现代心理与教育统计学课后题完整版14145
现代心理与教育统计学(张厚粲)课后习题答案
现代心理与教育统计学（张厚粲）课后习题答案第一章绪论（略）第二章统计图表（略）第三章集中量数4、平均数约为36.14；中位数约为36.635、总平均数为91.726、平均联想速度为5.27、平均增加率约为11%；10年后的毕业人数约有3180人8、次数分布表的平均数约为177.6；中位数约为177.5；原始数据的平均数约为176.7第四章差异量数5、标准差约为1.37；平均数约为1.196、标准差为26.3；四分位差为16.037、5cm组的差异比10cm组的离散程度大8、各班成绩的总标准差是6.039、次数分布表的标准差约为11.82；第一四分位为42.89；第三四分位为58.41；四分位差为7.76第五章相关关系5、应该用肯德尔W系数。
6、r=0.8；r R=0.79；这份资料只有10对数据，积差相关的适用条件是有30对以上数据，因此这份资料适用等级相关更合适。
7、这两列变量的等级相关系数为0.97。
8、上表中成绩与性别有很强的相关，相关系数为0.83。
9、r b=0.069小于0.2.成绩A与成绩B的相关很小，成绩A与成绩B的变化几乎没有关系。
10、测验成绩与教师评定之间有一致性，相关系数为0.87。
11、9名被试的等级评定具有中等强度的相关，相关系数为0.48。
12、肯德尔一致性叙述为0.31。
第六章概率分布4、抽得男生的概率是0.355、出现相同点数的概率是0.1676、抽一黑球与一白球的概率是0.24；两次皆是白球与黑球的概率分别是0.36和0.167、抽一张K的概率是4/54=0.074；抽一张梅花的概率是13/54=0.241；抽一张红桃的概率是13/54=0.241；抽一张黑桃的概率是13/54=0.241；抽不是J、Q、K的黑桃的概率是10/54=0.1858、两个正面，两个反面的概率p=6/16=0.375；四个正面的概率p=1/16=0.0625；三个反面的概率p=4/16=0.25；四个正面或三个反面的概率p=0.3125；连续掷两次无一正面的概率p=0.18759、二项分布的平均数是5，标准差是210、(1)Z≥1.5，P=0.5-0.43=0.07(2)Z≤1.5，P=0.5-0.43=0.07(3)-1.5≤Z≤1.5，p=0.43+0.43=0.86(4)p=0.78，Z=0.77，Y=0.30(5)p=0.23，Z=0.61，Y=0.33(6)1.85≤Z≤2.10，p=0.482—0.467=0.01511、(1)P=0.35，Z=1.04(2)P=0.05，Z=0.13(3)P=0.15，Z=-0.39(4)P=0.077，Z=-0.19(5)P=0.406，Z=-1.3212、(1)P=0.36，Z=-1.08(2)P=0.12，Z=0.31(3)P=0.125，Z=-0.32(4)P=0.082，Z=-0.21(5)P=0.229，Z=0.6113、各等级人数为23,136,341,341,136,2314、T分数为：73.3、68.5、64.8、60.8、57、53.3、48.5、46.4、38.2、29.515、三次6点向上的概率为0.054，三次以上6点向上的概率为0.06316、回答对33道题才能说是真会不是猜测17、答对5至10到题的概率是0.002，无法确定答对题数的平均数18、说对了5个才能说看清了而不是猜对的19、答对5题的概率是0.015；至少答对8题的概率为0.1220、至少10人被录取的概率为0.1821、（1）t0.05=2.060，t0.01=2.784（2）t0.05=2.021，t0.01=2.704（3）t0.05=2.048，t0.01=2.76322、（1）χ20.05=43.8，χ20.0,1=50.9（2）χ20.05=7.43，χ20.0,1=10.923、（1）F0.05=2.31，F0.01=3.03（2）F0.05=6.18，F0.01=12.5324、Z值为3，大于Z的概率是0.0013525、大于该平均数以上的概率为0.0826、χ2以上的概率为0.1；χ2以下的概率为0.927、χ2是20.16，小于该χ2值以下概率是0.8628、χ2值是12.32，大于这个χ2值的概率是0.2129、χ2值是15.92，大于这个χ2值的概率是0.0730、两方差之比比小于F0.05第七章参数估计5、该科测验的真实分数在78.55—83.45之间，估计正确的概率为95%，错误概率为5%。
张厚粲现代心理与教育统计学答案完整版
心理学解答心理学考研第一章1．名词概念（1）随机变量答：在统计学上把取值之前，不能准确预料取到什么值的变量，称为随机变量。
（2）总体答：总体（population）又称为母全体或全域，是具有某种特征的一类事物的总体，是研究对象的全体。
（3）样本答：样本是从总体中抽取的一部分个体。
（4）个体答：构成总体的每个基本单元。
（5）次数是指某一事件在某一类别中出现的数目，又称作频数，用f表示。
（6）频率答：又称相对次数，即某一事件发生的次数除以总的事件数目，通常用比例或百分数来表示。
（7）概率答：概率(probability),概率论术语，指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值，称为事件A的概率，记为P（A）。
（8）统计量答：样本的特征值叫做统计量，又称作特征值。
（9）参数答：又称总体参数，是描述一个总体情况的统计指标。
（10）观测值答：随机变量的取值，一个随机变量可以有多个观测值。
2．何谓心理与教育统计学？学习它有何意义？答：（1）心理与教育统计学是专门研究如何运用统计学原理和方法，搜集、整理、分析心理与教育科学研究中获得的随机性数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲，就是在心理与教育研究中，通过调查、实验、测量等手段有意地获取一些数据，并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理，最后得出结论的一种研究方法。
（2）学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务是对客观事实进行预测和分类，从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力，就必须运用科学的方法。
统计学正是提供了这样一种科学方法。
统计方法是从事科学研究的一种必不可少的工具。
张厚粲《现代心理与教育统计学》笔记和课后习题(含考研真题)详解(绪论)【圣才出品】
第1章绪论1.1 复习笔记本章重点✓心理与教育统计的研究内容✓选择使用统计方法的基本步骤✓统计数据的基本类型✓心理与教育统计的基本概念一、统计方法在心理和教育科学研究中的作用（一）心理与教育统计的定义与性质1．心理与教育统计学是专门研究如何运用统计学原理和方法，搜集、整理、分析心理与教育科学研究中获得的随机性数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育活动规律的一门学科。
2．具体讲，就是在心理与教育研究中，通过调查、实验、测量等手段有意地获取一些数据，并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理，最后得出结论的一种研究方法。
3．统计学大致分为理论统计学（theoretical statistics）和应用统计学（appliedstatistics）两部分。
前者侧重统计理论与方法的数理证明，后者侧重统计理论与方法在各个实践领域中的应用。
心理与教育统计学属于应用统计学范畴，是应用统计学的一个分支。
类似的还有生物统计、社会统计、医学统计、人口统计、经济统计等。
（二）心理与教育科学研究数据的特点1．心理与教育科学研究数据与结果多用数字形式呈现。
2．心理与教育科学研究数据具有随机性和变异性。
3．心理与教育科学研究数据具有规律性。
4．心理与教育科学研究的目标是通过部分数据来推测总体特征。
（三）学习心理与教育统计应注意的事项1．学习心理与教育统计学要注意的几个问题：（1）学习心理与教育统计学时，必须要克服畏难情绪。
心理与教育统计学偏重于应用，只要有中学数学知识就具备了学好心理与教育统计学的前提。
（2）在学习时要注意重点掌握各种统计方法使用的条件。
（3）要做一定的练习。
2．应用心理与教育统计方法时要做到：（1）克服“统计无用”与“统计万能”的思想，注意科研道德。
（2）正确选用统计方法，防止误用和乱用统计。
二、心理与教育统计学的内容心理与教育统计学的研究内容，可依不同的分类标志划分为不同的类别：（一）分类一依据统计方法的功能进行分类，统计学可分为下述三种类别，这是由于数理统计的发展历史所决定的，也是最常见的分类方法。
张厚璨《现代心理与教育统计学》书后习题详...
有多少。 1978 1979 1980 1981 1982 1983 1984 1985
毕业人数
542
601
750
760
810
930
1050
1120
解：该题是关于平均增加率的，应运用几何平均数计算。 N ＝8 X1＝542 X8＝1120
Mg＝ 8 1
1120 ＝1.10925 542
10
1.10925－1＝0.10925＝10.925% 10 年后的毕业人数为 1120* 1.10925 ＝3158（人）
2
16.93 1.37 9 11.0 11.1 13.0 11.1 10.5 11.1
i
N 9 答 : 这列数据的标准差是1.37, 平均数是1.19。
1.19
7/107 今有一画线实验，标准线分别为 5 厘米与 7 厘米。实验结果 5 厘米组的误差平均数 为 1.3 厘米，标准差为 0.7 厘米。10 厘米组的误差平均数为 4.3 厘米，标准差为 1.2 厘米。 请问用什么方法比较其离散程度的大小？并具体比较之。
i
x
2
( 1 ) 2 ( 2 ) 2 ( 9 )
(11.0 11.1) 2 (13.0 11.1) 2 (10.5 11.1) 2 16.93 (3)求标准差 N (4)求平均差 A.D. s
x
1
心理学统考专业资料店：/
QQ:382895420
次数分布表 分组区间 233～ 220～ 207～ 194～ 181～ 168～ 155～ 142～ 129～ 116～ 合计 由次数分布表可得累积次数分布表直方图,次数多边形图,如下: 累计次数分布表 分组区间 233～ 220～ 207～ 194～ 181～ 168～ 155～ 142～ 129～ c16～ 次数 2 1 7 5 11 18 6 11 3 1 向上累加次数 实际累加次数 65 63 62 55 50 39 21 15 4 1 相对累加次数 1 63/65 62/65 55/65 50/65 39/65 21/65 15/65 4/65 1/65 组中值（Xc） 239 226 213 200 187 174 161 148 135 122 次数（f） 2 1 7 5 11 18 6 11 3 1 65
现代心理与教育统计学课后答案
现代心理与教育统计学课后答案现代心理与教育统计学课后答案【篇一：现代心理与教育统计学第07章习题解答】点估计就是总体参数不清楚时，用一个特定的值，即样本统计量对总体参数进行估计，但估计的参数为数轴上某一点。
区间估计是用数轴上的一段距离来表示未知参数可能落入的范围，它不具体指出总体参数是多少，能指出总体未知参数落入某一区间的概率有多大。
点估计的优点是能够提供总体参数的估计值，缺点是点估计总以误差的存在为前提，且不能提供正确估计的概率。
区间估计的优点是用概率说明估计结果的把握程度，缺点是不能确定一个具体的估计值。
2以方差的区间估计为例说明区间估计的原理3.总体平均数估计的具体方法有哪些？总体方法为点估计好区间估计，区间估计又分为：（1）当总体分布正态方差已知时，样本平均的分布为正态分布，故依据正态分布理论估计其区间；（2）当总体分布正态方差未知时，样本平均数的分布为t分布，依据t分布理论估计其区间；（3）当总体非分布正态方差未知时，只有在n大于30时渐近t分布，样本平均数的分布渐近t分布，依据t分布理论估计其区间。
4总体相关系数的置信区间，应根据何种分布计算？应根据fisher的z分布进行计算5.解依据样本分布理论该样本平均数的分布呈正态5其标准误为： ?x1.25 nx?z?/2??xx?z?/2??x即81?1.96*1.2581?1.96*1.25所以：78.5583.45该科成绩的真实分数有95%的可能性在78.55----83.45之间。
x?t??xx?t?/2?x其置信区间为：即：80?1.987*0.780?1.987*0.778.6181.39该学区教学成绩的平均值有95%的可能在78.61---81.39之间。
7解：此题属于总体分布正态总体方差已知 ?8计算标准误 ?x1.789 n20x?z1x?171?1.96*1.789?171?3.506总体平均数的.95置信区间为所以总体平均数?在167.493―――174.506之间，作出这种判断的时候犯错误的比率是5％。
张厚粲《现代心理与教育统计学》(第3版)笔记和课后习题(含考研真题)详解
张厚粲《现代心理与教育统计学》（第3版）笔记和课后习题详解第1章绪论一、统计方法在心理和教育科学研究中的作用（一）心理与教育统计的定义与性质1．心理与教育统计学是专门研究如何运用统计学原理和方法，搜集、整理、分析心理与教育科学研究中获得的随机性数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育活动规律的一门学科。
2．具体讲，就是在心理与教育研究中，通过调查、实验、测量等手段有意地获取一些数据，并将得到的数据按统计学原理和步骤加以整理、计算、绘制图表、分析、判断、推理，最后得出结论的一种研究方法。
3．统计学大致分为理论统计学（theoretical statistics）和应用统计学（applied statistics）两部分。
前者侧重统计理论与方法的数理证明，后者侧重统计理论与方法在各个实践领域中的应用。
心理与教育统计学属于应用统计学范畴，是应用统计学的一个分支。
类似的还有生物统计、社会统计、医学统计、人口统计、经济统计等。
（二）心理与教育科学研究数据的特点1．心理与教育科学研究数据与结果多用数字形式呈现2．心理与教育科学研究数据具有随机性和变异性3．心理与教育科学研究数据具有规律性4．心理与教育科学研究的目标是通过部分数据来推测总体特征（三）学习心理与教育统计应注意的事项1．学习心理与教育统计学要注意的几个问题（1）学习心理与教育统计学时，必须要克服畏难情绪。
心理与教育统计学偏重于应用，只要有中学数学知识就具备了学好心理与教育统计学的前提。
（2）在学习时要注意重点掌握各种统计方法使用的条件。
（3）要做一定的练习。
2．应用心理与教育统计方法时要做到：（1）克服“统计无用”与“统计万能”的思想，注意科研道德。
（2）正确选用统计方法，防止误用和乱用统计。
二、心理与教育统计学的内容心理与教育统计学的研究内容，可依不同的分类标志划分为不同的类别。
（一）依据统计方法的功能进行分类，统计学可分为下述三种类别，这是由于数理统计的发展历史所决定的，也是最常见的分类方法。
现代心理学与教育统计学答案
现代心理学与教育统计学答案
名词概念
〔1〕随机变量
答：在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量.
〔2〕总体
答：总体〔population〕又称为母全体或全域,是具有某种特征的一类事物的总体,是研究对象的全体.
〔3〕样本
答：样本是从总体中抽取的一部分个体.
〔4〕个体
答：构成总体的每个基本单元.
〔5〕次数
是指某一事件在某一类别中出现的数目,又称作频数,用f表示.
〔6〕频率
答：又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示.
〔7〕概率
答：概率<probability>,概率论术语,指随机事件发生的可能性大小度量指标.其描述性定义.随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P〔A〕.
〔8〕统计量
答：样本的特征值叫做统计量,又称作特征值.
〔9〕参数
答：又称总体参数,是描述一个总体情况的统计指标. 〔10〕观测值
答：随机变量的取值,一个随机变量可以有多个观测值.。
《心理与教育统计学》习题答案
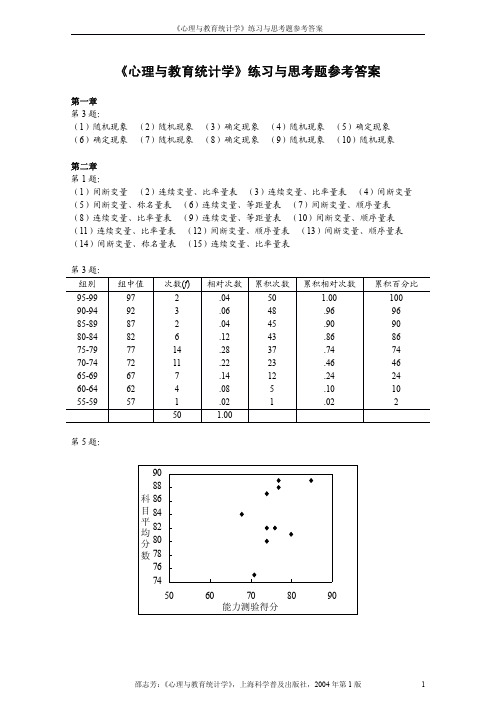
邵志芳： 《心理与教育统计学》 ，上海科学普及出版社，2004 年目 84 平 82 均 分 80 数 78 76 74 50 60 70 80 能力测验得分 90
邵志芳： 《心理与教育统计学》 ，上海科学普及出版社，2004 年第 1 版
1
《心理与教育统计学》练习与思考题参考答案
第三章 第 1 题： （1）84 （2）89 （3）420 （4）略 第 2 题： （1）13.5 （2）12 第 3 题：S2 = 8.5 S = 2.915 第 4 题：3159 第 5 题：男生 CV = 10%，女生 CV = 9.17%，男生成绩离散程度较高 第四章 第 2 题： （1）0.077 （2）0.25 （3）0.50 （4）0.25 （5）0.192 第 3 题： （1）0.0625 （2）0.0625 （3）0.25 （4）0.004 第 4 题： （1）0.008 （2）0.128 第五章 第 1 题： （1）1 （2）0.866 （3）0.0469 第 2 题： （1） 0.38493 （2） 0.30598 （3） 0.41924 （4） 0.89726 （5） 0.66141 （6） 0.78193 第 3 题：34.134 人；68.268% 第 4 题：A、B、C、D、E 等级人数分别为 18、119、226、119、18 第七章 第 1 题：95%的置信区间（66.08，73.92） ，99%的置信区间（64.84，75.16） 第 2 题： （67.30，75.70） 第 3 题： （73.27, 86.73） 第 4 题：Z = 9.09 > Z0.005 = 2.58 第 5 题：Z = – 2.68 < – Z0.01 = – 2.33 第八章 第 1 题： （– 8.573，9.538） 第 2 题：t = 0 第 3 题：|t| = | –1.033| < t0.025, 9＝2.262 第 4 题：|t| = | –3.4| > t0.01, 7 = 2.998 第九章 第 1 题： （5.30，14.06） 第 2 题：F = 186.67 > F0.01, 4, 6 = 9.15 第 3 题：Z = 4.187 > Z0.005 = 2.58 第十章 第 1 题：F = 25.70 < F0.05, 2, 9 = 4.26 第 2 题：F = 2.854 < F0.05, 2, 9 = 4.26 第 3 题：F = 4.495 > F0.05, 3, 21 = 3.07 第 4 题：FA =1.692，FB =0.884，FA*B =0.617，均小于 F0.05,1, 16 = 4.49 第 5 题： 差异来源 平方和 SS 自由度 df A 因素 B 因素 A*B 组内 180 300 3000 100 2 3 6 12 方差 MS 90 100 500 8.33
现代心理与教育统计学课后题完整版
第一章绪论1.名词解释随机变量：在统计学上，把取值之前不能预料取到什么值的变量称之为随机变量总体：又称为母全体、全域，指据有某种特征的一类事物的全体样本：从总体中抽取的一部分个体，称为总体的一个样本个体：构成总体的每个基本单元称为个体次数：指某一事件在某一类别中出现的数目，又成为频数，用f表示频率：又称相对次数，即某一事件发生的次数被总的事件数目除，亦即某一数据出现的次数被这一组数据总个数去除。
频率通畅用比例或百分数表示概率：又称机率。
或然率，用符号P表示，指某一事件在无限的观测中所能预料的相对出现的次数，也就是某一事物或某种情况在某一总体中出现的比率统计量：样本的特征值叫做统计量，又叫做特征值参数：总体的特性成为参数，又称总体参数，是描述一个总体情况的统计指标观测值：在心理学研究中，一旦确定了某个值，就称这个值为某一变量的观测值，也就是具体数据2.何谓心理与教育统计学？学习它有何意义心理与教育统计学是专门研究如何运用统计学原理和方法，搜集。
整理。
分析心理与教育科学研究中获得的随机数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育活动规律的一门学科。
3.选用统计方法有哪几个步骤？首先要分析一下试验设计是否合理，即所获得的数据是否适合用统计方法去处理，正确的数量化是应用统计方法的起步，如果对数量化的过程及其意义没有了解，将一些不着边际的数据加以统计处理是毫无意义的其次要分析实验数据的类型，不同数据类型所使用的统计方法有很大差别，了解实验数据的类型和水平，对选用恰当的统计方法至关重要第三要分析数据的分布规律，如总体方差的情况，确定其是否满足所选用的统计方法的前提条件4.什么叫随机变量？心理与教育科学实验所获得的数据是否属于随机变量随机变量的定义：①率先无法确定，受随机因素影响，成随机变化，具有偶然性和规律性②有规律变化的变量5.怎样理解总体、样本与个体？总体N：据有某种特征的一类事物的全体，又称为母体、样本空间，常用N表示，其构成的基本单元为个体。
心理和教育统计学课后题答案解析
张厚粲现代心理与教育统计学第一章答案1名词概念（1）随机变量答:在统计学上把取值之前,不能准确预料取到什么值的变量,称为随机变量。
（2）总体答:总体(population)又称为母全体或全域,就是具有某种特征的一类事物的总体,就是研究对象的全体。
（3）样本答:样本就是从总体中抽取的一部分个体。
（4）个体答:构成总体的每个基本单元。
(5)次数就是指某一事件在某一类别中出现的数目,又称作频数,用f表示。
（6）频率答:又称相对次数,即某一事件发生的次数除以总的事件数目,通常用比例或百分数来表示。
（7）概率答:概率(probability),概率论术语,指随机事件发生的可能性大小度量指标。
其描述性定义。
随机事件A在所有试验中发生的可能性大小的量值,称为事件A的概率,记为P(A)。
（8）统计量答:样本的特征值叫做统计量,又称作特征值。
（9）参数答:又称总体参数,就是描述一个总体情况的统计指标。
(10)观测值答:随机变量的取值,一个随机变量可以有多个观测值。
2何谓心理与教育统计学？学习它有何意义？答:(1)心理与教育统计学就是专门研究如何运用统计学原理与方法,搜集、整理、分析心理与教育科学研究中获得的随机性数据资料,并根据这些数据资料传递的信息,进行科学推论找出心理与教育统计活动规律的一门学科。
具体讲,就就是在心理与教育研究中,通过调查、实验、测量等手段有意地获取一些数据,并将得到的数据按统计学原理与步骤加以整理、计算、绘制图表、分析、判断、推理,最后得出结论的一种研究方法。
（2）学习心理与教育统计学有重要的意义。
①统计学为科学研究提供了一种科学方法。
科学就是一种知识体系。
它的研究对象存在于现实世界各个领域的客观事实之中。
它的主要任务就是对客观事实进行预测与分类,从而揭示蕴藏于其中的种种因果关系。
要提高对客观事实观测及分析研究的能力,就必须运用科学的方法。
统计学正就是提供了这样一种科学方法。
统计方法就是从事科学研究的一种必不可少的工具。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章绪论1.名词解释随机变量：在统计学上，把取值之前不能预料取到什么值的变量称之为随机变量总体：又称为母全体、全域，指据有某种特征的一类事物的全体样本：从总体中抽取的一部分个体，称为总体的一个样本个体：构成总体的每个基本单元称为个体次数：指某一事件在某一类别中出现的数目，又成为频数，用f表示频率：又称相对次数，即某一事件发生的次数被总的事件数目除，亦即某一数据出现的次数被这一组数据总个数去除。
频率通畅用比例或百分数表示概率：又称机率。
或然率，用符号P表示，指某一事件在无限的观测中所能预料的相对出现的次数，也就是某一事物或某种情况在某一总体中出现的比率统计量：样本的特征值叫做统计量，又叫做特征值参数：总体的特性成为参数，又称总体参数，是描述一个总体情况的统计指标观测值：在心理学研究中，一旦确定了某个值，就称这个值为某一变量的观测值，也就是具体数据2.何谓心理与教育统计学学习它有何意义心理与教育统计学是专门研究如何运用统计学原理和方法，搜集。
整理。
分析心理与教育科学研究中获得的随机数据资料，并根据这些数据资料传递的信息，进行科学推论找出心理与教育活动规律的一门学科。
3.选用统计方法有哪几个步骤首先要分析一下试验设计是否合理，即所获得的数据是否适合用统计方法去处理，正确的数量化是应用统计方法的起步，如果对数量化的过程及其意义没有了解，将一些不着边际的数据加以统计处理是毫无意义的其次要分析实验数据的类型，不同数据类型所使用的统计方法有很大差别，了解实验数据的类型和水平，对选用恰当的统计方法至关重要第三要分析数据的分布规律，如总体方差的情况，确定其是否满足所选用的统计方法的前提条件4.什么叫随机变量心理与教育科学实验所获得的数据是否属于随机变量随机变量的定义：①率先无法确定，受随机因素影响，成随机变化，具有偶然性和规律性②有规律变化的变量5.怎样理解总体、样本与个体总体N：据有某种特征的一类事物的全体，又称为母体、样本空间，常用N表示，其构成的基本单元为个体。
特点：①大小随研究问题而变（有、无限）②总体性质由组成的个体性质而定样本n：从总体中抽取的一部分交个体，称为总体的一个样本。
样本数目用n表示，又叫样本容量。
特点：①样本容量越大，对总体的代表性越强②样本不同，统计方法不同总体与样本可以相互转化。
个体：构成总体的每个基本单元称为个体。
有时个体又叫做一个随机事件或样本点6.统计量与参数之间有何区别和关系参数：总体的特性称参数，又称总体参数，是描述一个总体情况的统计指标统计量：样本的特征值叫做统计量，又称特征值二者关系：参数是一个常数，统计量随样本而变化参数常用希腊字母表示，统计量用英文字母表示当试验次数=总体大小时，二者为同一指标当总体无限时，二者不同，但统计量可在某种程度上作为参数的估计值7.试举例说明各种数据类型之间的区别8.下述一些数据，哪些是测量数据哪些是计数数据其数值意味着什么千克厘米秒分是测量数据17人25本是计数数据9.说明下面符号代表的意义μ反映总体集中情况的统计指标，即总体平均数或期望值X反映样本平均数ρ表示某一事物两个特性总体之间关系的统计指标，相关系数r 样本相关系数σ反映总体分散情况的统计指标标准差s样本标准差β表示两个特性中体之间数量关系的回归系数第三章 集中量数1. 应用算术平均数表示集中趋势要注意什么问题应用算术平均数必须遵循以下几个原则：① 同质性原则。
数据是用同一个观测手段采用相同的观测标准，能反映某一问题的同一方面特质的数据。
② 平均数与个体数据相结合的原则 ③ 平均数与标准差、方差相结合原则2. 中数、众数、几何平均数、调和平均数个适用于心理与教育研究中的哪些资料中数适用于：① 当一组观测结果中出现两个极端数目时 ② 次数分布表两端数据或个别数据不清楚时 ③ 要快速估计一组数据代表值时众数适用于：①要快速且粗略的求一组数据代表值时 ②数据不同质时，表示典型情况③次数分布中有两极端的数目时 ④粗略估计次数分布的形态时，用M-Mo 作为表示次数分布是否偏态的指标（正态：M=Md=Mo ； 正偏：M>Md>Mo; 负偏：M<Md<Mo ）⑤当次数分布中出现双众数时几何平均数适用于①少数数据偏大或偏小，数据的分布成偏态 ②等距、等比量表实验③平均增长率，按一定比例变化时调和平均数适用于①工作量固定，记录各被试完成相同工作所用时间 ②学习时间一定，记录一定时间内各被试完成的工作量3. 对于下列数据，使用何种集中量数表示集中趋势其代表性更好并计算它们的值。
⑴ 4 5 6 6 7 29 中数=6 ⑵ 3 4 5 5 7 5 众数=5⑶ 2 3 5 6 7 8 9 平均数=4. 求下列四个年级的总平均成绩。
年级一 二 三 四 x91 92 94 n236318215200解：i iTiX 91.72n236318215200===+++∑∑5. 三个不同被试对某词的联想速度如下表，求平均联想速度被试 联想词数 时间（分）词数/分（Xi ）A 13 2 13/2B 13 3 13/3 C1325-解：C 被试联想时间25分钟为异常数据，删除H i11M 5.211123()N X 21313===+∑调和平均数6. 下面是某校几年来毕业生的人数，问平均增加率是多少并估计10年后的毕业人数有多少。
年份 1978 1979 1980 1981 1982 1983 1984 1985 毕业人数54260175076081093010501120解：用几何平均数变式计算：Mg= 1.10925== 所以平均增加率为11% 10年后毕业人数为1120×=3159人第四章 差异量数1. 度量离中趋势的差异量数有哪些为什么要度量离中趋势度量离中趋势的差异量数有全距、四分位差、百分位差、平均差、标准差与方差等等。
在心理和教育研究中，要全面描述一组数据的特征，不但要了解数据的典型情况，而且还要了解特殊情况。
这些特殊性常表现为数据的变异性。
如两个样本的平均数相同但是整齐程度不同，如果只比较平均数并不能真实的反映样本全貌。
因此只有集中量数不可能真实的反映出样本的分布情况。
为了全面反映数据的总体情况，除了必须求出集中量数外，这时还需要使用差异量数。
2. 各种差异量数各有什么特点见课本103页“各种差异量数优缺点比较”3. 标准差在心理与教育研究中除度量数据的离散程度外还有哪些用途 可以计算差异系数（应用）和标准分数（应用）4. 应用标准分数求不同质的数据总和时应注意什么问题 要求不同质的数据的次数分布为正态5.计算下列数据的标准差与平均差Xi 11.013.010.09.011.512.213.19.710.5X 11.1N9++++++++===∑Xi-X 10.7A.D.=1.19n9==∑ 6.7. 今有一画线实验，标准线分别为5cm 和10cm ，实验结果5cm 组的误差平均数为，标准差为，10cm 组的误差平均数为，标准差为，请问用什么方法比较其离散程度的大小并具体比较之。
用差异系数来比较离散程度。
CV1=(s1/1X )×100%=×100%=% CV2=(s2/2X )×100%= ×100%=%<CV1 所以标准线为5cm 的离散程度大。
8. 求下表所列各班成绩的总标准差班级 平均数 标准差 人数 di 1 40 2 51 3 48 443iN40514843182=+++=∑ii T iN X 90.54091.05192.04889.54316525.5X 90.80N182182⨯+⨯+⨯+⨯====∑∑T i i d X X =- 其值见上表22222i iN s 40 6.251 6.548 5.843 5.26469.79=⨯+⨯+⨯+⨯=∑22222i iN d 400.351(0.2)48(1.2)43 1.3147.43=⨯+⨯-+⨯-+⨯=∑Ts 6.03=== 即各班成绩的总标准差是第五章 相关关系1. 解释相关系数时应注意什么（1） 相关系数是两列变量之间相关成都的数字表现形式，相关程度指标有统计特征数r 和总体系数ρ （2） 它只是一个比率，不是相关的百分数，更不是等距的度量值，只能说r 大比r 小相关密切，不能说r大=是r 小=的两倍（不能用倍数关系来解释）（3） 当存在强相关时，能用这个相关关系根据一个变量的的值预测另一变量的值 （4） -1≤r ≤1，正负号表示相关方向，值大小表示相关程度；（0为无相关，1为完全正相关，-1为完全负相关）（5） 相关系数大的事物间不一定有因果关系（6） 当两变量间的关系收到其他变量的影响时，两者间的高强度相关很可能是一种假象 （7） 计算相关要成对数据，即每个个体有两个观测值，不能随便2个个体计算（8） 非线性相关的用r 得可能性小，但并不能说不密切2. 假设两变量为线性关系，计算下列各情况的相关时，应用什么方法 （1） 两列变量是等距或等比的数据且均为正态分布（积差相关） （2） 两列变量是等距或等比的数据且不为正态分布（等级相关）（3） 一变量为正态等距变量，另一列变量也为正态变量，但人为分为两类（二列相关） （4） 一变量为正态等距变量，另一列变量也为正态变量，但人为分为多类（多列相关） （5） 一变量为正态等距变量，另一列变量为二分称名变量（点二列相关） （6） 两变量均以等级表示（等级相关、交错系数、相容系数） 3. 如何区分点二列相关与二列相关主要区别在于二分变量是否为正态。
二列相关要求两列数据均为正态，其中一列被人为地分为两类；点二列相关一列数据为等距或等比测量数据，且其总体分布为正态，另一列变量是二分称名变量，且两列数存在一一对应关系。
4. 品质相关有哪几种各种品质相关的应用条件是什么品质相关分析的总条件是两因素多项分类之间的关联程度，分为一下几类：（1） 四分相关，应用条件是：两因素都为正态连续变量（eg.学习能力，身体状态））人为分为两个类别；同一被试样品中，分别调查两个不同因素两项分类情况（2） Φ系数：除四分相关外的2×2表（最常用） （3） 列联表相关C ：R ×C 表的计数资料分析相关程度5. 预考查甲乙丙丁四人对十件工艺美术品的等级评定是否具有一致性，用哪种相关方法等级相关6. 下表是平时两次考试成绩分数，假设其分布成正态，分别用积差相关与等级相关方法计算相关系数，并回答，就这份资料用哪种相关法更恰当被试 A B A 2 B 2 AB R A R B R A R B D=R A -R B D 2 1 86 83 7396 6889 7138 2 3 6 -1 1 2 58 52 3364 2704 3016 7 8 56 -1 1 3 79 89 6241 7921 7031 4 1 4 3 9 4 64 78 4096 6084 4992 6 4 24 2 4 5 91 85 8281 7225 7735 1 2 2 -1 1 6 48 68 2304 4624 3264 9 6 54 3 9 7 55 47 3025 2209 2585 8 9 72 -1 1 8 82 76 6724 5776 6232 3 5 15 -2 4 9 32 25 1024 625 800 10 10 100 0 0 10 75 56 5625 3136 4200 5 7 35 -2 4 ∑670659480804719346993555536834N XY X Y0.82-==2R 226D 634r 110.794N(N -1)10(101)⨯=-=-=⨯-∑或 X Y R 4R R 334368r [(N+1)]110.794N-1N(N+1)9110⨯⎛⎫=-=⨯-= ⎪⎝⎭∑用积差相关的条件成立，故用积差相关更精确7. 下列两列变量为非正态，选用恰当的方法计算相关 本题应用等级相关法计算，且含有相同等级X 有3个数据的等级相同，等级的数据中有2个数据的等级相同，等级为和的数据中也分别有2个数据相同；Y 有3个数据等级相同，等级为3的数据中有3个数据等级相同，等级为的数据中有2个数据等级相同，等级为9的数据中有3个数据等级相同。