怎样得到园偏振光
椭圆偏振光与园偏振光的产生和检验

一、 圆偏振光和椭圆偏振光起偏 晶体相移器件
1、椭圆和圆偏振光获得(思路及装置) (一种相移元件)
思路: 根据振动方向相互垂直、频率相同的两个简谐振动能够合
成椭圆和圆的原理,可有双折射现象获得椭圆和圆偏振光。
分析: 自然光入射到晶片上,
光轴
出射光仍为自然光。(无恒定的相位差)晶片
d
自然光透过晶片是得不到椭圆和圆偏振光的。 o e
线偏振光入射到晶片上,可分解为振动方向相 互垂直的 e 光和 o 光。
晶片:光轴 平行于表面 的晶体薄片
出射光为振动方向相互垂直的、具有固定位相关
系的线偏振光 椭圆和圆偏振光
2、椭圆和圆偏振光起偏装置(光路图) 光轴
y
λ
Ae
A0
? x
P2 A2e
若单色光入射,且d不均匀, 则屏上出现等厚干涉条纹。色
若若dd均不匀均不匀变,,且而以以白白光光入入射射,,则则屏屏上上出出现现彩均色匀条的纹颜。色。偏振
色偏振: 由于某种颜色干涉相消,而呈现它的互补色
如 红色相消→绿色;蓝色相消→黄色
二、人为双折射
人为地造成介质的各向异性,而产生双折射。
A出
Ae 正最大时,Ao为负最大
A入
线偏振光振动面转过2 角度 A0出
A0入
1/2波片的作用—— 使线偏振光振动面转过2 角度
二、椭圆偏振光与圆偏振光的检偏
用1/4 波片C 和偏振片P 可把自然光与圆偏振光
(或部分偏振光与椭圆偏振光)区分开来。
自然光 圆偏振光
自然光 四 分 线偏振光 之
一、偏振光的干涉
P1
AC
Ao
椭圆和圆偏振光的检验与获得
E
E
r
r
二、产生
用一束平面偏振光垂直入射在一块光轴与表面 平行的单轴晶体薄片 C上,设C的光轴与入射的平 面偏振光的振动方向成 角,在晶片C内产生双折 射,且o、e 光沿同一方向传播,振动矢量相互垂直。 振幅分别为:
AO A sin , Ae A cos
A
消第1项
x cos 2 y cos 1 A1 A2
得
x cos 2 y cos1 sin t sin( 2 1 ) A1 A2
x A1 (cost cos1 sin t sin 1 ) y A2 (cost cos2 sin t sin 2 )
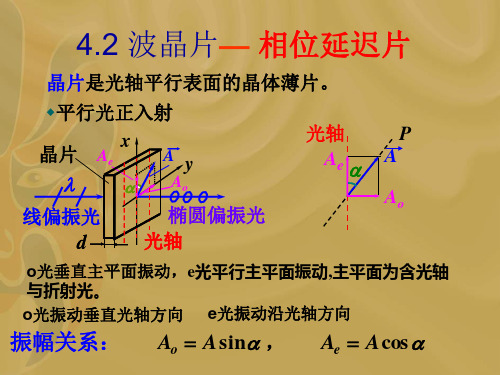
4.2 波晶片— 相位延迟片
晶片是光轴平行表面的晶体薄片。
平行光正入射
晶片
Ae
x
A
线偏振光 d
Ao
y
光轴 Ae
P
A Ao
椭圆偏振光 光轴
o光垂直主平面振动,e光平行主平面振动,主平面为含光轴 与折射光。 o光振动垂直光轴方向 e光振动沿光轴方向
振幅关系:
Ao A sin ,
Ae A cos
即 : 线偏振光 园偏振光
三、椭圆偏振光与部分偏振光的检定:
让椭圆偏振光和部分偏振光通过一个偏振片时,旋转中均会出现光强 大小变化但无消光的相同现象,无法区分。 方法:在偏振片前放入一块四分之一波片,并设法使椭圆的一个轴与四分 之一波片的光轴平行;以入射光为轴旋转偏振片。
1 波片且 450 4
光轴平行最大光强或最小光强方向放置 或光轴平行椭圆偏振光的长轴或短轴放置
2. 2 1 2
两个相互垂直的同频率的谐振动可以合成为一直线谐振动、 匀速圆周运动和椭圆运动。 由此可见,任一直线谐振动、匀速圆周运动和椭圆运动 都可分解为两个相互垂直的同频率的谐振动。
圆偏振光、椭圆偏振光如何检验?【最新】

圆偏振光、椭圆偏振光如何检验?首先讨论它们产生的原理。
圆偏振光、椭圆偏振光产生的原理如图10— 2所示图10 — 2当一束自然光经起偏器后,得到线偏振光再入射到波片时,被分成E。
和Ee两个振动分量,由于它们在晶体内的传播速度不同,通过波片后产生一定的位相差,出射后两束光速度相同,合成后一般得到椭圆偏振光,o光相对e光的位相差为=2π/λ ×(no- ne)dd —波片厚度在满足以下两个条件时,出射光是圆片振光:1.起偏器的透光轴与波片的快(慢)轴夹角α= 45°2.两束光在波片中产生位相差=(2m +1)× π/ 2 (m = 0; ±1; ±2; )或Δ= ( no – ne ) d =(m + 1/ 4)λ可见,该波片是λ/4波片,因此线偏振光只有通过λ/4波片才可能产生圆偏振光。
如何检验圆偏振和椭圆偏振光呢?一般采用以下两种方法:1、让圆或椭圆偏振光透过检偏器,通过旋转检偏器观察能量变化,来确定光的偏振态。
2、将圆偏振或椭圆偏振光变换成线偏振光,再通过马吕斯定律进行检验为什么圆偏振光经1/8 波片后成为椭圆偏振光?圆偏振光相位差不是PI/2吗。
+PI/4后怎么就变成了线偏振光。
这个很好解释么,圆偏振光原来的相位差是pi/2,线偏振光的相位差是pi或者是0,除了这个之外,所有的相位差,造成的偏振态形状都是椭圆的。
圆偏振本来pi/2,你经过λ/8波片,相位差加pi/4,那你用你的原来的pi/2+pi/4=3pi/4,相位差既不是0,也不是pi,自然就不是线偏振光,所以自然是个椭圆偏振的,怎么可能变成线偏振的?还有你这个问题太诡异了,题目里面问,为什么变成椭圆光,内容里面却问怎么就变成线偏振光,你到底是要问什么?只有经过λ/4波片的圆偏振,才能变成线偏振,还有通常都没有人用什么λ/8波片,都是λ/4的或者λ/2的波片,不知道楼主从哪里看来的λ/8波片?λ/4波片合成椭圆偏振光的原理是什么原理就是给本来没有相位差或者相位差是pi的线偏振光,附加上了pi/2的相位。
圆偏光片原理

圆偏光片原理
圆偏光片是一种常用的光学元件,其原理主要是利用了偏振光的性质。
偏振光是一种在特定方向上振动的光波,而圆偏光则是一种特殊类型的偏振光,其振动方向在平面内呈圆周运动。
圆偏光片的工作原理可以通过其结构和材料的特性来解释。
圆偏光片通常由具有双折射性质的晶体材料制成,如石英或偏光玻璃。
这些材料在电场的作用下会发生双折射现象,即光线在进入材料后会分成两束光线,一束是普通光,另一束则是振动方向旋转的偏振光。
当偏振光通过圆偏光片时,根据其振动方向和光线传播方向之间的关系,可以将偏振光转换成左旋或右旋的圆偏光。
这种转换是通过圆偏光片内部的结构和材料的双折射效应实现的。
具体来说,当偏振光穿过圆偏光片时,其振动方向会被旋转一个特定的角度,从而产生左旋或右旋的圆偏光。
圆偏光片在光学领域有着广泛的应用。
其中,最常见的用途是在偏振光实验和设备中,用于控制和调节光的偏振状态。
通过调整圆偏光片的旋转角度,可以改变光的偏振方向和强度,从而实现光学器件的功能。
此外,圆偏光片还常用于显微镜、激光器、偏振片等光学系统中,起到优化光学性能和增强光学效果的作用。
总的来说,圆偏光片原理是基于偏振光的特性和双折射效应,通过特定的结构和材料来实现对偏振光的控制和调节。
其在光学领域的
应用非常广泛,为光学技术的发展和应用提供了重要的支持和帮助。
通过深入理解圆偏光片的原理和工作机制,可以更好地利用其优势,推动光学技术的进步和创新。
圆偏振发光光谱发展历程

圆偏振发光光谱的发展历程可以追溯到20世纪初,当时科学家们开始研究光的偏振性质。
随着技术的发展,圆偏振光的性质逐渐被应用于光学、电磁学和光谱学等领域。
本文将介绍圆偏振发光光谱的发展历程。
早期研究:基础理论在早期的研究中,科学家们主要关注于基础理论的研究,如光的偏振态、偏振光的干涉和衍射等。
他们发现,圆偏振光在传播过程中,其振动面始终围绕传播方向旋转,这种现象被称为圆偏振。
光学元件:圆偏振的应用随着光学元件的发展,如线性偏振分束器、反射器等,圆偏振光的性质被广泛应用于各种光学实验中。
例如,通过控制光源和光学元件的参数,可以实现特定的圆偏振光的产生和调控。
光源:发光光谱的改进随着光源技术的进步,如激光器的出现,发光光谱的质量得到了显著提高。
科学家们开始尝试利用圆偏振光的特点来改进发光光谱的性质,如提高光谱的纯度和亮度。
实验方法:圆偏振光谱的测量为了准确地测量圆偏振发光光谱,科学家们发展了多种实验方法,如傅里叶变换光谱仪、圆偏振光干涉仪等。
这些仪器能够准确地测量圆偏振光的偏振态和强度,进而获取发光光谱的信息。
应用领域:新兴领域近年来,圆偏振发光光谱在许多新兴领域中得到了广泛应用,如生物医学、材料科学和环境科学等。
科学家们利用圆偏振发光光谱技术来研究生物分子的结构和功能,以及材料的光学性质和环境响应等。
未来展望:发展趋势随着科技的不断进步,圆偏振发光光谱技术将会在更多的领域得到应用。
未来,我们期待看到更多的创新和突破,如开发新型的光学元件和测量方法,以及将圆偏振发光光谱与其他技术相结合,如量子点技术和机器学习等。
这些技术的发展将为圆偏振发光光谱的应用开辟新的领域和可能性。
总之,圆偏振发光光谱的发展历程是一个不断探索、创新和应用的过程。
它从基础理论到实际应用,经历了多个阶段的发展,为科学和技术的发展做出了重要贡献。
未来,我们期待着圆偏振发光光谱技术在更多领域中的应用和发展。
线偏振光与圆偏振光的关系

1设单色平面光波沿z 方向传播,即k //z :
(1) 线偏振光可沿任意两个垂直方向分解,分量仍然是线偏振光,例如: e z t E E r r )2cos(0λ
πω−=线 (e r 是偏振方向的单位矢量,此情况在x 、y 平面内) 可分解为: )2cos()sin cos (00z t e E e E E y x λπωαα−⋅+⋅=r r r 线
(2) 圆偏振光可沿任意两个垂直方向分解为两个线偏振光,例如: y x e z t E e z t E E r r r ⋅−+⋅−−=)2cos()22cos(00λ
πωπλπω右圆 y x e z t E e z t E E r r r ⋅−+⋅+−=)2cos()22cos(00λ
πωπλπω左圆 给定一个z 值,则在此位置处,光矢量运动是两个垂直的、相位差2π
的简谐运动的合成。
(3) 线偏振光可分解为左右圆偏振光,例如用上面的两个式子可得: y e z t E E E E r r r r ⋅−=+=)2cos(20λ
πω左圆右圆线 (y 轴现在是偏振方向)
注意:上面的命题是普适的,但公式给的都是特例。
y z k x
x x
e r y e。
圆及椭圆偏振光的获得和检验

自然光
P196
偏振片,透振方向 绕光束旋转
光强不变
先通过1/4波片,再通过偏 振片
光强不变(鉴定)
圆偏振光
平面偏振光 部分偏振光 椭圆偏振光
光强不变
光强改变,在某一 角度消光(鉴定) 光强改变,但不消 光 光强改变,但不消 光
光强改变,出现消光(鉴定)
光强改变,但不消光 转动1/4波片和偏振片,出 现消光(鉴定)
2、进一步鉴定
• 先让光通过1/4波片! • 自然光:仍是自然光 • 圆偏振光:变为平面偏振光 • 部分偏振光:仍是部分偏振光 • 椭圆偏振光:仍是椭圆偏振光,当光轴与 椭圆长短轴重合,可以得到平面偏振光。 • 再通过线检偏器,可以将自然光与圆偏振 光鉴别;部分偏振光与椭圆偏振光鉴别。
偏振态的鉴定
都是左旋的
与坐标系的取法无关
快轴就加,慢轴就减!
线偏振光通过1/4波片也可获得圆偏振光
• 如果入射光的电矢量与光轴间的夹角为45o
Ex Ax cos t E y Ay cos(t 0) Ex Ax cos t E y Ay cos(t )
圆偏振光
椭圆偏振 光
e或o光轴与波片同椭圆主轴一致 其它位置
线偏振光 椭圆偏振光
光的偏振态的鉴定
• 1、使用线检偏器,可鉴定平面(线)偏振光
• 旋转检偏器,观察透射光强度的变化 • 自然光:光强不变 • 圆偏振光:光强不变 • 平面偏振光:光强改变,在某一角度消光 • 部分偏振光:光强改变,但不消光 • 椭圆偏振光:光强改变,但不消光
I0 A12 2 c (1 cos c ) cos 2 2 2
二、讨 论
• 在 c k (n0 ne )d 相同的条件下,两偏振片 平行和正交时,两者总相位差为π。 • 这两种情况的干涉光强互补,即
6-02 圆偏振光和椭圆偏振光的获得

e光
找出 长短轴
4
波片
偏振片
作业
p.201: 1, 2, 3
in Eo
2 2
( A x A y e i 2 ) e i t Aein e i e i t
out E e out Eo
2 2
( A x A y e i 2 ) e i 2 e i t Ae i ( 3
2 )
e i t
第六章:晶体偏振光学 § 3 圆偏振光和椭圆偏振光的获得和检验
3.1 垂直振动的合成 3.2 圆偏振光的椭圆偏振光的获得 3.3 圆偏振光的椭圆偏振光通过检偏器后的强度变化 3.4 圆偏振光的椭圆偏振光通过波片后偏振态的改变 3.5 圆偏振光的椭圆偏振光的检验
第六章:晶体偏振光学 § 3 圆偏振光和椭圆偏振光的获得和检验
例
入射光为右旋椭圆偏振光,四分之一波片,光轴与椭 圆长轴夹角0、90、45°时出射光的偏振态。
out i t E A e 0 e x out i i t i t E A e e A e y y o Ay
Ay
e光
o光
Ax
e光 o光
Ax
out i 2 i t E A e e 90 e y out i 2 i t E A e e x o
o光
Ay
右旋椭圆偏振光: e光
Ax
2 Ax A y
in i i t E ( A cos A sin e ) e x y 波片入射: ein i i t E ( A sin A cos e ) e x y o 四分之一波片: 2 out i i t E ( A cos A sin e ) e x y 波片出射: eout i i i t E ( A sin A cos e ) e e x y o
椭圆偏振光、圆偏振光、偏振光的检验

垂直射入波片的线偏光,分解成O光其振动方向垂直于入射面,
垂直光轴;分解成的e光振动方向平行于入射面,平行于光轴。 入射波片的线偏光的振幅 A I 0 / 2
Ae A cos
AO A sin
若C为1/4波片,即=/2,且若=450,则从C出射圆偏振光 若C为1/4波片,且450、 900或00,则出射椭圆偏振光 若C不为波长片也不是半波片,即 k 时,且450、
起偏器
o
椭圆 偏光
线偏光
M
c
Ae
N
AO A sin
Ae A cos
AO
AON
(no ne )d 2 /
o
AeN
AO A sin Ae A cos
AON A sin cos
AeN A cos sin
M
c
Ae
N
2 / (no ne )d
17-8 旋光现象 实验发现,线偏光通过某些透明介质后,它的电振动方 向将绕着光的传播方向旋转过某一角度,称为旋光现象。
这种介质称为旋光物质。如石英、糖、酒石酸钾钠等
F
M
C
N
C 是旋光物质,例如是晶面与光轴垂直的石英片 F 为滤色片;M为起偏器;旋光物体放在两个正交的偏振片 M与N之间,将会看到视场由原来的零变亮,把检偏器 N 旋 转一个角度,又可得到零视野。
2
若入射光的线偏振方向与外电场方向成450角,且M与N 偏振方向相互垂直,调节电压使其发生相长干涉,则有:
2k '1 l (ne no ) klE 2
2
k ' 0,1,2,
圆偏振光实验报告

圆偏振光实验报告圆偏振光实验报告引言:圆偏振光是一种特殊的光波,它具有固定的振动方向和相位差。
本实验旨在通过实际操作,观察和研究圆偏振光的性质,并探讨其在光学领域的应用。
实验装置:本次实验所用的装置主要包括:光源、偏振片、四分之一波片、检偏器以及光电探测器。
实验步骤:1. 将光源打开,调整其亮度适中。
2. 在光源前方放置一个偏振片,通过旋转偏振片,观察光的强度变化。
3. 将四分之一波片放置在光源后方,通过旋转四分之一波片,观察光的强度变化。
4. 在光源和四分之一波片之间加入一个检偏器,通过旋转检偏器,观察光的强度变化。
5. 使用光电探测器来测量不同光强度下的电流值,并记录数据。
6. 根据实验数据,分析圆偏振光的特性和应用。
实验结果与分析:通过实验观察和数据记录,我们得到了以下结果:1. 偏振片的旋转会导致光强度的变化。
当偏振片与光源的偏振方向垂直时,光强度最小;当两者平行时,光强度最大。
这说明偏振片可以选择性地通过或阻挡特定方向的光振动。
2. 四分之一波片的旋转会导致光强度的变化。
当四分之一波片的快轴与光振动方向平行时,光强度最大;当快轴与光振动方向垂直时,光强度最小。
这说明四分之一波片可以将线偏振光转化为圆偏振光。
3. 检偏器的旋转会导致光强度的变化。
当检偏器的透光轴与光振动方向平行时,光强度最大;当透光轴与光振动方向垂直时,光强度最小。
这说明检偏器可以选择性地通过或阻挡特定方向的圆偏振光。
4. 根据实验数据,我们发现圆偏振光的电流值随着光强度的变化而变化。
这说明光电探测器可以用来测量圆偏振光的强度,并提供定量的数据。
结论:通过本次实验,我们深入了解了圆偏振光的性质和应用。
我们发现圆偏振光可以通过偏振片、四分之一波片和检偏器来选择性地通过或阻挡特定方向的光振动。
此外,我们还发现圆偏振光的强度可以通过光电探测器来测量和记录。
这些发现对于光学领域的研究和应用具有重要意义。
进一步探讨:在实验过程中,我们还可以尝试使用其他光学元件,如半波片、全波片等,来观察圆偏振光的效果。
第五章光的偏振椭圆偏振光与圆偏振光

Ey Ay
,sin(t kz0 ) 1
2 Ey 2 Ay
cos (t kz0 ) (t kz0 ) cos(t kz0 ) cos(t kz0 ) sin(t kz0 ) sin(t kz0 )
Ay Y
Ax
Ay
X
Ax
5
Ex Ax cos(t kz0 )
轨迹方程 推导过程:
E y Ay cos(t kz0 )
2 Ex Ex cos(t kz0 )= ,sin(t kz0 )= 1 2 Ax Ax
cos(t kz0 ) cos
E x Ax cos(t kz) E y Ay cos(t kz )
当Δφ =±π/2,且 Ax=Ay,为圆偏振光。取+π/2为 右旋圆偏振光,取-π/2为左旋圆偏振光。 当Δφ =0或±π,光矢量在一条直线上的两个方向上, 即线偏振光。 当Δφ 取除±π 以及±π/2且 Ax=Ay 之外的值,为椭 圆偏振光。 特别地,当Δφ 取±π/2,是正椭圆偏振光。 当Δφ 随时间变化取0~2π之间的随机值,且Ax=Ay, 则是自然光。 当Δφ 随时间变化取0~2π之间的随机值,但Ax≠Ay, 则是部分偏振光。
E y Ex E y Ex 2 cos Ay Ax Ay Ax 2 2 Ey E E Ex 2 2 2 y x cos = sin 2 Ax Ay Ay Ax
2
2 2 Ey Ex 2 1 2 A Ax y
Ay y
0.8
0.6
0.4
¦ ¤ ¦ Õ=pi/6 Ax=Ay
Ax x
圆偏振光的产生

圆偏振光的产生一、圆偏振光的产生1、理论上的分析:圆偏振光是指按其几何构造,极化状况由圆环形变化,极化状况变化表现为由交叉状变为平行状,然后再变成交叉状的电磁波。
圆偏振光的产生可以通过以下几种方式:2、利用现有的偏振光的射光结构控制方法:常见的有偏振光调制器、变极化器、偏振片或玻璃片、偏振物镜等方式来控制光束手段,以达到激发出圆偏振光。
3、通过圆偏振光反射结构激发:设计一个单层折射率不同或多层表面折射率不同、表面形状不同特殊结构,当投射线束入射于该结构时,由于反射和折射,就可以产生圆偏振光。
4、利用物理玻璃结构调控:在利用普通玻璃片可以把偏振状态非对称的处理,可以达到将普通的或者角偏振光调节成圆偏振光,用于特殊领域的分析、识别等目的。
5、利用氩星灯的滤光片:把它放置在氩星灯的前端,将对话光束转换成圆偏振光,从而给该光束增加一定的吸收度,也可以降低混杂光的影响,实现有效的高精度分析。
二、圆偏振光的实际应用1、光学镜头:圆偏振光可以用来制作光学镜头,因为这种光可以实现表面光滑、通透性和互相抵消极化等特性,可以有效减少传递的杂散光,达到抑制反射的特殊效果,从而提升图像的清晰度。
2、荧光显微镜:通过调整圆偏振光的双极化,可以提高实验的精确度,可有效抑制普通双极化下图像的反光污染,从而实现更精确的样品成像。
3、显示器:圆偏振光可以加快显示器的响应速度,可以提高显示器的色度性能,能够达到高精度的阴影、灰度和色标准,有效抑制眩光和闪烁,具有表面反射率低、透射亮度高的优点,可以有效改善用户的视觉体验。
4、三维打印:通过圆偏振光技术可以有效提高三维打印的精度和稳定性,抑制了非理想的多重偏振、炎光、反射和衍射,从而达到更精确的打印效果;同时还有削减低反射率材料打印时间和准确度的作用,在工业上有广泛应用。
5、新能源材料:圆偏振光可以用于新能源材料的研发与应用,有效改善器件的性能,提升光电转换效率,具有提高器件强度、节约能源、降低成本等优势,广泛应用于航空航天、汽车、智能设备和太阳能发电等领域。
圆偏振光相关知识

圆偏振光相关知识
圆偏振光是一种偏振光的特殊形式,它的电场矢量在特定方向上进行旋转。
与线偏振光只在一个平面上振动不同,圆偏振光的电场矢量会在垂直于传播方向的平面上进行旋转。
根据旋转方向的不同,圆偏振光可以分为两种类型:左旋圆偏振光和右旋圆偏振光。
圆偏振光可以通过两种方式产生:
1. 使用波片:将线偏振光经过适当的波片(如1/4波片或1/2波片)转换成圆偏振光。
1/4波片能够将线偏振光转换为某个方向上的圆偏振光,而1/2波片则能够将线偏振光转换为相反方向上的圆偏振光。
2. 使用光学器件:一些光学器件,如克尔效应或波片阵列,能够直接产生圆偏振光。
圆偏振光在许多领域中有广泛应用,包括光学通信、光学显微镜、光学激光器等。
同时,圆偏振光也在许多实验室中用于研究光的物理性质和光与物质的相互作用。
放大自发发射圆偏振光

放大自发发射圆偏振光
圆偏振光呢,本身就像是光世界里的小机灵鬼。
它有着独特的性质,和我们平常所熟知的线偏振光可不一样哦。
圆偏振光就像是在一个圆形的轨道上欢快地跳舞的小光子们组成的队伍。
那什么是放大自发发射呢?这就像是给一群本来就很活跃的小光子们注入了超级能量。
想象一下,有一群小光子们原本在那里自娱自乐地发射着,然后突然有了一个神奇的力量,让它们发射得更厉害了,数量更多了,就好像是原本一个小乐队在轻声演奏,突然有了一个超级大音响,声音一下子就放大了好多倍呢。
在实际应用方面,那也是相当厉害的。
在显示技术里,它可以让我们看到更清晰、更鲜艳、更逼真的图像。
就像我们看电影的时候,如果运用了这种技术,电影里的那些美景、人物就像是要从屏幕里跳出来一样真实。
再比如说在光通信领域,它可以提高信号的传输质量和效率。
这就像是给信息传递修了一条超级高速公路,让信息能够又快又好地到达目的地。
另外,外部的环境也很重要。
就像小光子们也需要一个合适的舞台一样。
温度、压力等环境因素都会影响到这个过程。
如果温度不合适,就可能像小光子们在一个过热或者过冷的房间里,不能很好地发挥它们的能力。
圆偏振光和椭圆偏振光的获得和检验

(3)区分依据: (a)若圆偏振光为右旋光,则
入 / 2, / 2,
出射线偏振光的偏振方向位于二四象限。
出=
(b)若圆偏振光为左旋光,则
入 / 2, / 2,
出射线偏振光的偏振方向位于一三象限。
出 0
作业:2、3、4
旋转偏振片P一周,出射光强不变化
I
1 2
I0
E2
P I
2)椭圆偏振光通过旋转的检偏器后光强的变化
y Ey
E
P
x O Ex
I0
椭圆偏振光
P I
偏振片处于任意位置时:
Em E EM
旋转偏振片一周,没有消光现象。
出射光强为:
Im I IM
4.通过波晶片后光束偏振态的变化
1)光路:
结论:
0<</2,右旋椭圆,且向1~3象限倾斜;
/2< <,右旋椭圆,且向2~4象限倾斜;
< <3/2(或-< <-/2),左旋椭圆,且向
2~4象限倾斜;
3/2< <2 (或-/2< <0),左旋椭圆,且向
1~3象限倾斜。
右旋
左旋
=0
/4
/2
3/4
5/4
/4
3)具体区分步骤: (1)将偏振片放入光路,然后慢慢旋转一周。
(a)若出射光强有变化,且有消光位置, 则入射光是线偏振光。
(b)若出射光强没有变化,则入射光 为自然光或圆偏振光。
(c)若出射光强虽有变化,但没有消光位置, 则入射光为部分偏振光或椭圆偏振光。
(2)在第二组入射光前依次放置 波晶片 和偏振片,旋转偏振片一周若出射光有 消光位置,则该入射光为圆偏振光, 否则为自然光。
获得圆偏振光的方法

获得圆偏振光的方法
圆偏振光是一种特殊的光线,其电矢量随时间呈现圆周运动。
获取圆偏振光的方法包括以下几种:
1. 使用偏振片:将线偏振光通过四分之一波片或半波片,可以将电矢量的振动方向旋转90度,从而得到圆偏振光。
2. 液晶偏振器:利用液晶分子的排列结构,可以通过调节电场来改变电矢量的振动方向,从而得到圆偏振光。
3. 磁场:在一定的磁场下,电磁波的振动方向会发生旋转,从而得到圆偏振光。
4. 自然产生:某些物质在光的传播过程中,会使电矢量呈现圆周运动,从而产生圆偏振光。
例如,一些有机物质和细胞组织就能够自然产生圆偏振光。
总之,获得圆偏振光的方法多种多样,可以根据具体情况进行选择。
圆偏振光在光学领域有着广泛的应用,例如在生物医学影像学中,可以用圆偏振光来提高图像的对比度和分辨率。
- 1 -。
圆偏振片原理

圆偏振片原理圆偏振片是一种重要的光学元件,广泛应用于光学仪器和光学传感器等领域。
它可以将入射光线中的线性偏振光转化为圆偏振光,或者将圆偏振光转化为线性偏振光。
本文将介绍圆偏振片的原理、特点、制备方法和应用。
一、圆偏振光的定义在电磁波中,如果一个电场向一个方向振动,并且其振动方向与光波传播方向垂直,那么这种光为线偏振光。
如果电场向一个方向振动,并且其振动方向沿光波传播方向旋转,那么这种光为圆偏振光。
圆偏振光是一种特殊的偏振光,其振动方向呈螺旋状,可以分为左旋圆偏振光和右旋圆偏振光两种。
二、圆偏振片的原理圆偏振片是利用一种叫做旋光性质的物理现象制成的。
旋光性质是指某些物质(如葡萄糖、蔗糖等)对通过它的偏振光产生的旋转。
圆偏振片一般是由多层透明膜叠加在一起制成的。
在这些膜层中,每一层都是用旋光性质不同的材料制成的。
当线偏振光穿过这些膜层时,其振动方向会被旋转一定角度,最终形成圆偏振光。
圆偏振片的旋光方向由其材料的旋光性质决定。
如果材料对光的旋转方向是左旋的,那么制成的圆偏振片就是左旋圆偏振片;如果材料对光的旋转方向是右旋的,那么制成的圆偏振片就是右旋圆偏振片。
通常,材料的旋光性质是用旋光仪进行测量的,以确定材料的旋光方向和强度。
三、圆偏振片的特点1、具有转化线偏振光为圆偏振光的能力。
2、具有转化左旋圆偏振光为线偏振光的能力。
3、具有转化右旋圆偏振光为线偏振光的能力。
4、具有色散和吸收的特性,不同波长的光对其的作用有所不同。
5、对于不同的入射角度,其转换效率也不同。
6、制备过程复杂,成本较高。
四、圆偏振片的制备方法圆偏振片的制备方法通常有两种:玻璃制片法和薄膜堆积法。
1、玻璃制片法玻璃制片法是最早用于制备圆偏振片的方法之一。
这种方法是先将对光具有旋光性质的材料放在两片玻璃片之间,形成一个光学薄片。
然后,将若干这样的薄片堆叠在一起,并用特殊的胶粘结在一起,形成一个整体的圆偏振片。
这种方法制备的圆偏振片具有较高的品质和光学性能,但成本较高。
获得偏振光的方法

获得偏振光的方法嘿,你问获得偏振光的方法呀?那咱就来好好唠唠。
要得到偏振光呢,有好几种办法。
一种是用偏振片。
这偏振片就像个小魔法道具似的。
你把光通过偏振片,就能得到偏振光啦。
偏振片有不同的方向,你可以转一转偏振片,看看光的变化。
就像玩一个小魔术,可有意思了。
还有一种方法是用反射。
当光以一定的角度照在某些表面上的时候,反射光就会变成偏振光。
比如说照在水面上或者玻璃上。
这时候你就得找好角度,可不能随便乱照。
就像你拍照的时候要找好角度才能拍出好看的照片一样。
另外呢,还可以用双折射晶体。
这种晶体很神奇哦,它能把一束光分成两束,其中一束就是偏振光。
就好像把一个东西分成两半,一半是你想要的偏振光。
不过这得有点专业知识才能用好这种方法。
再说说散射也能得到偏振光。
当光被一些小颗粒散射的时候,散射光可能会变成偏振光。
就像太阳光被空气中的灰尘散射,有时候你就能看到偏振光的效果。
举个例子哈,我有个朋友,他对摄影很感兴趣。
有一次他想拍一些有偏振光效果的照片。
他就买了一个偏振片,装在相机镜头上。
他出去拍照的时候,就转一转偏振片,看看不同角度下的光的变化。
他拍出来的照片可漂亮了,有那种很特别的效果。
他可高兴了,说以后还要用偏振光拍出更多好看的照片。
总之呢,获得偏振光的方法有偏振片、反射、双折射晶体和散射等。
你可以根据自己的需要选择合适的方法。
试试这些方法,说不定你也能发现偏振光的神奇之处哦。
加油吧!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
5
7 6
x
4
5
4
5 6 7
3
2 1
8
x
2. / 2
y
8 7 6 5 5 6
y
7 8
1 2
3
1 2 2 1
6 7 8
4
4
3 3
x
4
5
x
3. / 4
y
8
y
8 7 6 5 5 6 7
1 2
3
1 2
x
4
4 4
5 6 7
3 3
2 1
8
x
两 相 互 垂 直 同 频 率 不 同 相 位 差
5、说明: • 波片是对某一波长而言的;
4.3 两相互垂直同频率谐振动的合成
分振动
x A1 cos(t 1 )
y A2 cos(t 2 )
① ② ③ ④
①、②式消 t 。 x A1 (cost cos1 sin t sin 1 )
y A 2 (cos t cos 2 sin t sin 2 )
2
y
A2
x
x y A A 0 2 1 A1 o A2 合振动轨迹为过原点 y x A1 且在二四象限直线。
合振动方程为同频率的谐振动
x y 2 xy cos( 2 1 ) 2 sin ( 2 1 ) A A A1 A2 1 2
2 2
为椭圆轨迹方程。 • 合运动一般是取向任意的椭圆。 • 椭圆的性 质 ( 方位 、长短 轴、左 右旋 ) 在 A1 、 A2确定之后, 主要决定于位相差 = 2– 1。
讨论
x y 2 xy cos( 2 1 ) 2 sin ( 2 1 ) A A A1 A2 1 2
⑤
③ ④
消第2项 得
2
x sin 2 y sin 1 A1 A2
x sin 2 y sin 1 cost sin( 2 1 ) A1 A2
2
⑥
⑤ ⑥
有
合振动的轨迹方程为
x y 2 xy cos( 2 1 ) 2 sin ( 2 1 ) A A A1 A2 1 2
简 谐 运 动 的 合 成 图
4.4椭园偏振光和园偏振光
一、定义 当晶体中产生双折射时,若 o、e 光沿同一方向传播,此 时它们满足频率相同、振动方向相互垂直的条件,如能使位相 差为定值,则当光连续通过晶体中任一点(该点上相差为恒定 值)时,在垂直于传播方向的平面内,合光矢(针对某一时刻) 的端点的投影将描出个一椭圆。 在晶体内的整个传播过程中,合光矢量将以传播方向为轴, 螺旋式向前传播。故称椭圆偏振光;若合振动矢量大小不变,仅 方向随时间变化,称圆偏振光。
2
2
1. 1 2 0 二分振动同相(位)
x y 2 xy A A AA 0 1 2 1 2
x y A A 0 2 1
2
2
2
y
A2
o
A2 y x A1
合振动轨迹为过原点 且在一三象限直线。
2
2
3. 2 1 / 2
x y A A 1 1 2
2 2
y
A2
o x
为顺时针正椭圆(见后)
•当 A1 A2
x y A
2 2 2
A1
为顺时针圆.
一般地,如果
1. 0 2 1
其合振动的轨迹 为顺时针的椭圆 其合振动的轨迹 为逆时针的椭圆
E
E
r
r
1 ∴ 该晶片称为 波片或 移相器。 4 2
1 4、 2 波片(半波片):
2
其厚度 : d
2k 1 4no ne
当晶片厚度满足: no ne d 2k 1 时, k 0,1,2,3, 2 2k 1 2k 1 1 其厚度 : d ∴ 该晶片称为 波片或 移相器。 2 2no ne
4.2 波晶片— 相位延迟片
晶片是光轴平行表面的晶体薄片。
平行光正入射
晶片
Ae
x
A
线偏振光 d
Ao
y
光轴 Ae
ቤተ መጻሕፍቲ ባይዱ
P
A Ao
椭圆偏振光 光轴
o光垂直主平面振动,e光平行主平面振动,主平面为含光轴 与折射光。 o光振动垂直光轴方向 e光振动沿光轴方向
振幅关系:
Ao A sin ,
Ae A cos
消第1项
x cos 2 y cos 1 A1 A2
得
x cos 2 y cos1 sin t sin( 2 1 ) A1 A2
x A1 (cost cos1 sin t sin 1 ) y A2 (cost cos2 sin t sin 2 )
e光 o光
由于传播速度不同
o光的位相比e光的 位相滞后或超前 出射波晶片时,两光经历的光程差为
Lo Le no ne d
d
通过厚为d的晶片,o、e光产生相位差: 2 ne no d
通常将这个位相差称作波晶片的位相延迟
1 3、 4 波片:
当晶片厚度满足: no ne d 2k 1 时, k 0,1,2,3, 4 2k 1
2. 2 1 2
两个相互垂直的同频率的谐振动可以合成为一直线谐振动、 匀速圆周运动和椭圆运动。 由此可见,任一直线谐振动、匀速圆周运动和椭圆运动 都可分解为两个相互垂直的同频率的谐振动。
用旋转矢量法确定合振动轨迹和方向 y y 0 1. 1
2
8
2
7 6 3
1
8
3
A1
x
x y 2 xy cos( 2 1 ) 2 sin ( 2 1 ) A A A1 A2 1 2
2
2
2.
| 2 1 | 二分振动反相(位) 2 2 x y 2 xy A A AA 0 1 2 1 2
