计算语言学4 Neural Language Model(1)
计算语言学(CL)与自然语言处理(NLP)

通过文本挖掘技术对大量文本进行情感倾向性分析,应用于产品 评价、舆情监控等领域。
信息提取
从非结构化文本中提取出关键信息,如实体识别、关系抽取等,用 于构建知识图谱、智能推荐等。
搜索引擎
信息检索技术是实现搜索引擎的核心,通过高效的索引和查询算法 ,为用户提供准确的搜索结果。
其他领域应用及案例
。
计算语言学作为语言学与计算 机科学的交叉学科,为自然语 言处理提供了理论基础和技术
支持。
发展趋势及应用前景
深度学习技术在自然语言处理领域的应 用日益广泛,如循环神经网络(RNN )、长短期记忆网络(LSTM)和自注
意力机制(Self-Attention)等。
随着预训练语言模型(如BERT、GPT 系列)的兴起,自然语言处理任务在性
和高效性能。
无监督与半监督学习
利用大量未标注数据进行无监督或半 监督学习,减少对标注数据的依赖。
多模态融合
探索将文本、图像、音频等多种模态 信息融合的方法,提高NLP系统的理 解和生成能力。
THANKS。
编程语言与编译原理
研究计算机编程语言的语法、 语义和编译技术,实现人类与 计算机之间的交互。
算法与数据结构
研究如何有效地组织和处理数 据,以及设计解决问题的算法 。
操作系统
管理计算机硬件与软件资源, 为应用程序提供运行环境和服 务。
数据库与信息系统
研究如何有效地存储、管理和 检索大量数据,以及构建基于 数据库的信息系统。
自然语言生成
根据特定主题或要求,自动生成 结构合理、语义通顺的自然语言 文本,应用于新闻报道、文学创 作等领域。
对话系统
实现更加自然、流畅的人机对话 ,提高用户体验和满意度,应用 于智能家居、智能车载等领域。
计算语言学

计算语言学计算语言学(computationallanguagetry)是20世纪80年代后期发展起来的一门语言学新分支。
它将语言的自然属性与功能性计算结合在一起,它从信息论的观点出发,用计算机去处理语言的各种特征和规律,因此也称为信息处理语言学。
目前,这一领域已经成为国际上语言学研究中的一个热点。
因为随着语言理解技术的不断改进,需要处理的信息越来越多,计算机的速度、容量等指标也不断提高,因此对语言理解算法的研究也逐渐引起了人们的重视。
对于计算机而言,从本质上看,它就是一种代码,如同程序员所编写的源程序一样。
但是,计算机是由人来控制的,它可以依据人的指令对数据进行加工和运算,实现特定的功能。
也就是说,计算机只能按照人事先确定的方式来执行,无法根据客观实际情况来作出相应的改变。
1、认知主义和行为主义。
语言学中一般把计算语言学分成两大派别:认知主义和行为主义。
认知主义的主要观点是:语言是知识系统的一部分,语言是我们从事交际活动的工具。
语言是在人脑中表示意义的符号系统,是外界事物的概括的反映,并借助词的形式表现出来。
行为主义的主要观点是:语言是人类交际过程中约定俗成的,符号形式能够描述人们所指的客观世界的思维过程。
人们使用语言来进行交际,是通过手势或面部表情表达他们的内心思想感情的。
他们把人的语言看作是一种人造的符号系统,其作用仅仅是向外部世界传递信息。
2、神经科学和心理语言学。
20世纪70年代以后,计算机和信息论的研究蓬勃兴起,并与人类语言学的研究产生了紧密的联系。
人们逐步发现,计算机的行为模式直接来自人的行为模式,即直接来自于大脑的某些脑区。
人脑的某些脑区被称之为高级认知中心,具有推理、解决问题、记忆和逻辑判断等功能,其主要功能是对外界事物的知觉、学习、记忆、存贮和对事物的归类,并做出适当的行为反应。
计算机是电子设备,电子设备在很大程度上都是按照人们事先制定的程序设计的,这样就保证了整个计算机的操作必须严格按照人们事先确定的规则来执行。
人工智能导论-第四课自然语言处理
研究表示,在大脑皮层中局部回路的基本连接 可以通过一系列的互联规则所捕获,而且这些 规则在大脑皮层中处于不断循环之中。
模拟人脑利用历史信息来做决策
两种不同神经网络的缩写。
时间递归神经网络(recurrent neural network) 结构递归神经网络(recursive neural network)
无法对词向量做比较,任意两个词之间都是孤立的
34
自然语言处理
词向量
使用上下文来表示单词
使用共现矩阵(Cooccurrence matrix) 一个基于窗口的共现矩阵例子
窗口长度是1(一般是5-10) 语料样例
▪ I like deep learning. ▪ I like NLP. ▪ I enjoy flying
7
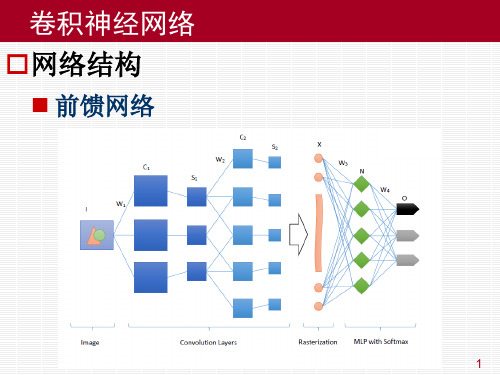
卷积神经网络 卷积网络训练过程
反向传播过程
从高层到底层,逐层进行分析
光栅化层 ▪ 从上一层传过来的残差为
▪ 重新整理成为一系列矩阵即可,若上一层 Q 有 q 个 池化核,则传播到池化层的残差为
8
卷积神经网络 卷积网络训练过程
反向传播过程
从高层到底层,逐层进行分析
池化层 ▪ 应池化过程中常用的两种池化方案,反传残差的时 候也有两种上采样方案 ▪ 最大池化:将1个点的残差直接拷贝到4个点。 ▪ 均值池化:将1个点的残差平均到4个点。 ▪ 传播到卷积层的残差为
9
卷积神经网络 卷积网络训练过程
反向传播过程
从高层到底层,逐层进行分析
卷积层 ▪ 卷积层有参数,所以卷积层的反传过程需要更新权 值,并反传残差。 ▪ 先考虑权值更新,考虑卷积层某个“神经中枢”中 的第一个神经元 ▪ 多层感知器的梯度公式
3分钟带你看懂大语言模型基础知识

大语言模型(Large Language Models,LLMs)是人工智能领域的一种重要技术,主要用于处理和理解自然语言文本。
以下是关于大语言模型的基础知识简介:什么是大语言模型?大语言模型是一种基于深度学习的模型,它通过训练大量的文本数据来学习语言的规律,从而实现对自然语言的理解和生成。
这些模型通常包含数十亿甚至万亿的参数,因此被称为“大”模型。
大语言模型的工作原理是什么?大语言模型的工作原理基于神经网络,特别是循环神经网络(RNN)和变换器(Transformer)结构。
这些模型通过逐层传递信息,从输入文本中提取特征,并生成相应的输出。
在训练过程中,模型会调整其参数以最小化预测错误,从而提高对自然语言的理解和生成能力。
大语言模型有哪些应用场景?大语言模型在多个领域都有广泛的应用,如自然语言处理(NLP)、机器翻译、文本生成、聊天机器人等。
它们可以自动完成句子、生成摘要、回答问题、进行对话等,为用户提供更智能的服务。
大语言模型的优势和挑战是什么?优势:大语言模型具有强大的语言理解和生成能力,可以处理复杂的自然语言任务。
此外,随着数据量的增加和模型规模的扩大,其性能会不断提高。
挑战:大语言模型需要大量的计算资源和数据来训练,这使得其成本高昂。
此外,随着模型规模的扩大,训练时间也会显著增加。
此外,大语言模型在某些情况下可能会产生不准确的预测或产生误导性的输出。
大语言模型的未来发展趋势是什么?随着技术的不断进步和计算资源的日益丰富,大语言模型将继续向更大、更复杂的方向发展。
未来,我们可能会看到更多基于大语言模型的创新应用,如自然语言生成、情感分析、智能写作等。
同时,随着模型性能的提高,大语言模型将在更多领域发挥重要作用,为人类提供更智能、更便捷的服务。
总之,大语言模型是人工智能领域的一项重要技术,它在自然语言处理、机器翻译、文本生成等领域具有广泛的应用前景。
虽然目前还存在一些挑战和限制,但随着技术的不断进步和计算资源的日益丰富,大语言模型有望在未来发挥更大的作用。
large language model综述

一、介绍大型语言模型(large language model)是近年来人工智能领域的热门话题之一。
它是指采用深度学习技术训练得到的能够自动处理和理解自然语言的模型。
随着深度学习技术的发展,大型语言模型在自然语言处理、对话系统、翻译等领域展现出了巨大的潜力和应用前景。
本文将对大型语言模型进行综述,包括其定义、发展历程、应用领域以及未来发展方向。
二、定义大型语言模型是指由大规模语料库训练得到的能够自动处理和理解自然语言的模型。
其核心技术是深度学习,特别是基于神经网络的模型。
大型语言模型能够对自然语言进行语义理解、生成文本,甚至进行对话交互,是自然语言处理领域的重要技术支撑。
三、发展历程从早期的基于规则的自然语言处理技术到近年来的基于深度学习的大型语言模型,该领域经历了不断的发展和进步。
2018年,Open本人发布了首个大型语言模型GPT(Generative Pre-tr本人ned Transformer),引起了广泛关注。
随后,GPT-2、GPT-3等版本相继发布,模型规模不断扩大,性能不断提升。
Google、Facebook等公司也纷纷推出了自己的大型语言模型,加速了该领域的发展。
四、应用领域大型语言模型在自然语言处理、对话系统、翻译等领域有着广泛的应用。
在自然语言处理中,大型语言模型可以用于文本分类、情感分析、实体识别等任务;在对话系统中,大型语言模型可以实现智能问答、聊天对话等功能;在翻译领域,大型语言模型可以实现自动翻译、跨语言交流等功能。
大型语言模型还可以应用于知识图谱建设、搜索引擎优化等领域。
五、未来发展方向未来,大型语言模型将继续向着更大规模、更高性能的方向发展。
随着深度学习技术的不断进步,大型语言模型将会更加强大,能够处理更加复杂的自然语言任务。
大型语言模型还有望与其他人工智能技术结合,如计算机视觉、增强学习等,实现更加智能化的应用。
大型语言模型还有望应用于更多领域,如医疗、金融、教育等,为人类社会带来更多智能化的便利。
计算语言学4Part1_283305576

4.2. Estimating Probability of Sentences
1. Unigram approximation to Shakespeare
4.2. Estimating Probability of Sentences
4.2. Estimating Probability of Sentences
4.2. Estimating Probability of Sentences
bigram probabilities:
PROB(for|prepare)=0.17 PROB(leap|for)=0.0000011 PROB(in|leap)=0.096 PROB(the|in)=0.27 PROB(dark|the)=0.0017 PROB(lip|for)=0.0000022 PROB(in|lip)=0.016
/corpora.html English Language Corpora and Corpus resources
4.2. Estimating Probability of Sentences
unigram probabilities: PROB(prepare)= 0.000030 PROB(leap)=0.00001 PROB(the)=0.022 PROB(lip)=0.000016
4.1. Rationalism and Empiricism
歧义难以处理 List the sales of the products produced in 1973 with the products produced in 1972. (Martin et al. 1987) 455种可能的parse
Selectional restriction 当遇到比喻修辞时,变得非常脆弱
计算机语言学

1. 什么是计算机语言学?发展史?计算语言学:指的是这样一门学科,它通过建立形式化的数学模型来分析,处理自然语言,并在计算机上用程序来实现分析和处理的过程,从而达到一机器来模拟人的全部或者部分语言能力的目的。
计算语言学是利用电子数字计算机进行的语言分析。
虽然许多其他类型的语言分析也可以运用计算机,计算分析最常用于处理基本的语言数据-例如建立语音、词、词元素的搭配以及统计它们的频率。
计算语言学是语言学的一个研究分支,用计算技术和概念来阐述语言学和语音学问题。
已开发的领域包括自然语言处理,言语识别,自动翻译,语法的检测,以及许多需要统计分析的领域。
发展史:第一个时期是计算语言的萌芽期(1950 -1960年代)第二个时期是计算语言的发展期(1970 -1980年代)第三那个时期是计算语言的繁荣期(1990 -至今)2什么是语言资料库?它与语言知识库有什么区别?语言库在自然语言处理方面有什么应用?答:语料库顾名思义就是存放语言材料的仓库。
它是以电子计算机为载体承载语言知识的基础资源;语料库中存放的是在语言的实际使用中真实出现过的语言材料;真实语料需要经过加工(分析和处理),才能成为有用的资源;语言资料库与语言知识库的区别是:语料库是一种承载自然语言的形式,它的特点是以语言的真实材料为基础来呈现语言知识的。
语言知识库可以说是由专家从大量的实例中提炼、概括出来的系统的语言知识,语料库则基本上是以知识的原始形态表现出来。
在自然语言处理方面的应用如:基于大规模语料库的语音识别;基于大规模语料库的音字转换技术(中文输入);基于大规模语料库的自动文本校对技术;利用语料库训练HMM模型进行分词,词性标注,词义标注等等;基于语料库的句法分析;局域原料库的机器翻译;基于机器学习技术,通过语料库获取语言知识,包括搭配特征,句法规则,等等;基于语料钜的语言模型训练以及语言模型的评价;3. 中文自动分词的重要性;举例说明分词算法中的主要难点有哪些类型?答:中文分词的重要性:首先自动分词是汉语信息处理系统的重要组成部分;其次,自动分词是中文信息处理的基础。
自然语言处理及计算语言学相关术语中英对译表三_计算机英语词汇

multilingual processing system 多语讯息处理系统multilingual translation 多语翻译multimedia 多媒体multi-media communication 多媒体通讯multiple inheritance 多重继承multistate logic 多态逻辑mutation 语音转换mutual exclusion 互斥mutual information 相互讯息nativist position 语法天生假说natural language 自然语言natural language processing (nlp) 自然语言处理natural language understanding 自然语言理解negation 否定negative sentence 否定句neologism 新词语nested structure 崁套结构network 网络neural network 类神经网络neurolinguistics 神经语言学neutralization 中立化n-gram n-连词n-gram modeling n-连词模型nlp (natural language processing) 自然语言处理node 节点nominalization 名物化nonce 暂用的non-finite 非限定non-finite clause 非限定式子句non-monotonic reasoning 非单调推理normal distribution 常态分布noun 名词noun phrase 名词组np (noun phrase) completeness 名词组完全性object 宾语{语言学}/对象{信息科学}object oriented programming 对象导向程序设计[面向对向的程序设计]official language 官方语言one-place predicate 一元述语on-line dictionary 线上查询词典 [联机词点]onomatopoeia 拟声词onset 节首音ontogeny 个体发生ontology 本体论open set 开放集operand 操作数 [操作对象]optimization 最佳化 [最优化]overgeneralization 过度概化overgeneration 过度衍生paradigmatic relation 聚合关系paralanguage 附语言parallel construction 并列结构parallel corpus 平行语料库parallel distributed processing (pdp) 平行分布处理paraphrase 转述 [释意;意译;同意互训]parole 言语parser 剖析器 [句法剖析程序]parsing 剖析part of speech (pos) 词类particle 语助词part-of relation part-of 关系part-of-speech tagging 词类标注pattern recognition 型样识别p-c (predicate-complement) insertion 述补中插pdp (parallel distributed processing) 平行分布处理perception 知觉perceptron 感觉器 [感知器]perceptual strategy 感知策略performative 行为句periphrasis 用独立词表达perlocutionary 语效性的permutation 移位petri net grammar petri 网语法philology 语文学phone 语音phoneme 音素phonemic analysis 因素分析phonemic stratum 音素层phonetics 语音学phonogram 音标phonology 声韵学 [音位学;广义语音学] phonotactics 音位排列理论phrasal verb 词组动词 [短语动词]phrase 词组 [短语]phrase marker 词组标记 [短语标记]pitch 音调pitch contour 调形变化pivot grammar 枢轴语法pivotal construction 承轴结构plausibility function 可能性函数pm (phrase marker) 词组标记 [短语标记] polysemy 多义性pos-tagging 词类标记postposition 方位词pp (preposition phrase) attachment 介词依附pragmatics 语用学precedence grammar 优先级语法precision 精确度predicate 述词predicate calculus 述词计算predicate logic 述词逻辑 [谓词逻辑]predicate-argument structure 述词论元结构prefix 前缀premodification 前置修饰preposition 介词prescriptive linguistics 规定语言学 [规范语言学] presentative sentence 引介句presupposition 前提principle of compositionality 语意合成性原理privative 二元对立的probabilistic parser 概率句法剖析程序problem solving 解决问题program 程序programming language 程序设计语言 [程序设计语言] proofreading system 校对系统proper name 专有名词prosody 节律prototype 原型pseudo-cleft sentence 准分裂句psycholinguistics 心理语言学punctuation 标点符号pushdown automata 下推自动机pushdown transducer 下推转换器qualification 后置修饰quantification 量化quantifier 范域词quantitative linguistics 计量语言学question answering system 问答系统queue 队列radical 字根 [词干;词根;部首;偏旁]radix of tuple 元组数基random access 随机存取rationalism 理性论rationalist (position) 理性论立场 [唯理论观点]reading laboratory 阅读实验室real time 实时real time control 实时控制 [实时控制]recursive transition network 递归转移网络reduplication 重叠词 [重复]reference 指涉referent 指称对象referential indices 指针referring expression 指涉词 [指示短语]register 缓存器[寄存器]{信息科学}/调高{语音学}/语言的场合层级{社会语言学}regular language 正规语言 [正则语言]relational database 关系型数据库 [关系数据库]relative clause 关系子句relaxation method 松弛法relevance 相关性restricted logic grammar 受限逻辑语法resumptive pronouns 复指代词retroactive inhibition 逆抑制rewriting rule 重写规则rheme 述位rhetorical structure 修辞结构rhetorics 修辞学robust 强健性robust processing 强健性处理robustness 强健性schema 基朴school grammar 教学语法scope 范域 [作用域;范围]script 脚本search mechanism 检索机制search space 检索空间searching route 检索路径 [搜索路径]second order predicate 二阶述词segmentation 分词segmentation marker 分段标志selectional restriction 选择限制semantic field 语意场semantic frame 语意架构semantic network 语意网络semantic representation 语意表征 [语义表示] semantic representation language 语意表征语言semantic restriction 语意限制semantic structure 语意结构semantics 语意学sememe 意素semiotics 符号学sender 发送者sensorimotor stage 感觉运动期sensory information 感官讯息 [感觉信息]sentence 句子sentence generator 句子产生器 [句子生成程序]sentence pattern 句型separation of homonyms 同音词区分sequence 序列serial order learning 顺序学习serial verb construction 连动结构set oriented semantic network 集合导向型语意网络 [面向集合型语意网络]sgml (standard generalized markup language) 结构化通用标记语言shift-reduce parsing 替换简化式剖析short term memory 短程记忆sign 信号signal processing technology 信号处理技术simple word 单纯词situation 情境situation semantics 情境语意学situational type 情境类型social context 社会环境sociolinguistics 社会语言学software engineering 软件工程 [软件工程]sort 排序speaker-independent speech recognition 非特定语者语音识别spectrum 频谱speech 口语speech act assignment 言语行为指定speech continuum 言语连续体speech disorder 语言失序 [言语缺失]speech recognition 语音辨识speech retrieval 语音检索speech situation 言谈情境 [言语情境]speech synthesis 语音合成speech translation system 语音翻译系统speech understanding system 语音理解系统spreading activation model 扩散激发模型standard deviation 标准差standard generalized markup language 标准通用标示语言start-bound complement 接头词state of affairs algebra 事态代数state transition diagram 状态转移图statement kernel 句核static attribute list 静态属性表statistical analysis 统计分析statistical linguistics 统计语言学statistical significance 统计意义stem 词干stimulus-response theory 刺激反应理论stochastic approach to parsing 概率式句法剖析 [句法剖析的随机方法]stop 爆破音stratificational grammar 阶层语法 [层级语法]string 字符串[串;字符串]string manipulation language 字符串操作语言string matching 字符串匹配 [字符串]structural ambiguity 结构歧义structural linguistics 结构语言学structural relation 结构关系structural transfer 结构转换structuralism 结构主义structure 结构structure sharing representation 结构共享表征subcategorization 次类划分 [下位范畴化] subjunctive 假设的sublanguage 子语言subordinate 从属关系subordinate clause 从属子句 [从句;子句] subordination 从属substitution rule 代换规则 [置换规则] substrate 底层语言suffix 后缀superordinate 上位的superstratum 上层语言suppletion 异型[不规则词型变化] suprasegmental 超音段的syllabification 音节划分syllable 音节syllable structure constraint 音节结构限制symbolization and verbalization 符号化与字句化synchronic 同步的synonym 同义词syntactic category 句法类别syntactic constituent 句法成分syntactic rule 语法规律 [句法规则]syntactic semantics 句法语意学syntagm 句段syntagmatic 组合关系 [结构段的;组合的] syntax 句法systemic grammar 系统语法tag 标记target language 目标语言 [目标语言]task sharing 课题分享 [任务共享] tautology 套套逻辑 [恒真式;重言式;同义反复] taxonomical hierarchy 分类阶层 [分类层次] telescopic compound 套装合并template 模板temporal inference 循序推理 [时序推理] temporal logic 时间逻辑 [时序逻辑] temporal marker 时貌标记tense 时态terminology 术语text 文本text analyzing 文本分析text coherence 文本一致性text generation 文本生成 [篇章生成]text linguistics 文本语言学text planning 文本规划text proofreading 文本校对text retrieval 文本检索text structure 文本结构 [篇章结构]text summarization 文本自动摘要 [篇章摘要] text understanding 文本理解text-to-speech 文本转语音thematic role 题旨角色thematic structure 题旨结构theorem 定理thesaurus 同义词辞典theta role 题旨角色theta-grid 题旨网格token 实类 [标记项]tone 音调tone language 音调语言tone sandhi 连调变换top-down 由上而下 [自顶向下]topic 主题topicalization 主题化 [话题化]trace 痕迹trace theory 痕迹理论training 训练transaction 异动 [处理单位]transcription 转写 [抄写;速记翻译]transducer 转换器transfer 转移transfer approach 转换方法transfer framework 转换框架transformation 变形 [转换]transformational grammar 变形语法 [转换语法] transitional state term set 转移状态项集合transitivity 及物性translation 翻译translation equivalence 翻译等值性translation memory 翻译记忆transparency 透明性tree 树状结构 [树]tree adjoining grammar 树形加接语法 [树连接语法] treebank 树图数据库[语法关系树库]trigram 三连词t-score t-数turing machine 杜林机 [图灵机]turing test 杜林测试 [图灵试验]type 类型type/token node 标记类型/实类节点type-feature structure 类型特征结构typology 类型学ultimate constituent 终端成分unbounded dependency 无界限依存underlying form 基底型式underlying structure 基底结构unification 连并 [合一]unification-based grammar 连并为本的语法 [基于合一的语法] universal grammar 普遍性语法universal instantiation 普遍例式universal quantifier 全称范域词unknown word 未知词 [未定义词]unrestricted grammar 非限制型语法usage flag 使用旗标user interface 使用者界面 [用户界面]valence grammar 结合价语法valence theory 结合价理论valency 结合价variance 变异数 [方差]verb 动词verb phrase 动词组 [动词短语]verb resultative compound 动补复合词verbal association 词语联想verbal phrase 动词组verbal production 言语生成vernacular 本地话v-o construction (verb-object) 动宾结构vocabulary 字汇vocabulary entry 词条vocal track 声道vocative 呼格voice recognition 声音辨识 [语音识别]vowel 元音vowel harmony 元音和谐 [元音和谐]waveform 波形weak verb 弱化动词whorfian hypothesis whorfian 假说word 词word frequency 词频word frequency distribution 词频分布word order 词序word segmentation 分词word segmentation standard for chinese 中文分词规范word segmentation unit 分词单位 [切词单位]word set 词集working memory 工作记忆 [工作存储区]world knowledge 世界知识writing system 书写系统x-bar theory x标杠理论 ["x"阶理论]zipf's law 利夫规律 [齐普夫定律]。
计算语言学(2024)

造性。
18
2024/1/29
05
CATALOGUE
语音识别与合成
19
语音识别的原理
声学建模
将输入的语音信号转换为声学特 征向量,如梅尔频率倒谱系数( MFCC),以描述语音的声学特
性。
2024/1/29
语言建模
构建语言模型来描述词与词之间的 概率关系,常用的有N-gram模型 和神经网络语言模型。
2024/1/29
12
句法分析
句子结构分析
确定句子中词汇之间的结构关系,如主谓宾、定状补 等。
依存关系分析
分析句子中词汇之间的依存关系,如动词与其宾语、 形容词与其修饰的名词等。
短语结构分析
识别并分析句子中的短语结构,如名词短语、动词短 语等。
2024/1/29
13
语义理解
词汇语义
理解词汇在特定上下文中的含义和用法。
1 2
个性化语言处理技术的发展
随着个性化需求的不断增长,计算语言学将更加 注重个性化语言处理技术的研究和应用,如个性 化推荐、情感分析等。
多模态语言处理的深度融合
未来计算语言学将更加注重多模态语言处理的深 度融合,实现文本、语音、图像等多种信息的联 合处理和应用。
语言智能的进一步提升
3
随着计算语言学技术的不断发展,语言智能将得 以进一步提升,实现更加自然、高效的人机交互 和智能应用。
基于规则的翻译
通过预设的语法和词汇规则进行翻译,这种方法需要大量的手工编 码规则。
基于统计的翻译
利用大量的双语语料库进行统计学习,构建翻译模型。这种方法可 以自动从语料库中学习翻译规则,避免了手工编码的繁琐。
基于神经网络的翻译
通过深度学习技术,构建大规模的神经网络模型进行翻译。这种方法 可以自动学习语言的复杂特征,并实现更加准确的翻译。
计算语言学概论课件

计算语言学的重要性
社会需求
随着信息技术的快速发展,社会 对自然语言处理的需求日益增长 ,计算语言学在信息检索、机器 翻译、语音识别等领域具有广泛
的应用前景。
学术价值
计算语言学为语言学、计算机科 学等相关学科提供了新的研究方 法和思路,有助于推动相关学科
的发展。
技术创新
计算语言学的技术突破和创新, 将推动人工智能、大数据等领域 的进步,为社会发展带来更多机
信息抽取是从非结构化文本中提 取结构化信息的过程,如从新闻 报道中提取事件、时间、地点等
关键信息。
信息抽取技术广泛应用于知识图 谱构建、问答系统等领域。
信息抽取的关键技术包括实体识 别、关系抽取、事件抽取等。
机器翻译
机器翻译是利用计算机自动将一 种语言的文本转换为另一种语言
的文本的过程。
机器翻译技术已经取得了显著的 进步,如基于神经网络的机器翻
深度学习在NLP领域的应用取得了显著成果,如词向量表示、序列标注、生成模型 等。
文本挖掘
文本挖掘是从大量文本数据中 提取有用信息的过程,包括文 本分类、聚类、情感分析等。
文本挖掘技术广泛应用于信息 检索、舆情分析、企业竞争情 报等领域。
文本挖掘的关键技术包括特征 提取、文本表示、模型评估等 。
信息抽取
感谢观看
REPORTING
情感分析
计算语言学可以帮助智能客服系统识别用户的情感倾向,从而提供 更加贴心、个性化的服务。
自动回复
利用计算语言学的方法,智能客服系统可以自动回复用户的咨询, 提高服务效率。
在机器翻译中的应用
1 2
语言对齐
计算语言学可以帮助机器翻译系统识别源语言和 目标语言之间的对应关系,提高翻译的准确度。
计算语言学

语音合成: 语音合成:将可视的文本信息转化为可听的 语音信息。 语音信息。 现在语音识别技术还在发展, 现在语音识别技术还在发展,据说可以哑人 手语识别系统借助数据手套, 手语识别系统借助数据手套,将哑人在会话过 程中的手的运动信息提取出来进行识别, 程中的手的运动信息提取出来进行识别 , 提 取其中的语义,并通过语音合成, 取其中的语义,并通过语音合成,最终将他们 的手语信息翻译成语音并输出, 的手语信息翻译成语音并输出 , 便于听力健 全人理解。 全人理解。
印刷汉字识别技术主要包括:
(1) 扫描输入文本图象。 扫描输入文本图象 输入文本图象。 (2) 图象的预处理,包括倾斜校正和滤除干扰噪声等。 图象的预处理 包括倾斜校正和滤除干扰噪声等。 预处理, (3) 图象版面分析和理解。区分出文本段落及排版顺序,图象、 图象版面分析和理解。区分出文本段落及排版顺序,图象、 表格的区域;对于文本区域将进行识别处理, 表格的区域;对于文本区域将进行识别处理,对于表格区域进行 专用的表格分析及识别处理,对于图象区域进行压缩或简单存储。 专用的表格分析及识别处理,对于图象区域进行压缩或简单存储。 (4)行字切分:图象的行切分和字切分。 行字切分: 行字切分 图象的行切分和字切分。 (5)特征提取:提取单字图象统计特征或结构特征。 特征提取: 特征提取 提取单字图象统计特征或结构特征。 (6)文字识别:基于单字图象特征的模式分类。将被分类的模式 文字识别: 文字识别 基于单字图象特征的模式分类。 赋予识别结果。 赋予识别结果。 (7)后处理:识别结果的编辑修改后处理。利用词义、词频、语 后处理:识别结果的编辑修改后处理。利用词义、词频、 后处理 法规则或语料库等语言先验知识对识别结果进行校正的过程。 法规则或语料库等语言先验知识对识别结果进行校正的过程。 其中(4)、(5)和(6),是印刷汉字识别中最为核心的技术。 、 其中 和 ,是印刷汉字识别中最为核心的技术。
计算语言学

计算语言学计算语言学(computer-aidedgrammars)又称“电脑辅助语言学”或“计算机辅助语言研究”。
它是计算机科学和人工智能技术与语言学相结合的产物,是20世纪50年代末到60年代初语言学中一个新兴的分支学科。
计算语言学的主要任务是利用现代科学技术手段来研究人类的自然语言及其形成过程。
它的研究对象就是大量的自然语言材料,通过建立各种模型、方法、理论来进行定量研究。
计算语言学作为当前语言学中一个崭新的领域,得到了很多语言学家和数学家们的重视。
语言是人类最重要的交际工具,社会上绝大部分的交际活动都需要借助语言才能完成。
人们也离不开语言,可以说没有语言就没有人类社会。
人类的自然语言也在发展变化,人们总结出许多的规律,我们将这些规律运用到语言教学之中,使教学更加符合实际,更加有效。
这是人们对自然语言规律的研究,在此基础上出现了语言教学法,现在应用的还只是一小部分,而且,目前还没有普及化,还不是每个学校都能普及的。
但随着时间的推移,它必将普及。
计算机作为人类科学文化发展的一个标志,已经深入到人类生活的各个角落,深入到生产和科研等领域,并且逐渐走向了社会的各个层面。
然而,如果有一天,计算机不再被当作某种工具,而真正成为人类的一种思维工具,计算机语言也就将成为一种有血有肉的社会语言,以后人们讲话也就将不再是那么困难。
从此,人们不仅可以像今天这样把语言看作是一门科学,而且,还可以像数学那样将语言视作人类智慧的结晶。
这种改变是革命性的,是人类历史上划时代的事件。
语言学家和语言学爱好者正是因为有了这种客观精神,所以才坚持走语言研究的道路,因为这条路可以给他们带来希望。
即使是这种希望并非一定会成功,但至少它会使人们意识到人类文明的进步与伟大,同时,也使他们在探索过程中感到幸福,感到充实。
语言学家们的每一次发现,语言学上的每一点进步,都会促使他们感受到真正的快乐。
每一项科研成果都会带来社会的进步和文明的提高,这种科研和探索本身是幸福的。
语言模型发展综述

语⾔模型发展综述语⾔模型发展综述摘要语⾔模型(language model)是⾃然语⾔处理中⾮常基础且重要的问题。
本⽂⾸先介绍了语⾔模型的定义及其应⽤场景,接着说明了语⾔模型的发展历史,本⽂将语⾔模型分为统计语⾔模型和神经⽹络语⾔模型两个⼤阶段,对各个阶段中出现的语⾔模型的特点、数学原理、对之前模型的改进,以及存在的缺点进⾏了详细的说明。
最后,本⽂对⽬前先进的⼤规模预训练语⾔模型进⾏了评价,指出了其存在的根本性问题,并对语⾔模型的未来做出了展望。
问题定义语⾔模型是定义在单词序列上的概率模型。
通过将⼀个句⼦或者⼀段⽂字视作单词序列,可以运⽤概率论,统计学,信息论,机器学习等⽅法对语⾔进⾏建模,从⽽实现对单词序列的概率进⾏计算。
⼀般来说,概率更⼤的单词序列意味着其在语⾔交流中出现的可能性更⼤,也即其可能更加符合语⾔习惯和会话逻辑。
例如将原始句⼦"美联储主席本伯南克昨天告诉媒体7000亿美元的救助资⾦将借给上百家银⾏,保险公司和汽车公司。
"调整语序变为"本伯南克美联储主席昨天7000亿美元的救助资⾦告诉媒体将借给银⾏,保险公司和汽车公司上百家。
"其可读性就下降了很多,出现在⽇常对话中的概率就下降了。
⽽倘如进⼀步将其打乱为⼀个完全不通顺的句⼦"联主美储席本伯诉南将借天的救克告媒咋助资⾦70元亿00美给上百败百家银保⾏,汽车险公司公司和。
"则其概率会进⼀步下降。
[1]语⾔模型可以应⽤于分词,搜索引擎,输⼊法,机器翻译等任务中。
例如,在分词时,我们可以认为其本质上就是求得⼀种分割⽅式,使得分词后得到的单词序列的语⾔模型概率最⼤化;搜索引擎和输⼊法通过应⽤语⾔模型预估⽤户要输⼊的单词,从⽽提⾼⽤户的使⽤体验;机器翻译任务可以通过语⾔模型来检查翻译后的句⼦的通顺程度,从中选最优秀的翻译结果等。
总⽽⾔之,语⾔模型是⾃然语⾔处理中⾮常重要的⼀块基⽯,其发展历史也象征了整个⾃然语⾔处理学科的发展历史,值得我们的深⼊研究和思考。
神经语言程序学(NLP)概况

神经语言程序学(NLP)概况神经语言程序学(Natural Language Processing, NLP)是人工智能领域中的一个重要分支,旨在使计算机能够理解、处理和生成自然语言。
NLP的目标是建立能够与人类进行自然对话的智能系统,使计算机能够像人类一样理解和使用语言。
NLP的发展历史可以追溯到20世纪50年代,当时研究人员开始尝试使用计算机处理自然语言。
然而,由于自然语言的复杂性和多义性,NLP的发展一直面临着巨大的挑战。
直到20世纪80年代,随着神经网络的兴起,NLP取得了一些重要的突破。
神经网络是一种模拟人脑神经元之间相互连接的数学模型,它可以通过学习和训练来提取和理解语言中的特征。
神经网络在NLP中的应用主要包括语言模型、词向量表示、句法分析和机器翻译等方面。
在语言模型方面,神经网络可以通过学习大量的语料库数据来预测下一个单词或句子的概率分布,从而实现自动语言生成。
通过训练神经网络模型,可以使计算机能够生成具有语法正确性和语义连贯性的自然语言文本。
词向量表示是NLP中的另一个重要研究方向。
传统的词袋模型将每个单词表示为一个离散的符号,无法捕捉到单词之间的语义关系。
而神经网络可以将每个单词表示为一个连续的向量,使得相似含义的单词在向量空间中距离较近,从而更好地捕捉到单词的语义信息。
句法分析是NLP中的一个重要任务,旨在分析句子的结构和语法关系。
传统的句法分析方法主要基于规则和规则库,但由于语法规则的复杂性和多样性,传统方法往往难以处理复杂的句子结构。
而基于神经网络的句法分析方法可以通过学习大量的句子数据来自动学习句子的结构和语法关系,从而实现更准确和高效的句法分析。
机器翻译是NLP中的一个重要应用领域,旨在将一种语言的文本自动翻译成另一种语言。
传统的机器翻译方法主要基于规则和统计模型,但由于语言的复杂性和多义性,传统方法往往难以处理复杂的语言现象。
而基于神经网络的机器翻译方法可以通过学习大量的平行语料数据来自动学习语言之间的对应关系,从而实现更准确和流畅的翻译效果。
计算语言学(全套课件114P)

计算语言学的发展简史
• 1950 - 1960年代 Warren Weaver(1949) Turing Test(1950)The first MTs(1954) • 1960 - 1970年代 ALPAC(1964-1966) • 1970 - 1990年代 Searle’s Chinese Room(1980) The first PC version of MTs(early 1980s) • 1990 - 至今 MT is available on the Web(1994)
主要的技术和方法基于知识的方法17上下文无关文法的扩充hpsg文法headdrivenphrasestructuregrammar对文法增加复杂特征主要的技术和方法基于知识的方法18上下文无关文法的扩充hpsg主要的技术和方法基于知识的方法19上下文无关文法的扩充hpsg主要的运算合一运算1检查特征属性是否兼容2如果兼容那么将两个负责特征集的信息合并主要的技术和方法基于知识的方法20上下文无关文法的扩充hpsg主要的技术和方法基于知识的方法21树邻接文法初始树i树
6
思考 • 人用来交际的“语言”具有什么样的性质? 这些性质又是如何影响交际过程的? • 人用来交际的“语言”跟机器可以“理解” 的语言有什么样的关系? • 人是如何运用“语言”进行交际的? • 人运用语言进行交际的过程是否可以描述 为一个机械的过程? • 什么叫做“理解”一种语言?
7
机器语言 vs自然语言
我是四川大学的老师。
27
主要的技术和方法 – 基于知识的方法(7) • 汉语句子切分存在的问题 交集型歧义 AB和BC都是词典中的词,如果待切分字串 中包含ABC,则可能切分成AB和C,以及A 和BC。如 网球场 组合型歧义 AB和A,B都是词典中的词,如果待切分字 串中包含AB,则可能切分为AB以及A和B。 如 个人
语言学模型

语言学模型语言学模型(Language Model)是自然语言处理中非常重要的一个概念,它可以帮助计算机理解和处理自然语言。
本文将分步骤讲解什么是语言学模型,它的作用以及如何构建语言学模型。
一、什么是语言学模型?语言学模型是一种数学模型,它能够预测一个句子或是一段文本的出现概率。
在语音识别、机器翻译、自动摘要、问答系统等自然语言处理任务中,语言学模型都发挥着至关重要的作用。
二、语言学模型的作用1.语音识别在语音识别中,使用语言学模型可以帮助判断识别结果是否正确。
比如说,一个语音识别系统在听到“我爱你”这句话时,还有可能把它误识别成“我爱牛”。
但是如果加入语言学模型,根据普遍的语法规则,“我爱牛”这种说法出现的概率要比“我爱你”要小很多,因此语音识别引擎就能够排除这种错误的结果。
2.机器翻译在机器翻译中,语言学模型可以帮助计算机正确地翻译原文。
在翻译过程中,一个单词的含义往往是根据上下文来确定的。
而语言学模型可以帮助计算机确定正确的上下文环境,从而得出准确的翻译结果。
3.自动摘要在文章自动摘要中,使用语言学模型可以帮助计算机快速地找到文章的主要内容。
语言学模型可以帮助计算机识别出哪些句子更具有重要性,从而提取出文章的主要内容,并生成摘要。
4.问答系统在问答系统中,语言学模型可以帮助计算机理解自然语言问题,并给出准确的答案。
通过对大量的问题进行训练,语言学模型可以学习到问题和答案之间的联系,从而回答各种问题。
三、如何构建语言学模型?构建一个好的语言学模型需要考虑很多因素。
通常,我们需要收集大量的文本数据,并且对这些数据进行语言学分析和处理,从而得到一个完整的语言学模型。
具体步骤如下:1.数据收集首先,我们需要收集大量的文本数据,比如论文、新闻、小说、网页等。
数据的来源越广泛,建立的语言学模型就越准确。
2.语言学处理在收集足够的数据之后,需要进行一些语言学处理工作。
这些工作包括分词、词性标注、语法分析等。
第六讲 计算语言学

• 1898年,德国学者F.W.Kaeding统计了德语 词汇的在文本中的出现频率,编制了世界上 一部频率词典《德语频率词典》。 • 1904年,波兰语言学家Baudouin De Courtenay指出,语言学家不仅应当掌握初 等数学,而且还要掌握高等数学。他表示坚 信,语言学将日益接近精密科学,并将根据 数学的模式,更多地扩展量的概念,发展新 的演绎思想的方法。
• • • •
4、计算语言学的进一步发展 音字转换:语音识别、拼音输入 自动文摘:自动给出一篇或多篇文章的摘要 信息检索:在海量的信息准确找到你所需要的信 息 • 信息过滤:信息过滤是大规模内容处理的另一种 典型应用。它是对陆续到达的信息进行过滤操作, 将符合用户需求的信息保留,将不符合用户需求 的信息过滤掉。通常可分为不良信息过滤和个性 化信息过滤:不良信息过滤一般指过滤掉暴力反 动色情等信息;个性化信息过滤类似于信息检索, 帮助用户返回感兴趣的东西。
语言学
计算机 计算语言学
数学
•计算语言学(Computational
Linguistics)指的是这样一门学科,它通过建立 形式化的数学模型, 来分析、处理自然语言,
/
/并在计算机上用程序来实现分析和处理的过程, /从而达到以机器来模拟人的部分乃利用计算计研究和 处理自然语言的学科。
语言学自己的准备: • 1、《圣经· 创世纪》中“巴比塔”的传说。
《旧约·创世纪》第11章讲述了“通天塔”的故事。 很久很久以前,天下的人都居住在一个叫做古巴比伦 的地方,那时候人们都使用同一种语言。后来,古巴 比伦人计划修建一座塔,塔顶要高耸入云,直达天庭, 以显示人们的团结和力量。塔越建越高,惊动了天庭 的耶和华。他想,现在天下的人都是一个民族,都说 一种语言,他们团结一致,什么奇迹都可以创造,那 神还怎么去统治人类?于是上帝便决定要惩罚惩罚人 类。他施魔法变乱了人们的口音,使他们无法沟通, 高塔因此无法继续建造下去。最后,上帝还把人类驱 散到地球的各个角落。
自然语言处理中的语言模型算法

自然语言处理中的语言模型算法自然语言处理(Natural Language Processing, NLP)是一项基于人工智能和计算语言学的技术,旨在让计算机理解、分析和生成自然语言。
而语言模型(Language Modeling)则是NLP中的一项核心技术,它可以对自然语言进行概率建模,并用于自动语音识别、机器翻译、自动文摘、对话系统等领域。
语言模型通常是基于一定的统计规则和机器学习算法来构建的。
其中,最为经典的语言模型算法包括n-gram模型、神经网络模型和BERT模型,下面就分别介绍这三种模型。
一、n-gram模型在NLP中,n-gram(n元语法)经常被用于对自然语言进行建模。
在一个由单词组成的句子中,n-gram模型就是指由n个相邻的单词构成的序列。
比如,一个3-gram模型就是由3个相邻的单词构成的序列,如“这是没有”。
n-gram模型的核心思想就是根据历史信息来预测下一个单词。
它通过统计文本中各个n元序列出现的频率,从而得到不同序列的概率分布。
在生成一段新的文本时,模型会根据已知的历史信息,选择概率最大的下一个单词作为预测结果。
n-gram模型具有简单、易于实现的优点。
但也存在一些问题,比如: 1)语义信息不足:n-gram模型是基于局部的语言统计规则,往往无法捕捉到整个句子的全局上下文信息; 2)数据稀疏问题:由于单词组合的种类过于庞大,n-gram模型在处理长文本时容易出现数据稀疏问题。
二、神经网络模型神经网络模型利用深度学习技术,通过多层神经网络对自然语言进行建模。
与传统的n-gram模型不同,神经网络模型可以捕捉到复杂的语言规律和语义信息,从而在自然语言处理的各个任务上表现出色。
对于语言模型问题,神经网络模型采用了RNN(Recurrent Neural Network)和LSTM(Long Short-Term Memory)等序列模型来完成。
其中LSTM模型通过引入门控机制,能够有效学习长文本中的信息。
nlu模型原理

nlu模型原理自然语言理解(Natural Language Understanding, NLU)是人工智能领域中的一个重要研究方向,其目标是使计算机能够理解和处理自然语言。
NLU模型是实现自然语言理解的关键技术之一。
本文将介绍NLU模型的原理和应用。
NLU模型的原理基于深度学习和自然语言处理技术。
它通常包含以下几个关键组件:词嵌入、编码器、解码器和意图识别。
词嵌入是将单词映射到高维向量空间的技术。
通过学习语料库中的上下文信息,词嵌入能够捕捉单词之间的语义关系。
常见的词嵌入模型有Word2Vec和GloVe等。
接下来是编码器,它将输入的自然语言文本转换为固定长度的向量表示。
编码器通常采用循环神经网络(RNN)或者Transformer模型。
循环神经网络通过逐个处理输入序列中的每个单词,并利用记忆单元来捕捉上下文信息。
而Transformer模型则通过自注意力机制来实现并行处理,能够更好地捕捉全局上下文信息。
解码器是将编码器输出的向量表示转换为人类可理解的形式。
解码器通常包括生成式模型和分类模型。
生成式模型通过逐个生成单词来构建自然语言文本,常见的方法有循环神经网络和转换器模型。
分类模型则将输入的向量表示映射到预定义的意图集合,通过预测最可能的意图来实现分类。
意图识别是NLU模型中的重要任务之一,它可以将用户的自然语言输入转化为机器可理解的形式。
意图识别通常采用分类模型,通过训练大量的标注数据,使模型能够识别出用户输入的意图。
常见的方法有支持向量机(SVM)、逻辑回归和深度神经网络等。
NLU模型在实际应用中有着广泛的应用。
例如,在智能客服系统中,NLU模型可以将用户的问题转化为机器可以理解的形式,并根据用户的意图提供相应的回答。
在智能助手中,NLU模型可以理解用户的指令,并根据指令执行相应的操作。
此外,NLU模型还可以应用于情感分析、机器翻译、智能搜索等领域。
然而,NLU模型仍然面临一些挑战。
首先,不同的语言和文化背景之间存在差异,如何进行跨语言和跨文化的自然语言理解仍然是一个难题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Model
2019/11/19
王小捷 智能科学与技术中心
北京邮电大学
绪论
1
大纲
• 引言 • 词表示 • Neural Probabilistic Language Model
(NPLM) • 总结
引言
•
N-gram语言模型中: P(w1T )
• 问题2
– 没有考虑词的相似性
• The cat is walking in the bedroom的训练样本对 A dog was running in a room的句子概率无贡献
– 没有相同的bigram
• 更细节:p(is/cat)和p(is/dog)无关
– cat 和 dog无关,所以两个概率无关,需分别找,因此, 在某些语料中,这两个值可能差别很大
w1
C ( w1 )
…
w2
C(w2 )
…
w|V |
C (w|V | )
|V | m维矩阵
…
• 2.神经模型
– 模型目标:训练一个映射 g 来建模n元语言模型, 即
g(C(xt ), C(xt1),.., C(xtn1);) P(C(xt ) | C(xt1),.., C(xtn1))
• 总参数个数
– |V|* (1+mn+h)+h*(1+ (n-1)m)
• 模型计算:对每一个输入的n元串
– 前向计算
• 隐层输入为:y=b+W*C(x)+Utanh(d+HC(x))
• 隐层输出为:
P(xt | xt1,...,wtn1)
e yxt e yxi
i
• 其中:C(x)是词x的向量表示
• A Neural Probabilistic Language Model,JMLR,2003
– M&H 2007,2008
• log-bilinear language (LBL) model
– Mikolov 2010,2013
• Recurrent neural network based language model
softmax
…
…
输出层|V|个神经元
…
C( … xtn1)
C xt n 1
C(xt … n2 ) … C(xt…1)
C xt n2
C xt 1
神经映射g
隐层h个神经元
词表式层 (t-1)×m个神经元
模型f
词表映射C
词层 :t-1个词
• 整体模型的训练目标中把C也纳入,则为极
大化:
L 1
T
T
log g(C(xt ),C(xt1),..,C(xtn1);)
t 1
1 T
T
log
t 1
f (xt , xt1,..,xt ; n1 C,)
• 加上正则化项,则为:
L
1 T
T t 1
log
f (xt , xt1,..,
xt ; n1 C,) R(C,)
– 基于分布式表示的语言模型
p(w)|w1, w2,…wn) <==p(c(w)|c(w1),c(w2),…c(wn))
• NPLM获得的distributed表示从其获得表示时利 用的信息来看,是distributional类的方法,利 用上下文词来表示目标词
• 为何叫distributed: 与1个位置1个词(local)相对 应
One-hot
distributional
distributed 从distributional基于 SVD等降维
每一个维度的含义 一个词 一个词 不明 不明
利用什么信息 词本身 词的上下文 词的上下文 词的上下文
• 后面专门将词表示时再说,本处词表示是为了 引导出神经语言模型
• NPLM
– Bengio 2001,2003模型
…
…
输出层|V|个神经元
神经映射g
…
隐层h个神经元
…
……
…
词表式层 (t-1)×m个神经元
深度网络
• 合并词表映射与神经网络模型-2
给定C时有 : P(C(xt ) | C(xtn1),..,C(xt1)) P(xt | xtn1,..,xt1)
第i个神经元输出 P(xt wi | xtn1,..., xt1)
softmax
…
…
输出层|V|个神经元
虚线是从输入层到
输出层的直接连接
…
隐层h个神经元
…
C( xtn1)
……
C( xtn2 )
…
C ( xt1)
输入层 (n-1)×m个神经元
• 合并词表映射与神经网络模型-1
第i个神经元输出 P(xt wi | xtn1,..., xt1)
softmax
• fine
• 无论是one-hot 还是distributional 维度都很 高,词表维度,每一个维度表示一个词,
– one-hot :该词本身 – distributional :该词上下文中的词
• 高维的问题:维数灾难
• 降维
– 直接基于one-hot 或distributional 的降维方法很 多SVD分解等,后续LDA模型时再提
化了
• 词表示
– 符号表示
• cat、dog、table…
– 分布表示:一个词用一个多维向量表示
• One-hot:向量维数=词表大小
– (1,0,0,….), (0,1,0,……)…
• Distributional :向量维数=词表大小
– 布尔式、频率式
• Distributional 词表示
• 参数集: (b,W,C,U, d, H)
– 反向随机梯度下降
log P(xt | xt1,...,wtn1)
• 为学习率
• 不在输入窗口中的Байду номын сангаас向量值不需要调整
• 混合模型
– 神经网络模型+插值trigram
• 算法的并行执行
•…
• 实验语料
训练语料规模
• 模型结构=1+2融合
– 1.词表映射
• 目标:对词表V 中的词(w1,…wi ,.. w|V|) 得到其m维向 量表示
• 实现方式
– 查表映射C:将任意词映射为一个m维向量
– 或者说是一个2层的神经网络(输入1个节点,输出m个节点)
C(x)
x
…
– 对于V中所有词:将V中第i词wi映射为C(wi),简记为C(i)
– 则p(C(is)/C(cat)) 与 p(C(is)/C(dog)) 比 p(C(is)/C(cat)) 与 p(C(is)/C(he)) 更接近
• NPLM
– 利用m个神经元的状态组合(x1,x2,…,xm)编码词
• 例如:
– Cat C(cat)=(x11,x12,…,x1m) – Dog C(dog)=(x21,x22,…,x2m) – Table C(dog)=(x31,x32,…,x3m) –…
Brown语料 1,181,041词的前800000词
AP新闻 13,994,528词
发展语料规模(模型选择、 随后的200,000词 权重衰减、early stopping)
测试语料规模
其余181,041词
963,138词 963,071词
语料实际含的不同词 使用的词,即|V|
47,578(含标点、大小写不同、 148,721词 分割段落与文本的标记符)
• 其中 为神经网络参数
– 训练的目标是使得该n元模型对于测试词序列
x即1,极x2,小…化xT(:xi均PP为(C(词x1),表...,CV(x中T ))的 P词(C)(具x1),有...,C最(xT小))PT1 P值。
T
1
( P(C(xt ) | C(xt1),..,C(xtn1))) T
• 可否直接获得低维表示?
• 词表示
– 符号表示
• cat、dog、table…
– 分布表示:一个词用一个多维向量表示
• One-hot:向量维数=词表大小
– (1,0,0,….), (0,1,0,……)…
• Distributional :向量维数=词表大小
– 布尔式、频率式 (下页)
• Distributed :向量维数=指定大小
– 即极大化
t 1
L 1
T
T
log P(C(xt ) | C(xt1),..,C(xtn1))
t 1
1 T
T
log g(C(xt ),C(xt1),..,C(xtn1);)
t 1
• 神经网络结构
第i个神经元输出为 P(C(xt ) C(wi ) | C(xtn1),.., C(xt1))
• interpolated or smoothed trigram model (Jelinek and Mercer, 1980)
– state-of-the-art n-gram models
• back-off n-gram models with theModified Kneser-Ney algorithm (Kneser and Ney, 1995, Chen and Goodman., 1999)
• 模型参数
– 各层
• 词层n-1个节点,n元语法的n-1个历史词 • 词表示层(n-1)×m个节点,每个词用m维向量表示 • 隐层h个节点,阈值为d,h维 • 输出层|V|个节点,阈值为b,|V|维
