C++递归函数汉诺塔原理一步步详解
证明并推导汉诺塔(河内之塔)问题公式

证明并推导汉诺塔(河内之塔)问题公式本⽂链接: 第⼀次遇到汉诺塔问题时我瞬间就被搞蒙了之后果断扔下不管了,今天再次遇到这个问题被搞蒙again ,在⽹上搜了好久愣是没让我找到证明汉诺塔问题可解和推导公式过程的资料,于是花了⼏个⼩时(谁让咱不太聪明呢,嘿嘿),最后终于想通了,记录下来希望对像我⼀样不聪明的⼈有所帮助。
证明可解汉诺塔问题:我⽤的是数学归纳法,假设圆盘的个数为n ,圆盘编号从上到下依次为1,2,3,4,……n ,证明如下①当 n = 1 时,从 A 移动到 C 显然能够完成,设需要移动的次数是a 。
②当 n = 2 时,由①可知从把 1 号盘⼦从 A 移动到 B 能够完成(B 和 C 是等效的)此时移动次数为a 。
之后把2号盘⼦移动到C 上⾯此时移动次数为a + 1。
这时把1号盘⼦从B 移动到C 和①是等价的,移动后总的移动次数是a = a + 1 + a 。
③当n = 3时,由②可知移动成下图的效果是可以实现的,此时移动的次数是a2,接着把3号盘⼦移动到C 上⾯此时移动的次数是a + 1,这时把1和2号盘⼦移动到C 上⾯(移动过程中3号盘⼦始终不会动)和②等效的,移动完成之后如下移动的总次数是a = a + 1 + a ④当n=4时,由③可知移动成下图的效果是可以实现的,此时移动的次数是a 把4号盘⼦从A 移动到C此时移动的次数是a + 1接下来把123号盘⼦从B 移动到C 的过程⼜和③等效了移动之后如下移动的总次数是a = a + 1 + a 假设当n= k 时,从A 移动到C 是可以实现的,那么当n=k+1时,可以移动到A 上⾯只剩k+1号盘⼦,B 上⾯依次是1,2,3,.....,k 号盘字,此时移动次数是a把k+1号盘⼦移动到C 上⾯,这时移动次数是a + 1接下来和n=k 时移动过程等效,移动完成后移动总次数是a = a + 1+ a可以得知移动k+1个盘⼦需要的次数与移动k 个盘⼦的次数之间的关系是:a = a + 1+ a = 2a + 1111 2 1 12 3 2 233 4 3 3k k k+1k kk+1 k k k所以a + 1 = 2*(a + 1)【这是个等⽐数列⾼中学过的】即a + 1 = (a1 +1)* 2 = 2 因此a = 2 - 1⾄此,证明完毕。
【C语言程序设计】汉诺塔问题,用C语言实现汉诺塔!
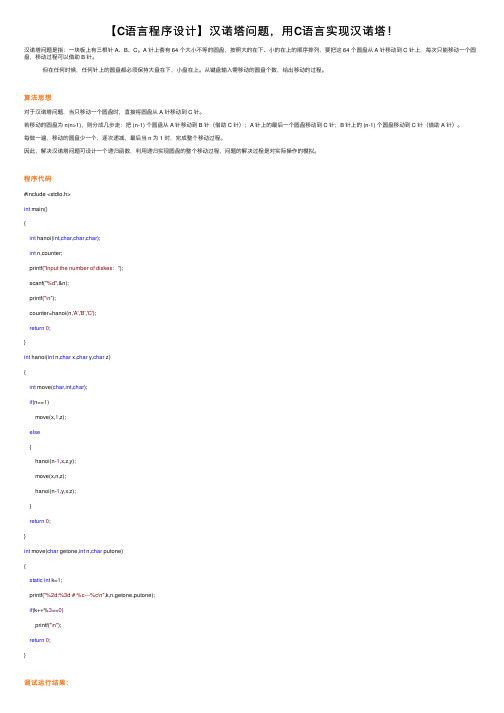
【C语⾔程序设计】汉诺塔问题,⽤C语⾔实现汉诺塔!汉诺塔问题是指:⼀块板上有三根针 A、B、C。
A 针上套有 64 个⼤⼩不等的圆盘,按照⼤的在下、⼩的在上的顺序排列,要把这 64 个圆盘从 A 针移动到 C 针上,每次只能移动⼀个圆盘,移动过程可以借助 B 针。
但在任何时候,任何针上的圆盘都必须保持⼤盘在下,⼩盘在上。
从键盘输⼊需移动的圆盘个数,给出移动的过程。
算法思想对于汉诺塔问题,当只移动⼀个圆盘时,直接将圆盘从 A 针移动到 C 针。
若移动的圆盘为 n(n>1),则分成⼏步⾛:把 (n-1) 个圆盘从 A 针移动到 B 针(借助 C 针);A 针上的最后⼀个圆盘移动到 C 针;B 针上的 (n-1) 个圆盘移动到 C 针(借助 A 针)。
每做⼀遍,移动的圆盘少⼀个,逐次递减,最后当 n 为 1 时,完成整个移动过程。
因此,解决汉诺塔问题可设计⼀个递归函数,利⽤递归实现圆盘的整个移动过程,问题的解决过程是对实际操作的模拟。
程序代码#include <stdio.h>int main(){int hanoi(int,char,char,char);int n,counter;printf("Input the number of diskes:");scanf("%d",&n);printf("\n");counter=hanoi(n,'A','B','C');return0;}int hanoi(int n,char x,char y,char z){int move(char,int,char);if(n==1)move(x,1,z);else{hanoi(n-1,x,z,y);move(x,n,z);hanoi(n-1,y,x,z);}return0;}int move(char getone,int n,char putone){static int k=1;printf("%2d:%3d # %c---%c\n",k,n,getone,putone);if(k++%3==0)printf("\n");return0;}调试运⾏结果:当移动圆盘个数为 3 时,具体移动步骤如下所⽰:Input the number of diskes:31: 1 # A---C2: 2 # A---B3: 1 # C---B4: 3 # A---C5: 1 # B---A6: 2 # B---C7: 1 # A---C总结:本实例中定义的 hanoi() 函数是⼀个递归函数,它有四个形参"n""x""y""z"。
汉诺塔原理

汉诺塔原理
汉诺塔原理是一种经典的数学问题,它涉及到如何将一堆盘子从一个柱子上移动到另一个柱子上,而且要保证每个盘子的顺序不变。
这个问题看似简单,但实际上却涉及到很多数学原理和技巧。
我们需要了解汉诺塔问题的基本规则。
假设有三个柱子,分别为A、
B、C,其中A柱子上有n个盘子,从上到下依次编号为1、2、
3、……、n。
我们的目标是将这n个盘子从A柱子上移动到C柱子上,每次只能移动一个盘子,并且不能将大盘子放在小盘子上面。
接下来,我们可以通过递归的方式来解决汉诺塔问题。
具体来说,我们可以将问题分解为三个子问题:将n-1个盘子从A柱子上移动到B柱子上;将第n个盘子从A柱子上移动到C柱子上;将n-1个盘子从B柱子上移动到C柱子上。
这样,我们就可以通过递归的方式来解决汉诺塔问题。
汉诺塔原理不仅仅是一种数学问题,它还具有很多实际应用。
例如,在计算机科学中,汉诺塔问题被广泛应用于算法设计和数据结构的研究中。
此外,汉诺塔问题还可以用来解决其他问题,例如排序、搜索、图形处理等。
汉诺塔原理是一种非常有趣和有用的数学问题,它不仅可以帮助我们提高数学思维能力,还可以帮助我们解决实际问题。
如果你对数
学感兴趣,不妨尝试一下汉诺塔问题,相信你一定会有很多收获。
汉诺塔问题求解思路

汉诺塔问题求解思路汉诺塔问题是⼀个经典的问题。
汉诺塔(Hanoi Tower),⼜称河内塔,源于印度⼀个古⽼传说。
⼤梵天创造世界的时候做了三根⾦刚⽯柱⼦,在⼀根柱⼦上从下往上按照⼤⼩顺序摞着64⽚黄⾦圆盘。
⼤梵天命令婆罗门把圆盘从下⾯开始按⼤⼩顺序重新摆放在另⼀根柱⼦上。
并且规定,任何时候,在⼩圆盘上都不能放⼤圆盘,且在三根柱⼦之间⼀次只能移动⼀个圆盘。
问应该如何操作?分析如果是初次接触类似的问题,乍看之下肯定会感觉⽆从下⼿。
要把64个圆盘从a柱⼦移动到c柱⼦上,第⼀步应该怎么做?虽然可以肯定,第⼀步唯⼀的选择是移动a最上⾯的那个圆盘,但是应该将其移到b还是c呢?很难确定。
因为接下来的第⼆步、第三步……直到最后⼀步,看起来都是很难确定的。
能⽴即确定的是最后⼀步:最后⼀步的盘⼦肯定也是a最上⾯那个圆盘,并且是由a或b移动到c——此前已经将63个圆盘移动到了c上。
也许你会说,管他呢,先随便试着移动⼀下好了。
如果你这么做,你会发现,接下来你会⾯临越来越多类似的选择,对每⼀个选择都“试”⼀下的话,你会偏离正确的道路越来越远,直到你发现你接下来⽆法进⾏为⽌。
如果将这个问题的盘⼦数量减为10个或更少,就不会有太⼤的问题了。
但盘⼦数量为64的话,你⼀共需要移动约1800亿亿步(18,446,744,073,709,551,615),才能最终完成整个过程。
这是⼀个天⽂数字,没有⼈能够在有⽣之年通过⼿动的⽅式来完成它。
即使借助于计算机,假设计算机每秒能够移动100万步,那么约需要18万亿秒,即58万年。
将计算机的速度再提⾼1000倍,即每秒10亿步,也需要584年才能够完成。
注:在我的笔记本电脑上,每秒⼤约能够移动6~8百万步。
虽然64个盘⼦超出了⼈⼒和现代计算机的能⼒,但⾄少对于计算机来说,这不是⼀个⽆法完成的任务,因为与我们⼈类不同,计算机的能⼒在不断提⾼。
分解问题⼀股脑地考虑每⼀步如何移动很困难,我们可以换个思路。
汉诺塔问题数学解法

汉诺塔问题数学解法
一、建立递归模型
汉诺塔问题是一个经典的递归问题,可以通过建立递归模型来求解。
递归模型的基本思想是将问题分解为更小的子问题,然后通过对子问题的求解来得到原问题的解。
二、定义变量
在汉诺塔问题中,我们可以定义以下变量:
n:表示盘子的数量;
A、B、C:表示三个柱子,其中A柱子是起始柱子,B 柱子是辅助柱子,C柱子是目标柱子;
m:表示当前需要移动的盘子数量。
三、递归关系
汉诺塔问题的递归关系可以表示为:
将m个盘子从A移动到C,需要先将m-1个盘子从A移动到B,然后将最后一个盘子从A移动到C,最后将m-1个盘子从B移动到C。
将m个盘子从A移动到B,需要先将m-1个盘子从A移动到C,然后将最后一个盘子从A移动到B,最后将m-1个盘子从C移动到B。
将m个盘子从B移动到C,需要先将m-1个盘子从B移动到A,然后将最后一个盘子从B移动到C,最后将m-1个盘子从A移动到C。
四、寻找规律
通过观察递归关系,我们可以发现以下规律:
每次移动都需要经过三个柱子,即起始柱子、辅助柱子和目标柱子;
每次移动都需要将n-1个盘子从起始柱子移动到辅助柱子,然后将最后一个盘子从起始柱子移动到目标柱子,最后将n-1个盘子从辅助柱子移动到目标柱子;
每次移动都需要将n-1个盘子从起始柱子移动到辅助柱子,然后将最后一个盘子从起始柱子移动到目标柱子,最后将n-1个盘子从辅助柱子移动到目标柱子。
五、验证解决方案
通过以上规律,我们可以得到汉诺塔问题的解法。
为了验证解法的正确性,我们可以使用递归函数来实现解法,并使用测试数据来验证解法的正确性。
用C语言解决汉诺塔问题的方法及过程分析

( )将 原 问题 转化 成 新 问题 后 ,能使 求 解算法 的规模减 小. 2
( )递归 有一 个 明显 的 出 口,或称 为递 归的边 界 ,而边 界 问题 的解是显 而 易见 的或 已知 的. 3
3 用 C语 言 编 程
C语 言是 一种 在 国内外 广泛 流行 的高 级程 序设 计语 言 ,它 的语 言 功能 丰富 ,表达 力 强 ,使 用 灵 活 ,应
言 中 ,用 递归 法编 写 条件
2 1 递 归程序 定义 .
《 C程 序设 计 》 数 据结 构 》等教科 书 中 ,都对 递 归 程 序 给 出 了基本 相 同的定 义 ,归纳 如下 :在调 用 、《
一
个 函数 的过 程 中 ,又直接 或 间接地 调用 了该 函数本 身 ,称 为 函数 的递 归调 用 ,使用 了递 归调用 函数 的程
第 3期
{ a ( 一 , o e t r e t ) hn n1 n , h e , wo ;
mo e ( ne, t e ); v o hr e
h n ( 一 ,t a n 1 wo,o e h e ) ) n ,t r e ;)
ma n ( i )
{n i tn;
prn f ( “ e s nt rt mbe ike ” it Pla e e e he nu rofd s s: );
维普资讯
维普资讯
2 0 年 6月 06
河 北 北 方 学 院学 报 ( 自然 科 学 版 )
第 3 期
上操 作 的实质 是把移 动 n个 盘子 的 问题转 化 为移 动 n 一1个盘 .那 一 、三 步 如何解 决 ?事 实 上 ,上述 方法 设盘 子数 为 n ,n可 为任 意数 ,该 法 同样 适 用于 移动 n 1 盘. 因此 ,依 据 上 法 ,可解 决 n 一 个 一1个 盘子从 A杆 移 到 B杆 ( 一 步)或 从 B杆 移到 C杆 ( 第 第三 步 ) 问题 .现 在 ,问题 由移 动 n个 盘 子 的操 作转 化 为 移动 n 一2个 盘子 的操作 .依 据该 原 理 ,层 层递 推 ,即可将 原 问题 转化 为 解 决移 动 n 、n … …3 、 一2 一3 、2 直 到移动 1 盘 的操 作 ,而移 动一 个 盘 的操 作 是可 以 直接 完成 的. 至 此 ,我 们 的任 务 算作 是 真 正完 成 了. 个 而这 种 由繁化 简 ,用简单 的问题 和 已知 的操 作 运算来 解决 复杂 问题 的方 法 ,就是 递归法 . 在计算 机设计 语
汉诺塔递归算法及详解

汉诺塔递归算法及详解
汉诺塔(Tower of Hanoi)是一个经典的数学谜题和递归问题。
它由三个塔杆和一些不同大小的圆盘组成,开始时圆盘按从大到小的顺序叠放在一个塔杆上。
目标是将所有圆盘从起始塔杆移动到目标塔杆上,同时遵守以下规则:
1. 一次只能移动一个圆盘。
2. 任何时刻,大的圆盘不能放在小的圆盘上面。
递归算法是解决汉诺塔问题的常用方法。
其基本思想是将问题分解为较小规模的子问题,然后通过递归地解决子问题来解决原问题。
以下是汉诺塔递归算法的详解:
1. 如果只有一个圆盘需要移动,则直接将圆盘从起始塔杆移动到目标塔杆上。
2. 如果有多个圆盘需要移动,则按以下步骤进行操作:
- 将除最下方的圆盘以外的上方圆盘从起始塔杆移动到辅助塔杆上。
这可以通过递归调用解决较小规模的子问题来实现,即将上方圆盘从起始塔杆移动到目标塔杆上(目标塔杆作为新的辅助塔杆)。
- 然后将最下方的圆盘从起始塔杆直接移动到目标塔杆上。
- 最后,将辅助塔杆上的所有圆盘移动到目标塔杆上,这可以通过递归调用解决较小规模的子问题来实现,即将上方圆盘从辅助塔杆移动到起始塔杆上(起始塔杆作为新的目标塔杆)。
通过递归地应用以上步骤,就可以实现将所有圆盘从起始塔杆移动到目标塔杆上的操作。
数据结构求解汉诺塔问题的递归算法

数据结构求解汉诺塔问题的递归算法汉诺塔问题是一个经典的数学问题,它可以通过递归算法来求解。
在这个问题中,我们需要将一堆盘子从一个柱子移动到另一个柱子,同时遵守以下规则:一次只能移动一个盘子,大盘子不能放在小盘子上面。
为了解决这个问题,我们可以使用数据结构中的栈来模拟柱子的堆叠。
我们可以将每个柱子表示为一个栈,每个盘子表示为一个元素。
初始时,所有的盘子都在第一个柱子上,我们需要将它们移动到第三个柱子上。
下面是求解汉诺塔问题的递归算法的伪代码:```1. 定义一个函数hanoi,接受参数n、起始柱子A、辅助柱子B、目标柱子C2. 如果n等于1,则直接将盘子从A移动到C3. 否则,将n-1个盘子从A移动到B,借助C作为辅助柱子4. 将第n个盘子从A移动到C5. 将n-1个盘子从B移动到C,借助A作为辅助柱子```接下来,我们来详细解释一下这个算法。
首先,我们定义了一个函数hanoi,它接受四个参数:n表示盘子的数量,起始柱子A、辅助柱子B和目标柱子C。
在函数内部,我们首先判断如果n等于1,那么我们直接将盘子从A移动到C即可。
这是递归算法的终止条件。
如果n大于1,我们需要将n-1个盘子从A移动到B,借助C作为辅助柱子。
这一步是通过递归调用hanoi函数来实现的。
在递归调用中,我们将n-1作为新的盘子数量,A作为起始柱子,B作为目标柱子,C作为辅助柱子。
接下来,我们将第n个盘子从A移动到C。
这一步是直接操作的,不需要递归调用。
最后,我们需要将n-1个盘子从B移动到C,借助A作为辅助柱子。
同样地,我们通过递归调用hanoi函数来实现这一步。
在递归调用中,我们将n-1作为新的盘子数量,B作为起始柱子,C作为目标柱子,A作为辅助柱子。
通过这样的递归调用,我们可以将所有的盘子从起始柱子A移动到目标柱子C,同时遵守汉诺塔问题的规则。
总结起来,数据结构中的栈可以很好地模拟汉诺塔问题中的柱子堆叠,而递归算法则可以很好地解决这个问题。
c语言 汉诺塔问题 递归 步骤

c语言汉诺塔问题递归步骤汉诺塔问题是一个经典的递归问题,涉及将一组圆盘从一个塔移到另一个塔,其中有三个塔:源塔、目标塔和辅助塔。
汉诺塔问题的规则如下:1. 只能一次移动一个圆盘。
2. 大盘不能放在小盘上面。
递归解法的基本思路是将问题分解为更小的子问题。
以下是C语言中的递归解法步骤:```c#include <stdio.h>// 汉诺塔函数,n是圆盘数量,source是源塔,target是目标塔,auxiliary是辅助塔void hanoi(int n, char source, char target, char auxiliary) {// 基本情况:只有一个圆盘时直接移动到目标塔if (n == 1) {printf("Move disk 1 from %c to %c\n", source, target);return;}// 递归步骤// 1. 将n-1 个圆盘从源塔移动到辅助塔hanoi(n - 1, source, auxiliary, target);// 2. 将第n 个圆盘从源塔移动到目标塔printf("Move disk %d from %c to %c\n", n, source, target);// 3. 将n-1 个圆盘从辅助塔移动到目标塔hanoi(n - 1, auxiliary, target, source);}int main() {int n;printf("Enter the number of disks: ");scanf("%d", &n);// 调用汉诺塔函数hanoi(n, 'A', 'C', 'B');return 0;}```在这个例子中,`hanoi` 函数是递归的核心,它将问题分解为三个步骤:将n-1 个圆盘从源塔移动到辅助塔,将第n 个圆盘从源塔移动到目标塔,最后将n-1 个圆盘从辅助塔移动到目标塔。
c++汉诺塔问题递归算法

c++汉诺塔问题递归算法汉诺塔问题是经典的递归问题,它可以帮助我们理解和掌握递归算法的思想。
在C++中,我们可以通过递归来解决汉诺塔问题。
汉诺塔问题的描述如下:有三根柱子A、B、C,A柱子上有n 个盘子,盘子的大小不一,大的在下,小的在上。
现在要将A 柱子上的盘子移动到C柱子上,并且每次只能移动一个盘子,并且大的盘子不能放在小的盘子上面。
要求通过借助柱子B来实现移动。
下面我们先给出解决汉诺塔问题的递归代码:```cpp#include <iostream>void hanoi(int n, char A, char B, char C) {if (n == 1) {std::cout << "Move disk 1 from " << A << " to " << C << std::endl;return;}hanoi(n - 1, A, C, B);std::cout << "Move disk " << n << " from " << A << " to " << C << std::endl;hanoi(n - 1, B, A, C);}int main() {int n = 3; // 盘子的个数hanoi(n, 'A', 'B', 'C');return 0;}```上面的代码使用了递归的思想来解决汉诺塔问题。
函数`hanoi()`接受四个参数,n表示盘子的个数,A、B、C表示三根柱子的名称。
当n等于1时,表示只有一个盘子需要移动,直接将它从A柱子移动到C柱子即可。
当n大于1时,我们可以把问题简化为两个步骤:将n-1个盘子从A柱子通过借助C柱子移动到B柱子,然后将最后一个盘子从A柱子移动到C柱子,最后将n-1个盘子从B柱子通过借助A柱子移动到C 柱子。
c课程设计汉诺塔

c 课程设计汉诺塔一、教学目标本课程的教学目标是让学生掌握汉诺塔的基本概念、原理和解决方法,培养学生的逻辑思维能力和问题解决能力。
具体来说,知识目标包括了解汉诺塔的历史背景、基本规则和递归算法;技能目标包括能够运用递归算法解决汉诺塔问题,并进行简单的优化;情感态度价值观目标包括培养学生的团队合作意识、挑战自我和探索未知的勇气。
二、教学内容教学内容主要包括汉诺塔的基本概念、递归算法的原理和应用。
首先,介绍汉诺塔的历史背景和基本规则,让学生了解汉诺塔的起源和演变。
然后,讲解递归算法的原理,引导学生理解递归的思维方式和实现方法。
最后,通过实例分析,让学生学会如何运用递归算法解决汉诺塔问题,并进行简单的优化。
三、教学方法为了激发学生的学习兴趣和主动性,本课程将采用多种教学方法。
首先,运用讲授法,清晰地传达汉诺塔的基本概念和递归算法的原理。
其次,通过讨论法,让学生在课堂上相互交流、分享心得,培养学生的团队合作意识。
此外,结合案例分析法,让学生通过分析实际问题,提高问题解决能力。
最后,运用实验法,让学生动手实践,加深对汉诺塔解决方法的理解。
四、教学资源为了支持教学内容和教学方法的实施,我们将选择和准备适当的教学资源。
教材方面,将选用权威、实用的汉诺塔教材,确保学生掌握准确的知识。
参考书方面,将推荐一些经典的汉诺塔相关书籍,拓展学生的知识视野。
多媒体资料方面,将收集一些关于汉诺塔的动画、视频等资料,丰富学生的学习体验。
实验设备方面,将准备相应的设备,让学生进行实践活动,提高操作技能。
五、教学评估本课程的评估方式包括平时表现、作业和考试三个部分。
平时表现主要评估学生在课堂上的参与程度、提问回答和团队协作等情况,占总评的30%。
作业分为练习题和项目任务,主要评估学生对知识的理解和应用能力,占总评的40%。
考试为闭卷笔试,涵盖课程全部内容,主要评估学生的知识掌握和问题解决能力,占总评的30%。
评估方式客观、公正,全面反映学生的学习成果。
汉诺塔动画演示课件

汉诺塔的规则和玩法
01
02
03
04
05
规则:汉诺塔的规则是 要求将所有的圆盘从起 始柱子移到目标柱子上, 移动过程中必须遵循以 下三个原 则
1. 每次只能移动一个圆 盘;
2. 圆盘只能放在比它大 3. 圆盘只能放在空柱子
的圆盘上;
上。
玩法:汉诺塔的玩法是 从起始柱子开始,按照 规则将圆盘逐个移到目 标柱子上。在移动过程 中,需要不断地将圆盘 进行分解和组合,以找 到最优的移动方案。
03
人工智能与机器学习
汉诺塔问题可以作为人工智能和机器学习领域的基准测试案例,用于评
估和优化算法和模型的性能。
在物理学中的应用
力学与运动学
汉诺塔问题涉及到物体的运动和相互作用,可以用来解释和演示力学和运动学的基本原理,如牛顿运 动定律、动量守恒定律等。
光学与视觉
汉诺塔问题中的不同颜色和形状的盘子可以用来模拟光线和颜色的传播和反射,可以用来解释和演示 光学和视觉的基本原理。
效地降低时间复杂度,提高求解效率。
优化二:使用遗传算法求解
总结词
遗传算法是一种基于生物进化原理的优化算法,可以用于求解组合优化问题。
详细描述
遗传算法是一种基于生物进化原理的优化算法,它通过模拟生物进化过程中的基因选择、交叉和变异等过程来寻 找最优解。在汉诺塔问题中,我们可以使用遗传算法来求解。首先,我们定义一个表示汉诺塔问题的染色体,然 后通过模拟选择、交叉和变异等过程来不断优化染色体的适应度,最终得到最优解。
02
汉诺塔动画演示
演示一:移动三个盘子
总结词:通过演示,展示汉诺塔问题最简单的情形,即只 有三个盘子需要移动。
详细描述
1. 起始状态:三个盘子叠在一起,放在第一个柱子上。
C语言递归调用实例——汉诺塔问题动画实现(附完整代码)

二、程序框架
古人云,不谋全局者,不足谋一域。同样,在编写代码之前,我们必 须得有个大体的思路和整体上的把握。不能一上来就稀里糊涂地乱敲一通。 当然,这里我也只能仅仅谈自己的个人想法,不一定就是最优的解决方案, 还希望能和大家一起相互交流,共同进步。整个程序的框架,我把它分为 动画效果和核心算法两大部分。我首先实现的是动画效果部分,等能够实 现盘子的随意移动后,我才开始研究核心算法的实现。这样一来,在核心 算法部分,我们正好可以利用前面的动画效果来直观地反映出我们的思路, 有助于代码的调试和缩短程序的开发周期。为了尽量减少废话,我们可以 用一张图来进行表示:
图 1-1 移动第一个圆盘..................................................................................................................... 4 图 1-2 移动第二个圆盘...................................................................................................................... 5 图 1-3 移动最后一个圆盘................................................................................................................. 6
能移动一个圆盘,且圆盘在放到棒上时,大的不能放在小的上面。中间的一根
棒作为辅助移动用。” 事实上,对此曾经有人作过分析,按这个规则,众僧耗尽毕生精力也
不可能完成圆盘的移动,因为需要移动圆盘的次数是一个天文数字 18446744073709551615(64 个圆盘需要移动的次数为 2 的 64 次方)。假设 1us 进行一次移动,也需要约一百万年的时间,使用计算机也很难解决 64
汉诺(Hanoi)塔问题(C#版)

汉诺(Hanoi)塔问题(C#版)
⼀个只能⽤递归解决的数学问题;问题描述:古代有⼀个梵塔,塔内有3个座,A、B、C,开始时A座有64个盘,盘⼦⼤⼩不等,⼤的在上,⼩的在下。
有⼀个⽼和尚想把这64个盘⼦从A座移到C座(如图所⽰),但每次只允许移动⼀个盘,且在移动过程中在3个座上始终保持⼤盘在下,⼩盘在上。
在移动地程中可以⾏⽤B座,要求编程序打印出移动的步骤。
逆向推理:1.假如⼀个和尚能把上⾯63个盘⼦先搬到B座,第⼆个和尚再把最⼤的那个移到C,第三个和尚再把63个盘⼦移到C座;⾄此整个⼯作就完成的。
2.问题是怎么才能把63个盘⼦移到B座,按照同样的⽅法,先把62个盘⼦选移到C座
,再把第63个盘⼦移到B座,最后再将62个盘⼦移到B座。
3……如此类推;
4.从上⾯分析可以看出:只有等后⾯那个和尚搬完盘⼦,前⾯的和尚才能够去完成任。
让我们来栈的数据结构:数据的处理只在⼀端处理,且是先进后出。
所以⽤递归的⽅法去处理是正确的。
(汉诺塔图)
汉诺塔问题解决⽅案
如果你发现有什么错误之处,请指出!谢谢了。
汉诺塔演示

汉诺塔演示.txt你不能让所有人满意,因为不是所有的人都是人成功人士是—在牛B的路上,一路勃起你以为我会眼睁睁看着你去送死吗?我会闭上眼睛的摘要:该文对经典的“汉诺塔”问题进行了详细的分析,并用C语言实现。
通过问题的具体实现,使学习者了解问题的全过程,推广到一般。
关键词:汉诺塔;递归;C语言Algorithm Analysis and C Realization of Hanio IssueBAI Hui-bo1,GAO Rui-ping2(1.Qinhuangdao Branch of Daqing Petroleum Institute, Qinhuangdao 066004, China;2.Hebei Normal University of Science and Technology, Qinhuangdao 06600, China)Abstract: This text carries on detailed analysis about classical Hanio issue and provides realization of algorithm in C.Through concrete realization of the problem,can make learners observe the whole course which solves this issue and Extend to the general.Key words: hanio; recursive; the C programming language1 问题描述汉诺塔是一个经典的数学问题,其具体描述如下:有三根相邻的塔子,标号为A,B,C,A塔子上从下到上按金字塔状叠放着n个不同大小的圆盘,现在把所有盘子借助于A,B,C三个塔子一个一个移动到塔子C上,并且每次移动在同一根塔子上都不能出现大盘子在小盘子上方.根据问题描述得到以下规则:1)圆盘必须一个一个的移动;2)大的圆盘必须在小圆盘的下方或单一圆盘;3)满足规则2)的序列可以出现在A,B,C任意一根塔子上。
递归及递归算法图解

递归问题的提出
第一步:将问题简化。 – 假设A杆上只有2个圆盘,即汉诺塔有2层,n=2。
A
B
C
递归问题的提出
A
B
C
对于一个有 n(n>1)个圆盘的汉诺塔,将n个圆盘分 为两部分:上面的 n-1 个圆盘和最下面的n号圆盘。将 “上面的n-1个圆盘”看成一个整体。
– 将 n-1个盘子从一根木桩移到另一根木桩上
1
当n 1时
n ! n (n 1)! 当n 1时
long int Fact(int n)
{ long int x;
if (n > 1)
{ x = Fact(n-1);
/*递归调用*/
return n*x; }
else return 1;
/*递归基础*/
}
Fact(n) 开始 传进的参数n N n>1
两种不同的递归函数--递归与迭代
21
(2)递归和迭代有什么差别?
递归和迭代(递推)
迭代(递推):可以自递归基础开始,由前向后依次计算或直
接计算;
递归:可以自递归基础开始,由前向后依次计算或直接计算;
但有些,只能由后向前代入,直到递归基础,寻找一条路径, 然后再由前向后计算。
递归包含了递推(迭代),但递推(迭代)不能覆盖递归。
递归的概念 (5)小结
战德臣 教授
组合 抽象
构造 递归
用递归 定义
用递归 构造
递归计 算/执行
递归 基础
递归 步骤
两种不同的递归函数
递归
迭代
两种不同的递归函数--递归与迭代
20
(1)两种不同的递归函数?
递归和递推:比较下面两个示例
c++汉诺塔问题递归算法

c++汉诺塔问题递归算法汉诺塔问题是一个经典的数学问题,也是计算机科学中常用的递归问题。
该问题的描述是:有三个柱子(A、B、C),A柱子上放着从小到大依次排列的n个圆盘,目标是将这些圆盘从A柱子移动到C柱子,每次只能移动一个圆盘,并且在移动过程中,大的圆盘不能放在小的圆盘上。
要解决这个问题,可以使用递归算法来实现。
递归是一种解决问题的方法,通过将问题简化为规模更小的子问题来解决。
对于汉诺塔问题,我们可以将其简化为将n-1个圆盘从A柱子移动到B柱子,然后将最大的圆盘从A柱子移动到C柱子,最后再将n-1个圆盘从B柱子移动到C柱子。
下面是一个使用C++编写的递归算法解决汉诺塔问题的示例代码:```cpp#include<iostream>using namespace std;void hanoi(int n, char a, char b, char c) {if (n == 1) {cout << "Move disk 1 from " << a << " to " << c << endl;return;}hanoi(n - 1, a, c, b);cout << "Move disk " << n << " from " << a << " to " << c << endl;hanoi(n - 1, b, a, c);}int main() {int n;cout << "Enter the number of disks: ";cin >> n;cout << "The moves are:" << endl;hanoi(n, 'A', 'B', 'C');return 0;}```在这段代码中,hanoi函数用于解决汉诺塔问题。
汉诺塔通项公式推导

汉诺塔通项公式推导汉诺塔通项公式证明:
设三个塔分别为A、B、C。
并设当A塔初始有n个盘⼦的时候,转移到C塔需要⽤T(n)步。
⾸先,有如下规律:
T(0) = 0 (当没有盘⼦的时候当然为0)
T(1) = 1
T(2) = 3
T(3) = 7
.....
T(n) = T(n - 1) + 1 + T(n - 1) = 2* T(n - 1) + 1
为什么T(n) = 2 * T(n -1 )+ 1 呢?
很容易可以想到,当n = n - 1 的时候,
(1)从A塔将所有盘⼦移动到C塔需要的步数是 T(n - 1)。
(2)如果从A到C移动的步数是T(n - 1),那么从A移动到B也需要T(n - 1)
那么当n = n 时:
(1)⾸先将A塔的全部盘⼦移动到B塔,需要T(n -1 )步。
(2)将A塔的最后⼀个盘⼦移动到C塔,需要1步
(3)将B塔的全部盘⼦移动到C塔,需要T( n - 1 )步。
最终结果需要 2* T(n - 1)+ 1 步。
所以T(n) = 2 * T( n - 1 ) + 1
那么通项公式是什么呢?该怎么证明呢?
很简单~
令等式左右两端同时加1,有:
T(n) + 1 = 2 * (T(n - 1) + 1)
设T(n) + 1 = S(n)
那么:S(n) = 2 *S(n - 1)
并且当n = 1 的时候,S(1) = 1;
那么S(n) = 2 ^ n
所以: T(n) + 1 = S(n) = 2 ^ n
即 T(n) = 2 ^ n - 1
证毕。
汉诺塔递归算法

汉诺塔递归算法
1. 简介
汉诺塔(Hanoi Tower)是一种经典的数学问题,它由法国数学家Edouard Lucas于1883年引入,并以法国一个寺庙的名字命名。
汉诺塔问题是一个经典的递归问题,它可以通过递归算法来解决。
2. 问题描述
汉诺塔问题的问法如下:
有三根柱子A、B、C,初始时柱子A上有若干个大小不同的盘子,按照从小到大的顺序从上往下叠放。
现在需要将这些盘子从柱子A移动到柱子C,移动过程中需要满足以下条件:
1.每次只能移动一个盘子;
2.每根柱子上的盘子都必须保持原有的从小到大的顺序。
问:如何才能将这些盘子从柱子A移动到柱子C,并且满足以上条件?
3. 解决方法
汉诺塔问题的解决方法之一是使用递归算法。
递归算法是一种通过函数自身调用来解决问题的方法。
对于汉诺塔问题,可以通过以下的递归算法来解决:
步骤
1.如果只有一个盘子需要移动,直接将盘子从柱子A移动到柱子C即可;
2.如果有多个盘子需要移动,将其分成三个步骤:
1.将n-1个盘子从柱子A移动到柱子B;
2.将最大的盘子从柱子A移动到柱子C;
3.将n-1个盘子从柱子B移动到柱子C。
递归实现
以下是使用递归实现汉诺塔问题的Python代码:
```python def hanoi(n, A, B, C): if n == 1: print(f。
基于TurboC的“汉诺塔”问题CAI课件

程序 设计 的盘 子规模 n可 以选择 从 1到 1 , 0 并且可 以选 择 人 工控 制 演 示 和 系 统 自动 运行 演
对 C语 言程序 设计 这 门课 程 认识 不清 楚 , 习 目 学
的不 明确 , 不知 道学这 门课 程究竟 能做 什么. 导 这 致 了大 多数学 生对 学 习 这 门课 程 不 感 兴趣 . 以 所
・
图 1 6 个 盘 子 的 原 始 图
) 男 , 南镇 雄 人 , , 云 副教 授 , 士 , 要从 事 软 件 工 程 研 究 硕 主
4 ・ 2
付 明柏
基 于 T r oC 的“ 诺 塔” u b 汉 问题 C 课 件 AI
第 5期
移动 到 C座 上 , 图 2所示 . 如 为了更好 地理 解 递 归 过 程 , 界 面 的上 方 显 在
示, 自动 演示 时要输 人演示 速度 ( 毫秒 ) 尽可能慢 ,
一
点, 以便能看 清楚 其移 动过 程.
用 Tub ro C编写 实 现 汉 诺 塔 问题 的计 算 机 辅 助 教学 ( AI课 件 , 仅 能让 学 生 很 好 地理 解 汉 诺 C ) 不 塔 问题 , 还有 助 于 其 学 习 C语 言 的兴 趣 , 高 学 提
第3 2卷
第 5期
昭通 师范 高 等专 科 学 校 学报
J u n I fZh o o gTe c e ’ l g o r a a t n a h rSCol e o e
21 00年 1 0月
OC . 0 0 t2 1
Vo. 2No 5 I3 .
●计算 机应 用技术
所 无 法 做 到 的.
教 学难点之 一 , 得上是 教 师讲不 清楚 , 算 学生难 于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,move(n,a ,b,c)表示讲 n 个盘子从 A 塔(借助于 B 塔)移到 C 塔。 所以 move(3,a ,b,c)表示讲 3 个盘子从 A 塔(借助于 B 塔)移到 C 塔。 2,move(2,a,c,b):即讲 2 个盘子从 A 塔(借助于 C 塔)移到 B 塔。目 的是让 A 塔上第 3 个盘子(最下面的盘子)上无其他盘子。 3,将底下的第 3 个盘子从 A 塔移到 C 塔。 4,move(2,b,a,c):即将 2 个叠放在 B 塔上的盘子(借助于 A 塔)移到 C 塔。 printf("step%d:%c-->%c\n",step,a,c)这个代码就是打印ove(n,chara, charb, charc)函数了,这里请注 意 char a 只是一个字符变量,就是一个只能赋值字符的变量,它现在 对应的是 b,同理 charb 对应 a,charc 对应 a,这样下去就一目了然 了
有 3 个塔,每个都可以对方若干个盘子。开始时,所有盘子均在塔 A 上,应且,盘从上到 下,按直径增大的次序放置(如图所示)。设计一个移动盘子的程序,使得塔 A 上的所有盘 子借助于塔 B 移到塔 C 上,但有两个限制条件:一是一次只能搬到一个盘子,而是任何时 候不能大盘子放在比它小的盘子的上面。
程序如下:
#include<stdio.h>——————不解释 int step=0;—————————赋初值 move(int n,char a,char b,char c);——函数声明 main()——————————不解释 {
int n;——————————不解释 scanf("%d",&n);——————不解释 printf("n=%d\n",n);—————不解释 move(n,'a','b','c');——————调用函数 move return 0;—————————不解释 } move(int n,char a,char b,char c)————不解释 {
if(n>0) {
move(n-1,a,c,b); step++; printf("step%d:%c-->%c\n",step,a,c); move(n-1,b,a,c); } } 现在开始详解: 现在开始解释 move 在 main 函数的具体发挥。 设 n=3 只有 3 个盘子 move(int 3,char a,char b,char c) ————n=3 { if(3>0)————n 变为 3 { move(2,a,c,b);————n 减 1 变为 2 //////step++; printf("step%d:%c-->%c\n",step,a,c);\\\\\注意斜杠里是个整体, 不是分开讨论的。 move(n-1,b,a,c); }
