材料力学习题解答弯曲应力
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
材料力学专项习题练习弯曲应力

材料⼒学专项习题练习弯曲应⼒弯曲应⼒1. 圆形截⾯简⽀梁A 、B 套成,A 、B 层间不计摩擦,材料的弹性模量2B A E E =。
求在外⼒偶矩e M 作⽤下,A 、B 中最⼤正应⼒的⽐值maxminA B σσ有4个答案: (A)16; (B)14; (C)18; (D)110。
答:B2. 矩形截⾯纯弯梁,材料的抗拉弹性模量t E ⼤于材料的抗压弹性模量c E ,则正应⼒在截⾯上的分布图有以下4种答案:答:C3. 将厚度为2 mm 的钢板尺与⼀曲⾯密实接触,已知测得钢尺点A 处的应变为11000-,则该曲⾯在点A 处的曲率半径为 mm 。
答:999 mm4. 边长为a 的正⽅形截⾯梁,按图⽰两种不同形式放置,在相同弯矩作⽤下,两者最⼤正应⼒之⽐max a max b ()()σσ= 。
答:2/15. ⼀⼯字截⾯梁,截⾯尺⼨如图,, 10h b b t ==。
试证明,此梁上,下翼缘承担的弯矩约为截⾯上总弯矩的88%。
证:412, (d ) 1 8203B A z z zMy M Mt M y yb y I I I σ==?=?? 4690z I t =, 41411 82088%3690M t M t =??≈B t A M =+=为翼缘弯矩(a)6. 直径20 mm d =的圆截⾯钢梁受⼒如图,已知弹性模量200 GPa E =, 200 mm a =,欲将其中段AB 弯成 m ρ=12的圆弧,试求所需载荷,并计算最⼤弯曲正应⼒。
解:1M EIρ= ⽽M Fa = 4840.78510 m , 0.654 kN 64d EI I F aπρ-==?==33max 80.654100.220102220.78510M d Fad I I σ--====??7. 钢筋横截⾯积为A ,密度为ρ,放在刚性平⾯上,⼀端加⼒F ,提起钢筋离开地⾯长度/3l 。
试问F解:截⾯C 曲率为零2(/3)0, 326C Fl gA l gAlM F ρρ=-==8. 矩形截⾯钢条长l ,总重为F ,放在刚性⽔平⾯上,在钢条A 端作⽤/3F 向上的拉⼒时,试求钢条内最⼤正应⼒。
材料力学习题解答(弯曲变形)

Pl 2
梁的挠曲线方程和转角方程是
D1 = 0
D2
=
−
1 24
Pl 3
⎧⎪⎪⎨⎪⎪⎩ 2EEIvI2'v1'==P2P2xx2212−−PPlxlx2 1+
3 16
Pl
2
⎧⎪⎪⎨⎪⎪⎩ 2EEIvI2v1==P6P6xx2313−−P2Pl2lxx2212+
3 16
Pl 2 x2
−
1 24
Pl 3
(6) 最大挠度和最大转角发生在自由端 令x2=l:
⋅a
=
−
qa4 3EI
上海理工大学 力学教研室
7
θB
= θ B(1)
+ θB(2)
+ θ B(3)
=
−
qa3 4EI
fB
=
f B (1)
+
fB(2)
+
f B ( 3)
= − 5qa4 24EI
7.10. 桥式起重机的最大载荷为 P=20 kN。起重机大梁为 32a 工字钢,E=210 GPa,l=8.7 m。 规定[f]=l/500,试校核大梁刚度。
⎪ ⎪⎩
M
2
(
x2
)
=
−
q
(l
− x2 2
∈
[
l 2
,
l
]
(2) 挠曲线近似微分方程
⎧ ⎪⎪
EIv1"
=
M1( x1)
=
− 3ql 2 8
+
ql 2
x1
⎨
⎪ ⎪⎩
EIv2"
=
M2(x2 )
17材料力学习题解答弯曲应力
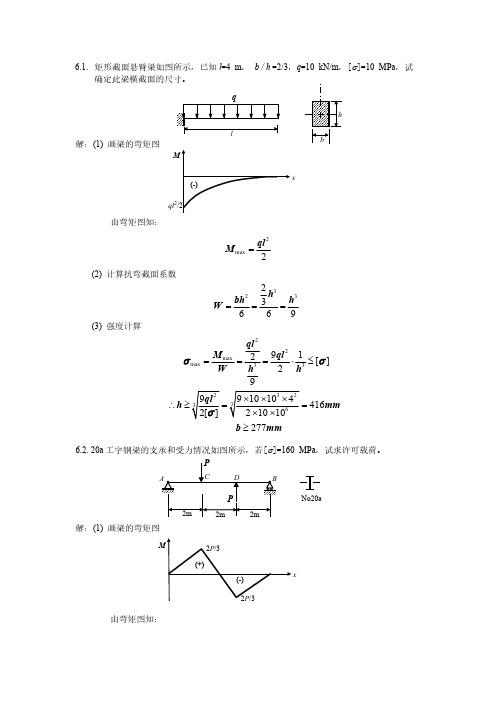
q
h
解:(1) 画梁的弯矩图
ql2/2
由弯矩图知:
(2) 计算抗弯截面系数
(3) 强度计算
M
h
l
x (-)
max
3
9ql 2 2[ ]
W
M max W
308 1.568 106
2
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
材料力学习题册答案-第5章 弯曲应力5页word文档

第 五 章 弯 曲 应 力一、是非判断题1、设某段梁承受正弯矩的作用,则靠近顶面和靠近底面的纵向纤维分别是伸长的和缩短的。
(×)2、中性轴是梁的横截面与中性层的交线。
梁发生平面弯曲时,其横截面绕中性轴旋转。
(√)3、 在非均质材料的等截面梁中,最大正应力maxσ不一定出现在maxM的截面上。
( × )4、等截面梁产生纯弯曲时,变形前后横截面保持为平面,且其形状、大小均保持不变。
5、梁产生纯弯曲时,过梁内任一点的任一截面上的剪应力都等于零。
( × )6、控制梁弯曲强度的主要因素是最大弯矩值。
( × )7、横力弯曲时,横截面上的最大切应力不一定发生在截面的中性轴上。
( √ )二、填空题1、应用公式y I Mz=σ时,必须满足的两个条件是 满足平面假设 和 线弹性 。
2、跨度较短的工字形截面梁,在横力弯曲条件下,危险点可能发生在 翼缘外边缘 、 翼缘腹板交接处 和 腹板中心 处。
3、 如图所示的矩形截面悬臂梁,其高为h 、宽为b 、长为l ,则在其中性层的水平剪力4、梁的三种截面形状和尺寸如图所示,则其抗弯截面系数分别为226161bH BH -、 H Bh BH 66132- 和 Hbh BH 66132- 。
)2、 如图所示的两铸铁梁,材料相同,承受相同的载荷F 。
则当F 增大时,破坏的情况是 ( C )。
A 同时破坏 ;B (a )梁先坏 ;C (b )梁先坏3、为了提高混凝土梁的抗拉强度,可在梁中配置钢筋。
若矩形截面梁的弯矩图如图所示,则梁内钢筋(图中虚线所示)配置最合理的是( D )x四、计算题1、长为l 的矩形截面梁,在自由端作用一集中力F ,已知m h 18.0=,m b 12.0=,m y 06.0=,m a 2=,kN F 1=,求C 截面上K 点的正应力。
解:MPa I y M Z C K1.21218.012.006.0210133=⨯⨯⨯⨯==σ2、⊥形截面铸铁悬臂梁,尺寸及载荷如图所示。
材料力学典型例题及解析 5.弯曲应力典型习题解析

9m q
4 ≤ [σ ]
A
1 πd 2
4
解得 q ≤ 1 π d 2 [σ ] = 1 × 20 ×10 −6 m 2 ×160 ×10 6 Pa = 22300 N/m = 22.3 kN/m
9m
9m
4、确定结构的许用载荷 取 AC 梁、BD 杆的许用 q 值中的小值,即为结构的许用载荷。
所以 [ q ] = 15.68 kN / m 。
切口,如图 a 所示。已知材料的许用应力 [σ ] = 100 MPa , (1) 计算切口许可的最大深度,并
画出切口处截面的应力分布图。(2) 如在杆的另一侧切出同样的切口,正应力有何变化?
F
y
(a)
38MPa
h=40mm
F
C'
M
F
CF F
F
100MPa
b=5mm (b)
(c)
(d)
题6图
解题分析:此题为偏心拉伸问题,可利用弯曲与拉伸组合变形的强度条件求出切口的允许深 度。若另一侧开同样深度切口,偏心拉伸问题变为轴向拉伸问题。 解:1、计算切口许可的最大深度
得 F B y = 12.75 kN
2、作弯矩图,确定危险截面
1
弯矩图如图 b 所示,峰值为 M C = 3.75kN ⋅ m 和 M B = − 4.5kN ⋅ m 。
B 截面的上边缘各点受拉,下边缘各点受压;C 截面的上边缘各点受压,下边缘各 点受拉。由于不能直观确定最大拉、压应力的位置,需要进一步计算。 3、计算 B、C 截面上的应力
设 A 处支反力为 F A y ,B 处支反力为 F B y ,均竖直向上。考虑梁 AD 的平衡,有
∑ M B = 0 , − F A y × 2 m − 4.5×103 N ×1m + 12×103 N ×1m = 0
材料力学习题及答案4-6

第四章弯曲应力判断图弯矩的值等于梁截面一侧所有外力的代数和。
()负弯矩说明该截面弯矩值很小,在设计时可以忽略不计。
()简支梁上向下的集中力对任意横截面均产生负弯矩。
()横截面两侧所有外力对该截面形心力矩的代数和就是该截面的弯矩值。
()梁的任一横截面上的弯矩在数值上等于该截面任一侧所有外力对该截面形心的力矩代数和。
()在计算指定截面的剪力时,左段梁向下的荷载产生负剪力。
()在计算指定截面的剪力时,右段梁向下的荷载产生正剪力。
()梁纯弯曲时中性轴一定通过截面的形心。
()简支梁上受一集中力偶作用,当集中力偶在不改变转向的条件下,在梁上任意移动时,弯矩图发生变化,剪力图不发生变化。
()图示梁弯矩图的B点是二次抛物线的顶点。
()图示梁段上集中力偶作用点两侧的弯矩直线一定平行。
()(M图)下列三种斜梁A截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁B截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁C截面的弯矩均相同。
()l/2l/2l/2l/2l/2l/2梁弯曲时的内力有剪力和弯矩,剪力的方向总是和横截面相切,而弯矩的作用面总是垂直于横截面。
()一端(或两端)向支座外伸出的简支梁叫做外伸梁。
()##√悬臂梁的一端固定,另一端为自由端。
()##√弯矩的作用面与梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
()##√弯曲时剪力对细长梁的强度影响很小,所以在一般工程计算中可忽略。
()##√图示,外伸梁BC段受力F作用而发生弯曲变形,AB段无外力而不产生弯曲变形()##×由于弯矩是垂直于横截面的内力的合力偶矩,所以弯矩必然在横截面上形成正应力。
()##√抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
()##×无论梁的截面形状如何,只要截面面积相等,则抗弯截面系数就相等。
()##×梁弯曲变形时,弯矩最大的截面一定是危险截面。
(修订)第9章 弯曲应力与弯曲变形-习题解答

第9章 弯曲应力与弯曲变形 习题解答题9 – 1 试计算下列各截面图形对z 轴的惯性矩I z (单位为mm )。
解:(a )mm 317400250500350200400250250500350≈⨯-⨯⨯⨯-⨯⨯=c y()()49323mm 107314002502003171240025050035025031712500350⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (b )mm 431550400800500375550400400800500≈⨯-⨯⨯⨯-⨯⨯=c y()()410323mm 1054615504003754311255040080050040043112800500⨯≈⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯-⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.I Z (c )()mm 3060202060506020102060=⨯+⨯⨯⨯+⨯⨯=c y()()46323mm103616020503012602020601030122060⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯+⎪⎪⎭⎫ ⎝⎛⨯⨯-+⨯=.Z I(a)(b) (c)题9-1图题9–2 悬臂梁受力及截面尺寸如图所示。
设q = 60kN/m ,F = 100kN 。
试求(1)梁1– 1截面上A 、B 两点的正应力。
(2)整个梁横截面上的最大正应力和最大切应力。
解:(1)求支反力kN 220100260=+⨯=A F (↑)m kN 32021001260⋅=⨯+⨯⨯=A M ( ) (2)画F S 、M 图(3)求1-1截面上A 、B 两点的正应力 m kN 1305016011001⋅=⨯⨯+⨯=.MF MA 点:MPa 254Pa 1025412150100550101306331=⨯≈⨯⨯⨯==...I y M zA t σB 点:MPa 162Pa 107816112150100*********331=⨯≈⨯⨯⨯==....I y M σzB c (4)求最大正应力和最大切应力M P a 853Pa 10385361501010320623max max =⨯≈⨯⨯==...W M σzM P a 22Pa 10221501010220232363max =⨯≈⨯⨯⋅=⋅=..A F τS 题9 - 3 简支梁受力如图所示。
材料力学习题解答弯曲应力
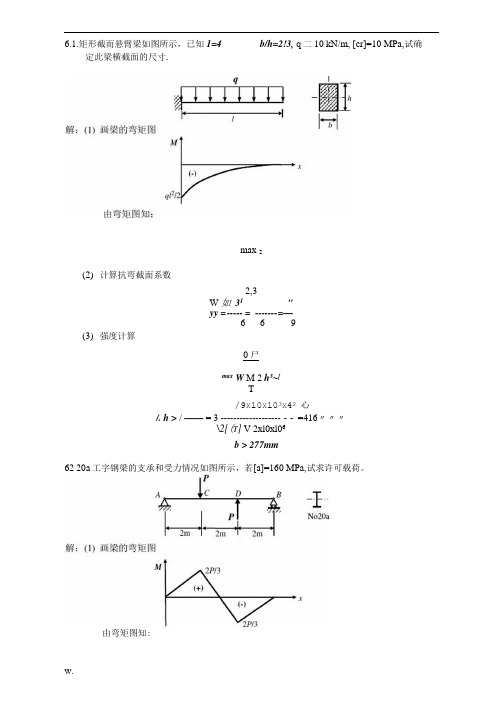
6.1.矩形截而悬臂梁如图所示,已知1=4 b/h=2!3, q二10 kN/m, [cr]=10 MPa,试确定此梁横截面的尺寸.max 2(2)计算抗弯截面系数2,3W 如31"yy = ----- = ------- =—6 6 9(3)强度计算0尸max W M 2 h3~[T/9X10X103X42心/. h > / —— = 3 ------------------- - - =416〃〃〃\2[(T] V 2xl0xl06b > 277mm62 20a工字钢梁的支承和受力情况如图所示,若[a]=160 MPa,试求许可载荷。
由弯矩图知:2P= = J_.pgEW W 3W.• A 哄=3x237xl0F60>d。
”= %.8 球2取许可载荷[P] = 57AN解:(1)画梁的弯矩图M c M c 32xl.34xl03=—=—Y = :— = 63.2MPaW c诚;. n x 0.06?"3TB截面:0.9xlO3 5z 4——;------------ -- = 62.1 MPa力以八d;、〃x0.06 〃 0.045、---- U ——r)------------ (1 —----- r-)32 矶32 0.064(3)轴内的最大正应力值(2)查表得抗弯截面系数(3)强度计算2P、=——W =237x10^7/1maxbfmax63.图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.由弯矩图知:可能危险截面是C和B截而(2)计算危险截而上的最大正应力值C截面:解:(1)画梁的弯矩图M t = 308M H(2)计算抗弯截面系数(3)强度计算 许用应力[(r] = ^- = — = 253MPa n 1.5强度校核308 inA1/rn r 】b” = —- = ------------------ I T = 1961"“ Y b maxW 1.568x1 Of压板强度足够。
材料力学习题册答案-第5章 弯曲应力

第 五 章 弯 曲 应 力一、是非判断题1、设某段梁承受正弯矩的作用,则靠近顶面和靠近底面的纵向纤维分别是伸长的和缩短的。
( × )2、中性轴是梁的横截面与中性层的交线。
梁发生平面弯曲时,其横截面绕中性轴旋转。
( √ )3、 在非均质材料的等截面梁中,最大正应力maxσ不一定出现在maxM的截面上。
( × )4、等截面梁产生纯弯曲时,变形前后横截面保持为平面,且其形状、大小均保持不变。
( √ )5、梁产生纯弯曲时,过梁内任一点的任一截面上的剪应力都等于零。
( × )6、控制梁弯曲强度的主要因素是最大弯矩值。
( × )7、横力弯曲时,横截面上的最大切应力不一定发生在截面的中性轴上。
( √ )二、填空题1、应用公式y I Mz=σ时,必须满足的两个条件是 满足平面假设 和 线弹性 。
2、跨度较短的工字形截面梁,在横力弯曲条件下,危险点可能发生在 翼缘外边缘 、 翼缘腹板交接处 和 腹板中心 处。
3、 如图所示的矩形截面悬臂梁,其高为h 、宽为b 、长为l ,则在其中性层的水平剪力=S FbhF23 。
4、梁的三种截面形状和尺寸如图所示,则其抗弯截面系数分别为226161bH BH -、 H Bh BH 66132- 和 Hbh BH 66132- 。
x三、选择题1、如图所示,铸铁梁有A,B,C和D四种截面形状可以供选取,根据正应力强度,采用( C )图的截面形状较合理。
2、如图所示的两铸铁梁,材料相同,承受相同的载荷F。
则当F增大时,破坏的情况是( C )。
A 同时破坏;B (a)梁先坏;C (b)梁先坏3、为了提高混凝土梁的抗拉强度,可在梁中配置钢筋。
若矩形截面梁的弯矩图如图所示,则梁内钢筋(图中虚线所示)配置最合理的是( D )A B C DA BDx四、计算题1、长为l 的矩形截面梁,在自由端作用一集中力F ,已知m h 18.0=,m b 12.0=,m y 06.0=,m a 2=,kN F 1=,求C 截面上K 点的正应力。
弯曲应力习题答案

弯曲应力习题答案在材料力学中,弯曲应力是结构分析中的一个重要概念,它涉及到梁或板在受到弯曲作用时内部产生的应力。
以下是一些弯曲应力习题的答案示例:习题一:简单梁的弯曲应力计算问题描述:一根长为 \( L \) 米,截面为矩形的梁,宽 \( b \) 米,高 \( h \) 米,材质为钢,弹性模量 \( E \) 为 \( 200 \) GPa。
梁的一端固定,另一端自由,中间受到一个集中力 \( P \) 的作用。
解答:1. 首先,确定梁的截面惯性矩 \( I \):\[ I = \frac{b \cdot h^3}{12} \]2. 根据梁的受力情况,计算梁的弯曲应力 \( \sigma \):\[ \sigma = \frac{M \cdot c}{I} \]其中 \( M \) 是弯矩,对于集中力 \( P \) 作用在梁的中点,弯矩 \( M \) 为 \( \frac{PL}{4} \)。
3. 将弯矩代入弯曲应力公式中:\[ \sigma = \frac{P \cdot L \cdot c}{4 \cdot I} \] 其中 \( c \) 是梁截面上距离中性轴的距离,对于矩形截面,\( c = \frac{h}{2} \)。
4. 将已知数值代入公式,计算出弯曲应力。
习题二:悬臂梁的弯曲应力分析问题描述:一根悬臂梁,长度 \( L \) 米,材料的弹性模量 \( E \) 为 \( 200 \) GPa,梁的一端固定,另一端受到一个向下的集中力 \( P \)。
解答:1. 悬臂梁在末端受到集中力作用时,最大弯矩 \( M \) 出现在梁的末端,其值为 \( P \cdot L \)。
2. 假设梁的截面为圆形,半径 \( r \),则截面惯性矩 \( I \) 为: \[ I = \frac{\pi r^4}{4} \]3. 计算弯曲应力 \( \sigma \):\[ \sigma = \frac{M}{I} = \frac{P \cdot L}{\frac{\pir^4}{4}} \]4. 将已知数值代入公式,计算出弯曲应力。
材料力学试题库精选题解精选题6_弯曲应力17页

弯曲应力1. 圆形截面简支梁A,B 套成,层间不计摩擦,材料的弹性模量E 严2E A 。
求在外力偶矩A/。
作用下,A,3中最大正应力的比值也有4个答案: (心;O(c)r 答:B2. 矩形截面纯弯梁,材料的抗 拉弹性模量耳大于材料的抗压 弹性模量瓦,则正应力在截面 上的分布图有以下4种答案:答:C3. 将厚度为2 mm 的钢板尺与一曲面密实接触,已 知测得钢尺点A 处的应变为-岛,则该曲面在点A 处的曲率半径为 ___________ mm ° 答:999 mm4. 边长为"的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比竺4= ________(bnux)b5•—工字截面梁,截面尺寸如图,h = b 」= 15。
的弯矩约为截面上总弯矩的88%o•工 My “ 2M 严彳 “t M/ 证: b = -j —, = —j — x J y( y^dy) = 1 820 x其中:积分限B = t + - , A = - 为翼缘弯矩2 26.直径d = 20 mm 的圆截面钢梁受力如图,已知弹性模量 E = 200 GPa , d = 200mm ,欲将其中段A3弯成 ° = 12 m 的圆弧,试求所需载荷,并计算最大弯曲北应力。
7. 钢筋横截面积为密度为° ,放在刚性平面上,一端加力提起钢筋离F2//3厂P(B)r试证明,此梁上,下翼缘承担 解:14而—第57页Ah/2h/2B开地面长度丄。
试问F应多大?3解:截面C曲率为零8.矩形截面钢条长/,总重为F,放在刚性水平面上,在钢条A端作用乂向上3 的拉力时,试求钢条内最大正应力。
解:在截面C处,有丄=^=0p EIAC段可视为受均布载荷§作用的简支梁9.图示组合梁山正方形的铝管和正方形钢杆套成,在两端用刚性平板牢固联接。
已知:钢和铝的弹性模量关系为£s=3£a;在纯弯曲时,应力在比例极限内。
材料力学典型例题及解析 5.弯曲应力典型习题解析

q
h1
h2
A
B
b l
题3图
解题分析:两板叠放在一起,在均布载荷 q 作用下,两梁一起变形,在任一截面上,两者弯 曲时接触面的曲率相等。小变形情况下,近似认为两者中性层的曲率相等。根据该条件,可 计算出各梁分别承担的弯矩。然后再分别计算两梁的最大应力。两板胶合在一起时,按一个 梁计算。 解:1、计算两板简单叠放在一起时的最大应力
= 0.5 m 2q ≤ σ Wz
解得 q ≤ W z [σ ] = 49 ×10−6 m 3 ×160 ×106 Pa = 15 680 N/m = 15.68 kN/m
0.5 m2
0.5 m2
3、BD 杆的强度条件
BD 杆横截面上各点拉伸正应力相同,强度条件为
σ
≤ [σ ] 或σ = F NBD =
F
Ay
=
3m 4
q
,
F
By
=
9m 4Leabharlann q2、梁的强度条件
画梁的弯矩图如图 b。显然,B 截面为危险截面。 M B = 0.5 m2 q ,查表知 10 号工 字钢 W z = 49 ×10−6 m 3 ,于是 B 截面上弯曲正应力强度条件为
[ ] [ ] σ m a x ≤ σ
或
σ ma x
=
M max Wz
=
I I
1 2
M
2
=( h1)3 h2
M
2
=
1M 8
2
梁中间截面弯矩为
M
=
M
1
+
M
2
=
1 ql 8
2
于是
M
1
=
1 72
材料力学专项习题练习弯曲应力解读

材料力学专项习题练习弯曲应力解读(C)弯曲应力1. 圆形截面简支梁A 、B 套成,A 、B 层间不计摩擦,材料的弹性模量2B A E E =。
求在外力偶矩e M 作用下,A 、B 中最大正应力的比值maxminA B σσ有4个答案: (A)16; (B)14; (C)18; (D)110。
答:B2. 矩形截面纯弯梁,材料的抗拉弹性模量t E 大于材料的抗压弹性模量c E ,则正应力在截面上的分布图有以下4种答案:答:C3. 将厚度为2 mm 的钢板尺与一曲面密实接触,已知测得钢尺点A 处的应变为11000-,则该曲面在点A 处的曲率半径为 mm 。
答:999 mm4. 边长为a 的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比max a max b ()()σσ= 。
答:2/15. 一工字截面梁,截面尺寸如图,, 10h b b t ==。
试证明,此梁上,下翼缘承担的弯矩约为截面上总弯矩的88%。
证:412, (d ) 1 8203B A z z zMy M Mt M y yb y I I I σ==?=?? 4690z I t=, 41411 82088%3690M t M t =??≈ 其中:积分限1 , 22h hB t A M =+=为翼缘弯矩(a)6. 直径20 mm d =的圆截面钢梁受力如图,已知弹性模量200 GPa E =, 200 mm a =,欲将其中段AB 弯成m ρ=12的圆弧,试求所需载荷,并计算最大弯曲正应力。
解:1M EIρ= 而M Fa = 4840.78510 m , 0.654 kN 64d EI I F aπρ-==?==33max 80.654100.220102220.78510M d Fad I I σ--====??7. 钢筋横截面积为A ,密度为ρ,放在刚性平面上,一端加力F ,提起钢筋离开地面长度/3l 。
试问F解:截面C 曲率为零2(/3)0, 326C Fl gA l gAlM F ρρ=-==8. 矩形截面钢条长l ,总重为F ,放在刚性水平面上,在钢条A 端作用/3F 向上的拉力时,试求钢条内最大正应力。
材料力学习题解答弯曲应力
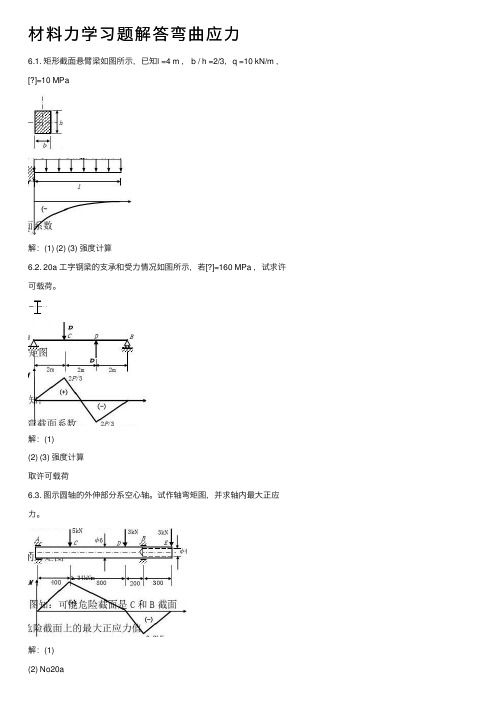
材料⼒学习题解答弯曲应⼒6.1. 矩形截⾯悬臂梁如图所⽰,已知l =4 m , b / h =2/3,q =10 kN/m ,[?]=10 MPa解:(1) (2) (3) 强度计算6.2. 20a ⼯字钢梁的⽀承和受⼒情况如图所⽰,若[?]=160 MPa ,试求许可载荷。
解:(1)(2) (3) 强度计算取许可载荷6.3. 图⽰圆轴的外伸部分系空⼼轴。
试作轴弯矩图,并求轴内最⼤正应⼒。
解:(1)(2) No20axxxC截⾯:B截⾯:(3) 轴内的最⼤正应⼒值6.5. 把直径d=1 m的钢丝绕在直径为2 m的卷筒上,设E=200 GPa,试计算钢丝中产⽣的最⼤正应⼒。
解:(1) 由钢丝的曲率半径知(2) 钢丝中产⽣的最⼤正应⼒6.8. 压板的尺⼨和载荷如图所⽰。
材料为45钢,?s=380 MPa,取安全系数n=1.5。
试校核压板的强度。
解:(2)(3) 强度计算许⽤应⼒强度校核压板强度⾜够。
6.12. 图⽰横截⾯为⊥形的铸铁承受纯弯曲,材料的拉伸和压缩许⽤应⼒之⽐为[?t]/[?c]=1/4。
求⽔平翼缘的合理宽度b。
A-A x解:(1) 梁截⾯上的最⼤拉应⼒和最⼤压应⼒(2) 由截⾯形⼼位置6.13. ⊥形截⾯铸铁梁如图所⽰。
若铸铁的许⽤拉应⼒为[?t]=40 MPa,许zc=10180 cm4,h1解:(1)(2)A截⾯的最⼤压应⼒A截⾯的最⼤拉应⼒C截⾯的最⼤拉应⼒取许⽤载荷值6.14. 铸铁梁的载荷及截⾯尺⼨如图所⽰。
许⽤拉应⼒[?l]=40 MPa,许⽤压应⼒[?c变,但将解:(1)(3) 强度计算B截⾯的最⼤压应⼒B 截⾯的最⼤拉应⼒C 截⾯的最⼤拉应⼒梁的强度⾜够。
(4) 讨论:当梁的截⾯倒置时,梁内的最⼤拉应⼒发⽣在B 截⾯上。
梁的强度不够。
6.19. 试计算图⽰⼯字形截⾯梁内的最⼤正应⼒和最⼤剪应⼒。
解:(3)计算应⼒最⼤剪应⼒最⼤正应⼒6.22. 起重机下的梁由两根⼯字钢组成,起重机⾃重Q=50 kN ,起重量P=10kN 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1. 矩形截面悬臂梁如图所示,已知l =4 m , b / h =2/3,q =10 kN/m ,[σ]=10 MPa ,试确定此梁横截面的尺寸。
解:(1) 画梁的弯矩图由弯矩图知:2max2ql M = (2) 计算抗弯截面系数32323669hbh h W === (3) 强度计算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥ 6.2. 20a 工字钢梁的支承和受力情况如图所示,若[σ]=160 MPa ,试求许可载荷。
解:(1) 画梁的弯矩图由弯矩图知:No20a xql 2xmax 23P M =(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度计算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤== 取许可载荷[]57P kN =6.3. 图示圆轴的外伸部分系空心轴。
试作轴弯矩图,并求轴内最大正应力。
解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是C 和B 截面 (2) 计算危险截面上的最大正应力值C 截面:3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯ B 截面:3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯-- (3) 轴内的最大正应力值MPa C 2.63max max ==σσx6.5. 把直径d =1 m 的钢丝绕在直径为2 m 的卷筒上,设E =200 GPa ,试计算钢丝中产生的最大正应力。
解:(1) 由钢丝的曲率半径知1M E M EI Iρρ=∴= (2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示。
材料为45钢,σs =380 MPa ,取安全系数n=1.5。
试校核压板的强度。
解:(1) 画梁的弯矩图由弯矩图知:危险截面是A 截面,截面弯矩是308A M Nm =(2) 计算抗弯截面系数232363330.030.0212(1)(1) 1.568106620bH h W m H -⨯=-=-=⨯(3) 强度计算许用应力380[]2531.5SMPa nσσ=== 强度校核max 6308196[]1.56810A M MPa W σσ-===⨯ 压板强度足够。
A-Ax6.12. 图示横截面为⊥形的铸铁承受纯弯曲,材料的拉伸和压缩许用应力之比为[σt ]/[ σc ]=1/4。
求水平翼缘的合理宽度b 。
解:(1) 梁截面上的最大拉应力和最大压应力()[][]11,max ,max ,max 1,max 11400 40014320 t c zzt t c c M y My I I y y y mmσσσσσσ-==-====(2) 由截面形心位置()()304006017060370320304006060510 i CiCiA y b y Ab b mm⨯-⨯+⨯⨯===⨯-+⨯=∑∑6.13. ⊥形截面铸铁梁如图所示。
若铸铁的许用拉应力为[σt ]=40 MPa ,许用压应力为[σc ]=160 MPa ,截面对形心z c 的惯性矩I zc =10180 cm 4,h 1=96.4 mm ,试求梁的许用载荷P 。
解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是A 和C 截面 (2) 强度计算A 截面的最大压应力Bz C x()22max 86320.8[][]101801016010132.60.80.825096.410A C C zC zCzC C M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯A 截面的最大拉应力11max 86310.8[][]1018010401052.80.80.896.410A t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==⨯⨯C 截面的最大拉应力()22max 86320.6[][]1018010401044.20.60.625096.410C t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯取许用载荷值[]44.2P kN =6.14. 铸铁梁的载荷及截面尺寸如图所示。
许用拉应力[σl ]=40 MPa ,许用压应力[σc ]=160MPa 。
试按正应力强度条件校核梁的强度。
若载荷不变,但将T 形截面倒置成为⊥形,是否合理?何故?解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是B 和C 截面 (2) 计算截面几何性质形心位置和形心惯性矩42.572.522264157.542.53020021520030100157.5 30200200303020060.12510i Ci C i zCAA y y mmAIy dA y dy y dy m --⨯⨯+⨯⨯===⨯+⨯==⨯⨯+⨯⨯=⨯∑∑⎰⎰⎰x(3) 强度计算B 截面的最大压应力3max620100.157552.4 []60.12510B C C C zC M y MPa I σσ-⨯⨯===⨯ B 截面的最大拉应力3max6(0.23)2010(0.230.1575)24.12 []60.12510B C t t zC M y MPa I σσ--⨯-===⨯C 截面的最大拉应力3max610100.157526.2 []60.12510C C t t zC M y MPa I σσ-⨯⨯===⨯ 梁的强度足够。
(4) 讨论:当梁的截面倒置时,梁内的最大拉应力发生在B 截面上。
3max620100.157552.4 []60.12510B C t t ZC M y MPa I σσ-⨯⨯===⨯梁的强度不够。
6.19. 试计算图示工字形截面梁内的最大正应力和最大剪应力。
解:(1) 画梁的剪力图和弯矩图最大剪力和最大弯矩值是max max 15 20 Q kN M kNm ==(2) 查表得截面几何性质3*max14113.8 6z z I W cm cm b mm S===(3) 计算应力最大剪应力No16 Qxx*3max max max151018.10.0060.138Z Z Q S MPa bI τ⨯===⨯最大正应力3max max62010141.814110M MPa W σ-⨯===⨯ 6.22. 起重机下的梁由两根工字钢组成,起重机自重Q=50 kN ,起重量P=10 kN 。
许用应力[σ]=160 MPa ,[τ]=100 MPa 。
若暂不考虑梁的自重,试按正应力强度条件选定工字钢型号,然后再按剪应力强度条件进行校核。
解:(1) 分析起重机的受力由平衡方程求得C 和D 的约束反力10 50C D R kN R kN ==(2) 分析梁的受力由平衡方程求得A 和B 的约束反力x R x R B A 610 650+=-=(3) 确定梁内发生最大弯矩时,起重机的位置及最大弯矩值C 截面:()(506)()501204.17C C M x x x dM x x dxx m=-=-==BR此时C 和D 截面的弯矩是104.25 134.05C D M kNm M kNm ==D 截面:()(106)(8)()381203.17D D M x x x dM x x dxx m=+-=-== 此时C 和D 截面的弯矩是98.27 140.07C D M kNm M kNm ==最大弯矩值是max 140.07 M kNm =(4) 按最大正应力强度条件设计maxmax 33max 6[]2140.0710438 2[]216010M WM W cm σσσ=≤⨯∴≥==⨯⨯查表取25b 工字钢(W=423 cm 3),并查得*max1021.3z z I b mm cm S ==(5) 按剪应力强度校核当起重机行进到最右边时(x =8 m ),梁内剪应力最大;最大剪力值是max 58 Q kN =xQ剪应力强度计算*3max max max581013.6[]220.010.213z z Q S MPa bI ττ⨯===⨯⨯剪应力强度足够。
6.23. 由三根木条胶合而成的悬臂梁截面尺寸如图所示,跨度l =1 m 。
若胶合面上的许用切应力为0.34 MPa ,木材的许用弯曲正应力为[σ]=10 MPa ,许用切应力为[τ]=1 MPa ,试求许可载荷P 。
解:(1) 截面上的最大剪力和弯矩max max Q P M Pl ==(2) 梁弯曲正应力强度条件max max 2262[]16[]10100.10.15 3.75 661M PlW bhbh P kNl σσσ==≤⨯⨯⨯≤==⨯ (3) 梁弯曲切应力强度条件max max 633[]222[]21100.10.1510 33Q PA bhbh P kNτττ==≤⨯⨯⨯⨯≤== (4)胶合面上切应力强度条件2222max 1336312222[]244212[]0.34100.10.15 3.825 0.15660.02544z Q h P h y y bh I bh P kN h y τττ⎛⎫⎛⎫=-=-≤ ⎪ ⎪⎝⎭⎝⎭⨯⨯⨯⨯≤==⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭许可载荷:[P ]=3.75 kN 。
6.27. 在图中,梁的总长度为l ,受均布载荷q 作用。
若支座可对称地向中点移动,试问移动距离为若干时,最为合理?AD解:(1) 约束反力2B C ql R R ==(2) 截面上的最大正弯矩和最大负弯矩22,max2,max 228822ql l ql ql qla M a qa M +-⎛⎫=--=- ⎪⎝⎭=-(3) 二者数值相等时最为合理222282244010.2072ql qla qa a la l a l l-=+-=-+===。
