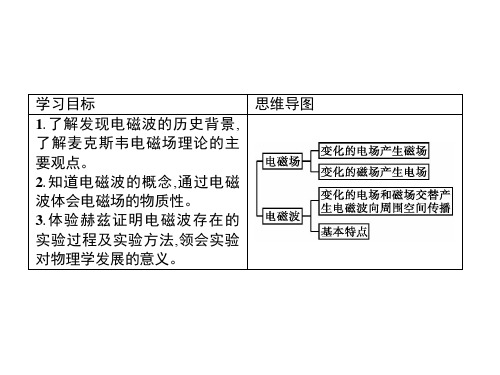
变化的电磁场精选课件PPT
合集下载
《电磁学电磁场》课件

电磁场实验
1
实验目的和方法
电磁场实验的目的是通过实践探究电磁场的特性和规律,方法包括搭建实验装置和测量相关 参数。
2
实验步骤和设备
实验步骤包括电磁场产生、测量和调整等过程,设备包括电磁铁、导线、磁罗盘等。
3
实验结果和数据分析
通过实验得到的数据和观察结果,进行数据分析和结论总结,验证电磁场的理论知识。
《电磁学电磁场》PPT课 件
课程介绍:本课程将介绍电磁学和电磁场的基本概念和原理,帮助学生了解 电磁场的特性和应用。
电磁场的特性
定义和起源
电磁场是电荷和电流所产生 的物理场,源自麦克斯韦方 程组的理论。
麦克斯韦方程组
麦克斯韦方程组描述了电场 和磁场的相互作用和传播规 律,是电磁学的基本定律。
特性和属性
电磁场的挑战
电磁场的环境污染
电磁场的不当使用会对人体健康 和环境造成潜在的污的影响
电磁场可能对其他设备和系统产 生干扰,影响其正常运行和通信。
长期接触电磁场可能对人体健康 产生潜在影响,需要加强相关研 究和安全措施。
电磁场具有电场和磁场的强 度、方向、能量和传播速度 等特性和属性。
电磁场的应用
电磁感应
电磁感应现象是将磁场转化为 电场或电流,应用于发电机、 变压器等设备。
电磁波
电磁波的传播是通过电场和磁 场相互耦合形成的,应用于通 信、雷达等领域。
电磁场在生活中的应 用案例
电磁场的应用包括无线充电、 电磁炉、磁悬浮等,为我们的 生活带来了便利和创新。
随时间变化的电磁场可场生场(精)

∴
jφ1 jφ2 · H(z)=j▽×Ė(z)/μω=k[eyE1e - exE2e ]exp(-jkz)/μω
H(z,t) =√2 k [eyE1 cos (ωt - kz+φ1) - exE2 cos (ωt - kz+φ2) ] /μω z
10、沿其它方向传播的均匀平面波 沿x 轴正向的电、磁场解:
⑹
5、∵上式中各分量⊥即独立∴上式若成立只有各分量为零: 2Ėz 2Ėy 2Ėx 2Ėz(z)=0 ⑼ 2 2Ėx(z)=0 ⑺ + k —— + k Ė y(z)=0 ⑻ —— —— + k 2 2 z2
z
z Ėx Ėy Ėz 6、∵无源∴ ▽· Ė(z ) =—— ex + —— ey+ —— x y z
j · 1 · 1 · H ▽× E k ×E = ek× E μω η
·
· ▽× H 1 · · · E= k ×H ηek× H jεω εω 1 E k ×H ηek× H εω 1 1 H k ×E = ek× E μω η
磁场能量密度:
实数表达形式
1 we E 2 2
wm
we wm 电磁波的能量密度: w we wm E 2 H 2
1 H 2 1 ( E )2 1 E 2 2 2 2
理想媒质中均匀平面波的电场能量等于磁场能量。
11、 场量 E、H 的关系
在实际应用中,纯粹的均匀平面波并不存在。但某些实际存在的波型,在远 离波源的一小部分波阵面,仍可近似看作均匀平面波。
解:∵是均匀平面波
∴E 只是z的函数E(z),故可有: 1、 设: Ė( z)=Ėx( z)ex+Ėy(z )ey+Ėz( z)ez ⑶ 2、对式⑶进行▽2运算 (
电磁学讲——变化的电场产生磁场电磁场与电磁波

cos (t
x) u
1)电 磁波是横波 E
u
E0 ,H
cos(t
u ;
kx)
E
k 2π
u
2) E 和 H 同相位 ;
H
3) E 和 H 数值成比例 H E ;
4)电磁波传播速度 u 1 , 真空中波速
等于光速 u c 1 00 2.998108 m/s.
例1 有一圆形平行平板电容器, R 3.0cm.现对
其充电,使电路上的传导电流 Ic dQ dt 2.5A,
若略去边缘效应, 求(1)两极板间的位移电流;(2)两
极板间离开轴线的距离为 r 2.0cm 的点 P 处的磁
感强度 .
解 如图作一半径
Q Q
为 r平行于极板的圆形
回路,通过此圆面积的 电位移通量为
B
0r
2π R2
dQ dt
代入数据计算得 Id 1.1A B 1.11105T
二、电磁场 麦克斯韦电磁场方程组
静电场高斯定理
D
ds
dV
q
S
V
静电场环流定理
l E dl 0
磁场高斯定理
SB
ds
0
安培环路定理
H dl
电能
We
Q2 2C
,
磁能 W m
1 2
LI 2 ,
LC回路总能量 1 Q2 1 LI 2 常量 2C 2
Q dQ LI dI 0 I dQ
C dt dt
dt
电5.变化的电磁场.ppt

mR ) t
22
• [例] 在垂直于均匀磁场B的某平面上,有一 长为R的金属细棒AB绕A端在平面上以角速度 ω转动,试求金属棒两端间的电势差.如果以半 径为R的金属盘取代本题的AB棒,仍在此平面 内绕盘心而转动,盘面与平面一致,其他不变, 再求盘心与边缘之间的电势差.
[解] 任取一金属棒线元dr,其位置距A端为r,其速度大 小v=rω,则dr上的动生电动势为
12
在一段导线中的动生电动势:
B ab
b
动ab
(b)
(V
B) d l
dl ab
(a)
若B const . ,V const . ,则
(b)
ab
B
动ab (V B) d l (V B) ab
7
解:(1)螺绕环内的磁感应强度为:
B 0nI
因为磁场完全集中于环内,故通过线圈A的磁通量 Φ为
BS 0nIS
因此,线圈A中感应电动势 的量值为
|
N
d dt
|
0nNS
|
dI dt
|
6.28105V
8
(2)线圈A接入一冲击电流计,形成闭合回路,E
在此回路中产生感应电流Ii,且
解: 动OA
(A)(V
B)
d
l
(O)
B
A
(A) (O)
VB d
l
V
dl
l
O
金属杆
L
0
大学物理第十二章变化的电磁场

是匀强磁场吗? 是!
m = BScos ( t+o)
= Bosin t Scos t
i
dm
dt
= -BoS cos2 t
13
例12.1.4 长直电流I与ABC共面, AB=a, BC=b。
(1) I =Iocos t (Io 和为常量) , ABC 不 动, 求: ABC=?
解:
m
Bdscos
方向成右手螺旋关系。3
感应电流总是“企图”阻碍原磁通的改变,但又 阻止不了。
楞次定律是能量守恒定律的必然结果。
fm
fm
楞次定律能量守恒
“阻碍”改为“助长”则,不需外力作功,导线便会 自动运动下去,从而不断获得电能。这显然违背 能量守恒定律。
4
感应电动势和感应电流的关系
对闭合导体回路, 感应电动势的方向和感应电 流的方向是相同的。
B)
dl
a
b ++ B
dl
(1)若i 若i
>0, <0,
则i 则i
沿 dl方向,即ab的方向; 与dl的方向相反,即ba的方向。
-a-
(2)动生电动势只存在于运动导体内,无论导体是否构
成闭合回路,只要导体 B在 磁0场中运动切割磁场线,即
(3)若整个导体回路在磁场中运动,则在回路中产生的
动生电动势:
用法拉第电磁感应定律解题的步骤如下:
(i)首先求出回路面积上的磁通量(取正值):
m
B dS
S
对匀强磁场中的平面线圈:
m B S BS cos
(ii)求导:
i
dm
dt
(ⅲ)判断i 的方向。
8
例12.1.1 圆线圈,m=8×10-5sin100t(wb), N=100匝,
大学物理下变化的电磁场

3、讨论:
•若有N匝线圈,它们彼此串联,总电动势等于各匝线圈所产生 的电动势之和。令每匝的磁通量为 1、 2 、 3
d1 d 2 dt dt
磁通链数:
1 2 3
d (1 2 3 ) d dt dt
故本题的结果为: r=2cm时
r dB 0.02 Ek =- 0.2 2 10 3V m 1 2 dt 2
R dB 0.05 Ek =- 0.2 5 10 3V m 1 2 dt 2
R 2 dB 0.052 Ek 0.2 2.5 10 3V m 1 2r dt 2 0.1
演示
11-2 动生电动势
引起磁通量变化的原因有两种: 1.磁场不变,回路全部或局部在稳恒磁场中运动——动生电动势 2.回路不动,磁场随时间变化——感生电动势 当上述两种情况同时存在时,则同时存在动生电动势与感生电 动势。 a
d
1、从运动导线切割磁场线导出 动生电动势公式
d d Blx d x i Bl Blv dt dt dt
d B i B dS dS S t dt S
不论空间是否存在导 体,变化的磁场总是 在周围空间激发电场
•感生电场的电场线是无头无尾的闭合曲线,所以又叫涡旋电场。
B dl 0 j dS
L S•感生电场和磁感应强Fra bibliotek的变化连在一起。
(b) 0, increase
n
n
i
direction
i
direction
(c) 0, decrease
(d ) 0, decrease
大学物理电磁学第十章电磁感应PPT课件

d Idq n2Rd 2 R R dR
dI在圆心处产生的磁场
16
dB20R dI120 dR
由于整个带电园盘旋转,在圆心产生的B为
BR2d R1
B 1 20( R2R 1)
穿过导体小环的磁通
R2
Bd 1 2 S 0( R 2R 1)r2
r R1
R
导体小环中的感生电动势
d d t1 20 (R 2R 1)r2d d t
本质 :能量守恒定律在电磁感应现象上的具体体现
影响感生电流的因素 dm i
6
相对运动
dt R
B
切割磁力线
磁通量m变化
m变化的数量和方向 m变化的快慢
I感
I
•
v
感生电流
3. 电动势
Q
-Q
7
(1)电源
++ ++
仅靠静电力不能维持稳恒电流。
+ +
+ +
维持稳恒电流需要非静电力。
++ ++
F非
____________
r nˆ
B
o
d0
x
13
这是一个磁场非均匀且
随时间变化的题目。
h
r nˆ
1、求通过矩形线圈磁通 o
B
dBd cso s2 0rIbdx rx
d0
x
d d 0 0 a 2 a 2Bc do s sd d 0 0 a 2 a 22 0Ibx2 x h d 2 x
0Ibln 4
例1 有一水平的无限长直导线,线中通有交变电流 12
II0cost,导线距地面高为 h,D点在通电导线的
dI在圆心处产生的磁场
16
dB20R dI120 dR
由于整个带电园盘旋转,在圆心产生的B为
BR2d R1
B 1 20( R2R 1)
穿过导体小环的磁通
R2
Bd 1 2 S 0( R 2R 1)r2
r R1
R
导体小环中的感生电动势
d d t1 20 (R 2R 1)r2d d t
本质 :能量守恒定律在电磁感应现象上的具体体现
影响感生电流的因素 dm i
6
相对运动
dt R
B
切割磁力线
磁通量m变化
m变化的数量和方向 m变化的快慢
I感
I
•
v
感生电流
3. 电动势
Q
-Q
7
(1)电源
++ ++
仅靠静电力不能维持稳恒电流。
+ +
+ +
维持稳恒电流需要非静电力。
++ ++
F非
____________
r nˆ
B
o
d0
x
13
这是一个磁场非均匀且
随时间变化的题目。
h
r nˆ
1、求通过矩形线圈磁通 o
B
dBd cso s2 0rIbdx rx
d0
x
d d 0 0 a 2 a 2Bc do s sd d 0 0 a 2 a 22 0Ibx2 x h d 2 x
0Ibln 4
例1 有一水平的无限长直导线,线中通有交变电流 12
II0cost,导线距地面高为 h,D点在通电导线的
时变电磁场专题教育课件

已知在任何边界上,电场强度旳切向分量及磁感应强度 旳法向分量是连续旳,所以理想导体表面上不可能存在电 场切向分量及磁场法向分量,即时变电场必须垂直于理想 导电体旳表面,而时变磁场必须与其表面相切。
en et ,
E
H
H2t JS
②
①
H1t
因 D1n ,0 由前式得
D2n S
或
en D S
因为理想导电体表面存在表面电流 Js ,设表面电流密度
J S e y (H x H z ) ez H x ex H z
在 y = b 旳内壁上
S e y ( E y ) E y J S e y (H x H z ) ez H x ex H z
在 x = 0 旳侧壁上,H x 0
J S ex ez H z0 sin( t k z z) e y H z0 sin( t k z z)
主要内容
位移电流,麦克斯韦方程,边界条件,正弦电 磁场。
6.1 法拉第电磁感应定律
由物理学知,穿过闭合线圈中旳磁通发生变化时,线 圈中产生旳感应电动势 e 为
e d
dt
式中电动势 e 旳正方向要求为与磁通方向构成右旋关系。 所以,当磁通增长时,感应电动势旳实际方向与磁通
方向构成左旋关系;反之,当磁通降低时,电动势旳实 际方向与磁通方向构成右旋关系。
例题 计算感应电动势 书P149
6.2 位移电流
位移电流不是电荷旳运动,而是一种人为定义旳概念。
电荷守恒原理表白
SJ
dS
q t
J
t
对于静态场,因为电荷分布与时间无关,所以取得电流连续性原理, 即
SJ dS 0
J 0
对于时变电磁场,因电荷随时间变化,不可能根据电荷守恒原理推出 电流连续性原理。但是电流连续是客观存在旳物理现象,为此必须扩充 前述旳电流概念。
电磁场与电磁波ppt完美版课件
探究一
探究二
随堂检测
画龙点睛变化的磁场周围产生电场,与是否有闭合电路存在无关。
2.对麦克斯韦电磁场理论的理解
探究一
探究二
随堂检测
实例引导例1根据麦克斯韦电磁场理论,下列说法正确的是( )A.有电场的空间一定存在磁场,有磁场的空间也一定能产生电场B.在变化的电场周围一定产生变化的磁场,在变化的磁场周围一定产生变化的电场C.均匀变化的电场周围一定产生均匀变化的磁场D.周期性变化的磁场周围空间一定产生周期性变化的电场解析:根据麦克斯韦电磁场理论,只有变化的电场才能产生磁场,均匀变化的电场产生恒定的磁场,非均匀变化的电场产生变化识
自我检测
1.正误判断。(1)电磁波也能产生干涉、衍射现象。( )答案:√(2)电磁波的传播不需要介质,可以在真空中传播。答案:√2.探究讨论。为什么电磁波是横波?答案:根据麦克斯韦电磁场理论,电磁波在真空中传播时,它的电场强度和磁感应强度是相互垂直的,且二者均与波的传播方向垂直。因此,电磁波是横波。
探究一
探究二
随堂检测
规律方法理解麦克斯韦的电磁场理论的关键掌握四个关键词:“恒定的”“均匀变化的”“非均匀变化的”“周期性变化的(即振荡的)”,这些都是对时间来说的,是时间的函数。
探究一
探究二
随堂检测
变式训练1如图所示的四种电场中,哪一种能产生电磁波( )
解析:由麦克斯韦电磁场理论,当空间出现恒定的电场时(如A图),由于它不激发磁场,故无电磁波产生;当出现均匀变化的电场时(如B、C图),会激发出磁场,但磁场恒定,不会激发出电场,故也不会产生电磁波;只有振荡的电场(即周期性变化的电场)(如D图),才会激发出振荡的磁场,振荡的磁场又激发出振荡的电场……如此周而复始,便会形成电磁波。答案:D
电磁场与电磁波 课件

国际标准
国际非电离辐射防护委员会( ICNIRP)制定了电磁辐射的安全标 准,限制了公众暴露在特定频率和强 度的电磁场中的最大容许暴露量。
各国标准
不同国家和地区根据自身情况制定了 相应的电磁辐射安全标准,以确保公 众的健康安全。
电磁波的防护措施
远离高强度电磁场
尽量减少在高压线、变电站、雷 达站等高强度电磁场区域的停留
射电望远镜是射电天文学的主要观测设备,可以接收来自宇宙的微弱射电信号。
射电天文学的发展对于人类认识宇宙、探索宇宙奥秘具有重要意义。
电磁波探测与成像
电磁波探测与成像技术利用电磁波的 特性,实现对物体内部结构的探测和 成像。
电磁波探测与成像技术对于医学诊断 、无损检测等领域具有重要意义。
医学上常用的超声波、核磁共振等技 术都是基于电磁波的探测与成像原理 。
这些物理量在电磁场与物质相互作用中起着重要作用,例如在光子与物 质的相互作用中,光子的能量和动量会与物质的能量和动量发生交换。
06
电磁场与电磁波的计算机模 拟
时域有限差分法(FDTD)
总结词
一种用于模拟电磁波传播的数值方法,通过在时域上逐步推进电磁场的变化来求解波动 方程。
详细描述
时域有限差分法(FDTD)是一种基于麦克斯韦方程组的数值计算方法,通过将电磁场 分量在空间和时间上交替离散化,将波动方程转化为差分方程,从而在计算机上实现电 磁波传播过程的模拟。这种方法在计算电磁波传播、散射、吸收等过程中具有广泛的应
磁场
磁Hale Waihona Puke 和电流周围存在的一种特殊 物质,对其中运动的磁体和电流 施加力。
电磁场与电磁波的产生
1 2
3
变化的电场产生磁场
根据麦克斯韦的电磁场理论,变化的电场在其周围产生磁场 。
国际非电离辐射防护委员会( ICNIRP)制定了电磁辐射的安全标 准,限制了公众暴露在特定频率和强 度的电磁场中的最大容许暴露量。
各国标准
不同国家和地区根据自身情况制定了 相应的电磁辐射安全标准,以确保公 众的健康安全。
电磁波的防护措施
远离高强度电磁场
尽量减少在高压线、变电站、雷 达站等高强度电磁场区域的停留
射电望远镜是射电天文学的主要观测设备,可以接收来自宇宙的微弱射电信号。
射电天文学的发展对于人类认识宇宙、探索宇宙奥秘具有重要意义。
电磁波探测与成像
电磁波探测与成像技术利用电磁波的 特性,实现对物体内部结构的探测和 成像。
电磁波探测与成像技术对于医学诊断 、无损检测等领域具有重要意义。
医学上常用的超声波、核磁共振等技 术都是基于电磁波的探测与成像原理 。
这些物理量在电磁场与物质相互作用中起着重要作用,例如在光子与物 质的相互作用中,光子的能量和动量会与物质的能量和动量发生交换。
06
电磁场与电磁波的计算机模 拟
时域有限差分法(FDTD)
总结词
一种用于模拟电磁波传播的数值方法,通过在时域上逐步推进电磁场的变化来求解波动 方程。
详细描述
时域有限差分法(FDTD)是一种基于麦克斯韦方程组的数值计算方法,通过将电磁场 分量在空间和时间上交替离散化,将波动方程转化为差分方程,从而在计算机上实现电 磁波传播过程的模拟。这种方法在计算电磁波传播、散射、吸收等过程中具有广泛的应
磁场
磁Hale Waihona Puke 和电流周围存在的一种特殊 物质,对其中运动的磁体和电流 施加力。
电磁场与电磁波的产生
1 2
3
变化的电场产生磁场
根据麦克斯韦的电磁场理论,变化的电场在其周围产生磁场 。
《交变电磁场》课件

电场对物质的极化作用
在电场的作用下,物质的分子或原子会发生极化现象,即正 负电荷中心分离,形成电偶极子。
磁场对物质的作用
磁场对物质的磁化作用
在磁场的作用下,物质的分子或原子会发生磁化现象,即产生磁偶极矩,形成磁畴结构 。
磁场对物质的洛伦兹力作用
在磁场和运动电荷的共同作用下,电荷会受到洛伦兹力的作用,导致电荷的运动轨迹发 生偏转。
THANKS
新型材料在交变电磁场领域的应用将进 一步拓展,为电磁场理论和技术的发展 提供新的思路和方向。
VS
详细描述
随着科技的不断发展,新型材料如碳纳米 管、石墨烯等在交变电磁场领域的应用逐 渐受到关注。这些新型材料具有优异的电 学、热学和力学性能,为交变电磁场的发 展提供了新的可能性。
高频、高强度交变电磁场的研究
《交变电磁场》PPT课件
contents
目录
• 交变电磁场概述 • 电磁场基本理论 • 交变电磁场的产生与变化 • 交变电磁场对物质的作用 • 交变电磁场的应用实例 • 交变电磁场的发展趋势与展望
01
交变电磁场概述
定义与特性
总结词
交变电磁场的定义和特性
详细描述
交变电磁场是指电磁场的强度、方向和相位随时间变化的电磁场。它具有周期 性、振荡性和方向性的特点,是电磁波传播的媒介。
交变电磁场对物质的综合作用
交变电磁场对物质的电动力学效应
在交变电磁场的作用下,物质中的电荷和电流会受到电动力学的效应,如电磁感应、电磁波的传播等 。
交变电磁场对物质的热效应
在交变电磁场的作用下,物质会产生热效应,即电磁能转化为热能,引起物质温度的升高。
05
交变电磁场的应用实例
交流电机的原理与应用
在电场的作用下,物质的分子或原子会发生极化现象,即正 负电荷中心分离,形成电偶极子。
磁场对物质的作用
磁场对物质的磁化作用
在磁场的作用下,物质的分子或原子会发生磁化现象,即产生磁偶极矩,形成磁畴结构 。
磁场对物质的洛伦兹力作用
在磁场和运动电荷的共同作用下,电荷会受到洛伦兹力的作用,导致电荷的运动轨迹发 生偏转。
THANKS
新型材料在交变电磁场领域的应用将进 一步拓展,为电磁场理论和技术的发展 提供新的思路和方向。
VS
详细描述
随着科技的不断发展,新型材料如碳纳米 管、石墨烯等在交变电磁场领域的应用逐 渐受到关注。这些新型材料具有优异的电 学、热学和力学性能,为交变电磁场的发 展提供了新的可能性。
高频、高强度交变电磁场的研究
《交变电磁场》PPT课件
contents
目录
• 交变电磁场概述 • 电磁场基本理论 • 交变电磁场的产生与变化 • 交变电磁场对物质的作用 • 交变电磁场的应用实例 • 交变电磁场的发展趋势与展望
01
交变电磁场概述
定义与特性
总结词
交变电磁场的定义和特性
详细描述
交变电磁场是指电磁场的强度、方向和相位随时间变化的电磁场。它具有周期 性、振荡性和方向性的特点,是电磁波传播的媒介。
交变电磁场对物质的综合作用
交变电磁场对物质的电动力学效应
在交变电磁场的作用下,物质中的电荷和电流会受到电动力学的效应,如电磁感应、电磁波的传播等 。
交变电磁场对物质的热效应
在交变电磁场的作用下,物质会产生热效应,即电磁能转化为热能,引起物质温度的升高。
05
交变电磁场的应用实例
交流电机的原理与应用
高二物理竞赛电磁场课件(共15张PPT)

各截面的磁通量Φ应该相等:
BΦ S
NI
en, B
B1S B2S 0 Φ1 Φ2
en
在气隙内,由于 l ,磁场
散开不大,故仍可认为磁场集
中在其截面与铁芯截面相等的 空间内:
Φ B0 S B
计算 B 值:应用磁场强度 H 的环路定理
r
L H dllH dlH dlNI
l
Hl H0NI
NI
又 H0Br, H0B0 0 B0
Φ( l )NI 0rS 0S
同电阻 R l 对比 S
同全电流欧姆定律 I(Rr)对比
结论:磁通、磁阻和磁动势在形式上服从欧姆定律。并且 可以证明它们也形式的服从相应的串并联规律。
无外磁场时抗磁质分子磁矩为零 m0
B0
m
B0
抗
磁 质 的 磁
q
v
F
m
q F
m v
化
m
, B0 同向时
, B0 反向时
第十一章 麦克斯韦方程组和电磁辐射
本章将对电磁规律加以总结。
首先给出麦克斯韦方程组,然后介绍电磁波的一般性质
。
1、 麦克斯韦方程组
静止电荷和恒定电流的电磁现象
静电场的高斯定律
q
E dS
S
0
静电场的环路定理
稳恒磁场的高斯定律 (磁通连续定理)
Edr 0
L
LEi drSB t dS
BdS 0
抗磁质内磁场 BB0B
三. 电磁波的能量
辐射能:以电磁波的形式传播出去的能量。
在气隙内,由于
,磁场散开不大,故仍可认为磁场集中在其截面与铁芯截面相等的空间内:
真空中的电磁场规律——
电磁波的能流密度 S wu 红外线 紫外线
BΦ S
NI
en, B
B1S B2S 0 Φ1 Φ2
en
在气隙内,由于 l ,磁场
散开不大,故仍可认为磁场集
中在其截面与铁芯截面相等的 空间内:
Φ B0 S B
计算 B 值:应用磁场强度 H 的环路定理
r
L H dllH dlH dlNI
l
Hl H0NI
NI
又 H0Br, H0B0 0 B0
Φ( l )NI 0rS 0S
同电阻 R l 对比 S
同全电流欧姆定律 I(Rr)对比
结论:磁通、磁阻和磁动势在形式上服从欧姆定律。并且 可以证明它们也形式的服从相应的串并联规律。
无外磁场时抗磁质分子磁矩为零 m0
B0
m
B0
抗
磁 质 的 磁
q
v
F
m
q F
m v
化
m
, B0 同向时
, B0 反向时
第十一章 麦克斯韦方程组和电磁辐射
本章将对电磁规律加以总结。
首先给出麦克斯韦方程组,然后介绍电磁波的一般性质
。
1、 麦克斯韦方程组
静止电荷和恒定电流的电磁现象
静电场的高斯定律
q
E dS
S
0
静电场的环路定理
稳恒磁场的高斯定律 (磁通连续定理)
Edr 0
L
LEi drSB t dS
BdS 0
抗磁质内磁场 BB0B
三. 电磁波的能量
辐射能:以电磁波的形式传播出去的能量。
在气隙内,由于
,磁场散开不大,故仍可认为磁场集中在其截面与铁芯截面相等的空间内:
真空中的电磁场规律——
电磁波的能流密度 S wu 红外线 紫外线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t2 t1
Iidt
1 R
2 1
d i
1 R
( 2
1)
1.
i
与
d
dt
有关,
与
无关,
与回路的材料无关.
2. i 的存在与回路是否闭合无关, 而Ii的存在与回路是
否闭合有关.
第5页 共48页
S n
Bi i
B
N
i
n
N NN
S NN
SS
SS
第6页 共48页
例题1. 导线ab弯成如图形状, 半径R=0.10m, B=0.50T, n =360转/分. 电路总电阻为1000. 求: 感应电动势和感应电 流以及最大感应电动势和最大感应电流.
第12页 共48页
2非.静动电生力电:动F势m的表达e(式v
B)
非静电: Ek v B
电动势: b
i
L Ek dl
(v B) dl a
1. 动生电动势存在于运动导体上; 不动的导体不产生电动 势, 是提供电流运行的通路.
2. 没有回路的导体, 在磁场中运动, 有动生电动势但没有感 应(动生)电流.
一、电磁感应现象及其基本规律
1.电磁出线 圈回路时, 在线圈回路中会 产生电流; 而当磁铁与线圈 保持相对静止时, 回路中不 存在电流.
第2页 共48页
结论:当穿过闭合回 路的磁通量发生变化时, 不管这种变化是由什么 原因的,回路中有电流产 生. 这一现象称为电磁 感应现象.
解1:
i
L
0
(v
B)
dl
0L
vBdl
L
0
lBdl
1 2
BL2
动生电动势方向: aO
解2: S π L2 1 L2 BS
2π
2
i
d dt
1 BL2 d
2 dt
1 BL2
2
动生电动势方向: aO
第16页 共48页
三、感生电动势 蜗旋电场
1.蜗旋电场的产生和性质
由法i 拉 d 第d t电 磁 d d 感t应S B 定 d 律S : S B t d S
转换定律.
(超导演示1) (超导演示2)
第4页 共48页
2.法拉第电磁感应定律
当穿过回路所包围面积的磁通量发生变化时,回路中产生
的感应电动势的大小与穿过回路的磁通量对时间的变化率
成正比.
i
d
dt
“-”号反映感应电动势的方 向与磁通量变化之间的关系.
感应电流: 感应电量:
Ii
i
R
1 R
dΦi dt
qi
B
i
dΦ dt
0.05cos 314t
第10页 共48页
二、动生电动势
根据磁通量变化的不同原因,把感应电动势分为两种情况.
动生电动势: 在稳恒磁场中运动着的导体内产生的感应 电动势.
感生电动势: 导体不动, 因磁场的变化产生的感应电动势.
动生电动势
感生电动势
恒定磁场中运动的导体
B B r
导体不动B , 磁B 场r 发,t生变化
解: 2π n 120π rad/s -1
Φ
B
S
60 BS
cos
B
π
r2
cos t
i
dΦ dt
Bπ r 2
2
2 sin
t
im
1 2
Bπ
r 2
2.96
V
Ii
i
R
Bπ r 2
2R
sin
t
Bπ r2
Iim 2R 2.96 mA
第7页 共48页
例题2. 一长直导线通以电流 i I0 sin t , 旁边有一个共面
电磁感应现象中产生的电流称为感应电流,相应的电 动势称为感应电动势.
电磁感应现象的本质由感应电动势反映。
第3页 共48页
• 楞次定律
电磁感应现象产生的感应电 流的方向,总是使感应电流的 磁场通过回路的磁通量阻碍原 磁通量的变化.
感应电流的效果总是反抗 引起感应电流的原因.
bB
c
v
I
a
d
楞次定律符合能量守恒和
电动势.
b
解1:
i
(v B) dl
a
l
0 vBdl vBl
电动势方向 AB
解2:
i
d
dt
Blx
i
d
dt
Bl dx dt
i vBl 电动势方向 AB
第15页 共48页
例题6. 长为L的铜棒,在均匀磁场B中以角速度在与磁场方
向垂直的平面上作匀速转动.求棒的两端之间的感应电动势.
第8页 共48页
例题3. 某空间区域存在垂直向里且随时间变化的非均匀磁
场B=kxcost. 其中有一弯成角的金属框COD,OD与x轴重
合, 一导体棒沿x方向以速度v匀速运动. 设t =0时x =0, 求框
内的感应电动势. 解: 设某时刻导体棒位于l 处
y B
C
任取 dS ydx x tan dx
例题4. 在亥姆霍兹线圈中间轴上放一半径为0.1m的小线 圈, 在小线圈所包围的面积内磁场近似均匀. 设在亥姆霍 兹线圈中通以交变磁场5.010-3(sin100t). 求小线圈中的 感应电动势.
解: B 5.0 103 sin 314t
I
I
Φ πr 2B
0.12 π 5103 sin 314t
磁通量发生变化的原因
d dt
第11页 共48页
1.动生电动势
导线运动时,内部 自由电子受到向下洛
伦兹 力: Fm e(v B)
导体内部上、下端
正、负电荷的积聚,
形成静电场.自由电
子受到向上的静电
力.
Fe eE
平衡时,电子不再因导体运动而移动, 导体两端相应具有一定的电势差,数值
上就等于动生电动势.
v
l
dS
Φ SB dS
kxcos t x tan dx
0
O
1 kl3 tan cos t
x dx
lD x
3
根据法拉第电磁感应定律:
i
dΦ dt
1 kl3 3
tan
sin
t
kl2
dl dt
tan
cost
l vt
i
1 3
kv3t 2
tan
(
t
sin
t
3cos
t)
第9页 共48页
3. 导线切割磁感线时才产生动生电动势.
第13页 共48页
• 动生电动势的计算
两种方法:
1. 公式求解:
b
i
(v B) dl
a
2. 法拉第电磁感应定律求解:
i
d
dt
若回路不闭合, 需增加辅助线使其闭合.
计算时只计大小, 方向由楞次定律决定.
第14页 共48页
例题5. 一矩形导体线框, 宽为l, 与运动导体棒构成闭合回 路. 如果导体棒以速度v作匀速直线运动, 求回路内的感应
问题: 是不是洛仑兹力?
的矩形线圈abcd. 求: 线圈中的感应电动势.
解:
Φ
S
B
dS
r
r
l1
0i
2π x
l2dx
0I0l2 sin t ln r l1
2π
r
i
d
dt
0I0
2π
l2
cos t ln
r
l1 r
当0 t π 时,cost 0,
2
i 0
为逆时针转向
当 π t π时,cost 0,
2
i 0 为顺时针转向
