机器人技术大作业
机器人测控技术大作业

机器人测控技术大作业题目: 电气工程学院学院名称:电气工程学院专业班级:自动学生姓名:学号: 2015指导教师:***考虑如图1所示的双关节刚性机械臂,试分析以下问题:图1 双关节机械臂示意图(1) 用D-H 建模法建立上述机械臂的运动学方程;(2) 忽略重力、摩擦力和干扰项的情况下,建立该机械臂的动力学方程;(3) 如果取11l =,20.8l =,120.5m m ==,初始状态:11220.100.10q q q q ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 试设计一个PD 控制器,让其跟踪一条如下指定的曲线:12sin 2sin 2d d q tq t ππ=⎧⎨=⎩,并利用Matlab 中给出仿真结果。
解:Y 0X 0X 1Y 1X 2Y2①建立坐标系a 、机座坐标系{0}b 、杆件坐标系{i } ②确定参数d i ——相邻坐标系x 轴之间的距离; θi ——相邻坐标系x 轴之间的夹角; l i ——相邻坐标系z 轴之间的距离; αi ——相邻坐标系z 轴之间的夹角。
③相邻杆件位姿矩阵M 01=Rot(z,θ1)·Trans(l 1,0,0)=1000010000110011θθθθc s s c -1000010000101l 001 = 100001001101111011θθθθθθs L c s c L s c -同理可得:M 12=Rot(z,θ2)·Trans(l 2,0,0)=100001002202222022θθθθθθs L c s c L s c -M 23(h )=Rot(z,θ3)·Trans(l 3,0,0)=100001003303333033θθθθθθs L c s c L s c -④建立方程。
将相邻杆件位置矩阵依次相乘,得:M 0h =M 01·M 12·M 23(h)=1000010012331221101231231233122110123123θθθθθθθθθθc l s l s l c s c l c l c l s c ++++-结果中一些字母的含义如下:C θ123=cos(θ1+θ2+θ3) s θ123=sin(θ1+θ2+θ3) c θ12=cos(θ1+θ2) s θ12=sin(θ1+θ2)(2)二连杆机械臂的动能和势能:21111111111111,,,cos 2K m v v d P m gh h d θθ====-22111111111,cos 2K m d P m gd θθ==-2222221,2K m v P mgy ==()()222222211212211212sin sin cos cos v x y x d d y d d θθθθθθ=+=++=--+()()()222222211221221221122211221211cos 22cos cos K m d m d m d d P m gd m gd θθθθθθθθθθ⎧=++++⎪=>⎨⎪=--+⎩21K K K +=2222121122122212211211()()22cos ()m m d m d m d d θθθθθθθ=+++++其中:连杆1的动能K 1 和势能 P 1:连杆2的动能K 2 和势能 P 2 : 总动能和总势能:21P P P +=)cos(cos )(21221121θθθ+-+-=gd m gd m m二连杆机械臂的拉格朗日函数L:P K L -=)2(21)(21222121222212121θθθθθ ++++=d m d m m)cos(cos )()(cos 2122112121212212θθθθθθθ++++++gd m gd m m d d m n i q Lq L dt d ii i ,2,1,=∂∂-∂∂=F动力学方程:111d L L T dt θθ∂∂=-∂∂ 222d L L T dt θθ∂∂=-∂∂矩阵形式orm:⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2112212212121211122221222211122111212221121121D D D D D D D D D D D D D D T T θθθθθθθθ (3)自适应PD 跟踪轨迹的simulink 模型① S-Function 的s 函数如下:② S-Function1的t函数如下:图1 PD自适应关节1的跟踪输出和给定信号图2 PD自适应关节2的跟踪输出和给定信号上面的是关节1和关节2的跟踪输出和相对应的给定信号。
机器人大作业
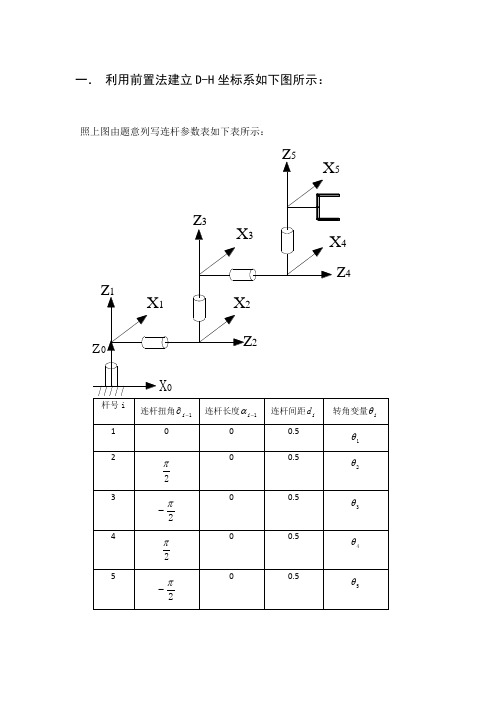
一. 利用前置法建立D-H 坐标系如下图所示:照上图由题意列写连杆参数表如下表所示:4其中初始位置时:12πθ=,2345T 0θθθθθ=====。
2 计算各i 1iT-由所学知道ii i 1i 1i i 1i i 1i 1i i 1ii i 1i i 1i 1i i 1c s 0s c c c sd s T s s c s c d c 001θθαθθθθ----------⎡⎤-⎢⎥⋅∂⋅∂-∂-⋅∂⎢⎥=⎢⎥⋅∂⋅∂∂⋅∂⎢⎥⎢⎥⎣⎦, 将上表中的各个值代入可得:110111c s 00s c 00T 0010.50001⎡⎤-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦221222c s 000010.5T s c 000001⎡⎤-⎢⎥--⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦332333c s 000010.5T sc 000001⎡⎤-⎢⎥⎢⎥=⎢⎥--⎢⎥⎢⎥⎣⎦443444c s 000010.5T s c 000001⎡⎤-⎢⎥--⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦554555c s 000010.5T sc 000001⎡⎤-⎢⎥⎢⎥=⎢⎥--⎢⎥⎢⎥⎣⎦TT 5T T T c s 000010.5T sc 0001⎡⎤-⎢⎥--⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦4 任意设定各关节变量,计算0TT 。
0012345T12345T111213x 212223y 313233z T T T T T T Tr r r p r r r p r r r p 001=∙∙∙∙∙⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦其中:1112345T 1345T 145T 245T 1235T 135T 134T1234T 14T 24Tr c c c c c c s s c c c c s c c s s c c c c s s c s c s c s s s s c c c s s c c s s c s =-+---+-+-2112345T 1345T 1235T 135T 1235T 1234T134T 124Tr s c c c c c c s c c c s s s c c c c s c s c s s c s c c s s c s s s s s c s =+-+----312345T 245T 235T 234T 24T r s c c c c c s c c s s s c s c s s c c s =+--+1212345T 1345T 145T 245T 1235T 135T 134T 1234T 14T 24Tr c c c c c s s s c c s c s c s s s c s c c s s s s c s s s s s c c c c s c c c c s c c =-+-++++-+-2212345T 1345T 1245T 135T 1235T 1234T 134T 124Tr s c c c c s c s c c s s s s c s c c s s s c s s s s c c s c c s s c s s c c =--+-+---322345T 245T 235T 234T 24Tr s c c c s c s c s s s s s s c s c c c c =--+-+131234513451452451235135r c c c c s s s c s c s s s s s c c s c s c c =-+-++2312345134512451235135r s c c c s c s c s s s s s s c s c c c c =+-+- 332345245235r s c c s c s s s s c =++x 12345134512451235135134123412412313121y 12345134512451235135123131211234134124z 2p 0.5(c c c c s s s c s c s s s c c s c s c c s s s c c c s c s c c c s s c c s s )p 0.5(s c c c s c s c c s s s s s c s c c c c s c s c c s s c s c c s c s s s s s )p 0.5(s c =--+++--++-+=+-+-+------=34524523523223424c s c s s s s c s s c 1s c s c c )+++++-+令15234T ,02πθθθθθθ======;代入以上各式并计算0T T 得:0012345T12345TT T T T T T T 01001000100010000010.50010.5=0010.5010001000001000100011000010010000010.50010.5001010010000001001=∙∙∙∙∙⎡⎤⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥∙∙∙⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤-⎢⎥⎢⎥----⎢⎥⎢⎥∙∙⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦0.5010000110010010.5010 1.50001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤-⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦5 根据上面得到的TT0,利用Paul 反变换法求解各关节变量。
机器人技术及应用-大作业1
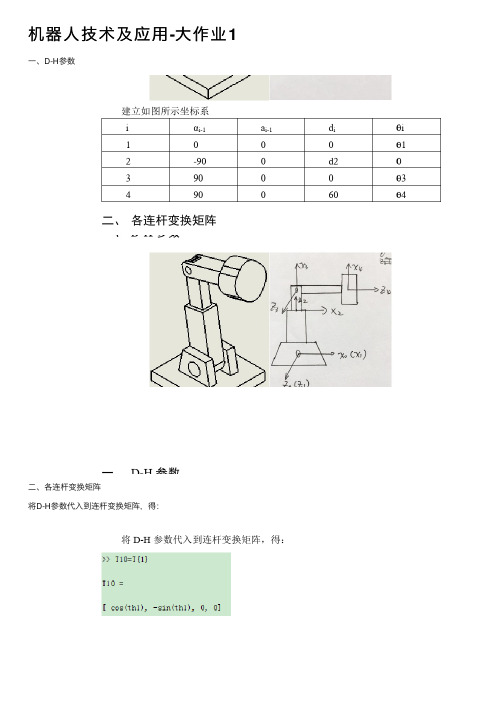
机器⼈技术及应⽤-⼤作业1⼀、D-H参数⼆、各连杆变换矩阵将D-H参数代⼊到连杆变换矩阵,得:三、各连杆⾄末端连杆的变换矩阵T43=T43T42=T32*T43;T41=T21*T42;Matlab 编程:clcclear allsyms af a d th realsyms d2 th1 th3 th4 realDH=[ 0 0 0 th1 ;-90 0 d2 0 ;90 0 0 th3 ;90 0 60 th4 ]; %DH参数for i=1:4af=DH(i,1) ; %取出DH参数a=DH(i,2) ;d=DH(i,3) ;th=DH(i,4);T{i}=[cos(th) -sin(th) 0 a;sin(th)*cos(af) cos(th)*cos(af) -sin(af) -d*sin(af) ; sin(th)*sin(af) cos(th)*sin(af) cos(af) d*cos(af) ;0 0 0 1 ] ; %连杆变换⽅程endT10=T{1}T21=T{2}T32=T{3}T43=T{4}T42=T32*T43T41=T21*T42四、雅可⽐矩阵雅可⽐矩阵结果:Matlab编程:clcclear allsyms d2 realsyms th1 th3 th4 realT21 =[ 1, 0, 0, 0;0, cos(90), sin(90), d2*sin(90);0, -sin(90), cos(90), d2*cos(90);0, 0, 0, 1];T32 =[ cos(th3), -sin(th3), 0, 0;cos(90)*sin(th3), cos(90)*cos(th3), -sin(90), 0;sin(90)*sin(th3), sin(90)*cos(th3), cos(90), 0;0, 0, 0, 1];T44=[ 1, 0, 0, 0;0, 1, 0, 0;0, 0, 1, 0;0, 0, 0, 1];T43 =[ cos(th4), -sin(th4), 0, 0;cos(90)*sin(th4), cos(90)*cos(th4), -sin(90), -60*sin(90); sin(90)*sin(th4), sin(90)*cos(th4), cos(90), 60*cos(90); 0, 0, 0, 1];T42=T32*T43n1=T41(1:3,1);o1=T41(1:3,2);a1=T41(1:3,3);p1=T41(1:3,4);n2=T42(1:3,1);o2=T42(1:3,2);a2=T42(1:3,3);p2=T42(1:3,4);n3=T43(1:3,1);o3=T43(1:3,2);a3=T43(1:3,3);p3=T43(1:3,4);n4=T44(1:3,1);o4=T44(1:3,2);a4=T44(1:3,3);p4=T44(1:3,4);Sp1=[0 -p1(3) p1(2);p1(3) 0 -p1(1);-p1(2) p1(1) 0] ; %位置⽮量的反对称矩阵Sp2=[0 -p2(3) p2(2);p2(3) 0 -p2(1);p2(2) p2(1) 0];Sp3=[0 -p3(3) p3(2);p3(3) 0 -p3(1);p3(2) p3(1) 0];Sp4=[0 -p4(3) p4(2);p4(3) 0 -p4(1);p4(2) p4(1) 0];pxn1=Sp1*n1;pxo1=Sp1*o1;pxa1=Sp1*a1;pxn2=Sp2*n2;pxo2=Sp2*o2;pxa2=Sp2*a2;pxo3=Sp3*o3;pxa3=Sp3*a3;pxn4=Sp4*n4;pxo4=Sp4*o4;pxa4=Sp4*a4;JL1=[pxn1(3) pxo1(3) pxa1(3)].' ;JL2=[pxn2(3) pxo2(3) pxa2(3)].' ;JL3=[pxn3(3) pxo3(3) pxa3(3)].' ;JL4=[pxn4(3) pxo4(3) pxa4(3)].' ;Ja1=[n1(3) o1(3) a1(3)].' ;Ja2=[n2(3) o2(3) a2(3)].' ;Ja3=[n3(3) o3(3) a3(3)].' ;Ja4=[n4(3) o4(3) a4(3)].' ;J1=[JL1 ; Ja1] ;J2=[JL2 ; Ja2] ;J3=[JL3 ; Ja3] ;J4=[JL4 ; Ja4] ;Jn=[J1 J2 J3 J4];JJn=vpa(Jn,2)五、关节驱动⼒如下图所⽰,杆各长设为li,受外⼒4F=(fx,fy)T静⼒传递:关节驱动⼒:设⼿抓坐标系原点受⼒:4F=[fx,fy,0]T 杆3受⼒:=fz fx f 033-=???=3030010*333fxl fzl fz fx l n杆2受⼒:-+=--===fz c fz s c fx s fz s s fx c fz fx c s s c c c s s s s c c f x R z R f R f 22112110*2202121121121)*,(*),(3321332322θθ-++-=?+=32232131321313332332322fxl c fxl fxl s c fzl s fxl s s fzl c f P n R n杆1受⼒:+---+=??-+-===fz c c fzs c fxs s fzs c fzs c fxs c s fzs fx c fz c fz s c fx s fz s s fx c c s s c f x R f R f 21)211(112)211(12112211211*110110001)*1,(22221211θ-+++++-=?+=321)231132(1132)231132(1213312221221211fxl c c s fxl c s fzl fxl s s fxl c s fxl c s fzl fxl c s s fxl fzl c f P n R n关节驱动⼒:关节1为转动关节:321)231132(11fxl c c s fxl c s fzl fxl s -++=τ关节2为移动关节:fz c 22=τ关节3为转动关节:33fxl -=τ六、速度与加速度分析操作臂的速度和加速度分析该机械⼿由四个关节组成,其中第⼆个关节为移动关节其余三个为转动关节,俩个连杆为l1和l2,应⽤递推法对末端构件的速度、⾓速度和雅克⽐矩阵计算如下所⽰,平⾯简图如下所⽰。
机器人大型作业内容与要求.

机器人大型作业内容与要求
1、内容(范围)
围绕下列内容之一,撰写研究报告/论文。
1)机器人重解选择方法
2)机器人奇异问题解决方法
3)机器人轨迹生成方法
4)机器人位置控制方法
5)机器人控制系统
6)机器人路径规划方法
7)机器人任务规划方法
8)机器人视觉
9)机器人视觉伺服方法
10)其它内容:可结合本人所学专业与研究方向,选择自己感兴趣且与本课程相关的内容。
报告的形式:(1)自己设计方法或系统;(2)国内/国外研究综述。
2、要求(评分标准)
1)在广泛调研分析的基础上独立完成,内容充实,严禁抄袭和下载;(50%)2)要有自己的分析和思路;(20%)
3)内容新颖,层次分明,条理清晰,系统性、逻辑性强;(10%)
4)报告书写规范,文笔流畅;(10%)
5)设计或提出的方法或系统具有一定的新意或原创性。
(10%)
3、报告/论文的格式
参照国家核心期刊科技论文的格式与规范撰写。
作业提交时间:2010年2月5日前
作业提交方式:必须同时以如下2种提交:
1)打印报告/论文全文(含附件)放入本人院办信箱;
2)将报告/论文全文(含附件)通过电子邮件发至:zdmeng@。
机器人技术基础大作业格式

《机器人技术基础》大作业题目:班级:姓名:成绩:一、机器人功能描述(200字)具有供人观赏,娱乐为目的,具有机器人的外部特征,也可以像人,像某种动物等。
同时具有机器人的功能,可以行走或完成动作,有语言能力,会唱歌,有一定的感知能力,可以自主的连续表演事先编好的多套动作。
二、机器人系统的功能构成(框图+文字说明)驱动:电动传动机械结构系统:感受系统:智能传感器基本思路:通过对人类动作的深入了解,分析人类的动作特性,并且与控制对象跳舞机器人的工作原理、动作过程进行比较,从而确定机器人的基本构成并选择合适的机械构件,组装完成机器人的造型。
分析机器人动作的局限性与优势,设定机器人的舞蹈动作,按动作编写程序,完成作品设计。
跳舞机器人的结构完全模仿真人,并实现了双腿分立走路,双臂有很强的自由度,可以完成多种高难度动作。
机器人的双脚为轮式结构,这样不仅可以实现转身和滑步,更突出的优点是在走路时减少了重心的调整,从而减少了机器人的倾斜度,实现了类似真人的走路及跳舞模式。
舞蹈机器人的控制方式是将uC/OS-Ⅱ操作系统嵌入Atmega128处理器中,采用PID算法,对电机、舵机进行实时可靠的控制,进而对机器人主动轮的速度、方向进行有效的控制,使机器人的动作定位更加准确,动作过程更加优美协调。
机器人的双脚为轮式结构,此结构可以很完美地实现转身和滑步。
更突出的优点是在走路时减少了重心的调整,同时也克服了塑料构件机械强度不够高的局限性。
跳舞机器人完全实现了智能化运行,可以用相应软件通过编程实现对舵机的控制,做出各种不同的动作,带给人们另类娱乐。
它可以走进各种不同的场合,如:在学校用于科技教育学习;在家庭用于提供丰富的生活享受;用于社会可以增加更多的新型娱乐项目等。
随着社会对服务业的需求不断扩大,可以代替人的机器人将会有更广阔的前景从近几年世界范围内推出的机器人产品来看,机器人技术正在向智能化、模块化和系统化的方向发展。
其发展趋势主要为:结构的模块化和可重构化;控制技术的的开放化;PC化和网络化;伺服驱动技术的数字化和分散化。
机器人技术大作业

《机器人技术》大作业(2015年秋季学期)题目工业机器人概述姓名学号班级专机械设计制造及其自动化业报告提交日期2015年12月5日哈尔滨工业大学内容及要求1.以某种机器人(如搬运、焊接、喷漆、装配等工业机器人;服务机器人;仿生鱼、蛇等仿生机器人;军用及其它机器人等)为例,撰写一篇大作业,题目自拟,以下内容仅作参考:1)机器人得机械结构设计(包括各部分名称、功能、传动等);2) 机器人得运动学及动力学分析;3) 机器人得控制及轨迹规划;4)驱动及伺服系统设计;5)电气控制电路图及部分控制子程序。
2.题目自拟,拒绝雷同与抄袭;3.参考文献不少于7篇,其中至少有2篇外文文献;4.报告统一用该模板撰写,字数不少于5000字,上限不限;5.正文为小四号宋体,1、25倍行距;图表规范,标注为五号宋体;6.用A4纸单面打印;左侧装订,1枚钉;7.提交打印稿及03版word电子文档,由班长收齐。
8.此页不得删除。
评语:成绩(20分): 教师签名:年月日工业机器人概述机器人学就是当今世界极为活跃得研究领域之一,它涉及计算机科学、机械学、电子学、自动控制、人工智能等多种学科。
随着计算机、人工智能与光机电一体化技术得迅速发展,机器人已经成为人类得好帮手。
在航空航天,深海探测中,往往使用机器人代替人类去完成复杂得极限工作任务。
工业机器人就是一个多功能、多自由度得机械与电气一体化得自动机械设备与系统,它可以在制造过程中完成各种任务。
它结合制造主机或生产线,可以形成一个单一得或多台机器自动化系统,在无人参与下,实现搬运、焊接、装配与喷涂等多种生产作业。
目前,工业机器人技术飞速发展,在生产中得应用日益广泛,已成为现代制造业重要得生产高度自动化设备。
一、工业机器人特性自20世纪60年代美国第一代机器人得开始,工业机器人得发展与应用迅速发展起来,工业机器人得最重要得特性概括如下。
1、可编程。
生产自动化得进一步发展就是柔性自动化。
机器人大作业综述

IRB1600型机器人的运动学分析及仿真目录1.引言................................................................................................................ - 2 -1.1 ABB公司简介.................................................................................... - 3 -1.2ABB发展历史 .................................................................................... - 4 -2. IRB1600 ........................................................................................................ - 5 -2.1 IRB1600的资料................................................................................. - 6 -2.2建立基于D-H方法的连杆坐标系 ................................................... - 8 -2.3建立六自由度点焊机器人的运动学方程....................................... - 10 -3. 虚拟样机的建立........................................................................................ - 12 -3.1 导入.................................................................................................. - 12 -3.2 添加约束副...................................................................................... - 13 -3.3 基于ADAMS的机器人运动学仿真 ............................................. - 14 -4. 结语............................................................................................................ - 18 -5. 参考资料.................................................................................................... - 19 -1.引言通过这学期对《机器人技术基础》这门课的学习,我对工业机器人有了一定的了解。
大作业(搬运机器人)

无锡科技职业学院中德机电学院
工业机器人技术大作业
设计题目搬运机器人设计与检修
学生姓名
系别控制系
专业
班级
授课教师龚运新
大作业的内容和要求(含技术要求、图表要求等):
1、论述搬运机器人的机械设计部分
⑴叙述搬运机器人机械各部分名称及功能
⑵各部件图纸设计及要求(最低画出一个部件图纸)
2、叙述搬运机器人电气设计各部分名称及功能
3、画出搬运机器人电气控制电路图
4、编写部分搬运机器人控制子程序
5、叙述搬运机器人故障检修方法
1。
机器人技术基础大作业整理版

KUKA KR40PA码垛机器人运动学仿真目录摘要 (3)1 引言 (4)1.1机器人发展 (4)1.1.1 发展 (4)1.1.2 现状 (5)2 KUKA机器人综述 (6)2.1 公司简介 (6)2.2 产品 (6)3 机器人理论基础 (7)3.1.求正运动学公式 (7)3.2运动学逆解 (8)3.3 静力分析 (9)4机器人建模 (10)4.1问题描述 (10)4.2模型描述 (10)5 仿真 (11)5.1 轨迹规划 (11)5.2特征曲线 (13)5.2.1 位移曲线 (13)5.2.2 速度曲线 (14)5.2.3 加速度曲线 (16)总结 (17)参考文献 (18)摘要本次作业主要针对KUKA KR40PA码垛机器人进行运动学仿真,根据已知的条件和需要以KUKA机器人为研究对象,对KUKA机器人进行运动学仿真,通过讨论该机器人的运动学问题,然后在matlab环境下,用simmechanics工具箱对该机器人的正运动学、逆运动学、轨迹规划进行了仿真, 通过仿真,观察到了机器人各个关节的运动,并得到了所需的数据,从而能够达到预定的目标.关键字:KUKA KR40PA码垛机器人运动学仿真 matlab1 引言1.1机器人发展1.1.1 发展虽然机器人已经历了30 多个春秋, 繁衍了三代, 是一个拥有几十万台机器人的大家族, 可是至今还没有统一的定义。
什么叫做机器人? 在世界范围内, 对于什么是机器人, 以及什么不属护机器人, 在看法上存在着很大的差差别。
为此在第18 届ISIR (国际机器人学术讨论会)期间, 专门成立了一个工作小组, 它的任务是制定机器人分类的标准, 并确定机器人数量的原则。
总之,不管机器人的定义如何, 现在的工业机器人已从原来概念的“纲领工人”或“通用自动机”逐步演进为从事专门任务的柔性机械。
进入80年代以后, 机器人的发展十分迅速。
198 0年, 全世界工业机器人仅有1万多台,可是到1984 年,除了中国、前苏联和东欧国家之外,全世界已有工业机器人102444 台, 其中以日本为最多, 高达4.4万台, 其次是美国,共有1.3万台, 以下依次是: 德国6600台、法国3380台、瑞典2400台。
工业机器人技术课后作业

成绩:《工业机器人》大作业学期:2014~2015学年第一学期指导教师:李敏姓名:学号:年级、专业:2011级机制班西南交通大学峨眉校区机械工程系2.6 已知齐次变换矩阵H=0100001010000001⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦要求ot(,)R θƒ=H 。
确定ƒ和θ的值解:0100001010000001H ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥⎣⎦,∴由式(2.46)得001x y z n n n =⎧⎪=⎨⎪=-⎩;100x y z o o o =⎧⎪=⎨⎪=⎩;010x y z a a a =⎧⎪=-⎨⎪=⎩; 由式(2.48)得:111cos (1)(0001)222x y z n o a θ=++-=++-=- 又:把旋转规定为绕矢量ƒ的正向旋转,使得0≤θ≤180 ,故120θ= 。
由式(2.52)得:2sin 3z y x o a θ-ƒ===2sin x z y a n θ-ƒ===;2sin 3y x z n o θ-ƒ===-综上,=⎡⎤⎢⎥⎢⎥⎢⎥ƒ⎢⎥⎢⎢⎢⎢⎥⎣⎦,120θ=。
2.10 {A}和{B}两坐标系仅仅方向不同。
坐标系{B}是这样得到的:首先与坐标系{A}重合,然后绕单位矢量ƒ旋转θ弧度,即()AA B B R R θ=ƒ,求证A B R e θƒ= ,式中 000z y zx y x⎡⎤-ƒƒ⎢⎥ƒ=ƒ-ƒ⎢⎥⎢⎥-ƒƒ⎣⎦ 证明:cos sin f e f θθθ=+ 且000zy zx y xf f f f f f f ⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦0sin sin cos sin 0sin sin sin 0z y f z x y x f f e f f f f θθθθθθθθ⎡⎤-⎢⎥∴=+-⎢⎥⎢⎥-⎣⎦···········(a )根据式(2.45)和式(2.47),令=ot()R R θƒ, 即0000000101xx x x x y x z z x y y y y x yz y y z y x z z z x z y y z x z z n o a f f vers c f f vers f s f f vers f s n o a f f vers f s f f vers c f f vers f s n o a f f vers f s f f vers f s f f vers c θθθθθθθθθθθθθθθθθθ+-+⎡⎤⎡⎤⎢⎥⎢⎥++-⎢⎥⎢⎥=⎢⎥⎢⎥-++⎢⎥⎢⎥⎣⎦⎣⎦··(b ) 由已知:()A A B B R R θ=ƒ,,将此式作式(b )变换,可得=0x y f f vers θ,即cos =0θ1-,则=90θ 。
机器人大作业

语音系统在机器人中的应用07机电2班组员:吴斯栋、李敏裕马李、林荣毅(一)语音系统的进展概况语音合成与识别技术是智能机器人领域的一个重要研究方向,也是智能机器人的一项关键技术。
多年来国际国内都有大量的科技工作者致力于这方面的研究开发工作,因而对许多问题的认识与求解都取得了长足的发展。
机器人“robot”一词起源于捷克语,意为强迫劳动力或奴隶。
1921年,捷克剧作家KarlCapeek在剧本《Rossum,SUnivesralRobots》中,描述了一个具有人的外表,特征和功能的机器,并命名为认Robota。
英语的Robot,一词就是由此演变而来的。
基本上,一个机器人包括:机械设备,如可以与周围环境进行交互的车轮平台、手臂或其它构造。
设备上或周围的传感器,可以感知周围环境并向设备提供有用的反馈。
根据设备当前的情况处理传感输入,并按照情况指示系统执行相应动作的系统。
语音识别和语音合成技术是一种人机语言通信技术,属于计算机智能接口技术。
多媒体技术也主要是利用计算机语音处理和图象处理的能力为人们提供一种更加方便,直观的人机界面。
机器人技术和语音技术的结合就成为了一项新的技术课题:智能语音机器人。
人们一直以来对自由交流方式的本能渴望正是语音识别技术坚定不移的发展动力。
自从工业革命以来,各种机械化设备虽然提高了劳动生产率,创造了巨大的物质财富,但是我们在面对它们时却不得不放弃最习惯、最自然的沟通方式一一自然语言。
因此,我们从来就没有放弃过这样一个梦想:让机器与人之间也能像人与人之间一样进行交流。
而成就人类这种梦想的最关键技术之一就是语音识别与合成技术。
今天,随着语音识别技术已经取得了巨大的进展。
一些智能语音机器人技术已经开始得到广泛的应用,具有语音识别功能的产品也不断出现,这些都标志着智能语音机器人技术距离人类的日常生活己经越来越近了。
我国的语音识别技术研究起步并不晚,但由于各种客观条件的限制,早期的研究工作进展缓慢。
工业机器人大作业

一、简答题
1.什么是机器人的内部传感器和外部传感器?举例说明之。
2. 按机器人的开发内容与应用进行分类,机器人应分为那几类?分别举例说明之。
3.齐次向量是怎样定义的?试举例说明之。
二、计算题
1.一个两关节机器人,关节1、2的齐次变换矩阵分别为A1和A2,试求该机器人的坐标变换矩阵。
2.已知R 为旋转矩阵,b 为平移向量,试写出相应的齐次矩阵。
三. 设计题:
1、MSO —CP -020型垂直六关节机器人的坐标结构简图如图1所示,其各连杆的D -H 参数和关节变量列于表1,(1)写出连杆D-H 参数及关节变量;(2)求出各连杆坐标系间变换矩阵A i ;(3)并写出机器人运动学方程。
111
11c 0s 0s 0c 001000
00
1θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦A 2
2
222
2c 0s 0s 0c 00100
00
1d θθθθ⎡⎤
⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦
A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=010100001R ⎥⎥
⎥⎦⎤
⎢⎢⎢⎣⎡--=523b
图1:垂直六关节机器人的坐标结构简图表1:连杆D-H参数及关节变量。
黑龙江哈尔滨工业大学机械课程机器人技术课程大作业
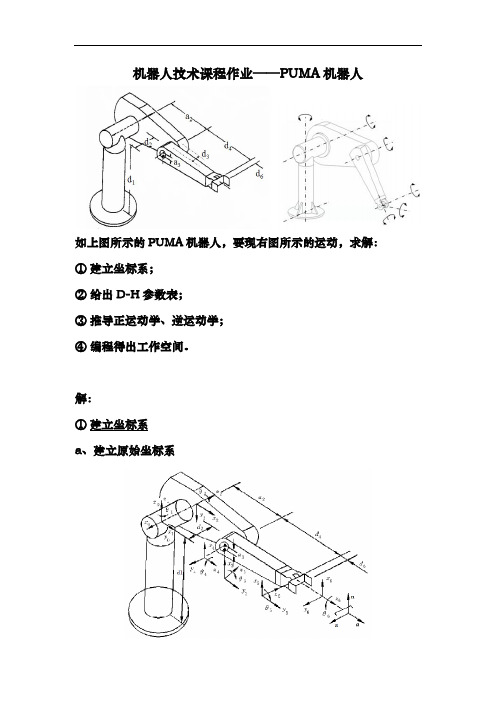
机器人技术课程作业——PUMA机器人如上图所示的PUMA机器人,要现右图所示的运动,求解:①建立坐标系;②给出D-H参数表;③推导正运动学、逆运动学;④编程得出工作空间。
解:①建立坐标系a、建立原始坐标系b 、坐标系简化② 给出D-H 参数表a 、PUMA 机器人的杆件参数1d 0.6604m =,2d 0.14909m =,4d 0.43307m =,6d 0.05625m = 2a 0.4318m =,3a 0.02032m =b 、D-H 参数表关节i i θ i α i L i d运动围 1 90 0 0 0-160o ~160o2 0 -90 02d 0.14909m = -225o ~45o3-902a 0.4318m =-45o ~225o4 0 -90 3a 0.02032m = 4d 0.43307m =-110 o~170 o 590-100 o~100 o③ 推导正运动学、逆运动学 a 、正运动学推导由式111111111100001ii i i i i i i i i i ii i i i i i i c s a s c c c s d s T s s c s c d c θθθαθαααθαθααα-----------⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦可得: 111101000000100001c s s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦222122200001000001c s d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦33233230000010001c s a s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦44343444000100001c s a d T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦ 554555000010000001c s T s c -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦ 665666000010000001c s T s c -⎡⎤⎢⎥⎢⎥=⎢⎥--⎢⎥⎣⎦由00123456123456T T T T T T T =,得机械手变换矩阵:601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦23654164123651654164123654164123651654164123654642365()()()x y z n c c c c c s s c s c s c c c s s s c s n c c c c s s s s s c s s c c s c s c c n s c c c s s c c s =--++=----=--- 23654164123651654164123654164123651645164123654642365()()()x y z o c s c c c c s c s s s c s c s s c c s o c s c c s c s s s s s s s s c c c c c o s s c c s s c c s =-++-+=-+++-=++2354123515412354123515412352354x y z a c s c c s c c s s s a c s c s s c s s s c a c c s s c =---=--+=-+3231221423121323122142312142332322x y z p a c c a c c d s c d s p a c s a c s d s s d c p d c a s a s =+--=+-+=---b 、逆运动学推导 1).求1θ用逆变换011T -左乘方程00123456123456T T T T T T T =两边:10123451623456T T T T T T T -=11111600000010000101xx x x yy y y zz z z c s n o a p s c n o a p T n o a p ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦得112x y s p c p d -+=三角代换 cos x p ρφ=,sin y p ρφ=式中,ρ=tan 2(,)x y a p p φ=得到1θ的解12a tan 2(,)a tan 2(,y x p p d θ=-2).求3θ矩阵方程两端的元素(1,4)和(2,4)分别对应相等113232242342332322x y z c p s p a c a c d s p d c a s a s +=+-⎧⎨-=++⎩ 平方和为:4333d s a c k += 其中 2222222242322x y z p p p d d a a k a ++----=解得:334a tan 2(,)a tan 2(,a d k θ=- 3).求θ在矩阵方程00123456123456T T T T T T T =两边左乘逆变换013T -。
机器人技术大作业

机器人技术大作业:PUMA机器人作业要求:1.建立坐标系;2.给出D-H参数表;3.推导正运动学,逆运动学;4.编程得出工作空间;1.建立坐标系由坐标系的建立规则:Oi:设在Li与Ai+1轴线的交点上;Zi轴:与Ai+1关节轴重合,指向任意;Xi轴:与公法线Li重合,指向沿Li由Ai轴线指向Ai+1轴线;Yi轴:按右手定则确定;可以建立PUMA机器人各关节坐标系如下:图1 PUMA机器人各关机坐标系2.给出D-H参数表由各参数的确定规则:杆件长度Li:沿xi 轴,zi-1 轴与xi 轴交点到0i 的距离;杆件扭转角αi:绕xi 轴,由zi-1 转向zi;杆件偏移量di:沿zi-1 轴,zi-1 轴和xi 交点至∑0i –1 坐标系原点的距离;杆件回转角θi:绕zi-1 轴,由xi-1转向xi;可以得到PUMA机器人的D-H参数表:表1 PUMA 机器人D-H 参数表3. 推导正运动学,逆运动学解3.1正运动学以下以c 代表cos 函数,s 代表sin 函数 由D-H 参数表易得:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=100001000001111110d c s s c T θθθθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10001000022222222221d s a c s c a s c T θθθθθθ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=10000010003333333332θθθθθθs a c s c a s c T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=100001000004444443d c s s c T θθθθ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=1000100000555554θθθθc s s c T ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=10010000006666665d c s s c T θθθθ将以上六个矩阵依次右乘,即可得到末端机械手的齐次变换矩阵:65544332211060T T T T T T T =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1060z z z z y y y yx x x x p a o n p a o n p a o n T 利用MATLAB 程序可以求出此变换矩阵各参数: syms a2 d2 a3 d4 d6syms c1 s1 c2 s2 c3 s3 c4 s4 c5 s5 c6 s6 T01=[c1 0 -s1 0;s1 0 c1 0;0 -1 0 d1;0 0 0 1]; T12=[c2 -s2 0 a2*c2;s2 c2 0 a2*s2;0 0 1 d2;0 0 0 1]; T23=[c3 0 -s3 a3*c3;s3 0 c3 a3*s3;0 -1 0 0;0 0 0 1]; T34=[c4 0 -s4 0;s4 0 c4 0;0 -1 0 d4;0 0 0 1]; T45=[c5 0 -s5 0;s5 0 c5 0;0 -1 0 0;0 0 0 1]; T56=[c6 -s6 0 0;s6 c6 0 0;0 0 1 d6;0 0 0 1]; T06=T01*T12*T23*T34*T45*T56 得到:nx=c6(s5c1s23 + c5(s1s4+c4c1c23)) - s6(c4s1 - s4c1c23) ny=c6(s5s1s23 - c5(c1s4-c4s1c23)) + s6(c1c4 + s4s1c23) nz=c6s5c23-c4c5s23-s4s6s23ox=-s6(s5c1c23+c5(s1s4 + c4c1c23)) - c6(c4s1-s4c1c23) oy=c6(c1c4+s4s1c23)-s6s5s1s23-c5(c1s4-c4s1c23) oz=-s6(s5c23 - c4c5s23- c6s4s23) ax=c5(c1s23- s5(s1s4 + c4c1c23)) ay=c5(s1s23+ s5(c1s4 - c4s1c23)) az=c5(c23 + c4s5s23)px=d6(c5c1s23-s5(s1s4+c4c1c23))-d2s1-d4c1s23+ a2c1c2 - a3c1s2s3 + a3c1c2c3 py=d6(c5s1s23+s5(c1s4-c4s1c23))+d2c1-d4s1c23+ a2c2s1- a3s1s2s3 + a3c2c3s1 pz=d1- a2s2 -d4c23+ d6(c5c23+ c4s5s23) - a3c2s3 - a3c3s2 其中:c23=cos(θ2+θ3),s23=sin(θ2+θ3). 带入:c1=0; s1=1; c2=1; s2=0; c3=0; s3=-1; c4=-1; s4=0; c5=-1; s5=0; c6=-1; s6=0;得到:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-++--=100013001642100201060d a d d a d T与图中实际位置相符,故正解正确。
大学机器人选修课的大作业2

《机器人技术基础》课程考核大作业一、进行课程学习考核(大作业形式)的目的:工业机器人系统设计是专业选修课的一个理论与实践相结合的教学环节,是机械类基础课程的延伸,可以巩固和加强机械类基础课程学习和工程应用知识的拓展,可以为毕业设计和就业工作打下良好基础,其目的是:1、通过资料查询与整理,联系生产实际,运用所学过的知识,使学生得到对课题的论证与分析、问题解决对策、自主学习、团队合作等能力的培养。
2、利用机械类的前序课知识,学会并掌握工业机器人系统设计的特点及方法,学会并掌握工业机器人系统设计中“总体方案设计”、“参数设计”、“组成机构原理与分析”、“机械结构装置设计”、“控制系统设计”等方面的一般方法和技术要求。
3、加强机械设计中基本技能的训练,如:设计计算能力,运用有关设计资料、设计手册、标准、规范及经验数据的能力,以及机械、电气系统的综合运用能力。
二、同学可以选择的课题领域:1.玻璃、陶瓷加工业用的工业机器人2.化学工业中应用的工业机器人3.建筑行业应用的工业机器人4.塑料工业中应用的工业机器人(如:装配、搬运)5.用于包装工业的工业机器人6.电气和电子工业中应用的工业机器人:工件搬运和存放的工业机器人7.特殊行业应用的工业机器人(如:医疗、残疾、家庭)8.用于金属生产和加工的工业机器人9.用于木加工业的工业机器人:木加工行业装配和搬运的工业机器人10.用于食品供应和加工的工业机器人:食品工业中的装配和搬运的工业机器人11.承担复杂机具搬运任务的工业机器人12.搬运和托盘堆码应用的工业机器人13.普通机械制造领域的装配和搬运作业的工业机器人14.用于机床上下料件的工业机器人15.用于粘接和密封的工业机器人16.用于金属生产和加工的工业机器人17.锻冶场所装卸的工业机器人18.金属生产和加工业的装配和搬运的工业机器人19.用于压铸和注模成型机装卸的工业机器人三、设计内容与要求:1.介绍所选工业机器人系统的组成及各部分的关系,理解其机、电组成系统的要求(包括:需求分析、功能分析与分解、功能求解与集成、设计方案的形成、方案的评价等),掌握工业机器人系统方案设计的主要进程以及各阶段的主要工作内容,初步领会工业机器人系统的设计方案及一般程序。
PUMA机器人正逆运动学推导及运动空间解算-机器人技术大作业全

PUMA机器人正逆运动学推导及运动空间解算求解:①建立坐标系;②给出D-H参数表;③推导正、逆运动学;④编程得工作空间1.建立坐标系根据PUMA机器人运动自由度,在各关节处建立坐标系如图2所示。
图1 PUMA560机器人坐标系图2.D-H参数表D-H 参数表可根据坐标系设定而得出,见表1。
(1)i θ为绕1i Z -轴从1i X -到i X 的角度; (2)1i α-为绕i X 轴从1i Z -到i Z 的角度;(3)1i a -为沿i X 轴从1i Z -与i X 交点到i O 的距离; (4)i d 为沿1i Z -轴从1i Z -与i X 交点到1i O -的距离。
表1 PUMA 机器人的杆件参数表3. 正运动学推导由坐标系图及各杆件参数可得个连杆变换矩阵。
111101000001100001c s s c T θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦ 22222222122000010001c s c a s c s a T d θθθθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦3333333323000100001c s c a s c s a T θθθθθθ-⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥⎣⎦ 444434400000100001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦5555450000010001c s s c T θθθθ⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦ 66665660000001001c s s c T d θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦根据各连杆变换矩阵相乘,可以得到PUMA560的机械手变换矩阵,其矩阵为关节变量的函数。
()()()()()()00123456112233445566T T T T T T T θθθθθθ=将上述变换矩阵逐个依次相乘可以得到06T 。
601x x x x yy y y z z z z n o a p n o a p T n o a p ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦()()()()()()()()6514142315236411234651442311523614231446236235452365141423152364112346514423115236x y z x y n c c s s c c c c s s s c s c c s n c c c s c c s s s s s c c c s s n s s s c c s c c s o s c s s c c c c s s c c s c c s o s c c s c c s s s s c =--+-+⎡⎤⎣⎦=+-+-⎡⎤⎣⎦=-+=-+-+⎡⎤⎣⎦=-+-+⎡⎤⎣⎦()()()()()()()()142314623545236423152351414235123514423152345231223232165141423152314231223231265144231z x y z x y c c c s s o s c s c c s c s s a c c s s s s c c c a c s s s c s c c s a a c c s s p c a c a c d s d s s s c c c c c s c d s p s a c a c c d d s c s c c s c -=++=--=++=-=-----+⎡⎤⎣⎦=-++++()512341232342232365234523z s s d s s p c d a s a s d c c c s s ⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪+⎡⎤⎣⎦⎪=-++-⎪⎭上式中()()23232323cos ,sin c s θθθθ=+=+。
机器人技术及应用-大作业1
for q1=q1_s:step1:q1_end
for d2=d2_s:step2:d2_end
for q3=q3_s:step3:q3_end
for q4=q4_s:step4:q4_end
% T=p560.fkine([q1*du d2 q3*du q4*du ]);%正向运动学仿真函数
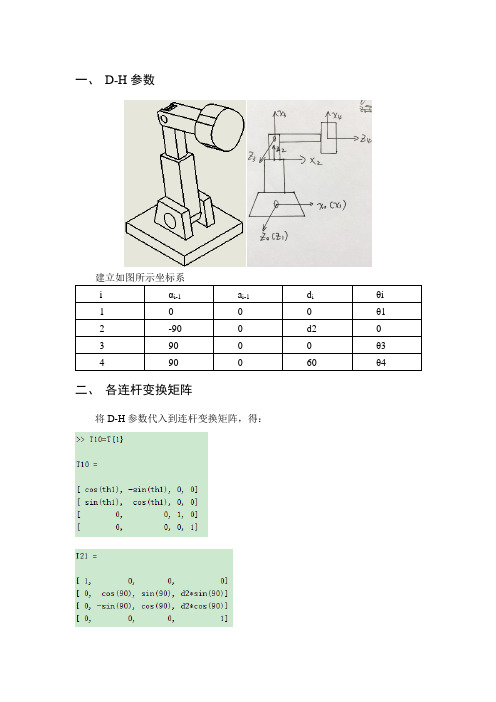
一、D-H参数
建立如图所示坐标系
i
αi-1
ai-1
di
θi
1
0
0
0
θ1
2
-90
0
d2
0
3
90
0
0
θ3
4
90
0
60
θ4
二、各连杆变换矩阵
将D-H参数代入到连杆变换矩阵,得:
三、各连杆至末端连杆的变换矩阵
T43=T43
T42=T32*T43;
T41=T21*T42;
Matlab编程:
clc
clear all
T10=[cos(q1) -sin(q1) 0 0; sin(q1) cos(q1) 0 0; 0 0 1 0;0 0 0 1];
T21=[1 0 0 0; 0 0 1 d2; 0 -1 0 0; 0 0 0 1];
T32=[cos(q3) -sin(q3) 0 0; 0 0 -1 0; sin(q3) cos(q3) 0 0;0 0 0 1];
plot3(T_x,T_y,T_z,'r.','MarkerSize',3);
disp(['绘制工作空间运行时间:',num2str(etime(clock,t1))]);
机器人技术与应用-大作业3
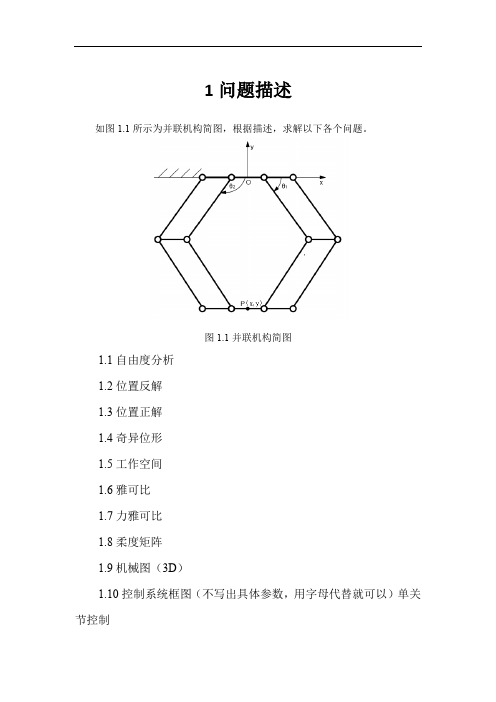
1问题描述如图1.1所示为并联机构简图,根据描述,求解以下各个问题。
图1.1并联机构简图图1.1并联机构简图1.1自由度分析1.2位置反解1.3位置正解1.4奇异位形1.5工作空间1.6雅可比1.7力雅可比1.8柔度矩阵1.9机械图(3D)1.10控制系统框图(不写出具体参数,用字母代替就可以)单关节控制2.问题解答2.0前言并联机构可以定义为动平台和定平台通过至少两个独立的运动链相连接,机构具有两个或两个以上自由度,且以并联方式驱动的一种闭环机构。
在工程上,机械手需在一个平面内做快速平动,而在与该平面的方向做长矩步进运动。
为此,黄田教授利用平行四边形的性质,提出了一种称之为Diamond 的全铰接二平动自由度平面并联机构,该机构包括了机架、动平台和两个结构相同的支链,各支链含两个平行四边形。
2.1分析自由度分析此机构的自由度,我们将并联机构图简化成图2所示简图进行分析。
图2 Diamond 并联机构简图根据G -K 公式,得如下自由度的计算公式:()∑=+--=ji i f j n F 11λ (1)其中:λ——位形空间的维数; n——构件个数,含机架; j——运动副的个数;f i ——第i 个运动副的自由度数。
现在空间为平面,所以λ=3。
故:F =3(5−5−1)+5=2所以上述的并联机构的自由度为2,若该机构需要确定的运动,就需要两个原动构件。
2.2-2.3位置反解与正解由图2可知,杆i i B A 通过转动副i A 与基座连接在一起,杆i i B A 通过转动副iB 与杆'O B i 连接在一起。
建立坐标系,参考坐标系Oxy 与基座位于同一平面,原点O 位于两基座的中心。
设11θ、12θ、21θ、22θ为机构的输入变量,运动平台的原点'O 在x 轴和y 轴方向上的位移x 和y 为输出变量。
i i B A 杆的杆长为i a ,'O B i 杆的杆长为i b ,O 距离基座i A 的距离为i e 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可编辑版《机器人技术》大作业(2015年秋季学期)题目工业机器人概述姓名学号班级专业机械设计制造及其自动化报告提交日期2015年12月5日哈尔滨工业大学.内容及要求1.以某种机器人(如搬运、焊接、喷漆、装配等工业机器人;服务机器人;仿生鱼、蛇等仿生机器人;军用及其它机器人等)为例,撰写一篇大作业,题目自拟,以下内容仅作参考:1) 机器人的机械结构设计(包括各部分名称、功能、传动等);2) 机器人的运动学及动力学分析;3) 机器人的控制及轨迹规划;4) 驱动及伺服系统设计;5) 电气控制电路图及部分控制子程序。
2.题目自拟,拒绝雷同和抄袭;3.参考文献不少于7篇,其中至少有2篇外文文献;4.报告统一用该模板撰写,字数不少于5000字,上限不限;5.正文为小四号宋体,1.25倍行距;图表规范,标注为五号宋体;6.用A4纸单面打印;左侧装订,1枚钉;7.提交打印稿及03版word电子文档,由班长收齐。
8.此页不得删除。
评语:成绩(20分):教师签名:年月日工业机器人概述机器人学是当今世界极为活跃的研究领域之一,它涉及计算机科学、机械学、电子学、自动控制、人工智能等多种学科。
随着计算机、人工智能和光机电一体化技术的迅速发展,机器人已经成为人类的好帮手。
在航空航天,深海探测中,往往使用机器人代替人类去完成复杂的极限工作任务。
工业机器人是一个多功能、多自由度的机械和电气一体化的自动机械设备和系统,它可以在制造过程中完成各种任务。
它结合制造主机或生产线,可以形成一个单一的或多台机器自动化系统,在无人参与下,实现搬运、焊接、装配和喷涂等多种生产作业。
目前,工业机器人技术飞速发展,在生产中的应用日益广泛,已成为现代制造业重要的生产高度自动化设备。
一、工业机器人特性自20世纪60年代美国第一代机器人的开始,工业机器人的发展和应用迅速发展起来,工业机器人的最重要的特性概括如下。
1、可编程。
生产自动化的进一步发展是柔性自动化。
工业机器人能根据工作环境不同、做出相应规划和变化,因而在小批量多品种的高效柔性制造过程可以起到很好的作用,是柔性制造系统(FMS)的重要组成部分。
2、拟人化。
工业机器人在机械结构上类似于人体行走、腰转、大臂、小臂、手腕、手爪和部分,在控制上有计算机类似大脑。
此外,智能工业机器人具有许多类似生物传的感器,如皮肤接触传感器、力传感器、负载传感器、视觉传感器、声传感器、语言功能等。
该传感器提高了自适应能力。
3、通用性。
除了专门的特种工业机器人外,一般工业机器人在执行不同任务时具有很好的通用性。
例如,更换工业机器人末端执行器(夹具、工具等)可以执行不同的任务。
4、机电一体化。
工业机器人技术涉及的学科相当广泛,但总结起来就是是机电一体化技术。
第三代智能机器人不仅具有获取外界环境信息的能力,而且具有记忆、语言理解、图像识别、推理和判断等能力,这与微电子技术、特别是计算机技术的应用有着密切的关系。
因此,机器人技术的发展将带动其他技术的发展,机器人技术的发展和应用也可以验证一个国家科技和工业技术的发展和水平。
二、工业机器人组成工业机器人系统由三大部分和六个子系统组成。
三大部分:机部分、传感部分、控制部分。
六个子系统:驱动系统、机械结构系统、感觉系统、机器人环境交互系统、人机交互系统、控制系统。
1、驱动系统,要使机器人运行起来,就需给各个关节即每个运动自由度安置传动装置,这就是驱动系统。
驱动系统可以是液压传动、气动传动、电动传动,或者把它们结合起来应用的综合系统;可以直接驱动或者通过同步带、链条、轮系、谐波齿轮等机械传动机构进行间接驱动。
2、机械结构系统,工业机器人的机械结构系统是工业机器人为完成各种运动的机械部件。
系统由骨骼(杆件)和连接它们的关节(运动副)构成,具有多个自由度,主要包括手部、腕部、臂部、机身等部件。
3、感觉系统由内部传感器模块和外部传感器模块组成,用以获得内部和外部环境状态中有意义的信息。
智能传感器的使用提高了机器人的机动性、适应性和智能化的水准。
人类的感受系统对感知外部世界信息是极其灵巧的,然而,对于一些特殊的信息,传感器比人类的感受系统更有效。
4、机器人一环境交换系统是现代工业机器人雨外部环境中的设备互换联系和协调的系统。
工业机器人与外部设备集成为一个功能单元,如加工单元、焊接单元、装配单元等。
当然,也可以是多台机器人、多台机床或设备、多个零件存储装置等集成为一个去执行复杂任务的功能单元。
5、人工交换系统是操作人员与机器人控制并与机器人联系的装置,例如,计算机的标准终端,指令控制台,信息显示板,危险信号报警器等。
该系统归纳起来分为两大类:指令给定装置和信息显示装置。
6、控制系统的任务是根据机器人的作业指令程序以及传感器反馈回来的信号支配机器人的执行机构去完成规定的运动和功能。
假如工业机器人不具备信息反馈特征,则为开环控制系统;若具备信息反馈特征,则为闭环控制系统。
根据控制原理,控制系统可分为程序控制系统、适应性控制系统和人工智能控制系统。
根据控制运行的形式,控制系统可分为点位控制和轨迹控制。
三、工业机器人种类应用工业机器人主要有以下几类1、移动机器人移动机器人是工业机器人的一种类型,它由计算机控制,具有移动、自动导航、多传感器控制、网络交互等功能,它可广泛应用于机械、电子、纺织、卷烟、医疗、食品、造纸等行业的柔性搬运、传输等功能,也用于自动化立体仓库、柔性加工系统、柔性装配系统;同时可在车站、机场、邮局的物品分捡中作为运输工具。
国际物流技术发展的新趋势之一,而移动机器人是其中的核心技术和设备,是用现代物流技术配合、支撑、改造、提升传统生产线,实现点对点自动存取的高架箱储、作业和搬运相结合,实现精细化、柔性化、信息化,缩短物流流程,降低物料损耗,减少占地面积,降低建设投资等的高新技术和装备。
2、点焊机器人用于点焊自动作业的工业机器人。
使用点焊机器人最多领域为汽车车身的自动装配车间。
点焊机器人由机器人本体、计算机控制系统、示教盒和点焊焊接系统几部分组成,由于为了适应灵活动作的工作要求,通常电焊机器人选用关节式工业机器人的基本设计,一般具有六个自由度:腰转、大臂转、小臂转、腕转、腕摆及腕捻。
3、弧焊机器人弧焊机器人主要应用于各类汽车零部件的焊接生产。
在该领域,国际大型工业机器人生产企业主要以向成套装备供应商提供单元产品为主。
4、激光加工机器人激光加工机器人是将机器人技术应用于激光加工中,通过高精度工业机器人实现更加柔性的激光加工作业。
本系统通过示教盒进行在线操作,也可通过离线方式进行编程。
该系统通过对加工工件的自动检测,产生加工件的模型,继而生成加工曲线,也可以利用CAD 数据直接加工。
可用于工件的激光表面处理、打孔、焊接和模具修复等。
四、工业机器人的发展趋势1、工业机器人的技术发展趋势从近几年世界机器人推出的产品来看,工业机器人技术正在向智能化、模块化和系统化的方向发展,其发展趋势主要为:结构的模块化和可重构化;控制技术的开放化、PC化和网络化;伺服驱动技术的数字化和分散化;多传感器融合技术的实用化;工作环境设计的优化和作业的柔性化以及系统的网络化和智能化等方面。
2、工业机器人的产业发展趋势国际机器人联盟(IFR)与联合国欧洲经济委员会(UNECE)发布的数据显示,全球多用途工业机器人销售从2003年开始恢复增长,预计在2005年到2008年间,全球工业机器人销量预计年均增长6.1%,到2008年增至12.1万台。
以具体地区而言,亚太地区仍将是工业机器人使用量最高的地区,预计日本的工业机器人销量将由2004年的3.71万台增至2008年的4.59万台。
而整体亚太地区的工业机器人销量将由2004年的5.2万台增至2008年的7.04万台。
北美地区的工业机器人销量也将稳定增加,预计将由2004年的1.34万台增至2008年的1.65万台。
而欧洲地区的工业机器人销量预计到2008年将增至3.37万台。
3、我国工业机器人的发展历程与现状我国工业机器人起步于20世纪70年代初期,经过20多年的发展,大致经历了3个阶段:70年代的萌芽期、80年代的开发期和90年代的适用化期。
目前,我国研制的工业机器人已达到了工业应用水平。
现在,国家更加重视机器人工业的发展,也有越来越多的企业和科研人员投入到机器人的开发研究中。
经过五十多年的发展,工业机器人已在越来越多的领域得到了应用。
在制造业中,尤其是在汽车产业中,工业机器人得到了广泛的应用。
如在毛坯制造(冲压、压铸、锻造等)、机械加工、焊接、热处理、表面涂覆、上下料、装配、检测及仓库堆垛等作业中,机器人都已逐步取代了人工作业。
随着工业机器人向更深更广方向的发展以及机器人智能化水平的提高,机器人的应用范周还在不断地扩大,已从汽车制造业推广到其他制造业,进而推广到诸如采矿机器人、建筑业机器人以及水电系统维护维修机器人等各种非制造行业。
此外,在国防军事、医疗卫生、生活服务等领域机器人的应用也越来越多,如无人侦察机(飞行器)、警备机器人、医疗机器人、家政服务机器人等均有应用实例。
机器人正在为提高人类的生活质量发挥着重要的作用。
工业机器人在许多生产领域的使用实践证明,它在提高生产自动化水平,提高劳动生产率和产品质量以及经济效益,改善工人劳动条件等方面,有着令世人瞩目的作用,引起了世界各国和社会各层人士的广泛关注。
在新的世纪,机器人工业必将得到更加快速的发展和更加广泛的应用。
从近几年世界机器人推出的产品来看,工业机器人技术正在向智能化、模块化和系统化的方向发展,其发展趋势主要为:结构的模块化和可重构化;控制技术的开放化、PC化和网络化;伺服驱动技术的数字化和分散化;多传感器融合技术的实用化;工作环境设计的优化和作业的柔性化以及系统的网络化和智能化等方面。
机器人技术是高技术的重要组成部分,其产业化的进程在我国刚刚起步,虽然取得了一定的成绩,但仍然存在很多困难和不足,因此更需要多方面的关心和支持。
国家政策支持,是加速高新技术产业化的重要前提。
根据我国政府有关部门应组织力量进行充分地调查研究,在此基础上,制定切实可行的推广、应用机器人和促进机器人研究开发的倾斜政策。
如在税收、投资和贷款方面对机器人产业实行扶持政策。
日本政府通过制定政策,采取一系列措施鼓励企业应用机器人,为日本机器人在国内开拓市场的经验值得我们借鉴。
另外,对机器人用户,可以考虑给予一定的资金补贴,以鼓励购买.为了避免危险恶劣的工作环境导致的工伤事故和职业病,保护工人的身心安全,对一些特殊工种,如喷涂,铸造等通过劳动法强制采用工业机器人来代替.这样可以大大增加工业机器人的需求数量。
我国的机器人产业化必须由市场来拉动。
机器人作为高技术,它的发展与社会的生产、经济状况密切相关。
