一级倒立摆的Simulink仿真.docx
直线一级倒立摆的自动起摆与稳摆控制

直线一级倒立摆的自动起摆与稳摆控制(Simulink仿真)通过对倒立摆系统的力学及运动学分析,建立系统的非线性数学模型为可见,直线一级倒立摆为单输入双输出系统,利用Simulink可建立上式的框图模型,如图1所示。
图1 直线一级倒立摆系统的非线性Simulink模型倒立摆的起摆问题,是控制理论中的一个经典实验,其实质是倒立摆系统从一个稳定的平衡状态(垂直向下)在外力的作用下自动转移到另一个平衡状态(垂直向上)。
在这个过程中,要求起摆快速,但又不能过于超调。
由于输入、输出之间的非线性,许多常用的线性控制理论都不适用。
基于非线性理论,目前常用的几种起摆方法为:Bang-Bang控制、能量控制、仿人智能控制等。
这里采用Bang-Bang控制作为起摆方法,LQR控制作为稳摆方法,Simulink框图如图2所示。
图2 倒立摆自动起摆控制Simulink框图(Bang-Bang + LQR)图2中,子系统“Inverted Pendulum”是直线一级倒立摆的非线性模型,如图1所示;S函数“ang_proc”模块用于摆杆角度的处理,即将任意角度信号转换为“ -π ~ π”之间的对应值;子系统“Bang-Bang Controller”为Bang-Bang控制器;子系统“LQR Controller”为LQR 控制器。
双击“Bang-Bang Controller”模块可打开Bang-Bang控制器框图如下:图3 Bang-Bang控制器框图图3中,bang_controller是为实现Bang-Bang控制算法而编写的S函数,信号Ang_s是Bang-Bang控制切换角,F_bang是Bang-Bang控制作用力。
双击“LQR Controller”子系统,打开LQR控制器框图如下:图4 LQR控制器框图运行图2中的仿真框图,则基于Bang-Bang控制和LQR控制算法的直线一级倒立摆自动起摆控制效果如图5所示。
(完整word版)一级倒立摆的Simulink仿真

单级倒立摆稳定控制直线-级倒立摆系统在忽略了空'(阻力及各种摩擦Z后,町抽象成小车和匀质摆杆组成的系统,如图1所示。
图2控制系统结构假设小车质量M=0.5kg,匀质摆朴质量m=0.2kg,摆朴长度21 =0.6m, x(t)为小车的水半位移,〃为摆杆的角位移,g = 9.8m/s2o控制的目标是通过外力u⑴使得摆直立向上(即&(t) = 0) o该系统的非线性模型为:(J +inl‘)典(nilcos^)&= niglsin^ (ml cos。
)翼(M其中J二一ml+ m)&= (mlsin0)6^ + u一、非线性模型线性化及建立状态空间模型因为在工作点附近(& = 0.必0)对系统进行线竹:•化,所以可以做如下线性化处理: 03 Q1sin0« 0 --------- 、COS&Q 1-----------------3! 2!当e很小时,由COS0V sine的幕级数展开式可知,忽略高次项后, 可得cos0~l, sin0=0, 0Z 2=0:因此模型线性化后如下:(J+nil A2)0r z +mlx z z =mgl0 (a)取系统的状态变量为% = x,x2 =仪X3 = x4=灰输出y = [x OF包扌舌小车位移和摆杆的角位移.由线性化后运动方程组得故空间状态方程如下:■010 0 ■「xT■ ■x2*00-2.6727 0x21 1.8182 x3f =000 1x3+0_x4J|_x40031.1818 0-4.5455uml0f r + (M+m) x''二u (b) 其中J = -ml3■ ■ xl ■ ■Xx2x1 x30 x4&Y=xlx3X1/二x'=x2—沁—册4(M + m) 一3m44(M + m) - 3m u3(M +m)g4(M + m)l 一3ni-34(M + m)l 一311119 1 00 ''xlM00 -3mg0am xl x2‘ _4(M + m) 一3m x2 x3* ~00 01x3x4J00 3(M + m)g0[_x44(M + m)l - 3ml 044(M + m) - 3m 0一34(M + m)l - 3nil二. 通过Matlab 仿真判断系统的可控与可观性,并说明其物理意义。
一级倒立摆系统仿真及分析

一级倒立摆系统仿真及分析1.摘要本次课程设计,我们小组选择一级倒立摆系统作为物理模型,首先通过物理分析建立数学模型,得到系统的传递函数,通过对传递函数的极点,根轨迹,单位阶跃响应来分析系统稳定性。
建立状态空间模型,利用matlab进行能控能观性分析,输入阶跃信号,分析系统输出响应。
通过设定初始条件,查看系统稳定性,利用simulink绘制系统状态图。
再对系统进行极点配置,进行状态反馈,使得系统在初始状态下处于稳定状态,并绘制系统状态图。
2.课程设计目的倒立摆系统是一个经典的快速、多变量、非线性、绝对不稳定系统,是用来检验某种控制理论或方法的典型方案。
倒立摆控制理论产生的方法和技术在半导体及精密仪器加工、机器人技术、导弹拦截控制系统和航空器对接控制技术等方面具有广阔的开发利用前景。
因此研究倒立摆系统具有重要的实践意义。
3.课程设计题目描述和要求本次课程设计我们小组选择环节项目三:系统状态响应、输出响应的测量。
环节目的:1.利用MATLAB分析线性定常系统。
2.利用SIMULINK进行系统状态空间控制模型仿真,求取系统的状态响应及输出响应。
环节内容、方法:1.给定系统状态空间方程,对系统进行可控性、可观性分析。
并利用SIMULINK 绘制系统的状态图,求取给定系统输入信号和初始状态时的状态响应及输出响应。
2.给定两个系统的状态空间模型,分别求两个系统的特征值;将两个系统的系统矩阵化为标准型;求出给定系统初始状态时,状态的零输入响应;求两个系统的传递函数并分析仿真结果。
4.课程设计报告内容4.1 数学模型的建立及分析对于倒立摆系统,由于其本身是自不稳定的系统,实验建模存在一定的困难。
但是经过小心的假设忽略掉一些次要的因素后,倒立摆系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。
下面我们采用其中的牛顿-欧拉方法建立直线型一级倒立摆系统的数学模型。
在忽略了空气阻力,各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如下图1所示图l 直线一级倒立摆系统我们不妨做以下假设:M小车质量、m摆杆质量、b小车摩擦系数、l摆杆转动轴心到杆质心的长度、I 摆杆惯、F加在小车上的力、x 小车位置、φ摆杆与垂直向上方向的夹角、θ摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下)。
一阶直线倒立摆双闭环PID控制仿真报告

目录摘要 (2)一、一阶倒立摆系统建模 (3)1、对象模型 (3)2、电动机、驱动器及机械传动装置的模型 (4)二、双闭环PID控制器设计 (5)1、仿真验证 (6)2、内环控制器的设计 (9)3、系统外环控制器设计 (12)三、仿真实验 (15)1、绘图子程序 (15)2、仿真结果 (16)四、结论 (18)摘要本报告旨在借助Matlab 仿真软件,设计基于双闭环PID 控制的一阶倒立摆控制系统。
在如图0.1所示的“一阶倒立摆控制系统”中,通过检测小车的位置与摆杆的摆动角,来适当控制驱动电动机拖动力的大小,控制器由一台工业控制计算机(IPC )完成。
图0.1 一阶倒立摆控制系统分析工作原理,可以得出一阶倒立摆系统原理方框图:图0.2 一阶倒立摆控制系统动态结构图本报告将借助于“Simulink 封装技术——子系统”,在模型验证的基础上,采用双闭环PID 控制方案,实现倒立摆位置伺服控制的数字仿真实验。
一、一阶倒立摆系统建模1、对象模型如图1.1所示,设小车的质量为m 0,倒立摆均匀杆的质量为m ,摆长为2l ,摆的偏角为θ,小车的位移为x ,作用在小车上的水平方向的力为F ,O 1为摆角质心。
θxyOFF xF x F yF yllxO 1图1.1 一阶倒立摆的物理模型根据刚体绕定轴转动的动力学微分方程,转动惯量与角加速度乘积等于作用于刚体主动力对该轴力矩的代数和,则 1)摆杆绕其中心的转动方程为θθθcos sin y l F l F J x-= (1-1) 2)摆杆重心的水平运动可描述为)sin (22x θl x dtd m F += (1-2)3)摆杆重心在垂直方向上的运动可描述为)cos (22y θl dtd m mg F =- (1-3)4)小车水平方向上的运动可描述为220dtxd m F F x =- (1-4)由式(1-2)和式(1-4)得F ml x m m =⋅-⋅++)sin (cos )(20θθθθ (1-5) 由式(1-1)、(式1-2)和式(1-3)得θθθsin g cos 2ml x ml ml J =⋅++ )( (1-6) 整理式(1-5)和式(1-6),得⎪⎪⎩⎪⎪⎨⎧++-+-⋅+⋅=-++-⋅+++=))((cos sin )(cos sin cos cos ))((cos sin sin )()(x 2022202222220222222m l J m m l m m l m m l m F m l l m m m m l J g l m m l J lm F m l J θθθθθθθθθθθθ(1-7) 以上式1-7为一阶倒立摆精确模型。
倒立摆控制系统的Simulink仿真

倒立摆控制系统的Simulink 仿真本文针对一个倒立摆系统进行了系统的建模、求解、控制系统的设计,并且使用Simulink 对控制算法进行了仿真。
一、模型的描述倒立摆系统如图(1),设有一个倒立摆装在只能沿x 轴方向移动的小车上,图中1m 为小车的质量,2m 为摆球的质量,g 为重力加速度,l 为摆长,J 为摆的转动惯量。
当小车受到外力()f t 的作用时,小车产生位移()x t ,且摆产生角位移()t θ。
二、模型的建立下面针对该倒立摆系统进行建模求解。
当小车1m 在外力作用下产生位移()x t 时,摆球受力情况如图(2)所示。
图中2m g 为摆球2m 所受重力,222()d x t m dt 为x 方向的惯性力,2sin ()m g t θ为垂直于摆杆方向的重力分量。
在x 方向上,小车的惯性力矩为212()d x t m dt ,摆球产生的位移量为()sin ()x t l t θ+;在垂直于摆杆的方向上,摆球的转动惯性力为22()d t J dt θ;222()d x t m dt的分力为222()cos ()d x t m t dt θ。
图(1)装有倒立摆的小车 图(2)倒立摆受力图根据牛顿运动定律,按照力的平衡原理,可以分别列出该系统在x 方向上和垂直于摆杆方向上的的运动方程222122222()()[sin ()]()d x t d x t d l t m m m f t dt dt dt θ++=(1) 222222()()cos ()sin ()d t d x t J m l t m lg t dt dtθθθ+= (2) 三、模型的求解3.1微分方程组的求解联立式(1)、(2),经过方程组的恒等变形得2222222122222()()2[()cos ()]sin 2()2sin ()()2()d x t d t m m J m l t m l g t Jm l t dt dtJf t θθθθ+-=-++ (3) 2222222212221222()()[cos ()()]sin ()cos ()()()sin ()()d t d t m l t m m J m l t t dt dtm m m lg t m lf t θθθθθθ-+=-++ (4) 由式(3)、(4)令''121343()(),(),()(),()()x t t x x t x t x t x t x t θ====,可建立如下的微分方程组进行求解'12'2222221222222122'34'222422222122()()1()()(sin ()cos ()()()sin ()cos ()()())()()1()()(sin 2()2sin ()()2())2[()cos ()]x t x t d t x t x m l t t m m m lg t m l t m m J dt m lf t x t x t d t x t m l g t Jm l t Jf t m m J m l t dt θθθθθθθθθ⎧=⎪⎪=-+⎪-+⎪+⎨==-+++-⎪⎪⎪⎪⎩3.2控制系统的分析与设计在该模型中,对该倒立摆系统实施角度环、速度换的控制,并假设小车在运行过程中受到空气阻力,阻力大小与小车的速度成正比。
一级倒立摆的Simulink仿真

一级倒立摆的Simulink仿真第一篇:一级倒立摆的Simulink仿真单级倒立摆稳定控制直线一级倒立摆系统在忽略了空气阻力及各种摩擦之后,可抽象成小车和匀质摆杆组成的系统,如图1所示。
杆长为2λmguθ图1 直线一级倒立摆系统图2 控制系统结构假设小车质量M =0.5kg,匀质摆杆质量m=0.2kg,摆杆长度2l =0.6m,x(t)为小车的水平位移,θ为摆杆的角位移,g=9.8m/s2。
控制的目标是通过外力u(t)使得摆直立向上(即θ(t)=0)。
该系统的非线性模型为:&&+(mlcosθ)&12&=mglsinθ(J+ml2)θxJ=ml。
,其中2&&&3&=(mlsinθ)θ+u(mlcosθ)θ+(M+m)&x解:一、非线性模型线性化及建立状态空间模型&=0)对系统进行线性化,所以因为在工作点附近(θ=0,θsinθ≈θ-θ33!可以做如下线性化处理:,cosθ≈1-θ22!当θ很小时,由cosθ、sinθ的幂级数展开式可知,忽略高次项后,可得cosθ≈1,sinθ≈θ,θ’^2≈0;因此模型线性化后如下:(J+ml^2)θ’’+mlx’’=mglθ(a)mlθ’’+(M+m)x’’=u(b)其中J=ml13&,输出y=[x&,x3=θ,x4=θ取系统的状态变量为x1=x,x2=x的角位移.θ]T包括小车位移和摆杆⎡x1⎤⎡x⎤⎢x2⎥⎢x'⎥⎡x⎤⎡x1⎤即X=⎢⎥=⎢⎥ Y=⎢⎥=⎢⎥⎢x3⎥⎢θ⎥⎣θ⎦⎣x3⎦⎢⎥⎢⎥⎣x4⎦⎣θ'⎦由线性化后运动方程组得-3mg4X1’=x’=x2 x2’=x’’=x3+u4(M+m)-3m4(M+m)-3m3(M+m)g-3X3’ =θ’=x4 x4’=θ’’=x3+u4(M+m)l-3ml4(M+m)l-3ml故空间状态方程如下:⎡0⎢⎡x1'⎤⎢0⎢x2'⎥⎢X’=⎢⎥=⎢⎢x3'⎥⎢0⎢⎥⎢⎣x4'⎦⎢0⎣100⎤⎡0⎤⎥⎢⎥-3mgx14⎡⎤⎢⎥00⎥⎢⎥4(M+m)-3m⎥x2⎢4(M+m)-3m⎥⎢⎥+ ⎢⎥001⎥0⎥⎢x3⎥⎢⎥⎢⎥⎥x4⎢⎥3(M+m)g-300⎥⎣⎦⎢⎥4(M+m)l-3ml⎦⎣4(M+m)l-3ml ⎦u⎡x1'⎤⎡0⎢x2'⎥⎢0⎢⎥⎢X’=⎢x3'⎥=⎢⎥⎢0⎣x4'⎦⎢⎣0100⎤0⎡⎤x1⎡⎤⎢1.8182⎥⎢x2⎥0-2.67270⎥⎥⎢⎥ + ⎢⎥ ux3⎥001⎥⎢⎢0⎥⎢⎥⎥⎣x4⎦⎢⎥031.18180⎦⎣-4.5455⎦⎡x1⎤⎢⎥⎡x1⎤⎡1000⎤⎢x2⎥Y= ⎢⎥=⎢⎥⎢⎥⎣x3⎦⎣0010⎦x3⎢⎥⎣x4⎦二、通过Matlab仿真判断系统的可控与可观性,并说明其物理意义。
基于一阶倒立摆的matlab仿真实验

成都理工大学工程技术学院基于一阶倒立摆的matlab仿真实验实验人员: --------------学号:-----------------实验日期:20150618摘要本文主要研究的是一级倒立摆的控制问题,并对其参数进行了优化。
倒立摆是典型的快速、多变量、非线性、强耦合、自然不稳定系统。
由于在实际中有很多这样的系统,因此对它的研究在理论上和方法论上均有深远的意义。
本文首先简单的介绍了一下倒立摆以及倒立摆的控制方法,并对其参数优化算法做了分类介绍。
然后,介绍了本文选用的优化参数的状态空间极点的配置和PID控制。
接着建立了一级倒立摆的数学模型,并求出其状态空间描述。
本文着重讲述的是利用状态空间中极点配置实现方法。
最后,用Simulink对系统进行了仿真,得出在实际控制中是两种比较好的控制方法。
目录1 引言 (4)1.1 倒立摆介绍以及应用 (4)1.2 倒立摆的控制方法 (5)2单级倒立摆数学模型的建立 (6)2.1传递函数 (8)2.2状态空间方程 (9)3系统Matlab 仿真和开环响应 (10)4 系统设计 (15)4.1极点配置与控制器的设计 (15)4.2系统仿真: (16)4.3仿真结果 (17)4.4根据传递函数设计第二种控制方法-----PID串级控制 (18)5结论 (19)1 引言1.1 倒立摆介绍以及应用倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。
通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。
通过对它的研究不仅可以解决控制中的理论和技术实现问题,还能将控制理论涉及的主要基础学科:力学,数学和计算机科学进行有机的综合应用。
其控制方法和思路无论对理论或实际的过程控制都有很好的启迪,是检验各种控制理论和方法的有效的“试金石”。
倒立摆控制系统的Simulink仿真

倒立摆控制系统的Simulink 仿真本文针对一个倒立摆系统进行了系统的建模、求解、控制系统的设计,并且使用Simulink 对控制算法进行了仿真。
一、模型的描述倒立摆系统如图(1),设有一个倒立摆装在只能沿x 轴方向移动的小车上,图中1m 为小车的质量,2m 为摆球的质量,g 为重力加速度,l 为摆长,J 为摆的转动惯量。
当小车受到外力()f t 的作用时,小车产生位移()x t ,且摆产生角位移()t θ。
二、模型的建立下面针对该倒立摆系统进行建模求解。
当小车1m 在外力作用下产生位移()x t 时,摆球受力情况如图(2)所示。
图中2m g 为摆球2m 所受重力,222()d x t m dt 为x 方向的惯性力,2sin ()m g t θ为垂直于摆杆方向的重力分量。
在x 方向上,小车的惯性力矩为212()d x t m dt ,摆球产生的位移量为()sin ()x t l t θ+;在垂直于摆杆的方向上,摆球的转动惯性力为22()d t J dt θ;222()d x t m dt的分力为222()cos ()d x t m t dt θ。
图(1)装有倒立摆的小车 图(2)倒立摆受力图根据牛顿运动定律,按照力的平衡原理,可以分别列出该系统在x 方向上和垂直于摆杆方向上的的运动方程222122222()()[sin ()]()d x t d x t d l t m m m f t dt dt dt θ++=(1) 222222()()cos ()sin ()d t d x t J m l t m lg t dt dtθθθ+= (2) 三、模型的求解3.1微分方程组的求解联立式(1)、(2),经过方程组的恒等变形得2222222122222()()2[()cos ()]sin 2()2sin ()()2()d x t d t m m J m l t m l g t Jm l t dt dtJf t θθθθ+-=-++ (3) 2222222212221222()()[cos ()()]sin ()cos ()()()sin ()()d t d t m l t m m J m l t t dt dtm m m lg t m lf t θθθθθθ-+=-++ (4) 由式(3)、(4)令''121343()(),(),()(),()()x t t x x t x t x t x t x t θ====,可建立如下的微分方程组进行求解'12'2222221222222122'34'222422222122()()1()()(sin ()cos ()()()sin ()cos ()()())()()1()()(sin 2()2sin ()()2())2[()cos ()]x t x t d t x t x m l t t m m m lg t m l t m m J dt m lf t x t x t d t x t m l g t Jm l t Jf t m m J m l t dt θθθθθθθθθ⎧=⎪⎪=-+⎪-+⎪+⎨==-+++-⎪⎪⎪⎪⎩3.2控制系统的分析与设计在该模型中,对该倒立摆系统实施角度环、速度换的控制,并假设小车在运行过程中受到空气阻力,阻力大小与小车的速度成正比。
直线一级倒立摆MATLAB仿真报告

1便携式倒立摆实验简介倒立摆装置被公认为是自动控制理论中的典型试验设备,是控制理论教学和科研中不可多得的典型物理模型。
本实验基于便携式直线一级倒立摆试验系统研究其稳摆控制原理。
1.1主要实验设备及仪器便携式直线一级倒立摆实验箱一套控制计算机一台便携式直线一级倒立摆实验软件一套1.2便携式倒立摆系统结构及工作原理便携式直线一级倒立摆试验系统总体结构如图1所示:图1便携式一级倒立摆试验系统总体结构图主体结构包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主体、驱动器、电源和数据采集卡都置于实验箱内,实验箱通过一条USB数据线与上位机进行数据交换,另有一条线接220v交流电源。
便携式直线一级倒立摆的工作原理如图2所示:图2 便携式一级倒立摆工作原理图数据采集卡采集到旋转编码器数据和电机尾部编码器数据,旋转编码器与摆杆同轴,电机与小车通过皮带连接,所以通过计算就可以得到摆杆的角位移以及小车位移,角位移差分得角速度,位移差分可得速度,然后根据自动控制中的各种理论转化的算法计算出控制量。
控制量由计算机通过USB数据线下发给伺服驱动器,由驱动器实现对电机控制,电机尾部编码器连接到驱动器形成闭环,从而可以实现摆杆直立不倒以及自摆起。
2便携式倒立摆控制原理方框图便携式倒立摆是具有反馈功能的闭环系统,其控制目标是实现在静态和动态下的稳摆。
∅g=0当输入量为理想摆角,即时,偏差为0,控制器不工作;当输入量不为理想摆角时,偏差存在,控制器做出决策,驱动电机,使小车摆杆系统发生相应位移,输出的摆角通过角位移传感器作用于输出量,达到减小偏差的目的。
根据控制原理绘制出控制方框图如图3所示:图3 便携式一级倒立摆控制原理方框图3建立小车-摆杆数学模型便携式倒立摆系统主要由小车、摆杆等组成,它们之间自由连接。
小车可以在导轨上自由移动,摆杆可以在铅垂的平面内自由地摆动。
在忽略了空气阻力和各种摩擦之后,可将便携式倒立摆系统抽象成小车和匀质杆组成的刚体系统,在惯性坐标内应用经典力学理论建立系统的动力学方程,采用力学分析方法建立小车-摆杆的数学模型。
单级倒立摆控制系统设计及MATLAB中的仿真

单级倒立摆控制系统设计及simulink仿真摘要:倒立摆系统是一个典型的多变量、非线性、强藕合和快速运动的自然不稳定系统。
因此倒立摆在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义,相关的科研成果己经应用到航天科技和机器人学等诸多领域。
单级倒立摆系统是一种广泛应用的物理模型。
控制单级倒立摆载体的运动是保证倒立摆稳定性的关键因素。
为了避免常用的物理反馈分析方法和运动轨迹摄像制导控制方法的某些缺点,本文从力学的角度提出对倒立摆的运动进行纯角度制导分析,完成了对倒立摆载体的角度制导运动微分方程的数学建模,设计了该模型的模糊控制系统,并利用 Matlab\simulink软件工具对倒立摆的运动进行了计算机仿真。
实验表明,这种模糊控制配合代数解析方法的运算速度和计算机仿真的效果均较物理反馈制导控制方法有了一定的提高。
该方法可以有效地改善单级倒立摆控制系统的性能。
本论文的主要工作是研究了直线一级倒立摆系统的模糊控制问题,用Matlab和Simulink对一级倒立摆模糊控制系统进行了仿真,验证了设计的可行性。
本文论述了一级倒立摆数学建模方法,推导出他们的微分方程,以及线性化后的状态方程。
讨论了单级倒立摆系统的模糊控制方法和操作步骤。
用Simulink实现了单级倒立摆模糊控制仿真系统,分别给出一级倒立摆系统控制量的响应曲线。
通过仿真说明控制器的有效性和实现性。
关键词:单级倒立摆;仿真;模糊控制;运动;建模;SimulinkDesign of single stage inverted pendulum control systemand Simulink simulationAbstract: inverted pendulum system is unstable system with a typical multi variable, nonlinear, strong coupled and fast motion. So the research on the attitude adjustment of the double foot robot and the attitude adjustment of the rocket launching process and the helicopter flight control field have practical,significance. The related scientific research achievements have been applied to many fields such as aerospace science and robotics. Single inverted pendulum system is a widely used physical model. Controlling the movement of the single inverted pendulum is the key factor to guarantee the stability of the inverted pendulum. In order to avoid some shortcomings of common physical feedback analysis method and motion trajectory camera guidance control method, this paper presents a pure angle guidance analysis on the motionof the inverted pendulum, and designs the fuzzy control system of the model. Experimental results show that the operation speed and computer simulation of this kind of fuzzy control combined with algebraic analysis method are improved by the physical feedback control method. This method can effectively improve the performance of a single stage inverted pendulum control system. In this paper, the main work of this paper is to study the fuzzy control of a linear inverted pendulum system, and the Matlab and Simulink to simulate the fuzzy control system of a single inverted pendulum, verify the feasibility of the design. And a mathematical modeling method of an inverted pendulum is described, their differential equations are derived, and the equation of state is linearized. The fuzzy control method and operation steps of single stage inverted pendulum system are discussed. Using Simulink to realize the fuzzy control simulation system of a single inverted pendulum, the response curve of the control of an inverted pendulum system is given. The effectiveness and the implementation of the controller are illustrated by simulation.Keywords: Inverted pendulum; Simulation; Fuzzy control; Motion; modeling; Simulink 引言倒立摆系统是研究控制理论的一种典型实验装置,具有成本低廉,结构简单,物理参数和结构易于调整的优点,是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不稳定系统。
(完整word版)一级倒立摆控制系统设计

基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统.二、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度.当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
三、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡.四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:分析工作原理,可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图下面的工作是根据结构框图,分析和解决各个环节的传递函数!1.一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中:M:小车质量m:为摆杆质量J :为摆杆惯量 F:加在小车上的力 x :小车位置θ:摆杆与垂直向上方向的夹角l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知:(1) 摆杆绕其重心的转动方程为(2) 摆杆重心的运动方程为得(3)小车水平方向上的运动为22..........(4)x d xF F M d t -=联列上述4个方程,可以得出一阶倒立精确气模型:()()()()()()()2222222222222222sin .sin cos cos cos .sin cos .lg sin cos J ml F ml J ml m l g x J ml M m m l ml F m l M m m m l M m J ml θθθθθθθθθθθθ⎧+++-⎪=++-⎪⎨+-+⎪=⎪-++⎩式中J 为摆杆的转动惯量:32m l J =sin cos ..........(1)y x J F l F l θθθ=-2222(sin ) (2)(cos ) (3)x y d F m x l d td F mg m l d t θθ=+=-若只考虑θ在其工作点附近θ0=0附近(︒︒≤≤-1010θ)的细微变化,则可以近似认为:⎪⎩⎪⎨⎧≈≈≈1cos sin 02θθθθ ⎪⎪⎩⎪⎪⎨⎧++-+=++-+=2..2222..)(lg )()()(Mml m M J mlF m m M Mml m M J g l m F ml J x θθθ 若取小车质量M=2kg,摆杆质量m=1kg,摆杆长度2 l =1m ,重力加速度取g=2/10s m ,则可以得一阶倒立摆简化模型:....0.44 3.330.412x F F θθθ⎧=-⎪⎨⎪=-+⎩ 拉氏变换即 G 1(s )= ; G 2(s)=一阶倒立摆环节问题解决!2.电动机驱动器选用日本松下电工MSMA021型小惯量交流伺服电动机,其有关参数如下: 驱动电压:U=0~100V 额定功率:PN=200W 额定转速:n=3000r/min 转动惯量:J=3×10-6kg 。
直线一级倒立摆MATLAB仿真报告
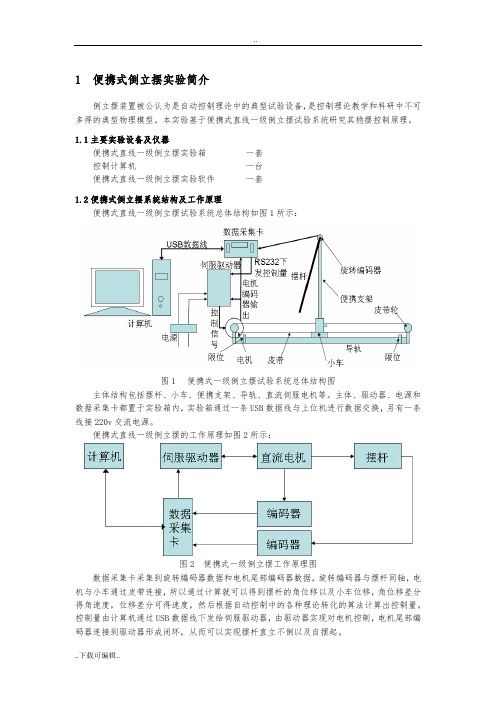
1便携式倒立摆实验简介倒立摆装置被公认为是自动控制理论中的典型试验设备,是控制理论教学和科研中不可多得的典型物理模型。
本实验基于便携式直线一级倒立摆试验系统研究其稳摆控制原理。
1.1主要实验设备及仪器便携式直线一级倒立摆实验箱一套控制计算机一台便携式直线一级倒立摆实验软件一套1.2便携式倒立摆系统结构及工作原理便携式直线一级倒立摆试验系统总体结构如图1所示:图1 便携式一级倒立摆试验系统总体结构图主体结构包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主体、驱动器、电源和数据采集卡都置于实验箱内,实验箱通过一条USB数据线与上位机进行数据交换,另有一条线接220v交流电源。
便携式直线一级倒立摆的工作原理如图2所示:图2 便携式一级倒立摆工作原理图数据采集卡采集到旋转编码器数据和电机尾部编码器数据,旋转编码器与摆杆同轴,电机与小车通过皮带连接,所以通过计算就可以得到摆杆的角位移以及小车位移,角位移差分得角速度,位移差分可得速度,然后根据自动控制中的各种理论转化的算法计算出控制量。
控制量由计算机通过USB数据线下发给伺服驱动器,由驱动器实现对电机控制,电机尾部编码器连接到驱动器形成闭环,从而可以实现摆杆直立不倒以及自摆起。
2便携式倒立摆控制原理方框图便携式倒立摆是具有反馈功能的闭环系统,其控制目标是实现在静态和动态下的稳摆。
当输入量为理想摆角,即∅∅=0时,偏差为0,控制器不工作;当输入量不为理想摆角时,偏差存在,控制器做出决策,驱动电机,使小车摆杆系统发生相应位移,输出的摆角通过角位移传感器作用于输出量,达到减小偏差的目的。
根据控制原理绘制出控制方框图如图3所示:图3 便携式一级倒立摆控制原理方框图3建立小车-摆杆数学模型便携式倒立摆系统主要由小车、摆杆等组成,它们之间自由连接。
小车可以在导轨上自由移动,摆杆可以在铅垂的平面内自由地摆动。
在忽略了空气阻力和各种摩擦之后,可将便携式倒立摆系统抽象成小车和匀质杆组成的刚体系统,在惯性坐标内应用经典力学理论建立系统的动力学方程,采用力学分析方法建立小车-摆杆的数学模型。
一阶倒立摆建模及simulink仿真

《现代控制理论》三级项目报告题目:一级倒立摆控制系统设计姓名:刘然学号:160103010258专业:过程控制4班指导教师:吴忠强分数:2019年4月一级倒立摆控制系统设计倒立摆是处于倒置不稳定状态,人为控制使其处于动态平衡的一种摆。
对于倒立摆系统的控制研究长期以来被认为是控制理论及其应用领域里引起人们极大兴趣的问题,倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统。
研究倒立摆控制能有效地反映控制中的许多问题,倒立摆研究具有重要的理论价值和应用价值,理论上,它是检验各种新的控制理论和方法的有效实验装置。
应用上,倒立摆广泛应用于控制理论研究!航空航天控制,机器人、杂技顶杆表演等领域,在自动化领域中具有重要的价值。
另外,由于此装置成本低廉,结构简单,便于用模拟、数字等不同方式控制,在控制理论教学和科研中也有很多应用。
本文中,以一级倒立摆为研究对象,对它的起摆以及稳定控制做了研究,主要工作如下:1.首先介绍了倒立摆系统的组成和控制原理,建立了一级倒立摆的数学模型,对倒立摆系统进行定性分析,说明在平衡点是能控的。
2.分析了倒立摆的起摆过程,对倒立摆的起摆能量反馈控制进行分析与说明。
3.在matlab2018a的simulink库下对倒立摆构造单级倒立摆状态反馈控制系统的仿真模型。
4.对这次仿真的总结。
一、倒立摆的控制目标倒立摆的控制问题就是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
二、建立单级倒立摆系统的状态空间模型其中,质量为M的小车在水平方向滑动,质量为m的球连在长度为L的刚性摆一端,x表示小车的位移,u是作用在小车上的力,通过移动小车使带有小球的摆杆始终处于垂直的位置。
为了简单起见,假设小车和摆仅在一个平面内运动,且不考虑摩擦、摆杆的质量和空气阻力。
如图1图1设系统的动态特性可以用小车的位移和速度及杆偏离垂线的角度θ和角速度⋅θ来描述。
直线一级倒立摆系统的建模及仿真

计算机控制技术课程设计实验:直线一级倒立摆系统的建模及仿真一、已知条件:图1倒立摆简化模型摆杆角度为输出,小车的位移为输入。
导轨中点为坐标轴的中心即零点,右向为坐标值增加的方向,杆偏移其瞬时平衡位置右侧的角度为正值。
二、任务要求:总体任务通过调节PID参数,设计PID控制器实现摆杆在受到干扰的情况下,依然能恢复平衡。
具体包括以下几部分:1. 理论推导包括倒立摆系统的动力学模型,传递函数,离散传递函数,状态空间或差分方程,稳定性分析,PID控制器设计2. 程序实现实现内容:倒立摆系统模型,控制器以及仿真结果的显示。
开发语言和工具:Matlab m 文件或C/C++ (工具:VC++或其它)3. PID控制参数设定及仿真结果。
分别列出不同杆长的仿真结果(例如:L=0.25 和L=0.5)。
4. 将理论推导、程序实现、仿真结果写成实验报告。
具体求解过程如下:一,倒立摆系统动力学模型的建立图1 摆杆的受力分析图以摆杆为研究对象,对其进行受力分析,如图1所示。
根据质点系的达朗贝尔原理得IC I 0F CP mg CP M →→⨯+⨯-= (1)式中,IC F 为杆的惯性力,表达式为()IC C P CP CP IP ICP ICP t n t nF ma m a a a F F F ==++=++,m 为杆的质量,g 为重力加速度,I M 为杆的惯性力偶。
惯性力及惯性力偶的大小分别为2222IP P ICP I c 2221,,3t d x d d F ma m F m m M J mL dt dt dt θθαα======(2)式中,α为杆的角加速度,P a 为小车的加速度,2L 为杆的长度,θ为杆偏离中心位置的角度,x 偏离轨道中心的位移。
对(2)式代入(1)式,并整理可得22224sin cos 3d d x L g dt dt θθθ-=-(3) 当摆动较小时,可以进行近似处理sin ,cos 1θθθ≈≈。
一阶倒立摆系统建模与仿真研究

一阶倒立摆系统建模与仿真研究一阶倒立摆系统是一种典型的非线性控制系统,具有多种状态和复杂的运动特性。
在实际生活中,倒立摆被广泛应用于许多领域,如机器人平衡控制、航空航天、制造业等。
因此,对一阶倒立摆系统进行建模与仿真研究具有重要的理论价值和实际意义。
ml''(t) + b*l'(t) + k*l(t) = F(t)其中,m为质量,b为阻尼系数,k为弹簧常数,l(t)为摆杆的位移,l'(t)为摆杆的加速度,l''(t)为摆杆的角加速度,F(t)为外界作用力。
在仿真过程中,需要设定摆杆的初始位置和速度。
一般而言,初始位置设为0,初始速度设为0。
边界条件则根据具体实验需求进行设定,如限制摆杆的最大位移、最大速度等。
利用MATLAB/Simulink等仿真软件进行建模和实验,可以方便地通过改变输入信号的参数(如力F)或系统参数(如质量m、阻尼系数b、弹簧常数k)来探究一阶倒立摆系统的性能和反应。
通过仿真实验,我们可以观察到一阶倒立摆系统在受到不同输入信号的作用下,会呈现出不同的运动规律。
在适当的输入信号作用下,摆杆能够达到稳定状态;而在某些特定的输入信号作用下,摆杆可能会出现共振现象。
在仿真过程中,我们可以发现一阶倒立摆系统具有一定的鲁棒性。
在一定范围内,即使输入信号发生变化或系统参数产生偏差,摆杆也能够保持稳定状态。
然而,当输入信号或系统参数超过一定范围时,摆杆可能会出现共振现象,导致系统失稳。
因此,在实际应用中,需要对输入信号和系统参数进行合理控制,以保证系统的稳定性。
为了避免共振现象的发生,可以通过优化系统参数或采用其他控制策略来实现。
例如,适当增加阻尼系数b能够减小系统的振荡幅度,有利于系统尽快达到稳定状态。
可以采用反馈控制策略,根据摆杆的实时运动状态调整输入信号,以抑制系统的共振响应。
本文对一阶倒立摆系统进行了建模与仿真研究,通过观察不同参数设置下的系统性能和反应,对其运动规律、鲁棒性及稳定性进行了分析。
基于Simulink的单级倒立摆仿真对比

关键词 :非线性系统 ;单级倒立摆 ;极点配置 ; T2S模糊控制模型 ; Simulink仿真
中图分类号 : TP273. 4
文献标识码 : A
An S im ula tion Study of S ingle Inverted Pendulum Ba sed on T2S Fuzzy Con trol M odel L I Guo2hui
4,故系统可控 , 可任意配置极点. 然后进行稳定性检查 : 由 MA TLAB 中 的 e ig ( A ) 求 得 特 征 值
70
大连交通大学学报
第 29卷
[ 0 0 4. 949 7 - 4. 949 7 ],故系统不稳定. 采用状态反馈方法使系统稳定并配置极点. 设期望的闭环 极点位置为 S1, 2 = - 3 ±j4. 457, S3, 4 = - 2,由 MATLAB求得反馈增益矩阵 K = [ - 160. 970 1 - 108. 151 3 - 485. 944 7 - 102. 075 6 ]. 2. 3 仿真研究与结果分析
M j ( x) ; A =
μ i
(
x)
Ai;
B
=
μ i
( x)
B i;
j=1
i =1
i =1
l
l
n
∑ ∑ ∏ C =
μ i
(
x)
Ci;
D
=
μ i
(
x)
D i;
Mi
( x)
=
M
i j
( x)
i =1
i =1
j =1
l
∑ 假设 : M i ( x) ≥ 0, M j ( x) > 0, M i ( x) 表示 x属于 M i 的隶属度函数 ,同时它也表示第 i条模糊规则的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单级倒立摆稳定控制
直线一级倒立摆系统在忽略了空气阻力及各种摩擦之后,可抽象成小车和匀质摆杆组成的系统,如图1所示。
mg θ
杆长为λ
2u
图1 直线一级倒立摆系统
图2 控制系统结构
假设小车质量M =0.5kg ,匀质摆杆质量m=0.2kg ,摆杆长度2l =0.6m ,x (t )为小车的水平
位移,θ为摆杆的角位移,2
/8.9s m g =。
控制的目标是通过外力u (t)使得摆直立向上(即
0)(=t θ)。
该系统的非线性模型为:
u
ml x m M ml mgl x ml ml J +=++=++22)sin ()()cos (sin )cos ()(θθθθθ
θθ&&&&&&&&&,其中2
31
ml J =。
解:
一、 非线性模型线性化及建立状态空间模型
因为在工作点附近(0,0==θθ&
)对系统进行线性化,所以
可以做如下线性化处理:
3
2
sin ,cos 13!
2!θθθθθ≈-
≈-
当θ很小时,由cos θ、sin θ的幂级数展开式可知,忽略高次项后, 可得cos θ≈1,sin θ≈θ,θ’^2≈0;
因此模型线性化后如下: (J+ml^2)θ’’+mlx ’’=mgl θ (a)
ml θ’’+(M+m) x ’’=u (b) 其中2
31ml J =
取系统的状态变量为,
,,,4321θθ&&====x x x x x x 输出T
x y ][θ=包括小车位移和摆杆
的角位移.
即X=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x =⎥⎥⎥⎥⎦⎤
⎢⎢⎢⎢⎣⎡''θθx x Y=⎥⎦⎤⎢⎣⎡θx =⎥⎦⎤⎢⎣⎡31x x 由线性化后运动方程组得
X1’=x ’=x2 x2’=x ’’=m m M mg 3)(43-+-x3+m m M 3)(44
-+u
X3’ =θ’=x4 x4’=θ’’=ml l m M g m M 3)(4)(3-++x3+ml l m M 3)(43
-+-u
故空间状态方程如下:
X ’=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'4'3'2'1x x x x =⎥⎥⎥⎥⎥⎥
⎥⎦⎤
⎢⎢⎢⎢⎢⎢⎢⎣⎡-++-+-03)(4)(300100003)(4300001
0ml l m M g m M m m M mg ⎥⎥⎥
⎥⎦⎤
⎢⎢⎢⎢⎣⎡4321x x x x + ⎥
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-+--+ml l m M m m M 3)(43
03)(440
u
X ’=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡'4'3'2'1x x x x =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣
⎡-01818.3100100006727.20000
1
⎥⎥⎥
⎥⎦⎤
⎢⎢⎢⎢⎣⎡4321x x x x + ⎥⎥⎥
⎥⎦⎤
⎢⎢⎢⎢⎣⎡-5455.408182.10 u
Y= ⎥⎦⎤⎢⎣⎡31x x =⎥⎦⎤⎢⎣
⎡01000001 ⎥
⎥⎥
⎥⎦⎤⎢⎢⎢⎢⎣⎡4321x x x x 二、通过Matlab 仿真判断系统的可控与可观性,并说明其物理意义。
(1)判断可控性
代码:
A=[0 1 0 0;
0 0 -2.627 0; 0 0 0 1; 0 0 31.1818 0];
B=[0;1.8182;0;-4.5455];
P=ctrb(A,B); n=rank(P); 运行了得n= 4
所以P 为满秩,系统能控
(2)判断可观性 代码:
A=[0 1 0 0;
0 0 -2.627 0; 0 0 0 1; 0 0 31.1818 0];
B=[0;1.8182;0;-4.5455]; C=[1 0 0 0;
0 0 1 0]; P=obsv(A,C); n=rank(P); 运行了得n= 4
所以P 为满秩,系统能观。
三、能否通过状态反馈任意配置系统的极点?若能,通过Matlab 仿真确定反馈控制规律K (如图2),使得闭环极点配置在
j
±-=-=-=1,2,14.321λλλ上。
并给出系统在施加一个单位脉冲输入时
状态响应曲线;
答: 因为系统完全能控,所以能通过状态反馈任意配置系统的极点。
要将闭环极点配置在
j
±-=-=-=1,2,14.321λλλ上,所以期望特征方程为
|λI —(A-BK)|=(λ+1)*(λ+2)*((λ+1)^2+1) =λ^4+5λ^3+10λ^2+10λ+4
Matlab求解K如下:
A=[0 1 0 0;
0 0 -2.627 0;
0 0 0 1;
0 0 31.1818 0];
B=[0;1.8182;0;-4.5455];
J=[-1 -2 -1+i -1-i];
K=place(A,B,J);
运行得:
K=[ -0.089378 -0.22345 -9.0957 -1.1894];
未加入极点配置。
仿真图:
未进行极点配置仿真电路图(1)X的响应图:
Θ的响应图:
配置后:
加入极点配置仿真图(2)X的响应图:
Θ的响应图:
四、用MatLab中的lqr函数,可以得到最优控制器对应的K。
要求用LQR控制算法控制倒立摆摆动至竖直状态,并可以控制倒立摆左移和右移;
欲对系统进行最优状态反馈设计,及小化性能指标为:
J= 1 2 0∞XTQX+UTRU dt
编写matalab程序如下:
A=[0 1 0 0;
0 0 -2.627 0;
0 0 0 1;
0 0 31.1818 0];
B=[0;1.8182;0;-4.5455];
C=[1 0 0 0;
0 0 1 0];
D=[0;0]
x=1;
y=1;
Q=[x 0 0 0;
0 0 0 0;
0 0 y 0;
0 0 0 0];
R=1;
G=lqr(A,B,Q,R);
A1=[(A-B*G)];
B1=[B];
C1=[C];
D1=[D];
t=0:0.01:5;
U=zeros(size(t));
x0=[0.1 0 0.1 0];
[Y,X]=lsim(A1,B1,C1,D1,U,t,x0); plot(t,Y);
legend('小车','倒立摆');
运行可得:
G=[-1 -1.5495 -18.68 -3.4559]
由图分析可得调节时间很长,所以增加Q的比重,将上程序中的x,y改为x=150,y=150.运行可得:
G=[-12.247 -9.3413 -41.934 -7.7732]
比较可得,控制效果明显改善。
但反馈增益变大,意味着控制作用变强,消耗能量变大。
将G放入系统中,进行simulink仿真可得:
仿真电路图:
仿真结果:X的响应图:
Θ的响应图:
五、写出本次仿真实验的心得体会。
本实验,从数学建模到仿真系统的搭建,再到加进控制环节进行实时控制,最后得出结果的过程中,参考了大量的资料,通过对比整合,设计出了适合自己的一套实验方法:倒立摆数学模型推导部分:首先用线性化数学模型,接着用动态系统空间状态方程法导出状态方程系数矩阵,然后用MATLAB对系统进行可控可观判断及进行几点配置,加入配置后在Simulink软件上进行系统仿真。
最后通过matlab求解线性二次型最优控制的G矩阵,然后加入形同进行Simulink 仿真。
通过本实验,掌握了倒立摆仿真的整个过程,熟悉了MATLAB的仿真软件Simulink的使用,也对系统控制有了较好的理解。
通过仿真,再次认识到了自动控制在改善系统性能方面的重要性,并激发了良好的关于系统控制方面的学习兴趣。
除此之外,通过本次大作业,让我学会了很多word的操作,在此基础上,相信在以后的学习将会有较大帮助。
------------word文档可编辑-------------。
