穷举法与粒子群算法的比较_王得燕

合集下载

基于改进粒子群算法的多阈值图像分割_武燕

Microcomputer Applications Vol. 27, No.5, 2011 技术交流微型电脑应用 2011年第27卷第5期 ·59·文章编号：1007-757X(2011)05-0059-03基于改进粒子群算法的多阈值图像分割武燕，张冰摘要：提出了一种改进的粒子群算法，在初始化种群时采用相对基学习原理，以获得较优的初始候选解；在后期迭代过程中引入扩张模型，使粒子不易陷入局部极小值点，并将其用于多阈值图像分割。

由最大熵阈值法得到所要优化的目标函数，用改进的粒子群算法对其进行优化，使其能够准确并迅速的得到分割的最佳阈值组合，并用该阈值组合对图像进行分割。

将此分割结果与遗传算法的多阈值分割结果相比较可以看出，该算法可更为准确快速的实现图像分割。

关键词：粒子群优化算法；相对基学习；扩张模型；多阈值；图像分割中图法分类号：TP301 文献标志码：A0 引言图像分割是目标识别的首要和关键步骤，其目的是将背景与目标分离，为计算机视觉的后续处理提供依据。

图像分割的方法主要包括阈值法、边缘检测等[1]。

其中，阈值分割因其快速简单使其成为图像分割中最基本最常用的方法。

常用的阈值法有最大熵阈值法、最大类间方差阈值法及最小误差阈值法等。

最大熵阈值法的原则使得总熵最大。

所以确定阈值是阈值分割的关键，根据阈值的个数，图像阈值分割可以分为单阈值分割和多阈值分割。

多阈值分割问题可转化为一系列单阈值分割问题来进行解决，但此需要在全灰度范围内搜索一个最佳门限的组合，耗时较多，难于实际应用。

为了简化计算，可以利用遗传、免疫等进化算法来搜索最佳阈值[2]。

而在本文中，将改进的粒子群算法引入图像分割中的多阈值选择，对最大熵阈值法(ME)进行了优化，使其能够准确并迅速地找到图像分割的最佳阈值，对图像进行多阈值分割。

1 基于最大熵的多阈值图像分割最大熵阈值法的基本依据是使得图像中目标与背景分布的信息量最大，即通过测量图像灰度直方图的熵，找出最佳阈值。

粒子群算法和遗传算法比较

粒子群算法（PSO）和遗传算法(GA)都是优化算法，都力图在自然特性的基础上模拟个体种群的适应性，它们都采用一定的变换规则通过搜索空间求解。

PSO和GA的相同点：(1)都属于仿生算法。

PSO主要模拟鸟类觅食、人类认知等社会行为而提出；GA主要借用生物进化中“适者生存”的规律。

(2)都属于全局优化方法。

两种算法都是在解空间随机产生初始种群，因而算法在全局的解空间进行搜索，且将搜索重点集中在性能高的部分。

(3)都属于随机搜索算法。

都是通过随机优化方法更新种群和搜索最优点。

PSO 中认知项和社会项前都加有随机数；而GA的遗传操作均属随机操作。

(4)都隐含并行性。

搜索过程是从问题解的一个集合开始的，而不是从单个个体开始，具有隐含并行搜索特性，从而减小了陷入局部极小的可能性。

并且由于这种并行性，易在并行计算机上实现，以提高算法性能和效率。

(5)根据个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等。

(6)对高维复杂问题，往往会遇到早熟收敛和收敛性能差的缺点，都无法保证收敛到最优点。

PSO和GA不同点(1)PSO有记忆，好的解的知识所有粒子都保存，而GA没有记忆，以前的知识随着种群的改变被破坏。

(2)在GA算法中，染色体之间相互共享信息，所以整个种群的移动是比较均匀地向最优区域移动。

PSO中的粒子仅仅通过当前搜索到最优点进行共享信息，所以很大程度上这是一种单项信息共享机制，整个搜索更新过程是跟随当前最优解的过程。

在大多数情况下，所有粒子可能比遗传算法中的进化个体以更快速度收敛于最优解。

(3)GA的编码技术和遗传操作比较简单，而PSO相对于GA，不需要编码，没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。

(4)在收敛性方面，GA己经有了较成熟的收敛性分析方法，并且可对收敛速度进行估计；而PSO这方面的研究还比较薄弱。

尽管已经有简化确定性版本的收敛性分析，但将确定性向随机性的转化尚需进一步研究。

粒子群算法的研究现状及其应用

智能控制技术课程论文中文题目: 粒子群算法的研究现状及其应用姓名学号:指导教师：年级与专业：所在学院：XXXX年XX月XX日1 研究的背景优化问题是一个古老的问题，可以将其定义为：在满足一定约束条件下，寻找一组参数值，使系统的某些性能指标达到最大值或最小值。

在我们的日常生活中，我们常常需要解决优化问题，在一定的范围内使我们追求的目标得到最大化。

为了解决我们遇到的最优化问题，科学家，们进行了不懈的努力，发展了诸如牛顿法、共轭梯度法等诸多优化算法，大大推动了优化问题的发展，但由于这些算法的低运行效率，使得在计算复杂度、收敛性等方面都无法满足实际的生产需要。

对此，受达尔文进化论的影响，一批新的智能优化算法相继被提出。

粒子群算法（PSO ）就是其中的一项优化技术。

1995 年Eberhart 博士和Kennedy 博士[1]-[3]通过研究鸟群捕食的行为后，提出了粒子群算法。

设想有一群鸟在随机搜索食物，而在这个区域里只有一块食物，所有的鸟都不知道食物在哪里。

那么找到食物最简单有效的办法就是鸟群协同搜寻，鸟群中的每只鸟负责离其最近的周围区域。

粒子群算法是一种基于群体的优化工具，尤其适用于复杂和非线性问题。

系统初始化为一组随机解，通过迭代搜寻最优值，通过采用种群的方式组织搜索，同时搜索空间内的多个区域，所以特别适合大规模并行计算，具有较高的效率和简单、易操作的特性。

目前使用的粒子群算法的数学描述[3]为：设粒子的寻优空间是m 维的，粒子的数目为ps ，算法的最大寻优次数为Iter 。

第i 个粒子的飞行速度为T i i1i2im v [v v ]= ,,,v ，位置为T i i1i2im x [x x x ]= ,,,，粒子的个体极值T i i1i2im Pbest [,]P = ,P ,P ，全局极值为T i i1i2im Gbest [,]g = ,g ,g 。

粒子群算法的寻优过程主要由粒子的速度更新和位置更新两部分组成，其更新方式如下：i+11122v ()()i i i i i v c r Pbest x c r Gbest x =+−+−；i+1i+1i x x v =+，式中：12c c ，为学习因子，一般取2；12r r ，是均与分布着[0,1]上的随机数。

粒子群优化算法的研究及改进

ｏｒ
ｏｐｔｉｍｉｚｅｄｆｕｎｃｔｉｏｎｉｓｄｉｆｆｅｒｅｎｔｉａｂｌｅ，ｄｅｒｉｖａｔｉｖｅ
ｃｏｎｔｉｎｕｏｕｓ．ＴｈｅＰＳＯ
ｉｓ
ｓｉｍｐｌｅｉｎｓｔｒｕｃｔｕｒｅ，ｆａｓｔｉｎ
ｃｏｎｖｅｒｇｅｎｃｅ，ｆｅｗ
ｉｎｐａｒａｍｅｔｅｒｓａｎｄｅａｓｙｉｎｐｒｏｇｒａｍｍｉｎｇ．
Ｓｏｉｔｈａｓａｔｔｒａｃｔｅｄｒｅｓｅａｒｃｈｅｒｓａｔｈｏｍｅａｎｄａｂｒｏａｄａｎｄａｐｐｌｙｅｄｉｎｍａｎｙａｒｅａｓｓｉｎｃｅｉｔｉｓ
ｓｙｓｔｅｍａｔｉｃ
ｓｔｕｄｙ
ＰＳＯ
ｏｎ
ｔｈｅａｓｐｅｃｔｓｏｆ
ａｌｇｏｒｉｔｈｍｍｏｄｉｆｉｃａｔｉｏｎ
ａｎｄｕｓｅｄ
ａｎｄｉｔｓａｐｐｌｉｃａｔｉｏｎ．Ｔｈｅｍａｉｎ
ｃｏｎｔｅｎｔ
ｉｓ
ａｒｒａｎｇｅｄａｓ
（１）Ｕｐｏｎａｎａｌｙｓｉｎｇｔｈｅ
ｃａｐａｂｉｌｉｔｉｅｓｓｙｓｔｅｍｓｉｓ
１３ｂｅｎｃｈｍａｒｋｆｕｎｃｔｉｏｎｓ．ＴｈｅｒｅｓｕｌｔｓｉｎｄｉｃａｔｅｔｈａｔＧＰＳＯａｌｇｏｒｉｔｈｍｈａｖｅｉｍｐｒｏｖｅｄ
ｐｅｒｆｏｒｍａｎｃｅ
（３）Ｂａｓｅｄ
ｏｎ
ｏｆｔｈｅ
ｃｏｎｖｅｒｇｅｎｃｅ
ｓｐｅｅｄａｎｄｔｈｅｓｅａｒｃｈａｃｃｕｒａｃｙ．ｔｈｅ
ａｎｄｔｈｅａｌｇｏｒｉｔｈｍ
ｔｏ‘＇ｐｒｅｍａｔｕｒｅ
ｃｏｎｖｅｒｇｅｎｃｅ”．Ｆｉｎａｌｌｙ，ｔｈｅ
ＰＳＯａｌｇｏｒｉｔｈｍｉｓｎｏｔｓｔｒｏｎｇｉｎｏｆｔｈｅ
ａ
ｃｌｉｍｂｉｎｇａｂｉｌｉｔｙａｎｄｌａｃｋｏｆ

粒子群算法

粒子群算法原理及简单案例[ python ]介绍粒子群算法（Particle swarm optimization，PSO）是模拟群体智能所建立起来的一种优化算法，主要用于解决最优化问题（optimization problems）。

1995年由 Eberhart和Kennedy 提出，是基于对鸟群觅食行为的研究和模拟而来的。

假设一群鸟在觅食，在觅食范围内，只在一个地方有食物，所有鸟儿都看不到食物（即不知道食物的具体位置。

当然不知道了，知道了就不用觅食了），但是能闻到食物的味道（即能知道食物距离自己是远是近。

鸟的嗅觉是很灵敏的）。

假设鸟与鸟之间能共享信息（即互相知道每个鸟离食物多远。

这个是人工假定，实际上鸟们肯定不会也不愿意），那么最好的策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素综合考虑找到最好的搜索位置。

粒子群算法与《遗传算法》等进化算法有很多相似之处。

也需要初始化种群，计算适应度值，通过进化进行迭代等。

但是与遗传算法不同，它没有交叉，变异等进化操作。

与遗传算法比较，PSO的优势在于很容易编码，需要调整的参数也很少。

一、基本概念与遗传算法类似，PSO也有几个核心概念。

粒子（particle）：一只鸟。

类似于遗传算法中的个体。

1.种群（population）：一群鸟。

类似于遗传算法中的种群。

2.位置（position）：一个粒子（鸟）当前所在的位置。

3.经验（best）：一个粒子（鸟）自身曾经离食物最近的位置。

4.速度（velocity ）：一个粒子（鸟）飞行的速度。

5.适应度（fitness）：一个粒子（鸟）距离食物的远近。

与遗传算法中的适应度类似。

二、粒子群算法的过程可以看出，粒子群算法的过程比遗传算法还要简单。

1）根据问题需要，随机生成粒子，粒子的数量可自行控制。

2）将粒子组成一个种群。

这前2个过程一般合并在一起。

3）计算粒子适应度值。

4）更新种群中每个粒子的位置和速度。

各种群体寻优算法的比较

各种群体寻优算法的⽐较【蚁群优化算法、粒⼦群优化算法、细菌觅⾷算法、萤⽕⾍算法、⼈⼯鱼群算法】计算机技术不断发展，算法技术也在不断更新。

群体智能 (Swarm Intelligent，SI) 算法始于 20 世纪 90 年代初，主要是受⾃然界⽣物群体智能现象的启发，通过模仿社会性动物的⾏为，⽽提出的⼀种随机优化算法。

群体智能是基于种群⾏为对给定的⽬标进⾏寻优的启发式搜索算法，其的核⼼是由众多简单个体组成的群体能够通过相互之间的简单合作来实现某⼀较复杂的功能。

所以群体智能可以在没有集中控制并且缺少全局信息和模型的前提下，为寻找复杂的分布式问题的解决⽅案提供了基础。

作为计算智能的⼀个重要的学科分⽀,群体智能优化算法是⼀类通过模仿⽣物界的遗传进化机理和群体协作⾏为⽽提出的仿⽣类随机搜索算法。

该算法以其⾼效的寻优速度,⽆需考虑问题的过多初始信息等特点⽽受到⼈们的普遍关注。

群体智能优化算法是⼀类基于概率的随机搜索进化算法，各个算法之间存在结构、研究内容、计算⽅法等具有较⼤的相似性。

因此，群体智能优化算法可以建⽴⼀个基本的理论框架模式：Step1：设置参数，初始化种群；Step2：⽣成⼀组解，计算其适应值；Step3：由个体最有适应着，通过⽐较得到群体最优适应值；Step4：判断终⽌条件⽰否满⾜？如果满⾜，结束迭代；否则，转向Step2；各个群体智能算法之间最⼤不同在于算法更新规则上，有基于模拟群居⽣物运动步长更新的（如PSO,AFSA与SFLA），也有根据某种算法机理设置更新规则（如ACO）。

统⼀框架下的群体智能优化算法，可以根据优化对象的特性只能地选择适合的更新规则，进⾏运算得到理想的优化结果。

蚁群算法（Ant Colony, ACO）：是模拟真实的蚁群秘觅⾷过程寻求最短路径的原理，由意⼤利学者Dorigo等在20世纪90年代⾸先提出。

最初的蚁群算法成为蚂蚁系统，对于旅⾏商问题（TSP）及⼆次分配问题（QAP）等取得了较好效果，经过改进后成为蚂蚁算法或蚁群算法。

鸟群算法和粒子群算法

鸟群算法和粒子群算法1.引言1.1 概述鸟群算法和粒子群算法是两种基于群体的智能优化算法，都受到了自然界中动物行为的启发。

鸟群算法模拟了鸟类在觅食、迁徙和群体行为中的协同行动，而粒子群算法则模拟了鸟类或昆虫等生物在群体中相互协作的行为。

鸟群算法中，鸟群被抽象为一组代表解空间中候选解的个体，这些个体通过觅食行为来寻找最优解。

每个鸟个体根据自身的经验和邻近鸟个体的信息进行位置的更新和调整，从而逐步优化解的质量。

鸟群算法具有全局搜索的能力，并且能够自适应地调整搜索策略。

粒子群算法则从粒子在解空间中的位置和速度变化角度出发，通过个体最优和群体最优两个方面来指导搜索过程。

每个粒子通过自身的经验以及邻近粒子的信息进行位置的调整，并逐渐趋向于全局最优解。

粒子群算法具有较快的收敛速度和较高的搜索精度。

这两种算法在解空间中的搜索能力和收敛性能方面有着相似之处，都可以用于求解优化问题。

不同的是，鸟群算法更侧重于模拟鸟类在现实生活中协同行动的策略，而粒子群算法则更注重于个体之间信息的传递和共享。

在应用场景上，鸟群算法和粒子群算法都可以应用于优化问题的求解，如函数优化、组合优化、机器学习等领域。

鸟群算法主要适用于复杂优化问题，特别是大规模问题，而粒子群算法更适用于连续型和离散型问题。

本文将对鸟群算法和粒子群算法的原理和应用场景进行详细介绍，并对其相似之处和差异之处进行对比分析。

最后，通过总结和展望，提出对这两种算法的进一步研究方向和应用前景的展望。

1.2 文章结构文章结构部分是对整篇文章进行一个简要的概括，提供读者一个清晰的导读，使其能够更好地理解文章的组织架构和内容安排。

在本文中，文章结构部分可以写成如下内容：文章结构:本文主要分为五个部分，即引言、鸟群算法、粒子群算法、对比分析和结论。

引言部分将对本文要讨论的主题进行概述，包括鸟群算法和粒子群算法的概念和应用。

在鸟群算法部分，将详细介绍鸟群算法的原理，包括鸟群算法的基本思想、运行机制以及常用的优化策略。

一种全局优化的两阶段算法

一种全局优化的两阶段算法张玉芬;王永军【摘要】为了提高算法的有效性,利用梯度算法和粒子群算法独立的运行机制,采用驱赶技术和重新初始化部分群体的技术,提出了一种基于梯度下降法和粒子群算法的两阶段优化算法,并对新算法进行了理论分析和数值仿真.数值结果显示新算法比单纯梯度算法有更好的全局优化能力,比单纯粒子群算法有更快的收敛速度和更高的精度.新算法求解质量更高,运行更稳定.%To enhance effectiveness of algorithm, on the basis of analyzing the independent operating mechanism of both gradient algorithm and particle swarm algorithm, a two-phase optimization algorithm based on gradient descent and particle swarm algorithm is presented; it adopts the driving technique and the re-initialization technique of part of population. Then, the theoretical analysis and numerical simulation about the new algorithm are made. The numerical simulation shows this new algorithm has better global optimization ability than the gradient algorithm, and it has faster convergences speed and lighter solution accuracy than particle swarm algorithm. This new algorithm produces a lighter quality solution and has more stable operation.【期刊名称】《河北大学学报（自然科学版）》【年(卷),期】2012(032)002【总页数】5页(P207-211)【关键词】全局优化;两阶段算法;梯度算法;粒子群算法【作者】张玉芬;王永军【作者单位】河北大学数学与计算机学院,河北保定071002;东方地球物理公司研究院数据处理中心,河北涿州 072751【正文语种】中文【中图分类】O241.3全局优化问题广泛应用于金融模型、网络交通、图像处理、集成电路设计、分子生物学、数据库、物流配送系统设计中.因为这些优化问题存在多个不同于全局最优解的局部最优解，所以传统的非线性规划中的局部优化方法不能有效地处理这类问题.而且，随着科学的发展，工程中遇到的优化问题的规模越来越大、复杂性越来越高，这使得全局优化问题的求解变得更加困难.全局优化问题的难以解决阻滞了许多学科的发展，因而全局优化方法的研究显得尤为重要.梯度类算法是一种确定性的局部优化方法，它能够快速高效地找到临近初始点的局部最优值.常见的算法有最速下降法、牛顿法、拟牛顿法、共轭梯度方法等.它们已经广泛地应用于许多领域［1－5］.此类算法的主要缺点是对初始点的严重依赖性、目标函数和约束区域的拓扑结构的严格要求性.粒子群算法是一种群体智能优化方法［1］，在粒子群算法中，群体中的一个粒子根据它本身找到的最优位置以及整个群体当前为止找到的最优位置，来不断地调整它本身的位置.算法的核心思想是用当前最好的已知的位置来引导群体朝搜索空间的最优位置移动.粒子群算法设计简单，参数少，容易实现，且表现出了较好的局部跳跃性，已经被应用到许多领域.但算法有时搜索到的只是局部解，找到高精度的解需要较长的运行时间，解决大规模优化问题至今还没有涉及.文献［2］提出了一种把梯度信息混合到粒子的速度更新公式中加快算法收敛的方法.这种方法没有使用现存的梯度算法的有效性和群体搜索中找到的最优信息.过于强调启发，而改变了传统粒子群算法的核心思想.文献［6］提出了一种基于梯度方法和动态隧道法的混合技术（用GRDT表示）来解决全局优化问题.在GRDT方法中，梯度用来加快局部搜索，动态方程用来寻找好的初始点.但是，该方法需要多次积分动态方程，对高维函数耗时较多，填充函数法和隧道法中的参数较难调节. 1.1 算法原理不同于一般意义下的进化算法，即局部搜索限制在进化算法的框架内，本文设计了一种新的混和算法.在新算法中，粒子群按照其独有的进化机制演化，而梯度算法使用目标函数的梯度信息进行独立的搜索.粒子群算法起着全局搜索的作用，而梯度搜索起着局部探测的作用.从而把2种算法混合为一个两阶段方法，发挥出它们各自的优点以解决复杂函数的优化问题是本文的核心思想所在.具体而言，第1步，从可行域中随机产生的一点出发，使用梯度算法得到目标函数的一个局部最优点.其次，以得到的最优点为均值，使用高斯分布函数初始化粒子群.然后，在最大的迭代次数内，运用粒子群算法找到一个更好的点.以找到的点作为初始点，回到第1步，重新开始梯度搜索.另外，为了利用算法已经得到的最优值信息（所有已经找到的局部最优点）防止群体早熟现象，把一种驱赶群体技巧［7］以及部分初始化群体方法加入到新算法中.驱赶技术利用当前点与已经找到的局部最优点之间的距离，建立起一种屏障，使得新产生的点不要落到已经找到的局部最优点太近的范围内，这可以使粒子向着更有希望的区域飞行，同时避免重复搜索.文献［7］已经证明了此方法可以有效地加快群智能算法的收敛.部分初始化群体方法是在群体搜索不能取得全局进展时，使用均匀分布函数产生的部分群体代替当前群体中同等规模的较差个体的一种做法.1.2 算法步骤假设群体规模是NP，n是问题的规模，M是一个随机生成的数值，M∈｛1，2，…，NP｝.本文使用的驱赶技术见算法1，更多的信息可以参考文献［5］.本文使用的部分初始化群体技术执行如下：根据当前群体的适应值进行排序，在可行域中按均匀分布随机产生M个样本点，执行驱赶技术，然后代替当前群体中M个较差的个体，其余NP－M个个体保留在群体中，进而形成同等规模的新群体.新群体继续执行粒子群算法搜索.新算法记做GRPSO（gradient based particle swarm optimization method），见算法2.算法1 驱赶技术［5］步骤0.输入算法找到的极小点集S＊＝｛X＊j（j＝1，2，…，m）｝，这里的m 是找到的极小点的个数.给定小生境的半径rij与驱赶因子mij.步骤1.对群体中的每一个粒子Xi，i＝1，2，…，NP.步骤1a.计算距离d ij＝｜X i－X＊j｜j＝1，2，m.步骤1b.对集合S＊中的每一个元素X＊j，j＝1，2，…，m.如果d ij＜rij，那么令Zij＝（X i－X＊j）／d ij.然后置X i＝Xi＋Pij Z ij.步骤2.输出群体Xi，i＝1，2，…，NP.算法2 提出的新算法（GRPSO）步骤0.随机生成可行域中的初始点X0，并置局部搜索计数器k＝0.给定粒子群内部的最大迭代次数Smax和计数器Npso＝1、调用粒子群算法的最大次数SSmax.设最优点集合S＊＝Φ.步骤1.（局部搜索）从Xk出发，应用梯度下降法找到可行域中的1个极小点X＊k，同时保留到集合S＊中.步骤2.（使用粒子群算法的全局搜索）步骤2a.根据高斯分布，以X＊k为均值，在可行域中初始化群体，并找出最好个体gbest.若f（X＊k）＜f（gbest），令gbest＝X＊k，k＝1转步骤1.否则，令gbest＝X＊k，计数器SS＝1，转入步骤2b.步骤2b.当最大迭代次数Smax没有达到时1）更新pbest，如果当前个体适应值好于f（pbest），i＝1，2，…，NP.2）更新gbest，如果当前群体中的最优个体适应值好于f（gbest）.3）如果f（gbest）＜f（X＊k），令X＊k＝gbest，结束循环.4）根据速度更新公式（1）和位置更新公式（2）更新群体的速度和位置.5）把当前群体和极小点集S＊作为输入集，执行算法1的驱赶技术（Algorithm 1）.然后，令Npso＝Npso＋1.步骤2c.如果gbest＝X＊k，SS＝SS＋1.如果SS＞SSmax，停止计算并输出gbest＝X＊k.否则，重新初始化M∈｛1，2，…，NP｝个粒子，并执行算法1的驱赶技术，保证此M个粒子远离找到的局部最优点.令Npso＝＋1，转入步骤2b.否则，令X＊k＋1＝gbest，k＝k＋1，转入步骤1.2.1 实验结果用文献［3］中已经被GRDT测试过的10个函数来检验新算法的优化性能.首先，把函数值的计算次数设定为2 100，比较最终解的质量，数值结果见表1.用新算法GRPSO对10个标准测试函数进行优化，把运算的结果与其他的算法，如GRDT （梯度算法和动态隧道法的混合方法［3］）、HGPSO（混合粒子群算法［6］）和专门设计处理高维函数的GRADSA（混合梯度和模拟退火技术的算法［4］）做比较.由于解的质量、收敛速度（计算机的CPU时间或目标函数值的计算次数）、算法的寻优成功率是衡量算法优劣的主要标准，对10个复杂函数［3］的20次独立运行后这几个指标的平均结果总结如表1.然后，在给定的最大函数值计算次数下，比较算法找到给定精度的解的成功率，数值结果见表2和3.2.2 结果分析从表1可以看出，GRPSO可以找到所有测试函数的最优值，其结果接近理论上的分析值.与GRDT和其他文献报道的结果相比，新算法找到的结果更好一些，比如函数H3和SH是2个典型的例子.从表2和3可以看到，新算法HGPSO运行效果更好，尽管它们都是基于梯度搜索的混PSO算法.同时，数值结果意味着在同样给定的计算时间内，新算法可以得到比GRPSO更高精度的解.说明两阶段的独立搜索更有助于各个算法发挥其基本功能.从表2可以看出，根据函数值的计算次数，新算法优化性能高于GRDT和HGPSO方法，尤其对于GP和H3函数的优化效果更明显.与其他典型方法如PRS （纯随机搜索）、MS（多起点方法）、SA1（基于微分方程的模拟退火方法）、SA2（基本模拟退火方法）、TS（禁忌搜索）、TA（树退火）和TT（信赖方法TRUST）相比，新算法的计算量大大降低.总之，梯度算法帮助新算法加快局部收敛，并找到高精度的解.加入了驱赶技术和部分初始化群体的粒子群算法增加了群体多样性，防止了群体早熟，进而使新算法能有效地跳出局部最优.所有这些显示新算法对低维的复杂函数优化效果好.提出了一种基于梯度算法和粒子群算法的两阶段混和算法.从有效的局部搜索（使用梯度算法）开始，然后借助进化算法（采用粒子群算法）的全局跳跃性质探索更有希望区域，为局部搜索找到更好的出发点.寻找高精度的解由局部搜索完成，因而省却了演化算法的进化时间，粒子群算法的全局搜索信息得以利用.不同于一般框架下的演化算法，该算法有效地利用了梯度算法和粒子群算法独立的运行机制.另外，新算法中采用了驱赶技术和重新初始化部分群体的技术.数值结果显示新算法比单纯梯度算法有更好的全局优化能力，比单纯粒子群算法有更快的收敛速度、解的精度.【相关文献】［1］KENNEDY J，EBERHART R C.Particle swarm optimization［Z］.Proceedings of IEEE International Conference on Neural Networks，Perth Australia，1995.［2］ROY C P，SINGH Y P，CHANSARKAR R A.Hybridization of gradient descent algorithms with dynamic tunneling methods for global optimization［J］.IEEE T Syst Man Cy，2000，30（3）：384－390.［3］NOEL M M，JANNETT T C.Simulation of a new hybrid particle swarm optimization algorithm［J］.System Symposium，2004，32（4）：150－153.［4］SUGANTHAN P N.Particle swarm optimiser with neighbourhood operator［Z］.Proceedings of the IEEE Congress on Evolutionary Computation，Piscataway，NJ，1999.［5］PARSOPOULOS K E，VRAHATIS M N.On the computation of all global optimizers through particles warm optimization［J］.IEEE Trans on Evolutionary Computation，2004，8（3）：211－224.［6］刘星宝，蔡自兴，王勇.用于全局优化问题的混合免疫进化算法［J］.西安电子科技大学学报，2010，37（5）：971－980.LIU Xingbao，CAI Zixing，WANG Yong.Hybrid immune evolutionary algorithm for global optimization problems［J］.Journal of Xidian University，2010，37（5）：971－980. ［7］路克中，王汝传，章家顺.最优化问题全局寻优的PSO－BFGS混合算法［J］.计算机应用研究，2007，24（5）：17－19.LU Kezhong，WANG Ruchuan，ZHANG Jiashun.PSO－BFGS algorithm of global optimum for optimization problems［J］.Application Research of Computers，2007，24（5）：17－19.。

粒子群算法可视化

粒子群算法可视化全文共四篇示例，供读者参考第一篇示例：粒子群算法（Particle Swarm Optimization）是一种基于群体智能的优化算法，最早由Kennedy和Eberhart提出。

它通过模拟鸟群或鱼群的行为来搜索问题的最优解。

粒子群算法的基本原理是将候选解看作是粒子，然后这些粒子在解空间中移动，寻找最优解的过程可以看作是粒子在解空间中飞翔。

在粒子群算法的优化过程中，每个粒子代表一个候选解，在整个解空间里进行搜索。

每个粒子的位置和速度都可以调整，以便获得更好的解。

粒子在搜索过程中会根据自身的位置和速度进行更新，同时也会受到其他粒子的影响，从而实现全局搜索和局部搜索的平衡。

为了更直观地展示粒子群算法的搜索过程，我们可以对算法进行可视化处理。

一种常见的方法是将解空间投影到二维平面上，并通过动态的图像展示粒子在解空间中的移动过程。

下面我们将介绍如何使用Python语言和matplotlib库实现粒子群算法的可视化。

我们需要定义一个适合优化的目标函数。

在这里，我们以一个简单的二维函数f(x, y) = x^2 + y^2为例。

然后，我们初始化粒子群中的粒子数量、最大迭代次数、学习因子等参数。

接下来，我们随机初始化每个粒子的位置和速度。

在每次迭代过程中，根据当前位置和速度更新粒子的位置和速度，并计算每个粒子的适应度。

根据适应度的大小，更新全局最优解和每个粒子的局部最优解。

可视化地展示每个粒子在解空间中的移动过程，并显示最终的最优解。

通过可视化的方式，我们可以清晰地观察粒子在解空间中的搜索过程，以及最优解的收敛情况。

这有助于我们更直观地理解粒子群算法的工作原理，并为参数调优提供参考。

粒子群算法的可视化不仅方便了我们对算法过程的理解，也增加了算法的趣味性。

第二篇示例：粒子群算法（Particle Swarm Optimization, PSO）是一种基于仿生学的优化算法，灵感来源于鸟群或鱼群的集体行为。

粒子群算法粒子群算法简介

粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天，那些都是科研工作者写论文的语气，不过，PSO的历史就像上面说的那样。

下面通俗的解释PSO算法。

PSO算法就是模拟一群鸟寻找食物的过程，每个鸟就是PSO中的粒子，也就是我们需要求解问题的可能解，这些鸟在寻找食物的过程中，不停改变自己在空中飞行的位置与速度。

大家也可以观察一下，鸟群在寻找食物的过程中，开始鸟群比较分散，逐渐这些鸟就会聚成一群，这个群忽高忽低、忽左忽右，直到最后找到食物。

这个过程我们转化为一个数学问题。

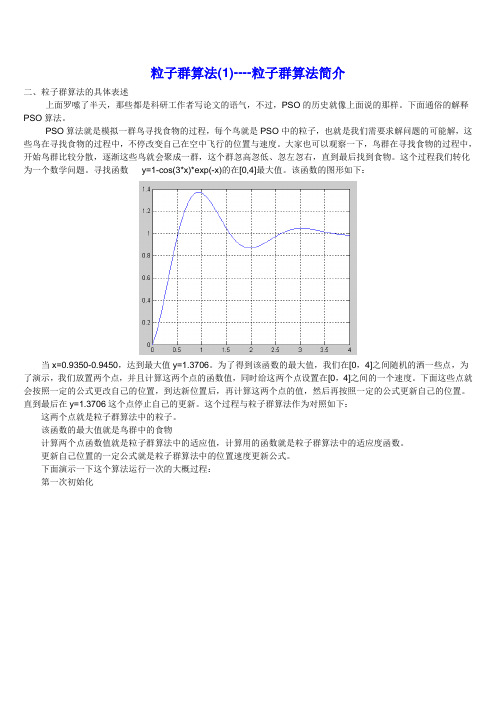
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。

该函数的图形如下：当x=0.9350-0.9450，达到最大值y=1.3706。

为了得到该函数的最大值，我们在[0，4]之间随机的洒一些点，为了演示，我们放置两个点，并且计算这两个点的函数值，同时给这两个点设置在[0，4]之间的一个速度。

下面这些点就会按照一定的公式更改自己的位置，到达新位置后，再计算这两个点的值，然后再按照一定的公式更新自己的位置。

直到最后在y=1.3706这个点停止自己的更新。

这个过程与粒子群算法作为对照如下：这两个点就是粒子群算法中的粒子。

该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值，计算用的函数就是粒子群算法中的适应度函数。

更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。

下面演示一下这个算法运行一次的大概过程：第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果（30次迭代）最后所有的点都集中在最大值的地方。

粒子群算法(2)----标准的粒子群算法在上一节的叙述中，唯一没有给大家介绍的就是函数的这些随机的点（粒子）是如何运动的，只是说按照一定的公式更新。

这个公式就是粒子群算法中的位置速度更新公式。

下面就介绍这个公式是什么。

在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。

粒子群优化算法(PSO)在智能组卷中的应用

可能会以牺牲ｕｌ作为代价，往往不能达到预期的效果Ｉ，选择ｌ，Ｊ＂￣此个高效、科学、合理的算法是自动组卷的关键．以往的自动组卷系．
一
① 种群随机初始化。 ② 对种群内的每一个个体汁算适应值（ｔｓｖｌ）ｉｅｕｆｎｓａｅ，适应值与最
粒子群优化算法以其简单容易实现及精确的智能搜索技术，来越越多地受到广泛的关注。将此算法应用于智能汁算机辅助教学系统的自动组卷，取代常用的遗传算法，从而大大提高了组卷的效率和精确
度。自动组卷的效率与质量完全取决于抽题算法的设计。如何没计一个算法从题库中既怏又好的抽出一组最佳解或是抽出一组非常接近最佳解的实体，涉及到—个全局寻优和收敛速度怏慢的问题，受到了广泛的关注。粒子群优化算法的优势在下简单容易实现并且没有许多参数需要调整。目前已广泛应用于函数优化、神经蚓络洲练、模糊系统控制以及其他遗传算法的应用领域。通过理论推导和事实运用，发现粒子群优化算法在寻优和收敛性方面部是非常有效的本文结合粒子、群优化算法（Ｓ）ＰＯ的原理和思想，对考试自动出题组卷的ｆ题进行了 “ １研究，找到了一种获得与考试试题控制指标符合的试题模型的解决方
后再依据一定卷生成完毕或退回出发点为止。但是在实际到一个应用时发现这种算法对内存的占用量很大，程序结构相对比较复杂，而且选取试题缺乏随机性，组卷时问长，两点是用户无法接受的，凶后此它也不是一种很好的用来自动组卷的算法。遗传算法（ｅｅｃＧｎｔｉＡｇｒｈｓ以其具有自适应全局寻优和智能搜索技术，并且收敛性ｌｉｍ）ｏｔ好的特性能很好地满足自动考试组卷的要求。但是遗传算法需要复杂的许多参数需要凋整，搜索不够精确，我们引进粒子群优化算法（Ｓ）ＰＯ，系统初始化为一组随机解，通过叠代搜寻最优值。优势在于简单容易实现，并且没有许多参数需要渊整。目前已广泛应用于函数优化，神经络训练，模糊系统控制以及其他遗传算法的应用领域，本研究就是把此算法应用于智能组卷系统

人工智能中的遗传算法与粒子群优化算法比较分析

人工智能中的遗传算法与粒子群优化算法比较分析遗传算法和粒子群优化算法都是优化问题中常用的智能算法，它们分别基于生物进化和鸟群行为的启发，通过模拟自然选择和信息交流的过程来求解问题的最优解。

下面将从原理、优势与劣势、应用领域等方面对遗传算法和粒子群优化算法进行比较分析。

一、原理比较1.遗传算法遗传算法基于达尔文的进化论，通过模拟自然选择、交叉、变异等操作来搜索问题的最优解。

其中，个体表示问题的候选解，适应度函数用于评估个体的优劣程度，选择操作根据个体适应度选择优秀的个体参与繁殖，交叉操作模拟基因的交换，变异操作模拟基因的突变。

通过多代的进化，逐渐优化个体，最终找到最优解。

2.粒子群优化算法粒子群优化算法基于社会行为模拟鸟群，通过个体间的信息交流和位置的调整来寻找问题的最优解。

其中，个体表示问题的解，位置表示个体的候选解，速度表示个体的搜索方向和步长，适应度函数用于评估个体的优劣程度，个体位置根据历史最优解和全局最优解进行更新，从而逐步优化个体的位置，最终找到最优解。

二、优势与劣势比较1.优势比较-遗传算法的优势：a.全局搜索能力较强：遗传算法采用随机搜索的策略，具有良好的全局搜索能力，适用于复杂问题的求解。

b.可以处理离散和连续问题：遗传算法适用于离散和连续优化问题，对问题的表达方式较为灵活。

c.可以处理多目标优化问题：遗传算法通过引入多个适应度函数，可以同时优化多个目标。

-粒子群优化算法的优势：a.收敛速度快：粒子群优化算法通过个体间的信息交流和位置更新，可以快速收敛到最优解。

b.可以处理连续和离散问题：粒子群优化算法适用于连续和离散优化问题，对问题的表达方式较为灵活。

c.具有自适应性：粒子群优化算法通过个体间的协作和自适应调整，有较好的适应性和稳定性。

2.劣势比较-遗传算法的劣势：a.搜索过程可能陷入局部最优：遗传算法基于随机搜索策略，可能陷入局部最优解而无法全局最优解。

b.参数调整和运算复杂性较高：遗传算法的参数设置和运算复杂性较高，需要经验和大量的计算。

基于粒子群算法的动态考试安排研究

表２ｔａｂ — ｋｓ仿真数据
算法过多地依赖了数据记录的位置，对于字段唯一性和字段之间的关联没有作深入的研究。文献［４］中主要研究准考证号的制作，数据是在Ｅｘｃｅｌ表格
上完成的。在实际考试安排系统开发中通常出现的问题
图１座位号生成界面
号中即可。
说明：对于任意考场，每位考生的座位号是唯一
的，且应该在１到３０之间；每３０人为一个考场，共有ｎｕｍ／（３０＋１）个考场。
虽然粒子群算法在很多实际应用中容易出现陷入局部最优中，通常需要加入扰动因子进行调整，而
个考场的人员如何调整和安排，对于最基本的考场
安排很少提到。文献［３］中提到运用随机函数Ｒｅｃｎ（）给报名表添加随机号ｓｊｈ，运用复合函数Ｃｅｉｌｉｎｇ
（Ｒｅｃｎ（）／Ｎ）实现考场号的安排，运用复合函数Ｒｅｃｎ（）一（Ｋｃｈ一１）Ｎ实现座位号的安排。整个
是：从招生办得到的数据主要是学生个人信息，如姓名、性别、身份证号码、报考种类等。对于开发系统设计界面以图１作为参考模型。
者来讲，在这张信息表的基础上需要安排学生的准
考证号、考场、对应的座位号、考试科目、考试时间等，然后生成报表，打印准考证。本文就是在这个需求基础上提出应用粒子群优化算法，以安排考生座位号为例，降低程序的时间复杂度。实践证明这种

粒子群算法

粒子群算法粒子群算法（Particle Swarm Optimization，PSO）是一种群体智能优化算法，它模拟了鸟群觅食行为中个体在信息交流、合作与竞争中寻找最优解的过程。

粒子群算法在解决优化问题中具有较好的效果，尤其适用于连续优化问题。

粒子群算法的基本思想是模拟粒子在解空间中的移动过程，每个粒子代表一个候选解，粒子的位置表示解的一组参数。

每个粒子都有一个速度向量，表示粒子在解空间中的移动方向和速率。

算法的核心是通过更新粒子的位置和速度来搜索目标函数的最优解。

具体来说，粒子的位置和速度更新通过以下公式计算：$$v_i^{t+1} = w\cdot v_i^{t} + c_1 \cdot rand() \cdot (p_i^{best}-x_i^{t}) + c_2 \cdot rand() \cdot (p_g^{best}-x_i^{t})$$$$x_i^{t+1} = x_i^{t} + v_i^{t+1}$$其中，$v_i^{t}$是粒子$i$在时间$t$的速度，$x_i^{t}$是粒子$i$在时间$t$的位置，$p_i^{best}$是粒子$i$自身经历过的最好位置，$p_g^{best}$是整个种群中经历过的最好位置，$w$是惯性权重，$c_1$和$c_2$是加速度因子，$rand()$是一个0到1的随机数。

粒子群算法的优点在于简单、易于理解和实现，同时具有较好的全局搜索能力。

其收敛速度较快，可以处理多维、非线性和非光滑的优化问题。

另外，粒子群算法有较少的参数需要调节，因此适用于许多实际应用中的优化问题。

粒子群算法的应用领域非常广泛，包括机器学习、数据挖掘、图像处理、模式识别、人工智能等。

例如，在机器学习中，粒子群算法可以应用于神经网络的训练和参数优化；在数据挖掘中，粒子群算法可以用于聚类、分类和关联规则挖掘等任务；在图像处理中，粒子群算法可以用于图像分割、边缘检测和特征提取等；在模式识别中，粒子群算法可以用于目标检测和模式匹配等。

粒子群优化算法【精品文档】(完整版)

扬州大学物理科学与技术学院本科生毕业设计论文课题：粒子群优化算法作者：张雷学号： 050702156 专业：电子信息科学与技术指导教师：朱海梅二零零九年五月十五日摘要近年来，智能优化算法—粒子群算法（particle swarm optimization，简称PSO）越来越受到学者的关注。

粒子群算法是美国社会心理学家JamesKennedy 和电气工程师Russell Eberhart在1995年共同提出的，它是受到鸟群社会行为的启发并利用了生物学家Frank Heppner的生物群体模型而提出的。

它用无质量无体积的粒子作为个体，并为每个粒子规定简单的社会行为规则，通过种群间个体协作来实现对问题最优解的搜索。

由于算法收敛速度快，设置参数少，容易实现，能有效地解决复杂优化问题，在函数优化、神经网络训练、图解处理、模式识别以及一些工程领域都得到了广泛的应用。

PSO是首先由基于不受约束的最小化问题所提出的基于最优化技术。

在一个PSO系统中，多元化解决方案共存且立即返回。

每种方案被称作“微粒”，寻找空间的问题的微粒运动着寻找目标位置。

一个微粒，在他寻找的时间里面，根据他自己的以及周围微粒的经验来调整他的位置。

追踪记忆最佳位置，遇到构建微粒的经验。

因为那个原因，PSO占有一个存储单元（例如，每个微粒记得在过去到达时的最佳位置）。

PSO系统通过全局搜索方法（通过）搜索局部搜索方法（经过自身的经验），试图平衡探索和开发。

粒子群优化算法是一种基于群体的自适应搜索优化算法，存在后期收敛慢、搜索精度低、容易陷入局部极小等缺点，为此提出了一种改进的粒子群优化算法，从初始解和搜索精度两个方面进行了改进，提高了算法的计算精度，改善了算法收敛性，很大程度上避免了算法陷入局部极小．对经典函数测试计算，验证了算法的有效性。

关键词：粒子群优化算法；粒子群；优化技术；最佳位置；全局搜索;搜索精度Particle swarm optimization (PSO) algorithm is a novel evolutionary algorithm. It is a kind of stochastic global optimization technique. PSO finds optimal regions of complex search spaces through the interaction of individuals in a population of particles. The advantages of PSO lie in simple and powerful function. In this paper , classical particle swarm optimization algorithm , the present condition and some applications of the algorithms are introduced , and the possible research contents in future are also discussed.PSO is a population-based optimization technique proposed firstly for the aboveunconstrained minimization problem. In a PSO system, multiple candidate solutions coexist and collaborate simultaneously. Each solution called a ‘‘particle’’, flies in the problem search space looking for the optimal position to land. A particle, as time passe s through its quest, adjusts its position according to its own ‘‘experience’’ as well as the experience of neighboring particles. Tracking and memorizing the best position encountered build particle_s experience. For that reason, PSO possesses a memory (i.e. every particle remembers the best position it reached during the past). PSO system combines local search method(through self experience) with global search methods (through neighboring experience), attempting to balance exploration and exploitation.Abstract Particle Swarm Optimization Algorithm is a kind of auto-adapted search optimization based on community.But the standard particle swarm optimization is used resulting in slow after convergence, low search precision and easily leading to local minimum. A new Particle Swarm Optimization algorithm is proposed to improve from the initial solution and the search precision. The obtained results showed the algorithm computation precision and the astringency are improved, and local minimum is avoided. The experimental results of classic functions show that the improved PSO is efficientand feasible.Key words ：particle swarm optimization algorithms ; unconstrained minimization problem;the bestposition;global search methods; the search precision目录一．引言二．PSO算法的基本原理和描述（一）概述（二）粒子群优化算法（三）一种改进型PSO算法——基于遗传交叉因子的粒子群优化算法简介1 自适应变化惯性权重2 交叉因子法（四） PSO与GA算法的比较1 PSO算法与GA算法2 PSO算法与GA算法的相同点3 PSO算法与GA算法的不同点三．PSO算法的实现及实验结果和仿真（一）基本PSO算法（二）算法步骤（三）伪代码描述（四）算法流程图（五）六个测试函数的运行结果及与GA算法结果的比较四结论五. 致谢六．参考文献一、引言混沌是一种有特点的非线形系统，它是一种初始时存在于不稳定的动态状态而且包含着无限不稳定时期动作的被束缚的行为。

粒子群算法简介优缺点及其应用

10
式(1)的第一部分称为动量部分，表示粒子对当前自身运动状态的信任，为粒子提供了一个必要动量，使其依据自身速度进行惯性运动；
第二部分称为个体认知部分，代表了粒子自身的思考行为，鼓励粒子飞向自身曾经发现的最优位置；
第三部分称为社会认知部分，表示粒子间的信息共享与合作，它引导粒子飞向粒子群中的最优位置。
粒子群算法(Particle Swarm Optimization，简称PSO)，是一种基于群体智能的进化计算方法。PSO由Kennedy和Eberhart博士于1995年提出。
粒子群算法源于复杂适应系统（Complex Adaptive System,CAS）。CAS理论于1994年正式提出，CAS中的成员称为主体。比如研究鸟群系统，每个鸟在这个系统中就称为主体。主体有适应性，它能够与环境及其他的主体进行交流，并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括：新层次的产生（小鸟的出生）；分化和多样性的出现（鸟群中的鸟分成许多小的群）；新的主题的出现（鸟寻找食物过程中，不断发现新的食物）。
改变这些常数会改变系统的“张力”，较低的c1 和 c2值使得粒子徘徊在远离目标的区域，较高的c1 和 c2值产生陡峭的运动或越过目标区域。
Shi和Eberhart建议，为了平衡随机因素的作用，一般情况下设置c1 ＝ c2，大部分算法都采用这个建议。
2021/3/22
13
(4)粒子的最大速度vmax ：粒子的速度在空间中的每一维上都有一个最大速度限制值vdmax ，用来对粒子的速度进行钳制，使速度控制在范围[－vdmax，＋vdmax ]内，这决定问题空间搜索的力度，该值一般由用户自己设定。
19

粒子群算法研究及其工程应用案例

粒子群算法研究及其工程应用案例一、概述随着现代制造业对高精度生产能力和自主研发能力需求的提升，优化指导技术在精确生产制造领域中的应用日益广泛。

粒子群优化算法（Particle Swarm Optimization，PSO）作为一种基于群体智能的优化算法，因其结构简单、参数较少、对优化目标问题的数学属性要求较低等优点，被广泛应用于各种工程实际问题中。

粒子群算法起源于对鸟群捕食行为的研究，通过模拟鸟群或鱼群等群体行为，利用群体中的个体对信息的共享，使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而找到最优解。

自1995年由Eberhart博士和kennedy博士提出以来，粒子群算法已成为一种重要的进化计算技术，并在工程应用中展现出强大的优势。

在工程应用中，粒子群算法可用于工艺参数优化设计、部件结构轻量化设计、工业工程最优工作路径设计等多个方面。

通过将粒子群算法与常规算法融合，可以形成更为强大的策略设计。

例如，在物流路径优化、机器人路径规划、神经网络训练、能源调度优化以及图像分割等领域，粒子群算法都取得了显著的应用成果。

本文旨在深入研究粒子群算法的改进及其工程应用。

对优化理论及算法进行分析及分类，梳理粒子群算法的产生背景和发展历程，包括标准粒子群算法、离散粒子群算法（Discrete Particle Swarm Optimization, DPSO）和多目标粒子群算法（Multi Objective Particle Swarm Optimization Algorithm, MOPSO）等。

在此基础上，分析粒子群算法的流程设计思路、参数设置方式以及针对不同需求得到的改进模式。

结合具体工程案例，探讨粒子群算法在工程实际中的应用。

通过构建基于堆栈和指针概念的离散粒子群改进方法，分析焊接顺序和方向对高速铁路客车转向架构架侧梁的焊接残余应力和变形的影响。

同时，将粒子群算法应用于点云数据处理优化设计，提高曲面重建和粮食体积计算的精度和效率。

一种改进的粒子群优化算法-《价值工程》武燕张冰

一种改进的粒子群优化算法武燕Wu Yan；张冰Zhang Bing（江苏科技大学电子信息学院，镇江212003）（School of Electronics and Information，Jiangsu University of Science and Technology，Zhenjiang 212003，China）摘要：介绍基本粒子群优化算法的原理、特点，并在此基础上提出了一种改进的粒子群算法。

通过在粒子初始化时引入相对基的原理使粒子获得更好的初始解，以及在迭代过程中引入变异模型，部分粒子生成相对应的扩张及收缩粒子，比较其适应度，保留最佳粒子进行后期迭代，使算法易跳出局部最优。

通过经典函数的测试结果表明，新算法的全局搜索能力有了显著提高，并且能够有效避免早熟问题。

Abstract: This paper introduces the principles and characteristics of Particle Swarm Optimization algorithm，and puts forward an improved particle swarm optimization algorithm. It adopted Opposition-Based Learning in initialization to get a better solution and adopted variation model which make some particles generate two corresponding shrink and expand particles and keep the best fitness particle iterate in later iteration to avoid getting into local minumum. The experimental results of classical function show this algorithm improves the global convergence ability and efficiently prevents the algorithm from the local optimization and early maturation.关键词：粒子群优化算法；相对基；变异模型Key words: Particle Swarm Optimization（PSO）；Opposition-Based Learning；variation model中图分类号：TP301.6 文献标识码：A 文章编号：1006-4311（2011）07-0161-020 引言粒子群优化算法（Particle Swarm Optimization，PSO）是一种新型的仿生算法，由Kennedy和Eberhart于1995年提出[1，2]。

穷举法与粒子群算法的比较_王得燕

基于改进粒子群算法的多阈值图像分割_武燕

粒子群算法和遗传算法比较

粒子群算法的研究现状及其应用

粒子群优化算法的研究及改进

粒子群算法

各种群体寻优算法的比较

鸟群算法和粒子群算法

一种全局优化的两阶段算法

粒子群算法可视化

粒子群算法粒子群算法简介

粒子群优化算法(PSO)在智能组卷中的应用

人工智能中的遗传算法与粒子群优化算法比较分析

基于粒子群算法的动态考试安排研究

粒子群算法

粒子群优化算法【精品文档】(完整版)

粒子群算法简介优缺点及其应用

粒子群算法研究及其工程应用案例

一种改进的粒子群优化算法-《价值工程》武燕 张冰

一种改进的粒子群优化算法-《价值工程》武燕张冰