多目标粒子群算法matlab源代码

合集下载

有约束多目标粒子群算法matlab程序

有约束多目标粒子群算法matlab程序摘要：一、多目标粒子群优化算法（MOPSO）概述二、MOPSO 的原理及应用三、MATLAB 实现MOPSO 的步骤四、MOPSO 在多目标优化问题中的优势与局限性五、总结与展望正文：一、多目标粒子群优化算法（MOPSO）概述多目标粒子群优化算法（Multi-objective Particle Swarm Optimization，MOPSO）是一种基于粒子群优化算法的多目标优化方法。

它通过模拟鸟群觅食的自然现象，搜索最优解空间中的全局最优解。

MOPSO 在处理多目标优化问题时，具有较强的全局搜索能力和适应性。

二、MOPSO 的原理及应用MOPSO 的基本原理是在粒子群优化算法的基础上，引入多目标优化问题的特性，即多个目标函数。

在MOPSO 中，每个粒子对应一个解，粒子群通过速度和位置的不断更新，寻找满足多个目标函数的最优解。

MOPSO 广泛应用于各种多目标优化问题，如配电网储能选址、非线性优化问题、多目标路径规划等。

通过MATLAB 实现MOPSO，可以方便地解决这些领域的多目标优化问题。

三、MATLAB 实现MOPSO 的步骤1.构建MOPSO 模型：包括定义目标函数、选择优化算法、设置粒子群参数等。

2.初始化粒子群：随机生成粒子群的位置和速度。

3.迭代更新：根据粒子群优化算法更新粒子的速度和位置。

4.判断收敛：当达到预设的最大迭代次数或满足其他收敛条件时，结束迭代。

5.输出结果：输出满足多个目标函数的最优解。

四、MOPSO 在多目标优化问题中的优势与局限性MOPSO 的优势在于其全局搜索能力和适应性，能够处理复杂的多目标优化问题。

同时，MOPSO 算法简单易懂，易于实现和调试。

然而，MOPSO 也存在一定的局限性。

由于多目标优化问题的特殊性，MOPSO 容易陷入局部最优解，导致算法收敛速度较慢。

此外，MOPSO 对初始粒子群的选择较为敏感，可能会影响算法的性能。

粒子群算法matlab程序

粒子群算法matlab程序粒子群算法（PSO）是一种基于群体智能的求解优化问题的算法。

其通过模拟鸟群等大规模群体行为，实现全局搜索和基于群体协作的局部搜索。

在PSO中，通过一组粒子（每个粒子代表一个解）来搜索问题的解空间，在搜索过程中，粒子的位置表示该解在解空间中的位置，速度表示该解在该方向（即属性）上的变化速率，最终达到全局最优解或局部最优解。

PSO算法有着简单易懂、实现简便、计算速度快以及易于与其他算法结合等优点。

下面我将介绍一下如何使用matlab编写简单的粒子群算法程序。

程序主要分为以下步骤：1.初始化在程序开始之前需要对粒子进行初始化操作，其中需要确定粒子群的大小、每个粒子的位置、速度等初始参数。

2.计算适应值计算每个粒子的适应值，即根据当前位置计算该解的适应值。

适应值可以根据实际问题进行定义，如最小化目标函数或最大化收益等。

3.更新粒子速度和位置这一步是PSO算法的核心步骤，通过改变粒子的速度和位置来找到更优的解。

其核心公式为：v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t)) x(t+1) = x(t) + v(t+1)其中w是惯性权重，c1、c2是学习因子，pbest是该粒子的历史最优解，gbest 是当前全局最优解。

4.更新pbest和gbest在每次更新位置之后需要更新每个粒子自己的历史最优解以及全局最优解。

5.停止条件判断设定停止条件，如最小适应值误差、迭代次数、最大迭代次数等，如果达到了停止条件，则程序结束，输出全局最优解。

下面是一份简单的PSO算法的matlab代码：function [best_fit, best_x] = pso(func, dim, lb, ub, max_iter, swarm_size, w, c1, c2)%初始化粒子v = zeros(swarm_size, dim);x = repmat(lb, swarm_size, 1) + repmat(ub - lb, swarm_size, 1) .* rand(swarm_size, dim);pbest = x;[best_fit, best_idx] = min(func(x));gbest = x(best_idx,:);%开始迭代for iter = 1 : max_iter%更新速度和位置v = w * v + c1 * rand(swarm_size, dim) .* (pbest - x) + c2 * rand(swarm_size, dim) .* repmat(gbest, swarm_size, 1) - x;x = x + v;%边界处理x = max(x, repmat(lb, swarm_size, 1));x = min(x, repmat(ub, swarm_size, 1));%更新pbest和gbestidx = func(x) < func(pbest);pbest(idx,:) = x(idx,:);[min_fit, min_idx] = min(func(pbest));if min_fit < best_fitbest_fit = min_fit;best_x = pbest(min_idx,:);endendend在使用上述代码时，需要定义适应值函数（func）、解空间维度（dim）、每个维度的上界（ub）与下界（lb）、最大迭代次数（max_iter）、粒子群大小（swarm_size）、惯性权重（w）、学习因子（c1、c2）等参数。

改进粒子群算法matlab代码

改进粒子群算法matlab代码粒子群算法是一种基于群体智能的优化算法，其主要思想是将优化问题转化为粒子在搜索空间中寻找最优解的过程。

粒子群算法的运作方式是通过定义一群随机粒子，并根据它们在搜索空间中的位置和速度，来引导粒子向着更好的解决方案进行搜索。

以下是改进版粒子群算法的MATLAB代码：%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 粒子群算法-改进版%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 初始化参数和粒子群function [gbest_x, gbest_y] = PSO(num_particles,max_iterations, f, lower_bound, upper_bound)% 定义粒子群基本参数w = 0.7; % 惯性权重c1 = 1.4; % 学习因子1c2 = 1.4; % 学习因子2% 初始化粒子位置和速度particles_position = unifrnd(lower_bound, upper_bound, [num_particles, 2]);particles_velocity = zeros(num_particles, 2);% 初始化个体最优解和全局最优解pbest_position = particles_position;pbest_value = zeros(num_particles, 1);for i = 1:num_particlespbest_value(i) = f(particles_position(i,:));end[global_min_value, global_min_index] = min(pbest_value); gbest_position = particles_position(global_min_index, :);gbest_value = global_min_value;% 迭代优化for iter = 1:max_iterationsfor i = 1:num_particles% 更新粒子速度particles_velocity(i,:) = w *particles_velocity(i,:) ...+ c1 * rand() * (pbest_position(i,:) -particles_position(i,:)) ...+ c2 * rand() * (gbest_position -particles_position(i,:));% 限制粒子速度范围particles_velocity(i,1) = max(particles_velocity(i,1), lower_bound);particles_velocity(i,1) = min(particles_velocity(i,1), upper_bound);particles_velocity(i,2) = max(particles_velocity(i,2), lower_bound);particles_velocity(i,2) = min(particles_velocity(i,2), upper_bound);% 更新粒子位置particles_position(i,:) = particles_position(i,:) + particles_velocity(i,:);% 限制粒子位置范围particles_position(i,1) = max(particles_position(i,1), lower_bound);particles_position(i,1) = min(particles_position(i,1),upper_bound);particles_position(i,2) = max(particles_position(i,2), lower_bound);particles_position(i,2) = min(particles_position(i,2), upper_bound);% 更新个体最优解temp_value = f(particles_position(i,:));if temp_value < pbest_value(i)pbest_value(i) = temp_value;pbest_position(i,:) = particles_position(i,:);endend% 更新全局最优解[temp_min_value, temp_min_index] = min(pbest_value);if temp_min_value < gbest_valuegbest_value = temp_min_value;gbest_position = pbest_position(temp_min_index,:);endend% 返回全局最优解gbest_x = gbest_position(1);gbest_y = gbest_position(2);end其中，num_particles为粒子数目，max_iterations为最大迭代次数，f为目标函数句柄，lower_bound和upper_bound为搜索空间的下界和上界。

12QoS路由问题的粒子群算法MATLAB源代码

QoS路由问题的粒子群算法MATLAB源代码粒子群算法在离散优化领域的应用比较少见，为了将粒子群算法应用在QoS 路由领域，而又不偏离粒子群算法的基本思想，定义并设计了一种“⊕算子”，并且设计了一种“随机游动算子”，将基于路径的变异算子引入算法，增强算法的全局搜索能力。

%% 第一步：产生网络拓扑结构BorderLength=10; %正方形区域的边长，单位：kmNodeAmount=30; %网络节点的个数Alpha=10; %网络特征参数，Alpha越大，短边相对长边的比例越大Beta=5; %网络特征参数，Beta越大，边的密度越大PlotIf=1; %是否画网络拓扑图，如果为1则画图，否则不画FlagIf=0; %是否标注参数，如果为1则将标注边的参数，否则不标注[Sxy,AM,Cost,Delay,DelayJitter,PacketLoss]=NetCreate(BorderLength,NodeAmount,Alpha,Beta, PlotIf,FlagIf);%% 第二步：使用粒子群算法搜索最优路径，存储数据，输出最优结果和收敛曲线% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensimS=[2,4]; %源节点的集合，用向量存储T=[25,27,29]; %目的节点的几何，用向量存储Alpha=1; %适应值计算式中费用的系数Beta=5e5; %适应值计算式中延时的系数Gamma=3e6; %适应值计算式中延时抖动的系数Delta=1000; %适应值计算式中丢包率的系数QoSD=100e-6; %延时的QoS约束QoSDJ=100e-6; %延时抖动的QoS约束QoSPL=0.02; %丢包率的QoS约束r1=0.1; %单个粒子的历史最优个体对当前粒子的影响系数，0<r1<=1r2=0.3; %粒子群的全局最优个体对当前粒子的影响系数，0<r2<=1r3=0.2; %粒子随机游动的影响系数，0<=r3<=1，r3可以为0，这时将关闭随机游动功能P=10; %粒子的个数Q=20; %迭代次数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%m=length(S);n=length(T);AllRoutes=cell(m,n);%各粒子经过的全部路径AllFitness=cell(m,n);HistoryBestRoutes=cell(m,n);%各粒子的历史最优路径HistoryBestFitness=cell(m,n);AllBestRoutes=cell(m,n);%全局最优路径AllBestFitness=cell(m,n);for i=1:mfor j=1:ns=S(i);t=T(j);[ROUTEst,FitFlag,HR,HFF,AR,AFF]=PSOUC(s,t,r1,r2,r3,P,Q,AM,Cost,Delay,DelayJitter,Packet Loss,QoSD,QoSDJ,QoSPL,Alpha,Beta,Gamma,Delta);AllRoutes{i,j}=ROUTEst;AllFitness{i,j}=FitFlag;HistoryBestRoutes{i,j}=HR;HistoryBestFitness{i,j}=HFF;AllBestRoutes{i,j}=AR;AllBestFitness{i,j}=AFF;endend%下面整理最优结果SYZ=Inf;FinalRoute=[];%最终的最优路由FinalFitness=[];%最终的最优路由对应的参数LearnCurve1=zeros(1,Q);%收敛曲线LearnCurve2=zeros(1,Q);%收敛曲线for q=1:QTT=[];for i=1:mfor j=1:nABR=HistoryBestRoutes{i,j};ABF=HistoryBestFitness{i,j};for p=1:PABRq=ABR{p,q};ABFq=ABF{p,q};TT=[TT,ABFq(1,1)];if ABFq(1,1)<SYZFinalRoute=ABRq;FinalFitness=ABFq;SYZ=ABFq(1,1);endendendendLearnCurve1(q)=mean(TT);LearnCurve2(q)=min(TT);endfigure(2)plot(LearnCurve1,'bs-')xlabel('迭代次数')ylabel('平均适应值')figure(3)plot(LearnCurve2,'bs-')xlabel('迭代次数')ylabel('最优粒子适应值')function[ROUTEst,FitFlag,HR,HFF,AR,AFF]=PSOUC(s,t,r1,r2,r3,P,Q,AM,Cost,Delay,DelayJitter,Packet Loss,QoSD,QoSDJ,QoSPL,Alpha,Beta,Gamma,Delta)%% 使用粒子群算法求源节点s到目的节点t的满足QoS约束的最小费用路径，将这些路径及其参数记录下来% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%% 输入参数列表% s 单个的源节点% t 单个的目的节点% r1 单个粒子的历史最优个体对当前粒子的影响系数，0<r1<=1% r2 粒子群的全局最优个体对当前粒子的影响系数，0<r2<=1% r3 粒子随机游动的影响系数，0<=r3<=1，r3可以为0，这时将关闭随机游动功能% P 粒子的个数% Q 迭代次数% AM 01形式存储的邻接矩阵% Cost 边的费用邻接矩阵% Delay 边的时延邻接矩阵% DelayJitter 边的延时抖动邻接矩阵% PacketLoss 边的丢包率邻接矩阵% QoSD 延时的QoS约束% QoSDJ 延时抖动的QoS约束% QoSPL 丢包率的QoS约束% Alpha 适应值计算式中费用的系数% Beta 适应值计算式中延时的系数% Gamma 适应值计算式中延时抖动的系数% Delta 适应值计算式中丢包率的系数%% 输出参数列表% ROUTEst P×Q的细胞结构，存储所有粒子经历过的从s到t的路径% FitFlag P×Q的细胞结构，存储与ROUTEst对应的Fitness和Flag数据% HR P×Q的细胞结构，存储所有粒子的历史最优路径% HFF P×Q的细胞结构，存储所有粒子的历史最优路径对应的参数% AR 1×Q的细胞结构，存储全局最优路径% AR 1×Q的细胞结构，存储全局最优路径对应的参数%% 粒子群初始化ROUTEst=cell(P,Q);FitFlag=cell(P,Q);HR=cell(P,Q);%各粒子的历史最优路径HFF=cell(P,Q);%各粒子的历史最优路径对应的参数AR=cell(1,Q);%全局最优路径AFF=cell(1,Q);%全局最优路径对应的参数TRACK=Initialize(AM,s,P);for p=1:PRoute=TRACK{p};pos=find(Route==t);Route=Route(1:pos(1));Route=Fresh(Route);ROUTEst{p,1}=Route;HR{p,1}=Route;[Fitness,Flag]=Fit(Route,Cost,Delay,DelayJitter,PacketLoss,QoSD,QoSDJ,QoSPL,Alpha,Beta,Ga mma,Delta);FitFlag{p,1}=[Fitness;Flag];HFF{p,1}=[Fitness;Flag];endSYZ=Inf;for p=1:PRoute=HR{p,1};FF=HFF{p,1};if FF(1,1)<SYZAR{1}=Route;SYZ=FF(1,1);AFF{1}=FF;endend%%for q=2:Q%按照粒子群迭代公式计算各个粒子的下一个位置for p=1:PRoute=ROUTEst{p,q-1};OptRoute1=HR{p,q-1};OptRoute2=AR{1,q-1};Route=SpecialAdd(Route,OptRoute1,r1,Cost);%向自己的历史最优位置靠近Route=SpecialAdd(Route,OptRoute2,r2,Cost);%向全局历史最优位置靠近Route=RandMove(Route,r3,AM);%随机游动[Fitness,Flag]=Fit(Route,Cost,Delay,DelayJitter,PacketLoss,QoSD,QoSDJ,QoSPL,Alpha,Beta,Ga mma,Delta);ROUTEst{p,q}=Route;FitFlag{p,q}=[Fitness;Flag];end%更新各粒子的历史最优位置for p=1:PF1=HFF{p,q-1};F2=FitFlag{p,q};if F2(1,1)<F1(1,1)HR{p,q}=ROUTEst{p,q};HFF{p,q}=FitFlag{p,q};elseHR{p,q}=HR{p,q-1};HFF{p,q}=HFF{p,q-1};endend%更新全局历史最优位置for p=1:PRoute=HR{p,q};FF=HFF{p,q};if FF(1,1)<SYZ&&FF(2,1)==1AR{q}=Route;SYZ=FF(1,1);AFF{q}=FF;elseAR{q}=AR{q-1};AFF{q}=AFF{q-1};endendend。

粒子群算法解决VRP代码（matlab）

粒子群算法解决VRP代码（matlab）particle_swarm_optimization.m文件：function PSOforTSP%初始化Alpha=0.25; %个体经验保留概率Beta=0.25; %全局经验保留概率NC_max=100; %最大迭代次数m=80; %微粒数CityNum=14; %问题的规模（城市个数）[dislist,Clist]=tsp(CityNum);NC=1;%迭代计数器R_best=zeros(NC_max,CityNum); %各代最佳路线L_best=inf.*ones(NC_max,1);%各代最佳路线的长度L_ave=zeros(NC_max,1);%各代路线的平均长度%产生微粒的初始位置for i=1:mx(i,:)=randperm(CityNum);L(i)=CalDist(dislist,x(i,:));endp=x; %p为个体最好解pL=L;[L_best(1,1) n_best]=min(L);R_best(1,:)=x(n_best,:);L_ave(1,1)=mean(L);%初始交换序v=ones(CityNum-1,2,m)*(round(rand*(CityNum-1))+1);figure(1);while NC<=NC_max %停止条件之一：达到最大迭代次数for i=1:mxnew(i,:)=changeFun(x(i,:),v(:,:,i));A=changeNum(x(i,:),p(i,:));Arand=randFun(A,Alpha);xnew(i,:)=changeFun(xnew(i,:),Arand);B=changeNum(x(i,:),R_best(NC,:));Brand=randFun(B,Beta);xnew(i,:)=changeFun(xnew(i,:),Brand);v(:,:,i)=changeNum(x(i,:),xnew(i,:));L(i)=CalDist(dislist,xnew(i,:));if L(i)<pl(i)< p="">p(i,:)=xnew(i,:);pL(i)=L(i);endend[L_bestnew n_best]=min(L);R_bestnew=xnew(n_best,:);L_ave(NC+1,1)=mean(L);if L_bestnew<l_best(nc,1)< p="">L_best(NC+1,1)=L_bestnew;R_best(NC+1,:)=R_bestnew;elseL_best(NC+1,1)=L_best(NC,1);R_best(NC+1,:)=R_best(NC,:);endx=xnew;drawTSP10(Clist,R_best(NC,:),L_best(NC,1),NC,0); %pause;NC=NC+1;end%输出结果Pos=find(L_best==min(L_best));Shortest_Route=R_best(Pos(1),:);Shortest_Length=L_best(Pos(1)); figure(2);plot([L_best L_ave]);legend('最短距离','平均距离'); endfunction xnew=changeFun(x,C); changeLen=size(C,1);xnew=x;for i=1:changeLena=xnew(C(i,1));xnew(C(i,1))=xnew(C(i,2));xnew(C(i,2))=a;endendfunction C=changeNum(x,y); CityNum=size(x,2);C=ones(CityNum-1,2);for i=1:CityNum-1pos=find(x==y(i));C(i,:)=[i pos];x=changeFun(x,C(i,:));endendfunction v=randFun(v,w);randLen=size(v,1);for i=1:randLenif rand>wv(i,2)=v(i,1);endendendfunction F=CalDist(dislist,s)%计算回路路径距离DistanV=0;n=size(s,2);for i=1:(n-1)DistanV=DistanV+dislist(s(i),s(i+1));endDistanV=DistanV+dislist(s(n),s(1));F=DistanV;endfunction [DLn,cityn]=tsp(n)city14=[0 0;0.3 0.334;0.08 0.433;0.166 0.456;0.5 0.4439;0.2439 0.1463;0.1207 0.2293;0.2293 0.761;0.6171 0.9414;0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];for i=1:14for j=1:14DL14(i,j)=((city14(i,1)-city14(j,1))^2+(city14(i,2)-city14(j,2))^2)^0.5;endendDLn=DL14;cityn=city14;enddrawTSP10.m文件：function m=drawTSP(Clist,BSF,bsf,p,f)CityNum=size(Clist,1);for i=1:CityNum-1plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i +1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');hold on;endaxis([0,1,0,1]);plot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNu m),2),Clist(BSF(1), 2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');title([num2str(CityNum),'城市TSP']);if f==0text(0.1,0.1,['第',int2str(p),' 步',' 最短距离为',num2str(bsf)]);elsetext(0.1,0.1,['最终搜索结果：最短距离',num2str(bsf)]);endhold off;pause(0.05);</l_best(nc,1)<></pl(i)<>。

粒子群算法 matlab源代码

%相关参数的设置UB=600; %函数的上界LB=300; %函数的下界PopSize=40; %种群的大小Dim=10; %微粒的维数c1=2; %学习因子c2=2; %学习因子w_start=0.9;%惯性权重的开始值w_end=0.4;%惯性权重的最后值Vmax=100;%微粒的最大速度MaxIter=1500;%最大迭代次数Iter=0;%初始迭代次数%初始化群和速度X=rand(PopSize,Dim)*(UB-LB)+LB;%微粒位置随机初始化V=rand(PopSize,Dim);%微粒速度随机初始化；%测试函数：Griewank函数ind=repmat(1:Dim,PopSize,1);FX=sum(((X.^2)/4000)')'- prod(cos(X./sqrt(ind))')'+1;%设定当前位置为粒子的最好位置，并记录其最好值PBest=X;FPBest=FX;%找到初始微粒群体的最好微粒[Fgbest,r]=min(FX);CF=Fgbest;%记录当前全局最优值Best=X(r,:);%用于保存最优粒子的位置FBest=Fgbest;%循环while(Iter<=MaxIter)Iter=Iter+1;%更新惯性权重的值；w_now=((w_start-w_end)*(MaxIter-Iter)/MaxIter)+w_end;A=repmat(X(r,:),PopSize,1);%生成随机数R1=rand(PopSize,Dim);R2=rand(PopSize,Dim);%速度更新V=w_now*V+c1*R1.*(PBest-X)+c2*R2.*(A-X);%对进化后速度大于最大速度的微粒进行处理changeRows=V>Vmax;VStep(find(changeRows))=Vmax;%对进化后速度小雨最小速度的微粒进行处理changeRows=V<-Vmax;V(find(changeRows))=-Vmax;%微粒位置进行更新X=X+1.0*V;%重新计算新位置的适应度值ind=repmat(1:Dim,PopSize,1);FX=sum(((X.^2)/4000)')'- prod(cos(X./sqrt(ind))')'+1;%更新每个微粒的最好位置P=FX<FPBest;FPBest(find(P))=FX(find(P));%适应值更换PBest(find(P),:)=X(find(P),:)%粒子位置更换[Fgbest,g]=min(FPBest);%保存最好适应值if Fgbest<CF %如果本次适应值好于上次则保存[fBest,b]=min(FPBest);%最好适应值为fBestBest=PBest(b,:);%最好位置为BestendCF=Fgbest;%保留本次适应值准备与下次比较end %循环结束。

粒子群算法详解matlab代码

粒子群算法(1)----粒子群算法简介一、粒子群算法的历史粒子群算法源于复杂适应系统（Complex Adaptive System,CAS）。

CAS理论于1994年正式提出，CAS中的成员称为主体。

比如研究鸟群系统，每个鸟在这个系统中就称为主体。

主体有适应性，它能够与环境及其他的主体进行交流，并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。

整个系统的演变或进化包括：新层次的产生（小鸟的出生）；分化和多样性的出现（鸟群中的鸟分成许多小的群）；新的主题的出现（鸟寻找食物过程中，不断发现新的食物）。

所以CAS系统中的主体具有4个基本特点（这些特点是粒子群算法发展变化的依据）：首先，主体是主动的、活动的。

主体与环境及其他主体是相互影响、相互作用的，这种影响是系统发展变化的主要动力。

环境的影响是宏观的，主体之间的影响是微观的，宏观与微观要有机结合。

最后，整个系统可能还要受一些随机因素的影响。

粒子群算法就是对一个CAS系统－－－鸟群社会系统的研究得出的。

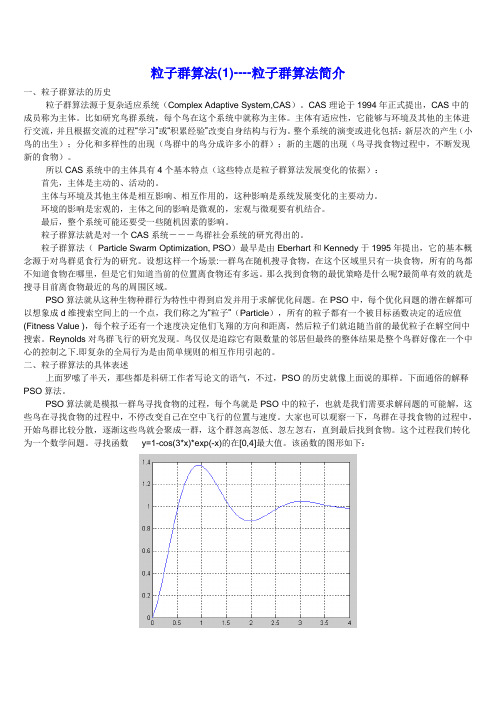
粒子群算法（Particle Swarm Optimization, PSO）最早是由Eberhart和Kennedy于1995年提出，它的基本概念源于对鸟群觅食行为的研究。

设想这样一个场景:一群鸟在随机搜寻食物，在这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但是它们知道当前的位置离食物还有多远。

那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

PSO算法就从这种生物种群行为特性中得到启发并用于求解优化问题。

在PSO中，每个优化问题的潜在解都可以想象成d维搜索空间上的一个点，我们称之为“粒子”（Particle），所有的粒子都有一个被目标函数决定的适应值(Fitness Value )，每个粒子还有一个速度决定他们飞翔的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索。

Reynolds对鸟群飞行的研究发现。

粒子群算法matlab(算法已经调试)

程序1当22111==c c ，5.12212==c c ，2.1=w 。

a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ）%------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数%------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=1.5;c22=1.5;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用） %------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif (rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48), char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b ）适应度函数%适应度函数（fitness.m ）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序2当22111==c c 于2.1,2,02212===w c c 对比a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ）%------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数%------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=0;c22=2;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用）%------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48),char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:));x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b）适应度函数%适应度函数（fitness.m）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序3当2.1,22111===w c c 于2.1,0,22212===w c c 对比a)%主函数源程序（main.m ）%------基本粒子群算法（particle swarm optimization ） %------名称：基本粒子群算法%------初始格式化clear all ; %清除所有变量clc; %清屏format long ; %将数据显示为长整形科学计数 %------给定初始条条件------------------N=40; %³初始化群体个数D=10; %初始化群体维数T=100; %初始化群体最迭代次数c11=2; %学习因子1c21=2; %学习因子2c12=2;c22=0;w=1.2; %惯性权重eps=10^(-6); %设置精度（在已知最小值的时候用） %------初始化种群个体（限定位置和速度）------------x=zeros(N,D);v=zeros(N,D);for i=1:Nfor j=1:Dx(i,j)=randn; %随机初始化位置v(i,j)=randn; %随机初始化速度endend%------显示群位置----------------------figure(1)for j=1:Dif (rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始位置')tInfo=strcat('第',char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48)，char(rem(j,10)+48),'维');endtitle(tInfo)end%------显示种群速度figure(2)for j=1:Dif(rem(D,2)>0)subplot((D+1)/2,2,j)elsesubplot(D/2,2,j)endplot(x(:,j),'b*');grid onxlabel('粒子')ylabel('初始速度')tInfo=strcat('第,char(j+48),'维');if(j>9)tInfo=strcat('第',char(floor(j/10)+48), char(rem(j,10)+48),'维);endtitle(tInfo)endfigure(3)%第一个图subplot(1,2,1)%------初始化种群个体（在此限定速度和位置）------------x1=x;v1=v;%------初始化个体最优位置和最优值---p1=x1;pbest1=ones(N,1);for i=1:Npbest1(i)=fitness(x1(i,:),D);end%------初始化全局最优位置和最优值---------------g1=1000*ones(1,D);gbest1=1000;for i=1:Nif(pbest1(i)<gbest1)g1=p1(i,:);gbest1=pbest1(i);endendgb1=ones(1,T);%-----浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x1(j,:),D)<pbest1(j))p1(j,:)=x1(j,:);pbest1(j)=fitness(x1(j,:),D);endif(pbest1(j)<gbest1)g1=p1(j,:);gbest1=pbest1(j);endv1(j,:)=w*v1(j,:)+c11*rand*(p1(j,:)-x1(j,:))+c21*rand*(g1-x1(j,:));x1(j,:)=x1(j,:)+v1(j,:);endgb1(i)=gbest1;endplot(gb1)TempStr=sprintf('c1= %g ,c2=%g',c11,c21);title(TempStr);xlabel('迭代次数');ylabel('适应度值');%第二个图subplot(1,2,2)%-----初始化种群个体（在此限定速度和位置）------------x2=x;v2=v;%-----初始化种群个体最有位置和最优解-----------p2=x2;pbest2=ones(N,1);for i=1:Npbest2(i)=fitness(x2(i,:),D);end%-----初始化种全局最有位置和最优解------g2=1000*ones(1,D);gbest2=1000;for i=1:Nif(pbest2(i)<gbest2)g2=p2(i,:);gbest2=pbest2(i);endendgb2=ones(1,T);%------浸入主循环，按照公式依次迭代直到满足精度或者迭代次数---for i=1:Tfor j=1:Nif (fitness(x2(j,:),D)<pbest2(j))p2(j,:)=x2(j,:);pbest2(j)=fitness(x2(j,:),D);endif(pbest2(j)<gbest2)g2=p2(j,:);gbest2=pbest2(j);endv2(j,:)=w*v2(j,:)+c12*rand*(p2(j,:)-x2(j,:))+c22*rand*(g2-x2(j,:)); x2(j,:)=x2(j,:)+v2(j,:);endgb2(i)=gbest2;endplot(gb2)TempStr=sprintf('c1= %g ,c2=%g',c12,c22);title(TempStr);xlabel('迭代次数');ylabel('适应度值');b ）适应度函数%适应度函数（fitness.m ）function result=fitness(x,D)sum=0;for i=1:Dsum=sum+x(i)^2;endresult=sum;程序4对21c c ≠，21w w ≠分别对其取值1.11=c ，22=c ，2.11=w ，5.12=w 测试函数。

有约束多目标粒子群算法matlab程序

有约束多目标粒子群算法matlab程序【实用版】目录一、多目标粒子群算法的概念和原理二、MATLAB 实现多目标粒子群优化算法的步骤三、多目标粒子群算法在配电网储能选址定容中的应用四、多目标粒子群优化算法的优缺点五、总结与展望正文一、多目标粒子群算法的概念和原理多目标粒子群算法（Multi-objective Particle Swarm Optimization，MOPSO）是一种基于启发式的多目标全局优化算法。

它起源于鸟群觅食的自然现象，通过模拟鸟群中个体的觅食行为，寻找全局最优解。

与传统的单目标粒子群算法不同，MOPSO 需要处理多个目标函数，因此需要在算法中加入目标函数权重的概念，以确定每个目标函数在优化过程中的重要性。

二、MATLAB 实现多目标粒子群优化算法的步骤1.确定优化问题：首先，需要明确优化问题的具体内容，包括目标函数、约束条件和搜索空间等。

2.初始化粒子群：根据搜索空间的大小和目标函数的个数，生成一定数量的粒子，并随机分配它们在搜索空间中的位置和速度。

3.更新粒子速度和位置：根据粒子群算法的更新规则，结合目标函数的梯度和约束条件，更新每个粒子的速度和位置。

4.评估适应度：根据目标函数的值，计算每个粒子的适应度，并选择最优的粒子作为全局最优解。

5.结束条件：当达到预设的最大迭代次数或全局最优解的适应度满足预设的标准时，结束优化过程。

6.输出结果：输出全局最优解及其对应的适应度。

三、多目标粒子群算法在配电网储能选址定容中的应用多目标粒子群算法在配电网储能选址定容问题中具有很好的应用前景。

该问题涉及到多个目标函数，如储能设备的投资成本、运行维护费用、电网的运行安全性等。

MOPSO 可以通过调整目标函数权重，很好地平衡这些目标之间的关系，从而找到最优的储能设备容量和位置。

四、多目标粒子群优化算法的优缺点MOPSO 的优点在于其全局搜索能力，能够处理多个目标函数，并在搜索过程中自动平衡各目标之间的关系。

有约束多目标粒子群算法matlab程序

有约束多目标粒子群算法matlab程序约束多目标粒子群算法（Constrained Multi-Objective Particle Swarm Optimization，CMOPSO）是一种用于处理多目标优化问题的进化算法。

以下是一个简单的MATLAB 示例程序，演示了如何实现CMOPSO。

请注意，这只是一个基本的框架，你可能需要根据你的具体问题进行适当的修改。

```matlabfunction [paretoFront, paretoSet] = cmopso(objectiveFunction, constraintFunction, nParticles, nIterations, nObjectives)% 参数设置nVariables = 2; % 例子中假设有两个变量w = 0.5; % 权重因子c1 = 2; % 学习因子1c2 = 2; % 学习因子2vMax = 0.2; % 最大速度nConstraints = 2; % 约束数量% 初始化粒子群particles.position = rand(nParticles, nVariables);particles.velocity = rand(nParticles, nVariables);particles.bestPosition = particles.position;particles.bestValue = inf(nParticles, nObjectives);% 迭代优化for iteration = 1:nIterations% 更新粒子位置和速度for i = 1:nParticles% 计算适应值fitness = objectiveFunction(particles.position(i, :));% 计算约束违反度constraintViolation = constraintFunction(particles.position(i, :));% 更新粒子最优解if all(constraintViolation <= 0) && dominates(fitness, particles.bestValue(i, :))particles.bestPosition(i, :) = particles.position(i, :);particles.bestValue(i, :) = fitness;end% 更新全局最优解if all(constraintViolation <= 0) && dominates(fitness, globalBestValue)globalBestPosition = particles.position(i, :);globalBestValue = fitness;end% 更新粒子速度和位置r1 = rand(1, nVariables);r2 = rand(1, nVariables);particles.velocity(i, :) = w * particles.velocity(i, :) + ...c1 * r1 .* (particles.bestPosition(i, :) - particles.position(i, :)) + ...c2 * r2 .* (globalBestPosition - particles.position(i, :));% 速度限制particles.velocity(i, :) = min(max(particles.velocity(i, :), -vMax), vMax);% 更新粒子位置particles.position(i, :) = particles.position(i, :) + particles.velocity(i, :);endend% 获取Pareto 前沿和Pareto 集paretoFront = [];paretoSet = [];for i = 1:nParticlesif all(constraintFunction(particles.position(i, :)) <= 0)isDominated = false;for j = 1:size(paretoFront, 1)if dominates(particles.bestValue(i, :), paretoFront(j, :))isDominated = true;break;elseif dominates(paretoFront(j, :), particles.bestValue(i, :))paretoFront(j, :) = [];break;endendif ~isDominatedparetoFront = [paretoFront; particles.bestValue(i, :)];paretoSet = [paretoSet; particles.bestPosition(i, :)];endendendendfunction result = dominates(a, b)% 判断a 是否支配bresult = all(a <= b) && any(a < b);end```请注意，这只是一个简单的示例，具体问题的约束函数和目标函数需要根据你的应用进行修改。

matlab汽车传动系多目标优化原程序

汽车传动系统，多目标优化（粒子群法）matlab原程序代码，供参考学习！可以根据实际情况进行更改进行运算。

原码：function apso% 参数设置定义全局变量global lamda1 lamda2 m ua_max eta_T r G f alpha Cd A rou K Ttq_max Fz fai ge_ne_pe dulamda1 = 0.2; % 动力性发挥程度加权因子；lamda2 = 0.8; % 经济性加权因子；m = 1092; % 整车质量（kg）；ua_max = 50; % 最大车速(km/h)；eta_T = 0.9; % 传动系的传动效率；r = 0.3; % 车轮半径(m)；g = 9.8; % 重力加速度（g*m/s^2）G = m*g; % 汽车重力G=mg，(N)；f = 0.015; % 汽车的滚动阻力系数；alpha = 25*pi/180; % 道路坡度角-->弧度；Cd = 0.32; % 空气阻力系数；A = 1.5; % 迎风面积，即汽车行驶方向的投影面积(m^2)；rou = 7.0; % 燃油重度，N/L等同于密度；K = 1.05; % 考虑连续加速,加权系数；Ttq_max = 132; % 发动机的最大转矩(N.m)；Fz = G/4; % 驱动轮上的法向反作用力(N)；fai = 0.7; % 地面附着系数；ge_ne_pe = 205; % 发动机的燃油消耗率(g/kW.h)；du = 0.1; % 步长% 变量Lb=[ 1 1 0.5 0.5 0.3 2]; %下边界Ub=[5.0 4.0 3.0 2.0 1.0 6]; %上边界% 默认参数para=[25 150 0.95]; %[粒子数，迭代次数，gama参数]% APSO 优化求解函数[gbest,fmin]=pso_mincon(@cost,@constraint,Lb,Ub,para);% 输出结果Bestsolution=gbest % 全局最优个体fmin%% 目标函数function fy=cost(x)% ig1 = x(1); %变速器第1挡的传动比% ig2 = x(2); %变速器第2挡的传动比% ig3 = x(3); %变速器第3挡的传动比% ig4 = x(4); %变速器第4挡的传动比% ig5 = x(5); %变速器第5挡的传动比% ig0 = x(6); %主减速器传动比global lamda1 lamda2 m ua_max eta_T r G f alpha Cd A rou K Ttq_max Fz fai ge_ne_pe du% 发动机功率(Pe)T = 0; % 时间Q = 0; % 耗油量for ua = 0.1:0.1:ua_maxif ua<=10delta = 1.06+0.04*x(1).^2; % 汽车旋转质量换算系数ne = ua*x(6)*x(1)/0.377/r; % 转速（r/min）Pe=(G*f*ua/3600+Cd*A*ua.^3/76140+delta*m*ua*du/3600)/eta_T;Me = 9549*Pe./ne; % 发动机转矩(N.m)Ft = Me*x(1)*x(6)*eta_T/r; % 汽车的驱动力elseif ua>10 && ua<=20delta = 1.06+0.04*x(2).^2; % 汽车旋转质量换算系数ne = ua*x(6)*x(2)/0.377/r; % 转速（r/min）Pe = ( G*f*ua/3600 + Cd*A*ua.^3/76140 + delta*m*ua*du/3600)/eta_T;Me = 9549*Pe./ne; % 发动机转矩(N.m)Ft = Me*x(2)*x(6)*eta_T/r; % 汽车的驱动力elseif ua>20 && ua<=30delta = 1.06+0.04*x(3).^2; % 汽车旋转质量换算系数ne = ua*x(6)*x(3)/0.377/r; % 转速（r/min）Pe = ( G*f*ua/3600 + Cd*A*ua.^3/76140 + delta*m*ua*du/3600)/eta_T;Me = 9549*Pe./ne; % 发动机转矩(N.m)Ft = Me*x(3)*x(6)*eta_T/r; % 汽车的驱动力elseif ua>30 && ua<=40delta = 1.06+0.04*x(4).^2; % 汽车旋转质量换算系数ne = ua*x(6)*x(4)/0.377/r; % 转速（r/min）Pe = ( G*f*ua/3600 + Cd*A*ua.^3/76140 + delta*m*ua*du/3600)/eta_T;Me = 9549*Pe./ne; % 发动机转矩(N.m)Ft = Me*x(4)*x(6)*eta_T/r; % 汽车的驱动力elseif ua>40 && ua<=ua_maxdelta = 1.06+0.04*x(4).^2; % 汽车旋转质量换算系数ne = ua*x(6)*x(5)/0.377/r; % 转速（r/min）Pe = ( G*f*ua/3600 + Cd*A*ua.^3/76140 + delta*m*ua*du/3600)/eta_T;Me = 9549*Pe./ne; % 发动机转矩(N.m)Ft = Me*x(5)*x(6)*eta_T/r; % 汽车的驱动力endFf = G*f*cos(alpha); % 汽车的滚动阻力Fw = Cd*A*ua.^2/21.15; % 汽车的空气阻力% f1(x)动力性分目标函数T = T + delta*m*du/(Ft-Ff-Fw); % 从0到最大速度ua_max所用时间% f2(x)经济性分目标函数delta_S = (ua + ua+du)/2; % 单位距离Q = Q + K*Pe*ge_ne_pe*delta_S./102./ua./rou; % 耗油量endfy = lamda1*T + lamda2*Q;% 非线性约束function [g,geq]=constraint(x)global lamda1 lamda2 m ua_max eta_T r G f alpha Cd A rou K Ttq_max Fz fai ge_ne_pe du% 不等式限制条件q = (x(1)./x(5)).^(1/4);g(1)= Ttq_max*x(1)*x(6)*eta_T/r - Fz*fai;g(2)= 0.85*q-x(1)./x(2);g(3)= x(1)./x(2)-1.15*q;g(4)= 0.80*q-x(2)./x(3);g(5)= x(2)./x(3)-1.1*q;g(6)= 0.75*q-x(3)./x(4);g(7)= x(3)./x(4)-1.05*q;g(8)= 0.7*q-x(4)./x(5);g(9)= x(4)./x(5)-1.0*q;g(10)= x(2)./x(3)-0.95*x(1)./x(2);g(11)= x(3)./x(4)-0.95*x(2)./x(3);g(12)= x(4)./x(5)-0.95*x(3)./x(4);g(13)= x(2)-x(1);g(14)= x(3)-x(2);g(15)= x(4)-x(3);g(16)= x(5)-x(4);g(17)= x(1)-x(6);% 如果没有等式约束，则置geq=[]；geq=[];%% APSO Solverfunction [gbest,fbest]=pso_mincon(fhandle,fnonlin,Lb,Ub,para) if nargin<=4,para=[20 150 0.95];endn=para(1); % 粒子种群大小time=para(2); % 时间步长，迭代次数gamma=para(3); % gama参数scale=abs(Ub-Lb); % 取值区间% 验证约束条件是否合乎条件if abs(length(Lb)-length(Ub))>0,disp('Constraints must have equal size');returnendalpha=0.2; % alpha=[0,1]粒子随机衰减因子beta=0.5; % 收敛速度(0->1)=(slow->fast);% 初始化粒子群best=init_pso(n,Lb,Ub);fbest=1.0e+100;% 迭代开始for t=1:time,%寻找全局最优个体for i=1:n,fval=Fun(fhandle,fnonlin,best(i,:));% 更新最有个体if fval<=fbest,gbest=best(i,:);fbest=fval;endend% 随机性衰减因子alpha=newPara(alpha,gamma);% 更新粒子位置best=pso_move(best,gbest,alpha,beta,Lb,Ub);% 结果显示str=strcat('Best estimates: gbest=',num2str(gbest));str=strcat(str,' iteration='); str=strcat(str,num2str(t));disp(str);fitness1(t)=fbest;plot(fitness1,'r','Linewidth',2)grid onhold ontitle('适应度')end% 初始化粒子函数function [guess]=init_pso(n,Lb,Ub)ndim=length(Lb);for i=1:n,guess(i,1:ndim)=Lb+rand(1,ndim).*(Ub-Lb);end%更新所有的粒子toward (xo,yo)function ns=pso_move(best,gbest,alpha,beta,Lb,Ub)% 增加粒子在上下边界区间内的随机性n=size(best,1); ndim=size(best,2);scale=(Ub-Lb);for i=1:n,ns(i,:)=best(i,:)+beta*(gbest-best(i,:))+alpha.*randn(1,ndim).*scale; endns=findrange(ns,Lb,Ub);% 边界函数function ns=findrange(ns,Lb,Ub)n=length(ns);for i=1:n,% 下边界约束ns_tmp=ns(i,:);I=ns_tmp<Lb;ns_tmp(I)=Lb(I);% 上边界约束J=ns_tmp>Ub;ns_tmp(J)=Ub(J);%更新粒子ns(i,:)=ns_tmp;end% 随机性衰减因子function alpha=newPara(alpha,gamma); alpha=alpha*gamma;% 带约束的d维目标函数的求解function z=Fun(fhandle,fnonlin,u)% 目标z=fhandle(u);z=z+getconstraints(fnonlin,u); % 非线性约束function Z=getconstraints(fnonlin,u)% 罚常数>> 1PEN=10^15;lam=PEN; lameq=PEN;Z=0;% 非线性约束[g,geq]=fnonlin(u);%通过不等式约束建立罚函数for k=1:length(g),Z=Z+ lam*g(k)^2*getH(g(k));end% 等式条件约束for k=1:length(geq),Z=Z+lameq*geq(k)^2*geteqH(geq(k)); end% Test if inequalitiesfunction H=getH(g)if g<=0,H=0;elseH=1;end% Test if equalities hold function H=geteqH(g) if g==0,H=0;elseH=1;end。

matlab自带的粒子群算法

matlab自带的粒子群算法粒子群算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，可用于解决各种实数空间的优化问题。

在Matlab中，PSO算法由函数“particleswarm”实现。

本文将简要介绍该函数的使用方法和一些相关参考内容，以便读者熟悉和使用该算法。

首先，为了使用Matlab中的PSO算法，需要了解“particleswarm”函数的基本用法和语法。

该函数的基本语法如下：[pbest,fval] = particleswarm(fun,nvars,lb,ub)其中，fun是优化目标函数的句柄，nvars是问题变量的维数，lb和ub分别是每个变量的下界和上界。

该函数返回优化结果pbest和对应的目标函数值fval。

除了基本用法外，“particleswarm”函数还提供了许多可选参数，用于进一步控制粒子群算法的行为。

例如，可以通过设置“MaxIterations”参数来指定最大迭代次数，或者通过设置“MaxStallIterations”参数来指定停滞迭代次数。

为了更好地理解PSO算法，读者可以参考以下相关内容：1. 书籍：《Swarm Intelligence: Principles, Advances, and Applications》（英文版），作者：Russel C. Eberhart等。

这本书对群体智能算法的原理、应用和进展进行了全面介绍，其中包括对PSO算法的详细解释和实例应用。

2. 学术论文：《Particle swarm optimization》（2008），作者：Maurice Clerc。

这篇经典的学术论文详细阐述了PSO算法的原理、参数设置和改进策略，对理解和应用PSO算法具有重要参考价值。

3. Matlab官方文档：Matlab官方网站提供了针对“particleswarm”函数的详细文档和示例代码。

用户可以通过访问Matlab官方网站并搜索“particleswarm”来获取相关信息。

粒子群算法matlab代码

一、粒子群主程序psize=20; %粒子个数的设置pd=12; %粒子的维数lz=zeros(psize,pd);for i=1:psize %随机生成粒子群，psize行pd列，pd维。

suiji=rand(1,pd);for j=1:pd/2if suiji(j)<0.5lz(i,j)=fix(unifrnd(0,100))*100;elselz(i,j)=fix(unifrnd(0,100)+1)*100;endendfor j=pd/2+1:1:pdif suiji(j)<0.5lz(i,j)=fix(unifrnd(0,45))/100;elselz(i,j)=fix(unifrnd(0,45)+1)/100;endendlz(i,1:pd/2)=sort(lz(i,1:pd/2));lz(i,pd/2+1:pd)=sort(lz(i,pd/2+1:pd));endlv=lz;goodvalue=lz; %每个粒子自己历史最好值初始化，psize行pd列。

vmax=20; %速度上限c1=2;c2=2; %学习因子w=0.729; %随机因子和惯性因子bestvalue=zeros(1,pd); %全局最好值初始化，1行pd列for j=1:pdbestvalue(1,j)=goodvalue(1,j);endfnew=zeros(1,psize);for j=1:psizefnew(j)=fpso(lz(1,:));endfold=fnew;flagstop=0; %终止标志k=0; %迭代次数记录f0=fpso(bestvalue); %适应值初始化while flagstop==0for i=1:psize %适应值比较，更新各自历史最好值（位置）fnew(i)=fpso(lz(i,:)); %记录每次每个粒子的适应值，便于以后设置终止条件if fnew(i)<fold(i)fold(i)=fnew(i); %fold记录每个粒子的最好历史值goodvalue(i,j)=lz(i,j);endendendfor i=1:psize%每个粒子历史最好值比较，更新全局最好值f1=fold(i);if f1<f0f0=f1;for j=1:pdbestvalue(1,j)=goodvalue(i,j);endendend%*********粒子趋一点终止条件*********%flagstop0=max(abs(fold)); %比较当次的所有粒子的适应值，flagstop1=min(abs(fold)); %若它们之间差别较小，则可以停止。

粒子群算法matlaB程序

qu(k)=-160/100*(k-350)+1680;
end
for k=451:540
qu(k)=1520;
end
for k=541:700
qu(k)=1520+80/100*(k-540);
end
for k=701:800
qu(k)=qu(700);
legend('Expext Line','PID')
xlabel('时间/分')
subplot(2,2,4)
plot(qut(1:end-1)/3,r,'-.')
legend('r(t)')
xlabel('时间/分')
rou(k+1)=rou(k)+alpha*qu(k)-alpha*vf*(rou(k)-rou(k)^2/rou_jam)+alpha*r(k)/lambda;
end
%%
%显示构造的期望密度
figure(1)
subplot(2,2,1)
plot(qut/3,qu)
xlabel('时间/分')
end00)-90/100*(k-800);
end
for k=951:1100
qu(k)=qu(950);
end
for k=1101:1200
qu(k)=qu(950)+120/100*(k-1100);
end
qu(k)=qu(1520)+70/100*(k-1650);
end
for k=1701:1850

粒子群算法的matlab代码实现

粒子群算法的matlab代码实现function swarmwarning off MATLAB:divideByZero%%% Script Particle Swarm Optimization%%% Author: Ivan Candelas del Toro%%% e-mail: ivanct@%%%%%% Control variables%%%%%global numberOfParticles;numberOfParticles = 40;global numberOfNeighbors;numberOfNeighbors = 4;maxIterations = 1000;%% Limites para cambio de localizaciónglobal deltaMin;deltaMin = -4.0;global deltaMax;deltaMax = 4.0;%% individuality and socialityiWeight = 2.0;iMin = 0.0;iMax = 1.0;sWeight = 2.0;sMin = 0.0;sMax = 1.0;%%%%%%%%%%%%% Related variables to the problem space solutions %%%%%%%%%%%initialFitness = -100000;targetFitness = 0;global dimensions;dimensions = 4;%%%% Program Startglobal particles;for p = 1:numberOfParticlesfor d = 1:dimensionsparticles(p).next(d) = randint(1,10); %%%%%%%%%%%%%%%%%particles(p).velocity(d) =randint(deltaMin,deltaMax); %%%%%%%%%%%particles(p).current(d) = particles(p).next(d);endparticles(p).bestSoFar = initialFitness;endfor p = 1:numberOfParticlesneighborVector = getNeighborIndexVector(p,numberOfNeighbors);for n = 1:numberOfNeighborsparticles(p).neighbor(n) = neighborVector(n);endenditerations = 0;ticwhile iterations <= maxIterationsfor p = 1:numberOfParticlesfor d = 1:dimensionsparticles(p).current(d) = particles(p).next(d);endfitness = test(p);if fitness > particles(p).bestSoFar;particles(p).bestSoFar = fitness;for d = 1:dimensionsparticles(p).best(d) = particles(p).current(d);endendif fitness == targetFitnessX=particles(p).current(1)Y=particles(p).current(2)Z=particles(p).current(3)W=particles(p).current(4)total_time=tocdisp('Success!!');returnendendfor p = 1:numberOfParticlesn = getNeighborIndexWithBestFitness(p);for d = 1:dimensionsiFactor = iWeight * randint(iMin,iMax); %%%%%%%%%%%%%%sFactor = sWeight * randint(sMin,sMax); %%%%%%%%%%%%%pDelta(d) = particles(p).best(d) - particles(p).current(d); nDelta(d) = particles(n).best(d) - particles(p).current(d);delta = (iFactor * pDelta(d)) + (sFactor * nDelta(d));delta = particles(p).velocity(d) + delta;particles(p).velocity(d) = constrict(delta);particles(p).next(d) = particles(p).current(d) +particles(p).velocity(d);endenditerations = iterations + 1enddisp('Failure');%%%%%%%%%%%%% Support Functions%%%%%%%%%%%%-------------function fitness = test(p)global particles;x = particles(p).current(1);y = particles(p).current(2);z = particles(p).current(3);w = particles(p).current(4);f = 5 * (x^2) + 2 * (y^3) - (z/w)^2 + 4;if ( x * y ) == 0n = 1;elsen = 0;endfitness = 0 - abs(f) - n;%%-------------function d = constrict(delta)global deltaMin;global deltaMax;if delta < deltaMind = deltaMin;returnendif delta > deltaMaxd = deltaMax;returnendd = delta;%%--------function p = getNeighborIndex(pindex,n)global numberOfParticles;global dimensions;global particles;dista=zeros(1,numberOfParticles);for i = 1:numberOfParticlessuma = 0;for d = 1:dimensionssuma = suma + (particles(pindex).current(d) - particles(i).current(d))^2;enddista(i)=sqrt(suma);end[X,I] = sort(dista);p = I(n);%%--------function p = getNeighborIndexVector(pindex,n) global numberOfParticles;global dimensions;global particles;dista=zeros(1,numberOfParticles);for i = 1:numberOfParticlessuma = 0;for d = 1:dimensionssuma = suma + (particles(pindex).current(d) - particles(i).current(d))^2;enddista(i)=sqrt(suma);end[X,I] = sort(dista);p = I(1:n);%%---------function p = getNeighborIndexWithBestFitness(pindex) global dimensions;global particles;global numberOfNeighbors;fit = zeros(1,4);for d = 1:numberOfNeighbors;fit(d) = test(particles(pindex).neighbor(d));end[X,I] = sort(fit);p = particles(pindex).neighbor(I(1));%%-------------%%return a random integer between min and max%function num = randint(min,max)array = min:max;index = mod(floor(rand(1)*1000),size(array,2))+1; num = array(index);。

双目标粒子群算法

对照程序：MPSO MATLAB 1,其中fl.m 是目标函数1, f2.m 是目标函数2, PSOl.m 是粒子群算法程序 (一个集合，里面有N 个点，每个点有它自己的位置 xi= (xi1,xi2…)向量，和速度vi=(vi1,vi2…)向量，i 表示第i 个点。

初始化基本变量， vmax ，xmax ，a ，b ，Tmax ， cl ， c2，wmax ，wmin ， D ， N ，Nmax ;第1步给位置xi 和速度vi 随机的赋值；end第2步通过公式计算适应值，就是函数值向量，(f1i,f2i )，f1，f2是 xi 向量的函数，有公式；将计算得到的适应值赋值给一个新的保存每个函数值向量的个体极值矩阵 Py ，并将函数值对应的位置存放到对第3步通过支配关系求出矩阵 Py 中的非支配成员，这些成员构成非劣解集C ，然后将非劣解集加入到集合 B (外部集或精英集)，B 集合初始为空；向量支配关系：定义1 (Pareto 支配)称一个向量u= (u1, u2,…，um )支配(或非劣于)向量v= (v1, v2,…，vm ),当且仅当对于任意的i €( 1, 2,…，m ) , ui < vi 人存在 i €( 1, 2,…，m )使得ui <vi ，记为u 支配v 。

每个向量有两个分量(f1i,f2i ),即定义中的m=2o 例子，有两个适应值向量F 仁(5,8) F2= (5,9)则F1支配F2;若 F1= (5,8) F2= (6,4),则 F1 和 F2无支配关系；若F1= (5,8) F2= (6,9)for i=1:Nfor j=1:D x(i,j)=rand*(b_a)+a; v(i,j)=ra nd*vma x; end %矩阵，N 行D 列%随机初始化位置%随机初始化速度应的Xy 矩阵中;for i=1:NPy(i,1)=f1(x(i,1:D)); Py(i,2)=f2(x(i,1:D)); Xy(i,1:D)=x(i,1:D); end %初始化个体极值 %计算目标f1的适应值 %计算目标f2的适应值 %记录个体极值的坐标位则F1支配F2;非劣解集中的每个元素都要更其余成员构成非支配的关系，即比较时把被该成员支配的成员均删掉，循环比较，每个成员都要更其余成员比较一次，最后只留下之间没有支配关系的成员。