2008年全国Ⅱ高考试题(文)
2008年高考试题——文综(全国卷2)含答案和详解

2008年普通高等学校招生全国统一考试文科综合能力测试(二)解析读图l.完成1~2题图11.①、②、③、④四地段中平均坡度最大的为A①B.②C③D.④2.海拔低于400米的区域面积约为A.0.05km2B0.5k m2C.5ki m2 D.50k m2[解析]等高线地形图中坡度考查,直接运用的知识是分析等高线的疏密程度,缩小范围B、D中选择,但此题中问到了平均坡度最大的地区,需要考虑起止点的高差,运用原理,水平距离相同,相对高度越大,坡度越大。
故1题选D选项。
在图中找到海拔低于400米的区域,结合比例尺,估算出边长为200米的正方形的面积即可,最接近A选项[点评]此组题考查了等值线类型中最典型的等高线地形图及其分析、判断、计算能力,在基础知识基础上,考查学生的能力又有所升华,起到了高考试题选拔人才的目的。
难度适中。
[参考答案]D A图2示意某雏形生态工业目区的产业链.箭头表示物、能量流动过程,其中虚线箭头表示副产品或废弃物的流动。
完成3~5题。
3.图中a、b、c分别代表A.电厂、化工厂、盐场B.盐场、电厂、化工厂C.电厂、盐场、化工厂D.盐场、化工厂、电厂4.该生态工业园区中A.发电厂的废水、废气与废渣得到有效利用B.制盐的副产品得到利用C.建材厂有效利用了盐场的废弃物D.化工厂的废弃物得到利用5.该生态工业园区可能位于A.晋南B.粤北C.冀东D.闽西[解析]第3题中的a与图中各个产业都有非常明显的关联性,肯定是电厂,再在A与C中衡量,考虑到太阳能的加入是晒盐的主要因素,答案即得。
结合第4题中的选项,去关注产业链中各个箭头的示意。
图示中反映该地临海、化工发达,盐业也很突出,这一点尤其重要,还要注意到闽西并不临海。
[点评]此组题考查了生态文明与循环经济、清洁生产等的相关知识点,更要注意的是,考生要在图示中找到相关知识之间的联系(必然与因果关系),试题较为简单。
[参考答案]C B C图3示意不同纬度四地白昼长度变化。
2008年高考文科综合试题及参考答案(全国卷二)

下载文档收藏2008年高考文科综合试题及参考答案(全国卷二)一、选择题(每小题 2 分,共 40 分) 1、以下生物体的结构最简单的是( A、细菌病毒 B、植物 D ) C、动物 D、肝炎 2、能将细胞中的有机物分解并释放出能量的结构是( A、细胞膜叶绿体 B、细胞核 C ) D、 C、线粒体 3、面对毒品我们不应有的态度是( A、坚决拒绝,决不沾染 C、有新鲜感,好奇地试一试 C ) B、举报你身边有吸毒行为的人 D、积极参加反吸毒的宣传活动 4、有些现存的动物仍与它们在一百万年以前生存的形式几乎相同,这一现象最好用什么来解释?(B) A、这些动物一直发生着变异 C、这些动物用有性生殖来繁殖 B、这些动物的生活环境变化不大 D、这些动物又演化成简单的生物 D ) 5、当你在家中自行用药时,为了安全,必须考虑什么?(①该药生产企业与日期、有效期、批准文号药品③该药的功能用量、不良反应、禁忌症等方药 A、①②③ ③④ DCCBD B、①②④ ABDCA A BDCBA )②该药是不是广告推荐的④该药是处方药还是非处 C、②③④ CBBDD D、① 6、染色体和基因的正确关系是( A、很多基因排列在染色体上 C、基因是染色体的另一种叫法 B、很多染色体排列在基因上 D、染色体在细胞核时叫基因 7、小明假期在农村老家的岩石上发现了许多斑点,这些斑点有大有小,就象是岩石的花纹一样,他不能确定这些斑点是什么,是不是生物?你能想办法帮他判断吗?( B ) A、不是生物,因为它们不能动 C、不是生物,因为刮下来就象是泥土西来的 B、是生物,因为它们能生长和繁殖 D、是生物,因为岩石是不会长出东 8、下列哪一项不是提高植物光合作用,增加作物产量的措施?( D ) A.增加光照时间,利用相关照明设施输送二氧化碳 C.合理灌溉,保证植物生长所需的水分 B.增加农田中二氧化碳的含量,向农田 D.尽力密植,让植物充分利用太阳光 9、过去航海的水手容易得坏血病,是因为在长期的航海过程中不易得到新鲜的蔬菜水果,新鲜的蔬菜水果中富含(C) A、维生素 A B、维生素 B C、维生素 C D、维生素 D 10、人体吸气时呼吸肌收缩,胸廓向上向外移动,如尽力吸气膈肌还会收缩,使膈顶下降,结果( A ) A、肺内气压减小,外界气体入肺肺 C、肺内气压减小,外界气体出肺肺 11、下列有关体循环的叙述中正确的是(B ) A、是把心脏的血输送到身体各部分的循环途径 B、通过体循环为全身各处输送氧和养料 C、通过体循环后,血液由静脉血变成动脉血 D、是把血输送回心脏的循环途径 12、下列关于小肠是消化和吸收的主要场所的叙述中不正确的是( A、小肠长 D ) B、肺内气压增大,外界气体入 D、肺内气压增大,外界气体出 B、小肠内壁有皱襞和小肠绒毛 C、小肠中含有丰富的消化液 13、眼球的结构中,有感光细胞的是( C A、角膜 B、巩膜 D、小肠的蠕动速度快) C、视网膜 D、虹膜 14、当电鳗捕到猎物时,会以极高的频率放电,同种电鳗闻讯而来,它交流信息的“语言”是( B )A、动作 B、电流 C、声音 D、气味 15、大多数鱼类依次产卵量可达数万粒至数百万粒以上,但鱼苗死亡率很高,因此发育成鱼的数量很少,这些鱼的高产卵量的现象是( A ) A、一种适应性 C、长期的遗传与变异的结果 B、适应的相对性 D、受非生物因素制约的结果 16、科学家推测生命起源经理了四个化学进化过程,其中小分子有机物(如氨基酸)的形成和原始生命诞生的场所分别是( C ) A、原始海洋和原始大气 C、都在原始海洋中 B、原始大气和原始海洋 D、都在原始大气中 17、豌豆的高茎为显性基因(用 D 表示),矮茎为隐基因(用d 表示),下列亲本组合中可能出现矮茎的是( B ) A、和 Dd DD DD 和 DD B、和 Dd Dd C、和 dd DD D、 18、玲玲旅游时看到一种大雁,经过查阅资料,她找到了这种大雁在分类学上的位置,请你帮助玲玲确定下列哪一项是正确的?( B ) A、鸭科、雁目、雁鸭亚科、雁属雁属 C、雁鸭亚科、雁目、鸭科、雁属目 B、雁目、鸭科、雁鸭亚科、 D、雁属、鸭科、雁鸭亚科、雁 19、要想使一株结酸味苹果的苹果树结出甜味苹果,下列哪项是错误的 D ( A、将酸味苹果作为砧木 B、将甜味苹果作为接穗) C、接穗和砧木的韧皮部必须想吻合 D、将酸味苹果作为接穗 D ) 20、下列关于青春期的说法中,不正确的一项是( A、进入青春期,人的神经系统和心脏等的功能明显增强 B、进入青春期后,男孩和女孩的性器官都迅速发育 C、人的青春期是一生中身体发育和智力发展的黄金时期 D、青春期女性出现月经,不应该让异性知道二、技能题(每空 1 分,共 30 分) 21、地球上最大的生态系统是,它是地球上所有生物共同的家园。
2008年高考语文试题及参考答案(全国卷Ⅱ)

2008年普通高等学校招生全国统一考试语文(全国卷Ⅰ)(供河南、河北、山西、广西使用)详细解答本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至4页,第Ⅱ卷5至9页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3.本试卷共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、(12分,每小题3分)1、下列词语中加点的字,读音全都正确的一组是A.刍议(chú)条分缕析(lǚ) 圈养(quān) 愀然不乐(qiǎo)B.倏忽(shū) 越俎代庖(páo) 牛虻(máng ) 自惭形秽(huì)C.靛蓝(dián)毁家纾难(shū)干涸(hé)白头偕老(xié)D.手帕(pà)相互龃龉(yǔ)麾下(huī)探本溯源(shuò)【参考答案】C【解析】【本题重点考查考生识记现代汉语普通话的字音的能力,多音字需要结合语境来分析。
A项中“圈养”的“圈”应读“juàn”,B项中“牛虻”的“虻”应读“méng”,D项中“探本溯源”的“溯”应读“sù”。
C项的几个字读音完全正确。
】2、下列各项中,加点的成语使用不恰当的一项是A、土耳其举重选手穆特鲁身高只有1.50米,多次参加世界男子举重56公斤级比赛,拿4金牌如探囊取物,人送绰号“举重神童”。
B.冬天老年人要增加营养,也要适当运动,在户外锻炼时一定要量入为出,以步行为宜,时间最好选在傍晚,还要注意保暖,防止着凉。
C.中国茶艺与日本茶道各有特点,但异曲同工,都强调“和”的精神。
2008年高考语文试题及参考答案(全国卷Ⅱ)

2008年高考语文试题及参考答案(全国卷Ⅱ)语文本试卷分第Ⅰ卷和第Ⅱ卷两部分,共8页,满分为150分,考试用时150分钟,考试结束后将试卷和答题卡一并交回。
注意事项:1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、考试科目填写在每件事题卡和试题卷规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把每件事题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能每件事在试题卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔作弊,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷;上需改动,先划掉原来的答案,然后再写上新的答案,不问候语使用涂改液,胶带纸、修正带和其他笔。
不按以上要求作每件事的答案无效。
第Ⅰ卷(共36分)一、(15分,每小题3分)1.下列词语中没有错别字的一组是A.宫阙蓝宝石珠光宝器攻城踏地B.貂婵踩高跷伏案疾书额手称庆C.缴税捅漏子各行其是螳臂当车D.思辨订书机无上光荣挑肥拣瘦2.依次填入下列横肉线处的词语,最恰当的一组是①在西藏高原的雪山中也有变速这风光,也长着香蕉和菠萝,这实在是一件令人喷喷的事。
②中国文物信息网日前公布了已入围2005年度全国考古手大新发现的24个项目名单。
适当“新发现”了石器时代至宋元时期的文化遗銌。
③这里不光生长有益的植物,还有一些的植物,其中有一种一人多高的小树,树干细细的,叶子像叶,一年开一次花,果实像豌豆,它的花和叶子都有毒。
④那时,北大的学生好幸运生的借书证,可以借十元钱装书。
A.移道涵盖有害竟然B.移奇囊括有毒居然C.称奇涵盖有害居然D.称道囊括有毒竟然3.下列各句中,加点的成语使用恰当的一句是A.各类配套完善的高新园区的建成使用,不仅带动了房地产开发,取得了经济效益,而且在潜移默化....中聚集着人气,改善若人居环境。
B.“中国印·舞动的北京”中的运动人形刚柔相济....,形象友善,在蕴含中国文化的同时,充满了动感,体现了“更快、更亮、更强”的奥林区克精神,以及以运动员为核心的奥林匹克运动原则。
2008年全国统一高考语文试卷(全国二卷)

2008年全国统一高考语文试卷(全国卷Ⅱ)第I卷一、(12分,每小题3分)1.下列词语中加点的字,读音全都正确的一组是A. 迸.发(bèng)不掘不挠.(ráo)怆.然(chuàng)婀.娜多姿(ē)。
B. 跻.身(jī)岿.然不动(kuī)女娲.(wō)谆.谆教导(zhūn)C. 恫吓.(xià)病入膏肓.(huāng)浣.衣(huàn)神情尴尬.(gà)D. 粗糙.(cāo)徘徊.观望(huái)糟粕.(pò)锲.而不舍(qiè)2.下列各句中,加点的成语使用不恰当的一项是A. 新来的王老师为人不苟言笑,同事们一般都产跟他嘻嘻哈俣,只有谭校长有时还会跟他开点无伤大雅....的玩笑。
B. 近几年,来中国演出的外国艺术团络绎不绝....,不过人们对俄罗斯芭蕾舞团的《天鹅湖》还是情有独钟,屡看不厌。
C. 美国博物馆的收费可谓各尽所能....:有的一部分收费,有的分时段收费,还有的是否交费、交费多少由参观者自行决定。
D. 中、日、韩三国参加这次围棋比赛的运动员,水平都在伯仲之间....,谁能胜出,就要看谁具有更好的竞技状态和心理素质了。
3.下列各句中,没有语病的一句是A. 金乌炭雕工艺精湛,采用纯天然颜料着色,具有高雅、时尚、个性的艺术享受,还能吸附有毒有害气体,是一种环保艺术品。
B. 该县认真实施“村村通”这一全省规划的八件实事之一,到10月底,在全地区率先解决了农村百姓听广播看电视难的问题。
C. 中俄两国元首在致辞中一致表示,要以举办“国家年”为契机,增进两国人民的相互了解和友谊,深化两国各领域的交流合作。
D. 听说博士村官潘汪聪要给大家讲农技课,大家兴致很高,还没到时间,村委会会议室就挤满了很多村民来听课,场面好不热闹。
4.依次填入下面一段文字横线处的语句,衔接最恰当的一组是铁路客车动车组先进的计算机网络控制技术。
2008年高考文科综合试题及参考答案(全国卷二)

江苏北部沿海滩涂围垦,需要经过筑堤、挖渠等工程措施和种植适应性植物等生物措施改造,4~5年后才能种植粮食作物。
据此完成1~2题。
1、改造滩涂所种植的适应性植物应A.耐湿B.耐旱C.耐盐D.抗倒伏2.若缩短滩涂改造时间,需投入更多的A.花费B.农家肥C.农药D.淡水北京的王女士登录总部位于上海的M公司(服装公司)网站,订购了两件衬衣,两天后在家受到货。
图1示意M公司的企业组织、经营网络。
据此完成3~5题。
图13.王女士此次购买的衬衣,在M公司员工完成的环节是A设计B提供面料C加工D.送货上门4.M公司的产品销售依靠A大型服装超市B服装专卖店C.代理销售商D信息交流平台5.在M公司的组织、经营网络中,区位选择最灵活的是A配送仓库B面料厂C制衣厂D仓储中心自谋城市市中心向南、向北分别设若干站点,监测城市气温的时空分布。
监测时间为8日(多云)9时到9日9(晴)18时。
监测结果如图2所示。
据此完成6-8题。
6.图示的最大温差可能是A.4℃B.12C. 16℃D. 18℃7.监测时段被监测区域气温A.最高值多云天高于晴天B.白天变化晴天比多云天强烈C.从正午到午夜逐渐降低D.白天变化比夜间变化平缓8.下午时间中热岛效应最强的是A.8日15时左右B.8日22时左右C. 9日15时左右D.9日18时左右假设从空中R点看到地表的纬线m和晨昏线n如图3所示。
R点在地表的垂直投影为S.据此完成9~11题。
9.S地的纬度A.与M第相同B. 介于M、N两地之间C.高于N地D. 低于M地10.如果在位于大陆上的N地看见太阳正在落下,则这一时期A.S地的白昼比N地长B. 美国加利福尼亚州火险等级高C.巴西东南部正值雨季D. 长江口附近海水盐度处于高值期11.若R点沿直线RSA.上升,看到m、n的两焦点间距离加大B.下降,看到m、n的两焦点间距离加大C.上升,看到m、n呈现弯曲方向相反的相交曲线D.上升或下降,看到m、n的形状保持不变12.中国古代常用五行相生相克解释朝代更替,称作“伍德”。
2008年高考语文试题全国卷ⅱ详细解答

2008年普通高等学校招生全国统一考试语文试题(全国卷II)(供贵州、黑龙江、吉林、云南、甘肃、新疆、内蒙古、青海、西藏使用)详细解答(311261)杭州市萧山区第六高级中学曾良策本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至4页,第Ⅱ卷5至 10页。
考试结束后,将本试卷和答题卡一并交回。
第I卷注意事项1.答题前,考生在答题卡上务必用直径0.5毫米黑色签字笔将自己的姓名、准考证号填写清楚。
请认真核准准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.本试卷共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项符合要求。
一、(12分,每小题3分)1、下列词语中加点的字,读音全都正确的一组是A.迸.发(bâng)不屈不挠.(ráo)怆.然(chuàng)婀.娜多姿(ē)B.跻.身(jī)岿.然不动(kuī)女娲.(wō)谆.谆教导(zhūn)C.恫吓.(xià)病入膏肓.(huāng)浣.衣(huàn)神情尴尬.(gà)D.粗糙.(cāo)徘徊.观望(huái)糟粕.(pò)锲.而不舍(qiâ)【参考答案】D【解析】【本题重点考查考生识记现代汉语普通话的字音的能力,多音字需要结合语境来分析。
A项中“不屈不挠”的“挠”应读“náo”,B项中“女娲”的“娲”应读“wā”,C项中“恫吓”的“吓”应读“hâ”,D项几个加点字读音完全正确。
】2、下列各句中,加点的成语使用不恰当的一项是A.新来的王老师为人不苟言笑,同事们一般都不跟他嘻嘻哈哈,只有谭校长有时还会跟他开点无伤大...雅.的玩笑。
B.近几年,来中国演出的外国艺术团络绎不绝....,不过人们对俄罗斯芭蕾舞团的《天鹅湖》还是情有独钟,屡看不厌。
2008年高考文综试卷及答案

2008年普通高等学校招生全国统一考试文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至8页,第Ⅱ卷9至15页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色签字笔将自己的姓名、准考证号填写清楚,并帖好条形码。
请认真核准条形码的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效。
3.本试卷共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是符合题目要求。
张某承包了0.5化顷耕地,种植结构变化如图1。
当地1月平均气温3℃。
完成1-2题。
1.张某承包的耕地可能位于A.珠江三角洲B.太湖平原C.华北平原D.松嫩平原2.导致种植结构变化的主要因素是A.市场需求B.生产经验C.自然条件D.国家政策下表为我国某城市人口资料。
读下表完成3-4题。
1982年 1990年 2000年总人口(万人) 35 167 7010-14岁(%) 35.27 14.63 8.515-64岁(%) 58.36 83.15 90.3965岁及以上(%) 6.37 2.22 1.113.该城市自1982年至2000年A.人口自然增长率很高,人口增长迅速B.人口出生率增高,人口老龄化问题得到缓解C.人口出生率大幅度降低,人口死亡率大幅度增高D.人口增长率很高,有大量青壮年人口迁入4.该城市是A.南京B.深圳C.西安D.沈阳产业重心是区城产业产值空间分布的重心。
图2示意中国三次产业重心的经、纬度变化(不含台湾、香港、澳门的统计资料)。
完成5-7题。
5.图中①、②、③线依次代表A.第一产业、第二产业、第三产业B.第二产业、第三产业、第一产业C.第一产业、第三产业、第二产业D.第三产业、第一产业、第二产业6.从产业重心的纬度变化看A.三次产业重心均向北移动 C.第一产业重心移动最快C.第二产业重心移动最快D.第三产业重心移动最快7.自1985年至2003年,产业重心移动的趋势是A.第二产业向东南B.第二产业向东北C.第一产业向东南D.第三产业向东南图3中a是经线,Q点为晨昏线与该经线的交点。
2008年全国统一高考语文试卷(含答案)

2008年普通高等学校招生全国统一考试本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分,其中第Ⅰ卷第三、四题为选考题,其他题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项1、答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证,并将条形码粘贴在答题卡的指定位置上。
2、答题时使用0.5 毫米黑色中性(签字)笔或碳素笔书写,字体工整\笔迹清楚.3、请按照题号在答题卡上各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效.4、保持卡面清洁,不折叠,不破损.5、做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑.第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1-3题。
所谓“变形”,是相对于“常形”而言。
“常形”是指显示生活中客观物象的正常自然形态;“变形”是指客观五香反映带艺术中的形态的改变。
在显示生活中,由于种种原因,物象的形态有时会出现变异,例如两头蛇、三脚鸡等,这种“变形”虽然怪异,但不是艺术美学研究的对象。
艺术美学所研究的,是正常的自然形态在艺术边县中的变化及其美学意义。
二、艺术上的“变形”氛围广义和狭义两种。
从广义上说,任何种类和流派的艺术,不论其创作思想和手法多么不同,它所塑造的形象较之原形都会有某些强调、选择、集中乃至改变。
从这个意义上说,变形乃是不是艺术反映生活的一种普遍现象。
不过一般地说,艺术上关于“变形”的观念是指狭义的“变形”,它表现为客观物象的几何图形所发生的改变。
例如杜甫的《古柏行》:“霜皮溜雨四十围,黛色参天二千尺。
”宋代科学家沈括(字存中)分析道:“四十围乃是径七尺,无乃大细长乎?此亦文章病也。
”沈括生得太早一些,他不懂得艺术变形的美学意义。
比沈括稍晚的王观国有所不同,他:“‘四十围’、‘二千尺’者,姑言其大且高也。
2008高考语文全国卷2(含答案)

全国卷2一、(12分,每小题3分)1.下列词语中加点的字,读音全都正确的一组是A.迸.发(bèng)不掘不挠.(ráo)怆.然(chuàng)婀.娜多姿(ē)。
B.跻.身(jī)岿.然不动(kuī)女娲.(wō)谆.谆教导(zhūn)C.恫吓.(xià)病入膏肓.(huāng)浣.衣(huàn)神情尴尬.(gà)D.粗糙.(cāo)徘徊.观望()糟粕.(pò)锲.而不舍(qiè)2.下列各句中,加点的成语使用不恰当的一项是A.新来的王老师为人不苟言笑,同事们一般都产跟他嘻嘻哈俣,只有谭校长有时还会跟他开点无伤大雅的玩笑。
B.近几年,来中国演出的外国艺术团络绎不绝,不过人们对俄罗斯芭蕾舞团的《天鹅湖》还是情有独钟,屡看不厌。
C.美国博物馆的收费可谓各尽所能:有的一部分收费,有的分时段收费,还有的是否交费、交费多少由参观者自行决定。
D.中、日、韩三国参加这次围棋比赛的运动员,水平都在伯仲之间,谁能胜出,就要看谁具有更好的竞技状态和心理素质了。
3.下列各句中,没有语病的一句是A.金乌炭雕工艺精湛,采用纯天然颜料着色,具有高雅、时尚、个性的艺术享受,还能吸附有毒有害气体,是一种环保艺术品。
B.该县认真实施“村村通”这一全省规划的八件实事之一,到10月底,在全地区率先解决了农村百姓听广播看电视难的问题。
C.中俄两国元首在致辞中一致表示,要以举办“国家年”为契机,增进两国人民的相互了解和友谊,深化两国各领域的交流合作。
D.听说博士村官潘汪聪要给大家讲农技课,大家兴致很高,还没到时间,村委会会议室就挤满了很多村民来听课,场面好不热闹。
4.依次填入下面一段文字横线处的语句,衔接最恰当的一组是铁路客车动车组先进的计算机网络控制技术。
,,,,。
列车防火系统也很先进,重要设施都附有防火装置①并与地面通讯,实现地面对列车的监控②能实现对动车组各个系统的控制③一旦出现异常情况,动车组即可自动减速或停车④同时对系统进行监视和故障诊断⑤无需人为干预A.②①⑤④③ B.②④①③⑤ C.⑤④③②① D.⑤④①③②二、(9分,每小题3分)阅读下面的文字,完成5~7题。
2008年普通高等学校招生全国统一考试数学卷(全国Ⅱ.文)含详解

2008年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至10页. 考试结束后,将本试卷和答题卡一并交回.第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.不能答在试题卷上.3.本卷共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 参考公式:如果事件A B ,互斥,那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ,相互独立,那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ,那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(012)k k n kk n P k C p p k n -=-=,,,,一、选择题1.若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,3.原点到直线052=-+y x 的距离为( ) A .1B .3C .2D .54.函数1()f x x x=-的图像关于( )A .y 轴对称B . 直线x y -=对称C . 坐标原点对称D . 直线x y =对称5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-7.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( ) A .1 B .12C .12-D .1-8.正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( ) A .3B .6C .9D .189.44)1()1(x x +-的展开式中x 的系数是( )A .4-B .3-C .3D .410.函数x x x f cos sin )(-=的最大值为( ) A .1B .2 C .3D .211.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( ) A .221+ B .231+ C . 21+ D .31+12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1 B .2C .3D .22008年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于 .16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分) 在ABC △中,5cos 13A =-,3cos 5B =. (Ⅰ)求sinC 的值;(Ⅱ)设5BC =,求ABC △的面积. 18.(本小题满分12分)等差数列{}n a 中,410a =且3610a a a ,,成等比数列,求数列{}n a 前20项的和20S .19.(本小题满分12分)甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹.根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2.设甲、乙的射击相互独立.(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率. 20.(本小题满分12分)如图,正四棱柱1111ABCD A BC D -中,124AA AB ==,点E 在1CC 上且EC E C 31=. (Ⅰ)证明:1AC ⊥平面BED ; (Ⅱ)求二面角1A DE B --的大小. 21.(本小题满分12分)设a ∈R ,函数233)(x ax x f -=.(Ⅰ)若2=x 是函数)(x f y =的极值点,求a 的值;(Ⅱ)若函数()()()[02]g x f x f x x '=+∈,,,在0=x 处取得最大值,求a 的取值范围. 22.(本小题满分12分)设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点. (Ⅰ)若6ED DF =,求k 的值; (Ⅱ)求四边形AEBF 面积的最大值.AB CD EA 1B 1C 1D 12008年普通高等学校招生全国统一考试 文科数学试题(必修+选修Ⅰ)参考答案和评分参考评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要 考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和 难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数.选择题不给中间分.一、选择题1.C 2.B 3.D 4.C 5.C 6.D 7.A 8.B 9.A 10.B 11.B 12.C 二、填空题13.2 14.420 15.216.两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.1.若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角 【答案】C【解析】sin 0α<,α在三、四象限;tan 0α>,α在一、三象限,∴选C 2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,【答案】B【解析】{}1,0,1,2--=M ,{}3,2,1,0,1-=N ,∴{}1,0,1-=N M 【高考考点】集合的运算,整数集的符号识别 3.原点到直线052=-+y x 的距离为( ) A .1B .3C .2D .5【答案】D【解析】52152=+-=d【高考考点】点到直线的距离公式4.函数1()f x x x=-的图像关于( ) A .y 轴对称 B . 直线x y -=对称 C . 坐标原点对称 D . 直线x y =对称【答案】C 【解析】1()f x x x=-是奇函数,所以图象关于原点对称 【高考考点】函数奇偶性的性质5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a【答案】C 【解析】由0ln 111<<-⇒<<-x x e,令x t ln =且取21-=t 知b <a <c6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-【答案】D【解析】如图作出可行域,知可行域的顶点是A (-2,2)、B(32,32)及C(-2,-2) 于是8)(min -=A z7.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-【答案】A【解析】ax y 2'=,于是切线的斜率a y k x 2'1===,∴有122=⇒=a a8.正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( ) A .3 B .6C .9D .18【答案】B【解析】高360sin 32=︒=h ,又因底面正方形的对角线等于32,∴底面积为 6332212=⨯⨯⨯=S ,∴体积63631=⨯⨯=V【备考提示】在底面积的计算时,要注意多思则少算 9.44)1()1(x x +-的展开式中x 的系数是( )A .4-B .3-C .3D .4【答案】A【解析】41666141404242404-=-+=-+C C C C C C 【易错提醒】容易漏掉1414C C 项或该项的负号10.函数x x x f cos sin )(-=的最大值为( ) A .1 B .2 C .3D .2【答案】B【解析】)4sin(2cos sin )(π-=-=x x x x f ,所以最大值是2【高考考点】三角函数中化为一个角的三角函数问题【备考提示】三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题 11.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( ) A .221+ B .231+ C . 21+ D .31+【答案】B【解析】由题意BC c =2,所以c c AC 3260sin 220=⨯⨯=,由双曲线的定义,有c a c c BC AC a )13(2322-=⇒-=-=,∴231131+=-==a c e 【高考考点】双曲线的有关性质,双曲线第一定义的应用12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1 B .2C .3D .2【答案】C【解析】设两圆的圆心分别为1O 、2O ,球心为O ,公共弦为AB ,其中点为E ,则21EO OO 为矩形,于是对角线OE O O =21,而3122222=-=-=AE OA OE ,∴321=O O 【高考考点】球的有关概念,两平面垂直的性质13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 【答案】 2【解析】λ+a b =)32,2(++λλ则向量λ+a b 与向量(47)=--,c 共线274322=⇒--=++⇔λλλ14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答) 【答案】 420【解析】4202701501621026110=+=+C C C C15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于 .【答案】 2 【解析】设过M的直线方程为)2(2-=-x k y ,由0)1(444)2(22222=-+-⇒⎩⎨⎧=-=-k kx x k xy x k y ∴k x x 421=+,2221)1(4kk x x -=,由题意144=⇒=k k ,于是直线方程为x y = 421=+x x ,021=x x ,∴24=AB ,焦点F (1,0)到直线x y =的距离21=d∴ABF △的面积是216.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)【答案】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.三、解答题17.解:(Ⅰ)由5cos 13A =-,得12sin 13A =, 由3cos 5B =,得4sin 5B =. ··········································································· 2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=. ····································· 5分(Ⅱ)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===. ··········································· 8分 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=. ····················· 10分18.解:设数列{}n a 的公差为d ,则3410a a d d =-=-, 642102a a d d =+=+,1046106a a d d =+=+. ················································································ 3分 由3610a a a ,,成等比数列得23106a a a =,即2(10)(106)(102)d d d -+=+, 整理得210100d d -=,解得0d =或1d =.······················································································· 7分 当0d =时,20420200S a ==. ······································································ 9分 当1d =时,14310317a a d =-=-⨯=, 于是2012019202S a d ⨯=+207190330=⨯+=. ············································· 12分 19.解:记12A A ,分别表示甲击中9环,10环,12B B ,分别表示乙击中8环,9环,A 表示在一轮比赛中甲击中的环数多于乙击中的环数,B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,12C C ,分别表示三轮中恰有两轮,三轮甲击中环数多于乙击中的环数.(Ⅰ)112122A A B A B A B =++,··································································· 2分 112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++112122()()()()()()P A P B P A P B P A P B =++0.30.40.10.40.10.40.2=⨯+⨯+⨯=. ····························································· 6分(Ⅱ)12B C C =+, ······················································································ 8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=,332()[()]0.20.008P C P A ===,1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=. ··························· 12分 20.解法一:依题设,2AB =,1CE =.(Ⅰ)连结AC 交BD 于点F ,则BD AC ⊥.由三垂线定理知,1BD AC ⊥. ········································································· 3分 在平面1ACA 内,连结EF 交1AC 于点G ,由于1AA ACFC CE== 故1Rt Rt A AC FCE △∽△,1AAC CFE ∠=∠, CFE ∠与1FCA ∠互余.于是1AC EF ⊥. 1AC 与平面BED 内两条相交直线BD EF ,都垂直, 所以1AC ⊥平面BED . ·················································································· 6分 (Ⅱ)作GH DE ⊥,垂足为H ,连结1A H .由三垂线定理知1A H DE ⊥,故1A HG ∠是二面角1A DE B --的平面角.························································ 8分EF =CE CF CG EF ⨯==EG ==. AB CDEA 1B 1C 1D 1 FH G13EG EF =,13EF FD GH DE ⨯=⨯=又1AC ==113AG AC CG =-=.11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ················································· 12分 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴, 建立如图所示直角坐标系D xyz -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,.(021)(220)DE DB ==,,,,,,11(224)(204)AC DA =--=,,,,,. ······························ 3分 (Ⅰ)因为10AC DB =,10AC DE =, 故1AC BD ⊥,1AC DE ⊥. 又DBDE D =,所以1AC ⊥平面DBE . ·················································································· 6分 (Ⅱ)设向量()x y z =,,n 是平面1DA E 的法向量,则DE ⊥n ,1DA ⊥n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n . ····················································· 9分1AC <>,n 等于二面角1A DE B --的平面角, 11114cos 42AC AC AC <>==,n n n 所以二面角1A DE B --的大小为arccos42. ················································· 12分21.解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =的极值点,所以(2)0f '=,即6(22)0a -=,因此1a =. 经验证,当1a =时,2x =是函数()y f x =的极值点. ········································· 4分 (Ⅱ)由题设,3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+. 当()g x 在区间[02],上的最大值为(0)g 时,(0)(2)g g ≥,即02024a -≥.故得65a ≤. ································································································ 9分 反之,当65a ≤时,对任意[02]x ∈,, 26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+- 3(25)(2)5xx x =+- 0≤,而(0)0g =,故()g x 在区间[02],上的最大值为(0)g . 综上,a 的取值范围为65⎛⎤-∞ ⎥⎝⎦,. ··································································· 12分22.(Ⅰ)解:依题设得椭圆的方程为2214x y +=, 直线AB EF ,的方程分别为22x y +=,(0)y kx k =>. ····································· 2分 如图,设001122()()()D x kx E x kx F x kx ,,,,,,其中12x x <,且12x x ,满足方程22(14)4k x +=, 故21x x =-=.①由6ED DF =知01206()x x x x -=-,得021215(6)77x x x x =+==; 由D 在AB 上知0022x kx +=,得0212x k=+.所以212k =+, 化简得2242560k k -+=,解得23k =或38k =. ······················································································ 6分 (Ⅱ)解法一:根据点到直线的距离公式和①式知,点E F ,到AB的距离分别为1h ==2h ==······················································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 1525(14k =+==≤当21k =,即当12k =时,上式取等号.所以S 的最大值为 ························ 12分 解法二:由题设,1BO =,2AO =.设11y kx =,22y kx =,由①得20x >,210y y =->, 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ···································································································· 9分===当222x y =时,上式取等号.所以S 的最大值为 ······································· 12分。
2008年全国统一高考语文试卷(全国卷ⅱ)(含解析版)

D.⑤④①③②
二、(9 分,每小题 3 分) 阅读下面的文字,完成 5~7 题。
在明王朝统治中国的 276 年间,白银经历了一个不同寻常的货币化过程。明 初,明朝禁用金银交易,到了明后期,白银则已经通行于全社会。迄今为止,对 于这一货币化过程,中外学术界无不以《明史》正统初年明英宗“弛用银之 禁”、“朝野率皆用银”的诏令为根据,以为是朝廷推行的结果。实际上,明代 白银的货币化是自民间开始,到明英宗以后才逐渐为官方认可、自每一个角落,使得市场前所未 有地活跃起来。到了嘉靖年间,整个中国对白银产生了巨大的需求,标志着这一 货币化过程基本完成。
此时,一方面明朝国家财政白银入不敷出,另一方面从皇族到平民都有对于 白银的大量需求。在国内白银开采和供应远远不能满足要求的情况下,人们开始 将寻求的目光投向海外。中国外来白银最早的源头是日本,虽然日本出产的金银 在 16 世纪中叶以前就有向外出口的记载,但那时日本向中国输出的主要是刀剑、 扇子、屏风、硫磺等。情况的转变是自 16 世纪 40 年代开始的。当时,来自中国 福建、广东、浙江的船只不断到到日本九州。它们的目的不再以物易物,而是以 物易银。有需求就有开发和供给。也正是这一时期,日本银矿的开发得到了迅速 发展,16 世纪后半叶日本的输出品中,白银独占重要地位,而对中国丝与丝织 品的巨大需求,则构成了银产量激增的日本方面的原因。在美洲方面,当西方走 向世界寻求财富时,最早寻找的是黄金,但也是从 16 世纪 40 年代开始,西班牙 在美洲转而开采白银且产量激增。当时达到菲律宾的西班牙人几乎立刻了解到中
国商品对于他们的意义,立即开始与中国海商的贸易。美洲白银不仅从马来西亚 流向中国,带动了整个东南亚贸易。也从欧洲运至印度,再流到中国,以换取中 国的丝绸、瓷器、水银、麝香、朱砂等。从 1540 年到 1644 年这一百年间,日本 白银产量的绝大部分和美洲白银产量的一半流入了中国,葡萄牙学者加良斯·戈 迪尼奥因此将中国形容为一个“吸泵”。
08 年高考现代文阅读 4 篇

2008年普通高等学校招生全国统一考试五、(22分)阅读下面的文字,完成14~17题。
马缨花季羡林曾经有很长的一段时间,我孤零零一个人住在一个很深的大院子里。
从外面走进去,越走越静,自己的脚步声越听越清楚,仿佛从闹市走向深山。
等到脚步声成为空谷足音的时候,我住的地方就到了。
院子不小,都是方砖铺地,三面有走廊。
天井里遮满了树枝,走到下面,浓荫迎地,清凉蔽体。
从房子的气势来看,依稀可见当年的富贵气象。
等到我住进去的时候,富贵气象早已成为陈迹,但是阴森凄苦的气氛却是原封未动。
再加上走廊上陈列的那一些汉代的石棺石椁、古代的刻着篆字和隶字的石碑,我一走回这院子里,就仿佛进入古墓。
这样的气氛同我当时的心情是相适应的,我一向又不相信有什么鬼神,所以我住在这里,也还处之泰然。
我是不是也有孤寂之感呢?应该说是有的。
当时正是“万家墨面没蒿莱”的时代,北平城一片黑暗。
白天在学校里的时候,同青年同学在一起,从他们那蓬蓬勃勃的斗争意志和生命活力里,还可以吸取一些力量和快乐,精神十分振奋。
但是,一到晚上,当我孤零一个人走回这个所谓家的时候,我仿佛遗世而独立。
没有一点活气。
寂寞像毒蛇似地偷偷地袭来,折磨着我,使我无所逃于天地之间。
有一天,在傍晚的时候,我从外面一走进那个院子,蓦地闻到一股似浓似淡的香气。
我抬头一看,原来是遮满院子的马缨花开花了。
我站在树下,仰头观望:细碎的叶子密密地搭成了一座天棚,天棚上面是一层粉红色的细丝般的花瓣,远处望去,就像是绿云层上浮上一团团的红雾。
香气就是从这一片绿云里洒下来的,洒满了整个院子,洒满了我的全身。
花开也是常有的事,开花有香气更是司空见惯。
但是,在这样一个时候,这样一个地方,有这样的花,但是。
在这样的时候和地方,有这样的香,我就觉得很不寻常,甚至有感激的心情了。
从此,我就爱上了马缨花,把它当成了自己的知心朋友。
可惜不久我就搬出了那个院子,同那些可爱的马缨花告别了。
时间也过得真快,才一转眼的工夫,已经过去了十三年。
2008高考数学试卷含答案(全word版)

2008年普通高等学校招生全国统一考试数学(文科)卷一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{|0}A x x =>,{|12}B x x =-≤≤,则A B =(A ){|1}x x ≥- (B ){|2}x x ≤ (C ){|02}x x <≤ (D ){|12}x x -≤≤ (2)函数2(sin cos )1y x x =++的最小正周期是 (A )2π(B )π (C )32π (D )2π(3)已知a ,b 都是实数,那么“22b a >”是“a >b ”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 (4)已知{}n a 是等比数列,41252==a a ,,则公比q =(A )21-(B )2- (C )2 (D )21(5)0,0a b ≥≥,且2a b +=,则(A )12ab ≤(B )12ab ≥(C )222a b +≥ (D )223a b +≤(6)在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是(A )-15 (B )85 (C )-120 (D )274(7)在同一平面直角坐标系中,函数])20[)(232cos(ππ,∈+=x x y 的图象和直线21=y 的交点个数是(A )0 (B )1 (C )2 (D )4 (8)若双曲线12222=-by ax 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是(A )3 (B )5 (C )3 (D )5 (9)对两条不相交的空间直线a 和b ,必定存在平面α,使得(A ),a b αα⊂⊂ (B ),//a b αα⊂ (C ),a b αα⊥⊥ (D ),a b αα⊂⊥ABCD(10)若0,0≥≥b a ,且当⎪⎩⎪⎨⎧≤+≥≥1,0,0y x y x 时,恒有1≤+by ax ,则以a ,b 为坐标点(,)P a b 所形成的平面区域的面积等于 (A )12(B )4π(C )1 (D )2π二.填空题:本大题共7小题,每小题4分,共28分。
2008年全国高考各省语文试题作文题目(目前最全).

2008年各省高考语文作文试题全国卷I(河北、河南、山西、广西)作文题:与“抗震救灾”有关的材料作文作文要求:与“抗震救灾”有关的材料作文。
提供了包括捐款、救援队等六条与抗震救灾有关的素材,要求考生完成作文,不限题材。
全国卷II(贵州、黑龙江、吉林、云南、甘肃、新疆、内蒙古、青海、西藏) 作文题:海龟和老鹰材料作文作文要求:材料是:一个人在沙滩走,走着走着见到一只刚出壳的小海龟即将遭到老鹰袭击,于是他上前把老鹰赶走了。
然而那只小海龟其实是侦察兵,如果遭遇袭击他会退回去,如果未回壳则其他海龟会大量出壳。
于是大批小海龟争先恐后从壳中出来。
好心人走了,那只等待已久的老鹰协同其他鹰冲向在毫无遮拦的沙滩上爬行的小海龟群……根据以上材料自命题作文,体裁不限。
北京卷(分小作文和大作文)大作文题:材料作文-放入杯子的石头、沙子和水作文要求:学生根据材料自选角度,自拟题目写一篇不少于800字的文章,除诗歌外体裁不限。
在课堂上,老师拿了一个玻璃杯,里面放了一个大石头,差不多和杯子一样大,老师问大家:杯子满了吗?一个学生回答:没满,还可以放沙子。
待学生放完沙子,老师又问:满了吗?全班同学回答满了,有一个男孩却回答没有满,还可以放水。
老师笑了,接着把沙子和石头倒出来,杯子是空的。
这回老师是往杯子里放沙子和水,然后问大家,杯子满了吗?如果要放石头进去,该怎么放?男孩就把杯子里的沙子和水倒出来,先把石头放进去。
小作文题:地震的废墟中作文要求:今年考题中出现了关于地震的内容,语言表述题要求学生用45个字对一幅漫画写出自己的感想:地震的废墟中,一只时钟停在了2点28分。
作文题:他们作文要求:平时我们关注更多的是我们自己,请以“他们”为题写一篇作文。
除了诗歌外,文体不限,字数800左右。
天津卷作文题:人之常情作文要求:请以“人之常情”为题写一篇作文。
800字作文,除诗歌和话剧外体裁不限。
四川卷作文题:坚强作文要求:以“坚强”为话题写作文一篇。
2008年高考文综试卷及答案(全国卷II)

2008年普通高等学校招生全国统一考试文科综合能力测试(二)本试卷分第1卷(选择题)和第ll卷(非选择题)两部分。
第1卷1至8页,第11卷9至15页。
考试结束后,将本试卷和答题卡一井交回。
第1卷注意事项:1答第l卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
3本卷共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是符合题目要求的。
读图l.完成1~2题图11.①、②、③、④四地段中平均坡度最大的为A①B.②C③D.④2.海拔低于400米的区域面积约为A.0.05 km2 B 0.5km2C.5 km2 D.50km2图2示意某雏形生态工业目区的产业链.箭头表示物、能量流动过程,其中虚线箭头表示副产品或废弃物的流动。
完成3~5题。
3.图中a、b、c分别代表A.电厂、化工厂、盐场 B.盐场、电厂、化工厂C.电厂、盐场、化工厂 D.盐场、化工厂、电厂4.该生态工业园区中A.发电厂的废水、废气与废渣得到有效利用B.制盐的副产品得到利用C.建材厂有效利用了盐场的废弃物D.化工厂的废弃物得到利用5.该生态工业园区可能位于A.晋南 B.粤北 C.冀东 D.闽西图3示意不同纬度四地白昼长度变化。
完成6~8题。
6.若该圈表示上半年a、b两月(a月早于b月).则①、②、③、④四地纬度依次是 A.66.5°N、66°N、40°N、40°SB.66.5°S、66°S、40°S、40°NC.66.5°N、66°N、0°、40°SD.66.5°S、66°S、0°、40°N7.根据图中各地的白昼长度变化可知A.a月内①—④各地的夜长均长于昼长B.b月内①—④各地的昼长均长于夜长C.③地较②地昼夜长短的年变幅大D.③地与④地之间的某一纬度上昼夜长短变化为零8. ①地在a月与b月的平均昼长变化Pa与Pb的关系应符合A.O<Pa/Pb<1 B.Pa/Pb=0 C.Pa/Pb=1 D. Pa/Pb>l图4示意日本本州岛部分地区樱花初放日期。
2008年高考文科综合试题及参考答案(全国卷二)
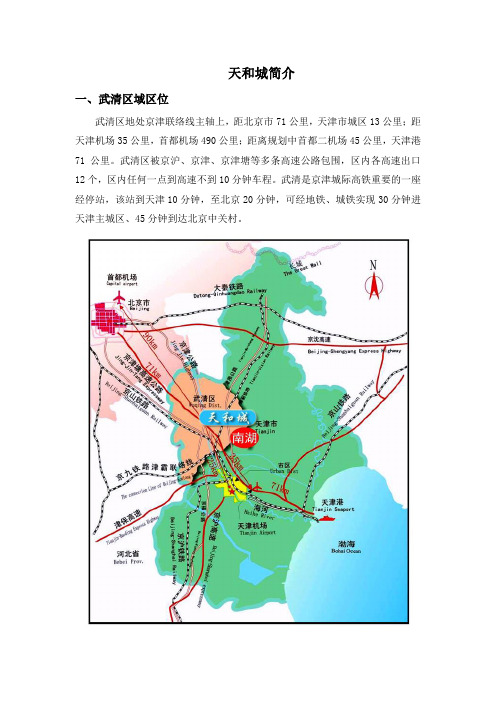
天和城简介一、武清区域区位武清区地处京津联络线主轴上,距北京市71公里,天津市城区13公里;距天津机场35公里,首都机场490公里;距离规划中首都二机场45公里,天津港71公里。
武清区被京沪、京津、京津塘等多条高速公路包围,区内各高速出口12个,区内任何一点到高速不到10分钟车程。
武清是京津城际高铁重要的一座经停站,该站到天津10分钟,至北京20分钟,可经地铁、城铁实现30分钟进天津主城区、45分钟到达北京中关村。
二、天和城区域交通天和城项目周边环绕着京津高速、京沪高速、津保高速及103国道,这些高速路在天和城均有入口,可实现5分钟到高速。
正在修建的天津外环北延长线与项目主干道--天和路相连接,实现5分钟车程至天津外环。
三、天和城城市规划天和城项目位于武清区新城东南部,规划用地面积11.85平方公里,总建筑规模550万平方米,规划居住人口10万人。
四、天和城定位以创造健康生活方式为目标,通过环境培育提升人居环境品质,以全民休闲运动为核心吸引,打造集商务会议、主题商业、休闲居住、田园风光为一体的具备旅游与城市双功能的京津旅居小镇。
五、天和城功能会议度假中心占地约38公顷,是集会议、休闲、度假等功能为一体的生态型休闲度假村(区)。
其中包括会议中心、滨水度假别墅、生态绿岛、迎宾广场、中央河道、休闲水广场、滨湖漫步公园等。
城市综合服务区占地约38公顷。
按欧式建筑风格打造商业小镇及城市公共服务功能群,实现休闲、娱乐、购物、活动等功能一体化。
其中包括欧式小镇商业街、星级度假酒店、SHOPPINGMALL、生态游乐广场、商业综合体、行政中心、中央水廊、亲水广场、滨湖带状公园等。
水街特色休闲区占地约16公顷,其中包括特色(滨水)酒吧街、特色展览馆、游船码头、喷泉休憩广场、滨湖带状公园等。
滨湖商住区占地约48公顷,是以文化娱乐为主题的大型商业混合社区。
其中包括文化娱乐中心、社区服务中心、高层景观公寓、花园公寓、湖景公寓、游客中心、南湖湾生态公园、观湖亲水平台、滨湖带状公园等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年普通高等数学招生全国统一考试(全国Ⅱ)文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.参考公式: 如果事件A 、B 互斥,那么)()()(B P A P B A P +=+如果事件A 、B 相互独立,那么)()()(B P A P B A P ⋅=⋅如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率:()(1)k k n kn n P k C P P -=-球是表面积公式24R S π=其中R 表示球的半径 球的体积公式334R V π=其中R 表示球的半径第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若sin 0α<且tan 0α>则α是A .第一象限角B .第二象限角C .第三象限角D .第四象限角 2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,, 3.原点到直线250x y +-=的距离为A .1BC .2D4.函数1()f x x x=-的图像关于 A .y 轴对称 B .直线x y -=对称 C .坐标原点对称D .直线x y =对称5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则A .a <b <cB .c <a <bC .b <a <cD .b <c <a6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值A .2-B .4-C .6-D .8-7.设曲线2y ax =在点(1,)a 处的切线与直线260x y --=平行,则a =A .1B .12C .12-D .1-8.正四棱锥的侧棱长为60°,则该棱锥的体积为A .3B .6C .9D .189.44(1(1的展开式中x 的系数是A .4-B .3-C .3D .410.函数()sin cos f x x x =-的最大值为A .1B C D .211.设△ABC 是等腰三角形,120ABC ∠=,则以A 、B 为焦点且过点C 的双曲线的离心率为A .12+ B C .1+D .112.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于 A .1B .2C .3D .2第Ⅱ卷(非选择题共90分)注意事项:用钢笔或圆珠笔直接答在答题卡上.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.13.设向量(12)(23)== ,,,a b ,若向量λ+ a b 与向量(47)=--,c 共线,则=λ .14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答).15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(2,2)M ,则△ABF 的面积等于 .16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)在ABC △中,5cos 13A =-,3cos 5B =. (1)求sinC 的值;(2)设5BC =,求ABC △的面积.18.(本小题满分12分)等差数列{}n a 中,410a =,且3610,,a a a 成等比数列,求数列{}n a 前20项的和20S .19.(本小题满分12分)甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹.根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2. 设甲、乙的射击相互独立.(1)求在一轮比赛中甲击中的环数多于乙击中环数的概率;(2)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率.20.(本小题满分12分)如图,正四棱柱1111ABCD A BC D -中,124AA AB ==,点E 在1CC 上且EC E C 31=.(1)证明:1AC ⊥平面BED ; (2)求二面角1A DE B --的大小.21.(本小题满分12分)设a R ∈,函数32()3f x ax x =-. (1)若2x =是函数()y f x =的极值点,求a 的值;(2)若函数()()()g x f x f x '=+,[0,2]x ∈,在0x =处取得最大值,求a 的取值范围.22.(本小题满分12分)设椭圆中心在坐标原点,(20)(01)A B ,,,是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相交于E 、F 两点.(1)若6ED DF =,求k 的值;(2)求四边形AEBF 面积的最大值.AB CDEA 1B 1C 1D 12008年普通高等学校招生全国统一考试 文科数学试题(必修+选修Ⅰ)参考答案和评分参考评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要 考查内容比照评分参考制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和 难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数.选择题不给中间分.一、选择题1.C 2.B 3.D 4.C 5.C 6.D 7.A 8.B 9.A 10.B 11.B 12.C 二、填空题13.2 14.420 15.216.两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形. 注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.1.若sin 0α<且tan 0α>是,则α是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角 【答案】C【解析】sin 0α<,α在三、四象限;tan 0α>,α在一、三象限,∴选C2.设集合{|32}M m m =∈-<<Z ,{|13}N n n M N =∈-=Z 则,≤≤( ) A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,,【答案】B【解析】{}1,0,1,2--=M ,{}3,2,1,0,1-=N ,∴{}1,0,1-=N M 【高考考点】集合的运算,整数集的符号识别 3.原点到直线052=-+y x 的距离为( ) A .1B .3C .2D .5【答案】D【解析】52152=+-=d【高考考点】点到直线的距离公式4.函数1()f x x x=-的图像关于( ) A .y 轴对称 B . 直线x y -=对称 C . 坐标原点对称 D . 直线x y =对称【答案】C 【解析】1()f x x x=-是奇函数,所以图象关于原点对称 【高考考点】函数奇偶性的性质5.若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( ) A .a <b <cB .c <a <bC . b <a <cD . b <c <a【答案】C 【解析】由0ln 111<<-⇒<<-x x e,令x t ln =且取21-=t 知b <a <c6.设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值为( )A .2-B .4-C .6-D .8-【答案】D【解析】如图作出可行域,知可行域的顶点是A (-2,2)、B(32,32)及C(-2,-2) 于是8)(min -=A z7.设曲线2ax y =在点(1,a )处的切线与直线062=--y x 平行,则=a ( )A .1B .12C .12-D .1-【答案】A【解析】ax y 2'=,于是切线的斜率a y k x 2'1===,∴有122=⇒=a a8.正四棱锥的侧棱长为32,侧棱与底面所成的角为︒60,则该棱锥的体积为( ) A .3 B .6C .9D .18【答案】B【解析】高360sin 32=︒=h ,又因底面正方形的对角线等于32,∴底面积为6332212=⨯⨯⨯=S ,∴体积63631=⨯⨯=V【备考提示】在底面积的计算时,要注意多思则少算 9.44)1()1(x x +-的展开式中x 的系数是( )A .4-B .3-C .3D .4【答案】A【解析】41666141404242404-=-+=-+C C C C C C 【易错提醒】容易漏掉1414C C 项或该项的负号10.函数x x x f cos sin )(-=的最大值为( ) A .1 B .2 C .3D .2【答案】B【解析】)4sin(2cos sin )(π-=-=x x x x f ,所以最大值是2【高考考点】三角函数中化为一个角的三角函数问题【备考提示】三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题11.设ABC △是等腰三角形,120ABC ∠=,则以A B ,为焦点且过点C 的双曲线的离心率为( ) A .221+ B .231+ C . 21+ D .31+【答案】B【解析】由题意BC c =2,所以c c AC 3260sin 220=⨯⨯=,由双曲线的定义,有c a c c BC AC a )13(2322-=⇒-=-=,∴231131+=-==a c e 【高考考点】双曲线的有关性质,双曲线第一定义的应用12.已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( ) A .1 B .2C .3D .2【答案】C【解析】设两圆的圆心分别为1O 、2O ,球心为O ,公共弦为AB ,其中点为E ,则21EO OO 为矩形,于是对角线OE O O =21,而3122222=-=-=AE OA OE ,∴321=O O【高考考点】球的有关概念,两平面垂直的性质13.设向量(12)(23)==,,,a b ,若向量λ+a b 与向量(47)=--,c 共线,则=λ . 【答案】 2【解析】λ+a b =)32,2(++λλ则向量λ+a b 与向量(47=--,c 共线274322=⇒--=++⇔λλλ14.从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答) 【答案】 420【解析】4202701501621026110=+=+C C C C15.已知F 是抛物线24C y x =:的焦点,A B ,是C 上的两个点,线段AB 的中点为(22)M ,,则ABF △的面积等于 . 【答案】 2 【解析】设过M的直线方程为)2(2-=-x k y ,由0)1(444)2(22222=-+-⇒⎩⎨⎧=-=-k kx x k xy x k y ∴k x x 421=+,2221)1(4k k x x -=,由题意144=⇒=k k ,于是直线方程为x y = 421=+x x ,021=x x ,∴24=AB ,焦点F (1,0)到直线x y =的距离21=d∴ABF △的面积是216.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)【答案】两组相对侧面分别平行;一组相对侧面平行且全等;对角线交于一点;底面是平行四边形.注:上面给出了四个充要条件.如果考生写出其他正确答案,同样给分.三、解答题17.解:(Ⅰ)由5cos 13A =-,得12sin 13A =, 由3cos 5B =,得4sin 5B =. ······························································································· 2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=. ··············································· 5分(Ⅱ)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===. ······················································ 8分 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=. ··························· 10分18.解:设数列{}n a 的公差为d ,则3410a a d d =-=-, 642102a a d d =+=+,1046106a a d d =+=+. ····································································································· 3分 由3610a a a ,,成等比数列得23106a a a =,即2(10)(106)(102)d d d -+=+, 整理得210100d d -=,解得0d =或1d =. ············································································································· 7分 当0d =时,20420200S a ==. ························································································· 9分 当1d =时,14310317a a d =-=-⨯=, 于是2012019202S a d ⨯=+207190330=⨯+=. ·························································· 12分 19.解:记12A A ,分别表示甲击中9环,10环,12B B ,分别表示乙击中8环,9环,A 表示在一轮比赛中甲击中的环数多于乙击中的环数,B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,12C C ,分别表示三轮中恰有两轮,三轮甲击中环数多于乙击中的环数.(Ⅰ)112122A A B A B A B =++, ···················································································· 2分 112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++112122()()()()()()P A P B P A P B P A P B =++0.30.40.10.40.10.40.2=⨯+⨯+⨯=. ············································································· 6分(Ⅱ)12B C C =+, ············································································································· 8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=,332()[()]0.20.008P C P A ===,1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=. ···································· 12分 20.解法一:依题设,2AB =,1CE =.(Ⅰ)连结AC 交BD 于点F ,则BD AC ⊥.由三垂线定理知,1BD AC ⊥. ···························································································· 3分 在平面1ACA 内,连结EF 交1AC 于点G ,由于1AA ACFC CE== 故1Rt Rt A AC FCE △∽△,1AAC CFE ∠=∠, CFE ∠与1FCA ∠互余.于是1AC EF ⊥. 1AC 与平面BED 内两条相交直线BD EF ,都垂直, 所以1AC ⊥平面BED .········································································································ 6分 (Ⅱ)作GH DE ⊥,垂足为H ,连结1A H .由三垂线定理知1A H DE ⊥,故1A HG ∠是二面角1A DE B --的平面角. ······································································ 8分 AB CDEA 1B 1C 1D 1 FH GEFCE CF CG EF ⨯==EG ==. 13EG EF =,13EF FD GH DE ⨯=⨯=又1AC ==113AG AC CG =-=.11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ······························································· 12分 解法二:以D 为坐标原点,射线DA 为x 轴的正半轴, 建立如图所示直角坐标系D xyz -.依题设,1(220)(020)(021)(204)B C E A ,,,,,,,,,,,.(021)(220)DE DB ==,,,,,,11(224)(204)AC DA =--= ,,,,,. ······································ 3分 (Ⅰ)因为10AC DB = ,10AC DE =, 故1AC BD ⊥,1AC DE ⊥. 又DB DE D = ,所以1AC ⊥平面DBE . ········································································································ 6分 (Ⅱ)设向量()x y z =,,n 是平面1DA E 的法向量,则DE ⊥ n ,1DA ⊥ n .故20y z +=,240x z +=.令1y =,则2z =-,4x =,(412)=-,,n . ··································································· 9分1AC <> ,n 等于二面角1A DE B --的平面角,111cos AC AC AC <>==,n n n 所以二面角1A DE B --的大小为arccos 42. ······························································ 12分 21.解:(Ⅰ)2()363(2)f x ax x x ax '=-=-.因为2x =是函数()y f x =的极值点,所以(2)0f '=,即6(22)0a -=,因此1a =. 经验证,当1a =时,2x =是函数()y f x =的极值点. ···················································· 4分 (Ⅱ)由题设,3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+.当()g x 在区间[02],上的最大值为(0)g 时, (0)(2)g g ≥,即02024a -≥.故得65a ≤. ························································································································· 9分 反之,当65a ≤时,对任意[02]x ∈,, 26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+- 3(25)(2)5xx x =+- 0≤,而(0)0g =,故()g x 在区间[02],上的最大值为(0)g . 综上,a 的取值范围为65⎛⎤-∞ ⎥⎝⎦,. ······················································································ 12分22.(Ⅰ)解:依题设得椭圆的方程为2214x y +=, 直线AB EF ,的方程分别为22x y +=,(0)y kx k =>. ················································ 2分 如图,设001122()()()D x kx E x kx F x kx ,,,,,,其中12x x <, 且12x x ,满足方程22(14)4k x +=,故21x x =-=.①由6ED DF = 知01206()x x x x -=-,得021215(6)77x x x x =+==;由D 在AB 上知0022x kx +=,得0212x k=+. 所以212k =+, 化简得2242560k k -+=,解得23k =或38k =. ············································································································ 6分 (Ⅱ)解法一:根据点到直线的距离公式和①式知,点E F ,到AB 的距离分别为1h ==2h ==. ····································································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 12===≤当21k =,即当12k =时,上式取等号.所以S 的最大值为 ······························· 12分 解法二:由题设,1BO =,2AO =.设11y kx =,22y kx =,由①得20x >,210y y =->, 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+······························································································································· 9分===当222x y =时,上式取等号.所以S 的最大值为 ·················································· 12分。
