功率谱分析ppt课件
合集下载
随机信号的功率谱密度课件
出端信噪比之比。即：
F
( Si / N i )
( So / N o )
四、白序列（RND伪随机序列）
设随机序列Zn的自相关函数满足：
2 Z , RZ (k ) 0,
k 0 k 0
2 Z
或
RZ (k ) (k )
对于白序列其功率谱：
GZ ()
2 Z ,
jt
d
将上式代入信号平均功率表达式中得:
1 W lim T 2T lim 1 T 2T
T T T
f T (t , ) dt 1 2
jt F ( , ) e d ]dt T
2
T T
f T (t , )[
1 lim T 2T 1 lim T 2T 1 2
GN(), FN()
RN()
N0 N0/2
N0/2
0 (a) 功率谱密度
0 (b) 自相关函数
白噪声的自相关函数：
1 RN ( ) 2 N 0 j N0 2 e d 2 ( )
白噪声的相关系数 N ( )为:
C N ( ) RN ( ) RN () RN ( ) N ( ) C N (0) RN (0) RN () RN (0)
2/
低通限带白噪声
W , G N ( ) 0,
0 | | 0
otherwise
sin RN ( ) W cos 0
4.6 功率谱估值的经典法
谱估值的基本问题是已知随机过程X(t)或Xj某个 实现： , x
2 , x1 , x0 , x1 , x2 ,, xN 1 ,
铁路轨道不平顺功率谱分析与数值模拟毕业设计答辩PPT
结果应用前景
根据对比分析结果，提出针对性的改善措施和建议，为铁路轨道 维护和优化提供参考。
05
结论与展望
研究结论
1 2 3
结论一
通过功率谱分析，成功提取了轨道不平顺的主要 频率成分，为后续的数值模拟提供了基础数据。
结论二
数值模拟结果显示，轨道不平顺对列车运行平稳 性和安全性有显著影响，其中高频不平顺的影响 尤为突出。
期刊论文
学位论文
会议论文
THANKS
感谢观看
滤波处理
对轨道不平顺信号进行滤 波处理，以去除噪声和异 常值，提高分析精度。
轨道不平顺数据采集
数据采集设备
01
使用高精度的测量设备，如激光位移传感器、加速度计等，对
轨道不平顺数据进行采集。
数据预处理
02
对采集到的数据进行预处理，包括数据清理、格式转换等，以
便进行后续分析。
数据存储与传输
03
将采集到的数据存储在计算机中，并采用适当的数据传输方式，
VS
功率谱分析是研究随机过程功率随频 率变化的一种方法，广泛应用于信号 处理、振动分析等领域。在铁路轨道 不平顺研究中，功率谱分析可以用于 分析轨道不平顺的特性，如幅值、频 率等，为轨道结构的优化设计和车辆 动力学性能的改善提供理论支持。
研究目的和意义
研究目的
本毕业设计旨在通过功率谱分析和数值模拟方法，深入研究铁路轨道不平顺的 特性，分析其对车辆动力学性能的影响，为铁路轨道结构的优化设计和车辆动 力学性能的改善提供理论依据和实践指导。
结论三
本研究提出的数值模拟方法能够较为准确地模拟 轨道不平顺对列车运行的影响，为实际工程应用 提供了有益参考。
研究不足与展望
不足
根据对比分析结果，提出针对性的改善措施和建议，为铁路轨道 维护和优化提供参考。
05
结论与展望
研究结论
1 2 3
结论一
通过功率谱分析，成功提取了轨道不平顺的主要 频率成分，为后续的数值模拟提供了基础数据。
结论二
数值模拟结果显示，轨道不平顺对列车运行平稳 性和安全性有显著影响，其中高频不平顺的影响 尤为突出。
期刊论文
学位论文
会议论文
THANKS
感谢观看
滤波处理
对轨道不平顺信号进行滤 波处理，以去除噪声和异 常值，提高分析精度。
轨道不平顺数据采集
数据采集设备
01
使用高精度的测量设备，如激光位移传感器、加速度计等，对
轨道不平顺数据进行采集。
数据预处理
02
对采集到的数据进行预处理，包括数据清理、格式转换等，以
便进行后续分析。
数据存储与传输
03
将采集到的数据存储在计算机中，并采用适当的数据传输方式，
VS
功率谱分析是研究随机过程功率随频 率变化的一种方法，广泛应用于信号 处理、振动分析等领域。在铁路轨道 不平顺研究中，功率谱分析可以用于 分析轨道不平顺的特性，如幅值、频 率等，为轨道结构的优化设计和车辆 动力学性能的改善提供理论支持。
研究目的和意义
研究目的
本毕业设计旨在通过功率谱分析和数值模拟方法，深入研究铁路轨道不平顺的 特性，分析其对车辆动力学性能的影响，为铁路轨道结构的优化设计和车辆动 力学性能的改善提供理论依据和实践指导。
结论三
本研究提出的数值模拟方法能够较为准确地模拟 轨道不平顺对列车运行的影响，为实际工程应用 提供了有益参考。
研究不足与展望
不足
功率谱分析及其应用
S x Rx e j d
Rx S x e j d
随机信号的功率谱密度
自功率谱密度函数(Auto-power spectral density function)的性质
自功率谱密度函数是实偶函数。 自功率谱密度函数是双边谱。
Cxy 2 R cos d 单边互谱密度函数 (One-sided cross-power spectrum) xy Qxy 2 Rxy sin d 其中 j
实部 Gxy Gxy e 虚部
单边功率谱(one-sided power spectrum)（非负频率 上的谱） G 2S
x x
2 Rx e j d
0
随机信号的功率谱密度
1 T 2 Rxx 0 lim x t x t 0 dt x T T 0
输入x(t)与输出y(t)的互相关函数(crosscorrelation function )为：
Rxy Rx ' x Rx 'n1 Rx 'n2 Rx 'n3
Rxy Rx ' x
S xy f
由于噪音与输入无关，所以后3项为零，于是有
可利用互谱求系统的
X(t)
系统1 系统2 可在强噪声背景下分析系统的传输特性
n1 t
n2 t
y(t)
n3 t
随机信号的功率谱密度 正弦加随机
随机信号
yt x ' t n1 ' t n2 ' t n3 ' t
§6.7信号通过线性系统的自相关函数能量谱和功率谱分析
h(t) r(t) H (jw ) R (jw )
时域
r(t) h(t)* e(t)
频域 R(jw ) H(jw ) E(jw )
假定e(t)是能量有限信号，
e(t)的能量谱密度为
(w ) e
r(t)的能量谱密度为
r (w )
e(w ) E(jw ) 2
r (w ) R(jw ) 2
显然
物理意义：响应的功率谱等于激励的功率谱与|H(jw)|2
的乘积。
返回
二．信号经线性系统的自相关函数
由 r (w ) H (jw ) 2e (w ) Sr (w ) H (jw ) 2 Se (w )
得 r (w ) H (jw )H *(jw )e (w )
Sr (w ) H (jw )H *(jw )Se (w )
§6.7 信号通过线性系统的自相关 函数、能量谱和功率谱分析
前面，从
时域
频域 中研究了
S域
激励 响应 系统
三者的关系
现在，从激励和响应的自相关函数，能量谱，功 率谱所发生的变化来研究线性系统所表现的传输特性。
一、能量谱和功率谱分析 二、信号经线性系统的自相关函数
返回
一．能量谱和功率谱分析
e(t ) E(jw )
所以响应r(t)的自相关函数
Rr ( ) Re ( ) h(t) h*( t)
N ( )
1
( ) 1 t
e RC u t
1
e
1 RC
t
u(
t
)
RC
RC
N
1 t
e RC
2RC
求响应r(t)的自相关函数的另一种方法
由
Rr
§3.2 周期信号的频谱和功率谱
不变，T增大，谱线间隔
1
2 T
减小，谱线逐渐密集，幅度
A T
பைடு நூலகம்
减
小
当 T
1 0
A 0 T
非周期信号连续频谱
非周期信号 n1 连续频率
2.当T不变， 减小时
T不变
1
2 间隔不变
T
A 振幅为0的谐波频率
T
2
,
4
,......
信号与系统
练习：周期信号的频谱描绘
不改变 不改变 不改变
Fn
2 T
2
f (t)dt
T
2 A
2
Adt
2
T
信号与系统
练习：周期信号的频谱描绘
a 2 nT
T
2 T
2
f (t) cos n1tdt
2A sin n n T
2 A
T
sin n
T
n
2A Sa(n )
T
T
T
f (t)
A
T
2 A
T
n 1
Sa( n
T
)
cos(n1t )
A 2A
TT
S a(
立叶展开式并画出其频谱图。
1
解: f(t) 在一个周期内可写为如下形式
Tt
f (t) 2 t T t T
T
22
f(t) 是奇函数，故 an 0
信号与系统
4
bn T
T 2 0
f (t) sin n1tdt
4 T
T 2 0
2t T
sin
n1tdt
(1
2
T
)
An &n 2
信号分析3.05功率谱和能量谱
1
一．周期信号的功率谱 （离散谱）
第 页
描述功率信号在频域中随ω分布情况
瞬时功率
p(t)
Ri2 (t)
u2 (t) R
f
2 (t)
fT 2 (t)
平均功率
P
1 T
T
0
fT 2 (t) d t
1 T
T
0
fT
(t)(
Fne
jn1tn
[1 T
T
0
fT (t)e jn1t dt]
Fn
Fn
3) Fn 2 ~ 绘成的线状图形，表示 各次谐波的平均功 率随频率分布的情况，称为功率谱系数。离散谱。可
绘单边谱也可绘双边谱. 4)功率谱只与幅频谱有关，与相位无关，由于其收敛性，
能量主要集中在低频段 。
X
3
二．非周期信号的能量谱
第
（连续谱）页
时域中：E
f
2 (t)dt
f
(t)[ 1
2
F(
j)e jtd]dt
页
不同频率下信号的实际振幅为无穷小,能 量实际也为无穷小,为描述不同频率下能量的 分布情况,引入能量密度频谱函数G(w),
E
G
(
)d
G() 1 F 2 ( j) 2
说明： 表示单位频率下的信号能量。
1)能量是整个频域范围内能量谱曲线下的面积
2)能量谱只取决于信号的幅频特性,而与相位无关.
通过能量谱曲线可以了解信号能量在频域
1
2
F(
j
)[
f
(t)e jtdt]d
时域法
1
2
F
(
j )F (
j )d
1
一．周期信号的功率谱 （离散谱）
第 页
描述功率信号在频域中随ω分布情况
瞬时功率
p(t)
Ri2 (t)
u2 (t) R
f
2 (t)
fT 2 (t)
平均功率
P
1 T
T
0
fT 2 (t) d t
1 T
T
0
fT
(t)(
Fne
jn1tn
[1 T
T
0
fT (t)e jn1t dt]
Fn
Fn
3) Fn 2 ~ 绘成的线状图形，表示 各次谐波的平均功 率随频率分布的情况，称为功率谱系数。离散谱。可
绘单边谱也可绘双边谱. 4)功率谱只与幅频谱有关，与相位无关，由于其收敛性，
能量主要集中在低频段 。
X
3
二．非周期信号的能量谱
第
（连续谱）页
时域中：E
f
2 (t)dt
f
(t)[ 1
2
F(
j)e jtd]dt
页
不同频率下信号的实际振幅为无穷小,能 量实际也为无穷小,为描述不同频率下能量的 分布情况,引入能量密度频谱函数G(w),
E
G
(
)d
G() 1 F 2 ( j) 2
说明： 表示单位频率下的信号能量。
1)能量是整个频域范围内能量谱曲线下的面积
2)能量谱只取决于信号的幅频特性,而与相位无关.
通过能量谱曲线可以了解信号能量在频域
1
2
F(
j
)[
f
(t)e jtdt]d
时域法
1
2
F
(
j )F (
j )d
1
第5章 功率谱分析及其应用3
▪ 谱相干函数的定义 ➢ 评测输入、输出信号间的因果性，即输出信号 的功率谱中有多少是所测试输入量引起的响应。
2 xy
Gxy 2 Gx Gy
相干函数是表示两个信号在频域内的相似 性。
随机信号的功率谱密度
▪ 频率响应函数的定义
H
Gxy Gx
▪ 谱相干函数的性质
2
Sxy ( f ) Sx ( f )Sy ( f )
油管振动自谱
第五章 信号分析技术
机械工程测试技术基础
§5.2 功率谱分析及其应用
一、自功率谱密度函数
1 定义
Sx ( f )
Rx
(
)e
j
2
f
d
称 Sx(f) 为 x(t) 的自功率谱密度函数
7
第五章 信号分析技术
机械工程测试技术基础
2 功率谱分析及其应用
2.1 自功率谱密度函数
1 定义 ➢ 根据维纳—辛钦公式，平稳随机过程的功率谱密
Sy f Sx f
测量中经常用这个公式计算频率响应函数的幅值， 但无法计算它的相位、实部和虚部。
随机信号的功率谱密度
▪ 互功率谱密度函数定义
➢
如果互相关函数满足付氏变换条件
Rxy
d
Sxy
R xy
e j d
Rxy
1
2
S xy
e j d
▪ 单边互谱密度函数
Gxy
➢ 虚部
Qxy
2
R xy
sin d
Gxy Gxy e jxy
Gxy Cxy 2 Qxy 2
xy
arctan
Qxy Cxy
第五章 信号分析技术
机械工程测试技术基础
2 xy
Gxy 2 Gx Gy
相干函数是表示两个信号在频域内的相似 性。
随机信号的功率谱密度
▪ 频率响应函数的定义
H
Gxy Gx
▪ 谱相干函数的性质
2
Sxy ( f ) Sx ( f )Sy ( f )
油管振动自谱
第五章 信号分析技术
机械工程测试技术基础
§5.2 功率谱分析及其应用
一、自功率谱密度函数
1 定义
Sx ( f )
Rx
(
)e
j
2
f
d
称 Sx(f) 为 x(t) 的自功率谱密度函数
7
第五章 信号分析技术
机械工程测试技术基础
2 功率谱分析及其应用
2.1 自功率谱密度函数
1 定义 ➢ 根据维纳—辛钦公式，平稳随机过程的功率谱密
Sy f Sx f
测量中经常用这个公式计算频率响应函数的幅值， 但无法计算它的相位、实部和虚部。
随机信号的功率谱密度
▪ 互功率谱密度函数定义
➢
如果互相关函数满足付氏变换条件
Rxy
d
Sxy
R xy
e j d
Rxy
1
2
S xy
e j d
▪ 单边互谱密度函数
Gxy
➢ 虚部
Qxy
2
R xy
sin d
Gxy Gxy e jxy
Gxy Cxy 2 Qxy 2
xy
arctan
Qxy Cxy
第五章 信号分析技术
机械工程测试技术基础
功率谱分析
谐波分析
准5年 准2年
准3年
Fig. 5 The time series curve for the standardized interannual component(1 and a half years to 8 years) of the IAAM
功率谱检验
65.1 m
38 m 24 m
End
Thanks
距平序列
Pic.3 The time series curve for the anomaly of the IAAM
功率谱分析
19a 3a 2a
Pic.4 The curve for the continuous spectrum and the check line of the red noise.
• 结果分析 • 结论
资料与方法介绍
NCAR/NCEP资料
NCAR/NCEP月平均风场资料（1948～2004年，30°E～ 180°E，40°S～40°N),水平分辨率2.5°*2.5°。
垂直方向上取对流层下层1000hPa，925hPa，850hPa， 700hPa四层经向风V平均作为低层，和对流层上层300hPa， 250hPa，200hPa，150hPa，100hPa五层经向风V平均作为高层。
影响aam的系统在低空有澳大利亚的冷性反气旋沿100e以东的越赤道气流西太平洋副高和赤道东风气流等各个系统在高空有南亚高压南半球强大的反气旋和高空自北半球向南半球的越赤道气流等
主要内容
• 资料与方法介绍 • 季风环流指数定义
(IAAM=Index of Asia-Australia Monsooneries on the high level of the troposphere, the black line is the time series of the IAAM.
《功率谱估计》课件
《功率谱估计》 PPT课件
目录
• 引言 • 功率谱估计的基本原理 • 常见功率谱估计方法 • 现代功率谱估计方法 • 功率谱估计的性能评估 • 实际应用案例分析
01
引言
功率谱估计的定义
功率谱估计是对信号的频率内容进行描述的方法，通过分析信号在不同频率的功 率分布情况，可以了解信号的特性。
功率谱估计可以分为非参数方法和参数方法两类，其中非参数方法包括傅里叶变 换、Welch方法等，而参数方法则包括AR模型、MA模型、和ARMA模型等。
非参数模型
不假设信号的功率谱具有特定参数形式，而是直接从数据中估计功率谱。
03
常见功率谱估计方法
直接法
定义
直接法是通过测量信号的样本值，利用离散 傅里叶变换（DFT）直接计算信号的频谱。
特点
计算简单，但容易受到频率偏移和相位失真的影响 。
应用场景
适用于信号频率稳定且对相位精度要求不高 的场合。
间接法
THANKS
感谢观看
分辨率与假峰率
分辨率（Resolution）
衡量功率谱估计中能够区分两个相近频率成分的能力。分辨率越高，说明估计的功率谱能够更好地分 辨出相近的频率成分。
假峰率（False Peak Rate）
衡量估计的功率谱中出现的虚假频率峰的概率。假峰率越低，说明估计的功率谱中虚假频率峰的出现 概率越小。
06
特点
能够减小频谱泄漏效应，提高频 谱分辨率。
应用场景
适用于信号持续时间较短或需要 高分辨率频谱分析的场合。
最大熵法
定义
最大熵法是一种基于信息论的方法，通过最 大化熵函数来估计信号的功率谱。
特点
能够提供平滑且连续的功率谱估计，但计算 复杂度较高。
目录
• 引言 • 功率谱估计的基本原理 • 常见功率谱估计方法 • 现代功率谱估计方法 • 功率谱估计的性能评估 • 实际应用案例分析
01
引言
功率谱估计的定义
功率谱估计是对信号的频率内容进行描述的方法，通过分析信号在不同频率的功 率分布情况，可以了解信号的特性。
功率谱估计可以分为非参数方法和参数方法两类，其中非参数方法包括傅里叶变 换、Welch方法等，而参数方法则包括AR模型、MA模型、和ARMA模型等。
非参数模型
不假设信号的功率谱具有特定参数形式，而是直接从数据中估计功率谱。
03
常见功率谱估计方法
直接法
定义
直接法是通过测量信号的样本值，利用离散 傅里叶变换（DFT）直接计算信号的频谱。
特点
计算简单，但容易受到频率偏移和相位失真的影响 。
应用场景
适用于信号频率稳定且对相位精度要求不高 的场合。
间接法
THANKS
感谢观看
分辨率与假峰率
分辨率（Resolution）
衡量功率谱估计中能够区分两个相近频率成分的能力。分辨率越高，说明估计的功率谱能够更好地分 辨出相近的频率成分。
假峰率（False Peak Rate）
衡量估计的功率谱中出现的虚假频率峰的概率。假峰率越低，说明估计的功率谱中虚假频率峰的出现 概率越小。
06
特点
能够减小频谱泄漏效应，提高频 谱分辨率。
应用场景
适用于信号持续时间较短或需要 高分辨率频谱分析的场合。
最大熵法
定义
最大熵法是一种基于信息论的方法，通过最 大化熵函数来估计信号的功率谱。
特点
能够提供平滑且连续的功率谱估计，但计算 复杂度较高。
第4章 随机信号的功率谱密度.ppt
➢ 二、互谱密度的性质 1. GXY (ω ) GYX ( ω ) GYX (ω )。
2. Re GXY ( ) 和 Re G YX( ) 是 的偶函数； Im GXY ( ) 和 Im G YX( ) 是 的奇函数。
因为任一复函数 f ( )满足：
| E[lim
T
XT (, i ) |2 ]
2T
| E[lim
T
xT (t , i ) |2 ]
2T
GX ( ) 称为随机过程的功率谱密度函数。由此可得随机过程的
平均功率：
P 1
2
GX ( )d
1
lim T 2T
T T
E[
xT ( t , i
1
[ lim
T 2T
T T
RX
(t,
t
)dt
]e j d
令：RX
(
)
lim
T
1 2T
T
T RX ( t , t )dt
RX ( ) 可看成非平稳过程自相关函数的时间平均。
➢ 若 X( t )为平稳过程，则 RX ( t , t ) RX ( ) ，故有
三、带限白噪声定义：
一个均值为零，功率谱密度为
GN (
)
N0 2
,
( 0 , 0 )
的平稳过程，称为带限白噪声。 其中ω0为有限值。
对应于带限白噪声的自相关函数为：
RN ( )
其中，Sa (
0
21)GsiNn(0)e 0
j d 。
由
XT (, i )
随机过程的功率谱密度解析
第五讲：小 结
平稳随机过程
严格平稳随机过程 广义平稳随机过程 平稳随机过程自相关函数性质
相关函数示意图
第五讲：小 结
平稳随机过程
相关系数
相关时间
随机过程的遍历性 平稳随机过程满足：
相关时间示意图
一、联合分布
二维联合分布函数：
二维联合概率密度：
一、联合分布
n+m维联合分布函数：
n+m维联合概率密度：
上均匀分布，求互协方差函数。
频谱：
复习
信号的 总能量
能谱密度：信号的能 量按频率分布的情况
一、随机过程的功率谱密度
截取数：
随机过程的样本函数及其截尾函数
时间平 均功率
功率谱密度：信 号的平均功率按 频率分布的情况
时间平 均功率
随机过程的平均功率 随机过程的功率谱密度：
功率谱密度：信 号的平均功率按 频率分布的情况
二、两随机过程的相互关系
互相关函数：
互协方差函数：
两随机过程的相互关系：
X(t)与Y(t)独立
若
，则X(t)与Y(t)正交；
若
，则X(t)与Y(t)不相关；
联合平稳的定义：如果随机过程X(t),Y(t)平稳，且满足 性质：
若 与 是联合平稳的，则 互相关系数：
是平稳的
例1、设 其中 为常数， 在
(1) Z(t)的功率谱密度； (2) X(t)、Y(t)不相关时Z(t)的功率谱密度； (3) X(t)、Y(t)分别与Z(t)的互谱密度。
第六讲：小 结
随机过程的联合分布
互相关函数： 互协方差函数： 互相关系数：
广义联合平稳的定义：
随机过程的功率谱密度 作业：2.31, 2.36, 2.39
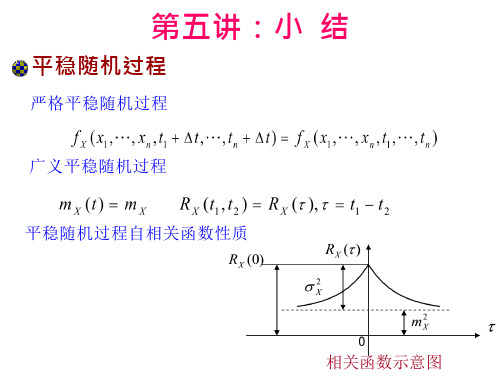
平稳随机过程
严格平稳随机过程 广义平稳随机过程 平稳随机过程自相关函数性质
相关函数示意图
第五讲：小 结
平稳随机过程
相关系数
相关时间
随机过程的遍历性 平稳随机过程满足：
相关时间示意图
一、联合分布
二维联合分布函数：
二维联合概率密度：
一、联合分布
n+m维联合分布函数：
n+m维联合概率密度：
上均匀分布，求互协方差函数。
频谱：
复习
信号的 总能量
能谱密度：信号的能 量按频率分布的情况
一、随机过程的功率谱密度
截取数：
随机过程的样本函数及其截尾函数
时间平 均功率
功率谱密度：信 号的平均功率按 频率分布的情况
时间平 均功率
随机过程的平均功率 随机过程的功率谱密度：
功率谱密度：信 号的平均功率按 频率分布的情况
二、两随机过程的相互关系
互相关函数：
互协方差函数：
两随机过程的相互关系：
X(t)与Y(t)独立
若
，则X(t)与Y(t)正交；
若
，则X(t)与Y(t)不相关；
联合平稳的定义：如果随机过程X(t),Y(t)平稳，且满足 性质：
若 与 是联合平稳的，则 互相关系数：
是平稳的
例1、设 其中 为常数， 在
(1) Z(t)的功率谱密度； (2) X(t)、Y(t)不相关时Z(t)的功率谱密度； (3) X(t)、Y(t)分别与Z(t)的互谱密度。
第六讲：小 结
随机过程的联合分布
互相关函数： 互协方差函数： 互相关系数：
广义联合平稳的定义：
随机过程的功率谱密度 作业：2.31, 2.36, 2.39
第五章功率谱估计1-2节
28/113
经FFT变换,得:
ˆ ˆ ˆ Pxx (k ) FFT xx (m) xx (m)e
m0 L -1 -j 2 km L
k 0,1, 2, L -1
29/113
三、相关图法功率谱估计质量
用x(n)的N 个有限值得到 ˆ 自相关函数的估计 ( m)，
13/113
（a）间接法（BT法）
BT法又称为相关图法 对信号序列估计求其自相关函数值 对自相关函数的估计进行加权 对加权的自相关函数做傅里叶变换 获得功率谱估计。
直到1965年快速傅里叶变换算法（FFT） 问世以前，是最流行的谱估计方法。
14/113
（b）直接法（又称周期图 （periodogram)法）
对观测到的数据样本直接进行傅里叶变换 取模的平方，再除以N 得到功率谱估计。 不用估计自相关函数，且可以用FFT进行计算， 在FFT出现以后，周期图法才得到了广泛的应 用。
15/113
（2）现代谱估计
其基本思想是根据已有的观测数据，建 立信号所服从的模型，从而在观测不到 的区间上，信号的取值服从模型的分布 情况，不再认为是零。 主要讨论参数模型（AR、MA、ARMA） 法。
N
2 xx (l ) xx (l m)xx (l - m) (N - m - l )
N - m -1 2 l -( N - m -1) N - m -1 2 l -( N - m -1)
N - m
N
所以在实际中必须兼顾分辨率与方差的要求来适当选择信号仍然是均值为方差为的白噪声观察数据长度为了利用平均周期法估计其功率谱将它分成段分别按照平均周期图法估计其功率谱得到功率谱曲线如图从图中可以看出随着分段数的增加功率谱估计值在附近的幅度愈来愈小显示出分段平均对周期图方差减少有明显效果
经FFT变换,得:
ˆ ˆ ˆ Pxx (k ) FFT xx (m) xx (m)e
m0 L -1 -j 2 km L
k 0,1, 2, L -1
29/113
三、相关图法功率谱估计质量
用x(n)的N 个有限值得到 ˆ 自相关函数的估计 ( m)，
13/113
（a）间接法（BT法）
BT法又称为相关图法 对信号序列估计求其自相关函数值 对自相关函数的估计进行加权 对加权的自相关函数做傅里叶变换 获得功率谱估计。
直到1965年快速傅里叶变换算法（FFT） 问世以前，是最流行的谱估计方法。
14/113
（b）直接法（又称周期图 （periodogram)法）
对观测到的数据样本直接进行傅里叶变换 取模的平方，再除以N 得到功率谱估计。 不用估计自相关函数，且可以用FFT进行计算， 在FFT出现以后，周期图法才得到了广泛的应 用。
15/113
（2）现代谱估计
其基本思想是根据已有的观测数据，建 立信号所服从的模型，从而在观测不到 的区间上，信号的取值服从模型的分布 情况，不再认为是零。 主要讨论参数模型（AR、MA、ARMA） 法。
N
2 xx (l ) xx (l m)xx (l - m) (N - m - l )
N - m -1 2 l -( N - m -1) N - m -1 2 l -( N - m -1)
N - m
N
所以在实际中必须兼顾分辨率与方差的要求来适当选择信号仍然是均值为方差为的白噪声观察数据长度为了利用平均周期法估计其功率谱将它分成段分别按照平均周期图法估计其功率谱得到功率谱曲线如图从图中可以看出随着分段数的增加功率谱估计值在附近的幅度愈来愈小显示出分段平均对周期图方差减少有明显效果
第5讲动态信号特征分析4_功率谱
第5讲动态信号特征分析4_功率谱功率谱是一种用于分析信号特征的工具，它能够将信号在频域上的能量分布情况展示出来。
在动态信号分析中，功率谱常常被用来研究信号的频谱特性和能量分布情况，从而揭示信号中的规律和隐含的信息。
功率谱是一种频谱密度估计方法，能够提供信号在不同频率上的能量分布情况。
它用于将时域信号转换成频域信号，通过分析在不同频率上的功率大小来了解信号的频谱特性。
功率谱通常由傅立叶变换（Fourier Transform）或自相关函数（Autocorrelation Function）得到。
在实际应用中，常用的功率谱估计方法有傅立叶变换、周期图法、Welch法等。
其中，傅立叶变换是一种基本的功率谱估计方法，通过将时域信号转换为频域信号，并计算信号在各个频率上的能量分布。
周期图法则是一种通过对信号进行周期性拓展和分析来得到频谱信息的方法，适用于非平稳信号的分析。
而Welch法是一种将信号分成不同的段，对每个段进行傅立叶变换，并对各个段的谱进行平均得到功率谱的方法，适用于平稳和非平稳信号的分析。
通过功率谱分析，可以得到信号中各个频率上的能量大小。
从功率谱图上可以观察到信号的频谱特性，包括频率的分布情况、频率的峰值位置和宽度等。
通过对功率谱的分析，可以了解信号中的主要频率成分和能量分布情况，从而揭示信号的特征和隐含信息。
功率谱分析在振动分析、音频处理、通信系统等领域中都有广泛的应用。
在实际应用中，功率谱分析往往需要注意一些问题。
首先，信号的采样率和采样点数要足够高，以满足对信号频谱的要求。
其次，对信号进行预处理，去除可能对功率谱分析造成影响的噪声或干扰。
另外，选择适当的功率谱估计方法和参数也是重要的，以获得准确和可靠的分析结果。
总之，功率谱是一种用于分析信号特征的工具，通过对信号在频域上能量分布的分析，可以了解信号的频谱特性和能量分布情况，从而揭示信号的规律和隐含信息。
在实际应用中，需要注意信号的采样率和采样点数、信号的预处理以及选择适当的功率谱估计方法和参数。
功率谱与功率谱密度.ppt
S X () S X () 0
记 SX
, , 为双边功率谱
GX , 0, 为单边功率谱
10
2.互功率谱密度 联合平稳信号X(t)与Y(t)的互功率谱密度为
S XY ( ) RXY ( )e j d
SYX () RYX ( )e
6
(2) 随机信号的平均功率及平均功率谱密度
对样本功率取平均，即为平均功率
PX E PX
对样本功率谱取平均，即为平均功率谱
2 1 S X E S , lim E X , X T 2T T
XT 是截断信号xT t 的傅里叶变换
xT t
x t
t
T
T
4
令
2 1 S lim X T T 2T
S ( ) 为功率谱密度，简称功率谱
S d 则 可见，信号的能量谱密度或功率谱密度沿整个频率 轴上的积分正好是信号的的能量或功率。
7
随机信号的平均功率与相关函数的关系
PX ARX t , t
0
v t dt
当x(t)为广义平稳时， P RX X 记算数平均算子为
1 A lim v t T 2T
T
T
平稳随机信号的功率谱密度满足
R S
8
3.4.2基本概念
2
| X j | d密度，简称能量谱。
E:归一化能量（单位电阻上消耗的平均能量）
3
（2）功率型信号 1 T 2 1 P lim x t dt T 2T T 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R S (0)
( f )df
x
x
（2.38）
由相关函数定义得， 0 时，有
R (0) lim 1
T
x(t)x(t 0)dt
x
T 0
x lim 1 T x T T 0
2(t)dt lim T T 0
2 (t) T dt （2.39）
Page 7
功率谱密度函数的物理意义
比较以上两式可得：
T 2 (t)
x ( f )df lim
dt
S x
T T 0
（2.40）
上式表明：Sx( f ) 曲线下的总面积与 x2(t) T 曲线下的总面积相等，如图2.17所示
从物理意义讲，x2(t) 是信号x（t）的能量，x2(t) T 是信号x（t）的功率，从而，
T 2 (t)
x lim
dt
T T 0
功率谱分析及其应用
主讲人：冯启涛 导师：蔡明仪
随机信号的功率谱密度
随机信号是时域无限信号，不具备可积分条件，因此不能 直接进行傅里叶变换。又因为随机信号的频率、幅值、相 位都是随机的，因此从理论上讲，一般不作幅值谱和相位 谱分析，而是用具有统计特性的功率谱密度(power spectral density)来作谱分析。 自功率谱密度函数(Auto-power spectral density function) 互功率谱密度函数(cross-power spectral density function)
随机信号的互功率谱密度函数（互谱）为
S R e
(f)
xy
( ) d j 2f （2.36）
xy
其逆变换为
R S e
( )
xy
( f ) j 2 f df
xy
（2.37）
Page 4
功率谱密度函数的定义
由于S ( f ) 与 R( ) 的傅里叶变换对的关系，两者是唯一对应的。S ( f )
yx
T
Page 13
Page 14
是信号x（t）的总功率。
Page 8
功率谱密度函数的物理意义
这一总功率与 S x ( f ) 曲线下 的总面积相等，故 S x ( f )曲
线下的总面积就是信号的总 功率。 这一总功率由无数不同频率
S上x (的f )频表率示元总S功x (率f )在df 不组同成频，率
处的功率分布，因此 S x ( f )
|X
(
f
)|2
Page 12
功率谱的计算
数字信号自谱的估值计算式：
S
(k )
x
1 | X (k )|2
N
G x(k )
2 N
|X
(k )|2 其中k
0,1,2..... N 1
模拟信号互谱的估值计算式：
S X ( f ) 1
xy
T
( f )Y ( f )
Gห้องสมุดไป่ตู้Y
1
(f) X(f)
( f )
因此可在 (0, ) 频率范围内 Gx( f ) 2Sx( f ) 表示信号的全部功率谱。Gx( f ) 称为x（t）
信号的单边功率谱密度函数。如下图所示：
Page 10
功率谱密度函数的物理意义
Sx ( f ), Gx ( f )
Gx ( f )
0
Sx( f )
f
单边谱和双边谱
Page 11
功率谱的计算
中包含着 R( ) 的全部信息。因为 RX ( )为实偶函数， S x ( f ) 亦为实偶
函数。互相关函数
Rxy( ) 并非偶函数，因此
S (f) xy
具有虚、实两个部
分，同样
S( xy
f
)
保留了
R ( ) xy
的全部信息。
Page 5
功率谱密度函数的物理意义
S
(
x
f
)
和
S (f) xy
是随机信号的频域描述函数。因为随机信号的积分不收敛，
Page 2
功率谱密度函数的定义
随机信号的自功率谱密度函数（自谱）是该随机信号自相关函数的傅 里叶变换，记为 SX ( f )
S R e
(f )
() j2f d
X
X
（2.34）
其逆变换为
R S e ( )
( f ) j 2f df
X
X
Page 3
（2.35）
功率谱密度函数的定义
2 (t)dt
1
lim
2
df
T av T 0
T T
再由式（2.38）、（2.39）、（2.41）得：
（2.41）
S
x
lim
T
1 T
|X
(
f
)|2
自功率谱密度函数是偶函数，频率范围 (,) ，故称双边自功率谱密度函
数。它的频率范围在(,0) 的函数值是在 (0,) 频率范围内函数值的对称映射。
不满足狄里赫利条件，因此其傅里叶变换不存在，无法直接得到频谱。
但均值为零的随机信号的相关函数 时是收敛的，即
Rx ( ) 0
时，满足傅里叶变换条件
R| ( ) | d
x
根据傅里叶变换理论，自相关函数 Rx ( ) 绝对可积。
Page 6
功率谱密度函数的物理意义
所以对于式子（2.35），当 0 时，有
布拉克-杜开法：首先根据原始信号计算出相关函数，然后进行傅里叶变 换而得到相应的功率谱函数；
模拟滤波器法：采用模拟分析仪进行分析计算； 库利-杜开法 ：即用FFT（快速傅里叶变换）计算功率谱。
以下是库利-杜开法的估值计算式： 模拟信号自谱的估值计算式：
S
(
x
f
)
1 T
|X
(
f
)|2
Gx(
f
)
2 T
表示信号功率密度沿着频率
轴的分布，所以称 S x ( f ) 为功
率谱密度函数。
Page 9
功率谱密度函数的物理意义
下面说明自功率谱密度函数 Sx ( f ) 和幅值谱 X ( f ) 或能谱 |X ( f )|2 之间的关
系。由巴塞法尔定理，在整个时间轴上的信号平均功率为
P x |X ( f )| lim 1 T