薄壁球壳内部爆炸的变形与破坏模拟
爆炸力学讲义

爆炸力学讲义第一章绪论§1.1 爆炸力学的基本概念爆炸效应是多种多样的,包括物理、力学、化学等多个学科领域,如主要以力学的观点和方法来研究爆炸,则可称之为“爆炸力学”。
郑哲敏教授和朱兆祥教授提出:“爆炸力学是力学的一个分支,是主要研究爆炸的发生和发展规律以及爆炸的力学效应的应用和防护的学科”。
爆炸力学从力学角度研究化学爆炸、核爆炸、电爆炸、粒子束爆炸(也称辐射爆炸)、高速碰撞等能量突然释放或急剧转化的过程,以及由此产生的强冲击波(又称激波)、高速流动、大变形和破坏、抛掷等效应。
自然界的雷电、地震、火山爆发、陨石碰撞、星体爆发等现象也可用爆炸力学方法来研究。
爆炸力学是流体力学、固体力学和物理学、化学之间的一门交叉学科,在武器研制、交通运输和水利建设、矿藏开发、机械加工、安全生产等方面有广泛的应用。
§1.2 爆炸力学的发展历程人们知道利用爆炸能为自己服务已经有很长的历史了,可以说从炸药发明以后就开始了。
黑火药是我国古代四大发明之一,这在我国是家喻户晓的常识,但在西方国家却不这么认为。
丁儆教授在1980年参加美国国际烟火技术会议(IPS),在会上作报告述及中国发明火药和烟火技术的事实,引起许多欧美学者的惊异,因为西方教材中都说火药是英国的罗吉•培根(Roger Bacon)发明的,为了纠正西方的错误,丁儆教授回国后进行了中国古代火药和爆炸方面历史的研究,研究表明,大约在公元8世纪(唐朝),中国就出现了火药的原始配方,在十世纪已应用于军事,北宋初官修著的《武经总要》中记载有火炮、蒺藜火球和毒烟火球等几种实战武器的火药配方。
宋代周密揆在《葵辛杂记》中记载了火药产生的爆炸事故:“……守兵百余人皆糜碎无余,盈栋皆寸裂,或为炮风崩至十余里外。
”《宋史》记载元兵破静江时有:“……娄乃令所都人拥一火炮燃之,声如雷霆,震城土皆崩,烟气涨天外,兵多惊死者。
”火药的知识由阿拉伯人传入欧洲,直到十三世纪,英国人罗吉•培根才涉及火药的配方和应用,他的工作比中国人晚300~500年。
冲击作用下夹层充液薄壁半球壳组合结构的动力响应

冲击作用下夹层充液薄壁半球壳组合结构的动力响应路国运;秦斌;张国权;韩志军;雷建平【摘要】Experiments were carried out to study the dynamic response of the liquid-filled thin-wall hemispherical shell under impact using the DHR9401 drop hammer as the loading device. According to the configurations of the hemispherical shells, the experimental device was elaborately designed to achieve the ideal seal for filling liquid. The time histories of the impact force and the internal pressure were recorded for different hemispherical shells. Four distinct deformation modes of the hemispherical shells under impact were observed as follows: (1) flattening of the upwardly protruding points, (2) inward dimpling with plastic hinges followed by outward expanding, (3) flattening of the plastic edge regions, and (4) elastic recovering. The experimental results show that double-wall liquid-filled hemispherical shells have better impact resistance than the single-wall hemispherical shells, for the liquid filled can reduce the deformation of the internal shell by turning point impact into even surface impact under the experimental impact conditions. So the double or multi-layer liquid-filled hemispherical shells can provide satisfying protection under a certain impact loading.%采用DHR9401作为加载工具对充液夹层构形的薄壁半球壳组合结构受质量块冲击的动力响应进行了实验研究.给出了冲击力和内压力时程曲线,结合实验变形过程的观察可以看出,冲击引起半球壳的动力响应可分为4个阶段:冲击点处的扁平化;壳面凹陷形成塑性铰并向外扩张;冲头对塑性棱区的压平以及弹性恢复.实验结果表明,双层充液球壳在受到载荷冲击时,由于液体作用使外壳受到的局部冲击转化成面载荷均匀加载在内壳上,使之具有更大的承载能力.采用夹层充液组合构形的半球壳组合结构的耐撞性有了很大的提高,在一定的冲击能量下,内部的球壳变形量很小,可以提供有效的安全防护空间.【期刊名称】《爆炸与冲击》【年(卷),期】2012(032)006【总页数】7页(P561-567)【关键词】固体力学;动力响应;冲击;半球壳;充液【作者】路国运;秦斌;张国权;韩志军;雷建平【作者单位】太原理工大学应用力学与生物医学工程研究所,山西太原030024;太原理工大学应用力学与生物医学工程研究所,山西太原030024;中航工业西安飞机工业(集团)有限责任公司,陕西西安710089;太原理工大学应用力学与生物医学工程研究所,山西太原030024;太原理工大学应用力学与生物医学工程研究所,山西太原030024【正文语种】中文【中图分类】O347.3薄壁球壳作为一种基本结构元件,广泛应用于各种运载工具和压力容器,如航天器和深水工程的压力容器等。
化工设备基础内压薄壁圆筒和球壳设计剖析

材料选择:需要考虑材料的强度、耐腐蚀性和耐高温性等性能
结构设计:需要考虑结构的稳定性、安全性和可维护性等要求
制造工艺:需要考虑制造工艺的可行性、成本和效率等因素
测试与验证:需要考虑测试方法和验证标准,确保设计的安全性和有效性
解ቤተ መጻሕፍቲ ባይዱ方案
采用先进的制造工艺,如焊接、锻造等,提高设备的可靠性和耐久性
04
材料加工性能:选择易于加工成型的材料,以降低制造成本和周期
结构优化
优化检测方法:采用先进的检测方法,如超声波、射线等,确保产品质量
04
优化制造工艺:采用先进的制造工艺,如焊接、冲压等
03
优化结构设计:采用合理的结构形式,如加强筋、肋板等
02
优化材料选择:选择高强度、轻质、耐腐蚀的材料
01
内压薄壁球壳设计
采用有限元分析方法,对内压薄壁圆筒和球壳进行应力分析
优化设计参数,如壁厚、材料、结构等,以降低应力水平
定期进行设备检查和维护,确保设备安全运行
设计优化方向
提高安全性能
优化材料选择:选择具有更高强度和耐腐蚀性的材料
01
优化结构设计:采用更加合理的结构设计,提高设备的稳定性和可靠性
02
优化制造工艺:采用更加先进的制造工艺,提高设备的加工精度和质量
03
优化检测方法:采用更加精确的检测方法,确保设备的安全性能符合要求
04
降低成本
优化材料选择:选择价格较低、性能可靠的材料
1
优化结构设计:减少不必要的结构,降低制造成本
2
优化生产工艺:采用先进的生产工艺,降低生产成本
3
优化设计方案:选择最优的设计方案,降低整体成本
4
薄壁扁球壳结构在撞击载荷下的变形控制方法研究

摘 要 对薄壁扁球壳结构撞击刚性板的变形特性和控制方法进行了研究。使用 L — Y A软件建立了薄壁扁 S DN
球壳结构撞击刚性板的有限元模 型 , 并通过试验结果对模 型的有效性进行 了验证。利用数值仿 真方法 , 薄壁球壳结 构 对
/
M
扁球 壳
/
0 性地 板—\
\
\ N N \ ' , N N \ NN ' N N\ \ N N 'N N N NN N N N N NN N N NN \ N N NN N NN N N NN X N'N . - , , .
图 1 薄壁球壳结构撞击过程简化模 型
撞 击过 程 中 , 在质 量块 上布 置加 速度传 感 器 , 测 量撞 击过程 中质 量块 上 的加 速度 响 应 。使 用 高速 摄像 拍摄撞 击过 程 , 过 图像 分 析 测 量球 壳 的 底 部 的动 态 通 变形 , 拍摄速 率 为 1 0 0帧/ 。 0 秒
第一作者 马春生 男 , 博士生 ,9 9年期
马春生等 :薄壁扁球壳结构在撞击载荷下 的变形控制方法研究
2 结构变形特性和动态响应分析
2 1 变 形模式 .
维普资讯
振
动
与
冲
击
第 2 卷第 4 6 期
J OURNAL OF VI BRAT ON AND S I HOCK
薄 壁扁 球 壳结构 在撞 击载 荷下 的 变形 控 制方 法研 究
马春生 , 杜汇 良, 张金换 , 黄世 霖
12 有 限元模 型建立 .
根据 简 化 模 型 , 用 通 用 显 式 有 限 元 软 件 L 利 s— DN Y A建立 了有 限元 模 型 。其 中薄 壁 球壳 采 用 全 积分
实验2 厚壁圆筒爆实验室

实验2 厚壁圆筒爆实验室一.实验目的1. 测定圆管塑性变形开始和结束时的屈服压力值:2. 测定圆管破坏时的爆破压力,并通过计算验证理论公式;3. 了解过程装备控制专业数据自动采集系统基本原理;4. 观察爆破断口的形貌,作宏面分析,了解韧性断裂与脆性断裂的特征;5. 了解容器受力变形直至破坏的三个阶段。
二.试验原理1. 屈服压力值的理论计算(1) 初始屈服压力(A 点对应压力)2s p =(2) 全屈服压力(材料为理想弹塑性)(C 点对应压力)0ln s s p k = 2. 爆破压力值的理论计算承受内压的高压管体,其爆破压力计算方法有如下六种:(1) 福贝尔(Faupel )——爆破失效准则(2)lns b s b p k σσ=- (2) 中径公式——弹性失效准则 121b bk p k σ-=+ (3) 最大主应力理论(第一强度理论)——弹性失效准则2211b b k p k σ⎛⎫-= ⎪+⎝⎭(4) 最大主应变理论22`11.30.4b b k p k σ⎛⎫-= ⎪+⎝⎭(5) 最大剪应力理论(第三强度理论)——弹性失效准则2212b b k p k σ⎛⎫-= ⎪⎝⎭(6) 最大变形能理论(第四强度理论)——弹性失效准则2b b p σ= 上述公式中:K ——容器外径与内径的比值(实验值为准)s σ——容器材料的屈服极限,245s MPa σ=b σ——容器材料的强度极限,410b MPa σ=。
3. 爆破试验原理过程三.实验装置四.实验操作步骤及注意事项1. 了解试验装置的结构2. 测量试件尺寸,其中内径为36mm 。
3. 关闭卸荷阀10与11,观察仪器面板的油标,看油缸是否有足够的介质油,若油缸中油不足,可从导油杯中直接加油。
4. 启动电机前须对试验机的十字头滑块、活塞杆等运动磨损件加润滑油;开机后待试件接口3处有油溢出,再关闭电机。
5. 将测量好欲爆破的厚壁圆筒试件预先灌满油(必须排除里面的空气),在出口上贴上一层薄纸,倒转后快速旋转到爆破试件接口上,用管子钳上紧罩好保护罩。
剪切带演化模型及其在模拟柱壳内外爆剪切失稳中的应用

剪切带演化模型及其在模拟柱壳内外爆剪切失稳中的应用柱壳在内部或外部炸药爆轰驱动下的断裂行为有很强的应用背景,对该问题已经有几十年的研究历史。
大量试验研究结果表明:绝热剪切带的形成和演化在爆轰加载柱壳高应变率膨胀断裂和厚壁圆筒向内塌陷破坏的过程中起着关键作用,其是裂纹的先导,断裂面沿着剪切带路径传播发展。
目前,对该问题的研究主要以实验和理论探讨为主,数值模拟分析相对较少。
本文以柱壳在内部炸药爆轰驱动下的高应变率膨胀断裂和厚壁圆筒在外部炸药驱动下的向内塌陷问题为需求背景,探索适合于模拟多条剪切带自组织行为的材料模型,针对金属材料强烈的粘塑性效应,探索适合于粘塑性本构计算的数值算法。
文章主要内容和创新性成果如下:1)通过在宏观本构中引入概率因子来描述材料缺陷导致的材料屈服应力分布不均匀性,假定该概率因子在空间服从正态分布。
在分析绝热剪切带形成过程各阶段特点的基础上,给出了剪切带形成的多阶段本构模型。
金属材料中广泛存在着各种缺陷,如位错、晶界、沉淀项、微孔洞、微裂纹等,某些缺陷导致材料局部屈服应力提高,某些缺陷导致材料局部屈服应力降低,屈服强度在材料内呈不均匀分布,但这种不均匀性在现有的宏观本构中并不体现。
剪切带的形成是扰动导致变形失稳的结果,扰动源在其形成过程中起关键作用,因此要模拟多条剪切带的形成发展过程,必须在本构中考虑屈服强度的分布不均匀性。
本文通过在宏观本构中引入一个概率因子建立概率型本构关系来描述材料内屈服强度的不均匀分布,假定概率因子在空间服从正态分布。
绝热剪切带的形成需要经历三个阶段:稳定塑性流动阶段、成核阶段和类流体阶段。
在高应变率变形时,材料与环境的热传导可以忽略,因此使用一个绝热的J-C本构描述材料在稳定塑性流动阶段的力学行为;在成核阶段,孔洞软化效果增强,孔洞的发展与材料内的存储能相关,温度软化效果与材料的热能相关,而热能和存储能都由塑性功转化而来,因此温度软化效果和孔洞软化效果可表述为塑性应变的函数;使用粘性流体本构描述材料在类流体阶段抵抗剪切变形的能力。
韧性金属圆球壳的动态膨胀和碎裂过程的数值模拟

韧性金属圆球壳的动态膨胀和碎裂过程的数值模拟作者:段忠,陈磊来源:《科技创新导报》 2011年第12期段忠陈磊(宁波大学机械工程与力学学院工程力学系浙江宁波 315211)摘要:本文通过ABAQUS软件建立韧性金属膨胀球壳的有限元模型,采用包含内聚力失稳断裂准则和温度软化效应的Johnson-Cook型损伤断裂模型描述材料的断裂和分离过程,采用断裂能量判据来判断单元是否失效,采用结合单元消去技术的ABAQUS/Explicit计算程序进行数值分析,通过分析膨胀球壳向外沿径向膨胀、碎裂的全过程和膨胀球壳的碎片断裂特征,发现韧性金属材料在二维均匀冲击拉伸载荷作用下,表现出多重损伤和碎裂的现象,损伤发展、演化和断裂(碎裂)的发生都有着明显的先后顺序。
关键词:韧性金属膨胀球壳数值模拟二维碎裂中图分类号:TP2 文献标识码:A 文章编号:1674-098X(2011)04(c)-0084-021 引言固体材料的动态碎裂问题是固体力学领域的一个重要的研究课题。
金属材料在高速变形过程中发生断裂和碎裂是爆炸力学中常见的现象。
Mott[1]在二战时期开创了材料的碎片化现象研究,Grady和Kipp[2,3]对Mott模型进行关键性修正,Glenn和Chudnovky[4]、Miller[5]、Wang 和Ramesh[6]等研究了材料一维冲击拉伸断裂问题。
由于应力状态的复杂性,针对材料的多维碎裂物理机制的分析较为困难。
国防应用之外,在日常生活中也存在着许多材料多维碎裂的例子,如平板玻璃的碎裂、河床干裂等。
目前研究材料二维及三维的实验手段相当有限,膨胀圆球壳是实现材料双轴均匀拉伸破坏的有效模型。
如果圆球壳壁厚远小于球体半径,球壳周向处于近似的平面应力状态。
当圆球壳沿径向均匀向外膨胀时,膨胀球壳受面内均匀的双轴拉伸载荷作用。
Becker[7]利用有限元方法对球壳均匀膨胀碎裂现象进行了初步探索性的研究。
本文采用ABAQUS[8]有限元软件建立韧性金属膨胀圆球壳的模型,采用无氧铜材料的Johnson-Cook[9]模型,采用包含内聚力失稳断裂准则和温度软化效应的Johnson-Cook型损伤断裂模型描述材料的断裂和分离过程,采用断裂能量判据来判断单元是否失效,采用结合单元消去技术的ABAQUS/Explicit计算程序进行数值分析。
钢箱内部爆炸破坏的SPH 数值模拟

桥梁是公路、铁路等交通网的咽喉。为了减小恒载,对斜拉桥、悬索桥等大跨度桥广泛采用钢箱梁 作其结构支撑的主梁。随着恐怖袭击的不断演化,战略性桥梁成为恐怖主义爆炸破坏的重点目标,因 此,有必要对钢箱结构内部爆炸过程中钢箱的变形规律进行研究[1-4]。Tang 等[5] 运用 LS-DYNA 软件研 究了汽车炸弹爆炸冲击作用下桥塔、桥墩、桥面结构的局部破坏模式;姚术健等[2,6] 通过实验,研究了钢 箱内部爆炸过程中内壁失效变形的模式, 并利用 ANSYS 软件分析了箱体的损伤特性。钢箱内部爆炸相 比外部爆炸而言,爆炸冲击波在约束空间内多次反射、叠加、汇聚,该物理过程相当复杂,目前的研究大 多局限于爆炸过程中钢箱变形的宏观现象。光滑粒子流体动力学 (smoothed particle hydrodynamics, SPH) 作为一种无网格的粒子方法,因其在计算过程中可避免网格重分和算法耦合,被广泛用于研究爆炸 冲击问题。自 Monaghan 等[7] 修正的人工黏度解决了 SPH 计算结果的非物理震荡问题后,强洪夫等[8]、 Qiang 等[9] 和 Liu 等[10] 利用该方法对爆炸冲击波冲击钢板的过程成功地进行了数值模拟。本文中,拟利 用自编的 SPH 程序对钢箱内部爆炸过程进行数值模拟,并与实验对比,验证 SPH 算法在模拟钢箱内部 爆炸问题上的有效性;分析爆炸过程中钢箱表面压力、应力波的传播规律以及特定点处速度变化趋势; 得到钢箱表面的 von Mises 应力分布;进一步对钢箱内不同位置爆炸的过程进行数值模拟,得到不同工 况下钢箱的失效变形模式,以期通过研究为钢箱类结构的爆炸毁伤提供一种评估方法。
薄壁球壳压缩非对称屈曲特性的实验及有限元分析

薄壁球壳压缩非对称屈曲特性的实验及有限元分析周刚毅;董新龙;郝伟伟【摘要】The deformation behaviors of thin-walled spherical shells subject to quasi-state and dynamic com-pression are studied experimentally. The process of deformation, the non-axisymmetric buckling characteristic and its influence factors are analyzed in detail using ABAQUS finite element code. The results show that the deformation modes are dependent on the impact velocity. It is found that, if impact loading speed increases, the collapse modes shift from pentagons to hexagons. The dynamic loading-deformation curve on which the impact velocity is not very high is in good consistence with its quasi-static one. Meanwhile, the load-deformation curves of FEM simulation conform well to the experimental results at the stage of axi-symmetric inward dimple, but it is not so at the non-axisymmetric buckling stage. Furthermore, the process of deformation of spherical shells and its effect factors are discussed, suggesting that the contact constraints of surface between spherical shell and rigid plate play a significant role in the process of non-asymmetric deformation.%采用实验方法研究了球壳在刚性板准静态和冲击压缩下变形特性及非对称屈曲模态,结合ABAQUS有限元分析了球壳冲击压缩下的屈曲变形过程、非对称屈曲特性,探讨了其影响因素。
内部爆载荷下薄壁柱壳膨胀断裂的研究

为 断 开 主 同路 的脱 扣 装 置 。 是 , 于 断 路 器 但 对 来 说 , 于它 的 脱 扣 器 采 用 的 是 机 械 开 关 , 由 分
断时 间在 几十毫 秒甚 至于 数百 毫秒 以上 , 不
分 布 人 手 , 出 了 当 内 壁 压 力 降 到 材 料 屈 服 导 强 度 时 , 体 即完 成 贯 穿 断 裂 的 简 单 判 据 。 壳 C. Ho g t口 等 认 为 , 强 载 荷 下 壳 内 形 R. g e t 在
材 料 参 数 。 此 , 一 步 寻 求 材 料 动 态 破 坏 过 因 进 程 的 简 化 模 型 是 必 要 的 1 物 理 模 型 及 其 简 化
大 载 流 体 超 高 速 关 断 装 置 是 关 于 电 力 系
统 关 断 技术 的 新 概 念 研 究 。 随 着 社 会 经 济 的
时 间 为 微 秒 级 , 很 好 地 满 足 保 护 设 备 的 要 能 求。
ma 等 从 材 料 破 坏 的 微 观 结 构 的 发 展 过 程 n
大 载 流 体 高 速 关 断 装 置 是 由 一 个 中 空 的 内 置炸药 的铜棒 ( 炸桥 ) 主回路 导体 , 爆 作 触 发 装 置 给 安 装 在 爆 炸 桥 中 心 的 电雷 管 发 出 触 发 信 号 . 雷 管 引 爆 炸 药 , 断 爆 炸 桥 , 而 电 炸 从 达到 断 开 主 回 路 的 目的 。 爆 炸 桥 的 拄 形 壳 体 内装 有 炸 药 , 炸 药 当 起 爆 后 , 轰 产 物 和 壳 体 发 生 作 用 , 爆 轰 产 爆 在 物 作 用 下 , 体 不 断 变 形 、 胀 直 至 断 裂 。 为 壳 膨 了研 究 方 便 , 用 下 列 简 化 条 件 和 处 理 办 法 : 采
内压薄壁圆筒的强度设计

15
设计压力p:设定的容器顶部的最高压力---设计载荷。
取值方法:
(1)容器上装有安全阀
取不低于安全阀开启压力 : p ≤(1.05~1.1)pw
系数取决于弹簧起跳压力 。
16
(2)容器内有爆炸性介质,安装有防爆膜时: 防 爆 膜 装 置 示 意 图
取 设计压力为爆破片设计爆破压力加制造范围上限。 P44 表3-1。
0 (1)极限应力
极限应力的选取与结构的使 用条件和失效准则有关 极限应力可以是 t t t b、 s ( 0.2 )、 st ( 0 ) 、 、 .2 D n
24
常温容器
b s 0.2 =min{ , }
nb ns
t t b st 0 .2
2
一、强度设计的基本知识
(一)、关于弹性失效的设计准则
1、弹性失效理论
容器上一处的最大应力达到材料在设计温度下的屈服点,容器即告失效 (失去正常的工作能力),也就是说,容器的每一部分必须处于弹性变形范围 内。
保证器壁内的相当应力必须小于材料由单向拉伸时测得的屈服点。
当 s
3
2、强度安全条件
pD 1 2
适用于 脆性材料
强度条件
I 当
pD [ ] 2
第三强度理论
(最大剪应力理论)Fra bibliotekIII 当
III 当
pD 1 3 2
适用于 塑性材料
强度条件
pD [ ] 2
6
第四强度理论
(能量理论)
IV 当
1 2 2 2 1 [( 1 2 ) ( 2 3 ) ( 3 1 ) ] 2 2 pD 2 2 1 2 1 2 2.3
爆炸碎片撞击圆柱薄壁储罐的有限元模拟分析

的影响 , 采用 L S—D N Y A软件 , 对爆炸碎 片撞 击下的圆柱薄壁储罐 动力学响应进行 了数值模 拟研 究. 结果表 明,随 着碎 片撞 击速度 、 横截 面积 的增加及撞 击角度的减 少, 罐 变得越 来越不稳 定. 储 随着碎 片撞击速 度 、 截 面积 的增 横
加 及 碎 片 密 度 的 减 小 , 罐 结 构 强度 逐 渐 失 效 、 片撞 击速 度 相 同 时 , 方 体 碎 片 的撞 击 对 储 罐 稳 定 性 和 结 构 强 度 储 碎 立
的影响 大于圆柱形碎 片. 片撞 击 角度为 1 。 合 成加 速度 最大, 15m s, 碎 0 时, 为 1 / 此时储罐 强度损 失源自 大, 导致 储罐 维普资讯
第3 0卷第 3期
20 0 8年 5月
南
京
工
业
大
学
学
报
( 然 科 学 版) 自
Vo . 0 No 3 13 .
M a 00 v2 8
J U N LO A JN N V R IY O E H O O Y ( a r cec dt n O R A FN N I G U IE ST FT C N L G N t a SineE io ) ul i
Fi ie e e e i u a i n a l ss o x l so e i m pa tng n t l m ntsm l to na y i n e p o i n d br s i ci
t i wa lc lnd i a a ks h n- l y i r c lt n
薄球壳模型

31 32 33 E3
0
薄球壳的压电方程为
S1 S11T1 S12T 2 d31E3 S 2 S 21T1 S 22T 2 d32 E3
D3 d31T1 d32T 2 33E3
E3 Er Eme jwt
F Fme jwt
假设
Ur U me jwt
将上述的已知条件代入方程(7)中,经行求解得到:
Ur
{(
Fm
4r 2 Lt
d 31
rSc
Em) /(w2
1
r 2 Sc
)}
*
e
jwt
(8)
假如令
上述的(8)式可改写成
Ur
{(
Fm
4r 2 Lt
d 31
rSc
Em) /(w2
wr2 )}* e jwt
(9)
根据麦克斯韦方程可求的球面上的电荷Q
D3
d 31(S1 d 31E3) Sc
33E3
d 31Ur d 312 E3 33E3
rSc
Sc
d 31Ur d 312Ur 33Ur
rSc
ScLt
0
0
E 3
S 21S 22...S 26 T S 31S 32...S 36 0 S 41S 42...S 46 0 S 51S 52...S 56 0
2
1
S 6 d 61d 62d 63
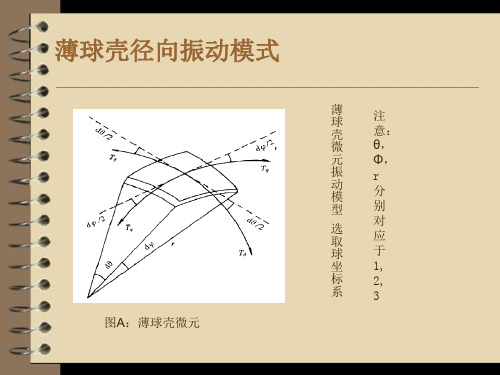
压电方程(1)ຫໍສະໝຸດ 由于球对称,θ和Φ方向上各向同性,则有
低速大质量球头弹冲击下薄板穿甲破坏机理数值分析

关键词 :爆炸力学 ; 薄板 ; 有限元分析 ; 甲 ; 穿 破坏机理 ; 低速 ; 冲击
中图分类号 :0 4 . 34 7 文献标识码 :A
薄板 穿 甲 问题 在 实 际 中广 泛存 在 , 在 实 验 和 理 并
元 分 析 了薄 板在 低速 大质 量球 头 弹 体 冲击 下 的 穿 甲破
矩 的作用 。 随后 人 们认 识 到 , 要 理 论 和 实 际 比较 一 若 致, 必须 同时考 虑弯矩 和膜力 的作用 , 考 虑 了弹 并 靶撞 击 区的局部 变形 能 J 。
但实 际冲击 过 程 中 , 板 的 变形 及 破 坏 模 式 往 往 靶
I l 一 ・ .
图 1 低速大质量球 头弹对
维普资讯
第1 期
侯海量 等 :低 速大质量 球头弹冲击下薄板穿 甲破坏机理数值分析
表 2 实 验 主 要 参 数 及 结 果
4 1
固支薄板的冲击示意 图
表 1 靶 板 材 料 力 学 性 能
图 2 弹体结 构
示 意 图
不是单一的…j而是多种模式的耦合 , , 其变形破坏机理 也是 复杂 的 。文 献 [2 通 过对 弹 速 在 30 / 1] 2 m s左 右 的 大锥 角锥头 弹对 薄 板 的 穿 甲实验 研 究 , 出 靶 板 的 主 指 要破坏形式 的为隆起一剪切破坏和碟形弯曲一花瓣开 裂 破坏 , 并应 用 能 量 分 析 原 理 建立 了 它 们 的 变形 功 计 算公式 , 得到了与实验吻合较好的结果 。 2 有 限 元分 析模 型 为探讨 薄板 穿 甲破 坏 机 理 , 文 采 用 非 线 性 有 限 本 采用动态非线 性有限元分析程序 M C D T A S/ Y R N 建 立三 维有 限元模 型 , 薄板 的穿 甲过程 进 行模 拟 , 对 弹 收稿 日期 :2 0 0 7一o 0 修改稿 收到 日期 :0 7— 5—2 4— 2 20 0 2 体 和靶 板均 采用六 面 体单元 进 行模 拟 。为考察 靶板 上 第一作者 侯海量 男 , 士生 ,97年生 博 17
金属薄壁球壳整体无模爆炸成形技术

金属薄壁球壳整体无模爆炸成形技术
佟铮;何风曼;马万珍
【期刊名称】《新技术新工艺》
【年(卷),期】2000(000)009
【摘要】薄板球面体成形一直是板料成形工艺中的难点,本文对薄壁球壳的制造提出了一种整体高能成形的新技术.通过应用这项无模爆炸成形技术,成功地制造出薄壁球壳,并通过大量工程实践验证了整体结构设计原则和炸药量理论计量公式,揭示了这一新技术在工业球罐制造中的的广阔应用前景.
【总页数】2页(P28-29)
【作者】佟铮;何风曼;马万珍
【作者单位】内蒙古工业大学,010062;内蒙古工业大学,010062;内蒙古工业大学,010062
【正文语种】中文
【中图分类】TG3
【相关文献】
1.大型超薄壁球壳无模爆炸成形 [J], 佟铮;李振声;何风曼
2.扁球壳体的整体无模成形理论与实验 [J], 尚彦凌;张士宏;曾元松;王仲仁
3.双金属球罐整体无模爆炸成形 [J], 佟铮
4.扁球壳体的整体无模成形理论与实验 [J], 尚彦凌;张士宏;曾元松;王仲仁
5.爆炸冲击载荷下球壳无模成形过程研究 [J], 佟铮;马万珍;张芮
因版权原因,仅展示原文概要,查看原文内容请购买。
薄球壳模型
Lt
F
jwmUr
SLt jwr 2Sc
Ur
d 31S rSc
Ur
令
N Sd31 rSc
Zm
jwm
SLt jwr 2 Sc
四端口网络模型如下:
NUr F ZmUr
I NUr S ( d 312 33)Ur
I Lt 1:N Sc
ur
四端口网络等效方程(1)
Ur C0
m Cm F
壳的内外表面涂上电极,沿球壳的径向经行极化,在径向施加电
压即产生逆向压电效应,从而球壳产生振动,继而向外产生声辐
射。
由声学理论可知,在外加电场激励的条件下,球壳产生振动。
振动模式有两种:一是沿径向的对称性的径向振动(称为轮廓振
动),另一种是沿球壳的径向(厚度方向)的伸缩振动。
对于薄球壳,Lt<<r,沿径向振动伸缩振动的固有谐振频率远
球壳沿径向产生整体运动。
假设薄球壳的内表面为力学端,外表面为声学端,因此此类
模型就可以用集总参数四端机电网络描述。
将上述的讨论结果代入矩阵形式的压电方程得到(1)和(2):
S1 d11d12d13
S11S12... S16 T1
S 2 S3 S 4 S5
d d d d
21d 31d 41d 51d
rSc
Sc
d 31Ur d 312Ur 33Ur
rSc
ScLt
Lt
Q D3dS 4r 2 D3
有根据 I dQ jwQ Ur jwUr dt m 4r 2Lt
S 4r 2
解得电流和力为
I dQ ( d 31Ur d 312Ur 33 Ur )S
dt
弹上薄壁部件应变分析付森 王霞

弹上薄壁部件应变分析付森王霞摘要:为满足导弹轻量化要求,弹上部件多用薄壁件。
当导弹做大机动行为时,弹上薄壁部件外部压力急剧变化,部件内压力变化速率小于外部压力变化速率,内外压差使外壁受力变形。
为解决这一问题,本文尝试用解析法计算弹上薄壁部件内外压差,得出薄壁部件内压力变化速率的影响因素有部件内温度、小孔孔径、小孔数量、部件外压力变化规律。
建议在满足总体其他要求条件下,适当增大小孔孔径和数量。
关键字:薄壁应变解析一、背景:弹上部件为适应产品轻量化要求,常将产品外壳设计为薄壁,且结构紧凑[1]。
当导弹做快速俯冲、爬升等大机动行为时,弹上薄壁部件外部压力急剧变化,部件内压力变化速率小于外部压力变化速率,内外压差使外壳受力变形,与其他元器件产生干涉,影响产品正常工作,甚至导致导弹发射失败[2]。
为减小薄壁部件的外壳变形程度,常在外壳上开多个小孔(下文称之为平衡孔),以减小内外压差[3]。
同时为满足电磁兼容要求,孔径不能过大,开孔数量不能过多[4]。
现有应变计算方法主要有两种,一是试验法,即通过地面试验模拟飞行环境,对不同孔径和小孔数量的多个产品测试,得到形变情况;二是基于流固耦合的瞬态数值仿真。
试验法受限于试验条件(设备有无、精度高低),往往成本较高,且通常很难复现实际飞行条件而出现误差[5]。
基于流固耦合的瞬态数值仿真计算量极大,单个算例所需时间往往数天,甚至数周,且流体项对网格质量、计算格式和精度较为敏感,与实际结果相比误差较大[6]。
为解决这一问题,本文尝试用解析法计算弹上薄壁部件内外压差。
二、计算状态已知某导弹做快速俯冲,然后巡航飞行,其中弹上薄壁部件外部压力在0~1s 时,压力从0.054Mpa变化到0.189Mpa,之后压力基本保持恒定。
部件内初始压力为0.054Mpa,体积5.4e-3m3。
部件上开有n个孔径为r的小孔。
三、解析推导本问题为瞬态绝热流动,薄壁部件小孔内外的能量方程为(1)(2)因为部件为薄壁,且部件外空气速度为0,则有(3)将气体状态方程代入(3)求得空气质量流率(4)薄壁部件内空气状态方程为(5)对(5)求导,有(6)结合公式(4)和(6)有(7)又因为,联合上述公式,得四、计算结果及分析1.设有8个小孔,孔径为1mm,薄壁部件外压力呈线性变化。
内压薄壁圆筒和球壳的强度设计36页PPT

END
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
内压薄壁圆筒和球壳的强度设计
6
、
露
凝
无
游
氛
,天高风源自景澈。7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Θ 0d 0E 0 2 ) ]。 Χ
( 13)
碎片飞散的初始速度, 可以认为等于在壳体破 坏时刻的径向扩展速度:
2
( 12)
由此可得球壳均匀破碎时的碎片数的计算式:
N = [Π k(
式中, e ij = Εij - Εkk ∆ij 3, 是变形速度张量偏量; s ij = Ρij - Ρkk ∆ij 3, 是应力张量偏量, Ρ= Ρkk 3; G 为剪切模 量; Γ 为材料动态粘度; J 0 为简单拉伸时的静弹性极 限, H ( x ) 为阶梯单位函数。 根据弹塑性理论, 变形 速度可以分解为弹性和塑性, 且塑性流动是不可压 缩的。 e p p ( 5) Ε 。 ij = Ε ij + Ε ij , Ε kk = 0 而对于一维球壳, 则: ΡΗ= Ρ+ S Η, ΡΥ= ΡΗ, Ρr = Ρ+ S r = 0, 2S Η+ S r = 0,
第 5 卷
对于圆柱壳破碎时碎片的预计数 N , 可由弹性 变形能和材料飞散时的表面能平衡得到: Θ d 0h ) E 0 = Χ hN , 0 (Π
( 10)
它当作一维球壳来研究。 因此, 运动方程为: ΡΗ p ( t) Θ v= - 2 ,
h r
・
( 1)
式中, Θ为密度, v 为径向速度, r 为壳的流动半径, ΡΗ 为环向应力 ( 壳体厚度上的平均应力) , v 表示对时 间的导数 ( 以下式中相同) 。 环向变形的速率为: Ε Η = v r。
Ke y w o rds : p ellicle ba ll; exp lo sive; d isto rt ion and fragm en ta t ion; fragm en t
研究壳体在其内部炸药爆炸作用下的破裂与碎 片的飞散, 对研究炸药的性能、 炸药的爆燃物及其变 形和破坏的力学问题等可以提供重要的方法。 目前, 国内外的研究对象通常是圆柱壳[ 1 ] , 且壳体材料的 破碎和炸药抛射破碎的典型圆柱壳的相对厚度取为 半径的 1 10, 1 8 和 1 6, 但由于火箭的燃料箱和飞 行器等薄壁容器的相对壁厚仅为半径的 1 100~ 1 1 000, 且以球形容器为主, 在近地轨道上爆炸会 形成以宇宙速度飞行的大小不等的空间垃圾, 且薄 壁球壳内爆炸引起破裂与碎片的飞散对防护屏障也 构成威胁, 从而对航天器形成严重的安全隐患。 评估 防护屏的安全可靠性就需要研究薄壁球壳内爆炸引
(D 1 为极限损耗比常量, 它是从平面板冲击破裂破
坏的试验中获得的[ 8 ] ) 。
S Η = S Η +
(1)
(0)
2 ・ (1 2) G ΕΗ ∃ t3
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
(0)
ΡΗ e ΡΗ p Ε , D = 2 Ε 。 Η Η Θ Θ
・ ・
可以确定 t= ∃ t 2 时壳的速度 v (1 2) ( 步长 ∃ t 应选择 较好地作用在壳上的压力 p = p ( t) 近似表达出来) :
( 7)
v
(1 2)
= v
(- 1 2)
+
比内能为: U = E + D 。 弹性变形速度和塑性变形速度分别为:
薄壁球壳内部爆炸的变形与破坏模拟
葛 涛1 , 潘越峰2 , 罗昆升1 , 王德荣1 , 王明洋1
( 1. 解放军理工大学 工程兵工程学院, 江苏 南京 210007; 2. 第二炮兵工程设计研究所, 北京 100011)
摘 要: 根据薄壁球壳内爆炸引起的动态变形和破坏特征, 建立了其分析模型。计算表明: 壳体发生破坏, 是 由于开始时刻在壳内积聚的弹性能的耗散, 所以忽略外力功, 不考虑剥落破坏; 碎片数目与施加荷载密切相 关; 脉冲荷载较小时与初始速度接近平方关系, 而脉冲荷载较大时, 则脉冲荷载与初始速度及脉冲荷载与碎 片数目均接近线性关系。 关键词: 薄壁球壳; 爆炸; 变形与破坏; 碎片 中图分类号: TU 435 文献标识码: A
1 2 1 1 1
( 1. Engineering In stitu te of Engineering Co rp s, PLA U n iv. of Sci . & T ech. , N an jing 210007, Ch ina; 2. Engineering D esign & R esea rch In stitu te of Stra tegic M issile Co rp s, B eijing 100011, Ch ina )
第5卷 第1期 2004 年 2 月
解 放 军 理 工 大 学 学 报 ( 自 然 科 学 版) Jou rna l of PLA U n iversity of Science and T echno logy
Vol . 5 N o. 1 Feb. 2004
文章编号: 100923443 ( 2004) 0120053204
Si m u la tion to D is to rtion a nd F ra gm e n ta tion of Th in S phe rica l S he ll Und e r Inne r Exp los ive
G E T ao , PA N Y ue2f eng , L UO K un 2sheng , W A N G D e2rong , W A N G M ing 2y ang
・
式中, Χ 为耗散在形成单位自由表面上的比能, E 0 为在 t= 0 时刻累积弹性能密度, d 0 为壳体的初始直 径。 要得到球面壳的碎片数, 需再做一个补充假设: 所有碎片的尺寸相同 ( 碎片外表面特征面积为 S , 碎 片厚度为 h ) , 面积 S 与碎片周边长一半 p 的平方的 比值都相等, 即:
第 1 期
葛 涛, 等: 薄壁球壳内部爆炸的变形与破坏模拟
SΗ
(0)
5 5
G
Γ
∃ tS Η
(0)
SΗ
(0)
1 J0 3
材料 的 变 形 速 率 效 应 ( 动 态 流 动 极 限 J = J 0 +
H ( SΗ
(0)
1 J 0) , 3
( 18)
2Γ
p 3 Εp ij Ε ij 2, 在指数分布模型中 J = J 0 + 3 Α Γ Εp Η
t0
(1) 和变形 Ε Η :
( 8)
Ε Η
(1 2) (1)
= 2Τ
(0)
(1 2)
( r (0) + r (1) ) ,
(1 2)
壳体的初始破坏指标——极限损耗比为:
D = 2
Ε Η = Ε Η + Ε Η
( 9)
∃ t。
( 17)
∫
0
ΡΗ p Ε Ηd t = D 1 Θ
′ 由式 ( 3) 得到 t = ∃ t′ 的密度 Θ ′ = Θ 0 exp ( - Ε Η) 对 式 ( 6) 积分, 可得:
A bs tra c t: A cco rd ing to the cha racters of d isto rt ion and fragm en ta t ion of p ellicle ba ll under inner exp lo sive
an ana lysis m odel is estab lished. Ca lcu la t ion ind ica tes tha t becau se of the d issip a t ion of the accum u la ted e2 la st ic energy in the ba ll a t the beg inn ing, ex terna l energy and crum b ling fragm en ta t ion a re igno red, tha t the num ber of fragm en t is clo sely rela ted w ith the load, and tha t w hen the p u lse is sm a ller, it ha s a squa re rela t ion w ith in it ia l velocity, and w hen b igger, a linea r rela t ion tha t is a s w ell a s the num ber of fragm en t.
k = S p = C。
2
( 2)
因为是薄壳, 其它变形不计。 由质量守恒定律
= - 2 ΕΗ, 可得: ΘΘ )。 Θ= Θ 2Ε 0 exp ( Η
・ ・
( 11)
( 3)
在计算时, 形状系数 k 取为 0. 2 ( 为了比较, 列 出一些 k 值: 正方形 k = 0. 25, 正三角形 k = 0. 19, 圆 形 k = 0. 32) 。 这样, 可以得到计算球壳的平均碎片数的公式:
收稿日期: 2003206218. 作者简介: 葛 涛 (1978) , 男, 硕士生.
起的动态变形和破坏问题。
1 物理力学模型
在求解该问题时, 对相对几何形状、 构件材料性 能和荷载特点等作了如下假设 [ 2~ 4 ]: ①薄壁球 壳 h rν 1 ( h 为壁厚, r 为壳的半径) ; ②爆炸荷载简化 为与时间有关的压力 p = p ( t ) , 且在内壳面上均匀 分布, 荷载作用的特征时间 Σµ h c0 ( c0 为壳体材料 中的声速) ; ③壳体材料用弹粘塑性模型模拟, 变形 过程为绝热过程; ④把极限损耗比作初始破坏的指 标; ⑤认为壳体发生破坏, 是由于开始破坏时刻 ( 设 为 t = 0 ) 在壳内积聚的弹性能的耗散, 而破坏时外 力功忽略, 不考虑剥落破坏[ 5, 6 ]。
