2018-2019学年第1学期工程数学I第5次作业
南京工业大学工程数学第5章作业

学号:642081701046 姓名:苗洁班级:化工2班第五章作业1.解:第一类边界条件的三次样条插值计算如下:>>x=[0.520,3.1,8.0,17.95,28.65,39.62,50.65,78,104.6,156.6,208.6,260.7,312.5,364.4,416.3,46 8,494,507,520];>>y=[5.288,9.4,13.84,20.20,24.90,28.44,31.10,35,36.9,36.6,34.6,31.0,26.34,20.9,14.8,7.8,3.7,1.5,0.2];>> pp2=csape(x,y,'complete',[1.86548,-0.046115])pp2 =form: 'pp'breaks: [0.5200 3.1000 8 17.9500 28.6500 39.6200 50.6500 78 104.6000 156.6000 208.6000 260.7000 312.5000 364.4000 416.3000 468 494 507 520]coefs: [18x4 double]pieces: 18order: 4dim: 1pp2.coefsans =-0.0029 -0.0979 1.8655 5.28800.0080 -0.1201 1.3031 9.4000-0.0003 -0.0029 0.7007 13.84000.0003 -0.0128 0.5447 20.20000.0000 -0.0039 0.3655 24.90000.0000 -0.0038 0.2803 28.44000.0000 -0.0030 0.2052 31.1000-0.0000 -0.0009 0.0990 35.00000.0000 -0.0013 0.0403 36.9000-0.0000 -0.0000 -0.0301 36.60000.0000 -0.0004 -0.0527 34.60000.0000 -0.0002 -0.0816 31.00000.0000 -0.0001 -0.0979 26.3400-0.0000 -0.0001 -0.1109 20.9000-0.0000 -0.0002 -0.1254 14.8000-0.0000 -0.0002 -0.1462 7.80000.0001 -0.0009 -0.1748 3.70000.0000 0.0030 -0.1467 1.5000>> fnplt(pp2)再求x=2,30,130,350,515各点上的函数值,则输入 >> xi=[2,30,130,350,515]; >> yi=ppval(pp2,xi) yi =7.8252 25.3862 37.2138 22.4751 0.5427 三次样条插值函数为)(x s =i i i h x x M 6)(31-++ii i h x x M 6)(31-++[)(i x f -62i i h M ]i i h x x -+1+[)(1+i x f -621i i h M +]iih x x - 由以上结果可得:当∈x [0.520,3.1]时:4333() 1.873410( 3.1) 6.32410(0.520) 4.15311.486s x x x x --=⨯--⨯-+-当∈x [28.65,39.62]时:53() 5.92510(28.65)0.329915.448s x x x -=-⨯-+-当∈x [104.6,156.6]时:633() 4.16710(104.6) 5.5131036.33s x x x --=-⨯-+⨯+当∈x [312.5,364.4]时:73() 3.21110(312.5)0.103958.808s x x x -=-⨯--+当∈x [507,520]时:53() 3.84610(507)0.106559.564s x x x -=⨯--+2.解:(1)复化Simpson 公式的余项估计,nS R =)(2180)()4(2ηf h a b ⎪⎭⎫ ⎝⎛-⇒nS R =)(2180)()4(2ηf h a b ⎪⎭⎫ ⎝⎛--≤4201114max 18021x n x≤≤⎛⎫ ⎪+⎝⎭≤9110-⨯ ⇒9441041802n ⨯≥⨯⇒≥n 35 采用复化的Simpson 要求具有9位有效数字则至少要取35个点,则()135b a h n -== 利用MATLAB 程序计算先求()f x 的四阶导数:>> syms xf=4/(1+x^2) %定义函数f (x )n=input('输入所求导数阶数:') f2=diff(f,x,n) f =4/(x^2 + 1) 输入所求导数阶数:4 n =4 f2 =96/(x^2+1)^3-(1152*x^2)/(x^2+1)^4+(1536*x^4)/(x^2+1)^5复化辛普森程序:>> syms x f=inline('(4/(1+x^2))','x');f2=inline('(96/(x^2 + 1)^3 - (1152*x^2)/(x^2 + 1)^4 + (1536*x^4)/(x^2 + 1)^5)','x'); f3='-(96/(x^2 + 1)^3 - (1152*x^2)/(x^2 + 1)^4 + (1536*x^4)/(x^2 + 1)^5)' ; e=1*10^(-9); a=0 ; b=1;x1=fminbnd(f3,0,1); for n=2:100000Rn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) ; if abs(Rn)<e break endendh=(b-a)/n ;Sn1=0 ;Sn2=0 ;for k=0:n-1xk=a+k*h ;xk1=xk+h/2 ;Sn1=Sn1+f(xk1) ;Sn2=Sn2+f(xk) ;endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b));z=exp(2);Rn=Sn-z ;format long;fprintf('Sn=')disp(Sn)fprintf('n=')disp(n)fprintf('Rn=')disp(Rn)计算结果:Sn= 3.141592653589789n= 76Rn= -4.247463445340861结果分析:与上述的余项估算结果对比可知,在其估算的范围之内,但是Rn的值不符合题目要求,不知错在哪里还请老师指正。
国开2020工程数学最新5次形考完整版

国开2020工程数学最新5次形考完整版工程数学作业(一)答案第2章矩阵一)单项选择题(每小题2分,共20分)1.设b1a2 - b2a1 = 2,则2a1 - 3b1.2a2 - 3b2.2a3 - 3b3 = (D).2.若a2 = 1,则a = (A).3.乘积矩阵1 -1.2 4]1 3.5 21]中元素c23 = (C).4.设A,B均为n阶可逆矩阵,则下列运算关系正确的是(B).5.设A,B均为n阶方阵,k。
0且k ≠ 1,则下列等式正确的是(D).6.下列结论正确的是(A).7.矩阵1 3.2 5]的伴随矩阵为(C).8.方阵A可逆的充分必要条件是(B).9.设A,B,C均为n阶可逆矩阵,则(ACB')^-1 = (D).10.设A,B,C均为n阶可逆矩阵,则下列等式成立的是(A).二)填空题(每小题2分,共20分)1.1/(1-4) = 7.2.若1 - x + 11x - x^2是关于x的一个一次多项式,则该多项式一次项的系数是2.3.乘积矩阵1 -1.2 4]1 3.5 21]中元素c23 = 10.4.设A,B均为n阶可逆矩阵,则A(B^-1 + A^-1) = A^-1 + B^-1.5.设A,B均为n阶方阵,k。
0且k ≠ 1,则下列等式正确的是(-k)A = (-k)^n A.6.若A是正交矩阵,则A^-1也是正交矩阵.7.矩阵1 3.2 5]的伴随矩阵为5 -3.-2 1].8.方阵A可逆的充分必要条件是A ≠ 0.9.设A,B,C均为n阶可逆矩阵,则(ACB')^-1 = (B^-1)'C^-1A^-1.10.设A,B,C均为n阶可逆矩阵,则下列等式成立的是(A).(A + B)C = A + 2AB + B。
(A + B)B = BA + B。
(2ABC)^-1 = 2C^-1B^-1A^-1,(2ABC)' = 2C'B'A'.1.若矩阵A为3×4,矩阵B为2×5,且切乘积AC' B' 有意义,则矩阵C为5×4.2.给出二阶矩阵A = [1 2.-1 3],B = [-13.-3 1],求(A + B')'。
工程数学作业(第一次)(满分100分).#精选

工程数学作业(第一次)(满分100分)第2章 矩阵(一)单项选择题(每小题2分,共20分)⒈设a a a b b b c c c 1231231232=,则a a a a b a b a b c c c 123112233123232323---=( ).A. 4B. -4C. 6D. -6⒉若000100002001001a a=,则a =( ).A.12 B. -1 C. -12D. 1 ⒊乘积矩阵1124103521-⎡⎣⎢⎤⎦⎥-⎡⎣⎢⎤⎦⎥中元素c 23=( ). A. 1 B. 7 C. 10 D. 8⒋设A B ,均为n 阶可逆矩阵,则下列运算关系正确的是( ). A. A BAB +=+---111 B. ()AB BA --=11C. ()A B A B +=+---111 D. ()AB A B ---=111⒌设A B ,均为n 阶方阵,k >0且k ≠1,则下列等式正确的是( ). A. A B A B +=+ B. AB n A B =C. kA k A =D. -=-kA k A n()⒍下列结论正确的是( ).A. 若A 是正交矩阵,则A -1也是正交矩阵B. 若A B ,均为n 阶对称矩阵,则AB 也是对称矩阵C. 若A B ,均为n 阶非零矩阵,则AB 也是非零矩阵D. 若A B ,均为n 阶非零矩阵,则AB ≠0⒎矩阵1325⎡⎣⎢⎤⎦⎥的伴随矩阵为( ). A. 1325--⎡⎣⎢⎤⎦⎥ B. --⎡⎣⎢⎤⎦⎥1325 C. 5321--⎡⎣⎢⎤⎦⎥ D. --⎡⎣⎢⎤⎦⎥5321 ⒏方阵A 可逆的充分必要条件是( ).A.A ≠0B.A ≠0C. A *≠0D. A *>0 ⒐设A B C ,,均为n 阶可逆矩阵,则()ACB '=-1( ).A. ()'---B A C 111 B. '--B C A 11 C. A C B ---'111() D. ()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵,则下列等式成立的是( ). A. ()A B A AB B +=++2222 B. ()A B B BA B +=+2C. ()221111ABC C B A ----= D. ()22ABC C B A '='''(二)填空题(每小题2分,共20分)⒈210140001---= . ⒉---11111111x 是关于x 的一个一次多项式,则该多项式一次项的系数是 . ⒊若A 为34⨯矩阵,B 为25⨯矩阵,切乘积AC B ''有意义,则C 为 矩阵.⒋二阶矩阵A =⎡⎣⎢⎤⎦⎥=11015. ⒌设A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=--⎡⎣⎢⎤⎦⎥124034120314,,则()A B +''= . ⒍设A B ,均为3阶矩阵,且A B ==-3,则-=2AB .⒎设A B ,均为3阶矩阵,且A B =-=-13,,则-'=-312()A B .⒏若A a =⎡⎣⎢⎤⎦⎥101为正交矩阵,则a = . ⒐矩阵212402033--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥的秩为 . ⒑设A A 12,是两个可逆矩阵,则A O OA 121⎡⎣⎢⎤⎦⎥=- .(三)解答题(每小题8分,共48分)⒈设A B C =-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥123511435431,,,求⑴A B +;⑵A C +;⑶23A C +;⑷A B +5;⑸AB ;⑹()AB C '.⒉设A B C =--⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥121012103211114321002,,,求AC BC +.⒊已知A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥310121342102111211,,求满足方程32A X B -=中的X . ⒋写出4阶行列式1020143602533110--中元素a a 4142,的代数余子式,并求其值.⒌用初等行变换求下列矩阵的逆矩阵:⑴ 122212221--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥; ⑵ 1234231211111026---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥; ⑶1000110011101111⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥. ⒍求矩阵1011011110110010121012113201⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥的秩. (四)证明题(每小题4分,共12分)⒎对任意方阵A ,试证A A +'是对称矩阵.⒏若A 是n 阶方阵,且AA I '=,试证A =1或-1. ⒐若A 是正交矩阵,试证'A 也是正交矩阵.工程数学作业(第二次)(满分100分)第3章 线性方程组(一)单项选择题(每小题2分,共16分)⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为( ).A. [,,]102-'B. [,,]--'722C. [,,]--'1122D. [,,]---'1122⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪( ). A. 有无穷多解 B. 有唯一解 C. 无解 D. 只有零解⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为( ). A. 3 B. 2 C. 4 D. 5⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,则( )是极大无关组.A. αα12,B. ααα123,,C. ααα124,,D. α1⒌A 与A 分别代表一个线性方程组的系数矩阵和增广矩阵,若这个方程组无解,则( ). A. 秩()A =秩()A B. 秩()A <秩()A C. 秩()A >秩()A D. 秩()A =秩()A -1⒍若某个线性方程组相应的齐次线性方程组只有零解,则该线性方程组( ). A. 可能无解 B. 有唯一解 C. 有无穷多解 D. 无解 ⒎以下结论正确的是( ).A. 方程个数小于未知量个数的线性方程组一定有解B. 方程个数等于未知量个数的线性方程组一定有唯一解C. 方程个数大于未知量个数的线性方程组一定有无穷多解D. 齐次线性方程组一定有解⒏若向量组ααα12,,, s 线性相关,则向量组内( )可被该向量组内其余向量线性表出.A. 至少有一个向量B. 没有一个向量C. 至多有一个向量D. 任何一个向量(二)填空题(每小题2分,共16分)⒈当λ= 时,齐次线性方程组x x x x 121200+=+=⎧⎨⎩λ有非零解.⒉向量组[][]αα12000111==,,,,,线性 .⒊向量组[][][][]123120100000,,,,,,,,,,,的秩是 .⒋设齐次线性方程组ααα1122330x x x ++=的系数行列式ααα1230=,则这个方程组有 解,且系数列向量ααα123,,是线性 的.⒌向量组[][][]ααα123100100===,,,,,的极大线性无关组是 . ⒍向量组ααα12,,, s 的秩与矩阵[]ααα12,,, s 的秩 .⒎设线性方程组AX =0中有5个未知量,且秩()A =3,则其基础解系中线性无关的解向量有 个.⒏设线性方程组AX b =有解,X 0是它的一个特解,且AX =0的基础解系为X X 12,,则AX b =的通解为 .(三)解答题(第1小题9分,其余每小题11分) 1.设有线性方程组λλλλλ11111112⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥x y z λ为何值时,方程组有唯一解?或有无穷多解?2.判断向量β能否由向量组ααα123,,线性表出,若能,写出一种表出方式.其中βααα=---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥83710271335025631123,,, 3.计算下列向量组的秩,并且(1)判断该向量组是否线性相关;(2)求出该向量组的一个极大无关组。
工程数学作业(第一次)(满分100分).

工程数学作业(第一次)(满分100分)第2章 矩阵(一)单项选择题(每小题2分,共20分)⒈设a a a b b b c c c 1231231232=,则a a a a b a b a b c c c 123112233123232323---=( ).A. 4B. -4C. 6D. -6⒉若000100002001001a a=,则a =( ). A.12 B. -1 C. -12D. 1 ⒊乘积矩阵1124103521-⎡⎣⎢⎤⎦⎥-⎡⎣⎢⎤⎦⎥中元素c 23=( ). A. 1 B. 7 C. 10 D. 8⒋设A B ,均为n 阶可逆矩阵,则下列运算关系正确的是( ). A. A BAB+=+---111B. ()AB BA--=11C. ()A B A B +=+---111D. ()AB A B ---=111⒌设A B ,均为n 阶方阵,k >0且k ≠1,则下列等式正确的是( ). A. A B A B +=+ B. AB n A B = C. kA k A = D. -=-kA k A n () ⒍下列结论正确的是( ).A. 若A 是正交矩阵,则A -1也是正交矩阵B. 若A B ,均为n 阶对称矩阵,则AB 也是对称矩阵C. 若A B ,均为n 阶非零矩阵,则AB 也是非零矩阵D. 若A B ,均为n 阶非零矩阵,则AB ≠0⒎矩阵1325⎡⎣⎢⎤⎦⎥的伴随矩阵为( ). A. 1325--⎡⎣⎢⎤⎦⎥ B. --⎡⎣⎢⎤⎦⎥1325 C. 5321--⎡⎣⎢⎤⎦⎥ D. --⎡⎣⎢⎤⎦⎥5321 ⒏方阵A 可逆的充分必要条件是( ).A.A ≠0B.A ≠0C. A *≠0D. A *>0⒐设A B C ,,均为n 阶可逆矩阵,则()ACB '=-1( ).A. ()'---B A C 111 B. '--B C A 11 C. A C B ---'111() D. ()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵,则下列等式成立的是( ). A. ()A B A AB B +=++2222 B. ()A B B BA B +=+2 C. ()221111ABC C B A ----= D. ()22ABC C B A '=''' (二)填空题(每小题2分,共20分)⒈210140001---= .⒉---11111111x 是关于x 的一个一次多项式,则该多项式一次项的系数是 . ⒊若A 为34⨯矩阵,B 为25⨯矩阵,切乘积AC B ''有意义,则C 为 矩阵.⒋二阶矩阵A =⎡⎣⎢⎤⎦⎥=11015.⒌设A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=--⎡⎣⎢⎤⎦⎥124034120314,,则()A B +''= . ⒍设A B ,均为3阶矩阵,且A B ==-3,则-=2AB .⒎设A B ,均为3阶矩阵,且A B =-=-13,,则-'=-312()A B .⒏若A a =⎡⎣⎢⎤⎦⎥101为正交矩阵,则a = . ⒐矩阵212402033--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥的秩为 . ⒑设A A 12,是两个可逆矩阵,则A O OA 121⎡⎣⎢⎤⎦⎥=- .(三)解答题(每小题8分,共48分)⒈设A B C =-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥123511435431,,,求⑴A B +;⑵A C +;⑶23A C +;⑷A B +5;⑸AB ;⑹()AB C '.⒉设A B C =--⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥121012103211114321002,,,求AC BC +. ⒊已知A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥310121342102111211,,求满足方程32A X B -=中的X . ⒋写出4阶行列式1020143602533110--中元素a a 4142,的代数余子式,并求其值.⒌用初等行变换求下列矩阵的逆矩阵:⑴ 122212221--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥; ⑵ 1234231211111026---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥; ⑶1000110011101111⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥. ⒍求矩阵1011011110110010121012113201⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥的秩. (四)证明题(每小题4分,共12分)⒎对任意方阵A ,试证A A +'是对称矩阵.⒏若A 是n 阶方阵,且AA I '=,试证A =1或-1. ⒐若A 是正交矩阵,试证'A 也是正交矩阵.工程数学作业(第二次)(满分100分)第3章 线性方程组(一)单项选择题(每小题2分,共16分)⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪的解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为( ).A. [,,]102-'B. [,,]--'722C. [,,]--'1122D. [,,]---'1122⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪( ).A. 有无穷多解B. 有唯一解C. 无解D. 只有零解⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,的秩为( ). A. 3 B. 2 C. 4 D. 5⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,则( )是极大无关组.A. αα12,B. ααα123,,C. ααα124,,D. α1⒌A 与A 分别代表一个线性方程组的系数矩阵和增广矩阵,若这个方程组无解,则( ). A. 秩()A =秩()A B. 秩()A <秩()A C. 秩()A >秩()A D. 秩()A =秩()A -1⒍若某个线性方程组相应的齐次线性方程组只有零解,则该线性方程组( ). A. 可能无解 B. 有唯一解 C. 有无穷多解 D. 无解 ⒎以下结论正确的是( ).A. 方程个数小于未知量个数的线性方程组一定有解B. 方程个数等于未知量个数的线性方程组一定有唯一解C. 方程个数大于未知量个数的线性方程组一定有无穷多解D. 齐次线性方程组一定有解⒏若向量组ααα12,,, s 线性相关,则向量组内( )可被该向量组内其余向量线性表出.A. 至少有一个向量B. 没有一个向量C. 至多有一个向量D. 任何一个向量(二)填空题(每小题2分,共16分) ⒈当λ= 时,齐次线性方程组x x x x 121200+=+=⎧⎨⎩λ有非零解.⒉向量组[][]αα12000111==,,,,,线性 .⒊向量组[][][][]123120100000,,,,,,,,,,,的秩是 .⒋设齐次线性方程组ααα1122330x x x ++=的系数行列式ααα1230=,则这个方程组有 解,且系数列向量ααα123,,是线性 的.⒌向量组[][][]ααα123100100===,,,,,的极大线性无关组是 . ⒍向量组ααα12,,, s 的秩与矩阵[]ααα12,,, s 的秩 .⒎设线性方程组AX =0中有5个未知量,且秩()A =3,则其基础解系中线性无关的解向量有 个.⒏设线性方程组AX b =有解,X 0是它的一个特解,且AX =0的基础解系为X X 12,,则AX b =的通解为 .(三)解答题(第1小题9分,其余每小题11分) 1.设有线性方程组λλλλλ11111112⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥x y z λ为何值时,方程组有唯一解?或有无穷多解?2.判断向量β能否由向量组ααα123,,线性表出,若能,写出一种表出方式.其中βααα=---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥83710271335025631123,,, 3.计算下列向量组的秩,并且(1)判断该向量组是否线性相关;(2)求出该向量组的一个极大无关组。
2018-2019工程数学试题与答案

( ) ( ) R (r ) = CJ0 λr + DY0 λr . D = 0
( ) 固有值λm = µm(0) 2 , µm(0)为J0 ( x)正零点
( ) 固有函数Rm (r ) = J0 µm(0)r
( ) ( ) Tm
t
= C e−
µm(0)a
2
t
m
∑ ( ) ( ) ( ) u
r,t
=
f ( z=) ( z − z0 )m ϕ ( z),
f ′( z) = m ( z − z0 )m−1 ϕ ( z) + ϕ′( z)( z − z0 )m ,
f f
′((zz))=
(
z
1 −
z0
)
m
+
ϕ′(z) ϕ(z)
(
z
−
z0
)
,
∴Res
f ′(z)
f
(
z)
,
z0
(sin θ
∂u ) ∂θ
=
0,0 <
r
< 1,0 ≤ θ
≤π,
u r=1 = 3cos 2θ + 1,0 ≤ θ ≤ π .
(本题的u 只与 r,θ 有关,与ϕ 无关)
解:由分离变量法,令 u(r,θ ) = R(r)Φ(θ ) ,得到
∞
∑ u(r,θ ) = Cn r n Pn (cosθ ) ,由边界条件有 n=0 ∞
l
anπ
l
l
x sin
0
nπ l
xdx −
l 0
x2 sin
nπ l
xdx
=
西南交大《工程数学Ⅰ》1-4次离线作业

工程数学Ⅰ第1次离线作业三、主观题(共15道小题)29.求5元排列52143的逆序数。
解答:在排列52143中,排在5之后,并小于5的数有4个;排在2之后,并小于2的数有1个;排在1之后,并小于1的数有0个;排在4之后,并小于4的数有1个。
所以30.计算行列式解答:容易发现D的特点是:每列(行)元素之和都等于6,那么,把二、三、四行同时加到第一行,并提出第一行的公因子6,便得到由于上式右端行列式第一行的元素都等于1,那么让二、三、四行都减去第一行得31.求行列式中元素a和b的代数余子式。
解答:行列式展开方法==32.计算行列式解答:容易发现D的特点是:每列元素之和都等于6,那么,把二、三、四行同时加到第一行,并提出第一行的公因子6,便得到由于上式右端行列式第一行的元素都等于1,那么让二、三、四列都减去第一列,第一行就出现了三个零元素,即33.设,求解答:34.,求解答:35.求矩阵X使之满足解答:36.解矩阵方程,其中解答:首先计算出,所以A是可逆矩阵。
对矩阵(A,B)作初等行变换所以所以秩(A)= 4。
37.解答:38.求向量组解答:设39.求解非齐次线性方程组解答:对增广矩阵施行初等行变换化成简单阶梯形矩阵40.设解答:若41.设,求A的特征值和特征向量。
解答:42.求一个正交矩阵P,将对称矩阵化为对角矩阵。
解答:43.已知二次型,问:满足什么条件时,二次型 f 是正定的;满足什么条件时,二次型 f 是负定的。
解答:二次型 f 的矩阵为计算 A 的各阶主子式得工程数学Ⅰ第2次离线作业三、主观题(共14道小题)30.判断(1);(2)是否是五阶行列式 D5 中的项。
解答:(1)是;(2)不是;31.设求的根。
解答:行列式特点是:每行元素之和都等于 a+b+c+x,那么,把二、三、四列同时加到第一列,并提出第一列的公因子a+b+c+x,便得到二、三、四列-a依次减去第一列的-a、-b、-c倍得32.计算四阶行列式解答:D的第一行元素的代数余子式依次为由行列式的定义计算得33.用克莱姆法则解方程组解答:34.解答:35.解答:36.用初等行变换把矩阵化为阶梯形矩阵和简单阶梯形矩阵。
工程数学线性代数第五版答案

线性代数重点第一章 行列式8. 计算下列各行列式(D k 为k 阶行列式): (1)aa D n 11⋅⋅⋅=, 其中对角线上元素都是a , 未写出的元素都是0; 解aa a a a D n 0 0010 000 00 000 0010 00⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=(按第n 行展开) )1()1(10 000 00 000 0010 000)1(-⨯-+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-=n n n aa a )1()1(2 )1(-⨯-⋅⋅⋅⋅-+n n n a a an n n nn a a a+⋅⋅⋅-⋅-=--+)2)(2(1)1()1(=a n -a n -2=a n -2(a 2-1).(2)xa aa x a a a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; 解 将第一行乘(-1)分别加到其余各行, 得ax x a ax x a a x x a aa a x D n --⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--⋅⋅⋅--⋅⋅⋅=000 0 00 0, 再将各列都加到第一列上, 得ax ax a x aaa a n x D n -⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-+=0000 0 000 00 )1(=[x +(n -1)a ](x -a )n -1. (3)111 1 )( )1()( )1(1111⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅--⋅⋅⋅-=---+n a a a n a a a n a a a D n n n nn n n ; 解 根据第6题结果, 有 nnn n n n n n n n a a a n a a a n a a aD )( )1()( )1( 11 11)1(1112)1(1-⋅⋅⋅--⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=---++ 此行列式为范德蒙德行列式. ∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏≥>≥++---=112)1()]([)1(j i n n n j i∏≥>≥++⋅⋅⋅+-++-⋅-⋅-=1121)1(2)1()()1()1(j i n n n n n j i∏≥>≥+-=11)(j i n j i .(4)n nnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112; 解nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=11112(按第1行展开) nn n n n nd d c d c b a b a a 00011111111----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=0)1(1111111112c d c d c b a b a b nn n n n nn ----+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-+. 再按最后一行展开得递推公式D 2n =a n d n D 2n -2-b n c n D 2n -2, 即D 2n =(a n d n -b n c n )D 2n -2.于是 ∏=-=ni i i i i n D c b d a D 222)(.而 111111112c b d a d c b a D -==, 所以 ∏=-=n i i i i i n c b d a D 12)(. (5) D =det(a ij ), 其中a ij =|i -j |; 解 a ij =|i -j |, 04321 4 01233 10122 21011 3210)det(⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅==n n n n n n n n a D ij n 043211 11111 11111 11111 1111 2132⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅--⋅⋅⋅-=====n n n n r r r r 15242321 0 22210 02210 00210 0001 1213-⋅⋅⋅----⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅----⋅⋅⋅---⋅⋅⋅--⋅⋅⋅-+⋅⋅⋅+=====n n n n n c c c c =(-1)n -1(n -1)2n -2.(6)nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121, 其中a 1a 2 ⋅ ⋅ ⋅ a n≠0.解nn a a a D +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅+=1 11 1 1111121 nn n n a a a a a a a a a c c c c +-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-⋅⋅⋅-=====--100001 000 100 0100 0100 0011332212132 11113121121110 00011 000 00 11000 01100 001 ------+-⋅⋅⋅-⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-⋅⋅⋅⋅⋅⋅=n n n a a a a a a a a∑=------+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=n i i n n a a a a a a a a 1111131******** 000100 10000 01000 001)11)((121∑=+=ni in a a a a .第二章 矩阵及其运算14. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|.解 因为*||11A A A =-, 所以|||521||*5)2(|111----=-A A A A A |2521|11---=A A=|-2A -1|=(-2)3|A -1|=-8|A |-1=-8⨯2=-16.15. 设⎪⎪⎭⎫⎝⎛-=321011330A , AB =A +2B , 求B .解 由AB =A +2E 可得(A -2E )B =A , 故⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-=--321011330121011332)2(11A E A B ⎪⎪⎭⎫⎝⎛-=011321330.16. 设⎪⎪⎭⎫⎝⎛=101020101A , 且AB +E =A 2+B , 求B .解 由AB +E =A 2+B 得 (A -E )B =A 2-E , 即 (A -E )B =(A -E )(A +E ).因为01001010100||≠-==-E A , 所以(A -E )可逆, 从而⎪⎪⎭⎫⎝⎛=+=201030102E A B .17. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B .解 由A *BA =2BA -8E 得 (A *-2E )BA =-8E , B =-8(A *-2E )-1A -1 =-8[A (A *-2E )]-1 =-8(AA *-2A )-1 =-8(|A |E -2A )-1 =-8(-2E -2A )-1 =4(E +A )-1=4[diag(2, -1, 2)]-1 )21 ,1 ,21(diag 4-==2diag(1, -2, 1).18. 已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A , 且ABA -1=BA -1+3E , 求B . 解 由|A *|=|A |3=8, 得|A |=2. 由ABA -1=BA -1+3E 得 AB =B +3A ,B =3(A -E )-1A =3[A (E -A -1)]-1A11*)2(6*)21(3---=-=A E A E⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫⎝⎛--=-1030060600600006603001010010000161.第三章 矩阵的初等变换与线性方程组例10 求解齐次线性方程组(略)12. 设⎪⎪⎭⎫⎝⎛----=32321321k k k A , 问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3.解 ⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ⎪⎪⎭⎫ ⎝⎛+-----)2)(1(0011011 ~k k k k k r . (1)当k =1时, R (A )=1; (2)当k =-2且k ≠1时, R (A )=2; (3)当k ≠1且k ≠-2时, R (A )=3.第四章 向量组的线性相关性例11. (略)27.(以填空形式出现) 设四元非齐次线性方程组的系数矩阵的秩为3, 已知η1, η2, η3是它的三个解向量. 且η1=(2, 3, 4, 5)T , η2+η3=(1, 2, 3, 4)T ,求该方程组的通解.解 由于方程组中未知数的个数是4, 系数矩阵的秩为3, 所以对应的齐次线性方程组的基础解系含有一个向量, 且由于η1, η2, η3均为方程组的解, 由非齐次线性方程组解的结构性质得2η1-(η2+η3)=(η1-η2)+(η1-η3)= (3, 4, 5, 6)T为其基础解系向量, 故此方程组的通解:x =k (3, 4, 5, 6)T +(2, 3, 4, 5)T , (k ∈R ).第五章待定第五章 相似矩阵及二次型1. 试用施密特法把下列向量组正交化:(1)⎪⎪⎭⎫⎝⎛=931421111) , ,(321a a a ;解 根据施密特正交化方法,⎪⎪⎭⎫⎝⎛==11111a b ,⎪⎪⎭⎫ ⎝⎛-=-=101],[],[1112122b b b a b a b ,⎪⎪⎭⎫ ⎝⎛-=--=12131],[],[],[],[222321113133b b b a b b b b a b a b .(2)⎪⎪⎪⎭⎫ ⎝⎛---=011101110111) , ,(321a a a .解 根据施密特正交化方法,⎪⎪⎪⎭⎫ ⎝⎛-==110111a b ,⎪⎪⎪⎭⎫ ⎝⎛-=-=123131],[],[1112122b b b a b a b ,⎪⎪⎪⎭⎫ ⎝⎛-=--=433151],[],[],[],[222321113133b b b a b b b b a b a b .2. 下列矩阵是不是正交阵:(1)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---121312112131211;解 此矩阵的第一个行向量非单位向量, 故不是正交阵.(2)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------979494949198949891.解 该方阵每一个行向量均是单位向量, 且两两正交, 故为正交阵.3. 设x 为n 维列向量, x T x =1, 令H =E -2xx T , 证明H 是对称的正交阵.证明 因为H T =(E -2xx T )T =E -2(xx T )T =E -2(xx T )T=E -2(x T )T x T =E -2xx T ,所以H 是对称矩阵.因为H T H =HH =(E -2xx T )(E -2xx T )=E -2xx T -2xx T +(2xx T )(2xx T )=E -4xx T +4x (x T x )x T=E -4xx T +4xx T=E ,所以H 是正交矩阵.4. 设A 与B 都是n 阶正交阵, 证明AB 也是正交阵. 证明 因为A , B 是n 阶正交阵, 故A -1=A T , B -1=B T ,(AB )T (AB )=B T A T AB =B -1A -1AB =E ,故AB 也是正交阵.5. 求下列矩阵的特征值和特征向量:(1)⎪⎪⎭⎫ ⎝⎛----201335212; 解 3)1(201335212||+-=-------=-λλλλλE A , 故A 的特征值为λ=-1(三重).对于特征值λ=-1, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=+000110101101325213~E A , 得方程(A +E )x =0的基础解系p 1=(1, 1, -1)T , 向量p 1就是对应于特征值λ=-1的特征值向量.(2)⎪⎪⎭⎫ ⎝⎛633312321; 解 )9)(1(633312321||-+-=---=-λλλλλλλE A , 故A 的特征值为λ1=0, λ2=-1, λ3=9.对于特征值λ1=0, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=000110321633312321~A , 得方程A x =0的基础解系p 1=(-1, -1, 1)T , 向量p 1是对应于特征值λ1=0的特征值向量.对于特征值λ2=-1, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=+000100322733322322~E A , 得方程(A +E )x =0的基础解系p 2=(-1, 1, 0)T , 向量p 2就是对应于特征值λ2=-1的特征值向量.对于特征值λ3=9, 由⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=-00021101113333823289~E A , 得方程(A -9E )x =0的基础解系p 3=(1/2, 1/2, 1)T , 向量p 3就是对应于特征值λ3=9的特征值向量.(3)⎪⎪⎪⎭⎫ ⎝⎛0001001001001000. 解 22)1()1(001010010100||+-=----=-λλλλλλλE A , 故A 的特征值为λ1=λ2=-1, λ3=λ4=1.对于特征值λ1=λ2=-1, 由⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=+00000000011010011001011001101001~E A , 得方程(A +E )x =0的基础解系p 1=(1, 0, 0, -1)T , p 2=(0, 1, -1, 0)T , 向量p 1和p 2是对应于特征值λ1=λ2=-1的线性无关特征值向量. 对于特征值λ3=λ4=1, 由⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=-00000000011010011001011001101001~E A , 得方程(A -E )x =0的基础解系p 3=(1, 0, 0, 1)T , p 4=(0, 1, 1, 0)T , 向量p3和p4是对应于特征值λ3=λ4=1的线性无关特征值向量.6.设A为n阶矩阵,证明A T与A的特征值相同.证明因为|A T-λE|=|(A-λE)T|=|A-λE|T=|A-λE|,所以A T与A的特征多项式相同,从而A T与A的特征值相同.7.设n阶矩阵A、B满足R(A)+R(B)<n,证明A与B有公共的特征值,有公共的特征向量.证明设R(A)=r,R(B)=t,则r+t<n.若a1,a2,⋅⋅⋅,a n-r是齐次方程组A x=0的基础解系,显然它们是A的对应于特征值λ=0的线性无关的特征向量.类似地,设b1,b2,⋅⋅⋅,b n-t是齐次方程组B x=0的基础解系,则它们是B的对应于特征值λ=0的线性无关的特征向量.由于(n-r)+(n-t)=n+(n-r-t)>n,故a1,a2,⋅⋅⋅,a n-r,b1,b2,⋅⋅⋅,b n-t 必线性相关.于是有不全为0的数k1,k2,⋅⋅⋅,k n-r,l1,l2,⋅⋅⋅,l n-t,使k1a1+k2a2+⋅⋅⋅+k n-r a n-r+l1b1+l2b2+⋅⋅⋅+l n-r b n-r=0.记γ=k1a1+k2a2+⋅⋅⋅+k n-r a n-r=-(l1b1+l2b2+⋅⋅⋅+l n-r b n-r),则k1,k2,⋅⋅⋅,k n-r不全为0,否则l1,l2,⋅⋅⋅,l n-t不全为0,而l1b1+l2b2+⋅⋅⋅+l n-r b n-r=0,与b1,b2,⋅⋅⋅,b n-t线性无关相矛盾.因此,γ≠0,γ是A的也是B的关于λ=0的特征向量,所以A 与B有公共的特征值,有公共的特征向量.8.设A2-3A+2E=O,证明A的特征值只能取1或2.证明设λ是A的任意一个特征值,x是A的对应于λ的特征向量,则(A2-3A+2E)x=λ2x-3λx+2x=(λ2-3λ+2)x=0.因为x≠0,所以λ2-3λ+2=0,即λ是方程λ2-3λ+2=0的根,也就是说λ=1或λ=2.9.设A为正交阵,且|A|=-1,证明λ=-1是A的特征值.证明因为A为正交矩阵,所以A的特征值为-1或1.因为|A|等于所有特征值之积,又|A|=-1,所以必有奇数个特征值为-1,即λ=-1是A的特征值.10.设λ≠0是m阶矩阵A m⨯n B n⨯m的特征值,证明λ也是n阶矩阵BA的特征值.证明设x是AB的对应于λ≠0的特征向量,则有(AB)x=λx,于是B(AB)x=B(λx),或BA(B x)=λ(B x),从而λ是BA的特征值,且B x是BA的对应于λ的特征向量.11.已知3阶矩阵A的特征值为1, 2, 3,求|A3-5A2+7A|.解令ϕ(λ)=λ3-5λ2+7λ,则ϕ(1)=3,ϕ(2)=2,ϕ(3)=3是ϕ(A)的特征值,故|A3-5A2+7A|=|ϕ(A)|=ϕ(1)⋅ϕ(2)⋅ϕ(3)=3⨯2⨯3=18.12. 已知3阶矩阵A 的特征值为1, 2, -3, 求|A *+3A +2E |. 解 因为|A |=1⨯2⨯(-3)=-6≠0, 所以A 可逆, 故A *=|A |A -1=-6A -1,A *+3A +2E =-6A -1+3A +2E .令ϕ(λ)=-6λ-1+3λ2+2, 则ϕ(1)=-1, ϕ(2)=5, ϕ(-3)=-5是ϕ(A )的特征值, 故|A *+3A +2E |=|-6A -1+3A +2E |=|ϕ(A )|=ϕ(1)⋅ϕ(2)⋅ϕ(-3)=-1⨯5⨯(-5)=25.13. 设A 、B 都是n 阶矩阵, 且A 可逆, 证明AB 与BA 相 似.证明 取P =A , 则P -1ABP =A -1ABA =BA ,即AB 与BA 相似.14. 设矩阵⎪⎪⎭⎫ ⎝⎛=50413102x A 可相似对角化, 求x . 解 由)6()1(50413102||2---=---=-λλλλλλx E A , 得A 的特征值为λ1=6, λ2=λ3=1.因为A 可相似对角化, 所以对于λ2=λ3=1, 齐次线性方程组(A -E )x =0有两个线性无关的解, 因此R (A -E )=1. 由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-00030010140403101)(~x x E A r 知当x =3时R (A -E )=1, 即x =3为所求.15. 已知p =(1, 1, -1)T是矩阵⎪⎪⎭⎫ ⎝⎛---=2135212b a A 的一个特征向量.(1)求参数a , b 及特征向量p 所对应的特征值;解 设λ是特征向量p 所对应的特征值, 则(A -λE )p =0, 即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛------0001112135212λλλb a , 解之得λ=-1, a =-3, b =0.(2)问A 能不能相似对角化?并说明理由.解 由3)1(201335212||--=-------=-λλλλλE A , 得A 的特征值为λ1=λ2=λ3=1.由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛----=-00011010111325211~r b E A 知R (A -E )=2, 所以齐次线性方程组(A -E )x =0的基础解系只有一个解向量. 因此A 不能相似对角化.16. 试求一个正交的相似变换矩阵, 将下列对称阵化为对角阵:(1)⎪⎪⎭⎫ ⎝⎛----020212022; 解 将所给矩阵记为A . 由λλλλ-------=-20212022E A =(1-λ)(λ-4)(λ+2), 得矩阵A 的特征值为λ1=-2, λ2=1, λ3=4.对于λ1=-2, 解方程(A +2E )x =0, 即0220232024321=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----x x x , 得特征向量(1, 2, 2)T , 单位化得T )32 ,32 ,31(1=p . 对于λ2=1, 解方程(A -E )x =0, 即0120202021321=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-----x x x , 得特征向量(2, 1, -2)T , 单位化得T )32 ,31 ,32(2-=p . 对于λ3=4, 解方程(A -4E )x =0, 即0420232022321=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-------x x x ,得特征向量(2, -2, 1)T , 单位化得T )31 ,32 ,32(3-=p . 于是有正交阵P =(p 1, p 2, p 3), 使P -1AP =diag(-2, 1, 4).(2)⎪⎪⎭⎫ ⎝⎛----542452222. 解 将所给矩阵记为A . 由λλλλ-------=-542452222E A =-(λ-1)2(λ-10), 得矩阵A 的特征值为λ1=λ2=1, λ3=10.对于λ1=λ2=1, 解方程(A -E )x =0, 即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----000442442221321x x x , 得线性无关特征向量(-2, 1, 0)T 和(2, 0, 1)T , 将它们正交化、单位化得T 0) 1, ,2(511-=p , T 5) ,4 ,2(5312=p . 对于λ3=10, 解方程(A -10E )x =0, 即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-------000542452228321x x x , 得特征向量(-1, -2, 2)T , 单位化得T )2 ,2 ,1(313--=p . 于是有正交阵P =(p 1, p 2, p 3), 使P -1AP =diag(1, 1, 10).17. 设矩阵⎪⎪⎭⎫ ⎝⎛------=12422421x A 与⎪⎪⎭⎫ ⎝⎛-=Λy 45相似, 求x , y ; 并求一个正交阵P , 使P -1AP =Λ.解 已知相似矩阵有相同的特征值, 显然λ=5, λ=-4, λ=y 是Λ的特征值, 故它们也是A 的特征值. 因为λ=-4是A 的特征值, 所以0)4(9524242425|4|=-=---+---=+x x E A , 解之得x =4.已知相似矩阵的行列式相同, 因为100124242421||-=-------=A , y y2045||-=-=Λ, 所以-20y =-100, y =5.对于λ=5, 解方程(A -5E )x =0, 得两个线性无关的特征向量(1, 0, -1)T , (1, -2, 0)T . 将它们正交化、单位化得T )1 ,0 ,1(211-=p , T )1 ,4 ,1(2312-=p . 对于λ=-4, 解方程(A +4E )x =0, 得特征向量(2, 1, 2)T , 单位化得T )2 ,1 ,2(313=p .于是有正交矩阵⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=23132212343102313221P , 使P -1AP =Λ. 18. 设3阶方阵A 的特征值为λ1=2, λ2=-2, λ3=1; 对应的特征向量依次为p 1=(0, 1, 1)T , p 2=(1, 1, 1)T , p 3=(1, 1, 0)T , 求A . 解 令P =(p 1, p 2, p 3), 则P -1AP =diag(2, -2, 1)=Λ, A =P ΛP -1. 因为⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛=--11011101101111111011P , 所以 ⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=Λ=-1101110111000200020111111101P P A ⎪⎪⎭⎫ ⎝⎛------=244354331. 19. 设3阶对称阵A 的特征值为λ1=1, λ2=-1, λ3=0; 对应λ1、λ2的特征向量依次为p 1=(1, 2, 2)T , p 2=(2, 1, -2)T , 求A .解 设⎪⎪⎭⎫ ⎝⎛=653542321x x x x x x x x x A , 则A p 1=2p 1, A p 2=-2p 2, 即 ⎪⎩⎪⎨⎧=++=++=++222222122653542321x x x x x x x x x , ---① ⎪⎩⎪⎨⎧=-+-=-+-=-+222122222653542321x x x x x x x x x . ---② 再由特征值的性质, 有x 1+x 4+x 6=λ1+λ2+λ3=0. ---③由①②③解得612131x x --=, 6221x x =, 634132x x -=, 642131x x -=, 654132x x +=. 令x 6=0, 得311-=x , x 2=0, 323=x , 314=x , 325=x . 因此 ⎪⎪⎭⎫ ⎝⎛-=022********A . 20. 设3阶对称矩阵A 的特征值λ1=6, λ2=3, λ3=3, 与特征值λ1=6对应的特征向量为p 1=(1, 1, 1)T , 求A .解 设⎪⎪⎭⎫ ⎝⎛=653542321x x x x x x x x x A . 因为λ1=6对应的特征向量为p 1=(1, 1, 1)T , 所以有⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛1116111A , 即⎪⎩⎪⎨⎧=++=++=++666653542321x x x x x x x x x ---①. λ2=λ3=3是A 的二重特征值, 根据实对称矩阵的性质定理知R (A -3E )=1. 利用①可推出⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=-331113333653542653542321~x x x x x x x x x x x x x x x E A . 因为R (A -3E )=1, 所以x 2=x 4-3=x 5且x 3=x 5=x 6-3, 解之得x 2=x 3=x 5=1, x 1=x 4=x 6=4.因此 ⎪⎪⎭⎫ ⎝⎛=411141114A . 21. 设a =(a 1, a 2, ⋅⋅⋅, a n )T , a 1≠0, A =aa T .(1)证明λ=0是A 的n -1重特征值;证明 设λ是A 的任意一个特征值, x 是A 的对应于λ的特征向量, 则有A x =λx ,λ2x =A 2x =aa T aa T x =a T a A x =λa T ax ,于是可得λ2=λa T a , 从而λ=0或λ=a T a .设λ1, λ2, ⋅ ⋅ ⋅, λn 是A 的所有特征值, 因为A =aa T 的主对角线性上的元素为a 12, a 22, ⋅ ⋅ ⋅, a n 2, 所以a 12+a 22+ ⋅ ⋅ ⋅ +a n 2=a T a =λ1+λ2+ ⋅ ⋅ ⋅ +λn ,这说明在λ1, λ2, ⋅ ⋅ ⋅, λn 中有且只有一个等于a T a , 而其余n -1个全为0, 即λ=0是A 的n -1重特征值.(2)求A 的非零特征值及n 个线性无关的特征向量. 解 设λ1=a T a , λ2= ⋅ ⋅ ⋅ =λn =0.因为A a =aa T a =(a T a )a =λ1a , 所以p 1=a 是对应于λ1=a T a 的特征向量.对于λ2= ⋅ ⋅ ⋅ =λn =0, 解方程A x =0, 即aa T x =0. 因为a ≠0, 所以a T x =0, 即a 1x 1+a 2x 2+ ⋅ ⋅ ⋅ +a n x n =0, 其线性无关解为p 2=(-a 2, a 1, 0, ⋅⋅⋅, 0)T , p 3=(-a 3, 0, a 1, ⋅⋅⋅, 0)T ,⋅ ⋅ ⋅,p n =(-a n , 0, 0, ⋅⋅⋅, a 1)T .因此n 个线性无关特征向量构成的矩阵为⎪⎪⎪⎭⎫ ⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-=⋅⋅⋅112212100), , ,(a a a a a a a nn n p p p . 22. 设⎪⎪⎭⎫ ⎝⎛-=340430241A , 求A 100. 解 由 )5)(5)(1(340430241||+---=----=-λλλλλλλE A , 得A 的特征值为λ1=1, λ2=5, λ3=-5.对于λ1=1, 解方程(A -E )x =0, 得特征向量p 1=(1, 0, 0)T . 对于λ1=5, 解方程(A -5E )x =0, 得特征向量p 2=(2, 1, 2)T . 对于λ1=-5, 解方程(A +5E )x =0, 得特征向量p 3=(1, -2, 1)T . 令P =(p 1, p 2, p 3), 则P -1AP =diag(1, 5, -5)=Λ,A =P ΛP -1,A 100=P Λ100P -1.因为Λ100=diag(1, 5100, 5100),⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-=--1202105055112021012111P , 所以⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=12021050555112021012151100100100A ⎪⎪⎭⎫ ⎝⎛-=1001001005000501501. 23. 在某国, 每年有比例为p 的农村居民移居城镇, 有比例为q 的城镇居民移居农村, 假设该国总人口数不变, 且上述人口迁移的规律也不变. 把n 年后农村人口和城镇人口占总人口的比例依次记为x n 和y n (x n +y n =1).(1)求关系式⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++n n n n y x A y x 11中的矩阵A ; 解 由题意知x n +1=x n +qy n -px n =(1-p )x n +qy n ,y n +1=y n +px n -qy n = px n +(1-q )y n ,可用矩阵表示为⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛++n n n n y x q p q p y x 1111, 因此 ⎪⎭⎫ ⎝⎛--=q p q p A 11. (2)设目前农村人口与城镇人口相等, 即⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛5.05.000y x , 求⎪⎭⎫ ⎝⎛n n y x . 解 由⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++n n n n y x A y x 11可知⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛00y x A y x n n n . 由 )1)(1(11||q p q p q p E A ++--=----=-λλλλλ, 得A 的特征值为λ1=1, λ2=r , 其中r =1-p -q .对于λ1=1, 解方程(A -E )x =0, 得特征向量p 1=(q , p )T . 对于λ1=r , 解方程(A -rE )x =0, 得特征向量p 2=(-1, 1)T .令⎪⎭⎫ ⎝⎛-==11) ,(21p q P p p , 则 P -1AP =diag(1, r )=Λ,A =P ΛP -1,A n =P Λn P -1.于是 11100111-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=p q r p q A n n ⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+=q p r p q q p n 11001111 ⎪⎭⎫ ⎝⎛+--++=n n n n qr p pr p qr q pr q q p 1, ⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+--++=⎪⎭⎫ ⎝⎛5.05.01n n n n n n qr p pr p qr q pr q q p y x ⎪⎭⎫ ⎝⎛-+-++=n n r p q p r q p q q p )(2)(2)(21. 24. (1)设⎪⎭⎫ ⎝⎛--=3223A , 求ϕ(A )=A 10-5A 9;解 由)5)(1(3223||--=----=-λλλλλE A , 得A 的特征值为λ1=1, λ2=5.对于λ1=1, 解方程(A -E )x =0, 得单位特征向量T )1 ,1(21. 对于λ1=5, 解方程(A -5E )x =0, 得单位特征向量T )1 ,1(21-. 于是有正交矩阵⎪⎭⎫ ⎝⎛-=111121P , 使得P -1AP =diag(1, 5)=Λ, 从而A =P ΛP -1, A k =P Λk P -1. 因此ϕ(A )=P ϕ(Λ)P -1=P (Λ10-5Λ9)P -1=P [diag(1, 510)-5diag(1, 59)]P -1=P diag(-4, 0)P -1⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=1111210004111121 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛----=111122222. (2)设⎪⎪⎭⎫ ⎝⎛=122221212A , 求ϕ(A )=A 10-6A 9+5A 8. 解 求得正交矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=20223123161P , 使得P -1AP =diag(-1, 1, 5)=Λ, A =P ΛP -1. 于是ϕ(A )=P ϕ(Λ)P -1=P (Λ10-6Λ9+5Λ8)P -1=P [Λ8(Λ-E )(Λ-5E )]P -1=P diag(1, 1, 58)diag(-2, 0, 4)diag(-6, -4, 0)P -1 =P diag(12, 0, 0)P -1⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=222033211001220223123161 ⎪⎪⎭⎫ ⎝⎛----=4222112112. 25. 用矩阵记号表示下列二次型:(1) f =x 2+4xy +4y 2+2xz +z 2+4yz ;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=z y x z y x f 121242121) , ,(. (2) f =x 2+y 2-7z 2-2xy -4xz -4yz ;解 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-------=z y x z y x f 722211211) , ,(. (3) f =x 12+x 22+x 32+x 42-2x 1x 2+4x 1x 3-2x 1x 4+6x 2x 3-4x 2x 4.解 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛------=432143211021013223111211) , , ,(x x x x x x x x f . 26. 写出下列二次型的矩阵:(1)x x x ⎪⎭⎫ ⎝⎛=1312)(T f ; 解 二次型的矩阵为⎪⎭⎫ ⎝⎛=1312A .(2)x x x ⎪⎪⎭⎫ ⎝⎛=987654321)(T f . 解 二次型的矩阵为⎪⎪⎭⎫ ⎝⎛=987654321A . 27. 求一个正交变换将下列二次型化成标准形:(1) f =2x 12+3x 22+3x 33+4x 2x 3;解 二次型的矩阵为⎪⎪⎭⎫ ⎝⎛=320230002A . 由 )1)(5)(2(320230002λλλλλλλ---=---=-E A , 得A 的特征值为λ1=2, λ2=5, λ3=1.当λ1=2时, 解方程(A -2E )x =0, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-0001002101202100002~E A , 得特征向量(1, 0, 0)T . 取p 1=(1, 0, 0)T .当λ2=5时, 解方程(A -5E )x =0, 由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-0001100012202200035~E A , 得特征向量(0, 1, 1)T . 取T )21 ,21 ,0(2=p . 当λ3=1时, 解方程(A -E )x =0, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-000110001220220001~E A , 得特征向量(0, -1, 1)T . 取T )21 ,21 ,0(3-=p . 于是有正交矩阵T =(p 1, p 2, p 3)和正交变换x =T y , 使f =2y 12+5y 22+y 32.(2) f =x 12+x 22+x 32+x 42+2x 1x 2-2x 1x 4-2x 2x 3+2x 3x 4.解 二次型矩阵为⎪⎪⎪⎭⎫ ⎝⎛----=1101111001111011A . 由 2)1)(3)(1(1101111001111011--+=--------=-λλλλλλλλE A , 得A 的特征值为λ1=-1, λ2=3, λ3=λ4=1. 当λ1=-1时, 可得单位特征向量T )21 ,21 ,21 ,21(1--=p . 当λ2=3时, 可得单位特征向量T )21 ,21 ,21 ,21(2--=p . 当λ3=λ4=1时, 可得线性无关的单位特征向量T )0 ,21 ,0 ,21(3=p , T )21 ,0 ,21 ,0(4=p . 于是有正交矩阵T =( p 1, p 2, p 3, p 4)和正交变换x =T y , 使f =-y 12+3y 22+y 32+y 42.28. 求一个正交变换把二次曲面的方程3x 2+5y 2+5z 2+4xy -4xz -10yz =1化成标准方程.解 二次型的矩阵为⎪⎪⎭⎫⎝⎛----=552552223A .由)11)(2(552552223||---=-------=-λλλλλλλE A , 得A 的特征值为λ1=2, λ2=11, λ3=0, .对于λ1=2, 解方程(A -2E )x =0, 得特征向量(4, -1, 1)T , 单位化得)231 ,231 ,234(1-=p .对于λ2=11, 解方程(A -11E )x =0, 得特征向量(1, 2, -2)T , 单位化得)32 ,32 ,31(2-=p .对于λ3=0, 解方程A x =0, 得特征向量(0, 1, 1)T , 单位化得)21 ,21 ,0(3=p .于是有正交矩阵P =(p 1, p 2, p 3), 使P -1AP =diag(2, 11, 0), 从而有正交变换⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛w v u z y x 21322312132231031234,使原二次方程变为标准方程2u 2+11v 2=1.29. 明: 二次型f =x T A x 在||x ||=1时的最大值为矩阵A 的最大特征值.证明 A 为实对称矩阵, 则有一正交矩阵T , 使得TAT -1=diag(λ1, λ2, ⋅ ⋅ ⋅, λn )=Λ成立, 其中λ1, λ2, ⋅ ⋅ ⋅, λn 为A 的特征值, 不妨设λ1最大. 作正交变换y =T x , 即x =T T y , 注意到T -1=T T , 有 f =x T A x =y T TAT T y =y T Λy =λ1y 12+λ2y 22+ ⋅ ⋅ ⋅ +λn y n 2. 因为y =T x 正交变换, 所以当||x ||=1时, 有||y ||=||x ||=1, 即y 12+y 22+ ⋅ ⋅ ⋅ +y n 2=1.因此f =λ1y 12+λ2y 22+ ⋅ ⋅ ⋅ +λn y n 2≤λ1,又当y 1=1, y 2=y 3=⋅ ⋅ ⋅=y n =0时f =λ1, 所以f max =λ1.30. 用配方法化下列二次形成规范形, 并写出所用变换的矩阵.(1) f (x 1, x 2, x 3)=x 12+3x 22+5x 32+2x 1x 2-4x 1x 3; 解 f (x 1, x 2, x 3)=x 12+3x 22+5x 32+2x 1x 2-4x 1x 3 =(x 1+x 2-2x 3)2+4x 2x 3+2x 22+x 32 =(x 1+x 2-2x 3)2-2x 22+(2x 2+x 3)2.令 ⎪⎩⎪⎨⎧+==-+=323223211222x x y x y x x x y , 即⎪⎪⎩⎪⎪⎨⎧+-==+-=323223*********y y x y x y y y x ,二次型化为规范形f =y 12-y 22+y 32,所用的变换矩阵为⎪⎪⎪⎪⎪⎭⎫⎝⎛--=12002102251C .(2) f (x 1, x 2, x 3)=x 12+2x 32+2x 1x 3+2x 2x 3; 解 f (x 1, x 2, x 3)=x 12+2x 32+2x 1x 3+2x 2x 3 =(x 1+x 3)2+x 32+2x 2x 3; =(x 1+x 3)2-x 22+(x 2+x 3)2.令 ⎪⎩⎪⎨⎧+==+=32322311x x y x y x x y , 即⎪⎩⎪⎨⎧+-==-+=323223211y y x y x y y y x ,二次型化为规范形f =y 12-y 22+y 32,所用的变换矩阵为⎪⎪⎭⎫⎝⎛--=110010111C . (3) f (x 1, x 2, x 3)=2x 12+x 22+4x 32+2x 1x 2-2x 2x 3. 解 f (x 1, x 2, x 3)=2x 12+x 22+4x 32+2x 1x 2-2x 2x 3.3223222212421)21(2x x x x x x -+++=232322212)2(21)21(2x x x x x +-++=.令 ⎪⎪⎩⎪⎪⎨⎧=-=+=333222112)2(21)21(2x y x x y x x y , 即⎪⎪⎩⎪⎪⎨⎧=+=--=33322321121222212121y x y y x y y y x , 二次型化为规范形f =y 12+y 22+y 32,所用的变换矩阵为⎪⎪⎭⎫ ⎝⎛--=10022011121C . 31. 设f =x 12+x 22+5x 32+2ax 1x 2-2x 1x 3+4x 2x 3为正定二次型, 求a .解 二次型的矩阵为⎪⎪⎭⎫⎝⎛--=5212111a a A , 其主子式为a 11=1, 2111a a a -=, )45(5212111+-=--a a a a . 因为f 为正主二次型, 所以必有1-a 2>0且-a (5a +4)>0, 解之得054<<-a .32. 判别下列二次型的正定性:(1) f =-2x 12-6x 22-4x 32+2x 1x 2+2x 1x 3;解 二次型的矩阵为⎪⎪⎭⎫⎝⎛---=401061112A . 因为0211<-=a , 0116112>=--, 038||<-=A , 所以f 为负定.(2) f =x 12+3x 22+9x 32+19x 42-2x 1x 2+4x 1x 3+2x 1x 4-6x 2x 4-12x 3x 4. 解 二次型的矩阵为⎪⎪⎪⎭⎫⎝⎛------=19631690230311211A . 因为 0111>=a ,043111>=--, 06902031211>=--, 024>=A , 所以f 为正定.33. 证明对称阵A 为正定的充分必要条件是: 存在可逆矩阵U , 使A =U T U , 即A 与单位阵E 合同.证明 因为对称阵A 为正定的, 所以存在正交矩阵P 使P T AP =diag(λ1, λ2, ⋅ ⋅ ⋅, λn )=Λ, 即A =P ΛP T ,其中λ1, λ2, ⋅ ⋅ ⋅, λn 均为正数.令), , ,diag(211n λλλ⋅⋅⋅=Λ, 则Λ=Λ1Λ1, A =P Λ1Λ1T P T . 再令U =Λ1T P T , 则U 可逆, 且A =U T U .第六章线性空间与线性变换1.验证所给矩阵集合对于矩阵的加法和乘数运算构成线性空间,并写出各个空间的一个基.(1) 2阶矩阵的全体S1;解设A,B分别为二阶矩阵,则A,B∈S1.因为(A+B)∈S1,kA∈S1,所以S 1对于矩阵的加法和乘数运算构成线性空间.⎪⎭⎫ ⎝⎛=00011ε, ⎪⎭⎫ ⎝⎛=00102ε, ⎪⎭⎫ ⎝⎛=01003ε, ⎪⎭⎫ ⎝⎛=10004ε 是S 1的一个基.(2)主对角线上的元素之和等于0的2阶矩阵的全体S 2;解 设⎪⎭⎫ ⎝⎛-=a c b a A , ⎪⎭⎫ ⎝⎛-=d f e d B , A , B ∈S 2. 因为 2)(S d a a c b c d a B A ∈⎪⎭⎫ ⎝⎛++++-=+, 2S ka kc kb ka kA ∈⎪⎭⎫ ⎝⎛-=, 所以S 2对于矩阵的加法和乘数运算构成线性空间.⎪⎭⎫ ⎝⎛-=10011ε, ⎪⎭⎫ ⎝⎛=00102ε, ⎪⎭⎫ ⎝⎛=01003ε 是S 2的一个基.(3) 2阶对称矩阵的全体S 3.解 设A , B ∈S 3, 则A T =A , B T =B . 因为 (A +B )T =A T +B T =A +B , (A +B )∈S 3, (kA )T =kA T =kA , kA ∈S 3,所以S 3对于加法和乘数运算构成线性空间.⎪⎭⎫ ⎝⎛=00011ε, ⎪⎭⎫ ⎝⎛=01102ε, ⎪⎭⎫ ⎝⎛=10003ε是S 3的一个基.2. 验证: 与向量(0, 0, 1)T 不平行的全体3维数组向量, 对于数组向量的加法和乘数运算不构成线性空间.解设V={与向量(0,0,1)T不平行的全体三维向量},设r1=(1, 1, 0)T,r2=(-1, 0, 1)T,则r1,r2∈V,但r1+r2=(0, 0, 1)T∉V,即V不是线性空间.3.设U是线性空间V的一个子空间,试证:若U与V的维数相等,则U=V.证明设ε1,ε2,⋅⋅⋅,εn为U的一组基,它可扩充为整个空间V 的一个基,由于dim(U)=dim(V),从而ε1,ε2,⋅⋅⋅,εn也为V的一个基,则:对于x∈V可以表示为x=k1ε1+k2ε2+⋅⋅⋅+k rεr.显然,x∈U,故V⊆U,而由已知知U⊆V,有U=V.4.设V r是n维线性空间V n的一个子空间,a1,a2,⋅⋅⋅,a r是V r 的一个基.试证:V n中存在元素a r+1,⋅⋅⋅,a n,使a1,a2,⋅⋅⋅,a r, a r+1,⋅⋅⋅,a n成为V n的一个基.证明设r<n, 则在V n中必存在一向量a r+1∉V r,它不能被a1,a2,⋅⋅⋅,a r线性表示,将a r+1添加进来,则a1,a2,⋅⋅⋅,a r+1是线性无关的.若r+1=n,则命题得证,否则存在a r+2∉L(a1,a2,⋅⋅⋅,a r+1),则a1,a2,⋅⋅⋅,a r+2线性无关,依此类推,可找到n个线性无关的向量a1,a2,⋅⋅⋅,a n,它们是V n的一个基.5.在R3中求向量α=(3, 7, 1)T在基α1=(1, 3, 5)T,α2=(6, 3, 2)T,α3=(3, 1, 0)T下的坐标.解 设ε1, ε2, ε3是R 3的自然基, 则 (α1, α2, α3)=(ε1, ε2, ε3)A , (ε1, ε2, ε3)=(α1, α2, α3)A -1,其中⎪⎪⎭⎫ ⎝⎛=025133361A , ⎪⎪⎭⎫⎝⎛-----=-1528981553621A .因为 ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=-173) , ,(173) , ,(1321321A αααεεεα⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-----=173152898155362) , ,(321ααα⎪⎪⎭⎫⎝⎛-=1548233) , ,(321ααα,所以向量α在基α1, α2, α3下的坐标为(33, -82, 154)T .6. 在R 3取两个基α1=(1, 2, 1)T , α2=(2, 3, 3)T , α3=(3, 7, 1)T ; β1=(3, 1, 4)T , β2=(5, 2, 1)T , β3=(1, 1, -6)T . 试求坐标变换公式.解 设ε1, ε2, ε3是R 3的自然基, 则 (β1, β2, β1)=(ε1, ε2, ε3)B , (ε1, ε2, ε3)=(β1, β2, β1)B -1,(α1, α2, α1)=(ε1, ε2, ε3)A =(β1, β2, β1)B -1A ,其中 ⎪⎪⎭⎫ ⎝⎛=131732121A , ⎪⎪⎭⎫⎝⎛-=614121153B .设任意向量α在基α1, α2, α3下的坐标为(x 1, x 2, x 3)T , 则⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=-3211321321321) , ,() , ,(x x x A B x x x βββαααα,故α在基β1, β2, β3下的坐标为⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛'''-3211321x x x A B x x x ⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=32149910726313941811913x x x .7. 在R 4中取两个基e 1=(1,0,0,0)T , e 2=(0,1,0,0)T , e 3=(0,0,1,0)T , e 4=(0,0,0,1)T ; α1=(2,1,-1,1)T , α2=(0,3,1,0)T , α3=(5,3,2,1)T , α3=(6,6,1,3)T . (1)求由前一个基到后一个基的过渡矩阵; 解 由题意知⎪⎪⎪⎭⎫⎝⎛-=3101121163316502) , , ,() , , ,(43214321e e e e αααα, 从而由前一个基到后一个基的过渡矩阵为⎪⎪⎪⎭⎫⎝⎛-=3101121163316502A . (2)求向量(x 1, x 2, x 3, x 4)T 在后一个基下的坐标; 解 因为⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=-43211432143214321) , , ,() , , ,(x x x x A x x x x αααααe e e e ,向量α在后一个基下的坐标为⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-4321143213166123501301112x x x x y y y y ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-------=432126937180092391213327912271x x x x . (3)求在两个基下有相同坐标的向量.解 令⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-------4321432126937180092391213327912271x x x x x x x x , 解方程组得⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛11114321k x x x x (k 为常数).8. 说明xOy 平面上变换⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛y x A y x T 的几何意义, 其中(1)⎪⎭⎫ ⎝⎛-=1001A ; 解 因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛y x y x y x T 1001,所以在此变换下T (α)与α关于y 轴对称.(2)⎪⎭⎫ ⎝⎛=1000A ; 解 因为⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛y y x y x T 01000,所以在此变换下T (α)是α在y 轴上的投影.(3)⎪⎭⎫ ⎝⎛=0110A ; 解 因为⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛x y y x y x T 0110, 所以在此变换下T (α)与α关于直线y =x 对称.(4)⎪⎭⎫ ⎝⎛-=0110A .解 因为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛x y y x y x T 0110, 所以在此变换下T (α)是将α顺时针旋转2π.9.n阶对称矩阵的全体V对于矩阵的线性运算构成一个2)1(+nn维线性空间. 给出n阶矩阵P,以A表示V中的任一元素,变换T(A)=P T AP称为合同变换. 试证合同变换T是V中的线性变换.证明设A,B∈V,则A T=A,B T=B.T(A+B)=P T(A+B)P=P T(A+B)T P=[(A+B)P]T P=(AP+BP)T P=(P T A+P T B)P=P T AP+P T BP=T(A)+T(B),T(kA)=P T(kA)P=kP T AP=kT(A),从而,合同变换T是V中的线性变换.10.函数集合V3={α=(a2x2+a1x+a0)e x | a2,a1,a0∈R}对于函数的线性运算构成3维线性空间,在V3中取一个基α1=x2e x,α2=xe x,α3=e x.求微分运算D在这个基下的矩阵.解设β1=D(α1)=2xe x+x2e x=2α2+α1,β2=D(α2)=e x+xe x=α3+α2,β3=D(α3)=e x=α3.易知β1,β2,β3线性无关,故为一个基.由 ⎪⎪⎭⎫⎝⎛=110012001) , ,() , ,(321321αααβββ,知即D 在基α1, α2, α3下的矩阵为⎪⎪⎭⎫⎝⎛=110012001P .11. 2阶对称矩阵的全体},,|{32132213R x x x x x x x A V ∈⎪⎭⎫⎝⎛==对于矩阵的线性运算构成3维线性空间. 在V 3中取一个基⎪⎭⎫ ⎝⎛=00011A , ⎪⎭⎫ ⎝⎛=01102A , ⎪⎭⎫ ⎝⎛=10003A .在V 3中定义合同变换⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=10111101)(A A T ,求T 在基A 1, A 2, A 3下的矩阵. 解 因为⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=101100011101)(1A T 3211111A A A ++=⎪⎭⎫ ⎝⎛=,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=101111101101)(2A T 3222110A A +=⎪⎭⎫ ⎝⎛=,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=101110001101)(3A T 31000A =⎪⎭⎫ ⎝⎛=,故 ⎪⎪⎭⎫⎝⎛=121011001) , ,())( ),( ),((321321A A A A T A T A T ,从而, T 在基A 1, A 2, A 3下的矩阵⎪⎪⎭⎫⎝⎛=121011001A .。
福建工程学院《高等数学AI》2018-2019期末试卷
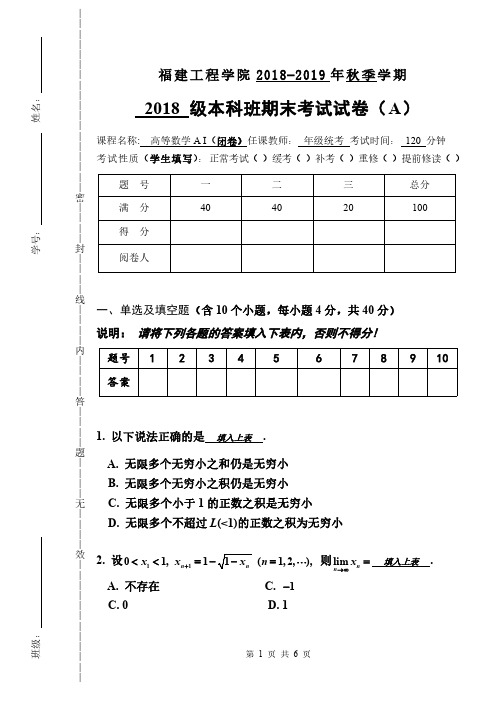
第1页共6页福建工程学院2018-2019年秋季学期2018级本科班期末考试试卷(A )课程名称:高等数学A I (闭卷)任课教师:年级统考考试时间:120分钟考试性质(学生填写):正常考试()缓考()补考()重修()提前修读()题号一二三总分满分404020100得分阅卷人一、单选及填空题(含10个小题,每小题4分,共40分)说明:请将下列各题的答案填入下表内,否则不得分!题号12345678910答案1.以下说法正确的是填入上表.A.无限多个无穷小之和仍是无穷小B.无限多个无穷小之积仍是无穷小C.无限多个小于1的正数之积是无穷小D.无限多个不超过L (<1)的正数之积为无穷小2.设1101,11,2,),n x x n +<<=-= 则lim n n x →∞=填入上表.A.不存在 C.1-C.0 D.1——————————————————密————封————线————内————答————题————无————效————————————班级:学号:姓名:第2页共6页3.函数()(1)x e e f x x x -=-的间断点0x =,1x =的类型依次是填入上表.A.第一类,第一类B.第一类,第二类C.第二类,第一类D.第二类,第二类4.设3sin y x x =,则(100)(0)y =填入上表.A.100B.10099⋅C.1009998⋅⋅D.100999897⋅⋅⋅5.设0()20x b e a x f x x x ⎧+>⎪=⎨+≤⎪⎩连续、可导,则(,)a b =填入上表.6.设()f x 在(0,)+∞内连续,(1)1f =,且对所有,(0,)x t ∈+∞,满足111()()()xtx t f u du t f u du x f u du =+⎰⎰⎰,则()f x =填入上表.7.曲线21x y e -=在(1,1)-处的切线方程是填入上表.A.230x y -+= B.230x y --=C.230x y +-= D.230x y +-=8.设函数()f x 在区间[1,1]-上可导,()0f x '<,(1)0f ->,(1)0f <,则方程()0f x =在区间(1,1)-内填入上表.A .至少有两个实根B .有且仅有一个实根C .没有实根D .根的个数不能确定9.设[]lim (),lim lim ()(1)x x x x x c f x e f x f x x c →∞→∞→∞+⎛⎫'==-- ⎪-⎝⎭,则c =填入上表.A .0B.0.5C.1D. 1.510.曲线211x x y e x -+=-的渐近线有填入上表.A.1条 B.2条 C.3条D.0条第3页共6页二、计算下列各题(含8个小题,每小题5分,共40分)11.计算212lim n n n →∞+++ .12.求2lim 1.x x x →∞⎛⎫+ ⎪⎝⎭13.求020(sin 1)lim .x x x e x dx x →+-⎰14.直接计算()12336y x x =-的高阶导数比较复杂,可以先将两边3次方,然后再按照隐函数求导法计算.试按这种方法计算,.y y '''得分——————————————————密————封————线————内————答————题————无————效————————————第4页共6页15.利用二阶导数判断星形线33cos sin x a t y a t ⎧=⎪⎨=⎪⎩对应04t π≤≤段的凹凸性.16.计算.ln ln ln dx x x x⋅⎰17.利用换元法计算10.I =⎰18.计算20.x I x e dx +∞-=⎰第5页共6页三、完成下列各题(含2个小题,每小题10分,共20分)19.在区间[0,1]上给定函数2y x ,问t 为何值时,图中的阴影部分1S 与2S 的面积之和S 最小?最小值是多少?得分——————————————————密————封————线————内————答————题————无————效————————————第6页共6页20.(1)证明:方程53330x x x ++-=有且仅有一个正根.(2)设()f x 为奇函数,证明0()()xF x f t dt =⎰为偶函数.。
工程数学I(离线作业)

工程数学I第一次作业三、主观题(共9道小题)22.参考答案:t=523.参考答案:2424.参考答案:-325.参考答案:26.参考答案:x= -4 , y= 227.参考答案:428.参考答案:相关29.参考答案:1=2= 0 ,3=230.参考答案:3二次作业三、主观题(共6道小题)13.参考答案:a=614.参考答案:4815.参考答案:-216.参考答案:或不定17.参考答案:a=b=c=118.参考答案:4第三次作业三、主观题(共6道小题)13.参考答案:令,则A的阶梯形有零行,所以向量组线性相关。
14.求解齐次方程组参考答案:对方程组的系数矩阵作初等行变换化成简单阶梯形矩阵15.已知四元线性方程组参考答案:16.设,求A的特征值和特征向量。
参考答案:17.求一个正交矩阵P,将对称矩阵化为对角矩阵。
参考答案:18.设二次型经过正交变换化为求参数a、b及所用的正交变换矩阵。
参考答案:变换前后的两个二次型的矩阵分别为第四次作业三、主观题(共7道小题)13.计算行列式参考答案:容易发现D的特点是:每列(行)元素之和都等于6,那么,把二、三、四行同时加到第一行,并提出第一行的公因子6,便得到由于上式右端行列式第一行的元素都等于1,那么让二、三、四行都减去第一行得14.求行列式中元素a和b的代数余子式。
参考答案:行列式展开方法==15.设,判断A是否可逆?若可逆,求出参考答案:即所以16.求矩阵X使之满足参考答案:17.用初等行变换求矩阵的逆矩阵参考答案:于是同样道理,由算式可知,若对矩阵(A,B)施行初等行变换,当把A 变为E时,B就变为18.讨论向量组,,的线性相关性。
参考答案:即19.用正交变换把二次型化为标准型。
参考答案:二次型的矩阵正交化得位化得第五次作业三、主观题(共7道小题)14.参考答案:15.参考答案:16.参考答案:17.参考答案:18.计算四阶行列式参考答案:将行列式D按第三行展开得19.求方程组的一个基础解系并求其通解。
工程数学--线性代数课后题答案_第五版5

工程数学--线性代数课后题答案_第五版第五章 相似矩阵及二次型1. 试用施密特法把下列向量组正交化:(1)⎪⎪⎭⎫⎝⎛=931421111) , ,(321a a a ;解 根据施密特正交化方法,⎪⎪⎭⎫⎝⎛==11111a b ,⎪⎪⎭⎫⎝⎛-=-=101],[],[1112122b b b a b a b ,⎪⎪⎭⎫⎝⎛-=--=12131],[],[],[],[222321113133b b b a b b b b a b a b .(2)⎪⎪⎪⎭⎫⎝⎛---=011101110111) , ,(321a a a .解 根据施密特正交化方法,⎪⎪⎪⎭⎫ ⎝⎛-==110111a b ,⎪⎪⎪⎭⎫⎝⎛-=-=123131],[],[1112122b b b a b a b ,⎪⎪⎪⎭⎫⎝⎛-=--=433151],[],[],[],[222321113133b b b a b b b b a b a b .2. 下列矩阵是不是正交阵:(1)⎪⎪⎪⎪⎪⎭⎫⎝⎛---121312112131211;解 此矩阵的第一个行向量非单位向量, 故不是正交阵.(2)⎪⎪⎪⎪⎪⎭⎫⎝⎛------979494949198949891.解 该方阵每一个行向量均是单位向量, 且两两正交, 故为正交阵.3. 设x 为n 维列向量, x T x =1, 令H =E -2xx T , 证明H 是对称的正交阵. 证明 因为H T =(E -2xx T )T =E -2(xx T )T =E -2(xx T )T=E -2(x T )T x T =E -2xx T ,所以H 是对称矩阵. 因为H T H =HH =(E -2xx T )(E -2xx T ) =E -2xx T -2xx T +(2xx T )(2xx T ) =E -4xx T +4x (x T x )x T =E -4xx T +4xx T =E , 所以H 是正交矩阵.4. 设A 与B 都是n 阶正交阵, 证明AB 也是正交阵. 证明 因为A , B 是n 阶正交阵, 故A -1=A T , B -1=B T ,(AB )T (AB )=B T A T AB =B -1A -1AB =E ,故AB 也是正交阵.5. 求下列矩阵的特征值和特征向量:(1)⎪⎪⎭⎫ ⎝⎛----201335212;解3)1(201335212||+-=-------=-λλλλλE A ,故A 的特征值为λ=-1(三重). 对于特征值λ=-1, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----=+000110101101325213~E A ,得方程(A +E )x =0的基础解系p 1=(1, 1, -1)T , 向量p 1就是对应于特征值λ=-1的特征值向量.(2)⎪⎪⎭⎫ ⎝⎛633312321;解)9)(1(633312321||-+-=---=-λλλλλλλE A ,故A 的特征值为λ1=0, λ2=-1, λ3=9. 对于特征值λ1=0, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=000110321633312321~A , 得方程A x =0的基础解系p 1=(-1, -1, 1)T , 向量p 1是对应于特征值λ1=0的特征值向量. 对于特征值λ2=-1, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=+000100322733322322~E A ,得方程(A +E )x =0的基础解系p 2=(-1, 1, 0)T , 向量p 2就是对应于特征值λ2=-1的特征值向量. 对于特征值λ3=9, 由⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛---=-00021101113333823289~E A ,得方程(A -9E )x =0的基础解系p 3=(1/2, 1/2, 1)T , 向量p 3就是对应于特征值λ3=9的特征值向量.(3)⎪⎪⎪⎭⎫⎝⎛0001001001001000. 解22)1()1(001010010100||+-=----=-λλλλλλλE A ,故A 的特征值为λ1=λ2=-1, λ3=λ4=1. 对于特征值λ1=λ2=-1, 由⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫⎝⎛=+00000000011010011001011001101001~E A , 得方程(A +E )x =0的基础解系p 1=(1, 0, 0, -1)T , p 2=(0, 1, -1, 0)T , 向量p 1和p 2是对应于特征值λ1=λ2=-1的线性无关特征值向量. 对于特征值λ3=λ4=1, 由⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛----=-0000000001101001101011001101001~E A , 得方程(A -E )x =0的基础解系p 3=(1, 0, 0, 1)T , p 4=(0, 1, 1, 0)T , 向量p 3和p 4是对应于特征值λ3=λ4=1的线性无关特征值向量.6. 设A 为n 阶矩阵, 证明A T 与A 的特征值相同. 证明 因为|A T-λE|=|(A-λE)T|=|A-λE|T=|A-λE|,所以A T与A的特征多项式相同,从而A T与A的特征值相同.7.设n阶矩阵A、B满足R(A)+R(B)<n,证明A与B有公共的特征值,有公共的特征向量.证明设R(A)=r,R(B)=t,则r+t<n.若a1,a2,⋅⋅⋅,a n-r是齐次方程组A x=0的基础解系,显然它们是A的对应于特征值λ=0的线性无关的特征向量.类似地,设b1,b2,⋅⋅⋅,b n-t是齐次方程组B x=0的基础解系,则它们是B的对应于特征值λ=0的线性无关的特征向量.由于(n-r)+(n-t)=n+(n-r-t)>n,故a1,a2,⋅⋅⋅,a n-r,b1,b2,⋅⋅⋅,b n-t 必线性相关.于是有不全为0的数k1,k2,⋅⋅⋅,k n-r,l1,l2,⋅⋅⋅,l n-t,使k1a1+k2a2+⋅⋅⋅+k n-r a n-r+l1b1+l2b2+⋅⋅⋅+l n-r b n-r=0.记γ=k1a1+k2a2+⋅⋅⋅+k n-r a n-r=-(l1b1+l2b2+⋅⋅⋅+l n-r b n-r),则k1,k2,⋅⋅⋅,k n-r不全为0,否则l1,l2,⋅⋅⋅,l n-t不全为0,而l1b1+l2b2+⋅⋅⋅+l n-r b n-r=0,与b1,b2,⋅⋅⋅,b n-t线性无关相矛盾.因此,γ≠0,γ是A的也是B的关于λ=0的特征向量,所以A 与B有公共的特征值,有公共的特征向量.8.设A2-3A+2E=O,证明A的特征值只能取1或2.证明设λ是A的任意一个特征值,x是A的对应于λ的特征向量,则(A2-3A+2E)x=λ2x-3λx+2x=(λ2-3λ+2)x=0.因为x≠0,所以λ2-3λ+2=0,即λ是方程λ2-3λ+2=0的根,也就是说λ=1或λ=2.9.设A为正交阵,且|A|=-1,证明λ=-1是A的特征值.证明因为A为正交矩阵,所以A的特征值为-1或1.因为|A|等于所有特征值之积,又|A|=-1,所以必有奇数个特征值为-1,即λ=-1是A的特征值.10.设λ≠0是m阶矩阵A m⨯n B n⨯m的特征值,证明λ也是n阶矩阵BA的特征值.证明设x是AB的对应于λ≠0的特征向量,则有(AB)x=λx,于是B(AB)x=B(λx),或BA(B x)=λ(B x),从而λ是BA的特征值,且B x是BA的对应于λ的特征向量.11.已知3阶矩阵A的特征值为1, 2, 3,求|A3-5A2+7A|.解令ϕ(λ)=λ3-5λ2+7λ,则ϕ(1)=3,ϕ(2)=2,ϕ(3)=3是ϕ(A)的特征值,故|A3-5A2+7A|=|ϕ(A)|=ϕ(1)⋅ϕ(2)⋅ϕ(3)=3⨯2⨯3=18.12.已知3阶矩阵A的特征值为1, 2,-3,求|A*+3A+2E|.解因为|A|=1⨯2⨯(-3)=-6≠0,所以A可逆,故A*=|A|A-1=-6A-1,A*+3A+2E=-6A-1+3A+2E.令ϕ(λ)=-6λ-1+3λ2+2, 则ϕ(1)=-1, ϕ(2)=5, ϕ(-3)=-5是ϕ(A )的特征值, 故|A *+3A +2E |=|-6A -1+3A +2E |=|ϕ(A )|=ϕ(1)⋅ϕ(2)⋅ϕ(-3)=-1⨯5⨯(-5)=25. 13. 设A 、B 都是n 阶矩阵, 且A 可逆, 证明AB 与BA 相 似.证明 取P =A , 则P -1ABP =A -1ABA =BA ,即AB 与BA 相似. 14.设矩阵⎪⎪⎭⎫⎝⎛=50413102x A 可相似对角化,求x .解 由)6()1(50413102||2---=---=-λλλλλλx E A ,得A 的特征值为λ1=6, λ2=λ3=1.因为A 可相似对角化, 所以对于λ2=λ3=1, 齐次线性方程组(A -E )x =0有两个线性无关的解, 因此R (A -E )=1. 由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-00030010140403101)(~x x E A r知当x =3时R (A -E )=1, 即x =3为所求.15. 已知p =(1, 1, -1)T是矩阵⎪⎪⎭⎫⎝⎛---=2135212b a A 的一个特征向量.(1)求参数a , b 及特征向量p 所对应的特征值; 解 设λ是特征向量p 所对应的特征值, 则 (A -λE )p =0,即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛------0001112135212λλλb a ,解之得λ=-1, a =-3, b =0.(2)问A 能不能相似对角化?并说明理由. 解 由3)1(201335212||--=-------=-λλλλλE A ,得A 的特征值为λ1=λ2=λ3=1. 由⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛----=-00011010111325211~r b E A知R (A -E )=2, 所以齐次线性方程组(A -E )x =0的基础解系只有一个解向量. 因此A 不能相似对角化.16. 试求一个正交的相似变换矩阵, 将下列对称阵化为对角阵:(1)⎪⎪⎭⎫ ⎝⎛----020212022;解 将所给矩阵记为A . 由λλλλ-------=-20212022E A =(1-λ)(λ-4)(λ+2),得矩阵A 的特征值为λ1=-2, λ2=1, λ3=4. 对于λ1=-2, 解方程(A +2E )x =0, 即0220232024321=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛----x x x , 得特征向量(1, 2, 2)T , 单位化得T )32 ,32 ,31(1=p .对于λ2=1, 解方程(A -E )x =0, 即0120202021321=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-----x x x , 得特征向量(2, 1, -2)T , 单位化得T )32 ,31 ,32(2-=p .对于λ3=4, 解方程(A -4E )x =0, 即0420232022321=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-------x x x , 得特征向量(2, -2, 1)T , 单位化得T )31 ,32 ,32(3-=p .于是有正交阵P =(p 1, p 2, p 3), 使P -1AP =diag(-2, 1, 4).(2)⎪⎪⎭⎫ ⎝⎛----542452222.解 将所给矩阵记为A . 由λλλλ-------=-542452222E A =-(λ-1)2(λ-10),得矩阵A 的特征值为λ1=λ2=1, λ3=10. 对于λ1=λ2=1, 解方程(A -E )x =0, 即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----000442442221321x x x , 得线性无关特征向量(-2, 1, 0)T 和(2, 0, 1)T , 将它们正交化、单位化得T 0) 1, ,2(511-=p , T 5) ,4 ,2(5312=p .对于λ3=10, 解方程(A -10E )x =0, 即⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-------000542452228321x x x , 得特征向量(-1, -2, 2)T , 单位化得T )2 ,2 ,1(313--=p .于是有正交阵P =(p 1, p 2, p 3), 使P -1AP =diag(1, 1, 10). 17.设矩阵⎪⎪⎭⎫⎝⎛------=12422421x A 与⎪⎪⎭⎫ ⎝⎛-=Λy 45相似,求x , y ; 并求一个正交阵P , 使P -1AP =Λ.解 已知相似矩阵有相同的特征值, 显然λ=5, λ=-4, λ=y 是Λ的特征值, 故它们也是A 的特征值. 因为λ=-4是A 的特征值, 所以0)4(9524242425|4|=-=---+---=+x x E A ,解之得x =4.已知相似矩阵的行列式相同, 因为100124242421||-=-------=A , y y2045||-=-=Λ,所以-20y =-100, y =5.对于λ=5, 解方程(A -5E )x =0, 得两个线性无关的特征向量(1, 0, -1)T , (1, -2, 0)T . 将它们正交化、单位化得T )1 ,0 ,1(211-=p , T )1 ,4 ,1(2312-=p . 对于λ=-4, 解方程(A +4E )x =0, 得特征向量(2, 1, 2)T , 单位化得T )2 ,1 ,2(313=p .于是有正交矩阵⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=23132212343102313221P , 使P -1AP =Λ. 18. 设3阶方阵A 的特征值为λ1=2, λ2=-2, λ3=1; 对应的特征向量依次为p 1=(0, 1, 1)T , p 2=(1, 1, 1)T , p 3=(1, 1, 0)T , 求A . 解 令P =(p 1, p 2, p 3), 则P -1AP =diag(2, -2, 1)=Λ, A =P ΛP -1. 因为⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛=--11011101101111111011P ,所以⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=Λ=-1101110111000200020111111101P P A ⎪⎪⎭⎫⎝⎛------=244354331.19. 设3阶对称阵A 的特征值为λ1=1, λ2=-1, λ3=0; 对应λ1、λ2的特征向量依次为p 1=(1, 2, 2)T , p 2=(2, 1, -2)T , 求A .解设⎪⎪⎭⎫⎝⎛=653542321x x x x x x x x x A , 则A p 1=2p 1, A p 2=-2p 2,即⎪⎩⎪⎨⎧=++=++=++222222122653542321x x x x x x x x x , ---① ⎪⎩⎪⎨⎧=-+-=-+-=-+222122222653542321x x x x x x x x x . ---② 再由特征值的性质, 有x 1+x 4+x 6=λ1+λ2+λ3=0. ---③由①②③解得612131x x --=, 6221x x =, 634132x x -=,642131x x -=, 654132x x +=.令x 6=0, 得311-=x , x 2=0, 323=x , 314=x , 325=x .因此⎪⎪⎭⎫ ⎝⎛-=022********A .20. 设3阶对称矩阵A 的特征值λ1=6, λ2=3, λ3=3, 与特征值λ1=6对应的特征向量为p 1=(1, 1, 1)T , 求A .解设⎪⎪⎭⎫ ⎝⎛=653542321x x x x x x x x x A .因为λ1=6对应的特征向量为p 1=(1, 1, 1)T , 所以有⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛1116111A , 即⎪⎩⎪⎨⎧=++=++=++666653542321x x x x x x x x x ---①. λ2=λ3=3是A 的二重特征值, 根据实对称矩阵的性质定理知R (A -3E )=1. 利用①可推出⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛---=-331113333653542653542321~x x x x x x x x x x x x x x x E A .因为R (A -3E )=1, 所以x 2=x 4-3=x 5且x 3=x 5=x 6-3, 解之得x 2=x 3=x 5=1, x 1=x 4=x 6=4.因此⎪⎪⎭⎫⎝⎛=411141114A .21. 设a =(a 1, a 2, ⋅⋅⋅, a n )T , a 1≠0, A =aa T .(1)证明λ=0是A的n-1重特征值;证明设λ是A的任意一个特征值,x是A的对应于λ的特征向量,则有A x=λx,λ2x=A2x=aa T aa T x=a T a A x=λa T ax,于是可得λ2=λa T a,从而λ=0或λ=a T a.设λ1,λ2,⋅⋅⋅,λn是A的所有特征值,因为A=aa T的主对角线性上的元素为a12,a22,⋅⋅⋅,a n2,所以a12+a22+⋅⋅⋅+a n2=a T a=λ1+λ2+⋅⋅⋅+λn,这说明在λ1,λ2,⋅⋅⋅,λn中有且只有一个等于a T a,而其余n-1个全为0,即λ=0是A的n-1重特征值.(2)求A的非零特征值及n个线性无关的特征向量.解设λ1=a T a,λ2=⋅⋅⋅=λn=0.因为A a=aa T a=(a T a)a=λ1a,所以p1=a是对应于λ1=a T a的特征向量.对于λ2=⋅⋅⋅=λn=0,解方程A x=0,即aa T x=0.因为a≠0,所以a T x=0,即a1x1+a2x2+⋅⋅⋅+a n x n=0,其线性无关解为p2=(-a2,a1, 0,⋅⋅⋅, 0)T,p3=(-a3, 0,a1,⋅⋅⋅, 0)T,⋅⋅⋅,p n=(-a n, 0, 0,⋅⋅⋅,a1)T.因此n个线性无关特征向量构成的矩阵为⎪⎪⎪⎭⎫⎝⎛⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅-⋅⋅⋅-=⋅⋅⋅112212100), , ,(a a aa a a a n n n p p p . 22.设⎪⎪⎭⎫⎝⎛-=340430241A ,求A 100.解 由)5)(5)(1(340430241||+---=----=-λλλλλλλE A ,得A 的特征值为λ1=1, λ2=5, λ3=-5.对于λ1=1, 解方程(A -E )x =0, 得特征向量p 1=(1, 0, 0)T . 对于λ1=5, 解方程(A -5E )x =0, 得特征向量p 2=(2, 1, 2)T . 对于λ1=-5, 解方程(A +5E )x =0, 得特征向量p 3=(1, -2, 1)T . 令P =(p 1, p 2, p 3), 则P -1AP =diag(1, 5, -5)=Λ, A =P ΛP -1,A 100=P Λ100P -1. 因为Λ100=diag(1, 5100, 5100), ⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛-=--1202105055112021012111P , 所以⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=12021050555112021012151100100100A⎪⎪⎭⎫ ⎝⎛-=1001001005000501501.23. 在某国, 每年有比例为p 的农村居民移居城镇, 有比例为q 的城镇居民移居农村, 假设该国总人口数不变, 且上述人口迁移的规律也不变. 把n 年后农村人口和城镇人口占总人口的比例依次记为x n 和y n (x n +y n =1). (1)求关系式⎪⎭⎫⎝⎛=⎪⎭⎫⎝⎛++n n n n y x A y x 11中的矩阵A ; 解 由题意知x n +1=x n +qy n -px n =(1-p )x n +qy n , y n +1=y n +px n -qy n = px n +(1-q )y n , 可用矩阵表示为⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛--=⎪⎭⎫ ⎝⎛++n n n n y x q pq py x 1111, 因此 ⎪⎭⎫⎝⎛--=q p qp A 11.(2)设目前农村人口与城镇人口相等, 即⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛5.05.000y x , 求⎪⎭⎫⎝⎛n n y x . 解 由⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++n n n n y x A y x 11可知⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛00y x A y x n n n . 由)1)(1(11||q p q p qp E A ++--=----=-λλλλλ,得A 的特征值为λ1=1, λ2=r , 其中r =1-p -q .对于λ1=1, 解方程(A -E )x =0, 得特征向量p 1=(q , p )T . 对于λ1=r , 解方程(A -rE )x =0, 得特征向量p 2=(-1, 1)T . 令⎪⎭⎫⎝⎛-==11) ,(21p q P p p , 则 P -1AP =diag(1, r )=Λ, A =P ΛP -1, A n =P Λn P -1. 于是 11100111-⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛-=p q r p q A nn ⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+=q p r p q q p n 11001111⎪⎭⎫⎝⎛+--++=n n n n q r p p r p q r q p r q q p 1,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+--++=⎪⎭⎫⎝⎛5.05.01n n n n n n qr p pr p qr q pr q q p y x ⎪⎭⎫ ⎝⎛-+-++=n n r p q p r q p q q p )(2)(2)(21.24. (1)设⎪⎭⎫ ⎝⎛--=3223A , 求ϕ(A )=A 10-5A 9;解 由)5)(1(3223||--=----=-λλλλλE A ,得A 的特征值为λ1=1, λ2=5.对于λ1=1, 解方程(A -E )x =0, 得单位特征向量T )1 ,1(21.对于λ1=5, 解方程(A -5E )x =0, 得单位特征向量T )1 ,1(21-.于是有正交矩阵⎪⎭⎫⎝⎛-=111121P , 使得P -1AP =diag(1, 5)=Λ,从而A =P ΛP -1, A k =P Λk P -1. 因此 ϕ(A )=P ϕ(Λ)P -1=P (Λ10-5Λ9)P -1 =P [diag(1, 510)-5diag(1, 59)]P -1 =P diag(-4, 0)P -1⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=1111210004111121 ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛----=111122222.(2)设⎪⎪⎭⎫⎝⎛=122221212A ,求ϕ(A )=A 10-6A 9+5A 8.解 求得正交矩阵为⎪⎪⎪⎭⎫⎝⎛---=20223123161P , 使得P -1AP =diag(-1, 1, 5)=Λ, A =P ΛP -1. 于是 ϕ(A )=P ϕ(Λ)P -1=P (Λ10-6Λ9+5Λ8)P -1=P [Λ8(Λ-E )(Λ-5E )]P -1=P diag(1, 1, 58)diag(-2, 0, 4)diag(-6, -4, 0)P -1=P diag(12, 0, 0)P -1⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---=222033211001220223123161⎪⎪⎭⎫ ⎝⎛----=4222112112.25. 用矩阵记号表示下列二次型: (1) f =x 2+4xy +4y 2+2xz +z 2+4yz ; 解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=z y x z y x f 121242121) , ,(.(2) f =x 2+y 2-7z 2-2xy -4xz -4yz ; 解⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-------=z y x z y x f 722211211) , ,(.(3) f =x 12+x 22+x 32+x 42-2x 1x 2+4x 1x 3-2x 1x 4+6x 2x 3-4x 2x 4.解 ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫⎝⎛------=432143211021013223111211) , , ,(x x x x x x x x f . 26. 写出下列二次型的矩阵:(1)x x x ⎪⎭⎫⎝⎛=1312)(T f ;解 二次型的矩阵为⎪⎭⎫ ⎝⎛=1312A .(2)x x x ⎪⎪⎭⎫⎝⎛=987654321)(T f .解二次型的矩阵为⎪⎪⎭⎫⎝⎛=987654321A .27. 求一个正交变换将下列二次型化成标准形: (1) f =2x 12+3x 22+3x 33+4x 2x 3; 解二次型的矩阵为⎪⎪⎭⎫⎝⎛=320230002A .由)1)(5)(2(320230002λλλλλλλ---=---=-E A ,得A 的特征值为λ1=2, λ2=5, λ3=1. 当λ1=2时, 解方程(A -2E )x =0, 由⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-0001002101202100002~E A ,得特征向量(1, 0, 0)T . 取p 1=(1, 0, 0)T . 当λ2=5时, 解方程(A -5E )x =0, 由⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛---=-0001100012202200035~E A ,得特征向量(0, 1, 1)T . 取T )21 ,21 ,0(2=p .当λ3=1时, 解方程(A -E )x =0, 由⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=-000110001220220001~E A ,得特征向量(0, -1, 1)T . 取T )21 ,21 ,0(3-=p .于是有正交矩阵T =(p 1, p 2, p 3)和正交变换x =T y , 使f =2y 12+5y 22+y 32.(2) f =x 12+x 22+x 32+x 42+2x 1x 2-2x 1x 4-2x 2x 3+2x 3x 4. 解二次型矩阵为⎪⎪⎪⎭⎫⎝⎛----=111111001111011A . 由 2)1)(3)(1(1101111001111011--+=--------=-λλλλλλλλE A ,得A 的特征值为λ1=-1, λ2=3, λ3=λ4=1.当λ1=-1时, 可得单位特征向量T )21 ,21 ,21 ,21(1--=p .当λ2=3时, 可得单位特征向量T )21 ,21 ,21 ,21(2--=p .当λ3=λ4=1时, 可得线性无关的单位特征向量T )0 ,21 ,0 ,21(3=p , T)21 ,0 ,21 ,0(4=p . 于是有正交矩阵T =( p 1, p 2, p 3, p 4)和正交变换x =T y , 使f =-y 12+3y 22+y 32+y 42.28. 求一个正交变换把二次曲面的方程3x 2+5y 2+5z 2+4xy -4xz -10yz =1化成标准方程. 解二次型的矩阵为⎪⎪⎭⎫⎝⎛----=552552223A .由)11)(2(552552223||---=-------=-λλλλλλλE A ,得A 的特征值为λ1=2, λ2=11, λ3=0, .对于λ1=2, 解方程(A -2E )x =0, 得特征向量(4, -1, 1)T , 单位化得)231 ,231 ,234(1-=p .对于λ2=11, 解方程(A -11E )x =0, 得特征向量(1, 2, -2)T , 单位化得)32 ,32 ,31(2-=p .对于λ3=0, 解方程A x =0, 得特征向量(0, 1, 1)T , 单位化得)21 ,21,0(3=p . 于是有正交矩阵P =(p 1, p 2, p 3), 使P -1AP =diag(2, 11, 0), 从而有正交变换⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛w v u z y x 21322312132231031234, 使原二次方程变为标准方程2u 2+11v 2=1.29. 明: 二次型f =x T A x 在||x ||=1时的最大值为矩阵A 的最大特征值.证明 A 为实对称矩阵, 则有一正交矩阵T , 使得TAT -1=diag(λ1, λ2, ⋅ ⋅ ⋅, λn )=Λ成立, 其中λ1, λ2, ⋅ ⋅ ⋅, λn 为A 的特征值, 不妨设λ1最大. 作正交变换y =T x , 即x =T T y , 注意到T -1=T T , 有 f =x T A x =y T TAT T y =y T Λy =λ1y 12+λ2y 22+ ⋅ ⋅ ⋅ +λn y n 2. 因为y =T x 正交变换, 所以当||x ||=1时, 有||y ||=||x ||=1, 即y 12+y 22+ ⋅ ⋅ ⋅ +y n 2=1.因此f =λ1y 12+λ2y 22+ ⋅ ⋅ ⋅ +λn y n 2≤λ1,又当y 1=1, y 2=y 3=⋅ ⋅ ⋅=y n =0时f =λ1, 所以f max =λ1.30. 用配方法化下列二次形成规范形, 并写出所用变换的矩阵.(1) f (x 1, x 2, x 3)=x 12+3x 22+5x 32+2x 1x 2-4x 1x 3; 解 f (x 1, x 2, x 3)=x 12+3x 22+5x 32+2x 1x 2-4x 1x 3 =(x 1+x 2-2x 3)2+4x 2x 3+2x 22+x 32 =(x 1+x 2-2x 3)2-2x 22+(2x 2+x 3)2.令⎪⎩⎪⎨⎧+==-+=323223211222x x y x y x x x y , 即⎪⎪⎩⎪⎪⎨⎧+-==+-=323223211221225y y x y x yy y x ,二次型化为规范形f =y 12-y 22+y 32,所用的变换矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=12002102251C .(2) f (x 1, x 2, x 3)=x 12+2x 32+2x 1x 3+2x 2x 3; 解 f (x 1, x 2, x 3)=x 12+2x 32+2x 1x 3+2x 2x 3 =(x 1+x 3)2+x 32+2x 2x 3;=(x 1+x 3)2-x 22+(x 2+x 3)2. 令⎪⎩⎪⎨⎧+==+=32322311x x y x y x x y , 即⎪⎩⎪⎨⎧+-==-+=323223211y y x y x y y y x , 二次型化为规范形f =y 12-y 22+y 32,所用的变换矩阵为⎪⎪⎭⎫⎝⎛--=110010111C . (3) f (x 1, x 2, x 3)=2x 12+x 22+4x 32+2x 1x 2-2x 2x 3. 解 f (x 1, x 2, x 3)=2x 12+x 22+4x 32+2x 1x 2-2x 2x 3. 3223222212421)21(2x x x x x x -+++=232322212)2(21)21(2x x x x x +-++=.令⎪⎪⎩⎪⎪⎨⎧=-=+=333222112)2(21)21(2x y x x y x x y , 即⎪⎪⎩⎪⎪⎨⎧=+=--=33322321121222212121y x y y x y y y x , 二次型化为规范形f =y 12+y 22+y 32,所用的变换矩阵为⎪⎪⎭⎫ ⎝⎛--=10022011121C .31. 设f =x 12+x 22+5x 32+2ax 1x 2-2x 1x 3+4x 2x 3为正定二次型, 求a . 解二次型的矩阵为⎪⎪⎭⎫⎝⎛--=5212111a a A ,其主子式为a 11=1,2111a a a-=, )45(5212111+-=--a a a a .因为f 为正主二次型, 所以必有1-a 2>0且-a (5a +4)>0, 解之得054<<-a .32. 判别下列二次型的正定性:(1) f =-2x 12-6x 22-4x 32+2x 1x 2+2x 1x 3; 解二次型的矩阵为⎪⎪⎭⎫⎝⎛---=401061112A .因为0211<-=a ,0116112>=--, 038||<-=A , 所以f 为负定.(2) f =x 12+3x 22+9x 32+19x 42-2x 1x 2+4x 1x 3+2x 1x 4-6x 2x 4-12x 3x 4. 解二次型的矩阵为⎪⎪⎪⎭⎫⎝⎛------=19631690230311211A . 因为 0111>=a ,043111>=--, 06902031211>=--, 024>=A , 所以f 为正定.33. 证明对称阵A 为正定的充分必要条件是: 存在可逆矩阵U , 使A =U T U , 即A 与单位阵E 合同.证明 因为对称阵A 为正定的, 所以存在正交矩阵P 使P T AP =diag(λ1, λ2, ⋅ ⋅ ⋅, λn )=Λ, 即A =P ΛP T ,其中λ1, λ2, ⋅ ⋅ ⋅, λn 均为正数. 令), , ,diag(211n λλλ⋅⋅⋅=Λ, 则Λ=Λ1Λ1, A =P Λ1Λ1T P T .再令U =Λ1T P T , 则U 可逆, 且A =U T U .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正确答案:说法错误
解答参考:
13.
正确答案:说法正确
解答参考:
(注意:若有主观题目,请按照题目,离线完成,完成后纸质上交学习中心,记录成绩。在线只需提交客观题答案。)
三、主观题(共7道小题)
14.
参考答案:主观题答案暂不公布,请先自行离线完成。
15.
参考答案:主观题答案暂不公布,请先自行离线完成。
16.
2018-2019
一、单项选择题(只有一个选项正确,共6道小题)
1.
(A)
(B)
(C)
(D)
正确答案:B
解答参考:
2.
(A)
(B)
(C)
(D)
正确答案:C
解答参考:
3.
(A)
(B)
(C)
(D)
正确答案:D
解答参考:
4.
(A) m+n
((D) n-m
正确答案:D
解答参考:
5.
(A)
(B)
(C)
(D)
正确答案:D
解答参考:
6.
(A)
(B)
(C)
(D)
正确答案:B
解答参考:
二、判断题(判断正误,共7道小题)
7.
正确答案:说法错误
解答参考:
8.
正确答案:说法错误
解答参考:
9.
正确答案:说法错误
解答参考:
10.
正确答案:说法错误
解答参考:
11.
正确答案:说法正确
解答参考:
12.
参考答案:主观题答案暂不公布,请先自行离线完成。
17.
参考答案:主观题答案暂不公布,请先自行离线完成。
18.
计算四阶行列式
参考答案:主观题答案暂不公布,请先自行离线完成。
19.
求方程组
的一个基础解系并求其通解。
参考答案:主观题答案暂不公布,请先自行离线完成。
20.
a、b为何值时,线性方程组
有唯一解,无解或有无穷多解?在有无穷多解时,求其通解?
