FFT 算法详解
FFT快速傅里叶变换(蝶形算法)详解概要

5.4 按频率抽取的基2-FFT算法
算法原理
先把输入按n的顺序分成前后两半 再把输出X(k)按k的奇偶分组 设序列长度为N=2L,L为整数 前半子序列x(n) 后半子序列 x(n
nk x ( n ) W N
N 1
rk k rk x1 (r )W N WN x ( r ) W 2 N 2 2
k X 1 (k ) WN X 2 (k )
式中,X1(k)和X2(k)分别是x1(n)和x2(n)的N/2的DFT。
另外,式中k的取值范围是:0,1, …,N/2-1 。
N 2M , 第L级:
r WN W2jL , j 0,1,2,,2 L1 1
2 L 2 M 2 LM N 2 LM
W W
r N j N 2 L M
e
j
2 N 2 L M
j
e
j
2 j 2 M L N
W
j 2 M L N
r WN
的确定
25
序列的逆序排列
序列的逆序排列
由于 x(n) 被反复地按奇、偶分组,所以流图输入端的 排列不再是顺序的,但仍有规律可循: 因为 N=2M , 对于任意 n(0≤n ≤N-1),可以用M个 二进制码表示为:
n( DEC) (nM 1nM 2 n2 n1n0 ) ( BIN )
(2)周期性 (3)可约性 另外,
( n N ) k n( k N ) nk WN WN WN
mnk nk WmN WN
nk nk / m WN WN /m
( k N / 2) k WN WN
N /2 WN 1
8
FFT算法详解

FFT算法详解FFT (Fast Fourier Transform) 是一种高效的离散傅里叶变换算法,用于将时域信号转换为频域信号。
它在信号处理、图像处理、通信领域等具有广泛的应用。
本文将详细介绍FFT算法的原理和实现。
一、傅里叶变换的基本原理傅里叶变换是一种将信号从时域转换到频域的方法。
它将时域信号分解成多个不同频率的正弦和余弦函数的叠加。
傅里叶变换的基本公式为:F(k) = Σ_{n=0}^{N-1} f(n)e^{-2πikn/N}其中,F(k)是频域信号的复数表示,f(n)是时域信号的复数表示,N是信号长度,k是频率。
二、傅里叶变换的问题传统的傅里叶变换算法的时间复杂度为O(N^2),计算量较大,不适用于实时处理大型信号。
FFT算法通过分治的思想,将DFT(Digital Fourier Transform)问题转化为多个子问题,从而降低了计算复杂度。
三、蝶形运算蝶形运算的公式为:y_0=x_0+W_N^k*x_1y_1=x_0-W_N^k*x_1其中,x_0、x_1是输入,y_0、y_1是输出,W_N^k是旋转因子,N是信号长度,k是频率。
四、FFT算法的步骤1.将输入信号分成偶数下标和奇数下标的两个子序列。
2.对两个子序列分别进行FFT变换,得到两个子序列的频域表示。
3.将两个子序列的频域表示合并成完整的频域信号。
4.重复上述步骤,直到得到最终的频域信号。
五、FFT算法的实现1.初始化输入信号和旋转因子。
2.将输入信号按照偶数下标和奇数下标分成两个子序列。
3.对两个子序列分别进行FFT变换,递归调用FFT函数。
4.将两个子序列的频域表示合并成完整的频域信号。
5.返回最终的频域信号。
总结:FFT算法是一种高效的离散傅里叶变换算法,通过分治的思想将DFT问题分解为多个子问题,从而降低了计算复杂度。
它在信号处理、图像处理、通信领域等有着广泛的应用。
掌握FFT算法的原理和实现对于理解信号处理技术和提高算法效率具有重要意义。
现代通信中的FFT算法

现代通信中的FFT算法现代通信技术的发展离不开算法的支持,其中FFT算法是通信领域中最重要的数学算法之一。
在通信领域,FFT算法通过将连续时间函数转化为离散时间函数,大大地提高了通信的速度和效率。
本文将介绍FFT算法的基本原理、应用场景以及优化对策。
一、FFT算法基本原理FFT算法是快速傅立叶变换(Fast Fourier Transform)的缩写,是一种高效的信号处理算法,在信号压缩、遥感等领域有着广泛的应用。
FFT算法的基本原理是把连续的信号在一定的时间间隔内取样,然后用傅里叶变换公式将其转化为频域上的信息,再通过逆傅里叶变换将其转换回时域信号。
在通信领域,我们通常使用的是离散傅立叶变换(DFT),即将连续信号按照时间间隔取样,然后再进行傅立叶变换。
然而,直接通过DFT计算机算量巨大,效率低下。
FFT算法通过巧妙地将DFT分解为多个小的子问题,从而减少计算量,提高了算法的效率。
二、FFT算法的应用场景FFT算法广泛应用于数字信号处理、信道估计、多载波调制等领域。
以OFDM(Orthogonal Frequency-Division Multiplexing)技术为例,OFDM技术中的多载波信号可以通过FFT算法实现快速的频域处理,从而实现多载波信号的调制和解调。
此外,FFT算法还广泛应用于卫星遥感、医学影像处理等领域。
三、FFT算法的优化对策虽然FFT算法在通信领域中十分重要,但是其高算法复杂度限制了其在实际中的应用。
为了提高FFT算法的效率和性能,研究人员提出了许多优化对策。
以下是一些优化对策的介绍。
1.快速傅立叶变换算法:FFT算法的核心是快速傅立叶变换算法,其中最知名的是Cooley-Tukey算法。
该算法通过将DFT分解为多个小的子问题,在一定的时间复杂度内实现快速傅立叶变换。
2.算法并行化:随着计算机硬件性能的提高,通过并行化算法可以充分利用计算机多核CPU或GPU的并行计算能力,从而提高FFT算法的运算速度。
fft的计算原理

fft的计算原理FFT(Fast Fourier Transform)是一种高效地计算离散傅里叶变换(Discrete Fourier Transform, DFT)的算法。
FFT能够将一个时域上的离散信号转换到频域上,并可以用于信号分析、滤波、图像处理以及编码等领域。
FFT的计算原理可以从两个角度来讲解:一是从离散傅里叶变换(DFT)的定义出发,二是从FFT的具体计算过程中各个步骤的推导和实现。
首先,从DFT的定义出发,对一个离散信号x(n)进行DFT计算,可以得到其频域表示X(k),表示为:X(k) = Σ(x(n) * exp(-j2πkn/N))其中,N为信号的长度,k为频域采样点的索引,n为时域采样点的索引。
直接按照DFT的定义计算的复杂度是O(N^2),当信号长度很大时,计算量非常大。
FFT算法通过对DFT的变换矩阵进行分解,将复杂度降低到O(NlogN)。
然后,从FFT的具体计算过程中各个步骤的推导和实现来看。
以下是常见的快速傅里叶变换算法,即Cooley-Tukey算法的计算过程:1. 将信号x(n)分为两个部分:偶数索引部分x_e(n)和奇数索引部分x_o(n),分别由原信号的偶数索引和奇数索引采样得到。
2. 对x_e(n)和x_o(n)分别进行FFT计算,得到频域表示X_e(k)和X_o(k)。
3. 将得到的频域表示X_e(k)和X_o(k)按照以下公式合并得到最终的频域表示X(k):X(k) = X_e(k) + W_N^k * X_o(k)其中,W_N^k = exp(-j2πk/N)为旋转因子,可由欧拉公式得到。
4. 重复以上步骤,直到计算得到所有频域采样点的值。
以上就是FFT算法的基本原理和计算过程。
通过对信号进行分解和合并的方式,FFT算法能够大大减少计算量,快速地计算得到离散信号的频域表示。
后续还有一些对FFT算法进行改进和优化的方法,如快速傅里叶变换的再加工算法(Radix-2 FFT Algorithm)以及快速余弦和正弦变换(Fast Cosine and Sine Transform)等。
fft的用法 -回复

fft的用法-回复FFT,即快速傅里叶变换(Fast Fourier Transform),是一种高效的信号处理算法,用于快速计算傅里叶变换。
它广泛应用于数字信号处理、图像处理、通信和音频处理等领域。
在本文中,我将详细介绍FFT的原理、算法步骤以及应用。
一、傅里叶变换简介傅里叶变换是一种将信号从时域转换为频域的数学工具,它可以将一个信号分解为不同频率成分的叠加。
傅里叶变换公式为:F(w) = ∫f(t)e^(-jwt)dt其中,F(w)表示频域的复数函数,f(t)表示时域的函数,w为频率。
二、快速傅里叶变换原理FFT算法是在1965年由J.W. Cooley和J.W. Tukey发现的,它利用了傅里叶变换的对称性质,将O(n^2)复杂度的计算降低为O(nlogn)的复杂度。
FFT算法通过将信号采样点划分为不同的子集进行计算,并利用了旋转因子运算的特性,实现了快速的计算。
三、FFT算法步骤1. 输入信号首先,我们需要准备一个输入信号,该信号是以时间为自变量的实数函数。
通常,我们会对信号进行采样,得到一组离散的采样点。
2. 信号的长度针对采样点的数量,我们需要确定信号的长度为N。
在实际应用中,为了确保FFT的正确性,通常会选择2的整数次幂,即N=2^k。
3. 填充零如果信号的长度小于N,我们需要对其进行零填充,使其长度等于N。
这样做是为了保证FFT算法的正确性以及计算的高效性。
4. 快速傅里叶变换采用分治法的思想,FFT算法将信号分为两个子集,并分别计算它们的频谱。
然后,通过合并这些子集的结果以及旋转因子的运算,得到整个信号的频谱。
5. 频谱结果最后,我们可以得到信号的频谱结果,它表示了信号中不同频率成分的振幅和相位。
四、FFT的应用1. 音频处理在音频处理中,FFT被广泛应用于音频信号的频谱分析、波形绘制和滤波处理等方面。
通过FFT算法,我们可以将音频信号转化为频域表示,实现音频特征提取、音频识别以及音频效果的处理。
新手小白一看就会FFT算法的原理详解

新手小白一看就会FFT算法的原理详解傅里叶变换(Fourier Transform)是一种用于信号分析和图像处理的重要数学方法,它基于信号可以用一组正弦和余弦函数加权和表示的基本原理。
傅里叶变换主要通过将一个信号从时域变换到频域,实现信号的频谱分析和频域处理。
而快速傅里叶变换(Fast Fourier Transform,FFT)则是一种高效实现傅里叶变换的算法。
FFT算法的核心思想是分治策略,即将一个规模为N的问题分解为若干规模为N/2的子问题。
FFT算法借鉴了分治算法的优点,使得傅里叶变换的计算时间复杂度从O(N^2)下降到了O(NlogN),大大提高了计算效率。
下面将详细介绍FFT算法的原理。
首先,考虑需要进行傅里叶变换的一个离散的序列f(x),其中x为序列的下标。
这个序列可以看作是一个多项式的系数,傅里叶变换的目的是求得该多项式的根。
FFT算法的基本思路是将这个多项式分解为奇次和偶次项两个多项式的和,并分别对其进行傅里叶变换。
然后再将变换后的结果合并为最终的结果。
设序列f(x)的长度为N,可以将其分为两部分:f_e(x)=f(2x),其中x为偶数f_o(x)=f(2x+1),其中x为奇数那么f(x)可以表示为f_e(x^2)+f_o(x^2)*x对序列f_e(x)和f_o(x)分别进行N/2点的傅里叶变换,得到变换后的序列F_e(x)和F_o(x)。
接下来将F_e(x)和F_o(x)合并为最终的结果F(x)。
根据频域上两个序列的关系可知:F(x)=F_e(x)+W_N^x*F_o(x)其中W_N^x表示复数的单位根,即在单位圆上的第x个点。
根据Euler公式可知 W_N = exp(-2πi/N),则 W_N^x = exp(-2πi/N)^x,在计算机中可以通过查表或者递推的方式计算出。
最后,递归地将N个点的傅里叶变换转化为两个N/2个点的傅里叶变换,并利用合并的方式得到最终的结果。
总体而言,FFT算法可以通过递归的方式将一个长度为N的序列的傅里叶变换转化为两个长度为N/2的序列的傅里叶变换,并通过合并得到最终结果。
FFT算法详解

FFT算法详解2.3 快速傅⽴叶变换问题1) 问题背景在数值电路的传输中,为了避免信号⼲扰,需要把⼀个连续信号 x(t)先通过取样离散化为⼀列数值脉冲信号x(0), x(1), …… ,然后再通过编码送到传输电路中。
如果取样间隔很⼩,⽽连续信号的时间段⼜很长,则所得到的数值脉冲序列将⾮常庞⼤。
因此,传输这个编码信号就需要长时间的占⽤传输电路,相应地也需要付出昂贵的电路费⽤。
那么能否经过适当处理是使上述的数值脉冲序列变短,⽽同时⼜不会丧失有⽤的信息?的经过研究,⼈们发现,如果对上述数值脉冲序列作如下的变换处理:∑-=--=-==1/21,1,...,1,0,)()(N k Nnki i N n ek x n X π (1)则所得到的新序列X(0), X(1) , ……将⾮常有序,其值⽐较⼤的点往往集中在某⼀很狭窄的序列段内,这将⾮常有利于编码和存储,从⽽达到压缩信息的⽬的。
公式(1)就是所谓的离散傅⽴叶变换,简称DFT 。
现在我们来分析⼀下计算DFT 所需要的⼯作量。
如果我们不考虑公式(7.1)中指数项的运算,那么计算其每⼀个点X (n) 需要N 次复数乘法和N-1次的复数加法。
显然当N 很⼤时,这个⼯作量也⾮常巨⼤。
正是由于这个原因,使得DFT 的应⽤范围在过去很长的时间⾥受到了严格的限制。
注意到公式(1)是⾮常有规律性的,那么能否利⽤这种规律性来降低DFT 的计算时间?1965年,凯莱和塔柯的提出了⼀种⽤于计算DFT 的数学⽅法,⼤⼤减少了DFT 的计算时间,同时⼜特别适⽤于硬件处理,这就是所谓的快速傅⾥叶变换,简称FFT 。
鉴于DFT 的数据结构可以通过傅⽴叶变换的离散化获得,亦可通过三⾓插值得到,⽽本质上⼜同连续傅⾥叶分析有着极为密切的关系。
下⾯我们从傅⽴叶级数级数和傅⽴叶积分⼊⼿,导出DFT 结构的来源和FFT 的⼯作原理。
2)傅⽴叶变换如果x(t)是定义在整个实轴上的实值或复值函数,则其傅⽴叶变换可由下式给出:∞∞---==1,)()(/2i dt et x f X Tnift (2)若对任意参数f ,上述积分都存在,则(2)式确定了⼀个函数X(f),称为x(t) 的傅⽴叶变换。
fft计算公式

fft计算公式摘要:一、引言二、FFT 计算公式简介1.离散傅里叶变换2.快速傅里叶变换三、FFT 计算公式推导1.基2 递归算法2.蝴蝶运算四、FFT 在实际应用中的优势五、总结正文:一、引言在数字信号处理、图像处理等领域,傅里叶变换是一种非常重要的数学工具。
然而,对于大规模的信号处理问题,直接应用傅里叶变换的计算复杂度较高,因此,快速傅里叶变换(FFT)应运而生。
本文将详细介绍FFT 的计算公式及应用。
二、FFT 计算公式简介为了便于理解FFT 的计算公式,我们先简要介绍一下离散傅里叶变换(DFT)和快速傅里叶变换(FFT)。
1.离散傅里叶变换(DFT)DFT 是一种将离散信号从时域转换到频域的方法,其计算公式如下:X[k] = ∑N/2^n i^(-k+n) * x[n]其中,X[k] 表示频域的系数,x[n] 表示时域的信号,k 和n 分别为频域和时域的下标,N 为信号长度。
2.快速傅里叶变换(FFT)FFT 是DFT 的高效实现方法,它采用分治策略和循环移位技术,将DFT 的计算复杂度从O(N^2) 降低到O(NlogN)。
FFT 的计算公式如下:X[k] = ∑(N/2^n)^(2m) * C[m, k] * x[n]其中,m 为迭代次数,k 和n 分别为频域和时域的下标,N 为信号长度,C[m, k] 为复合基函数。
三、FFT 计算公式推导为了更直观地理解FFT 的计算过程,我们分两步进行推导。
1.基2 递归算法(1)首先,将输入序列x[n] 进行零填充,使其长度变为2 的整数次幂,即N = 2^n。
(2)将x[n] 和x[n+N/2] 进行旋转,得到x[n] 和x[n+N/2],其中x[n] 为原始序列,x[n+N/2] 为旋转后的序列。
(3)对旋转后的序列进行DFT 计算,得到频域系数X[k] 和X[k+N/2]。
(4)根据旋转序列的关系,可以得到频域系数X[k+N/2] = X[k],因此,我们只需计算一半的频域系数。
详解FFT(快速傅里叶变换FFT

knN W N N第四章 快速傅里叶变换有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长 序列.但其计算量太大,很难实时地处理问题,因此引出了快速傅里叶变换 (FFT). 1965 年,Cooley 和 Tukey 提出了计算离散傅里叶变换(DFT )的快 速算法,将 DFT 的运算量减少了几个数量级。
从此,对快速傅里叶变换(FFT ) 算法的研究便不断深入,数字信号处理这门新兴学科也随 FFT 的出现和发 展而迅速发展。
根据对序列分解与选取方法的不同而产生了 FFT 的多种算 法,基本算法是基2DIT 和基2DIF 。
FFT 在离散傅里叶反变换、线性卷积 和线性相关等方面也有重要应用。
快速傅里叶变换(FFT )是计算离散傅里叶变换(DFT )的快速算法。
DFT 的定义式为N −1X (k ) = ∑ x (n )W NR N (k )n =0在所有复指数值 W kn 的值全部已算好的情况下,要计算一个 X (k ) 需要 N 次复数乘法和 N -1 次复数加法。
算出全部 N 点 X (k ) 共需 N 2次复数乘法和 N ( N − 1) 次复数加法。
即计算量是与 N 2成正比的。
FFT 的基本思想:将大点数的 DFT 分解为若干个小点数 DFT 的组合, 从而减少运算量。
W N 因子具有以下两个特性,可使 DFT 运算量尽量分解为小点数的 DFT运算:(1) 周期性:( k + N ) nN= W kn= W ( n + N ) k(2) 对称性:W( k + N / 2 )= −W kNN利用这两个性质,可以使 DFT 运算中有些项合并,以减少乘法次数。
例子:求当N=4 时,X(2)的值4 NNN3∑44444X (2) = n =0x (n )W 2 n = x (0)W 0 + x (1)W 2 + x (2)W 4 + x (3)W 6= [ x (0) + x (2)]W 0 + [ x (1) + x (3)]W 2(周期性)4=[ x (0) + x (2)]-[ x (1) + x (3)]W 04(对称性)通过合并,使乘法次数由 4 次减少到 1 次,运算量减少。
按时间抽取的FFT算法讲义

按时间抽取的FFT算法讲义1. 引言FFT(快速傅里叶变换)算法是一种高效的计算离散傅里叶变换(DFT)的方法,被广泛应用于信号处理、图像处理和科学计算等领域。
在本讲义中,我们将按照时间的顺序介绍FFT 算法的基本原理和步骤。
2. DFT的定义离散傅里叶变换(DFT)将离散时间域的信号转换为频域的复数信号,其定义为:X(k) = Σ[x(n) * exp(-j*2πnk/N)]其中,X(k) 表示频域的复数信号,x(n) 是输入的离散时间域信号,N 是信号的样本点数,k 是频率索引(0 ≤ k < N)。
3. DFT的计算DFT的直接计算方法是通过遍历所有频率索引 k,并计算上述公式。
但这种方法的时间复杂度为 O(N^2),当样本点数较大时计算开销较大。
4. 快速傅里叶变换的思想FFT算法的核心思想是将 DFT 的计算过程分解为多个规模较小的 DFT 计算,以降低计算的复杂度。
具体而言,FFT算法利用了信号的周期性质,将输入信号划分为奇数索引和偶数索引的两个子序列,分别进行 DFT 的计算。
5. 雷德算法(Radix-2)雷德算法是FFT算法的一种常用实现方式,其基本思路是将DFT 计算递归地分解为规模为 M/2 的子问题,并利用旋转因子求解。
6. FFT算法的步骤(1)输入信号 x(n) 的样本点数为 N,其中 N 必须为2的幂次,否则需要进行零填充。
(2)将输入信号分解为奇数索引和偶数索引的两个子序列。
(3)对两个子序列分别进行 FFT 的计算。
(4)通过旋转因子和蝶形结构计算两个子序列的 DFT。
(5)将两个子序列的 DFT 结果合并得到整个信号的 DFT。
7. FFT算法的优势相较于直接计算DFT,FFT算法具有以下优势:- 时间复杂度为 O(NlogN),较直接计算的 O(N^2) 更高效。
- 适用于样本点数为2的幂次的信号。
- 算法实现简单易懂,且可以通过并行计算进一步提高效率。
FFT(快速傅里叶变换)算法详解

FFT (快速傅⾥叶变换)算法详解多项式的点值表⽰(Point Value Representation)设多项式的系数表⽰(Coefficient Representation):P a (x )=a 0+a 1x +a 2x 2+⋯+a n −1x n −1=n −1∑i =0a ix i则我们对上⾯的式⼦可以代⼊不同的 n 个 x 的值,构成⼀个 n 维向量:P a (x 0)P a (x 1)P a (x 2)⋮P a (x n −1)=1x 0x 20⋯x n −101x 1x 21⋯x n −111x 2x 22⋯x n −12⋮⋮⋮⋱⋮1x n −1x 2n −1⋯x n −1x −1a 0a 1a 2⋮a n −1更简洁的写法:P a =X α对上式观察后发现,X 是所谓的范德蒙德矩阵(Vandermonde's Matrix),在 n 个 x 的值不同的情况下,其⾏列式的值为:det (X )=∏0⩽i <j ⩽n −1(x j −x i )很明显,当所有 n 个 x 取值不同时,其⾏列式不为零,因此 X 可逆。
所以我们可以唯⼀确定多项式系数构成的向量 α:α=X −1P a也就是说,多项式 P a (x ) 还可以由 n 个 x 代⼊得到的 n 个点值来唯⼀表⽰:{x 0,P(x 0),x 1,P(x 1),x 2,P(x 2),⋯,x n −1,P(x n −1)}这就是多项式的点值表⽰。
多项式的点值表⽰是指,对于 n 次多项式,可以⽤ n 个不同的 x 和与之对应的多项式的值 P(x ) 构成⼀个长度为 n 的序列,这个序列唯⼀确定多项式,并且能够与系数表⽰相互转化。
n 次单位根了解了多项式的点值表⽰,⼀个很⾃然的问题是:如何选择 x 的值,来防⽌其指数⼤⼩爆炸型增长呢?这⾥可以借⽤复数的单位根。
简单回顾⼀下,复数有两种表⽰⽅法:迪卡尔积坐标表⽰和极坐标表⽰,这⾥我们⽤到的是后者:z =re i θi 是虚数单位,r 表⽰模长,θ 表⽰相⾓。
详解快速傅里叶变换FFT算法

详解快速傅里叶变换FFT算法快速傅里叶变换(FFT)算法是一种高效的计算离散傅里叶变换的方法。
它通过将傅里叶变换问题分解为更小的子问题,从而减少计算量。
FFT算法广泛应用于信号处理、图像处理和其他科学与工程领域。
FFT算法的核心思想是将一个长度为N的复数序列分解为两个长度为N/2的复数序列,并重用其计算结果。
这种分解是通过将序列的奇数项与偶数项分为两组来实现的。
分解后可以继续将长度为N/2的序列分解为长度为N/4的序列,直到序列长度为1时停止。
然后,通过合并这些子问题的解,我们可以得到原始问题的解。
FFT算法的关键步骤可以概括为以下几点:1.首先,将输入序列通过位逆序操作重新排列。
这是为了便于分解和合并子问题的解。
2.然后,将序列分解为两个长度为N/2的子序列。
一组是奇数项,另一组是偶数项。
3.对两个子序列进行递归调用FFT算法,分别计算它们的傅里叶变换。
4.将子问题的解合并为原始问题的解。
这是通过使用每个子问题的解的一部分和一些旋转因子来完成的。
5.重复以上步骤,直到得到最终的傅里叶变换结果。
FFT算法的时间复杂度是O(NlogN),相对于朴素的傅里叶变换(时间复杂度为O(N^2)),有着显著的性能优势。
这个优势主要来自于FFT算法中子问题的重用和分治思想的应用。
FFT算法的应用非常广泛。
在信号处理中,FFT算法可以用来分析信号的频域特征,还可以用于滤波、频谱分析和频率估计等。
在图像处理中,FFT算法被用来进行图像变换,包括傅里叶变换、离散余弦变换等。
此外,FFT算法还被广泛应用于通信、雷达和声音等领域中的数据处理和分析。
总的来说,FFT算法通过分解和重用子问题的解,实现了高效的计算离散傅里叶变换的目的。
它的应用范围广泛,并且在在很多领域中被广泛使用。
快速傅里叶变换(FFT)的原理及公式
快速傅里叶变换(FFT)的原理及公式原理及公式非周期性连续时间信号x(t)的傅里叶变换可以表示为式中计算出来的是信号x(t)的连续频谱。
但是,在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。
因此需要利用离散信号x(nT)来计算信号x(t)的频谱。
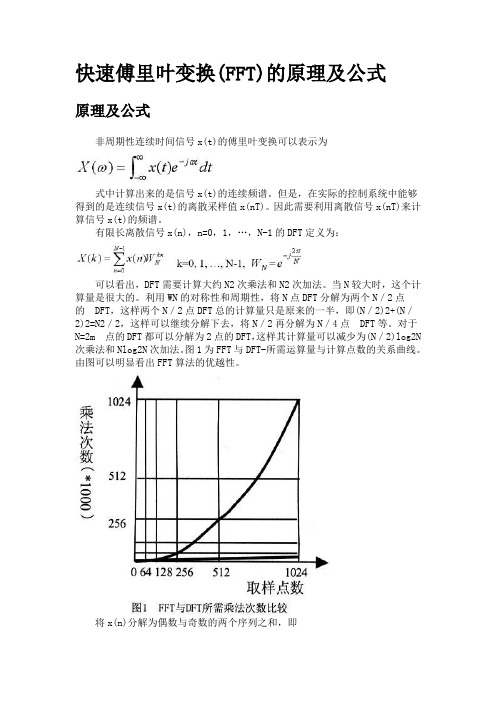
有限长离散信号x(n),n=0,1,…,N-1的DFT定义为:可以看出,DFT需要计算大约N2次乘法和N2次加法。
当N较大时,这个计算量是很大的。
利用WN的对称性和周期性,将N点DFT分解为两个N/2点的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。
对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N 次乘法和Nlog2N次加法。
图1为FFT与DFT-所需运算量与计算点数的关系曲线。
由图可以明显看出FFT算法的优越性。
将x(n)分解为偶数与奇数的两个序列之和,即x1(n)和x2(n)的长度都是N/2,x1(n)是偶数序列,x2(n)是奇数序列,则其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。
由于X1(k)和X2(k)均以N/2为周期,且WN k+N/2=-WN k,所以X(k)又可表示为:上式的运算可以用图2表示,根据其形状称之为蝶形运算。
依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。
图3为8点FFT的分解流程。
FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换,降低了运算要求,提高了与运算速度。
FFT不是DFT的近似运算,它们完全是等效的。
关于FFT精度的说明:因为这个变换采用了浮点运算,因此需要足够的精度,以使在出现舍入误差时,结果中的每个组成部分的准确整数值仍是可辨认的。
为了FFT的舍入误差,应该允许增加几倍log2(log2N)位的二进制。
FFT快速傅里叶变换详解

FFT快速傅里叶变换详解FFT(Fast Fourier Transform)快速傅里叶变换是一种高效的算法,用于将一个信号的时域表示转换为频域表示。
它基于分治思想,通过递归的将输入序列划分为较小的子序列,然后合并子序列的变换结果来获得整个序列的变换结果。
蝶形算法是FFT的核心思想之一、它通过将输入序列分为两组,每组包含偶数索引和奇数索引的元素,然后对每组执行蝶形计算。
蝶形计算的基本思想是,将输入序列中的每个元素与另一个元素进行乘积,并根据一定的规则进行合并。
具体而言,蝶形算法的步骤如下:1.将输入序列分为两组,一组包含偶数索引的元素,另一组包含奇数索引的元素。
2.对每组执行蝶形计算。
蝶形计算的基本公式为:Y[k]=X1[k]+W_N^k*X2[k],其中X1[k]和X2[k]分别表示输入序列的两个子序列的第k个元素,Y[k]表示计算结果,W_N^k表示旋转因子,N表示序列的长度。
旋转因子的计算公式为:W_N^k=e^(-j*2πk/N),其中j表示虚数单位。
3.重复步骤2,直到计算完所有的蝶形计算。
4.最后,将两组子序列的变换结果合并。
合并的方式是,将两个子序列的变换结果分别与旋转因子进行乘积,并按照一定的规则相加。
通过蝶形算法,FFT可以将一个长度为N的序列的变换时间复杂度从O(N^2)降低到O(NlogN)。
这使得FFT在信号处理、图像处理、通信等领域得到广泛应用,例如音频信号的频谱分析、图像的频域滤波等。
需要注意的是,蝶形算法要求输入序列的长度为2的幂次。
对于长度不是2的幂次的序列,可以通过补零或者裁剪的方式使其长度变为2的幂次,但这可能会引入一定的误差。
总结起来,FFT快速傅里叶变换通过蝶形算法实现高效的频域变换。
蝶形算法将输入序列分为两组,对每组执行蝶形计算,并最终合并结果。
通过蝶形算法,FFT的时间复杂度由O(N^2)降低到O(NlogN),使得其在信号处理等领域发挥重要作用。
FFT算法详解

FFT算法详解快速傅里叶变换(Fast Fourier Transform, FFT)算法是一种高效的计算离散傅里叶变换(Discrete Fourier Transform, DFT)的方法,广泛应用于信号处理、图像处理、通信等领域。
本文以详细的解释为主,全面讲解FFT算法。
傅里叶变换将一个信号从时域转换到频域,即将信号表示为不同频率分量的叠加。
如果信号为离散的,则称为离散傅里叶变换(DFT)。
DFT 的计算复杂度为O(N^2),其中N是信号的长度。
然而,通过观察DFT的计算过程,我们可以发现其中存在着很多重复计算。
FFT算法就是通过减少这些重复计算的方式,降低了DFT的计算复杂度到O(NlogN)。
FFT算法的核心思想是DFT分治思想,将DFT递归地分解为更小的DFT,最终合并得到原始信号的DFT结果。
具体来说,FFT算法将长度为N 的信号分为两半,分别计算这两部分信号的DFT,然后再将它们合并成N/2个长度为2的DFT,重复这个过程直到计算得到最小粒度的DFT。
假设N为2的整数次幂,一个长度为N的信号X可以表示为X=x[0],x[1],...,x[N-1]。
FFT的计算可以分为两个步骤:分解和合并。
分解步骤:1.如果N=1,直接返回x;2.将长度为N的信号X分为两半,分别记作X0和X1,其中X0=x[0],x[2],...,x[N-2],X1=x[1],x[3],...,x[N-1];3.对X0和X1分别递归地执行FFT计算,得到长度为N/2的结果Y0和Y1;4.构造长度为N的结果Y,其中Y[k]=Y0[k]+W_N^k*Y1[k],其中W_N=e^(-2πi/N),0<=k<N/2;5.返回Y。
合并步骤:将长度为N/2的结果Y0和Y1合并为长度为N的结果Y,其中Y[k]=Y0[k]+W_N^k*Y1[k],其中W_N=e^(-2πi/N),0<=k<N/2通过分解和合并的操作,FFT算法可以高效地计算DFT。
FFT算法设计(含程序设计)

FFT算法设计(含程序设计)FFT算法设计(含程序设计)一、概述FFT(快速傅里叶变换)是一种高效的计算DFT(离散傅里叶变换)的算法,它可以将一个长度为N的复数序列在O(NlogN)的时间复杂度内进行变换。
FFT广泛应用于信号处理、图像处理、通信系统等领域。
二、FFT算法原理1. DFT的定义离散傅里叶变换(DFT)用于将一个时域上的离散信号转换为频域上的复数序列。
对于长度为N的输入序列x(n),DFT的定义如下:其中,W是N次单位根的复数。
2. FFT的基本思想FFT是通过分治法将一个长度为N的DFT问题分解成多个长度小于N的DFT问题来求解的。
其基本思想如下:当N为奇数时,将输入序列分成两部分,奇数下标部分和偶数下标部分;分别对奇数下标部分和偶数下标部分进行长度为N/2的DFT变换;利用旋转因子进行结果合并。
通过以上步骤,可以将一个长度为N的DFT问题转化为两个长度为N/2的DFT问题。
3. 快速傅里叶变换的递归算法快速傅里叶变换(FFT)是一种基于递归的计算DFT的算法。
其基本过程如下:若N=1,则直接返回输入序列作为结果;将输入序列分成两部分,奇数下标部分和偶数下标部分;对奇数下标部分和偶数下标部分分别进行FFT变换;利用旋转因子进行结果合并。
通过递归的方式,可以将一个长度为N的DFT问题分解为多个长度为1的DFT问题,从而实现FFT的求解。
三、FFT算法实现下面是一个基于C语言的FFT算法的实现示例:cinclude <stdio.h>include <math.h>include <complex.h>define PI 3.149323846void fft(complex double x, int n) {if (n == 1) {return;}complex double odd = malloc(sizeof(complex double) (n / 2));complex double even = malloc(sizeof(complex double) (n / 2));for (int i = 0; i < n / 2; i++) {even[i] = x[2 i];odd[i] = x[2 i + 1];}fft(odd, n / 2);fft(even, n / 2);for (int k = 0; k < n / 2; k++) {complex double t = cexp(-I 2 PI k / n) odd[k];x[k] = even[k] + t;x[k + n / 2] = even[k] t;}free(odd);free(even);}int mn() {int n;printf(\。
FFT算法详解

FFT算法详解快速傅里叶变换(Fast Fourier Transform,FFT)是一种高效的计算傅里叶变换的算法。
傅里叶变换是一种将信号从时域转换到频域的方法,它能够将一个时域上的信号表示为一系列不同频率的正弦和余弦函数。
FFT算法的基本思想是将一个N点的离散傅里叶变换分解为多个较小规模的离散傅里叶变换,并利用这些较小规模的变换的结果快速计算出原始信号的傅里叶变换。
这种分治的思想使得FFT算法的时间复杂度为O(NlogN),远远优于朴素的傅里叶变换算法的时间复杂度O(N^2)。
下面详细介绍FFT算法的过程:1.假设有一个长度为N的输入序列x[n],其中n从0到N-1、首先将序列x[n]划分为偶数下标序列x_e[n]和奇数下标序列x_o[n],即x_e[n]=x[2n]和x_o[n]=x[2n+1]。
2.分别对序列x_e[n]和x_o[n]进行FFT变换。
对于每个序列,可以继续进行递归的分解,将其划分为更小规模的序列,直到序列长度为1为止。
3.利用蝴蝶运算的方法,将两个较小规模的FFT变换的结果合并为一个较大规模的FFT变换的结果。
蝴蝶运算是指将两个复数相乘后加到另一个复数上的运算。
4.重复第3步,直到所有序列都合并为一个长度为N的FFT变换。
上述步骤可以通过递归的方式实现,也可以通过迭代的方式实现。
下面介绍一种迭代的方式:1.初始化一个长度为N的输入序列x[n],将其按照倒位序重新排列,得到一个新的序列X[n]。
具体的排列方式为,将x[n]的二进制位反转后所得到的二进制数转换为十进制数。
2.设置一个变量m,初始值为2(即每两个元素合并为一个的步长),进行迭代。
3. 对于每个步长m,分别计算W_m^0, W_m^1, ..., W_m^{m-1}的值,其中W_m^k = e^{-2 \pi i k/m}。
这些值可以预先计算并保存,以减少重复计算。
4.对于每个步长m,将序列X[n]划分为m个长度为N/m的子序列,分别为X_0[n],X_1[n],...,X_{m-1}[n]。
常用FFT算法

常用FFT 算法总结一、DFT 及IDFT 的定义对于N 点有限长序列)(n x ,其DFT 及IDFT 定义如下: DFT :∑-==10)()(N n nk N W n x k XIDFT :∑-=-=1)(1)(N k nk NWk X Nn x其中,Np j p NeW/2π-=称为旋转因子,p 称为旋转因子的指数。
二、基2-FFT 算法 设序列)(n x 的长度N 满足MN2=,M 为自然数。
1、时间域抽取FFT (DIT-FFT ) (1)算法原理按n 的奇偶把)(n x 分解为两个N/2点的子序列:)12()()2()(21+==r x r x r x r x则)(n x 的DFT 为)()()12()2()(2112/0)12(12/02k X W k X Wr x Wr x k X kN N r k r NN r rk N+=++=∑∑-=+-=其中)(1k X 和)(2k X 分别为)(1r x 和)(2r x 的N/2点DFT 。
利用)(1k X 和)(2k X 的周期性,)(k X 可以表示为⎪⎩⎪⎨⎧-=++=)()()2()()()(2121k X W k X N k X k X W k X k X kN k N 上式表明一个N 点的DFT 可以用两个N/2点的DFT 来表示。
(2)运算量 当MN2=时,共有M 级蝶形,每级N/2个蝶形,每个蝶形有1次复数乘法2次复数加法。
复数乘法:NN M N mF2log22==复数加法:NN NM a F2log==NN NN NFFT m DFT m F F 222log2log 2)()(==(3)蝶形运算⎪⎩⎪⎨⎧-=+=----)()()()()()(1111j X W k X j X j X W k X k X m pN m m m pN m m m表示第m 级迭代,k 和j 表示数据所在的行数,12-+=m k j ,m M k p -⋅=2。
FFT原理讲解及实现指南

FFT原理讲解及实现指南FFT(快速傅里叶变换)是一种高效的算法,用于将一个离散的时间域信号转换为频域信号。
在信号处理、图像处理以及通信领域,FFT是一种非常重要的工具。
一、FFT原理讲解傅里叶变换是一种将一个连续时间域信号转换为频域信号的方法。
其数学表达式为:X(f) = ∫x(t)e^(-j2πft)dt其中,X(f)表示频域信号,x(t)表示时间域信号,f表示频率,j表示虚数单位。
然而,对于离散时间信号,我们可以使用离散傅里叶变换(DFT)来对其进行频域分析。
DFT的公式如下:X(k) = Σx(n)e^(-j2πnk/N)其中,X(k)表示离散频域信号,x(n)为离散时间信号,N为采样点数,k表示频率。
FFT是一种用于快速计算DFT的算法,其基本原理是将DFT的计算复杂度从O(N^2)降低到O(NlogN)。
FFT的算法思路是:将N个采样点分为偶数和奇数序列,然后对偶数和奇数序列分别进行DFT变换,得到两个较小的DFT结果。
然后再将这两个较小的DFT结果合并,得到最终的DFT结果。
二、FFT实现指南1.选择合适的FFT库:在实际应用中,我们可以选择一些已有的FFT库来实现FFT算法,例如FFTW、MKL等。
2.确定输入信号:首先,需要确定待处理的离散时间信号x(n)。
3.计算FFT:使用FFT库提供的函数,对输入信号进行FFT计算。
常见的FFT库一般提供了相应的API,通过输入参数,得到计算出的离散频域信号X(k)。
4.获取频域信息:根据需要,可以从计算出的离散频域信号X(k)中提取相应的频域信息,例如频率分量、频谱等。
5.可选步骤:根据实际需求,可以进行滤波、频率域增强等操作。
6.反变换:如果需要将频域信号转换为时间域信号,可以使用反变换。
需要注意的是,FFT算法主要适用于离散时间信号的频域分析。
在实际应用中,可能还需要考虑信号预处理、采样率等因素。
三、总结FFT是一种高效的算法,用于离散时间信号的频域分析。
fft计算公式

fft计算公式摘要:1.傅里叶变换与快速傅里叶变换2.傅里叶级数3.快速傅里叶变换计算公式4.实际应用中的快速傅里叶变换正文:一、傅里叶变换与快速傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的数学方法,它可以帮助我们分析信号的频率成分。
在实际应用中,对于大规模的信号处理,傅里叶变换的计算复杂度较高,因此,为了提高计算效率,人们提出了快速傅里叶变换(FFT)算法。
二、傅里叶级数傅里叶级数是傅里叶变换的数学表达形式,它可以将一个周期函数表示为一系列正弦和余弦函数之和。
傅里叶级数的公式如下:f(x) = a0/2 + Σ[an*cos(nx) + bn*sin(nx)] (n 从0 到N-1)其中,a0 表示直流分量,an 和bn 表示正弦和余弦分量的幅值,n 表示频率。
三、快速傅里叶变换计算公式快速傅里叶变换的计算公式是基于傅里叶级数的逆变换得到的。
其基本思想是将傅里叶级数中的每个频率分量的计算分解成更小的子问题,从而减少计算量。
快速傅里叶变换的计算公式如下:X(k) = Σ[ak*cos(Nk*x) + bk*sin(Nk*x)] (k 从0 到N-1)其中,X(k) 表示频域信号,ak 和bk 表示频域信号的幅值,N 表示信号长度。
四、实际应用中的快速傅里叶变换快速傅里叶变换在实际应用中具有广泛的应用,例如信号处理、图像处理、音频处理等领域。
在信号处理中,快速傅里叶变换可以帮助我们提取信号的频率特征,从而识别信号的来源;在图像处理中,快速傅里叶变换可以用于图像的频域滤波,提高图像的质量;在音频处理中,快速傅里叶变换可以用于音频信号的频谱分析,实现音色识别等功能。
总之,快速傅里叶变换作为一种高效的频域信号处理方法,在各个领域都有着重要的应用价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 快速傅立叶变换问题1) 问题背景在数值电路的传输中,为了避免信号干扰,需要把一个连续信号 x(t)先通过取样离散化为一列数值脉冲信号x(0), x(1), …… ,然后再通过编码送到传输电路中。
如果取样间隔很小,而连续信号的时间段又很长,则所得到的数值脉冲序列将非常庞大。
因此,传输这个编码信号就需要长时间的占用传输电路,相应地也需要付出昂贵的电路费用。
那么能否经过适当处理是使上述的数值脉冲序列变短,而同时又不会丧失有用的信息?的经过研究,人们发现,如果对上述数值脉冲序列作如下的变换处理:∑-=--=-==1/21,1,...,1,0,)()(N k Nnki i N n ek x n X π (1)则所得到的新序列X(0), X(1) , ……将非常有序,其值比较大的点往往集中在某一很狭窄的序列段内,这将非常有利于编码和存储,从而达到压缩信息的目的。
公式(1)就是所谓的离散傅立叶变换,简称DFT 。
现在我们来分析一下计算DFT 所需要的工作量。
如果我们不考虑公式(7.1)中指数项的运算,那么计算其每一个点X (n) 需要N 次复数乘法和N-1次的复数加法。
显然当N 很大时,这个工作量也非常巨大。
正是由于这个原因,使得DFT 的应用范围在过去很长的时间里受到了严格的限制。
注意到公式(1)是非常有规律性的,那么能否利用这种规律性来降低DFT 的计算时间?1965年,凯莱和塔柯的提出了一种用于计算DFT 的数学方法,大大减少了DFT 的计算时间,同时又特别适用于硬件处理,这就是所谓的快速傅里叶变换,简称FFT 。
鉴于DFT 的数据结构可以通过傅立叶变换的离散化获得,亦可通过三角插值得到,而本质上又同连续傅里叶分析有着极为密切的关系。
下面我们从傅立叶级数级数和傅立叶积分入手,导出DFT 结构的来源和FFT 的工作原理。
2) 傅立叶变换如果x(t)是定义在整个实轴上的实值或复值函数,则其傅立叶变换可由下式给出:⎰∞∞---==1,)()(/2i dt et x f X Tnift (2)若对任意参数f ,上述积分都存在,则(2)式确定了一个函数X(f),称为x(t) 的傅立叶变换。
如果已知X(f) 则利用如下的傅立叶逆变换,还可复原x(t) :⎰∞∞--==1,)()(/2i df ef X t x Tnift (3)若x(t) 和 X(f) 同时满足(2)、(3)式,则称他们是一个傅立叶变换对,记为)()(f X t x ⇔。
通常X(f) 是一个复函数,因此可以写成如下两部分:i f I f R f X )()()(+= , 1-=i (4)式子中R(f) ,I(f) 分别是X(f) 的实部和虚部。
将上式表示为指数形式:)()()(f i ef X f X φ= 1-=i (5)其中)()()(22f I f R f X +=(6)))()(()(1f R f I tgf -=φ工程技术中,常将x(t) 看成一时间信号,相应的空间,称为时间域和空域;将其傅立叶变换X(f) 看成频率函数,相应的空间称为频域。
)(f X 称为x(t) 的傅立叶谱,而)(f φ称为其相角,这在物理上是有良好背景的。
的譬如此频率的的含义可以这样来理解:应用欧拉公式可将指数项表示成正弦-余弦的形式,如果把(2)式解释成离散项和的极限,则显然X(f)是包含了无限项正弦-余弦的和,而且f 的每一个值确定了所对应的正弦-余弦的频率。
在以后的叙述中,我们不妨用t 表示时间,用f 表示频率;同时用小写字母表示时间函数,并用相应的大写字母表示其傅立叶变换。
傅立叶变换可很容易地推广到二维情形。
假设x(t , s)是连续的和可积的,且X(f , g)是可积的,则相应的傅立叶变换对如下:⎰⎰∞∞-∞∞-+--==1,),(),(/)(2i dtds es t x g f X Tgs ft ni (7)⎰∞∞-+-==1,),(),(/)(2i dfdg eg f X s t x Tgs ft ni (8)3) 离散傅立叶变换尽管傅立叶级数和傅立叶变换具有非常优美的数学结构,但并不实用,并为他们都无法用有限字长的计算机作逻辑上的运算。
为此,我们必须建立傅立叶变换的数值方法,并由此导出DFT 数据结构的来源。
a. 傅立叶积分的离散化由于傅立叶变换无法用数字计算机进行逻辑运算,工程分析中,通常采用抽样的方法,观测x(t)的一些离散值,然后利用数值积分将傅立叶变换离散化。
函数抽样是函数插值的逆过程,假定用取2N+1 个互相间隔为 t ∆的节点的方法,当一个连续函数x(t) 离散化为的一个序列:}),(),...,(),0(),(),...,({t N x t x x t x t N x ∆∆∆-∆-于是当N 充分大时,有:⎰∆∆--≈tN tN niftdtet x f X 2)()( (9)现在我们把(9)式中的求积函数当成周期为t N ∆2的函数,以Nj t j ±±±=∆,...2,1,0,为节点,对(9)式用复化梯形公式做数值积分得∑-=∆-∆∆≈NNn tnifn et n x tf X 12)()( (10)对f 进行离散化,取1,...2,1,0),/(-=∆=N j t N j f , 则上式可改写:∑-=--=∆∆≈∆NNn Nnijn N j et n x ttN j X 1/21,...,1,0,)()((11)这就是一维傅立叶积分的离散表达式。
b 离散傅立叶变换在上面,我们普便的遇到了带有复指数乘积项的和式。
实际上,这种特殊的数据结构可利用以下更为一般的方式定义。
给定N 个实或复的数列{x(0), x(1),……x(N-1)},定义∑-=--=-==1/21,1,...,1,0,)()(N k Nnki i N n ek x n X π (12)为{x(k)}的离散傅立叶变换,简称DFT 。
我们指出,(11)式可以转化成上述一般形式。
这说明(12)式与傅立叶变换之间存在内在的联系,渴望获得与连续傅立叶变换相类似的性质,事实上确实如此。
下面我们就来做这件事。
首先说明,由(12)式确定的序列{X(n)}可以恢复为原序列{x(k)}。
事实上,在(12)式两边同乘以Nnijn e/2,并对n 从0 到n-1求和得:∑∑∑-=--=-==1/)(211/2)()(N k Ni k j n N n N n Nnji ek x en X ππ∑∑-=--==1/)(21][)(N n nNi k j n N k ek x πNi k j n ik j n N jk k eek x j Nx /)(2)(21,011)()(---≠=--+=∑ (13)注意到(13)式的和式中分子部分为0,从而∑-=-==1/21,...,1,0,)(1)(N n Nnji N j en X Nj x π (14)今后我们称(14)式是(12)式的逆变换,并称{x(k)}和{X(n)}为离散傅立叶变换对,简记为)()(n X k x ⇔离散傅立叶变换的这种可恢复性质,在工程技术中有着极为重要的应用。
因为,可以通过抽样获得一组的离散值,并利用DFT 转换为另一组数据,通过对变换数据的修改以及逆变换,达到对原数据的修正。
这也正是DFT 最具魅力的地方。
应用DFT 作数值分析,抽样也变得相当简单。
这时,可以抽取函数的任一片断,而无需象傅立叶变换离散化那样做对称抽样。
4) 快速傅里叶变换本节我们将把注意力集中在如何计算DFT 上。
如果我们不考虑(12)式中的复指数部分的运算,则求解(12)式共需要N * N 次乘法和N * (N-1)次加法。
显然当N 很大时,其工作量是相当可观的。
为此,凯莱和卡柯提出了一种专门用于处理DFT 的快速算法(FFT), 大大减少了DFT 的计算时间。
充分理解FFT 的工作原理,这并不需要高深的数学知识,只要时刻的盯住DFT 的数据结构即可。
为了便于理解,我们先从最简单的情形入手。
a FFT 直观发展注意到(12)式可以表示成一个矩阵运算,而FFT 实际上是一个矩阵分解算法,它对N 的要求有一定的限制,通常N 取成r2,其中r 是正整数。
为了更加直观,这里我们假定r=2, N =4 ,并引进记号1,/2-==-i eW Ni N π (15)则(12)式可改写为如下的矩阵形式:⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)3()2()1()0()3()2()1()0(946434464442404342414044040404x x x x W W W W W W W W W W W W W W W W X X X X (16)注意到1=knN W ,k 为整数,则(16)式还可简化为⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)3()2()1()0(1111111)3()2()1()0(142434240424342414x x x x W W W W W W W W W X X X X (17)上式以及以后的式子中没有把04W 写成1 ,完全是为了以后推广的需要。
第二步我们要做的是,把上述矩阵分解为两个矩阵的乘积:⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)3()2()1()0(010010100011100001001)3()2()1()0(2424040434142404x x x x W W W W W W W W X X X X (18)上述分解基于以后要讲到的FFT 算法理论,其中第一行和第二行的位置做了变换,,这是FFT 本身所要求的。
以后将会看到,这种交换有利于数据存储,成为输出倒置。
今引进⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)3()2()1()0(01001010001)3()2()1()0(242404041111x x x x W W W W x x x x (19)则⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛)3()2()1()0(1100001001)3()2()1()0()3()2()1()0(1111341424042222x x x x W W W W x x x x X X X X (20)于是求解X(n)分成了两次矩阵运算。
下面我们来分析一下这个过程的工作量。
计算)0(1x 需要的一个复数乘法和一个复数加法,即)2()0()0(041x W x x += 这里没有用1代替04W 是因为在一般情况下这一项通常不为1。
计算)1(1x 同样需要一个复数乘法和一个复数加法。
计算)2(1x 只需要一个复数加法,这是因为424W W -=,从而)2()0()2()0()2(04241x W x x W x x -=+=其中)2(04x W 在计算)0(1x 时已经计算过。
