FFT算法(查表法)
利用Excel进行FFT和Fourier分析的基本步骤
6
上面基于杭州人口密度数据的 FFT,实际上是一种空间自相关分析过程,属于 FT 的第 二类应用。这种过程不以寻找周期为目标,实际上也不存在任何周期。
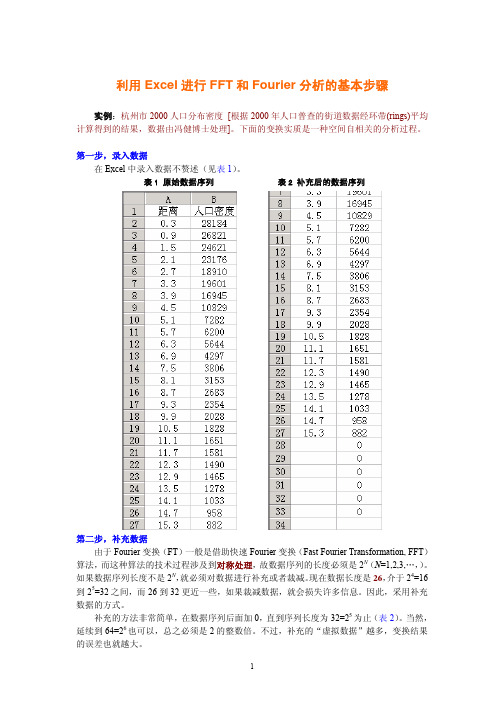
不论目标是什么,都必须借助频谱图(频率-功率谱密度图)进行分析和解释。下面第 一步就是绘制频谱图。首先要计算频率,线频或角频都可以,因为二者相差常数倍(2π)。 一个简单的办法是,用 0 到 T=32 的自然数列除以 T=32(表 6)。
如果采用的频率变化范围 0~1,则绘制的频谱图是对称的(图 6)。实际上,另一半是多 余的,Mathcad2000 自动生成的频谱图就没有考虑另外一半儿(图 7)。因此,我们可以以对 称点 f=0.5 为界,截取前面一半的数据,在 Excel 上绘制频谱图(图 8)。
功率谱密度
1600000000
1400000000
9 6.238?06
10 8.908?06
11 1.073?07
12 1.042?07
13 9.42?06
14 6.494?06
15 4.79?06
16 4.697?06
第六步,功率谱分析 功率谱分析目前主要用于两个方面,一是侦测系统变化的某种周期或者节律,据此寻找
因果关系(解释)或者进行某种发展预测(应用);二是寻找周期以外的某些规律,据此对 系统的时空结构特征进行解释。
a
2
b 图 3 傅立叶分析(Fourier Analysis) 注意:如果“输入区域”设为“$B$2:$B$33”,则不选“标志位于第一行(L)”(图 3b)。
表 3 FFT 的结果
3
第四步,输出 FFT 结果 选项设置完毕以后,确定(OK),立即得到 FFT 结果(表 3)。 显然,表 3 给出的都是复数(complex numbers)。假定一个数据序列表为 f(t),则理论
数字预失真基本原理

17数字预失真基本原理马 进(西安电子科技大学 通信工程学院,陕西 西安 710071)摘 要 对高功率放大器的失真特性进行了数学分析,介绍了数字预失真的基本原理,总结了常用的几种预失真线性化方法,着重详细介绍了查找表数学模型的建模方法。
关键词 功率放大器;线性化;预失真中图分类号 TN722.7+5The Principle of Digital Pre-distortionMa Jin(School of Telecommunications Engineering, Xidian University, Xi ′ an 710071, China)Abstract This paper makes a mathematical analysis of the HPA's distortion characteristic and introduces the principle of digital pre-distortion. It also summarizes some common techniques for linearizing pre-distortion with emphasis on the LUT mathematical model's modeling method.Keywords PA; linearization; pre-distortion; LUT1 数字预失真的实测图表数字预失真的目的是改善功放的线性度,而对功放线性度评估是用ACPR 这个指标进行评估的,因此数字预失真目的就是改善功放的ACPR 指标。
预失真效果见表1所示。
2 功放的非线性特性分析功放的各种失真特性[1]如下:(1)AM-AM 失真特性:就是放大器的增益压缩现象,即AM-AM 失真,可以采用非线性的多项式来表征放大器的这种特性,其数值由输入信号的幅度(AM )决定。
DSP常见算法的实现

DSP常见算法的实现3.6常见的算法实现在实际应用中虽然信号处理的方式多种多样,但其算法的基本要素却大多相同,在本节中介绍几种较为典型的算法实现,希望通过对这些例子(单精度,16bit)的分析,能够让大家熟悉DSP编程中的一些技巧,在以后的工作中可以借鉴,达到举一反三的效果。
1.函数的产生在高级语言的编程中,如果要使用诸如正弦、余弦、对数等数学函数,都可以直接调用运行库中的函数来实现,而在DSP编程中操作就不会这样简单了。
虽然TI公司提供的实时运行库中有一些数学函数,但它们所耗费的时间大多太长,而且对于大多数定点程序使用双精度浮点数的返回结果有点“大材小用”的感觉,因此需要编程人员根据自身的要求“定制”数学函数。
实现数学函数的方法主要有查表法、迭代法和级数逼近法等,它们各有特点,适合于不同的应用。
查表法是最直接的一种方法,程序员可以根据运算的需要预先计算好所有可能出现的函数值,将这些结果编排成数据表,在使用时只需要根据输入查出表中对应的函数值即可。
它的特点是速度快,但需要占用大量的存储空间,且灵活度低。
当然,可以对上述查表法作些变通,仅仅将一些关键的函数值放置在表中,对任意一个输入,可根据和它最接近的数据采用插值方法来求得。
这样占用的存储空间有所节约,但数值的准确度有所下降。
迭代法是一种非常有用的方法,在自适应信号处理中发挥着重要的作用。
作为函数产生的一种方法,它利用了自变量取值临近的函数值之间存在的关系,如时间序列分析中的AR、MA、ARMA等模型,刻画出了信号内部的特征。
因为它只需要存储信号模型的参量和相关的状态变量,所以所占用的存储空间相对较少,运算时间也较短。
但它存在一个致命的弱点,由于新的数值的产生利用了之前的函数值,所以它容易产生误差累积,适合精度要求不高的场合。
级数逼近法是用级数的方法在某一自变量取值范围内去逼近数学函数,而将自变量取值在此范围外的函数值利用一些数学关系,用该范围内的数值来表示。
基4FFT算法的FPGA实现

基-4算法原理
我们也同样采用按时间抽取的方式讲解基-4算 法的蝶形单元。 设A、B 、C 、D 为时间序列,A’、B’、C’、D’ rk 为频率序列, WN r = 0 , 1 , 2 , 3 为旋转因子,则蝶形 单元运算表达式为式1-3: A' B' C' D'
= ( A + CW 2k ) + ( BW k + DW 3k ) = ( A - CW 2k ) - j ( BW k - DW 3k ) 3k k = ( A + CW 2k + ) ( BW k DW ) 2k = ( A - CW ) + j ( BW - DW 3k )
(1-3)
基-4蝶形单元信号流图如下: A B
0k WN k WN
A’ B’
C’ D’
图 1-2 基-4单元信号流图
W
2k
N
C
W
3k
N
D
由 1-3 式可以看出 ,基 -4 蝶形单元需要三个复数 乘法器及十二个复数加法(减)器,而且对于 N= 4M 有 log 4 N = M 次迭代运算,每次迭代运算 包含 N/4 次蝶形运算,每个基 -4 的蝶形单元与四个 基-2 蝶形相比较,减少一次复数乘法,在相同 N点 的 FFT运算过程中,基 -4 运算的迭代运算和每次迭 代包含的蝶形单元要少于基 -2FFT算法,可以看出 基-4 算法的研究可以大大提高 FFT运算的速度,更 加 发 挥 F F T 运 算 快 的 优 势 。
0k N
- BW
k N
(1-1)
图 1-1 基2按时间抽取单元蝶形图
设 A = a + jb (1-1)式得:
数字信号处理主要知识点整理复习总结

求出对应
的各种可能的序列的表达式。
解: 有两个极点,因为收敛域总是以极点为界,因此收敛域有以下三种情况: 三种收敛域对应三种不同的原序列。
时,
(1)当收敛域
令
,因为c内无极点,x(n)=0;
,C内有极点0,但z=0是一个n阶极点,改为求圆外极点留数,圆外极点有
数字信号处理课程 知识点概要
第1章 数字信号处理概念知识点
1、掌握连续信号、模拟信号、离散时间信号、数字信号的特点及相互关系(时间和幅度的连续性考量) 2、数字信号的产生; 3、典型数字信号处理系统的主要构成。
量化、编码 ——————
采样 ————
模拟信号
离散时间信号
数字信号
5、部分分式法进行逆Z变换 求极点 将X(z)分解成部分分式形式 通过查表,对每个分式分别进行逆Z变换 注:左边序列、右边序列对应不同收敛域 将部分分式逆Z变换结果相加得到完整的x(n)序列 6、Z变换的性质 移位、反向、乘指数序列、卷积
常用序列z变换(可直接使用)
7、DTFT与Z变换的关系
(a) 边界条件 时,是线性的但不是移不变的。
(b) 边界条件 时,是线性移不变的。
令
….
所以:
….
所以:
可见 是移一位的关系, 亦是移一位的关系。因此是移不变系统。
代入差分方程,得:
……..
所以:
因此为线性系统。
3. 判断系统是否是因果稳定系统。
Causal and Noncausal System(因果系统) causal system: (1) 响应不出现于激励之前 (2) h(n)=0, n<0 (线性、时不变系统) Stable System (稳定系统) (1) 有界输入导致有界输出 (2) (线性、时不变系统) (3) H(z)的极点均位于Z平面单位圆内(因果系统)
通信课程设计——双音多频信号检测

通信技术方向课程设计题目:双音多频信号检测物联网工程学院电子信息工程专业学号0703070106学生姓名时雅茹二〇一〇年六月一、原理介绍双音多频(Dual Tone Multi Frequency, DTMF )信号是音频电话中的拨号信号,由美国AT&T 贝尔公司实验室研制,并用于电话网络中。
这种信号制式具有很高的拨号速度,且容易自动监测识别,很快就代替了原有的用脉冲计数方式的拨号制式。
这种双音多频信号制式不仅用在电话网络中,还可以用于传输十进制数据的其它通信系统中,用于电子邮件和银行系统中。
这些系统中用户可以用电话发送DTMF 信号选择语音菜单进行操作。
DTMF 信号系统是一个典型的小型信号处理系统,它要用数字方法产生模拟信号并进行传输,其中还用到了D/A 变换器;在接收端用A/D 变换器将其转换成数字信号,并进行数字信号处理与识别。
为了系统的检测速度并降低成本,还开发一种特殊的DFT 算法,称为戈泽尔(Goertzel)算法,这种算法既可以用硬件(专用芯片)实现,也可以用软件实现。
下面首先介绍双音多频信号的产生方法和检测方法,包括戈泽尔算法,最后进行模拟实验。
二、内容及结论1、双音多频(DTMF )信号的组成在电话中,数字0~9的中每一个都用两个不同的单音频传输,所用的8个频率分成高频带和低频带两组,低频带有四个频率:679Hz,770Hz,852Hz 和941Hz ;高频带也有四个频率:1209Hz,1336Hz,1477Hz 和1633Hz.。
每一个数字均由高、低频带中各一个频率构成,例如1用697Hz 和1209Hz 两个频率,信号用)2sin()2sin(21t f t f ππ+表示,其中Hz f 6791=,Hz f 12092=。
这样8个频率形成16种不同的双频信号。
具体号码以及符号对应的频率如表1所示。
表中最后一列在电话中暂时未用。
表1 双频拨号的频率分配列 行 1209Hz1336Hz1477Hz 633Hz 697Hz 1 2 3 A 770Hz 4 5 6 B852Hz 7 8 9 C 942Hz*#DDTMF 信号在电话中有两种作用,一个是用拨号信号去控制交换机接通被叫的用户电话机,另一个作用是控制电话机的各种动作,如播放留言、语音信箱等。
DSP课程设计参考题目

DSP课程设计任务书钱满义高海林编北京交通大学电工电子教学基地2006年1月目录一、综合设计性实验题目 (2)二、《DSP应用课程设计》教学大纲 (16)三、实验报告格式 (19)四、评分标准格式 (21)一、综合设计参考题目1.DSP系统定时及其应用2.DSP系统的自举设计3.任意信号发生器的设计4.DTMF信号的产生及检测5.信号的调制与解调6.语音压缩、存储与回放7.语音噪声滤波8.语音识别9.利用DSP实现信号滤波10.利用DSP实现自适应滤波11.实时信号的谱分析12.DCT离散余弦变换的DSP实现1. D SP系统定时及其应用定时器是DSP处理器最基本的片上外设,使用定时器可以构建系统程序基本的定时单元,为周期性执行某些程序提供时间基准,或者为片外有时钟要求的电路,如A/D和D/A电路提供定时时钟。
本设计要求采用DSP的片内定时器实现应用程序的周期性运行。
1.设计要求及目标基本部分:(1)对定时器进行初始化(2)编写定时服务程序实现3个LED指示灯分别以1秒、2秒、4秒的周期进行闪烁(3)编写定时服务程序实现3个LED指示灯以流水灯的形式进行闪烁,流水周期在0.6秒~6秒之间进行循环改变发挥部分:使用定时器在Tout输出引脚产生频率为10K~100KHz连续可调的方波信号,实现方波信号发生器的功能。
2.设计思路首先使用DSP的定时器实现最基本的定时功能,例如当DSP的系统时钟为100MHZ时,基本定时时间可确定为10ms。
然后可使用查询方式或中断方式编写定时器的定时服务程序,在服务程序中设置定时变量进一步计算时间。
根据设计要求编写定时服务程序。
Tout引脚即XTOUT引脚,已连接到扩展板接口上,可以使用示波器来测量所产生的信号波形,如果要求产生方波信号,还要增加一点附加电路。
3.要求完成的任务(1)编写C语言程序,并在CCS集成开发环境下调试通过。
(2)实现设计所要求的各项功能。
(3)按要求撰写设计报告。
数字控制振荡器NCO

本文设计的 NCO 工作时钟为 100MHz,相位累加器的位数为 16 位,输入的频率控制字为 4CCCH,根据公式:
因此在实际设计中,采用的是图 2 所示的由 16 级 CORDIC 运算单元组成的流水线结构, 正常工作时只需 1 个时钟周期就能输出 1 个数据,为数据实现高速实时处理提供了前提。每 一级实现的功能是根据式(5)进行一次迭代,移位的位数等于当前的迭代级数,加减法选择 由该级中 Z 的最高位(符号位)决定,得到下一级的 X 、Y 和 Z 的值。经过 16 级流水线运 算后,Z 的值变为 0,X 和 Y 的值则为初始值 z0 的余弦和正弦值。每一级电路结构主要包 括 2 个移位器和 3 个加(减)法器,级与级之间直接相连,不需要额外的寄存器。θi 的值为 arctan(2-i),可将该小数转换为二进制数后,存储于存储单元中,为每一级流水线提供查 找表。若对于 16 级的流水线结构,则的范围是 0~15。
数控振荡器的 FPGA 实现
图 1 是数控振荡器的顶层电路。由图可见,频率控制字寄存器将接收到的的频率控制字 送入相位累加器,相位累加器对系统时钟进行计数,每到达输入频率控制字的值即对相位进 行累加,随后将累加值送入相位相加器,与相位控制字寄存器接收到的初始相位进行相加, 得到当前的相位值。其中,相位累加器是决定 NCO 性能的一个关键模块,可以利用 FPGA 器 件的进位链实现快速、高效的电路结构。然而,由于进位链必须位于临近的逻辑阵列块 CLB 和逻辑单元 LC 内,所以长的进位链会减少其它逻辑使用的布线资源;同时,过长的进位链 也会制约整个系统速度的提高。因此,设计中采用进位链和流水线技术相结合的办法。所谓 流水线技术,即把在一个时钟内要完成的逻辑操作分成几步较小的操作,并插入几个时钟周 期来提高系统的数据吞吐率。采用以上做法实现的相位累加器既能保证具有较高的资源利用 率,又能大幅提高系统的性能和速度。
嵌入式系统中FFT算法研究 (128点参考)

摘要:首先分析实数FFT算法的推导过程,然后给出一种具体实现FFT算法的C语言程序,可以直接应用于需要FFT运算的单片机或DSP等嵌入式系统中。
关键词:嵌入式系统FFT算法单片机DSP目前国内有关数字信号处理的教材在讲解快速傅里叶变换(FFT)时,都是以复数FFT为重点,实数FFT算法都是一笔带过,书中给出的具体实现程序多为BASIC或FORTRAN程序并且多数不能真正运行。
鉴于目前在许多嵌入式系统中要用到FFT运算,如以DSP为核心的交流采样系统、频谱分析、相关分析等。
本人结合自己的实际开发经验,研究了实数的FFT算法并给出具体的C语言函数,读者可以直接应用于自己的系统中。
1 倒位序算法分析按时间抽取(DIT)的FFT算法通常将原始数据倒位序存储,最后按正常顺序输出结果X(0),X(1),...,X(k),...。
假设一开始,数据在数组float dataR[128]中,我们将下标i表示为(b6b5b4b3b2b1b0)b,倒位序存放就是将原来第i个位置的元素存放到第(b0b1b2b3b4b5b6)b的位置上去.由于C语言的位操作能力很强,可以分别提取出b6、b5、b4、b3、b2、b1、b0,再重新组合成b0、b1、b2、b3、b4、b5、b6,即是倒位序的位置。
程序段如下(假设128点FFT):/* i 为原始存放位置,最后得invert_pos 为倒位序存放位置 */ int b0=b1=b2=b3=b4=b5=6=0; b0=i&0x01; b1=(i/2)&0x01; b2=(i/4)&0x01; b3=(i/8)&0x01; b4=(i/16)&0x01; b5=(i/32)&0x01; b6=(i/64)&0x01;/*以上语句提取各比特的0、1值*/invert_pos=b0*64+b1*32+b2*16+b3*8+b4*4+b5*2+b6; 大家可以对比教科书上的倒位序程序,会发现这种算法充分利用了C 语言的位操作能力,非常容易理解而且位操作的速度很快。
51用FFT程序

851,878,903,926,946,964,980,993,1004,1013,
1019,1023,1024,1023,1019,1013,1004,993,980,964,
946,926,903,878,851,822,792,759,724,688,
650,610,569,526,483,438,392,345,297,249,
-792,-799,-807,-815,-822,-830,-837,-844,-851,-858,
-865,-872,-878,-885,-891,-897,-903,-909,-915,-920,
-926,-931,-936,-941,-946,-951,-955,-960,-964,-968,
#define IN_TYPE int
#define OUT_TYPE long int
#define LEN_TYPE long int
#define PI 3.1415926535897932384626433832795
void InitBitRev(void);
void FftInput(IN_TYPE *pIn);
822,807,792,775,759,742,724,706,688,669,
650,630,610,590,569,548,526,505,483,460,
438,415,392,369,345,321,297,273,249,224,
200,175,150,125,100,75,50,25
extern enum eepromtype EepromType;
bit RW24XX(unsigned char *DataBuff,unsigned char ByteQuantity,unsigned int Address,
付立叶变换理解及excel实现

傅里叶变换的本质傅里叶变换的公式为dt e t f F t j ⎰+∞∞--=ωω)()(可以把傅里叶变换也成另外一种形式:t j e t f F ωπω),(21)(= 可以看出,傅里叶变换的本质是内积,三角函数是完备的正交函数集,不同频率的三角函数的之间的内积为0,只有频率相等的三角函数做内积时,才不为0。
)(2,21)(2121Ω-Ω==⎰Ω-ΩΩΩπδdt e e e t j t j t j下面从公式解释下傅里叶变换的意义因为傅里叶变换的本质是内积,所以f(t)和t j e ω求内积的时候,只有f(t)中频率为ω的分量才会有内积的结果,其余分量的内积为0。
可以理解为f(t)在t j e ω上的投影,积分值是时间从负无穷到正无穷的积分,就是把信号每个时间在ω的分量叠加起来,可以理解为f(t)在t j eω上的投影的叠加,叠加的结果就是频率为ω的分量,也就形成了频谱。
傅里叶逆变换的公式为 ωωπωd e F t f t j ⎰+∞∞-=)(21)( 下面从公式分析下傅里叶逆变换的意义傅里叶逆变换就是傅里叶变换的逆过程,在)(ωF 和t j e ω-求内积的时候,)(ωF 只有t 时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t 时刻上的分量叠加起来,叠加的结果就是f(t)在t 时刻的值,这就回到了我们观察信号最初的时域。
离散付立叶变换的理解FFT 是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FF T 变换的原因。
另外,FFT 可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT 是什么,可以用来做什么,怎么去做,但是却不知道FFT 之后的结果是什意思、如何决定要使用多少点来做FFT 。
DSP课程设计---DTMF信号的产生及检测

DSP课程设计实验报告DTMF信号的产生及检测院(系):电子信息工程学院通信工程专业设计人员:宋佳阳学号:08211042目录一、设计任务书.........................................................................- 3 -二、设计内容.............................................................................- 3 -三、设计方案、算法原理说明.................................................- 4 -1.DTMF信号的产生 .........................................................- 4 -2.DTMF信号的检测 .........................................................- 5 -四、程序设计、调试与结果分析.............................................- 7 -1.程序设计部分: ...................................................................- 7 -2.调试与结果分析部分: ................................................... - 28 -五、设计(安装)与调试的体会.......................................... - 33 -六、参考文献.......................................................................... - 34 -一、设计任务书设计要求及目标基本部分:(1)使用C语言编写DTMF信号的发生程序,要求循环产生0~9、*、#、A、B、C、D对应的DTMF信号,并且符合CCITT对DTMF信号规定的指标。
利用单片机实现实现频谱显示的快速傅里叶变换算法并进行优化

利用单片机实现实现频谱显示的快速傅里叶变换算法并进行优化1 引言在家庭影院、卡拉OK等音响系统中,实时显示音乐信号的频谱将为音响系统增添不少色彩。
目前实际生产的音响系统产品,大多采用以下两种方法实现音频频谱显示:一是利用硬件滤波器和A/D转换器;二是利用DSP处理频谱显示。
前者实现简单,但硬件成本高,后者软件和硬件实现都较复杂。
这里针对单片机RAM资源少、运算速度慢的特点,提出一种切实可行的快速傅里叶变换算法实现频谱显示。
2 系统整体设计及原理该系统设计由单片机SST89V58RD2、音频数据采样电路、A/D转换电路、频谱显示电路等部分组成。
图1为系统整体设计原理框图。
该系统从功能上可划分成3部分:(1)音频数据采集电路实现模拟音频信号的采样保持和量化处理,包括音频采样电路和加转换电路;(2)频谱显示电路实现模拟音频信号频谱的分段显示,它将音频信号频谱划分成14段,每段按照14级量化,由VFD显示器件显示;(3)主控制器采用SST89V58RD2单片机。
在完成系统其他控制任务的前提下,充分利用单片机剩余计算资源,采用优化FFT算法计算音频信号频谱,并将计算结果输出到频谱显示电路。
3 音频信号的采集和预处理3.1 采样频率根据香农采样定理,一般采样频率至少应为所采样音频信号最高频率的2倍。
由于人耳能够感受的频率为20 Hz~20 kHz,所以理论上采样频率最高取40 kHz。
目前工业上广泛采用的采样频率大致有3种:44 kHz、16 bit的声音称作CD音质:22 kHz、16 bit的声音效果近似于立体声广播(FMStereo),称作广播音质;11 kHz、8 bit的声音称作电话音质。
本文为提高频谱计算的精度,拟采用40 kHz的采样频率和8Bit的数据位长。
3.2 样本大小。
基于相位旋转法的NCO设计与实现

基于相位旋转法的NCO设计与实现张青林;罗义军;陈淑珍;颜佳【摘要】针对信道化接收机的低通滤波器组结构中NCO消耗资源巨大的问题,提出了一种基于三角函数的相位旋转法.介绍了该算法的结构,然后在FPGA上实现了该方法.最后通过产生八路NCO所占用资源的对比,说明该方法与直接使用查表法或CORDIC算法相比最少能节省50%的逻辑单元和存储器单元.该方法可以很容易推广到频谱监测、多频移键控调制、跳频接收等应用中.【期刊名称】《系统工程与电子技术》【年(卷),期】2010(032)005【总页数】4页(P908-911)【关键词】信道化接收机;低通滤波器组;数控振荡器;相位旋转;FPGA【作者】张青林;罗义军;陈淑珍;颜佳【作者单位】武汉大学电子信息学院,湖北,武汉,430079;武汉大学电子信息学院,湖北,武汉,430079;武汉大学电子信息学院,湖北,武汉,430079;武汉大学电子信息学院,湖北,武汉,430079【正文语种】中文【中图分类】TN914.30 引言信道化接收机具有瞬时频带宽、动态范围大、可以处理同时到达信号等特点,能实现宽带接收,对提高接收效率、捕获跳频信号、进行频谱分析以及同时接收多个信号等十分有用。
目前,对于多个信号的同时接收一般都采用滤波器组并接的模拟信道化体制,或者采用多部接收机同时工作的方案。
但这两种实现途径都具有设备组成复杂、成本高、可扩展性差等弊端,无法适应不断变化的新需求。
基于软件无线电(software defined radio,SDR)[1]思想的数字信道化接收机采用FPGA实现,能够克服上述诸多弊端,具有良好的重置性,可扩展性以及较强的实时处理能力,并且能有效地简化接收设备。
信道化接收机的基本思想就是采用信道划分的方法,将输入的宽带信号S(n)按频率均匀分成若干段(D段),然后分别移到零中频,再通过多个低通滤波器输出。
由于输出的信号yk(n)(k=0,1,…,D-1)的带宽仅为原带宽的1/D,故可以对其进行D倍抽取,并不会影响yk(n)的频谱结构[2]。
数字信号处理—原理、实现及应用(第4版)第2章 时域离散信号和系统的频域分析 学习要点及习题答案

·22· 第2章 时域离散信号和系统的频域分析2.1 引 言数字信号处理中有三个重要的数学变换工具,即傅里叶变换、Z 变换和离散傅里叶变换,利用它们可以将信号和系统在时域空间和频域空间相互转换,这大大方便了对信号和系统的分析和处理。
三种变换互有联系,但又不同。
表征一个信号和系统的频域特性用傅里叶变换;Z 变换是傅里叶变换的一种扩展,在Z 域对系统进行分析与设计更加既灵活方便。
单位圆上的Z 变换就是傅里叶变换,因此用Z 变换分析频域特性也很方便。
离散傅里叶变换是离散化的傅里叶变换,因此用计算机分析和处理信号时,全用离散傅里叶变换进行。
离散傅里叶变换具有快速算法FFT ,使离散傅里叶变换在应用中更加重要。
但是离散傅里叶变换不同于傅里叶变换和Z 变换,其优点是将信号的时域和频域都进行了离散化,便于计算机处理。
但实际使用中,一定要注意它的特点,例如对模拟信号进行频域分析,只能是近似的,如果使用不当,会引起较大的误差。
因此掌握好这三种变换是学习好数字信号处理的关键。
本章只学习前两种变换,离散傅里叶变换及其FFT 在下一章中讲述。
2.2 本章学习要点(1) 求序列的傅里叶变换—序列频率特性。
(2) 求周期序列的傅里叶级数和傅里叶变换—周期序列频率特性。
(3) 0(),(),(),1,cos()n N n a u n R n n δω,0sin()n ω和0j e n ω的傅里叶变换,02/ωπ为有理数。
(4) 傅里叶变换的性质和定理:傅里叶变换的周期性、移位与频移性质、时域卷积定理、巴塞伐尔定理、频域卷积定理、频域微分性质、实序列和一般序列的傅里叶变换的共轭对称性。
(5) 求序列的Z 变换及其收敛域。
(6) 序列Z 变换收敛域与序列特性之间的关系。
(7) 求逆Z 变换:部分分式法和围线积分法。
(8) Z 变换的定理和性质:移位、反转、Z 域微分、共轭序列的Z 变换、时域卷积定理、初值定理、终值定理、巴塞伐尔定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ARM或单片机用的FFT算法,用于信号处理。
经过愚昧的本人优化,提高了计算效率(在aduc7026 @41MHz FFT256点环境下运算时间为0.06s左右)PS:以下有两部分(fft.h和fft.c)【复制以下内容改名为fft.h】#ifndef __FFT_H__#define __FFT_H__#include<math.h>#ifdef FFT_GLOBALS#define FFT_EXT#else#define FFT_EXT extern#endif#define PI 3.1415926#define FFT_POINT 8 //设置点数(此值变,下面的也要变)(0~11)#define SAMPLE_NUM 256 //可设256或512两种数//count[n]//count[]={1,2,4,8,16,32,64,128,256,512,1024,2048}FFT_EXT float dataR[SAMPLE_NUM];FFT_EXT float dataI[SAMPLE_NUM];FFT_EXT void SetData(float data,unsigned int i); //采集数据到第i个点(0~SAMPLE_NUM)FFT_EXT void FFT(void);//采样来的数据放在dataR[ ]数组中//***************FFT结果数值处理*******************************************************//计算和返回峰(模)值,k表示第几个值(0~SAMPLE_NUM-1),type为0返回峰值,1返回模值,2返回有效值FFT_EXT float GetPeak(unsigned int k,unsigned int type);//FFT_EXT float GetPhase(unsigned int k,unsigned int type); //计算和返回相位,k同上//type为0返回角度,1返回弧度//speed为采样速率,返回第k(0~SAMPLE_NUM)个点代表的频率FFT_EXT float GetStepF(float speed,unsigned int k);FFT_EXT float GetPower1(unsigned int k); //返回功率谱的第k点FFT_EXT float GetPower2(unsigned int k,float total); // 返回k点所占的功率百分比(单位是%) total为总功率FFT_EXT float GetTotalPower(void); //计算功率谱总和FFT_EXT float GetTHD(void); //计算失真度#endif///////////////////////////////////////////////////////////////////////////////【复制以下内容改名为fft.c】//查表式FFT算法#define FFT_GLOBALS#include "fft.h"#if SAMPLE_NUM==256const float sin_tab[256]={0.000000,0.024541,0.049068,0.073565,0.098017,0.122411,0.146730,0.170962,0.1 95090,0.219101,0.242980,0.266713,0.290285,0.313682,0.336890,0.359895,0.382683,0.405241,0.427555,0.449611,0.471397,0.492898,0.514103,0.534998,0.555570,0.575808,0.5 95699,0.615232,0.634393,0.653173,0.671559,0.689541,0.707107,0.724247,0.740951,0.757209,0.773010,0.788346,0.803208,0.817585,0.831470,0.844854,0.8 57729,0.870087,0.881921,0.893224,0.903989,0.914210,0.923880,0.932993,0.941544,0.949528,0.956940,0.963776,0.970031,0.975702,0.980785,0.985278,0.9 89177,0.992480,0.995185,0.997290,0.998795,0.999699,1.000000,0.999699,0.998795,0.997290,0.995185,0.992480,0.989177,0.985278,0.980785,0.975702,0.9 70031,0.963776,0.956940,0.949528,0.941544,0.932993,0.923880,0.914210,0.903989,0.893224,0.881921,0.870087,0.857729,0.844854,0.831470,0.817585,0. 803208,0.788346,0.773010,0.757209,0.740951,0.724247,0.707107,0.689541,0.671559,0.653173,0.634393,0.615232,0.595699,0.575808,0.555570,0.534998,0. 514103,0.492898,0.471397,0.449611,0.427555,0.405241,0.382683,0.359895,0.336890,0.313682,0.290285,0.266713,0.242980,0.219101,0.195090,0.170962,0. 146730,0.122411,0.098017,0.073565,0.049068,0.024541,0.000000,-0.024541,-0.049068,-0.073565,-0.098017,-0.122411,-0.146730,-0.170962,-0.195090,-0.219 101,-0.242980,-0.266713,-0.290285,-0.313682,-0.336890,-0.359895,-0.382683,-0.405241,-0.427555,-0.449611,-0.471397,-0.492898,-0.514103,-0.534998,-0.555570,-0.575 808,-0.595699,-0.615232,-0.634393,-0.653173,-0.671559,-0.689541,-0.707107,-0.724247,-0.740951,-0.757209,-0.773010,-0.788346,-0.803208,-0.817585,-0.831470,-0.844 854,-0.857729,-0.870087,-0.881921,-0.893224,-0.903989,-0.914210,-0.923880,-0.932993,-0.941544,-0.949528,-0.956940,-0.963776,-0.970031,-0.975702,-0.980785,-0.985 278,-0.989177,-0.992480,-0.995185,-0.997290,-0.998795,-0.999699,-1.000000,-0.999699,-0.998795,-0.997290,-0.995185,-0.992480,-0.989177,-0.985278,-0.980785,-0.975 702,-0.970031,-0.963776,-0.956940,-0.949528,-0.941544,-0.932993,-0.923880,-0.914210,-0.903989,-0.893224,-0.881921,-0.870087,-0.857729,-0.844854,-0.831470,-0.817 585,-0.803208,-0.788346,-0.773010,-0.757209,-0.740951,-0.724247,-0.707107,-0.689541,-0.671559,-0.653173,-0.634393,-0.615232,-0.595699,-0.575808,-0.555570,-0.534 998,-0.514103,-0.492898,-0.471397,-0.449611,-0.427555,-0.405241,-0.382683,-0.359895,-0.336890,-0.313682,-0.290285,-0.266713,-0.242980,-0.219101,-0.195090,-0.170 962,-0.146730,-0.122411,-0.098017,-0.073565,-0.049068,-0.024541};#endif#if SAMPLE_NUM==512const float sin_tab[512]={0.000000,0.012272,0.024541,0.036807,0.049068,0.061321,0.073565,0.085797,0.0 98017,0.110222,0.122411,0.134581,0.146730,0.158858,0.170962,0.183040,0.195090,0.207111, 0.219101,0.231058,0.242980,0.254866,0.266713,0.278520,0.290285,0.302006,0.313682,0.3253 10,0.336890,0.348419,0.359895,0.371317,0.382683,0.393992,0.405241,0.416430,0.427555,0.438616,0.449611,0.460539,0.471397,0.482184,0. 492898,0.503538,0.514103,0.524590,0.534998,0.545325,0.555570,0.565732,0.575808,0.585798 ,0.595699,0.605511,0.615232,0.624859,0.634393,0.643832,0.653173,0.662416,0.671559,0.6806 01,0.689541,0.698376,0.707107,0.715731,0.724247,0.732654,0.740951,0.749136,0.757209,0.765167,0.773010,0.780737,0.7 88346,0.795837,0.803208,0.810457,0.817585,0.824589,0.831470,0.838225,0.844854,0.851355, 0.857729,0.863973,0.870087,0.876070,0.881921,0.887640,0.893224,0.898674,0.903989,0.90916 8,0.914210,0.919114,0.923880,0.928506,0.932993,0.937339,0.941544,0.945607,0.949528,0.953306,0.956940,0.960431,0. 963776,0.966976,0.970031,0.972940,0.975702,0.978317,0.980785,0.983105,0.985278,0.987301, 0.989177,0.990903,0.992480,0.993907,0.995185,0.996313,0.997290,0.998118,0.998795,0.9993 22,0.999699,0.999925,1.000000,0.999925,0.999699,0.999322,0.998795,0.998118,0.997290,0.996313,0.995185,0.993907,0. 992480,0.990903,0.989177,0.987301,0.985278,0.983105,0.980785,0.978317,0.975702,0.972940, 0.970031,0.966976,0.963776,0.960431,0.956940,0.953306,0.949528,0.945607,0.941544,0.9373 39,0.932993,0.928506,0.923880,0.919114,0.914210,0.909168,0.903989,0.898674,0.893224,0.887640,0.881921,0.876070,0.8 70087,0.863973,0.857729,0.851355,0.844854,0.838225,0.831470,0.824589,0.817585,0.810457, 0.803208,0.795837,0.788346,0.780737,0.773010,0.765167,0.757209,0.749136,0.740951,0.732654,0.724247,0.715731,0.707107,0.698376,0.689541,0.680601,0.671559,0.662416,0.653173,0.643832,0.634393,0.624859,0. 615232,0.605511,0.595699,0.585798,0.575808,0.565732,0.555570,0.545325,0.534998,0.524590 ,0.514103,0.503538,0.492898,0.482184,0.471397,0.460539,0.449611,0.438616,0.427555,0.4164 30,0.405241,0.393992,0.382683,0.371317,0.359895,0.348419,0.336890,0.325310,0.313682,0.302006,0.290285,0.278520,0. 266713,0.254866,0.242980,0.231058,0.219101,0.207111,0.195090,0.183040,0.170962,0.158858 ,0.146730,0.134581,0.122411,0.110222,0.098017,0.085797,0.073565,0.061321,0.049068,0.0368 07,0.024541,0.012272,0.000000,-0.012272,-0.024541,-0.036807,-0.049068,-0.061321,-0.073565,-0.085797,-0.098017,-0.110 222,-0.122411,-0.134581,-0.146730,-0.158858,-0.170962,-0.183040,-0.195090,-0.207111,-0.219 101,-0.231058,-0.242980,-0.254866,-0.266713,-0.278520,-0.290285,-0.302006,-0.313682,-0.325 310,-0.336890,-0.348419,-0.359895,-0.371317,-0.382683,-0.393992,-0.405241,-0.416430,-0.427555,-0.438616,-0.449611,-0.460539,-0.471397,-0.482 184,-0.492898,-0.503538,-0.514103,-0.524590,-0.534998,-0.545325,-0.555570,-0.565732,-0.575 808,-0.585798,-0.595699,-0.605511,-0.615232,-0.624859,-0.634393,-0.643832,-0.653173,-0.662 416,-0.671559,-0.680601,-0.689541,-0.698376,-0.707107,-0.715731,-0.724247,-0.732654,-0.740951,-0.749136,-0.757209,-0.765167,-0.773010,-0.780 737,-0.788346,-0.795837,-0.803208,-0.810457,-0.817585,-0.824589,-0.831470,-0.838225,-0.844 854,-0.851355,-0.857729,-0.863973,-0.870087,-0.876070,-0.881921,-0.887640,-0.893224,-0.8986 74,-0.903989,-0.909168,-0.914210,-0.919114,-0.923880,-0.928506,-0.932993,-0.937339,-0.941544,-0.945607,-0.949528,-0.953306,-0.956940,-0.960 431,-0.963776,-0.966976,-0.970031,-0.972940,-0.975702,-0.978317,-0.980785,-0.983105,-0.9852 78,-0.987301,-0.989177,-0.990903,-0.992480,-0.993907,-0.995185,-0.996313,-0.997290,-0.9981 18,-0.998795,-0.999322,-0.999699,-0.999925,-1.000000,-0.999925,-0.999699,-0.999322,-0.998795,-0.998118,-0.997290,-0.996313,-0.995185,-0.993 907,-0.992480,-0.990903,-0.989177,-0.987301,-0.985278,-0.983105,-0.980785,-0.978317,-0.9757 02,-0.972940,-0.970031,-0.966976,-0.963776,-0.960431,-0.956940,-0.953306,-0.949528,-0.94560 7,-0.941544,-0.937339,-0.932993,-0.928506,-0.923880,-0.919114,-0.914210,-0.909168,-0.903989,-0.898674,-0.893224,-0.887640,-0.881921,-0.876 070,-0.870087,-0.863973,-0.857729,-0.851355,-0.844854,-0.838225,-0.831470,-0.824589,-0.8175 85,-0.810457,-0.803208,-0.795837,-0.788346,-0.780737,-0.773010,-0.765167,-0.757209,-0.74913 6,-0.740951,-0.732654,-0.724247,-0.715731,-0.707107,-0.698376,-0.689541,-0.680601,-0.671559,-0.662416,-0.653173,-0.643832,-0.634393,-0.624 859,-0.615232,-0.605511,-0.595699,-0.585798,-0.575808,-0.565732,-0.555570,-0.545325,-0.534998,-0.524590,-0.514103,-0.503538,-0.492898,-0.482184,-0.471397,-0.460539,-0.449611,-0.4386 16,-0.427555,-0.416430,-0.405241,-0.393992,-0.382683,-0.371317,-0.359895,-0.348419,-0.336890,-0.325310,-0.313682,-0.302006,-0.290285,-0.278 520,-0.266713,-0.254866,-0.242980,-0.231058,-0.219101,-0.207111,-0.195090,-0.183040,-0.170 962,-0.158858,-0.146730,-0.134581,-0.122411,-0.110222,-0.098017,-0.085797,-0.073565,-0.061 321,-0.049068,-0.036807,-0.024541,-0.012272};#endifvoid SetData(float data,unsigned int i){dataR[i]=data;}/* 采样来的数据放在dataR[ ]数组中,运算前dataI[ ]数组初始化为0 */void FFT(void){const int count[]={1,2,4,8,16,32,64,128,256,512,1024,2048};int i,xx,n;int L,j,k,b;float TR,TI,temp,Tsin,Tcos;//,p;long m;int x[11]={0};n=FFT_POINT;/********** following code invert sequence ************/for(i=0;i<count[n];i++){xx=0;for(j=0;j<n;j++) {x[j]=0;}for(j=0;j<n;j++) {x[j]=(i/count[j])&0x01;}for(j=0;j<n;j++) {xx=xx+x[j]*count[n-j-1];}dataI[xx]=dataR[i];}for(i=0;i<count[n];i++){dataR[i]=dataI[i];dataI[i]=0;}/************** following code FFT *******************/for(L=1;L<=n;L++) /* for(1) */{b=1; // i=L-1;b<<=(L-1); //整型2的n次方简化运算(加快计算速度)m=SAMPLE_NUM/count[L];for(j=0;j<=b-1;j++) /* for (2) */{Tsin=sin_tab[(m*j)%SAMPLE_NUM];Tcos=sin_tab[(m*j+SAMPLE_NUM/4)%SAMPLE_NUM];for(k=j;k<count[n];k=k+2*b) /* for (3) */{TR=dataR[k];TI=dataI[k];temp=dataR[k+b];dataR[k] = dataR[k]+dataR[k+b]*Tcos+dataI[k+b]*Tsin;dataI[k] = dataI[k]-dataR[k+b]*Tsin+dataI[k+b]*Tcos;dataR[k+b] = TR-dataR[k+b]*Tcos-dataI[k+b]*Tsin;dataI[k+b] = TI+temp*Tsin-dataI[k+b]*Tcos;} /* END for (3) */} /* END for (2) */} /* END for (1) */}/**********************FFT数值计算处理(可自行增删)**********************/float GetPeak(unsigned int k,unsigned int type) //计算峰(模,有效)值{float result;result=sqrt(dataR[k]*dataR[k]+dataI[k]*dataI[k]);switch(type){case 1:return result;case 0:case 2:if(k==0) result=result/SAMPLE_NUM;else result=result/(SAMPLE_NUM/2);if(type==2) result=result/1.41421356; //峰值除以根号2return result;default:return result;}}float GetPower1(unsigned int k) //返回功率谱的一点{float temp;temp=GetPeak(k,2);temp*=temp;return temp;}float GetPower2(unsigned int k,float total) //返回比例{float temp;temp=GetPeak(k,2);temp*=temp;return 100.0*temp/total;}float GetTotalPower(void){unsigned int i;float total=0;for(i=0;i<SAMPLE_NUM/2;i++){total+=GetPower1(i);}return total;}/*float GetPhase(unsigned int k,unsigned int type) //计算相位{if(type) return atan2(dataI[k],dataR[k]);else return(180.0*atan2(dataI[k],dataR[k])/PI);}*/float GetStepF(float speed,unsigned int k){return k*speed/(SAMPLE_NUM*1.0);}float GetTHD(void) //计算失真度{float total,temp1=0,temp2=0;unsigned int i,n=0;total=GetTotalPower();for(i=0;i<(SAMPLE_NUM/2);i++){temp2=GetPeak(i,2);if(temp2>temp1) {temp1=temp2;n=i;}}temp1=GetPower1(n);temp2=sqrt((total-temp1)/temp1);return temp2;}。
