(完整word版)stm32F103进行FFT算法教程
(完整word版)基于DSP的快速傅立叶变换(FFT)的实现(汇编语言)

快速傅立叶变换(FFT )的实现一、实验目的1.了解FFT 的原理及算法;2.了解DSP 中FFT 的设计及编程方法;3.熟悉FFT 的调试方法;二、实验原理FFT 是一种高效实现离散付立叶变换的算法,把信号从时域变换到频域,在频域分析处理信息。
对于长度为N 的有限长序列x (n ),它的离散傅里叶变换为:(2/)j N nk N W e π-=,称为旋转因子,或蝶形因子。
在x (n )为复数序列的情况下,计算X (k ):对某个k 值,需要N 次复数乘法、(N -1)次复数加法;对所有N 个k 值,需要2N 次复数乘法和N (N -1)次复数加法。
对于N 相当大时(如1024)来说,直接计算它的DFT 所作的计算量是很大的,FFT 的基本思想在于: 利用2()j nk N N W e π-=的周期性即:k N k N N W W +=对称性:/2k k N N N W W +=-将原有的N 点序列分成两个较短的序列,这些序列的DFT 可以很简单的组合起来得到原序列的DFT 。
按时间抽取的FFT ——DIT FFT 信号流图如图5.1所示:图5.1 时间抽取的FFT —DIT FFT 信号流图FFT 算法主要分为以下四步。
第一步 输入数据的组合和位倒序∑=-=10)()(N n nk N W n x k X把输入序列作位倒序是为了在整个运算最后的输出中得到的序列是自然顺序。
第二步 实现N 点复数FFT第一级蝶形运算;第二级蝶形运算;第三级至log2N 级蝶形运算;FFT 运算中的旋转因子N W 是一个复数,可表示:为了实现旋转因子N W 的运算,在存储空间分别建立正弦表和余弦表,每个表对应从0度到180度,采用循环寻址来对正弦表和余弦表进行寻址。
第三步 功率谱的计算X (k )是由实部()R X k 和虚部()I X k 组成的复数:()()()R I X k X k jX k =+;计算功率谱时只需将FFT 变换好的数据,按照实部()R X k 和虚部()I X k 求它们的平方和,然后对平方和进行开平方运算。
STM32F103中文教程及参考手册

3.2
电源管理器 --------------------------------------------------------------------------------- 25
3.2.1 上电复位(POR)和掉电复位(PDR)-------------------------------------------------25 3.2.2 可编程电压监测器(PVD) -----------------------------------------------------------25
3.3
低功耗模式 --------------------------------------------------------------------------------- 26
3.3.1 3.3.2 3.3.3 3.3.4 3.3.5 3.3.6
降低系统时钟 -------------------------------------------------------------------------27 外部时钟的控制 ----------------------------------------------------------------------27 睡眠模式 -------------------------------------------------------------------------------27 停止模式 -------------------------------------------------------------------------------28 待机模式 -------------------------------------------------------------------------------29 低功耗模式下的自动唤醒(AWU) -------------------------------------------------31
STM32F103编程入门

STM32F103单片机编程入门一款单片机入门,至少四样:时钟、端口、定时、串口、中断。
系统时钟RCC系统内部有8M_RC晶振和32678Hz_RC晶振有大约2%的温飘。
当外部有8M晶振时,自动选择外部晶振,失效时自动切换成内部。
程序自动倍频成72M。
如果用于通信最好加个外部晶振。
判断是否使用外部晶振的方法:短接外部晶振引脚观察工作情况。
分为两个桥,对应不同的外设,每个外设又可以单独设定时钟。
初步学习,先不用单独设定,均选用系统时钟72M。
可根据情况做一步分频。
用到某外设时,配置RCC(打开外设时钟),一般只有一句指令。
一般临时查找。
呵呵,我也没找到好办法。
GPIO:RCC_APB2PeriphClockCmd( RCC_APB2Periph_GPIOC , ENABLE);USART:RCC_APB2PeriphClockCmd(RCC_APB2Periph_USART1,ENABLE);Timer2:RCC_APB1PeriphClockCmd(RCC_APB1Periph_TIM2 , ENABLE);端口GPIO端口配置思路:1,先定义一个结构体配置成员参数值,类型是GPIO_InitTypeDef,下划线是结构体名;结构体名是GPIO_InitStructure:名称可以自定义。
在后面利用参数初始化函数时要一致。
2,打开相对应的端口时钟RCC。
3,声明要配置的管脚,可以用“|”复选4,配置模式,4种输入,4种输出5,配置管脚频率,一般都是50Mhz6,最后调用函数GPIO_Init(GPIOA, &GPIO_InitStructure);第2个参数是,结构体地址指针。
Eg:GPIO_InitTypeDef GPIO_InitStructure;RCC_APB2PeriphClockCmd( RCC_APB2Periph_GPIOC , ENABLE);GPIO_InitStructure.GPIO_Pin = GPIO_Pin_13;GPIO_InitStructure.GPIO_Mode =GPIO_Mode_Out_PP;GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;GPIO_Init(GPIOC, &GPIO_InitStructure);一、串口USART串口配置思路:1,定义结构体,类型是USART_InitTypeDef;2,打开串口时钟,可以选择和端口GPIO一起3,设置波特率,—————省去了复杂的烦人的计算4,设置字长。
stm32自相关算法

stm32自相关算法摘要:1.简介2.stm32自相关算法的基本原理3.stm32自相关算法的实现步骤4.stm32自相关算法的应用领域5.总结正文:1.简介STM32是一款由意法半导体公司开发的基于ARM Cortex-M内核的微控制器。
自相关算法是一种在信号处理领域广泛应用的算法,主要用于信号的时域分析。
在STM32平台上实现自相关算法,可以更好地对信号进行处理和分析。
2.stm32自相关算法的基本原理自相关算法基于信号的叠加原理,通过计算信号的自身相关函数,得到信号的频率信息。
在STM32平台上,自相关算法主要通过计算信号的离散傅里叶变换(DFT)实现。
DFT可以将信号从时域转换到频域,从而得到信号的频谱信息。
3.stm32自相关算法的实现步骤在STM32平台上实现自相关算法,主要分为以下几个步骤:(1) 数字信号处理:将模拟信号转换为数字信号,并进行采样。
(2) 窗函数处理:为了减少频谱泄漏和旁瓣干扰,需要对信号进行窗函数处理。
常用的窗函数有汉宁窗、汉明窗、布莱克曼窗等。
(3) 离散傅里叶变换:对窗函数处理后的信号进行DFT,将时域信号转换为频域信号。
(4) 逆离散傅里叶变换:对频域信号进行逆DFT,得到时域信号的自身相关函数。
(5) 结果处理:根据自身相关函数,提取信号的频率信息,进行进一步分析和处理。
4.stm32自相关算法的应用领域STM32自相关算法广泛应用于各种信号处理领域,如通信、声学、图像处理、振动分析等。
通过自相关算法,可以更好地分析信号的频率特性,从而实现更高效、准确的信号处理。
5.总结STM32自相关算法是一种在信号处理领域广泛应用的算法,通过计算信号的自身相关函数,得到信号的频率信息。
stm32fft相位差

stm32fft相位差(原创实用版)目录1.什么是相位差2.STM32FFT 与相位差的关系3.如何使用 STM32FFT 计算相位差4.相位差的应用正文一、什么是相位差相位差是指两个同频率正弦量的相位之差,它反映了两个同频率正弦量的相对位置。
相位差与时间起点的选择无关,只与它们的初相有关。
在交流电路中,如果电路是纯电阻,那么交流电压和电流的相位差等于零。
二、STM32FFT 与相位差的关系STM32FFT 是一款基于 STM32 微控制器的快速傅里叶变换(FFT)库,它可以帮助我们快速地计算信号的频谱。
在计算频谱时,我们需要了解信号的相位差,因为相位差可以帮助我们更好地分析信号的特性。
三、如何使用 STM32FFT 计算相位差使用 STM32FFT 计算相位差的步骤如下:1.首先,需要安装并配置 STM32FFT 库。
详细的安装步骤可以参考STM32FFT 的官方文档。
2.准备输入信号。
输入信号可以是实时采集的数据,也可以是预先录制的数据。
输入信号应该是一个包含多个样本的数组,每个样本都是一个复数,表示信号的幅值和相位。
3.使用 STM32FFT 库计算输入信号的频谱。
在计算频谱之前,需要对输入信号进行窗函数处理,以减少频谱泄漏和旁瓣干扰。
窗函数可以选择汉宁窗、汉明窗或布莱克曼窗等。
4.根据计算得到的频谱,可以提取相位差信息。
相位差可以通过比较相邻频率成分的相位来计算。
相位差的大小反映了信号在不同频率下的相对相位关系。
四、相位差的应用相位差在许多领域都有广泛的应用,例如通信、控制和信号处理等。
在通信领域,相位差可以用于衡量信号的同步程度。
在控制领域,相位差可以用于控制电机的转速和位置。
在信号处理领域,相位差可以用于消除噪声和提高信号的质量。
单片机fft计算频率

单片机fft计算频率在单片机上进行FFT(快速傅里叶变换)可以用于计算信号的频谱,从而分析信号中的不同频率分量。
在单片机上执行FFT通常需要一些数学库或专门的FFT库,因为FFT是一个计算密集型的算法,需要较多的计算资源。
以下是在单片机上执行FFT的一般步骤:选择FFT库:选择适合你的单片机架构的FFT库。
一些流行的嵌入式系统FFT库包括CMSIS-DSP库、FFTW(Fastest Fourier Transform in the West)等。
这些库提供了实现FFT所需的函数和算法。
获取信号数据:从传感器、模拟输入或其他来源获取信号数据。
这可以是一维的时间域信号,比如声音或振动信号。
初始化FFT库:使用FFT库的初始化函数进行设置,包括FFT 的大小和其他参数。
输入信号数据:将获取到的信号数据输入到FFT库中。
这可能涉及到对数据进行预处理,例如去直流分量、窗函数处理等。
执行FFT:调用FFT库的计算函数执行FFT算法。
获取频谱数据:从FFT库中获取计算得到的频谱数据。
频谱数据表示信号在不同频率上的幅度。
分析频谱数据:使用频谱数据进行进一步的分析。
你可以识别信号中的主要频率分量,了解信号的频谱特性。
下面是一个简单的例子,使用CMSIS-DSP库在ARM Cortex-M微控制器上执行FFT的步骤:cCopy code#include "arm_math.h"#define FFT_SIZE 1024#define SAMPLING_FREQ 1000// 定义信号数组float32_t signal[FFT_SIZE];// 定义FFT输出数组float32_t fftOutput[FFT_SIZE * 2];int main(void) {// 初始化CMSIS-DSP库SystemInit();// 初始化FFT库arm_cfft_radix4_instance_f32 fftInstance;arm_cfft_radix4_init_f32(&fftInstance, FFT_SIZE, 0, 1);// 获取信号数据(示例中使用随机数据)for (int i = 0; i < FFT_SIZE; i++) {signal[i] = rand() % 100;}// 执行FFTarm_cfft_radix4_f32(&fftInstance, signal);// 获取频谱数据arm_cmplx_mag_f32(signal, fftOutput, FFT_SIZE);// 在这里进行进一步的频谱数据分析while (1) {// 主循环}}这只是一个简单的例子,实际上需要根据具体的硬件和需求进行更详细的配置和处理。
(完整word版)fft算法代码注释及流程框图

sub(x[j+k],product,&down);
x[j+k]=up; //up为蝶形单元右上方的值
x[j+k+l]=down; //down为蝶形单元右下方的值
}
}
}
}
void initW() //计算W的实现函数
{
int i;
W=(complex *)malloc(sizeof(complex) * size_x); /*申请size_x个复数W的空间(这部申请的空间有点多,实际上只要申请size_x/2个即可)*/
{
l=1<<i;
for(j=0;j<size_x;j+=2*l)
//算出第m=i级的结果【i从0到(log(size_x)/log(2))-1】
{
for(k=0;k<l;k++) //算出第i级内j组蝶形单元的结果
{ //算出j组中第k个蝶形单元
mul(x[j+k+l],W[(size_x/2/l)*k],&product); /*size/2/l是该级W的相邻上标差,l是该级该组取的W总个数*/
fft(); //利用fft快速算法进行DFT变化
output(); //顺序输出size_x个fft的结果
return 0;
}
/*进行基-2 FFT运算,蝶形算法。这个算法的思路就是,
先把计算过程分为log(size_x)/log(2)-1级(用i控制级数);
然后把每一级蝶形单元分组(用j控制组的第一个元素起始下标);
scanf("%d",&size_x);
(完整版)STM32F103通用教程

STM32F103_使用心得IO端口输入输出模式设置:...........;Delay延时函数:..............;IO端口使用总结:...............;IO口时钟配置:................;初始化IO口参数:...............;注意:时钟使能之后操作IO口才有效!......;IO端口输出高低电平函数:...........;IO的输入IO端口输入输出模式设置: (1)Delay延时函数: (2)IO端口使用总结: (2)IO口时钟配置: (2)初始化IO口参数: (2)注意:时钟使能之后操作IO口才有效! (2)IO端口输出高低电平函数: (2)IO的输入和输出宏定义方式: (3)读取某个IO的电平函数: (3)IO口方向切换成双向 (3)IO 口外部中断的一般步骤: (3)内部ADC使用总结: (4)LCDTFT函数使用大全 (5)TFTLCD使用注意点: (5)IO端口宏定义和使用方法: (6)Keil使用心得: (6)ucGUI移植 (6)DDS AD9850测试程序: (6)ADC 使用小结: (7)ADC测试程序: (9)DAC—tlv5638测试程序 (9)红外测试程序: (9)DMA使用心得: (9)通用定时器使用: (9)BUG发现: (10)编程总结: (10)时钟总结: (10)汉字显示(外部SD卡字库): (11)字符、汉字显示(内部FLASH) (12)图片显示: (16)触摸屏: (17)引脚连接: (19)IO端口输入输出模式设置:Delay延时函数:delay_ms(u16 nms);delay_us(u32 nus);IO端口使用总结:1)使能IO 口时钟。
调用函数为RCC_APB2PeriphClockCmd()。
2)初始化IO 参数。
调用函数GPIO_Init();3)操作IO。
IO口时钟配置:RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOA,ENABLE);RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOB,ENABLE);RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOC,ENABLE);RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOD,ENABLE);RCC_APB2PeriphClockCmd(RCC_APB2Periph_GPIOE,ENABLE);初始化IO口参数:注意:时钟使能之后操作IO口才有效!GPIO_InitTypeDefGPIO_InitStructure; GPIO_InitStructure.GPIO_Pin = GPIO_Pin_13|GPIO_Pin_15; GPIO_InitStructure.GPIO_Mode = GPIO_Mode_IPU; GPIO_Init(GPIOA, &GPIO_InitStructure); //上拉输入GPIO_InitTypeDefGPIO_InitStructure;GPIO_InitStructure.GPIO_Pin = GPIO_Pin_8;GPIO_InitStructure.GPIO_Mode = GPIO_Mode_Out_PP;GPIO_InitStructure.GPIO_Speed = GPIO_Speed_50MHz;GPIO_Init(GPIOA, &GPIO_InitStructure); //LED0-->PA.8 端口配置 //推挽输出技巧:如果为同一端口的不同引脚,可以使用或运算,如GPIO_InitStructure.GPIO_Pin =GPIO_Pin_13|GPIO_Pin_15;IO端口输出高低电平函数:GPIO_SetBits(GPIOA,GPIO_Pin_8|GPIO_Pin_9); //PA.8 输出高GPIO_ResetBits(GPIOA,GPIO_Pin_8);GPIO_WriteBit(GPIO_TypeDef* GPIOx, uint16_t GPIO_Pin, BitActionBitVal);//可以输出1,也可以输出0GPIO_Write(GPIO_TypeDef* GPIOx, uint16_t PortVal);//整体输出一个值IO的输入和输出宏定义方式:#define DATAOUT(x) GPIOB->ODR=x; //数据输出#define DATAIN GPIOB->IDR; //数据输入#define DATAOUT(DataValue){GPIO_Write(GPIOB,(GPIO_ReadOutputData(GPIOB)&0xff00)|(DataValu e&0x00FF));} //PB0~7,作为数据线读取某个IO的电平函数:(一) 读出一个IO口电平GPIO_ReadInputDataBit(GPIO_TypeDef* GPIOx, uint16_t GPIO_Pin)#define KEY0 GPIO_ReadInputDataBit(GPIOA,GPIO_Pin_13) //PA13#define KEY1 GPIO_ReadInputDataBit(GPIOA,GPIO_Pin_15) //PA15#define KEY2 GPIO_ReadInputDataBit(GPIOA,GPIO_Pin_0)(二) 读出某个IO口的全部电平GPIO_ReadInputData(GPIOC)IO口方向切换成双向IIC里面的一个实例#define SDA_IN() {GPIOC->CRH&=0XFFFF0FFF;GPIOC->CRH|=8<<12;} //PC12#define SDA_OUT() {GPIOC->CRH&=0XFFFF0FFF;GPIOC->CRH|=3<<12;}IO 口外部中断的一般步骤:1)初始化IO 口为输入。
stm32正弦波频率计算

stm32正弦波频率计算
摘要:
1.STM32简介
2.正弦波频率计算方法
3.STM32实现正弦波频率计算的步骤
4.代码示例及解析
5.总结
正文:
STM32是一款高性能、低成本的微控制器,广泛应用于各种嵌入式系统中。
在很多应用场景中,需要根据需求产生一定频率的正弦波信号。
本文将介绍如何使用STM32计算并生成正弦波频率,同时提供一段代码示例。
一、STM32简介
STM32是STMicroelectronics推出的一款基于ARM Cortex-M内核的微控制器。
它具有丰富的外设接口、高性能的运算能力以及低功耗的特点。
由于其强大的功能,STM32在很多领域都有广泛的应用,如工业控制、医疗设备、消费电子等。
二、正弦波频率计算方法
正弦波频率的计算公式为:f = n / T,其中f表示频率,n表示波形周期数,T表示周期时长。
在实际应用中,我们可以根据需求计算出所需的频率,进而确定微控制器的时钟频率和晶振频率。
三、STM32实现正弦波频率计算的步骤
1.确定目标频率:根据应用需求,计算所需的正弦波频率。
2.选择合适的晶振频率:根据目标频率,选择合适的晶振频率,以满足频率精度要求。
3.配置微控制器时钟:根据晶振频率,配置微控制器的内部时钟,以产生所需频率的正弦波信号。
4.编写程序:编写程序实现正弦波信号的生成和计算。
STM32F103中文教程及参考手册

时钟控制寄存器(RCC_CR) ---------------------------------------------------------42 时钟配置寄存器(RCC_CFGR) -----------------------------------------------------43 时钟中断寄存器 (RCC_CIR) -------------------------------------------------------46 APB2 外设复位寄存器 (RCC_APB2RSTR) -------------------------------------48 APB1 外设复位寄存器 (RCC_APB1RSTR) -------------------------------------50 AHB外设时钟使能寄存器 (RCC_AHBENR) -----------------------------------52 APB2 外设时钟使能寄存器(RCC_APB2ENR) ---------------------------------53 APB1 外设时钟使能寄存器(RCC_APB1ENR) ---------------------------------54 备份域控制寄存器 (RCC_BDCR) -------------------------------------------------56 控制/状态寄存器 (RCC_CSR)------------------------------------------------------57
3.3
低功耗模式 --------------------------------------------------------------------------------- 26
FFT算法STM32

void divi(complex ,complex ,complex *);/*复数除法*/
/******************************/
/*快速傅里叶变换*/
void fft()
x[j+k]=up;
x[j+k+l]=down;
}
}
}
}
/*初始化变换核*/
void initW()
{int s;
for(s=0;s<size_x;s++)
{
W[s].real=cos(2*PI/size_x*s);
W[s].img=-1*sin(2*PI/size_x*s);
}
}
/*变址计算,将x(n)码位倒置*/
void change()
{complex temp;
unsigned short s=0,j=0,k=0;
double t;
for(s=0;s<size_x;s++)
{
k=s;j=0;
t=(log(size_x)/log(2));
while( (t--)>0 )
{
j=j<<1;
j|=(k & 1);
k=k>>1;
}
if(j>s)
{
temp=x[s];
x[s]=x[j];
x[j]=temp;
} Βιβλιοθήκη } /************************************/
(完整word版)fft算法代码注释及流程框图

{
double real;
double img;
}complex; //定义复数型变量的结构体
void fft(); //快速傅里叶变换函数声明
void initW(); //计算W(0)~W(size_x-1)的值函数声明
void change(); //码元位置倒置函数函数声明
scanf("%d",&size_x);
printf("Please input the data in x[N]:(such as:5 6)\n"); /*输入序列对应的值*/
for(i=0;i<size_x;i++)
scanf("%lf %lf",&x[i].real,&x[i].img);
initW(); //计算W(0)~W(size_x-1)的值
}
}
void change() //输入的码组码位倒置实现函数
{
complex temp;
unsigned short i=0,j=0,k=0;
double t;
for(i=0;i<size_x;i++)
{
k=i;
j=0;
t=(log(size_x)/log(2));
while((t--)>0)
{
j=j<<1;
printf("\n");
else
printf("-j%.4f\n",fabs(x[i].img));
//如果虚部的值小于-0.0001,输出-jx.img的形式
}
STM32F103通用教程

STM32F103通用教程
对于初学者来说,学习STM32F103 的第一步是了解它的硬件组成和
特点。
STM32F103 是基于ARM Cortex-M3内核的微控制器,内置了多种外
设模块,如通用串行总线(USART)、SPI(Serial Peripheral Interface)、I2C(Inter-Integrated Circuit)、定时器、通用输入/输出口等等。
此外,它还具有片上闪存和SRAM,可以方便地存储程序代码和数据。
STM32F103 还具有多种引脚、工作电压和工作频率选择,适应了不同的应
用需求。
在使用STM32F103 进行开发之前,需要准备一个基于ARM Cortex-M3
内核的开发板和开发环境。
开发板提供了对STM32F103 的外设模块的物
理连接和输入/输出接口,而开发环境则提供了对STM32F103 的编程和调
试的支持。
常见的开发环境有Keil、IAR和STM32Cube IDE等。
搭建好开
发环境后,可以开始编写代码,对STM32F103 进行开发。
除了学习和开发STM32F103的硬件和固件程序,还可以参考相关的教
程和文档,了解更多关于STM32F103的知识。
ST微电子公司提供了丰富
的STM32F103相关的文档和教程,包括官方参考手册、应用笔记和培训课
程等。
此外,还可以参考网络上的STM32F103教程和开发案例,学习其他
人的经验和技巧。
使用STM32_的DSP库进行FFT变换

使用STM32 的DSP库进行FFT变换STM32 2010-08-11 10:41:39 阅读802 评论7字号:大中小订阅/******************************************************************************** **************************FileName:dsp_asm.h******************************************************************************* ***************************/#ifndef __DSP_ASM_H__#define __DSP_ASM_H__******************************************************************************* *************************** FUNCTION PROTOTYPES******************************************************************************* ***************************/void dsp_asm_test(void);void dsp_asm_init(void);#endif /* End of module include. *//*8888888888888888888888888888888888888888888888888888888888888888*//*8888888888888888888888888888888888888888888888888888888888888888*//** FileName:dsp_asm.c* Author:Bobby.Chen* Email:heroxx@* Date:2010-08-11* Description:This file showes how to use the dsp library in mdk project.* 使用三角函数生成采样点,供FFT计算* 进行FFT测试时,按下面顺序调用函数即可:* dsp_asm_init();* dsp_asm_test();*/#include "stm32f10x.h"#include "dsp_asm.h"#include "stm32_dsp.h"#include "table_fft.h"#include <stdio.h>#include <math.h>/******************************************************************************** *************************** LOCAL CONSTANTS******************************************************************************* ***************************/#define PI2 6.28318530717959// Comment the lines that you don't want to use.// 要模拟FFT,请注释掉其他的预定义// 此处也可以全部注释掉,在MDK的工程属性->"C/C++"->"Preprocessor Symbols"-"Define:"中添加NPT_XXX项目// 但是这样做法的缺点是每次修改XXX数据,都会导致MDK下次编译时会编译全部文件,速度太慢。
STM32-FFT代码说明

FFT 代码说明FFT 为Fast Fourier Transformation ,即快速傅里叶变换,本项目中,FFT 的目标是识别频率为形如式(1.1)的一个正弦信号:()sin(2)f x A ft π=• (1.1) 其中,21Hz 5%f =±;因为单片机通过ADC 接口读取该正弦信号的电压值,而12位精度的ADC 的值范围在0-4096之间,如信号经过放大器后映射到0-3.3V 之间,则振幅A 的取值0-4096之间。
假设,信号经过放大器后,其电压值最大为3.3V ,最小为0V ,则此信号的振幅为1.65V ,对应A=2048,即该信号为:()20482048sin(221)f x t π=+•⨯• (1.2) 本文中给出的例程即通过FFT 识别式(1.2)这种正弦信号。
假设采样频率为Fs ,信号频率Fn ,采样点数为N 。
那么FFT 之后结果就是一个为N 点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A ,那么FFT 的结果的每个点(除了第一个点直流分量之外)的模值就是A 的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N 倍。
第一个点表示直流分量(即0Hz ),而最后一个点N 的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs ,这中间被N -1个点平均分成N 等份,每个点的频率依次增加。
例如某点n 所表示的频率为:()1*/Fn n Fs N =- (1.3) 频率分辨率(/f Fs N ∆=)等于采样时间的倒数。
例如要分辨0.1Hz ,则需要采集10s 。
1 基于STM32官方DSP 库的FFT 算法工程文件中包含三个函数库,分别为:cr4_fft_64_stm32.scr4_fft_256_stm32.scr4_fft_1024_stm32.s分别对应数据点数为64,256和1024时的FFT算法。
(完整word版)基于KEIL的STM32F103系统的开发与调试
-->
调试中经常需要观察存储器,点相应图标
输入地址后即可显示后续的存储空间的内容。
在存储区间点击右键可以选择显示类型,如无符号32位
若修改代码,再按 退出调试界面。
图形界面中有时可以自由摆放所用的工具。
DEBUG时,左边是寄存器组信息,右边通常会出现“上面机器码与汇编-下面程序”结构。上方的黄箭头表时当前取指地址(PC值),下面的双三角表示即将执行的程序代码。
11、调试操作。从左到右:重启、执行、停止、单步、单行、返回、执行到当前行。单步是指按照指令的实际操作一步步执行;单行是指完成该指令所到实现的功能,并不关心该指令所导致的实际操作过程。
4、运行环境选择。暂不选,按确定。
5、建立了一个空项目。
6、设置OPTION,右键点击TARTGET1
target 1'
7、构建软仿真环境,在Ddbug栏设置。
8、添加汇编文件startup.s
9、添加代码
10、先编译,再链接,最后调试。(底部有编译和链接信息,出错的话会提示)
微处理器系统原理与设计课程实践参考文档之
基于KEIL的STM32F103系统的开发与调试
1、建立工程
2、选择工作目录,输入项目名test1。
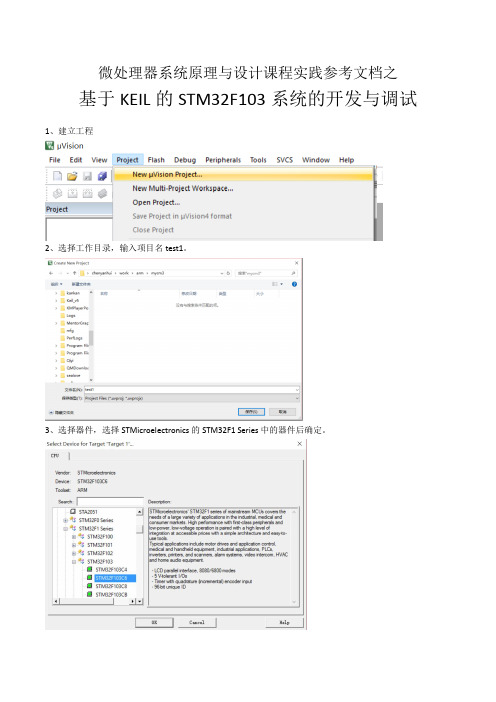
3、选择器件,选择STMicroelectronics的STM32F1 Series中的器件后确定。
对于KEIL5来说,若没有该器件,需要装PACKE,选择Pack Installer后选择相应PACK安装即可。
基于STM32的FFT算法实现

离散傅里叶变换(DFT)是分析信号频域特性的重要 工具,其运算复杂度随处理序列的长度增加大幅上升,不利 于计算机对实时的大数据信号进行处理,快速傅里叶变换 (FFT)的出现解决了这一问题。FFT 是将 DFT 算法进行 高效化、计算机化的一种改进算法。FFT 之所以能够改善运 算量,是因为其充分利用了 DFT 运算中的对称性和周期性, 从而能够将运算量从 N 2 减少到 N*log2 (N ) ,其中 N 为待计算的 序列的长度。当 N 越大,FFT 算法提高计算效率的效果就 越突出。
则又可进一步得到四个
N 4
点的序列,如式(5)、(6)所示:
X
X= 1 (k )
1(k
+
N 4
X )=
3(k ) + WNk/2 X 4 (k ) = , k
X 3(k ) −WNk/2 X 4 (k )
0,1, 2,,
N 4
−1
(5)
X
X= 2 (k)
2 (k
+
N 4
X )=
5 (k ) + WNk/2 X 6 (k ) = , k
d=1;
d = 1<<(M-L); // 第 L 级的各旋转因子WNk
中 k 的数值间隔是 d
k=1;
k=j*d; // 计算第 L 级中第 j 种旋转因子的 k 值
for(i=0;i<=d-1;i++) // 第 j 种旋转因子第 i
次参与运算,共 d 次
{
结语
根据 FFT 原理推导出能用 C 语言表达的 FFT 算法,并 在 STM32 上实现。经过 matlab 仿真对比发现,本系统得
图 7 给定输入信号 y=3.4cos(2Π×54×t)+3.5cos (2Π×450×t+Π/2)频谱对比图
fft滤波算法范文

fft滤波算法范文FFT (Fast Fourier Transform) 滤波算法是一种常见的信号分析和滤波技术。
它基于快速傅里叶变换(FFT)算法,可以将信号从时域转换到频域,并对频域信号进行处理和滤波操作。
以下将详细介绍FFT滤波算法的原理及其应用。
一、原理:FFT滤波算法的原理基于傅里叶变换,其基本思想是将时域信号分解成一系列正弦波的频域信号,并对频域信号进行处理和滤波操作。
具体步骤如下:1.采样信号:首先对待处理的信号进行采样,通常是通过模拟到数字转换器(ADC)将连续信号转化为离散的数据点。
2.傅里叶变换:通过应用快速傅里叶变换(FFT),将离散采样的信号从时域转换为频域。
FFT算法快速高效地计算出信号的频率和相位谱。
3.频域处理:在频域上,可以对信号进行各种操作和处理,如滤波、增益调整等。
其中最常见的应用是滤波操作,通过选择感兴趣的频率范围,可以将噪声或其他频率成分从信号中滤除。
4.逆傅里叶变换:对处理后的频域信号应用逆傅里叶变换(IFFT),将频域信号转换回时域,得到处理后的信号。
二、应用:FFT滤波算法广泛应用于各个领域,包括信号处理、音频处理、图像处理等。
以下列举几个典型的应用案例:1.语音信号去噪:通过将语音信号转换到频域,可以根据频率成分的特点,选择性地滤除背景噪声,从而实现清晰的音频输出。
2.图像去噪:将图像转换到频域后,可以通过频域滤波操作去除噪声和伪像,提高图像质量。
3.信号谱分析:将信号转换到频域,可以分析信号中的频率成分,识别出信号的频率特征,如音乐信号的音调、语音信号的共振峰等。
4.音频合成:通过合成不同频率和幅度的正弦波,可以生成各种音频信号,如合成乐器音色、产生特定频率的声音等。
5.数字通信中的调制和解调:FFT滤波算法用于将数字信号转化为模拟信号,或将模拟信号转化为数字信号,用于数字通信系统中的调制和解调。
总结:FFT滤波算法通过傅里叶变换将信号从时域转换到频域,可应用于各种信号处理和滤波方面的任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
STM32F103 12-15元左右
本文将以一个实例来介绍如何使用STM32提供的DSP库函数进行FFT。
1.FFT运算效率
使用STM32官方提供的DSP库进行FFT,虽然在使用上有些不灵活(因为它是基4的FFT,所以FFT的点数必须是4^n),但其执行效率确实非常高效,看图1所示的FFT运算效率测试数据便可见一斑。
该数据来自STM32 DSP库使用文档。
图1 FFT运算效率测试数据
由图1可见,在STM32F10x系列处理器上,如果使用72M的系统主频,进行64点的FFT运算,仅仅需要0.078ms而已。
如果是进行1024点的FFT运算,也才需要2.138ms。
2.如何使用STM32提供的DSP库函数
2.1下载STM32的DSP库
大家可以从网上搜索下载得到STM32的DSP库,这里提供一个下载的地址:https:///public/STe2ecommunities/mcu/Lists/cortex_ mx_stm32/DispForm.aspx?ID=30831&RootFolder=%2fpublic%2fST e2ecommunities%2fmcu%2fLists%2fcortex%5fmx%5fstm32%2fST M32F10x%20DSP%20library%2c%20where%20is%20it
2.2添加DSP库到自己的工程项目中
下载得到STM32的DSP库之后,就可以将其添加到自己的工程项目中了。
其中,inc文件夹下的stm32_dsp.h和table_fft.h两个文件是必须添加的。
stm32_dsp.h是STM32的DSP库的头文件。
src文件夹下的文件可以有选择的添加(用到那个添加那个即可)。
因为我只用到了256点的FFT,所以这里我只添加了cr4_fft_256_stm32.s文件。
添加完成后的项目框架如图2所示。
图2 项目框架
2.3模拟采样数据
根据采样定理,采样频率必须是被采样信号最高频率的2倍。
这里,我要采集的是音频信号,音频信号的频率范围是20Hz到20KHz,所以我使用的采用频率是44800Hz。
那么在进行256点FFT时,将得到44800Hz / 256 = 175Hz的频率分辨率。
为了验证FFT运算结果的正确性,这里我模拟了一组采样数据,并将该采样数据存放到了long类型的lBufInArray数组中,且该数组中每个元素的高16
位存储采样数据的实部,低16位存储采样数据的虚部(总是为0)。
为什么要这样做呢?是因为后面要调用STM32的DSP库函数,需要传入的参数规定了必须是这样的数据格式。
下面是具体的实现代码:
1
/****************************************************************** 2函数名称:InitBufInArray()
3函数功能:模拟采样数据,采样数据中包含3种频率正弦波(350Hz,8400Hz,18725Hz)
4参数说明:
5备注:在lBufInArray数组中,每个数据的高16位存储采样数据的实部, 6低16位存储采样数据的虚部(总是为0)
7作者:博客园依旧淡然(/menlsh/)
8
*******************************************************************/
9void InitBufInArray()
10 {
11 unsigned short i;
12float fx;
13for(i=0; i<NPT; i++)
14 {
15 fx = 1500 * sin(PI2 * i * 350.0 / Fs) +
162700 * sin(PI2 * i * 8400.0 / Fs) +
174000 * sin(PI2 * i * 18725.0 / Fs);
18 lBufInArray[i] = ((signed short)fx) << 16;
19 }
20 }
其中,NPT是采样点数256,PI2是2π(即6.28318530717959),Fs是采样频率44800。
可以看到采样数据中包含了3种频率的正弦波,分别为350Hz,8400Hz和18725Hz。
2.4调用DSP库函数进行FFT
进行256点的FFT,只需要调用STM32 DSP库函数中的cr4_fft_256_stm32()函数即可。
该函数的原型为:
void cr4_fft_256_stm32(void *pssOUT, void *pssIN, uint16_t Nbin);
其中,参数pssOUT表示FFT输出数组指针,参数pssIN表示要进行FFT
运算的输入数组指针,参数Nbin表示了点数。
至于该函数的具体实现,因为是用汇编语言编写的,我也不懂,这里就不妄谈了。
下面是具体的调用实例:
cr4_fft_256_stm32(lBufOutArray, lBufInArray, NPT);
其中,参数lBufOutArray同样是一个long类型的数组,参数lBufInArray就是存放模拟采样数据的采样数组,NPT为采样点数256。
调用该函数之后,在lBufOutArray数组中就存放了进行FFT运算之后的结果数据。
该数组中每个元素的数据格式为;高16位存储虚部,低16位存储实部。
2.5计算各次谐波幅值
得到FFT运算之后的结果数据之后,就可以计算各次谐波的幅值了。
下面是具体的实现代码:
1
/****************************************************************** 2函数名称:GetPowerMag()
3函数功能:计算各次谐波幅值
4参数说明:
5备注:先将lBufOutArray分解成实部(X)和虚部(Y),然后计算幅值(sqrt(X*X+Y*Y)
6作者:博客园依旧淡然(/menlsh/)
7
*******************************************************************/
8void GetPowerMag()
9 {
10 signed short lX,lY;
11float X,Y,Mag;
12 unsigned short i;
13for(i=0; i<NPT/2; i++)
14 {
15 lX = (lBufOutArray[i] << 16) >> 16;
16 lY = (lBufOutArray[i] >> 16);
17 X = NPT * ((float)lX) / 32768;
18 Y = NPT * ((float)lY) / 32768;
19 Mag = sqrt(X * X + Y * Y) / NPT;
20if(i == 0)
21 lBufMagArray[i] = (unsigned long)(Mag * 32768);
22else
23 lBufMagArray[i] = (unsigned long)(Mag * 65536);
24 }
25 }
其中,数组lBufMagArray存储了各次谐波的幅值。
2.6实验结果
通过串口,我们可以将lBufMagArray数组中各次谐波的幅值(即各个频率分量的幅值)输出打印出来,具体实验数据如下所示:
View Code
在以上的实验数据中,我们分别打印出来了点数、频率、幅值、实部、虚部信息。
由以上的实验数据,我们可以看出,在频率为350Hz,8400Hz和18725Hz 时,幅值出现峰值,分别为1492、2696和3996,这与我们所预期的结果正好相符,从而验证了实验结果的正确性。
