confidence intervals总结置信区间SPSS计算解释 及APA 报告规范-zhaomf
置信区间(详细定义及计算)

2. 估计的精度要尽可能的高.如要求区间长度 ˆ2 ˆ1
尽可能短,或能体现该要求的其它准则.
可靠度与精度是一对矛盾, 一般是在保证可靠度的
条件下尽可能提高精度.
16
已知某种油漆的干燥时间X(单位:小时)
服从正态分布 X ~ N (,1), 其中μ未知,现在抽取
25个样品做试验, 得数据后计算得
t
2
(n
1),
X
S n
t
2
(n
1)]
[X
S n
t
2
(n
1)]
19
为了调查某地旅游者的消费额为X, 随机访问了
40名旅游者。得平均消费额为 x 105 元,样本方差
s2 282 设 X ~ N (, 2 )求该地旅游者的平均消费额
μ的置信区间。 0.05 解 本题是在σ2未知的条件下求正态总体参数μ的
0.04
X
P{ z0.04 P{X
n
2 z0.01}
n
z0.01 X
0.95
n z0.04}
0.95
z0.04
0.01
z0.01
则μ的置信度为0.95的置信区间为
[ X n z0.01 , X n z0.04 ]
与上一个置信区间比较,同样是 1 0.95
[ X n t 2 (n 1)]
则所求μ的2 置信区间为 [1259 24.58 , 1259 24.58] 21
为了估计一批钢索所能承受的平均张力(单位
kg/cm2), 随机选取了9个样本作试验,由试验所得数据得
置信区间的通俗理解

置信区间的通俗理解统计学是一门研究数据分析和推断的学科,它的发展历程也伴随着人类社会的发展而逐步完善。
在实际应用中,我们常常需要对样本数据进行分析,以得出总体的特征和性质。
但是样本的结果并不能完全代表总体的结果,因此我们需要通过一定的方法来推断总体的特征和性质。
而置信区间就是这样一种方法。
一、什么是置信区间置信区间,英文名为Confidence Interval,简称CI,是指对总体某一参数的区间估计。
这个区间的构造方法是,利用样本数据计算出一个区间,这个区间的两端分别是样本统计量的值,这个区间的范围就是置信区间。
这个区间的意义是,我们可以通过这个区间来推断总体参数的真实值,而这个推断的结果是有一定的置信度的。
二、置信区间的计算方法置信区间的计算方法主要有两种,一种是基于t分布的方法,另一种是基于正态分布的方法。
这两种方法的具体步骤如下:1.基于t分布的方法(1)计算样本的均值和标准差;(2)确定置信水平和自由度;(3)查t分布表,确定t值;(4)计算置信区间。
2.基于正态分布的方法(1)计算样本的均值和标准差;(2)确定置信水平和样本容量;(3)查正态分布表,确定z值;(4)计算置信区间。
三、置信区间的解释置信区间的解释是指,这个区间的范围是我们对总体参数真实值的推断结果。
这个推断的结果是有一定的置信度的,通常以置信水平的形式来表示。
例如,我们可以说“在95%的置信水平下,总体参数的真实值在置信区间内”。
四、置信区间的应用置信区间的应用非常广泛,例如:1.在医学研究中,可以通过置信区间来推断某种治疗方法的效果;2.在市场调查中,可以通过置信区间来推断某种产品的市场占有率;3.在工程设计中,可以通过置信区间来推断某种材料的强度特性。
总之,置信区间是一种非常重要的统计方法,它可以帮助我们对总体参数的真实值进行推断,并且这个推断结果是有一定置信度的。
在实际应用中,我们需要根据具体情况选择合适的置信水平和计算方法,以得到准确可靠的结果。
置信区间的计算与解读

置信区间的计算与解读置信区间是统计学中常用的一种方法,用于估计总体参数的范围。
在实际应用中,我们往往无法获得总体的全部数据,而只能通过抽样得到一部分样本数据。
通过计算置信区间,我们可以利用样本数据对总体参数进行估计,并给出一个范围,以表明我们对估计结果的不确定性程度。
一、置信区间的计算方法置信区间的计算方法主要有两种:参数估计法和非参数估计法。
1. 参数估计法参数估计法是基于总体参数的已知分布进行计算的。
常见的参数估计法有正态分布的置信区间和二项分布的置信区间。
正态分布的置信区间计算方法如下:假设总体服从正态分布N(μ, σ^2),样本容量为n,样本均值为x̄,样本标准差为s。
置信水平为1-α,α为显著性水平。
置信区间的计算公式为:x̄± Z(1-α/2) * (σ/√n)其中,Z(1-α/2)为标准正态分布的上分位数,可以在标准正态分布表中查找。
二项分布的置信区间计算方法如下:假设总体服从二项分布B(n, p),样本容量为n,样本成功次数为x,置信水平为1-α,α为显著性水平。
置信区间的计算公式为:p̄± Z(1-α/2) * √(p̄(1-p̄)/n)其中,p̄为样本成功率,可以通过样本成功次数除以样本容量得到。
2. 非参数估计法非参数估计法是基于样本数据的分布进行计算的。
常见的非参数估计法有中位数的置信区间和百分位数的置信区间。
中位数的置信区间计算方法如下:假设样本容量为n,样本数据按升序排列,第k个观测值为中位数,置信水平为1-α,α为显著性水平。
置信区间的计算公式为:[x(k-1)/2, x(n-k+1)/2]其中,x(k-1)/2为第k-1个观测值,x(n-k+1)/2为第n-k+1个观测值。
百分位数的置信区间计算方法类似,只需将中位数的位置换成相应的百分位数的位置。
二、置信区间的解读置信区间给出了对总体参数的估计范围,通常以置信水平来表示。
置信水平越高,估计结果的可信度越高,但估计范围也会相应增大。
置信区间(详细定义及计算)

5 1
4
s2 5
28.5 5.339
n 1 4 0.01
S
查表 t0.01 (4) t0.005(4) 4.6041
[ X n t 2 (n 1)]
则所求μ的2 置信区间为 [1259 24.58 , 1259 24.58] 21
为了估计一批钢索所能承受的平均张力(单位
kg/cm2), 随机选取了9个样本作试验,由试验所得数据得
只依赖于样本的界限(构造统计量) (ˆ1 ˆ2 )
ˆ1 ˆ1( X1, X 2 , X n ) ˆ2 ˆ2 ( X1, X 2 , X n )
一旦有了样本,就把 估计在区间 [ˆ1,内ˆ2 .]
这里有两个要求:
1. 要求 很大的可能被包含在区间 [ˆ内1,,ˆ2 ]
就是说,概率 P{ˆ1 ˆ2} 要尽可能大.
求温度真值的置信度为 0.99 的置信区间。
解 设μ为温度的真值, X表示测量值,通常是一个
正态随机变量 EX .
问题是在未知方差的条件下求μ的置信区间。 由公式
x 1250 1 [0 15 510 25] 1259
s2
1
5 [(1250
1259)2
(1275
1259)2 ]
570
程度为0.95. 或“该区间包含μ”这一事实的可信程度 为0.95.
注: μ的置信水平1-α的置信区间不唯一。
11
μ的置信区间是总体 X ~ N (, 2)的前提下提出的。
分布,都近似有
当 n 充分大时,无论X服从什么
Z X EX ~ N (0,1) DX n
[X
n
z 2 ,
X
n
z 2 ]
均可看作EX的置信区间。
95%CI,置信区间ConfidenceInterval

95%CI,置信区间ConfidenceInterval什么是置信区间 置信区间⼜称估计区间,是⽤来估计参数的取值范围的。
常见的52%-64%,或8-12,就是置信区间(估计区间)。
置信区间的概述1、对于具有特定的发⽣概率的,其特定的价值区间:⼀个确定的数值范围(“⼀个区间”)。
2、在⼀定置信⽔平时,以测量结果为中⼼,包括总体均值在内的可信范围。
3、该区间包含了参数θ真值的可信程度。
4、参数的置信区间可以通过点估计量构造,也可以通过构造。
关于置信区间的宽窄 窄的置信区间⽐宽的置信区间能提供更多的有关的信息。
假设全班考试的平均分数为65分,则置信区间、间隔、宽窄度、表达的意思是: 0-100分 100 宽等于什么也没告诉你 30-80分 50 较窄你能估出⼤概的平均分了(55分) 60-70分 10 窄你⼏乎能判定全班的平均分了(65分)置信区间与置信⽔平、样本量的关系 1、对置信区间的影响:在固定的情况下,越多,置信区间越窄。
实例分析: 经过实践计算的样本量与置信区间关系的变化表(假设置信⽔平相同):样本量置信区间间隔宽窄度10050%-70%20宽80056.2%-63.2%7较窄1,60057.5%-63% 5.5较窄3,20058.5%-62% 3.5更窄 由上表得出: 1、在置信⽔平相同的情况下,样本量越多,置信区间越窄。
2、置信区间变窄的速度不像样本量增加的速度那么快,也就是说并不是样本量增加⼀倍,置信区间也变窄⼀倍(实践证明,样本量要增加4倍,置信区间才能变窄⼀倍),所以当样本量达到⼀个量时(通常是1,200,如上例三个国家各抽了1,200个),就不再增加样本了。
通过置信区间的计算公式来验证置信区间与样本量的关系 置信区间=样本的推断值±(可靠程度系数× ) 从上述公式中可以看出: 1、在其他因素不变的情况下,样本量越多(⼤),置信区间越窄(⼩)。
2、置信⽔平对置信区间的影响:在相同的情况下,置信⽔平越⾼,置信区间越宽。
置信区间(详细定义及计算)

2
z } 1
2
n
2
2
P{z 2
X 2
z 2} 1
z
z
n
2
2
P{
n
z
2
X
n
z
2}
1
P{X
n
z 2
X
n
z 2} 1
这就是说随机区间
[ X n z 2 , X n z 2 ]
P{1 2} 1
由于正态随机变量广泛存在,特别是很多产品的 指标服从正态分布,我们重点研究一个正态总体情形
数学期望和方差 2的区间估计。 5
设 X1, X 2 ,, X n 为总体 X ~ N (, 2 ) 的样本,
X , S 2 分别是样本均值和样本方差。 对于任意给定的α,我们的任务是通过样本寻找一
也就是说,我们希望确定一个区间,使我们能以比 较高的可靠程度相信它包含真参数值.
这里所说的“可靠程度”是用概率来度量的,
称为置信概率,置信度或置信水平.
习惯上把置信水平记作 1 ,这里 是一个很小
的正数,称为显著水平。
2
若由总体X的样本 X1,X2,…Xn 确定的 两个统计量
1 1( X1, X 2 ,, X n ),
我们称其为置信度为0.95的μ的置信区间。其含义是:
若反复抽样多次,每个样本值(n =16) 按公式
(x 1.96 , x 1.96) 即 (x 0.49) 确定一个区间。
4
4
10
(x 0.49, x 0.49) 确定一个区间。
【最新精选】使用SPSS求置信区间
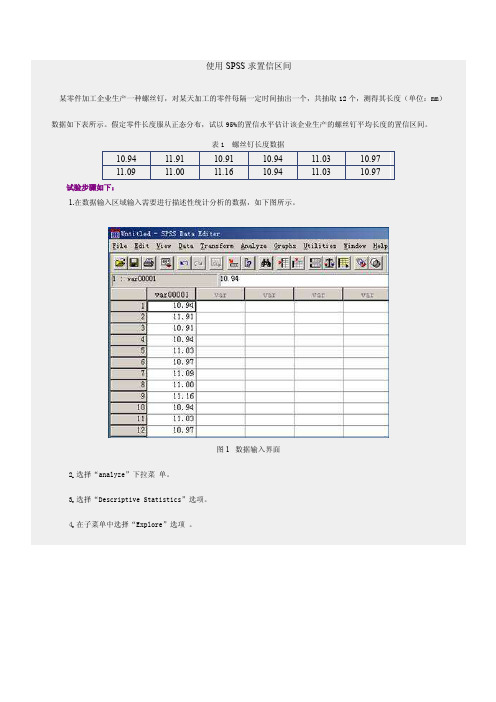
图2 选择分析工具5.在左侧选择需要进行区间估计的V ar00001参数进入右侧的“Dependent List”。
图3 选择变量进入右侧的分析列表6.在“Statistics”选项中设定置信水平为95%。
【附加总结类文档一篇,不需要的朋友可以下载后编辑删除,谢谢】2015年文化馆个人工作总结在XXXX年X月,本人从XXXX学院毕业,来到了实现我梦想的舞台--XX区文化馆工作。
在这里我用艰辛的努力,勤劳的付出,真诚而认真地工作态度认真的做好自身的每一项文化馆相关工作,取得了较为良好的工作业绩。
随着一场场活动的成功举办、一台台戏剧的成功出演,在这个带有着梦想和希望的舞台上,转眼之间我已在这里渡过了XX年的青春事业,我亦与舞台共同成长,逐步由一名青涩的毕业生,历练成为了今天的XXX。
梦想在于不断坚持,未来的旅途在于不断的前进,在这个承载着梦的舞台上,我持以坚定的信心和丰富的工作能力与工作经验,一步一步超前迈进着。
下面我将自身XX年来的工作能力情况总结如下:一、一专多能服务1、高端学识水平。
本人于XXXX年XX月毕业于XXXX大学XX专业。
随后于XXXX年X 月进入XX区文化馆从事XX工作,至今已有XX年的时间。
在本人从事文化馆XX工作的XX年里,我始终坚持积极探索、勤奋学习,做到辅助教学与实际工作相长,坚定与时俱进的思想理念,努力攻克各项困难,将提高效益型,能力型的工作绩效作为自己的奋斗目标,并在自身的素质方面进行了坚持不懈的强化与提高。
我深知,要不断充实自身能力,深化提升自身素质,才能够不断更新自我,超越自我,为我XX区文化馆的发展与活动做出奉献。
为此,我树立起了牢固的学习思想,除积极参加上级机关以及本馆内组织的各项思想教育以及业务培训活动外,我还一直坚持,利用业余时间阅读和学习各类与我文化馆工作相关的理论书籍与系列杂志等相关信息书籍,通过专业的培训和广泛的阅读,我吸取了优秀工作者以及高级文化工作人员的先进经验和优秀成果,在理论和实践结合的层面上逐渐开拓了视野,以高效提升了自身的专业能力和学识水平。
置信区间计算

置信区间计算
置信区间是指由样本统计量所构造的总体参数的估计区间。
在统计学中,一个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。
置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度,其给出的是被测量参数的测量值的可信程度,即前面所要求的“一个概率”。
置信区间的计算公式取决于所用到的统计量。
置信区间是在预先确定好的显著性水平下计算出来的,显著性水平通常称为α(希腊字母alpha),如前所述,绝大多数情况会将α设为0.05。
置信度为(1-α),或者100×(1-α)%。
于是,如果α=0.05,那么置信度则是0.95或95%,后一种表示方式更为常用。
置信区间的常用计算方法如下:
Pr(c1<=μ<=c2)=1-α
其中:α是显著性水平(例:0.05或0.10);
Pr表示概率,是单词probablity的缩写;
100%*(1-α)或(1-α)或指置信水平(例如:95%或0.95);
表达方式:interval(c1,c2) - 置信区间。
求解步骤
第一步:求一个样本的均值
第二步:计算出抽样误差。
经过实践,通常认为调查:100个样本的抽样误差为±10%;500个样本的抽样误差为±5%;1200个样本时的
抽样误差为±3%。
第三步:用第一步求出的“样本均值”加、减第二步计算的“抽样误差”,得出置信区间的两个端点。
在样本量相同的情况下,置信水平越高,置信区间越宽。
置信区间法

置信区间法一、概述置信区间法(Confidence interval)是统计学中常用的一种方法,用于估计总体参数的范围。
在实际应用中,我们通常无法获得全体数据,只能通过从总体中抽取样本来进行推断。
而置信区间法可以帮助我们利用样本数据来估计总体参数,并给出一个可信的范围。
二、置信水平置信水平(Confidence level)是指在重复抽样的情况下,置信区间包含真实参数值的比例。
通常情况下,我们使用95%或99%作为置信水平。
三、构建置信区间构建置信区间需要以下三个步骤:1. 确定总体分布类型和总体参数;2. 根据样本数据估计总体参数;3. 利用统计方法确定置信区间。
四、正态分布情况下的置信区间当总体分布为正态分布时,可以使用t分布或标准正态分布来构建置信区间。
1. 样本量大于30且已知总体标准差时,使用标准正态分布构建置信区间;2. 样本量小于30或未知总体标准差时,使用t分布构建置信区间。
五、t分布情况下的置信区间当样本量小于30或未知总体标准差时,使用t分布构建置信区间。
1. 确定置信水平和自由度;2. 根据样本数据计算样本均值和样本标准差;3. 计算t值;4. 根据t分布表查找临界值;5. 构建置信区间。
六、实例假设我们想要估计一批产品的平均重量。
我们从该批产品中随机抽取了20个样本,得到平均重量为100g,标准差为10g。
现在我们希望以95%的置信水平来估计总体平均重量的范围。
1. 确定总体分布类型和总体参数:假设总体分布为正态分布,未知总体参数;2. 根据样本数据估计总体参数:样本均值为100g,样本标准差为10g;3. 利用统计方法确定置信区间:(1)因为样本量大于30且已知总体标准差,所以使用标准正态分布构建置信区间;(2)查找标准正态分布表可得到95%置信水平下的临界值为1.96;(3)根据公式:(x̄-zα/2 * σ/√n, x̄+zα/2 * σ/√n),计算置信区间为(96.08g, 103.92g)。
置信区间(Confidence Interval)

置信区间(Confidence Interval)分类:专业学习2010-04-28 13:32阅读(6841)评论(5)一直做着的不确定性分析,很多时候会涉及到置信区间的概念,但一直没能有个清晰的认识,今天终于从网上查资料,具体核实了置信区间的含义。
95%置信区间(Confidence Interval,CI):当给出某个估计值的95%置信区间为【a,b】时,可以理解为我们有95%的信心(Confidence)可以说样本的平均值介于a到b之间,而发生错误的概率为5%。
有时也会说90%,99%的置信区间,具体含义可参考95%置信区间。
置信区间具体计算方式为:(1)知道样本均值(M)和标准差(ST)时:置信区间下限:a=M - n*ST; 置信区间上限:a=M + n*ST;当求取90% 置信区间时n=1.645当求取95% 置信区间时n=1.96当求取99% 置信区间时n=2.576(2)通过利用蒙特卡洛(Monte Carlo)方法获得估计值分布时:先对所有估计值样本进行排序,置信区间下限:a为排序后第lower%百分位值; 置信区间上限:b为排序后第upper%百分位值.当求取90% 置信区间时 lower=5 upper=95;当求取95% 置信区间时lower=2.5 upper=97.5当求取99% 置信区间时lower=0.5 upper=99.5当样本足够大时,(1)和(2)获取的结果基本相等。
参考资料:http://140.116.72.80/~smallko/ns2/confidence_interval.htm附刚准备MATLAB 求取置信区间源码:……………………………………………………………………………………………………………………%%% 置信区间的定义90%,95%,99%clearclcsampledata=randn(10000,1);a=0.01; %0.01 对应99%置信区间,0.05 对应95%置信区间,0.1 对应90%置信区间if a==0.01n=2.576; % 2.576 对应99%置信区间,1.96 对应95%置信区间,1.645 对应90%置信区间elseif a==0.05n=1.96;elseif a==0.1n=1.645;end%计算对应百分位值meana=mean(sampledata);stda=std(sampledata);sorta=sort(sampledata); %对数据从小到大排序leng=size(sampledata,1);CIa(1:2,1)=[sorta(leng*a/2);sorta(leng*(1-a/2))]; %利用公式计算置信区间CIf(1:2,1)=[meana-n*stda;meana+n*stda];。
置信区间的解释及求取

置信区间的解释及求取-学习了解95%置信区间(Confidence Interval,CI):当给出某个估计值的95%置信区间为【a,b】时,可以理解为我们有95%的信心(Confidence)可以说样本的平均值介于a到b之间,而发生错误的概率为5%。
有时也会说90%,99%的置信区间,具体含义可参考95%置信区间。
置信区间具体计算方式为:(1) 知道样本均值(M)和标准差(ST)时:置信区间下限:a=M - n*ST; 置信区间上限:a=M + n*ST;当求取90% 置信区间时n=1.645当求取95% 置信区间时n=1.96当求取99% 置信区间时n=2.576(2) 通过利用蒙特卡洛(Monte Carlo)方法获得估计值分布时:先对所有估计值样本进行排序,置信区间下限:a为排序后第lower%百分位值; 置信区间上限:b为排序后第upper%百分位值.当求取90% 置信区间时 lower=5 upper=95;当求取95% 置信区间时lower=2.5 upper=97.5当求取99% 置信区间时lower=0.5 upper=99.5当样本足够大时,(1)和(2)获取的结果基本相等。
参考资料:http://140.116.72.80/~smallko/ns2/confidence_interval.htmConfidence Limits: The range of confidence interval附MATLAB 求取置信区间源码:%%% 置信区间的定义90%,95%,99%-------Liumin 2010.04.28clearclcsampledata=randn(10000,1);a=0.01; %0.01 对应99%置信区间,0.05 对应95%置信区间,0.1 对应90%置信区间if a==0.01n=2.576; % 2.576 对应99%置信区间,1.96 对应95%置信区间,1.645 对应90%置信区间elseif a==0.05n=1.96;elseif a==0.1n=1.645;end%计算对应百分位值meana=mean(sampledata);stda=std(sampledata);sorta=sort(sampledata); %对数据从小到大排序leng=size(sampledata,1);CIa(1:2,1)=[sorta(leng*a/2);sorta(leng*(1-a/2))];%利用公式计算置信区间CIf(1:2,1)=[meana-n*stda;meana+n*stda]; …………………………………………………………………………………………。
置信区间(详细定义及计算)

18
2.未知σ2时,μ的置信区间
当总体X的方差未知时, 容易想到用样本方差Ѕ 2代替σ2。
已知 T X ~ t(n 1)
S2
n X
则对给定的α, 令
P{ S2
n
t (n 1)} 1
2
查t 分布表, 可得 t (n 1) 的值。
P{X
S n
t
2 (n
2
1)
X
S n
t
2
(n
1)}
1
则μ的置信度为1- α的置信区间为
S
2
的概率分布是难以计算的,
2
而
p
y
2
(n 1)S 2
2
~
2 (n 1)
2
2
对于给定的 (0 1).
P{12 2
(n 1)
(n 1)S 2
2
2
2
(n 1)} 1
2 1
(n
1)
2
(n
1)
2
2
x
24
即 py
2
2
12 (n1) 2
p( y)d
y
0
2
2 1
(n
1)
2
(n
1)
x
2
2
p(y)d y
2
( n 1)
2
P{12 2
(n 1)
(n 1)S 2
2
2
2
(n
1)}
2
1
(n 1)S 2
P{
2
(n
1)
2
(n 1)S
2 1
(n
2
} 1)
1
置信区间(Confidenceinterval)是啥

置信区间(Confidenceinterval)是啥
可信程度那种~
对这个样本的某个总体参数的区间估计。
置信区间展现的是这个参数的真实值有⼀定概率落在测量结果的周围的程度。
置信区间给出的是被测量参数测量值的可信程度范围,即前⾯所要求的“⼀定概率”。
这个概率被称为置信⽔平
如果在⼀次⼤选中某⼈的⽀持率为55%,⽽置信⽔平0.95上的置信区间是(50%,60%),那么他的真实⽀持率有百分之九⼗五的机率落在百分之五⼗和百分之六⼗之间,因此他的真实⽀持率不⾜⼀半的可能性⼩于百分之2.5(假设分布是对称的)。
如例⼦中⼀样,置信⽔平⼀般⽤百分⽐表⽰,因此置信⽔平0.95上的置信区间也可以表达为:95%置信区间。
置信区间的两端被称为置信极限。
对⼀个给定情形的估计来说,置信⽔平越⾼,所对应的置信区间就会越⼤。
置信度置信区间计算方法-置信区间公式表

置信度置信区间计算方法-置信区间公式表置信度置信区间计算方法置信区间公式表在统计学中,置信度和置信区间是非常重要的概念。
它们帮助我们在对总体参数进行估计时,给出一个可能包含真实参数值的范围,以及我们对这个范围的确定程度,也就是置信度。
首先,让我们来理解一下什么是置信度。
置信度通常用百分数表示,比如 95%或 99%。
它反映了我们在多次重复抽样和估计的过程中,得到的置信区间能够包含真实总体参数值的比例。
比如说,95%的置信度意味着如果我们进行 100 次抽样和估计,大约有 95 次得到的置信区间能够包含真实的总体参数值。
而置信区间则是一个可能包含总体参数真实值的范围。
这个范围的宽窄取决于我们所选择的置信度、样本数据的特征以及样本量的大小。
接下来,我们重点介绍几种常见的置信区间计算方法和相应的公式。
对于正态总体均值的置信区间计算,当总体方差已知时,我们使用的公式是:\\bar{X} \pm Z_{\alpha/2} \frac{\sigma}{\sqrt{n}}\其中,\(\bar{X}\)是样本均值,\(Z_{\alpha/2}\)是标准正态分布的双侧分位数(对应于置信度\(1 \alpha\)),\(\sigma\)是总体标准差,\(n\)是样本量。
例如,如果我们有一个样本均值为 50,总体标准差为 10,样本量为 100,并且想要计算 95%置信度下的置信区间,那么首先找到\(Z_{\alpha/2}\),对于 95%的置信度,\(\alpha = 005\),\(\alpha/2 = 0025\),对应的\(Z_{\alpha/2} \approx 196\)。
然后代入公式计算:\50 \pm 196 \times \frac{10}{\sqrt{100}}= 50 \pm 196\得到的置信区间就是 4804, 5196。
当总体方差未知时,我们用样本方差\(s\)来代替总体方差\(\sigma\),此时使用的是\(t\)分布,公式变为:\\bar{X} \pm t_{\alpha/2}(n 1) \frac{s}{\sqrt{n}}\其中,\(t_{\alpha/2}(n 1)\)是自由度为\(n 1\)的\(t\)分布的双侧分位数。
置信区间——精选推荐

置信区间在统计学中,⼀个概率样本的置信区间(Confidence interval)是对这个样本的某个总体参数的区间估计。
置信区间展现的是这个参数的真实值有⼀定概率落在测量结果的周围的程度。
置信空间给出的是被测量参数的测量值的可信程度,即前⾯所要求的“⼀定概率”。
这个概率被称为置信⽔平。
举例来说,如果在⼀次⼤选中某⼈的⽀持率为55%,⽽置信⽔平0.95上的置信区间是(50%,60%),那么他的真实⽀持率有百分之九⼗五的机率落在百分之五⼗和百分之六⼗之间,因此他的真实⽀持率不⾜⼀半的可能性⼩于百分之五。
95%置信区间(Confidence Interval,CI):当给出某个估计值的95%置信区间为【a,b】时,可以理解为我们有95%的信⼼(Confidence)可以说样本的平均值介于a到b之间,⽽发⽣错误的概率为5%。
⼀、置信区间的概念置信区间⼜称估计区间,是⽤来估计参数的取值范围的。
常见的52%-64%,或8-12,就是置信区间(估计区间)。
置信区间是按下列三步计算出来的:第⼀步:求⼀个样本的均值第⼆步:计算出抽样误差。
⼈们经过实践,通常认为调查:100个样本的抽样误差为±10%500个样本的抽样误差为±5%1,200个样本时的抽样误差为±3%第三步:⽤第⼀步求出的“样本均值”加、减第⼆步计算的“抽样误差”,得出置信区间的两个端点。
举例说明:美国Gallup(盖洛普)公司就消费者对美国产品质量的看法,对美国、德国和⽇本三国共计3,500名消费者(每个国家约1,200名)分别进⾏了调查,调查结果:有55%的美国⼈认为美国产品质量好,⽽只有26%的德国⼈和17%的⽇本⼈持同样看法。
抽样误差为±3%,置信⽔平为95%。
则这三个国家消费者的置信区间分别为:国别样本均值抽样误差置信区间美国 55% ±3% 52%-58%德国 26% ±3% 23%-29%⽇本 17% ±3% 14%-20%⼆、关于置信区间的宽窄窄的置信区间⽐宽的置信区间能提供更多的有关总体参数的信息。
置信区间的计算与解释

置信区间的计算与解释在统计学中,置信区间是用来估计总体参数的范围,通常以一定的置信水平表示。
置信区间的计算与解释在实际应用中非常重要,可以帮助我们更好地理解数据和做出正确的决策。
本文将介绍置信区间的计算方法,并解释如何正确理解和解释置信区间的含义。
一、置信区间的计算方法1. 样本均值的置信区间计算当我们想要估计总体均值的置信区间时,可以使用样本均值和标准误差来计算。
一般情况下,我们使用 t 分布来计算置信区间,计算公式如下:置信区间 = 样本均值± t * 标准误差其中,t 是自由度为 n-1 时对应于所选置信水平的 t 分布的临界值,标准误差的计算公式为标准差/ √n。
2. 样本比例的置信区间计算当我们想要估计总体比例的置信区间时,可以使用二项分布来计算。
计算公式如下:置信区间 = 样本比例± z * 标准误差其中,z 是对应于所选置信水平的标准正态分布的临界值,标准误差的计算公式为√(样本比例 * (1-样本比例) / n)。
二、置信区间的解释1. 置信水平的含义置信水平是指在重复抽样的过程中,置信区间包含总体参数的概率。
例如,95% 的置信水平表示在进行多次抽样时,有95% 的置信区间会包含总体参数。
2. 置信区间的解释当我们得到一个置信区间时,我们可以解释为:我们有95%(以95%置信水平为例)的把握认为总体参数落在这个区间内。
换句话说,如果我们进行多次抽样,大约有95% 的样本会包含总体参数。
3. 置信区间的宽度置信区间的宽度取决于样本大小和置信水平。
一般来说,置信水平越高,置信区间就越宽;样本大小越大,置信区间就越窄。
因此,在解释置信区间时,我们需要考虑到置信水平和置信区间的宽度。
4. 置信区间与假设检验的关系置信区间和假设检验是统计推断中常用的两种方法。
置信区间可以帮助我们估计总体参数的范围,而假设检验则用来判断总体参数是否符合我们的假设。
在实际应用中,我们通常会同时使用这两种方法来进行推断。
置信区间的通俗解释,统计学的精髓

置信区间的通俗解释,统计学的精髓“置信区间”的英文是confidence interval,也译为“可信区间”、“信赖区间”或“信心区间”。
“confidence interval”这个术语跟“logit”类似,没有既精确又易懂的译法(translation),我努力提供一个平易的“解释”(interpretation)。
先咬文嚼字。
confidence interval由两个词组成,主词是“interval”(区间);“confidence”(置信)是对“interval”的“界定”,名词扮演形容词。
“置信”这个译法比较“雅”,但把问题复杂化了,因为“置信”的通常联想是“难以置信”,有否定意味,老老实实译为“信心”较好。
我追求简单明白,但也愿意附庸风雅,下文既用“信心区间”,也用“置信区间”。
这样做,不是为了制造混乱,而是提醒各位两个词同义,可以交换使用。
“区间”指的是处在两个端点之间的范围。
例如,课间休息的十分钟就是两节课之间的区间,两个端点分别是上节课结束和下节课开始。
“信心区间”的区间是个由“下限”(lower bound,即较小的数)和“上限”(upper bound,即较大的数)界定的数值区间,其中的每个值都是对于总体参数的一个估计。
做显著度检验时,“信心”指的是我们放弃零假设时的信心度,比如90%,95%,99%。
这个信心度就是100减去p值,p值是犯一类错误的风险。
零假设指的是“总体参数是0”,设立零假设的目的是为了放弃它。
在这个语境下,“信心”的对象是“犯一类错误”,有95%的信心,意思是“犯一类错误的风险是5%”。
“信心区间”的信心,意思比较绕。
在这个语境下,“信心”的对象不是“这个区间”,不是“这个区间中的任何一个数”,也不是“这个区间的中间数”,而是“得到这个区间的程序”,即抽样程序。
说“我们有95%的信心认为眼前这个样本统计值(可以是平均值、回归系数或净回归系数)的置信区间包含总体参数”,意思是:如果我们采用同一个抽样程序,从一个总体中抽到样本量相同的无数个样本,每个样本中得到一个样本统计值,每个样本统计值有一个置信区间,假设这无数个置信区间是百分之百,那么其中95%包括总体参数,我们有95%的信心认为眼前这个置信区间包括总体参数,也就是说,我们有95%的信心认为眼前这个置信区间包括总体参数是那95%中的一个。
置信区间(详细定义及计算)

t
2
(n
1),
X
S n
t
2
(n
1)]
[X
S n
t
2
(n
1)]
19
为了调查某地旅游者的消费额为X, 随机访问了
40名旅游者。得平均消费额为 x 105 元,样本方差
s2 282 设 X ~ N (, 2 )求该地旅游者的平均消费额
μ的置信区间。 0.05 解 本题是在σ2未知的条件下求正态总体参数μ的
(双侧置信区间).
1 为置信度, 为显著水平.
4
置信水平的大小是根据实际需要选定的.
例如,通常可取显著水平 0.025, 0.05, 0.1, 等. 即取置信水平 1 0.975 或 0.95,0.9 等.
根据一个实际样本,由给定的置信水平,我们求出
一个尽可能小的区间 ,使 [1,2 ]
[ X n t 2 (n 1)]
则所求μ的2 置信区间为 [1259 24.58 , 1259 24.58] 21
为了估计一批钢索所能承受的平均张力(单位
kg/cm2), 随机选取了9个样本作试验,由试验所得数据得
x 6720 s2 282 设钢索所能承受的张力X, X ~ N (, 2 ) 分别估计这批钢索所能承受的平均张力
2.306]
即 [6650.9 , 6889.1]
3
则钢索所能承受的平均张力为 6650.9 kg/cm2
22
已知总体 X ~ N (, 2 )
下面我们将根据样本找出σ2 的置信区间,这在研究
生产的稳定性与精度问题是需要的。 我们利用样本方差对σ2进行估计,由于不知道S2与
σ2差多少?容易看出把 S 2 看成随机变量,又能找到
confidence intervals总结置信区间SPSS计算解释 及APA 报告规范-zhaomf

How to Report Confidence Intervals and Read Pictures of Data
Zhao MF 2015/3/11 LAB MEETING Email:576880153@
Bibliography and Tools for this Presentation
Outstanding Issues Complex Experimental Designs
4*2(between) mixed design
References and Tools for this Presentation
• • American Psychological Association (2009). Publication Manual of the American Psychological Association. (6th ed.) American Psychological Association, Washington, DC: Author. Cumming, G., & Finch, S. (2005). Inference by eye: confidence intervals and how to read pictures of data. American Psychologist, 60(2), 170. Thompson, B. (2002). What future quantitative social science research could look like: Confidence intervals for effect sizes. Educational Researcher, 31(3), 25-32. SPSS TOOLS(excel): DANCE WITH p, C(confidence) .au/psy/research/cognitive-anddevelopmental-psychology/esci
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Descriptive statistics (for CIs)
HOW TO REPORT (APA)?
APA, 2009, p117: When reporting confidence intervals, use the format 95% Cl [LL UL]
Displaying results APA, 2009, P130
Inference by Eye
2. For a comparison of two independent means, 1) p < .05 when proportion overlap of the 95% CIs is about .50 or less. (Proportion
overlap is expressed as a proportion of the average margin of error for the two groups.)
1. Identify what the means and error bars represent. Do bars show confidence intervals (CIs) or standard errors (SEs)? What is the experimental design?
Outstanding Issues Complex Experimental Designs
4*2(between) mixed design
References and Tools for this Presentation
• • American Psychological Association (2009). Publication Manual of the American Psychological Association. (6th ed.) American Psychological Association, Washington, DC: Author. Cumming, G., & Finch, S. (2005). Inference by eye: confidence intervals and how to read pictures of data. American Psychologist, 60(2), 170. Thompson, B. (2002). What future quantitative social science research could look like: Confidence intervals for effect sizes. Educational Researcher, 31(3), 25-32. SPSS TOOLS(excel): DANCE WITH p, C(confidence) .au/psy/research/cognitive-anddevelopmental-psychology/esci
Inference by Eye
4. For paired data, interpret the mean of the differences and error bars for this mean. In general, beware of bars on separate means for a repeated-measure independent variable: They are irrelevant for inferences about differences.
Confidence Intervals (CIs)
• • • • • WHAT IS? WHY REPORT/USE? HOW TO CALCULATE? HOW TO REPORT (APA)? HOW TO INFERENCE BY E2)normal distribution
Why Use CIs?
• (a) they give point and interval estimates in measurement units that should be readily comprehensible; • (b) there is a link between CIs and p values • (c) CIs help combine evidence over experiments (meta-analytic thinking) • (d) CIs give information about value of the t statistic
What Is a CI ?
1) × 2)normal distribution
What Is a CI ?
• n=36; M = 62; SD = 30 • a 95% CI, which is an interval estimate that indicates the precision, or likely accuracy, of our point estimate; • W (the margin of error) = SE × ; SE= • e.g., 95%CI [M-W, M+W]
as a proportion of the average SE for the two groups.)
2) p < .01 when the proportion gap is at least about 2 (see Figure 6).
NOTE. SE bars are about half the size of 95% CI bars and give approximately a 68% CI, when n is at least 10.
Cumming & Finch, 2005
HOW TO CALCULATE BY SPSS?
T-test in SPSS
T-test: Interpreting the output
One way ANOVA
One way ANOVA
Paired samples Test
ANOVAs— With-subject variables pairwise comparisons CIs
Displaying results APA, 2009, p143
Inference by Eye Introduce some TAKE HOME Messages
Please refer to : Cumming, G., & Finch, S. (2005). Inference by eye: confidence intervals and how to read pictures of data. American Psychologist, 60(2), 170.
Cumming & Finch, 2005
What Is a CI ?
• For C=95, 5% of cases in the long
run, e.g., will not include
Cumming & Finch, 2005
μ.
Why report CI?
1. Publish our research papers: e.g., motivated by the request of reviewers…. • APA, 2009, p.34 [Results]: “The inclusion of confidence intervals (for estimates of parameters, for functions of parameters such as differences in means, and for effect sizes) can be an extremely effective way of reporting results.” • “plete reporting of all tested hypotheses and estimates of appropriate effect sizes and confidence intervals are the minimum expectations for all APA journals…”
•
• •
THANK YOU!
P138: 5.15 Confidence Intervals in Tables
• When a table includes point estimates, for example, means, correlations, or regression slopes, it should also, where possible, include confidence intervals. You may report confidence intervals in tables either by using brackets, as in text (see section 4.10) and in Table 5.8, or by giving lower and upper limits in separate columns, as in Table 5.9. In every table that includes confidence intervals, state the confidence level, for example, 95%. It is usually best to use the same confidence level throughout a paper.
How to Report Confidence Intervals and Read Pictures of Data
Zhao MF 2015/3/11 LAB MEETING Email:576880153@
