2020年中考数学中考专题训练——存在性问题 (2)

合集下载

苏教版初三数学下册《专题讲座：存在性问题(2)》

特殊四边形的存在性问题一、重点知识和解题策略一般有平行四边形、矩形、菱形或正方形存在性问题。

解题策略首先根据图形的定义或性质来确定动点的位置，明确分类，画出相应的图形，然后利用图形的性质或适当转化，构造方程（组）或直接计算求出满足存在条件的量。

二、热身运动1.已知直线与直线相交于点．（1）求、的值；（2）设交轴于点，交轴于点，若点与点、、能构成平行四边形，请直接写出点坐标．三、例题学习例1、如图．如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B （5，0）两点．（1）求抛物线的解析式；（2）在第二象限内取一点C，作CD垂直x轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m 的值；（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q 为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．例2、如图，抛物线y=﹣x2+2x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求直线AD的解析式；（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH周长的最大值；（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM 所在直线对称，求点T的坐标．四、自我挑战1．如图1，在平面直角坐标系xOy 中，抛物线2:C y ax bx c =++与x 轴相交于,A B 两点，顶点为()0,4D ，42AB =，设点(),0F m 是x 轴的正半轴上一点，将抛物线C 绕点F 旋转180°，得到新的抛物线C '．（1）求抛物线C 的函数表达式；（2）若抛物线C '与抛物线C 在y 轴的右侧有两个不同的公共点，求m 的取值范围；（3）如图2，P 是第一象限内抛物线C 上一点，它到两坐标轴的距离相等，点P 在抛物线C '上的对应点为P '，设M 是C 上的动点，N 是C '上的动点，试探究四边形PMP N '能否成为正方形，若能，求出m 的值；若不能，请说明理由．特殊四边形的存在性问题参考答案二、热身运动1.解：（1）将点代入，，，，解得：，．（2）当时，，∴点；当时，， ∴点．当为对角线时，点，，即；当为对角线时，点，，即；当为对角线时，点，，即．故若点与点、、能构成平行四边形，点坐标为、或．三、自我挑战 1.（1）y =﹣21x 2+4; （2）结论：四边形PMP ′N 能成为正方形．理由：1情形1，如图，作PE ⊥x 轴于E ，MH ⊥x 轴于H ．由题意易知P （2，2），当△PFM 是等腰直角三角形时，四边形PMP ′N 是正方形，∴PF =FM ，∠PFM =90°，易证△PFE ≌△FMH ，可得PE =FH =2，EF =HM =2-m ，∴M （m +2，m -2），∵点M 在y=-21x 2+4上，∴m-2=-21（m+2）2+4，解得m=17-3或-17-3（舍弃）， ∴m=17-3时，四边形PMP′N 是正方形．情形2，如图，四边形PMP′N 是正方形，同法可得M （m-2，2-m ），把M （m-2，2-m ）代入y=-21x 2+4中，2-m=-21（m-2）2+4，解得m=6或0（舍弃），∴m=6时，四边形PMP′N 是正方形．综上，四边形PMP′N 能成为正方形，m=17-3或6．。

2020年中考数学压轴题训练平行四边形的存在性问题

2020年中考数学压轴题训练平⾏四边形的存在性问题2020年中考数学压轴题训练平⾏四边形的存在性问题针对训练1、如图已知抛物线y=-x 2-2x+3与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C 顶点为P .若以A 、C 、P 、M 为顶点的四边形是平⾏四边形，求点M 的坐标2、如图，在平⾯直⾓坐标系xOy 中，已知抛物线y=-x 2+2x+3与x 轴交于A 、B 两点，点M 在这条抛物线上，点P 在y 轴上，如果以点P 、M 、A 、B 为顶点的四边形是平⾏四边形，求点M 的坐标3、将抛物线c1:y=23x 3-+沿x 轴翻折，得到抛物线c2如图所⽰现将抛物线c1向左平移m 个单位长度，平移后得到新抛物线的顶点为M ，与x 轴的交点从左到右依次为A 、B ：将抛物线c2向右也平移m 个单位长度，平移后得到新抛物线的顶点为N ，与x 轴的交点从左到右依次为D E 在平移过程中，是否存在以点A 、N 、F,M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理⽈如图，4、抛物线y=25x bx c 4-++与y 轴交于点A （0,1），过点A 的直线与抛物线交于为⼀点B （3.2），过点B 作BC ⊥x 轴，垂⾜为C（1）求抛物线的表达式；（2）点P是x轴正半轴上的⼀动点，过点P作PN⊥x轴交直线AB于点M，交抛物线于点N设OP的长度为m，连结CM、BN，当m 为何值时，四边形BCMN为平⾏四边形？5、如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C秒1个单位长度的速度运动，动点Q从点C 开始沿边CB向点B以每秒2个单位长度的速度过点P作PD∥BC，交AB于点D，连结PQ点P、Q分别从点A、C同时出发，当其中⼀点到达终点时，另⼀点也随之停⽌运动，设运动的时间为t秒（t≥0）（1）直接⽤含t的代数式分别表⽰：QB= ，PD=（2）是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由，并探究如何改变点Q的速度（匀速运动），使四边形PDBQ在某⼀时刻为菱形，求点Q的速度6、如图，在平⾯直⾓坐标系中，直线AB与x轴、y轴分别交于点A（4,0）、B（0,3），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴正半轴上的⼀动点，且满⾜O=2x，连结DE，以DE、DA为边作平⾏匹边形DEFA（1）如果平⾏四边形DEFA为矩形，求m的值（2）如果平⾏四边形DEFA为菱形，请直接写出m的值真题演练7、（18衢州24）如图，Rt△OAB的直⾓边OA在x轴上，顶点B的坐标为（6,8），直线CD 交AB 于点D （6，3），交x 轴于点C （12,0）（1）求直线CD 的函数表达式；（2）动点P 在x 轴上从点（-10,0）出发，以每秒1个单位的速度向x 轴正⽅向运动，过点P 作直线l 垂直于x 轴，设运动时间为t①点P 在运动过程中，是否存在某个位置，使得∠PDA=∠B ？若存在，请求出点P 的坐标；若不存在，请说明理由②请探索当t 为何值时，在直线l 上存在点M ，在直线CD 上存在点Q ，使得以OB 为⼀边，O 、B 、M 、Q 为顶点的四边形是菱形？并求出此时t 的值8、（19连云港26）如图，在平⾯直⾓坐标系xOy 中，抛物线L1：y=x 2+bx+c 过点C （0，-3），与抛物线L2：y=213222x x --+的⼀个交点为A ，且点A 的横坐标为2，点P 、Q 分别是抛物线L1，L2上的动点（1）求抛物线L1的函数表达式（2）若以A 、C 、P 、Q 为顶点的四边形恰为平⾏四边形，求点P 的坐标；（3）设点R 为抛物线L1上另⼀个动点，且CA 平分∠PCR 若OQ ∥PR ，求点Q 的坐标9、（19南充25）抛物线y=ax 2+bx+c 与x 轴交于点A （-1,0）、点B （-3,0）与y 轴交于点C ，且OB=OC （如图所⽰）（1）求抛物线的解析式；（2）若点P 在抛物线上，且∠POB=∠ACB ，求点P 的坐标；（3）抛物线上有两点M 、N ，点M 的横坐标为m ，点N 的横坐标为m+4.点D 是抛物线上M 、N 之间的动点，过点D 作y 轴的平⾏线交MN 于点①求DE 的最⼤值②点D 关于点E 的对称点为F ，当m 为何值时，四边形MDNF 为矩形？10（17泰安28）如图是将抛物线y=-x2平移后得到的抛物线，其中对称轴为x=1，与x轴的⼀个交点为A（-1,0），另⼀个交点为B，与y轴的交点为C.（1）求抛物线的函数表达式；（2）若点N为抛物线上⼀点，且BC⊥NC，求点N的坐标；（3）点P是抛物线上⼀点，点Q是⼀次函数y=2x+2的图象上⼀点，若四边形OAPQ 为平⾏四边形，这样的点P、Q是否存在？若存在，分别求出点P、Q的坐标；若不存在，请说明理由模拟训练11、（2018年长沙市中考模拟（三）第26题）如图，已知抛物线y=x2-2x+a（a<0）与y轴相交于点A，顶点为M直线y=2x-a分别与x轴、y轴相交于B、C两点，并且与直线M相交于点N.（1）试⽤含a的代数式分别表⽰点M与N的坐标；（2）如图，将△NAC沿y轴翻折，若点N的对应点N恰好落在抛物线上，AN与x 轴交于点D，连结CD，求a的值和四边形ADCN的⾯积；（3）在抛物线y=x2-2x+a上是否存在⼀点P，使得以P、A、C、N为顶点的四边形是平⾏四边形？若存在，求出点P的坐标；若不存在，试说明理由12、（2019年内蒙古准格尔旗中考模拟第24题）如图所⽰，已知抛物线y=-x2+bx+c与⼀直线相交于A（-1,0）、C（2,3）两点，其顶点为D（1）求抛物线及直线AC的函数关系式（2）若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意⼀点，过点E 作EF∥BD交抛物线于点F，以B、D、E、F为顶4O点的四边形能否为平⾏四边形？若能，求点E的坐标；若不能，请说明理由（3）若P是抛物线上位于直线AC上⽅的⼀个动点，直接写出△APC的⾯积的最⼤值及此时点P的坐标专题预测13、如图，在平⾯直⾓坐标系中，矩形1BC的顶点A、C分别在x轴和y轴上，点B的坐标为（3.33）。

2020年九年级数学中考经典几何题讲义系列：动点存在性问题

中考经典几何题系列：动点存在性问题目录一、建立函数解析式二、动态几何型压轴题三、双动点问题四、函数中因动点产生的相似三角形问题五、圆的动点问题六、经典练习题（一）七、经典练习题（二）“动点存在性问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静.数学思想：分类思想函数思想方程思想数形结合思想转化思想函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1（上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意.②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2. 二、应用比例式建立函数解析式例2（山东）如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；2222233621419x x x MH PH MP +=-+=+=HM NGPOAB图1x y(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴ACBD CEAB =,∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立,∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式x y 1=成立.例3（上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长.解:(1)连结OD. 根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54xAD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58.∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.AED CB 图2A 3(2)3(1)∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE, ∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE.∴5-x 58=4,得85=x .可求得2=y ,即AP=2.②若EP 交线段CB 于点F,如图3(2), 则CF=2. 类似①,可得CF=CE.∴5-x 58=2,得815=x .可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6.三、应用求图形面积的方法建立函数关系式例4（上海）如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H. ∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x .∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ).(2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21. AB CO图8HC动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

中考数学专题训练存在性问题及答案

第二节存在性问题【例题经典】条件探索性问题例1 如图，AB ⊥BC 于B ，DC ⊥BC 于C ．（1）当AB=4，DC=1，BC=4时，在线段BC 上是否存在点P ，使AP ⊥PD ．•若存在，•求线段BP 的长；如果不存在，请说明理由．（2）设AB=a ，DC=b ，AD=c ，那么当a ，b ，c 之间满足什么关系时，在直线BC 上存在点P ，使AP ⊥PD ．【分析】（1）假设AP ⊥PD ，有△APB ∽△PDC ，进而求出BP ．（2）方法如（1），•但相比之下，添了分类思想．【点评】本例为条件探索型，此类题的解法类似于分析法，假设结论成立，•逐步探索其成立的条件．存在探索性问题例2 （浙江省）如图，平面直角坐标系中，直线AB 与x 轴，y 轴分别交于A （3，0），B （0，）两点，点C 为线段AB 上的一动点，过点C 作CD ⊥x 轴于点D ．（1）求直线AB 的解析式；（2）若S 梯形OBCD =，求点C 的坐标；（3）在第一象限内是否存在点P ，使得以P ，O ，B 为顶点的三角形与△OBA 相似．若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．【评析】本题是一道存在探索性问题的题型，（1）、（2）两问是常规题，•容易解决．（3）问较难，要分不同情况考虑，首先画出符合题意的图形，•然后结合图形进行计算或推理，若能推导出符合条件的结论或计算出某些未知数的值，则表示存在；•若推出矛盾结论或求不出未知数的值，则所求的点就不存在．3【考点精练】1．如图，在平面直角坐标系中，点A 是动点且纵坐标为4，点B 是线段OA 上的一个动点．过点B 作直线MN 平行于x 轴，设MN 分别交射线OA 与X•轴所形成的两个角的平分线于点E 、F ．（1）求证：EB=BF ；（2）当为何值时，四边形AEOF 是矩形？并证明你的结论；（3）是否存在点A 、B ，使四边形AEOF 为正方形．若存在，求点A 与点B 的坐标；• 若不存在，请说明理由．2．（辽宁省）如图，Rt △OAC 是一张放在平面直角坐标系中的直角三角形纸片，点O 与原点重合，点A 在x 轴上，点C 在y 轴上，CAO=30°，将Rt △OAC•折叠，•使OC 边落在AC 边上，点O 与点D 重合，折痕为CE ．（1）求折痕CE 所在直线的解析式；（2）求点D 的坐标；（3）设点M 为直线CE 上的一点，过点M 作AC 的平行线，交y 轴于点N ，是否存在这样的点M ，使得以M 、N 、D 、C 为顶点的四边形是平行四边形？若存在，请求出符合条件的点M 的坐标；若不存在，请说明理由．OBOA3．如图所示的平面直角坐标系中，有一条抛物线y=ax2+bx+c交x轴于A、B两点，交y 轴于点C，已知抛物线的对称轴为x=1，B（3，0），C（0，-3）．（1）求二次函数y=ax2+bx+c的解析式；（2）在抛物线对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出P点坐标；若不存在，请说明理由．4．如图，AB是⊙O的直径，MN是⊙O的切线，C为切点，AC=6cm，AB=10cm．（1）试猜想∠ACM与∠B的大小有什么关系？并说明理由．（2）在切线MN上是否存在一点D，使得以A、C、D为顶点的三角形与△ABC相似？若存在，请确定点D的位置；若不存在，请说明理由．B5．（龙岩市）如图，抛物线y=ax +bx 过点A （4，0），正方形OABC 的边BC•与抛物线的一个交点为D ，点D 的横坐标为3，点M 在y 轴负半轴上，直线L 过D 、M•两点且与抛物线的对称轴交于点H ，tan ∠OMD=．（1）写出a ，b 的值：a=_____，b=______，并写出点H 的坐标（______，______）．（2）如果点Q 是抛物线对称轴上的一个动点，那么是否存在点Q ，使得以点O ，M ，•Q ，H 为顶点的四边形是平行四边形？若存在，求出点Q 的坐标；若不存在，请说明理由．6．（莆田市）已知：如图，抛物线经过A （-3，0），B （0，4）和C （4，0）三点．（1）求抛物线的解析式；（2）已知AD=AB （D 在线段AC 上），有一动点P 从点A 沿线段AC 以每秒1•个单位长度的速度移动；同时．．另一动点Q 以某一速度从点B 沿线段BC 移动，经过t 秒的移动，线段PQ 被BD 垂直平分，求t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点M ，使MQ+MC 的值最小？•若存在，请求出点M 的坐标；若不存在，请说明理由．（注：抛物线y=ax 2+bx+c 的对称轴为x=-）132ba7．如图，已知抛物线L1：y=x-4的图像与x轴交于A、C两点．（1）若抛物线L1与L2关于x轴对称，求L2的解析式；（2）若点B是抛物线L1上的一个动点（B不与A、C重合），以AC为对角线，A、B、C•三点为顶点的平行四边形的第四个顶点定为D，求证：点D在L2上；（3）探索：当点B分别位于L1在x轴上、下两部分的图像上时，平行四边形ABCD 的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，•并求出它的面积；若不存在，请说明理由．8．（无锡市）如图，在等腰梯形ABCD中，AB∥DC，AB=8cm，CD=2cm，AD=6cm，点P从点A出发，以2cm/s的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD、DA向终点A运动（P、Q两点中，有一个点运动到终点时，所有运动即终止），设P、Q同时出发并运动了t秒．（1）当PQ将梯形ABCD分成两个直角梯形时，求t的值；（2）试问是否存在这样的t，使四边形PBCQ的面积是梯形ABCD面积的一半？若存在，求出这样的t的值，若不存在，请说明理由．答案:例题经典例1．（1）如果存在点P ，使AP ⊥PD ，那么∠APD=90°，∴∠APB+•∠CPD=90°，∵AB ⊥BC ，DC ⊥BC ，∴∠B=∠C=90°，∴∠APB+∠BAP=90°．∴∠BAP=∠CPD ，∴△APB ∽△PDC ，∴．设BP=x ，则PC=4-x ，∴，解得x=2， ∴在线段BC 上存在点P ，使AP•⊥PD ，此时，BP=2．（2）如果在直线BC 上存在点P ，使AP ⊥PD ，那么点P 在以AD 为直径的圆上，且圆的半径为c ，取AD 的中点O ，过点O 作OE ⊥BC ，垂足为E ． ∵∠B=∠OEC=∠C=90°，∴AB ∥OE ∥DC ．∵AO=DO ，∴BE=CE ，∴OE=（AB+DC ）=（a+b ），当OE<c ，即a+b<c 时，以AD•为直径的圆与直线BC 相交，此时，存在⊙O 和直线BC 的交点P 1、P 2，使AP 1⊥P 1D ，AP 2⊥P 2D ， •当OE=c ，即a+b=c 时，以AD 为直径的圆与直线BC 相切．此时，存在切点P ，使AP ⊥PD ． ∴当OE>c 时，即a+b>c 时，以AD 为直径的圆与直线BC 相离．此时，在直线BC 上不存在点P ，•使AP ⊥PD ．综上，当a+b ≤c 时，在直线BC 上存在点P ，使AP ⊥PD ．例2．（1）直线AB 解析式为：（2）设点C 坐标为（x ，，那么OD=x ，∴S 梯形OBCD ==-x 2AB BPPC CD =441xx =-121212121212()2OB CD OD +⨯6由题意：2x1=2，x2=4（舍去），∴（2．（3）当∠OBP=Rt∠时，如图：①若△BOP∽△OBA，则∠BOP=∠OBA=60°，，∴P1（3①③②若△BPO∽△OBA，则∠POB=∠BAO=30°，，∴P2（1．当∠OPB=Rt∠时③过点O作OP⊥BC于点P（如图），此时△PBO∽△OBA，∠BOP=∠BAO=30°，过点P作PM⊥OA于点M．在Rt△PBO中，BP=．∵在Rt△PMO中，∠OPM=30°，∴OM=OP=；，∴P3（）④若△POB∽△OBA（如图），则∠OBP=∠BAO=30°，∠POM=30°，∴P4（（由对称性也可得到点P4的坐标）．当∠OPB=Rt∠时，点P在x轴上，不符合要求，综合得，•符合条件的点有四个，分别是：P1（3，P2（1，P3（，），P4（，）．考点精练1．解：（1）如图①，∵OF是角平分线，∴∠1=∠2，∵MN平行于x轴，∴∠3=∠1，∴∠2=∠3，∴BO=BF．同理可证BO=BE，∴BE=BF．123212343434344344（2）当=时，四边形AEOF 是矩形，∵=， ∴OB=AB ．又∵BE=BF ，∴四边形AEOF 是平行四边形，∵OE 、OF 是角平分线，∴∠EOF=90°，∴四边形AEOF 是矩形．（3）如图②，∵MN 平行于x 轴，∴当A 点在y 轴时，即A 点坐标为（0，4）时，有OA ⊥EF ，• 此时，取OA 的中点，由（2）知四边形AEOF 是矩形， ∴四边形AEOF 是正方形， ∴存在点A （0，4），B （0，2），使四边形AEOF 为正方形． 2．（1）直线CE 的解析式为（2）D （（3）（若此点在第四象限）M 1（，-），（•若此点在第二象限）M 2（-，）3．（1）y=x 2-2x-3（2）在抛物线对称轴上存在一点P ，使点P 到B 、C•两点的距离之差最大．作直线AC 交抛物线对称轴于点P ，连结PB ，∵对称轴x=1是线段AB•的垂直平分线，∴PB=PA ， ∴PB-PC=PA-PC=AC ．（线段AC 为差值最大值），设直线AC 的解析式为y=•kx+b ．把A （-1，0），C （0，-3）代入上式，得，∴k=-3，b=-3，∴直线AC 的解析式为：y=-3x 1-3，•当x=1时，y=-3×1-3=-6， ∴点P 的坐标为（1，-6）．4．（1）∠ACM=∠B ，连结OC ，利用圆的切线性质和等腰三角形的性质可证得结论．OB OA 12OB OA 123232232203k b b -+=⎧⎨=-⎩（2）存在两个点D 1、D 2，使得以A 、C 、D 为顶点的三角形与△ABC 相似．过点A 作AD 1⊥MN 于D 1，过点A 作AD 2⊥AC 交MN 于D 2．由相似三角形对应边成比例可分别求得CD 1和CD 2的长． 5．（1）a=-，b=，H （2，1）（2）答：存在这样的点Q ，使得点O 、M 、Q 、H 为顶点的四边形为平行四边形．由题意可知，△MDC 是直角三角形，CD=3，OC=4，∵tan ∠OMD=， ∴=，•∴CM=9，∴OM=9-4=5． ①要使OMQH 是平行四边形，由题意知OM ∥HQ ，只须OM=OQ ， ∵点H•的坐标是1，∴点Q 1（2，-4）②要使OMHQ 是平行四边形，由题意知OM ∥HQ ，只须OM=HQ ，• ∵点H 的坐标是1，∴点Q 2（2，6）．6．解：设抛物线的解析式为y=ax 2+bx+c （a ≠0），根据题意得：c=4，且，∴所求的抛物线的解析式为y=-x 2+x+4．4316313CD CM 13193403,1644013a a b a b b ⎧=-⎪-+=⎧⎪⎨⎨++=⎩⎪=⎪⎩解得1313（2）连结DQ ．在Rt △AOB 中，，∴AD=AB=•5，•∵AC=AO+CO=3+4=7，∴CD=AC-AD=7-5=2． ∵BD 垂直平分PQ ，∴PD=QD ，PQ ⊥BD ，∴∠PDB=∠QDB ， ∵AD=AB ，∴∠ABD=∠ADB ，∵∠ABD=∠QDB ，∴DQ ∥AB ， ∴∠CQD=∠CBA ，∠CDQ=•∠CAB ，∴△CDQ ∽△CAB ，∴． ∴AP=AD-DP=AD-DQ=5-=，t=÷1=（秒）， ∴t 的值为秒．（3）答：对称轴上存在一点M ，使MQ+MC 的值最小．理由：∵抛物线的对称轴为：x=-=，• ∴A （-3，0），C （4，0）两点关于直线x=对称．连结AQ 交直线x=于点M ，则MQ+MC 的值最小．•过点Q 作QE ⊥x 轴，垂足为E ，∴∠QED=∠BOA=90°， ∵DQ ∥AB ，∴∠BAO=∠QDE ，∴△DQE ∽△ABO ，∴， ∴QE=，DE=，OE=OD+DE=2+=，∴Q （，），设直线AQ 的解析式为y=kx+m （k ≠0），则， 210,577DQ CD DQ DQ AB CA ===即1072572572572572b a 121212107453QE DQ DE QE DE BO AB AO ====即:8767672072078782084177243041k k m k m m ⎧=⎧⎪+=⎪⎪⎨⎨⎪⎪-+==⎩⎪⎩得∴直线AQ 的解析式为y=， ∴M （，），则：在对称轴上存在点M （，），使MQ+MC 值最小． 7．解：设L 2的解析式为y=a （x-h ）2+k ，∵L 1与x 轴的交点A （-2，0），C （2，0），顶点坐标是（0，-4），L 1与L 2关于x 轴对称，∴L 2过A （-2，0），C （2，0），顶点坐标是（0，4）， ∴y=ax 2+4，∴0=4a+a 得a=-1，∴L 2的解析式为y=-x 2+4．（2）设B （x 1，y 1），∵点B 在L 1上，∴B （x 1，x 12-4），∵四边形ABCD 是平行四边形，A 、C 关于0对称，∴B 、D 关于0对称， ∴D （-x 1，-x 12+4），将D （-x 1，-x 12+4）的坐标代入L 2：y=-x 2+4，∴左边=右边， ∴点D 在L 2上．（3）设平行四边形ABCD 的面积为S ，则S=2×S △ABC =AC ×│y 1│=4│y 1│，a ．当点B 在x 轴上方时，y 1>0，∴S=4y 1，•它是关于y 1的正比例函数且S 随y 1的增大而增大，∴S 既无最大值也无最小值．b ．当点B 在x•轴下方时，-4≤y 1<0，∴S=-4y 1，它是关于y 1的正比例函数且S 随y 1的增大而减小，∴当y 1=-4时，•S 有最大值16，但它没有最小值．此时B （0，-4）在y 轴上，它的对称点D 也在y 轴上，∴AC ⊥BD ，∴平行四边形ABCD 是菱形，此时S 最大=16．8．解：（1）过D 作DE ⊥AB 于E ，过C 作CF ⊥AB 于F ，如图1，∵ABCD 是等腰梯形，•∴四边形CDEF 是矩形，∴DE=CD ．又∵AD=BC ，∴Rt △ADE ≌Rt △BCF ，AE=BF ．又CD=2cm ，AB=8cm ，∴EF=CD=cm ，AE=AF=（8-2）=3cm ．若四边形APQD 是直角梯形，则四边形DEPQ 为知形，∵CQ=t ，∴DQ=EP=2-t ，∵AP=AE+EP ，∴2t=3+2-t ，∴t=秒． 1182422,824284141414141x x x y x y ⎧⎧==⎪⎪⎪⎪+⎨⎨⎪⎪=+=⎪⎪⎩⎩联立得1228411228411253（2）在Rt △ADE 中，cm ），S 梯形ABCD=（8+2）×cm 2）．当S 四边形PBCQ=S 梯形ABCD 时，①如图2，若点Q•在CD 上，即0≤t ≤2，则CQ=t ，BP=8-2t ．S 四边形PBCQ =（t+8-2t ）×．解之得t=3（舍去）． ②如图3，若点Q 在AD 上，即2<t ≤4，过点Q 作HG ⊥AB 于G ，交CD 的延长线于H ．由图1知：sin ∠ADE=，∴∠ADE=30°，则∠A=60°．在Rt △ADG 中，AQ=8-t ，QG=AQ ·sin60°=，在Rt△QDH 中，∠QDH=60°，DQ=t-2，QH=DQ·sin60°=．由题意知，S 四边形PBCQ =S △APQ +S △CDQ =×2t ×+×2×，即t 2-9t+17=0，•解之得t 1（不合题意，舍去），t 2．答：存在t=，使四边形PBCQ 的面积是梯形ABCD•面积的一半．12121212AE AD =)2t -121292。

初中存在性问题(二)

存在性问题（二）1.y=ax2+bx+4与x轴的一个交点为A(﹣2,0)，与y轴的交点为C，对称轴是x=3,对称轴与x轴交于点B. （1）求抛物线的函数表达式；（2）经过B，C的直线l平移后与抛物线交于点M，与x轴交于点N，当以B，C，M，N为顶点的四边形是平行四边形时，求出点M的坐标；（3）若点D在x轴上，在抛物线上是否存在点P，使得△PBD≌△PBC？若存在，直接写出点P的坐标；若不存在，请说明理由．2．l：y=ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．（1）y=x2﹣2x﹣3的衍生抛物线的解析式是,衍生直线的解析式是;（2）若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1，求这条抛物线的解析式；（3）设（1）中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x 轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．3．y=ax2+bx+c经过A（3，0）、B（0，3）、C（1，0）三点．（1）求抛物线的解析式；（2）若点D的坐标为(-1,0),在直线AB上有一点P，使△ABO与△ADP相似，求出点P的坐标；（3）在(2)的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．4．如图①,点A坐标为(1,-2),点B坐标为(3,-1),二次函数y=-x2图象为l1．（1）平移抛物线l1，使平移后的抛物线经过点A，但不过点B．①满足此条件函数解析式有个．②写出向下平移且经点A解析式．（2）平移抛物线l1，使平移后的抛物线经过A，B两点，所得的抛物线l2，如图②，求抛物线l2的函数解析式及顶点C的坐标，并求△ABC的面积．（3）在y轴上是否存在点P，使S△ABC=S△ABP？若存在，求出点P的坐标；若不存在，请说明理由．5．对称轴为x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M（0，1），E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点．（1）求此抛物线的解析式；（2）当a=1时,求四边形MEFP面积的最大值，并求此时点P的坐标；（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．6.与x 轴交于A 、D 两点,与y 轴交于点B,四边形OBCD 是矩形,点A 的坐标为（1，0），点B 的坐标为（0，4），已知点E （m ，0）是线段DO 上的动点，过点E 作PE ⊥x 轴交抛物线于点P ，交BC 于点G ，交BD 于点H ．（1）求该抛物线的解析式；（2）当点P 在直线BC 上方时，请用含m 的代数式表示PG 的长度；（3）在（2）的条件下，是否存在这样的点P ，使得以P 、B 、G 为顶点的三角形与△DEH 相似？若存在，求出此时m 的值；若不存在，请说明理由．24y x bx c 3=-++7.直线y =-x +2与x 轴交于点B,与y 轴交于点C.二次函数图象经过点B ，C 和点A （-1，0）．（1）求B ，C 两点坐标；（2）求该二次函数的关系式；（3）若抛物线的对称轴与x 轴的交点为点D ，点E 是线段BC 上的一个动点，过点E 作x 轴的垂线与抛物线相交于点F ，当点E 运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF 的最大面积及此时E 点的坐标；（4）在抛物线的对称轴上是否存在点P ，使△PCD 是等腰三角形？如果存在，直接写出P 点的坐标；如果不存在，请说明问题．8.如图，在平面直角坐标系中，已知点A 的坐标是（4，0），并且OA =OC =4OB ，动点P 在过A ，B ，C 三点的抛物线上．（1）求抛物线的解析式；（2）是否存在点P ，使得△ACP 是以AC 为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由；（3）过动点P 作PE 垂直于y 轴于点E ，交直线AC 于点D ，过点D 作x 轴的垂线．垂足为F ，连接EF ，当线段EF 的长度最短时，求出点P 的坐标．129.对称轴为直线x =−的抛物线经过点A(-6，0）和点B （0，4）．（1）求抛物线的解析式和顶点坐标；（2）设点E （x ，y ）是抛物线上的一个动点，且位于第三象限，四边形OEAF 是以OA 为对角线的平行四边形，求▱OEAF 的面积S 与x 的函数关系式，并写出自变量x 的取值范围；①当▱OEAF 的面积为24时，请判断▱OEAF 是否为菱形？②是否存在点E ，使▱OEAF 为正方形？若存在，求出点E 的坐标；若不存在，请说明理由．72。

两年中考模拟2020年中考数学：存在性问题(学生版)

第七篇专题复习篇专题40存在性问题知识点名师点晴抛物线的存在性等腰、直角三角形掌握等腰三角形与直角三角形的性质,并能求出相关的点的存在性问题平行四边形问题理解并掌握抛物线与特殊的平行四边形的求法相似三角形理解并掌握抛物线与相似三角形问题的解法等腰梯形、直角梯形理解并掌握抛物线与梯形的存在性问题的求法线段最值掌握线段最大值或线段和的最小值的求法面积最值问题解决相关的三角形或四边形的面积最大（小）值问题归纳1：抛物线的存在性问题基础知识归纳：抛物线的存在性问题主要涉及等腰三角形、直角三角形、相似三角形、等腰梯形、直角梯形、线段的最值与面积的最值问题．基本方法归纳：等腰三角形要注意顶点问题的讨论、直角三角形主要讨论斜边、相似三角形的涉及对应边问题、梯形的上底和下底互相平行、平行四边形的对边平行且相等、对角线互相平分、线段的最值注意二次函数配方法的应用和对称问题．注意问题归纳：点的存在性问题中,关键是点的找法,点不要漏找．【例1】（2019内蒙古鄂尔多斯市,第24题,12分）如图,抛物线y=ax2+bx﹣2（a≠0）与x轴交于A（﹣3,0）,B （1,0）两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点．（1）求抛物线的解析式．（2）P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值．（3）以点C为圆心,1为半径作圆,⊙C上是否存在点M,使得△BCM是以CM为直角边的直角三角形？若存在,直接写出M点坐标；若不存在,说明理由．【例2】（2019内蒙古包头市,第26题,12分）如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2（a≠0）与x轴交于A（﹣1,0）,B（3,0）两点,与y轴交于点C,连接BC．（1）求该抛物线的解析式,并写出它的对称轴；（2）点D为抛物线对称轴上一点,连接CD、BD,若∠DCB=∠CBD,求点D的坐标；（3）已知F（1,1）,若E（x,y）是抛物线上一个动点（其中1＜x＜2）,连接CE、CF、EF,求△CEF面积的最大值及此时点E的坐标．（4）若点N为抛物线对称轴上一点,抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形？若存在,请直接写出所有满足条件的点M的坐标；若不存在,请说明理由．【2019年题组】一、选择题二、填空题三、解答题1．（2019内蒙古赤峰市,第25题,14分）如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c 经过点B、C,与x轴另一交点为A,顶点为D．（1）求抛物线的解析式；（2）在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值；（3）在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB？若存在,求出P点坐标；若不存在,请说明理由．2．（2019四川省内江市,第28题,12分）两条抛物线C1：y1=3x2﹣6x﹣1与C2：y2=x2﹣mx+n的顶点相同．（1）求抛物线C2的解析式；（2）点A是抛物线C2在第四象限内图象上的一动点,过点A作AP⊥x轴,P为垂足,求AP+OP的最大值；（3）设抛物线C2的顶点为点C,点B的坐标为（﹣1,﹣4）,问在C2的对称轴上是否存在点Q,使线段QB绕点Q顺时针旋转90°得到线段QB',且点B'恰好落在抛物线C2上？若存在,求出点Q的坐标；若不存在,请说明理由．3．（2019四川省凉山州,第28题,12分）如图,抛物线y=ax2+bx+c的图象过点A（﹣1,0）、B（3,0）、C（0,3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在一点P,使得△P AC的周长最小,若存在,请求出点P的坐标及△P AC的周长；若不存在,请说明理由；（3）在（2）的条件下,在x轴上方的抛物线上是否存在点M（不与C点重合）,使得S△P AM=S△P AC？若存在,请求出点M的坐标；若不存在,请说明理由．4．（2019四川省宜宾市,第24题,12分）如图,在平面直角坐标系xOy中,已知抛物线y=ax2﹣2x+c与直线y=kx+b 都经过A（0,﹣3）、B（3,0）两点,该抛物线的顶点为C．（1）求此抛物线和直线AB的解析式；（2）设直线AB与该抛物线的对称轴交于点E,在射线EB上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点？若存在,求点M的坐标；若不存在,请说明理由；（3）设点P是直线AB下方抛物线上的一动点,当△P AB面积最大时,求点P的坐标,并求△P AB面积的最大值．5．（2019四川省成都市,第27题,10分）如图1．在△ABC中,AB=AC=20,tanB34=,点D为BC边上的动点（点D不与点B,C重合）．以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF．（1）求证：△ABD∽△DCE；（2）当DE∥AB时（如图2）,求AE的长；（3）点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF？若存在,求出此时BD的长；若不存在,请说明理由．6．（2019自贡,第26题,14分）如图,已知直线AB与抛物线C：y=ax2+2x+c相交于点A（﹣1,0）和点B（2,3）两点．（1）求抛物线C函数表达式；（2）若点M是位于直线AB上方抛物线上的一动点,以MA、MB为相邻的两边作平行四边形MANB,当平行四边形MANB的面积最大时,求此时平行四边形MANB的面积S及点M的坐标；（3）在抛物线C的对称轴上是否存在定点F,使抛物线C上任意一点P到点F的距离等于到直线y174=的距离？若存在,求出定点F的坐标；若不存在,请说明理由．7．（2019四川省资阳市,第24题,13分）如图,抛物线y12=-x2+bx+c过点A（3,2）,且与直线y=﹣x72+交于B、C两点,点B的坐标为（4,m）．（1）求抛物线的解析式；（2）点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+P A的最小值；（3）设点M为抛物线的顶点,在y轴上是否存在点Q,使∠AQM=45°？若存在,求点Q的坐标；若不存在,请说明理由．8．（2019山东省泰安市,第24题,13分）若二次函数y=ax2+bx+c的图象与x轴、y轴分别交于点A（3,0）、B （0,﹣2）,且过点C（2,﹣2）．（1）求二次函数表达式；（2）若点P为抛物线上第一象限内的点,且S△PBA=4,求点P的坐标；（3）在抛物线上（AB下方）是否存在点M,使∠ABO=∠ABM？若存在,求出点M到y轴的距离；若不存在,请说明理由．9．（2019山东省济南市,第27题,12分）如图1,抛物线C：y=ax2+bx经过点A（﹣4,0）、B（﹣1,3）两点,G 是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C'．（1）求抛物线C的函数解析式及顶点G的坐标；（2）如图2,直线l：y=kx125经过点A,D是抛物线C上的一点,设D点的横坐标为m（m＜﹣2）,连接DO并延长,交抛物线C'于点E,交直线l于点M,若DE=2EM,求m的值；（3）如图3,在（2）的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB？若存在,求出点P的横坐标；若不存在,请说明理由．10．（2019莱芜区,第24题,12分）如图,抛物线y=ax2+bx+c经过A（﹣3,0）,B（1,0）,C（0,3）三点．（1）求抛物线的函数表达式；（2）如图1,P为抛物线上在第二象限内的一点,若△P AC面积为3,求点P的坐标；（3）如图2,D为抛物线的顶点,在线段AD上是否存在点M,使得以M,A,O为顶点的三角形与△ABC相似？若存在,求点M的坐标；若不存在,请说明理由．11．（2019济宁,第22题,11分）如图1,在矩形ABCD中,AB=8,AD=10,E是CD边上一点,连接AE,将矩形ABCD 沿AE折叠,顶点D恰好落在BC边上点F处,延长AE交BC的延长线于点G．（1）求线段CE的长；（2）如图2,M,N分别是线段AG,DG上的动点（与端点不重合）,且∠DMN=∠DAM,设AM=x,DN=y．①写出y关于x的函数解析式,并求出y的最小值；②是否存在这样的点M,使△DMN是等腰三角形？若存在,请求出x的值；若不存在,请说明理由．12．（2019山东省淄博市,第24题,9分）如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A（3,0）,B（﹣1,0）两点,与y轴交于点C．（1）求这条抛物线对应的函数表达式；（2）问在y轴上是否存在一点P,使得△P AM为直角三角形？若存在,求出点P的坐标；若不存在,说明理由．（3）若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值．13．（2019青岛,第24题,12分）已知：如图,在四边形ABCD中,AB∥CD,∠ACB=90°,AB=10cm,BC=8cm,OD 垂直平分AC．点P从点B出发,沿BA方向匀速运动,速度为1cm/s；同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s；当一个点停止运动,另一个点也停止运动．过点P作PE⊥AB,交BC于点E,过点Q作QF ∥AC,分别交AD,OD于点F,G．连接OP,EG．设运动时间为t（s）（0＜t＜5）,解答下列问题：（1）当t为何值时,点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2）,求S与t的函数关系式；（3）在运动过程中,是否存在某一时刻t,使四边形PEGO的面积最大？若存在,求出t的值；若不存在,请说明理由；（4）连接OE,OQ,在运动过程中,是否存在某一时刻t,使OE⊥OQ？若存在,求出t的值；若不存在,请说明理由．14．（2019山西省,第23题,13分）综合与探究如图,抛物线y=ax2+bx+6经过点A（﹣2,0）,B（4,0）两点,与y轴交于点C,点D是抛物线上一个动点,设点D 的横坐标为m（1＜m＜4）．连接AC,BC,DB,DC．（1）求抛物线的函数表达式；（2）△BCD的面积等于△AOC的面积的34时,求m的值；（3）在（2）的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形？若存在,请直接写出点M的坐标；若不存在,请说明理由．15．（2019广西桂林市,第26题,12分）如图,抛物线y=﹣x2+bx+c与x轴交于点A（﹣2,0）和B（1,0）,与y 轴交于点C．（1）求抛物线的表达式；（2）作射线AC,将射线AC绕点A顺时针旋转90°交抛物线于另一点D,在射线AD上是否存在一点H,使△CHB的周长最小．若存在,求出点H的坐标；若不存在,请说明理由；（3）在（2）的条件下,点Q为抛物线的顶点,点P为射线AD上的一个动点,且点P的横坐标为t,过点P作x 轴的垂线l,垂足为E,点P从点A出发沿AD方向运动,直线l随之运动,当﹣2＜t＜1时,直线l将四边形ABCQ 分割成左右两部分,设在直线l左侧部分的面积为S,求S关于t的函数表达式．16．（2019江苏省常州市,第27题,10分）如图,二次函数y=﹣x2+bx+3的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为（﹣1,0）,点D为OC的中点,点P在抛物线上．（1）b= ；（2）若点P在第一象限,过点P作PH⊥x轴,垂足为H,PH与BC、BD分别交于点M、N．是否存在这样的点P,使得PM=MN=NH？若存在,求出点P的坐标；若不存在,请说明理由；（3）若点P的横坐标小于3,过点P作PQ⊥BD,垂足为Q,直线PQ与x轴交于点R,且S△PQB=2S△QRB,求点P 的坐标．17．（2019江苏省徐州市,第28题,11分）如图,平面直角坐标系中,O为原点,点A、B分别在y轴、x轴的正半轴上．△AOB的两条外角平分线交于点P,P在反比例函数y9x的图象上．P A的延长线交x轴于点C,PB的延长线交y轴于点D,连接CD．（1）求∠P的度数及点P的坐标；（2）求△OCD的面积；（3）△AOB的面积是否存在最大值？若存在,求出最大面积；若不存在,请说明理由．18．（2019江苏省无锡市,第28题,12分）如图1,在矩形ABCD中,BC=3,动点P从B出发,以每秒1个单位的速度,沿射线BC方向移动,作△P AB关于直线P A的对称△P AB',设点P的运动时间为t（s）．（1）若AB=23．①如图2,当点B'落在AC上时,显然△P AB'是直角三角形,求此时t的值；②是否存在异于图2的时刻,使得△PCB'是直角三角形？若存在,请直接写出所有符合题意的t的值？若不存在,请说明理由．（2）当P点不与C点重合时,若直线PB'与直线CD相交于点M,且当t＜3时存在某一时刻有结论∠P AM=45°成立,试探究：对于t＞3的任意时刻,结论“∠P AM=45°”是否总是成立？请说明理由．19．（2019浙江省湖州市,第23题,10分）已知在平面直角坐标系xOy中,直线l1分别交x轴和y轴于点A（﹣3,0）,B（0,3）．（1）如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长；（2）如图2,已知直线l2：y=3x﹣3分别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心2为半径画圆．①当点Q与点C重合时,求证：直线l1与⊙Q相切；②设⊙Q与直线l1相交于M,N两点,连结QM,QN．问：是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标；若不存在,请说明理由．20．（2019金华,第24题,12分）如图,在等腰Rt△ABC中,∠ACB=90°,AB=142,点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90°得到EF．（1）如图1,若AD=BD,点E与点C重合,AF与DC相交于点O．求证：B D=2DO．（2）已知点G为AF的中点．①如图2,若AD=BD,CE=2,求DG的长．②若AD=6BD,是否存在点E,使得△DEG是直角三角形？若存在,求CE的长；若不存在,试说明理由．21．（2019湖北省襄阳市,第25题,13分）如图,在直角坐标系中,直线y12=-x+3与x轴,y轴分别交于点B,点C,对称轴为x=1的抛物线过B,C两点,且交x轴于另一点A,连接AC．（1）直接写出点A,点B,点C的坐标和抛物线的解析式；（2）已知点P为第一象限内抛物线上一点,当点P到直线BC的距离最大时,求点P的坐标；（3）抛物线上是否存在一点Q（点C除外）,使以点Q,A,B为顶点的三角形与△ABC相似？若存在,求出点Q的坐标；若不存在,请说明理由．22．（2019湖南省岳阳市,第24题,10分）如图1,△AOB的三个顶点A、O、B分别落在抛物线F1：y13=x273+x的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2．（点A在点B的左侧）（1）求点A、B的坐标；（2）将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2：y=ax2+bx+4经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积；（3）如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似．若存在,请求出点D的坐标；若不存在,请说明理由．23．（2019湖南省湘西州,第26题,22分）如图,抛物线y=ax2+bx（a＞0）过点E（8,0）,矩形ABCD的边AB 在线段OE上（点A在点B的左侧）,点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA：A D=1：3．（1）求抛物线的解析式；（2）F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值；（3）在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为105？若存在,求出点P的坐标；若不存在,请说明理由；（4）矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离．24．（2019湖南省衡阳市,第26题,12分）如图,在等边△ABC中,AB=6cm,动点P从点A出发以1cm/s的速度沿AB匀速运动．动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动．设运动时间为t（s）．过点P作PE⊥AC于E,连接PQ交AC边于D．以CQ、CE 为边作平行四边形CQFE．（1）当t为何值时,△BPQ为直角三角形；（2）是否存在某一时刻t,使点F在∠ABC的平分线上？若存在,求出t的值,若不存在,请说明理由；（3）求DE的长；（4）取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B'PM,连接AB',当t为何值时,AB'的值最小？并求出最小值．【2018年题组】一、选择题二、填空题三、解答题1．（2018广东,第23题,9分）如图,已知顶点为C（0,﹣3）的抛物线y=ax2+b（a≠0）与x轴交于A,B两点,直线y=x+m过顶点C和点B．（1）求m的值；（2）求函数y=ax2+b（a≠0）的解析式；（3）抛物线上是否存在点M,使得∠MCB=15°？若存在,求出点M的坐标；若不存在,请说明理由．2．（2018内蒙古包头市,第26题,12分）如图,在平面直角坐标系中,已知抛物线y=12x2+32x﹣2与x轴交于A,B两点（点A在点B的左侧）,与y轴交于点C,直线l经过A,C两点,连接BC．（1）求直线l的解析式；（2）若直线x=m（m＜0）与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD．当OD⊥AC时,求线段DE的长；（3）取点G（0,﹣1）,连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG？若存在,求出点P的坐标；若不存在,请说明理由．3．（2018内蒙古呼和浩特市,第20题,8分）如图,已知A（6,0）,B（8,5）,将线段OA平移至CB,点D在x轴正半轴上（不与点A重合）,连接OC,AB,CD,BD．（1）求对角线AC的长；（2）设点D的坐标为（x,0）,△ODC与△ABD的面积分别记为S1,S2．设S=S1﹣S2,写出S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等？如果存在,用坐标形式写出点D的位置；如果不存在,说明理由．4．（2018内蒙古赤峰市,第26题,14分）已知抛物线y=﹣12x2﹣32x的图象如图所示：（1）将该抛物线向上平移2个单位,分别交x轴于A、B两点,交y轴于点C,则平移后的解析式为．（2）判断△ABC的形状,并说明理由．（3）在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形？若存在,求出点P 的坐标；若不存在,说明理由．5．（2018内蒙古通辽市,第26题,12分）如图,抛物线y=ax2+bx﹣5与坐标轴交于A（﹣1,0）,B（5,0）,C（0,﹣5）三点,顶点为D．（1）请直接写出抛物线的解析式及顶点D的坐标；（2）连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点（点P不与B、C两点重合）,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m．①是否存在点P,使四边形PEDF为平行四边形？若存在,求出点P的坐标；若不存在,说明理由．②过点F作FH⊥BC于点H,求△PFH周长的最大值．6．（2018四川省乐山市,第26题,13分）如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C（0,43-）,OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD34=．（1）求抛物线的解析式；（2）动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒．①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值；若不存在,请说明理由．②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大？若存在,求出t的值；若不存在,请说明理由．7．（2018四川省凉山州,第28题,12分）已知直线y=x+3与x轴、y轴分别相交于A、B两点,抛物线y=x2+bx+c 经过A、B两点,点M在线段OA上,从O点出发,向点A以每秒1个单位的速度匀速运动；同时点N在线段AB上,从点A出发,向点B以每秒2个单位的速度匀速运动,连接MN,设运动时间为t秒（1）求抛物线解析式；（2）当t为何值时,△AMN为直角三角形；（3）过N作NH∥y轴交抛物线于H,连接MH,是否存在点H使MH∥AB,若存在,求出点H的坐标,若不存在,请说明理由．8．（2018四川省南充市,第25题,10分）如图,抛物线顶点P（1,4）,与y轴交于点C（0,3）,与x轴交于点A,B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点,△BCQ与△BCP的面积相等,求点Q的坐标．（3）若M,N为抛物线上两个动点,分别过点M,N作直线BC的垂线段,垂足分别为D,E．是否存在点M,N使四边形MNED为正方形？如果存在,求正方形MNED的边长；如果不存在,请说明理由．9．（2018四川省广安市,第26题,10分）如图,已知抛物线y12=x2+bx+c与直线y12=x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A（0,3）,C（﹣3,0）．（1）求此抛物线的解析式；（2）在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值；（3）点P为y轴右侧抛物线上一动点,连接P A,过点P作PQ⊥P A交y轴于点Q,问：是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相似？若存在,请求出所有符合条件的点P的坐标；若不存在,请说明理由．10．（2018四川省德阳市,第24题,14分）如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B在y轴上,点C（3,1）,二次函数y13=x2+bx32-的图象经过点C．（1）求二次函数的解析式,并把解析式化成y=a（x﹣h）2+k的形式；（2）把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积；（3）在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形？如果存在,请求出所有符合条件的点P的坐标；如果不存在,请说明理由．11．（2018四川省成都市,第27题,10分）在Rt △ABC 中,∠ACB =90°,AB7=,AC =2,过点B 作直线m ∥AC ,将△ABC 绕点C 顺时针旋转得到△A 'B 'C （点A ,B 的对应点分别为A ',B '）,射线CA ',CB '分别交直线m 于点P ,Q ．（1）如图1,当P 与A '重合时,求∠ACA '的度数；（2）如图2,设A 'B '与BC 的交点为M ,当M 为A 'B '的中点时,求线段PQ 的长；（3）在旋转过程中,当点P ,Q 分别在CA ',CB '的延长线上时,试探究四边形P A 'B 'Q 的面积是否存在最小值．若存在,求出四边形P A 'B 'Q 的最小面积；若不存在,请说明理由．12．（2018四川省攀枝花市,第24题,12分）如图,对称轴为直线x =1的抛物线y =x 2﹣bx +c 与x 轴交于A （x 1,0）、B （x 2,0）（x 1＜x 2）两点,与y 轴交于C 点,且121123x x +=-．（1）求抛物线的解析式；（2）抛物线顶点为D ,直线BD 交y 轴于E 点；①设点P 为线段BD 上一点（点P 不与B 、D 两点重合）,过点P 作x 轴的垂线与抛物线交于点F ,求△BDF 面积的最大值；②在线段BD 上是否存在点Q ,使得∠BDC =∠QCE ？若存在,求出点Q 的坐标；若不存在,请说明理由．13．（2018四川省眉山市,第26题,11分）如图①,已知抛物线y=ax2+bx+c的图象经过点A（0,3）、B（1,0）,其对称轴为直线l：x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m．（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值；（3）如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在,直接写出所有符合条件的点P的坐标；若不存在,请说明理由．14．（2018四川省绵阳市,第25题,14分）如图,已知抛物线y=ax2+bx（a≠0）过点A3,﹣3）和点B（3,0）．过点A作直线AC∥x轴,交y轴于点C．（1）求抛物线的解析式；（2）在抛物线上取一点P,过点P作直线AC的垂线,垂足为D．连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标；（3）抛物线上是否存在点Q,使得S△AOC13S△AOQ？若存在,求出点Q的坐标；若不存在,请说明理由．15．（2018四川省自贡市,第26题,14分）如图,抛物线y=ax2+bx﹣3过A（1,0）、B（﹣3,0）,直线AD交抛物线于点D,点D的横坐标为﹣2,点P（m,n）是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q．（1）求直线AD及抛物线的解析式；（2）求线段PQ的长度l与m的关系式,m为何值时,PQ最长？（3）在平面内是否存在整点（横、纵坐标都为整数）R,使得P、Q、D、R为顶点的四边形是平行四边形？若存在,直接写出点R的坐标；若不存在,说明理由．16．（2018四川省资阳市,第24题,12分）已知：如图,抛物线y=ax2+bx+c与坐标轴分别交于点A（0,6）,B（6,0）,C （﹣2,0）,点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时,△P AB的面积有最大值？（3）过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形？若存在,求出点P的坐标；若不存在,说明理由．17．（2018四川省达州市,第25题,12分）如图,抛物线经过原点O（0,0）,点A（1,1）,点72B⎛⎫ ⎪⎝⎭，．（1）求抛物线解析式；（2）连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积；（3）点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N．问：是否存在点M,使以点O,M,N为顶点的三角形与（2）中的△AOC相似,若存在,求出点M的坐标；若不存在,说明理由．18．（2018四川省遂宁市,第25题,12分）如图,已知抛物线y=ax232+x+4的对称轴是直线x=3,且与x轴相交于A,B两点（B点在A点右侧）与y轴交于C点．（1）求抛物线的解析式和A、B两点的坐标；（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合）,则是否存在一点P,使△PBC的面积最大．若存在,请求出△PBC的最大面积；若不存在,试说明理由；（3）若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标．19．（2018山东省东营市,第25题,12分）如图,抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式；（3）在（2）的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大？若存在,请求出点P的坐标；若不存在,请说明理由．20．（2018山东省临沂市,第26题,13分）如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B 的坐标为（1,0）．抛物线y=﹣x2+bx+c经过A、B两点．（1）求抛物线的解析式；（2）点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=12 DE．①求点P的坐标；②在直线PD上是否存在点M,使△ABM为直角三角形？若存在,求出符合条件的所有点M的坐标；若不存在,请说明理由．21．（2018山东省威海市,第25题,12分）如图,抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣4,0）,B（2,0）,与y轴交于点C（0,4）,线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x 轴交于点H．（1）求抛物线的函数表达式；（2）求点D的坐标；（3）点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R．求点P的坐标；（4）点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M,N为顶点的四边形是平行四边形？若存在,则直接写出N点坐标；若不存在,请说明理由．22．（2018山东省德州市,第25题,14分）如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A（m,0）、B（4,n）,该抛物线与y轴交于点C,与x轴交于另一点D．（1）求m、n的值及该抛物线的解析式；（2）如图2,若点P为线段AD上的一动点（不与A、D重合）,分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标；（3）如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标；若不存在,请说明理由．23．（2018山东省日照市,第21题,13分）如图,已知点A（﹣1,0）,B（3,0）,C（0,1）在抛物线y=ax2+bx+c 上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P,使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC？若存在,求出Q点坐标；若不存在,说明理由．24．（2018山东省泰安市,第24题,11分）如图,在平面直角坐标系中,二次函数y=ax2+bx+c交x轴于点A（﹣4,0）、B（2,0）,交y轴于点C（0,6）,在y轴上有一点E（0,﹣2）,连接AE．（1）求二次函数的表达式；（2）若点D为抛物线在x轴负半轴上方的一个动点,求△ADE面积的最大值；（3）抛物线对称轴上是否存在点P,使△AEP为等腰三角形？若存在,请直接写出所有P点的坐标,若不存在请说明理由．25．（2018山东省济宁市,第22题,11分）如图,已知抛物线y=ax2+bx+c（a≠0）经过点A（3,0）,B（﹣1,0）,C （0,﹣3）．（1）求该抛物线的解析式；（2）若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标；（3）若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形？若存在,求点P的坐标；若不存在,请说明理由．。

中考数学专题复习——存在性问题

中考数学专题复习——存在性问题一、二次函数中相似三角形的存在性问题1.如图，把抛物线2=向左平移1个单位，再向下平移4个单位，得到抛物线2y x=-+.y x h k()所得抛物线与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D.（1）写出h k、的值；（2）判断△ACD的形状，并说明理由；（3）在线段AC上是否存在点M，使△AOM∽△ABC？若存在，求出点M的坐标；若不存在，说明理由.2.如图，抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．（1）求抛物线的解析式；（2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．二、二次函数中面积的存在性问题3.如图，抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ，B ．已知点B 的坐标为（－2，－2），点A 在第一象限内，且tan ∠AOX ＝4．过点A 作直线AC ∥x 轴，交抛物线于另一点C ．（1）求双曲线和抛物线的解析式；（2）计算△ABC 的面积；（3）在抛物线上是否存在点D ，使△ABD 的面积等于△ABC 的面积．若存在，写出点D 的坐标；若不存在，说明理由．4.如图，抛物线y ＝ax 2＋c （a ＞0）经过梯形ABCD 的四个顶点，梯形的底AD 在x 轴上，A （－2,0），B （－1, －3）．（1）求抛物线的解析式；（3分）（2）点M 为y 轴上任意一点，当点M 到A 、B 两点的距离之和为最小时，求此时点M 的坐标；（2分）（3）在第（2）问的结论下，抛物线上的点P 使S △PAD ＝4S △ABM 成立，求点P 的坐标．（4分）(4)在抛物线的BD 段上是否存在点Q 使三角形BDQ 的面积最大，若有，求出点Q 的坐标，若没有，说明理由。

2020中考数学专题17—存在性问题之特殊三角形

2020中考专题17——存在性问题之特殊三角形姓名____________ . 【方法解读】特殊二和形存化件问题L婪足指寻找符介条件的点使之构成等腰二角形、江用三角形、全第一;角形等特殊二用形.解决此类问题的美犍在于恰当地分类4M避免M籽.【例题分析】例L如图，直线产3x-3交x轴例点A,交y轴J点B,过A, B两点的他物线交x例J另一点C(3, 0).(1)求点A,B的坐标.(2)求旭物线对应的函数表认式.(3)在附物线的对称轴上是否存在点Q,使△ABQ皓笔腰三角形?若存在，求出符合条件的点Q的坐标: 若不存在.请说明毋山.例2.如凰tl知直线.kx 6与抛物线y』x'b乂，c相交十A, 3两点，口点A(l,⑷为抛物段的顶点, 点B 在x轴上.⑴求旭利线对应的函数及辽揖⑵任⑴中：次函数的第.拿限的图象上是否存在•点P,便△FOB与APOC全等?若存在，求出点P 的％标:若不存在,请说明理由.(3)若点Q是y轴上…点,HAABQ为直角三角形,求点Q的坐标.D.【巩固训练】1.（2019•止宾〉已刈抛物纹y = x'-l，j轴文于点A.。

宜纹/=代内为任总实数）出文于S , C两点.则下列结论不正确的是（）A.存在实数使得448C为等腰三角形民存在实数A ,使得&46C的内角中仃两角分别为3伊和60）C.任意实数A,伐得部为血角三角形D.存在实数4,使得M8c为等边三处形2. M图.在平行四边形ABCD中,AB 7 cm, BC 4 c0 NA-30' .点P从点A出发沿着AB边向燃B运劭, 速度为I cm/.连结印，若以运动时间为则当〔二 w时,AADP为等小」角形.3.（2019 •泰安）已知次函数】七公十）的图象。

反比例函数y =巴的图象大丁点T,与x他交丁x 点用 5.U）.若 08 二4 8, H.S^=y .（1）求反比例函数与一次函数的表达式，<2）苦点P为x粕上一点,是等股三角形.求点「的坐乐.1. （2D18・ F州）如图，池物线y = a/+bx-4经过,4（-3.0）.£（5.-4）两点, I j•地文于点C ,性接力&•4C. RC.（1）求抛物线的表达式，（2）求证，.48平分NO6（3）抛物线的对称轴卜.是否存在点M,使得M8W是以48为宜用边的汽角H角形，若存在，求山点M的坐标：苍不存在，请说刚理由.5.(2019•的卅)如图I.在平面直用坐标系中•点。

数学：存在性问题专项训练(二九年级训练考试卷)

学生做题前请先回答以下问题问题1：菱形存在性问题通常转化成什么问题来处理？利用的是菱形的哪个判定？问题2：正方形的存在性问题通常转化为什么问题来处理？利用的是正方形的哪个判定？问题3：对比平行四边形存在性，菱形的存在性以及正方形的存在性问题处理思路，总结处理存在性问题的一般方法．存在性问题专项训练（二）一、单选题(共6道，每道16分)1.如图，已知抛物线经过点A（-2，0）及原点O，点B在抛物线上，点C在抛物线的对称轴上，若以点A，O，B，C为顶点的四边形是平行四边形，则点B的坐标为( )A. B.C. D.2.如图，抛物线与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴为直线．点P从点C出发沿y轴负方向运动，点Q从点B出发沿x轴正方向运动，P，Q两点同时出发，速度均为每秒1个单位长度，过点P作x轴的平行线交抛物线于点E．设运动的时间为t（秒），若以P，A，Q，E为顶点的四边形是平行四边形，则t的值为( )A. B.C. D.3.如图，已知抛物线经过原点O和x轴上的一点A，抛物线的顶点为E，对称轴与x轴交于点D．N是坐标平面内任一点，M是对称轴上的一点，使得以N，A，E，M为顶点的四边形是菱形，则点N的坐标为( )A.B.C.D.4.如图，直线与x轴交于点A，与y轴交于点P．M为线段OA上一动点，过点M作MN⊥PM，交AP于点N．Q为坐标平面内一点，若以A，M，N，Q为顶点的四边形为菱形，则点M的横坐标为( )A.8B.C.6D.5.如图，抛物线交x轴于A，C两点（点A在点C的右侧），交y轴于点B．点D的坐标为（-1，0），若点P是直线AB上的动点，点Q是坐标平面内一点，则当以A，D，P，Q为顶点的四边形是正方形时，点Q的坐标为( )A.（-1，4）或（1，2）B.（-1，4），（1，2）或（5，-2）C.（3，4）或（1，-2）D.（2，2）或（-1，-2）6.如图，在平面直角坐标系中，抛物线与x轴交于点A(-1，0)，B(4，0)．点M，N在x轴上，且点N在点M右侧，MN=2．以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°．设点M的横坐标为m，将线段CN绕点N逆时针旋转90°后，得到对应线段DN．E是抛物线对称轴上一点，F是坐标平面内一点，若以D，N，E，F为顶点的四边形是以DN为边的正方形，则m的值为( )A. B.C. D.。

二次函数-存在性问题-备战2023年中考数学考点微专题

考向3.9 二次函数-存在性问题例1、（2021·湖南湘潭·中考真题）如图，一次函数333y x =-图象与坐标轴交于点A 、B ，二次函数233y x bx c =++图象过A 、B 两点．（1）求二次函数解析式；（2）点B 关于抛物线对称轴的对称点为点C ，点P 是对称轴上一动点，在抛物线上是否存在点Q ，使得以B 、C 、P 、Q 为顶点的四边形是菱形？若存在，求出Q 点坐标；若不存在，请说明理由．解：（1）对于33y x =：当x =0时，3y = 当y =0时，3303x -=，妥得，x =3 ∴A （3，0），B （0，3- 把A （3，0），B （0，3-23y bx c ++得： 33+3+=03b c c ⎧⎪⎨=-⎪⎩解得，233b c ⎧=⎪⎨⎪=⎩∴抛物线的解析式为：23233y =-（2）抛物线的对称轴为直线23312323b x a -=-=-=⨯故设P （1，p ），Q （m ，n ） ①当BC 为菱形对角线时，如图，∵B ，C 关于对称没对称，且对称轴与x 轴垂直， ∴∴BC 与对称轴垂直，且BC //x 轴 ∵在菱形BQCP 中，BC ⊥PQ ∴PQ ⊥x 轴 ∵点P 在x =1上， ∴点Q 也在x =1上，当x =1时，232343113=333y =⨯-⨯--∴Q （1，433-）； ②当BC 为菱形一边时，若点Q 在点P 右侧时，如图，∴BC //PQ ，且BC =PQ ∵BC //x 轴，∴令3y =23233=3y解得，120,2x x == ∴(2,3)C - ∴PQ =BC =2 ∵22(3)12+= ∴PB =BC =2 ∴迠P 在x 轴上， ∴P (1,0) ∴Q (3，0)；若点Q 在点P 的左侧，如图，同理可得，Q （-1，0）综上所述，Q 点坐标为（1，433-）或(3，0)或（-1，0）1、存在性问题的解题思路:假设存在,推理论证,得出结论；2、解決线段存在性问题的方法:将军饮马问题、垂线段问题、三角形三边关系、函数最值等；3、本题考查的知识点有用待定系数法求出二次函数的解析式，菱形的性质和判定，解一元二次方程，主要考查学生综合运用这些性质进行计算和推理的能力．同时注意用分类讨论思想解决问题。

中考数学专题复习教案-专题四存在性问题(2)

1专题四存在性问题(2)教学目标：通过复习,查缺补漏,发展学生直观想象、逻辑推理能力,提高综合应试水平. 复习重点：四边形的存在性复习策略：以题带知识点,基础过关,变式提升,分层要求,配套课件教学过程：例1.在平面直角坐标系中,以A (,0),B (2,0),C (0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( D ) A.(3,1)B.(4-,1)C.(1,1-)D.(3-,1)变式1.已知A ,B ,C 三点不在同一条直线上,则以这三点为顶点的平行四边形共有 3个. 2.如图,在平面直角坐标系中,二次函数2(0)y ax bx c a =++≠的图象经过点A (1-,0),B (3,0),C (0,3). (1)求二次函数的解析式；(2)若在x 轴上有一动点M ,在二次函数2y ax bx c =++的图象上有一动点N ,则M 、N 、B 、C 四点是否能构成平行四边形?若存在,请求出所有适合的点M 的坐标；若不存在,请说明理由. 解:(1)223y x x =-++；(2)设M (t ,0),根据题意,得能构成平行四边形时点N 的坐标有三种可能:分别是(3t -,3),(3t -,3),(3t +,3-) ∵点N 在抛物线223y x x =-++上∴把(3t -,3)代入得,2(3)2(3)33t t --+-+= 解得1t =或3t =(点M 与点B 重合,舍去) ∴M (1,0)同理得M (5,0),M (27-+,0)或M (27--,0)∴所求点M 的坐标为(1,0),(5,0),(27-+,0),(27--,0).例2.如图,在平面直角坐标系xOy 中,A ,B ,C 分别为坐标轴上的三个点,且1OA =,3OB =,4OC =.(1)求经过A ,B ,C 三点的抛物线的解析式；(2)是否存在一点P ,使得以A 、B 、C 、P 为顶点的四边形为菱形?若存在,请求出点P 的坐标；若不存在,请说明理由；解:(1)239344y x x =--+；(2)(5,3).A BCxy xyA BCO2变式1.如图,抛物线2y ax bx c =++经过△ABC 的三个顶点,与y 轴相交于(0,94),点A 坐标为(1-,2),点B是点A 关于y 轴的对称点,点C 在x 轴的正半轴上. (1)求抛物线的函数解析式；(2)点F 为线段AC 上一动点,过F 作FE ⊥x 轴,FG ⊥y 轴,垂足分别为E 、G ,当四边形OEFG 为正方形时,求出F 点的坐标. 解:(1)29144y x =-+；(2)①当点F 在第一象限时,F (1,1)；②当点F 在第二象限时,同理可得F (3-,3) 此时点F 不在线段AC 上,故舍去综上所述,所求点F 的坐标为(1,1).变式2.如图,在Rt △ABC 中,90C ∠=,6AC =,8BC =,动点P 从点A 开始沿边AC 向点C 以1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD ∥BC ,交AB 于点D ,连接PQ 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(0t ≥).(1)直接用含t 的代数式分别表示:QB =82t -,PD =43t ；(2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值；若不存在,说明理由.并探究如何改变Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度. 解：不存在理由:平行四边形PDBQ 不能为菱形设点Q 的速度为每秒m 个单位长度则8BQ mt =-,43PD t =,5103BD t =-要使四边形PDBQ 为菱形,则PD BD BQ == 当PD BD =时,541033t t =-,解得103t = 当PD BQ =时,101048333m ⨯=-,解得1615m = ∴当点Q 的速度为每秒1615个单位长度时,经过103秒,四边形PDBQ 为菱形.作业布置：配套练习专题4 选做题：教学反思：CB DQABC xyO。

存在性问题-中考数学综合专题训练试题

优秀教案欢迎下载第四节存在性问题这类问题是近几年来各地中考的“热点”．解决存在性问题就是：假设存在→推理论证→得出结论．若能导出合理的结果，就作出“存在”的判断，导出矛盾，就作出不存在的判断．尤其以二次函数中的是否存在相似三角形、三角形的面积相等、等腰( 直角) 三角形、平行四边形作为考查对象是中考命题热点．这类题型对基础知识，基本技能提出了较高要求，并具备较强的探索性，正确、完整地解答这类问题，是对知识、能力的一次全面的考查．, 中考重难点突破)1 23【例 1】 ( 汇川中考模拟 ) 抛物线 y＝4x －2x＋ 2 与 x 轴交于 A， B 两点 (OA<OB)，与 y 轴交于点 C.(1)求点 A， B，C 的坐标；(2) 点 P 从点 O出发，以每秒 2 个单位长度的速度向点 B 运动，同时点 E 也从点 O出发，以每秒 1 个单位长度的速度向点 C 运动，设点 P 的运动时间为 t s(0<t<2)．①过点 E 作 x 轴的平行线，与11BC 相交于点 D(如图所示 ) ，当 t 为何值时，＋的值最小，求出这个最小值OP ED并写出此时点 E， P 的坐标；②在满足①的条件下，抛物线的对称轴上是否存在点F，使△ EFP 为直角三角形？若存在，请直接写出点 F 的坐标；若不存在，请说明理由．【解析】 (1) 在抛物线的解析式中，令y＝ 0，令 x＝ 0，解方程即可得到结果；(2) ①由题意得： OP＝ 2t ， OE＝CE ED2－ t＝DE11yt ，通过△ CDE∽△ CBO 得到＝，即，求得＋有最小值 1，即可求得结果；②存在，求得抛物线CO OB24OP ED123＝4x －2x＋ 2 的对称轴为直线 x＝ 3，设 F(3 ，m)，当△ EFP 为直角三角形时，①当∠ EPF＝ 90°时，②当∠ EFP＝90°时，③当∠ PEF＝ 90°时，根据勾股定律列方程即可求得结果．【答案】解： (1) 在抛物线的解析式中，令y＝ 0，23得4x －2x＋ 2＝ 0，解得 x1＝ 2， x2＝ 4.1∵OA<OB，∴ A(2 ，0) ， B(4 ， 0) ，在抛物线的解析式中，令 x＝ 0，得 y＝ 2，∴ C(0 ， 2) ；(2)①由题意，得 OP＝ 2t ， OE＝ t.∵DE∥OB，∴△ CDE∽△ CBO，CE ED2－t＝DE∴ ＝，即24，CO OB∴DE＝4－ 2t ，1111＝112，∴ ＋＝2t ＋2＝1－（ t － 1）OP ED4－2t－ t ＋2t∵0 <t<2 ， 1－ (t －1) 2始终为正数，且t ＝1 时， 1－(t － 1) 2有最大值 1，1∴ t ＝ 1 时，1－（t－1）2有最小值1，1 1即 t ＝1 时，＋有最小值 1，OP ED此时 OP＝ 2， OE＝ 1，∴E(0，1) ，P(2，0) ；②存在． F 的坐标为 (3 ，2) 或 (3 ， 7) ．【规律总结】这类问题一般是对结论作出肯定的假设，然后由肯定的假设出发，结合已知条件建立方程，解出方程的解的情况和结合题目的已知条件确定“存在与否”．解题的方法主要是建立方程模型，由方程有无符合条件的解来肯定“存在与否”的问题．◆模拟题区1． ( 汇川升学二模 ) 在平面直角坐标系中，抛物线 y＝ x2＋ (k －1)x － k 与直线 y＝ kx＋ 1 交于 A， B 两点，点 A 在点B 的左侧．(1)如图①，当 k＝ 1 时，写出 A， B两点的坐标；(2) 在 (1) 的条件下，点P 为抛物线上的一个动点，且在直线AB 下方，试求出△ ABP 面积的最大值及此时点P 的坐标；(3)如图②，抛物线 y＝ x2＋ (k －1)x － k(k>0) 与 x 轴交于点上是否存在唯一一点 Q，使得∠ OQC＝ 90°？若存在，请求出此时C， D 两点 ( 点 C 在点 D 的左侧 ) ，在直线y＝ kx ＋ 1 k的值；若不存在，请说明理由．解： (1) 当 k＝ 1 时，抛物线的解析式为y＝ x2－1，直线的解析式为y＝ x＋ 1. 联立两个解析式，得 x2－ 1＝ x＋ 1，解得 x＝－ 1 或 x＝2，当 x＝－ 1 时， y＝ x＋ 1＝0；当 x＝2 时， y＝x＋ 1＝ 3，∴A(－1，0) ，B(2，3) ；(2)设 P(x ， x2－ 1) ．如图①所示，过点 P 作 PF∥y轴，交直线AB 于点 F，则 F(x ， x＋1) ．∴PF＝(x ＋ 1) －(x 2－ 1) ＝－ x2＋ x＋ 2.S＝S＋S＝1－ x ) ＋1132PF(x2PF(x － x ) ＝2PF(x － x ) ＝2PF，△ ABP△ PFA△PFB F A BF BA∴S△ABP＝3( － x2＋ x＋ 2) ＝－3x－1 2＋27，282223当 x＝2时， y P＝ x －1＝－4.127∴△ ABP面积最大值为8 ，1 3此时点 P 坐标为2，－4；(3)存在，理由如下：设直线 AB： y＝ kx ＋ 1 与 x 轴， y 轴分别交于点 E，F ，11则 E －k， 0 ，F(0 ， 1) ，OE＝k，OF＝ 1.在 Rt△EOF中，由勾股定理得：EF＝121＋ k2 k＋ 1＝.k令 y＝x2＋ (k － 1)x － k＝ 0，即 (x ＋ k)(x － 1) ＝0，解得 x＝－ k 或 x＝ 1，∴ C(－k， 0) ， OC＝ k.设以 OC为直径的圆与直线AB 相切于点 Q，根据圆周角定理，此时∠OQC＝90° .设点 N为 OC中点，连接NQ，如图②所示，k则 NQ⊥EF， NQ＝ CN＝ ON＝2，1k∴EN＝ OE－ ON＝k－2.∵∠ NEQ＝∠ FEO，∠ EQN＝∠ EOF＝ 90°，∴△ EQN∽△ EOF，NQ EN∴＝，OF EFk1－ k2 52k 2即＝，∴ k＝±.11＋k25∵k>0，25∴ k＝，525∴当 k＝时，存在唯一一点Q，5使得∠ OQC＝ 90° .◆中考真题区优秀教案欢迎下载1 22． ( 黔东南中考 ) 如图，在平面直角坐标系xOy 中，抛物线 y＝－6x＋bx＋ c 过点 A(0， 4) 和 C(8 ， 0) ， P(t ，0) 是 x 轴正半轴上的一个动点， M是线段 AP 的中点，将线段 MP绕点 P 顺时针旋转90°得线段 PB. 过点 B 作 x 轴的垂线，过点 A 作 y 轴的垂线，两直线相交于点 D.(1)求 b， c 的值；(2)当 t 为何值时，点D落在抛物线上；(3)是否存在 t ，使得以 A， B， D 为顶点的三角形与△ AOP 相似？若存在，求此时t 的值；若不存在，请说明理由．解： (1) ∵A(0， 4) ， C(8， 0) 在抛物线上，c＝4，5∴1b＝6，2解得0＝－6×8＋ 8b＋ c，c＝ 4；(2)∵∠ AOP＝∠ PEB＝ 90°，∠OAP＝ 90°－∠ APO＝∠ EPB，AO AP∴△ AOP∽△ PEB，∴＝，PE PB∵AO＝4， AP＝ 2MP＝ 2PB，∴PE＝2， OE＝ OP＋ PE＝ t ＋ 2，又∵ DE＝ OA＝ 4，∴点 D的坐标为 (t ＋ 2， 4) ，当点 D落在抛物线上时，1有－ 6(t5＋ 2) 2＋ 6(t＋2) ＋ 4＝4，解得 t ＝ 3 或 t ＝－ 2，∵t ＞ 0，∴ t ＝ 3，故当 t 为 3 时，点 D 落在抛物线上；(3)存在 t ，能够使得以 A， B， D 为顶点的三角形与△ AOP相似．理由如下：①当 0＜ t ＜ 8 时，若△ POA∽△ ADB，PO AO t＝42＋16＝ 0，则＝，即整理，得 t AD BD t ＋214－2t∴ t 无解；若△ POA∽△ BDA，同理，解得 t ＝－ 2±2 5( 负值舍去 ) ；②当 t ＞ 8 时，若△ POA∽△ ADB，则PO AO＝，AD BDt4，即＝t ＋ 214－2t解得 t ＝8±4 5( 负值舍去 ) ；若△ POA∽△ BDA，同理，解得t 无解．综上所述，当t ＝－ 2＋ 2 5或 8＋4 5时，优秀教案欢迎下载以 A，B， D 为顶点的三角形与△ AOP 相似 .。

2020年中考数学压轴解答题02 因动点产生的直角三角形问题(学生版)

备战2020中考数学之解密压轴解答题命题规律专题02 因动点产生的直角三角形问题【类型综述】解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根．一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便．【方法揭秘】我们先看三个问题：1．已知线段AB,以线段AB为直角边的直角三角形ABC有多少个？顶点C的轨迹是什么？2．已知线段AB,以线段AB为斜边的直角三角形ABC有多少个？顶点C的轨迹是什么？3．已知点A(4,0),如果△OAB是等腰直角三角形,求符合条件的点B的坐标．图1 图2 图3如图1,点C在垂线上,垂足除外．如图2,点C在以AB为直径的圆上,A、B两点除外．如图3,以OA为边画两个正方形,除了O、A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个．如图4,已知A(3, 0),B(1,－4),如果直角三角形ABC的顶点C在y轴上,求点C的坐标．我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C．如果作BD⊥y轴于D,那么△AOC∽△CDB．设OC＝m,那么341mm-=．这个方程有两个解,分别对应图中圆与y轴的两个交点．【典例分析】【例1】如图1,已知抛物线E1：y＝x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y轴的对称点分别为点A′、B′．（1）求m的值及抛物线E2所表示的二次函数的表达式；（2）如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形？若存在,求出点Q的坐标；若不存在,请说明理由；（3）如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连结OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比．图1 图2【例2】已知在平面直角坐标系xOy中,直线l别交x轴和y轴于点A（－3,0）,B（0,3）．（1）如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长；（2）如图2,已知直线l2：y＝3x－别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,22为半径画圆．①当点Q与点C重合时,求证：直线l1与⊙Q相切；②设⊙Q与直线l1相交于M,N两点,连结QM,QN．问：是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标；若不存在,请说明理由．【例3】如图1,在Rt△ABC中,∠ACB＝90°,AB＝13,CD//AB,点E为射线CD上一动点（不与点C重合）,联结AE交边BC于F,∠BAE的平分线交BC于点G．（1）当CE＝3时,求S△CEF∶S△CAF的值；（2）设CE＝x,AE＝y,当CG＝2GB时,求y与x之间的函数关系式；（3）当AC＝5时,联结EG,若△AEG为直角三角形,求BG的长．图1【例4】综合与实践折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船等,折纸活动也伴随着我们初中数学的学习．在折纸过程中,我们可以通过研究图形的性质和运动、确定图形位置等,进一步发展空间观念,在经历借助图形思考问题的过程中,我们会初步建立几何直观,折纸往往从矩形纸片开始,今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论．实践操作如图1,将矩形纸片ABCD沿对角线AC翻折,使点B′落在矩形ABCD所在平面内,B′C和AD相交于点E,连接B′D．解决问题(1)在图1中,①B′D和AC的位置关系为；②将△AEC剪下后展开,得到的图形是；(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中的一个结论加以证明,若不成立,请说明理由；(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为；拓展应用(4)在图2中,若∠B=30°,AB=43,当△AB′D恰好为直角三角形时,BC的长度为．【例5】如图,已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0),B(3,0)两点,与y轴交于点C（1）求此二次函数解析式；（2）点D为抛物线的顶点,试判断△BCD的形状,并说明理由；（3）将直线BC向上平移t(t>0)个单位,平移后的直线与抛物线交于M,N两点（点M在y轴的右侧）,当△AMN为直角三角形时,求t的值．【例6】如图,抛物线y＝mx2+nx﹣3（m≠0）与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y＝﹣x 与该抛物线交于E,F两点．（1）求点C坐标及抛物线的解析式．（2）P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值．（3）以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形？若存在,直接写出D点坐标；若不存在,请说明理由．【变式训练】1．如图,点M是直线y=2x+3上的动点,过点M作MN垂直于x轴于点N,y轴上是否存在点P,使得△MNP为等腰直角三角形,则符合条件的点P有（提示：直角三角形斜边上的中线等于斜边的一半）（）A．2个B．3个C．4个D．5个2．如图,已知A、B两点的坐标分别为（8,0）、（0,8）,点C、F分别是直线x＝﹣5和x轴上的动点,CF＝10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是（）A．817B．717C．49D．593．如图,在△ABC中,AB=2,AO=BO,P是直线CO上的一个动点,∠AOC=60°,当△PAB是以BP为直角边的直角三角形时,AP的长为（）A．,1,2 B．,,2 C．,,1 D．,24．如图,是的直径,弦,是弦的中点,．若动点以的速度从点出发沿着方向运动,设运动时间为,连结,当是直角三角形时,（s）的值为A．B．1 C．或1 D．或1 或5．若D点坐标(4,3),点P是x轴正半轴上的动点,点Q是反比例函数12(0)y xx=>图象上的动点,若△PDQ为等腰直角三角形,则点P的坐标是________．6．如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=6,AD=BC=10,点E为射线AD上的一个动点,若△ABE与△A′BE关于直线BE对称,当△A′BC为直角三角形时,AE的长为______．7．如图,AB 为O e 的直径,C 为O e 上一点,过B 点的切线交AC 的延长线于点D ,E 为弦AC 的中点,10AD =,6BD =,若点P 为直径AB 上的一个动点,连接EP ,当AEP ∆是直角三角形时,AP 的长为__________．8．如图,Rt △ABC 中,∠C=90°,AC=2,BC=5,点D 是BC 边上一点且CD=1,点P 是线段DB 上一动点,连接AP,以AP 为斜边在AP 的下方作等腰Rt △AOP ．当P 从点D 出发运动至点B 停止时,点O 的运动路径长为_____．9．如图,AB 是⊙O 的直径,弦BC=6cm ,AC=8cm ．若动点P 以2cm/s 的速度从B 点出发沿着B→A 的方向运动,点Q 以1cm/s 的速度从A 点出发沿着A→C 的方向运动,当点P 到达点A 时,点Q 也随之停止运动．设运动时间为t(s),当△APQ 是直角三角形时,t 的值为___________．10．定义：在平面直角坐标系中,对于任意两点A （a ,b ）,B （c ,d ）,若点T （x ,y ）满足x ＝3+a c ,y ＝3+b d那么称点T 是点A ,B 的融合点．例如：A （﹣1,8）,B （4,﹣2）,当点T （x ,y ）满足x ＝143-+＝1,y ＝8(2)3+-＝2时,则点T （1,2）是点A ,B 的融合点．（1）已知点A （﹣1,5）,B （7,7）,C （2,4）,请说明其中一个点是另外两个点的融合点．（2）如图,点D （3,0）,点E （t ,2t +3）是直线l 上任意一点,点T （x ,y ）是点D ,E 的融合点． ①试确定y 与x 的关系式．②若直线ET 交x 轴于点H ．当△DTH 为直角三角形时,求点E 的坐标．11．如图,在矩形ABCO 中,AO=3,tan ∠ACB=43,以O 为坐标原点,OC 为x 轴,OA 为y 轴建立平面直角坐标系．设D,E 分别是线段AC,OC 上的动点,它们同时出发,点D 以每秒3个单位的速度从点A 向点C 运动,点E 以每秒1个单位的速度从点C 向点O 运动,设运动时间为t 秒．（1）求直线AC 的解析式；（2）用含t 的代数式表示点D 的坐标；（3）当t 为何值时,△ODE 为直角三角形？（4）在什么条件下,以Rt △ODE 的三个顶点能确定一条对称轴平行于y 轴的抛物线？并请选择一种情况,求出所确定抛物线的解析式.12．如图,顶点为M 的抛物线23y ax bx =++与x 轴交于()3,0A ,()1,0B -两点,与y 轴交于点C ．（1）求这条抛物线对应的函数表达式；（2）问在y 轴上是否存在一点P ,使得PAM ∆为直角三角形？若存在,求出点P 的坐标；若不存在,说明理由．（3）若在第一象限的抛物线下方有一动点D ,满足DA OA =,过D 作DG x ⊥轴于点G ,设ADG ∆的内心为I ,试求CI 的最小值．13．如图,在等腰Rt ABC V 中,90,142ACB AB ∠==o ．点D,E 分别在边AB,BC 上,将线段ED 绕点E 按逆时针方向旋转90º得到EF ．（1）如图1,若AD BD =,点E 与点C 重合,AF 与DC 相交于点O ．求证：2BD DO =．（2）已知点G 为AF 的中点．①如图2,若,2AD BD CE ==,求DG 的长．②若6AD BD =,是否存在点E,使得DEG △是直角三角形？若存在,求CE 的长；若不存在,试说明理由． 14．已知在平面直角坐标系xOy 中,直线1l 分别交x 轴和y 轴于点()()3,0,0,3A B -. (1)如图1,已知P e 经过点O ,且与直线1l 相切于点B ,求P e 的直径长；(2)如图2,已知直线2: 33l y x =-分别交x 轴和y 轴于点C 和点D ,点Q 是直线2l 上的一个动点,以Q 为圆心,22为半径画圆.①当点Q 与点C 重合时,求证: 直线1l 与Q e 相切；②设Q e 与直线1l 相交于,M N 两点, 连结,QM QN . 问:是否存在这样的点Q ,使得QMN ∆是等腰直角三角形,若存在,求出点Q 的坐标；若不存在,请说明理由.15．如图1,已知抛物线y ＝﹣23384x +x +3与x 轴交于A 和B 两点,（点A 在点B 的左侧）,与y 轴交于点C ．（1）求出直线BC 的解析式．（2）M 为线段BC 上方抛物线上一动点,过M 作x 轴的垂线交BC 于H ,过M 作MQ ⊥BC 于Q ,求出△MHQ 周长最大值并求出此时M 的坐标；当△MHQ 的周长最大时在对称轴上找一点R ,使|AR ﹣MR |最大,求出此时R 的坐标．（3）T 为线段BC 上一动点,将△OCT 沿边OT 翻折得到△OC ′T ,是否存在点T 使△OC ′T 与△OBC 的重叠部分为直角三角形,若存在请求出BT 的长,若不存在,请说明理由．16．在平面直角坐标系中,抛物线y=x 2+（k ﹣1）x ﹣k 与直线y=kx+1交于A,B 两点,点A 在点B 的左侧．（1）如图1,当k=1时,直接写出A,B 两点的坐标；（2）在（1）的条件下,点P 为抛物线上的一个动点,且在直线AB 下方,试求出△ABP 面积的最大值及此时点P 的坐标；（3）如图2,抛物线y=x 2+（k ﹣1）x ﹣k （k ＞0）与x 轴交于点C 、D 两点（点C 在点D 的左侧）,在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°？若存在,请求出此时k 的值；若不存在,请说明理由． 17．在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A,B 两点（A 在B 的左侧）,与y 轴交于点C,顶点为D ．（1）请直接写出点A,C,D 的坐标；（2）如图（1）,在x 轴上找一点E,使得△CDE 的周长最小,求点E 的坐标；（3）如图（2）,F 为直线AC 上的动点,在抛物线上是否存在点P,使得△AFP 为等腰直角三角形？若存在,求出点P 的坐标,若不存在,请说明理由．18．如图,已知抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =-,且抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(1,0)A ,(0,3)C .（1）若直线y mx n =+经过B 、C 两点,求直线BC 和抛物线的解析式；（2）在抛物线的对称轴1x =-上找一点M ,使点M 到点A 的距离与到点C 的距离之和最小,求出点M 的坐标；（3）设点P 为抛物线的对称轴1x =-上的一个动点,求使BPC ∆为直角三角形的点P 的坐标.19．已知：如图,抛物线y=ax 2+bx+c 与坐标轴分别交于点A （0,6）,B （6,0）,C （﹣2,0）,点P 是线段AB 上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P 运动到什么位置时,△PAB 的面积有最大值？（3）过点P 作x 轴的垂线,交线段AB 于点D,再过点P 做PE ∥x 轴交抛物线于点E,连结DE,请问是否存在点P 使△PDE 为等腰直角三角形？若存在,求出点P 的坐标；若不存在,说明理由．20．如图①,已知抛物线y=ax 2+bx+c 的图像经过点A （0,3)、B （1,0）,其对称轴为直线l ：x=2,过点A 作AC ∥x 轴交抛物线于点C,∠AOB 的平分线交线段AC 于点E,点P 是抛物线上的一个动点,设其横坐标为m.（1）求抛物线的解析式；（2）若动点P 在直线OE 下方的抛物线上,连结PE 、PO,当m 为何值时,四边形AOPE 面积最大,并求出其最大值；（3）如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形？若存在,直接写出所有符合条件的点P 的坐标；若不存在,请说明理由.21．如图,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0,）,点M 是抛物线C 2：2y mx 2mx 3m =--（m ＜0）的顶点．（1）求A 、B 两点的坐标；（2）“蛋线”在第四象限上是否存在一点P,使得△PBC 的面积最大？若存在,求出△PBC 面积的最大值；若不存在,请说明理由；（3）当△BDM 为直角三角形时,求m 的值．22．如图,矩形OABC 中,点O 为原点,点A 的坐标为（0,8）,点C 的坐标为（6,0）．抛物线249y x bx c =-++经过A 、C 两点,与AB 边交于点D ．（1）求抛物线的函数表达式；（2）点P 为线段BC 上一个动点（不与点C 重合）,点Q 为线段AC 上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ 的面积为S ．①求S 关于m 的函数表达式,并求出m 为何值时,S 取得最大值；②当S 最大时,在抛物线249y x bx c =-++的对称轴l 上若存在点F,使△FDQ 为直角三角形,请直接写出所有符合条件的F 的坐标；若不存在,请说明理由．。

2020年中考数学复习专题——平行四边形动点及存在性问题

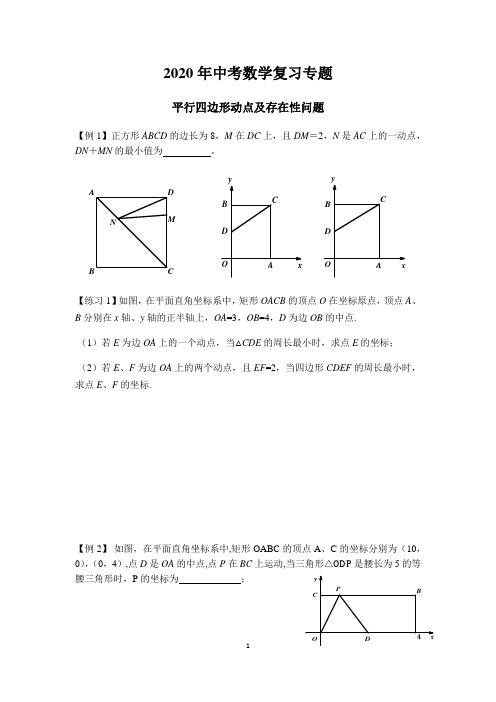
2020年中考数学复习专题平行四边形动点及存在性问题【例1】正方形ABCD 的边长为8，M 在DC 上，且DM ＝2，N 是AC 上的一动点，DN ＋MN 的最小值为。

【练习1】如图，在平面直角坐标系中，矩形OACB 的顶点O 在坐标原点，顶点A 、B 分别在x 轴、y 轴的正半轴上，OA =3，OB =4，D 为边OB 的中点.（1）若E 为边OA 上的一个动点，当△CDE 的周长最小时，求点E 的坐标；（2）若E 、F 为边OA 上的两个动点，且EF =2，当四边形CDEF 的周长最小时，求点E 、F 的坐标.【例2】如图，在平面直角坐标系中,矩形OABC 的顶点A 、C 的坐标分别为（10，0），（0，4）,点D 是OA 的中点,点P 在BC 上运动,当三角形△ODP 是腰长为5的等腰三角形时，P 的坐标为；【练习2】如图，在平面直角坐标系中，AB∥OC，A（0，12），B（a，c），C（b，0），并且a，b满足16b=．一动点P从点A出发，在线段AB上以每秒2个单位长度的速度向点B运动；动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动，点P、Q分别从点A、O同时出发，当点P运动到点B时，点Q随之停止运动．设运动时间为t（秒）（1）求B、C两点的坐标；（2）当t为何值时，四边形PQCB是平行四边形？并求出此时P、Q两点的坐标；（3）当t为何值时，△PQC是以PQ为腰的等腰三角形？并求出P、Q两点的坐标．【例3】（1）如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为；（2）在直角坐标系中，有A（-1，2），B（3，1），C（1，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．【练习3】如图，四边形ABCD 为矩形，C 点在x 轴上，A 点在y 轴上，D 点坐标是（0，0），B 点坐标是（3，4），矩形ABCD 沿直线EF 折叠，点A 落在BC 边上的G 处，E 、F 分别在AD 、AB 上，且F 点的坐标是（2，4）．（1）求G 点坐标；（2）求直线EF 解析式；（3）点N 在x 轴上，直线EF 上是否存在点M ，使以M 、N 、F 、G 为顶点的四边形是平行四边形？若存在，请直接写出M 点的坐标；若不存在，请说明理由．【例4】在Rt △ABC 中，∠B =90°，AC =60cm ，∠A =60°，点D 从点C 出发沿CA 方向以4cm /s 的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以2cm /s 的速度运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D ，E 运动的时间是ts （0<t 15）．过点D 作DF ⊥BC 于点F ，连接DE ，EF ．（1）求证：AE =DF ；（2）四边形AEFD 能够成为菱形吗？如果能，求出相应的t 值；如果不能，请说明理由；（3）当t 为何值时，△DEF 为直角三角形？请说明理由．xE【练习4】如图，等腰三角形OAB的一边OB在x轴的正半轴上，点A的坐标为（6，8），OA=OB，动点P从原点O出发，在线段OB上以每秒2个单位的速度向点B匀速运动，动点Q从原点O出发，沿y轴的正半轴以每秒1个单位的速度向上匀速运动，过点Q作x轴的平行线分别交OA，AB于E，F，设动点P，Q同时出发，当点P到达点B时，点Q也停止运动，他们运动时间为t秒（0t ）（1）点E的坐标为，F的坐标为；（2）当t为何值时，四边形POFE是平行四边形；（3）是否存在某一时刻，使△PEF为直角三角形？若存在，请求出此时t的值；若不存在，请说明理由．【巩固练习】1、菱形ABCD中，AB=2，∠BAD=60°，点E是AB的中点，P一个动点，则PE+PB的最小值为。

2020中考数学压轴题全揭秘精品专题16 二次函数的存在性问题

决胜2020中考数学压轴题全揭秘精品专题16二次函数的存在性问题【典例分析】【考点1】二次函数与相似三角形问题【例1】已知抛物线23y ax bx =++与x 轴分别交于(3,0)A -，(1,0)B 两点，与y 轴交于点C ．（1）求抛物线的表达式及顶点D 的坐标；（2）点F 是线段AD 上一个动点． ①如图1，设AF k AD =，当k 为何值时，2CF AD =1. ②如图2，以A ，F ，O 为顶点的三角形是否与ABC ∆相似？若相似，求出点F 的坐标；若不相似，请说明理由．【答案】（1）223y x x =--+，D 的坐标为(1,4)-；（2）①12k =；②以A ，F ，O 为顶点的三角形与ABC ∆相似，F 点的坐标为618,55⎛⎫- ⎪⎝⎭或(2,2)-．【解析】(1)将A 、B 两点的坐标代入二次函数解析式，用待定系数法即求出抛物线对应的函数表达式，可求得顶点D(1,4)-；(2)①由A 、C 、D 三点的坐标求出AC =DC =，AD =，可得ΔACD 为直角三角形，若1CF AD 2=，则点F 为AD 的中点，可求出k 的值； ②由条件可判断DAC OBC ∠∠=，则OAF ACB ∠∠=，若以A ，F ，O 为顶点的三角形与ΔABC 相似，可分两种情况考虑：当AOF ABC ∠∠=或AOF CAB 45∠∠︒==时，可分别求出点F 的坐标．【详解】(1)抛物线2y ax bx 3=++过点A(3,0)-，B(1,0)，933030a b a b -+=⎧∴⎨++=⎩，解得：12a b =-⎧⎨=-⎩，∴抛物线解析式为2y x 2x 3=--+；()22y x 2x 3x 14=--+=-++， ∴顶点D 的坐标为(1,4)-；(2)①在Rt ΔAOC 中，OA 3=，OC 3=，222AC OA OC 18∴=+=，()D 1,4-，()C 0,3，()A 3,0-，222CD 112∴=+=， 222AD 2420∴=+=，222AC CD AD ∴+=，ΔACD ∴为直角三角形，且ACD 90∠︒=，1CF AD 2=， ∴F 为AD 的中点，AF 1AD 2∴=， 1k 2∴=；②在Rt ΔACD中，DC 1tan ACD AC 3∠===，在Rt ΔOBC 中，OB 1tan OCB OC 3∠==， ACD OCB ∠∠∴=， OA OC =，OAC OCA 45∠∠︒∴==，FAO ACB ∠∠∴=，若以A ，F ，O 为顶点的三角形与ΔABC 相似，则可分两种情况考虑：当AOF ABC ∠∠=时，ΔAOF ΔCBA ∽，OF BC ∴，设直线BC 的解析式为y kx b =+，03k b b +=⎧∴⎨=⎩，解得：33k b =-⎧⎨=⎩，∴直线BC 的解析式为y=3x+3-，∴直线OF 的解析式为y=3x -，设直线AD 的解析式为y=mx+n ，430k b k b -+=⎧∴⎨-+=⎩，解得：26k b =⎧⎨=⎩， ∴直线AD 的解析式为y=2x 6+，263y x y x =+⎧∴⎨=-⎩，解得：65185x y ⎧=-⎪⎪⎨⎪=⎪⎩，618F ,55⎛⎫∴- ⎪⎝⎭．当AOF CAB 45∠∠︒==时，ΔAOF ΔCAB ∽，CAB 45∠︒=， OF AC ∴⊥，∴直线OF 的解析式为y=x -，26y x y x =-⎧∴⎨=+⎩，解得：22x y =-⎧⎨=⎩， ()F 2,2∴-，综合以上可得F 点的坐标为618,55⎛⎫- ⎪⎝⎭或(2,2)-．【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、相似三角形的判定与性质和直角三角形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．【变式1-1】如图，抛物线2y 2ax x c =++经过(1,0)A -，B 两点，且与y 轴交于点(0,3)C ，抛物线与直线1y x =--交于A ，E 两点．（1）求抛物线的解析式；（2）坐标轴上是否存在一点Q ，使得AQE ∆是以AE 为底边的等腰三角形？若存在，请直接写出点Q 的坐标；若不存在，说明理由．（3）P 点在x 轴上且位于点B 的左侧，若以P ，B ，C 为顶点的三角形与ABE ∆相似，求点P 的坐标．【答案】（1）2y x 2x 3=-++；（2）存在，()40Q ，或()04-，，理由见解析；（3）3p 05⎛⎫ ⎪⎝⎭，或9p 02⎛⎫- ⎪⎝⎭，．【解析】（1）将A 、C 的坐标代入2y 2ax x c =++求出a 、c 即可得到解析式；（2）先求出E 点坐标，然后作AE 的垂直平分线，与x 轴交于Q ，与y 轴交于Q'，根据垂直平分线的性质可知Q 、与A 、E ，Q'与A 、E 组成的三角形是以AE 为底边的等腰三角形，设Q 点坐标(0,x)，Q'坐标(0,y)，根据距离公式建立方程求解即可；（3）根据A 、E 坐标，求出AE 长度，然后推出∠BAE=∠ABC=45°，设()p 0m ，，由相似得到PB ABBC AE=或PB AEBC AB=，建立方程求解即可．【详解】（1）将(1,0)A -，(0,3)C 代入2y 2ax x c =++得：203a c c -+=⎧⎨=⎩，解得13a c =-⎧⎨=⎩ ∴抛物线解析式为2y 23=-++x x （2）存在，理由如下：联立y 1x =--和2y x 2x 3=-++，2y 123x y x x =--⎧⎨=-++⎩，解得10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩∴E 点坐标为(4,-5)，如图，作AE 的垂直平分线，与x 轴交于Q ，与y 轴交于Q'，此时Q 点与Q'点的坐标即为所求，设Q 点坐标(0,x)，Q'坐标(0,y)，由QA=QE ，Q'A= Q'E 得：()()()221405--=-++x x ()()()()2222010045++-=-++y y 解得4x =，4y =故Q 点坐标为()40，或()04-，（3）∵(1,0)A -，()45E -，∴()22145=52=--+AE当2230x x -++=时，解得1x =-或3 ∴B 点坐标为(3,0)， ∴3OB OC ==∴45ABC ∠=︒，4AB =，32BC =，由直线1y x =--可得AE 与y 轴的交点为(0,-1)，而A 点坐标为(-1,0) ∴∠BAE=45°设()p 0m ，则3m BP =-， ∵PBC ∆和ABE ∆相似 ∴PB AB BC AE =或PB AE BC AB =，即3252=或52432=解得35m =或92m =-， ∴3p 05⎛⎫ ⎪⎝⎭，或9p 02⎛⎫- ⎪⎝⎭，．【点睛】本题考查二次函数的综合问题，是中考常见的压轴题型，熟练掌握待定系数法求函数解析式，等腰三角形的性质，以及相似三角形的性质是解题的关键．感谢关注公众号“数学一二三”【变式1-2】如图，已知抛物线1(2)()y x x m m=-+-(m ＞0)与x 轴相交于点A ，B ，与y 轴相交于点C ，且点A 在点B 的左侧.（1）若抛物线过点（2，2），求抛物线的解析式；（2）在（1）的条件下，抛物线的对称轴上是否存在一点H ，使AH+CH 的值最小，若存在，求出点H 的坐标；若不存在，请说明理由；（3）在第四象限内，抛物线上是否存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似？若存在，求出m 的值；若不存在，请说明理由.【答案】（1）211242y x x =-++；（2）点H 的坐标为（1，32）；（3）当m=222+时，在第四象限内抛物线上存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似. 【解析】分析：（1）把点（2，2）代入1(2)()?(0)y x x m m m=-+->中，解出m 的值即可得到抛物线的解析式；（2）由（1）中所得解析式求出点A 、B 、C 的坐标，由题意可知，点A 、B 关于抛物线的对称轴对称，这样连接BC 与对称轴的交点即为所求的点H ，根据B 、C 的坐标求出直线BC 的解析式即可求得点H 的坐标；（3）由解析式1(2)()?(0)y x x m m m=-+->可得点A 、B 、C 的坐标分别为（-2，0）、（m ，0）和（0，2），如下图，由图可知∠ACB 和∠ABM 是钝角，因此存在两种可能性：①当△ACB ∽△ABM ，②△ACB ∽△MBA ，分这两种情况结合题中已知条件进行分析解答即可. 详解：（1）把点（2，2）代入抛物线，得2=()()1222m m-+-. 解得m=4.∴抛物线的解析式为()()2111y x 2x 4x x 2442=-+-=-++. （2）令211y x x 2042=-++=，解得12x 2x 4=-=，. 则A （-2，0），B （4，0）.对称轴x=-121124=⎛⎫⨯- ⎪⎝⎭. ∵ 211y x x 242=-++中当x=0时，y=2，∴点C 的坐标为（0，2）.∵点A 和点B 关于抛物线的对称轴对称，∴连接BC 与对称轴的交点即为点H ，此时AH+CH 的值最小，设直线BC 的解析式为y=kx+b ，把B （4，0），C （0，2）代入得：402k b b +=⎧⎨=⎩ ，解得：122k b ⎧=-⎪⎨⎪=⎩ ，∴直线BC 的解析式为y=1x 22-+. ∵当x=1时，y=1122-⨯+=32.∴点H 的坐标为（1，32）.（3）假设存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似. 如下图，连接AC ，BC ，AM ，BM ，过点M 作MN ⊥x 轴于点N ，由图易知，∠ACB 和∠ABM 为钝角， ①当△ACB ∽△ABM 时，有AC AB =ABAM，即2AB AC?AM =. ∵A （-2，0），C （0，2），即OA=OC=2， ∴∠CAB=∠BAM=o 45.∵MN ⊥x 轴，∴∠BAM=∠AMN=45°， ∴AN=MN.∴可设M 的坐标为：（x ，-x-2）（x ＞0），把点M 的坐标代入抛物线的解析式，得：-x-2=()()1x 2x m m-+-. 化简整理得：x=2m ，∴点M 的坐标为：（2m ，-2m-2）. ∴()())222m 22m 222m 1++--=+.∵2AB AC?AM =，AC=22AB=m+2， ∴())2m 22222m 1+=+. 解得：m=222±. ∵m ＞0， ∴m=222+.②当△ACB ∽△MBA 时，有AB MA =CBBA，即2AB CB?MA =. ∵∠CBA=∠BAM ，∠ANM=∠BOC=o 90， ∴△ANM ∽△BOC ，∴MN AN =COBO. ∵BO=m ，设ON=x ， ∴2MN x +=2m ，即MN=2m（x+2）.令M （x ，()2x 2m-+）（x ＞0），把M 点的坐标代入抛物线的解析式，得()2x 2m -+=()()1x 2x m m-+-.解得x=m+2.即M （m+2，()2m 4m-+）.∵2AB CB?MA =，CB=2m 4AN m 4+=+，，MN=()2m 4m+， ∴()()()222224m 4m 2m 4?m 4m ++=+++. 化简整理，得16=0，显然不成立.综上所述，当m=222+时，在第四象限内抛物线上存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似.点睛：本题是一道二次函数和几何图形综合的题目，解题的要点有以下两点：（1）“知道点A 、B 是关于抛物线的对称轴对称的，连接BC 与对称轴的交点即为所求的点H”是解答第2小题的关键；（2）“能根据题意画出符合要求的图形，知道∠ACB 和∠ABM 为钝角，结合题意得到存在：①当△ACB ∽△ABM ，②△ACB ∽△MBA 这两种可能情况”是解答第3小题的关键. 【考点2】二次函数与直角三角形问题【例2】如图，抛物线()20y ax bx c a =++≠的顶点坐标为()2,1-，图象与y 轴交于点()0,3C ，与x 轴交于A 、B 两点．()1求抛物线的解析式；()2设抛物线对称轴与直线BC 交于点D ，连接AC 、AD ，求ACD 的面积；()3点E 为直线BC 上的任意一点，过点E 作x 轴的垂线与抛物线交于点F ，问是否存在点E 使DEF 为直角三角形？若存在，求出点E 坐标，若不存在，请说明理由．【答案】(1)22(2)143y x x x =--=-+ ;(2)2;(3)见解析. 【解析】（1）可设抛物线解析式为顶点式，把C 点坐标代入可求得抛物线解析式；（2）由抛物线解析式可求得A 、B 坐标，利用待定系数法可求得直线BC 解析式，利用对称轴可求得D 点坐标，则可求得AD 2、AC 2和CD 2，利用勾股定理的逆定理可判定△ACD 为直角三角形，则可求得其面积；（3）根据题意可分∠DFE=90°和∠EDF=90°两种情况，当∠DFE=90°时，可知DF ∥x 轴，则可求得E 点纵坐标，代入抛物线解析式可求得E 点坐标；当∠EDF=90°时，可求得直线AD 解析式，联立直线AC 和抛物线解析式可求得点E 的横坐标，代入直线BC 可求得点E 的坐标．【详解】解：()1∵抛物线的顶点坐标为()2,1-， ∴可设抛物线解析式为()2(2)10y a x a =--≠，把()0,3C 代入可得2(02)13a --=，解得1a =，∴抛物线解析式为22(2)143y x x x =--=-+；()2在243y x x =-+中，令0y =可得2430x x -+=，解得1x =或3x =，∴()1,0A ，()3,0B ，设直线BC 解析式为3y kx =+，把()3,0B 代入得：330k +=，解得1k =-， ∴直线BC 解析式为3y x =-+，由()1可知抛物线的对称轴为2x =，此时231y =-+=， ∴()2,1D ，∴22AD =，210AC =，28CD =， ∵222AD CD AC +=，∴ACD 是以AC 为斜边的直角三角形，∴11222ACDSAD CD =⋅==； ()3由题意知//EF y 轴，则90FED OCB ∠=∠≠，∴DEF 为直角三角形，分90DFE ∠=和90EDF ∠=两种情况， ①当90DFE ∠=时，即//DF x 轴，则D 、F 的纵坐标相同， ∴F 点纵坐标为1，∵点F 在抛物线上，∴2431x x -+=，解得2x =E 的横坐标为2 ∵点E 在直线BC 上，∴当2x =31y x =-+=-2x =-31y x =-+=+∴E 点坐标为(2或(2-； ②当90EDF ∠=时， ∵()1,0A ，()2,1D ， ∴直线AD 解析式为1y x =-， ∵直线BC 解析式为3y x =-+， ∴AD BC ⊥，∴直线AD 与抛物线的交点即为E 点，联立直线AD 与抛物线解析式有2431x x x -+=-，解得1x =或4x =，当1x =时，32y x =-+=，当4x =时，31y x =-+=-， ∴E 点坐标为()1,2或()4,1-，综上可知存在满足条件的点E ，其坐标为(2或(2+或()1,2或()4,1-．【点睛】考查了待定系数法求函数解析式，利用已知的顶点坐标，列出方程组，可以求出函数解析式.【变式2-1】如图，经过x 轴上(10)(30)A B -，，，两点的抛物线2(1)4y m x m =--（0m <）交y 轴于点C ，设抛物线的顶点为D ，若以DB 为直径的⊙G 经过点C ，求解下列问题：（1）用含m 的代数式表示出C D ，的坐标；（2）求抛物线的解析式；（3）能否在抛物线上找到一点Q ，使BDQ △为直角三角形？如能，求出Q 点的坐标，若不能，请说明理由。