第五章光的干涉习题答案
光的干涉试题及答案

光的干涉试题及答案一、选择题1. 光的干涉现象是指:A. 光波的叠加B. 光波的衍射C. 光波的反射D. 光波的折射答案:A2. 以下哪个条件是产生光的干涉的必要条件?A. 光波的频率相同B. 光波的振幅相同C. 光波的传播方向相同D. 光波的相位差恒定答案:D3. 杨氏双缝干涉实验中,干涉条纹的间距与以下哪个因素无关?A. 双缝间的距离B. 光的波长C. 屏幕与双缝的距离D. 观察者与屏幕的距离答案:D二、填空题1. 在光的干涉中,当两列波的相位差为0时,光强增强,这种现象称为________。
答案:相长干涉2. 光的干涉条纹的间距可以通过公式________计算得出。
答案:Δx = (λL) / d三、简答题1. 请简述光的干涉现象是如何产生的?答案:光的干涉现象是由两列或多列光波在空间某点相遇时,由于光波的相位差,导致光强在某些区域增强,在另一些区域减弱,从而形成明暗相间的干涉条纹。
2. 光的干涉实验中,如何改变干涉条纹的间距?答案:可以通过改变光源的波长、改变双缝间的距离或者改变屏幕与双缝之间的距离来改变干涉条纹的间距。
四、计算题1. 已知杨氏双缝干涉实验中,双缝间的距离d=0.5mm,屏幕与双缝之间的距离L=1.5m,光的波长λ=600nm,求干涉条纹的间距。
答案:Δx = (λL) / d = (600×10^-9 m × 1.5m) / (0.5×10^-3 m) = 1.8×10^-4 m2. 如果在上述实验中,将双缝间的距离增加到1.0mm,求新的干涉条纹间距。
答案:Δx = (λL) / d = (600×10^-9 m × 1.5m) / (1.0×10^-3 m) = 9.0×10^-4 m。
光的干涉(答案)

光的干涉(参考答案)一、选择题1. 【答案】AB【解析】A .肥皂膜因为自重会上面薄而下面厚,因表面张力的原因其截面应是一个圆滑的曲面而不是梯形,A 正确;B .薄膜干涉是等厚干涉,其原因为肥皂膜上的条纹是前后表面反射光形成的干涉条纹,B 正确;C .形成条纹的原因是前后表面的反射光叠加出现了振动加强点和振动减弱点,形成到破裂的过程上面越来越薄,下面越来越厚,因此出现加强点和减弱点的位置发生了变化,条纹宽度和间距发生变化,C 错误;D .将肥皂膜外金属环左侧的把柄向上转动90︒,由于重力,表面张力和粘滞力等的作用,肥皂膜的形状和厚度会重新分布,因此并不会跟着旋转90°;D 错误。
2. 【答案】D【解析】从薄膜的上下表面分别反射的两列光是相干光,其光程差为△x =2d ,即光程差为薄膜厚度的2倍,当光程差△x =nλ时此处表现为亮条纹,故相邻亮条纹之间的薄膜的厚度差为12λ,在图中相邻亮条纹(或暗条纹)之间的距离变大,则薄膜层的厚度之间变小,因条纹宽度逐渐变宽,则厚度不是均匀变小。
选项D 正确。
3. 【答案】D【解析】【分析】本题考查折射定律以及双缝干涉实验。
【详解】由双缝干涉条纹间距的公式Lx d λ∆=可知,当两种色光通过同一双缝干涉装置时,波长越长条纹间距越宽,由屏上亮条纹的位置可知12λλ>反射光经过三棱镜后分成两束色光,由图可知M 光的折射角大,又由折射定律可知,入射角相同时,折射率越大的色光折射角越大,由于12λλ>则12n n <所以N 是波长为λ1的光出射位置,故D 正确,ABC 错误。
故选D 。
4. 【答案】C【解析】解:因为路程差即(膜的厚度的两倍)是半波长的偶数倍,振动加强,为亮条纹,路程差是半波长的奇数倍,振动减弱,为暗条纹。
所以人从同侧看,可看到亮条纹时,同一高度膜的厚度相同,则彩色条纹水平排列,因竖直放置的肥皂薄膜受到重力的作用,下面厚,上面簿,形状视如凹透镜,因此,在薄膜上不同的地方,来自前后两个面的反射光所走的路程差不同,导致上疏下密,故C 正确,ABD 错误。
光的干涉习题答案

学号 班级 姓名 成绩第十六章 光的干涉(一)一、选择题1、波长mm 4108.4-⨯=λ的单色平行光垂直照射在相距mm a 4.02=的双缝上,缝后m D 1=的幕上出现干涉条纹。
则幕上相邻明纹间距离是[ B ]。
A .0.6mm ;B .1.2 mm ;C .1.8 mm ;D . 2.4 mm 。
2、在杨氏双缝实验中,若用一片透明云母片将双缝装置中上面一条缝挡住,干涉条纹发生的变化是[ C ]。
A .条纹的间距变大;B .明纹宽度减小;C .整个条纹向上移动;D .整个条纹向下移动。
3、双缝干涉实验中,入射光波长为λ,用玻璃薄片遮住其中一条缝,已知薄片中光程比相同厚度的空气大2.5λ,则屏上原0级明纹处[ B ]。
A .仍为明条纹;B .变为暗条纹;C .形成彩色条纹;D .无法确定。
4、在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取的办法是[ B ]。
A .使屏靠近双缝; B .使两缝的间距变小; C .把两个缝的宽度稍微调窄; D .改用波长较小的单色光源。
5、在双缝干涉实验中,单色光源S 到两缝S 1、S 2距离相等,则中央明纹位于图中O 处,现将光源S 向下移动到S ’的位置,则[ B ]。
A .中央明纹向下移动,条纹间距不变;B .中央明纹向上移动,条纹间距不变;C .中央明纹向下移动,条纹间距增大;D .中央明纹向上移动,条纹间距增大。
二、填空题1、某种波长为λ的单色光在折射率为n 的媒质中由A 点传到B 点,相位改变为π,问光程改变了2λ , 光从A 点到B 点的几何路程是 2nλ 。
2、从两相干光源s 1和s 2发出的相干光,在与s 1和s 2等距离d 的P 点相遇。
若s 2位于真空中,s 1位于折射率为n 的介质中,P 点位于界面上,计算s 1和s 2到P 点的光程差 d-nd 。
3、光强均为I 0的两束相干光相遇而发生干涉时,在相遇区域内有可能出现的最大光强是04I ;最小光强是 0 。
光的干涉参考答案

光的干涉参考解答一 选择题1.如图示,折射率为n 2厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3,已知n 1<n 2<n 3,若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束之间的光程差是 (A )2n 2e (B )2n 2e -2λ (C )2n 2e -λ (D )2n 2e -22n λ[A ][参考解]:两束光都是在从光疏介质到光密介质的分界面上反射,都有半波损失存在,其光程差应为δ=(2n 2e +2λ)-2λ= 2n 2e 。
2.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2,路径S 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过一块厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径光的光程差等于 (A )(r 2+ n 2t 2)-(r 1+ n 1t 1)(B )[r 2+ (n 2-1)t 2] -[r 1+ (n 1-1)t 1] (C )(r 2-n 2t 2)-(r 1-n 1t 1) (D )n 2t 2-n 1t 1[ B ]3.如图,用单色光垂直照射在观察牛顿环的装置上,当平凸透镜垂直向上缓缓平移而离开平面玻璃板时,可以观察到环状干涉条纹 (A )向右移动 (B )向中心收缩 (C )向外扩张 (D )静止不动[ B ][参考解]:由牛顿环的干涉条件(k 级明纹)λλk ne k =+22 ⇒ nk e k 2)21(λ-= 可知。
4.在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传到B ,若A 、B 两点的相位差是3π,则此路径AB 的光程差是 (A )1.5λ (B )1.5n λ (C )3λ (D )1.5λ/n[ A ][参考解]:由相位差和光程差的关系λδπϕ2=∆可得。
3S 1PS 空气二 填空题1.如图所示,波长为λ的平行单色光斜入射到距离为d 的双缝上,入射角为θ,在图中的屏中央O 处(S 1O=S 2O ),两束相干光的相位差为λθπsin 2d 。
高中物理(新人教版)选择性必修一课后习题:光的干涉(课后习题)【含答案及解析】

光的干涉课后篇巩固提升必备知识基础练1.(多选)下列关于双缝干涉实验的说法正确的是()A.单缝的作用是获得频率保持不变的相干光源B.双缝的作用是获得两个振动情况相同的相干光源C.频率相同、相位差恒定、振动方向相同的两列单色光能够发生干涉现象D.照射单缝的单色光的波长越小,光屏上出现的条纹宽度越宽,单缝的作用是获得一个线光源,双缝的作用是获得两个振动情况完全相同的光源,故选项A错误,B正确;频率相同、相位差恒定的两列光可以发生干涉现象,选项C正确;由Δx=ldλ可知,波长越短,条纹间距越窄,选项D错误。
2.(2021河北博野中学高二开学考试)某一质检部门为检测一批矿泉水的质量,利用干涉原理测定矿泉水的折射率。
方法是将待测矿泉水填充到特制容器中,放置在双缝与光屏之间(可视为双缝与光屏之间全部为矿泉水),如图所示,特制容器未画出,通过比对填充后的干涉条纹间距x2和填充前的干涉条纹间距x1就可以计算出该矿泉水的折射率。
则下列说法正确的是(设空气的折射率为1)()A.x2=x1B.x2>x1C.该矿泉水的折射率为x1x2D.该矿泉水的折射率为x2x1n=cv和v=fλ可知光在水中的波长小于在空气中的波长,根据双缝干涉条纹的间距公式Δx=ldλ可知填充矿泉水后的干涉条纹间距x2小于填充前的干涉条纹间距x1,所以A、B错误;根据n=cv 和v=fλ可得n=λ1λ2,又由x1=ldλ1和x2=ldλ2得n=x1x2,故C正确,D错误。
3.如图所示,用频率为f 的单色光垂直照射双缝,在光屏上的P 点出现第3条暗条纹,已知光速为c ,则P 点到双缝距离之差S 2P-S 1P 应为( )A.c 2fB.3c 2fC.3c fD.5c 2fλ=c f ,又P 点出现第3级暗条纹,即S 2P-S 1P=5×λ2=5c 2f ,选项D 正确。
4.某同学自己动手利用如图所示的器材,观察光的干涉现象,其中,A 为单缝屏,B 为双缝屏,C 为像屏。
(参考资料)光的干涉习题(附答案)

光的干涉(附答案)一. 填空题1. 光强均为I 0的两束相干光相遇而发生干涉时,在相遇区域内有可能出现的最大光强是 4I 0 。
2. 在双峰干涉试验中,用折射率为n 的薄云母片覆盖其中的一条狭缝,这时屏幕上的第7级明纹恰好移到屏幕中央原零级明纹的位置,设入射光波长为λ,则云母片的厚度为 7λ/(n -1) 。
3. S 1和S 2是两个波长均为λ的相干波源,相距3λ4,S 1的相位比S 2超前π2。
若两波单独传播时,在过S 1和S 2的直线上各点的强度相同,不随距离变化,且两波的强度都是I 0,那么在S 1、S 2连线上,S 1和S 2的外侧各点,合成波的强度分别是 4 I 0,0 。
3λ44. 用波长为λ的单色光垂直照射牛顿环装置,观察牛顿环,如图所示。
若使凸透镜慢慢向上垂直移动距离d ,移过视场中某固定观察点的条纹数等于 2d/λ 。
S 1 S 25.空气中两块玻璃形成的空气劈形膜,一端厚度为零,另一端厚度为0.005 cm,玻璃折射率为1.5,空气折射率近似为1。
如图所示,现用波长为600 nm的单色平行光,沿入射角为30°角的方向射到玻璃板的上表面,则在劈形膜上形成的干涉条纹数目为144 。
解:通过折射定律,求空气劈形膜上表面的入射角:n空气sin30o=n玻璃sini入,得到sini入=1/3根据劈尖干涉的特点,可以得到相邻明纹中心的高度差Δe:Δe=λ/2(1-2.25/9)0.5得到最终的干涉条纹数目:m=5*10-5*2(1-2.25/9)0.5/6*10-7≈1446.维纳光驻波实验装置示意如图。
MM为金属反射镜,NN为涂有极薄感光层的玻璃板。
MM与NN之间夹角φ=3.0×10-4 rad,波长为λ的平面单色光通过NN板垂直入射到MM金属反射镜上,则反射光与入射光在相遇区域形成光驻波,NN板的感光层上形成对应于波腹波节的条纹。
实验测得两个相邻的驻波波腹感光垫A、B的间距1.0 mm,则入射光的波长为 6.0×10-4mm 。
光的干涉(有答案)

光的⼲涉(有答案)光的⼲涉⼀、⼲涉的相关知识点1、双缝⼲涉:由同⼀光源发出的光经双缝后,在屏上出现明暗相间的条纹.⽩光的双缝⼲涉的条纹是中央为⽩⾊条纹,两边为彩⾊条纹,单⾊光的双缝⼲涉中相邻亮条纹间距离为Δx = Δx =l dλ 2、薄膜⼲涉:利⽤薄膜(如肥皂液薄膜) 前后两⾯反射的光相遇⽽形成的.图样中同⼀条亮(或暗)条纹上所对应的薄膜厚度相同⼆、双缝⼲涉1、⼀束⽩光在真空中通过双缝后在屏上观察到的⼲涉条纹,除中央⽩⾊亮纹外,两侧还有彩⾊条纹,其原因是 ( )A .各⾊光的波长不同,因⽽各⾊光分别产⽣的⼲涉条纹的间距不同B .各⾊光的速度不同,因⽽各⾊光分别产⽣的⼲涉条纹的间距不同C .各⾊光的强度不同,因⽽各⾊光分别产⽣的⼲涉条纹的间距不同D .上述说法都不正确答案 A解析⽩光包含各种颜⾊的光,它们的波长不同,在相同条件下做双缝⼲涉实验时,它们的⼲涉条纹间距不同,所以在中央亮条纹两侧出现彩⾊条纹,A 正确.2、 (2011·北京·14)如图所⽰的双缝⼲涉实验,⽤绿光照射单缝S 时,在光屏P 上观察到⼲涉条纹.要得到相邻条纹间距更⼤的⼲涉图样,可以 ( )A .增⼤S1与S 2的间距B .减⼩双缝屏到光屏的距离C .将绿光换为红光D .将绿光换为紫光答案 C解析在双缝⼲涉实验中,相邻两条亮纹(或暗纹)间的距离Δx =l dλ,要想增⼤条纹间距可以减⼩两缝间距d ,或者增⼤双缝屏到光屏的距离l ,或者换⽤波长更长的光做实验.由此可知,选项C 正确,选项A 、B 、D 错误.3、双缝⼲涉实验装置如图所⽰,绿光通过单缝S 后,投射到具有双缝的挡板上,双缝S 1和S 2与单缝的距离相等,光通过双缝后在与双缝平⾏的屏上形成⼲涉条纹.屏上O 点距双缝S 1和S 2的距离相等,P 点是距O 点最近的第⼀条亮条纹.如果将⼊射的单⾊光换成红光或蓝光,讨论屏上O 点及其上⽅的⼲涉条纹的情况是 ( )A.O点是红光的亮条纹B.O点不是蓝光的亮条纹C.红光的第⼀条亮条纹在P点的上⽅D.蓝光的第⼀条亮条纹在P点的上⽅答案AC解析O点处波程差为零,对于任何光都是振动加强点,均为亮条纹,故B错;红光的波长较长,蓝光的波长较短,根据Δx=ldλ可知,C正确.4、关于光的⼲涉现象,下列说法正确的是()A.在波峰与波峰叠加处,将出现亮条纹;在波⾕与波⾕叠加处,将出现暗条纹B.在双缝⼲涉实验中,光屏上距两狭缝的路程差为1个波长的某位置,将出现亮纹C.把⼊射光由黄光换成紫光,两相邻亮条纹间的距离变窄D.当薄膜⼲涉的条纹是等间距的平⾏线时,说明薄膜的厚度处处相等答案BC解析在波峰与波峰叠加处,或在波⾕与波⾕叠加处,都是振动加强区,将出现亮条纹,选项A错误;在双缝⼲涉实验中,出现亮纹的条件是光屏上某位置距两狭缝的路程差为波长的整数倍,出现暗纹的条件是光屏上某位置距两狭缝的路程差为半波长的奇数倍,选项B正确;条纹间距公式Δx=ldλ,λ黄>λ紫,选项C正确;薄膜⼲涉实验中的薄膜是“楔形”空⽓膜,选项D错误.5、关于光的⼲涉,下列说法中正确的是()A.在双缝⼲涉现象⾥,相邻两明条纹和相邻两暗条纹的间距是不等的B.在双缝⼲涉现象⾥,把⼊射光由红光换成紫光,相邻两个明条纹间距将变宽C.只有频率相同的两列光波才能产⽣⼲涉D.频率不同的两列光波也能产⽣⼲涉现象,只是不稳定答案 C解析在双缝⼲涉现象⾥,相邻两明条纹和相邻两暗条纹的间距是相等的,A错误;由条纹间距Δx=ldλ,⼊射光的波长越长,相邻两个明条纹间距越⼤,因此,把⼊射光由红光换成紫光,相邻两个明条纹间距将变窄,B错误;两列光波产⽣⼲涉时,频率必须相同,C正确,D错误.6、如图所⽰,⼀束复⾊光由真空射向半圆形玻璃砖的圆⼼,经玻璃砖后分为两束单⾊光a、b,则()A.玻璃中a光波长⼤于b光波长B.玻璃中a光折射率⼤于b光折射率C .逐渐增⼤⼊射⾓i ,a 光⽐b 光先发⽣全反射D .利⽤同⼀双缝⼲涉实验装置,a 光产⽣的⼲涉条纹间距⽐b 光⼤ad7、在双缝⼲涉实验中,双缝到光屏上P 点的距离之差Δr =0.6 µm ;分别⽤频率为f 1=5.×1014 Hz 和f 2=7.5×1014 Hz 的单⾊光垂直照射双缝,则P 点出现明、暗条纹的情况是A .⽤频率为f 1的单⾊光照射时,出现明条纹B .⽤频率为f 2的单⾊光照射时,出现明条纹C .⽤频率为f 1的单⾊光照射时,出现暗条纹D .⽤频率为f 2的单⾊光照射时,出现暗条纹答案 AD解析根据c =λf ,可得两种单⾊光波长分别为:λ1=c f 1=3×1085×1014m =0.6 µm λ2=c f 2=3×1087.5×1014m =0.4 µm 与题给条件(Δr =0.6 µm)⽐较可知Δr =λ1=32λ2,故⽤频率为f 1的光照射双缝时,P 点出现明条纹;⽤频率为f 2的光照射双缝时,P 点出现暗条纹.8、如图所⽰,在双缝⼲涉实验中,S 1和S 2为双缝,P 是光屏上的⼀点,已知P 点与S 1、S 2距离之差为2.1×10-6 m ,分别⽤A 、B 两种单⾊光在空⽓中做双缝⼲涉实验,问P 点是亮条纹还是暗条纹?(1)已知A 光在折射率为1.5的介质中波长为4×10-7 m ;(2)已知B 光在某种介质中波长为3.15×10-7 m ,当B 光从这种介质射向空⽓时,临界⾓为37°;(3)若让A 光照射S 1,B 光照射S 2,试分析光屏上能观察到的现象.解析 (1)设A 光在空⽓中波长为λ1,在介质中波长为λ2,由n =c v =λ1λ2,得λ1=nλ2=1.5×4×10-7 m =6×10-7 m 根据路程差Δr =2.1×10-6m ,所以N 1=Δr λ1=2.1×10-66×10-7=3.5 由此可知,从S 1和S 2到P 点的路程差是波长λ1的3.5倍,所以P 点为暗条纹.(2)根据临界⾓与折射率的关系sin C =1n 得n =1sin 37°=53由此可知,B 光在空⽓中波长λ3为:λ3=nλ介=53×3.15×10-7 m =5.25×10-7 m 路程差Δr 和波长λ3的关系为:N 2=Δr λ3=2.1×10-65.25×10-7=4 可见,⽤B 光做光源,P 点为亮条纹.(3)若让A 光和B 光分别照射S 1和S 2,这时既不能发⽣⼲涉,也不发⽣衍射,此时在光屏上只能观察到亮光.答案 (1)暗条纹 (2)亮条纹 (3)见解析9、如图所⽰,在双缝⼲涉实验中,已知SS 1=SS 2,且S 1、S 2到光屏上P 点的路程差Δr =1.5×10-6 m. (1)当S 为λ=0.6 µm 的单⾊光源时,在P 点处将形成______条纹.(2)当S 为λ=0.5 µm 的单⾊光源时,在P 点处将形成______条纹.(均选填“明”或“暗”)答案 (1)暗 (2)明解析 (1)当λ=0.6 µm =0.6×10-6 m 时, Δr =1.5×10-6 m =212λ.在P 点处将形成暗条纹. (2)当λ=0.5 µm =0.5×10-6 m 时,Δr =1.5×10-6 m =3λ,在P 点处将形成明条纹10、如图所⽰,a 、b 为两束不同频率的单⾊光,以45°的⼊射⾓射到玻璃砖的上表⾯,直线OO ′与玻璃砖垂直且与其上表⾯交于N 点,⼊射点A 、B 到N 点的距离相等,经玻璃砖上表⾯折射后两束光相交于图中的P 点,则下列说法正确的是 ( )A .在真空中,a 光的传播速度⼤于b 光的传播速度B .在玻璃中,a 光的传播速度⼩于b 光的传播速度C .同时增⼤⼊射⾓(⼊射⾓始终⼩于90°),则a 光在下表⾯先发⽣全反射D .对同⼀双缝⼲涉装置,a 光的⼲涉条纹⽐b 光的⼲涉条纹宽答案 D解析各种光在真空中的光速相同,选项A 错误;根据题图,⼊射⾓相同,a 光的折射⾓较⼤,所以a 光的折射率较⼩,由光在介质中的光速v =c n得,a 光在介质中的传播速度较⼤,选项B 错误;根据临界⾓公式C =arcsin 1n可知,a 光的临界⾓较⼤,b 光在下表⾯先发⽣全反射,选项C 错误;a 光的折射率较⼩,波长较长,根据公式Δx =l dλ可知,对同⼀双缝⼲涉装置,a 光的⼲涉条纹⽐b 光的⼲涉条纹宽,选项D 正确.三、薄膜⼲涉11、劈尖⼲涉是⼀种薄膜⼲涉,其装置如图7甲所⽰.将⼀块平板玻璃放置在另⼀平板玻璃之上,在⼀端夹⼊两张纸⽚,从⽽在两玻璃表⾯之间形成⼀个劈形空⽓薄膜.当光垂直⼊射后,从上往下看到的⼲涉条纹如图⼄所⽰,⼲涉条纹有如下两个特点:图7(1)任意⼀条明条纹或暗条纹所在位置下⾯的薄膜厚度相等;(2)任意相邻明条纹或暗条纹所对应的薄膜厚度差恒定.现若在图甲装置中抽去⼀张纸⽚,则当光垂直⼊射到新劈形空⽓薄膜后,从上往下观察到的⼲涉条纹将如何变化?答案见解析解析光线在空⽓膜的上下表⾯上反射,并发⽣⼲涉,形成⼲涉条纹,设空⽓膜顶⾓为θ,d 1、d 2处为两相邻明条纹,如图所⽰,则两处光的路程差分别为Δx 1=2d 1,Δx 2=2d 2,因为Δx 2-Δx 1=λ,所以d 2-d 1=12λ. 设条纹间距为Δl ,则由⼏何关系得d 2-d 1Δl =tan θ,即Δl =λ2tan θ.当抽去⼀张纸⽚时,θ减⼩,Δl 增⼤,即条纹变疏.12、甲所⽰,在⼀块平板玻璃上放置⼀平凸薄透镜,在两者之间形成厚度不均匀的空⽓膜,让⼀束单⼀波长的光垂直⼊射到该装置上,结果在上⽅观察到如图⼄所⽰的同⼼内疏外密的圆环状⼲涉条纹,称为⽜顿环,以下说法正确的是 ( )A .⼲涉现象是由于凸透镜下表⾯反射光和玻璃上表⾯反射光叠加形成的B .⼲涉现象是由于凸透镜上表⾯反射光和玻璃上表⾯反射光叠加形成的C .⼲涉条纹不等间距是因为空⽓膜厚度不是均匀变化的D .⼲涉条纹不等间距是因为空⽓膜厚度是均匀变化的答案 AC解析由于在凸透镜和平板玻璃之间的空⽓形成薄膜,所以形成相⼲光的反射⾯是凸透镜的下表⾯和平板玻璃的上表⾯,故A 正确,由于凸透镜的下表⾯是圆弧⾯,所以形成的薄膜厚度不是均匀变化的,形成不等间距的⼲涉条纹,故C 正确,D 错.。
光的干涉_基外练习题(含答案)

一选择题 (共 3分)1. (本题 3分)(5888)在折射率n3 = 1.60的玻璃片表面镀一层折射率n2 = 1.38的MgF2薄膜作为增透膜.为了使波长为λ = 500 nm (1 nm = 10-9 m)的光,从折射率n1 = 1.00的空气垂直入射到玻璃片上的反射尽可能地减少,MgF2薄膜的厚度e至少是(A) 250 nm. (B) 181.2 nm.(C) 125 nm.(D) 90.6 nm.[]二填空题 (共24分)2. (本题 3分)(3936)得干涉条纹时,将一折射率为1.33的平行平面透明膜插入双棱镜上半棱镜的光路中,如图所示.发现干涉条纹的中心极大(零级)移到原来不放膜时的第五级极大处,则膜厚为__________________.(1 nm = 10-9 m)3. (本题 3分)(7501)用迈克耳孙干涉仪产生等厚干涉条纹,设入射光的波长为λ,在反射镜M2转动过程中,在总的观测区域宽度L内,观测到总的干涉条纹数从N1条增加到N2条.在此过程中M2转过的角度Δθ 是____________________4. (本题 3分)(7502)用迈克耳孙干涉仪作干涉实验,设入射光的波长为λ.在转动迈克耳孙干涉仪的反射镜M2过程中,在总的干涉区域宽度L内,观测到完整的干涉条纹数从N1开始逐渐减少,而后突变为同心圆环的等倾干涉条纹.若继续转动M2又会看到由疏变密的直线干涉条纹.直到在宽度L内有N2条完整的干涉条纹为止.在此过程中M2转过的角度Δθ是____________________.5. (本题 3分)(7937)太阳光以入射角i = 52°从空气射在折射率为n = 1.4的薄膜上,若要透射光中波长λ = 670 nm (1 nm = 10-9 m)的红光较强,薄膜的最小厚度应为______________________________________.6. (本题 3分)(3929)镉的一条光谱线的波长λ = 643.8 nm ,谱线宽度Δλ = 1.3×10-3 nm(1 nm = 10-9 m) ,则此准单色光的相干长度L = _______________cm.采用窄带钨丝作为双缝干涉实验的光源.已知与双缝平行的发光钨丝的宽度b = 0.24 mm,双缝间距d = 0.4 mm.钨丝发的光经滤光片后,得到中心波长为690nm (1 nm = 10-9 m) 的准单色光.钨丝逐渐向双缝移近,当干涉条纹刚消失时,钨丝到双缝的距离l是__________________.8. (本题 3分)(3932)以钠黄光(λ = 589.3 nm)照亮的一条缝作为双缝干涉实验的光源,光源缝到双缝的距离为20 cm,双缝间距为0.5 mm.使光源的宽度逐渐变大,当干涉条纹刚刚消矢时,光源缝的宽度是__________________.(1nm = 10-9m)9. (本题 3分)(7945)白光垂直照射在镀有e = 0.40 μm厚介质膜的玻璃板上,玻璃的折射率n=1.45,介质的折射率n′= 1.50.则在可见光(390 nm~760 nm) (1 nm = 10-9 m)范围内,波长λ = ____________的光在反射中增强.三计算题 (共115分)10. (本题 5分)(3939)图示一双棱镜,顶角α很小,狭缝光源S发出的光Array通过双棱镜分成两束,好像直接来自虚光源S1和S2,它们间距d = 2α a(n- 1),n为棱镜的折射率.设费涅耳双棱镜的折射率n = 1.5,顶角α = 0.5°,被照亮的狭缝S放在距双棱镜a = 100 mm远的地方,如图所示.在距双棱镜L = 1 m远的幕上获得干涉条纹的间距为0.8mm,求所用光波的波长.11. (本题 5分)(3940)图示一双棱镜,顶角α很小,狭缝光源S发出的光Array通过双棱镜分成两束,好像直接来自虚光源S1和S2,它们间距d = 2α a(n- 1),n为棱镜的折射率.在双棱镜干涉实验中,狭缝光源到双棱镜距离a = 10 cm,而双棱镜到屏幕距离L = 120 cm.双棱镜折射率为1.50,所用波长λ = 589.0 nm(1nm=10−9m),在屏幕上测得干涉明纹间距Δx = 0.10 cm,求双棱镜顶角α.12. (本题 5分)(3941)在费涅耳双面镜干涉装置中,两面镜之间的夹角φ = 20′,单色缝光源到双面镜交线的距离L1 = 10 cm,屏幕与双面镜之间的距离L2 = 210 cm,光波波长λ =0.6 μm,求干涉条纹的间距.如图所示,把一凸透镜L切成两半,并稍微拉开一个距离h,用一小遮光板把其间的缝挡住.将一波长为λ的单色点光源S放在轴线O′O上,且fOS2=′,f是透镜的焦距.在透镜后面放一观察屏C,已知fOO10=′.设x轴的原点O点处的光强为I0.求x轴上任一点P点的光强I随x而变化的函数关系(即把I表示成I0,λ,h,f和x的函数).14. (本题10分)(5892)钠黄光中包含着两条相近的谱线,其波长分别为λ1 = 589.0 nm和λ2= 589.6 nm (1nm = 10-9 m).用钠黄光照射迈克耳孙干涉仪.当干涉仪的可动反射镜连续地移动时,视场中的干涉条纹将周期性地由清晰逐渐变模糊,再逐渐变清晰,再变模糊,….求视场中的干涉条纹某一次由最清晰变为最模糊的过程中可动反射镜移动的距离d.15. (本题 5分)(7503)把折射率n = 1.38的透明薄膜放入迈克耳孙干涉仪的一条光路中,观测到干涉条纹移动了ΔN = 7条.若所用单色光的波长是λ = 589.3 nm (1 nm = 10-9 m),求薄膜的厚度.(空气的折射率为1)16. (本题 5分)(7504)沿光路长度为d = 28 mm的透明薄壁(厚度可忽略)容器放在迈克耳孙干涉仪的一条光路中,所用单色光的波长为λ = 589.3 nm (1 nm = 10-9 m).当以氨气注入容器代替容器中的空气时,观测到干涉条纹移动了ΔN = 36条.已知空气的折射率n1 = 1.000276,且氨气的折射率n2 > n1,求氨气的折射率(要求计算到小数点后六位).17. (本题 5分)(7505)在用迈克耳孙干涉仪的实验中所用单色光的波长为λ = 589.3 nm (1 nm = 10-9 m),在反射镜M2转动过程中,在观测的干涉区域宽度L = 12 mm内干涉条纹从N1 = 12条增加到N2 = 20条.求M2转过的角度.18. (本题10分)(5887)如图所示,用波长为λ= 632.8 nm (1 nm = 10-9 m)的单色点光源S照射厚度为e = 1.00×10-5m、折射率为n2 = 1.50、半径为R= 10.0 cm的圆形薄膜F,点光源S与薄膜F的垂直距离为d = 10.0 cm,薄膜放在空气(折射率n1 = 1.00)中,观察透射光的等倾干涉条纹.问最多能看到几个亮纹?(注:亮斑和亮环都是亮纹).S用波长为λ的单色光,观察迈克耳孙干涉仪的等倾干涉条纹.先看到视场中共有10个亮纹(包括中心的亮斑在内).在移动可动反射镜M2的过程中,看到往中心缩进去10个亮纹.移动M2后,视场中共有5个亮纹(包括中心的亮斑在内).设不考虑两束相干光在分束板G1的镀银面上反射时产生的相位突变之差,试求开始时视场中心亮斑的干涉级k.20. (本题10分)(5891)用波长为λ的单色光,观察迈克耳孙干涉仪的等倾干涉条纹.先看到视场中共有10个亮纹(包括中心的亮斑在内).在移动可动反射镜M2的过程中,看到往中心缩进去10个亮纹.移动M2后,视场中共有5个亮纹(包括中心的亮斑在内).设不考虑两束相干光在分束板G1的镀银面上反射时产生的相位突变之差,试求开始时视场中心亮斑的干涉级k.21. (本题 5分)(1763)= 200用某种放电管产生的镉(Cd)红光,其中心波长λ = 644 nm,相干长度lc mm,试估计此镉红光的线宽Δλ和频宽Δν.(1 nm = 10-9 m)22. (本题 5分)(1764)用铯(Cs)原子制成的铯原子钟能产生中心频率等于9300 MHz、频宽为50 Hz 的狭窄谱线.求谱线宽度Δλ和相干长度.23. (本题 5分)(1765)用迈克耳孙干涉仪精密测量长度,光源为Kr86灯,谱线波长为605.7 nm(橙红色),谱线宽度为0.001 nm,若仪器可测出十分之一个条纹的变化,求能测出的最小长度和测量量程.(1 nm = 10-9 m)24. (本题 5分)(3931)已知镉光的波长λ = 643.8 nm,谱线宽度Δλ = 1.3×10-3 nm,求镉光的相长度与相干时间.25. (本题 5分)(3927)在观察肥皂水薄膜(n =1.33)的反射光时,某处绿色光(λ = 500 nm)反射最强,且这时法线和视线间的角度i = 45°,求该处膜的最小厚度.(1 nm = 10-9 m) 26. (本题 5分)(3933)在折射率为1.58的玻璃表面镀一层MgF2(n = 1.38)透明薄膜作为增透膜.欲使它对波长为λ= 632.8 nm的单色光在正入射时尽量少反射,则薄膜的厚度最小应是多少?27. (本题 5分)(5754)n2).波长为λ的单色平行光从空气(折射率为n1)中以入射角i射到薄膜上,欲使反射光尽可能增强,所镀薄膜的最小厚度是多少?(设n1 < n2 < n3)四 理论推导与证明题 (共13分)28. (本题 8分)(5890) 用波长为λ 的单色光照射迈克耳孙干涉仪,产生等倾干涉条纹.试证明第k 级明纹与第( k + 1 )级明纹的角间隔( Δθ )k 近似是)sin 2/()(1k k k k e θλθθθ≈−=+Δ,式中e 是等效空气薄膜的厚度.29. (本题 5分)(1759) 如图所示,a 是入射光的振幅,r 是其反射光对入射光的振幅比值,称为振幅反射系数;t 是其折射光对入射光的振幅比值,称为振幅透射系数.现让反射光和折射光各作逆向进行,如果没有吸收,请作简图并根据光的可逆性原理证明下列关系 (1) 21r t t −=′ (2) r r −=′r ′、t ′各表示光在逆向进行(即从第二种介质射向两种介质交界面)时的振幅反射系数和振辐透射系数.aar atn 1n 2五 回答问题 (共40分)30. (本题 5分)(0457) 图示装置是在迈克耳孙干涉仪的一臂上用凸面反射镜M 2代替原平面镜M 2,且调节到光程OO 1 = OO 2.分束板G 与M 1、M 2成45°角.现以单色平行光入射.(1) 在E 处观察M 1表面,观察到的干涉图样呈现什么形状?试求出第k 级亮纹的位置. (2) 当M 1朝G 移动时,干涉条纹如何变化?S31. (本题10分)(1766) 什么是光的时间相干性?32. (本题10分)(1767) 试以双缝干涉为例说明什么是光的空间相干性?33. (本题10分)(1767) 试以双缝干涉为例说明什么是光的空间相干性?34. (本题 5分)(7941) 试画出三缝干涉条纹中,亮条纹中心处光振动叠加的振幅矢量图和两亮条纹之间最暗处光振动叠加的振幅矢量图.一 选择题 (共 3分)1. (本题 3分)(5888) (D)参考解:当从增透膜MgF 2薄膜的上、下两表面的反射光的光程差为λ21时,反射光为相消干涉: λ2122=e n ∴ =××==−38.141050004102n e λ90.6 nm .二 填空题 (共24分)2. (本题 3分)(3936) 8.9 μm 3分参考解: λ5)1(=−d n=−=)1/(5n d λ8.9 μm3. (本题 3分)(7501))(212N N L−λ3分4. (本题 3分)(7502))(212N N L+λ3分5. (本题 3分)(7937) 2.90×10-5 cm 3分参考解:透射光加强即反射光干涉减弱,由以下公式可求e minλλ)12(2121sin 222122+=+−k i n n e 令 k = 1 =°−=52sin 4.1222min λe 2.90×10-5 cm6. (本题 3分)(3929) 32 cm 3分参考解答:L = λ2 / Δλ = 32 cm7. (本题 3分)(3930) 1.4×102 mm 3分8. (本题 3分)(3932) 0.24 mm 3分480 nm 3分参考解:反射增强,有 λλk e n =+′212 =−′=124k en λ 480 nm (选k = 3)三 计算题 (共115分)10. (本题 5分)(3939) 解:两个虚相干光源的间距为d=−=a n d α)1(20.87 mm 2分(式中α = 0.5°= 0.0087 rad ))/(L a d x +⋅=Δλ 2分= 0.63 μm 1分11. (本题 5分)(3940) 解:由双棱镜干涉公式x L a a n D x d ΔΔ+−==)]/()1(2[/αλ 3分所以 =−+=Δ])1(2/[)]([x a n L a λα 0.44° 2分12. (本题 5分)(3941) 解:等效的两虚光源间距为 d = 2L 1φ 2分干涉条纹间距为 φλλ1212/)(/L L L d L x +==Δ 1分= 1.1 mm 2分解:根据几何光学作图法可知点光源S 发出的光束经过上半个透镜L 1和下半个透镜L 2分别折射后所形成的两光束和两个同相位的相干光源S 1和S 2的位置,如图所示.由透镜成像公式fu 111=+v 和 f u 2=得 f 2=v 又因SS 1和SS 2分别通过上下两个半透镜的中心,由图可得1:2:)(:21=+=u u h S S v∴ h S S 221=,且S 1S 2平面与屏的距离= 8f . 5分 根据类似双缝干涉的计算可知P 点的光强)21(cos 4)cos 1(22121φφΔΔ=+=I A I 2分其中 θλδλφsin )2(22h π=π=Δ fhx f x h λλ428)2(2π≈π≈ 2分 ∴ f hxI I λ4cos 421π=.当x = 0时,104I I =. fhxI I λ4cos 20π=. 1分S14. (本题10分)(5892) 解:设视场中的干涉条纹由最清晰(λ1 的明纹与λ2的明纹重合)变为最模糊(λ1的明纹与λ2的暗纹重合)的过程中,可动反射镜M 2移动的距离为d ,则在此过程中,对于λ1,光程差增加了12λp d = ① 3分对于λ2,光程差增加了 2)21(2λ−=p d ② 3分由①式和②式联立解得: )(2122λλλ−=p ③ 1分将③式代入①式得: )(41221λλλλ−=d )0.5896.589(46.5890.589−×= 2分= 1.45×105 nm =1.45×10-4 m 1分15. (本题 5分)(7503) 解: λN d n Δ=−)1(2 3分=−=Δ)1(2n N d λ 5.43×10-3mm 2分16. (本题 5分)(7504) 解: λN d n n Δ=−)(212 3分dN n n 212λΔ+= 1分= 1.000655 1分解: )(212N N L−=Δλθ 3分= 1.96×10-4rad 2分18. (本题10分)(5887) 解:对于透射光等倾条纹的第k 级明纹有:λk r e n =cos 22 3分中心亮斑的干涉级最高,为k max ,其r = 0,有:=××××==−−752max 10328.61000.150.122λe n k 47.4 应取较小的整数,k max = 47(能看到的最高干涉级为第47级亮斑). 3分最外面的亮纹干涉级最低,为k min ,相应的入射角为 i m = 45°(因R =d ),相应的折射角为r m ,据折射定律有 m m r n i n sin sin 21= ∴ 50.145sin 00.1sin )sin (sin 1211°==−−m m i n n r = 28.13° 由 λmin 2cos 2k r e n m = 得:752min 10328.613.28cos 1000.150.12cos 2−−×°×××==λmr e n k = 41.8 应取较大的整数,k min = 42(能看到的最低干涉级为第42级亮斑). 3分∴ 最多能看到6个亮斑(第42,43,44,45,46,47级亮斑). 1分19. (本题10分)(5891) 解:设开始时干涉仪的等效空气薄膜的厚度为e 1,则对于视场中心的亮斑有 λk e =12 ① 2分对于视场中最外面的一个亮纹有λ)9(cos 21−=k r e ② 2分设移动了可动反射镜M 2之后,干涉仪的等效空气薄膜的厚度变为e 2,则对于视场中心的亮斑有λ)10(22−=k e ③ 2分对于视场中最外面的一个亮纹有λ)14(cos 22−=k r e ④ 2分联立解①─④,得: k = 18 2分20. (本题10分)(5891) 解:设开始时干涉仪的等效空气薄膜的厚度为e 1,则对于视场中心的亮斑有 λk e =12 ① 2分对于视场中最外面的一个亮纹有λ)9(cos 21−=k r e ② 2分设移动了可动反射镜M 2之后,干涉仪的等效空气薄膜的厚度变为e 2,则对于视场中心的亮斑有λ)10(22−=k e ③ 2分对于视场中最外面的一个亮纹有λ)14(cos 22−=k r e ④ 2分联立解①─④,得: k = 18 2分解:线宽 Δλ = λ2 / l c = 2.07×10-3nm 3分 频宽 Δν = | -c Δλ / λ2 | = c / l c= 1.5×109Hz 2分22. (本题 5分)(1764) 解: ∵ λν = c , ∴ λΔν = - νΔλΔλ = | ( - λΔν ) / ν |= c Δν / ν 2 = 0.173 nm 2分 l c = λ 2 / Δλ = ( c / ν )2 / (c Δν / ν 2 ) = c / Δν= 6000 km 3分23. (本题 5分)(1765) 解:每变化一个条纹,干涉仪的动镜移动半个波长,故能测出十分之一个条纹,则能测出长度的最小值为=×λ21)10/1(30.3 nm 3分用迈克耳孙干涉仪动镜可以测量的量程为光的相干长度之半==Δλλ/21212c l 18 cm 2分24. (本题 5分)(3931) 解:镉光的相干长度 L = λ2 / Δλ = 32 cm 3分相干时间 Δt = L / c = 1.1×10-9 s 2分25. (本题 5分)(3927) 解:因为 λλk i n e =−−2/sin 222 2分令k = 0 , 2/sin 222λ=−i n e =−=i n e 22sin 2/)2/(λ111 nm 3分26. (本题 5分)(3933) 解:尽量少反射的条件为2/)12(2λ+=k ne (k = 0, 1, 2, …)令 k = 0 得 d min = λ / 4n 4分= 114.6 nm 1分27. (本题 5分)(5754) 解:设膜的厚度为e ,令膜的上下表面反射的光束为1和2,1、2两束反射光的光程差为 i n n e 22122sin 2−=δ 2分(因n 1 < n 2 < n 3,两束反射光都有相位π的突变,故因反射导致的附加光程差为零).相长干涉条件为 δ = k λ k = 1,2,3,…即 λk i n n e =−22122sin 2 ∴ )sin 2/(22122i n n k e −=λ 2分取k = 1,得最小厚度 )sin 2/(22122i n n e −=λ 1分。
第五章 1光的干涉作业答案

1光的干涉一、双缝干涉1.1801年,英国物理学家托马斯·杨在实验室里成功地观察到了光的干涉.2.双缝干涉实验(1)实验过程:激光束垂直射到两条狭缝S1和S2时,S1和S2相当于两个完全相同的光源,从S1和S2发出的光在挡板后面的空间叠加而发生干涉现象.(2)实验现象:在屏上得到明暗相间的条纹.(3)实验结论:光是一种波.3.出现明、暗条纹的条件光从两狭缝到屏上某点的路程差为半波长λ2的偶数倍(即波长λ的整数倍)时,这些点出现明条纹;当路程差为半波长λ2的奇数倍时,这些点出现暗条纹.二、薄膜干涉1.原理:以肥皂膜为例,单色光平行入射到肥皂泡液薄膜上,由液膜前后两个表面反射回来的两列光是相干光,它们相互叠加产生干涉,肥皂泡上就出现了明暗相间的条纹或区域.2.图样:以光照射肥皂泡为例,如果是单色光照射肥皂泡,肥皂泡上就会出现明暗相间的条纹或区域;如果是白光照射肥皂泡,液膜上就会出现彩色条纹.3.应用:检查平面的平整程度.原理:空气层的上下两个表面反射的两列光波发生干涉.1.判断下列说法的正误.(1)两只相同的手电筒射出的光在同一区域叠加后,看不到干涉图样的原因是干涉图样太细小看不清楚.(×)(2)屏上到双缝的路程差等于半波长的整数倍,此处为暗条纹.(×)(3)水面上的油膜呈现彩色条纹,是油膜表面反射光与入射光叠加的结果. (×)(4)观察薄膜干涉条纹时,应在入射光的另一侧.(×)2.如图1所示,在杨氏双缝干涉实验中,激光的波长为5.30×10-7 m,屏上P点距双缝S1和S2的路程差为7.95×10-7 m.则在这里出现的应是________(填“亮条纹”或“暗条纹”).图1答案暗条纹一、杨氏干涉实验1.杨氏双缝干涉实验(1)双缝干涉的装置示意图实验装置如图2所示,有光源、单缝、双缝和光屏.(2)单缝的作用:获得一个线光源,使光源有唯一的频率和振动情况.也可用激光直接照射双缝.(3)双缝的作用:将一束光分成两束频率相同且振动情况完全一致的相干光.2.光产生干涉的条件两束光的频率相同、相位差恒定、振动方向相同.杨氏双缝干涉实验是靠“一分为二”的方法获得两个相干光源的.3.干涉图样(1)单色光的干涉图样:干涉条纹是等间距的明暗相间的条纹.(2)白光的干涉图样:中央条纹是白色的,两侧干涉条纹是彩色条纹.例1 在双缝干涉实验中,以白光为光源,在屏幕上观察到了彩色干涉条纹,若在双缝中的一缝前放一红色滤光片(只能透过红光),另一缝前放一绿色滤光片(只能透过绿光),已知红光与绿光的频率、波长均不相等,这时( )A.只有红色和绿色的双缝干涉条纹,其他颜色的双缝干涉条纹消失B.红色和绿色的双缝干涉条纹消失,其他颜色的干涉条纹依然存在C.任何颜色的双缝干涉条纹都不存在,但屏上仍有光亮D.屏上无任何光亮答案 C解析 分别用绿色滤光片和红色滤光片挡住两条缝后,红光和绿光的频率不等,不能发生干涉,因此屏上不会出现干涉条纹,但仍有光亮.二、决定条纹间距的条件1.两相邻亮条纹(或暗条纹)间距离与光的波长有关,波长越长,条纹间距越大.白光的干涉条纹的中央是白色的,两侧是彩色的,这是因为:各种色光都能形成明暗相间的条纹,都在中央条纹处形成亮条纹,从而复合成白色条纹.两侧条纹间距与各色光的波长成正比,条纹不能完全重合,这样便形成了彩色干涉条纹.2.亮、暗条纹的判断如图3所示,设屏上的一点P 到双缝的距离分别为r 1和r 2,路程差Δr =r 2-r 1.(1)若满足路程差为波长的整数倍,即Δr =kλ(其中k =0,1,2,3…),则出现亮条纹.k =0时,PS 1=PS 2,此时P 点位于屏上的O 处,为亮条纹,此处的条纹叫中央亮条纹或零级亮条纹.k 为亮条纹的级次.(2)若满足路程差为半波长的奇数倍,即Δr =2k -12λ(其中k =1,2,3…),则出现暗条纹.k 为暗条纹的级次,从第1级暗条纹开始向两侧展开.例2 如图4所示是双缝干涉实验装置,使用波长为600 nm 的橙色光源照射单缝S ,在光屏中央P 处观察到亮条纹,在位于P 点上方的P 1点出现第一条亮条纹(即P 1到S 1、S 2的路程差为一个波长),现换用波长为400 nm 的紫色光源照射单缝,则( )A.P 和P 1仍为亮条纹B.P 为亮条纹,P 1为暗条纹C.P 为暗条纹,P 1为亮条纹D.P 、P 1均为暗条纹答案 B解析 从单缝S 射出的光波被S 1、S 2两缝分成两束相干光,由题意知屏中央P 点到S 1、S 2距离相等,即分别由S 1、S 2射出的光到P 点的路程差为零,因此中央是亮条纹,无论入射光是什么颜色的光、波长多大,P 点都是中央亮条纹.而分别由S 1、S 2射出的光到P 1点的路程差刚好是橙光的一个波长,即|P 1S 1-P 1S 2|=600 nm =λ橙.当换用波长为400nm 的紫光时,|P 1S 1-P 1S 2|=600 nm =32λ紫,则两列光波到达P 1点时振动情况完全相反,即分别由S 1、S 2射出的紫色光到达P 1点时相互削弱,因此,在P 1点出现暗条纹.综上所述,选项B 正确.三、薄膜干涉1.薄膜干涉中相干光的获得光照射到薄膜上,在薄膜的前、后两个面反射的光是由同一个实际的光源分解而成的,它们具有相同的频率,恒定的相位差.2.薄膜干涉的原理光照在厚度不同的薄膜上时,前、后两个面的反射光的路程差等于相应位置膜厚度的2倍,在某些位置,两列波叠加后相互加强,于是出现亮条纹;在另一些位置,叠加后相互削弱,于是出现暗条纹.3.薄膜干涉是经薄膜前、后表面反射的两束光叠加的结果出现亮条纹的位置,两束光的路程差Δr =kλ(k =0,1,2,3…),出现暗条纹的位置,两束光的路程差Δr =2k +12λ(k =0,1,2,3…).4.薄膜干涉的应用(1)检查平面平整度的原理光线经空气薄膜的上、下两面的反射,得到两束相干光,如果被检测平面是光滑平整的,得到的干涉条纹是等间距的.如果被检测平面某处凹下,则对应条纹提前出现,如果某处凸起,则对应条纹延后出现.(2)增透膜的原理在增透膜的前、后表面反射的两列光波形成相干波,当路程差为半波长的奇数倍时,两光波相互削弱,反射光的能量几乎等于零.例3 用单色光照射位于竖直平面内的肥皂液薄膜,所观察到的干涉条纹为( )答案 B解析 由于在光的干涉中亮、暗条纹的位置取决于两列光波相遇时通过的路程差,则在薄膜干涉中取决于入射点处薄膜的厚度.因肥皂液薄膜在重力作用下形成了一个上薄下厚的楔形膜,厚度相等的位置在同一条水平线上,故同一条干涉条纹必然是水平的,由此可知只有选项B 正确.1.由于薄膜干涉是经薄膜前、后表面反射的两束光叠加而形成的,所以观察时眼睛与光源应在膜的同一侧.2.在光的薄膜干涉中,前、后表面反射光的路程差由膜的厚度决定,所以薄膜干涉中同一亮条纹或同一暗条纹应出现在厚度相同的地方,因此又叫等厚干涉,每一条纹都是水平的.3.用单色光照射得到明暗相间的条纹,用白光照射得到彩色条纹.1.(双缝干涉实验)(2018·北京卷)用双缝干涉实验装置得到白光的干涉条纹,在光源与单缝之间加上红色滤光片后( )A.干涉条纹消失B.彩色条纹中的红色条纹消失C.中央条纹变成暗条纹D.中央条纹变成红色答案 D解析 在光源与单缝之间加上红色滤光片后,只透过红光,屏上出现红光(单色光)的干涉条纹,中央条纹变成红色.2.(亮、暗条纹的判断)在双缝干涉实验中,双缝到光屏上P 点的距离之差为0.6 μm ,若分别用频率为f 1=5.0×1014 Hz 和f 2=7.5×1014 Hz 的单色光垂直照射双缝,则P 点出现亮、暗条纹的情况是( )A.用单色光f 1和f 2分别照射时,均出现亮条纹B.用单色光f 1和f 2分别照射时,均出现暗条纹C.用单色光f 1照射时出现亮条纹,用单色光f 2照射时出现暗条纹D.用单色光f 1照射时出现暗条纹,用单色光f 2照射时出现亮条纹答案 C解析 单色光f 1的波长:λ1=c f 1=3×1085.0×1014 m =0.6×10-6 m =0.6 μm. 单色光f 2的波长:λ2=c f 2=3×1087.5×1014 m =0.4×10-6 m =0.4 μm. 因P 点到双缝的距离之差Δx =0.6 μm =λ1,所以用单色光f 1照射时P 点出现亮条纹.Δx =0.6 μm =32λ2, 所以用单色光f 2照射时P 点出现暗条纹,故选项C 正确.3.(多选)用红光做光的双缝干涉实验,如果将其中一条缝改用蓝光,下列说法正确的是( )A.在光屏上出现红蓝相间的干涉条纹B.只有相干光源发出的光才能在叠加时产生干涉现象,此时不产生干涉现象C.频率不同的两束光也能发生干涉现象,此时出现彩色条纹D.尽管亮、暗条纹都是光波相互叠加的结果,但此时红光与蓝光只叠加而不产生干涉现象答案 BD解析 频率相同、相位差恒定、振动方向相同是产生干涉现象的条件,红光和蓝光的频率不同,不能产生干涉现象,不会产生干涉条纹,A 、C 错误.4.(多选)用单色光做双缝干涉实验时( )A.屏上到双缝的路程差等于波长整数倍处出现亮条纹B.屏上到双缝的路程差等于半波长整数倍处,可能是亮条纹,也可能是暗条纹C.屏上的亮条纹一定是两列光波的波峰与波峰相遇的地方D.屏上的亮条纹是两列光波的波峰与波谷相遇的地方答案 AB解析在双缝干涉实验中,屏上到双缝的路程差等于波长整数倍处出现亮条纹,是振动加强处,不一定是两列光波的波峰与波峰相遇的地方,也可能是波谷与波谷相遇的地方,A选项正确,C选项错误;屏上到双缝的路程差等于半波长整数倍处,可能是半波长的奇数倍(暗条纹),也可能是半波长的偶数倍(亮条纹),B选项正确;两列光波的波峰与波谷相遇的地方,应是暗条纹,D选项错误.5.(多选)双缝干涉实验装置如图3所示,绿光通过单缝S后,投射到有双缝的挡板上,双缝S1和S2与单缝S的距离相等,光通过双缝后在与双缝平行的屏上形成干涉条纹.屏上O点距双缝S1和S2的距离相等,P点是O点上侧的第一条亮条纹,如果将入射的单色光换成红光或蓝光,已知红光波长大于绿光波长,绿光波长大于蓝光波长,则下列说法正确的是()A.O点是红光的亮条纹B.红光的同侧第一条亮条纹在P点的上方C.O点不是蓝光的亮条纹D.蓝光的同侧第一条亮条纹在P点的上方答案AB解析中央O点到S1、S2的路程差为零,所以换不同颜色的光时,O点始终为亮条纹,选项A正确,C错误;波长越长,条纹间距越宽,所以红光的同侧第一条亮条纹在P点上方,蓝光的同侧第一条亮条纹在P点下方,选项B 正确,D错误.6.(多选)下列现象中可以用薄膜干涉来解释的是()A.海市蜃楼B.水面上的油膜在阳光照射下呈彩色C.肥皂泡在阳光照射下呈现五颜六色D.荷叶上的水珠在阳光下晶莹透亮答案BC解析海市蜃楼是光在空气中发生折射形成的,故选项A错误;荷叶上的水珠在阳光下晶莹透亮是全反射的结果,故选项D错误;油膜在阳光照射下呈彩色、肥皂泡在阳光照射下呈现五颜六色都是薄膜干涉的结果,故选项B、C 正确.7.(多选)如图4所示,一束白光从左侧射入肥皂薄膜,下列说法中正确的是()A.人从右侧向左看,可以看到彩色条纹B.人从左侧向右看,可以看到彩色条纹C.彩色条纹水平排列D.彩色条纹竖直排列答案BC解析一束白光射到薄膜上,经前、后两个面反射回来的光相遇,产生干涉现象,从左侧向右看可看到彩色条纹,又由于薄膜同一水平线上的厚度相同,所以彩色条纹是水平排列的,故正确答案为B、C.8.如图所示是用干涉法检查某块厚玻璃板的上表面是否平整的装置,所用单色光是用普通光通过滤光片产生的,检查中所观察到的干涉条纹是由下列哪两个表面反射的光线叠加而成的()A.a的上表面和b的下表面B.a的上表面和b的上表面C.a 的下表面和b 的上表面D.a 的下表面和b 的下表面答案 C解析 干涉法的原理是利用单色光的薄膜干涉,这里的薄膜指的是标准样板与待测玻璃板之间的空气层.在空气层的上表面和下表面分别反射的光会发生干涉,观察干涉后形成的条纹是否为平行直线,可以判断厚玻璃板的上表面是否平整.因此选项C 正确.9在双缝干涉实验中,若双缝处的两束光的频率均为6×1014 Hz ,两光源S 1、S 2的振动情况恰好相反,光屏上的P 点到S 1与到S 2的路程差为3×10-6 m ,如图所示,则:(注意和同频同步结论刚好相反)(1)P 点是亮条纹还是暗条纹?(2)设O 为到S 1、S 2路程相等的点,则P 、O 间还有几条亮条纹,几条暗条纹?(不包括O 、P 两处的条纹) 答案 (1)暗条纹 (2)5条暗条纹,6条亮条纹解析 (1)由λ=c f得λ=5×10-7 m n =Δs λ=3×10-65×10-7=6 由于两光源的振动情况恰好相反,所以P 点为暗条纹.(2)O 点到S 1、S 2的路程差为0,也是暗条纹,OP 间还有5条暗条纹,6条亮条纹.。
鲁科版 高中物理 选修3-4 第5章 光的干涉 衍射 寒假复习题含答案

绝密★启用前鲁科版高中物理选修3-4 第5章光的干涉衍射寒假复习题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共100分,考试时间150分钟。
分卷I一、单选题(共10小题,每小题4.0分,共40分)1科学家利用激光干涉方法探测到由于引力波引起的干涉条纹的变化,这是引力波存在的直接证据.关于激光,下列说法中正确的是()A.激光是自然界中某种物质直接发光产生的,不是偏振光B.激光相干性好,任何两束激光都能发生干涉C.用激光照射不透明挡板上小圆孔时,光屏上能观测到等间距的光环D.激光全息照片是利用光的干涉记录下物体三维图象的信息2.为了提高汽车夜间行车安全,有人提出设想:将汽车的挡风玻璃和车灯罩做成偏振片,使司机只看到自己车灯的光而看不见对面车灯发出的光,从而大大降低对面的车灯造成的视线模糊,以下关于光的偏振的说法正确的是()A.只有振动方向和透振方向一致的光才能透过偏振片B.光的振动方向指的是磁场方向C.光的偏振现象不可争议地证明了光是一种机械波D.泊松亮斑就是一种偏振现象3.如图所示为红光和紫光通过相同的双缝和单缝所呈现的图样,则()A.甲为紫光的干涉图样B.乙为紫光的干涉图样C.丙为红光的干涉图样D.丁为红光的干涉图样4.如图所示,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线.则()A.在玻璃中,a光的传播速度大于b光的传播速度B.玻璃砖对a光的折射率小于对b光的折射率C.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失D.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距5.关于光的干涉现象,下列说法正确的是()A.波峰与波峰叠加处将出现亮条纹,波谷与波谷叠加处将出现暗条纹B.双缝干涉实验中光屏上距两狭缝的路程差为1个波长的某位置将出现亮纹C.把双缝干涉实验中入射光由黄光换成紫光,相邻两明条纹间距离变宽D.薄膜干涉的条纹是等间距的平行线时,说明薄膜的厚度处处相等6.对光的衍射现象的定性分析,不正确的是()A.光的衍射是光在传播过程中绕过障碍物继续传播的现象B.衍射条纹图样是光波相互叠加的结果C.光的衍射现象为光的波动说提供了有力的证据D.光的衍射现象完全否定了光的直线传播结论7.a、b两束单色光分别用同一双缝干涉装置进行实验,在距双缝恒定距离的屏上得到如图所示的干涉图样,图甲是a光照射时形成的干涉图样,图乙是b光照射时形成的干涉图样.下列关于a、b两束单色光的说法正确的是()A.a光的频率比b光大B.b光比a光易发生衍射现象C.a光比b光易发生全反射现象D.b光在水中的传播速度较小8.一个半径较大的透明玻璃球体,截去其下面的一部分,然后将这一部分放在标准的水平面上,现让单色光竖直射向截面,如图所示,从上往下看到的是()A.一片黑暗B.只能看到同颜色的平行的反射光C.环形的明暗相间的干涉条纹D.平行的明暗相间的干涉条纹9.如图所示,将一束由两种色光混合的复色光沿SE方向射向一上、下表面平行的厚玻璃平面镜上表面,得到三束光线A、B、C,若平面镜的上、下表面足够宽,则()A.光束A为单色光,光束B、C为复色光B.玻璃对光束C的折射率大于对光束B的折射率C.A、B、C三束光线一定互相平行D.通过相同的双缝干涉装置,光束B产生的相邻亮条纹间距要大于光束C产生的相邻亮条纹间距10.一束单色平行光通过双缝后,在屏上得到干涉条纹,下列说法正确的是()A.相邻两条亮纹间距比相邻两条暗纹间距大B.用红光做实验比用紫光做实验时,得到的亮条纹或暗条纹间的间距小C.用白光做此实验不能形成条纹D.用白光做此实验,屏上出现彩色条纹二、多选题(共4小题,每小题5.0分,共20分)11.(多选)在单缝衍射实验中,下列说法中正确的是().A.将入射光由黄色换成绿色,衍射条纹间距变窄B.使单缝宽度变小,衍射条纹间距变窄C.换用波长较长的光照射,衍射条纹间距变宽D.增大单缝到屏的距离,衍射条纹间距变宽12.(多选)关于光的衍射现象,下面说法正确的是()A.红光的单缝衍射图样是红暗相间的直条纹B.白光的单缝衍射图样是白黑相间的直条纹C.光照到不透明小圆盘上出现泊松亮斑,说明发生了衍射D.光照到较大圆孔上出现大光斑,说明光沿着直线传播,不存在光的衍射13.(多选)对于激光的认识,以下说法正确的是()A.普通光源发出的光都是激光B.激光是自然界普遍存在的一种光C.激光是一种人工产生的相干光D.激光已深入到我们生活的各个方面14.(多选)抽制细丝时可用激光监控其粗细,如图所示.激光束通过细丝时产生的条纹和它通过遮光板的同样宽度的窄缝时产生的条纹规律相同,则()A.这是利用光的干涉现象B.这是利用光的衍射现象C.如果屏上条纹变宽,表明抽制的丝变粗了D.如果屏上条纹变宽,表明抽制的丝变细了分卷II三、实验题(共1小题,每小题10.0分,共10分)15.在利用双缝干涉测定光波波长的实验中,将测量头的分划板中心刻度线与某亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图甲所示,然后同方向转动测量头,使分划板中心刻度线与第6 条亮纹中心对齐,记下此时手轮上的示数如图乙所示,已知双缝间距为 2.00×10-4m,双缝到屏的距离为0.700 m,(1)图甲所示示数为________ mm,图乙所示示数为________ mm.(2)相邻亮纹的间距Δx为________ mm.(3)计算波长的公式为λ=________,求得的波长值为________ m.四、计算题(共3小题,每小题10.0分,共30分)16.在双缝干涉实验中,用单色光照射双缝,双缝间距等于0.06 cm,双缝到光屏的距离为1.5 m,若测得屏上第1条亮条纹与第7条亮条纹之间相距9.0 mm,则此单色光的波长是多少?17.如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2距离之差为2.1×10-6m,分别用A、B两种单色光在空气中做双缝干涉实验,问P点处是亮条纹还是暗条纹?(1)已知A光在折射率为n=1.5的介质中波长为4×10-7m.(2)已知B光在某种介质中波长为3.15×10-7m,当B光从这种介质射向空气时,临界角为37°.(3)若让A光照射S1,B光照射S2,试分析光屏上能观察到的现象.18.在双缝干涉实验中,屏上一点P到双缝的距离之差为1.5×10-6m,若用频率为5.0×1014Hz的单色光照射双缝,该点处于亮条纹还是暗条纹?从屏中心算起这是第几条什么条纹?答案解析1.【答案】D【解析】激光是人造光,也是偏振光,故A错误;激光相干性好,只有频率相同的两束激光才会发生干涉,故B错误;用激光照射不透明挡板上小圆孔时,光屏上能观测到衍射条纹,间距不等,故C错误;激光全息照片是利用光的干涉记录下物体三维图象的信息,故D正确.2.【答案】A【解析】根据光的偏振原理,当只有振动方向和透振方向一致的光,才能透过偏振片,故A正确;光的振动方向指的是横波的振动方向,与磁场方向无关,故B错误;光的偏振现象不可争议地证明了光是一种横波,不是机械波,故C错误;泊松亮斑现象是光的衍射,故D错误;故选.3.【答案】B【解析】干涉条纹平行、等宽、等间距,选项C、D错误.干涉图样为明暗相间的条纹,且条纹间距为Δx=λ,光的波长越长,条纹间距越大,紫光的波长短,因而紫光干涉图样的条纹间距小,故正确选项为B.4.【答案】C【解析】光线a的偏折程度大,根据折射定律公式n=,知玻璃砖对a光的折射率大;再根据公式v=,知光线a在玻璃中的传播速度小,故A、B错误;若改变光束的入射方向使θ角逐渐变大,则折射光线a的折射角先达到90°,故a光先发生全反射,首先消失,故C正确;光线a 的折射率大,说明光线a的频率高,根据c=λf,光线a在真空中的波长较短,根据双缝干涉条纹间距公式Δx=λ,知分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距小于b光的干涉条纹间距,故D错误;故选C.5.【答案】B【解析】在波峰与波峰叠加处,波谷与波谷叠加处,都将出现亮条纹,故A错误;光屏上距两狭缝的路程差为波长的整数倍时出现亮纹,故B正确;把入射光由黄光换成紫光,紫光的波长小于黄光,根据Δx=λ知Δx减小,故C错误;从薄膜的上下表面分别反射的两列光是相干光,其光程差为薄膜厚度的2倍,当光程差Δx=nλ时此处表现为亮条纹,当光程差Δx=nλ+λ出现暗条纹,若薄膜的厚度处处相等,则各处光程差相等,若是亮的则都是亮的若是暗的则都是暗的,不会出现明暗相间的条纹,故D错误.6.【答案】D【解析】根据光的衍射现象的定义可知选项A正确;衍射图中有亮、暗条纹,这是光波相互叠加的结果,加强区为亮条纹,减弱区为暗条纹,选项B正确;因为衍射也是波特有的现象,所以光的衍射现象的发现为光的波动说提供了有力证据,选项C正确;当障碍物较大时,光的衍射很弱,光几乎沿直线传播,即光的直线传播只是特殊情况下的近似,二者是统一的,选项D错误.7.【答案】D【解析】根据双缝干涉条纹的间距公式Δx=λ,知甲图条纹间距大,则a光的波长较长.根据f =知,a光的频率较小,故A错误;a光的波长较长,则a光比b光易发生衍射现象,故B错误;频率小,则折射率小,根据sin C=可知,折射率越大的,临界角越小,因此a光临界角比b光大,那么b光比a光易发生全反射现象,故C错误;根据v=知,a光在水中的传播速度较大,b光在水中的传播速度较小.故D正确.8.【答案】C【解析】玻璃球体的下表面和水平面的反射光是两束相关光,频率相同,发生干涉现象,干涉条纹不是疏密均匀的同心圆,故选C.9.【答案】C【解析】两种色光在上表面都发生反射,反射角相同,则由图可知光束A是复色光.而光束B、C 由于折射率的不同导致偏折分离,因为厚玻璃平面镜的上下表面是平行的.根据光的可逆性,知两光速仍然平行射出,且光束B、C是单色光.故A错误;由图知:光束B的偏折程度大于光束C,根据折射定律可知光束B的折射率大于光束C,故B错误.一束由两种色光混合的复色光沿SE方向射出,经过反射、再折射后,光线仍是平行,因为光的反射时入射角与反射角相等.所以由光路可逆可得出射光线平行.改变α角,光线A、B、C仍保持平行,故C正确;光束B的折射率大于光束C的折射率,则光束B的频率大于光束C,光束B的波长小于光束C的波长,而双缝干涉条纹间距与波长成正比,则双缝干涉实验中光B产生的条纹间距比光束C的小,故D错误.10.【答案】D【解析】单色光的干涉条纹的宽度是相等的,A错误;条纹间距与波长成正比,所以用红光做实验比用紫光做实验时,得到的亮条纹或暗条纹间的间距大,B错误;用白光做此实验,屏上出现彩色干涉条纹,C错误,D正确.11.【答案】ACD【解析】当单缝宽度一定时,波长越长,衍射现象越明显,即光偏离直线传播的路径越远,条纹间距也越大;当光的波长一定时,单缝宽度越小,衍射现象越明显,条纹间距越大;光的波长一定、单缝宽度也一定时,增大单缝到屏的距离,衍射条纹间距也会变宽(如图所示).故选项A、C、D正确.12.【答案】AC【解析】单色光照到狭缝上产生的衍射图样是红暗相间的直条纹,白光的衍射图样是彩色条纹.光照到不透明小圆盘上,在其阴影中心处出现亮点,是衍射现象.光的衍射现象只有明显与不明显之分,D项中屏上大光斑的边缘模糊,正是光的衍射造成的,不能认为不存在衍射现象.13.【答案】CD【解析】激光是人工产生的相干光,并不能由普通光源发出,激光在我们日常生活中有着重要的应用.14.【答案】BD【解析】由图样可知,这是利用了光的衍射现象,当丝变细时(相当于狭缝变窄)条纹间距变宽,B、D选项正确.15.【答案】(1)2.32013.870(2)2.310 6.6×10-7【解析】(1)图甲中固定刻度读数为2 mm,可动刻度读数为0.01×32.0=0.320 mm,所以最终读数为2.320 mm.图乙中固定刻度读数为13.5 mm,可动刻度读数为0.01×37.0=0.370 mm,所以最终读数为13.870 mm.(2)相邻两条亮纹间的距离Δx=mm=2.310 mm;(3)根据双缝干涉条纹的间距公式Δx=λ,知λ=,代入数据得:λ=6.6×10-7m.16.【答案】6×10-7m【解析】本题考查干涉条纹宽度公式:Δx=λΔx==1.5×10-3m.Δx=1.5×10-3m,d=0.06 cm=6×10-4m,l=1.5 m,代入λ=可得:λ=6×10-7m.17.【答案】(1)暗条纹(2)亮条纹(3)光屏上只能观察到亮光【解析】(1)设A光在空气中的波长为λ1,在介质中的波长为λ2,由n=,得λ1=nλ2=1.5×4×10-7m=6×10-7m,根据路程差Δr=2.1×10-6m,所以n1===3.5由此可知,从S1和S2到P点的路程差是波长λ1的3.5倍,所以P点处为暗条纹.(2)根据临界角与折射率的关系sin C=,得n==由此可知,B光在空气中的波长λ2为:λ2=nλ介=×3.15×10-7m=5.25×10-7m由路程差Δr和波长λ的关系得n2===4可见,用B光做光源,P点处为亮条纹.(3)若让A光和B光分别照射S1和S2,这时既不能发生干涉,也不发生衍射,此时在光屏上只能观察到亮光.18.【答案】暗第3条暗条纹【解析】λ==6.0×10-7,Δr=1.5×10-6m=2.5λ;光程差为半波长的奇数倍,P点处于暗条纹,令2.5λ=(2k-1),k=3,这是第3条暗条纹.。
光的干涉计算题及答案

《光的干涉》计算题1.在双缝干涉实验中,用波长λ=546.1nm (1 nm=10-9m)的单色光照射,双缝与屏的距离D =300 mm.测得中央明条纹两侧的两个第五级明条纹的间距为12.2 mm,求双缝间的距离.解:由题给数据可得相邻明条纹之间的距离为∆x=12.2 / (2×5)mm=1.22 mm 2分由公式∆x=Dλ / d,得d=Dλ / ∆x=0.134 mm 3分2. 在图示的双缝干涉实验中,若用薄玻璃片(折射率n1=1.4)覆盖缝S1,用同样厚度的玻璃片(但折射率n2=1.7)覆盖缝S2,将使原来未放玻璃时屏上的中央明条纹处O变为第五级明纹.设单色光波长λ=480 nm(1nm=109m),求玻璃片的厚度d(可认为光线垂直穿过玻璃片).解:原来,δ = r2-r1= 0 2分覆盖玻璃后,δ=( r2 + n2d–d)-(r1 + n1d-d)=5λ3分∴(n2-n1)d=5λ125nnd-=λ2分= 8.0×10-6 m 1分3. 薄钢片上有两条紧靠的平行细缝,用波长λ=546.1 nm (1 nm=10-9 m)的平面光波正入射到钢片上.屏幕距双缝的距离为D=2.00 m,测得中央明条纹两侧的第五级明条纹间的距离为∆x=12.0 mm.(1) 求两缝间的距离.(2) 从任一明条纹(记作0)向一边数到第20条明条纹,共经过多大距离?(3) 如果使光波斜入射到钢片上,条纹间距将如何改变?解:(1) x=2kDλ / dd = 2kDλ /∆x2分此处k=5∴d=10 Dλ / ∆x=0.910 mm 2分(2) 共经过20个条纹间距,即经过的距离l=20 Dλ / d=24 mm 2分(3) 不变2分4. 在双缝干涉实验中,单色光源S0到两缝S1和S2的距离分别为l1和l2,并且l1-l2=3λ,λ为入射光的波长,双缝之间的距离为d,双缝到屏幕的距离为D(D>>d),如图.求:(1) 零级明纹到屏幕中央O点的距离.(2) 相邻明条纹间的距离.屏解:(1) 如图,设P 0为零级明纹中心则 D O P d r r /012≈- 3分(l 2 +r 2) - (l 1 +r 1) = 0∴ r 2 – r 1 = l 1 – l 2 = 3λ ∴()d D d r r D O P /3/120λ=-= 3分 (2) 在屏上距O 点为x 处, 光程差 λδ3)/(-≈D dx 2分 明纹条件 λδk ±= (k =1,2,....) ()d D k x k /3λλ+±=在此处令k =0,即为(1)的结果.相邻明条纹间距d D x x x k k /1λ=-=+∆ 2分5. 在双缝干涉实验中,用波长λ=500 nm 的单色光垂直入射到双缝上,屏与双缝的距离D =200 cm ,测得中央明纹两侧的两条第十级明纹中心之间距离为Δx =2.20 cm ,求两缝之间的距离d .(1nm=109m)解:相邻明纹间距 ∆x 0 = D λ / d 2分两条缝之间的距离 d = D λ / ∆x 0 =D λ / (∆x / 20) =20 D λ/∆x= 9.09×10-2 cm 3分6. 双缝干涉实验装置如图所示,双缝与屏之间的距离D =120 cm ,两缝之间的距离d =0.50 mm ,用波长λ=500 nm (1 nm=10-9 m)的单色光垂直照射双缝. (1) 求原点O (零级明条纹所在处)上方的第五级明条纹的坐标x . (2) 如果用厚度l =1.0×10-2 mm , 折射率n =1.58的透明薄膜复盖在图中的S 1缝后面,求上述第五级明条纹的坐标x '.解:(1) ∵ dx / D ≈ k λx ≈Dk λ / d = (1200×5×500×10-6 / 0.50)mm= 6.0 mm 4分(2) 从几何关系,近似有r 2-r 1≈ D x /d '有透明薄膜时,两相干光线的光程差 δ = r 2 – ( r 1 –l +nl ) = r 2 – r 1 –(n -1)l ()l n D x 1/d --'=对零级明条纹上方的第k 级明纹有 λδk = 零级上方的第五级明条纹坐标()[]d k l n D x /1λ+-=' 3分=1200[(1.58-1)×0.01±5×5×10-4] / 0.50mm=19.9 mm 3分P d λ x '7. 在如图所示的瑞利干涉仪中,T 1、T 2是两个长度都是l 的气室,波长为λ的单色光的缝光源S 放在透镜L 1的前焦面上,在双缝S 1和S 2处形成两个同相位的相干光源,用目镜E 观察透镜L 2焦平面C 上的干涉条纹.当两气室均为真空时,观察到一组干涉条纹.在向气室T 2中充入一定量的某种气体的过程中,观察到干涉条纹移动了M 条.试求出该气体的折射率n (用已知量M ,λ和l 表示出来).解:当T 1和T 2都是真空时,从S 1和S 2来的两束相干光在O 点的光程差为零.当T 1中充入一定量的某种气体后,从S 1和S 2来的两束相干光在O 点的光程差为(n – 1)l . 1分 在T 2充入气体的过程中,观察到M 条干涉条纹移过O 点,即两光束在O 点的光程差改变了M λ.故有(n -1)l -0 = M λ 3分 n =1+M λ / l . 1分8.用波长λ=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少?解: 明纹, 2ne +λ21=k λ (k =1,2,…)3分 第五条,k =5, ne 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分9. 在Si 的平表面上氧化了一层厚度均匀的SiO 2薄膜.为了测量薄膜厚度,将它的一部分磨成劈形(示意图中的AB 段).现用波长为600 nm 的平行光垂直照射,观察反射光形成的等厚干涉条纹.在图中AB 段共有8条暗纹,且B 处恰好是一条暗纹,求薄膜的厚度.(Si 折射率为3.42,SiO 2折射率为1.50)解:上下表面反射都有相位突变π,计算光程差时不必考虑附加的半波长. 设膜厚为e , B 处为暗纹,2ne =21( 2k +1 )λ, (k =0,1,2,…) 2分 A 处为明纹,B 处第8个暗纹对应上式k =7 1分 ()nk e 412λ+==1.5×10-3 mm 2分A ,膜10. 图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm .(1) 求入射光的波长.(2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.解:(1) 明环半径 ()2/12λ⋅-=R k r 2分()Rk r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ)对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分 故在OA 范围内可观察到的明环数目为50个. 1分11. 波长为λ的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹.(1) 从形膜顶部O 开始向右数起,第五条暗纹中心所对应的薄膜厚度e 5是多少?(2) 相邻的二明纹所对应的薄膜厚度之差是多少?解:∵ n 1<n 2<n 3,二反射光之间没有附加相位差π,光程差为δ = 2n 2 e第五条暗纹中心对应的薄膜厚度为e 5,2n 2 e 5 = (2k - 1)λ / 2 k = 5()2254/94/152n n e λλ=-⨯= 3分 明纹的条件是 2n 2 e k = k λ相邻二明纹所对应的膜厚度之差∆e = e k+1-e k = λ / (2n 2) 2分3。
第五章 光的干涉 习题答案

第五章光得干涉5-1 波长为589、3nm得钠光照射在一双缝上,在距双缝200cm得观察屏上测量20个条纹共宽3cm,试计算双缝之间得距离。
解:由题意,条纹间距为:∴双缝间距为:,两小孔得距离为1、5mm,观察屏离小孔得垂直距离为1m,若所用光源发出波长=650nm与=532nm得两种光波,试求两光波分别形成得条纹间距以及两组条纹得第8级亮纹之间得距离。
解:对于=650nm得光波,条纹间距为:对于=532nm得光波,条纹间距为:∴两组条纹得第8级条纹之间得距离为:5-3 一个长40mm得充以空气得气室置于杨氏装置中得一个小孔前,在观察屏上观察到稳定得干涉条纹系,继后抽去气室中得空气,注入某种气体,发现条纹系移动了30个条纹。
已知照射光波波长为656、28nm,空气折射率为1、000276,试求注入气体得折射率n g。
解:气室充入空气与充气体前后,光程得变化为:而这一光程变化对应于30个波长:∴5-4 在菲涅耳双面镜干涉实验中,光波长为600nm,光源与观察屏到双面镜交线得距离分别为0、6m与1、8m,双面镜夹角为10-3rad,求:(1)观察屏上得条纹间距;(2)屏上最多能瞧到多少亮条纹?解:如图所示,S1S2得距离为:∴条纹间距为:∵角很小∴屏上能产生条纹得范围,如图阴影所示∴最多能瞧到得亮条纹数为:5-5 在如图所示得洛埃镜实验中,光源S1到观察屏得距离为2m,光源到洛埃镜面得垂直距离为2、5mm。
洛埃镜长40cm,置于光源与屏得中央。
若光波波长为500nm,条纹间距为多少?在屏上可瞧见几条条纹?解:在洛埃镜实验中,S1与S1在平面镜中得像S2可瞧作就是产生干涉得两个光源。
条纹间距为:由图可知,屏上发生干涉得区域在P1P2范围内0 1 2mm mmmmmm OA O S AP tg AP P P 75.38005.21200102002=⨯===θ 由于经平面镜反射得光波有π得相位差,所以S 1与S 2可瞧作位相相反得相干光源。
第五章 光的干涉 习题答案

第五章 光的干涉5-1 波长为589.3nm 的钠光照射在一双缝上,在距双缝200cm 的观察屏上测量20个条纹共宽3cm ,试计算双缝之间的距离。
解:由题意,条纹间距为:cm e 15.0203==∴双缝间距为:m e D d 391079.015.0103.589200--⨯≈⨯⨯==λ5-2 在杨氏干涉实验中,两小孔的距离为1.5mm ,观察屏离小孔的垂直距离为1m ,若所用光源发出波长1λ=650nm 和2λ=532nm 的两种光波,试求两光波分别形成的条纹间距以及两组条纹的第8级亮纹之间的距离。
解:对于1λ=650nm 的光波,条纹间距为:m d D e 339111043.0105.1106501---⨯≈⨯⨯⨯==λ 对于2λ=532nm 的光波,条纹间距为:m d D e 339221035.0105.1105321---⨯≈⨯⨯⨯==λ ∴两组条纹的第8级条纹之间的距离为: m e e x 3211064.0)(8-⨯=-=∆5-3 一个长40mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系,继后抽去气室中的空气,注入某种气体,发现条纹系移动了30个条纹。
已知照射光波波长为656.28nm ,空气折射率为1.000276,试求注入气体的折射率n g 。
解:气室充入空气和充气体前后,光程的变化为: D n g )000276.1(-=∆δ 而这一光程变化对应于30个波长: λδ30=∆∴λ30)1(=-D n g000768.1000276.110401028.6563039=+⨯⨯⨯=--g n5-4 在菲涅耳双面镜干涉实验中,光波长为600nm ,光源和观察屏到双面镜交线的距离分别为0.6m 和1.8m ,双面镜夹角为10-3rad ,求:(1)观察屏上的条纹间距;(2)屏上最多能看到多少亮条纹?解:如图所示,S 1S 2的距离为:αsin 2l d =∴条纹间距为:αλλsin 2)(l q l d D e +== ∵α角很小∴mmm l q l e 2.1102.1106.0210600)8.16.0(2)(339=⨯=⨯⨯⨯⨯+=+≈---αλ屏上能产生条纹的范围,如图阴影所示mmmq qtg y 6.3108.12223=⨯⨯=≈=-αα∴最多能看到的亮条纹数为:32.16.3===e y n5-5 在如图所示的洛埃镜实验中,光源S 1到观察屏的距离为2m ,光源到洛埃镜面的垂直距离为2.5mm 。
华理工大学大学物理习题之光的干涉习题详解
此文件仅供参考,如有雷同,纯属巧合。
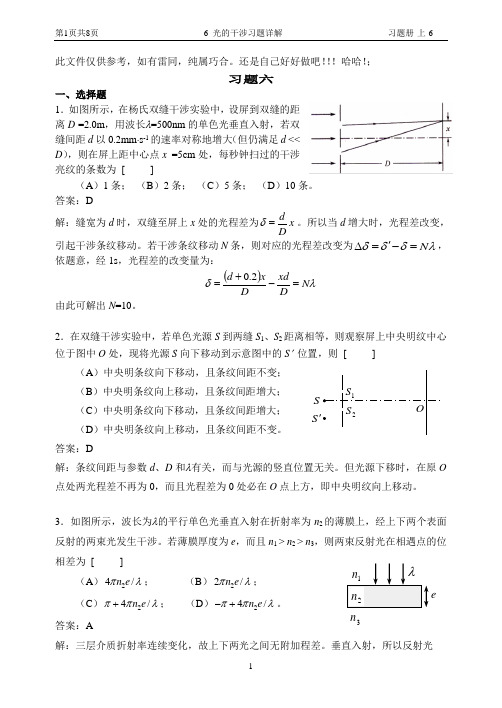
还是自己好好做吧!!!哈哈!;习题六一、选择题1.如图所示,在杨氏双缝干涉实验中,设屏到双缝的距离D =2.0m ,用波长λ=500nm 的单色光垂直入射,若双缝间距d 以0.2mm ⋅s -1的速率对称地增大(但仍满足d << D ),则在屏上距中心点x =5cm 处,每秒钟扫过的干涉亮纹的条数为 [ ] (A )1条; (B )2条; (C )5条; (D )10条。
答案:D解:缝宽为d 时,双缝至屏上x 处的光程差为dx Dδ=。
所以当d 增大时,光程差改变,引起干涉条纹移动。
若干涉条纹移动N 条,则对应的光程差改变为N δδδλ'∆=-=,依题意,经1s ,光程差的改变量为:()λδN Dxd D x d =-+=2.0 由此可解出N =10。
2.在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明纹中心位于图中O 处,现将光源S 向下移动到示意图中的S ' 位置,则 [ ](A )中央明条纹向下移动,且条纹间距不变; (B )中央明条纹向上移动,且条纹间距增大; (C )中央明条纹向下移动,且条纹间距增大; (D )中央明条纹向上移动,且条纹间距不变。
答案:D解:条纹间距与参数d 、D 和λ有关,而与光源的竖直位置无关。
但光源下移时,在原O 点处两光程差不再为0,而且光程差为0处必在O 点上方,即中央明纹向上移动。
3.如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉。
若薄膜厚度为e ,而且n 1 > n 2 > n 3,则两束反射光在相遇点的位相差为 [ ](A )24/n e πλ; (B )22/n e πλ; (C )24/n e ππλ+; (D )24/n e ππλ-+。
答案:A解:三层介质折射率连续变化,故上下两光之间无附加程差。
光的干涉练习题及答案

光的干涉练习题及答案三、分析题1、在双缝干涉实验中,在下列情况下,干涉条纹将如何变化?试说明理由。
(1) 入射光由红光换为紫光;(2) 屏与双缝的间距D 不断增大;(3) 在下面一条缝后放一块云母片。
【答案】:双缝干涉条纹相邻明条纹(或暗条纹)的间距为 λdD x =∆ (2分) (1) 红光变紫光波长λ减小,其他条件不变时,条纹变窄(或密或向屏中央集中)(3分)(2) D 不断增大时,x ∆增大,条纹变稀(或变宽)(3分)(3) 在下面一条缝后放一块云母片,通过它的光线的光程增大(2分),干涉条纹向下平移(2分)。
2、杨氏双缝干涉实验条件作如下变化,干涉条纹将如何变化?试说明理由。
(1)加大双缝间距d ;(2)把整套装置浸入水中;(3)在两缝后分别放红色和绿色的滤光片。
【答案】:根据:条纹宽度λdD x =∆(2分) (1)d 变大,其他条件不变,则x ∆变小,所以条纹变窄(或密或向屏中央集中)(2分)。
d 增大到一定程度,条纹过于细密而无法分辨,拥挤在一起成为一条明亮带。
(2分)(2)装置没入水中后的条纹宽度为λdD n x 1=∆,因为1>n (2分) 所以x ∆变小,条纹变窄(或密或向屏中央集中)。
(2分)(3)使通过两缝的光频率不同,不满足相干条件(2分),干涉条纹消失(2分)。
3、如图所示,A ,B 两块平板玻璃构成空气劈尖,分析在下列情况中劈尖干涉条纹将如何变化?(1) A 沿垂直于B 的方向向上平移[见图(a)];(2) A 绕棱边逆时针转动[见图(b)]。
【答案】:相邻明纹或暗纹介质膜厚度差n d 2λ=∆(2分),相邻明纹或暗纹间距θλn l 2=(2分)。
(1)上表面A 向上平移时,棱边明暗交替变化,相同厚度的空气薄模向棱边处移动,条纹间距不变。
(4分)(2) A 绕棱边逆时针转动时,棱边明暗不变,各级条纹向棱边方向移动,条纹变密。
(4分)4、在玻璃(5.1=n )上镀上25.1=n 的介质薄膜,波长 nm 500=λ的光从空气中垂直照射到此薄膜上,要使其为高反膜和增透膜求膜的厚度。
关于光的干涉的习题与答案

关于光的干涉的习题与答案
光的干涉习题与答案
光的干涉是光学中非常重要的一个现象,它揭示了光波的波动性质。
在干涉现象中,光波会相互叠加,形成明暗条纹,从而产生干涉图样。
下面我们来看一些关于光的干涉的习题与答案。
习题一:两束相干光波在空气中相遇,它们的波长分别为600nm和450nm,求它们的相位差。
解答:相位差可以用公式Δφ=2πΔx/λ来计算,其中Δx为两束光波的光程差,λ为光波的波长。
由于光程差Δx=0,所以相位差Δφ=0。
习题二:在双缝干涉实验中,两个狭缝间距为0.2mm,波长为500nm的光波垂直入射到狭缝上,求干涉条纹的间距。
解答:干涉条纹的间距可以用公式dλ/D来计算,其中d为狭缝间距,λ为光波的波长,D为观察屏到狭缝的距离。
代入数据可得,间距为0.1mm。
习题三:在双缝干涉实验中,两个狭缝间距为0.1mm,波长为600nm的光波垂直入射到狭缝上,观察屏到狭缝的距离为2m,求干涉条纹的间距。
解答:代入数据可得,间距为0.3mm。
通过以上习题与答案,我们可以看到光的干涉现象在实际问题中的应用。
对于学习光学的同学来说,掌握光的干涉原理和计算方法是非常重要的。
希望大家能够通过练习,加深对光的干涉现象的理解,提高解决实际问题的能力。
光的干涉习题答案

光学干涉测量技术
利用光的干涉现象测量长度、角 度、表面粗糙度等物理量,具有 高精度和高灵敏度。
光学干涉滤镜
利用光的干涉现象制作出的滤镜, 可以实现对特定波长的光进行过 滤或增强。
光学干涉仪
利用光的干涉现象测量光学元件 的表面形貌、折射率等参数,广 泛应用于光学研究和制造领域。
02 光的干涉原理
光的波动理论
光的干涉习题答案
目录
• 光的干涉现象 • 光的干涉原理 • 光的干涉实验 • 光的干涉习题解析 • 光的干涉理论的发展
01 光的干涉现象
光的干涉现象定义
1 2
光的干涉现象
当两束或多束相干光波在空间某一点叠加时,由 于光波的相互加强或减弱,形成明暗相间的干涉 条纹的现象。
相干光波
频率相同、振动方向相同、相位差恒定的光波。
题目:一束单色光垂直入射到一对相互平行的狭缝上, 光通过狭缝后形成的光斑可看作是什么图形?
解析:根据光的干涉原理,当单色光垂直入射到一对相 互平行的狭缝上,光通过狭缝后形成的光斑是圆形干涉 图样。
进阶习题解析
题目
如何通过双缝干涉实验验证光的波动性?
答案
通过观察干涉条纹的形状和分布,可以证明光具有波动性 。
光的波动理论。
20世纪初,爱因斯坦提出光的 量子理论,解释了光的干涉现象
的微观机制。
光的干涉理论在现代物理学中的应用
光的干涉理论在光学、 量子力学和凝聚态物 理学等领域有广泛应 用。
在量子力学中,光的 干涉被用于研究量子 纠缠和量子计算等前 沿领域。
在光学中,光的干涉 被用于制造高精度光 学仪器和检测技术。
光的干涉理论的前沿研究
01
目前,光的干涉理论的前沿研究主要集中在量子光 学和量子信息领域。
(完整版)光的干涉练习题及答案

(完整版)光的干涉练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一、选择题1、严格地讲,空气折射率大于1,因此在牛顿环实验中,若将玻璃夹层中的空气逐渐抽去而成为真空时,干涉环将:( )A.变大;B.缩小;C.不变;D.消失。
【答案】:A2、在迈克耳逊干涉仪的一条光路中,放入一折射率n ,厚度为h 的透明介质板,放入后,两光束的光程差改变量为:( )A.h n )1(2-;B.nh 2;C.nh ;D.h n )1(-。
【答案】:A3、用劈尖干涉检测工件(下板)的表面,当波长为λ的单色光垂直入射时,观察到干涉条纹如图。
图中每一条纹弯曲部分的顶点恰与左边相邻的直线部分的连线相切。
由图可见工件表面: ( )A.一凹陷的槽,深为λ/4;B.有一凹陷的槽,深为λ/2;C.有一凸起的埂,深为λ/4;D.有一凸起的埂,深为λ。
【答案】:B4、牛顿环实验装置是用一平凸透镜放在一平板玻璃上,接触点为C ,中间夹层是空气,用平行单色光从上向下照射,并从下向上观察,看到许多明暗相间的同心圆环,这些圆环的特点是:( )是明的,圆环是等距离的; 是明的,圆环是不等距离的;是暗的,圆环是等距离的; 是暗的,圆环是不等距离的。
【答案】:B5、若将牛顿环玻璃夹层中的空气换成水时,干涉环将: ( )A .变大;B .缩小;C .不变;D .消失。
【答案】:B6、若把牛顿环装置(都是用折射率为的玻璃制成的)由空气搬入折射率为的水中,则干涉条纹 ( )A .中心暗斑变成亮斑;B .变疏;C .变密;D .间距不变。
【答案】:C7、两个不同的光源发出的两个白光光束,在空间相遇是不会产生干涉图样的,这是由于( )A.白光是由许多不同波长的光组成;B.两个光束的光强不一样;C.两个光源是独立的不相干光源;D.两个不同光源所发出的光,频率不会恰好相等。
【答案】:C8、在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于O处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 光的干涉5-1 波长为的钠光照射在一双缝上,在距双缝200cm 的观察屏上测量20个条纹共宽3cm ,试计算双缝之间的距离。
解:由题意,条纹间距为:cm e 15.0203==∴双缝间距为:m e D d 391079.015.0103.589200--⨯≈⨯⨯==λ1.5mm ,观察屏离小孔的垂直距离为1m ,若所用光源发出波长1λ=650nm 和2λ=532nm 的两种光波,试求两光波分别形成的条纹间距以及两组条纹的第8级亮纹之间的距离。
解:对于1λ=650nm 的光波,条纹间距为:m d D e 339111043.0105.1106501---⨯≈⨯⨯⨯==λ 对于2λ=532nm 的光波,条纹间距为:m d D e 339221035.0105.1105321---⨯≈⨯⨯⨯==λ ∴两组条纹的第8级条纹之间的距离为: m e e x 3211064.0)(8-⨯=-=∆5-3 一个长40mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系,继后抽去气室中的空气,注入某种气体,发现条纹系移动了30个条纹。
已知照射光波波长为,空气折射率为,试求注入气体的折射率n g 。
解:气室充入空气和充气体前后,光程的变化为: D n g )000276.1(-=∆δ 而这一光程变化对应于30个波长: λδ30=∆ ∴λ30)1(=-D n g000768.1000276.110401028.6563039=+⨯⨯⨯=--g n5-4 在菲涅耳双面镜干涉实验中,光波长为600nm ,光源和观察屏到双面镜交线的距离分别为0.6m 和1.8m ,双面镜夹角为10-3rad ,求:(1)观察屏上的条纹间距;(2)屏上最多能看到多少亮条纹解:如图所示,S 1S 2的距离为:αsin 2l d =∴条纹间距为:αλλsin 2)(l q l d D e +== ∵α角很小 ∴mmm l q l e 2.1102.1106.0210600)8.16.0(2)(339=⨯=⨯⨯⨯⨯+=+≈---αλ 屏上能产生条纹的范围,如图阴影所示mmmq qtg y 6.3108.12223=⨯⨯=≈=-αα∴最多能看到的亮条纹数为:32.16.3===e y n5-5 在如图所示的洛埃镜实验中,光源S 1到观察屏的距离为2m ,光源到洛埃镜面的垂直距离为2.5mm 。
洛埃镜长40cm ,置于光源和屏的中央。
若光波波长为500nm ,条纹间距为多少在屏上可看见几条条纹解:在洛埃镜实验中,S 1和S 1在平面镜中的像S 2可看作是产生干涉的两个光源。
条纹间距为:mm d D e 2.01025.210500239=⨯⨯⨯⨯==--λ 由图可知,屏上发生干涉的区域在P 1P 2范围内mm mm mmmm OB O S BP tg BP P P 67.112005.2800101001≈⨯===θ mm mmmmmm OA O S AP tg AP P P 75.38005.21200102002=⨯===θ 由于经平面镜反射的光波有π的相位差,所以S 1和S 2可看作位相相反的相干光源。
若P 0点在干涉区内,它应该有一条暗条纹通过,并且P 1 P 0内包含的暗条纹数目:4.82.067.1011===e P P N P 2 P 0内包含的暗条纹数目为:8.182.075.3022===e P P N ∴P 1 P 2区域内可看见10个暗条纹,9个亮条纹P 01P 2E5-6 用λ=的绿光照射肥皂泡膜,若沿着与肥皂泡膜平面成30°角的方向观察,看到膜最亮。
假设此时干涉级次最低,并已知肥皂水的折射率为,求此时膜的厚度。
当垂直观察时,应改用多大波长的光照射才能看到膜最亮解:在观察膜最亮时,应满足干涉加强的条件:λλθm n n h =+-=∆2sin 212202 m =0,1,2,3,……按题意,m =1,︒=301θ∴肥皂膜厚度:m n n m h 7122021024.1sin 2)21(-⨯≈--=θλ若垂直观察时看到膜最亮,设m =1,应有:22λ=nh∴nm nh 6604≈=λ5-7 在如图所示的干涉装置中,若照明光波的波长λ=640nm平板厚度h =2mm ,折射率n (6.1>H n ),问(1是暗斑(2)由中心向外计算,第10个亮斑的半径是多少(3)第个亮环处的条纹间距是多少设望远镜物镜的焦距为25cm 。
解:(1(021==θθ)对应的光程差为: mm nh 4.626.122=⨯⨯==∆ 干涉级次为:10000106404.660=⨯=∆=-λm∴环中心是一亮斑。
(2)当中心是亮斑时,由中心向外计算,第10是:rad h nN 0716.0210640106.1610≈⨯⨯⨯==-λθ∴半径为:mm mm f r 9.172500716.01010=⨯==θ(3)第十个亮环处条纹的角间距为:rad mmmmh n 361010575.320716.02106406.12--⨯≈⨯⨯⨯⨯==∆θλθ∴间距为:mm f e 894.010575.32503≈⨯⨯=∆=-θS 照射平行平板G ,经反射后通过透镜L 在其焦平面E 上产生等倾干涉条纹,光源不直接照射透镜,光波长λ=600nm ,板厚d =2mm ,折射率n =,为了在给定系统下看到干涉环,照射在板上的谱线最大允许宽度是多少解:设干涉环中心的干涉级次为0m ,则:λλ0022m nd =+=∆ ∴21100002120+=+=λnd m将m 改写成:ε+=10m m ,则1m 是最靠近中心的亮条纹的干涉级次,100001=m为了能看到干涉环,最大允许谱线宽度λ∆应满足: λλλ)1()(11+=∆+m m ∴最大允许的谱线宽度为:nm m 06.01==∆λλ如图,G 1是待检物体,G 2是一标定长度的标准物,T是放在两物体上的透明玻璃板。
假设在波长λ=550nm 的单色光垂直照射下,玻璃板和物体之间的锲形空气层产生间距为1.8mm 的条纹,两物体之间的距离为80mm ,问两物体的长度之差为多少解:当垂直入射时,条纹间隔为:αλsin 2n e =∵在该题中是空气层的楔角,且α角很小∴αλ2≈e ∴rad e 3610153.08.12105502--⨯=⨯⨯==λα ∴两物体的长度之差为:mm mm R Rtg h 331024.1210153.080--⨯=⨯⨯=≈=∆αα5-10 如图所示的尖劈形薄膜,右端厚度d 为0.0417mm ,折射率n =,波长为μm 的光以30°角入射到表面上,求在这个面上产生的条纹数。
若以两块玻璃片形成的空气劈尖代替,产生多少条纹解:经劈尖上下两表面反射的光发生干涉,其光程差近似为: θ'=∆cos 2nh其中θ'是在上表面的折射角,h 表示平均厚度。
由折射定理:33.030sin sin =︒='nθ 计算得:943.0cos ='θ 在上表面产生的条纹数,即在劈尖最右端的暗纹或亮纹级数。
此时h =d =0.0417mm产生暗纹条件: λλθ)21(2cos 2+=+'m nd m =0,1,2,3,…… ∴20010589.0943.0100417.05.12cos 263=⨯⨯⨯⨯⨯='=--λθnd m劈尖棱线处是暗条纹,因此表面上有201条暗条纹,200条亮条纹 当用两块玻璃片形成的空气劈尖代替时,866.030cos cos =︒='θ 在劈尖最右端的暗纹级数为:6.12210589.0866.0100417.012cos 263=⨯⨯⨯⨯⨯='=--λθnd m因此表面上有123条暗条纹,122条亮条纹5-11 集成光学中的楔形薄膜耦合器如图所示。
楔形端从A 到B 厚度逐渐减小到零。
为测定薄膜的厚度,用波长λ=的He -Ne 激光垂直照明,观察到楔形端共出现11条暗纹,且A 处对应一条暗纹。
已知薄膜对激光的折射率为,求薄膜的厚度。
解:薄膜的折射率大于玻璃,因此入射光在楔形薄膜上表面反射有相位突变。
产生暗条纹满足条件: λλ)21(22+=+=∆m nh m =0,1,2,3,…… 在薄膜B 处,h =0,2λ=∆,所以B 处对应一暗纹。
∴第11条暗纹在薄膜A 处 ∴λλ)2111(22+=+nh ∴A 处薄膜的厚度为:mm n h 0014.021.22108.632102106≈⨯⨯⨯==-λ5-12 如图,在一块平面玻璃板上,放置一曲率半径R 很大的平凸镜,以观察牛顿环条纹。
(1)证明条纹间隔e 满足:NR e λ21=,式中N 是由中心向外计算的条纹数; (2)若分别测得相距k 个条纹的两个环的半径为N r 和k N r +,证明:λk r r R Nk N 22-=+证明:(1)透镜凸表面和玻璃板平面间的空气层中心O 的厚度为零,可知牛顿环中心为一暗斑。
设由中心向外计算,第N 个暗环的半径为N r ,则由图中几何关系可知:22222)(h Rh h R R r N -=--=∵h R >> ∴Rh r N 22=又∵N 个条纹对应的空气层厚度差为: 2λNh =∴λNR r N =2对上式微分,得:dN R dr r N λ=2当1=dN 时,e dr = ∴条纹间距为:NR r R e N λλ212==(2)由上面推得得结果: λNR r N =2 λR k N r k N )(2+=+ ∴λR N k N r r N k N )(22-+=-+∴ λk r r R Nk N 22-=+5-13 在观察牛顿环时,用1λ=580nm 的第五个亮环与用2λ的第七个亮环重合,求波长2λ为多少解:设由中心向外计算,第N 个亮环的半径为N r ,则:Rh r N 22=亮环满足的光程差条件为:λλN h =+22 ∴λ)21(-=N h ∴λR N r N )21(2-=由题意,用1λ=580nm 的第五个亮环与用2λ的第七个亮环重合∴21)217()215(λλR R -=-∴nm 54.40113912==λλ5-14 曲率半径为R 1的凸透镜和曲率半径为R 2的凹透镜相接触如图所示。
在钠黄光λ=垂直照射下,观察到两透镜之间的空气层形成10个暗环。
已知凸透镜的直径D =30mm ,曲率半径R 1=500mm ,试求凹透镜的曲率半径。
解:)11(4212R R D N -=λ∴)15001(103.58943010262R -⨯⨯=-∴mm R 63.5062≈5-15 假设照射迈克尔逊干涉仪的光源发出两种波长的单色光(设21λλ>)。
