飞行控制系统大作业
飞控大作业(蔡云鹏)
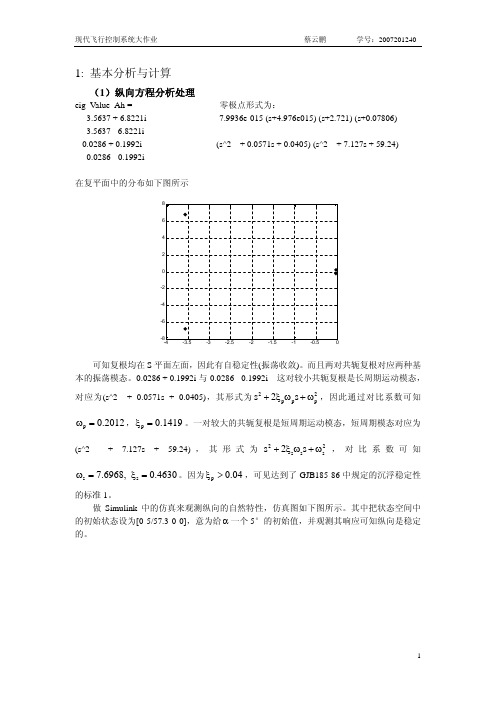
1: 基本分析与计算(1)纵向方程分析处理eig_Value_Ah = 零极点形式为: -3.5637 + 6.8221i -7.9936e-015 (s+4.976e015) (s+2.721) (s+0.07806) -3.5637 - 6.8221i ---------------------------------------------------------------------- -0.0286 + 0.1992i (s^2 + 0.0571s + 0.0405) (s^2 + 7.127s + 59.24) -0.0286 - 0.1992i在复平面中的分布如下图所示可知复根均在S 平面左面,因此有自稳定性(振荡收敛)。
而且两对共轭复根对应两种基本的振荡模态。
-0.0286 + 0.1992i 与-0.0286 - 0.1992i 这对较小共轭复根是长周期运动模态,对应为(s^2 + 0.0571s + 0.0405),其形式为22p p s 2s p +ξω+ω,因此通过对比系数可知,。
一对较大的共轭复根是短周期运动模态,短周期模态对应为p 0.2012ω=p 0.1419ξ=(s^2 + 7.127s + 59.24),其形式为2s s s s 2s 2+ξω+ω,对比系数可知。
因为s s 7.6968, 0.4630ω=ξ=p 0.04ξ>,可见达到了GJB185-86中规定的沉浮稳定性的标准1。
做Simulink 中的仿真来观测纵向的自然特性,仿真图如下图所示。
其中把状态空间中的初始状态设为[0 5/57.3 0 0],意为给α一个5°的初始值,并观测其响应可知纵向是稳定的。
上图中右图是空速V 的响应,左图是迎角α的响应。
可以看出其纵向自然特性是随着时间而自稳定的。
在讨论纵向操纵性时,给定升降舵偏角一个幅值为5=°e δ,宽度为1秒的一个脉冲,其中脉冲可用signal builder 来构造,Simulink 框图和各状态变量的响应的输出如下图所示:Vαqθ可见,,,V q αθ在升降舵受到脉冲干扰后,其均随时间而收敛,其中空速V 和仰俯角θ的变换范围较大,其稳定所需时间较长。
简单飞行器设计大作业

简单飞行器设计大作业
**一、设计目标**
本次设计的目标是设计一个简单的飞行器,能够在空中稳定飞行,并具备一定的操控性能。
**二、设计要求**
1. 飞行器能够安全起飞和降落。
2. 具备简单的航向控制能力。
3. 能够在空中稳定飞行一段时间。
**三、设计方案**
1. 飞行器整体采用轻量化材料制作,以减小重量,提高飞行效率。
2. 采用电动马达作为动力源,驱动螺旋桨产生升力。
3. 飞行器的控制系统采用遥控器进行控制,通过调整马达的转速实现飞行器的升降和航向控制。
**四、技术实现**
1. 选择合适的材料制作飞行器的机架和外壳。
2. 安装电动马达和螺旋桨,并进行动力系统的调试。
3. 设计并制作遥控器,实现对飞行器的远程控制。
4. 进行飞行测试,对飞行器的性能进行评估和优化。
**五、总结与展望**
通过本次简单飞行器设计大作业,我们初步掌握了飞行器设计的基本流程和方法。
在未来的工作中,可以进一步优化飞行器的设计,提高其性能和可靠性,为实际应用提供更好的解决方案。
以上示例仅供参考,你可以根据具体的设计要求和实际情况进行修改和完善。
飞行方案大作业(1)

[键入文档标题][键入作者姓名]2015300464第一部分飞行方案1、方案飞行2、弹道设计3、卫星摄动与机动第三部分卫星的摄动与机动第二部分弹道设计飞行方案大作业一、 问题描述在已知导弹质量、转动惯量、发动机推力等参数的情况下,导弹分为三个飞行方案,即三个阶段飞行。
阶段一:飞行距离在9100x m <,采用追踪法,其中方案高度与距离的关系、方案弹道倾角与高度的关系如下:***2000cos(0.000314 1.1)5000(-)+(-)z H x k H H k H H ϕϕδ=⨯⨯⨯+=⨯⨯ (1)阶段二:飞行距离在240009100m x m >>,采用追踪法,其中方案高度与距离的关系、方案弹道倾角与高度的关系、导弹因燃料消耗而质量改变参数如下:**3050(-)+z H mk H H k H ϕϕδ== (2)0.46/s m kg s = (3)阶段三:飞行方案24000&&0x m y >>,而最终目标位置为30000m x m = 采用比例导引法**00**sin sin tan ()(-)+()θθηηθθθδθθθθ=⨯--=-=-=-=-m T T Tm T mz dq r V V dty y q x x d dq k dt dtk q q k k (4) 要求:1) 计算纵向理想弹道,给出采用瞬时平衡假设0z z z z m m δααδ+=时所有纵向参数随时间的变化曲线。
2) 不考虑气动力下洗影响,计算飞行器沿理想弹道飞行时,你认为可以作为特性点的5个以上点处的纵向短周期扰动运动的动力系数,并分析其在特性点处的自由扰动的稳定性,以及计算在各个特性点处弹体传递函数(),(),()y n W s W s W s αδδϑδ 。
二、 建立模型基于“瞬时平衡”假设,导弹在铅垂平面内运动的质心运动方程组为:cos sin sin cos cos sin b b b b dV m P X mg dt d mV P Y mg dt dx V dt dy V dtαθθαθθθ⎧=--⎪⎪⎪=+-⎪⎪⎨⎪=⎪⎪⎪=⎪⎩ (5) 因为阶段一不考虑导弹质量随时间的变化,因此阶段一的模型需要联立公式(1)、公式(5); 其中攻角α可根据瞬时平衡假设从而可得到导弹攻角与弹道倾角之间的关系z =-z z zm m δαδα (6) 其中 X Y b x refb y ref C qS C qS == (7)其中假设公式(1)的**(-)+()θθδθθθθ=-z k k 中的=-9=-0.5,;θθk k又因为阶段二需要考虑导弹质量随时间的变化,因此阶段二的模型需要联立公式(2)公式(5)、公式(6)、公式(7)最后一阶段,因为利用了比例导引法公式(4)的k=2,可得导弹到达目标的相对微分方程为而导引率*θ=d dq k dt dt、其中k=2; 因为第三阶段的初始参数及终点坐标均为直角坐标系,由下图可知将代入到公式(4),得到直角坐标系下的微分方程组另外补充方程法向平衡方程:三、 算法实现编程使用MATLAB 软件,并运用欧拉方程解微分方程,即ode45函数;四、程序源代码*************************阶段一******************************function dy=jieduan1(t,y)dy=zeros(4,1);m=320;g=9.8;P=2000;q=0.5*1.2495*((288.15-0.0065*y(4))/288.15).^4.2558*y(1).^2;k=-9;dk=-0.5;Hi=2000*cos(0.000314*1.1*y(3))+5000;dHi=-2000*0.000314*1.1*sin(y(3));delta=k*(y(4)-Hi)+dk*(dy(3)-dHi);alpha=0.34*delta;Xb=(0.2+0.005*alpha^2)*q*0.45;Yb=(0.25*alpha+0.05*delta)*q*0.45;dy=zeros(4,1);dy(1)=P*cos(alpha)/m-Xb/m-g*sin(y(2));dy(2)=P*sin(alpha)/m/y(1)+Yb/m/y(1)-g*cos(y(2))/y(1);dy(3)=y(1)*cos(y(2));dy(4)=y(1)*sin(y(2));end******************************阶段二****************************** function dy=jieduan2(t,y)dy=zeros(4,1);m=320-0.46*t;g=9.8;P=2000;q=0.5*1.2495*((288.15-0.0065*y(4))/288.15).^4.2558*y(1).^2;k=-0.25;Hi=3050;delta=k*(y(4)-Hi);alpha=0.34*delta;Xb=(0.2+0.005*alpha^2)*q*0.45;Yb=(0.25*alpha+0.05*delta)*q*0.45;dy(1)=P*cos(alpha/180*pi)/m-Xb/m-g*sin(y(2)/180*pi);dy(2)=P*sin(alpha/180*pi)/m/y(1)+Yb/m/y(1)-g*cos(y(2)/180*pi)/y(1);dy(3)=y(1)*cos(y(2)/180*pi);dy(4)=y(1)*sin(y(2)/180*pi);end*******************************阶段三******************************** function dy=jieduan3(t,y)v=y(4);k=10;m=285.04-0.46*t;q0=-atan(3050/6000);g=9.8;q1=0.5*1.2495*((288.15-0.0065*y(2))/288.15).^4.2558*y(4).^2;k1=10;dk1=0.05;dy=zeros(4,1);r=sqrt(y(1)^2+y(2)^2);q=atan(y(2)/(y(1)-30000));elta=q-y(3);dr=-v*cos(elta);tht=q0+k*(q-q0);dq=v/r*sin(elta);dtht=k*dq;delta=k1*(y(3)-tht)+dk1*(dy(3)-dtht);alpha=0.34*delta;dy(1)=-dr*cos(q)+r*sin(q)*dq;dy(2)=-dr*sin(q)-r*cos(q)*dq;Yb=(0.25*alpha+0.05*delta)*q1*0.45;dy(3)=(2000*sin(alpha)/m+Yb/m-g*cos(y(3)))/v;y(4)=v;end***********************************main函数************************************ m(1)=287.2204; %导弹质量P=2000; %发动机推力g=9.8;k=5;det(1)=0.045;a(1)=0.6186;sit(1)=-0.000002024;V(1)=217.2867; %初始速度x(1)=24000; %初始位置H(1)=3071; %初始高度H1(1)=3050;S=0.45; %参考面积L=2.5; %参考长度k1=-0.14;k2=-0.06;sit1(1)=sit(1);p0=1.2495;T0=288.15;T(1)=T0-0.0065*H(1);p(1)=p0*(T(1)/T0)^4.25588;q(1)=1/2*p(1)*V(1)^2; %大气密度计算公式Cx(1)=0.2+0.005*a(1)^2;Cy(1)=0.25*a(1)+0.05*det(1)*180/pi; %升力系数Y(1)=Cy(1)*q(1)*S;X(1)=Cx(1)*q(1)*S;SIT(1)=(P*sind(a(1))+(Y(1)-m(1)*g*cos(sit(1))))/m(1)/V(1);Q(1)=atan(-H(1)/(30000-x(1)))+pi;r(1)=6708.2039;R(1)=-V(1)*cos(Q(1));n(1)=Q(1)+pi;SIT1(1)=k/r(1)*(V(1)*sin(n(1)));mza=-0.1; %俯仰力矩系数对攻角的偏导数mzdet=0.024; %俯仰力矩系数对舵偏角的偏导数t=0;i=0;dt=0.01;ms=0.46; %质量秒消耗量while H>0 & H1>0 %运用迭代法求解i=i+1;t=t+dt;det(i+1)=k1*(sit(i)-sit1(i))+k2*(SIT(i)-SIT1(i));a(i+1)=-mzdet/mza*det(i)*180/pi;Cy(i+1)=0.25*a(i)+0.05*det(i)*180/pi;Cx(i+1)=0.2+0.005*a(i)^2;Y(i+1)=Cy(i)*q(i)*S;X(i+1)=Cx(i)*q(i)*S;m(i+1)=m(i)-ms*dt;sit(i+1)=sit(i)+(P*sind(a(i))+(Y(i)-m(i)*g*cos(sit(i))))/m(i)/V(i)*dt;V(i+1)=V(i)+(P*cosd(a(i))-(X(i)+m(i)*g*sin(sit(i))))/m(i)*dt;x(i+1)=x(i)+V(i)*cos(sit(i))*dt;H(i+1)=H(i)+V(i)*sin(sit(i))*dt;Q(i+1)=atan(-H(i)/(30000-x(i)))+pi;sit1(i+1)=k*(Q(i)-Q(1));H1(i+1)=H(i)+V(i)*sin(sit1(i));SIT(i+1)=(sit(i+1)-sit(i))/dt;r(i+1)=(H(i)^2+(30000-x(i))^2)^(1/2);R(i+1)=(r(i+1)-r(i))/dt;n(i+1)=acos(-R(i)/V(i))+pi;SIT1(i+1)=k/r(i)*(V(i)*sin(n(i)));T(i+1)=T0-0.0065*H(i+1);p(i+1)=p0*(T(i+1)/T0)^4.25588;q(i+1)=1/2*p(i+1)*V(i+1)^2;endplot(x,H);hold on[t,y]=ode45('jieduan1',[0 39.0564],[250 0 0 7000]);plot(y(:,3),y(:,4));hold on[t,y]=ode45('jieduan2',[39.0564 115],[192.768 -0.009 9100 2998.71]);plot(y(:,3),y(:,4));其中每一段的初始值,均为上阶段的结束值所以每一阶段计算结束后,需要再给出所有数据的结果,找到每一段距离相对应的数据,即为初始值。
【VIP专享】北航飞机飞行操纵系统大作业

飞机飞行操纵系统实验报告教师:于黎明班级:130326姓名:xxx学号:130312xx一、飞机操纵系统传动机构的发展历史1、简单机械操纵系统驾驶员通过机械传动装置直接偏转舵面,舵面上的气动铰链力矩通过机械传动装置使驾驶员获得力和位移的感觉。
机械传动装置直接带动舵面,有软式和硬式两种基本型式。
软式传动装置由钢索和滑轮组成,特点是重量轻,容易绕过障碍,但是弹性变形和摩擦力较大。
硬式传动装置由传动拉杆和摇臂组成,优点是刚度大,操纵灵活。
软式和硬式可以混合使用。
2、可逆助力操纵系统在大型高速飞机上,舵面上的气动铰链力矩很大,虽然用气动补偿的方法可以减小力矩,但很难在高低速范围内达到同样效果。
40年代末出现了液压助力系统,舵面由液压助力器驱动,驾驶员通过中央操纵机构、机械传动装置控制助力器的伺服活门,间接地使舵面偏转。
它同时通过杠杆系统把舵面一部分气动载荷传给中央操纵机构,使驾驶员获得操纵力的感觉,构成所谓“机械反馈”,这就是可逆助力操纵系统。
3、不可逆助力操纵系统可逆助力操纵系统虽可解决杆力过大的问题,但在超音速飞机上还会出现杆力反向变化的问题。
由于杆力反向变化,会使驾驶员产生错觉而无法正确驾驶飞机。
为此,须把可逆助力操纵系统中的机械反馈取消,即舵面气动载荷全部由液压助力器承受。
为了使驾驶员获得操纵力感觉,在系统中增加了人工载荷机构(通常是弹簧的)以及其他改善操纵特性的装置,形成不可逆助力操纵系统。
在高空超音速飞行时,由于空气密度减小,飞机容易发生频率很高的俯仰和横侧振荡,驾驶员来不及作出反应。
为了克服振荡,在超音速飞机上普遍安装自动增稳装置,如俯仰阻尼器和方向阻尼器等。
4、电传操纵系统靠电信号传递飞行员的操纵指令,提高了响应速度性,并减轻了重量和体积。
消除了机械传动结构的非线性因素,改善了机械操纵直接固定在机体上面而引起的人机诱发振荡,改善了飞机的操纵品质,对飞机的结构变化的影响不敏感,可以降低和减少维护工作量以及更容易与自动飞行控制系统相结合。
飞控大作业

《飞行控制系统》课程实验报告班级 0314103学号 031410329 姓名嵇程成绩南京航空航天大学2017年4月《飞行控制系统》课程实验(8学时)一、目标通过本实验,学生能够掌握基本的飞行控制系统的结构,设计的方法,仿真验证方法及控制性能的分析,加深对课堂教学内容的理解。
二、环境在windows操作系统下,matlab/simulink下进行设计与仿真。
三、内容(一)飞机纵向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括短周期模态,长周期模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机俯仰角控制系统的设计;3、飞机速度控制系统的设计;4、飞机纵向运动的仿真与分析(二)飞机侧向飞行控制系统的设计与仿真(4学时)1、飞机纵向自然特性的分析与仿真,包括滚转模态,荷兰滚及螺旋模态的分析,求解阻尼与自然频率,分析开环响应特性。
2、飞机滚转角控制系统的设计;3、飞机航向控制系统的设计;4、飞机侧向航向协调控制仿真与分析四.要求1.在matlab下进行编程,系统设计与仿真;2.撰写实验报告,要求给出设计的参数,实验结果及曲线。
3.报告封面采用模板给定格式。
4.报告需提交打印稿,沿左侧装订。
(一)飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为:lon lon xA xB u =+& 其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T e T u δδ=∆∆ 问题:1、 分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
输入:[W n ,z,p]=damp(alon)%系统的自然频率、阻尼比和闭环极点输出:W n z p 2.7127 2.7127 0.0708 0.0708 0.0030 0.3890 0.3890 0.0875 0.0875 1.0000 -1.0553 + 2.4990i -1.0553 - 2.4990i -0.0062 + 0.0706i -0.0062 - 0.0706i -0.0030 + 0.0000i表1-1-1p 1p 2ζ W n 长周期 -0.0062 + 0.0706i -0.0062 - 0.0706i 0.0875 0.0708 短周期 -1.0553+2.4990i -1.0553 - 2.4990i0.3890 2.7127表1-1-22、 对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
飞机飞行控制系统
飞机飞行控制系统飞行控制系统(简称飞控系统)的作用是保证飞机的稳定性和操纵性,提高飞机飞行性能和完成任务的能力,增强飞行的安全性和减轻驾驶员的工作负担。
3.4.1. 飞行控制系统概述飞控系统分类飞控系统分为人工飞行控制系统和自动飞行控制系统两大类。
由驾驶员通过对驾驶杆和脚蹬的操纵实现控制任务的系统,称为人工飞行控制系统。
最简单的人工飞行控制系统就是机械操纵系统。
不依赖于驾驶员操纵驾驶杆和脚蹬指令而自动完成控制任务的飞控系统,称为自动飞行控制系统。
自动驾驶仪是最基本的自动飞行控制系统。
飞控系统构成飞控系统由控制与显示装置、传感器、飞控计算机、作动器、自测试装置、信息传输链及接口装置组成。
控制及显示装置是驾驶员输入飞行控制指令和获取飞控系统状态信息的设备,包括驾驶杆、脚蹬、油门杆、控制面板、专用指示灯盘和电子显示器(多功能显示器、平视显示器等)。
传感器为飞控系统提供飞机运动参数(航向角、姿态角、角速度、位置、速度、加速度等)、大气数据以及相关机载分系统(如起落架、机轮、液压源、电源、燃油系统等)状态的信息,用于控制、导引和模态转换。
飞控计算机是飞控系统的“大脑”,用来完成控制逻辑判断、控制和导引计算、系统管理并输出控制指令和系统状态显示信息。
作动器是飞控系统的执行机构,用来按飞控计算机指令驱动飞机的各种舵面、油门杆、喷管、机轮等,以产生控制飞机运动的力和力矩。
自测试装置用于飞行前、飞行中、飞行后和地面维护时对系统进行自动监测,以确定系统工作是否正常并判断出现故障的位置。
信息传输链用于系统各部件之间传输信息。
常用的传输链有电缆、光缆和数据总线。
接口装置用于飞控系统和其他机载系统之间的连接,不同的连接情况可以有多种不同的接口形式。
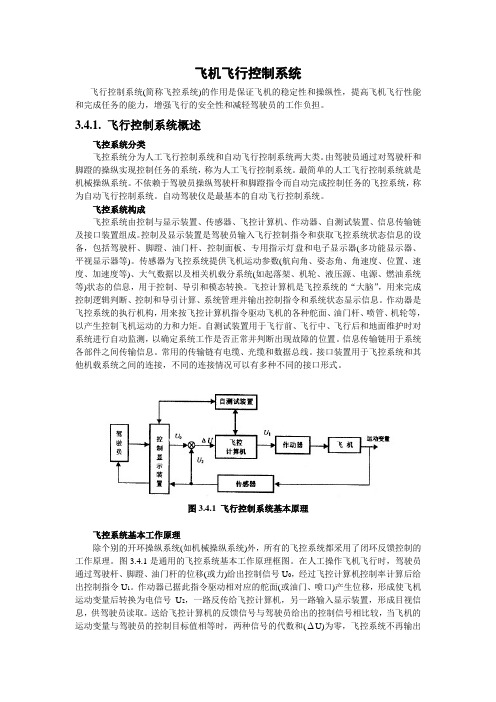
图3.4.1 飞行控制系统基本原理飞控系统基本工作原理除个别的开环操纵系统(如机械操纵系统)外,所有的飞控系统都采用了闭环反馈控制的工作原理。
图3.4.1是通用的飞控系统基本工作原理框图。
飞行动力学与控制大作业

飞行动力学与控制大作业报告院(系)航空科学与工程学院专业名称飞行器设计学号学生姓名目录一.飞机本体动态特性计算分析 (2)1.1飞机本体模型数据 (2)1.2模态分析 (2)1.3传递函数 (3)1.4升降舵阶跃输入响应 (3)1.5频率特性分析 (5)1.6短周期飞行品质分析 (6)二.改善飞行品质的控制器设计 (7)2.1SAS控制率设计 (7)2.1.1控制器参数选择 (8)2.1.2数值仿真验证 (12)2.2CAS控制率设计 (13)三.基于现代控制理论的飞行控制设计方法 (16)3.1特征结构配置问题描述 (16)3.1.1特征结构的可配置性 (16)3.1.2系统模型 (16)3.2系统的特征结构配置设计 (17)3.2.1设计过程 (17)3.2.2具体的设计数据 (17)3.2.3结果与分析 (18)四.附录 (20)一. 飞机本体动态特性计算分析1.1飞机本体模型数据本文选取F16飞机进行动态特性分析及控制器设计,飞机的纵向状态方程形式如下:.x =Ax +Bu y =Cx (1.1)状态变量为:[]Tu q αθ=x控制变量为:e δ=u基准状态选择为120,2000V m s H m ==的定直平飞。
选取状态向量()Tu q αθ=x ,控制量为升降舵偏角,则在此基准状态下线化全量方程所得到的矩阵数据如下:-0.0312 -1.1095 -9.8066 -0.5083-0.0013 -0.6543 0 0.9185 0 0 0 1.00000 -0.3828 0 -0.6901⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Α (1.2)[]-0.0167-0.0014-0.0956T=B(1.3)[]1.000057.295857.295857.2958diag =C(1.4)1.2模态分析矩阵A 的特征值算出为:1,23,4-0.6778 + 0.5926i-0.0100 + 0.0769iλλ==对应的特征向量如下:0.9874 0.9874 -1.0000 -1.0000 0.1137 - 0.0053i 0.1137 + 0.0053i 0.0011 - 0.0000i 0.0011 + 0.0000i 0.0521 - 0.0629i 0.0521 + 0.0629i 0.002=V 1 + 0.0078i 0.0021 - 0.0078i 0.0019 + 0.0735i 0.0019 - 0.0735i -0.0006 + 0.0001i -0.0006 - 0.0001i ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由系统特征值可知,系统具有两对共轭复根,也即具有两种运动模态:长周期模态与短周期模态,其对应的模态频率及阻尼比如下:表一 飞机长短周期模态特征可以看出,在此飞行状态下,飞机纵向具有明显的长周期模态,但不具备明显的短周期的模态特征,模态频率过低,需要使用纵向增稳系统,改善阻尼比和自然频率。
哈工大飞行器控制大作业

H/km V/m/s a1 a2 a3 a4 a5
1.067 546.9 1.488 104.7 66.54 1.296 0.129
4.526 609.2 0.132 91.97 54.93 1.126 0.106
8.21 701.5 0.7748 76.51 41.52 0.9 0.076
14.288 880.3 0.3528 46.44 21.59 0.514 0.036
加入这个惯性环节,相当于让系统的带宽降低,使高频段被及时的衰减,此时,系统的 时域响应和频域响应都有很大的好转。 最终,系统仿真的 Simiulink 框图如下图所示:
仿真时把������������������������ 、������������������������ 、������������������������ 都当做 1,������������1 、������������2 由公式求出后,设计控制器 C 和 I,以求系统可
������������ ������������5 ������������ 2 + ������������1 ������������5 ������������ + ������������2 ������������5 − ������������3 ������������4 ∙ ������������ ������������ 2 + (������������1 + ������������4 )������������ + ������������1 ������������4 + ������������2 公式中各个系数所对应的数据见下表:
此时,得到的系统时域及频域图像如下:
可以看出,在未加任何校正环节的情况下,系统的时域响应是发散的,很不稳定。由开 环 Bode 图可以看出,此时系统根本就没有穿越 0db 线,没有剪切频率,高频也没有衰减, 导致系统还没有进行工作就已经不稳定了。
航空工程中的飞行控制系统资料

航空工程中的飞行控制系统资料在航空工程领域中,飞行控制系统是起着至关重要作用的关键性组成部分。
它负责监控飞行器的状态,以及对其进行控制和调整,确保飞行器能够稳定、安全地进行飞行。
本文将介绍航空工程中飞行控制系统的一些基本资料。
一、飞行控制系统的概述飞行控制系统是航空器上的一套设备和软件系统,用于实时监控并控制飞行器的运动状态。
它包括飞行控制计算机、传感器、执行器和相关的软件等组件。
飞行控制系统利用传感器获取飞行器的姿态、速度、加速度等信息,并根据预设的飞行目标以及飞行员输入的指令,通过执行器控制飞行器进行转向、俯仰、升降等各种动作。
二、飞行控制系统的功能1. 姿态控制:飞行控制系统通过计算飞行器的当前姿态,并实时调整各个执行器以保持飞行器的平衡状态。
通过姿态控制,飞行器可以在各种环境和飞行条件下保持稳定飞行。
2. 导航控制:飞行控制系统使用导航传感器获取飞行器的位置和速度信息,以及目标航线等导航数据。
通过在空中导航控制系统的计算和调整,飞行器能够按照预定的航线进行飞行,并在需要时进行导航修正。
3. 自动驾驶:现代飞行器的飞行控制系统通常还具备自动驾驶功能。
自动驾驶功能能够实现自动起飞、巡航、降落等操作,减轻飞行员的负担。
同时,自动驾驶系统也能够避免人为因素导致的误操作,提高飞行安全性。
4. 应急控制:飞行控制系统还能够响应各种异常情况,例如遇到强风、气流干扰或系统故障等。
通过应急控制,飞行控制系统可以快速调整飞行器的姿态和航向,保持飞行器的稳定,并尽可能减轻对乘客和机组人员的影响。
三、飞行控制系统的重要性飞行控制系统是保证飞行安全的基本保障之一。
它的稳定性、精确性和可靠性对航空器的安全运行起到至关重要的作用。
过去的事故中,飞行控制系统的故障往往是导致事故发生的重要原因之一。
因此,在航空工程中,飞行控制系统的设计、测试和故障排除至关重要。
四、飞行控制系统的发展趋势随着科技的迅速发展,飞行控制系统也在不断地进步和演化。
自动飞行控制系统知到章节答案智慧树2023年中国民用航空飞行学院

自动飞行控制系统知到章节测试答案智慧树2023年最新中国民用航空飞行学院第一章测试1.人类历史上首次重于空气的航空器持续而且受控的动力飞行是有哪位实现的?参考答案:莱特兄弟2.自动飞行控制系统既可以控制飞机的姿态又可以控制飞机的轨迹。
参考答案:对3.自动飞行控制系统可以控制飞机的参考答案:偏航;推进力;俯仰;横滚4.FBW飞行控制系统已经成为了民用飞机操纵系统的发展方向参考答案:对5.自动飞行系统的主要作用是参考答案:实现飞机的自动飞行控制;改善飞机的性能6.自动飞行系统属于 ATA-()章的内容参考答案:227.自动驾驶仪可以在恶劣的气象条件下完成飞机的自动着陆。
参考答案:对8.飞行指引仪的功用是参考答案:指导驾驶员人工驾驶飞机;自动驾驶的时候,监控飞机的姿态9.偏航阻尼器的英语简写是参考答案:YD10.自动俯仰配平系统的英语简写是参考答案:APTS第二章测试1.系统具有稳定性需要同时具有哪两种力矩参考答案:稳定力矩;阻尼力矩2.对于不倒翁,()产生了稳定力矩参考答案:重力3.对于不倒翁,()产生了阻尼力矩参考答案:摩擦力;空气阻力4.倒立摆系统具有稳定性参考答案:错5.具有静稳定性的系统一定具有()参考答案:稳定力矩6.具有动稳定性的系统一定具有()参考答案:阻尼力矩7.阻尼力矩的作用是()扰动动能参考答案:消耗8.具有稳定性的飞机受到扰动后,必须飞行员手动操作才能回到平衡状态参考答案:错9.飞行器的稳定性包含()参考答案:方向稳定性;俯仰稳定性;横侧稳定性10.飞行器的俯仰稳定性主要影响飞行器的迎角参考答案:对第三章测试1.自动驾驶仪必须由俯仰、横滚和偏航三个通道,分别实现对升降舵、副翼和方向舵的自动控制。
参考答案:错2.在自动驾驶仪稳定飞机姿态的过程中,导致飞机姿态偏离原状态的原因是飞机受到了干扰。
参考答案:对3.无论如何想办法,比例式自动驾驶仪在常值干扰力矩作用下都会存在稳态误差。
参考答案:对4.只有使用速度反馈才能够实现积分式自动驾驶仪的控制律参考答案:错5.可以在姿态角偏差信号输入计算机之前,加一个积分信号,然后,再在反馈中使用速度反馈来实现积分式自动驾驶仪的控制律参考答案:错6.自动驾驶仪稳定回路的主要作用是:参考答案:稳定飞机的姿态7.关于自动驾驶仪同步回路的说法正确的是参考答案:在自动驾驶仪接通前始终处于工作状态8.在积分式自动驾驶仪中,舵回路用的主反馈信号是:参考答案:舵面速率反馈信号9.关于比例式自动驾驶仪稳态误差的大小,说法正确的是参考答案:与自动驾驶仪角度传递系数成反比10.在比例式自动驾驶仪稳定飞机姿态的过程中,当()时,舵面偏转到最大。
飞行控制系统大作业

飞行控制系统大作业一、 飞机纵向俯仰角与速度控制系统设计 某飞机的纵向线性小扰动方程为: lon lon x A x B u =+其中 状态[]T x u q h αθ=∆∆∆∆∆,控制量[]T eT u δδ=∆∆问题:1、 分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
2、 对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
3、 采用短周期简化方法,求出传递函数()e qG s δ∆∆。
采用根轨迹方法设计飞机的俯仰角控制系统,并进行仿真。
4、 基于长周期简化方法,求出传递函数()T uG s δ∆∆,设计飞机的速度控制系统,并进行仿真。
5、 基于纵向线性模型(状态方程),分别对速度控制与俯仰角控制进行仿真。
假设作动器特性为1010s +。
要求:给出相应的传递函数,画出相应的结构图根轨迹图及仿真曲线。
二、 飞机侧向滚转角控制系统设计 某飞机的侧向线性小扰动方程为: lat lat x A x B u =+其中 状态[]T x p rβφψ=∆∆∆∆∆,控制量[]T ar u δδ=∆∆问题:1、 求出侧向运动方程的特征根,及对应的模态,求出荷兰滚模态的阻尼及自然频率。
2、 对副翼与方向舵单位阶跃输入下的自然特性进行仿真。
3、 采用简化方法,求出传递函数()a pG s δ∆∆。
采用根轨迹方法设计飞机的滚转角控制系统,并进行仿真。
4、 设计飞机航向控制系统,并进行仿真。
5、设计飞机方向舵协调控制律,基于侧向线性模型(状态方程),进行航向控制系统的仿真。
假设作动器特性为1010s +。
要求:给出相应的传递函数,画出相应的结构图根轨迹图及仿真曲线,提交word 打印稿。
1. 数据文件在文件中,按照学号的最后一位选择相应的数据文件。
如学号最后一位为5,则选择文件作为你设计的数据。
2. 在matlab 中 输入load data5 则可将数据导入, 其中 alon 为纵向系统阵,blon 为纵向控制输入阵alat 为侧向系统阵,blat 为侧向控制输入阵控制量的单位为deg ,状态变量的单位为(deg ,deg/s , m ) 3、由状态方程求传递函数用ss2tf ()函数。
飞行控制系统大作业

飞行控制系统大作业《飞行控制系统》课程实验报告班级0314102学号*********姓名孙旭东成绩南京航空航天大学2017年4月(一)飞机纵向飞行控制系统的设计与仿真1、分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
在MATLAB环境下导入数据文件,输入damp(alon),得出结果:Eigenvalue Damping Freq.(rad/s)-2.29e+000+4.10e+000i 4.88e-001 4.69e+000-2.29e+000-4.10e+000i 4.88e-001 4.69e+000-3.16e-002 1.00e+000 3.16e-002-7.30e-003+3.35e-002i 2.13e-001 3.42e-002-7.30e-003-3.35e-002i 2.13e-001 3.42e-002长周期的根为-7.30e-003+3.35e-002i和-7.30e-003-3.35e-002i阻尼为 2.13e-001自然频率为 3.42e-002(rad/s)短周期的根为-2.29e+000+4.10e+000i和-2.29e+000-4.10e+000i阻尼为 4.88e-001自然频率为 4.69e+000(rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
sys=ss(alon,blon,clon,dlon)[y,t]=step(sys,500)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Delta\alpha(deg)'))g d (α ) / ( )g d (α 0 0 ) / ( /g d /g (q) ( ) )g d )g d ( (sm u∆400 0200 -2 e 0 ∆ -4-2000 200400 600-60 200400 600t(s)4004t(s)sm u ∆200 2 e ∆-2000 200400 600-20 200400 600t(s)subplot(221)plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\theta(deg)')54 t(s)s e q∆-52 s e 0 d ∆ -2-100 200400 600-40 200400 600t(s)t(s)e θ∆ 50-50-100e θ∆10050-150200400 600-500 200400 600t(s)t(s)m h m hsubplot(121)plot(t,y(:,5,1)) xlabel('t(s)') ylabel('\Deltah(m)') subplot(122)plot(t,y(:,5,2)) xlabel('t(s)') ylabel('\Deltah(m)')2.5 2 1.5x104x104-0.5-1)(1)(-1.50.5-0.50200-2-2.54006000200400600 t(s)t(s)以上各图为升降舵及油门单位阶跃输入下的飞机自然特性行仿真,左边一列为升降舵的阶跃输入,右边一列为油门的阶跃输入。
飞控大作业

现代飞行控制系统控制作业一、飞机的建模、配平与线性化1.1飞机的建模以现有的飞机六自由度模型为基础,使用S函数编写飞机气动力、发动机推力以及重力的力和力矩,空气密度 由Matlab中的 ISA Atomsphere Model,利用高度来计算。
模型主要有五大部分,一是空气密度模块,由simulink提供。
气动力、发动机推力和重力模块都是用s函数编写得到的。
使用edit sfuntmpl命令即可调用MATLAB自带的s函数的模板,修改其中部分就可以得到相应功能的s 函数模块。
此飞机模型包括六个输入(deltaF = 0):[deltaE deltaA deltaR deltaF n pz],12个状态: [V alpha beta p q r phi theta psi xe ye H]。
1.2 飞机的配平与线性化配平是通过调整各舵面默认角度来达到使飞机平稳飞机/保持某状态的目的。
飞机配平一个是俯仰配平,一个是副翼配平。
俯仰配平包括安定面配平、速度配平、马赫配平。
人工配平有人工电气配平、人工备用配平。
自动配平是衔接自动驾驶以后由FCC控制的配平,包括升降舵伺服系统来进行俯仰配平,有的机型叫自动驾驶配平。
在速度为50m/s,高度为3000m的初始条件下进行配平。
然后得到飞机的线性化矩阵,以及纵向和横侧向的矩阵。
线性化矩阵A B C D如下:CD横向矩阵A-lateralB-lateralC-lateralD-lateral纵向矩阵AhBhChDh二、 飞机特性分析2.1 特征根的求解由线性化方程可以很容易求出纵向和横侧向的特征根,如下:纵向-2.8775 + 2.5588i -2.8775 - 2.5588i -0.0164 + 0.2223i -0.0164 - 0.2223i特征根全部在负半平面,纵向是稳定的。
横侧向0.0000 + 0.0000i 0.0000 + 0.0000i -0.0267 + 0.8539i -0.0267 - 0.8539i横侧向有两个零根,所以横侧向是不稳定的。
飞行动力学与控制大作业

飞行动力学与控制大作业报告院(系)航空科学与工程学院专业名称飞行器设计学号学生姓名目录一.飞机本体动态特性计算分析 (2)飞机本体模型数据 (2)模态分析 (2)传递函数 (3)升降舵阶跃输入响应 (3)频率特性分析 (5)短周期飞行品质分析 (6)二.改善飞行品质的控制器设计 (7)SAS控制率设计 (7)控制器参数选择 (8)数值仿真验证 (12)CAS控制率设计 (13)三.基于现代控制理论的飞行控制设计方法 (17)特征结构配置问题描述 (17)特征结构的可配置性 (17)系统模型 (17)系统的特征结构配置设计 (18)设计过程 (18)具体的设计数据 (18)结果与分析 (19)四.附录 (22)一. 飞机本体动态特性计算分析1.1 飞机本体模型数据本文选取F16飞机进行动态特性分析及控制器设计,飞机的纵向状态方程形式如下:.x =Ax +Bu y =Cx(1.1)状态变量为:[]Tu q αθ=x控制变量为:e δ=u基准状态选择为120,2000V m s H m ==的定直平飞。
选取状态向量()Tu q αθ=x ,控制量为升降舵偏角,则在此基准状态下线化全量方程所得到的矩阵数据如下:-0.0312 -1.1095 -9.8066 -0.5083-0.0013 -0.6543 0 0.9185 0 0 0 1.00000 -0.3828 0 -0.6901⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦Α (1.2)[]-0.0167-0.0014-0.0956T=B(1.3)[]1.000057.295857.295857.2958diag =C(1.4)1.2 模态分析矩阵A 的特征值算出为:1,23,4-0.6778 + 0.5926i-0.0100 + 0.0769iλλ==对应的特征向量如下:0.9874 0.9874 -1.0000 -1.0000 0.1137 - 0.0053i 0.1137 + 0.0053i 0.0011 - 0.0000i 0.0011 + 0.0000i 0.0521 - 0.0629i 0.0521 + 0.0629i 0.002=V 1 + 0.0078i 0.0021 - 0.0078i 0.0019 + 0.0735i 0.0019 - 0.0735i -0.0006 + 0.0001i -0.0006 - 0.0001i ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦由系统特征值可知,系统具有两对共轭复根,也即具有两种运动模态:长周期模态与短周期模态,其对应的模态频率及阻尼比如下:表一 飞机长短周期模态特征可以看出,在此飞行状态下,飞机纵向具有明显的长周期模态,但不具备明显的短周期的模态特征,模态频率过低,需要使用纵向增稳系统,改善阻尼比和自然频率。
直升机显模型跟踪控制与仿真--直升机控制系统大作业

南京航空航天大学直升机控制系统大作业题目直升机显模型跟踪控制与仿真学生姓名Xx学号xxx学院xxx专业xxx指导教师xxx二〇一七年六月第一章 小型直升机的建模小型无人直升机要实现控制,首先要对小型直升机进行模型的建立,建立准确的模型能够简化直升机的设计的流程,缩短设计时间,大大提高设计的效率,而且对于仿真来说,是不需要成本的,这也大大减少了硬件调试时由于控制律的不合适导致的直升机的坠毁的情况。
基于准确的模型,设计出来的控制律,能够非常不错的用在实际的小型无人直升机上,大大缩短了调试时间。
1.1小型无人直升机建模方法简介小型直升机的模型表现为高阶非线性、非对称非定常等特点,而且很多参数很难通过仪器测量得到,而且与大型有人直升机相比,稳定性较差,抗干扰能力比较弱,因此建立小型直升机的模型非常困难,如今小型无人直升机的建模应用最广的方法主要为两种,分别为原理建模法和系统辨识法。
本文采用原理建模法。
原理建模法是将直升机分为主旋翼、机身、尾桨等部分,并对各部分进行动力学分析,从而获得各部分的动力学模型,然后建立位置,姿态,控制量之间的非线性方程组,获得比较精确地模型。
在某个平衡位置,要获得小型无人直升机的线性方程,可以对小型无人直升机的非线性模型进行线性化。
由于原理建模法是从小型无人直升机本身的动力学特性出发,因此适合直升机全包线飞行设计。
相对于系统辨识法来说,原理建模法比较复杂,建立的方程阶数比较高,而且很多参数获得比较困难,但是对于直升机建模来说,它有它自己独特的优势,仍然是无可替代的,比如随着时代的发展,人们对小型直升机的性能要求也越来越高,一些超机动的飞行动作,采用系统辨识法就很困难,因为一些超机动飞行操纵起来很困难,而且很危险,这时候就需要采用原理建模法。
1.2小型直升机模型的建立1.2.1坐标系在忽略弹性变形的情况下,小型直升机为六自由的刚体,选择合适的坐标系可以简化对直升机的研究,并且可以使对直升机的描述更简单准确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《飞行控制系统》课程实验报告班级 0314102学号 ********* 姓名孙旭东成绩南京航空航天大学2017年4月(一)飞机纵向飞行控制系统的设计与仿真1、分析飞机纵向动力学模态,求飞机的长周期与短周期阻尼与自然频率。
在MATLAB环境下导入数据文件,输入damp(alon),得出结果:Eigenvalue Damping Freq. (rad/s)-2.29e+000 + 4.10e+000i 4.88e-001 4.69e+000-2.29e+000 - 4.10e+000i 4.88e-001 4.69e+000-3.16e-002 1.00e+000 3.16e-002-7.30e-003 + 3.35e-002i 2.13e-001 3.42e-002-7.30e-003 - 3.35e-002i 2.13e-001 3.42e-002长周期的根为 -7.30e-003 + 3.35e-002i 和 -7.30e-003 - 3.35e-002i阻尼为 2.13e-001自然频率为 3.42e-002(rad/s)短周期的根为 -2.29e+000 + 4.10e+000i 和 -2.29e+000 - 4.10e+000i阻尼为 4.88e-001自然频率为 4.69e+000(rad/s)2、对升降舵及油门单位阶跃输入下的飞机自然特性进行仿真,画出相应的状态曲线。
sys=ss(alon,blon,clon,dlon)[y,t]=step(sys,500)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Delta\alpha(deg)')200400600-10-505t(s)∆q (d e g /s )200400600-4-2024t(s)∆q (d e g /s )200400600-150-100-50050t(s)∆θ(d e g )0200400600-50050100t(s)∆θ(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-6-4-2t(s)∆α(d e g )200400600-2000200400t(s)∆u (m /s )0200400600-2024t(s)∆α(d e g )subplot(221) plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltaq(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\theta(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\theta(deg)')subplot(121) plot(t,y(:,5,1)) xlabel('t(s)')ylabel('\Deltah(m)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)')ylabel('\Deltah(m)')2004006004t(s)∆h (m )200400600-2.5-2-1.5-1-0.54t(s)∆h (m )以上各图为升降舵及油门单位阶跃输入下的飞机自然特性行仿真,左边一列为升降舵的阶跃输入,右边一列为油门的阶跃输入。
3、采用短周期简化方法,求出传递函数()e qG s δ∆∆。
采用根轨迹方法设计飞机的俯仰角控制系统,并进行仿真。
输入命令:a1=alon((2:3),(2:3)) b1=blon((2:3),:)c1=clon((2:3),(2:3)) d1=dlon((2:3),:)[n,d]=ss2tf(a1,b1,c1,d1,1) g1=tf(n(2,:),d)得到传递函数()e qG s δ∆∆为 :-34.17 s - 82.55----------------------- s^2 + 4.579 s + 22.01根轨迹设计: 输入命令:g1=tf(n(2,:),d)g2=tf([-10],[1 10]) g3=series(g1,g2) sisotool(g3)1010101010Frequency (rad/sec)P h a s e (d e g)Open-Loop Bode E ditor for Open Loop 1 (OL1)M a g n i t u d e (d B )Root Locus E ditor for Open Loop 1 (OL1)1010101010Frequency (rad/sec)P h a s e (d e g )Open-Loop Bode E ditor for Open Loop 1 (OL1)M a g n i t u d e (d B )1010101010Frequency (rad/sec)Open-Loop Bode E ditor for Open Loop 1 (OL1)Root Locus E ditor for Open Loop 1 (OL1)Real AxisI m a g A x i s同样,可得Kth=1在Simulink 中搭建系统仿真模型:进行仿真:0.20.40.60.81t(s)∆θ(d e g )00.20.40.60.811.21.4∆ut(s)4、基于长周期简化方法,求出传递函数()T uG s δ∆∆,设计飞机的速度控制系统,并进行仿真。
输入命令:a1=alon([1,4],[1,4]) b1=blon([1,4],:) c1=clon([1,4],[1,4]) d1=dlon([1,4],:)[n,d]=ss2tf(a1,b1,c1,d1,2); g1=tf(n(1,:),d)得到传递函数为:7.971 s --------------- s^2 + 0.04847 s在Simulink 中搭建系统模型:使用经验试凑法得到PID 控制器参数:Kp=0.9 Ki=0.2 Kd=0仿真结果如下:5、基于纵向线性模型(状态方程),分别对速度控制与俯仰角控制进行仿真。
在Simulink中搭建仿真模型:先在速度通道加阶跃信号,输入命令:subplot(221)plot(t,x1)xlabel('t(s)')ylabel('\Deltau(m/s)')subplot(222)plot(t,x2)xlabel('t(s)')ylabel('\Delta\alpha(deg)')subplot(223)plot(t,x3)xlabel('t(s)')ylabel('\Deltaq(deg/s)')subplot(224)plot(t,x4)xlabel('t(s)')ylabel('\Delta\theta(deg)')和plot(t,x5)xlabel('t(s)')ylabel('\Deltah(m)')得到以下曲线:t(s)∆h (m)0510-0.015-0.01-0.0050t(s)∆u (m /s)0510-0.500.51t(s)∆α(d e g)-10123t(s)∆q (d e g /s)0.511.5t(s)∆θ(d e g)5100.511.5t(s)∆u (m /s)510-0.4-0.200.20.4t(s)∆α(d e g)510-4-2024t(s)∆q (d e g /s)510-0.200.20.40.6t(s)∆θ(d e g )再在俯仰角通道加阶跃信号,重复以上命令,得到如下曲线:0246810-30-20-10010t(s)h (m )(二)飞机侧向滚转角控制系统设计1、求出侧向运动方程的特征根,及对应的模态,求出荷兰滚模态的阻尼及自然频率。
在MATLAB环境下导入数据文件,输入damp(alon),得出结果:Eigenvalue Damping Freq. (rad/s)0.00e+000 -1.00e+000 0.00e+000-6.89e+000 1.00e+000 6.89e+000-1.55e-002 1.00e+000 1.55e-002-1.02e+000 + 5.08e+000i 1.97e-001 5.19e+000-1.02e+000 - 5.08e+000i 1.97e-001 5.19e+000侧向运动方程的特征根为:0.00e+000(航向随遇平衡模态)-1.55e-002(螺旋模态)-1.02e-001 +5.08e+000i,-1.02e-001 – 5.08e+000i(荷兰滚模态)-6.89e+000(侧向滚转收敛模态)荷兰滚模态的阻尼为:1.97e-001自然频率为:5.19e+000(rad/s)2、对副翼与方向舵单位阶跃输入下的自然特性进行仿真sys=ss(alat,blat,clat,dlat)[y,t]=step(sys,400)subplot(221)plot(t,y(:,1,1))xlabel('t(s)')ylabel('\Delta\beta(deg)')subplot(222)plot(t,y(:,1,2))xlabel('t(s)')ylabel('\Delta\beta(deg)')subplot(223)plot(t,y(:,2,1))xlabel('t(s)')ylabel('\Deltap(deg/s)')subplot(224)plot(t,y(:,2,2))xlabel('t(s)')ylabel('\Deltap(deg/s)')得到以下曲线:100200300400-3-2-101t(s)∆β(d e g )0100200300400-0.500.511.5t(s)∆β(d e g )100200300400-30-20-100t(s)∆p (d e g /s )0100200300400-15-10-5t(s)∆p (d e g /s )subplot(221) plot(t,y(:,3,1)) xlabel('t(s)')ylabel('\Deltar(deg/s)') subplot(222) plot(t,y(:,3,2)) xlabel('t(s)')ylabel('\Deltar(deg/s)') subplot(223) plot(t,y(:,4,1)) xlabel('t(s)')ylabel('\Delta\phi(deg)') subplot(224) plot(t,y(:,4,2)) xlabel('t(s)')ylabel('\Delta\phi(deg)')得到以下曲线:100200300400-2.5-2-1.5-1-0.504t(s)∆ψ(d e g )200400t(s)∆ψ(d e g )100200300400-80-60-40-200t(s)∆r (d e g /s )100200300400-40-2020t(s)∆r (d e g /s )100200300400-1500-1000-5000t(s)∆φ(d e g )0100200300400-800-600-400-2000t(s)∆φ(d e g )subplot(121) plot(t,y(:,5,1)) xlabel('t(s)')ylabel('\Delta\psi(deg)') subplot(122) plot(t,y(:,5,2)) xlabel('t(s)')ylabel('\Delta\psi(deg)'得到以下曲线:以上各图中左边为副翼输入单位阶跃响应的曲线,右边为方向舵输入单位阶跃响应的曲线。
