高一新生入学分班考试01(含答案)
2021年秋季高一新生入学分班考试物理试卷(一)(解析版)

F′=G=900N
货箱对地面的压强 故 D 正确。
p
=
F S
=
900N 20010−4 m2
=
4.5104 Pa
故选 D。
8.汽车行驶的过程中,经常会出现如下提示,下列 4 幅图片的情景说法正确的是( )
A.甲图是高速上的指示牌,上面的“95km”、“171km”等指的是位移
B.乙图是高速上的指示牌,上面的“120”“100”等指的是平均速度
11.如图所示是小丽正在吹气球时的情景,下列说法正确的是( )
A.气球越吹越大说明力可以改变物体的形状 B.气球被吹大后具有弹性势能 C.吹大的气球松手后会快速飞出是因为受到浮力的作用 D.气球飞行时向外喷出的气体对外做功,气体内能减小 【答案】ABD 【解析】 A.气球越吹越大,气球的形状发生变化,说明力可以改变物体的形状,故 A 正确; B.气球被吹大后,发生弹性形变,具有弹性势能,故 B 正确; C.吹大的气球松手后,气体将向后喷出,给气流一个向后的力,根据物体间力的作用是相互的可知, 气流会给气球一个向前的力,会快速飞出,故 C 错误; D.气球飞行时向外喷出的气体,气体对外做功,内能减小,温度降低,故 D 正确。 故选 ABD。 12.如图所示是一款行车记录仪,它左侧部分是平面镜,用于司机观察后方来车。右侧部分是一显示 屏,实时显示前方摄像头记录的路况信息。下列说法正确的是( )
v= s = 12m =0.6m/s t 20s
B.不计绳重和摩擦,动滑轮的重力
故 B 错误;
G 动=nF-G=3×500N-900N=600N
C.滑轮组的机械效率
= W有 = Gh = Gh = G = 900N =60% W总 Fs F 3h 3F 3500N
2024年重庆一中高一新生分班考生物模拟试卷(含答案)

2024年重庆一中高一新生分班考生物模拟试卷(含答案)考试说明本次考试为高一新生分班考试,旨在考察学生的生物基础知识掌握情况。
考试范围包括高中生物必修一的内容。
考试形式为选择题和填空题,满分100分,考试时间90分钟。
选择题第一部分:单项选择题(每题2分,共20分)1. 生物体的结构和功能的基本单位是____。
A. 细胞B. 组织C. 器官D. 系统2. 下列哪种生物属于真核生物?A. 细菌B. 蓝藻C. 酵母菌D. 原生动物3. 细胞膜的主要成分是____。
A. 蛋白质和脂肪B. 蛋白质和糖类C. 脂肪和糖类D. 蛋白质和核酸4. 光合作用的场所是____。
A. 细胞壁B. 叶绿体C. 线粒体D. 核糖体5. 下列哪种物质是构成染色体的主要成分?A. 蛋白质B. 核酸C. 脂肪D. 糖类6. 人体内分解有机物的过程叫做____。
A. 呼吸作用B. 光合作用C. 吸收作用D. 排泄作用7. 下列哪种生物可以通过有性生殖和无性生殖两种方式繁殖后代?A. 细菌B. 酵母菌C. 蓝藻D. 原生动物8. 植物根对矿质元素的吸收具有选择性,其选择性主要由植物根内的____决定。
A. 细胞壁B. 细胞膜C. 液泡D. 线粒体9. 下列哪种现象不属于物理吸附?A. 植物根对矿质元素的吸收B. 活性炭吸附色素和异味C. 蛋白质与金属离子的结合D. 免疫反应中的抗原-抗体结合10. 人体内糖类的代谢终产物是____。
A. 二氧化碳和水B. 尿素和氨C. 尿酸和尿素D. 乳酸和酒精第二部分:多项选择题(每题3分,共30分)11. 下列哪些属于细胞器?A. 核糖体B. 内质网C. 中心体D. 以上都是12. 光合作用的原料是____,产物是____。
A. 水、有机物B. 水、氧气C. 二氧化碳、有机物D. 二氧化碳、氧气13. 下列哪些生物可以通过有性生殖和无性生殖两种方式繁殖后代?A. 细菌B. 酵母菌C. 蓝藻D. 原生动物14. 植物吸收矿质元素的主要途径有____、____和____。
高一新生分班考试英语试题及答案

2018高一新生分班考试英语试题( 1)I.单项填空(共 20 小题;每题 1 分,满分 20 分)1.She is worried ______ her son’ s eyesight because he often plays online games.A. aboutB. forC. withD. of2.—Got any information about buying the Olympics Opening Ceremony tickets online?----Well, I was trying to, but found _____.A. someB.noneC. nothingD. no one3.When I can ’ t understand ______, I always raise my hand to ask.A. what the teacher saysB. how the teacher saysC. what does the teacher sayD. how does the teacher say4.—Who writes _______ in your class?—Kate does, of course.A. more carefullyB. the most carefulC. the most carefullyD. more careful5.—Two Yangtze Evening Paper, please!—Only one copy left. Would you like to have ______, sir?A. oneB. itC. this6.—Are you sure you have to? It’s been so late.D. them—I don’t know _______ I can do it if not now.7. Which do you enjoy ______ your coming weekend, going touring or staying at home?8.—What do you think the weather is like today?—It’ s still a little bit cold, though not so ______ as yesterday.A. coldB. colderC. coldest9. I ’m good at Chinese ______ my sister does very well in English.A. whileB. whenC. becauseD. as10. I was born ______ a warm spring afternoon of 1992. Now I am 16 years old.A. atB. inC. onD. much colderD. to11. Please come to me _______ you need my help.A. whereverB. whateverC. wheneverD.however12.—_____ will your father be back? I have something important to tell him.—Perhaps in two days, I think.A. How longB. How farC. How soonD. How much13. Mike _______ very hard.WhenI saw him at eleven last night,he was still studying in his room.A. has studiedB. studiesC. studiedD. will study14.—Could you please tell me the telephone number of Huian Guesthouse?— Wait a minute, please. I’ll _______ in the telephone book.A. look at itB. look for itC. look it upD. look it over15.— _____do the students in your school do outdoor activities every day?— At least an hour.A. How oftenB. How longC. How muchD. How far16.—Could I ride an electric bicycle to school, Mr. Wang?—No, you _____. Students under the age of 16 aren’t allowed to ride electric bicycles.A. couldn ’tB. needn’tC. can’tD. shouldn’t17.—I’m thirsty. I’d like a glass of orange j uice. What about you, Dad?— I prefer a cup of coffee ____nothing in it.A.withB. withoutC. forD. to18.—How do you like the sone Chenddu sung by Zhao Lei?— Oh, I have never enjoyed a ____one before.19. The newly-opened company _____the local people with more chances to work.20.The Reader has been a popular programme since last year, _____ there is still somethingnot satisfying.A. thoughB. untilC. ifD. unlessII.完形填空(共 15 小题;每题 2 分,满分 30 分)It was the last evening of the old year. In the cold and darkness there went 21 thestreet a poor littlegirl,with bare feet. She carried a small bundle of matches in her hand, and a lot 22 inher broken apron (围裙).No one had bought any all day long. Trembling with cold and hunger,the girl walked on and on. 23 poor little child!In a corner, she sat down, but she could not warm herself. She was 24 to go home,she had earned( 赚 ) not a coin, and perhaps her father would 25her, and her home was almost as cold asthe street. Herhands were nearly dead with cold. She struck one match against the wall, and held her hands26 the flame( 火焰 ). She wanted to warm her small hands. It was quite a magic light.She found herself27 before aLarge iron-stove. How warm it was! As the child wanted to warm her feet, the flame 28 ,and the stovedisappeared. The little girl sat cold and hungry, with the burnt match in her hand.A second match was lighted, she saw a table 29 delicious food. The roast goose stoodat one end, withknife and folk in her breast, jumped down from the dishes, and came to the poor child. Thematch was burnt outand only the thick, 30wall was beside her.She struck 31 match,this time, her gentle and loving grandmother came up, bright and happy as shehad never looked during her lifetime.“ Grandma ! ”32 the child,“ Oh, take me with you! I know that you will leave me33thematch goes out,” And she lighted all the matches hurriedly; she would like 34_____her old grandmotherdisappearing. Her kind, old and beautiful grandmother took the little girl in her arms, andthey both flew hightogether,until they were in that place where neither cold, nor hunger, nor 35 is ever known. The next morning, the little girl was found dead in the corner, with a smile on her face.21.A. away B. along C. off D. out22.A. many B. much C. most D. more23. A. What a B. What C. How a D. How24.A. happy B. willing C. afraid D. ready25.A. worry B. beat C. pay D. praise26.A. in B. across C. below D. over27.A, sit B. sitting C. sits D. sat28.A. died down B. put off C. broke away D. turned down29, A. made of B. next to C. full of D. close to30.A. hard B. warm C. deep D. soft31.A. another one B. other C. another D. the other32.A. asked B. talked C. nodded D. cried33.A. as soon as B. as if C. even though D. so that34.A. stopping B. to keep C. to stop D. keep35.A. hope B. pain C. feeling D. angerIII.阅读理解(共 20 小题;每题 2 分,满分 40 分)AThere are five exchange students in Zhao Hua’s class.Here is some information about them.Name Nationality Date of birth Hobby DreamMaria Canada Piano Basketball TeacherTim France Tennis Drawing PilotKatie America Reading Swimming En gineerPaul Germany Dancing Soccer ScientistJames Australia Drawing Volleyball Doctor36.When can Zhao Hua have a birthday party for Maria and James?A. In November.B. In September.C. In December.D. In October.37.Where does Paul come from?A. Australia.B. France.C. Canada.D. Germany.38.If Zhao Hua wants to l earn French, who can help her?A. Tim.B. Maria.C. James.D. Katie.39.What does Katie want to be?A. A teacher.B. A pilot.C. An engineer.D. A doctor.BA psychologist walked around a room while teaching stress management to audience. As sheraised a glass of water, everyone expected they ’d be asked the “half or half full ” question. Instead, with a smile on her face, she asked,“_______”Answers come out from 8 oz(盎司 ) to 20 oz.She replied,“The real weigh doesn’t matter. It depends on how long I hold it. If Ihold it for a minute, it’s not a problem. If I hold it for an hour, I’ll have an ache inmy arm. If I hold it for a day, my arm will feel numb(麻痹). In each case, the weigh of theglass doesn ’t change, but the longer I hold it, the heavier it becomes.”She continued,“ The stesses and worries in life are like the glass of water. Think about them for a while and nothing happens. Think about them a bit longer and they begin to hurt.And if you think about them all day long, you will feel numb—unable to do anything.”I t ’s important to remember to let go of your stresses.As early in the evening as you can, put all your burdens down. Don’t carry them through the evening and into the night. Remember to put the glass down!40. Which of the following can be put at the end of the first paragraph?A. How much is this glass of water?B. How heavy is this glass of water?C. How long can I hold this glass of water?D. How soon can I drink this glass ofwater?41. According to the passage, people often feel bad when having stresses because ______.A. they think about them for a whileB. they think about them for an hourC. they think about them too oftenD. they think about them too long42. The writer expressed his opinion through _______.A. taking an exampleB. giving a factC. having a discussionD. telling a story43. Which of the following can be the best title of the passage?A. Let go of your problemsB. Let’s think of our worries for a whileC. Let go of you stressesD. Lets’ put down our glasses of waterCDenny was famous photographer. Her travelled all over the world, taking pictures formagazines and newspapers, and won many prizes.“I ’ll do anything to get a good photo, ”he often said.“I’ll go anywhere at any time, even if it is dangerous.”And he told the truth. He had photos of earthquakes, forest fires, floods and evensomething ineresting happened, Denny went to photograph it.He was a married man and his wife often asked him take her with him, but he always refused.“I ’ll travel for my work, not for pleasure, ”he told her.“ You won’t have fun, and I won’t have time to look after you. Sometimes there ’s not even anywhere to stay, and I have to sleep outside. I often don’t have a good meal or a bath for days. You won’t like it.”“Denny, I am not a child,” his wife didn’t agree.“I can look after myself. Pleasetake me with you the next time you go overseas.”Denny didn ’t say anything, but he thought about it, and when he was asked to go to Africa,he said to his wife,“You can come to Africa with me if you want to. I have got to tak e photos of wild animals shoud be interesting and not too uncomfortable.”His wife was very excited, and at first she had a very enjoyable time. Then Denney wentto the forest to find some lions to photo. His wife went with him, but before long they became separated.She walked down one path while he walked down the other.Suddenly, Denny heard her crying. He ran back and saw her running towards him. A huge lionwas chasing her. Quickly Denny took his camera out of its case and pointed it at his wife andthe lion. Then he shouted,“Slow down, woman! I can’t get you both in the picture!”44.Denny had photos of all the following EXCEPT ______.A. natural disastersB.wild animalsC.travel magazinesD.interesting event45.The couple became separated in the African forest, probably because _____.A. one of them left to take a bathB. either of them had lost his/her wayC. they didn’t have a good meal for daysD. they had nowhere to stay for the night46.The underlined sentence in the last paragraph mainly tells us that ______.A. Denny was in fact playing a joke with his wifeB.Denny trained the wild lion to play with his wifeC.Denney loved wonderful pictures more than his wifeD.Denny was too busy taking photos to protect his wife47. According to the passage, a famous photographer’s live must be ______.A. safe, cheerful and colorfulB. pleasant, comfortable and meaningfulC. enjoyable,excting but regrettableD. interesting,successful but dangerousDImagine having a ear made out of an apple. It seems like a crazy idea from a horror But it could happen in the near future.Canadian biophysicist Andrew Pelling used an apple to grow a human ear. He think fruitand vegetables can be used to cheaply repair human body parts in the future.Scientists have been trying to grow organs( 器官 ) in labs to replace our old ones. But it is a hard job.For example, liver cells (肝细胞) can grow in a lab, but he cells still need things like blood vessels (血管) to actually things have to grow inside a scaffold( In the past, scientists have used man-made materials, animals parts and even dead peopleas scaffolds. But that has proved to be difficult and expensive.Pelling and his team, however, f ound the apple to be a cheap and easy-to-use scaffold. They first cut an apple into the shape of an ear. Then they used a special way to take outthe apple ’s cell and make it a scaffold. The team then added human cells to the apple, andwatched it grow.“You can implant these scaffolds into the body, and the body will send in cells and ablood supply and actually keep these thi ngs alive,” Pelling said during a Ted Talk speech.The team put the apple scaffold inside a living mouse and the mouse’s cells slowly took over the pieces of apple.Now Pelling is thinking of other fruit, plants or vegetables to use.He says that the shape of flower petals could be perfect for repairing skin. Andasparagus( 芦笋 ) could fix a broken spine(脊柱).Now, Pelling and his team are trying hard to put these crazy ideas into reality.48. Pelling’s idea of man-made ear seems crazy because he use _____as scaffolds.A. animal parts people materials apples49. The underlined word“implant” in Paragraph 7 probably means ______.A. pickB. putC. produceD. protect movie.支架 ).50.Which is the right order of making an ear out of an apple according to the passage?a. put the apple scaffold inside a mouseb.add human cells to the apple scaffoldc.cut an apple into the shape of an eard.make the apple ear a scaffolde.take out the apple’s cells in a special wayA. a-b-c-d-e51. From the last three paragraphs, we can infer that plants or vegetbales _____.A. to make human earsB. to repair burnt skinC. body parts Pellingto fixwill experimenta broken spinewithD.other fruit,to make humanEWe moved away from my grandmother when I was eight years old. I missed her a lot. I washer favorite granddaughter and she was my favorite grandma.Two years later my mother and father separated and soon divorced. I felt as if my worldwas falling apart. I lived with my mother for a time, next door to my grandma and grandpa inan apartment while my father was away during World WarⅡ .Grandma never had much in the way of money or material things. But it was the little things she gave me that let me feel warm, like letting me dip my fingers in the sugar bowl, lettingme sip the coffee from her cup or allowing me to sit on the table as I had meals.Though she didn ’t have much,she did something for my brother and me. I will alwaysremember she saved her coins in a glass jar. I thought my grandma could have used these coinsherself, but she saved them to give us when we came to visit her.I don’t remember how much we collected on our visits,nor was the amount( 数量 )important.It was the idea that she remembered us, and cared about us when we were away from her.52. What happened to the writer when she was eight years old?A. She moved away from her grandma.B. She moved away from her parents.C. She lived with her grandparents.D. She lived with her aunt.53. The writer’s grandma allowed her to do many things. Which of the following is not mentioned?A. The writer could dip her fingers in the sugar bowl.B. The writer was allowed to sip the coffee from her grandma’s cup.C. The writer could sit on the table while having meals.D. The writer was allowed to collect coins in a glass jar.54.For whom did the writer’s grandma save her coins?A. For her son.B. For her grandchildren.C. For the poor.D. For herself.55.What can we learn from the passage?A. The writer disliked her childhood.B. The writer complained about herparents.C. The writer missed her grandma so much.D. The writer wanted to have her grandma’s money.IV. 单词填空(共10小题;每题1分,满分10 分)56.The ______faces were a sight, covered with dust. (boy)57.You can enjoy water sports, or _______lie on the beach. (simple)58.Some complain that visitors are ______too much stress on the environment. (cause)59.People who often list things they are thankful for are happier and ______. (healthy)60.Never give up! Pain always comes with _________.(achieve)61.We can see different kinds of birds on this ______. (岛屿 )62.If you don ’t have a dream, you ’ve been old, even at _______. (二十)63.The temperature ______a lot last night. (降落 )64.Tom, look at the sign! We’re not ______to park our car here. (同意)65.When you think of Venice, does it bring any other ______ city to your mind? (欧洲的 ) V.书面表达 ( 共 1 小题;满分 20 分 )青少年是祖国的将来,也是城市的名片。
高一分班考试试题及答案

高一分班考试试题及答案一、选择题(每题3分,共30分)1. 下列哪项不是高一分班考试的目的?A. 评估学生的知识水平B. 确定学生的学科兴趣C. 选拔优秀学生参加竞赛D. 为学生提供个性化的学习建议答案:C2. 高一分班考试通常包括哪些科目?A. 语文、数学、英语B. 物理、化学、生物C. 历史、地理、政治D. 所有上述科目答案:D3. 高一分班考试的主要形式是什么?A. 口试B. 笔试C. 实验操作D. 面试答案:B4. 在高一分班考试中,学生应该如何准备?A. 只复习自己感兴趣的科目B. 忽略基础知识,专注于难题C. 平衡复习各科,注重基础知识D. 依赖临时抱佛脚答案:C5. 高一分班考试的结果将如何影响学生?A. 决定学生的班级分配B. 决定学生的座位安排C. 决定学生的课外活动D. 决定学生的升学机会答案:A6. 高一分班考试的评分标准通常是怎样的?A. 严格按照答案给分B. 根据学生的答题速度给分C. 根据学生的答题态度给分D. 根据学生的答题风格给分答案:A7. 高一分班考试通常在什么时候进行?A. 学年结束时B. 学年中期C. 新学年开始时D. 学期结束时答案:C8. 学生在高一分班考试中作弊的后果是什么?A. 被警告B. 被取消考试资格C. 被记过处分D. 所有上述后果答案:D9. 高一分班考试的试题难度通常如何设定?A. 非常难B. 适中C. 非常简单D. 随机变化答案:B10. 学生在高一分班考试中应该如何表现?A. 紧张焦虑B. 放松自信C. 随意答题D. 依赖他人答案:B二、填空题(每题2分,共20分)1. 高一分班考试的目的是_________、_________和_________。
答案:评估学生的知识水平、确定学生的学科兴趣、为学生提供个性化的学习建议2. 高一分班考试通常包括_________、_________和_________等科目。
答案:语文、数学、英语3. 高一分班考试的主要形式是_________。
高一新生分班考试化学试卷(含答案)(1)
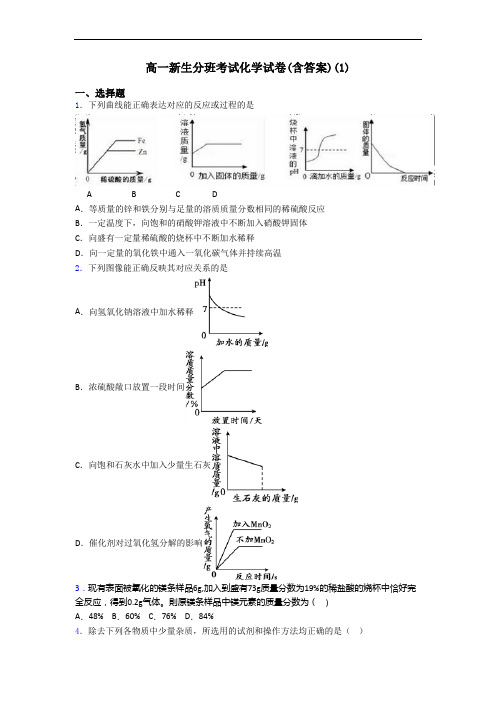
高一新生分班考试化学试卷(含答案)(1)一、选择题1.下列曲线能正确表达对应的反应或过程的是A B C DA.等质量的锌和铁分别与足量的溶质质量分数相同的稀硫酸反应B.一定温度下,向饱和的硝酸钾溶液中不断加入硝酸钾固体C.向盛有一定量稀硫酸的烧杯中不断加水稀释D.向一定量的氧化铁中通入一氧化碳气体并持续高温2.下列图像能正确反映其对应关系的是A.向氢氧化钠溶液中加水稀释B.浓硫酸敞口放置一段时间C.向饱和石灰水中加入少量生石灰D.催化剂对过氧化氢分解的影响3.现有表面被氧化的镁条样品6g,加入到盛有73g质量分数为19%的稀盐酸的烧杯中恰好完全反应,得到0.2g气体。
則原镁条样品中镁元素的质量分数为( )A.48% B.60% C.76% D.84%4.除去下列各物质中少量杂质,所选用的试剂和操作方法均正确的是()A.A B.B C.C D.D5.下列除杂(括号内为杂质)选用的试剂或方法正确的是 ( ) A.CuO(C):隔绝空气高温加热B.N a2SO4溶液(N a OH):加适量稀盐酸C.CO2(HCl):将气体通入足量的氢氧化钠溶液D.CaCl2溶液(HCl):加入过量碳酸钙,充分反应后过滤6.下列归纳和总结完全正确的一组是A.化学与生活B.化学与安全①用甲醛可保鲜海产品②用熟石灰改良酸性土壤③用生石灰作食品干燥剂①点燃氢气前一定要检验纯度②进行化学实验时配戴护目镜③发现厨房中天然气泄漏马上拨打119报警C.化学与资源D.化学与发现①塑料的使用一定程度上保护了金属资源②稀土是宝贵的不可再生资源③海洋中蕴藏着丰富的化学资源①卢瑟福确定了原子的核式结构②拉瓦锡第一个发现并提出了质量守恒定律③门捷列夫发现元素周期律并编制元素周期表A.A B.B C.C D.D7.等质量的镁、铝、锌分别与相同质量20%的盐酸充分反应,产生氢气的质量大小关系的猜测:①Al>Mg>Zn; ②Al=Mg=Zn; ③Al=Mg>Zn; ④Al=Zn>Mg; ⑤Al>Mg=Zn.其中错误的个数为A.5个 B.2个 C.3个 D.4个8.下列图象中,能正确反映其对应变化关系的是()A.服用胃舒平[主要成分是Al(OH)3]治疗胃酸过多,胃液pH的变化B.向一定质量的稀盐酸和氯化铜的混合溶液中加入氢氧化钠溶液C.将等质量的镁和铁分别投入到盛有足量同种稀硫酸的两个容器中D.浓盐酸敞口放置9.将一个不与盐酸反应的小球放入盛有盐酸的烧杯中,小球漂浮在液面上,将几枚洁净的小铁钉投入烧杯中,当不再有气泡逸出时(忽略溶液体积的变化),小球的位置与开始时比较,将()A.下沉一些 B.不变 C.上浮一些 D.无法判断10.向某AgNO3和Fe(NO3)2的混合溶液中加入一定质量的Zn粉,充分反应后过滤,得到滤渣和浅绿色溶液,关于该滤渣和滤液有下列四种说法,其中正确的说法有①向滤渣中加入稀盐酸,一定有气泡产生②滤渣中一定有Ag,可能含有Fe③向滤液中加入稀盐酸,一定有沉淀产生④滤液中一定含有Zn(NO3)2,可能含有Fe(NO3)2和AgNO3A.只有① B.只有② C.只有①②③ D.只有①③④11.除去下列各物质中的少量杂质所选用的试剂及操作方法均正确的是()项目物质杂质(少量)试剂操作方法A CaO固体CaCO3固体加入适量的稀盐酸过滤、洗涤、干燥B CO2CO通O2点燃C NaNO3Na2SO4适量氢氧化钡溶液过滤D KClO3MnO2水溶解、过滤、蒸发A.A B.B C.C D.D12.在相同的温度和压强下,相同体积的气体具有相同的分子数,反之亦然。
高一新生分班考试化学试卷(含答案)

高一新生分班考试化学试卷(含答案)第一部分:选择题 (共40分)
1. (2分) 以下哪个是元素周期表中的一行?
A. 周期
B. 基态
C. 分子
D. 能级
答案:A
2. (3分) 化学方程式H2 + O2 → H2O 表示什么化学变化?
A. 酸碱中和反应
B. 氧化反应
C. 还原反应
D. 合成反应
答案:D
3. (5分) 哪个元素的原子数量最多?
A. 半导体
B. 金属
C. 非金属
D. 停滞
答案:B
...
第二部分:填空题 (共30分)
1. (5分) 水的化学式是 H_2O,其中两个氢原子的总质量为\_\_\_\_ g。
答案:2
2. (5分) 原子核中的质子数等于 \_\_\_\_。
答案:核电荷数
...
第三部分:解答题 (共30分)
1. (15分) 简要解释离子化合物和共价化合物的区别。
答案:离子化合物是由阳离子和阴离子相互结合而成的化合物,离子间通过离子键结合。
共价化合物是由非金属原子通过共用电子
而结合的化合物,其化学键为共价键。
2. (15分) 简述酸和碱的性质及酸碱反应的特征。
答案:酸具有酸味、能腐蚀金属、能变红蓝石蕊试纸等性质。
碱具有苦味、有腻滑感、能中和酸等性质。
酸碱反应的特征是产生
氢气、生成盐和水等。
高一开学分班试题及答案

高一开学分班试题及答案一、语文(共100分)(一)选择题(每题3分,共30分)1. 下列词语中加点字的读音完全相同的一组是()A. 箴言缄默渐染缄口不言B. 蹊跷桎梏沏茶锲而不舍C. 蹒跚蹊径蹊跷蹊跷D. 砧板缜密砧木砧板答案:C2. 下列各句中,加点的成语使用恰当的一项是()A. 他虽然取得了一定的成绩,但离群众的要求还相去甚远,因此没有理由妄自菲薄,停滞不前。
B. 他性格内向,不善交际,因此朋友不多,但他和为数不多的几个朋友却能推心置腹,肝胆相照。
C. 他虽然有过失,但已表示愿意改正,我们不能求全责备他,更不能揪住不放。
D. 他为人正直,工作勤恳,但因过于严肃而被同事敬而远之。
答案:B(二)阅读理解(共40分)阅读下面的文言文,完成3-5题。
《桃花源记》晋太元中,武陵人捕鱼为业。
缘溪行,忘路之远近。
忽逢桃花林,夹岸数百步,中无杂树,芳草鲜美,落英缤纷。
渔人甚异之,复前行,欲穷其林。
林尽水源,便得一山,山有小口,仿佛若有光。
便舍船,从口入。
初极狭,才通人。
复行数十步,豁然开朗。
土地平旷,屋舍俨然,有良田美池桑竹之属。
阡陌交通,鸡犬相闻。
其中往来种作,男女衣着,悉如外人。
黄发垂髫,并怡然自乐。
3. 下列句子中加点词的解释不正确的一项是()A. 缘溪行:沿着溪水走B. 渔人甚异之:渔人对此感到非常奇怪C. 豁然开朗:形容心胸开阔D. 阡陌交通:田间小路交错相通答案:C4. 下列对文章理解不正确的一项是()A. 文章通过描绘桃花源的美景,表达了作者对美好生活的向往。
B. 文章中的桃花源是一个与世隔绝、自给自足的理想社会。
C. 文章通过渔人的视角,展现了桃花源的神秘和美丽。
D. 文章最后提到“后遂无问津者”,意味着桃花源是真实存在的。
答案:D5. 翻译下列句子。
“黄发垂髫,并怡然自乐。
”答案:老人和小孩都怡然自得,自得其乐。
(三)作文(共30分)请以“我眼中的高中生活”为题,写一篇不少于800字的作文。
2021年秋季高一新生入学分班考试英语试卷-01(新高考)(原卷卷)

2021年秋季高一新生入学分班考试01(新高考)英语试卷(满分150分,考试时间120分钟)适用于:重庆、湖北、辽宁、河北、福建、江苏、广东、湖南注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
第二部分阅读(共两节,满分50分)第一节(共15小题;每小题2.5分,满分37.5分)阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项。
AWant to make a difference to our planet? Bring your families and friends to our clubs in your free time These clubs are free and a lot of fun.Nature FirstCome and meet people of all ages who care about the environment at our beach project. We collectplastic to be recycled on the beach near you. Learn how waste in our oceans harms sea life and what you can do about it.Earths friendsWe get creative at Earth’s Friends! This youth club is for teens who want to take part in online projects such as making more people know about pollution in cities and how it is influencing the environment. Our website has a fantastic planner, so you can see how cycling reduces pollution in your local area.GeniusDon’t put your bottles, newspapers or cans in the recycling bin-bring them to any meeting on Monday morning, when our expert environmental artist shows you how to make art out of rubbish! Take part in planning the event to show off your creative projects to the public, and share tips on ways to reduce waste.Band TogetherYou won’t believe you’re in the middle of the city where our club meets every Sunday afternoon. Come and help clean up rubbish in our city parks! It’s not easy, but you’ll make lots of new friends. And it’s not all hard work-we have guest speakers and discussions about how to protect animals in the area. 21.Which one will you choose if you want to join a club that meets online?A.Nature First.B.Earth’s Friends.C.Genius.D.Band Together. 22.What is special about Genius?A.It provides beach project.B.It offers works of art for sale.C.It is for teens to set up online projects.D.It gives chances to make art out of rubbish.23.What can we infer from the passage?A.These clubs are only for fun.B.These clubs are open on weekends.C.These clubs all help the environment.D.These clubs always invite artists to give talks.BIn 1987, a small company named Huawei was started in Shenzhen. After more than 30 years of development, the company has now beaten Apple and become the world’s second - largest maker of smartphones behind Korea’s Samsung. It has also become the world’s largest supplier of 5G.But recently, Huawei faced some difficulties. The US government ordered a ban(禁止)on its sales in America. American officials said Huawei gave information that it collected to the Chinese government. At the same time, the US government planned to stop selling parts and services to Huawei, which was believed to hurt Huawei’s business.“We have never received such a request from the Chinese government and we have never tried to get into other systems to collect information,” Ren Zhengfei, Huangwei’s founder and president said. “The ban from the US would have little effect on our company. Huawei has enough ability to deal with the problems,” Ren added.In an interview several years ago, Ren Zhengfei said,“I started Huawei with only 20, 000 yuan, but now it has become a $100 billion company. The experience was not as romantic as you imagine.”Facing the ban of the US, Huawei is growing. Huawei’s smartphone sales around the world rose a lot compared to last year. At the same time, sales from both Samsung and Apple fell. So far, Huawei has grown into the world’s largest telecommumication equipment(电信设备)supplier, selling in 170 countries. It may beat Samsung as the largest smartphore maker in the near future.24.What is the corret order of the world’s largest smartphone maker according to the passage? A.Apple - Huawei - Samsung.B.Huawei - Apple - Samsung. C.Samsung - Apple - Huawei.D.Samsung - Huawei - Apple.25.What was the excuse of the US government to order a ban on Huawei?A.Huawei’s sales in America were growing faster than Apple.B.Huawei’s smartphones were not good enough to use.C.Huawei collected information for the Chinese government.D.Huawei refused to supply services to the US government.26.What does Ren Zhengfei mean by the underlined(划线的)sentence?A.Huawei’s development was a romantic story.B.Huawei went through hard times before its success.C.Success belonged to romantic people.D.People should work hard to achieve their goals.27.How does the writer support his prediction about Huawei’s bright future?a. By listing numbers.b. By telling stories.c. By comparing.d. By giving the definition(定义).A.a c B.a b C.a d D.b cCNature and culture are often seen as opposite ideas. What belongs to nature cannot be the result of human activities and on the other hand, cultural development is achieved against nature. However, this is not the only opinion on the relationship between nature and culture. Studies in the development of humans suggest that culture, whether taken as an effort against nature or a natural effort, is part of the development of the human species(物种).Several modern writers saw the process of education as a struggle(斗争) against human nature. We are born with wild natures, such as eating and behaving in a disorganized way or acting selfishly. Education uses culture as a way to get us out of our widest natures; it is thanks to culture that the human species could learn to adapt(适应) , progress and raise itself above and beyond other species.Over the past century and a half, however, studies in the history of human development have shown that the formation of culture is part of the biological adaptation. Consider, for example, hunting(打猎) . It seems to be an adaptation, which allowed humans to move into new and different areas, opening up the opportunity to change living habits. At the same time, the development of weapons(武器) is related to that adaptation-from rocks and stones to a set of hunting tools, and from hunting tools to rules relating to the proper use of weapons. Hunting also seems to be responsible for a whole set of bodily abilities, such as balancing on one foot. Just think of how this very simple thing is closely related to dance, a key expression of human culture. It is then clear that biological developmentand cultural development are closely tied.The transmission of culture seems to be directly related to what’s in our blood. Just as snails carry their shells, so do we bring along our culture. However, culture is also passed on among people of the same time or among people belonging to different populations. We can learn how to make jiaozi even if we were born from Russian parents in Paris just as we can learn how to speak English even if none of our family or friends speak that language.28.What is Paragraph 2 mainly about?A.Culture belongs to human nature.B.Nature teaches humans how to adapt.C.Humans are supposed to be well organized.D.Education pushes the human species to progress.29.Why does the writer talk about hunting in Paragraph 3?A.To suggest some possible ways of changing living habits.B.To stress the importance of tools in humans’ struggle for life.C.To show how culture develops as humans adapt to the environment.D.To explain why there is a need to call for the proper use of weapons.30.The word “transmission” in Paragraph 4 probably means “________”.A.system B.spread C.start D.spirit31.What is the writer’s opinion on the nature-culture relationship?A.Culture and nature are separate yet balanced.B.Culture depends much on nature to progress.C.Nature and culture are different but connected.D.Nature follows the unwritten rules set by culture.DIn 1987 a small company named Huawei was started in Shenzhen. After more than 30 years of development, the company has now beaten Apple and become the world’s second largest maker of smartphones. It has also become the world’s supplier (供应者) of 5G. In China and even in the world, Huawei is a wonder. Although it started producing mobile phones not many years ago, it has become one of the most famous phone companies.But recently, Huawei faces some difficulties. The US government made a law to stop its sales in America. American officials said Huawei gave information that it collected to the Chinese government. At the same time, the US government planned to stop selling parts and services to Huawei. They believed that Huawei’s business would be hurt this way.“We have never received such a request from the Chinese government and we have never tried to get into other systems to collect information,” Ren Zhengfei, Huawei’s president said. “The law wouldhave little effect on our company. Huawei has enough ability to deal with the problems,” Ren added.In an interview several years ago, Ren Zhengfei said, “I started Huawei with only £4000 at the beginning, but now it has become a 100 billion company. The experience was not as romantic as you imagine.”Facing the law of the US, Huawei is growing. Huawei’s smartphone sales around the world rose 50 percent compared with a year earlier in the first three months of 2019. At the same time, sales from both Samsung and Apple fell. So far Huawei has grown into the world’s largest telecommunication equipment supplier (供应商), selling in 170 countries. It may beat Samsung as the largest smartphone maker in the near future.32.How many kinds of smartphones are mentioned in total in this passage?A.One.B.Two.C.Three.D.Four.33.Which of the following sentences is TRUE according to the passage?A.Huawei collected the information for the Chinese government.B.Ren Zhengfei started Huawei with only £4000 in 1987.C.Huawei has beaten Samsung, a South-Korea phone maker so far.D.Huawei has developed its business smoothly.34.What does the underlined word “romantic” in Paragraph 4 mean in Chinese?A.浪漫的B.现实的C.成功的D.麻烦的35.The last paragraph mainly tells us ________.A.Huawei has become one of the most famous phone companies.B.Huawei has become the largest maker of smartphones in the world.C.Huawei has got into some systems of the US.D.Huawei is full of hope and must succeed in the future.第二节(共5小题;每小题2.5分,满分12.5分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
高一新生入学分班考试 含答案

2006
2005
2004
3
2
f(2)+ f(3)+ … + f(2004)+ f(2005)+ f(2006)=
.
三. 解答题(共 6 小题,共 80 分,解答应写出文字说明,证明过程或演算步骤)
16.(1)解不等式组:
2x 3
4
1
5
2
x
,并把解集在数轴上表示出来.
2 x 1 6 x
(2)先化简,再求值:已知 x
则 4 张贺年卡不同的拿法有__________种。
1
15. 对于正数 x,规定 f(x)= x ,例如 f(3)= 3 3 ,f( 1 )= 3 1 ,
1 x
13 4
3 1 1 4
3
2
计算 f( 1 )+ f( 1 )+ f( 1 )+ …f( 1 )+ f( 1 )+ f(1)+ f(1)+
1 2
)=0.
⑴ 求证:无论 k 取何值,这个方程总有实数根;⑵ 若等腰三角形 ABC 的一边长 a=4,另两边的长 b、c 恰
好是这个方程的两个根,求三角形 ABC 的周长.
解:(1)
7
(2k 1)2 16(k 1) 2
4k 2 12k 9
(2k 3)2
恒大于等于0
所以:无论 k 取何值,这个方程总有实数根。-------5 分
(2)三角形 ABC 为等腰三角形,可能有两种情况:
1)b 或 c 中至少有一个等于 a= 4,即:方程 x2-(2k+1)x+4(k-
1 2
)=0 有一根为 4,
可得 k= 5 ,方程为 x2-6x+8=0.另一根为 2,此时三角形 ABC 周长为 10;------9 分 2
高一新生分班考试物理试卷(含答案)(1)

高一新生分班考试物理试卷(含答案)(1)一、选择题1.利用下图探究电流通过导体产生的热量与哪些因素有关,下列说法正确的是()A.通电一段时间后,右边U形管两液面的高度差大B.U形管中两液面产生高度差是因为U形管中液体的热胀冷缩造成的C.容器外R3在本实验中主要起到分流的作用,在实验过程中也会发热D.通电一段时间后,左侧R1产生的热量等于R2、R3产生的热量之和2.如图甲所示是某校九年級的同学们在参加“青羊区中学生物理科技创新大赛”时设计的空气质量测仪的原理,电源电压恒为3V,R0为10 的定值电阻,R为可以感知空气污染指数的可变电阻,其阻值随污染指数交化的情况如图乙所示。
用电压表示数反映污染指数,污染指数在50以下为空气质量优,90-102之间为空气质量良,100~150为轻微污染,151~200为轻度污染,201~250为中度污染,251~300为轻度重污染,300以上为重度污染,下列分析正确的是()A.污染指数越小,电压表示数越大B.比赛当天电压表示数为1V时,属于轻微污染C.污染指数越大,电路中消耗的总功率越小 D.污染指数为50时,电压表的示数为2.5V 3.楼梯感应灯可由声控开关(有声响时开关闭合)和光控开关(光线较暗时开关闭合)共同控制,某同学设计并组装了一个楼梯感应灯电路,出现了以下异常情况:白天有声响时感应灯亮,无声响时感应灯不亮;晚上无论有无声响,感应灯都不亮.经检查各元件都能正常工作,则下列电路中可能出现以上异常情况的是()A. B. C.D.4.某大学两位研究生从蚂蚁身上得到启示,设计出如图所示的“都市蚂蚁”概念车.这款概念车小巧实用,有利于缓解城市交通拥堵.下列关于正在城市中心马路上行驶的此车说法正确的是()A.以路面为参照物,车是静止的B.以路旁的树木为参照物,车是静止的C.以路旁的房屋为参照物,车是运动的D.以车内的驾驶员为参照物,车是运动的5.如图所示A物体重力为20N,用滑轮组分别按甲、乙两种方法提升和水平移动物体A。
高一新生分班考试化学试卷(含答案)

高一新生分班考试化学试卷(含答案)注意:1.本卷共4页,满分60分,考试时间50分钟2.请将所有的答案填入答题纸的相应位置!可能用到的相对原子质量:H 1 C 12 O 16 Na 23 Mg 24 Si 28 S 32 Cl 35.5 K 39 Fe 56 Cu 64一、选择题(本题包括10小题,共25分。
1~5题每小题2分,共10分,每小题只有一个选项符合题意;6~10题每小题3分,共计15分,每小题有一个或两个选项符合题意,若正确答案只有一个选项,多选时,该题得0分,若正确答案有两个选项,只选一个且正确的得1分,选两个且都正确的得3分,但只要选错一个,该小题就得0分。
)请将选择题的答案填入下表中1.化学与新型材料、环境保护、能源开发等密切相关。
下列说法错误..的是A.聚乙烯、合成橡胶和玻璃都属于有机合成材料B.推广利用微生物发酵技术,将植物桔杆等制成沼气以替代液化石油气C.上海世博会很多展馆采用光电转化装置,体现当今“低碳”经济的理念D.利用二氧化碳等原料合成可降解塑料有利于减少白色污染2.M是一种活动性比铁强的金属,M2+与其他几种离子构成的化合物的溶解性见下表:根据以上信息判断下列各反应:①M+HCl;②M(NO3)2+BaCl2;③MO+HCl;④M(OH)2+NaCl;⑤M(OH)2+HCl;⑥M(NO3)2+HCl;⑦MCO3+HCl;⑧MSO4+BaCl2,不能发生的是A.①②④⑦B.⑤⑥⑦⑧C.②④⑥D.①③⑤⑧3.有Na、S、O、H四种元素中的二种或三种元素组成四种常见的化合物。
其中甲能跟盐酸反应生成盐和水;乙能跟氯化钡反应生成一种硫酸盐和另一种盐;丙能跟氢氧化钠反应生成盐和水;丁呈中性,且可以分别跟氧化钙或二氧化碳发生化合反应,生成相应的碱或酸。
下列推断:①甲一定是氢氧化钠;②乙一定是硫酸钠;③丙可能是硫酸;④丁一定是水。
其中正确的一组是A.①②③B.①②④C.①③④D.②③④4.下列除去杂质的方法正确的是A.除去N2中的少量O2:通过灼热的Cu网,收集气体B.除去CO2中的少量HCl:通入NaOH溶液,收集气体C . 除去氯化铵溶液中的氯化铁:向溶液中滴加适量氢氧化钠溶液,过滤D . 除去KCl 溶液中的少量MgCl 2:加入适量NaOH 溶液,过滤5.有一在空气中暴露过的KOH 样品,经分析测知其含水7.62%,含K 2CO 32.38%, KOH 90%,若将此样品加入10g20%的盐酸中,再用10.2%的KOH 溶液中和过量的酸,则蒸发中和后的溶液所得固体的质量约为 A .3.4g B .4.1g C .4.5g D .无法计算 6.下表中“一”表示相连的物质间能发生反应,“→”表示这种物质可转化为另一种物质。
高一新生分班考试生物试卷(含答案)

高一新生分班考试生物试卷(含答案)第一部分:单项选择题1. 下列哪个是生物研究的对象?A. 数学B. 语文C. 动物D. 物理答案:C2. 下列哪个是生物的基本单位?A. 细胞B. 分子C. 原子D. 组织答案:A3. 植物是通过什么进行光合作用的?A. 根B. 茎C. 叶D. 花答案:C4. 以下哪个是遗传物质?A. 蛋白质B. 脂肪C. 钙D. 糖答案:A5. 下列哪个是细胞内的电子库?A. 核糖体B. 线粒体C. 高尔基体D. 溶酶体答案:B第二部分:简答题1. 请简要解释细胞是什么?答案:细胞是生物体内最基本的结构和功能单位,具有自我复制和自我调控的能力。
2. 请简要说明光合作用的过程。
答案:光合作用是植物通过叶绿素吸收光能,利用二氧化碳和水合成光合产物(如葡萄糖)的过程。
3. 请简要介绍遗传物质的组成和功能。
答案:遗传物质主要由DNA和RNA组成,它们包含了生物遗传信息,并能够传递给下一代。
遗传物质的功能包括控制生物体的生长发育、遗传特征的传递和蛋白质合成等。
第三部分:实验题1. 设计一个简单的实验来观察植物的光合作用。
答案:材料:一株绿叶植物、水、光线;方法:将植物放在阳光下一段时间后,将其置于无光的环境中,同时检查植物的叶片颜色变化。
第四部分:操作题1. 根据下面的DNA序列,推导出RNA序列。
DNA序列:ATGCTGAAGCTT答案:AUGCUGAAGCUU2. 根据下面的RNA序列,推导出该序列对应的蛋白质序列。
RNA序列:UGACAUGGCAUC答案:Met-Asp-Gly-Ile以上为高一新生分班考试生物试卷的内容和答案。
注意:本试卷仅供参考,具体分数以实际考试结果为准。
请同学们在答题时仔细阅读题目,理解题意后再作答。
祝大家考试顺利!。
高一新生分班试题及答案

高一新生分班试题及答案一、选择题(每题2分,共20分)1. 下列哪项不是中国四大发明?A. 造纸术B. 指南针C. 火药D. 望远镜2. 地球的自转周期是多久?A. 24小时B. 12小时C. 36小时D. 48小时3. 以下哪种元素属于碱金属?A. 氢B. 氦C. 钠D. 钾4. 以下哪个国家是联合国常任理事国之一?A. 德国B. 日本C. 巴西D. 法国5. 以下哪个是光合作用的产物?A. 水B. 氧气C. 二氧化碳D. 氮气二、填空题(每题3分,共30分)6. 牛顿第一定律也被称为__________定律。
7. 人体最大的器官是__________。
8. 光年是__________单位。
9. 世界上最大的洋是__________洋。
10. 化学元素周期表中,原子序数为1的元素是__________。
三、简答题(每题10分,共40分)11. 请简述细胞的基本结构。
12. 描述一下牛顿第三定律。
13. 请解释什么是生态系统。
14. 简述电磁感应现象。
四、计算题(每题15分,共30分)15. 一辆汽车以60公里/小时的速度行驶,求它在2小时内行驶的总距离。
16. 一个物体从静止开始,以2米/秒²的加速度自由下落,求它在第3秒末的速度。
答案:一、选择题1. D2. A3. C4. D5. B二、填空题6. 惯性7. 皮肤8. 长度9. 太平洋10. 氢三、简答题11. 细胞的基本结构包括细胞膜、细胞质和细胞核。
12. 牛顿第三定律指出,对于两个相互作用的物体,它们之间的力是相互的,大小相等,方向相反。
13. 生态系统是指在一定区域内生物和非生物因素相互作用形成的一个整体。
14. 电磁感应现象是指当导体在磁场中运动时,会在导体中产生电动势的现象。
四、计算题15. 60公里/小时× 2小时 = 120公里16. 根据公式 v = u + at,其中v是最终速度,u是初始速度(0),a是加速度(2米/秒²),t是时间(3秒),所以v = 0 + 2 × 3 = 6米/秒。
高一分班考试题目及答案

高一分班考试题目及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的化学元素符号?A. 氢(H2)B. 氧(O2)C. 碳(C)D. 氮(N)答案:C2. 地球自转一周的时间是:A. 24小时B. 12小时C. 48小时D. 36小时答案:A3. 以下哪个不是中国四大发明之一?A. 造纸术B. 指南针C. 火药D. 印刷术答案:D4. 以下哪个选项是正确的数学公式?A. 圆的面积= πr²B. 圆的周长= 2πrC. 圆的面积= 2πrD. 圆的周长= πr²答案:A5. 以下哪种植物是单子叶植物?A. 玉米B. 玫瑰C. 竹子D. 松树答案:A6. 以下哪个选项是正确的英语语法?A. She is going to the park.B. She is going at the park.C. She is going in the park.D. She is going to park.答案:A7. 以下哪个选项是正确的物理公式?A. 功 = 力× 距离B. 功 = 力× 速度C. 功 = 力× 加速度D. 功 = 力× 时间答案:A8. 以下哪个选项是正确的历史事件?A. 秦始皇统一六国B. 秦始皇统一八国C. 秦始皇统一五国D. 秦始皇统一九州答案:A9. 以下哪个选项是正确的地理知识?A. 长江是中国最长的河流B. 黄河是中国最长的河流C. 珠江是中国最长的河流D. 黑龙江是中国最长的河流答案:A10. 以下哪个选项是正确的生物分类?A. 动物界、植物界、微生物界B. 动物界、植物界、真菌界C. 动物界、植物界、细菌界D. 动物界、植物界、病毒界答案:B二、填空题(每题4分,共20分)1. 光合作用是植物通过______和水,在光照条件下,产生______和氧气的过程。
答案:二氧化碳、葡萄糖2. 牛顿第二定律的公式是______。
高一分班试题及答案

高一分班试题及答案一、选择题(每题3分,共30分)1. 下列哪项不是高一分班的依据?A. 考试成绩B. 学生兴趣C. 教师推荐D. 家长意愿2. 高一分班通常在什么时候进行?A. 学期初B. 学期末C. 学期中D. 假期3. 学生在高一分班时,应该优先考虑的因素是什么?A. 班级人数B. 班级氛围C. 教师资质D. 班级位置4. 高一分班后,学生可以申请调换班级吗?A. 可以B. 不可以C. 只有特殊情况下可以D. 完全取决于学校政策5. 高一分班的目的是为了什么?A. 便于学校管理B. 促进学生个性化发展C. 提高教学质量D. 所有以上选项6. 高一分班时,学校通常会考虑哪些因素?A. 学生的学科成绩B. 学生的特长和兴趣C. 学生的社交能力D. 所有以上选项7. 在高一分班过程中,家长应该扮演什么角色?A. 决策者B. 咨询者C. 支持者D. 旁观者8. 高一分班后,学生通常需要多久适应新班级?A. 一周B. 一个月C. 一个学期D. 因人而异9. 高一分班对学生的学业成绩有何影响?A. 有积极影响B. 有消极影响C. 没有影响D. 取决于学生适应能力10. 高一分班时,学生应该如何准备?A. 复习考试B. 了解新班级情况C. 与新同学建立联系D. 所有以上选项二、填空题(每题2分,共20分)1. 高一分班通常基于学生的_________和_________。
2. 学生在高一分班时,应该关注班级的_________和_________。
3. 高一分班的目的是为了_________和_________。
4. 高一分班后,学生可以_________申请调换班级。
5. 高一分班时,学校通常会考虑学生的_________和_________。
6. 在高一分班过程中,家长应该扮演_________的角色。
7. 高一分班后,学生通常需要_________适应新班级。
8. 高一分班对学生的学业成绩有_________影响。
2021年秋季高一新生入学分班考试英语试卷 01(全国卷)(解析版)

2021年秋季高一新生入学分班考试01(全国卷)英语试卷(满分150分,考试时间120分钟)适用于:广西、贵州、四川、西藏、云南、山西安徽、甘肃、河南、黑龙江、吉林、江西、内蒙古、宁夏、青海、陕西、新疆注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £ 19. 15.B. £ 9. 18.C. £ 9. 15.答案是C。
1.How did the man get to Beijing?A.By plane.B.By train.C.By bus.【答案】B【原文】W: Did you have a nice trip to Beijing?M: Yes, it was very interesting on the train2.How long will the girl stay in Beijing?A.About a month.B.Three weeks.C.Half a year.【答案】A【原文】M: When are you leaving and how long are you going to stay in Beijing?W: I’m leaving this weekend and I’m going to stay there for four weeks.3.What does the boy’s hero do?A.A farmer.B.A sportsman.C.A doctor.【答案】C【原文】W: Who’s your hero?M: It’s Zhang Boli! He’s a great doctor. I think he is calm and brave in fighting against COVID-19! 4.What are the birds made of?A.Plastic.B.Wood.C.Paper.【答案】C【原文】W: Look at those birds. How cute they are!M: Yes. They are made of wasted paper. It’s so funny.5.When did the film begin?A.At 2:15.B.At 2:45.C.At 3:45.【答案】B【原文】M: Where did you go yesterday afternoon, Kate?W: I went to the cinema with my classmates. When we got there at three fifteen, the film had been on for half an hour.第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
高一分班考试试题及答案

高一分班考试试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是正确的?A. 地球是宇宙的中心B. 太阳是宇宙的中心C. 宇宙没有中心D. 地球是宇宙的边缘答案:C2. 以下哪个元素的化学符号是正确的?A. 铜 - CuB. 铁 - FeC. 氧 - O2D. 氢 - H2答案:A3. 以下哪个历史事件标志着中国近代史的开端?A. 鸦片战争B. 甲午战争C. 辛亥革命D. 五四运动答案:A4. 以下哪个选项是正确的?A. 光年是时间单位B. 光年是长度单位C. 光年是速度单位D. 光年是质量单位答案:B5. 以下哪个选项是正确的?A. 牛顿第一定律描述了物体在没有外力作用下的运动状态B. 牛顿第二定律描述了物体在没有外力作用下的运动状态C. 牛顿第三定律描述了物体在没有外力作用下的运动状态D. 牛顿定律不适用于微观粒子答案:A6. 以下哪个选项是正确的?A. 细胞是所有生物体的基本单位B. 病毒不是生物体C. 植物没有细胞结构D. 动物和植物的细胞结构相同答案:B7. 以下哪个选项是正确的?A. 光合作用是植物吸收二氧化碳和水,释放氧气和葡萄糖的过程B. 光合作用是植物吸收氧气和水,释放二氧化碳和葡萄糖的过程C. 光合作用是植物吸收氧气和二氧化碳,释放水和葡萄糖的过程D. 光合作用是植物吸收水和葡萄糖,释放二氧化碳和氧气的过程答案:A8. 以下哪个选项是正确的?A. 欧姆定律描述了电流、电压和电阻之间的关系B. 欧姆定律描述了电流、电压和电感之间的关系C. 欧姆定律描述了电流、电压和电容之间的关系D. 欧姆定律描述了电流、电阻和电感之间的关系答案:A9. 以下哪个选项是正确的?A. 相对论是描述宏观物体运动的物理理论B. 相对论是描述微观粒子运动的物理理论C. 相对论是描述天体运动的物理理论D. 相对论是描述电磁现象的物理理论答案:B10. 以下哪个选项是正确的?A. 遗传物质是蛋白质B. 遗传物质是核酸C. 遗传物质是糖类D. 遗传物质是脂质答案:B二、填空题(每题4分,共20分)11. 请填写下列化学反应方程式中缺失的反应物或生成物:2H2 + O2 → 2H2O答案:2H2 + O2 → 2H2O12. 请填写下列历史事件的时间:五四运动发生于______年。
高一新生分班试题及答案

高一新生分班试题及答案一、单项选择题(每题2分,共30分)1. 下列哪个选项是正确的?A. 地球是宇宙的中心B. 太阳是太阳系的中心C. 月球是地球的卫星D. 火星是太阳系的行星答案:B2. 以下哪个国家不是联合国安全理事会常任理事国?A. 中国B. 法国C. 印度D. 俄罗斯答案:C3. 以下哪个选项是正确的?A. 光年是时间单位B. 光年是长度单位C. 光年是质量单位D. 光年是速度单位答案:B4. 以下哪个选项是正确的?A. 牛顿第一定律描述了物体在没有外力作用下的运动状态B. 牛顿第二定律描述了物体在受到外力作用下的运动状态C. 牛顿第三定律描述了物体在受到外力作用下的运动状态D. 牛顿第四定律描述了物体在受到外力作用下的运动状态答案:A5. 以下哪个选项是正确的?A. 氧气是不可燃的B. 氢气是不可燃的C. 氮气是不可燃的D. 甲烷是可燃的答案:D6. 以下哪个选项是正确的?A. 酸雨是由于大气中的二氧化碳过多造成的B. 酸雨是由于大气中的二氧化硫过多造成的C. 酸雨是由于大气中的氮气过多造成的D. 酸雨是由于大气中的氧气过多造成的答案:B7. 以下哪个选项是正确的?A. 植物的光合作用需要阳光、水和二氧化碳B. 植物的光合作用需要阳光、水和氧气C. 植物的光合作用需要阳光、二氧化碳和氮气D. 植物的光合作用需要阳光、二氧化碳和氧气答案:A8. 以下哪个选项是正确的?A. 人类最早的文明起源于亚洲B. 人类最早的文明起源于非洲C. 人类最早的文明起源于欧洲D. 人类最早的文明起源于美洲答案:B9. 以下哪个选项是正确的?A. 牛顿是现代物理学的奠基人B. 爱因斯坦是现代物理学的奠基人C. 牛顿和爱因斯坦都是现代物理学的奠基人D. 牛顿和爱因斯坦都不是现代物理学的奠基人答案:C10. 以下哪个选项是正确的?A. 地球的自转周期是24小时B. 地球的公转周期是365天C. 地球的自转周期是365天D. 地球的公转周期是24小时答案:A11. 以下哪个选项是正确的?A. 细胞是所有生物体的基本单位B. 病毒不是生物体C. 细胞是所有生物体的基本单位,但病毒不是生物体D. 病毒是生物体,但细胞不是所有生物体的基本单位答案:C12. 以下哪个选项是正确的?A. 遗传信息存储在DNA中B. 遗传信息存储在RNA中C. 遗传信息存储在蛋白质中D. 遗传信息存储在脂肪中答案:A13. 以下哪个选项是正确的?A. 人类基因组计划的目标是确定人类基因组的全部DNA序列B. 人类基因组计划的目标是确定人类基因组的全部RNA序列C. 人类基因组计划的目标是确定人类基因组的全部蛋白质序列D. 人类基因组计划的目标是确定人类基因组的全部脂肪序列答案:A14. 以下哪个选项是正确的?A. 相对论是描述宏观物体运动的理论B. 相对论是描述微观物体运动的理论C. 相对论是描述宏观和微观物体运动的理论D. 相对论是描述宏观物体运动的理论,量子力学是描述微观物体运动的理论答案:D15. 以下哪个选项是正确的?A. 牛顿的三大定律只适用于宏观物体B. 牛顿的三大定律只适用于微观物体C. 牛顿的三大定律既适用于宏观物体,也适用于微观物体D. 牛顿的三大定律既适用于宏观物体,也适用于微观物体,但需要修正答案:A二、填空题(每题2分,共20分)16. 地球的自转方向是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) (2)
所以原不等式组的解集为: 1 x 4
-5
-4
-3
-2
-1
O
1
2
3
4
5
x
6
x x 1 1 (2)先化简,再求值:已知 x 2 1 ,求 2 2 的值. x x x 2x 1 x
B 图4
14.同室的 4 人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的 贺年卡, 则 4 张贺年卡不同的拿法有__________种。
1 x 3 3 1 1 ,f( )= 3 , 15. 对于正数 x,规定 f(x)= ,例如 f(3)= 1 4 1 x 1 3 4 3 1 3
A、2a B、2b
(
) C、2c D、0
6. 在物理实验课上,小明用弹簧称将铁块 A 悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出 水面一定高度,则下图能反映弹簧称的读数 y(单位 N)与铁块被提起的高度 x(单位 cm)之间的函 数关系的大致图象是 ( )
(N)
(N) (cm) (cm)
⑴ 求证:无论 k 取何值,这个方程总有实数根; ⑵ 若等腰三角形 ABC 的一边长 a=4,另两边的长 b、c 恰好是这个方程的两个根,求三角形 ABC 的周长.
19. (本小题满分 14 分) 在芦淞服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为 20 元/件(第 1 周价格) ,并且每周价格上涨,如图示,从第 6 周开始到第 11 周保持 30 元/件的价格平稳销售; 从第 12 周开始,当季节即将过去时,每周下跌,直到第 16 周周末,该服装不再销售。 ⑴求 销售价格 y (元/件)与周次 x 之间的函数关系式; ⑵若这种时装每件进价 Z(元/件)与周次 x 次之间的关系为 Z= 0.125x 8 12 (1≤ x ≤16) ,
17. (本小题满分 10 分) 如图,等腰三角形 ABC 中,AB=AC,以 AC 为直径作圆,交 AB 于 D,交 BC 于 E, (3) 求证:EC=ED (4) 已知:AB=5,BC=6,求 CD 长。 (1) 证明:
A
AC为直径, AE BC, AB=AC,
O
BAE=CAE
EC=ED
21. (本小题满分 14 分)若干个 1 与 2 排成一行:1,2,1,2,2,1,2,2,2,1,2,------ ,规则是: 第 1 个数是 1,第 2 个数是 2,第 3 个数是 1,一般地,先写一行 1,再在第 k 个 1 与第 k+1 个 1 之间插入 k 个 2(k=1,2,3,---).试问: (1)第 2006 个数是 1 还是 2? (2)前 2006 个数的和是多少?前 2006 个数的平方和是多少? (3)前 2006 个数两两乘积的和是多少?
点 C(0,b) ,O 为原点. (1)求 m 的取值范围; (2)若 m
1 且 OA+OB=3OC,求抛物线的解析式及 A、B、C 的坐标. 18
(3)在(2)的情形下,点 P、Q 分别从 A、O 两点同时出发以相同的速度沿 AB、OC 向 B、C 运动,联结 PQ 与 BC 交于 M,设 AP=k,问是否存在 k,使以 P、B、M 为顶点的三角形与⊿ABC 相似.若存在,求所有的 k 值,若不存在说明理由.
(2)解:由 AB=5,BC=6 得:BE=3,AE=4
D B E
C
AC为直径, CDA AEB 90,B B
BDC 6 CD 即: 5 4
2
BEA
BC CD AB AE 24 CD 5
1 )=0. 2
18. (本小题满分 12 分)已知关于x的方程 x -(2k+1)x+4(k-
1 x 3 3 1 1 15. 对于正数 x,规定 f(x)= ,例如 f(3)= ,f( )= 3 , 1 4 1 x 1 3 4 3 1 3 1 1 1 1 1 计算 f( )+ f( )+ f( )+ …f( )+ f( )+ f(1)+ f(1)+ 2006 2005 2004 3 2 f(2)+ f(3)+ … + f(2004)+ f(2005)+ f(2006)= 2006 .
x 1 中,自变量 x 的取值范围是 x2
.
12.在 Rt△ABC 中,∠ACB=90°, CD AB于D ,AC=10, CD=6,则 sinB 的值为_____。 13.如图 ,在⊙O 中,∠ACB=∠D=60°,OA=2,则 AC 的长为_________。 A
C
O .
A D B
D C
综上,三角形 ABC 周长为 10。 --------------------12 分 19. (本小题满分 14 分) 在芦淞服装批发市场,某种品牌的时装当季节将来临时,价格呈上升趋势,设这种时装开始时定价为 20 元/件(第 1 周价格) ,并且每周价格上涨,如图示,从第 6 周开始到第 11 周保持 30 元/件的价格平稳销售; 从第 12 周开始,当季节即将过去时,每周下跌,直到第 16 周周末,该服装不再销售。 ⑴求 销售价格 y (元/件)与周次 x 之间的函数关系式; ⑵若这种时装每件进价 Z(元/件)与周次 x 次之间的关系为 Z= 0.125x 8 12 (1≤ x ≤16) ,
17. (本小题满分 10 分) 如图,等腰三角形 ABC 中,AB=AC,以 AC 为直径作圆,交 AB 于 D,交 BC 于 E, (1) 求证:EC=ED (2) 已知:AB=5,BC=6,求 CD 长。
3
18. (本小题满分 12 分)已知关于x的方程 x -(2k+1)x+4(k-
2
1 )=0. 2
所以:无论 k 取何值,这个方程总有实数根。-------5 分 (2)三角形 ABC 为等腰三角形,可能有两种情况: 1)b 或 c 中至少有一个等于 a= 4,即:方程 x -(2k+1)x+4(k可得 k=
2
1 )=0 有一根为 4, 2
5 2 ,方程为 x -6x+8=0.另一根为 2,此时三角形 ABC 周长为 10;------9 分 2 1 2)b=c 时, (2k 1) 2 16(k ) 0 2 3 2 得 k= ,方程为 x - 4x+4=0.得 b=c=2, 此时 ABC 不能构成三角形; 2
高一新生入学分班考试 01
一. 选择题(本大题共 10 小题,每小题 5 分,共 50 分。在每小题给出的四个选项中,只有一项是符合题 目要求的。 ) 1.下列运算正确的是( ) 。 2 3 6 8 A、a ·a =a B、a ÷a4=a2
C、a3+a3=2a6
D、(a3)2=a6 ( )
2.一元二次方程 2x2-7x+k=0 的一个根是 x1=2,则另一个根和 k 的值是 A.x2=1 ,k=4 B.x2= - 1, k= -4 C .x2=
三. 解答题(共 6 小题,共 80 分,解答应写出文字说明,证明过程或演算步骤)
5 x 2x 4 1 16. (本题满分 16 分) (1)解不等式组: 3 2 ,并把解集在数轴上表示出来. 2 x 1 6 x 5 x 2x 4 1 解: 3 2 2 x 1 6 x
50
β B D C
D.不能确定
10.如图为由一些边长为 1cm 正方体堆积在桌面形成的立方体的三视图,则该立方体露在外
面部分的表面积是________ cm2。
正视图 A. 11 B.15
左视图 C.18
俯视图 D.22
二. 填空题(本大题共 5 小题,每小题 4 分,共 20 分)
11.函数 y
(N)
(N)
A
第 6 题图
(cm)
A
B
C
D
(cm)
7. 下列图中阴影部分的面积与算式 |
3 1 | ( ) 2 2 1 的结果相同的是 4 2
(
)
y (1,1) 0 x
y y=2x 0 1 B x
y y=x2-1
y
y
3 x
3x 0 x 0 x
8.已知四边形 S1 的两条对角线相等,但不垂直,顺次连结 S1 各边中点得四边形 S 2 ,顺次连结 S 2 各边中
2
计算 f(
1 1 1 1 1 )+ f( )+ f( )+ …f( )+ f( )+ f(1)+ f(1)+ 2006 2005 2004 3 2
.
f(2)+ f(3)+ … + f(2004)+ f(2005)+ f(2006)=
三. 解答题(共 6 小题,共 80 分,解答应写出文字说明,证明过程或演算步骤)
⑴ 求证:无论 k 取何值,这个方程总有实数根;⑵ 若等腰三角形 ABC 的一边长 a=4,另两边的长 b、c 恰 好是这个方程的两个根,求三角形 ABC 的周长. 解: (1)
7
1 (2k 1) 2 16( k ) 2 2 4k 12k 9 (2k 3) 2 恒大于等于0
3 ,k=6 2
D.x2=
3 ,k=-6 2
3.如果关于 x 的一元二次方程 x 2 kx 2 0 中,k 是投掷骰子所得的数字(1,2,3,4,5,6) ,则该 二次方程有两个不等实数根的概率 P= ( A. ) C.
2 3
B.
1 2
1 3
)
D.
