逻辑推理分类
推理必备常识

推理必备常识
1.推理的定义:推理是一种基于已知事实或信息,通过逻辑推断得出未知事实或信息的过程。
2. 推理的分类:归纳推理和演绎推理。
归纳推理是从具体到一般,通过观察事实得出规律性结论;演绎推理是从一般到具体,通过已知前提得出结论。
3. 推理中的逻辑学:推理过程需要遵循一定的逻辑规则,如排中律、矛盾律、排中律等,以保证推理的正确性。
4. 推理中的误区:推理过程中可能出现的误区包括谬误、非凡人假设、逻辑圈套等,需要注意避免。
5. 推理在生活中的应用:推理在生活中有广泛的应用,如破解谜题、分析证据、判断事实真伪等。
掌握推理常识可以提高分析问题的能力和解决问题的效率。
- 1 -。
高中政治必修二逻辑推导整理

高中政治必修二逻辑推导整理全文共四篇示例,供读者参考第一篇示例:高中政治必修二逻辑推导整理逻辑推导是一种推理方法,通过推演和论证,从假设或前提出发,得出结论或推论。
在政治学科中,逻辑推导常常被用来分析政治问题、推导政治观点和论证政治理论。
以下是高中政治必修二中常见的逻辑推导方法和技巧:1. 归纳推理:归纳推理是从特殊到一般的推理过程,即从具体事实或事例中总结出一般规律或结论。
在学习政治理论和实践时,可以通过归纳推理总结出相关政治观点和结论,帮助学生更好地理解和记忆知识点。
3. 比较推理:比较推理是通过对比和比较不同政治观点、政治理论或政治实践,找出它们的异同之处,并得出结论。
在学习政治学科时,比较推理可以帮助学生更全面地理解不同政治观点和理论,从而更好地进行分析和评价。
4. 推理论证:推理论证是通过逻辑推导、论证和证据,为自己的观点或立场提供有力的支持。
在学习政治学科时,学生可以运用推理论证方法分析政治问题、论证政治观点,提高自己的批判性思维能力。
5. 概念分类:概念分类是将不同的概念或观点按照一定的标准进行分类和归类,以便更好地理清思路和分析问题。
在学习政治学科时,学生可以运用概念分类方法整理和归纳政治知识,帮助自己更好地理解和记忆。
逻辑推导在高中政治必修二中扮演着重要的角色,可以帮助学生更好地理解政治理论和实践,培养学生的批判性思维能力。
通过掌握常见的逻辑推导方法和技巧,学生可以更好地运用逻辑推理,提高学习效率和学习成绩。
希望本文对学生在高中政治必修二中的学习有所帮助,让他们更好地掌握逻辑推导的重要性和方法。
【这篇文章在逻辑推导方面没有很具体的内容,可能需要进行补充】。
第二篇示例:高中政治必修二课程中,逻辑推导是一个非常重要的知识点,它帮助我们理清思路,分析问题,做出合理的判断。
逻辑推导的基本原理是根据已知的前提推出一个结论,通过推理关系来推断出未知的东西,是一种思维方法和技能,也是一种学科。
逻辑学划分举例

逻辑学划分举例以逻辑学划分为题,下面列举了10个不同的逻辑学划分的例子:1. 形式逻辑与实质逻辑形式逻辑研究逻辑推理的规则和形式,如命题逻辑和谓词逻辑;而实质逻辑研究具体领域中的逻辑问题,如科学推理、法律推理等。
2. 形式逻辑与非形式逻辑形式逻辑关注逻辑推理的形式和结构,不考虑具体内容;而非形式逻辑关注逻辑推理的内容和语义,考虑逻辑推理的实际应用。
3. 归纳逻辑与演绎逻辑归纳逻辑研究从具体事实中归纳出一般规律的推理过程,如从具体案例推断出普遍规律;而演绎逻辑研究从普遍规律推断出具体结论的推理过程。
4. 经典逻辑与非经典逻辑经典逻辑是传统的逻辑学,基于二值逻辑,即命题只有真和假两种取值;而非经典逻辑包括模糊逻辑、多值逻辑等,允许命题具有多种取值。
5. 符号逻辑与自然语言逻辑符号逻辑使用符号代表逻辑关系,以形式化的方式表达逻辑推理;而自然语言逻辑使用自然语言进行逻辑推理,如通过语义分析理解文章中的逻辑结构。
6. 形式逻辑与认知逻辑形式逻辑关注逻辑推理的形式和结构,与人的认知过程无关;而认知逻辑研究人类认知过程中的逻辑推理,如心理学中的思维过程。
7. 逻辑学与数理逻辑逻辑学是研究逻辑原理和逻辑推理的学科,包括形式逻辑和实质逻辑等;而数理逻辑是数学中的一个分支,使用数学方法研究逻辑原理和逻辑推理。
8. 形式逻辑与计算机逻辑形式逻辑是研究逻辑推理的规则和形式,如命题逻辑和谓词逻辑;而计算机逻辑是计算机科学中的一个分支,使用逻辑方法研究计算机的逻辑结构和逻辑推理。
9. 形而上学与逻辑学形而上学研究存在、本质和实体等超越经验的问题,涉及哲学的基本问题;而逻辑学研究逻辑推理和逻辑原理,是哲学的一个重要分支。
10. 命题逻辑与谓词逻辑命题逻辑研究命题的逻辑关系和推理规则,适用于形式化的推理;而谓词逻辑研究谓词的逻辑关系和推理规则,适用于包含变量和量词的逻辑推理。
通过以上的例子,我们可以看到逻辑学可以根据不同的划分标准进行分类,从而更好地理解和研究逻辑学的不同方面。
数学中常用的逻辑推理方法总结

数学中常用的逻辑推理方法总结逻辑推理是数学中不可或缺的一部分,它通过合理的演绎和归纳推断,使我们能够得出准确的结论。
在数学中,有许多常用的逻辑推理方法可以帮助我们解决问题。
本文将总结介绍一些常见的逻辑推理方法。
1. 直接证明法直接证明法是最常用的逻辑推理方法之一。
它的基本思路是通过一系列推理步骤,由已知的真实前提推导出所需的结论。
这种方法常用于证明数学中的等式、不等式、定理等。
例如,要证明一个等式A=B成立,可以通过对A和B进行一系列变换和等价关系的推理,直到得到相等的结果。
2. 反证法反证法是一种常用的逻辑推理方法,它通过假设所需结论不成立,推导出矛盾的结论,从而证明所需结论的正确性。
反证法常用于证明一些数学中的性质和存在性问题。
例如,要证明一个命题P成立,可以先假设P不成立,然后通过一系列逻辑推理和推导,导出矛盾的结论,从而证明反设假设的错误,进而证明P的正确性。
3. 数学归纳法数学归纳法是一种常见的数学推理方法,它常用于证明递推关系式、数列性质以及整数集合的性质。
数学归纳法的基本思想是:首先证明当n=1时,命题成立;然后假设当n=k(k≥1)时,命题成立;最后证明当n=k+1时,命题也成立。
通过这种归纳的推理方式,可以证明所需结论对所有自然数都成立。
4. 分类讨论法分类讨论法适用于将一个复杂的问题分解为若干个简单的情况,然后对每种情况进行独立的讨论。
通过分析每个情况,最终得出整体问题的解决方案。
分类讨论法在解决一些具有多种情况和条件的问题时非常有效。
例如,当解决一个不等式问题时,可以将问题分解为几种不同的情况,然后针对每种情况进行推理和讨论,最终得出整个问题的解。
5. 构造法构造法是一种通过构造具体的例子或集合来推理和证明数学问题的方法。
通过构造一些特殊的数或对象,可以帮助我们理解问题的本质和规律,进而得出结论。
构造法常用于解决一些具体问题和优化问题。
例如,当证明一个数的存在性时,可以通过构造一个满足条件的具体数来证明。
小学三年级数学思维总结逻辑推理与问题解决技巧

小学三年级数学思维总结逻辑推理与问题解决技巧在小学三年级的数学学习中,逻辑推理和问题解决技巧是非常重要的一部分。
通过锻炼逻辑思维和培养解决问题的能力,孩子们可以更好地理解数学概念,并在解决实际问题时做出正确的决策。
下面是对小学三年级数学思维总结的逻辑推理与问题解决技巧。
一、逻辑推理技巧逻辑推理是指根据事实和推理来得出结论的思维方式。
在小学三年级数学学习中,逻辑推理的技巧包括以下几点:1. 分类思维:通过将问题中的元素进行分类,找出规律和共性,从而解决问题。
例如,在解决加法问题时,可以将数字按照个位、十位进行分类,更好地理解进位的概念。
2. 排序思维:将一组数按照特定的顺序排列,可以更好地观察和比较数的大小关系。
例如,通过比较数的大小关系,可以解决大小比较问题。
3. 推理思维:通过观察已知条件和推理,得出未知情况的解答。
例如,通过观察等式关系和已知条件,可以进行代入推理,得出未知数的值。
4. 逆向思维:通过反向思考问题,从结果出发寻找问题的解决思路。
例如,在解决减法问题时,可以通过反向思考,将减法问题转化为加法问题。
二、问题解决技巧问题解决是数学学习中的核心能力之一。
在小学三年级数学学习中,通过培养问题解决技巧,可以提高孩子们解决实际问题的能力。
以下是一些问题解决技巧:1. 分析问题:在解决问题之前,先仔细阅读问题,理解问题的要求和所给出的条件。
将问题分解为更小的部分,有助于更好地理解和解决问题。
2. 制定计划:根据问题的要求和已知条件,制定解决问题的计划。
可以使用图表、模型或其他可视化工具来辅助解决问题。
3. 尝试不同的方法:解决问题的方法多种多样,可以尝试不同的方法来解决问题。
比较不同方法的效果,选择最有效的方法。
4. 反思和检查:在解决问题之后,进行反思和检查,确保答案的准确性。
可以通过重新计算、理解策略和验证等方式来检查答案是否正确。
总之,在小学三年级数学学习中,逻辑推理和问题解决技巧对培养孩子们的数学思维能力和解决实际问题的能力非常重要。
逻辑的一般分类 黑格尔

逻辑的一般分类(黑格尔)
黑格尔将逻辑分为三种不同的类型:
1. 分析逻辑(Analytic Logic):也称为形式逻辑,是研究逻辑形式和结构的分支。
它主要关注命题的真假和推理的正确性,不涉及命题所涉及的具体内容。
2. 合成逻辑(Dialectical Logic):也称为辩证逻辑,是研究事物的矛盾和对立面的分支。
它认为任何事物都存在着内部的矛盾和对立面,这些矛盾和对立面可以通过辩证的方法来解决。
3. 历史逻辑(Historical Logic):也称为历史哲学逻辑,是研究历史和社会变迁的分支。
它认为历史和社会是不断发展和变化的,逻辑也应该与时俱进,反映这些变化和发展。
黑格尔认为这三种逻辑类型是相互关联的,它们共同构成了逻辑的完整体系。
通过逻辑的研究,人们可以更好地理解和认识事物的本质和规律,为人类的思维和行动提供指导和支持。
(完整版)逻辑判断推理技巧大全

逻辑判断推理技巧大全一、演绎推理1. 指的是通过一些的前提来论证从而推断出某个结论。
2. 基本原则:头脑清空原则(按人家来,不要按自己的来)题设为真原则(人家题设说的是绝对不可怀疑的)形式统一原则3. 解题步骤:(1)看问题,定题型;(2)看题目,做简化;(3)据技巧,得答案。
4. 演绎推理的分类:(1)论证类——加强论证型——减弱论证型(2)结论类——形式推理结论类:侧重规则的考察——日常推理结论类:侧重脉络的考察(一)形式推理结论类1. 分类:有真有假型;翻译推理型(强调对于肯定确定信息的认识);排列组合型(匹配型的题型);集合运算型(很像数学的一种题型)2. 有真有假型:(1)首先看矛盾;其次看包容;然后看反对;最后带题中(实在不行就代入排除法)(2)矛盾关系:必然一真一假,两者构成整个全集,如生和死;——A:其矛盾关系为否AA且B:其矛盾关系为否(A且B)即否A或否BA或B:其矛盾关系为否(A或B)即否A且否BA能够推出B:其矛盾关系为A且否B所有:其矛盾关系为有的不必然:其矛盾关系为可能不——即首先要寻找矛盾关系,然后根据题目中的真假结论来得出其他几个关系的真假,从而得出相应的最后答案——能用在很多地方,不光是在这里。
比如说在后来的削弱关系中,矛盾是最强的削弱关系——构成矛盾关系的主体一定相同,这是观察矛盾关系的一个重要判断指标。
(3)包容关系:——当不能发现矛盾关系时,我们就要看包容关系,即寻找看几个关系之间是否存在包容。
——即要寻找包容关系,几个关系如果为包容关系,则他们同时为真或为假(这和矛盾关系刚好相反),然后根据题目中的真假结论来得出其他几个关系的真假,从而得出相应的最后答案。
——若A能推出B:则包容关系为若A为真则B为真+若B为假则A为假只有一真,则A必为假——即“一真前假”只有一假,则B必为真——即“一假后真”——所有:则包容关系是能够推出某人、有的A且B:则包容关系是能过推出A(B)、A或者B(4)反对关系:——对于两个“有的”的反对关系,“必有一真”;对于两个“所有”的反对关系,“必有一假”;(5)当题目中有多真多假时,可以利用矛盾或包容或反对关系将其转化为一个真或假再解。
行测逻辑推理题型分类与解题方法

行测逻辑推理题型分类与解题方法在行政职业能力测验(简称行测)中,逻辑推理是一个重要的板块,它考察的是考生的逻辑思维和分析能力。
掌握不同类型的逻辑推理题型以及相应的解题方法,对于提高行测成绩至关重要。
下面,我们将对行测逻辑推理的常见题型进行分类,并介绍一些实用的解题方法。
一、直言命题推理直言命题是指直接陈述对象具有或不具有某种性质的命题。
例如:“所有的苹果都是红色的”“有的学生不是勤奋的”。
解题方法:1、对当关系推理:根据直言命题之间的矛盾、反对、下反对和从属关系进行推理。
2、换位推理:改变命题中主项和谓项的位置,但不改变命题的真假性质。
二、联言命题推理联言命题是指同时断定几种事物情况都存在的复合命题。
例如:“小明既聪明又勤奋”。
解题方法:全真则真,一假则假。
三、选言命题推理选言命题分为相容选言命题和不相容选言命题。
相容选言命题,如“或者 A 或者B”,只要其中一个选言支为真,整个命题就为真。
不相容选言命题,如“要么 A 要么B”,只有一个选言支为真时,整个命题才为真。
解题方法:1、相容选言命题:否定肯定式。
2、不相容选言命题:否定肯定式和肯定否定式。
四、假言命题推理假言命题是反映事物情况之间条件关系的命题。
常见的有充分条件假言命题(如果 A 那么 B)、必要条件假言命题(只有 A 才 B)和充分必要条件假言命题(当且仅当 A 则 B)。
解题方法:1、充分条件假言命题:肯前肯后,否后否前。
2、必要条件假言命题:否前否后,肯后肯前。
五、归纳推理归纳推理是从个别性知识推出一般性结论的推理。
解题方法:1、注意样本的代表性和数量。
2、避免以偏概全、偷换概念等错误。
六、类比推理类比推理是根据两个或两类对象在某些属性上相同或相似,推出它们在其他属性上也相同或相似的推理。
解题方法:1、分析所给对象之间的内在逻辑关系。
2、比较选项与题干逻辑关系的一致性。
七、削弱论证这类题目要求找出能够削弱给定论点的选项。
解题方法:1、直接削弱论点。
三段论的逻辑规则

三段论的逻辑规则三段论是一种经典的逻辑推理形式,由两个前提和一个结论组成。
它基于一系列逻辑规则,用来确保推理的有效性和正确性。
以下是一些常见的逻辑规则,适用于三段论的推理:1.基本规则:(a)边界排中律:任何陈述或命题要么是真的,要么是假的,不存在中间值。
(b)合取析取律:陈述或命题可以使用合取(AND,表示为∧)或析取(OR,表示为∨)操作符进行组合。
2.分类:(a)分类完全性:任何事物都属于一些类别,不存在其它情况。
(b)分类排他性:一个事物只能属于一个类别,不可能同时属于两个以上的类别。
3.确定因果关系:(a)必要条件:如果一些命题为真,则它的必要条件也为真。
例如,如果A是B的必要条件,则当A为真时,B也必为真。
(b)充分条件:如果一些命题为真,则它的充分条件也为真。
例如,如果A是B的充分条件,则当B为真时,A也必为真。
4.假言推理:(a)假言推理:如果前提中的条件命题为真,则结论必为真。
例如,“如果A成立,则B成立。
A成立,所以B成立。
”(b)假言链:如果A成立则B成立,如果B成立则C成立,所以如果A成立则C成立。
5.抵消:(a)反证法:通过假设一个命题的反命题,来证明原命题的真实性。
(b)甄别拒斥1:如果一些命题的一个特殊情况成立,而普遍情况不成立,则拒斥普遍情况。
(c)甄别拒斥2:如果一些命题的普遍情况成立,而一个特殊情况不成立,则拒斥特殊情况。
6.并列关系:(a)等价关系:两个命题具有相同的真值,要么都为真,要么都为假。
例如,A等价于B,当且仅当A和B具有相同的真值。
(b)等价转换:如果两个命题等价,则它们可以互相替换。
以上是一些常见的逻辑规则,用于确保三段论推理的有效性和正确性。
当我们使用三段论进行推理时,必须遵守这些规则,并确保所使用的前提和结论符合这些逻辑关系。
通过正确应用这些规则,我们可以进行准确和有效的推理,以得出令人信服的结论。
说明逻辑涉及阶段的主要步骤和内容

说明逻辑涉及阶段的主要步骤和内容逻辑是一门研究思维规律和思维方法的学科,它涉及到许多阶段的步骤和内容。
在逻辑学中,通常将逻辑分为三个阶段:概念阶段、判断阶段和推理阶段。
下面将分别介绍这三个阶段的主要步骤和内容。
概念阶段概念是逻辑思维的基本单位,是人们对客观事物的抽象反映。
在概念阶段,主要包括以下步骤和内容:1. 概念的形成:概念的形成是指人们通过对客观事物的感性认识和思维活动,将其抽象出来,形成概念。
概念的形成需要具备感性认识和思维能力。
2. 概念的分类:概念的分类是指将概念按照其内在联系和特征进行分类。
概念的分类是逻辑思维的基础,它有助于人们更好地理解和认识事物。
3. 概念的定义:概念的定义是指对概念进行准确、明确的描述和解释。
概念的定义需要具备准确性、明确性和简洁性。
判断阶段判断是指根据已有的概念和事实,对新的事物进行判断和评价。
在判断阶段,主要包括以下步骤和内容:1. 判断的形式:判断的形式有三种,即肯定判断、否定判断和疑问判断。
肯定判断是指对某一事物进行肯定的评价,否定判断是指对某一事物进行否定的评价,疑问判断是指对某一事物进行疑问的评价。
2. 判断的真假:判断的真假是指判断是否符合客观事实。
判断的真假需要根据已有的概念和事实进行判断,不能凭空臆断。
3. 判断的关系:判断的关系是指判断之间的逻辑关系。
判断之间的逻辑关系有三种,即同一关系、对立关系和疑问关系。
推理阶段推理是指根据已有的概念和事实,通过逻辑推理得出新的结论。
在推理阶段,主要包括以下步骤和内容:1. 推理的形式:推理的形式有两种,即演绎推理和归纳推理。
演绎推理是指从一般到特殊的推理,归纳推理是指从特殊到一般的推理。
2. 推理的规则:推理的规则是指推理过程中需要遵循的规则。
推理的规则有三种,即排中律、矛盾律和归纳法则。
3. 推理的正确性:推理的正确性是指推理结论是否符合逻辑规律和客观事实。
推理的正确性需要根据已有的概念和事实进行判断,不能凭空臆断。
小学数学逻辑推理知识点的归纳与总结

小学数学逻辑推理知识点的归纳与总结数学是一门既有逻辑性又有创造力的学科,逻辑推理作为数学中的重要组成部分,对于小学生的思维发展和数学学习都起到了关键性的作用。
在小学阶段,数学的逻辑推理内容主要包括分类、排序、数列、模式等知识点。
本文将对这些知识点进行归纳与总结,让我们一起来了解一下。
首先,分类是逻辑推理的基本概念之一,也是小学数学中重要的知识点。
分类是指根据事物的相似性或不同性,将其划分为不同的类别或群体。
在小学数学中,分类常常涉及到形状、颜色、大小等特征。
比如,让学生将给定的一组图形分为圆形和非圆形,或者将一组不同颜色的球分为红球和非红球。
通过这种分析与划分,学生可以加深对事物特征的理解,并培养逻辑思维的能力。
其次,排序是逻辑推理的另一个重要知识点。
排序是根据一定的规则或条件将一组事物按照一定的顺序进行排列。
在小学数学中,排序常常涉及到数字、字母、长度等概念。
例如,要求学生按照从小到大的顺序排列一组给定的数字,或者按照字母表的顺序排列一组字母。
通过排序的练习,学生可以提高观察力和逻辑思维能力,培养他们的分析和推理能力。
此外,数列也是小学数学中的一个重要内容,与逻辑推理有着密切的关系。
数列是按照一定的规则将一组数字或形状排列起来的一种数学表达形式。
在小学数学中,常见的数列包括自然数数列、偶数数列、奇数数列等。
学生通过观察数列中数字的规律,可以找到其中的共同特点,并根据规律推测数列中后面的数字。
数列的学习有助于培养学生的归纳与推理能力,提高他们的逻辑思维水平。
最后,模式是小学数学中涉及逻辑推理的重要知识点之一。
模式是指事物中存在的一种特定的规律或形式。
在小学数学中,模式常常涉及到形状、图案、数字等方面。
例如,给学生展示一组图片,让他们观察其中的规律,并根据规律推测下一个图片是什么。
通过模式的学习,学生可以培养观察和推理能力,帮助他们更好地理解事物的规律性与普遍性。
综上所述,小学数学逻辑推理包括分类、排序、数列、模式等知识点。
小学奥数 逻辑推理 知识点+例题+练习 (分类全面)
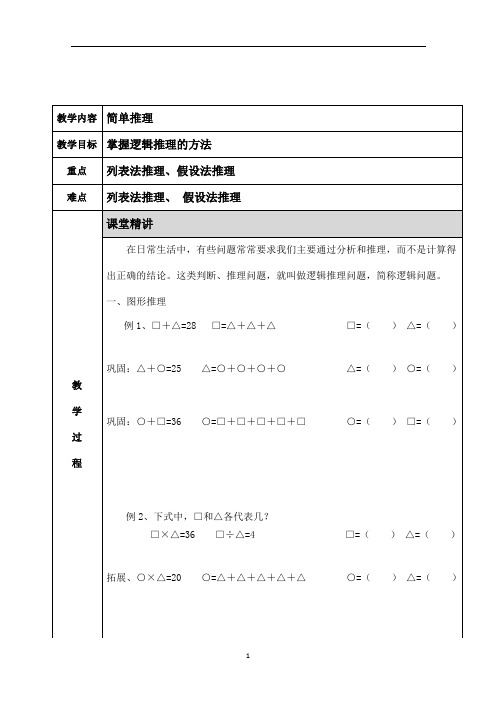
拓展、□=○+○+○+○○×□=16 □=()○=()
例3、下面三块正方体的六个面都是按相同的规律涂有红、黄、蓝、白、绿、黑六种颜色。
请判断黄色的对面是什么颜色?白色的对面是什么颜色?红色的对面是什么颜色?
(A)
黄
黑
白
(B)
红
白
绿
(C)
红
蓝
黄
拓展:一个正方体6个面上分别写着1、2、3、4、5、6。
根据下图摆放的三种情况,判断每个数字对面上的数字是几。
二、文字推理
例1、小王、小张和小李一位是工人,一位是农民,一位是教师,现在只知道:小李比教师年龄大;小王与农民不同岁;农民比小张年龄小。
问:谁是工人?谁是农民?谁是教师?
课后作业
1、☆+○=18 ☆=○+○☆=()○=()
2、○×□=16 □÷○=4 ○=()□=()
3、甲、乙、丙分别是来自中国、日本和英国的小朋友。
甲不会英文,乙不懂日语却与英国小朋友热烈交谈。
问:甲、乙、丙分别是哪国的小朋友?
4、根据一个正方体的三种不同的摆法,判断出相对的两个面上的字母各是什么?。
小学数学中的简单数学逻辑推理

小学数学中的简单数学逻辑推理数学是一门逻辑性强的学科,通过逻辑推理可以解决各种问题。
在小学阶段,学生们开始接触到简单的数学逻辑推理,这为他们打下了坚实的数学基础。
本文将介绍小学数学中的简单数学逻辑推理。
一、分类思维分类思维是小学数学中的重要逻辑推理方式之一。
通过观察事物的性质和特征,将其归类,有助于形成清晰的思维结构。
例如,给出一组数字:2、4、6、8、10,要求将其分类。
经过观察可以发现,这组数字中都是偶数,因此可以将其归为一类。
二、反证法反证法是逻辑思维中一种常用的方法。
当我们需要证明某个结论为真时,可以假设其反面为真,通过推导出矛盾的结论来证明原结论的正确性。
例如,对于一个等边三角形ABC,如果需要证明其内角都是60度,可以先假设其中一个内角不是60度,比如为70度,然后通过计算得出三条边不相等,与等边三角形的定义矛盾,因此可以证明原结论的正确性。
三、逻辑推理逻辑推理是指根据已知条件和逻辑关系,通过推理得出结论的过程。
在小学数学中,常见的逻辑推理题包括找规律、判断真假等。
例如,给出一组数字序列:1、4、9、16、25,要求找出规律并继续序列。
通过观察可以发现,这组数字是1的平方、2的平方、3的平方、4的平方、5的平方,因此可以判断下一个数字是6的平方,即36。
四、推理证明推理证明是通过已知条件和逻辑关系来证明一个数学结论的逻辑推理过程。
在小学数学中,常见的推理证明题涉及到类比、对称性、等差数列等。
例如,对于一个三角形ABC,已知AB=AC,要求证明∠B=∠C。
通过推理可以发现,根据等边三角形的定义,AB=AC,再结合三角形内角和等于180度的性质,可以得出∠B=∠C的结论。
五、数学模型数学模型是将实际问题抽象化成数学形式,通过逻辑推理解决问题的方法。
在小学数学中,数学模型的应用主要体现在代数方程的解答中。
例如,求解一个简单的一元一次方程2x+3=7。
可以将该方程看做一个数学模型,通过逻辑推理和运算可求得x=2的解。
逻辑学直言三段论举例-概述说明以及解释

逻辑学直言三段论举例-概述说明以及解释1.引言1.1 概述逻辑学是研究思维和推理方式的科学,而三段论则是逻辑学中的重要概念之一。
三段论是由亚里士多德提出的一种推理形式,包含前提、中介和结论三个部分,通过这种形式可以对逻辑关系进行清晰的表达和推理。
在逻辑学的研究中,三段论占据着重要地位,被广泛运用于不同领域的推理和论证中。
本文将通过对三段论的定义和原理、分类以及实际应用的介绍,探讨三段论在逻辑学中的重要性和影响。
1.2 文章结构文章结构部分的内容可以根据上面提供的大纲进行详细介绍,如下所示:文章结构部分的内容:本文将按照以下结构展开讨论三段论的相关内容:1. 引言部分将首先对三段论进行概述,介绍其基本概念和重要性。
接着会说明本文的结构和目的,为读者提供一个整体的框架。
2. 正文部分将分为三个子部分,首先会详细解释三段论的定义和原理,包括三段论的基本结构和推理规则。
其次会介绍三段论的分类,包括分类的标准和不同类型的例子。
最后会讨论三段论的实际应用,通过具体的案例展示三段论在逻辑推理中的应用。
3. 结论部分将对本文进行总结,强调三段论在逻辑学中的重要性,并探讨三段论对逻辑学的影响。
此外,还将展望三段论在未来的发展方向,指出其在逻辑学研究中的潜在作用和价值。
通过以上结构的安排,本文将全面而系统地介绍三段论的相关内容,帮助读者更好地理解和掌握这一重要的逻辑学理论。
1.3 目的本文旨在通过探讨逻辑学中的三段论,深入了解其在逻辑推理中的重要性和实际应用。
通过对三段论的定义、原理、分类及实际案例的讨论,旨在帮助读者更好地理解逻辑学的基础知识,并引导他们在日常生活和学术研究中更好地运用逻辑思维的方法。
同时,通过对三段论的重要性、对逻辑学的影响以及未来发展进行总结和展望,旨在激发读者对逻辑学的兴趣,并促进逻辑学领域的进一步研究和发展。
通过本文的阐述,希望读者能够加深对逻辑学的认识,并提高自己的逻辑思维能力,以更好地应对复杂的问题和情境。
小学中的逻辑推理知识点整理

小学中的逻辑推理知识点整理在小学阶段,逻辑推理是培养学生思维能力和分析问题的重要内容。
通过逻辑推理的训练,学生可以锻炼自己的观察力、思辨能力和解决问题的能力。
下面将整理一些小学中常见的逻辑推理知识点。
1. 奇偶数逻辑推理奇偶数逻辑推理是小学数学中的重要内容之一。
学生在这个阶段需要学会判断一个数的奇偶性,并运用奇偶数的性质解决问题。
例如,我们知道两个偶数相加的结果是偶数,奇数加偶数的结果是奇数,学生可以利用这些性质来推理和解决一些数学问题。
2. 数列逻辑推理数列逻辑推理是培养学生观察和分析能力的重要途径之一。
学生需要通过观察和分析找出数列中的规律,并运用这些规律来推理下一个数或下一个几个数是什么。
例如,给定一个数列:2, 4, 6, 8,学生可以观察到每个数都比前一个数大2,根据这个规律可以推理出下一个数是10。
3. 图形逻辑推理图形逻辑推理是小学数学中的一个重要内容,是培养学生观察力和图形分析能力的有效方法。
学生需要根据图形的形状、大小、角度等特征来进行推理和分析。
例如,给定一个图形序列:正方形、三角形、圆形,学生可以观察到每个图形都有不同的边数,根据这个规律可以推理出下一个图形是一个五边形。
4. 概率逻辑推理概率逻辑推理是小学数学中的一个重要内容,帮助学生理解和运用概率的概念。
学生需要通过观察和分析概率事件的可能性来进行推理和判断。
例如,在一个抽奖箱中有5个红色球、3个蓝色球,学生可以推理出从抽奖箱中抽出一个红色球的概率比抽出一个蓝色球的概率高。
5. 分类逻辑推理分类逻辑推理是培养学生分类和归纳能力的重要方式之一。
学生需要观察和分析对象的特点,将其归类,并根据特点进行推理和判断。
例如,给定一个分类序列:苹果、香蕉、橘子,学生可以观察到这些水果都是属于水果类别,根据这个规律可以推理出下一个水果是梨。
6. 逻辑问题推理逻辑问题推理是培养学生逻辑思维和解决问题能力的重要内容之一。
学生需要运用已有的信息和推理方法来分析和解决问题。
中考英语专题讲练:逻辑推理(解析版)

中考英语专题讲练:逻辑推理(解析版)知识精讲一、逻辑推理题的分类逻辑推理题可分为:反义推理、进一步推理、情绪推理和态度推理四类。
此中,前两类主要是从做题技能上举行的分类,而后两类主要是从考察内容上举行分类。
总结发觉,中考完形填空的考点通常是考察代表使命态度、看法和事件成长走向的。
通常环境下,同砚们此部分标题的失分率相当高,要引起注意。
二、反义推理题此类题型通常是指填空部分在语言表述上采取“否定之否定”的方法,进一步说明前后文或后文已表达的语义。
比方上文表述“我欣赏自己天才的一面”,下文说“我厌恶自己_________的一面”。
填空部分可以议决“欣赏”和“厌恶”两词反义,推知欣赏“天才”,而厌恶“平庸”。
正确答案“平庸”与原文“天才”相对应。
这类标题通常以一对反义词为线索,寻找另一对反义词,从而推知正确的答案。
通常,可以议决某条件不成立或有变化,从而推知终于相反或不同;可根据终于不同,从而推知原因不同;也可根据选择A,从而推知不能选择与A相反或相对的事物等等。
总之,这类题型解题要害便是找出反义的对应词。
三、进一步推理进一步推理主要指根据上下文所提供的故事线索和已经产生的故事脉络,根据因果干系或常识等推测故事走向的标题。
如上文说“奶奶给我几美元”,后文说“奶奶对我说,拿着_________去给需要的人买工具。
”可推知,空格处是拿着钱去买工具。
此类标题数量最多,难度不一,相比拟较纷乱。
有时是依据常识举行推理,大部分还是要根据上下文表露出的字里行间的语义举行合理推测。
四、情绪推理此类标题主要是指议决上下文线索,推测文章中人物的情绪状况和感情变化的一类标题。
情绪通常是指喜、怒、哀、乐等各种感情。
情绪推理题是从完形填空考察内容的角度举行分类。
情绪推理题的难点在于对各类不怜悯绪的辨析,明白相近情绪的差异。
这类标题出现的频率相当高,而且同砚们的失分率也相对较高。
五、态度推理此类标题主要是指议决上下文线索,合理地推测文章中人物的态度及其变化。
四种逻辑规律类型

四种逻辑规律类型人类思维的逻辑组织和推理是一个重要的课题,许多逻辑学家和心理学家认为,思考、解决问题和考虑复杂情况都是通常可以拆分成四种基本类型的逻辑规律。
这四种逻辑规律类型是分类法、递进法、因果法和类比法。
首先,分类法是基于一组属性分类的一种方法,每个类别有其独特的属性,从而使得复杂的事物可以更加容易地理解和分类。
它可以用于对对象分类,如物种,以及把对象放在更大的系统中,如生态系统中的动物类群。
分类法也被广泛应用于学术领域,其中包括心理学、数学、经济学、物理学和医学等学科。
其次,递进法是一种循序渐进的思维方式,以有序的步骤展开问题的讨论,从而得出一个结论。
它可以从特定的基本点开始,推导出一个递进的过程,从而形成一个明确的结果。
递进法可以用于把一个复杂的问题分解成小的、可以被理解和处理的不同部分,从而被用于编程、语法和叙述等方面。
第三,因果法是一种重要的思维方法,它认为“因”和“果”之间存在某种关系,并且可以根据经验判断出未来可能出现的“果”。
因果法可以用于分析和推理问题,从而定义一个特定的结果。
因果法在许多学科中都得到广泛的应用,包括经济学、心理学、生态学、统计学和社会学。
最后,类比法是一种比较、对比和模仿的技巧,可以帮助我们理解一个对象的结构和功能,以及它与其他对象之间的关系。
类比法可以用于解决许多复杂的问题,如设计、文学创作、科学研究和工程学等。
实际上,类比法是一种实用的思维方法,它在做出决策和决定时可以帮助人们更准确地判断其结果。
以上就是人类思考和推理基本类型的四种逻辑规律类型,它们是:分类法、递进法、因果法和类比法。
经过反复证明,它们是人类复杂思维的基础,可以帮助人们更好地理解和解决复杂的问题。
正是基于这四种逻辑规律类型,人们才能更加清晰地思考、记忆和推理问题。
未来,这些类型将继续在许多领域中发挥重要作用,并成为人类思维和解决问题的重要工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逻辑部分第一部分:模态判断1、什么是模态判断所谓模态判断是指一切包含“可能”、“必然”等模态概念的判断。
它判断事物的可能性或必然性;例如:今年我可能会结婚今年我必然会考上公务员2、模态判断的种类(1)、可能判断:分为可能肯定判断和可能否定判断小张可能是个帅哥----------------------------------S可能是P小张可能考不上成都省直公务员----------------S可能不是P(2)、必然判断:分为必然肯定判断和必然否定判断小张必然会成熟起来-------------------S必然是P小张必然离不开QZZN的朋友-------S必然不是P3、模态判断的真假关系就是要讨论:“必然P”、“必然非P”、“可能P”、“可能非P”之间的对当关系。
用一个逻辑方针来表示:1、上反对关系“必然P”和“必然非P”是上反对关系:不能同真,但是可以同假。
准确的说:如果其中一个是真,则令一个必然是假的;如果其中一个判断是假的,另一个判断不必然是真的,也可能是假的。
A:小张必然是个好人B:小张必然不是个好人如果A真,则B假如果A假,则B可能为真,也可能为假2、下反对关系“可能P”与“可能非P”是下反对关系:可以同真,但是不能同假。
即:如果其中一个判断是假的,则另一个判断必然是真的;如果其中一个判断是真的,则另一个判断不必然是假的,也可能是真的。
A:小张可能是个好人B:小张可能不是个好人如果A真,那B的真假性无法判断如果A假,那么B真3、矛盾关系“必然P”与“可能非P”、“必然非P”与“可能P”是矛盾关系:矛盾关系就是我们讲的:不能同真,也不能同假。
即:如果其中一个判断为真,另一个判断必然为假;如果其中一个判断假,另一个必然为真。
4、从属关系“必然P”与“可能P”、“必然非P”与“可能非P”是从属关系:可以同真,可以同假。
具体地说,即:必然判断真可能判断必真;可能判断假,必然判断必假。
第二部分1、联言判断:是判定若干事物情况共同存在的复合判断。
例如:成都即美丽,又时尚小张不但帅,而且还聪明表达联言判断的词语主要有:“即。
又。
”、“。
也。
”、“不是。
而是。
”、“一方面。
另一方面。
”、“尚且。
何况。
”、“虽然。
但是。
”、“尽管。
可是。
”2、选言判断:p或者q“或者”、“是。
还是。
”、“也许。
也许。
”、“不是。
就是。
”等等表示选择关系的词语3、假言判断:假言判断是判定一事物情况是另一事物情况存在的条件的判断,我们也称它为条件判断。
其中包括:充分条件、必要条件、充分必要条件。
(1)充分条件如果p,那么q。
p就是q 的充分条件表达充分条件假言判断的关联词语还有“假使。
就。
”、“倘若。
则。
”、“只要。
就,,,”、“当。
就(便)。
”等等。
(2)必要条件假言判断只有p,才q。
p就是q 的必要条件表达必要条件假言判断的关联词语还有:“除非。
才。
”、“除非。
不。
”、“。
才。
”(3)充分必要条件如果有p必有q;如果无p,则无q真假a且b: a真b真 a假b真,a假b假,a真b假a或b: a真b真,a真b假,a假b真 a假b假a=>b a真b真,a假b真,a假b假 a真b假(4)负判断负判断就是否定某个判断的判断①简单的负判断的等价判断(等值判断)顺口溜:否定全称得特称,否定特称得全称。
否定必然得可能,否定可能得必然。
例子:1、并非所有会飞的动物都是鸟--------------------------------------------------有的会飞的动物不是鸟2、并非所有失足青年都不是可教育的-----------------------------------------------------有的失足青年是可教育的3、并非有的人是生而知之的------------------------------------------------------所有的人都不是生而知之的4、并非有的知识不是有用的----------------------------------------------------------所有的知识都是有用的并非必然P等值于:可能非P并非必然非P等值于:可能P并非可能P等值于:必然非P并非可能非P等值于:必然P用云淡的话说就是其他类似的有:不必然p======可能不p不必然非p======可能不非p====可能p不可能p=======必然不p (必然非p)不可能非p=====必然不非p====必然p不所有p======有的p不不所有p不=====有的p不不====有的p不有的p======所有p不不有的p不======所有p不不===所有p②负复合判断及其等价判断(1):负联言判断是判定一个联言判断是假的,前面我们有讲过,什么时候联言判断为假?就是至少有一个联言支是假的(也可以都是假的)用公式表示为:“并非(P且q)”等值于“非P或者非q”例如:并非小张既有才华又帅气---------------------------------------------------小张或者没有才华,或者不帅气并非某些公务员既有才又有德--------------------------------------------------------某些公务员或者没才,或者没德(2)相容选言判断的负判断“并非(P或者q)”等值于“非P并且非q”例子:并非考不上公务员是因为或者没有才华,或者没关系-------------------------------------------------------------------------考不上公务员即不是因为没有才华,也不是因为没有关系(4)不相容选言判断的负判断“并非要么p要么q”等值于“P并且q,或者非p,并且非q”不相容判断不能同真同假,所以他的负判断就是要判定它可以同真,或者是可以同假。
(5)充分条件的负判断“并非(如果p,那么q)等值于“P并且非q”因为前面我们有讲过,充分条件命题假只有一种情况,即前真后假的时候为假!所以它的负判断就是判定它什么时候为假的判断!(6)必要条件的负判断并非(只有P,才q)等值于“非P且q”(7)充分必要条件的负判断“并非(当且仅当P,才q)”等值于(P并且非q)或者(非p并且q)第三部分:类比推理类比推理考察主要是一下16方面(我讲逐一和大家学习)1 同一事物的不同称谓2 原因和结果(因果关系)3 属种和种属关系(一般和特殊)4 同一类属下的两个并列关系5 相对概念6 作者、作品、人物7 整体和部分8 事物与空间9 事物、工具记以及相关功能、效用10物品与制作材料11比喻、引申和象征12人文、成语及其相关13特定人员或行为与其实施的对象14人文地理知识15行为(事物材料)与后果16特定的关系一、同一事物的不同称谓2007贵州买单:付账A远足:游历 B跳槽:转岗C沉默:保密 D派对:下海2006浙江罗曼蒂克:浪漫A博客:网络日志 B洗手间:厕所C一级棒:顶好 D厚道:老实2006江西地衣:苔藓A小姨子:妻弟 B腊月:十二月C竖子:叛徒 D蝉联:阔别桂圆:龙眼A桔:柚 B桂皮:陈皮C芒果:荔枝 D大料:八角答案AABD二、原因和结果2008中央通;牒A丑小鸭:白天鹅 B胚胎:婴儿C种子:花朵 D蝌蚪:青蛙2006中央二氧化碳:温室效应A石油:煤炭 B公路:汽车C洪水:水灾 D投资:奉献2008中央()对于知识相当于分析对于()A书本理论 B学习结论C学问:研究 D学生:研究员分析:1D 必然性的因果关系,蛹必然变成蝶,蝌蚪必然变成青蛙。
2C二氧化碳增多可能导致温室效应洪水泛滥可能导致水灾3C 学习的目的是获得知识,分析的目的是得出理论,学习和分析都是动词,知识和结论都是名词三、种属关系07浙江古诗:李白A国家:楼兰 B民间艺术:手工陶艺C运动:拳击 D民族冲突:加沙地带06中央自恋:爱A敌意:批评 B沉思:思想 C内疚:谴责 D贪婪:欲望分析:1D李白是古代诗人中的巅峰人物,加沙地区是民族冲突最激烈的地方2D自恋是爱的一种,而贪婪是欲望的一种四、同一类型下的两个并列06福建狗:鼠A马:牛 B猫:虎 C狼:狗 D鹅:鸭07浙江鼠标:键盘A电脑:音响 B门:窗户 C棉花:丝绸 D红花:绿叶06江苏鞭挞:抨击A架空:排挤 B斧正:修改 C数落:列举 D水印:胶印07湖南(也是06广东)山道:索道A客轮:渔船 B汽车:卡车 C楼梯:电梯 D筷子:刀叉07浙江客车:货车A居民楼:商务楼 B蝌蚪:青蛙 C男生:女生 D遥控器:电视机分析:1A都是十二生肖2B鼠标和键盘都是电脑必不可少的输入部件,并列关系3B鞭挞:比喻抨击斧正:比喻修改4C山道和索道是并列关系,同时后者比前者更具科技成分。
5A车辆由于分工用途不同而分为客车和货车,楼盘因为用途不同,分为居民楼和商务楼五、相对概念07浙江糖:苦A孤儿:可怜 B复杂:简单 C明确:模糊 D美国:弱小06中央费解:理解A难看:漂亮 B组合:合并 C坚固:塌陷 D疏忽:忽略06江苏聪明:狡猾A谦虚:自卑 B骄傲:自豪 C伟大:渺小 D杰出:拔尖分析;1D糖是甜的,甜的反义词是哭;美国是强大的,强大的反义词是弱小2C前一对词的词性分别是形容词和动词,并且描述的状态为相反的状态。
3A (褒义词对贬义词)六、作品对作者06江苏《平凡的世界》:路遥A《京华烟云》:梁实秋 B《射雕英雄传》:金庸C《编辑部的故事》:李冬宝 D《围城》:杨峰04江苏(多选)武松:《水浒传》A王熙凤:《红楼梦》 B范进:《儒林外史》C司马迁:《三国演义》 D姜子牙:《封神榜》范晔:《后汉书》A罗贯中:《三国志》 B魏征:《通典》63C孔子:《论语》 D徐光启:《农政全书》分析:前面两个比较简单1 B 2ABD(多选)主要讲下第三个选D 书对应的作者。
A罗贯中写的是三国演义 C《论语》是孔子弟子记录孔子言行的,而非孔子所作。
B我也不清楚(自己查查印象更深)七、整体和部分06中央电脑:鼠标A水壶:茶杯 B手机:短信 C船:锚 D录音机:磁带06江苏手指:手A春天:刮风 B树叶:树 C头发:梳子 D运动:流汗07中央正方形:边长A矩形:对角线 B菱形:高 C圆形:半径 D三角形:底边分析:1 C 2B 3C八、事物与空间07中央太空:卫星A铁轨:火车 B公路:自行车 C机场:直升飞机 D城市:公共汽车05江苏职员:公司A公务员:机关 B犯罪:沙漠 C嫌疑人:现场 D秘书:写字间分析:1A太空是卫星运行的空间,城市是公交车运行的空间。
卫星在太空“里面”运行,而火车在铁轨上面运行。
九、事物、工具以及相关功能07江西眼睛:眼镜A子弹:步枪 B鞋子:鞋带 C手:手套 D头:帽子08国家岩石:矿物:成分()A森林:树木:木材 B:粘土:沙子:石头C器官:组织:功能 D:酒精:饮料:果汁06浙江钟表:时光A潜艇:深度 B铅笔:素描 C毛衣:温暖 D天平:质量温度计:摄氏度A体积:立方米 B秒表:秒 C考试:成绩 D天平:重量分析:1D眼镜对眼睛起保护和美化作用,并且没把眼睛全部覆盖2C岩石的成分是矿物,器官的功能是组织3D钟表是计量时间的工具,天平是计量质量的工具。
