最新数据模型与决策课程大作业打印版.doc
数据模型与决策课程大作业(完整资料).doc

【最新整理,下载后即可编辑】数据模型与决策课程大作业以我国汽油消费量为因变量,乘用车销量、城镇化率和90#汽油吨价与城镇居民人均可支配收入的比值为自变量时行回归(数据为年度时间序列数据)。
试根据得到部分输出结果,回答下列问题:1)“模型汇总表”中的R方和标准估计的误差是多少?2)写出此回归分析所对应的方程;3)将三个自变量对汽油消费量的影响程度进行说明;4)对回归分析结果进行分析和评价,指出其中存在的问题。
1)“模型汇总表”中的R方和标准估计的误差是多少?答案:R方为0.993^2=0.986 ;标准估计的误差为120910.147^(0.5)=347.722)写出此回归分析所对应的方程;答案:假设汽油消费量为Y,乘用车销量为a,城镇化率为b,90#汽油吨价/城镇居民人均可支配收入为c,则回归方程为:Y=240.534+0.00s027a+8649.895b-198.692c3)将三个自变量对汽油消费量的影响程度进行说明;乘用车销量对汽油消费量相关系数只有0.00027,数值太小,几乎没有影响,但是城镇化率对汽油消费量相关系数是8649.895,具有明显正相关,当城镇化率每提高1,汽油消费量增加8649.895。
乘用90#汽油吨价/城镇居民人均可支配收入相关系数为-198.692,呈明显负相关,即乘用90#汽油吨价/城镇居民人均可支配收入每增加1个单位,汽油消费量降低198.692个单位。
a, b, c三个自变量的sig值为0.000、0.000、0.009,在显著性水平0.01情形下,乘用车消费量对汽油消费量的影响显著为正。
(4)对回归分析结果进行分析和评价,指出其中存在的问题。
在学习完本课程之后,我们可以统计方法为特征的不确定性决策、以运筹方法为特征的策略的基本原理和一般方法为基础,结合抽样、参数估计、假设分析、回归分析等知识对我国汽油消费量影响因素进行了模拟回归,并运用软件计算出回归结果,故根据回归结果,对具体回归方程,回归准确性,自变量影响展开分析。
数据模型与决策习题与参考答案

《数据模型与决策》复习题及参考答案第一章绪言一、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核心是运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据。
3.模型是一件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表示成一个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学用系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应用各学科交叉的方法,具有典型综合应用特性。
8.运筹学的发展趋势是进一步依赖于_计算机的应用和发展。
9.运筹学解决问题时首先要观察待决策问题所处的环境。
10.用运筹学分析与解决问题,是一个科学决策的过程。
11.运筹学的主要目的在于求得一个合理运用人力、物力和财力的最佳方案。
12.运筹学中所使用的模型是数学模型。
用运筹学解决问题的核心是建立数学模型,并对模型求解。
13用运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之一是用系统的观点研究功能关系。
15.数学模型中,"s·t"表示约束。
16.建立数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
二、单选题1.建立数学模型时,考虑可以由决策者控制的因素是〔 AA.销售数量B.销售价格C.顾客的需求D.竞争价格2.我们可以通过〔 C来验证模型最优解。
A.观察B.应用C.实验D.调查3.建立运筹学模型的过程不包括〔 A 阶段。
A.观察环境B.数据分析C.模型设计D.模型实施4.建立模型的一个基本理由是去揭晓那些重要的或有关的〔 BA数量 B变量 C 约束条件 D 目标函数5.模型中要求变量取值〔 DA可正 B可负 C非正 D非负6.运筹学研究和解决问题的效果具有〔 AA 连续性B 整体性C 阶段性D 再生性7.运筹学运用数学方法分析与解决问题,以达到系统的最优目标。
数据模型与决策习题与参考答案

数据模型与决策习题与参考答案《数据模型与决策》复习题及参考答案第⼀章绪⾔⼀、填空题1.运筹学的主要研究对象是各种有组织系统的管理问题,经营活动。
2.运筹学的核⼼是运⽤数学⽅法研究各种系统的优化途径及⽅案,为决策者提供科学决策的依据。
3.模型是⼀件实际事物或现实情况的代表或抽象。
4、通常对问题中变量值的限制称为约束条件,它可以表⽰成⼀个等式或不等式的集合。
5.运筹学研究和解决问题的基础是最优化技术,并强调系统整体优化功能。
运筹学研究和解决问题的效果具有连续性。
6.运筹学⽤系统的观点研究功能之间的关系。
7.运筹学研究和解决问题的优势是应⽤各学科交叉的⽅法,具有典型综合应⽤特性。
8.运筹学的发展趋势是进⼀步依赖于_计算机的应⽤和发展。
9.运筹学解决问题时⾸先要观察待决策问题所处的环境。
10.⽤运筹学分析与解决问题,是⼀个科学决策的过程。
11.运筹学的主要⽬的在于求得⼀个合理运⽤⼈⼒、物⼒和财⼒的最佳⽅案。
12.运筹学中所使⽤的模型是数学模型。
⽤运筹学解决问题的核⼼是建⽴数学模型,并对模型求解。
13⽤运筹学解决问题时,要分析,定议待决策的问题。
14.运筹学的系统特征之⼀是⽤系统的观点研究功能关系。
15.数学模型中,“s·t”表⽰约束。
16.建⽴数学模型时,需要回答的问题有性能的客观量度,可控制因素,不可控因素。
17.运筹学的主要研究对象是各种有组织系统的管理问题及经营活动。
⼆、单选题1.建⽴数学模型时,考虑可以由决策者控制的因素是( A )A.销售数量 B.销售价格 C.顾客的需求 D.竞争价格2.我们可以通过( C )来验证模型最优解。
A.观察 B.应⽤ C.实验 D.调查3.建⽴运筹学模型的过程不包括( A )阶段。
A.观察环境 B.数据分析 C.模型设计 D.模型实施4.建⽴模型的⼀个基本理由是去揭晓那些重要的或有关的( B )A数量 B变量 C 约束条件 D ⽬标函数5.模型中要求变量取值( D )A可正 B可负 C⾮正 D⾮负6.运筹学研究和解决问题的效果具有( A )A 连续性B 整体性C 阶段性D 再⽣性7.运筹学运⽤数学⽅法分析与解决问题,以达到系统的最优⽬标。
数据模型与决策作业
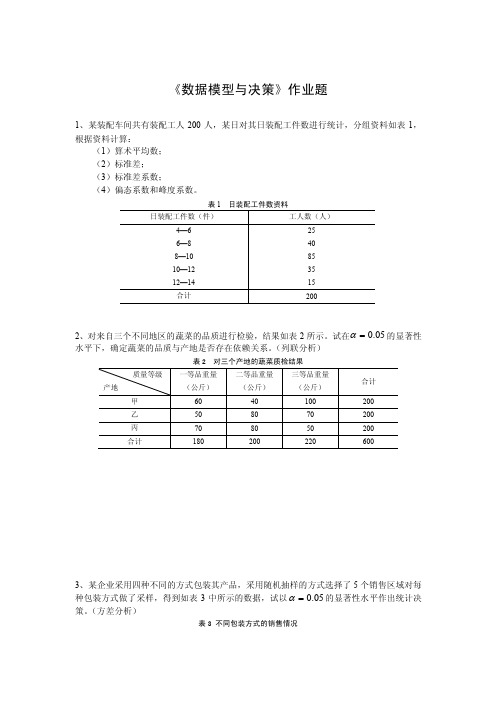
《数据模型与决策》作业题1、某装配车间共有装配工人200人,某日对其日装配工件数进行统计,分组资料如表1,根据资料计算:(1)算术平均数; (2)标准差;(3)标准差系数;(4)偏态系数和峰度系数。
表1 日装配工件数资料日装配工件数(件)工人数(人)4—6 6—8 8—10 10—12 12—14 25 40 85 35 15 合计2002、对来自三个不同地区的蔬菜的品质进行检验,结果如表2所示。
试在05.0=α的显著性水平下,确定蔬菜的品质与产地是否存在依赖关系。
(列联分析)表2 对三个产地的蔬菜质检结果质量等级 产地一等品重量 (公斤)二等品重量 (公斤)三等品重量 (公斤) 合计 甲 60 40 100 200 乙 50 80 70 200 丙 70 80 50 200 合计1802002206003、某企业采用四种不同的方式包装其产品,采用随机抽样的方式选择了5个销售区域对每种包装方式做了采样,得到如表3中所示的数据,试以05.0=α的显著性水平作出统计决策。
(方差分析)表3 不同包装方式的销售情况包装方式 销售区域方式一 方式二 方式三 方式四 1 66 32 46 25 2 45 16 32 15 3 78 66 12 30 4 25 23 45 16 5344650404、已知我国1990年~1999年的货运量y 、工业总产值x 1、农业总产值x 2资料如表4所示:表4 1990年~1999年我国货运量、工业总产值和农业总产值资料年份 货运量(万吨)工业总产值(亿元)农业总产值(亿元)1990 970602 23924 7662.1 1991 985793 26625 8157.0 1992 1045899 34599 9084.7 1993 1115771 48402 10995.5 1994 1180273 70176 15750.5 1995 1234810 91894 20340.9 1996 1296200 99595 22353.7 1997 1278087 113733 23788.4 1998 1267200 119048 24541.9 1999129265012611124519.1要求计算:(1)相关系数(2)二元线性回归方程(3)进行各种统计显著性检验。
数据模型与决策--作业大全详解
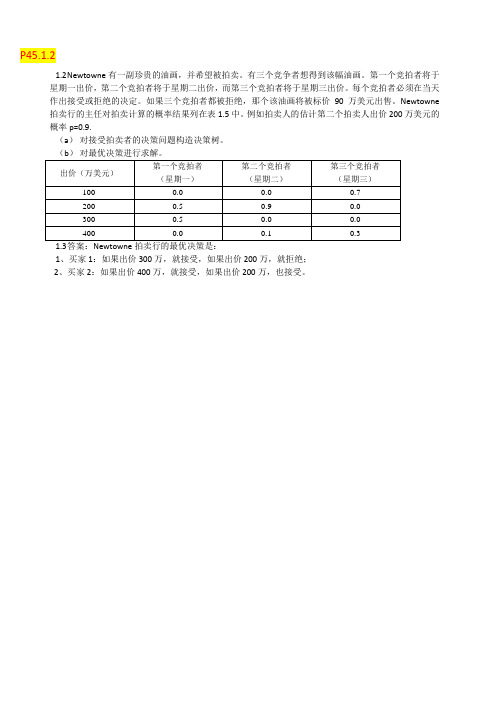
P45.1.21.2N ewtowne有一副珍贵的油画,并希望被拍卖。
有三个竞争者想得到该幅油画。
第一个竞拍者将于星期一出价,第二个竞拍者将于星期二出价,而第三个竞拍者将于星期三出价。
每个竞拍者必须在当天作出接受或拒绝的决定。
如果三个竞拍者都被拒绝,那个该油画将被标价90万美元出售。
Newtowne 拍卖行的主任对拍卖计算的概率结果列在表1.5中。
例如拍卖人的估计第二个拍卖人出价200万美元的概率p=0.9.(a)对接受拍卖者的决策问题构造决策树。
1、买家1:如果出价300万,就接受,如果出价200万,就拒绝;2、买家2:如果出价400万,就接受,如果出价200万,也接受。
接受买家1200 200200接受买家22002002000.50.9接受买家3买家1出价200万买家2出价200万0.7100 21买家3出价100万100100 0220020010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万400400拒绝买家1104000220拒绝买家3909090接受买家24004004000.1接受买家3买家2出价400万0.71001买家3出价100万100100040010100260拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万40040010400拒绝买家3909090接受买家1300 300300接受买家22002002000.50.9接受买家3买家1出价300万买家2出价200万0.7100 11买家3出价100万100100 0300020010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万400400拒绝买家1104000220拒绝买家3909090接受买家24004004000.1接受买家3买家2出价400万0.71001买家3出价100万100100040010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万40040010400拒绝买家39090902.9在美国有55万人感染HIV病毒。
数据模型与决策--作业大全
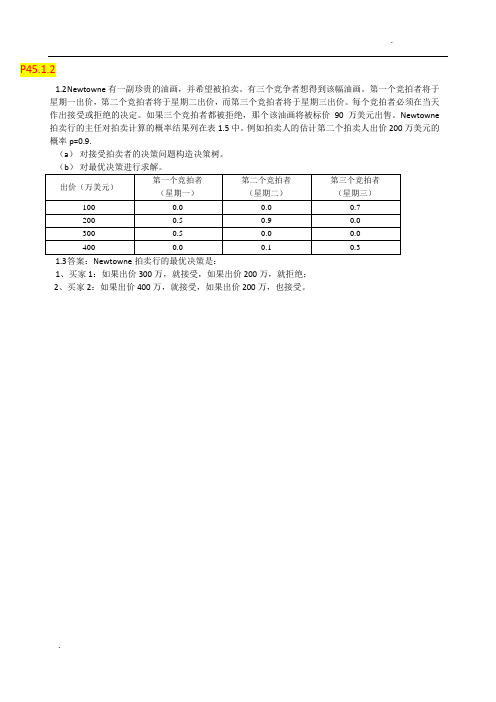
P45.1.21.2N ewtowne有一副珍贵的油画,并希望被拍卖。
有三个竞争者想得到该幅油画。
第一个竞拍者将于星期一出价,第二个竞拍者将于星期二出价,而第三个竞拍者将于星期三出价。
每个竞拍者必须在当天作出接受或拒绝的决定。
如果三个竞拍者都被拒绝,那个该油画将被标价90万美元出售。
Newtowne 拍卖行的主任对拍卖计算的概率结果列在表1.5中。
例如拍卖人的估计第二个拍卖人出价200万美元的概率p=0.9.(a)对接受拍卖者的决策问题构造决策树。
1、买家1:如果出价300万,就接受,如果出价200万,就拒绝;2、买家2:如果出价400万,就接受,如果出价200万,也接受。
接受买家1200 200200接受买家22002002000.50.9接受买家3买家1出价200万买家2出价200万0.7100 21买家3出价100万100100 0220020010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万400400拒绝买家1104000220拒绝买家3909090接受买家24004004000.1接受买家3买家2出价400万0.71001买家3出价100万100100040010100260拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万40040010400拒绝买家3909090接受买家1300 300300接受买家22002002000.50.9接受买家3买家1出价300万买家2出价200万0.7100 11买家3出价100万100100 0300020010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万400400拒绝买家1104000220拒绝买家3909090接受买家24004004000.1接受买家3买家2出价400万0.71001买家3出价100万100100040010100拒绝买家390拒绝买家290900190接受买家30.3400买家3出价400万40040012.9在美国有55万人感染HIV病毒。
数据模型与决策(运筹学)课后习题和案例答案(6)

CHAPTER 7NETWORK OPTIMIZATION PROBLEMS Review Questions7.1-1 A supply node is a node where the net amount of flow generated is a fixed positive number.A demand node is a node where the net amount of flow generated is a fixed negativenumber. A transshipment node is a node where the net amount of flow generated is fixed at zero.7.1-2 The maximum amount of flow allowed through an arc is referred to as the capacity of thatarc.7.1-3 The objective is to minimize the total cost of sending the available supply through thenetwork to satisfy the given demand.7.1-4 The feasible solutions property is necessary. It states that a minimum cost flow problemwill have a feasible solution if and only if the sum of the supplies from its supply nodesequals the sum of the demands at its demand nodes.7.1-5 As long as all its supplies and demands have integer values, any minimum cost flowproblem with feasible solutions is guaranteed to have an optimal solution with integervalues for all its flow quantities.7.1-6 Network simplex method.7.1-7 Applications of minimum cost flow problems include operation of a distribution network,solid waste management, operation of a supply network, coordinating product mixes atplants, and cash flow management.7.1-8 Transportation problems, assignment problems, transshipment problems, maximum flowproblems, and shortest path problems are special types of minimum cost flow problems. 7.2-1 One of the company’s most important distribution centers (Los Angeles) urgently needs anincreased flow of shipments from the company.7.2-2 Auto replacement parts are flowing through the network from the company’s main factoryin Europe to its distribution center in LA.7.2-3 The objective is to maximize the flow of replacement parts from the factory to the LAdistribution center.7.3-1 Rather than minimizing the cost of the flow, the objective is to find a flow plan thatmaximizes the amount flowing through the network from the source to the sink.7.3-2 The source is the node at which all flow through the network originates. The sink is thenode at which all flow through the network terminates. At the source, all arcs point awayfrom the node. At the sink, all arcs point into the node.7.3-3 The amount is measured by either the amount leaving the source or the amount entering thesink.7.3-4 1. Whereas supply nodes have fixed supplies and demand nodes have fixed demands, thesource and sink do not.2. Whereas the number of supply nodes and the number of demand nodes in a minimumcost flow problem may be more than one, there can be only one source and only onesink in a standard maximum flow problem.7.3-5 Applications of maximum flow problems include maximizing the flow through adistribution network, maximizing the flow through a supply network, maximizing the flow of oil through a system of pipelines, maximizing the flow of water through a system ofaqueducts, and maximizing the flow of vehicles through a transportation network.7.4-1 The origin is the fire station and the destination is the farm community.7.4-2 Flow can go in either direction between the nodes connected by links as opposed to onlyone direction with an arc.7.4-3 The origin now is the one supply node, with a supply of one. The destination now is theone demand node, with a demand of one.7.4-4 The length of a link can measure distance, cost, or time.7.4-5 Sarah wants to minimize her total cost of purchasing, operating, and maintaining the carsover her four years of college.7.4-6 When “real travel” through a network can end at more that one node, a dummy destinationneeds to be added so that the network will have just a single destination.7.4-7 Quick’s management must consider trade-offs between time and cost in making its finaldecision.7.5-1 The nodes are given, but the links need to be designed.7.5-2 A state-of-the-art fiber-optic network is being designed.7.5-3 A tree is a network that does not have any paths that begin and end at the same nodewithout backtracking. A spanning tree is a tree that provides a path between every pair of nodes. A minimum spanning tree is the spanning tree that minimizes total cost.7.5-4 The number of links in a spanning tree always is one less than the number of nodes.Furthermore, each node is directly connected by a single link to at least one other node. 7.5-5 To design a network so that there is a path between every pair of nodes at the minimumpossible cost.7.5-6 No, it is not a special type of a minimum cost flow problem.7.5-7 A greedy algorithm will solve a minimum spanning tree problem.17.5-8 Applications of minimum spanning tree problems include design of telecommunicationnetworks, design of a lightly used transportation network, design of a network of high- voltage power lines, design of a network of wiring on electrical equipment, and design of a network of pipelines.Problems7.1a)b)c)1[40] 6 S17 4[-30] D1 [-40] D2 [60] 5 8S2 6[-30] D37.2a)supply nodestransshipment nodesdemand nodesb)[200] P1560 [150]425 [125][0] W1505[150]490 [100]470 [100][-150]RO1[-200]RO2P2 [300]c)510 [175]600 [200][0] W2390 [125]410[150] 440[75]RO3[-150]7.3a)supply nodestransshipment nodesdemand nodesV1W1F1V2V3W2 F21P1W1RO1RO2P2W2RO3[-50] SE3000[20][0]BN5700[40][0]HA[50]BE 4000 6300[40][30] [0][0]NY2000[60]2400[20]3400[10] 4200[80][0]5900[60]5400[40]6800[50]RO[0]BO[0]2500[70]2900[50]b)c)7.4a)LA 3100 NO 6100 LI 3200 ST[-130] [70] [30] [40] [130]1[70]11b)c) The total shipping cost is $2,187,000.7.5a)[0][0] 5900RONY[60] 5400[0] 2900 [50]4200 [80][0] [40] 6800 [50]BO[0] 2500LA 3100 NO 6100 LI 3200 ST [-130][70][30] [40][130]b)c)SEBNHABERONYNY(80) [80] (50) [60](30)[40] ROBO (40)(50) [50] (70)[70]11d)e)f) $1,618,000 + $583,000 = $2,201,000 which is higher than the total in Problem 7.5 ($2,187,000). 7.6LA(70) NO[50](30)LI (30) ST[70][30] [40]There are only two arcs into LA, with a combined capacity of 150 (80 + 70). Because ofthis bottleneck, it is not possible to ship any more than 150 from ST to LA. Since 150 actually are being shipped in this solution, it must be optimal. 7.7[-50] SE3000 [20] [0] BN 5700 [40][0] HA[50] BE4000 6300[40][0] NY2000 [60] 2400 [20][30] [0]5900RO [60]17.8 a) SourcesTransshipment Nodes Sinkb)7.9 a)AKR1[75]A [60]R2[65] [40][50][60] [45]D [120] [70]B[55]E[190]T [45][80] [70][70]R3CF[130][90]SE PT KC SL ATCHTXNOMES S F F CAb)Oil Fields Refineries Distribution CentersTXNOPTCACHATAKSEKCME c)SLSFTX[11][7] NO[5][9] PT[8] [2][5] CA [4] [7] [8] [7] [4] [6][8] CH [7][5][9] [4] ATAK [3][6][6][12] SE KC[8][9][4][8] [7] [12] [11]MESL [9]SF[15][7]d)3Shortest path: Fire Station – C – E – F – Farming Community 7.11 a)A70D40 60O60 5010 B 20 C5540 10 T50E801c)Shortest route: Origin – A – B – D – Destinationd)Yese)Yes7.12a)31,00018,000 21,00001238,000 10,000 12,000b)17.13a) Times play the role of distances.B 2 2 G5ACE 1 31 1b)7.14D F1. C---D: Cost = 14.E---G: Cost = 5E---F: Cost = 1 *choose arbitrarilyD---A: Cost = 4 2.E---G: Cost = 5 E---B: Cost = 7 E---B: Cost = 7 F---G: Cost = 7 E---C: Cost = 4 C---A: Cost = 5F---G: Cost = 7C---B: Cost = 2 *lowestF---C: Cost = 3 *lowest5.E---G: Cost = 5 F---D: Cost = 4 D---A: Cost = 43. E---G: Cost = 5 B---A: Cost = 2 *lowestE---B: Cost = 7 F---G: Cost = 7 F---G: Cost = 7 C---A: Cost = 5F---D: Cost = 46.E---G: Cost = 5 *lowestC---D: Cost = 1 *lowestF---G: Cost = 7C---A: Cost = 5C---B: Cost = 2Total = $14 million7.151. B---C: Cost = 1 *lowest 4. B---E: Cost = 72. B---A: Cost = 4 C---F: Cost = 4 *lowestB---E: Cost = 7 C---E: Cost = 5C---A: Cost = 6 D---F: Cost = 5C---D: Cost = 2 *lowest 5. B---E: Cost = 7C---F: Cost = 4 C---E: Cost = 5C---E: Cost = 5 F---E: Cost = 1 *lowest3. B---A: Cost = 4 *lowest F---G: Cost = 8B---E: Cost = 7 6. E---G: Cost = 6 *lowestC---A: Cost = 6 F---G: Cost = 8C---F: Cost = 4C---E: Cost = 5D---A: Cost = 5 Total = $18,000D---F: Cost = 57.16B 34 2E HA D 2 G I K3C F 12J34B41E6A C41G2 FD1. F---G: Cost = 1 *lowest 6. D---A: Cost = 62. F---C: Cost = 6 D---B: Cost = 5F---D: Cost = 5 D---C: Cost = 4F---I: Cost = 2 *lowest E---B: Cost = 3 *lowestF---J: Cost = 5 F---C: Cost = 6G---D: Cost = 2 F---J: Cost = 5G---E: Cost = 2 H---K: Cost = 7G---H: Cost = 2 I---K: Cost = 8G---I: Cost = 5 I---J: Cost = 33. F---C: Cost = 6 7. B---A: Cost = 4F---D: Cost = 5 D---A: Cost = 6F---J: Cost = 5 D---C: Cost = 4G---D: Cost = 2 *lowest F---C: Cost = 6G---E: Cost = 2 F---J: Cost = 5G---H: Cost = 2 H---K: Cost = 7I---H: Cost = 2 I---K: Cost = 8I---K: Cost = 8 I---J: Cost = 3 *lowestI---J: Cost = 3 8. B---A: Cost = 4 *lowest4. D---A: Cost = 6 D---A: Cost = 6D---B: Cost = 5 D---C: Cost = 4D---E: Cost = 2 *lowest F---C: Cost = 6D---C: Cost = 4 H---K: Cost = 7F---C: Cost = 6 I---K: Cost = 8F---J: Cost = 5 J---K: Cost = 4G---E: Cost = 2 9. A---C: Cost = 3 *lowestG---H: Cost = 2 D---C: Cost = 4I---H: Cost = 2 F---C: Cost = 6I---K: Cost = 8 H---K: Cost = 7I---J: Cost = 3 I---K: Cost = 85. D---A: Cost = 6 J---K: Cost = 4D---B: Cost = 5 10. H---K: Cost = 7D---C: Cost = 4 I---K: Cost = 8E---B: Cost = 3 J---K: Cost = 4 *lowestE---H: Cost = 4F---C: Cost = 6F---J: Cost = 5G---H: Cost = 2 *lowest Total = $26 millionI---H: Cost = 2I---K: Cost = 8I---J: Cost = 37.17a) The company wants a path between each pair of nodes (groves) that minimizes cost(length of road).b)7---8 : Distance = 0.57---6 : Distance = 0.66---5 : Distance = 0.95---1 : Distance = 0.75---4 : Distance = 0.78---3 : Distance = 1.03---2 : Distance = 0.9Total = 5.3 miles7.18a) The bank wants a path between each pair of nodes (offices) that minimizes cost(distance).b) B1---B5 : Distance = 50B5---B3 : Distance = 80B1---B2 : Distance = 100B2---M : Distance = 70B2---B4 : Distance = 120Total = 420 milesHamburgBostonRotterdamSt. PetersburgNapoliMoscowA IRFIELD SLondonJacksonvilleBerlin RostovIstanbulCases7.1a) The network showing the different routes troops and supplies may follow to reach the Russian Federation appears below.PORTSb)The President is only concerned about how to most quickly move troops and suppliesfrom the United States to the three strategic Russian cities. Obviously, the best way to achieve this goal is to find the fastest connection between the US and the three cities.We therefore need to find the shortest path between the US cities and each of the three Russian cities.The President only cares about the time it takes to get the troops and supplies to Russia.It does not matter how great a distance the troops and supplies cover. Therefore we define the arc length between two nodes in the network to be the time it takes to travel between the respective cities. For example, the distance between Boston and London equals 6,200 km. The mode of transportation between the cities is a Starlifter traveling at a speed of 400 miles per hour * 1.609 km per mile = 643.6 km per hour. The time is takes to bring troops and supplies from Boston to London equals 6,200 km / 643.6 km per hour = 9.6333 hours. Using this approach we can compute the time of travel along all arcs in the network.By simple inspection and common sense it is apparent that the fastest transportation involves using only airplanes. We therefore can restrict ourselves to only those arcs in the network where the mode of transportation is air travel. We can omit the three port cities and all arcs entering and leaving these nodes.The following six spreadsheets find the shortest path between each US city (Boston and Jacksonville) and each Russian city (St. Petersburg, Moscow, and Rostov).The spreadsheets contain the following formulas:Comparing all six solutions we see that the shortest path from the US to Saint Petersburg is Boston → London → Saint Petersburg with a total travel time of 12.71 hours. The shortest path from the US to Moscow is Boston → London → Moscow with a total travel time of 13.21 hours. The shortest path from the US to Rostov is Boston →Berlin → Rostov with a total travel time of 13.95 hours. The following network diagram highlights these shortest paths.-1c)The President must satisfy each Russian city’s military requirements at minimum cost.Therefore, this problem can be solved as a minimum-cost network flow problem. The two nodes representing US cities are supply nodes with a supply of 500 each (wemeasure all weights in 1000 tons). The three nodes representing Saint Petersburg, Moscow, and Rostov are demand nodes with demands of –320, -440, and –240,respectively. All nodes representing European airfields and ports are transshipment nodes. We measure the flow along the arcs in 1000 tons. For some arcs, capacityconstraints are given. All arcs from the European ports into Saint Petersburg have zero capacity. All truck routes from the European ports into Rostov have a transportation limit of 2,500*16 = 40,000 tons. Since we measure the arc flows in 1000 tons, the corresponding arc capacities equal 40. An analogous computation yields arc capacities of 30 for both the arcs connecting the nodes London and Berlin to Rostov. For all other nodes we determine natural arc capacities based on the supplies and demands at the nodes. We define the unit costs along the arcs in the network in $1000 per 1000 tons (or, equivalently, $/ton). For example, the cost of transporting 1 ton of material from Boston to Hamburg equals $30,000 / 240 = $125, so the costs of transporting 1000 tons from Boston to Hamburg equals $125,000.The objective is to satisfy all demands in the network at minimum cost. The following spreadsheet shows the entire linear programming model.HamburgBoston Rotterdam St.Petersburg+500-320Napoli Moscow A IRF IELDSLondon -440Jacksonville Berlin Rostov+500-240Istanbul The total cost of the operation equals $412.867 million. The entire supply for SaintPetersburg is supplied from Jacksonville via London. The entire supply for Moscow is supplied from Boston via Hamburg. Of the 240 (= 240,000 tons) demanded by Rostov, 60 are shipped from Boston via Istanbul, 150 are shipped from Jacksonville viaIstanbul, and 30 are shipped from Jacksonville via London. The paths used to shipsupplies to Saint Petersburg, Moscow, and Rostov are highlighted on the followingnetwork diagram.PORTSd)Now the President wants to maximize the amount of cargo transported from the US tothe Russian cities. In other words, the President wants to maximize the flow from the two US cities to the three Russian cities. All the nodes representing the European ports and airfields are once again transshipment nodes. The flow along an arc is againmeasured in thousands of tons. The new restrictions can be transformed into arccapacities using the same approach that was used in part (c). The objective is now to maximize the combined flow into the three Russian cities.The linear programming spreadsheet model describing the maximum flow problem appears as follows.The spreadsheet shows all the amounts that are shipped between the various cities. The total supply for Saint Petersburg, Moscow, and Rostov equals 225,000 tons, 104,800 tons, and 192,400 tons, respectively. The following network diagram highlights the paths used to ship supplies between the US and the Russian Federation.PORTSHamburgBoston Rotterdam St.Petersburg+282.2 -225NapoliMoscowAIRFIELDS-104.8LondonJacksonvilleBerlin Rostov +240 -192.4Istanbule)The creation of the new communications network is a minimum spanning tree problem.As usual, a greedy algorithm solves this type of problem.Arcs are added to the network in the following order (one of several optimal solutions):Rostov - Orenburg 120Ufa - Orenburg 75Saratov - Orenburg 95Saratov - Samara 100Samara - Kazan 95Ufa – Yekaterinburg 125Perm – Yekaterinburg 857.2a) There are three supply nodes – the Yen node, the Rupiah node, and the Ringgit node.There is one demand node – the US$ node. Below, we draw the network originatingfrom only the Yen supply node to illustrate the overall design of the network. In thisnetwork, we exclude both the Rupiah and Ringgit nodes for simplicity.b)Since all transaction limits are given in the equivalent of $1000 we define the flowvariables as the amount in thousands of dollars that Jake converts from one currencyinto another one. His total holdings in Yen, Rupiah, and Ringgit are equivalent to $9.6million, $1.68 million, and $5.6 million, respectively (as calculated in cells I16:K18 inthe spreadsheet). So, the supplies at the supply nodes Yen, Rupiah, and Ringgit are -$9.6 million, -$1.68 million, and -$5.6 million, respectively. The demand at the onlydemand node US$ equals $16.88 million (the sum of the outflows from the sourcenodes). The transaction limits are capacity constraints for all arcs leaving from thenodes Yen, Rupiah, and Ringgit. The unit cost for every arc is given by the transactioncost for the currency conversion.Jake should convert the equivalent of $2 million from Yen to each US$, Can$, Euro, and Pound. He should convert $1.6 million from Yen to Peso. Moreover, he should convert the equivalent of $200,000 from Rupiah to each US$, Can$, and Peso, $1 million from Rupiah to Euro, and $80,000 from Rupiah to Pound. Furthermore, Jake should convert the equivalent of $1.1 million from Ringgit to US$, $2.5 million from Ringgit to Euro, and $1 million from Ringgit to each Pound and Peso. Finally, he should convert all the money he converted into Can$, Euro, Pound, and Peso directly into US$. Specifically, he needs to convert into US$ the equivalent of $2.2 million, $5.5 million, $3.08 million, and $2.8 million Can$, Euro, Pound, and Peso, respectively. Assuming Jake pays for the total transaction costs of $83,380 directly from his American bank accounts he will have $16,880,000 dollars to invest in the US.c)We eliminate all capacity restrictions on the arcs.Jake should convert the entire holdings in Japan from Yen into Pounds and then into US$, the entire holdings in Indonesia from Rupiah into Can$ and then into US$, and the entire holdings in Malaysia from Ringgit into Euro and then into US$. Without the capacity limits the transaction costs are reduced to $67,480.d)We multiply all unit cost for Rupiah by 6.The optimal routing for the money doesn't change, but the total transaction costs are now increased to $92,680.e)In the described crisis situation the currency exchange rates might change every minute.Jake should carefully check the exchange rates again when he performs thetransactions.The European economies might be more insulated from the Asian financial collapse than the US economy. To impress his boss Jake might want to explore other investment opportunities in safer European economies that provide higher rates of return than US bonds.。
数据模型与决策课程学习大作业.doc

数据模型与决策课程大作业以我国汽油消费量为因变量,乘用车销量、城镇化率和90#汽油吨价与城镇居民人均可支配收入的比值为自变量时行回归(数据为年度时间序列数据)。
试根据得到部分输出结果,回答下列问题:1)“模型汇总表”中的R方和标准估计的误差是多少?2)写出此回归分析所对应的方程;3)将三个自变量对汽油消费量的影响程度进行说明;4)对回归分析结果进行分析和评价,指出其中存在的问题。
1)“模型汇总表”中的R方和标准估计的误差是多少?答案:R方为0.993^2=0.986 ;标准估计的误差为120910.147^(0.5)=347.722)写出此回归分析所对应的方程;答案:假设汽油消费量为Y,乘用车销量为a,城镇化率为b,90#汽油吨价/城镇居民人均可支配收入为c,则回归方程为:Y=240.534+0.00s027a+8649.895b-198.692c3)将三个自变量对汽油消费量的影响程度进行说明;乘用车销量对汽油消费量相关系数只有0.00027,数值太小,几乎没有影响,但是城镇化率对汽油消费量相关系数是8649.895,具有明显正相关,当城镇化率每提高1,汽油消费量增加8649.895。
乘用90#汽油吨价/城镇居民人均可支配收入相关系数为-198.692,呈明显负相关,即乘用90#汽油吨价/城镇居民人均可支配收入每增加1个单位,汽油消费量降低198.692个单位。
a, b, c三个自变量的sig 值为0.000、0.000、0.009,在显著性水平0.01情形下,乘用车消费量对汽油消费量的影响显著为正。
(4)对回归分析结果进行分析和评价,指出其中存在的问题。
在学习完本课程之后,我们可以统计方法为特征的不确定性决策、以运筹方法为特征的策略的基本原理和一般方法为基础,结合抽样、参数估计、假设分析、回归分析等知识对我国汽油消费量影响因素进行了模拟回归,并运用软件计算出回归结果,故根据回归结果,对具体回归方程,回归准确性,自变量影响展开分析。
(完整word版)数据,模型与决策练习题含

1、某企业目前的损益情况如在下:销售收入〔 1000 件× 10 元 / 件〕10 000销售本钱:变动本钱〔 1000 件× 6 元/ 件〕 6 000固定本钱 2 000销售和管理费〔全部固定〕 1 000利润 1 000〔 1〕假设企业按国家规定普调薪水,使单位变动本钱增加4%,固定本钱增加1%,结果将会以致利润下降。
为了抵销这种影响企业有两个对付措施:一是提升价格5%,而提价会使销量减少10%;二是增加产量20%,为使这些产品能销售出去,要追加500 元广告费。
请做出选择,哪一个方案更有利?(2〕假设企业欲使利润增加 50%,即到达 1 500 元,能够从哪几个方面着手,采用相应的措施。
2、某企业每个月固定制造本钱 1 000 元,固定销售费100 元,固定管理费 150 元;单位变动制造本钱 6 元,单位变动销售费0.70 元,单位变动管理费0.30 元;该企业生产一种产品,单价 10元,所得税税率 50%;本月方案产销 600 件产品,问预期利润是多少?如拟实现净利 500 元,应产销多少件产品?3、某企业生产甲、乙、丙三种产品,固定本钱 500000 元,相关资料见下表〔单位:元〕:产品单价单位变动本钱销量甲1008012000乙907515000丙95808000要求:(1〕计算各产品的边缘奉献;(2〕计算加权平均边缘奉献率;(3〕依照加权平均边缘奉献率计算预期税前利润。
4、某企业每年耗用某种资料 3 600 千克,单位储藏本钱为 2 元,一次订货本钱25 元。
那么经济订货批量、每年最正确订货次数、最正确订货周期、与批量相关的存货总本钱是多少?5.有 10 个同类企业的生产性固定财富年平均价值和工业总产值资料以下:企业编生产性固定财富价值(万元 )工业总产值〔万元〕号131852429101019320063844098155415913650292873146058121015169102212191012251624合计65259801(1〕说明两变量之间的相关方向;(2〕建立直线回归方程;〔 3〕估计生产性固定财富〔自变量〕为1100 万元时总产值〔因变量〕的可能值。
数据模型与决策课

数据模型与决策课程大作业数据模型与决策课程大作业以我国汽油消费量为因变量,乘用车销量、城镇化率和90#汽油吨价与城镇居民人均可支配收入的比值为自变量时行回归(数据为年度时间序列数据)。
试根据得到部分输出结果,回答下列问题:1)“模型汇总表”中的R方和标准估计的误差是多少?2)写出此回归分析所对应的方程;3)将三个自变量对汽油消费量的影响程度进行说明;4)对回归分析结果进行分析和评价,指出其中存在的问题。
1)“模型汇总表”中的R方和标准估计的误差是多少?答案:R方为0.993^2=0.986 ;标准估计的误差为120910.147^(0.5)=347.722)写出此回归分析所对应的方程;答案:假设汽油消费量为Y,乘用车销量为a,城镇化率为b,90#汽油吨价/城镇居民人均可支配收入为c,则回归方程为:Y=240.534+0.00s027a+8649.895b-198.692c3)将三个自变量对汽油消费量的影响程度进行说明;乘用车销量对汽油消费量相关系数只有0.00027,数值太小,几乎没有影响,但是城镇化率对汽油消费量相关系数是8649.895,具有明显正相关,当城镇化率每提高1,汽油消费量增加8649.895。
乘用90#汽油吨价/城镇居民人均可支配收入相关系数为-198.692,呈明显负相关,即乘用90#汽油吨价/城镇居民人均可支配收入每增加1个单位,汽油消费量降低198.692个单位。
a, b, c三个自变量的sig 值为0.000、0.000、0.009,在显著性水平0.01情形下,乘用车消费量对汽油消费量的影响显著为正。
(4)对回归分析结果进行分析和评价,指出其中存在的问题。
在学习完本课程之后,我们可以统计方法为特征的不确定性决策、以运筹方法为特征的策略的基本原理和一般方法为基础,结合抽样、参数估计、假设分析、回归分析等知识对我国汽油消费量影响因素进行了模拟回归,并运用软件计算出回归结果,故根据回归结果,对具体回归方程,回归准确性,自变量影响展开分析。
《数据模型与决策》练习题及答案
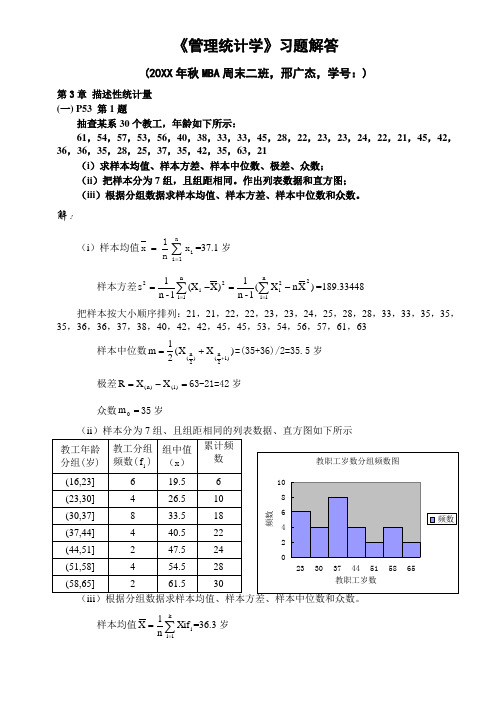
《管理统计学》习题解答(20XX 年秋MBA 周末二班,邢广杰,学号:)第3章 描述性统计量 (一) P53 第1题抽查某系30个教工,年龄如下所示:61,54,57,53,56,40,38,33,33,45,28,22,23,23,24,22,21,45,42,36,36,35,28,25,37,35,42,35,63,21(i )求样本均值、样本方差、样本中位数、极差、众数;(ii )把样本分为7组,且组距相同。
作出列表数据和直方图; (iii )根据分组数据求样本均值、样本方差、样本中位数和众数。
解:(i )样本均值∑==n1i ixn1x =37.1岁样本方差)X n X (1-n 1)X (X 1-n 1s 2n 1i 2i2n 1i i 2-=-=∑∑===189.33448 把样本按大小顺序排列:21,21,22,22,23,23,24,25,28,28,33,33,35,35,35,36,36,37,38,40,42,42,45,45,53,54,56,57,61,63样本中位数)X X (21m 1)2n ()2n (++==(35+36)/2=35.5岁极差=-=1)()n (X X R 63-21=42岁 众数=0m 35岁(ii )样本分为7组、且组距相同的列表数据、直方图如下所示样本均值i k1i f Xi n 1X ∑===36.3岁样本方差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i 2i i2k 1i i 2-=-=∑∑===174.3724 样本中位数810230730f F 2n i I m -+=-+==34.375岁 众数=--⨯-+=---+=+448248730f f 2f f f iI m 1m 1-m m 1-m m 033.5岁(二)P53 第2题某单位统计了不同级别的员工的月工资水平资料如下:解:样本均值i k1i f Xi n 1X ∑===1566.667元样本标准差)X n f X (1-n 1f )X (X 1-n 1s 2k 1i i2i i 2k 1i i -=-=∑∑===398.1751元 样本中位数在累计74人的那一组,m=1500元; 众数1500m 0=元。
运筹学数据模型与决策教材习题答案

教材习题答案1.2 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-22所示.130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为1.3 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:【解】 设x j (j =1,2,…,14)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为用单纯形法求解得到两个基本最优解X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 (2)余料最少数学模型为用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料650根 显然用料最少的方案最优。
1.7 图解下列线性规划并指出解的形式:(1) 121212max 2131,0Z x x x x x x x x =-++≥⎧⎪-≥-⎨⎪≥⎩【解】最优解X =(1/2,1/2);最优值Z=-1/2(2) 12121212min 32223120,0Z x x x x x x x x =---≥-⎧⎪+≤⎨⎪≥≥⎩【解】最优解X =(3/4,7/2);最优值Z=-45/4(3)121212121212min 322114102731,0Z x x x x x x x x x x x x =-++≤⎧⎪-+≤⎪⎪-≤⎨⎪-≤⎪⎪≥⎩【解】最优解X =(4,1);最优值Z=-10(4) 121212112max 3812223,0Z x x x x x x x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ 【解】最优解X =(3/2,1/4);最优值Z=7/4(5) ⎪⎪⎩⎪⎪⎨⎧≥≤≥≥-+=0,6322min 21212121x x x x x x x x Z 【解】最优解X =(3,0);最优值Z=3 (6) ⎪⎪⎩⎪⎪⎨⎧≥≤≥≥-+=0,6322max 21212121x x x x x x x x Z【解】无界解。
数据模型与决策

0.9185 和 28.6。
定义 设总体的概率函数为P(x; ), 是参数 可能取值的参数空间,x1, x2 , …, xn 是样本,将 样本的联合概率函数看成 的函数,用L( ; x1, x2, …, xn) 表示,简记为L( ),
总体与样本
1 添加标题
总体 美国2亿五千多万成年人
2 添加标题
样本 1015人
3 添加标题
抽取样本
4 添加标题
推断总体
5 添加标题
在全部美国2亿五千多万成 年人中克林顿政府外交政 策和经济政策支持率各是 多少?
6 添加标题
经统计:在样本1015人中各 有39%(396)的和42%(426) 的人分别支持克林顿政府的 外交政策和经济政策
样本均值x是总体均值的(点)估计
在样本容量 n 比较大的时候
关于比例和均值的 总体比例 P 的置信水平例如为 95%的区间估计为 估计 p1 p
p 1.96 n
总体均值的置信水平例如为 95%的区间估计为
x 1.96 s n
有些问题,由于种种原因例如希望试验成本低一
些,或希望试验时间短一些,或就只作了少数几次
观察,以至于样本容量比较小。在样本容量n比较
小的时候,在n样x s 本接近容N量0,1比的情较况小就比的较差。n越
小,情况越差。
时候
在总体的分布为正态分布N ,2 的时候,
样本n容x s量的小(精,确且)分总布体为t为n 正1分态布分布
圆钢强度的测量是一个破坏性试验,其样本容
量不会很大。现测得n 7根圆钢的强度数据:
p 分位数,
Vˆ ar(X) sn2
数据、模型与决策(运筹学)课后习题和案例答案001

CHAPTER 1INTRODUCTIONReview Questions1.1-1 The rapid development of the discipline began in the 1940’s and 1950’s.1.1-2 The traditional name given to the discipline is operations research.1.1-3 A management science study provides an analysis and recommendations, based onthe quantitative factors involved in the problem, as input to the managers.1.1-4 Management science is based strongly on some scientific fields, includingmathematics and computer science. It also draws upon the social sciences, especially economics.1.1-5 A decision support system is an interactive computer-based system that aidsmanagerial decision-making. The system draws current data from databases or management information systems and then solves the various versions of the model specified by the manager.1.1-6 Many managerial problems revolve around such quantitative factors as productionquantities, revenues, costs, the amounts available of needed resources, etc.1.2-1 The production and sales volume needs to exceed the break-even point to make itworthwhile to introduce a product.1.2-2 The number of clocks produced cannot be less than 0, nor should it exceed thenumber that can be sold. Also, the objective is to make the decision that maximizes the company’s profit.1.2-3 The purpose of sensitivity analysis is to check the effect on the recommendations of amodel if the estimates turn out to be wrong.1.2-4 Simply enter a variety of new values and see what happens.1.2-5 The MIN(a, b) function gives the minimum of a and b.1.2-6 The IF(a, b, c) function returns b if a is true, otherwise it returns c.1.3-1 These applications typically resulted in annual savings in the millions of dollars. Problems1.1 Answers will vary.1.2 Answers will vary.1.3 If Q units are produced per month, thenMonthly Profit = $0 {if Q= 0} and –$20,000 + ($20 –$10)Q{if Q> 0}.Break-even point = $20,000 / ($20 – $10) = 2000,so it will be profitable to produce if Q > 2000.1.4 a) $40,000b) $15.c) $15.1.5 a) Let Q be the number of units produced and sold. ThenMonthly Profit = $0 {if Q= 0} and –$500,000 + ($35 – $15)Q{if Q> 0}.Break-even point = $500,000 / ($35 – $15) = 25,000.b) Let Q be the number produced and s the number that can be sold. ThenProfit = [0 if Q = 0] and [-$500,000 + $35 * MIN(Q, s) – $15Q if Q > 0].c)d) Q≤ s.1.6 a) $150,000b) $733.33c) $566.671.7 a)b) Break-even point = ($50,000) / ($700 – $500) = 250.c) Maximize Profit = $0 {if Q= 0} and –$50,000 + $200Q{if Q> 0}subject to 0 ≤ Q≤ s.d)e)1.8 a) Jennifer must decide how much to ship from each plant (A and B) to each retailoutlet (1 and 2). Let xˆj = amount to ship from plant i (for i = A, B) to each retailoutlet j (for j = 1, 2).b) Shipping Cost = $700x A1 + $400x A2 + $800x B1 + $600x B2c) x A1 + x A2 = 30; x B1 + x B2≤ 500; x A1 + x B1 = 40; x A2 + x B2≥ 25; all x ij≥ 0.d) Minimize Shipping Cost = $700x A1+ $400x A2+ $800x B1+ $600x B2subject to x A1+ x A2= 30x B1+ x B2≤ 500x A1+ x B1= 40x A2+ x B2≥ 25 andall x ij≥ 0e) Jennifer should ship all of Retail Outlet 2’s 25 units from Plant A because it is $200cheaper than from Plant B. Retail Outlet 1 should get all it can from Plant A (5units) because it is $100 cheaper than from Plant B. The remaining 35 units shouldcome from Plant B. The decision variables would be x A1 = 5, x A2 = 25, x B1 = 35, x B2 =0.1.9 a)b) Break-even point = $1,000,000 / ($2,000 - $1,600) = 2,500.1.10 a)b) The make option appears to be better ($100,000 profit for the make option vs.$75,000 profit for the buy option).c) Q= number of grandfather clocks to produce for sale.Make Option: Profit = $0 {if Q= 0} and –$50,000 + $500Q{if Q> 0}.Buy Option: Profit = ($900 –$650)Q= $250QIncremental profit from choosing make option rather than buy option = $0 {if Q=0} and= –$50,000 + $500Q–$250Q= –$50,000 + $250Q{if Q> 0}.Mathematical model: Now interpret Q as the number to produce with the make option. The model is to find the value of Q so as toMaximize Incremental Profit = $0 {if Q=0} and= –$50,000 + $500Q–$250Q= –$50,000 + $250Q{if Q> 0}subject to Q≤ s(sales forecast)Q≥ 0.d)e) Make-option cost = $50,000 + $400QBuy-option cost = $650Q Break-even point = $50,000 / ($650 – $400) = 200 units.。
MBA数据、模型 课堂大作业

《数据、模型与决策》案例案例1 北方化工厂月生产计划安排(0.7+0.3)一. 问题提出根据经营现状和目标,合理制定生产计划并有效组织生产,是一个企业提高效益的核心。
特别是对于一个化工厂而言,由于其原料品种多,生产工艺复杂,原材料和产成品存储费用较高,并有一定的危险性,对其生产计划作出合理安排就显得尤为重要。
现要求我们对北方化工厂的生产计划做出合理安排。
二. 有关数据1.生产概况北方化工厂现在有职工120人,其中生产工人105名。
主要设备是2套提取生产线,每套生产线容量为800kg,至少需要10人看管。
该工厂每天24小时连续生产,节假日不停机。
原料投入到成品出线平均需要10小时,成品率约为60%,该厂只有4吨卡车1辆,可供原材料运输。
2.产品结构及有关资料该厂目前的产品可分为5类,多有原料15种,根据厂方提供的资料,经整理得表1。
3.供销情况①根据现有运出条件,原料3从外地购入,每月只能购入1车。
②根据前几个月的销售情况,产品1和产品3应占总产量的70%,产品2的产量最好不要超过总产量的5%,产品1的产量不要低于产品3与产品4的产量之和。
问题:a.请作该厂的月生产计划,使得该厂的总利润最高。
b.找出阻碍该厂提高生产能力的瓶颈问题,提出解决办法。
案例2 石华建设监理公司监理工程师配置问题(0.8+0.2)石华建设监理公司(国家甲级),侧重国家大中型项目的监理,仅在河北省石家庄市就正在监理七项工程,总投资均在5000万元以上。
由于工程开工的时间不同,多工程工期之间相互搭接,具有较长的连续性,2012年监理的工程量与2011年监理的工程量大致相同。
每项工程安排多少监理工程师进驻工地,一般是根据工程的投资,建筑规模,使用功能,施工的形象进度,施工阶段来决定的。
监理工程师的配置数量是随之而变化的。
由于监理工程师从事的专业不同,他们每人承担的工作量也是不等的。
有的专业一个工地就需要三人以上,而有的专业一人则可以兼管三个以上的工地。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据模型与决策课程大作业
以我国汽油消费量为因变量,乘用车销量、城镇化率和90#汽油吨价与城镇居民人均可支配收入的比值为自变量时行回归(数据为年度时间序列数据)。
试根据得到部分输出结果,回答下列问题:1)“模型汇总表”中的R方和标准估计的误差是多少?
2)写出此回归分析所对应的方程;
3)将三个自变量对汽油消费量的影响程度进行说明;
4)对回归分析结果进行分析和评价,指出其中存在的问题。
1)“模型汇总表”中的R方和标准估计的误差是多少?
答案:R方为0.993^2=0.986 ;标准估计的误差为120910.147^(0.5)=347.72
2)写出此回归分析所对应的方程;
答案:假设汽油消费量为Y,乘用车销量为a,城镇化率为b,90#汽油吨价/城镇居民人均可支配收入为c,则回归方程为:
Y=240.534+0.00s027a+8649.895b-198.692c
3)将三个自变量对汽油消费量的影响程度进行说明;
乘用车销量对汽油消费量相关系数只有0.00027,数值太小,几乎没有影响,但是城镇化率对汽油消费量相关系数是8649.895,具有明显正相关,当城镇化率每提高1,汽油消费量增加8649.895。
乘用90#汽油吨价/城镇居民人均可支配收入相关系数为-198.692,呈
明显负相关,即乘用90#汽油吨价/城镇居民人均可支配收入每增加1个单位,汽油消费量降低198.692个单位。
a, b, c三个自变量的sig 值为0.000、0.000、0.009,在显著性水平0.01情形下,乘用车消费量对汽油消费量的影响显著为正。
(4)对回归分析结果进行分析和评价,指出其中存在的问题。
在学习完本课程之后,我们可以统计方法为特征的不确定性决策、以运筹方法为特征的策略的基本原理和一般方法为基础,结合抽样、参数估计、假设分析、回归分析等知识对我国汽油消费量影响因素进行了模拟回归,并运用软件计算出回归结果,故根据回归结果,对具体回归方程,回归准确性,自变量影响展开分析。
Anova表中,sig值是t统计量对应的概率值,所以t和sig两者是等效的,sig要小于给定的显著性水平,越接近于0越好。
F是检验方程显著性的统计量,是平均的回归平方和平均剩余平方和之比,越大越好。
在图表中,回归模型统计值F=804.627,p值为0.000,因此证明回归模型有统计学意义,表现回归极显著。
即因变量与三个自变量之间存在线性关系。
系数表中,除了常数项系数显著性水平大于0.05,不影响,其它项系数都是0.000,小于0.005,即每个回归系数均具有意义。
当然,这其中也存在一定的问题:
在模型设计中,乘用车销量为、城镇化率为、90#汽油吨价/城镇居民人均可支配收入为三个自变量的单位均不同,因此会造成自变量前面的回归系数不具有准确的宏观意义,因此需要对模型进行实现标准化,也就是引入β系数,消除偏回归系数带来的数量单位影响。
根据共线性统计量中的变量的容差t和方差膨胀因子(VIF),自变量间存在共性问题,容差和膨胀因子为倒数关系,容差越小,膨胀因子越大,尤其是城镇化率VIF为11.213,说明共线性明显,可能原因是由于样本容量太小,也可能是城镇化之后乘用车销售量和、90#汽油吨价/城镇居民人均可支配收入本身就具有相关性。
缺乏模型异方差检验。
在多元回归模型中,由于数据质量原因、模型设定原因,异方差的存在会使回归系数估计结果误差较多,所以在建立模型分析的过程红要对异方差进行检验。
数据模型与决策使我们学会使用科学的分析和决策,对经营管理活动实现合理化、精细化、科学化,从而避免了盲目的生产活动。
通
过数据预测、假设检验、公式、分析、验证等一系列的步骤,将数据结果逐一展现。
为我们的学习和工作提供了一些非常有用、便捷的,处理问题的方法。
附表:t分布表:
df 单尾检验的显著水平
0.050 0.025 0.010 0.005 双尾检验的显著水平
0.10 0.05 0.02 0.01
3 2.353 3.182 4.541 5.841
4 2.132 2.776 3.747 4.604
5 2.015 2.571 3.365 4.032
6 1.943 2.44
7 3.143 3.707
7 1.895 2.365 2.998 3.499
8 1.860 2.306 2.896 3.355
9 1.833 2.262 2.821 3.250
10 1.812 2.228 2.764 3.169
11 1.796 2.201 2.718 3.106
12 1.782 2.179 2.681 3.055
13 1.771 2.160 2.650 3.012
赠送以下资料
新课程标准学习计划
为切实学习好新课程,把握好新课程标准的教学思想,实施好新课程,制定如下计划。
一、加强领导完善制度
1、建立以校长为组长的科研领导小组,由校长亲自抓新课程的实施;进一步完善教研教改制度,建立教科研工作制度,定期召开新课程研讨会,组织研究课,作好研究记录,保证研究探讨的连续性和完备性。
2、完善考评制度。
学校制定出详细的考评细则,对教师实践新课程进行考核,对教师成绩并入本学期综合考评,记入个人档案,作为评优的重要依据。
二、加强对新课程标准的学习
1、严格学习制度,规定每周三下午为固定学习时间,制定学习计划,明确学习内容,落实保障措施,将学习情况纳入对教师的考核
量化。
本学期的重点学习内容是各科新课程标准,《走进新课程》及有关新课程方面的理论文章,每位教师本学期做新课程学习笔记不少于5千字。
2、积极组织有关新课程方面的论文撰写、评选及征文活动和教案评选活动,要求教师围绕新课程的内涵、目标、任务、措施等展开进一步的讨论,并结合自己在实践新课程中的教学体会,写出有独到见解的优秀论文,鼓励教师精心设计教案,实践好新教材,对优秀论文和优秀教案及时向上推荐和上报。
3、通过走出去和请进来的办法,促进新课程的学习,本学期打算请区教研室的领导就新课程方面进行理论讲座和发表指导建议。
积极参加区教研室组织的外出培训学习,通过学习我们力求达到三个认识和四个转化:(1)提高对新课程的认识,增强教育改革的责任感。
(2)提高主体意识,让学生成为学习的主人。
(3)提高能力意识,树立新的教育质量观。
实现四个转变:(1)传授知识教学向培养学生学会学习的教学转变。
(2)实现由单向交流向多维互动转变。
(3)实现有封闭性课堂向选择性、开放性、实践性课堂转变。
(4)实现由重结果教学为重知识形成过程的转变。
三、努力提高教师素质
1、把年轻的教学能手、教学骨干作为实践新课程的领头兵,鼓励他们积极投身于新课程的学习实践和研究,为他们创造展现才能的时空。
2、有重点的培养。
寻找一切可能的机会,让他们参加大型的或较高层次的理论学习和研讨会,增强课程改革意识和改革能力。
3、充分发挥能动作用,鼓励教师从教学中发现问题,主动研究,从备课、上课、批改作业和课外活动等教学环节中,发现值得研究的问题,在教育理论的指导下,不断进行教学改革尝试,探索解决问题的有效方法。
4、压担子。
每学期给教师定目标、定任务:学校规定每位教师都要有自己的研究课题,对研究课题要有计划、有实施方案、有研究记录、有阶段性总结,每位教师都要结合教研教改实际,写出一篇高质量的论文和精心设计一篇教案,每人上好一堂公开课或示范课。
5、发挥示范作用,提高整体素质,采取一帮一结对子的形式,营造出一个互相激励,互相支持,互相帮助的改革氛围,用集体的智慧来解决新课程实践过程中碰到的问题。
总之,我们将在县局的领导下,依照区教研室及上级主管部门的要求,认真研究、勇于探索,积极学习外地先进经验,及时调整思路和方法,把新课程实施好,使我校教育教学水平有一个大提高。
孟津县横水镇第一初级中学
2012年3月16日计划。
