高考抛物线强化训练专题汇总,高中数学抛物线试题及答案解析
高中数学高考总复习抛物线习题及详解

高中数学高考总复习抛物线习题及详解一、选择题1.若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .4[答案] D[解析] 椭圆中,a 2=6,b 2=2,∴c =a 2-b 2=2, ∴右焦点(2,0),由题意知p2=2,∴p =4.2.已知点M 是抛物线y 2=2px (p >0)上的一点,F 为抛物线的焦点,若以|MF |为直径作圆,则这个圆与y 轴的关系是( )A .相交B .相切C .相离D .以上三种情形都有可能[答案] B[解析] 如图,由MF 的中点A 作准线l 的垂线AE ,交直线l 于点E ,交y 轴于点B ;由点M 作准线l 的垂线MD ,垂足为D ,交y 轴于点C ,则MD =MF ,ON =OF , ∴AB =OF +CM 2=ON +CM2=DM 2=MF 2, ∴这个圆与y 轴相切.3.已知抛物线y 2=2px (p >0),过焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2[答案] B[解析] 设A (x 1,y 1),B (x 2,y 2),则线段AB 的中点(x 1+x 22,y 1+y 22),∴y 1+y 22=2,∵A 、B 在抛物线y 2=2px 上,∴⎩⎪⎨⎪⎧y 12=2px 1 ①y 22=2px 2 ② ①-②得y 12-y 22=2p (x 1-x 2),∴k AB =y 1-y 2x 1-x 2=2p y 1+y 2=p 2,∵k AB =1,∴,p =2∴抛物线方程为y 2=4x ,∴准线方程为:x =-1,故选B.4.双曲线x 29-y 24=1的渐近线上一点A 到双曲线的右焦点F 的距离等于2,抛物线y 2=2px (p >0)过点A ,则该抛物线的方程为( )A .y 2=9xB .y 2=4xC .y 2=41313xD .y 2=21313x[答案] C[解析] ∵双曲线x 29-y 24=1的渐近线方程为y =±23x ,F 点坐标为(13,0),设A 点坐标为(x ,y ),则y =±23x ,由|AF |=2⇒(x -13)2+⎝⎛⎭⎫23x 2=2⇒x =913,y =±613,代入y 2=2px 得p =21313,所以抛物线方程为y 2=41313x ,所以选C.5.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172B .3 C. 5D.92[答案] A[解析] 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 与点(0,2)的距离,因此所求的最小值等于⎝⎛⎭⎫122+22=172,选A. 6.已知抛物线C :y 2=4x 的焦点为F ,准线为l ,过抛物线C 上的点A 作准线l 的垂线,垂足为M ,若△AMF 与△AOF (其中O 为坐标原点)的面积之比为3 1,则点A 的坐标为( )改填空题A .(2,22)B .(2,-22)C .(2,±2)D .(2,±22)[答案] D[解析] 如图,由题意可得,|OF |=1,由抛物线定义得,|AF |=|AM |,∵△AMF 与△AOF (其中O 为坐标原点)的面积之比为3∶1,∴S △AMFS △AOF =12×|AF |×|AM |×sin ∠MAF 12×|OF |×|AF |×sin (π-∠MAF )=3, ∴|AM |=3,设A ⎝⎛⎭⎫y 024,y 0,∴y 024+1=3,解得y 0=±22,∴y 024=2,∴点A 的坐标是(2,±22),故选D.7.(2010·河北许昌调研)过点P (-3,1)且方向向量为a =(2,-5)的光线经直线y =-2反射后通过抛物线y 2=mx ,(m ≠0)的焦点,则抛物线的方程为( )A .y 2=-2xB .y 2=-32xC .y 2=4xD .y 2=-4x[答案] D[解析] 设过P (-3,1),方向向量为a =(2,-5)的直线上任一点Q (x ,y ),则PQ →∥a ,∴x +32=y -1-5,∴5x +2y +13=0,此直线关于直线y =-2对称的直线方程为5x +2(-4-y )+13=0,即5x -2y +5=0,此直线过抛物线y 2=mx 的焦点F ⎝⎛⎭⎫m 4,0,∴m =-4,故选D.8.已知mn ≠0,则方程是mx 2+ny 2=1与mx +ny 2=0在同一坐标系内的图形可能是( )[答案] A[解析] 若mn >0,则mx 2+ny 2=1应为椭圆,y 2=-mnx 应开口向左,故排除C 、D ;∴mn <0,此时抛物线y 2=-mnx 应开口向右,排除B ,选A.9.(2010·山东聊城模考)已知A 、B 为抛物线C :y 2=4x 上的不同两点,F 为抛物线C 的焦点,若F A →=-4FB →,则直线AB 的斜率为( )A .±23B .±32C .±34D .±43[答案] D[解析] ∵F A →=-4FB →,∴|F A →|=4|FB →|,设|BF |=t ,则|AF |=4t ,∴|BM |=|AA 1|-|BB 1|=|AF |-|BF |=3t ,又|AB |=|AF |+|BF |=5t ,∴|AM |=4t ,∴tan ∠ABM =43,由对称性可知,这样的直线AB 有两条,其斜率为±43.10.已知抛物线C 的方程为x 2=12y ,过点A (0,-4)和点B (t,0)的直线与抛物线C 没有公共点,则实数t 的取值范围是( )A .(-∞,-1)∪(1,+∞) B.⎝⎛⎭⎫-∞,-22∪⎝⎛⎭⎫22,+∞ C .(-∞,-22)∪(22,+∞) D .(-∞,-22)∪(2,+∞) [答案] B[解析] 由题意知方程组⎩⎨⎧x 2=12y ①x t +y-4=1 ②无实数解由②得y =4xt -4,代入①整理得,2x 2-4x t +4=0,∴Δ=16t2-32<0,∴t >22或t <-22,故选B. [点评] 可用数形结合法求解,设过点A (0,-4)与抛物线x 2=12y 相切的直线与抛物线切点为M (x 0,y 0),则切线方程为y -y 0=4x 0(x -x 0), ∵过A 点,∴-4-2x 02=4x 0(0-x 0), ∴x 0=±2,∴y 0=4,∴切线方程为y -4=±42x -8, 令y =0得x =±22,即t =±22,由图形易知直线与抛物线无公共点时,t <-22或t >22. 二、填空题11.已知点A (2,0)、B (4,0),动点P 在抛物线y 2=-4x 上运动,则AP →·BP →取得最小值时的点P 的坐标是______.[答案] (0,0)[解析] 设P ⎝⎛⎭⎫-y 24,y ,则AP →=⎝⎛⎭⎫-y 24-2,y ,BP →=⎝⎛⎭⎫-y 24-4,y ,AP →·BP →=⎝⎛⎭⎫-y24-2⎝⎛⎭⎫-y 24-4+y 2=y 416+52y 2+8≥8,当且仅当y =0时取等号,此时点P 的坐标为(0,0).12.(文)(2010·泰安市模拟)如图,过抛物线y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,交抛物线于A 、B 两点,且|F A |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 设抛物线准线为l ,作AA 1⊥l ,BB 1⊥l ,FQ ⊥l ,垂足分别为A 1、B 1、Q ,作BM ⊥AA 1垂足为M ,BM 交FQ 于N ,则由条件易知∠ABM =30°,设|BF |=t ,则|NF |=t 2,|MA |=t +32,∵|AM |=|QN |,∴3-t +32=p -t 2,∴p =32,∴抛物线方程为y 2=3x .如图,过抛物线y 2=2px (p >0)的焦点的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 解法1:过A 、B 作准线垂线,垂足分别为A 1,B 1,则|AA 1|=3,|BB 1|=|BF |,∵|BC |=2|BF |,∴|BC |=2|BB 1|,∴|AC |=2|AA 1|=2|AF |=6,∴|CF |=3,∴p =12|CF |=32,∴抛物线方程为y 2=3x .解法2:由抛物线定义,|BF |等于B 到准线的距离,由|BC |=2|BF |得∠BCB 1=30°,又|AF |=3,从而A ⎝⎛⎭⎫p 2+32,332在抛物线上,代入抛物线方程y 2=2px ,解得p =32.点评:还可以由|BC |=2|BF |得出∠BCB 1=30°,从而求得A 点的横坐标为|OF |+12|AF |=p2+32或3-p 2,∴p 2+32=3-p 2,∴p =32. 13.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.[答案] 3+2 2[解析] 分别由A 和B 向准线作垂线,垂足分别为A 1,B 1,则由条件知, ⎩⎪⎨⎪⎧|AA 1|+|BB 1|=|AB |,|AA 1|-|BB 1|=22|AB |,解得⎩⎪⎨⎪⎧|AA 1|=2+24|AB ||BB 1|=2-24|AB |,∴|AA 1||BB 1|=3+22,即|F A ||FB |=3+2 2. 14.(文)若点(3,1)是抛物线y 2=2px 的一条弦的中点,且这条弦所在直线的斜率为2,则p =________.[答案] 2[解析] 设弦两端点P 1(x 1,y 1),P 2(x 2,y 2),则⎩⎪⎨⎪⎧y 12=2px 1y 22=2px 2,两式相减得,y 1-y 2x 1-x 2=2p y 1+y 2=2,∵y 1+y 2=2,∴p =2.(理)设抛物线x 2=12y 的焦点为F ,经过点P (2,1)的直线l 与抛物线相交于A 、B 两点,又知点P 恰为AB 的中点,则|AF |+|BF |=________.[答案] 8[解析] 过A 、B 、P 作准线的垂线AA 1、BB 1与PP 1,垂足A 1、B 1、P 1,则|AF |+|BF |=|AA 1|+|BB 1|=2|PP 1|=2[1-(-3)]=8.三、解答题15.(文)若椭圆C 1:x 24+y 2b 2=1(0<b <2)的离心率等于32,抛物线C 2:x 2=2py (p >0)的焦点在椭圆C 1的顶点上.(1)求抛物线C 2的方程;(2)若过M (-1,0)的直线l 与抛物线C 2交于E 、F 两点,又过E 、F 作抛物线C 2的切线l 1、l 2,当l 1⊥l 2时,求直线l 的方程.[解析] (1)已知椭圆的长半轴长为a =2,半焦距c =4-b 2, 由离心率e =c a =4-b 22=32得,b 2=1.∴椭圆的上顶点为(0,1),即抛物线的焦点为(0,1), ∴p =2,抛物线的方程为x 2=4y .(2)由题知直线l 的斜率存在且不为零,则可设直线l 的方程为y =k (x +1),E (x 1,y 1),F (x 2,y 2),∵y =14x 2,∴y ′=12x ,∴切线l 1,l 2的斜率分别为12x 1,12x 2,当l 1⊥l 2时,12x 1·12x 2=-1,即x 1·x 2=-4,由⎩⎪⎨⎪⎧y =k (x +1)x 2=4y得:x 2-4kx -4k =0, 由Δ=(-4k )2-4×(-4k )>0,解得k <-1或k >0. 又x 1·x 2=-4k =-4,得k =1. ∴直线l 的方程为x -y +1=0.(理)在△ABC 中,CA →⊥CB →,OA →=(0,-2),点M 在y 轴上且AM →=12(AB →+CD →),点C在x 轴上移动.(1)求B 点的轨迹E 的方程;(2)过点F ⎝⎛⎭⎫0,-14的直线l 交轨迹E 于H 、E 两点,(H 在F 、G 之间),若FH →=12HG →,求直线l 的方程.[解析] (1)设B (x ,y ),C (x 0,0),M (0,y 0),x 0≠0, ∵CA →⊥CB →,∴∠ACB =π2,∴2x 0·y 0-x 0=-1,于是x 02=2y 0① M 在y 轴上且AM →=12(AB →+AC →),所以M 是BC 的中点,可得 ⎩⎨⎧x 0+x 2=0y +02=y,∴⎩⎪⎨⎪⎧x 0=-x ②y 0=y2③ 把②③代入①,得y =x 2(x ≠0),所以,点B 的轨迹E 的方程为y =x 2(x ≠0). (2)点F ⎝⎛⎭⎫0,-14,设满足条件的直线l 方程为: y =kx -14,H (x 1,y 1),G (x 2,y 2),由⎩⎪⎨⎪⎧y =kx -14y =x 2消去y 得,x 2-kx +14=0.Δ=k 2-1>0⇒k 2>1,∵FH →=12HG →,即⎝⎛⎭⎫x 1,y 1+14=12(x 2-x 1,y 2-y 1), ∴x 1=12x 2-12x 1⇒3x 1=x 2.∵x 1+x 2=k ,x 1x 2=14,∴k =±233,故满足条件的直线有两条,方程为:8x +43y +3=0和8x -43y -3=0. 16.(文)已知P (x ,y )为平面上的动点且x ≥0,若P 到y 轴的距离比到点(1,0)的距离小1.(1)求点P 的轨迹C 的方程;(2)设过点M (m,0)的直线交曲线C 于A 、B 两点,问是否存在这样的实数m ,使得以线段AB 为直径的圆恒过原点.[解析] (1)由题意得:(x -1)2+y 2-x =1,化简得:y 2=4x (x ≥0). ∴点P 的轨迹方程为y 2=4x (x ≥0).(2)设直线AB 为y =k (x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -m )y 2=4x ,得ky 2-4y -4km =0, ∴y 1+y 2=4k ,y 1·y 2=-4m .∴x 1·x 2=m 2,∵以线段AB 为直径的圆恒过原点, ∴OA ⊥OB ,∴x 1·x 2+y 1·y 2=0.即m 2-4m =0⇒m =0或4.当k 不存在时,m =0或4. ∴存在m =0或4,使得以线段AB 为直径的圆恒过原点.[点评] (1)点P 到定点F (1,0)的距离比到y 轴的距离大1,即点P 到定点F (1,0)的距离与到定直线l :x =-1的距离相等.∴P 点轨迹是以F 为焦点,l 为准线的抛物线,∴p =2,∴方程为y 2=4x .(理)已知抛物线y 2=4x ,过点(0,-2)的直线交抛物线于A 、B 两点,O 为坐标原点. (1)若OA →·OB →=4,求直线AB 的方程.(2)若线段AB 的垂直平分线交x 轴于点(n,0),求n 的取值范围.[解析] (1)设直线AB 的方程为y =kx -2 (k ≠0),代入y 2=4x 中得,k 2x 2-(4k +4)x +4=0①设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k +4k 2,x 1x 2=4k 2.y 1y 2=(kx 1-2)·(kx 2-2)=k 2x 1x 2-2k (x 1+x 2)+4=-8k.∵OA →·OB →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=4k 2-8k =4,∴k 2+2k -1=0,解得k =-1±2.又由方程①的判别式Δ=(4k +4)2-16k 2=32k +16>0得k >-12,∴k =-1+2,∴直线AB 的方程为(2-1)x -y -2=0.(2)设线段AB 的中点的坐标为(x 0,y 0),则由(1)知x 0=x 1+x 22=2k +2k 2,y 0=kx 0-2=2k,∴线段AB 的垂直平分线的方程是 y -2k =-1k ⎝⎛⎭⎫x -2k +2k 2. 令y =0,得n =2+2k +2k 2=2k 2+2k +2=2⎝⎛⎭⎫1k +122+32.又由k >-12且k ≠0得1k <-2,或1k>0,∴n >2⎝⎛⎭⎫0+122+32=2.∴n 的取值范围为(2,+∞). 17.(文)(已知抛物线C :y 2=4x 的焦点为F ,过点K (-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D .(1)证明:点F 在直线BD 上;(2)设F A →·FB →=89,求△BDK 的内切圆M 的方程.[解析] 设A (x 1,y 1),B (x 2,y 2),D (x 1,-y 1),l 的方程为x =my -1(m ≠0) (1)将x =my -1(m ≠0)代入y 2=4x 并整理得 y 2-4my +4=0,从而y 1+y 2=4m ,y 1y 2=4① 直线BD 的方程为y -y 2=y 2+y 1x 2-x 1(x -x 2)即y -y 2=4y 2-y 1⎝⎛⎭⎫x -y 224 令y =0,得x =y 1y 24=1,所以点F (1,0)在直线BD 上.(2)由(1)知,x 1+x 2=(my 1-1)+(my 2-1)=4m 2-2, x 1x 2=(my 1-1)(my 2-1)=1因为F A →=(x 1-1,y 1),FB →=(x 2-1,y 2),F A →·FB →=(x 1-1,y 1)·(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+4=8-4m 2,故8-4m 2=89,解得m =±43,直线l 的方程为3x +4y +3=0,3x -4y +3=0. 从而y 2-y 1=±(4m )2-4×4=±437,故4y 2-y 1=±37因而直线BD 的方程为3x +7y -3=0,3x -7y -3=0.因为KF 为∠BKD 的角平分线,故可设圆心M (t,0),(-1<t <1),M (t,0)到直线l 及BD 的距离分别为3|t +1|5,3|t -1|4, 由3|t +1|5=3|t -1|4得t =19或t =9(舍去),故圆M 的半径为r =3|t +1|5=23, 所以圆M 的方程为⎝⎛⎭⎫x -192+y 2=49. (理)(2010·揭阳市模考)已知点C (1,0),点A 、B 是⊙O :x 2+y 2=9上任意两个不同的点,且满足AC →·BC →=0,设P 为弦AB 的中点.(1)求点P 的轨迹T 的方程;(2)试探究在轨迹T 上是否存在这样的点:它到直线x =-1的距离恰好等于到点C 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.[解析] (1)法一:连结CP ,由AC →·BC →=0知,AC ⊥BC ,∴|CP |=|AP |=|BP |=12|AB |, 由垂径定理知|OP |2+|AP |2=|OA |2,即|OP |2+|CP |2=9,设点P (x ,y ),有(x 2+y 2)+[(x -1)2+y 2]=9,化简得,x 2-x +y 2=4.法二:设A (x 1,y 1),B (x 2,y 2),P (x ,y ),根据题意知,x 12+y 12=9,x 22+y 22=9,2x =x 1+x 2,2y =y 1+y 2,∴4x 2=x 12+2x 1x 2+x 22,4y 2=y 12+2y 1y 2+y 22故4x 2+4y 2=(x 12+y 12)+(2x 1x 2+2y 1y 2)+(x 22+y 22)=18+2(x 1x 2+y 1y 2)①又∵AC →·BC →=0,∴(1-x 1,-y 1)·(1-x 2,-y 2)=0∴(1-x 1)×(1-x 2)+y 1y 2=0,故x 1x 2+y 1y 2=(x 1+x 2)-1=2x -1,代入①式得,4x 2+4y 2=18+2(2x -1),化简得,x 2-x +y 2=4.(2)根据抛物线的定义,到直线x =-1的距离等于到点C (1,0)的距离的点都在抛物线y 2=2px 上,其中p 2=1,∴p =2,故抛物线方程为y 2=4x ,由方程组⎩⎪⎨⎪⎧ y 2=4x x 2-x +y 2=4得,x 2+3x -4=0,解得x 1=1,x 2=-4,由于x ≥0,故取x =1,此时y =±2,故满足条件的点存在,其坐标为(1,-2)和(1,2).。
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.抛物线的焦点为,点在抛物线上,且,弦中点在其准线上的射影为,则的最大值为()A.B.C.D.【答案】A【解析】设,由抛物线定义,.而余弦定理,,再由,得到,所以的最大值为,故选:A.【考点】双曲线的简单性质.2.已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足·=0,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.【答案】(1)x2-x+y2=4(2)存在,(1,-2)和(1,2)【解析】(1)连接CP、OP,由·=0,知AC⊥BC,∴|CP|=|AP|=|BP|=|AB|.由垂径定理知|OP|2+|AP|2=|OA|2,即|OP|2+|CP|2=9.设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,化简,得到x2-x+y2=4.(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中=1,∴p=2,故抛物线方程为y2=4x.由方程组,得x2+3x-4=0,解得x1=1,x2=-4,由于x≥0,故取x=1,此时y=±2.故满足条件的点存在,其坐标为(1,-2)和(1,2).3.动直线l的倾斜角为60°,且与抛物线x2=2py(p>0)交于A,B两点,若A,B两点的横坐标之和为3,则抛物线的方程为________.【答案】x2=y【解析】设直线l的方程为y=x+b,联立,消去y,得x2=2p(x+b),即x2-2px-2pb=0,∴x1+x2=2p=3,∴p=,则抛物线的方程为x2=y.4.已知点在抛物线C:的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为()A.B.C.D.【答案】D【解析】由于点在抛物线C:的准线上,所以,设直线AB的方程为,将与联立,即,则(负值舍去),将k=2代入得y=8,即可求出x=8,故B(8,8),所以,故选D.【考点】1.直线与抛物线的位置关系;2.斜率公式.5.已知抛物线C:的焦点为F,过点F倾斜角为60°的直线l与抛物线C在第一、四象限分别交于A、B两点,则的值等于()(A)2 (B)3 (C)4 (D)5【答案】B【解析】由抛物线的方程可知焦点,直线的斜率为,则直线的方程为,设.将直线方程和抛物线方程联立削去并整理可得,解得.所以.故B正确.【考点】1直线与抛物线的位置关系;2数形结合思想.6.设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为________.【答案】【解析】设P(x0,x2),又y′=2x,则直线PQ的方程为y=-++x2.代入y=x2得x2+--x2=0,即(x-x)=0,所以点Q的坐标为.从而PQ2=2+2,令t=4x2,则PQ2=f(t)=t+++3(t>0),则f′(t)=,即f(t)在(0,2)上是减函数,在(2,+∞)上是增函数,故当t=2时,PQ有最小值.7.已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A ,B两点.(1)如图所示,若,求直线l的方程;(2)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值.【答案】(1);(2)长轴长的最小值为.【解析】(1)首先求得抛物线方程为.设直线方程为,并设利用,得到;联立,可得,应用韦达定理得到,从而得到,求得直线方程.(2)可求得对称点,代入抛物线中可得:,直线方程为,考虑到对称性不妨取,椭圆设为联立直线、椭圆方程并消元整理可得,由,可得,即得解.(1)由题知抛物线方程为。
高考数学专题《抛物线》习题含答案解析

专题9.5 抛物线1.(2020·全国高考真题(理))已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( ) A .2 B .3 C .6 D .9【答案】C 【解析】设抛物线的焦点为F ,由抛物线的定义知||122A p AF x =+=,即1292p=+,解得6p.故选:C.2.(2020·北京高三二模)焦点在x 轴的正半轴上,且焦点到准线的距离为4的抛物线的标准方程是( ) A .x 2=4y B .y 2=4x C .x 2=8y D .y 2=8x【答案】D 【解析】根据题意,要求抛物线的焦点在x 轴的正半轴上, 设其标准方程为22(0)y px p =>, 又由焦点到准线的距离为4,即p =4, 故要求抛物线的标准方程为y 2=8x , 故选:D.3.(全国高考真题)设F 为抛物线2:4C y x =的焦点,曲线()0ky k x=>与C 交于点P ,PF x ⊥轴,则k =( )A .12B .1C .32D .2【答案】D 【解析】由抛物线的性质可得(1,2)221kP y k ⇒==⇒=,故选D. 4.(2020·全国高考真题(文))设O 为坐标原点,直线2x =与抛物线C :22(0)y px p =>交于D ,E 两点,若OD OE ⊥,则C 的焦点坐标为( ) A .1,04⎛⎫⎪⎝⎭B .1,02⎛⎫ ⎪⎝⎭C .(1,0)D .(2,0)练基础【答案】B 【解析】因为直线2x =与抛物线22(0)y px p =>交于,E D 两点,且OD OE ⊥, 根据抛物线的对称性可以确定4DOx EOx π∠=∠=,所以()2,2D ,代入抛物线方程44p =,求得1p =,所以其焦点坐标为1(,0)2, 故选:B.5.(2019·四川高三月考(文))若抛物线22y px =的准线为圆2240x y x ++=的一条切线,则抛物线的方程为( ) A.216y x =- B.28y x =-C.216y x =D.24y x =【答案】C 【解析】∵抛物线22y px =的准线方程为x=2p-,垂直于x 轴. 而圆2240x y x ++=垂直于x 轴的一条切线为4x =-, 则42p=,即8p =. 故抛物线的方程为216y x =. 故选:C .6.(2019·北京高考真题(文))设抛物线y 2=4x 的焦点为F ,准线为l .则以F 为圆心,且与l 相切的圆的方程为__________. 【答案】(x -1)2+y 2=4. 【解析】抛物线y 2=4x 中,2p =4,p =2, 焦点F (1,0),准线l 的方程为x =-1, 以F 为圆心,且与l 相切的圆的方程为 (x -1)2+y 2=22,即为(x -1)2+y 2=4.7.(2019·山东高三月考(文))直线l 与抛物线22x y =相交于A ,B 两点,当AB 4=时,则弦AB 中点M 到x 轴距离的最小值为______. 【答案】32【解析】由题意,抛物线22x y =的焦点坐标为(0,12),根据抛物线的定义如图,所求d=111A B AF BF 113M 2222A B AB M ++--==≥= 故答案为:32. 8.(2021·沙湾县第一中学(文))设过抛物线y 2=4x 的焦点F 的直线交抛物线于A ,B 两点,且直线AB 的倾斜角为4π,则线段AB 的长是____,焦点F 到A ,B 两点的距离之积为_________.【答案】8 8 【分析】由题意可得直线AB 的方程为1y x =-,然后将直线方程与抛物线方程联立方程组,消去y 后,利用根与系数的关系,结合抛物线的定义可求得答案 【详解】解:由题意得(1,0)F ,则直线AB 的方程为1y x =-,设1122(,),(,)A x y B x y ,由241y x y x ⎧=⎨=-⎩,得2610x x -+=, 所以12126,1x x x x +==, 所以12628AB x x p =++=+=,因为11221,122=+=+=+=+p pAF x x BF x x , 所以()()1212121116118AF BF x x x x x x ⋅=+⋅+=+++=++=, 故答案为:8,89.(2021·全国高三专题练习)已知抛物线顶点在原点,焦点在坐标轴上,又知此抛物线上的一点(),3A m -到焦点F 的距离为5,则m 的值为__________;抛物线方程为__________. 【答案】答案见解析 答案见解析 【分析】由于抛物线的开口方向未定,根据点(),3A m -在抛物线上这一条件,抛物线开口向下,向左、向右均有可能,以此分类讨论,利用焦半径公式列方程可得p 的值,根据点(),3A m -在抛物线上可得m 的值. 【详解】根据点(),3A m -在抛物线上,可知抛物线开口向下,向左、向右均有可能, 当抛物线开口向下时,设抛物线方程为22x py =-(0p >), 此时准线方程为2py =,由抛物线定义知(3)52p --=,解得4p =.所以抛物线方程为28x y ,这时将(),3A m -代入方程得m =±当抛物线开口向左或向右时,可设抛物线方程为22y ax (0a ≠),从p a =知准线方程为2ax =-,由题意知()25232am am⎧+=⎪⎨⎪-=⎩,解此方程组得11192a m =⎧⎪⎨=⎪⎩,22192a m =-⎧⎪⎨=-⎪⎩,33912a m =⎧⎪⎨=⎪⎩,44912a m =-⎧⎪⎨=-⎪⎩,综合(1)、(2)得92m =,22y x =; 92m =-,22y x =-;12m =,218y x =; 12m =-,218y x =-;m =±28xy .故答案为:92,92-,12,12-,±22y x =,22y x =-,218y x =,218y x =-,28x y .10.(2019·广东高三月考(理))已知F 为抛物线2:4T x y =的焦点,直线:2l y kx =+与T 相交于,A B 两点.()1若1k =,求FA FB +的值;()2点(3,2)C --,若CFA CFB ∠=∠,求直线l 的方程.【答案】(1)10(2)3240x y +-= 【解析】(1)由题意,可得()0,1F ,设221212,,,44x x A x B x ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,联立方程组224y kx x y=+⎧⎨=⎩,整理得2480x kx --=,则124x x k +=,128x x =-,又由22121144x x FA FB +++=+()2121222104x x x x +-=+=.(2)由题意,知211,14x FA x ⎛⎫=- ⎪⎝⎭,222,14x FB x ⎛⎫=- ⎪⎝⎭,()3.3FC =--, 由CFA CFB ∠=∠,可得cos ,cos ,FA FC FB FC =又2114x FA =+,2214x FB =+,则FA FC FB FC FA FC FB FC =, 整理得()1212420x x x x ++-=,解得32k =-, 所以直线l 的方程为3240x y +-=.1.(2021·吉林长春市·高三(理))已知M 是抛物线24y x =上的一点,F 是抛物线的焦点,若以Fx 为始边,FM 为终边的角60xFM ∠=,则FM 等于( ) A .2 B C .D .4【答案】D 【分析】设点200,4y M y ⎛⎫ ⎪⎝⎭,取()1,0a =,可得1cos ,2FM a <>=,求出20y 的值,利用抛物线的定义可求练提升得FM 的值. 【详解】设点()00,M x y ,其中2004y x =,则()1,0F ,2001,4y FM y ⎛⎫=- ⎪⎝⎭,取()1,0a =,则211cos ,2y FM a FM a FM a-⋅<>===⋅⎛,可得4200340480y y -+=,因为20104y ->,可得204y >,解得2012y =,则20034y x ==,因此,014MF x=+=. 故选:D.2.(2017·全国高考真题(文))过抛物线2:4C y x =的焦点F 的直线交C 于点M (在x 轴上方),l 为C 的准线,点N 在l 上且MNl ⊥,则点M 到直线NF 的距离为()A. B. D.【答案】A 【解析】设直线l 与x 轴相交于点P ,与直线MN 相交于点Q ,(1,0)F ,设||||MN MF m ==,因为||2,30PF NQM =∠=,所以||4,||2QF QM m ==, 所以42m m +=,解得:4m =,设00(,)M x y ,由焦半径公式得:014x +=, 所以03x=,0y =,所以sin sin 42NP MNF NFP NF ∠=∠===,所以点M 到直线NF 的距离为||sin 4NM MNF ⋅∠=⋅=3.(2020·广西南宁三中其他(理))已知抛物线28C y x =:的焦点为F ,P 是抛物线C 的准线上的一点,且P 的纵坐标为正数,Q 是直线PF 与抛物线C 的一个交点,若PQ =,则直线PF 的方程为( )A .20x y --=B .20x y +-=C .20x y -+=D .20x y ++=【答案】B 【解析】过Q 点作QH PM ⊥于H ,因为PQ =,由抛物线的定义得PQ =,所以在Rt PQH ∆中,4PQH π∠=,所以4PFM π∠=,所以直线PF 的斜率为1k =-,所以直线PF 的方程为()()012y x -=--, 即20x y +-=, 故选B.4.(2020·浙江高三月考)如图,已知抛物线21:4C y x =和圆222:(1)1C x y -+=,直线l 经过1C 的焦点F ,自上而下依次交1C 和2C 于A ,B ,C ,D 四点,则AB CD ⋅的值为( )A .14B .12C .1D .2【答案】C 【解析】因为抛物线21:4C y x =的焦点为(1,0)F ,又直线l 经过1C 的焦点F ,设直线:(1)l y k x =-,由24(1)y x y k x ⎧=⎨=-⎩得2222(24)0k x k x k -++=, 设1122(,),(,)A x y B x y ,则121=x x由题意可得:1111=-=+-=AB AF BF x x , 同理2=CD x ,所以12cos01︒⋅=⋅⋅==AB CD AB CD x x . 故选C5.【多选题】(2022·全国高三专题练习)已知抛物线21:C y mx =与双曲线222:13y C x -=有相同的焦点,点()02,P y 在抛物线1C 上,则下列结论正确的有( )A .双曲线2C 的离心率为2B .双曲线2C 的渐近线为y x = C .8m =D .点P 到抛物线1C 的焦点的距离为4【答案】ACD 【分析】由双曲线方程写出离心率、渐近线及焦点,即可知A 、B 、C 的正误,根据所得抛物线方程求0y ,即知D 的正误. 【详解】双曲线2C 的离心率为2e ==,故A 正确;双曲线2C 的渐近线为y =,故B 错误; 由12,C C 有相同焦点,即24m=,即8m =,故C 正确; 抛物线28y x =焦点为()2,0,点()02,P y 在1C 上,则04y =±,故()2,4P 或()2,4P -,所以P 到1C 的焦点的距离为4,故D 正确. 故选:ACD .6.【多选题】(2021·海南鑫源高级中学)在下列四个命题中,真命题为( )A .当a 为任意实数时,直线(a -1)x -y +2a +1=0恒过定点P ,则过点P 且焦点在y 轴上的抛物线的标准方程是243x y =B .已知双曲线的右焦点为(5,0),一条渐近线方程为2x -y =0,则双曲线的标准方程为221205x y -= C .抛物线y =ax 2(a ≠0)的准线方程14y a=-D .已知双曲线2214x y m +=,其离心率()1,2e ∈,则m 的取值范围(-12,0)【答案】ACD 【分析】求出直线定点设出抛物方程即可判断A ;根据渐近线方程与焦点坐标求出,a b 即可判断B ;根据抛物线方程的准线方程公式即可判断C ;利用双曲线离心率公式即可判断D . 【详解】对A 选项,直线(a -1)x -y +2a +1=0恒过定点为()2,3P -,则过点P 且焦点在y 轴上的抛物线的标准方程设为22x py =,将点()2,3P -代入可得23p =,所以243x y =,故A 正确;对B 选项,知5,2bc a==,又22225a b c +==,解得225,20a b ==,所以双曲线的标准方程为221520x y -=,故B 错; 对C 选项,得21x y a =,所以准线方程14y a=-,正确;对D 选项,化双曲线方程为2214x y m-=-,所以()1,2e =,解得()12,0m ∈-,故正确.故选:ACD7.(2021·全国高二课时练习)已知点M 为抛物线2:2(0)C y px p =>上一点,若点M 到两定点(,)A p p ,,02p F ⎛⎫⎪⎝⎭的距离之和最小,则点M 的坐标为______.【答案】,2p p ⎛⎫⎪⎝⎭【分析】过点M 作抛物线准线的垂线,垂足为B ,根据抛物线的定义可得||||MF MB =, 易知当A ,B ,M 三点共线时||MB MA +取得最小值且为||AB ,进而可得结果. 【详解】过点M 作抛物线准线的垂线,垂足为B ,由抛物线的定义,知点M 到焦点,02p F ⎛⎫⎪⎝⎭的距离与点M 到准线的距离相等,即||||MF MB =,所以||||||||MF MA MB MA +=+, 易知当A ,B ,M 三点共线时,||MB MA +取得最小值, 所以min 3(||||)||2p MF MA AB +==,此时点M 的坐标为,2p p ⎛⎫⎪⎝⎭. 故答案为:2p p ⎛⎫⎪⎝⎭,8.(2021·全国高二课时练习)抛物线()220y px p =>的焦点为F ,已知点A ,B 为抛物线上的两个动点,且满足120AFB ∠=︒,过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,则MN AB的最大值为______.【分析】设=AF a ,=BF b ,根据中位线定理以及抛物线定义可得()12MN a b =+,在AFB △中,由余弦定理以及基本不等式可得)AB a b ≥+,即可求得MN AB 的最大值.【详解】设=AF a ,=BF b ,作AQ 垂直抛物线的准线于点Q ,BP 垂直抛物线的准线于点P .由抛物线的定义,知AF AQ =,BF BP =.由余弦定理得()2222222cos120AB a b ab a b ab a b ab =+=︒=++=+-.又22a b ab +⎛⎫≤ ⎪⎝⎭,∴()()()()22221344a b ab a b a b a b +-≥+-+=+,当且仅当a b =时,等号成立,∴)AB a b ≥+,∴()1a b MN AB +≤=MN AB9.(2020·山东济南外国语学校高三月考)抛物线C :22y x =的焦点坐标是________;经过点()4,1P 的直线l 与抛物线C 相交于A ,B 两点,且点P 恰为AB 的中点,F 为抛物线的焦点,则AF BF +=________.【答案】1,02⎛⎫⎪⎝⎭9【解析】抛物线C :22y x =的焦点1,02F ⎛⎫⎪⎝⎭. 过A 作AM ⊥准线交准线于M ,过B 作BN ⊥准线交准线于N ,过P 作PK ⊥准线交准线 于K ,则由抛物线的定义可得AM BN AF BF +=+. 再根据P 为线段AB 的中点,119(||||)||4222AM BN PK +==+=, ∴9AF BF +=,故答案为:焦点坐标是1,02⎛⎫ ⎪⎝⎭,9AF BF +=.10.(2019·四川高考模拟(文))抛物线C :()220x py p =>的焦点为F ,抛物线过点(),1P p .(Ⅰ)求抛物线C 的标准方程与其准线l 的方程;(Ⅱ)过F 点作直线与抛物线C 交于A ,B 两点,过A ,B 分别作抛物线的切线,证明两条切线的交点在抛物线C 的准线l 上.【答案】(Ⅰ)抛物线的标准方程为24x y =,准线l 的方程为1y =-;(Ⅱ)详见解析. 【解析】(Ⅰ)由221p p =⨯,得2p =,所以抛物线的标准方程为24x y =,准线l 的方程为1y =-.(Ⅱ)根据题意直线AB 的斜率一定存在,又焦点()0,1F ,设过F 点的直线方程为1y kx =+,联立241x yy kx ⎧=⎨=+⎩,得,2440x kx --=. 设()11,A x y ,()22,B x y ,则124x x k +=,124x x =-.∴()22221212122168x x x x x x k +=+-=+.由214y x =得,1'2y x =,过A ,B 的抛物线的切线方程分别为 ()()1112221212y y x x x y y x x x ⎧-=-⎪⎪⎨⎪-=-⎪⎩, 即21122211241124y x x x y x x x ⎧=-⎪⎪⎨⎪=-⎪⎩,两式相加,得()()2212121148y x x x x x =+-+,化简,得()221y kx k =-+,即()21y k x k =--, 所以,两条切线交于点()2,1k -,该点显然在抛物线C 的准线l :1y =-上.1.(2021·全国高考真题)抛物线22(0)y px p =>的焦点到直线1y x =+,则p =( ) A .1 B .2 C .D .4【答案】B 【分析】首先确定抛物线的焦点坐标,然后结合点到直线距离公式可得p 的值. 【详解】抛物线的焦点坐标为,02p ⎛⎫ ⎪⎝⎭,其到直线10x y -+=的距离:d == 解得:2p =(6p =-舍去). 故选:B.2.(2021·天津高考真题)已知双曲线22221(0,0)x y a b a b-=>>的右焦点与抛物线22(0)y px p =>的焦点重合,抛物线的准线交双曲线于A ,B 两点,交双曲线的渐近线于C 、D 两点,若|CD AB .则双曲线的离心率为( ) A B C .2D .3练真题【答案】A 【分析】设公共焦点为(),0c ,进而可得准线为x c =-,代入双曲线及渐近线方程,结合线段长度比值可得2212a c =,再由双曲线离心率公式即可得解. 【详解】设双曲线22221(0,0)x y a b a b-=>>与抛物线22(0)y px p =>的公共焦点为(),0c ,则抛物线22(0)y px p =>的准线为x c =-,令x c =-,则22221c ya b-=,解得2b y a =±,所以22b AB a =, 又因为双曲线的渐近线方程为b y x a =±,所以2bcCD a=,所以2bc a c ,所以222212a cbc =-=,所以双曲线的离心率ce a== 故选:A.3.(2020·北京高考真题)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ). A .经过点O B .经过点P C .平行于直线OP D .垂直于直线OP【答案】B 【解析】如图所示:.因为线段FQ 的垂直平分线上的点到,F Q 的距离相等,又点P 在抛物线上,根据定义可知,PQ PF =,所以线段FQ 的垂直平分线经过点P .故选:B.4.(2021·全国高考真题)已知O 为坐标原点,抛物线C :22y px =(0p >)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ OP ⊥,若6FQ =,则C 的准线方程为______. 【答案】32x =-【分析】先用坐标表示P Q ,,再根据向量垂直坐标表示列方程,解得p ,即得结果. 【详解】抛物线C :22y px = (0p >)的焦点,02p F ⎛⎫⎪⎝⎭,∵P 为C 上一点,PF 与x 轴垂直, 所以P 的横坐标为2p,代入抛物线方程求得P 的纵坐标为p ±, 不妨设(,)2pP p ,因为Q 为x 轴上一点,且PQ OP ⊥,所以Q 在F 的右侧, 又||6FQ =, (6,0),(6,)2pQ PQ p ∴+∴=- 因为PQ OP ⊥,所以PQ OP ⋅=2602pp ⨯-=, 0,3p p >∴=,所以C 的准线方程为32x =-故答案为:32x =-.5.的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则AB =________.【答案】163【解析】∵抛物线的方程为24y x =,∴抛物线的焦点F 坐标为(1,0)F ,又∵直线AB 过焦点F AB 的方程为:1)y x =- 代入抛物线方程消去y 并化简得231030x x -+=, 解法一:解得121,33x x ==所以12116||||3|33AB x x =-=-= 解法二:10036640∆=-=> 设1122(,),(,)A x y B x y ,则12103x x +=, 过,A B 分别作准线1x =-的垂线,设垂足分别为,C D 如图所示.12||||||||||11AB AF BF AC BD x x =+=+=+++1216+2=3x x =+故答案为:1636.(2020·浙江省高考真题)如图,已知椭圆221:12x C y +=,抛物线22:2(0)C y px p =>,点A 是椭圆1C 与抛物线2C 的交点,过点A 的直线l 交椭圆1C 于点B ,交抛物线2C 于M (B ,M 不同于A ).(Ⅰ)若116=p ,求抛物线2C 的焦点坐标; (Ⅱ)若存在不过原点的直线l 使M 为线段AB 的中点,求p 的最大值.【答案】(Ⅰ)1(,0)32;【解析】 (Ⅰ)当116=p 时,2C 的方程为218y x =,故抛物线2C 的焦点坐标为1(,0)32;(Ⅱ)设()()()112200,,,,,,:A x y B x y M x y I x y m λ=+,由()22222222220x y y my m x y mλλλ⎧+=⇒+++-=⎨=+⎩, 1200022222,,222m m my y y x y m λλλλλλ--∴+===+=+++, 由M 在抛物线上,所以()222222244222m pm mp λλλλλ=⇒=+++, 又22222()220y pxy p y m y p y pm x y mλλλ⎧=⇒=+⇒--=⎨=+⎩, 012y y p λ∴+=,2101022x x y m y m p m λλλ∴+=+++=+,2122222mx p m λλ∴=+-+.由2222142,?22x y x px y px ⎧+=⎪⇒+=⎨⎪=⎩即2420x px +-=12x p ⇒==-222221822228162p p p m p p p λλλλλ+⇒-=+⋅=++≥+,18p ≥,21160p ≤,p ≤ 所以,p,此时A . 法2:设直线:(0,0)l x my t m t =+≠≠,()00,A x y .将直线l 的方程代入椭圆221:12x C y +=得:()2222220m y mty t +++-=,所以点M 的纵坐标为22M mty m =-+.将直线l 的方程代入抛物线22:2C y px =得:2220y pmy pt --=,所以02M y y pt =-,解得()2022p m y m+=,因此()220222p m xm+=,由220012x y +=解得22212242160m m p m m ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,所以当m t ==p .。
高中抛物线知识点归纳总结与练习题及答案
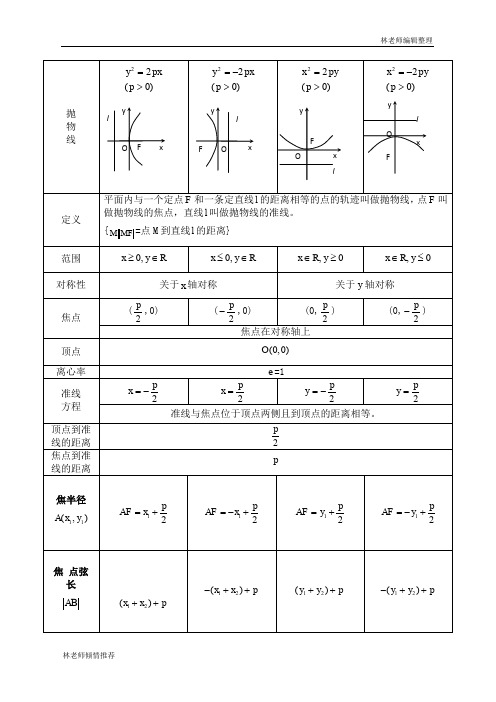
一. 直线与抛物线的位置关系 直线,抛物线,,消y 得:(1)当k=0时,直线l 与抛物线的对称轴平行,有一个交点; (2)当k ≠0时,Δ>0,直线l 与抛物线相交,两个不同交点; Δ=0, 直线l 与抛物线相切,一个切点; Δ<0,直线l 与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?(不一定)二. 关于直线与抛物线的位置关系问题常用处理方法 直线l :b kx y += 抛物线,)0( p① 联立方程法:⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k 设交点坐标为),(11y x A ,),(22y x B ,则有0 ∆,以及2121,x x x x +,还可进一步求出bx x k b kx b kx y y 2)(212121++=+++=+,2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长,中点,对称,面积等问题时,常用此法,比如 1. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M , 2210x x x +=, 2210y y y += ② 点差法:设交点坐标为),(11y x A ,),(22y x B ,代入抛物线方程,得1212px y = 2222px y =将两式相减,可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时,212y y pk AB +=b. 在涉及中点轨迹问题时,设线段AB 的中点为),(00y x M ,021*******y py p y y p x x y y ==+=--, 即0y pk AB =, 同理,对于抛物线)0(22≠=p py x ,若直线l 与抛物线相交于B A 、两点,点),(00y x M 是弦AB 的中点,则有px p x p x x k AB 0021222==+=(注意能用这个公式的条件:1)直线与抛物线有两个不同的交点,2)直线的斜率存在,且不等于零)抛物线练习及答案1、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为 。
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.过抛物线的焦点作直线与此抛物线相交于、两点,是坐标原点,当时,直线的斜率的取值范围是()A.B.C.D.【答案】D【解析】由题可知,点的横坐标时,满足,此时,故直线(即直线)的斜率的取值范围是.故选D.【考点】抛物线的几何性质以及直线与抛物线的位置关系.2.抛物线y=2ax2(a≠0)的焦点是( )A.(,0)B.(,0)或(-,0)C.(0,)D.(0,)或(0,-)【答案】C【解析】将方程改写为,可知2p=,当a>0时,焦点为(0,),即(0,);当a<0时,焦点为(0,-),即(0,);综合得,焦点为(0,),选C考点:抛物线的基本概念3.设F(1,0),M点在x轴上,P点在y轴上,且=2,⊥,当点P在y轴上运动时,点N的轨迹方程为()A.y2=2x B.y2=4xC.y2=x D.y2=x【答案】B【解析】设M(x0,0),P(0,y),N(x,y),∵⊥,=(x0,-y),=(1,-y0),∴(x0,-y)·(1,-y)=0,∴x0+y2=0.由=2,得(x-x0,y)=2(-x,y),∴即∴-x+=0,即y2=4x.故所求的点N的轨迹方程是y2=4x.故选B.4.已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足·=0,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.【答案】(1)x2-x+y2=4(2)存在,(1,-2)和(1,2)【解析】(1)连接CP、OP,由·=0,知AC⊥BC,∴|CP|=|AP|=|BP|=|AB|.由垂径定理知|OP|2+|AP|2=|OA|2,即|OP|2+|CP|2=9.设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,化简,得到x2-x+y2=4.(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中=1,∴p=2,故抛物线方程为y2=4x.由方程组,得x2+3x-4=0,解得x1=1,x2=-4,由于x≥0,故取x=1,此时y=±2.故满足条件的点存在,其坐标为(1,-2)和(1,2).5.设F为抛物线C:的焦点,过F且倾斜角为30°的直线交C于A,B两点,O为坐标原点,则△OAB的面积为()A.B.C.D.【答案】D【解析】由题意可知:直线AB的方程为,代入抛物线的方程可得:,设A、B,则所求三角形的面积为=,故选D.【考点】本小题主要考查直线与抛物线的位置关系,考查两点间距离公式等基础知识,考查同学们分析问题与解决问题的能力.6.若,则称点在抛物线C:外.已知点在抛物线C:外,则直线与抛物线C的位置关系是()A.相交B.相切C.相离D.不能确定【答案】A【解析】因为点在抛物线C:外,所以由与联立方程组消得:因此,所以直线与抛物线相交.【考点】直线与抛物线位置关系7.已知直线:与抛物线:交于两点,与轴交于,若,则_______.[【答案】【解析】解方程组得或,由得:.【考点】1、直线与圆锥曲线的关系;2、向量的运算.8.过抛物线焦点F的直线交抛物线于A、B两点,若A、B在抛物线准线上的射影分别为,则()A.B.C.D.【答案】D【解析】由抛物线的定义得,,,故,,故,,又,故,从而.【考点】抛物线定义.9.已知直线交抛物线于两点.若该抛物线上存在点,使得为直角,则的取值范围为________.【答案】【解析】根据题意不妨设,则⊥∴∵为直角,点C与点A不同,∴∴∵∴10.如图,设抛物线的顶点为A,与x 轴正半轴的交点为B,设抛物线与两坐标轴正半轴围成的区域为M,随机往M内投一点P,则点P落在AOB内的概率是( )A.B.C.D.【答案】C【解析】解:设抛物线与轴正半轴及轴的正半轴所围成的区域的面积为则设事件“随机往M内投一点P,则点P落在AOB内”则,故选:C.【考点】1、定积分;2、几何概型.11.已知抛物线C:,点A、B在抛物线C上.(1)若直线AB过点M(2p,0),且=4p,求过A,B,O(O为坐标原点)三点的圆的方程;(2)设直线OA、OB的倾斜角分别为,且,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.【答案】(1);(2)过定点【解析】(1)当直线斜率不存在时方程为,与的交点分别为M,N ,弦长。
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.设双曲线的离心率为2,且一个焦点与抛物线的焦点相同,则此双曲线的方程为__________.【答案】.【解析】抛物线的焦点坐标为(0,2),所以双曲线的焦点在y轴上且c=2,所以双曲线的方程为,即a2=n>0,b2=-m>0,所以a=,又e=,解得n=1,所以b2=c2-a2=4-1=3,即-m=3,m=-3,所以双曲线的方程为,故答案为:.【考点】1.抛物线的简单性质;2.双曲线的简单性质.2.已知点A(-1,0),B(1,-1)和抛物线.,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.(1)证明: 为定值;(2)若△POM的面积为,求向量与的夹角;(3)证明直线PQ恒过一个定点.【答案】(1)见解析; (2) ;(3)直线PQ过定点E(1,-4).【解析】(1)设点根据、M、A三点共线,得计算得到=5;(2)设∠POM=α,可得结合三角形面积公式可得tanα="1."根据角的范围,即得所求.(3)设点、B、Q三点共线,据此确定进一步确定的方程,化简为得出结论.试题解析:(1)设点、M、A三点共线,2分5分(2)设∠POM=α,则由此可得tanα=1. 8分又 10分(3)设点、B、Q三点共线,即 12分即 13分由(*)式,代入上式,得由此可知直线PQ过定点E(1,-4). 14分【考点】抛物线及其几何性质,直线方程,直线与抛物线的位置关系,转化与化归思想.3.已知抛物线C: y2 =2px(p>0)的准线L,过M(l,0)且斜率为的直线与L相交于A,与C的一个交点为B,若,则p=____ 。
【答案】2【解析】由题意可得,抛物线的焦点为,准线为.,为AB的中点.直线方程为,由题意可得,故由中点公式可得,把点B的坐标代入抛物线可得,解得.【考点】直线与抛物线的位置关系4.已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(,0).(1)求双曲线C的方程;(2)若直线l:y=kx+与双曲线C恒有两个不同的交点A和B,且·>2(其中O为原点),求k的取值范围.【答案】(1)-y2=1(2)(-1,-)∪(,1)【解析】(1)设双曲线C的方程为-=1(a>0,b>0).由已知得a=,c=2,再由c2=a2+b2得b2=1,所以双曲线C的方程为-y2=1.(2)将y=kx+代入-y2=1中,整理得(1-3k2)x2-6kx-9=0,由题意得,故k2≠且k2<1①.设A(xA ,yA),B(xB,yB),则xA+xB=,xAxB=,由·>2得xA xB+yAyB>2,x A xB+yAyB=xAxB+(kxA+)(kxB+)=(k2+1)xAxB+k(xA+xB)+2=(k2+1)·+k·+2=,于是>2,即>0,解得<k2<3②.由①②得<k2<1,所以k的取值范围为(-1,-)∪(,1).5.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )A.B.C.D.【答案】A【解析】圆的方程为,则其直径长圆心为,设的方程为,代入抛物线方程得:设,有∴线段的长按此顺序构成一个等差数列,,即,解得,故选A.【考点】1.抛物线的几何性质;2.直线与抛物线相交问题.6.已知F是抛物线的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为()A.B.1C.D.【答案】C【解析】过A,B及线段AB的中点C向抛物线的准线作垂线,垂足分别为M,N,Q,CQ交y轴于T,由抛物线的定义知|AM|+|BN|=|AF|+|BF|=3,因为CQ是直角梯形AMNB的中位线所以CQ|=(|AM|+|BN)=,所以|CT|=|CQ|-|TQ|=-=7.已知抛物线的准线与x轴交于点M,过点M作圆的两条切线,切点为A、B,.(1)求抛物线E的方程;(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.【答案】(1)y2=4x;(2)点N坐标为或.【解析】本题主要考查抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质等基础知识,考查学生分析问题解决问题的能力和计算能力.第一问,利用抛物线的准线,得到M点的坐标,利用圆的方程得到圆心C的坐标,在中,可求出,在中,利用相似三角形进行角的转换,得到的长,而,从而解出P的值,即得到抛物线的标准方程;第二问,设出N点的坐标,利用N、C点坐标写出圆C的方程,利用点C的坐标写出圆C的方程,两方程联立,由于P、Q是两圆的公共点,所以联立得到的方程即为直线PQ的方程,而O点在直线上,代入点O的坐标,即可得到s、t的值,即得到N点坐标.试题解析:(1)由已知得,C(2,0).设AB与x轴交于点R,由圆的对称性可知,.于是,所以,即,p=2.故抛物线E的方程为y2=4x. 5分(2)设N(s,t).P,Q是NC为直径的圆D与圆C的两交点.圆D方程为,即x2+y2-(s+2)x-ty+2s=0.①又圆C方程为x2+y2-4x+3=0.②②-①得(s-2)x+ty+3-2s=0.③ 9分P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.因为直线PQ经过点O,所以3-2s=0,.故点N坐标为或. 12分【考点】抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质.8.如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.(1)若直线PQ过定点,求点A的坐标;(2)对于第(1)问的点A,三角形APQ能否为等腰直角三角形?若能,试确定三角形APD的个数;若不能,说明理由.【答案】(1),(2)一个【解析】(1)确定抛物线标准方程只需一个独立条件,本题条件为已知通径长所以抛物线的方程为.直线过定点问题,实际是一个等式恒成立问题.解决问题的核心是建立变量的一个等式.可以考虑将直线的斜率列为变量,为避开讨论,可设的方程为,与联立消得,则,设点坐标为,则有,代入化简得:因此,点坐标为,(2)若三角形APQ为等腰直角三角形,则的中点与点A连线垂直于.先求出的中点坐标为,再讨论方程解的个数,这就转化为研究函数增减性,并利用零点存在定理判断零点有且只有一个.试题解析:(1)设抛物线的方程为,依题意,,则所求抛物线的方程为. (2分)设直线的方程为,点、的坐标分别为.由,消得.由,得,,.∵,∴.设点坐标为,则有.,,∴或.∴或, ∵恒成立. ∴.又直线过定点,即,代入上式得注意到上式对任意都成立,故有,从而点坐标为. (8分)(2)假设存在以为底边的等腰直角三角形,由第(1)问可知,将用代换得直线的方程为.设,由消,得.∴,.∵的中点坐标为,即,∵,∴的中点坐标为.由已知得,即.设,则,在上是增函数.又,,在内有一个零点.函数在上有且只有一个零点,所以满足条件的等腰直角三角形有且只有一个. (12分)【考点】直线与抛物线关系,零点存在定理9.在平面直角坐标系中,已知三点,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为,而直线AB恰好经过抛物线)的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则()A.9B.C.D.【答案】A【解析】由题意得,且.令,,则,所以,且,由此可解得.由抛物线的方程知焦点为,因此设直线的方程为,代入抛物线方程,得,解得或,所以由题意知,.由图形特征根据三角形相似易知.【考点】1、直线的斜率;2、直线方程;3、直线与抛物线的位置关系.10.抛物线y2=-8x的准线方程是________.【答案】x=2【解析】∵2p=8,∴p=4,故所求准线方程为x=2.11.下图是抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m.水位下降1m后,水面宽________m.【答案】2【解析】设抛物线的方程为x2=-2py,则点(2,-2)在抛物线上,代入可得p=1,所以x2=-2y.当y=-3时,x2=6,即x=±,所以水面宽为2.12.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y).若点M到该抛物线焦点的距离为3,则|OM|等于()A.2B.2C.4D.2【答案】B【解析】由题意设抛物线方程为y2=2px(p>0),则M到焦点的距离为xM+=2+=3,∴p=2,∴y2=4x. ∴=4×2,∴|OM|===2.故选B.13.已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点,|AF|=2,则|BF|=.【答案】2【解析】设A(x0,y),由抛物线定义知x+1=2,∴x=1,则直线AB⊥x轴,∴|BF|=|AF|=2.14.已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A、B两点,若·=0,则k等于()(A) (B) (C) (D)2【答案】D【解析】法一设直线方程为y=k(x-2),A(x1,y1)、B(x2,y2),由得k2x2-4(k2+2)x+4k2=0,∴x1+x2=,x 1x2=4,由·=0,得(x1+2,y1-2)·(x2+2,y2-2)=(x1+2)(x2+2)+[k(x1-2)-2][k(x2-2)-2]=0,代入整理得k2-4k+4=0,解得k=2.故选D.法二如图所示,设F为焦点,取AB中点P,过A、B分别作准线的垂线,垂足分别为G、H,连接MF,MP,由·=0,知MA⊥MB,则|MP|=|AB|=(|AG|+|BH|),所以MP为直角梯形BHGA的中位线,所以MP∥AG∥BH,所以∠GAM=∠AMP=∠MAP,又|AG|=|AF|,|AM|=|AM|,所以△AMG≌△AMF,所以∠AFM=∠AGM=90°,则MF⊥AB,所以k=-=2.15.已知F是抛物线y2=4x的焦点,P是圆x2+y2-8x-8y+31=0上的动点,则|FP|的最小值是() A.3B.4C.5D.6【答案】B【解析】圆x2+y2-8x-8y+31=0的圆心C坐标为(4,4),半径为1,∵|PF|≥|CF|-1,∴当P、C、F三点共线时,|PF|取到最小值,由y2=4x知F(1,0),∴|PF|min=-1=4.故选B.16.已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=-的垂线,垂足为M,则∠MAF的平分线所在直线的方程为.【答案】x-2y+4=0【解析】点A在抛物线上,所以16=4p,所以p=4,所以抛物线的焦点为F(1,0),准线方程为x=-1,垂足M(-1,4),由抛物线的定义得|AF|=|AM|,所以∠MAF的平分线所在的直线就是线段MF的垂直平分线,kMF==-2,所以∠MAF的平分线所在的直线方程为y-4=(x-4),即x-2y+4=0.17.设M(x0,y)为抛物线C:y2=8x上一点,F为抛物线C的焦点,若以F为圆心,|FM|为半径的圆和抛物线C的准线相交,则x的取值范围是()A.(2,+∞)B.(4,+∞) C.(0,2)D.(0,4)【答案】A【解析】∵(x0,y)为抛物线C:y2=8x上一点,∴x≥0,又∵以F为圆心,|FM|为半径的圆和抛物线C的准线相交,∴在水平方向上,点M应在点F的右侧,∴x>2.18.过抛物线y2=2px(p>0)上一定点P(x0,y)(y>0)作两直线分别交抛物线于A(x1,y1),B(x2,y2),当PA与PB的斜率存在且倾斜角互补时,的值为.【答案】-2【解析】设直线PA的斜率为kPA ,PB的斜率为kPB,由=2px1,=2px,得kPA==,同理kPB=,由于PA与PB的斜率存在且倾斜角互补,因此=-,即y1+y2=-2y(y>0),那么=-2.19.若抛物线y2=2px(p>0)的焦点在圆x2+y2+2x-3=0上,则p=()A.B.1C.2D.3【答案】C【解析】由已知(,0)在圆x2+y2+2x-3=0上,所以有+2×-3=0,即p2+4p-12=0,解得p=2或p=-6(舍去).20.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线共有()A.1条B.2条C.3条D.4条【答案】C【解析】作出图形,可知点(0,1)在抛物线y2=4x外.因此,过该点可作抛物线y2=4x的切线有两条,还能作一条与抛物线y2=4x的对称轴平行的直线,因此共有三条直线与抛物线只有一个交点.21.如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.(1)求实数b的值.(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.【答案】(1) b=-1 (2) (x-2)2+(y-1)2=4【解析】(1)由得x2-4x-4b=0(*)因为直线l与抛物线C相切,所以Δ=(-4)2-4×(-4b)=0.解得b=-1.(2)由(1)可知b=-1,故方程(*)为x2-4x+4=0.解得x=2,代入x2=4y,得y=1,故点A(2,1).因为圆A与抛物线C的准线相切,所以圆A的半径r就等于圆心A到抛物线的准线y=-1的距离,即r=|1-(-1)|=2,所以圆A的方程为(x-2)2+(y-1)2=4.22.过抛物线焦点的直线交其于,两点,为坐标原点.若,则的面积为()A.B.C.D.2【答案】C【解析】设直线的倾斜角为及,∵,∴点到准线的距离为,∴,则.∴的面积为.故选C.【考点】抛物线的几何性质,直线与抛物线的位置关系.23.如图X15-3所示,已知圆C1:x2+(y-1)2=4和抛物线C2:y=x2-1,过坐标原点O的直线与C2相交于点A,B,定点M的坐标为(0,-1),直线MA,MB分别与C1相交于点D,E.(1)求证:MA⊥MB;(2)记△MAB,△MDE的面积分别为S1,S2,若=λ,求λ的取值范围.【答案】(1)见解析(2)【解析】(1)证明:设直线AB的方程为y=kx,A(x1,y1),B(x2,y2),则x2-kx-1=0,所以x1+x2=k,x1x2=-1.又·=(x1,y1+1)·(x2,y2+1)=(k2+1)x1x2+k(x1+x2)+1=-k2-1+k2+1=0,∴MA⊥MB.(2)设直线MA的方程为y=k1x-1,MB的方程为y=k2x-1,k1k2=-1.解得或∴A(k1,-1),同理可得B(k2,-1),∴S1=|MA||MB|=|k1k2|.又解得或∴D ,同理可得E . ∴S 2=|MD||ME|=.=λ==≥.故λ的取值范围是.24. 已知抛物线C :y 2=2px(p>0)的焦点为F ,抛物线C 与直线l 1:y =-x 的一个交点的横坐标为8.(1)求抛物线C 的方程;(2)不过原点的直线l 2与l 1垂直,且与抛物线交于不同的两点A ,B ,若线段AB 的中点为P ,且|OP|=|PB|,求△FAB 的面积. 【答案】(1) y 2=8x (2) 24【解析】解:(1)易知直线与抛物线的交点坐标为(8,-8),∴82=2p×8, ∴2p =8,∴抛物线方程为y 2=8x. (2)直线l 2与l 1垂直,故可设l 2:x =y +m ,A(x 1,y 1),B(x 2,y 2),且直线l 2与x 轴的交点为M. 由得y 2-8y -8m =0,Δ=64+32m>0,∴m>-2. y 1+y 2=8,y 1y 2=-8m , ∴ x 1x 2==m 2.由题意可知OA ⊥OB ,即x 1x 2+y 1y 2=m 2-8m =0, ∴m =8或m =0(舍), ∴l 2:x =y +8,M(8,0).故S △FAB =S △FMB +S △FMA =·|FM|·|y 1-y 2|=3=24.25. 已知抛物线方程为x 2=4y ,过点M (0,m )的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,且x 1x 2=-4,则m 的值为________. 【答案】1【解析】设直线方程为y =kx +m ,代入抛物线方程得x 2-4kx -4m =0,所以x 1x 2=-4m ,所以m =1.26. 抛物线的焦点坐标是( ) A .(2,0) B .(0,2) C .(l ,0) D .(0,1)【答案】D 【解析】因为,所以,因为焦点在的正半轴,所以焦点坐标为即。
100高中数学高考总复习抛物线习题及详解100

高中数学高考总复习抛物线习题(附参考答案)一、选择题1.(2010·湖北黄冈)若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .4[答案] D[解析] 椭圆中,a 2=6,b 2=2,∴c =a 2-b 2=2, ∴右焦点(2,0),由题意知p2=2,∴p =4.2.已知点M 是抛物线y 2=2px (p >0)上的一点,F 为抛物线的焦点,若以|MF |为直径作圆,则这个圆与y 轴的关系是( )A .相交B .相切C .相离D .以上三种情形都有可能[答案] B[解析] 如图,由MF 的中点A 作准线l 的垂线AE ,交直线l 于点E ,交y 轴于点B ;由点M 作准线l 的垂线MD ,垂足为D ,交y 轴于点C ,则MD =MF ,ON =OF , ∴AB =OF +CM 2=ON +CM2=DM 2=MF 2, ∴这个圆与y 轴相切.3.(2010·山东文)已知抛物线y 2=2px (p >0),过焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2[答案] B[解析] 设A (x 1,y 1),B (x 2,y 2),则线段AB 的中点(x 1+x 22,y 1+y 22),∴y 1+y 22=2,∵A 、B 在抛物线y 2=2px 上,∴⎩⎪⎨⎪⎧y 12=2px 1 ①y 22=2px 2② ①-②得y 12-y 22=2p (x 1-x 2),∴k AB =y 1-y 2x 1-x 2=2p y 1+y 2=p 2,∵k AB =1,∴,p =2∴抛物线方程为y 2=4x ,∴准线方程为:x =-1,故选B.4.双曲线x 29-y 24=1的渐近线上一点A 到双曲线的右焦点F 的距离等于2,抛物线y 2=2px (p >0)过点A ,则该抛物线的方程为( )A .y 2=9xB .y 2=4xC .y 2=41313xD .y 2=21313x[答案] C[解析] ∵双曲线x 29-y 24=1的渐近线方程为y =±23x ,F 点坐标为(13,0),设A 点坐标为(x ,y ),则y =±23x ,由|AF |=2⇒(x -13)2+⎝⎛⎭⎫23x 2=2⇒x =913,y =±613,代入y 2=2px 得p =21313,所以抛物线方程为y 2=41313x ,所以选C.5.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172B .3 C. 5D.92[答案] A[解析] 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 与点(0,2)的距离,因此所求的最小值等于⎝⎛⎭⎫122+22=172,选A. 6.已知抛物线C :y 2=4x 的焦点为F ,准线为l ,过抛物线C 上的点A 作准线l 的垂线,垂足为M ,若△AMF 与△AOF (其中O 为坐标原点)的面积之比为,则点A 的坐标为( )A .(2,22)B .(2,-22)C .(2,±2)D .(2,±22)[答案] D[解析] 如图,由题意可得,|OF |=1,由抛物线定义得,|AF |=|AM |,∵△AMF 与△AOF (其中O 为坐标原点)的面积之比为3∶1,∴S △AMFS △AOF =12×|AF |×|AM |×sin ∠MAF 12×|OF |×|AF |×sin (π-∠MAF )=3, ∴|AM |=3,设A ⎝⎛⎭⎫y 024,y 0,∴y 024+1=3,解得y 0=±22,∴y 024=2,∴点A 的坐标是(2,±22),故选D.7.(2010·河北许昌调研)过点P (-3,1)且方向向量为a =(2,-5)的光线经直线y =-2反射后通过抛物线y 2=mx ,(m ≠0)的焦点,则抛物线的方程为( )A .y 2=-2xB .y 2=-32xC .y 2=4xD .y 2=-4x[答案] D[解析] 设过P (-3,1),方向向量为a =(2,-5)的直线上任一点Q (x ,y ),则PQ →∥a ,∴x +32=y -1-5,∴5x +2y +13=0,此直线关于直线y =-2对称的直线方程为5x +2(-4-y )+13=0,即5x -2y +5=0,此直线过抛物线y 2=mx 的焦点F ⎝⎛⎭⎫m 4,0,∴m =-4,故选D.8.已知mn ≠0,则方程是mx 2+ny 2=1与mx +ny 2=0在同一坐标系内的图形可能是( )[答案] A[解析] 若mn >0,则mx 2+ny 2=1应为椭圆,y 2=-mnx 应开口向左,故排除C 、D ;∴mn <0,此时抛物线y 2=-mnx 应开口向右,排除B ,选A.9.(2010·山东聊城模考)已知A 、B 为抛物线C :y 2=4x 上的不同两点,F 为抛物线C 的焦点,若F A →=-4FB →,则直线AB 的斜率为( )A .±23B .±32C .±34D .±43[答案] D[解析] ∵F A →=-4FB →,∴|F A →|=4|FB →|,设|BF |=t ,则|AF |=4t ,∴|BM |=|AA 1|-|BB 1|=|AF |-|BF |=3t ,又|AB |=|AF |+|BF |=5t ,∴|AM |=4t ,∴tan ∠ABM =43,由对称性可知,这样的直线AB 有两条,其斜率为±43.10.已知抛物线C 的方程为x 2=12y ,过点A (0,-4)和点B (t,0)的直线与抛物线C 没有公共点,则实数t 的取值范围是( )A .(-∞,-1)∪(1,+∞) B.⎝⎛⎭⎫-∞,-22∪⎝⎛⎭⎫22,+∞ C .(-∞,-22)∪(22,+∞) D .(-∞,-22)∪(2,+∞) [答案] B[解析] 由题意知方程组⎩⎨⎧x 2=12y ①x t +y-4=1 ②无实数解由②得y =4xt -4,代入①整理得,2x 2-4x t +4=0,∴Δ=16t2-32<0,∴t >22或t <-22,故选B. [点评] 可用数形结合法求解,设过点A (0,-4)与抛物线x 2=12y 相切的直线与抛物线切点为M (x 0,y 0),则切线方程为y -y 0=4x 0(x -x 0), ∵过A 点,∴-4-2x 02=4x 0(0-x 0), ∴x 0=±2,∴y 0=4,∴切线方程为y -4=±42x -8, 令y =0得x =±22,即t =±22,由图形易知直线与抛物线无公共点时,t <-22或t >22. 二、填空题11.已知点A (2,0)、B (4,0),动点P 在抛物线y 2=-4x 上运动,则AP →·BP →取得最小值时的点P 的坐标是______.[答案] (0,0)[解析] 设P ⎝⎛⎭⎫-y 24,y ,则AP →=⎝⎛⎭⎫-y 24-2,y ,BP →=⎝⎛⎭⎫-y 24-4,y ,AP →·BP →=⎝⎛⎭⎫-y24-2⎝⎛⎭⎫-y 24-4+y 2=y 416+52y 2+8≥8,当且仅当y =0时取等号,此时点P 的坐标为(0,0).12.(文)(2010·泰安市模拟)如图,过抛物线y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,交抛物线于A 、B 两点,且|F A |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 设抛物线准线为l ,作AA 1⊥l ,BB 1⊥l ,FQ ⊥l ,垂足分别为A 1、B 1、Q ,作BM ⊥AA 1垂足为M ,BM 交FQ 于N ,则由条件易知∠ABM =30°,设|BF |=t ,则|NF |=t 2,|MA |=t +32,∵|AM |=|QN |,∴3-t +32=p -t 2,∴p =32,∴抛物线方程为y 2=3x .(理)(2010·泰安质检)如图,过抛物线y 2=2px (p >0)的焦点的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 解法1:过A 、B 作准线垂线,垂足分别为A 1,B 1,则|AA 1|=3,|BB 1|=|BF |,∵|BC |=2|BF |,∴|BC |=2|BB 1|,∴|AC |=2|AA 1|=2|AF |=6,∴|CF |=3,∴p =12|CF |=32,∴抛物线方程为y 2=3x .解法2:由抛物线定义,|BF |等于B 到准线的距离,由|BC |=2|BF |得∠BCB 1=30°,又|AF |=3,从而A ⎝⎛⎭⎫p 2+32,332在抛物线上,代入抛物线方程y 2=2px ,解得p =32.点评:还可以由|BC |=2|BF |得出∠BCB 1=30°,从而求得A 点的横坐标为|OF |+12|AF |=p2+32或3-p 2,∴p 2+32=3-p 2,∴p =32. 13.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.[答案] 3+2 2[解析] 分别由A 和B 向准线作垂线,垂足分别为A 1,B 1,则由条件知, ⎩⎪⎨⎪⎧|AA 1|+|BB 1|=|AB |,|AA 1|-|BB 1|=22|AB |,解得⎩⎪⎨⎪⎧|AA 1|=2+24|AB ||BB 1|=2-24|AB |,∴|AA 1||BB 1|=3+22,即|F A ||FB |=3+2 2. 14.(文)若点(3,1)是抛物线y 2=2px 的一条弦的中点,且这条弦所在直线的斜率为2,则p =________.[答案] 2[解析] 设弦两端点P 1(x 1,y 1),P 2(x 2,y 2),则⎩⎪⎨⎪⎧y 12=2px 1y 22=2px 2,两式相减得,y 1-y 2x 1-x 2=2p y 1+y 2=2,∵y 1+y 2=2,∴p =2.(理)(2010·衡水市模考)设抛物线x 2=12y 的焦点为F ,经过点P (2,1)的直线l 与抛物线相交于A 、B 两点,又知点P 恰为AB 的中点,则|AF |+|BF |=________.[答案] 8[解析] 过A 、B 、P 作准线的垂线AA 1、BB 1与PP 1,垂足A 1、B 1、P 1,则|AF |+|BF |=|AA 1|+|BB 1|=2|PP 1|=2[1-(-3)]=8.三、解答题15.(文)若椭圆C 1:x 24+y 2b 2=1(0<b <2)的离心率等于32,抛物线C 2:x 2=2py (p >0)的焦点在椭圆C 1的顶点上.(1)求抛物线C 2的方程;(2)若过M (-1,0)的直线l 与抛物线C 2交于E 、F 两点,又过E 、F 作抛物线C 2的切线l 1、l 2,当l 1⊥l 2时,求直线l 的方程.[解析] (1)已知椭圆的长半轴长为a =2,半焦距c =4-b 2, 由离心率e =c a =4-b 22=32得,b 2=1.∴椭圆的上顶点为(0,1),即抛物线的焦点为(0,1), ∴p =2,抛物线的方程为x 2=4y .(2)由题知直线l 的斜率存在且不为零,则可设直线l 的方程为y =k (x +1),E (x 1,y 1),F (x 2,y 2),∵y =14x 2,∴y ′=12x ,∴切线l 1,l 2的斜率分别为12x 1,12x 2,当l 1⊥l 2时,12x 1·12x 2=-1,即x 1·x 2=-4,由⎩⎪⎨⎪⎧y =k (x +1)x 2=4y得:x 2-4kx -4k =0, 由Δ=(-4k )2-4×(-4k )>0,解得k <-1或k >0. 又x 1·x 2=-4k =-4,得k =1. ∴直线l 的方程为x -y +1=0.(理)在△ABC 中,CA →⊥CB →,OA →=(0,-2),点M 在y 轴上且AM →=12(AB →+CD →),点C在x 轴上移动.(1)求B 点的轨迹E 的方程;(2)过点F ⎝⎛⎭⎫0,-14的直线l 交轨迹E 于H 、E 两点,(H 在F 、G 之间),若FH →=12HG →,求直线l 的方程.[解析] (1)设B (x ,y ),C (x 0,0),M (0,y 0),x 0≠0, ∵CA →⊥CB →,∴∠ACB =π2,∴2x 0·y 0-x 0=-1,于是x 02=2y 0① M 在y 轴上且AM →=12(AB →+AC →),所以M 是BC 的中点,可得 ⎩⎨⎧x 0+x 2=0y +02=y,∴⎩⎪⎨⎪⎧x 0=-x ②y 0=y2③ 把②③代入①,得y =x 2(x ≠0),所以,点B 的轨迹E 的方程为y =x 2(x ≠0). (2)点F ⎝⎛⎭⎫0,-14,设满足条件的直线l 方程为: y =kx -14,H (x 1,y 1),G (x 2,y 2),由⎩⎪⎨⎪⎧y =kx -14y =x 2消去y 得,x 2-kx +14=0.Δ=k 2-1>0⇒k 2>1,∵FH →=12HG →,即⎝⎛⎭⎫x 1,y 1+14=12(x 2-x 1,y 2-y 1), ∴x 1=12x 2-12x 1⇒3x 1=x 2.∵x 1+x 2=k ,x 1x 2=14,∴k =±233,故满足条件的直线有两条,方程为:8x +43y +3=0和8x -43y -3=0. 16.(文)已知P (x ,y )为平面上的动点且x ≥0,若P 到y 轴的距离比到点(1,0)的距离小1.(1)求点P 的轨迹C 的方程;(2)设过点M (m,0)的直线交曲线C 于A 、B 两点,问是否存在这样的实数m ,使得以线段AB 为直径的圆恒过原点.[解析] (1)由题意得:(x -1)2+y 2-x =1,化简得:y 2=4x (x ≥0). ∴点P 的轨迹方程为y 2=4x (x ≥0).(2)设直线AB 为y =k (x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -m )y 2=4x ,得ky 2-4y -4km =0, ∴y 1+y 2=4k ,y 1·y 2=-4m .∴x 1·x 2=m 2,∵以线段AB 为直径的圆恒过原点, ∴OA ⊥OB ,∴x 1·x 2+y 1·y 2=0.即m 2-4m =0⇒m =0或4.当k 不存在时,m =0或4. ∴存在m =0或4,使得以线段AB 为直径的圆恒过原点.[点评] (1)点P 到定点F (1,0)的距离比到y 轴的距离大1,即点P 到定点F (1,0)的距离与到定直线l :x =-1的距离相等.∴P 点轨迹是以F 为焦点,l 为准线的抛物线,∴p =2,∴方程为y 2=4x .(理)已知抛物线y 2=4x ,过点(0,-2)的直线交抛物线于A 、B 两点,O 为坐标原点. (1)若OA →·OB →=4,求直线AB 的方程.(2)若线段AB 的垂直平分线交x 轴于点(n,0),求n 的取值范围.[解析] (1)设直线AB 的方程为y =kx -2 (k ≠0),代入y 2=4x 中得,k 2x 2-(4k +4)x +4=0①设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k +4k 2,x 1x 2=4k 2.y 1y 2=(kx 1-2)·(kx 2-2)=k 2x 1x 2-2k (x 1+x 2)+4=-8k.∵OA →·OB →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=4k 2-8k =4,∴k 2+2k -1=0,解得k =-1±2.又由方程①的判别式Δ=(4k +4)2-16k 2=32k +16>0得k >-12,∴k =-1+2,∴直线AB 的方程为(2-1)x -y -2=0.(2)设线段AB 的中点的坐标为(x 0,y 0),则由(1)知x 0=x 1+x 22=2k +2k 2,y 0=kx 0-2=2k,∴线段AB 的垂直平分线的方程是 y -2k =-1k ⎝⎛⎭⎫x -2k +2k 2. 令y =0,得n =2+2k +2k 2=2k 2+2k +2=2⎝⎛⎭⎫1k +122+32.又由k >-12且k ≠0得1k <-2,或1k>0,∴n >2⎝⎛⎭⎫0+122+32=2.∴n 的取值范围为(2,+∞). 17.(文)(2010·全国Ⅰ)已知抛物线C :y 2=4x 的焦点为F ,过点K (-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D .(1)证明:点F 在直线BD 上;(2)设F A →·FB →=89,求△BDK 的内切圆M 的方程.[解析] 设A (x 1,y 1),B (x 2,y 2),D (x 1,-y 1),l 的方程为x =my -1(m ≠0) (1)将x =my -1(m ≠0)代入y 2=4x 并整理得 y 2-4my +4=0,从而y 1+y 2=4m ,y 1y 2=4① 直线BD 的方程为y -y 2=y 2+y 1x 2-x 1(x -x 2)即y -y 2=4y 2-y 1⎝⎛⎭⎫x -y 224 令y =0,得x =y 1y 24=1,所以点F (1,0)在直线BD 上.(2)由(1)知,x 1+x 2=(my 1-1)+(my 2-1)=4m 2-2, x 1x 2=(my 1-1)(my 2-1)=1因为F A →=(x 1-1,y 1),FB →=(x 2-1,y 2),F A →·FB →=(x 1-1,y 1)·(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+4=8-4m 2,故8-4m 2=89,解得m =±43,直线l 的方程为3x +4y +3=0,3x -4y +3=0. 从而y 2-y 1=±(4m )2-4×4=±437,故4y 2-y 1=±37因而直线BD 的方程为3x +7y -3=0,3x -7y -3=0.因为KF 为∠BKD 的角平分线,故可设圆心M (t,0),(-1<t <1),M (t,0)到直线l 及BD 的距离分别为3|t +1|5,3|t -1|4, 由3|t +1|5=3|t -1|4得t =19或t =9(舍去),故圆M 的半径为r =3|t +1|5=23, 所以圆M 的方程为⎝⎛⎭⎫x -192+y 2=49. (理)(2010·揭阳市模考)已知点C (1,0),点A 、B 是⊙O :x 2+y 2=9上任意两个不同的点,且满足AC →·BC →=0,设P 为弦AB 的中点.(1)求点P 的轨迹T 的方程;(2)试探究在轨迹T 上是否存在这样的点:它到直线x =-1的距离恰好等于到点C 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.[解析] (1)法一:连结CP ,由AC →·BC →=0知,AC ⊥BC ,∴|CP |=|AP |=|BP |=12|AB |, 由垂径定理知|OP |2+|AP |2=|OA |2,即|OP |2+|CP |2=9,设点P (x ,y ),有(x 2+y 2)+[(x -1)2+y 2]=9,化简得,x 2-x +y 2=4.法二:设A (x 1,y 1),B (x 2,y 2),P (x ,y ),根据题意知,x 12+y 12=9,x 22+y 22=9,2x =x 1+x 2,2y =y 1+y 2,∴4x 2=x 12+2x 1x 2+x 22,4y 2=y 12+2y 1y 2+y 22故4x 2+4y 2=(x 12+y 12)+(2x 1x 2+2y 1y 2)+(x 22+y 22)=18+2(x 1x 2+y 1y 2)①又∵AC →·BC →=0,∴(1-x 1,-y 1)·(1-x 2,-y 2)=0∴(1-x 1)×(1-x 2)+y 1y 2=0,故x 1x 2+y 1y 2=(x 1+x 2)-1=2x -1,代入①式得,4x 2+4y 2=18+2(2x -1),化简得,x 2-x +y 2=4.(2)根据抛物线的定义,到直线x =-1的距离等于到点C (1,0)的距离的点都在抛物线y 2=2px 上,其中p 2=1,∴p =2,故抛物线方程为y 2=4x , 由方程组⎩⎪⎨⎪⎧y 2=4x x 2-x +y 2=4得,x 2+3x -4=0, 解得x 1=1,x 2=-4,由于x ≥0,故取x =1,此时y =±2,故满足条件的点存在,其坐标为(1,-2)和(1,2).。
高考数学专题练习-抛物线含解析

高考数学专题练习-抛物线含解析一、选择题(本大题共20小题,共100.0分)1.一桥拱的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于()A.h2B.2h2C.h2D.h22.若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为()A.2B.C.D.3.已知抛物线y2=2px的焦点为F,△ABC的三个顶点都在抛物线上,且A(1,2),+=,则BC边所在的直线方程为()A.2x-y-2=0B.2x-y-1=0C.2x+y-6=0D.2x+y-3=04.抛物线y2=4x的焦点为F,其准线与x轴的交点为N,过点F作直线与抛物线交于A,B两点,若,则|AF|-|BF|=()A.2B.3C.4D.55.已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点P是抛物线C上一点,过P 作PM⊥l,垂足为M,记与MN交于点T,若|NF|=2|PF|,且△PNT的面积为,则p=()A. B.2 C. D.6.过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,且|AF|=2|BF|,则直线AB的斜率为()A. B. C.或 D.7.过抛物线C:y2=2px(p>0)的焦点F作斜率为的直线l与C及其准线分别相交于A、B、D三点,则的值为()A.2或B.3或C.1D.4或8.设抛物线C:y2=4x的焦点为F,倾斜角为钝角的直线l过F且与C交于A,B两点,若|AB|=,则l的斜率为()A.-1B.-C.-D.-9.正三角形ABC的两个顶点A,B在抛物线x2=2py(p>0)上,另一个顶点C是此抛物线焦点,则满足条件的三角形ABC的个数为()A.0B.1C.2D.310.已知直线l:y=kx-k与抛物线C:y2=4x及其准线分别交于M,N两点,F为抛物线的焦点,若,则实数k等于()A. B.±1 C. D.±211.设F是抛物线C1:y2=2px(p>0)的焦点,点A是抛物线与双曲线C2:-=1(a>0,b>0)的一条渐近线的一个公共点,且AF⊥x轴,则双曲线的离心率为()A. B. C. D.212.过抛物线C:y2=2px(p>0)焦点F的直线l与C相交于A,B两点,与C的准线交于点D,若|AB|=|BD|,则直线l的斜率k=()A. B.±3 C. D.13.已知抛物线顶点在原点,焦点为双曲线的右焦点,则此抛物线的方程是()A.y2=2xB.y2=4xC.y2=10xD.y2=20x14.已知抛物线y2=8x的准线与双曲线-=1相交于A,B两点,点F为抛物线的焦点,△ABF为直角三角形,则双曲线的离心率为()A.3B.C.2D.15.设抛物线C:y2=4x的焦点为F,倾斜角为钝角的直线l过F且与C交于A,B两点,若|AB|=,则l的斜率为()A.±B.-C.±D.-16.抛物线的顶点在原点,焦点是椭圆4x2+y2=1的一个焦点,则此抛物线的焦点到准线的距离是()A. B. C. D.17.过抛物线y2=4x焦点的直线l交抛物线于P(x1,x2),Q(x2,y2)两点,若x1+x2=6,则|PQ|=()A.9B.8C.8D.618.已知O为坐标原点,F为抛物线y2=4x的焦点,直线l:y=m(x-1)与抛物线交于A,B两点,点A在第一象限,若|FA|=3|FB|.则m的值为()A.3B.C.D.19.已知F是抛物线x2=8y的焦点,若抛物线上的点A到x轴的距离为5,则|AF|=()A.4B.5C.6D.720.抛物线y2=-4x的焦点坐标为()A.(0,-2)B.(-2,0)C.(0,-1)D.(-1,0)二、填空题(本大题共20小题,共100.0分)21.已知抛物线y2=2px(p>0)的焦点为F,过抛物线上点P(2,y0)的切线为l,过点P作平行于x轴的直线m,过F作平行于l的直线交m于M,若|PM|=5,则p的值为______ .22.已知抛物线C:x2=2py(p>0),P,Q是C上任意两点,点M(0,-1)满足,则p的取值范围是 ______ .23.已知抛物线的方程为x2=2py(p>0),过点A(0,-a)(a>0)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,a),连接BP,BQ.且QB,QP与x轴分别交于M,N两点,如果QB的斜率与PB的斜率之积为-3,则∠PBQ= ______ .24.已知以F为焦点的抛物线C:y2=2px(p>0)上的两点A,B满足=3,若弦AB的中点到准线的距离为,则抛物线的方程为 ______ .25.斜率为k(k>0)的直线l经过点F(1,0)交抛物线y2=4x于A,B两点,若△AOF 的面积是△BOF面积的2倍,则k= ______ .26.已知点P(2,1)是抛物线上x2=4y上的一点,点M,N是抛物线上的动点(M,N,P 三点不共线),直线PM,PN分别交y轴于A,B两点,且|PA|=|PB|,则直线MN的斜率为 ______ .27.已知抛物线y2=6x上的一点到焦点的距离是到y轴距离的2倍,则该点的横坐标为______ .28.抛物线顶点在原点,焦点在y轴上,其上一点P(m,1)到焦点的距离为5,则抛物线的标准方程为 ______ .29.若抛物线y2=8x上的点P到焦点的距离为6,则P到y轴的距离是 ______ .30.已知抛物线y2=2px(p>0)的准线为l,若l与圆x2+y2+6x+5=0的交点为A,B,且|AB|=2.则p的值为 ______ .31.圆心在抛物线y=x2上,并且和该抛物线的准线及y轴都相切的圆的标准方程为______ .32.过抛物线x2=8y焦点F作直线l交抛物线于A、B两点,若线段AB中点M的纵坐标为4,则|AB|= ______ .33.在平面直角坐标系x O y中,抛物线y2=4x的焦点到其准线的距离为 ______ .34.抛物线y2=4x上一点M到焦点的距离为5,则点M的横坐标为 ______ .35.抛物线y2=4x上横坐标为3的点P到焦点F的距离为 ______ .36.以抛物线y2=4x的焦点为顶点,顶点为中心,离心率为2的双曲线的渐近线方程为______ .37.已知点,点F为抛物线y2=2px(p>0)的焦点,点P是该抛物线上的一个动点.若|PF|+|PM|的最小值为5,则p的值为 ______ .38.若点A(-6,y)在抛物线y2=-8x上,F为抛物线的焦点,则AF的长度为 ______ .39.已知圆心C在抛物线y2=4x上且与准线相切,则圆C恒过定点 ______ .40.已知抛物线y2=8x的准线过双曲线的左焦点,且被双曲线解得的线段长为6,则双曲线的渐近线方程为 ______ .三、解答题(本大题共20小题,共240.0分)41.在平面直角坐标系x O y中,抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交C 于A,B两点,交x轴于点D,B到x轴的距离比|BF|小1.(Ⅰ)求C的方程;(Ⅱ)若S△BOF=S△AOD,求l的方程.42.已知E(2,2)是抛物线C:y2=2px上一点,经过点D(2,0)的直线l与抛物线C 交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N(1)求抛物线方程及其焦点坐标,准线方程;(2)已知O为原点,求证:∠MON为定值.43.已知抛物线C:y2=2px(p>0)的焦点为F,直线y=2与y的轴的交点为P,与C的交点为Q,且|QF|=2|PQ|.(1)求C的方程;(2)边焦点F的直线l斜率为-1,判断C上是否存在两点M,N,使得M,N关于直线l 对称,若存在,求出|MN|,若不存在,说明理由.44.已知圆M:(x-a)2+(y-b)2=9,M在抛物线C:x2=2py(p>0)上,圆M过原点且与C的准线相切.(Ⅰ)求C的方程;(Ⅱ)点Q(0,-t)(t>0),点P(与Q不重合)在直线l:y=-t上运动,过点P作C 的两条切线,切点分别为A,B.求证:∠AQO=∠BQO(其中O为坐标原点).45.已知抛物线C:y2=2px(p>0)的焦点是F,点D(1,y0)是抛物线上的点,且|DF|=2.(I)求抛物线C的标准方程;(Ⅱ)过定点M(m,0)(m>0)的直线与抛物线C交于A,B两点,与y轴交于点N,且满足:=λ,=μ.(i)当m=时,求证:λ+μ为定值;(ii)若点R是直线l:x=-m上任意一点,三条直线AR,BR,MR的斜率分别为k AR,k BR,k MR,问是否存在常数t,使得.k AR+k BR=t•k MR.恒成立?若存在求出t的值;若不存在,请说明理由.46.已知抛物线C顶点在原点,焦点在y轴上,抛物线C上一点Q(a,2)到焦点的距离为3,线段AB的两端点A(x1,y1)、B(x2,y2)在抛物线C上.(1)求抛物线C的方程;(2)若y轴上存在一点M(0,m)(m>0),使线段AB经过点M时,以AB为直径的圆经过原点,求m的值;(3)在抛物线C上存在点D(x3,y3),满足x3<x1<x2,若△ABD是以角A为直角的等腰直角三角形,求△ABD面积的最小值.47.如图,O为坐标原点,点F为抛物线C1:x2=2py(p>0)的焦点,且抛物线C1上点M处的切线与圆C2:x2+y2=1相切于点Q.(Ⅰ)当直线MQ的方程为时,求抛物线C1的方程;(Ⅱ)当正数p变化时,记S1,S2分别为△FMQ,△FOQ的面积,求的最小值.48.如图是一座桥的截面图,桥的路面由三段曲线构成,曲线AB和曲线DE分别是顶点在路面A、E的抛物线的一部分,曲线BCD是圆弧,已知它们在接点B、D处的切线相同,若桥的最高点C到水平面的距离H=6米,圆弧的弓高h=1米,圆弧所对的弦长BD=10米.(1)求弧所在圆的半径;(2)求桥底AE的长.49.已知圆O:x2+y2=1和抛物线E:y=x2-2,O为坐标原点.(1)已知直线l和圆O相切,与抛物线E交于M,N两点,且满足OM⊥ON,求直线l的方程;(2)过抛物线E上一点P(x0,y0)作两直线PQ,PR和圆O相切,且分别交抛物线E于Q,R两点,若直线QR的斜率为,求点P的坐标.50.已知直线l过点P(2,0),斜率为,直线l和抛物线y2=2x相交于A,B两点,设线段AB的中点为M,求:(1)点M的坐标;(2)线段AB的长|AB|.51.已知动点P到点(,0)的距离比它到直线x=-的距离小2.(Ⅰ)求动点P的轨迹方程;(Ⅱ)记P点的轨迹为E,过点S(2,0)斜率为k1的直线交E于A,B两点,Q(1,0),延长AQ,BQ与E交于C,D两点,设CD的斜率为k2,证明:为定值.52.如右图抛物线顶点在原点,圆(x-2)2+y2=22的圆心恰是抛物线的焦点,(Ⅰ)求抛物线的方程;(Ⅱ)一直线的斜率等于2,且过抛物线焦点,它依次截抛物线和圆于A、B、C、D四点,求|AB|+|CD|的值.53.已知椭圆C的中心为原点O,焦点在x轴上,且经过点(Ⅰ)求椭圆C的标准方程;(Ⅱ)过抛物线y2=4x的焦点F的直线l与椭圆C交于不同两点M,N,且满足⊥,求直线l的方程.54.已知平面内一动点M到点F(1,0)距离比到直线x=-3的距离小2.设动点M的轨迹为C.(1)求曲线C的方程;(2)若过点F的直线l与曲线C交于A、B两点,过点B作直线:x=-1的垂线,垂足为D,设A(x1,y1),B(x2,y2).求证:①x1•x2=1,y1•y2=-4;②A、O、D三点共线(O为坐标原点).55.已知抛物线E:y2=2px(p>0)的焦点F,E上一点(3,m)到焦点的距离为4.(Ⅰ)求抛物线E的方程;(Ⅱ)过F作直线l,交抛物线E于A,B两点,若直线AB中点的纵坐标为-1,求直线l的方程.56.已知抛物线关于y轴对称,它的顶点在坐标原点,并且经过点M(,-2)(1)求抛物线的标准方程.(2)如果直线y=x+m与这个抛物线交于不同的两点,求m的取值范围.57.(1)已知抛物线y2=2px(p>0)的焦点在直线2x-y-4=0上,求p的值;(2)已知双曲线的渐近线方程为,准线方程为,求双曲线的标准方程.58.已知抛物线的顶点在原点,它的准线过双曲线的一个焦点,抛物线与双曲线交点为,求抛物线方程和双曲线方程.59.已知抛物线C:y2=4x的焦点为F,准线为l.⊙F与C交于A,B两点,与x轴的负半轴交于点P.(Ⅰ)若⊙F被l所截得的弦长为,求|AB|;(Ⅱ)判断直线PA与C的交点个数,并说明理由.60.已知动点M到点N(1,0)和直线l:x=-1的距离相等.(Ⅰ)求动点M的轨迹E的方程;(Ⅱ)已知不与l垂直的直线l'与曲线E有唯一公共点A,且与直线l的交点为P,以AP为直径作圆C.判断点N和圆C的位置关系,并证明你的结论.【答案】1.B2.D3.B4.C5.D6.C7.D8.D9.C 10.C 11.A 12.D 13.D 14.A 15 .D 16.B 17.B 18.C 19.D 20.D21.622.(0,2]23.24.y2=8x25.226.-127.28.x2=16y29.430.4或831.(x±1)2+(y-)2=132.1233.234.435.436.y=37.2或638.839.(1,0)40.y=±x41.解:(Ⅰ)解法一:抛物线C:x2=2py(p>0)的焦点为F(0,),C的准线方程为,(1分)由抛物线的定义,可知|BF|等于点B到C的准线的距离.(2分)又因为点B到x轴的距离比|BF|小1,所以点B到x轴的距离比点B到抛物线准线的距离小1,(3分)故,解得p=2,所以C的方程为x2=4y.(4分)解法二:C的焦点为,(1分)将代入x2=2py,得x=p或x=-p,故,因为点B到x轴的距离比|BF|小1,,即,(2分)解得p=2,所以C的方程为x2=4y,(3分)经检验,抛物线的方程x2=4y满足题意.(4分)(Ⅱ)由(Ⅰ)得C的焦点为F(0,1),设直线l的方程为y=kx+1(k≠0),A(x1,y1),B(x2,y2).则.(5分)联立方程组消去y,得x2-4kx-4=0.(6分)△=(-4k)2-4×1×(-4)=16k2+16>0,由韦达定理,得x1+x2=4k,x1x2=-4.(7分)设点O到直线l的距离为d,则,.又S△BOF=S△AOD,所以|BF|=|AD|.(8分)又A,B,D,F在同一直线上,所以,即,(9分)因为,(10分)所以,整理,得16k4+16k2-1=0,故,解得,(11分)所以l的方程为.(12分)42.解:(1)将E(2,2)代入y2=2px,得p=1,∴抛物线方程为y2=2x,焦点坐标为(,0),准线方程x=-;.…(3分)(2)证明:设A(,y1),B(,y2),M(x M,y M),N(x N,y N),因为直线l不经过点E,则直线l的斜率存在,设直线l方程为y=k(x-2),与抛物线方程联立得到,消去x,整理得:ky2-2y-4k=0,则由韦达定理得:y1+y2=,y1y2=-4,…(6分)直线AE的方程为:y-2=(x-2),即y=(x-2)+2,令x=-2,得y M=,…(9分)同理可得:y N=,…(10分)又∵=(-2,y M),=(-2,y N),则•=4+y M y N=4+×,=4+=4+=0…(13分)∴OM⊥ON,即∠MON为定值.…(14分).方法二:证明:设A(,y1),B(,y2),M(x M,y M),N(x N,y N),设直线l方程为x=my+2,于抛物线方程联立得,整理得:y2-2my-4=0,则由韦达定理得:y1+y2=2m,y1y2=-4,…(6分)直线AE的方程为:y-2=(x-2),即y=(x-2)+2,令x=-2,得y M=,…(9分)同理可得:y N=,…(10分)又∵=(-2,y M),=(-2,y N),则•=4+y M y N=4+×,=4+=4+=0…(13分)∴OM⊥ON,即∠MON为定值.…(14分)43.解:(1)设Q(x0,2),P(0,2)代入由y2=2px(p>0)中得x0=,所以|PQ|=,|QF|=+,由题设得+=2×,解得p=-2(舍去)或p=2.所以C的方程为y2=4x.(2)设直线l的方程为x+y-1=0,设M(x1,y1),N(x2,y2),则k MN=,MN的中点T的坐标为(,),∵M,N关于直线l对称,∴MN⊥l,∴=1①,∵中点T在直线l上,∴=-+1②,由①②可得y1+y2=4,y1y2=4,∴y1,y2是方程y2-4y+4=0的两个根,此方程有两个相等的根,∴C上不存在M,N,使得M,N关于直线l对称.44.解:(I)解法一:因为圆M的圆心在抛物线上且与抛物线的准线相切,且圆半径为3,故,(1分)因为圆过原点,所以a2+b2=9,所以,(2分)又a2=2pb,所以,(3分)因为p>0,所以p=4,所以抛物线C方程x2=8y.(4分)解法二:因为圆M的圆心在抛物线上且与抛物线的准线相切,由抛物线的定义,圆M必过抛物线的焦点,(1分)又圆M过原点,所以,(2分)又圆的半径为3,所以,又a2=2pb,(3分)又,得p2=16(p>0),所以p=4.所以抛物线C方程x2=8y.(4分)解法三:因为圆M与抛物线准线相切,所以,(1分)且圆过又圆过原点,故,可得,(3分)解得p=4,所以抛物线C方程x2=8y.(4分)(Ⅱ)解法一:设A(x1,y1),B(x2,y2),P(m,-t),C方程为,所以,(5分)∴抛物线在点A处的切线的斜率,所以切线PA方程为:,即,化简得,(6分)又因过点P(m,-t),故可得,,(7分)即,同理可得,(8分)所以x1,x2为方程x2-2mx-4t=0的两根,所以x1+x2=2m,x1x2=-4t,(9分)因为Q(0,-t),所以,(10分)化简=.(11分)所以∠AQO=∠BQO.(12分)解法二:依题意设点P(m,-t),设过点P的切线为y=k(x-m)-t,所以,所以x2-4kx+4km+4t=0,所以△=16k2-4(4km+4t)=0,即k2-km-t=0,(5分)不妨设切线PA、PB的斜率为k1、k2,点A(x1,y1),B(x2,y2),所以k1+k2=m,k1•k2=-t,又,所以,所以,(6分)所以x1=2k1,,即点,同理点,(7分)因为Q(0,-t),所以,同理,(9分)所以=+=,(11分)所以∠AQO=∠BQO.(12分)45.解:(I)∵点D(1,y0)是抛物线上的点,且|DF|=2.∴1+=2,解得p=2.∴抛物线C的标准方程为y2=4x.(II)证明:(i)设A(x1,y1),B(x2,y2),当m==1时,M(1,0),直线AB的斜率存在且不为0,可设直线AB的方程为:x=ty+1(t≠0),可得N.联立,可得:y2-4ty-4=0,∴y1+y2=4t,y1y2=-4.∵=λ,=μ,∴=λ(-y1),=μ(-y2),∴λ+μ=-1--1-=-2-=-2-=-1.为定值.(ii)先取特殊情况探索三条直线AR,BR,MR的斜率之间的关系,当AB⊥x轴时,设A(m,y0),B(m,-y0),R(-m,y3),则k AR=,k MR=,k BR=,则k AR+k BR=2•k MR.下面证明一般情况成立.设A(x1,y1),B(x2,y2),R(-m,y3),直线AB的斜率不等于0,可设直线AB的方程为:x=ty+m.联立,化为:y2-4ty-4m=0,∴y1+y2=4t,y1y2=-4m.则k AR=,k MR=,k BR=,则k AR+k BR=+=,又,.代入可得:k AR+k BR=,把y1+y2=4t,y1y2=-4m代入化简可得:k AR+k BR==2•k MR.综上可得:三条直线AR,BR,MR的斜率满足k AR+k BR=2•k MR.46.解:(1)设抛物线的C方程x2=2py(p>0),则焦点F(0,),准线方程:y=-,过点Q向准线l作垂线,垂足为Q1,由抛物线的定义可得:丨QF丨=丨QQ1丨,∴2-(-)=3,p=2,∴抛物线方程:x2=4y;(2)设直线AB的方程:y=kx+m,则,整理得:x2-4kx-4m=0,则x1+x2=4k,x1x2=-4m,由AB为直径的圆经过原点,则⊥,•=0,则x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0∴(1+k2)×(-4m)+km×4k+m2=0,整理得m2-4m=0,解得:m=4或m=0,由m>0,则m=4,∴m的值4;(3)设直线AB的斜率为k,k>0,其方程y-y1=k(x-x1),即y=kx+y1-kx1,∴,整理得:x2-4kx+4kx1-4y1=0,∴x1+x2=4k,x2=-x1+4k,丨AB丨2=(1+k2)[(x1+x2)2-4x1x2]=(1+k2)[(x1+x2)2-4x1x2],=(1+k2)[(4k)2-4x1(-x1+4k)],=4(1+k2)(x12-4kx1+4k2),同理丨AD丨=4[1+(-)2][x12-4(-)x1+4(-)2],=4(1+)(x12+x1+),由丨AB丨=丨AD丨,则丨AB丨2=丨AD丨2,4(1+k2)(x12-4kx1+4k2),=4(1+)(x12+x1+),整理得:x1==k-,则丨AB丨2=4(1+k2)[(k-)2-4k(k-)+4k2]=4(1+k2)(k+)2,丨AB丨=2(k+),丨AD丨2=4(1+)[(k-)2+(k-)+]4(1+)(k+)2,丨AD丨=2(k+),∴△ABD面积S=×丨AB丨×丨AD丨=×2(k+)×2(k+),==2(k+)3≥2(2)3=16,当且仅当k=时,即k2=1,即k=1,取等号,∴△ABD面积的最小值16.47.解:(Ⅰ)设点,由x2=2py(p>0)得,,求导,而直线MQ的斜率为1,∴且,解得:.∴抛物线的标准方程:x2=4y;…(4分)(Ⅱ)因为点M处的切线方程为:,即,根据切线又与圆相切,得d=r,即,化简得,4p2=x04-4x02>0,解得:丨x0丨>2,由方程组,解得:Q(,),由丨PQ丨=丨x P-x Q丨=丨x0-丨=(x02-2),点F(0,)到切线PQ的距离d===,则S1=丨PQ丨•d=(x02-2),S1=丨OF丨•丨x Q丨=,∴====++3≥2+3,当且仅当=时,取“=”号,即x02=4+2,此时p=,所以的最小值为.…(12分)48.解:(1)设弧所在圆的半径为r(r>0),由题意得r2=52+(r-1)2,则r=13,即弧所在圆的半径为13米.…(4分)(2)以线段AE所在直线为x轴,线段AE的中垂线为y轴,建立如图的平面直角坐标系.∵H=6米,BD=10米,弓高h=1米,∴B(-5,5),D(5,5),C(0,6),设所在圆的方程为x2+(y-b)2=r2,(r>0),则,,∴弧的方程为x2+(y+7)2=169(5≤y≤6)…6分设曲线AB所在抛物线的方程为:y=a(x-m)2,…(8分)由点B(-5,5),在曲线AB上∴5=a(5+m)2, …(10分)又弧与曲线段AB在接点B处的切线相同,且弧在点B处的切线的斜率为,由y=a(x-m)2,y′=2a(x-m),2a(-5-m)=,2a(5+m)=-,…(12分)由 得m=-29,A(-29,0),E(29,0)∴桥底AE的长为58米;…(13分)答:(1)弧所在圆的半径为13米;(2)桥底AE的长58米.(答和单位各1分)…(14分)49.解:(1)设l:y=kx+b,M(x1,y1),N(x2,y2),由l和圆O相切,得.∴b2=k2+1.由消去y,并整理得x2-kx-b-2=0,∴x1+x2=k,x1x2=-b-2.由OM⊥ON,得,即x1x2+y1y2=0.∴x1x2+(kx1+b)(kx2+b)=0.∴,∴(1+k2)(-b-2)+k2b+b2=0,∴b2(-b-2)+(b2-1)b+b2=0.∴b2+b=0.∴b=-1或b=0(舍).当b=-1时,k=0,故直线l的方程为y=-1.(2)设P(x0,y0),Q(x1,y1),R(x2,y2),则.∴.设l QR:y-y0=k1(x-x0),由直线和圆相切,得,即.设l PR:y-y0=k2(x-x0),同理可得:.故k1,k2是方程的两根,故.由得,故x0+x1=k1.同理x0+x2=k2,则2x0+x1+x2=k1+k2,即.∴,解或.当时,;当时,y0=1.故或.50.解:(1)∵直线l过点P(2,0),斜率为,设直线的倾斜角为α,tanα=,sinα=,cosα=,∴直线l的参数方程为(t为参数)(*)∵直线l和抛物线相交,将直线的参数方程代入抛物线方程y2=2x中,整理得8t2-15t-50=0,且△=152+4×8×50>0,设这个一元二次方程的两个根为t1、t2,由根与系数的关系,得t1+t2=,t1t2=-,由M为线段AB的中点,根据t的几何意义,因为中点M所对应的参数为,将此值代入直线l的参数方程的标准形式中,得M(,).(2)|AB|=|t2-t1|==.51.(Ⅰ)解:∵动点P到点(,0)的距离比它到直线x=-的距离小2,∴动点P到点(,0)的距离与它到直线x=-的距离相等,∴动点P的轨迹是以点(,0)为焦点的抛物线,∴动点P的轨迹方程为y2=2x;(Ⅱ)证明:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则直线AB的方程为y=k1(x-2),代入抛物线方程中,得,∴y1+y2=,y1y2=-4直线AC,BD过点Q(1,0),同理可得y1y3=y2y4=-2,∴y3=-,,∴k2===-=2k1,∴=2.52.解:(Ⅰ)设抛物线方程为y2=2px(p>0),∵圆(x-2)2+y2=22的圆心恰是抛物线的焦点,∴p=4.∴抛物线的方程为:y2=8x;(Ⅱ)依题意直线AB的方程为y=2x-4设A(x1,y1),D(x2,y2),则,得x2-6x+4=0,∴x1+x2=6,|AD|=x1+x2+p=6+4=10.|AB|+|CD|=|AD|-|CB|=10-4=6.53.解:(Ⅰ)由题意可知设椭圆的标准方程:(a>b>0),则a=2,将A2(,)代入,则b=1,∴椭圆的标准方程为:;(Ⅱ)方法一:抛物线y2=4x的焦点F(1,0),设直线l的方程为x=my+1,M(x1,y1),N(x2,y2),由⊥,则x1x2+y1y2=0(*),由,消去x,得得(m2+4)y2+2my-3=0,△=16m2+48>0∴y1+y2=-,y1y2=-,①x1x2=(1+my1)(1+my2)=1+m(y1+y2)+m2y1y2;=1+m×(-)+m2(-),=,②(9分)将①②代入(*)式,得+(-)=0,解得m=±,存在直线l满足条件,且直线l的方程为2x-y-2=0或2x+y-2=0.方法二:当直线l的斜率不存在时,不满足题意;当直线l的斜率存在时,设其方程为y=k(x-1),与C1的交点为M(x1,y1),N(x2,y2).联立,消去y并整理得(1+4k2)x2-8k2x+4(k2-1)=0,于是x1+x2=,x1x2=.①∴y1y2=k2(x1-1)(x2-1)=k2[x1x2-(x1+x2)+1]=k2[-+1]=-.② 由⊥,则•=0,即x1x2+y1y2=0(*),将①②代入③式,得+(-)==0,解得k=±2,∴存在直线l满足条件,且直线l的方程为2x-y-2=0或2x+y-2=0.54.解:(1)根据题意,点M到点F(1,0)的距离比它到直线x=-3的距离小1,即点M到点F(1,0)的距离与其到直线x=-1的距离相等,则点M的轨迹为抛物线,且其焦点为F(1,0),准线为x=-1,则其轨迹方程为y2=4x;…(6分)(2)①联立直线x=my+1与抛物线的方程,可得y2-4my-4=0,∴y1•y2=-4,x1•x2=1 …(9分)②设D(-1,y2),则k AO-k OD===0,所以A、O、D三点共线.…(12分)55.解:(Ⅰ)法一:抛物线E:y2=2px(p>0)的焦点F的坐标为,由已知…(2分)解得P=2或P=-14∵P>0,∴P=2∴E的方程为y2=4x.…(4分)法二:抛物线E:y2=2px(p>0)的准线方程为,由抛物线的定义可知解得p=2∴E的方程为y2=4x.…(4分)(Ⅱ)法一:由(Ⅰ)得抛物线E的方程为y2=4x,焦点F(1,0)设A,B两点的坐标分别为A(x1,y1),B(x2,y2),则…(6分)两式相减.整理得∵线段AB中点的纵坐标为-1∴直线l的斜率…(10分)直线l的方程为y-0=-2(x-1)即2x+y-2=0…(12分)法二:由(1)得抛物线E的方程为y2=4x,焦点F(1,0)设直线l的方程为x=my+1由消去x,得y2-4my-4=0设A,B两点的坐标分别为A(x1,y1),B(x2,y2),∵线段AB中点的纵坐标为-1∴解得…(10分)直线l的方程为即2x+y-2=0…(12分)56.解:(1)因为抛物线关于y轴对称,它的顶点在坐标原点,并且经过点M(,-2),则抛物线的焦点在y的负半轴上,∴可设它的标准方程为:x2=-2py(p>0),又因为点M在抛物线上,则3=-2p×(-2),解得:p=,∴椭圆的标准方程:x2=-y;(2)将直线方程代入抛物线方程:,整理得2x2+x+m=0,则△=b2-4ac=3-8m>0,解得:m<,m的取值范围(-∞,).57.解:(1)抛物线y2=2px(p>0)的焦点坐标为(p,0),又焦点在直线2x-y-4=0上,∴2p-0-4=0,解得p=2,(2)由题意知双曲线标准方程为:+=1,(a,b>0).∴=,=,又c2=a2+b2,解得a=4,b=3,∴所求双曲线标准方程为-=158.解:由题设知,抛物线以双曲线的右焦点为焦点,准线过双曲线的左焦点,∴p=2c.设抛物线方程为y2=4cx,∵抛物线过点,6=4c•.∴c=1,故抛物线方程为y2=4x.又双曲线过,∴=1.又a2+b2=c2=1,∴a2=或a2=9(舍).∴b2=,故双曲线方程为:4x2-=1.59.解:(Ⅰ)抛物线C:y2=4x的焦点为F(1,0),∵⊙F被l所截得的弦长为,∴圆的半径为=3,∴⊙F的方程为(x-1)2+y2=9,与y2=4x联立可得A(2,2),B(2,-2),∴|AB|=4;(Ⅱ)(x-1)2+y2=9,令y=0,可得P(4,0),∵A(2,2),∴直线PA与C的交点个数为2.60.解:(Ⅰ)设动点M(x,y),由抛物线定义可知点M的轨迹E是以N(1,0)为焦点,直线l:x=-1为准线的抛物线,所以轨迹E的方程为y2=4x.(Ⅱ)点N在以PA为直径的圆C上.理由:由题意可设直线l':x=my+n,由可得y2-4my-4n=0(*),因为直线l'与曲线E有唯一公共点A,所以△=16m2+16n=0,即n=-m2.所以(*)可化简为y2-4my+4m2=0,所以A(m2,2m),令x=-1得,因为n=-m2,所以所以NA⊥NP,所以点N在以PA为直径的圆C上.【解析】1. 解:由题意,建立如图所示的坐标系,设抛物线方程为y=ax2(a<0),则将(,-h)代入可得a=-,∴该抛物线拱的面积为h×3h+==2h2,故选B.建立坐标系,设抛物线方程为y=ax2(a<0),将(,-h)代入可得a=-,该抛物线拱的面积为h×3h+,即可得出结论.解决该试题的关键是利用定积分表示出抛物线拱的面积,然后借助于定积分得到结论.2. 解:根据题意,抛物线y=2x2上,设P到准线的距离为d,则有|PF|=d,抛物线的方程为y=2x2,即x2=y,其准线方程为:y=-,分析可得:当P在抛物线的顶点时,d有最小值,即|PF|的最小值为,故选:D.根据题意,设P到准线的距离为d,则有|PF|=d,将抛物线的方程为标准方程,求出其准线方程,分析可得d的最小值,即可得答案.本题考查抛物线的几何性质,要先将抛物线的方程化为标准方程.3. 解:A代入抛物线方程可得p=2,∴抛物线方程为y2=4x,F(1,0),∵+=,∴BC经过AF的中点(1,1),设直线方程为x=my+1-m,代入抛物线方程y2=4x,可得y2-4my-4+4m=0,∴4m=2,∴m=,∴直线方程为x=y+,即2x-y-1=0,故选B.A代入抛物线方程可得p=2,可得抛物线的方程,+=,BC经过AF的中点(1,1),设直线方程为x=my+1-m,代入抛物线方程y2=4x,可得y2-4my-4+4m=0,利用韦达定理,求出m,即可得出结论.本题考查抛物线的方程,考查直线与抛物线位置关系的运用,考查向量知识,属于中档题.4. 解:抛物线y2=4x的焦点为F(1,0),假设直线AN的斜率k存在,设AB方程为:y=k(x-1),,整理得:k2x2-2(k2+2)x+k2=0设两交点为A(x2,y2),B(x1,y1),∵,则∠NBF=90°,∴(x1-1)(x1+1)+y12=0,∴x12+y12=1,∴x12+4x1-1=0(x1>0),∴x1=-2+,∵x1x2=1,∴x2=2+,∴|AF|-|BF|=(x2+1)-(x1+1)=4,故选C.设直线l的方程,代入抛物线方程,利用韦达定理及向量数量积的坐标运算,分别求得A和B点横坐标,根据抛物线的焦半径公式,即可求得则|AF|-|BF|.本题考查直线与抛物线的位置关系,考查抛物线的定义,考查学生分析解决问题的能力,属于中档题.5. 解:如图所示,NF=∵|NF|=2|PF|,∴PM=PF=,由得x P=p∵PM∥NF,∴,∴s△NPT:s△NFT=1:2,∵△PNT的面积为,∴△PNF的面积为3×=9由,得,∵在抛物线y2=2px(p>0)上,即,解得p=.故选:D由NF|=2|PF|,得x P=p,由,得s△NPT:s△NFT=1:2,由,得,,点P在抛物线y2=2px(p>0)上,即,解得p.6. 解:如图,点A在第一象限.过A、B分别作抛物线的垂线,垂足分别为D、E,过A作EB的垂线,垂足为C,则四边形ADEC为矩形.由抛物线定义可知|AD|=|AF|,|BE|=|BF|,又∵|AF|=2|BF|,∴|AD|=|CE|=2|BE|,即B为CE中点,∴|AB|=3|BC|,在R t△ABC中,|AC|=2|BC|,∴直线l的斜率为=2;当点B在第一象限时,同理可知直线l的斜率为-2,∴直线l的斜率为±2,故选:C.当点A在第一象限,通过抛物线定义及|AF|=2|BF|可知B为CE中点,通过勾股定理可知|AC=2|BC|,进而计算可得结论.本题考查抛物线的简单性质,注意解题方法的积累,属于中档题.7. 解:抛物线C:y2=2px(p>0)的焦点F(,0),过A和B分别做准线的垂线,垂足分别为A′,B′,则直线AB的方程:y=(x-)设A(x1,y1),B(x2,y2),,整理得:y2-py-p2=0,则y1+y2=p,y1y2=-p2,设=λ,(-x1,-y1)=(x2-,y2),则-y1=λy2,由=++2=-,∴-λ-+2=-,整理得:λ2-17λ+4=0,解得:λ=4或λ=,当λ=4时,丨AF丨=4丨BF丨,则丨AB丨=5丨BF丨,由抛物线的定义可知:丨BF丨=丨BB′丨,由直线AB的斜率为,则sin∠∠BDB′=,即sin∠BDB′==,∴丨BD丨=丨BB′丨=丨BF丨,丨AD丨=丨AB丨+丨BD丨=,∴的值4,当λ=,4丨AF丨=丨BF丨,则丨AB丨=5丨AF丨,由抛物线的定义可知:丨AF丨=丨AB′丨,由直线AB的斜率为,则sin∠∠ADF′=,即sin∠ADF′==,∴丨AD丨=丨AB′丨=丨AF丨,丨BD丨=丨AB丨+丨AD丨=,∴的值,故选D.设抛物线方程,代入椭圆方程,设=λ,根据向量数量积的坐标运算,即可求得λ的值,分类讨论,根据抛物线的定义及相似性,即可求得丨BD丨及丨AD丨,即可求得的值.本题考查直线与抛物线的位置关系,考查韦达定理,向量的坐标运算,考查数形结合思想,考查计算能力,属于中档题.8. 解:由y2=4x,得F(1,0),设AB所在直线方程为y=k(x-1),联立y2=4x,得k2x2-(2k2+4)x+k2=0.∵|AB|=,∴2++2=,∵倾斜角为钝角,∴k=-,故选D.由题意设出直线AB的方程,联立直线和抛物线方程,利用韦达定理,结合弦长公式得答案.本题考查了抛物线的简单几何性质,考查了抛物线的定义,考查了学生的计算能力,是中档题.9. 解:由抛物线x2=2py(P>0)的焦点F(0,),等边三角形的一个顶点位于抛物线x2=2py(P>0)的焦点,另外两个顶点在抛物线上,则等边三角形关于x轴轴对称两个边的斜率k=±tan60°=±,其方程为:y=±x+,每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形.满足条件的三角形ABC的个数为2,故选C.由题意可知:x2=2py(P>0)的焦点F(0,),则两个边的斜率k=±tan60°=±,其方程为:y=±x+,每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形.满足条件的三角形ABC的个数为2,本题主要考查了抛物线的简单性质.主要是利用抛物线和正三角形的对称性,考查数形结合思想,属于基础题.10. 解:抛物线C:y2=4x的焦过抛物线的焦点,过N做NN′⊥准线x=-1,垂足为N′,由抛物线的定义,丨NN′丨=丨NF丨,由∠N′NM与直线l倾斜角相等,由,则cos∠N′NM==,则tan∠N′NM=±,∴直线l的斜率k=±,故选:C.由题意可知直线l过抛物线的焦点,由∠N′NM与直线l倾斜角相等,根据抛物线的定义即可求得tan∠N′NM,即可求得k的值.本题考查直线与抛物线的位置关系,抛物线的定义,考查数形结合思想,属于中档题.11. 解:由题意得F(,0),准线为x=-,设双曲线的一条渐近线为y=x,则点A (,),由抛物线的定义得|PF|等于点A到准线的距离,即=+,∴=1,e==,故选A.求出抛物线的焦点坐标和准线方程,利用抛物线的定义得到=+,利用离心率的定义求得双曲线的离心率.本题考查抛物线的定义和双曲线、抛物线的标准方程,以及双曲线、抛物线的简单性质的应用,利用抛物线的定义得到=+,是解题的关键.12. 解:如图,设A,B两点的抛物线的准线上的射影分别为A′,B′,过B作AA′的垂线BH,在三角形ABH中,∠BAH等于直线AB的倾斜角,其正切值即为丨k值,由抛物线的定义可知:设|BF|=n,B为AD中点,根据抛物线的定义可知:丨AF丨=丨AA′丨,丨BF丨=丨BB′丨,丨BB′丨=丨AA′丨,可得2|BF|=|AA′|,即|AF|=2|BF|,∴|AF|=2n,|AA′|=2n,|BF|=n,∴|AH|=n,在直角三角形ABH中,tan∠BAH===2,则直线l的斜率k=2;同理求得:直线l的斜率k=-2;故选:D.在三角形ABH中,∠BAH等于直线AB的倾斜角,其正切值即为k值,利用在直角三角形ABN中,tan∠BAH=,从而得出直线AB的斜率.本题主要考察了直线与抛物线的位置关系,抛物线的简单性质,特别是焦点弦问题,解题时要善于运用抛物线的定义解决问题,属于中档题.13. 解:双曲线的右焦点为(5,0)由题意,设抛物线方程为y2=2px(p>0)∵抛物线的焦点为双曲线的右焦点∴∴p=10所以抛物线方程为y2=20x故选D.先求双曲线的焦点坐标,再假设抛物线的方程,利用抛物线的焦点为双曲线的右焦点,可求抛物线方程.本题以双曲线的标准方程为载体,考查双曲线的焦点坐标,考查待定系数法求抛物线的标准方程,属于基础题.14. 解:依题意知抛物线的准线x=-2,代入双曲线方程得y=±•,不妨设A(-2,).∵△FAB是等腰直角三角形,∴=p=4,求得a=,∴双曲线的离心率为e====3,故选:A.先求解准线方程,代入双曲线方程求得y,根据双曲线的对称性可知△FAB为等腰直角三角形,进而可求得A或B的纵坐标为4,进而求得a,利用a,b和c的关系求得c,则双曲线的离心率可得.本题主要考查了双曲线的简单性质.解题的关键是通过双曲线的对称性质判断出△FAB 为等腰直角三角形,属于中档题.15. 解:由y2=4x,则焦点F(1,0),设AB所在直线方程为y=k(x-1),联立y2=4x,得k2x2-(2k2+4)x+k2=0.设A(x1,y1),B(x2,y2),则x1+x2=2+,∵|AB|=,∴2++2=,解得:k=±,∵倾斜角为钝角,∴k=-,故选D.由题意设出直线AB的方程,联立直线和抛物线方程,利用韦达定理,结合弦长公式得答案.本题考查了抛物线的简单几何性质,考查了抛物线的定义,考查了学生的计算能力,是。
抛物线【九大题型】(举一反三)(新高考专用)(解析版)—2025年高考数学一轮复习

抛物线【九大题型】专练【题型1 抛物线的定义及其应用】........................................................................................................................3【题型2 抛物线的标准方程】................................................................................................................................5【题型3 抛物线的焦点坐标及准线方程】............................................................................................................6【题型4 抛物线的轨迹方程】................................................................................................................................7【题型5 抛物线上的点到定点的距离及最值】....................................................................................................9【题型6 抛物线上的点到定点和焦点距离的和、差最值】..............................................................................11【题型7 抛物线的焦半径公式】..........................................................................................................................14【题型8 抛物线的几何性质】..............................................................................................................................16【题型9 抛物线中的三角形(四边形)面积问题】 (18)1、抛物线【知识点1 抛物线及其性质】1.抛物线的定义(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫作抛物线.点F叫作抛物线的焦点,直线l叫作抛物线的准线.(2)集合语言表示设点M(x,y)是抛物线上任意一点,点M到直线l的距离为d,则抛物线就是点的集合P={M||MF|=d}.2.抛物线的标准方程与几何性质(0,0)(0,0)3.抛物线与椭圆、双曲线几何性质的差异抛物线与椭圆、双曲线几何性质的差异:①它们都是轴对称图形,但椭圆和双曲线又是中心对称图形;②顶点个数不同,椭圆有4个顶点,双曲线有2个顶点,抛物线只有1个顶点;③焦点个数不同,椭圆和双曲线各有2个焦点,抛物线只有1个焦点;④离心率取值范围不同,椭圆的离心率范围是0<e<1,双曲线的离心率范围是e>1,抛物线的离心率是e=1;⑤椭圆和双曲线都有两条准线,而抛物线只有一条准线;⑥椭圆是封闭式曲线,双曲线和抛物线都是非封闭式曲线.【知识点2 抛物线标准方程的求解方法】1.抛物线标准方程的求解待定系数法:求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p,只需一个条件就可以确定抛物线的标准方程.【知识点3 抛物线的焦半径公式】1.焦半径公式设抛物线上一点P的坐标为,焦点为F.(1)抛物线:;(2)抛物线:(3)抛物线:;(4)抛物线:.注:在使用焦半径公式时,首先要明确抛物线的标准方程的形式,不同的标准方程对应于不同的焦半径公式.【知识点4 与抛物线有关的最值问题的解题策略】1.与抛物线有关的最值问题的两个转化策略(1)转化策略一:将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”“三角形两边之和大于第三边”,使问题得以解决.(2)转化策略二:将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.【方法技巧与总结】1.通径:过焦点与对称轴垂直的弦长等于2p.2.抛物线P,也称为抛物线的焦半径.【题型1 抛物线的定义及其应用】【例1】(2024·贵州贵阳·二模)抛物线y2=4x上一点M与焦点间的距离是10,则M到x轴的距离是()A.4B.6C.7D.9【解题思路】借助抛物线定义计算即可得.【解答过程】抛物线y2=4x的准线为x=―1,由抛物线定义可得x M+1=10,故x M=10―1=9,则|y M|===6,即M到x轴的距离为6.故选:B.【变式1-1】(2024·河北·模拟预测)已知点P为平面内一动点,设甲:P的运动轨迹为抛物线,乙:P到平面内一定点的距离与到平面内一定直线的距离相等,则()A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件【解题思路】根据已知条件,结合充分条件、必要条件的定义,即可求解.【解答过程】解:当直线经过定点时,点的轨迹是过定点且垂直于该直线的另一条直线,当直线不经过该定点时,点的轨迹为抛物线,故甲是乙的充分条件但不是必要条件.故选:A.【变式1-2】(2024·北京大兴·三模)已知抛物线y2=4x的焦点为F,过F且斜率为―1的直线与直线x=―1交于点A,点M在抛物线上,且满足|MA|=|MF|,则|MF|=()A.1B C.2D.【解题思路】由题意先求出过F且斜率为―1的直线方程,进而可求出点A,接着结合点M在抛物线上且|MA|=|MF|可求出x M,从而根据焦半径公式|MF|=x M+1即可得解.【解答过程】由题意可得F(1,0),故过F且斜率为―1的直线方程为y=―(x―1)=―x+1,令x=―1⇒y=2,则由题A(―1,2),因为|MA|=|MF|,所以MA垂直于直线x=―1,故y M=2,又M 在抛物线上,所以由22=4x M ⇒x M =1,所以|MF |=x M +1=2.故选:C.【变式1-3】(2024·福建莆田·模拟预测)若抛物线C 的焦点到准线的距离为3,且C 的开口朝左,则C 的标准方程为( )A .y 2=―6xB .y 2=6xC .y 2=―3xD .y 2=3x【解题思路】根据开口设抛物线标准方程,利用p 的几何意义即可求出.【解答过程】依题意可设C 的标准方程为y 2=―2px(p >0),因为C 的焦点到准线的距离为3,所以p =3,所以C 的标准方程为y 2=―6x .故选:A.【题型2 抛物线的标准方程】【例2】(2024·山东菏泽·模拟预测)已知点A (a,2)为抛物线x 2=2py (p >0)上一点,且点A 到抛物线的焦点F 的距离为3,则p =( )A .12B .1C .2D .4【解题思路】由题意,根据抛物线的性质,抛物线x 2=2py (p >0),则抛物线焦点为F 0,M (x 1,y 1)为 抛物线上一点,有|MF |=y 1+p 2,可得|AF |=2+p2=3,解得p =2.【解答过程】因为抛物线为x 2=2py (p >0),则其焦点在y 轴正半轴 上,焦点坐标为由于点A (a,2)为抛物线x 2=2py ,(p >0)为上一点,且点A 到抛物线的焦点F 的距离为3, 所以点A 到抛物线的焦点F 的距离为|AF |=2+p2=3,解得p =2,故选:C.【变式2-1】(2024·陕西安康·模拟预测)过点(2,―3),且焦点在y 轴上的抛物线的标准方程是( )A .x 2=―3yB .x 2=―43yC .x 2=―23yD .x 2=―4y【解题思路】利用待定系数法,设出抛物线方程,把点代入求解即可.【解答过程】设抛物线的标准方程为x 2=ay (a ≠0),将点点(2,―3)代入,得22=―3a,解得a=―43,所以抛物线的标准方程是x2=―43y.故选:B.【变式2-2】(2024·新疆·三模)已知抛物线y2=2px(p>0)上任意一点到焦点F的距离比到y轴的距离大1,则抛物线的标准方程为()A.y2=x B.y2=2x C.y2=4x D.y2=8x【解题思路】根据抛物线的定义求解.【解答过程】由题意抛物线y2=2px(p>0)上任意一点到焦点F的距离与它到直线x=―1的距离相,因此―p2=―1,p=2,抛物线方程为y2=4x.故选:C.【变式2-3】(2024·宁夏石嘴山·三模)如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于两点A、B,交其准线于C,AE与准线垂直且垂足为E,若|BC|=2|BF|,|AE|=3,则此抛物线的方程为()A.y2=3x2B.y2=9xC.y2=9x2D.y2=3x【解题思路】过点A,B作准线的垂线,设|BF|=a,得到|AC|=3+3a,结合抛物线的定义,求得a=1,再由BD//FG,列出方程求得p的值,即可求解.【解答过程】如图所示,分别过点B作准线的垂线,垂足为D,设|BF|=a,则|BC|=2|BF|=2a,由抛物线的定义得|BD|=|BF|=a,在直角△BCD中,可得sin∠BCD=|BD||BC|=12,所以∠BCD=30∘,在直角△ACE中,因为|AE|=3,可得|AC|=3+3a,由|AC |=2|AE |,所以3+3a =6,解得a =1,因为BD //FG ,所以1p =2a3a ,解得p =32,所以抛物线方程为y 2=3x .故选:C.【题型3 抛物线的焦点坐标及准线方程】【例3】(2024·内蒙古赤峰·二模)已知抛物线C 的方程为 x =―116y 2, 则此抛物线的焦点坐标为( )A .(-4,0)B .―14,C .(-2,0)D .―12,【解题思路】由抛物线的几何性质求解.【解答过程】依题意得:y 2=―16x ,则此抛物线的焦点坐标为:―4,0,故选:A.【变式3-1】(2024·黑龙江大庆·模拟预测)已知抛物线C:y =6x 2,则C 的准线方程为( )A .y =―32B .y =32C .y =―124D .y =124【解题思路】根据抛物线的准线方程直接得出结果.【解答过程】抛物线C :y =6x 2的标准方程为x 2=16y ,所以其准线方程为y =―124.故选:C.【变式3-2】(2024·河南·三模)抛物线y 2=―28x 的焦点坐标为( )A .(0,―14)B .(0,―7)C .(―14,0)D .(―7,0)【解题思路】根据抛物线的标准方程直接得出结果.【解答过程】∵2p =28,∴p =14,∴抛物线y 2=―28x 的焦点坐标为(―7,0).故选:D.【变式3-3】(2024·福建厦门·模拟预测)若抛物线y 2=mx 的准线经过双曲线x 2―y 2=2的右焦点,则m的值为()A.―4B.4C.―8D.8【解题思路】根据题意,分别求得双曲线的右焦点以及抛物线的准线方程,代入计算,即可得到结果.【解答过程】因为双曲线x2―y2=2的右焦点为(2,0),又抛物线y2=mx的准线方程为x=―m4,则―m4=2,即m=―8.故选:C.【题型4 抛物线的轨迹方程】【例4】(2024·湖南衡阳·三模)已知点F(2,0),动圆P过点F,且与x=―2相切,记动圆圆心P点的轨迹为曲线Γ,则曲线Γ的方程为()A.y2=2x B.y2=4x C.y2=8x D.y2=12x【解题思路】分析题意,利用抛物线的定义判断曲线是抛物线,再求解轨迹方程即可.【解答过程】由题意知,点P到点F的距离和它到直线x=―2的距离相等,所以点P的轨迹是以(2,0)为焦点的抛物线,所以Γ的方程为y2=8x,故C正确.故选:C.【变式4-1】(23-24高二上·北京延庆·期末)到定点F(1,0)的距离比到y轴的距离大1的动点且动点不在x轴的负半轴的轨迹方程是()A.y2=8x B.y2=C.y2=2x D.y2=x【解题思路】根据抛物线的定义即可得解.【解答过程】因为动点到定点F(1,0)的距离比到y轴的距离大1,所以动点到定点F(1,0)的距离等于到x=―1的距离,所以动点的轨迹是以F(1,0)为焦点,x=―1为准线的抛物线,所以动点的轨迹方程是y2=4x.故选:B.【变式4-2】(23-24高二上·重庆·期末)已知点P(x,y)=|x+1|,则点P的轨迹为()A.椭圆B.双曲线C.抛物线D.圆【解题思路】根据已知条件及抛物线的定义即可求解.P(x,y)到点(1,0)的距离;|x+1|表示点P(x,y)到直线x=―1的距离.=|x+1|,所以点P(x,y)到点(1,0)的距离等于点P(x,y)到直线x=―1的距离,所以P的轨迹为抛物线.故选:C.【变式4-3】(23-24高二上·宁夏石嘴山·阶段练习)一个动圆与定圆F:(x+2)2+y2=1相内切,且与定直线l:x=3相切,则此动圆的圆心M的轨迹方程是( )A.y2=8x B.y2=4x C.y2=―4x D.y2=―8x【解题思路】先利用圆与圆的位置关系,直线与圆的位置关系找到动点M的几何条件,再根据抛物线的定义确定动点M的轨迹,最后利用抛物线的标准方程写出轨迹方程.【解答过程】设动圆M的半径为r,依题意:|MF|=r―1,点M到定直线x=2的距离为d=r―1,所以动点M到定点F(―2,0)的距离等于到定直线x=2的距离,即M的轨迹为以F为焦点,x=2所以此动圆的圆心M的轨迹方程是y2=―8x.故选:D.【题型5 抛物线上的点到定点的距离及最值】【例5】(2024·全国·模拟预测)已知A是抛物线C:y2=4x上的点,N(4,0),则|AN|的最小值为()A.2B.C.4D.【解题思路】由抛物线的方程,利用二次函数的性质求最值【解答过程】设,t,则|AN|===≥当且仅当t=±故选:D.【变式5-1】(2024高三·全国·专题练习)已知P是抛物线y2=2x上的点,Q是圆(x―5)2+y2=1上的点,则|PQ |的最小值是( )A .2B .C .D .3【解题思路】将问题转化为求|PC|的最小值,根据两点之间的距离公式,求得|PC|的最小值再减去半径即可.【解答过程】如图,抛物线上点P (x,y )到圆心C (5,0)的距离为|PC |,|CP |≤|CQ |+|PQ |,因此|PQ |≥|CP |―1,当|CP |最小时,|PQ |=|CP |―1最小,而|CP |2=(x ―5)2+y 2=―52+y 2=2―82+9,当y =±|CP |min =3,因此|PQ |的最小值是2.故选:A.【变式5-2】(2024·湖南益阳·三模)已知M 是抛物线y²=4x 上一点,圆C 1:(x ―1)2+(y ―2)2=1关于直线y =x ―1对称的圆为C 2,N 是圆C 2上的一点,则|MN |的最小值为( )A .1B ―1C―1D .37【解题思路】根据对称性求出圆C 2的方程,设y 0,求出|MC 2|的最小值,即可求出|MN |的最小值.【解答过程】圆C 1:(x ―1)2+(y ―2)2=1圆心为C 1(1,2),半径r =1,设C 2(a,b ),=―1―1=0,解得a =3b =0,则C 2(3,0),所以圆C2 :(x ―3)2+y 2=1,设y 0,则|MC 2|==所以当y 20=4,即y 0=±2时,|MC 2|min=所以|MN |的最小值是―1.故选:A.【变式5-3】(2024·黑龙江齐齐哈尔·二模)已知抛物线C:y2=8x的焦点为F,M为C上的动点,N为圆A:x2+ y2+2x+8y+16=0上的动点,设点M到y轴的距离为d,则|MN|+d的最小值为()A.1B C D.2【解题思路】作出图形,过点M作ME垂直于抛物线的准线,垂足为点E,利用抛物线的定义可知d=|MF|―2,分析可知,当且仅当N、M为线段AF分别与圆A、抛物线C的交点时,|MN|+d取最小值,即可得解.【解答过程】根据已知得到F(2,0),圆A:(x+1)2+(y+4)2=1,所以A(―1,―4),圆A的半径为1,抛物线C的准线为l:x=―2,过点M作ME⊥l,垂足为点E,则|ME|=d+2,由抛物线的定义可得d+2=|ME|=|MF|,所以,|MN|+d=|MN|+|MF|―2≥|AM|+|MF|―1―2≥|AF|―1―2=1―2=2.当且仅当N、M为线段AF分别与圆A、抛物线C的交点时,两个等号成立,因此,|MN|+d的最小值为3.故选:D.【题型6 抛物线上的点到定点和焦点距离的和、差最值】【例6】(2024·四川成都·模拟预测)设点A(2,3),动点P在抛物线C:y2=4x上,记P到直线x=―2的距离为d,则|AP|+d的最小值为()A.1B.3C1D【解题思路】根据抛物线的定义,P到焦点F的距离等于P到准线的距离,可得d=|PF|+1,从而转化为求|AP|+|PF|+1的值,当A,P,F三点共线时,d=|PF|+1取得最小值,即可求解.【解答过程】由题意可得,抛物线C的焦点F(1,0),准线方程为x=―1,由抛物线的定义可得d=|PF|+1,所以|AP|+d=|AP|+|PF|+1,因为|AP|+|PF|≥|AF|==所以|AP|+d=|AP|+|PF|+1≥+1.当且仅当A,P,F三点共线时取等号,所以|AP|+d+1.故选:D.【变式6-1】(2024·湖南常德·一模)已知抛物线方程为:y2=16x,焦点为F.圆的方程为(x―5)2+(y―1)2 =1,设P为抛物线上的点,Q|PF|+|PQ|的最小值为()A.6B.7C.8D.9【解题思路】根据抛物线定义将点到焦点的距离转化为点到直线的距离,即|PF|=|PN|,从而得到|PF|+ |PQ|=|PN|+|PQ|,P、Q、N三点共线时和最小;再由Q在圆上,|QN|min=|MN|―r得到最小值.【解答过程】由抛物线方程为y2=16x,得到焦点F(4,0),准线方程为x=―4,过点P做准线的垂线,垂足为N,因为点P在抛物线上,所以|PF|=|PN|,所以|PF|+|PQ|=|PN|+|PQ|,当Q点固定不动时,P、Q、N三点共线,即QN垂直于准线时和最小,又因为Q在圆上运动,由圆的方程为(x―5)2+(y―1)2=1得圆心M(5,1),半径r=1,所以|QN|min=|MN|―r=8,故选:C.【变式6-2】(2024·全国·模拟预测)在直角坐标系xOy中,已知点F(1,0),E(―2,0),M(2,2),动点P满足线段PE的中点在曲线y2=2x+2上,则|PM|+|PF|的最小值为()A.2B.3C.4D.5【解题思路】设P(x,y),由题意求出P的轨迹方程,继而结合抛物线定义将|PM|+|PF|的最小值转化为M 到直线l的距离,即可求得答案.【解答过程】设P(x,y),则PE y2=2x+2,可得y2=4x,故动点P的轨迹是以F为焦点,直线l:x=―1为准线的抛物线,由于22<4×2,故M(2,2)在抛物线y2=4x内部,过点P作PQ⊥l,垂足为Q,则|PM|+|PF|=|PM|+|PQ|,(抛物线的定义),故当且仅当M,P,Q三点共线时,|PM|+|PQ|最小,即|PM|+|PF|最小,最小值为点M到直线l的距离,所以(|PM|+|PF|)min=2―(―1)=3,故选:B.【变式6-3】(2024·陕西西安·一模)设P为抛物线C:y2=4x上的动点,A(2,6)关于P的对称点为B,记P到直线x=―1、x=―4的距离分别d1、d2,则d1+d2+|AB|的最小值为()A B.C+3D.+3【解题思路】根据题意得到d1+d2+|AB|=2d1+3+2|PA|=2(d1+|PA|)+3,再利用抛物线的定义结合三角不等式求解.【解答过程】抛物线C:y2=4x的焦点为F(1,0),准线方程为x=―1,如图,因为d 2=d 1+3,且A (2,6)关于P 的对称点为B ,所以|PA |=|PB |,所以d 1+d 2+|AB |=2d 1+3+2|PA |=2(d 1+|PA |)+3 =2(|PF |+|PA |)+3≥2|AF |+3 ==.当P 在线段AF 与抛物线的交点时,d 1+d 1+|AB |取得最小值,且最小值为.故选:D.【题型7 抛物线的焦半径公式】【例7】(2024·青海西宁·一模)已知F 是抛物线C:x 2=4y 的焦点,点M 在C 上,且M 的纵坐标为3,则|MF |=( )A .B .C .4D .6【解题思路】利用抛物线的标准方程和抛物线的焦半径公式即可求解.【解答过程】由x 2=4y ,得2p =4,解得p =2.所以抛物线C:x 2=4y 的焦点坐标为F (0,1),准线方程为y =―1,又因为M 的纵坐标为3,点M 在C 上,所以|MF |=y M +p2=3+22=4.故选:C.【变式7-1】(2024·河南·模拟预测)已知抛物线C:y 2=2px (p >0)上的点(m,2)到原点的距离为为F ,准线l 与x 轴的交点为M ,过C 上一点P 作PQ ⊥l 于Q ,若∠FPQ =2π3,则|PF |=( )A .13B .12C D .23【解题思路】根据点(m,2)到原点的距离为再设点P 坐标,利用抛物线的定义和等腰三角形的性质列出方程即可求解.【解答过程】因为点(m,2)到原点的距离为所以m 2+22=8,解得m =2,(负值舍),将点(2,2)代入抛物线方程y 2=2px (p >0),得4=4p ,所以p =1,所以C:y 2=2x,F(12,0),l:x =―12.由于抛物线关于x 轴对称,不妨设,因为|PQ|=|PF|=x +12,∠FPQ =2π3,所以△PQF 为等腰三角形,∠PQF =π6,所以|QF|=+12),所以|QF|==+12),解得x =16或x =―12(舍),所以|PF |=16+12=23.故选:D.【变式7-2】(2024·新疆·三模)已知抛物线C :y 2=x 的焦点为F ,在抛物线C 上存在四个点P ,M ,Q ,N ,若弦PQ 与弦MN 的交点恰好为F ,且PQ ⊥MN ,则1|PQ |+1|MN |=( )A B .1C D .2【解题思路】由抛物线的方程可得焦点F 的坐标,应用抛物线焦点弦性质|PF |=p1―cos θ,|QF |=p1+cos θ,|MF |=p1+sin θ,|NF |=p1―sin θ,结合三角的恒等变换的化简可得1|PQ |+1|MN |=12p ,即可求解.【解答过程】由抛物线C:y 2=x 得2p =1,则p =12,F(14,0),不妨设PQ 的倾斜角为θ0<θ<则由|PF |cos θ+p =|PF |,p ―|QF |cos θ=|QF |,得|PF |=p 1―cos θ,|QF |=p1+cos θ,所以|MF |==p1+sin θ,|NF |==p1―sin θ,得|PQ |=|PF |+|QF |=p1―cos θ+p1+cos θ=2psin 2θ,|MN |==2pcos 2θ,所以1|PQ |+1|MN |=12p =1.故选:B.【变式7-3】(2024·北京西城·三模)点F 抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若FA +FB +FC =0,则|FA |+|FB |+|FC |=( )A .2B .C .3D .【解题思路】设A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),根据抛物线方程求出焦点坐标和准线方程,再由FA +FB +FC =0可得F 为△ABC 的重心,从而可求出x 1+x 2+x 3,再根据抛物线的定义可求得结果.【解答过程】设A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),由y 2=2x ,得p =1,所以F(12,0),准线方程为x =―12,因为FA +FB +FC =0,所以F 为△ABC 的重心,所以x 1+x 2+x 33=12,所以x 1+x 2+x 3=32,所以|FA |+|FB |+|FC |=x 1+12+x 2+12+x 3+12=x 1+x 2+x 3+32=32+32=3,故选:C.【题型8 抛物线的几何性质】【例8】(2024·重庆·模拟预测)A,B 是抛物线y 2=2px(p >0)上的不同两点,点F 是抛物线的焦点,且△OAB 的重心恰为F ,若|AF|=5,则p =( )A .1B .2C .3D .4【解题思路】根据重心可得x 1+x 2=3p 2y 1=―y 2,结合对称性可得x 1=3p4,再根据抛物线的定义运算求解.【解答过程】设A (x 1,y 1),B (x 2,y 2),因为△OAB 的重心恰为F=p2=0,解得x 1+x 2=3p2y 1=―y 2,由y 1=―y 2可知A,B 关于x 轴对称,即x 1=x 2,则x 1+x 2=2x 1=3p2,即x 1=3p 4,又因为|AF |=x 1+p2=5p 4=5,解得p =4.故选:D.【变式8-1】(23-24高二下·福建厦门·期末)等边三角形的一个顶点位于原点,另外两个顶点在抛物线y 2=2x 上,则这个等边三角形的边长为( )A .2B .C .4D.【解题思路】正三角形的另外两个顶点关于x 轴对称,设另外两个顶点坐标分别是A ),B―a),把顶点代入抛物线方程化简即可求解.【解答过程】设正三角形得边长为2a ,由图可知正三角形的另外两个顶点关于x 轴对称,可设另外两个顶点坐标分别是A),B―a ),把顶点代入抛物线方程得a 2=解得a =所以正三角形的边长为故选:D.【变式8-2】(23-24高三下·北京·阶段练习)设抛物线C 的焦点为F ,点E 是C 的准线与C 的对称轴的交点,点P 在C 上,若∠PEF =30°,则sin ∠PFE =( )A B C D 【解题思路】先设P(x 0,y 0),根据图形分别表示出tan ∠ P EF 和sin ∠ P FE 即可得解.【解答过程】由于抛物线的对称性,不妨设抛物线为C:y 2=2px(p >0),则其焦点为F(p2,0),点E 是C 的准线与C 的对称轴的交点,其坐标为E(―p2,0),点P 在C 上,设为P(x 0,y 0),若∠ P EF =30∘,则tan ∠ P EF =|y 0|x 0+p 2=且|PF|=x 0+p 2,则sin ∠ P FE =sin (π―∠ P FE )=|y 0||PF|=故选:B.【变式8-3】(23-24高二下·重庆·阶段练习)已知x 轴上一定点A (a,0)(a >0),和抛物线y 2=2px (p >0)上的一动点M ,若|AM |≥a 恒成立,则实数a 的取值范围为( )A .B .(0,p ]C .D .(0,2p ]【解题思路】设M (x 0,y 0) (x 0≥0),表示出|AM |,依题意可得x 20―(2a ―2p )x 0≥0恒成立,分x 0=0和x 0>0两种情况讨论,当x0>0时x0≥2a―2p恒成立,即可得到2a―2p≤0,从而求出a的取值范围.【解答过程】设M(x0,y0)(x0≥0),则y20=2px0,所以|AM|====因为|AM|≥a恒成立,所以x20―(2a―2p)x0+a2≥a2恒成立,所以x20―(2a―2p)x0≥0恒成立,当x0=0时显然恒成立,当x0>0时x0≥2a―2p恒成立,所以2a―2p≤0,则a≤p,又a>0,所以0<a≤p,即实数a的取值范围为(0,p].故选:B.【题型9 抛物线中的三角形(四边形)面积问题】【例9】(2024·江西新余·二模)已知点Q(2,―2)在抛物线C:y2=2px上,F为抛物线的焦点,则△OQF (O为坐标原点)的面积是()A.12B.1C.2D.4【解题思路】将点Q代入抛物线C的方程,即可求解p,再结合抛物线的公式,即可求解【解答过程】∵点Q(2,―2)在抛物线C:y2=2px上,F为抛物线C的焦点,∴4=4p,解得p=1,故抛物线C的方程为y2=2x,F(12,0),则△OQF的面积S△OQF=12×12×2=12.故选:A.【变式9-1】(23-24高二上·广东广州·期末)已知抛物线C:y2=2px(p>0)的焦点为F,直线l与C相交于A、B两点,与y轴相交于点E.已知|AF|=5,|BF|=3,若△AEF的面积是△BEF面积的2倍,则抛物线C的方程为()A .y 2=2xB .y 2=4xC .y 2=6xD .y 2=8x【解题思路】过A,B 分别作C 的准线的垂线交y 轴于点M,N ,根据抛物线定义可得|AM |=5―p2,|BN |=3―p 2,再由S △AEF S △BEF=|AE ||BE |=|AM ||BN |即可求参数p ,进而可得抛物线方程.【解答过程】如图,过A,B 分别作C 的准线的垂线交y 轴于点M,N ,则AM //BN ,故|AE ||BE |=|AM ||BN |,因为C 的准线为x =―p2,所以|AM |=|AF |―p2=5―p2,|BN |=|BF |―p2=3―p2,所以S △AEFS △BEF=12|EF ||AE |sin ∠AEF 12|EF ||BE |sin ∠BEF =|AE ||BE |=|AM ||BN |=5―p 23―p 2=2,解得p =2,故抛物线C 的方程为y 2=4x .故选:B.【变式9-2】(23-24高二上·广东广州·期末)设F 为抛物线y 2=4x 的焦点,A,B,C 为该抛物线上不同的三点,且FA +FB +FC =0,O 为坐标原点,若△OFA 、△OFB 、△OFC 的面积分别为S 1、S 2、S 3,则S 21+S 22+S 23=( )A .3B .4C .5D .6【解题思路】设点A,B,C 的坐标,再表示出△OFA,△OFB,△OFC 的面积,借助向量等式即可求得答案.【解答过程】设点A,B,C 的坐标分别为(x 1,y 1),(x 2,y 2),(x 3,y 3),而抛物线的焦点F(1,0),|OF|=1,FA =(x 1―1,y 1),FB =(x 2―1,y 2),FC =(x 3―1,y 3),由FA +FB +FC =0,得x 1+x 2+x 3=3,于是S 1=12|y 1|,S 2=12|y 2|,S 3=12|y 3|,所以S 21+S 22+S 23=14(y 21+y 22+y 23)=x 1+x 2+x 3=3.故选:A.【变式9-3】(23-24高二·全国·课后作业)已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2―4x+3=0作切线,切点分别为A,B,则四边形PADB的面积的最小值为()A.1B.2C D【解题思路】由题意圆的圆心与抛物线的焦点重合,可得连接PD,则S四边形PADB=2S Rt△PAD=|PA|,而|PA|=|PD|最小时,四边形PADB的面积最小,再抛物线的定义转化为点P到抛物线的准线的距离的最小值,结合抛物线的性质可求得结果【解答过程】如图,连接PD,圆D:(x―2)2+y2=1,该圆的圆心与抛物线的焦点重合,半径为1,则S四边形PADB=2S Rt△PAD=|PA|.又|PA|=PADB的面积最小时,|PD|最小.过点P向抛物线的准线x=―2作垂线,垂足为E,则|PD|=|PE|,当点P与坐标原点重合时,|PE|最小,此时|PE|=2.==故S四边形PADBmin故选:C.一、单选题1.(2024·江西·模拟预测)若抛物线x 2=8y 上一点(x 0,y 0)到焦点的距离是该点到x 轴距离的2倍.则y 0=( )A .12B .1C .32D .2【解题思路】根据抛物线的方程,结合抛物线的标准方程,得到抛物线的焦点和准线,利用抛物线的定义,得到抛物线上的点(x 0,y 0)到焦点的距离,根据题意得到关于y 0的方程,求解即可.【解答过程】已知拋物线的方程为x 2=8y ,可得p =4.所以焦点为F (0,2),准线为l :y =―2.抛物线上一点A (x 0,y 0)到焦点F 的距离等于到准线l 的距离,即|AF |=y 0+2,又∵A 到x 轴的距离为y 0,由已知得y 0+2=2y 0,解得y 0=2.故选:D .2.(2024·四川·模拟预测)已知抛物线C:x 2=8y 的焦点为F,P 是抛物线C 上的一点,O 为坐标原点,|OP |=4|PF |=( )A .4B .6C .8D .10【解题思路】求出抛物线焦点和准线方程,设P (m,n )(m ≥0),结合|OP |=n =4,由焦半径公式得到答案.【解答过程】抛物线C:x 2=8y 的焦点为F (0,2),准线方程为y =―2,设P (m,n )(m ≥0)=,解得n =4或n =―12(舍去),则|PF |=n +2=6.故选:B .3.(23-24高二下·甘肃白银·期中)若圆C 与x 轴相切且与圆x 2+y 2=4外切,则圆C 的圆心的轨迹方程为( )A .x 2=4y +4B .x 2=―4y +4C .x 2=4|y |+4D .x 2=4y ―4【解题思路】设圆心坐标为(x,y )=2+|y |,化简整理即可得解.【解答过程】设圆心坐标为(x,y)=2+|y|,化简得x2=4|y|+4,即圆C的圆心的轨迹方程为x2=4|y|+4.故选:C.4.(2024·北京海淀·三模)已知抛物线y2=4x的焦点为F、点M在抛物线上,MN垂直y轴于点N,若|MF|=6,则△MNF的面积为()A.8B.C.D.【解题思路】确定抛物线的焦点和准线,根据|MF|=6得到M.【解答过程】因为抛物线y2=4x的焦点为F(1,0),准线方程为x=―1,所以|MF|=x M+1=6,故x M=5,不妨设M在第一象限,故M×(5―0)×=所以S△MNF=12故选:C.5.(2024·西藏林芝·模拟预测)已知抛物线y2=8x上一点P到准线的距离为d1,到直线l:4x―3y+12=0的距离为d2,则d1+d2的最小值为()A.1B.2C.3D.4【解题思路】点P到直线l:4x―3y+12=0的距离为|PA|,到准线l1:x=―2的距离为|PB|,利用抛物线的定义得|PF|=|PB|,当A,P和F共线时,点P到直线l:4x―3y+12=0和准线l1:x=―2的距离之和的最小,由点到直线的距离公式求得答案.【解答过程】由抛物线y2=8x知,焦点F(2,0),准线方程为l:x=―2,根据题意作图如下;点P到直线l:4x―3y+12=0的距离为|PA|,到准线l1:x=―2的距离为|PB|,由抛物线的定义知:|PB|=|PF|,所以点P到直线l:4x―3y+12=0和准线l1:x=―2的距离之和为|PF|+|PA|,=4,且点F(2,0)到直线l:4x―3y+12=0的距离为d=|8―0+12|5所以d1+d2的最小值为4.故选:D.6.(2024·四川雅安·三模)已知过圆锥曲线的焦点且与焦点所在的对称轴垂直的弦被称为该圆锥曲线的通径,清代数学家明安图在《割圆密率捷法》中,也称圆的直径为通径.已知圆(x―2)2+(y+1)2=4的一条直径与拋物线x2=2py(p>0)的通径恰好构成一个正方形的一组邻边,则p=()B.1C.2D.4A.12【解题思路】根据圆的通径的上端点就是抛物线通径的上右端点,可得抛物线x2=2py(p>0)经过点(2,1),从而可得答案.【解答过程】因为圆(x―2)2+(y+1)2=4的一条直径与抛物线x2=2py(p>0)的通径恰好构成一个正方形的一组邻边,而抛物线x2=2py(p>0)的通径与y轴垂直,所以圆(x―2)2+(y+1)2=4的这条直径与x轴垂直,且圆的直径的上端点就是抛物线通径的右端点,因为圆(x―2)2+(y+1)2=4的圆心为(2,―1),半径为2,所以该圆与x轴垂直的直径的上端点为(2,1),即抛物线x2=2py(p>0)经过点(2,1),则4=2p,即p=2.故选:C.7.(2024·山西运城·三模)已知抛物线C:y 2=4x 的焦点为F ,动点M 在C 上,点B 与点A (1,―2)关于直线l:y =x ―1对称,则|MF ||MB |的最小值为( )AB .12CD .13【解题思路】根据对称性可得B(―1,0),即点B 为C 的准线与x 轴的交点,作MM ′垂直于C 的准线于点M ′,结合抛物线的定义可知|MF ||MB |=|MM ′||MB |= cos θ(∠MBF =θ),结合图象可得当直线MB 与C 相切时,cos θ最小,求出切线的斜率即可得答案.【解答过程】依题意,F(1,0),A(1,―2),设B(m,n)=―1m+12―1,解得m =―1n =0,即B(―1,0),点B 为C 的准线与x 轴的交点,由抛物线的对称性,不妨设点M 位于第一象限,作MM ′垂直于C 的准线于点M ′,设∠MBF =θ,θ∈ (0,π2),由抛物线的定义得|MM ′|=|MF |,于是|MF ||MB |=|MM ′||MB |= cos θ,当直线MB 与C 相切时,θ最大,cos θ最小,|MF||MB|取得最小值,此时直线BM 的斜率为正,设切线MB 的方程为x =my ―1(m >0),由x =my ―1y 2=4x消去x 得y 2―4my +4=0,则Δ=16m 2―16=0,得m =1,直线MB 的斜率为1,倾斜角为π4,于是θmax =π4,(cos θ)min =,所以|MF||MB|的最小值为故选:A.8.(2024·江西九江·二模)已知抛物线C:y 2=2px 过点A (1,2),F 为C 的焦点,点P 为C 上一点,O 为坐标原点,则( )A .C 的准线方程为x =―2B .△AFO 的面积为1C .不存在点P ,使得点P 到C 的焦点的距离为2D .存在点P ,使得△POF 为等边三角形【解题思路】求解抛物线方程,得到准线方程,判断A ;求解三角形的面积判断B ;利用|PF|=2.判断C ;判断P 的位置,推出三角形的形状,判断D .【解答过程】由题意抛物线C:y 2=2px 过点A(1,2),可得p =2,所以抛物线方程为C:y 2=4x ,所以准线方程为x =―1,A 错误;可以计算S △AFO =12×1×2=1,B 正确;当P(1,2)时,点P 到C 的焦点的距离为2,C 错误;△POF 为等边三角形,可知P 的横坐标为:12,当x =12时,纵坐标为:则12×=≠则△POF 为等腰三角形,不是等边三角形,故等边三角形的点P 不存在,所以D 错误.故选:B .二、多选题9.(2024·湖南长沙·二模)已知抛物线C 与抛物线y 2=4x 关于y 轴对称,则下列说法正确的是( )A .抛物线C 的焦点坐标是(―1,0)B .抛物线C 关于y 轴对称C .抛物线C 的准线方程为x =1D .抛物线C 的焦点到准线的距离为4【解题思路】依题意可得抛物线C 的方程为y 2=―4x ,即可得到其焦点坐标与准线方程,再根据抛物线的性。
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.抛物线的焦点为,点在抛物线上,且,弦中点在其准线上的射影为,则的最大值为()A.B.C.D.【答案】A【解析】设,由抛物线定义,.而余弦定理,,再由,得到,所以的最大值为,故选:A.【考点】双曲线的简单性质.2.已知点A(-1,0),B(1,-1)和抛物线.,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.(1)证明: 为定值;(2)若△POM的面积为,求向量与的夹角;(3)证明直线PQ恒过一个定点.【答案】(1)见解析; (2) ;(3)直线PQ过定点E(1,-4).【解析】(1)设点根据、M、A三点共线,得计算得到=5;(2)设∠POM=α,可得结合三角形面积公式可得tanα="1."根据角的范围,即得所求.(3)设点、B、Q三点共线,据此确定进一步确定的方程,化简为得出结论.试题解析:(1)设点、M、A三点共线,2分5分(2)设∠POM=α,则由此可得tanα=1. 8分又 10分(3)设点、B、Q三点共线,即 12分即 13分由(*)式,代入上式,得由此可知直线PQ过定点E(1,-4). 14分【考点】抛物线及其几何性质,直线方程,直线与抛物线的位置关系,转化与化归思想.3.以抛物线y2=8x上的任意一点为圆心作圆与直线x+2=0相切,这些圆必过一定点,则这一定点的坐标是()A.(0,2)B.(2,0)C.(4,0)D.(0,4)【答案】B【解析】x+2=0为抛物线的准线,根据抛物线的定义,圆心到准线的距离等于圆心到焦点的距离,故这些圆恒过定点(2,0).4.(5分)(2011•湖北)将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则()A.n=0B.n=1C.n=2D.n≥3【答案】C【解析】根据题意和抛物线以及正三角形的对称性,可推断出两个边的斜率,进而表示出这两条直线,每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形.进而可知这样的三角形有2个.解:y2=2px(P>0)的焦点F(,0)等边三角形的一个顶点位于抛物线y2=2px(P>0)的焦点,另外两个顶点在抛物线上,则等边三角形关于x轴轴对称两个边的斜率k=±tan30°=±,其方程为:y=±(x﹣),每条直线与抛物线均有两个交点,焦点两侧的两交点连接,分别构成一个等边三角形.故n=2,故选C点评:本题主要考查了抛物线的简单性质.主要是利用抛物线和正三角形的对称性.5.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线l,此直线与上述两曲线的四个交点,自左向右顺次记为A,B,C,D,如果线段AB,BC,CD的长按此顺序构成一个等差数列,则直线l的斜率为( )A.B.C.D.【答案】A【解析】圆的方程为,则其直径长圆心为,设的方程为,代入抛物线方程得:设,有∴线段的长按此顺序构成一个等差数列,,即,解得,故选A.【考点】1.抛物线的几何性质;2.直线与抛物线相交问题.6.抛物线上一点到直线的距离与到点的距离之差的最大值为()A.B.C.D.【答案】D【解析】作出抛物线的图象如下图所示,则点为抛物线的焦点,直线为抛物线的准线,过点作垂直于直线,垂足为点,由抛物线的定义的可知,则点到直线的距离与到点的距离之差等于,当、、三点不共线时,由三角形三边之间的关系可知,,当点为射线与抛物线的交点时,,此时点到直线的距离与到点的距离取到最大值,故选D.【考点】1.抛物线的定义;2.数形结合7.(2011•浙江)已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M(1)求点M到抛物线C1的准线的距离;(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.【答案】(1)(2)【解析】(1)由题意画出简图为:由于抛物线C1:x2=y准线方程为:y=﹣,圆C2:x2+(y﹣4)2=1的圆心M(0,4),利用点到直线的距离公式可以得到距离d==.(2)设点P(x0,x2),A(x1,x12),B(x2,x22);由题意得:x0≠0,x2≠±1,x1≠x2,设过点P的圆c2的切线方程为:y﹣x2=k(x﹣x)即y=kx﹣kx+x2①则,即(x02﹣1)k2+2x(4﹣x2)k+(x2﹣4)2﹣1=0设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,∴,;代入①得:x2﹣kx+kx0﹣x2="0" 则x1,x2应为此方程的两个根,故x1=k1﹣x,x2=k2﹣x∴kAB =x1+x2=k1+k2﹣2x=由于MP⊥AB,∴kAB •KMP=﹣1⇒故P∴.8.过抛物线焦点F的直线交抛物线于A、B两点,若A、B在抛物线准线上的射影分别为,则()A.B.C.D.【答案】D【解析】由抛物线的定义得,,,故,,故,,又,故,从而.【考点】抛物线定义.9.抛物线的焦点坐标为.【答案】【解析】由于,焦点在轴的正半轴,所以,抛物线的焦点坐标为.【考点】抛物线的几何性质.10.已知抛物线:和:的焦点分别为,交于两点(为坐标原点),且.(1)求抛物线的方程;(2)过点的直线交的下半部分于点,交的左半部分于点,点坐标为,求△面积的最小值.【答案】(1);(2)8.【解析】本题主要考查抛物线的标准方程及其几何性质、向量垂直的充要条件、两点间距离公式、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用抛物线的标准方程得到焦点的坐标,从而得到向量坐标,联立2个抛物线方程,解方程组,可求出A点坐标,从而得到向量的坐标,由于,所以,利用这个方程解出P的值,从而得到抛物线的方程;第二问,先设出过点O的直线方程,直线和抛物线联立,得到M点坐标,直线和抛物线联立得到N点坐标,由于,利用两点间距离公式得到3个边长,再利用基本不等式求面积的最小值.试题解析:(1)由已知得:,,∴ 1分联立解得或,即,,∴ 3分∵,∴,即,解得,∴的方程为. 5分『法二』设,有①,由题意知,,,∴1分∵,∴,有,解得, 3分将其代入①式解得,从而求得,所以的方程为. 5分(2)设过的直线方程为联立得,联立得 7分在直线上,设点到直线的距离为,点到直线的距离为则 8分10分当且仅当时,“”成立,即当过原点直线为时,11分△面积取得最小值. 12分『法二』联立得,联立得, 7分从而,点到直线的距离,进而9分令,有, 11分当,即时,即当过原点直线为时,△面积取得最小值. 12分【考点】抛物线的标准方程及其几何性质、向量垂直的充要条件、两点间距离公式、三角形面积公式.11.抛物线的焦点为,点在抛物线上,且,弦中点在准线上的射影为的最大值为( )A.B.C.D.【答案】B【解析】如图,设,,由抛物线定义,得.在中,由余弦定理,得,,,,故选B.【考点】1.抛物线的定义;2.基本不等式.12.已知抛物线的焦点为,点为抛物线上的一点,其纵坐标为,.(1)求抛物线的方程;(2)设为抛物线上不同于的两点,且,过两点分别作抛物线的切线,记两切线的交点为,求的最小值.【答案】(1);(2).【解析】(1)对于开口向上的抛物线来说,,代入坐标,解出;(2)设,利用导数的几何意义,利用点斜式方程,分别设出过两点的切线方程,然后求出交点的坐标,结合,所得到的关系式,设,以及的坐标,将点的坐标转化为一个未知量表示的函数,,用未知量表示,转化为函数的最值问题,利用二次函数求最值的方法求出.中档偏难题型. 试题解析:(1)由抛物线定义得: 2分抛物线方程为 4分(2)设且即 6分 又处的切线的斜率为 处的切线方程为和由得8分设,由得10分 当时,12分【考点】1.抛物线的定义;2.导数的几何意义;3.函数的最值.13. 已知抛物线x 2=4y 的焦点为F ,过焦点F 且不平行于x 轴的动直线交抛物线于A 、B 两点,抛物线在A 、B 两点处的切线交于点M.(1)求证:A 、M 、B 三点的横坐标成等差数列;(2)设直线MF 交该抛物线于C 、D 两点,求四边形ACBD 面积的最小值. 【答案】(1)见解析(2)32【解析】(1)证明:由已知,得F(0,1),显然直线AB 的斜率存在且不为0, 则可设直线AB 的方程为y =kx +1(k≠0),A(x 1,y 1),B(x 2,y 2), 由消去y ,得x 2-4kx -4=0,显然Δ=16k 2+16>0.所以x 1+x 2=4k ,x 1x 2=-4,由x 2=4y ,得y =x 2,所以y′=x,所以,直线AM 的斜率为k AM =x 1, 所以,直线AM 的方程为y -y 1=x 1(x -x 1),又=4y 1,所以,直线AM 的方程为x 1x =2(y +y 1)①,同理,直线BM 的方程为x 2x =2(y +y 2)②,②-①并据x 1≠x 2得点M 的横坐标x =,即A 、M 、B 三点的横坐标成等差数列.(2)解:由①②易得y =-1,所以点M 的坐标为(2k ,-1)(k≠0).所以k MF ==-,则直线MF 的方程为y =-x +1,设C(x 3,y 3),D(x 4,y 4)由消去y ,得x 2+x -4=0,显然Δ=+16>0,所以x 3+x 4=-,x 3x 4=-4,又|AB|===4(k 2+1),|CD|==,因为k MF ·k AB =-1,所以AB ⊥CD , 所以S ACBD =|AB|·|CD|=8≥32,当且仅当k =±1时,四边形ACBD 面积取到最小值32.14. 如图,过抛物线y 2=2px(p>0)的焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C.若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为________.【答案】y 2=3x【解析】由抛物线定义,|BF|等于B 到准线的距离. 由|BC|=2|BF|,得∠BCM =30°. 又|AF|=3,从而A.由A 在抛物线上,代入抛物线方程y 2=2px ,解得p =.15. 过抛物线y 2=4x 的焦点F 的直线交该抛物线于A,B 两点.若|AF|=3,则|BF|= . 【答案】【解析】由题意知,抛物线的焦点F 的坐标为(1,0),又|AF|=3,由抛物线定义知,点A 到准线x=-1的距离为3∴点A 的横坐标为2.将x=2代入y 2=4x 得y 2=8, 由图知点A 的纵坐标y=2, ∴A(2,2),∴直线AF 的方程为y=2(x-1). 由解得或由图知,点B 的坐标为,∴|BF|=-(-1)=.16. 若已知点Q(4,0)和抛物线y=x 2+2上一动点P(x,y),则y+|PQ|最小值为( ) A .2+2 B .11 C .1+2 D .6【答案】D【解析】抛物线y=+2的准线是y=1,焦点F(0,3).用抛物线的定义:设P 到准线的距离为d, 则y+|PQ|=d+1+|PQ|=|PF|+|PQ|+1≥|FQ|+1=5+1=6(当且仅当F,Q,P 共线时取等号), 故y+|PQ|的最小值是6.17. 设x 1,x 2∈R,常数a>0,定义运算“*”:x 1*x 2=(x 1+x 2)2-(x 1-x 2)2,若x≥0,则动点P(x,)的轨迹是( ) A .圆 B .椭圆的一部分C.双曲线的一部分D.抛物线的一部分【答案】D【解析】∵x1*x2=(x1+x2)2-(x1-x2)2,∴==2. 则P(x,2).设P(x1,y1),即消去x得=4ax1(x1≥0,y1≥0),故点P的轨迹为抛物线的一部分.18.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线共有()A.1条B.2条C.3条D.4条【答案】C【解析】作出图形,可知点(0,1)在抛物线y2=4x外.因此,过该点可作抛物线y2=4x的切线有两条,还能作一条与抛物线y2=4x的对称轴平行的直线,因此共有三条直线与抛物线只有一个交点.19.已知M是y=x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为()A.2B.4C.8D.10【答案】B【解析】【思路点拨】利用抛物线的定义,数形结合求解.由题意可知,焦点坐标为F(0,1),准线方程为l:y=-1.过点M作MH⊥l于点H,由抛物线的定义,得|MF|=|MH|.∴|MA|+|MF|=|MH|+|MA|,当C,M,H,A四点共线时,|MA|=|MC|-1,|MH|+|MC|有最小值, 于是,|MA|+|MF|的最小值为4-(-1) -1=4.20.过抛物线焦点的直线交其于,两点,为坐标原点.若,则的面积为()A.B.C.D.2【答案】C【解析】设直线的倾斜角为及,∵,∴点到准线的距离为,∴,则.∴的面积为.故选C.【考点】抛物线的几何性质,直线与抛物线的位置关系.21.已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.(1)求抛物线C的方程;(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.【答案】(1)y 2=8x .(2)24【解析】(1)易知直线与抛物线的交点坐标为(8,-8),∴82=2p ×8,∴2p =8,∴抛物线方程为y 2=8x .(2)直线l 2与l 1垂直,故可设l 2:x =y +m ,A (x 1,y 1),B (x 2,y 2),且直线l 2与x 轴的交点为M . 由得y 2-8y -8m =0,Δ=64+32m >0,∴m >-2.y 1+y 2=8,y 1y 2=-8m ,∴x 1x 2==m 2.由题意可知OA ⊥OB ,即x 1x 2+y 1y 2=m 2-8m =0,∴m =8或m =0(舍), ∴l 2:x =y +8,M (8,0),故S △FAB =S △FMB +S △FMA =|FM |·|y 1-y 2|=3=24.22. 抛物线y =x 2上的点到直线x +y +1=0的最短距离为________. 【答案】【解析】由于f ′(x )=2x ,设与直线x +y +1=0平行且与抛物线相切的直线与抛物线切于点A (x 0,y 0),由导数几何意义可知2x 0=-1,求得切点为.切点A到直线x +y +1=0的距离最小,由点到直线距离公式易得最小值为23. O 为坐标原点,F 为抛物线C :y 2=4x 的焦点,P 为C 上一点,若|PF|=4,则△POF的面积为( )A .2B .2C .2D .4【答案】C【解析】由题意知抛物线的焦点F(,0),如图,由抛物线定义知|PF|=|PM|,又|PF|=4,所以x P =3,代入抛物线方程求得y P =2,所以S △POF =·|OF|·y P =2.24. 抛物线y 2=4x 的焦点为F ,点P(x ,y)为该抛物线上的动点,又点A(-1,0),则的最小值是( ) A . B .C .D .【答案】B【解析】依题意知x≥0,焦点F(1,0),则|PF|=x +1,|PA|==.当x =0时,=1;当x>0时,1<=≤=(当且仅当x =1时取等号).因此当x≥0时,1≤≤,≤≤1,的最小值是.25.设为抛物线的焦点,为抛物线上三点,若为的重心,则的值为( )A.1B.2C.3D.4【答案】C【解析】由条件,∵是的重心,则有,即,而.【考点】1.重心公式;2.焦半径公式.26.已知点F为抛物线的焦点,O为原点,点P是抛物线准线上一动点,A在抛物线上,且=4,则+的最小值是【答案】【解析】∵|AF|=4,由抛物线的定义得,∴A到准线的距离为4,即A点的横坐标为-2,又点A在抛物线上,∴从而点A的坐标A(-2,4);坐标原点关于准线的对称点的坐标为B(4,0),则|PA|+|PO|的最小值为:|AB|=,故答案.【考点】抛物线的简单性质.27.已知抛物线,过其焦点且斜率为-1的直线交抛物线于两点,若线段的中点的纵坐标为-2,则该抛物线的准线方程为()A.B.C.D.【答案】C【解析】∵焦点为,∴设直线为,∵直线交抛物线于两点,∴∴消参得,设,∴,∵线段的中点的纵坐标为-2,∴,∴,∴抛物线的准线方程为.【考点】1.直线的方程;2.韦达定理;3.抛物线的焦点、准线;4.中点坐标公式.28.已知抛物线的焦点与双曲线的一个焦点重合,它们在第一象限内的交点为,且与轴垂直,则此双曲线的离心率为()A.B.2C.D.【答案】C.【解析】因为抛物线的焦点的坐标为又抛物线的焦点与双曲线的一个焦点重合,.由已知抛物线与双曲线在第一象限内的交点为,且与轴垂直,则点的横坐标为1,代入得再把代入,与联立得方程组消去得,解这个关于的双二次方程,得.【考点】抛物线与双曲线简单的几何性质(焦点、离心率).29.某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板长为2m,跳水板距水面的高为3m,=5m,=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点m()时达到距水面最大高度4m,规定:以为横轴,为纵轴建立直角坐标系.(1)当=1时,求跳水曲线所在的抛物线方程;(2)若跳水运动员在区域内入水时才能达到压水花的训练要求,求达到压水花的训练要求时的取值范围.【答案】(1);(2).【解析】(1)由题意可以将抛物线的方程设为顶点式.由顶点(3,4),然后代入点可将抛物线方程求出;(2)将抛物线的方程设为顶点式,由点得.将用表示.跳水运动员在区域内入水时才能达到压水花的训练要求,所以方程在区间[5,6]内有一解,根据抛物线开口向下,由函数的零点与方程的根的关系,令,由,且可得的取值范围.试题解析:(1)由题意知最高点为,,设抛物线方程为, 4分当时,最高点为(3,4),方程为,将代入,得,解得.当时,跳水曲线所在的抛物线方程. 8分(2)将点代入得,所以.由题意,方程在区间[5,6]内有一解. 10分令,则,且.解得. 14分达到压水花的训练要求时的取值范围. 16分【考点】1.抛物线的顶点式方程;2.函数的零点与方程的根.30.如图,已知抛物线焦点为,直线经过点且与抛物线相交于,两点(Ⅰ)若线段的中点在直线上,求直线的方程;(Ⅱ)若线段,求直线的方程【答案】(Ⅰ);(Ⅱ)【解析】(Ⅰ)根据已知条件设出未知的点的坐标和斜率,根据两点间的斜率公式和中点坐标公式找等价关系,求出直线的斜率,由已知得的根据斜截式求出直线方程; (Ⅱ)设出直线的方程为,这样避免讨论斜率的存在问题,与抛物线的方程联立方程组,得到根与系数的关系,根据直线与抛物线相交的交点弦的长来求参数的值试题解析:解:(Ⅰ)由已知得交点坐标为, 2分设直线的斜率为,,,中点则,,所以,又,所以4分故直线的方程是:6分(Ⅱ)设直线的方程为,7分与抛物线方程联立得,消元得,9分所以有,,11分所以有,解得,13分所以直线的方程是:,即15分【考点】1、直线的方程;2、直线与圆锥曲线的关系31.抛物线的准线截圆所得弦长为2,则= .【答案】2【解析】抛物线的准线为,而圆化成标准方程为,圆心,,圆心到准线的距离为,所以,即.【考点】1.抛物线的准线方程;2.勾股定理.32.在平面直角坐标系中,已知曲线上任意一点到点的距离与到直线的距离相等.(Ⅰ)求曲线的方程;(Ⅱ)设,是轴上的两点,过点分别作轴的垂线,与曲线分别交于点,直线与x轴交于点,这样就称确定了.同样,可由确定了.现已知,求的值.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)根据抛物线的定义及标准方程求解;(Ⅱ)先由求,再由求.试题解析:(Ⅰ)因为曲线上任意一点到点的距离与到直线的距离相等,根据抛物线定义知,曲线是以点为焦点,直线为准线的抛物线,故其方程为. 4分(Ⅱ)由题意知,,,则,故. 6分令,得,即. 8分同理,, 9分于是. 10分【考点】抛物线的概念、曲线的交点.33.已知抛物线的方程为,过点和点的直线与抛物线没有公共点,则实数的取值范围是()A.B.C.D.【答案】D【解析】据已知可得直线的方程为,联立直线与抛物线方程,得,消元整理,得,由于直线与抛物线无公共点,即方程无解,故有,解得或.【考点】1.直线与抛物线的位置关系;2.方程组的解法.34.如图所示,设抛物线的焦点为,且其准线与轴交于,以,为焦点,离心率的椭圆与抛物线在轴上方的一个交点为P.(1)当时,求椭圆的方程;(2)是否存在实数,使得的三条边的边长是连续的自然数?若存在,求出这样的实数;若不存在,请说明理由.【答案】(1);(2).【解析】(1)依题意由抛物线方程容易得椭圆的方程,代入既得椭圆方程;(2)假设存在满足条件的实数,由抛物线和椭圆方程求交点P,使得,求得.试题解析:(1)抛物线的焦点为, 1分椭圆的半焦距,离心率,所以椭圆的长半轴长,短半轴长,3分所以椭圆的方程为, 4分当时,椭圆的方程. 6分(2)假设存在满足条件的实数由,解得, 8分,,, 11分所以的三条边的边长分别是,,所以当时使得的三条边的边长是连续的自然数. 13分【考点】1、抛物线和椭圆的方程及性质;2.存在性问题.35.(5分)抛物线y2=8x的焦点到直线的距离是()A.B.2C.D.1【答案】D【解析】由抛物线y2=8x得焦点F(2,0),∴点F(2,0)到直线的距离d==1.故选D.36.过抛物线的焦点F作斜率分别为的两条不同的直线,且,相交于点A,B,相交于点C,D。
100高中数学高考总复习抛物线习题及详解100

高中数学高考总复习抛物线习题(附参考答案)一、选择题1.(2010·湖北黄冈)若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .4[答案] D[解析] 椭圆中,a 2=6,b 2=2,∴c =a 2-b 2=2, ∴右焦点(2,0),由题意知p2=2,∴p =4.2.已知点M 是抛物线y 2=2px (p >0)上的一点,F 为抛物线的焦点,若以|MF |为直径作圆,则这个圆与y 轴的关系是( )A .相交B .相切C .相离D .以上三种情形都有可能[答案] B[解析] 如图,由MF 的中点A 作准线l 的垂线AE ,交直线l 于点E ,交y 轴于点B ;由点M 作准线l 的垂线MD ,垂足为D ,交y 轴于点C ,则MD =MF ,ON =OF , ∴AB =OF +CM 2=ON +CM2=DM 2=MF 2, ∴这个圆与y 轴相切.3.(2010·山东文)已知抛物线y 2=2px (p >0),过焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2[答案] B[解析] 设A (x 1,y 1),B (x 2,y 2),则线段AB 的中点(x 1+x 22,y 1+y 22),∴y 1+y 22=2,∵A 、B 在抛物线y 2=2px 上,∴⎩⎪⎨⎪⎧y 12=2px 1 ①y 22=2px 2② ①-②得y 12-y 22=2p (x 1-x 2),∴k AB =y 1-y 2x 1-x 2=2p y 1+y 2=p 2,∵k AB =1,∴,p =2∴抛物线方程为y 2=4x ,∴准线方程为:x =-1,故选B.4.双曲线x 29-y 24=1的渐近线上一点A 到双曲线的右焦点F 的距离等于2,抛物线y 2=2px (p >0)过点A ,则该抛物线的方程为( )A .y 2=9xB .y 2=4xC .y 2=41313xD .y 2=21313x[答案] C[解析] ∵双曲线x 29-y 24=1的渐近线方程为y =±23x ,F 点坐标为(13,0),设A 点坐标为(x ,y ),则y =±23x ,由|AF |=2⇒(x -13)2+⎝⎛⎭⎫23x 2=2⇒x =913,y =±613,代入y 2=2px 得p =21313,所以抛物线方程为y 2=41313x ,所以选C.5.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172B .3 C. 5D.92[答案] A[解析] 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 与点(0,2)的距离,因此所求的最小值等于⎝⎛⎭⎫122+22=172,选A. 6.已知抛物线C :y 2=4x 的焦点为F ,准线为l ,过抛物线C 上的点A 作准线l 的垂线,垂足为M ,若△AMF 与△AOF (其中O 为坐标原点)的面积之比为3 1,则点A 的坐标为( )A .(2,22)B .(2,-22)C .(2,±2)D .(2,±22)[答案] D[解析] 如图,由题意可得,|OF |=1,由抛物线定义得,|AF |=|AM |,∵△AMF 与△AOF (其中O 为坐标原点)的面积之比为3∶1,∴S △AMFS △AOF =12×|AF |×|AM |×sin ∠MAF 12×|OF |×|AF |×sin (π-∠MAF )=3, ∴|AM |=3,设A ⎝⎛⎭⎫y 024,y 0,∴y 024+1=3,解得y 0=±22,∴y 024=2,∴点A 的坐标是(2,±22),故选D.7.(2010·河北许昌调研)过点P (-3,1)且方向向量为a =(2,-5)的光线经直线y =-2反射后通过抛物线y 2=mx ,(m ≠0)的焦点,则抛物线的方程为( )A .y 2=-2xB .y 2=-32xC .y 2=4xD .y 2=-4x[答案] D[解析] 设过P (-3,1),方向向量为a =(2,-5)的直线上任一点Q (x ,y ),则PQ →∥a ,∴x +32=y -1-5,∴5x +2y +13=0,此直线关于直线y =-2对称的直线方程为5x +2(-4-y )+13=0,即5x -2y +5=0,此直线过抛物线y 2=mx 的焦点F ⎝⎛⎭⎫m 4,0,∴m =-4,故选D.8.已知mn ≠0,则方程是mx 2+ny 2=1与mx +ny 2=0在同一坐标系内的图形可能是( )[答案] A[解析] 若mn >0,则mx 2+ny 2=1应为椭圆,y 2=-mnx 应开口向左,故排除C 、D ;∴mn <0,此时抛物线y 2=-mnx 应开口向右,排除B ,选A.9.(2010·山东聊城模考)已知A 、B 为抛物线C :y 2=4x 上的不同两点,F 为抛物线C 的焦点,若F A →=-4FB →,则直线AB 的斜率为( )A .±23B .±32C .±34D .±43[答案] D[解析] ∵F A →=-4FB →,∴|F A →|=4|FB →|,设|BF |=t ,则|AF |=4t ,∴|BM |=|AA 1|-|BB 1|=|AF |-|BF |=3t ,又|AB |=|AF |+|BF |=5t ,∴|AM |=4t ,∴tan ∠ABM =43,由对称性可知,这样的直线AB 有两条,其斜率为±43.10.已知抛物线C 的方程为x 2=12y ,过点A (0,-4)和点B (t,0)的直线与抛物线C 没有公共点,则实数t 的取值范围是( )A .(-∞,-1)∪(1,+∞) B.⎝⎛⎭⎫-∞,-22∪⎝⎛⎭⎫22,+∞ C .(-∞,-22)∪(22,+∞) D .(-∞,-22)∪(2,+∞) [答案] B[解析] 由题意知方程组⎩⎨⎧x 2=12y ①x t +y-4=1 ②无实数解由②得y =4xt -4,代入①整理得,2x 2-4x t +4=0,∴Δ=16t2-32<0,∴t >22或t <-22,故选B. [点评] 可用数形结合法求解,设过点A (0,-4)与抛物线x 2=12y 相切的直线与抛物线切点为M (x 0,y 0),则切线方程为y -y 0=4x 0(x -x 0), ∵过A 点,∴-4-2x 02=4x 0(0-x 0), ∴x 0=±2,∴y 0=4,∴切线方程为y -4=±42x -8, 令y =0得x =±22,即t =±22,由图形易知直线与抛物线无公共点时,t <-22或t >22. 二、填空题11.已知点A (2,0)、B (4,0),动点P 在抛物线y 2=-4x 上运动,则AP →·BP →取得最小值时的点P 的坐标是______.[答案] (0,0)[解析] 设P ⎝⎛⎭⎫-y 24,y ,则AP →=⎝⎛⎭⎫-y 24-2,y ,BP →=⎝⎛⎭⎫-y 24-4,y ,AP →·BP →=⎝⎛⎭⎫-y24-2⎝⎛⎭⎫-y 24-4+y 2=y 416+52y 2+8≥8,当且仅当y =0时取等号,此时点P 的坐标为(0,0).12.(文)(2010·泰安市模拟)如图,过抛物线y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,交抛物线于A 、B 两点,且|F A |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 设抛物线准线为l ,作AA 1⊥l ,BB 1⊥l ,FQ ⊥l ,垂足分别为A 1、B 1、Q ,作BM ⊥AA 1垂足为M ,BM 交FQ 于N ,则由条件易知∠ABM =30°,设|BF |=t ,则|NF |=t 2,|MA |=t +32,∵|AM |=|QN |,∴3-t +32=p -t 2,∴p =32,∴抛物线方程为y 2=3x .(理)(2010·泰安质检)如图,过抛物线y 2=2px (p >0)的焦点的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 解法1:过A 、B 作准线垂线,垂足分别为A 1,B 1,则|AA 1|=3,|BB 1|=|BF |,∵|BC |=2|BF |,∴|BC |=2|BB 1|,∴|AC |=2|AA 1|=2|AF |=6,∴|CF |=3,∴p =12|CF |=32,∴抛物线方程为y 2=3x .解法2:由抛物线定义,|BF |等于B 到准线的距离,由|BC |=2|BF |得∠BCB 1=30°,又|AF |=3,从而A ⎝⎛⎭⎫p 2+32,332在抛物线上,代入抛物线方程y 2=2px ,解得p =32.点评:还可以由|BC |=2|BF |得出∠BCB 1=30°,从而求得A 点的横坐标为|OF |+12|AF |=p2+32或3-p 2,∴p 2+32=3-p 2,∴p =32. 13.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.[答案] 3+2 2[解析] 分别由A 和B 向准线作垂线,垂足分别为A 1,B 1,则由条件知, ⎩⎪⎨⎪⎧|AA 1|+|BB 1|=|AB |,|AA 1|-|BB 1|=22|AB |,解得⎩⎪⎨⎪⎧|AA 1|=2+24|AB ||BB 1|=2-24|AB |,∴|AA 1||BB 1|=3+22,即|F A ||FB |=3+2 2. 14.(文)若点(3,1)是抛物线y 2=2px 的一条弦的中点,且这条弦所在直线的斜率为2,则p =________.[答案] 2[解析] 设弦两端点P 1(x 1,y 1),P 2(x 2,y 2),则⎩⎪⎨⎪⎧y 12=2px 1y 22=2px 2,两式相减得,y 1-y 2x 1-x 2=2p y 1+y 2=2,∵y 1+y 2=2,∴p =2.(理)(2010·衡水市模考)设抛物线x 2=12y 的焦点为F ,经过点P (2,1)的直线l 与抛物线相交于A 、B 两点,又知点P 恰为AB 的中点,则|AF |+|BF |=________.[答案] 8[解析] 过A 、B 、P 作准线的垂线AA 1、BB 1与PP 1,垂足A 1、B 1、P 1,则|AF |+|BF |=|AA 1|+|BB 1|=2|PP 1|=2[1-(-3)]=8.三、解答题15.(文)若椭圆C 1:x 24+y 2b 2=1(0<b <2)的离心率等于32,抛物线C 2:x 2=2py (p >0)的焦点在椭圆C 1的顶点上.(1)求抛物线C 2的方程;(2)若过M (-1,0)的直线l 与抛物线C 2交于E 、F 两点,又过E 、F 作抛物线C 2的切线l 1、l 2,当l 1⊥l 2时,求直线l 的方程.[解析] (1)已知椭圆的长半轴长为a =2,半焦距c =4-b 2, 由离心率e =c a =4-b 22=32得,b 2=1.∴椭圆的上顶点为(0,1),即抛物线的焦点为(0,1), ∴p =2,抛物线的方程为x 2=4y .(2)由题知直线l 的斜率存在且不为零,则可设直线l 的方程为y =k (x +1),E (x 1,y 1),F (x 2,y 2),∵y =14x 2,∴y ′=12x ,∴切线l 1,l 2的斜率分别为12x 1,12x 2,当l 1⊥l 2时,12x 1·12x 2=-1,即x 1·x 2=-4,由⎩⎪⎨⎪⎧y =k (x +1)x 2=4y得:x 2-4kx -4k =0, 由Δ=(-4k )2-4×(-4k )>0,解得k <-1或k >0. 又x 1·x 2=-4k =-4,得k =1. ∴直线l 的方程为x -y +1=0.(理)在△ABC 中,CA →⊥CB →,OA →=(0,-2),点M 在y 轴上且AM →=12(AB →+CD →),点C在x 轴上移动.(1)求B 点的轨迹E 的方程;(2)过点F ⎝⎛⎭⎫0,-14的直线l 交轨迹E 于H 、E 两点,(H 在F 、G 之间),若FH →=12HG →,求直线l 的方程.[解析] (1)设B (x ,y ),C (x 0,0),M (0,y 0),x 0≠0, ∵CA →⊥CB →,∴∠ACB =π2,∴2x 0·y 0-x 0=-1,于是x 02=2y 0① M 在y 轴上且AM →=12(AB →+AC →),所以M 是BC 的中点,可得 ⎩⎨⎧x 0+x 2=0y +02=y,∴⎩⎪⎨⎪⎧x 0=-x ②y 0=y2③ 把②③代入①,得y =x 2(x ≠0),所以,点B 的轨迹E 的方程为y =x 2(x ≠0). (2)点F ⎝⎛⎭⎫0,-14,设满足条件的直线l 方程为: y =kx -14,H (x 1,y 1),G (x 2,y 2),由⎩⎪⎨⎪⎧y =kx -14y =x 2消去y 得,x 2-kx +14=0.Δ=k 2-1>0⇒k 2>1,∵FH →=12HG →,即⎝⎛⎭⎫x 1,y 1+14=12(x 2-x 1,y 2-y 1), ∴x 1=12x 2-12x 1⇒3x 1=x 2.∵x 1+x 2=k ,x 1x 2=14,∴k =±233,故满足条件的直线有两条,方程为:8x +43y +3=0和8x -43y -3=0. 16.(文)已知P (x ,y )为平面上的动点且x ≥0,若P 到y 轴的距离比到点(1,0)的距离小1.(1)求点P 的轨迹C 的方程;(2)设过点M (m,0)的直线交曲线C 于A 、B 两点,问是否存在这样的实数m ,使得以线段AB 为直径的圆恒过原点.[解析] (1)由题意得:(x -1)2+y 2-x =1,化简得:y 2=4x (x ≥0). ∴点P 的轨迹方程为y 2=4x (x ≥0).(2)设直线AB 为y =k (x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -m )y 2=4x ,得ky 2-4y -4km =0, ∴y 1+y 2=4k ,y 1·y 2=-4m .∴x 1·x 2=m 2,∵以线段AB 为直径的圆恒过原点, ∴OA ⊥OB ,∴x 1·x 2+y 1·y 2=0.即m 2-4m =0⇒m =0或4.当k 不存在时,m =0或4. ∴存在m =0或4,使得以线段AB 为直径的圆恒过原点.[点评] (1)点P 到定点F (1,0)的距离比到y 轴的距离大1,即点P 到定点F (1,0)的距离与到定直线l :x =-1的距离相等.∴P 点轨迹是以F 为焦点,l 为准线的抛物线,∴p =2,∴方程为y 2=4x .(理)已知抛物线y 2=4x ,过点(0,-2)的直线交抛物线于A 、B 两点,O 为坐标原点. (1)若OA →·OB →=4,求直线AB 的方程.(2)若线段AB 的垂直平分线交x 轴于点(n,0),求n 的取值范围.[解析] (1)设直线AB 的方程为y =kx -2 (k ≠0),代入y 2=4x 中得,k 2x 2-(4k +4)x +4=0①设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k +4k 2,x 1x 2=4k 2.y 1y 2=(kx 1-2)·(kx 2-2)=k 2x 1x 2-2k (x 1+x 2)+4=-8k.∵OA →·OB →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=4k 2-8k =4,∴k 2+2k -1=0,解得k =-1±2.又由方程①的判别式Δ=(4k +4)2-16k 2=32k +16>0得k >-12,∴k =-1+2,∴直线AB 的方程为(2-1)x -y -2=0.(2)设线段AB 的中点的坐标为(x 0,y 0),则由(1)知x 0=x 1+x 22=2k +2k 2,y 0=kx 0-2=2k,∴线段AB 的垂直平分线的方程是 y -2k =-1k ⎝⎛⎭⎫x -2k +2k 2. 令y =0,得n =2+2k +2k 2=2k 2+2k +2=2⎝⎛⎭⎫1k +122+32.又由k >-12且k ≠0得1k <-2,或1k>0,∴n >2⎝⎛⎭⎫0+122+32=2.∴n 的取值范围为(2,+∞). 17.(文)(2010·全国Ⅰ)已知抛物线C :y 2=4x 的焦点为F ,过点K (-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D .(1)证明:点F 在直线BD 上;(2)设F A →·FB →=89,求△BDK 的内切圆M 的方程.[解析] 设A (x 1,y 1),B (x 2,y 2),D (x 1,-y 1),l 的方程为x =my -1(m ≠0) (1)将x =my -1(m ≠0)代入y 2=4x 并整理得 y 2-4my +4=0,从而y 1+y 2=4m ,y 1y 2=4① 直线BD 的方程为y -y 2=y 2+y 1x 2-x 1(x -x 2)即y -y 2=4y 2-y 1⎝⎛⎭⎫x -y 224 令y =0,得x =y 1y 24=1,所以点F (1,0)在直线BD 上.(2)由(1)知,x 1+x 2=(my 1-1)+(my 2-1)=4m 2-2, x 1x 2=(my 1-1)(my 2-1)=1因为F A →=(x 1-1,y 1),FB →=(x 2-1,y 2),F A →·FB →=(x 1-1,y 1)·(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+4=8-4m 2,故8-4m 2=89,解得m =±43,直线l 的方程为3x +4y +3=0,3x -4y +3=0. 从而y 2-y 1=±(4m )2-4×4=±437,故4y 2-y 1=±37因而直线BD 的方程为3x +7y -3=0,3x -7y -3=0.因为KF 为∠BKD 的角平分线,故可设圆心M (t,0),(-1<t <1),M (t,0)到直线l 及BD 的距离分别为3|t +1|5,3|t -1|4, 由3|t +1|5=3|t -1|4得t =19或t =9(舍去),故圆M 的半径为r =3|t +1|5=23, 所以圆M 的方程为⎝⎛⎭⎫x -192+y 2=49. (理)(2010·揭阳市模考)已知点C (1,0),点A 、B 是⊙O :x 2+y 2=9上任意两个不同的点,且满足AC →·BC →=0,设P 为弦AB 的中点.(1)求点P 的轨迹T 的方程;(2)试探究在轨迹T 上是否存在这样的点:它到直线x =-1的距离恰好等于到点C 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.[解析] (1)法一:连结CP ,由AC →·BC →=0知,AC ⊥BC ,∴|CP |=|AP |=|BP |=12|AB |, 由垂径定理知|OP |2+|AP |2=|OA |2,即|OP |2+|CP |2=9,设点P (x ,y ),有(x 2+y 2)+[(x -1)2+y 2]=9,化简得,x 2-x +y 2=4.法二:设A (x 1,y 1),B (x 2,y 2),P (x ,y ),根据题意知,x 12+y 12=9,x 22+y 22=9,2x =x 1+x 2,2y =y 1+y 2,∴4x 2=x 12+2x 1x 2+x 22,4y 2=y 12+2y 1y 2+y 22故4x 2+4y 2=(x 12+y 12)+(2x 1x 2+2y 1y 2)+(x 22+y 22)=18+2(x 1x 2+y 1y 2)①又∵AC →·BC →=0,∴(1-x 1,-y 1)·(1-x 2,-y 2)=0∴(1-x 1)×(1-x 2)+y 1y 2=0,故x 1x 2+y 1y 2=(x 1+x 2)-1=2x -1,代入①式得,4x 2+4y 2=18+2(2x -1),化简得,x 2-x +y 2=4.(2)根据抛物线的定义,到直线x =-1的距离等于到点C (1,0)的距离的点都在抛物线y 2=2px 上,其中p 2=1,∴p =2,故抛物线方程为y 2=4x , 由方程组⎩⎪⎨⎪⎧y 2=4x x 2-x +y 2=4得,x 2+3x -4=0, 解得x 1=1,x 2=-4,由于x ≥0,故取x =1,此时y =±2,故满足条件的点存在,其坐标为(1,-2)和(1,2).。
100高中数学高考总复习抛物线习题及详解100

高中数学高考总复习抛物线习题(附参考答案)一、选择题1.(2010·湖北黄冈)若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为( )A .-2B .2C .-4D .4[答案] D[解析] 椭圆中,a 2=6,b 2=2,∴c =a 2-b 2=2, ∴右焦点(2,0),由题意知p2=2,∴p =4.2.已知点M 是抛物线y 2=2px (p >0)上的一点,F 为抛物线的焦点,若以|MF |为直径作圆,则这个圆与y 轴的关系是( )A .相交B .相切C .相离D .以上三种情形都有可能[答案] B[解析] 如图,由MF 的中点A 作准线l 的垂线AE ,交直线l 于点E ,交y 轴于点B ;由点M 作准线l 的垂线MD ,垂足为D ,交y 轴于点C ,则MD =MF ,ON =OF , ∴AB =OF +CM 2=ON +CM2=DM 2=MF 2, ∴这个圆与y 轴相切.3.(2010·山东文)已知抛物线y 2=2px (p >0),过焦点且斜率为1的直线交抛物线于A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为( )A .x =1B .x =-1C .x =2D .x =-2[答案] B[解析] 设A (x 1,y 1),B (x 2,y 2),则线段AB 的中点(x 1+x 22,y 1+y 22),∴y 1+y 22=2,∵A 、B 在抛物线y 2=2px 上,∴⎩⎪⎨⎪⎧y 12=2px 1 ①y 22=2px 2② ①-②得y 12-y 22=2p (x 1-x 2),∴k AB =y 1-y 2x 1-x 2=2p y 1+y 2=p 2,∵k AB =1,∴,p =2∴抛物线方程为y 2=4x ,∴准线方程为:x =-1,故选B.4.双曲线x 29-y 24=1的渐近线上一点A 到双曲线的右焦点F 的距离等于2,抛物线y 2=2px (p >0)过点A ,则该抛物线的方程为( )A .y 2=9xB .y 2=4xC .y 2=41313xD .y 2=21313x[答案] C[解析] ∵双曲线x 29-y 24=1的渐近线方程为y =±23x ,F 点坐标为(13,0),设A 点坐标为(x ,y ),则y =±23x ,由|AF |=2⇒(x -13)2+⎝⎛⎭⎫23x 2=2⇒x =913,y =±613,代入y 2=2px 得p =21313,所以抛物线方程为y 2=41313x ,所以选C.5.已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172B .3 C. 5D.92[答案] A[解析] 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 与点(0,2)的距离,因此所求的最小值等于⎝⎛⎭⎫122+22=172,选A. 6.已知抛物线C :y 2=4x 的焦点为F ,准线为l ,过抛物线C 上的点A 作准线l 的垂线,垂足为M ,若△AMF 与△AOF (其中O 为坐标原点)的面积之比为3 1,则点A 的坐标为( )A .(2,22)B .(2,-22)C .(2,±2)D .(2,±22)[答案] D[解析] 如图,由题意可得,|OF |=1,由抛物线定义得,|AF |=|AM |,∵△AMF 与△AOF (其中O 为坐标原点)的面积之比为3∶1,∴S △AMFS △AOF =12×|AF |×|AM |×sin ∠MAF 12×|OF |×|AF |×sin (π-∠MAF )=3, ∴|AM |=3,设A ⎝⎛⎭⎫y 024,y 0,∴y 024+1=3,解得y 0=±22,∴y 024=2,∴点A 的坐标是(2,±22),故选D.7.(2010·河北许昌调研)过点P (-3,1)且方向向量为a =(2,-5)的光线经直线y =-2反射后通过抛物线y 2=mx ,(m ≠0)的焦点,则抛物线的方程为( )A .y 2=-2xB .y 2=-32xC .y 2=4xD .y 2=-4x[答案] D[解析] 设过P (-3,1),方向向量为a =(2,-5)的直线上任一点Q (x ,y ),则PQ →∥a ,∴x +32=y -1-5,∴5x +2y +13=0,此直线关于直线y =-2对称的直线方程为5x +2(-4-y )+13=0,即5x -2y +5=0,此直线过抛物线y 2=mx 的焦点F ⎝⎛⎭⎫m 4,0,∴m =-4,故选D.8.已知mn ≠0,则方程是mx 2+ny 2=1与mx +ny 2=0在同一坐标系内的图形可能是( )[答案] A[解析] 若mn >0,则mx 2+ny 2=1应为椭圆,y 2=-mnx 应开口向左,故排除C 、D ;∴mn <0,此时抛物线y 2=-mnx 应开口向右,排除B ,选A.9.(2010·山东聊城模考)已知A 、B 为抛物线C :y 2=4x 上的不同两点,F 为抛物线C 的焦点,若F A →=-4FB →,则直线AB 的斜率为( )A .±23B .±32C .±34D .±43[答案] D[解析] ∵F A →=-4FB →,∴|F A →|=4|FB →|,设|BF |=t ,则|AF |=4t ,∴|BM |=|AA 1|-|BB 1|=|AF |-|BF |=3t ,又|AB |=|AF |+|BF |=5t ,∴|AM |=4t ,∴tan ∠ABM =43,由对称性可知,这样的直线AB 有两条,其斜率为±43.10.已知抛物线C 的方程为x 2=12y ,过点A (0,-4)和点B (t,0)的直线与抛物线C 没有公共点,则实数t 的取值范围是( )A .(-∞,-1)∪(1,+∞) B.⎝⎛⎭⎫-∞,-22∪⎝⎛⎭⎫22,+∞ C .(-∞,-22)∪(22,+∞) D .(-∞,-22)∪(2,+∞) [答案] B[解析] 由题意知方程组⎩⎨⎧x 2=12y ①x t +y-4=1 ②无实数解由②得y =4xt -4,代入①整理得,2x 2-4x t +4=0,∴Δ=16t2-32<0,∴t >22或t <-22,故选B. [点评] 可用数形结合法求解,设过点A (0,-4)与抛物线x 2=12y 相切的直线与抛物线切点为M (x 0,y 0),则切线方程为y -y 0=4x 0(x -x 0), ∵过A 点,∴-4-2x 02=4x 0(0-x 0), ∴x 0=±2,∴y 0=4,∴切线方程为y -4=±42x -8, 令y =0得x =±22,即t =±22,由图形易知直线与抛物线无公共点时,t <-22或t >22. 二、填空题11.已知点A (2,0)、B (4,0),动点P 在抛物线y 2=-4x 上运动,则AP →·BP →取得最小值时的点P 的坐标是______.[答案] (0,0)[解析] 设P ⎝⎛⎭⎫-y 24,y ,则AP →=⎝⎛⎭⎫-y 24-2,y ,BP →=⎝⎛⎭⎫-y 24-4,y ,AP →·BP →=⎝⎛⎭⎫-y24-2⎝⎛⎭⎫-y 24-4+y 2=y 416+52y 2+8≥8,当且仅当y =0时取等号,此时点P 的坐标为(0,0).12.(文)(2010·泰安市模拟)如图,过抛物线y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,交抛物线于A 、B 两点,且|F A |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 设抛物线准线为l ,作AA 1⊥l ,BB 1⊥l ,FQ ⊥l ,垂足分别为A 1、B 1、Q ,作BM ⊥AA 1垂足为M ,BM 交FQ 于N ,则由条件易知∠ABM =30°,设|BF |=t ,则|NF |=t 2,|MA |=t +32,∵|AM |=|QN |,∴3-t +32=p -t 2,∴p =32,∴抛物线方程为y 2=3x .(理)(2010·泰安质检)如图,过抛物线y 2=2px (p >0)的焦点的直线l 依次交抛物线及其准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=3,则抛物线的方程是________.[答案] y 2=3x[解析] 解法1:过A 、B 作准线垂线,垂足分别为A 1,B 1,则|AA 1|=3,|BB 1|=|BF |,∵|BC |=2|BF |,∴|BC |=2|BB 1|,∴|AC |=2|AA 1|=2|AF |=6,∴|CF |=3,∴p =12|CF |=32,∴抛物线方程为y 2=3x .解法2:由抛物线定义,|BF |等于B 到准线的距离,由|BC |=2|BF |得∠BCB 1=30°,又|AF |=3,从而A ⎝⎛⎭⎫p 2+32,332在抛物线上,代入抛物线方程y 2=2px ,解得p =32.点评:还可以由|BC |=2|BF |得出∠BCB 1=30°,从而求得A 点的横坐标为|OF |+12|AF |=p2+32或3-p 2,∴p 2+32=3-p 2,∴p =32. 13.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.[答案] 3+2 2[解析] 分别由A 和B 向准线作垂线,垂足分别为A 1,B 1,则由条件知, ⎩⎪⎨⎪⎧|AA 1|+|BB 1|=|AB |,|AA 1|-|BB 1|=22|AB |,解得⎩⎪⎨⎪⎧|AA 1|=2+24|AB ||BB 1|=2-24|AB |,∴|AA 1||BB 1|=3+22,即|F A ||FB |=3+2 2. 14.(文)若点(3,1)是抛物线y 2=2px 的一条弦的中点,且这条弦所在直线的斜率为2,则p =________.[答案] 2[解析] 设弦两端点P 1(x 1,y 1),P 2(x 2,y 2),则⎩⎪⎨⎪⎧y 12=2px 1y 22=2px 2,两式相减得,y 1-y 2x 1-x 2=2p y 1+y 2=2,∵y 1+y 2=2,∴p =2.(理)(2010·衡水市模考)设抛物线x 2=12y 的焦点为F ,经过点P (2,1)的直线l 与抛物线相交于A 、B 两点,又知点P 恰为AB 的中点,则|AF |+|BF |=________.[答案] 8[解析] 过A 、B 、P 作准线的垂线AA 1、BB 1与PP 1,垂足A 1、B 1、P 1,则|AF |+|BF |=|AA 1|+|BB 1|=2|PP 1|=2[1-(-3)]=8.三、解答题15.(文)若椭圆C 1:x 24+y 2b 2=1(0<b <2)的离心率等于32,抛物线C 2:x 2=2py (p >0)的焦点在椭圆C 1的顶点上.(1)求抛物线C 2的方程;(2)若过M (-1,0)的直线l 与抛物线C 2交于E 、F 两点,又过E 、F 作抛物线C 2的切线l 1、l 2,当l 1⊥l 2时,求直线l 的方程.[解析] (1)已知椭圆的长半轴长为a =2,半焦距c =4-b 2, 由离心率e =c a =4-b 22=32得,b 2=1.∴椭圆的上顶点为(0,1),即抛物线的焦点为(0,1), ∴p =2,抛物线的方程为x 2=4y .(2)由题知直线l 的斜率存在且不为零,则可设直线l 的方程为y =k (x +1),E (x 1,y 1),F (x 2,y 2),∵y =14x 2,∴y ′=12x ,∴切线l 1,l 2的斜率分别为12x 1,12x 2,当l 1⊥l 2时,12x 1·12x 2=-1,即x 1·x 2=-4,由⎩⎪⎨⎪⎧y =k (x +1)x 2=4y得:x 2-4kx -4k =0, 由Δ=(-4k )2-4×(-4k )>0,解得k <-1或k >0. 又x 1·x 2=-4k =-4,得k =1. ∴直线l 的方程为x -y +1=0.(理)在△ABC 中,CA →⊥CB →,OA →=(0,-2),点M 在y 轴上且AM →=12(AB →+CD →),点C在x 轴上移动.(1)求B 点的轨迹E 的方程;(2)过点F ⎝⎛⎭⎫0,-14的直线l 交轨迹E 于H 、E 两点,(H 在F 、G 之间),若FH →=12HG →,求直线l 的方程.[解析] (1)设B (x ,y ),C (x 0,0),M (0,y 0),x 0≠0, ∵CA →⊥CB →,∴∠ACB =π2,∴2x 0·y 0-x 0=-1,于是x 02=2y 0① M 在y 轴上且AM →=12(AB →+AC →),所以M 是BC 的中点,可得 ⎩⎨⎧x 0+x 2=0y +02=y,∴⎩⎪⎨⎪⎧x 0=-x ②y 0=y2③ 把②③代入①,得y =x 2(x ≠0),所以,点B 的轨迹E 的方程为y =x 2(x ≠0). (2)点F ⎝⎛⎭⎫0,-14,设满足条件的直线l 方程为: y =kx -14,H (x 1,y 1),G (x 2,y 2),由⎩⎪⎨⎪⎧y =kx -14y =x 2消去y 得,x 2-kx +14=0.Δ=k 2-1>0⇒k 2>1,∵FH →=12HG →,即⎝⎛⎭⎫x 1,y 1+14=12(x 2-x 1,y 2-y 1), ∴x 1=12x 2-12x 1⇒3x 1=x 2.∵x 1+x 2=k ,x 1x 2=14,∴k =±233,故满足条件的直线有两条,方程为:8x +43y +3=0和8x -43y -3=0. 16.(文)已知P (x ,y )为平面上的动点且x ≥0,若P 到y 轴的距离比到点(1,0)的距离小1.(1)求点P 的轨迹C 的方程;(2)设过点M (m,0)的直线交曲线C 于A 、B 两点,问是否存在这样的实数m ,使得以线段AB 为直径的圆恒过原点.[解析] (1)由题意得:(x -1)2+y 2-x =1,化简得:y 2=4x (x ≥0). ∴点P 的轨迹方程为y 2=4x (x ≥0).(2)设直线AB 为y =k (x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -m )y 2=4x ,得ky 2-4y -4km =0, ∴y 1+y 2=4k ,y 1·y 2=-4m .∴x 1·x 2=m 2,∵以线段AB 为直径的圆恒过原点, ∴OA ⊥OB ,∴x 1·x 2+y 1·y 2=0.即m 2-4m =0⇒m =0或4.当k 不存在时,m =0或4. ∴存在m =0或4,使得以线段AB 为直径的圆恒过原点.[点评] (1)点P 到定点F (1,0)的距离比到y 轴的距离大1,即点P 到定点F (1,0)的距离与到定直线l :x =-1的距离相等.∴P 点轨迹是以F 为焦点,l 为准线的抛物线,∴p =2,∴方程为y 2=4x .(理)已知抛物线y 2=4x ,过点(0,-2)的直线交抛物线于A 、B 两点,O 为坐标原点. (1)若OA →·OB →=4,求直线AB 的方程.(2)若线段AB 的垂直平分线交x 轴于点(n,0),求n 的取值范围.[解析] (1)设直线AB 的方程为y =kx -2 (k ≠0),代入y 2=4x 中得,k 2x 2-(4k +4)x +4=0①设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k +4k 2,x 1x 2=4k 2.y 1y 2=(kx 1-2)·(kx 2-2)=k 2x 1x 2-2k (x 1+x 2)+4=-8k.∵OA →·OB →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=4k 2-8k =4,∴k 2+2k -1=0,解得k =-1±2.又由方程①的判别式Δ=(4k +4)2-16k 2=32k +16>0得k >-12,∴k =-1+2,∴直线AB 的方程为(2-1)x -y -2=0.(2)设线段AB 的中点的坐标为(x 0,y 0),则由(1)知x 0=x 1+x 22=2k +2k 2,y 0=kx 0-2=2k,∴线段AB 的垂直平分线的方程是 y -2k =-1k ⎝⎛⎭⎫x -2k +2k 2. 令y =0,得n =2+2k +2k 2=2k 2+2k +2=2⎝⎛⎭⎫1k +122+32.又由k >-12且k ≠0得1k <-2,或1k>0,∴n >2⎝⎛⎭⎫0+122+32=2.∴n 的取值范围为(2,+∞). 17.(文)(2010·全国Ⅰ)已知抛物线C :y 2=4x 的焦点为F ,过点K (-1,0)的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D .(1)证明:点F 在直线BD 上;(2)设F A →·FB →=89,求△BDK 的内切圆M 的方程.[解析] 设A (x 1,y 1),B (x 2,y 2),D (x 1,-y 1),l 的方程为x =my -1(m ≠0) (1)将x =my -1(m ≠0)代入y 2=4x 并整理得 y 2-4my +4=0,从而y 1+y 2=4m ,y 1y 2=4① 直线BD 的方程为y -y 2=y 2+y 1x 2-x 1(x -x 2)即y -y 2=4y 2-y 1⎝⎛⎭⎫x -y 224 令y =0,得x =y 1y 24=1,所以点F (1,0)在直线BD 上.(2)由(1)知,x 1+x 2=(my 1-1)+(my 2-1)=4m 2-2, x 1x 2=(my 1-1)(my 2-1)=1因为F A →=(x 1-1,y 1),FB →=(x 2-1,y 2),F A →·FB →=(x 1-1,y 1)·(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+4=8-4m 2,故8-4m 2=89,解得m =±43,直线l 的方程为3x +4y +3=0,3x -4y +3=0. 从而y 2-y 1=±(4m )2-4×4=±437,故4y 2-y 1=±37因而直线BD 的方程为3x +7y -3=0,3x -7y -3=0.因为KF 为∠BKD 的角平分线,故可设圆心M (t,0),(-1<t <1),M (t,0)到直线l 及BD 的距离分别为3|t +1|5,3|t -1|4, 由3|t +1|5=3|t -1|4得t =19或t =9(舍去),故圆M 的半径为r =3|t +1|5=23, 所以圆M 的方程为⎝⎛⎭⎫x -192+y 2=49. (理)(2010·揭阳市模考)已知点C (1,0),点A 、B 是⊙O :x 2+y 2=9上任意两个不同的点,且满足AC →·BC →=0,设P 为弦AB 的中点.(1)求点P 的轨迹T 的方程;(2)试探究在轨迹T 上是否存在这样的点:它到直线x =-1的距离恰好等于到点C 的距离?若存在,求出这样的点的坐标;若不存在,说明理由.[解析] (1)法一:连结CP ,由AC →·BC →=0知,AC ⊥BC ,∴|CP |=|AP |=|BP |=12|AB |, 由垂径定理知|OP |2+|AP |2=|OA |2,即|OP |2+|CP |2=9,设点P (x ,y ),有(x 2+y 2)+[(x -1)2+y 2]=9,化简得,x 2-x +y 2=4.法二:设A (x 1,y 1),B (x 2,y 2),P (x ,y ),根据题意知,x 12+y 12=9,x 22+y 22=9,2x =x 1+x 2,2y =y 1+y 2,∴4x 2=x 12+2x 1x 2+x 22,4y 2=y 12+2y 1y 2+y 22故4x 2+4y 2=(x 12+y 12)+(2x 1x 2+2y 1y 2)+(x 22+y 22)=18+2(x 1x 2+y 1y 2)①又∵AC →·BC →=0,∴(1-x 1,-y 1)·(1-x 2,-y 2)=0∴(1-x 1)×(1-x 2)+y 1y 2=0,故x 1x 2+y 1y 2=(x 1+x 2)-1=2x -1,代入①式得,4x 2+4y 2=18+2(2x -1),化简得,x 2-x +y 2=4.(2)根据抛物线的定义,到直线x =-1的距离等于到点C (1,0)的距离的点都在抛物线y 2=2px 上,其中p 2=1,∴p =2,故抛物线方程为y 2=4x , 由方程组⎩⎪⎨⎪⎧y 2=4x x 2-x +y 2=4得,x 2+3x -4=0, 解得x 1=1,x 2=-4,由于x ≥0,故取x =1,此时y =±2,故满足条件的点存在,其坐标为(1,-2)和(1,2).。
(完整版)高中抛物线知识点归纳总结与练习题及答案
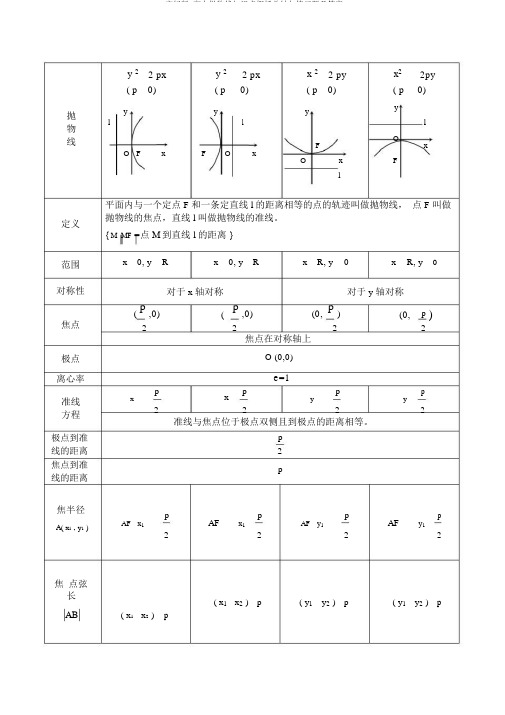
抛物线y 2 2 px y 2 2 px x 2 2 py x22py ( p0)( p0)( p0)( p0)y y yyl l lFOx O F x F O xO x Fl定义范围对称性焦点极点离心率准线方程极点到准线的距离焦点到准线的距离焦半径A( x1 , y1 )焦点弦长AB 平面内与一个定点 F 和一条定直线l的距离相等的点的轨迹叫做抛物线,点 F 叫做抛物线的焦点,直线 l 叫做抛物线的准线。
{ M MF =点 M到直线 l 的距离 }x 0, y R x 0, y R x R, y 0x R, y0对于 x 轴对称对于 y 轴对称(p,0)(p,0)(0,p)(0,p ) 2222焦点在对称轴上O (0,0)e=1pxp p p x y2y222准线与焦点位于极点双侧且到极点的距离相等。
p2ppAFp pAFp AF x1x1AF y1y1 2222( x1x2 ) p( y1y2 ) p( y1y2 )p ( x1x2 )pyA x1 , y1o FxB x2 , y2焦点弦AB 的几条性质以 AB 为直径的圆必与准线l相切A(x1, y1 ) 2 p 2 p若 AB 的倾斜角为若 AB 的倾斜角为,则 AB,则 ABB(x2 , y2 )sin 2cos2p22x1x2y1 y2p4切线方程11AF BF AB2AF BF AF ? BF AF ? BF py0 y p( x x0 )y0 y p( x x0 )x0 x p( y y0 )x0 x p( y y0 )一.直线与抛物线的地点关系直线,抛物线,,消 y 得:(1)当 k=0 时,直线 l 与抛物线的对称轴平行,有一个交点;(2)当 k≠ 0 时,>0,直线 l 与抛物线订交,两个不一样交点;=0,直线 l 与抛物线相切,一个切点;< 0,直线 l 与抛物线相离,无公共点。
(3)若直线与抛物线只有一个公共点, 则直线与抛物线必相切吗?(不必定)二.对于直线与抛物线的地点关系问题常用办理方法直线 l :y kx b抛物线, ( p0)①联立方程法:y kx bk2 x22(kb p)x b20y2 2 px设交点坐标为(,y1), B( x2 , y2 ) ,则有0, 以及 x1x2 , x1 x2,还可进一步求出A x1y1 y2kx1 b kx2 b k (x1x2 ) 2b,y1 y2( kx1b)(kx2b) k 2 x1 x2kb( x1x2 ) b2在波及弦长,中点,对称,面积等问题时,常用此法,比方1.订交弦 AB的弦长AB 1 k 2 x1x2 1 k 2(x1x2 )24x1x2 1 k 2a或1121 k 2AB1k 2 y1y21k 2( y1y2 ) 4 y1 y2ab. 中点M (x0, y0) , x0x1x2,y0y1y222②点差法:设交点坐标为 A( x1, y1 ) , B(x2 , y2 ) ,代入抛物线方程,得y12 2 px1y22 2 px2将两式相减,可得( y1y2 )( y1y2 ) 2 p(x1 x2 )y1y2 2 px1x2 y1 y2a.在波及斜率问题时,k AB 2 py1y2b.在涉及中点轨迹问题时,设线段 AB 的中点为 M ( x0 , y0 ) ,y1y2 2 p2p p ,x1x2y1 y2 2 y0y0即 k AB p ,y0同理,对于抛物线x 22(p0),若直线 l 与抛物线订交于A、, y0 ) py B 两点,点M ( x0是弦 AB 的中点,则有 k AB x1 x22x0x0 2 p 2 p p(注意能用这个公式的条件: 1)直线与抛物线有两个不一样的交点, 2)直线的斜率存在,且不等于零)抛物线练习及答案1、已知点 P 在抛物线 y 2 = 4x 上,那么点P 到点 Q ( 2,- 1)的距离与点P 到抛物线焦点距离之和获得最小值时,点P 的坐标为。
专题23--抛物线(解答题压轴题)(解析版)-【挑战压轴题】备战2023年高考数学高分必刷必过题

(1)若1l 过抛物线C 的焦点,且垂直于(2)若直线1l 的斜率k ∈2MN MQ =,且MNQ △【答案】(1)22y x =1(1)若B为线段AC的中点,求直线(2)若正方形DFMN的边长为实数λ,使得k1+k2=λk3?若存在,求出【答案】(1)22;λ=,理由见解析(2)存在2(1)由已知可得DN为抛物线的准线.(2)λ=,使得k1+k2=λk3,理由如下:存在2(1)若抛物线2C的焦点正好为椭圆1C的上顶点,求(2)椭圆1C与抛物线2C在第一象限的交点为于点Q,交抛物线2C于点M(Q,M值,并求当p取最大时直线l的斜率.(1)证明:以DE为直径的圆经过点(1)求点P的纵坐标的取值范围;(2)设D是抛物线2Γ上一点,且位于椭圆PCD的面积存在最大值.【答案】(1)3,22⎛⎫ ⎪⎝⎭;32⎛⎫(1)当k 取不同数值时,求直线l 与抛物线公共点的个数;(2)若直线l 与抛物线相交于A 、B (3)在x 轴上是否存在这样的定点均能使得MA MB k k ⋅为定值,若有,找出满足条件的点【答案】(1)答案见解析(2)证明见解析(3)存在,()0,0M (1)420240x y x y -+-=+-=(1)写出这条抛物线的焦点坐标和准线方程;(2)求证:1x 、0x 、2x 成等差数列,(3)若A ,F ,B 三点共线,求出动点【答案】(1)焦点坐标为()0,1F ,准线方程为(2)证明见解析(3)1y =-,4(1)(1)抛物线的标准方程为24x y =,于是焦点坐标为(1)若抛物线2C 的焦点恰为椭圆1C (2)若椭圆1C 与抛物线2C 在第一象限的交点为交抛物线2C 于M ,且AM MB =,求【答案】(1)28y x =(2)p 的最大值为3540,此时直线(1)求抛物线的方程;(2)若||||AB CD =,求凹四边形OEBC 面积的最小值.【答案】(1)24y x =(2)324+①若0m ≤,2(22)S m =++②若0m >,((21)2S m ⎡=+⎢⎣综上所述,凹四边形OEBC 面积的最小值是。
高考数学抛物线大题专练30题(含详解)经典收藏版

目录目录-------------------------------------------------------------------------------------------------1抛物线大题专练(一)--------------------------------------------------------------------------------2抛物线大题专练(二)--------------------------------------------------------------------------------5抛物线大题专练(三)--------------------------------------------------------------------------------8抛物线大题专练---------------------------------------------------------------------------------------11参考答案与试题解析---------------------------------------------------------------------------------11抛物线大题专练(一)1.已知抛物线C的方程为x2=2py,设点M(x0,1)(x0>0)在抛物线C上,且它到抛物线C的准线距离为;(1)求抛物线C的方程;(2)过点M作倾斜角互补的两条直线分别交抛物线C于A(x1,y1),B(x2,y2)两点(M、A、B三点互不相同),求当∠MAB为钝角时,点A的纵坐标y1的取值范围.2.在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为x=﹣,过点M(0,﹣2)作抛物线的切线MA,切点为A(异于点O).直线l过点M与抛物线交于两点B,C,与直线OA交于点N.(1)求抛物线的方程;(2)试问:的值是否为定值?若是,求出定值;若不是,说明理由.3.如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=﹣1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).(1)求抛物线E的方程;(2)若•+•=64,求直线l1、l2的方程.4.已知抛物线C:y2=2px(p>0),点A、B在抛物线C上.(Ⅰ)若直线AB过点M(2p,0),且|AB|=4p,求过A,B,O(O为坐标原点)三点的圆的方程;(Ⅱ)设直线OA、OB的倾斜角分别为α,β且α+β=,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.5.已知点A(2,1)在抛物线E:x2=ay上,直线l1:y=kx+1(k∈R,且k≠0)与抛物线E相交于B,C两点,直线AB,AC分别交直线l2:y=﹣1于点S,T.(1)求a的值;(2)若|ST|=2,求直线l1的方程;(3)试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.6.已知抛物线y2=2px(p>0),焦点为F,一直线l与抛物线交于A、B两点,且|AF|+|BF|=8,且AB的垂直平分线恒过定点S(6,0)①求抛物线方程;②求△ABS面积的最大值.7.已知抛物线y2=4x,直线l:y=﹣x+b与抛物线交于A,B两点.(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.8.抛物线M:y2=2px(p>0)的准线过椭圆N:+y2=1的左焦点,以原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的图象以及y轴的正半轴相交于点A和B,直线AB与x轴相交于点C.(Ⅰ)求抛物线M的方程;(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.9.已知抛物线y2=4x的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C,过点(1,),(Ⅰ)求椭圆C的标准方程;(Ⅱ)设T(2,0),过点F2作直线l与椭圆C交于A,B两点,且=λ,若λ∈[﹣2,﹣1],求|+|2的最小值.抛物线大题专练(二)10.(2015•福建模拟)如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.(Ⅰ)证明•的值与k1无关;(Ⅱ)记直线MN的斜率为k2,证明为定值.11.已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)当|AM|+4|BM|最小时,求直线l的方程.12.已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)若圆x2+y2﹣2x=0与直线l相交于以C,D(A,C两点均在第一象银),且线段AC,CD,DB长构成等差数列,求直线l的方程.13.已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.14.如图所示,已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.(1)求证:以AF为直径的圆与x轴相切;(2)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程:(3)设过抛物线x2=4y焦点F的直线l与椭圆+=1的交点为C、D,是否存在直线l使得|AF|•|CF|=|BF|•|DF|,若存在,求出直线l的方程,若不存在,请说明理由.15.已知抛物线C:y2=2px(p>0),直线交此抛物线于不同的两个点A(x1,y1)、B(x2,y2)(1)当直线过点M(p,0)时,证明y1.y2为定值;(2)如果直线过点M(p,0),过点M再作一条与直线垂直的直线l′交抛物线C于两个不同点D、E.设线段AB的中点为P,线段DE的中点为Q,记线段PQ的中点为N.问是否存在一条直线和一个定点,使得点N到它们的距离相等?若存在,求出这条直线和这个定点;若不存在,请说明理由.16.(2014•陕西)如图,曲线C由上半椭圆C1:+=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为.(Ⅰ)求a,b的值;(Ⅱ)过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.17.(2014•山东)已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有丨FA丨=丨FD丨.当点A的横坐标为3时,△ADF为正三角形.(Ⅰ)求C的方程;(Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E,(ⅰ)证明直线AE过定点,并求出定点坐标;(ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.18.(2014•安徽)如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1、A2两点,l2与E1、E2分别交于B1、B2两点.(Ⅰ)证明:A1B1∥A2B2;(Ⅱ)过O作直线l(异于l1,l2)与E1、E2分别交于C1、C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2,求的值.19.(2014•福建)已知曲线Γ上的点到点F(0,1)的距离比它到直线y=﹣3的距离小2.(Ⅰ)求曲线Γ的方程;(Ⅱ)曲线Γ在点P处的切线l与x轴交于点A.直线y=3分别与直线l及y轴交于点M,N,以MN为直径作圆C,过点A作圆C的切线,切点为B,试探究:当点P在曲线Γ上运动(点P与原点不重合)时,线段AB的长度是否发生变化?证明你的结论.20.(2014•江西)如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).(1)证明:动点D在定直线上;(2)作C的任意一条切线l(不含x轴),与直线y=2相交于点N1,与(1)中的定直线相交于点N2,证明:|MN2|2﹣|MN1|2为定值,并求此定值.抛物线大题专练(三)21.(2014•杭州二模)设抛物线Γ:y2=2px(p>0)过点(t,)(t是大于0的常数).(Ⅰ)求抛物线Γ的方程;(Ⅱ)若F是抛物线Γ的焦点,斜率为1的直线交抛物线Γ于A,B两点,x轴负半轴上的点C,D满足|FA|=|FC|,|FD|=|FB|,直线AC,BD相交于点E,当时,求直线AB的方程.22.(2014•包头一模)设抛物线C:y2=2px(p>0)的焦点为F,准线为l,l与x轴交于点R,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.(1)若∠BFD=120°,△ABD的面积为8,求p的值及圆F的方程;(2)在(1)的条件下,若A,B,F三点在同一直线上,FD与抛物线C交于点E,求△EDA的面积.23.(2014•长春三模)已知抛物线C:y2=2px(p>0)的焦点为F,若过点F且斜率为1的直线与抛物线相交于M,N两点,且|MN|=8.(1)求抛物线C的方程;(2)设直线l为抛物线C的切线,且l∥MN,P为l上一点,求的最小值.24.(2014•长沙二模)已知A、B为抛物线C:y2=4x上的两个动点,点A在第一象限,点B在第四象限,l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.(Ⅰ)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;(Ⅱ)设C、D为直线l1、l2与直线x=4的交点,求△PCD面积的最小值.25.(2015•上海模拟)如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2﹣x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).(1)用k、b表示出C点、D点的坐标,并证明CD垂直于x轴;(2)求△ABC的面积,证明△ABC的面积与k、b无关,只与h有关;(3)小张所在的兴趣小组完成上面两个小题后,小张连AC、BC,再作与AC、BC平行的切线,切点分别为E、F,小张马上写出了△ACE、△BCF的面积,由此小张求出了直线l与抛物线围成的面积,你认为小张能做到吗?请你说出理由.26.(2014•乌鲁木齐三模)已知抛物线y2=2px(p>0)的焦点过F,过H(﹣,0)引直线l交此抛物线于A,B两点.(1)若直线AF的斜率为2,求直线BF的斜率;(2)若p=2,点M在抛物线上,且+=t,求t的取值范围.27.(2014•太原二模)已知抛物线y2=4x的焦点为F,直线l1与抛物线交于不同的两点A、B,直线l2与抛物线交于不同的两点C、D.(Ⅰ)当l1过F时,在l1上取不同于F的点P,使得=,求点P的轨迹方程;(Ⅱ)若l1与l2相交于点Q,且倾斜角互补时,|QA|•|QB|=a|QC|•|QD|,求实数a的值.28.(2014•合肥一模)已知△ABC的三个顶点都在抛物线y2=2px(p>0)上,且抛物线的焦点F满足,若BC边上的中线所在直线l的方程为mx+ny﹣m=0(m,n为常数且m≠0).(Ⅰ)求p的值;(Ⅱ)O为抛物线的顶点,△OFA、△OFB、△OFC的面积分别记为S1、S2、S3,求证:为定值.29.(2014•呼和浩特一模)已知抛物线C:y2=2px(p>0),直线l过定点A(4,0)且与抛物线C交于P、Q两点,若以弦PQ为直径的圆E过原点O.(Ⅰ)求抛物线C的方程;(Ⅱ)当圆E的面积最小时,求E的方程.30.(2014•普陀区一模)已知点P(2,0),点Q在曲线C:y2=2x上.(1)若点Q在第一象限内,且|PQ|=2,求点Q的坐标;(2)求|PQ|的最小值.抛物线大题专练参考答案与试题解析1.已知抛物线C的方程为x2=2py,设点M(x0,1)(x0>0)在抛物线C上,且它到抛物线C的准线距离为;(1)求抛物线C的方程;(2)过点M作倾斜角互补的两条直线分别交抛物线C于A(x1,y1),B(x2,y2)两点(M、A、B三点互不相同),求当∠MAB为钝角时,点A的纵坐标y1的取值范围.考点:抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:(1)由抛物线的定义,求出p,即可求抛物线C的方程;(2)设直线AM的方程为:y=k(x﹣1)+1,与抛物线方程联立,求出k的范围,利用,即可求出点A的纵坐标y1的取值范围.解答:解:(1)由定义得,则抛物线C的方程:x2=y(2)设直线AM的方程为:y=k(x﹣1)+1联立方程得x2﹣kx+k﹣1=0,A(k﹣1,(k﹣1)2),△1>0即k≠2同理B(﹣k﹣1,(﹣k﹣1)2),△2>0即k≠﹣2,令,则所以k>2或,所以点评:本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.2.(2015•淮安一模)在平面直角坐标系xOy中,已知抛物线y2=2px(p>0)的准线方程为x=﹣,过点M(0,﹣2)作抛物线的切线MA,切点为A(异于点O).直线l过点M与抛物线交于两点B,C,与直线OA交于点N.(1)求抛物线的方程;(2)试问:的值是否为定值?若是,求出定值;若不是,说明理由.考点:抛物线的简单性质.专题:计算题;直线与圆;圆锥曲线的定义、性质与方程.分析:(1)由抛物线的准线方程可得p,进而得到抛物线方程;(2)求出函数y=﹣的导数,求出切线的斜率,以及切线方程,联立切线方程和抛物线方程求得切点A,进而直线OA的方程,设出直线BC的方程,联立抛物线方程运用韦达定理,求出N的坐标,代入所求式子化简即可得到定值2.解答:解:(1)由题设知,,即,所以抛物线的方程为y2=x;(2)因为函数的导函数为,设A(x0,y0),则直线MA的方程为,因为点M(0,﹣2)在直线MA上,所以﹣2﹣y0=﹣•(﹣x0).联立,解得A(16,﹣4),所以直线OA的方程为.设直线BC方程为y=kx﹣2,由,得k2x2﹣(4k+1)x+4=0,所以.由,得.所以,故的为定值2.点评:本题考查抛物线的方程和性质,考查直线方程和抛物线方程联立,运用韦达定理,以及导数的运用:求切线方程,考查运算能力,属于中档题和易错题.3.(2014•九江三模)如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=﹣1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).(1)求抛物线E的方程;(2)若•+•=64,求直线l1、l2的方程.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)确定△AFO外接圆的圆心在线段OF的垂直平分线y=上,求出p,即可求抛物线E的方程;(2)利用•+•=64,结合韦达定理,基本不等式,即可求直线l1、l2的方程.解答:解:(1)由题意,F(0,),△AFO外接圆的圆心在线段OF的垂直平分线y=上,∴+=3,∴p=4.∴抛物线E的方程是x2=8y;(2)设直线l1的方程y=k1x+2,代入抛物线方程,得y2﹣(8k12+4)y+4=0设A(x1,y1),B(x2,y2),则y1+y2=8k12+4,y1y2=4设C(x3,y3),D(x4,y4),同理可得y3+y4=+4,y3y4=4∴•+•=32+16(k12+)≥64,当且仅当k12=,即k1=±1时取等号,∴直线l1、l2的方程为y=x+2或y=﹣x+2.点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查向量知识的运用,属于中档题.4.(2014•浙江二模)已知抛物线C:y2=2px(p>0),点A、B在抛物线C上.(Ⅰ)若直线AB过点M(2p,0),且|AB|=4p,求过A,B,O(O为坐标原点)三点的圆的方程;(Ⅱ)设直线OA、OB的倾斜角分别为α,β且α+β=,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)求出A,B的坐标,可得三角形ABO是Rt△,从而可求过A,B,O三点的圆方程;(Ⅱ)直线AB的方程为:x=my+b,代入抛物线方程,利用韦达定理,结合α+β=,可得b=﹣2p﹣2mp,即可得出结论.解答:解:(Ⅰ)∵直线AB过点M(2p,0),且|AB|=4p,∴直线x=2p与抛物线y2=2px的两个交点坐标分别是:A(2p,2p),B(2p,﹣2p),∴三角形ABO是Rt△,∴过A,B,O三点的圆方程是:(x﹣2p)2+y2=4p2;(Ⅱ)设点,直线AB的方程为:x=my+b,它与抛物线相交,由方程组消去x可得y2﹣2mpy﹣2pb=0,故y1+y2=2mp,y1y2=﹣2pb,这样,tan==即1=,所以b=﹣2p﹣2mp,∴直线AB的方程可以写成为:x=my﹣2p﹣2mp,即x+2p=m(y﹣2p),∴直线AB过定点(﹣2p,2p).点评:本题考查圆的方程,考查直线与抛物线的位置关系,考查和角的正切公式,考查直线过定点,属于中档题.5.(2014•广州二模)已知点A(2,1)在抛物线E:x2=ay上,直线l1:y=kx+1(k∈R,且k≠0)与抛物线E相交于B,C两点,直线AB,AC分别交直线l2:y=﹣1于点S,T.(1)求a的值;(2)若|ST|=2,求直线l1的方程;(3)试判断以线段ST为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)根据点A(2,1)在抛物线E:x2=ay上,可求a的值;(2)y=kx+1代入抛物线方程,利用韦达定理,确定S,T的坐标,根据|ST|=2,即可求直线l1的方程;(3)确定以线段ST为直径的圆的方程,展开令x=0,即可求这两个定点的坐标.解答:解:(1)∵点A(2,1)在抛物线E:x2=ay上,∴a=4.…(1分)(2)由(1)得抛物线E的方程为x2=4y.设点B,C的坐标分别为(x1,y1),(x2,y2),依题意,,y=kx+1代入抛物线方程,消去y得x2﹣4kx﹣4=0,解得.∴x1+x2=4k,x1x2=﹣4.…(2分)直线AB的斜率,故直线AB的方程为.…(3分)令y=﹣1,得,∴点S的坐标为.…(4分)同理可得点T的坐标为.…(5分)∴=.…(6分)∵,∴.由,得20k2=16k2+16,解得k=2,或k=﹣2,…(7分)∴直线l1的方程为y=2x+1,或y=﹣2x+1.…(9分)(3)设线段ST的中点坐标为(x0,﹣1),则=.…(10分)而|ST|2=,…(11分)∴以线段ST为直径的圆的方程为=.展开得.…(12分)令x=0,得(y+1)2=4,解得y=1或y=﹣3.…(13分)∴以线段ST为直径的圆恒过两个定点(0,1),(0,﹣3).…(14分)点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查圆的方程,考查学生的计算能力,属于中档题.6.(2015•兴国县一模)已知抛物线y2=2px(p>0),焦点为F,一直线l与抛物线交于A、B两点,且|AF|+|BF|=8,且AB的垂直平分线恒过定点S(6,0)①求抛物线方程;②求△ABS面积的最大值.考点:抛物线的标准方程;抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:①利用点差法,确定AB中点M的坐标,分类讨论,根据AB的垂直平分线恒过定点S(6,0),即可求抛物线方程;②分类讨论,求出△ABS面积的表达式,即可求得其最大值.解答:解:①设A(x1,y1),B(x2,y2),AB中点M(x0,y0)当直线的斜率存在时,设斜率为k,则由|AF|+|BF|=8得x1+x2+p=8,∴又得,∴所以依题意,∴p=4∴抛物线方程为y2=8x﹣﹣﹣﹣(6分)当直线的斜率不存在时,2p=8,也满足上式,∴抛物线方程为y2=8x②当直线的斜率存在时,由(2,y0)及,令y=0,得又由y2=8x和得:∴=﹣﹣﹣﹣(12分)当直线的斜率不存在时,AB的方程为x=2,|AB|=8,△ABS面积为∵,∴△ABS面积的最大值为.点评:本题考查抛物线的标准方程,考查三角形面积的计算,考查学生的计算能力,属于中档题.7.(2015•路南区二模)已知抛物线y2=4x,直线l:y=﹣x+b与抛物线交于A,B两点.(Ⅰ)若x轴与以AB为直径的圆相切,求该圆的方程;(Ⅱ)若直线l与y轴负半轴相交,求△AOB面积的最大值.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)联立得y2+8y﹣8b=0.由此利用根的判别式、弦长公式,结合已知条件能求出圆的方程.(Ⅱ)由直线l与y轴负半轴相交,得﹣1<b<0,由点O到直线l的距离d=,得S△AOB=|AB|d=4.由此利用导数性质能求出△AOB的面积的最大值.解答:解:(Ⅰ)联立得:y2+8y﹣8b=0.依题意应有△=64+32b>0,解得b>﹣2.设A(x1,y1),B(x2,y2),设圆心Q(x0,y0),则应有x0=,y0==﹣4.因为以AB为直径的圆与x轴相切,得到圆半径为r=|y1|=4,又|AB|==.所以|AB|=2r,即=8,解得b=﹣.所以x0==2b+8=,所以圆心为(,﹣4).故所求圆的方程为(x﹣)2+(y+4)2=16..(Ⅱ)因为直线l与y轴负半轴相交,∴b<0,又l与抛物线交于两点,由(Ⅰ)知b>﹣2,∴﹣2<b<0,直线l:y=﹣x+b整理得x+2y﹣2b=0,点O到直线l的距离d==,所以∴S△AOB=|AB|d=﹣4b=4.令g(b)=b3+2b2,﹣2<b<0,g′(b)=3b2+4b=3b(b+),∴g(b)在(﹣2,﹣)增函数,在(﹣,0)是减函数,∴g(b)的最大值为g(﹣)=.∴当b=﹣时,△AOB的面积取得最大值.点评:本题主要考查圆的方程的求法,考查三角形面积的最大值的求法,考查直线与抛物线、圆等知识,同时考查解析几何的基本思想方法和运算求解能力.8.(2015•大庆二模)抛物线M:y2=2px(p>0)的准线过椭圆N:+y2=1的左焦点,以原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的图象以及y轴的正半轴相交于点A和B,直线AB与x轴相交于点C.(Ⅰ)求抛物线M的方程;(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)由椭圆方程求出椭圆左焦点坐标,得到抛物线准线方程,从而求得p值,则抛物线方程可求;(Ⅱ)写出A的坐标,由|OA|=t列式求得t与A的坐标间的关系,求出直线BC的方程,把A代入BC方程,得到a,c的关系,然后直接代入斜率公式求直线CD的斜率.解答:解:(Ⅰ)∵椭圆N:+y2=1,∴c2=a2﹣b2=﹣1=,∴椭圆的左焦点为F1(﹣,0),∴﹣=﹣,则p=1.故M:y2=2x;(Ⅱ)由题意知,A(a,2a),∵|OA|=t,∴a2+2a=t2.由于t>0,故有t=①由点B(0,t),C(c,0)的坐标知,直线BC的方程为+=1.又∵A在直线BC上,故有+=1.将①代入上式,得:+=1,解得c=a+2+.又∵D(a+2,2),∴直线CD的斜率为:k CD====﹣1.点评:本题主要抛物线方程的求法,考查了直线与圆锥曲线位置关系的应用,解答此题的关键是对抛物线定义的灵活应用,是高考试卷中的压轴题.9.(2015•黄冈模拟)已知抛物线y2=4x的焦点为F2,点F1与F2关于坐标原点对称,以F1,F2为焦点的椭圆C,过点(1,),(Ⅰ)求椭圆C的标准方程;(Ⅱ)设T(2,0),过点F2作直线l与椭圆C交于A,B两点,且=λ,若λ∈[﹣2,﹣1],求|+|2的最小值.考点:抛物线的简单性质.专题:综合题;圆锥曲线的定义、性质与方程.分析:(Ⅰ)设椭圆的半焦距为c,由y2=4x求得c=1.设椭圆C的标准方程为(a>b>0),由于椭圆C过点(1,),代入椭圆方程结合a2=b2+c2,联立解得即可;(II)设l:x=ky+1,与椭圆的方程联立可得根与系数的关系,由λ∈[﹣2,﹣1)可得到k2的取值范围.由于=(x1﹣2,y1),=(x2﹣2,y2),通过换元,令t=∈[,],即可得出|+|2的最小值.解答:解:(Ⅰ)设椭圆的半焦距为c,由y2=4x得c=1,设椭圆C的标准方程为(a>b>0),∵椭圆C过点(1,),∴,又a2=b2+1,联立解得b2=1,a2=2.故椭圆C的标准方程为椭圆方程为+y2=1…(5分)(Ⅱ)由题意可设l:x=ky+1,由得(k2+2)y2+2ky﹣1=0…(6分)设A(x1,y1),B(x2,y2),则有将①2÷②得+2=﹣⇒λ++2=…(8分)由λ∈[﹣2,﹣1]得﹣≤λ++2≤0⇒﹣≤≤0,0≤k2≤…(9分)=(x1﹣2,y1),=(x2﹣2,y2),+=(x1+x2﹣4,y1+y2)x1+x2﹣4=k(y1+y2)﹣2=﹣,|+|=+==16﹣+令t=∈[,],|+|2=8t2﹣28t+16∴t=时|+|2的最小值是4点评:本题综合考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数、换元法、分类讨论、向量相等及其向量运算和向量的模等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于中档题.10.(2015•福建模拟)如图,已知抛物线y2=4x的焦点为F,过点P(2,0)且斜率为k1的直线交抛物线于A(x1,y1),B(x2,y2)两点,直线AF、BF分别与抛物线交于点M、N.(Ⅰ)证明•的值与k1无关;(Ⅱ)记直线MN的斜率为k2,证明为定值.考点:抛物线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:(Ⅰ)依题意,设直线AB的方程为x=my+2,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得y1y2,进而求出x1x2,根据向量数量积运算公式,可得•的值与k1无关;(Ⅱ)设M(x3,y3),N(x4,y4),设直线AM的方程为x=ny+1,将其代入y2=4x,消去x,得到关于y的一元二次方程,从而得y1y3=﹣4,同理可得y2y4=﹣4,根据斜率公式可把表示成关于y1与y2的表达式,再借助(Ⅰ)的结果即可证明.解答:证明:(Ⅰ)依题意,设直线AB的方程为x=my+2(m≠0).…(1分)将其代入y2=4x,消去x,整理得y2﹣4my﹣8=0.…(2分)从而y1y2=﹣8,于是,…(3分)∴与k 1无关.…(5分)(Ⅱ)设M(x3,y3),N(x4,y4).则.…(8分)设直线AM的方程为x=ny+1(n≠0),将其代入y2=4x,消去x,整理得y2﹣4ny﹣4=0∴y1y3=﹣4.同理可得y2y4=﹣4.…(10分)故,…(11分)由(Ⅰ)知,y1y2=﹣8,∴为定值.…(12分)点评:本题考查直线与圆锥曲线的位置关系及抛物线的简单性质,考查学生综合运用知识分析问题解决问题的能力,难度较大.11.(2015•洛阳一模)已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)当|AM|+4|BM|最小时,求直线l的方程.考点:直线与圆锥曲线的关系.专题:计算题;平面向量及应用;直线与圆;圆锥曲线的定义、性质与方程.分析:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)运用抛物线的定义,及均值不等式,即可得到最小值9,注意等号成立的条件,求得B的坐标,代入直线方程,求得m,即可得到直线l的方程.解答:解:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,消去x,得,y2﹣2pmy﹣p2=0,y1+y2=2pm,y1y2=﹣p2,由于•=﹣3,即x1x2+y1y2=﹣3,x1x2==,即有﹣p2=﹣3,解得,p=2;(2)由抛物线的定义,可得,|AM|=x1+1,|BM|=x2+1,则|AM|+4|BM|=x 1+4x2+5+5=9,当且仅当x1=4x2时取得最小值9.由于x1x2=1,则解得,x2=(负的舍去),代入抛物线方程y2=4x,解得,y2=,即有B(),将B的坐标代入直线x=my+1,得m=.则直线l:x=y+1,即有4x+y﹣4=0或4x﹣y﹣4=0.点评:本题考查抛物线的定义、方程和性质,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理,考查基本不等式的运用:求最值,考查运算能力,属于中档题.12.(2015•洛阳一模)已知过点M(,0)的直线l与抛物线y2=2px(p>0)交于A,B两点,且•=﹣3,其中O为坐标原点.(1)求p的值;(2)若圆x2+y2﹣2x=0与直线l相交于以C,D(A,C两点均在第一象银),且线段AC,CD,DB长构成等差数列,求直线l的方程.考点:直线与圆锥曲线的关系;直线的一般式方程.专题:计算题;平面向量及应用;圆锥曲线的定义、性质与方程.分析:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,运用韦达定理,及平面向量的数量积的坐标表示,即可得到p=2;(2)求出AB的长,用m表示,再由等差数列的性质,以及CD为圆的直径,即可得到m的方程,解出m,即可得到直线l的方程.解答:解:(1)设A(x1,y1),Bx2,y2),直线l:x=my+,代入抛物线方程,消去x,得,y2﹣2pmy﹣p2=0,y1+y2=2pm,y1y2=﹣p2,由于•=﹣3,即x1x2+y1y2=﹣3,x1x2==,即有﹣p2=﹣3,解得,p=2;(2)由(1)得,y1+y2=4m,y1y2=﹣4,则(y1﹣y2)2=(y1+y2)2﹣4y1y2=16(1+m2),|AB|2=(y1﹣y2)2+(x1﹣x2)2=(y1﹣y2)2+()2=y1﹣y2)2[1+()2]=16(1+m2)2,即有|AB|=4(1+m2),由于线段AC,CD,DB长构成等差数列,则2|CD|=|AC|+|DB|=|AC|+|BC|﹣|CD|=|AB|﹣|CD|,又CD为圆x2+y2﹣2x=0的直径,即有|CD|=2,则4(1+m2)=6,解得,m=,则直线l的方程是x+y﹣=0或x﹣y﹣=0.点评:本题考查抛物线的定义、方程和性质,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理,考查等差数列的性质,考查运算能力,属于中档题.13.(2015•衡水模拟)已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(I)设M(x,y),由题意可得:,化简可得曲线C的轨迹方程为x2=4y且(x≠±4).(II)设Q(m,﹣1),切线方程为y+1=k(x﹣m),与抛物线方程联立化为x2﹣4kx+4(km+1)=0,由于直线与抛物线相切可得△=0,即k2﹣km﹣1=0.解得x=2k.可得切点(2k,k2),由k2﹣km﹣1=0.可得k1+k2=m,k1•k2=﹣1.得到切线QD⊥QE.因此△QDE为直角三角形,|QD|•|QE|.令切点(2k,k2)到Q的距离为d,则d2=(2k﹣m)2+(k2+1)2=(4+m2)(k2+1),利用两点之间的距离公式可得|QD|=,|QE|=,代入即可得出.解答:解:(I)设M(x,y),由题意可得:,化为x2=4y.∴曲线C的轨迹方程为x2=4y且(x≠±4).(II)设Q(m,﹣1),切线方程为y+1=k(x﹣m),联立,化为x2﹣4kx+4(km+1)=0,由于直线与抛物线相切可得△=0,即k2﹣km﹣1=0.∴x2﹣4kx+4k2=0,解得x=2k.可得切点(2k,k2),由k2﹣km﹣1=0.∴k1+k2=m,k1•k2=﹣1.∴切线QD⊥QE.∴△QDE为直角三角形,|QD|•|QE|.令切点(2k,k2)到Q的距离为d,则d2=(2k﹣m)2+(k2+1)2=4(k2﹣km)+m2+(km+2)2=4(k2﹣km)+m2+k2m2+4km+4=(4+m2)(k2+1),∴|QD|=,|QE|=,∴(4+m2)=≥4,当m=0时,即Q(0,﹣1)时,△QDE的面积S取得最小值4.点评:本题考查了直线与抛物线相切的性质、切线方程、相互垂直的斜率之间的关系、两点之间的距离公式、三角形的面积计算公式、二次函数的性质,考查了推理能力与计算能力,属于难题.14.(2015•郴州二模)如图所示,已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.(1)求证:以AF为直径的圆与x轴相切;(2)设抛物线x2=4y在A,B两点处的切线的交点为M,若点M的横坐标为2,求△ABM的外接圆方程:(3)设过抛物线x2=4y焦点F的直线l与椭圆+=1的交点为C、D,是否存在直线l使得|AF|•|CF|=|BF|•|DF|,若存在,求出直线l的方程,若不存在,请说明理由.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(1)如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x轴.利用抛物线的定义及梯形的中位线定理可得可得r====|O1O2|,即可证明;(2)设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).与抛物线方程联立化为x2﹣4kx﹣4=0,可得根与系数的关系,由x2=4y,可得.可得k MA•k MB==﹣1,可得△MAB为直角三角形,可得△MAB的外接圆的圆心为线段AB的中点.设线段AB的中点为P,可得⊙P与抛物线的准线相切,切点为点M,利用中点坐标公式与根与系数的关系可得圆心P(2,3),半径r=|MP|=|3﹣(﹣1)|=4,即可得出所求的△MAB的外接圆的方程.(3)假设存在直线l使得|AF|•|CF|=|BF|•|DF|,设=λ,可得,,设C(x3,y3),D (x4,y4).利用向量的坐标运算可得x1=﹣λx2,x4=﹣λx3.把x1=﹣λx2代入根与系数的关系可得.把y=kx+1代入椭圆方程可得(3k2+6)x2+6kx﹣1=0,把根与系数的关系与x4=﹣λx3联立可得,联立解得即可.解答:(1)证明:如图所示,设线段AF的中点为O1,过O1作O1O2⊥x轴,垂足为点O2,作AA1⊥x轴.则r====|O1O2|,∴r=|O1O2|,∴以AF为直径的圆与x轴相切;(2)解:设直线AB的方程为y=kx+1,A(x1,y1),B(x2,y2).联立,化为x2﹣4kx﹣4=0,∴x1+x2=4k,x1x2=﹣4.。
高二数学抛物线试题答案及解析

高二数学抛物线试题答案及解析1.过抛物线y2=4x的焦点F作倾斜角为的直线,它与抛物线交于A、B两点,求这两点间的距离.【答案】8【解析】抛物线y2=4x的焦点为F(1,0),则过焦点的直线的参数方程可设为(t为参数),将其代入抛物线方程并化简得t2+4t-8=0,由参数t的几何意义可知|AB|=|t1-t2|=8.试题解析:抛物线y2=4x的焦点为F(1,0),设过焦点F(1,0),倾斜角为π的直线的参数方程为(t为参数),将此代入y2=4x,得t2+4t-8=0,设这个方程的两个根为t1,t2,由根与系数的关系,有t 1+t2=-4,t1·t2=-8,∴|AB|=|t1-t2|====8.∴A、B两点间的距离是8.【考点】参数方程的应用2.准线为的抛物线的标准方程是()A.y2=﹣4x B.y2=﹣8x C.y2=4x D.y2=8x【答案】B【解析】设抛物线方程为,准线方程,解得,抛物线方程【考点】抛物线方程的应用.3.已知直线和直线,则抛物线上的动点到直线和的距离之和的最小值为___________.【答案】【解析】设抛物线上的动点的坐标为,它到到直线和的距离之和为,则=,当时,.【考点】直线与抛物线的位置关系及二次函数的最值.4.已知抛物线的方程为,直线l过定点,斜率为k.当k为何值时,直线l与该抛物线:只有一个公共点;有两个公共点;没有公共点?【答案】当,或,此时直线l与该抛物线只有一个公共点;当,此时直线l 与该抛物线有两个公共点;当或,此时直线l与该抛物线没有公共点.【解析】解题思路:联立直线方程与抛物线方程,得到关于的一元二次方程,利用判别式的符号判定直线与抛物线的交点个数.规律总结:解决直线与圆锥曲线的交点个数,一般思路是联立直线与圆锥曲线的方程,整理得到关于或的一元二次方程,利用判别式的符号进行判定.注意点:当整理得到的一元二次方程的二次项系数为字母时,要注意讨论二次项系数是否为0.试题解析:直线l的方程为,联立方程组得.①当时,知方程有一个解,直线l与该抛物线只有一个公共点.②当时,方程的判别式为,若,则或,此时直线l与该抛物线只有一个公共点.若,则,此时直线l与该抛物线有两个公共点.若,则或,此时直线l与该抛物线没有公共点.综上:当,或,此时直线l与该抛物线只有一个公共点;当,此时直线l与该抛物线有两个公共点;当或,此时直线l与该抛物线没有公共点.【考点】直线与抛物线的交点个数.5.已知点,直线,动点P到点F的距离与到直线的距离相等.(1)求动点P的轨迹C的方程;(2)直线与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.【答案】(1);(2)或。
高三数学抛物线试题答案及解析

高三数学抛物线试题答案及解析1.过抛物线的焦点作直线与此抛物线相交于、两点,是坐标原点,当时,直线的斜率的取值范围是()A.B.C.D.【答案】D【解析】由题可知,点的横坐标时,满足,此时,故直线(即直线)的斜率的取值范围是.故选D.【考点】抛物线的几何性质以及直线与抛物线的位置关系.2.抛物线y=ax2的准线方程为y=1,则实数a的值为()A.4B.C.D.-4【答案】C【解析】将抛物线方程改写为,可知由准线方程为,可得,即解得,选C【考点】抛物线的方程及其准线方程3.直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( ) A.B.2C.D.【答案】C【解析】∵抛物线方程为x2=4y,∴其焦点坐标为F(0,1),故直线l的方程为y=1.如图所示,可知l与C围成的图形的面积等于矩形OABF的面积与函数y=x2的图象和x轴正半轴及直线x=2围成的图形的面积的差的2倍(图中阴影部分的2倍),即S=4-2=4-2·=4-=.4.已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线C:x2=2py(p>0)上运动,MN为圆O′在x轴上所截得的弦.(1)当O′点运动时,|MN|是否有变化?并证明你的结论;(2)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.【答案】(1)|MN|不变化,其定值为2p 见解析(2)见解析【解析】(1)设O′(x0,y),则x2=2py(y≥0),则⊙O′的半径|O′A|=,⊙O′的方程为(x-x0)2+(y-y)2=x2+(y-p)2,令y=0,并把x02=2py,代入得x2-2xx+x2-p2=0,解得x1=x-p,x2=x+p,所以|MN|=|x1-x2|=2p,这说明|MN|不变化,其定值为2p.(2)不妨设M(x0-p,0),N(x+p,0).由题2|OA|=|OM|+|ON|,得2p=|x0-p|+|x+p|,所以-p≤x≤p.O′到抛物线准线y=-的距离d=y+=,⊙O′的半径|O′A|===.因为r>d⇔x04+4p4>(x2+p2)2⇔x2<p2,又x2≤p2<p2(p>0),所以r>d,即⊙O′与抛物线的准线总相交.5.已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足·=0,设P为弦AB的中点.(1)求点P的轨迹T的方程;(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.【答案】(1)x2-x+y2=4(2)存在,(1,-2)和(1,2)【解析】(1)连接CP、OP,由·=0,知AC⊥BC,∴|CP|=|AP|=|BP|=|AB|.由垂径定理知|OP|2+|AP|2=|OA|2,即|OP|2+|CP|2=9.设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,化简,得到x2-x+y2=4.(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中=1,∴p=2,故抛物线方程为y2=4x.由方程组,得x2+3x-4=0,解得x1=1,x2=-4,由于x≥0,故取x=1,此时y=±2.故满足条件的点存在,其坐标为(1,-2)和(1,2).6.在平面直角坐标系中,点到点的距离比它到轴的距离多1,记点的轨迹为. (1)求轨迹为的方程(2)设斜率为的直线过定点,求直线与轨迹恰好有一个公共点,两个公共点,三个公共点时的相应取值范围.【答案】(1);(2)当时直线与轨迹恰有一个公共点;当时,故此时直线与轨迹恰有两个公共点;当时,故此时直线与轨迹恰有三个公共点.【解析】(1)设点,根据条件列出等式,在用两点间的距离公式表示,化简整理即得;(2)在点的轨迹中,记,,设直线的方程为,联立方程组整理得,分类讨论①时;②;③或;④,确定直线与轨迹的公共点的个数.(1)设点,依题意,,即,整理的,所以点的轨迹的方程为.(2)在点的轨迹中,记,,依题意,设直线的方程为,由方程组得①当时,此时,把代入轨迹的方程得,所以此时直线与轨迹恰有一个公共点.当时,方程①的判别式为②设直线与轴的交点为,则由,令,得③(ⅰ)若,由②③解得或.即当时,直线与没有公共点,与有一个公共点,故此时直线与轨迹恰有一个公共点.(ⅱ)若或,由②③解得或,即当时,直线与有一个共点,与有一个公共点.当时,直线与有两个共点,与没有公共点.故当时,故此时直线与轨迹恰有两个公共点.(ⅲ)若,由②③解得或,即当时,直线与有两个共点,与有一个公共点.故当时,故此时直线与轨迹恰有三个公共点.综上所述,当时直线与轨迹恰有一个公共点;当时,故此时直线与轨迹恰有两个公共点;当时,故此时直线与轨迹恰有三个公共点.【考点】两点间的距离公式,抛物线方程,直线与抛物线的位置关系.7.抛物线的准线方程是()A.B.C.D.【答案】A【解析】题中抛物线的标准形式为,则其准线方程为,故先A.【考点】1.抛物线的准线方程.8.在平面直角坐标系中,抛物线上纵坐标为2的一点到焦点的距离为3,则抛物线的焦点坐标为.【答案】【解析】由题意,,因此焦点为.【考点】抛物线的性质.9.(12分)(2011•福建)如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.(Ⅰ)求实数b的值;(Ⅱ)求以点A为圆心,且与抛物线C的准线相切的圆的方程.【答案】(Ⅰ)b=﹣1(Ⅱ)(x﹣2)2+(y﹣1)2=4【解析】(I)由,得:x2﹣4x﹣4b=0,由直线l与抛物线C相切,知△=(﹣4)2﹣4×(﹣4b)=0,由此能求出实数b的值.(II)由b=﹣1,得x2﹣4x+4=0,解得x=2,代入抛物线方程x2=4y,得点A的坐标为(2,1),因为圆A与抛物线C的准线相切,所以圆A的半径r等于圆心A到抛物线的准线y=﹣1的距离,由此能求出圆A的方程.解:(I)由,消去y得:x2﹣4x﹣4b=0①,因为直线l与抛物线C相切,所以△=(﹣4)2﹣4×(﹣4b)=0,解得b=﹣1;(II)由(I)可知b=﹣1,把b=﹣1代入①得:x2﹣4x+4=0,解得x=2,代入抛物线方程x2=4y,得y=1,故点A的坐标为(2,1),因为圆A与抛物线C的准线相切,所以圆A的半径r等于圆心A到抛物线的准线y=﹣1的距离,即r=|1﹣(﹣1)|=2,所以圆A的方程为:(x﹣2)2+(y﹣1)2=4.点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.10.过抛物线C:上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.(1)求抛物线C的方程及点M的坐标;(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求面积的最大值.【答案】(1)y2=8x,(2,4);(2).【解析】本题主要考查抛物线的标准方程及其几何性质、韦达定理、点到直线的距离、三角形面积公式、利用导数求函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由题意结合抛物线图象得到M点坐标,代入抛物线方程中,解出P的值,从而得到抛物线的标准方程及M点坐标;第二问,设出A,B点坐标,利用M点,分别得到直线MA和直线MB的斜率,因为两直线倾斜角互补,所以两直线的斜率相加为0,整理得到y1+y2=-8,代入到中得到直线AB的斜率,设出直线AB的方程,利用M点在直线AB上方得到b 的范围,令直线与抛物线方程联立,图形有2个交点,所以方程的进一步缩小b的范围,,而用两点间距离公式转化,d是M到直线AB的距离,再利用导数求面积的最大值.(1)抛物线C的准线x=-,依题意M(4-,4),则42=2p(4-),解得p=4.故抛物线C的方程为y2=8x,点M的坐标为(2,4), 3分(2)设.直线MA的斜率,同理直线MB的斜率.由题设有,整理得y1+y2=-8.直线AB的斜率. 6分设直线AB的方程为y=-x+b.由点M在直线AB的上方得4>-2+b,则b<6.由得y2+8y-8b=0.由Δ=64+32b>0,得b>-2.于是-2<b<6. 9分,于是.点M到直线AB的距离,则△MAB的面积.设f(b)=(b+2)(6-b)2,则f¢(b)=(6-b)(2-3b).当时,f¢(x)>0;当时,f¢(x)<0.当时,f(b)最大,从而S取得最大值. 12分【考点】抛物线的标准方程及其几何性质、韦达定理、点到直线的距离、三角形面积公式、利用导数求函数的最值.11.(2011•浙江)已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M(1)求点M 到抛物线C 1的准线的距离;(2)已知点P 是抛物线C 1上一点(异于原点),过点P 作圆C 2的两条切线,交抛物线C 1于A ,B 两点,若过M ,P 两点的直线l 垂直于AB ,求直线l 的方程.【答案】(1)(2)【解析】(1)由题意画出简图为:由于抛物线C 1:x 2=y 准线方程为:y=﹣,圆C 2:x 2+(y ﹣4)2=1的圆心M (0,4), 利用点到直线的距离公式可以得到距离d==.(2)设点P (x 0,x 02),A (x 1,x 12),B (x 2,x 22); 由题意得:x 0≠0,x 2≠±1,x 1≠x 2,设过点P 的圆c 2的切线方程为:y ﹣x 02=k (x ﹣x 0)即y=kx ﹣kx 0+x 02① 则,即(x 02﹣1)k 2+2x 0(4﹣x 02)k+(x 02﹣4)2﹣1=0设PA ,PB 的斜率为k 1,k 2(k 1≠k 2),则k 1,k 2应该为上述方程的两个根, ∴,;代入①得:x 2﹣kx+kx 0﹣x 02="0" 则x 1,x 2应为此方程的两个根, 故x 1=k 1﹣x 0,x 2=k 2﹣x 0 ∴k AB =x 1+x 2=k 1+k 2﹣2x 0=由于MP ⊥AB ,∴k AB •K MP =﹣1⇒故P ∴.12. 过抛物线x 2=2py(p>0)焦点的直线与抛物线交于不同的两点A 、B ,则抛物线上A 、B 两点处的切线斜率之积是( )A.P 2B.-p 2C.-1D.1 【答案】C【解析】设A(x 1,y 1),B(x 2,y 2) ∵=x,∴过A 点的切线斜率为x 1, 过B 点的切线斜率为x 2, ∴过抛物线上A 、B 两点处的切线斜率之积是x 1x 2,设过抛物线焦点的直线方程为y=kx+与x 2=2py 联立消去y 得 x 2-2kpx-p 2=0x 1x 2=-p 2x 1x 2=-1.13. 抛物线的焦点坐标为 . 【答案】【解析】由于,焦点在轴的正半轴,所以,抛物线的焦点坐标为.【考点】抛物线的几何性质.14.抛物线的焦点坐标是( )A.B.C.(0,1)D.(1,0)【答案】C【解析】解抛物线的标准方程为,所以抛线以轴为对称轴,开口向上,且,,所以焦点坐标为,故选C.【考点】抛物线的标准方程与简单几何性质.15.已知抛物线的准线与x轴交于点M,过点M作圆的两条切线,切点为A、B,.(1)求抛物线E的方程;(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.【答案】(1)y2=4x;(2)点N坐标为或.【解析】本题主要考查抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质等基础知识,考查学生分析问题解决问题的能力和计算能力.第一问,利用抛物线的准线,得到M点的坐标,利用圆的方程得到圆心C的坐标,在中,可求出,在中,利用相似三角形进行角的转换,得到的长,而,从而解出P的值,即得到抛物线的标准方程;第二问,设出N点的坐标,利用N、C点坐标写出圆C的方程,利用点C的坐标写出圆C的方程,两方程联立,由于P、Q是两圆的公共点,所以联立得到的方程即为直线PQ的方程,而O点在直线上,代入点O的坐标,即可得到s、t的值,即得到N点坐标.试题解析:(1)由已知得,C(2,0).设AB与x轴交于点R,由圆的对称性可知,.于是,所以,即,p=2.故抛物线E的方程为y2=4x. 5分(2)设N(s,t).P,Q是NC为直径的圆D与圆C的两交点.圆D方程为,即x2+y2-(s+2)x-ty+2s=0.①又圆C方程为x2+y2-4x+3=0.②②-①得(s-2)x+ty+3-2s=0.③ 9分P,Q两点坐标是方程①和②的解,也是方程③的解,从而③为直线PQ的方程.因为直线PQ经过点O,所以3-2s=0,.故点N坐标为或. 12分【考点】抛物线的标准方程及其几何性质、圆的标准方程及其几何性质、圆的切线的性质.16.若抛物线的焦点在直线上,则_____;的准线方程为_____.【答案】;.【解析】抛物线的焦点坐标为,该点在直线上,则有,解得,此时抛物线的准线方程为.【考点】抛物线的几何性质17.已知直线和直线,抛物线上一动点到直线和直线的距离之和的最小值是()A.B.2C.D.3【答案】B【解析】由题可知是抛物线的准线,设抛物线的焦点为,则动点到的距离等于,则动点到直线和直线的距离之和的最小值,即焦点到直线的距离,所以最小值是,故选【考点】抛物线的定义。
高考数学一轮复习抛物线专题练习(含答案)

高考数学一轮复习抛物线专题练习(含答案)【常规证法】抛物线y2=2px(p0)的焦点为F,显然直线AB 的斜率不为0,当AB斜率不存在时,直线AP方程为x=,不妨设A在第一象限,则易知A,B,C,此时kOA==2,kOC==2.kOA=kOC,A,O,C三点共线,即直线AC经过原点O.当AB斜率存在且不为0时,设直线AB方程为y=k代入y2=2px 得k2x2-(k2+2)px+=0,设A(x1,y1),B(x2,y2),则x1x2=,(y1y2)2=p4,由题意知y1y20,y1y2=-p2kOC======kOA直线AC过原点O,综上,直线AC经过原点O.【巧妙证法】因为抛物线y2=2px(p0)的焦点为F,而直线AB的斜率不为零,所以经过点F的直线AB的方程可设为x=my+.代入抛物线方程消去x得y2-2pmy-p2=0.若记A(x1,y1),B(x2,y2),则y1,y2是该方程的两个根,所以y1y2=-p2.因为BCx轴,且点C在准线x=-上,所以点C的坐标为,故直线CO的斜率为k===,即k也是直线OA的斜率,所以直线AC经过原点O.3.(2019南师附中检测)设A(x1,y1),B(x2,y2)为抛物线y2=2px(p0)上位于x轴两侧的两点.(1)若y1y2=-2p,证明直线AB恒过一个定点;(2)若p=2,AOB(O是坐标原点)为钝角,求直线AB在x轴上的截距的取值范围.[解] (1)设直线AB在x轴上的截距为t,则可设直线AB的方程为x=my+t.代入y2=2px得y2=2p(my+t),即y2-2pmy-2pt=0,于是-2p=y1y2=-2pt,所以t=1,即直线AB 恒过定点(1,0).(2)因为AOB为钝角,所以0,即x1x2+y1y20.y=2px1,y=2px2,yy=2px12px2,于是x1x2===t2,故x1x2+y1y2=t2-2pt=t2-4t.解不等式t2-4t0,得00)把点P(-2,-4)代入得(-4)2=-2p(-2).解得p=4,抛物线方程为y2=-8x.当焦点在y轴负半轴上时,设方程为x2=-2py(p0),把点P(-2,-4)代入得(-2)2=-2p(-4).解得p=.抛物线方程为x2=-y.综上可知抛物线方程为y2=-8x或x2=-y.[答案] y2=-8x或x2=-y4.(2019广东高考)已知抛物线C的顶点为原点,其焦点F(0,c)(c0)到直线l:x-y-2=0的距离为.设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.(1)求抛物线C的方程;(2)当点P(x0,y0)为直线l上的定点时,求直线AB的方程;(3)当点P在直线l上移动时,求|AF||BF|的最小值.[解题思路] (1)由点到直线的距离求c的值,得到F(0,c)后可得抛物线的方程;(2)采用设而不求策略,先设出A(x1,y1),B(x2,y2),结合导数求切线PA,PB的方程,代入点P 的坐标,根据结构,可得直线AB的方程;(3)将|AF||BF|转化为关于x(或y)的函数,再求最值.[解] (1)依题意,设抛物线C的方程为x2=4cy(c0),由点到直线的距离公式,得=,解得c=1(负值舍去),故抛物线C的方程为x2=4y.(2)由x2=4y,得y=x2,其导数为y=x.设A(x1,y1),B(x2,y2),则x=4y1,x=4y2,切线PA,PB的斜率分别为x1,x2,所以切线PA的方程为y-y1=(x-x1),即y=x-+y1,即x1x-2y-2y1=0.同理可得切线PB的方程为x2x-2y-2y2=0.因为切线PA,PB均过点P(x0,y0),所以x1x0-2y0-2y1=0,x2x0-2y0-2y2=0,所以和为方程x0x-2y0-2y=0的两组解.所以直线AB的方程为x0x-2y-2y0=0.(3)由抛物线定义可知|AF|=y1+1,|BF|=y2+1,所以|AF||BF|=(y1+1)(y2+1)=y1y2+(y1+y2)+1.由消去x并整理得到关于y的方程为y2+(2y0-x)y+y=0.由一元二次方程根与系数的关系得y1+y2=x-2y0,y1y2=y.所以|AF||BF|=y1y2+(y1+y2)+1=y+x-2y0+1.又点P(x0,y0)在直线l上,所以x0-y0-2=0,即x0=y0+2,所以y+x-2y0+1=2y+2y0+5=22+,所以当y0=-时,|AF||BF|取得最小值,且最小值为.2019年高考数学一轮复习抛物线专题练习及答案的所有内容就为考生分享到这里,查字典数学网请考生认真练习。
