吸振器
第十二讲—动力吸振器
切向无外力,故切向加速度为0
( ) Rθ cosϕ + Rθ 2 sinϕ + r θ +ϕ = 0
cosϕ ≈ 1,sinϕ ≈ ϕ,θ ≈ ω
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
单摆运动方程
16
机械与运载工程学院
单摆运动方程 单摆固有频率
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
x2
无阻尼动力吸振器系统
m2
m1、 k1:主系统的质量和弹簧刚度
k2 x1
m1 上作用有简谐激振力
F1 sin ωt
m1
阻尼动力吸振器:
k1
质量 m2 弹簧 k2
4
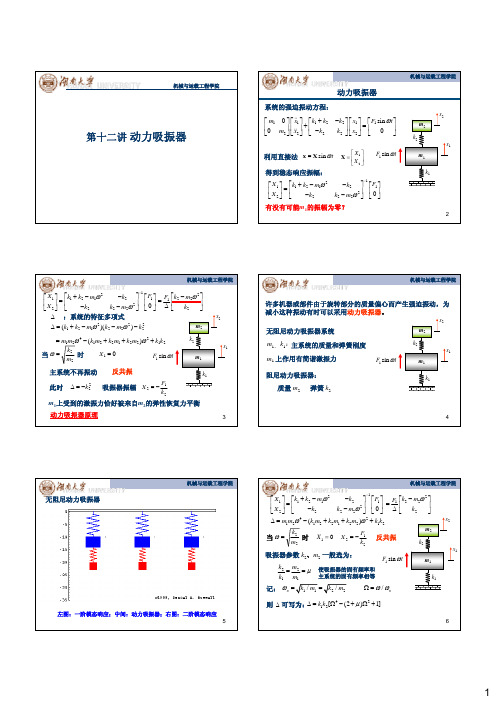
无阻尼动力吸振器
机械与运载工程学院
左图:一阶模态响应;中间:动力吸振器;右图:二阶模态响应 5
机械与运载工程学院
⎡ ⎢⎣
X1 X2
⎤ ⎥⎦
⎡X1 ⎤
⎢ ⎣
X
2
⎥ ⎦
=
F1 Δ
⎡⎢k2 ⎣
− m2ω k2
2
⎤ ⎥ ⎦
X 0 = F1 / k1
X1 =
1− Ω2
X 0 Ω4 − (2 + μ)Ω2 +1
X2 =
1
X0 Ω4 − (2 + μ)Ω2 +1
7
机械与运载工程学院
4 X1 / X0
2
X2 / X0
μ = 0.3 X1 =
1− Ω2
反共振
动力吸振器自

第22卷第324期2007年8月实 验 力 学J OU RNAL OF EXPERIM EN TAL M ECHANICSVol.22No.324Aug.2007文章编号:100124888(2007)03&0420429206磁流变弹性体自调谐式吸振器及其优化控制3王莲花,龚兴龙,邓华夏,倪正超,孔庆合(中国科学技术大学力学和机械工程系,中国科学院材料力学行为与设计重点实验室,安徽合肥230027)摘要:本文研制了一种基于磁流变弹性体的自调谐式吸振器,它利用磁流变弹性体这种新型智能材料作为吸振器的弹性元件和阻尼元件,通过外加磁场控制磁流变弹性体的剪切模量来改变吸振器的固有频率,实现吸振器的移频。
并将遗传算法改进移植到吸振器,对其进行优化控制。
实验结果表明,这种遗传算法具有全局搜索和快速收敛的特点,它能使吸振器快速找到吸振器减振效果最佳点,并且经过优化控制的磁流变弹性体自调谐式吸振器在移频范围内具有很好的减振效果,减振效果最高可达25dB。
关键词:磁流变弹性体;动力吸振器;振动控制;遗传算法中图分类号:O34;X593 文献标识码:A0 引言 动力吸振器自1911年问世以来[1],在实践中得到了广泛的应用。
它通过在需要减振的结构(称为主系统)上附加子结构,改变系统的振动能量的分布和传递特性,使振动能量转移到附加的子结构上,从而达到控制主系统振动的目的。
传统的动力吸振器多属被动控制,它对于主系统的窄带响应有着良好的吸振效果,但由于其吸振带宽不可调节,对于宽频激励引起的主系统的振动,吸振效果不是很理想。
近年来,对于主动吸振器的大量研究表明,主动吸振器可以根据主系统的振动状态,自动调节自身的结构参数或振动状态,实现宽频吸振,提高了吸振器减振效果,大大拓宽了吸振器的应用范围。
根据吸振器自动调节机理的不同,主动吸振器可分为全主动式吸振器和半主动式吸振器。
全主动式吸振器是根据主系统的振动状态反馈调节吸振器的振动状态,使其对主系统的动态作用力与主系统的振动加速度反相,从而实现主系统实时宽频振动控制。
阻尼动力吸振器减振问题的进一步研究

阻尼动力吸振器减振问题的进一步研究阻尼动力吸振器减振问题的进一步研究伍良生华中理工大学).塑二l=丑张阿舟(南京航空学院)丁?f摘要口有阻尼单自由度主系统,多自由度主系统可通过安装单个或多个吸振器来抑制其振动.为使系统指定点处的最大响应在某一频带内处于某一预先指定的范围,本文提出了决定吸振器匾量比,固有频率和阻尼比等参数的优化设计方法.一引言动力吸振器长期以来一直被证明是非常有效的减振手段之一.它的基本设计原理为许多学者所研究‟.],并且被广泛甩应用于工程设计实践中.然而可以说,到目前为止对它的研究还远没有完善.:~~首先,当用于单自由度主系统减振时,基于不动点原理的动力吸振器的设计方法一般都假定主系统是无阻尼的,但实际结构却往往存在一定的阻尼.为了提高吸振器的教能,不少学者进行了在一个单自由度主系统上附加多个动力吸振器的研究”“.从工程应用的观点来说,在这方面仍有很多有意义的工作要做. 多自由度主系统由于本身的复杂性,很多减振研究工作主要是针对系统的某一模态进行的,且只是在系统的某点附加一个动力吸振器.实际问题中,由于结构上的原因或使用的合理性.往往要求在几个点附加动力吸振器对系统的某一模态进行减振.对具有模态耦合的一般多自由度系统来说,其减振问题的研究则是一个较新的领域.这方面已有的工作的特点是:或者是对主系统一减振器组成的复合系统进行重复的动态性能计算,以得到吸振器参数,或者只是对一些比较特殊的结构作简化处理.本文以上述问题为背景,并直接以对系统的振动控制要求为出发点,较系统地提出了一套吸振器参数的优化设计方法.二有阻尼单自由度主系统安装单个动力吸振器有阻尼单自由度主系统附加一个动力吸振器的模型如图1所示.图中各符号的意义为K——主系统弹簧系数M——主系统质量C——主系统阻尼系数K——吸振器弹簧系数M——吸振器质量振动与冲击Cz——吸振器阻尼系数.再引入记号,—M/M.表示吸振器质量与主质量之比.设计问题的提法是:在一定的质量比下,确定吸振器的弹簧系数Kz和阻尼系数c,使主质量M在力F作用下的位移在全频带上的最大值最小.系统的运动方程为:.fxl-+-C1X-+-K1Xl—F(t)一M2-X;,一.(1)1%X2__C!(X2一X)一K2(X2一X.)一0设F(t)=FeX1=X】e2一X2引入放大因子3,使IX=?,可推得:卢一l登图l(2)上式中各记号的意义为:——主系统的固有频率P——吸振器的固有频率——主系统的阻尼比一C/2M——吸振器的阻尼比,一Cz/2MP(2)式中只有两个未知量P和≮,使在全频段上的最大值为最小的P 和即为最优解,具体计算可按如下步骤进行:1.在主系统固有频率的邻域内取一频段:ct,≤ct,≤(1jb,ct,.和(1jb可根据具体情况选定,一般可取=0.7,=13;2选定P,的初值,计算指定频带内的的最大Max~](P,);3.变更P,,直至求出Max~](P,)的极小值,则此时的P,即为最优解.三单自由度主系统安装多个动力吸振器吸振器由于其固有频率与主系统的固有频率很接近,吸振质量产生较大位移和速度.由于吸振器是有阻尼的,消耗的能量也较大,从而使主系统的振动得到抑制.若在一个单自由度主系统上并联安装若干个吸振器,使这些吸振器频率按一定的间隔错开,则在这些吸振器的总质量与原来单个吸振器的质量相同的情况下,主系统的振动将得到进一步降低.图2表示在一个单自由度主系统上并联安装s个动力吸振器的情况.引入放大因子,使Ix一0?,其中F表示简谐激振力的幅值,x表示主质量M的复振幅.类似上节的推导可得;一第l期阻尼动力吸振器减振问题的进一步研究一1+2篆.1意上式中各记号的意义为:——主系统的固有频率P.——各吸振器的固有频率—量比一般只需要附加一个吸振器时质量比的80左右,而附加三个吸振器时的质量比一般只需要附加一个吸振器时的质量比的70左右.因此,在可能情况下应尽量采用多个动力吸振器,只要适当地调整吸振器的固有频率和阻尼比,特别是使吸振器的固有频率错开一定值,就能得到耩意的结果. 表1不同质量比的放大因子值单十吸振器两个吸振器三个吸振器10.O38.207.296.90.047.156.356.1j0.056.405.7C.5.5O.065.86j.2l5.03O.075.544.844.60O.085.114.554.320.094.824.294.090.104.584.093.090.114.393.913.780.124.2l3.763.620.134.053.623.460.143_923.0380.153.793.393230.163.683.3O3.190.173.583.2l3.1l0.183.493.133.000.193.4O3.052.910.203.322.982.8402】3242.922.790.223.172.862.73O.233.112.812.680.243.02.762.620.253.002_712.58振动与冲击/J\/一.一一,.图3分别附加一个和两个动力吸振器时的放大因子1.附加一个动力吸振器2.附加两个动力吸振器四多自由度系统单模态振动控制对于多自由度系统,若各阶固有频率相隔较远,通常可忽略各模态之间的相互影响,在振动控制时,将各模态分别处理设多自由度系统的运动方程为:十一Ky—F(4)引入坐标变换Y一朔(5)其中为模态矩阵.将(5)代入(4),且(4)的两边都前乘甲下,可推得M1.+G0.+K.q一F(一1,2,…)(6)其中,M.CK..F分别表示第i阶模态质量,模态阻尼,模态刚度和模态力,方程(6)与单自由度系统的运动方程形式相同,它对应于系统第i阶模态的振动,在进行减振设计时,可用类似于单自由度主系统的方法处理对连续型主系统也可作类似处理以下分两种情况来研究单模态的减振问题.1.安装单个动力吸振器的单横态减振此时减振设计问题的提法为:在多自由度主系统上附加一个动力吸振器,确定吸振器的质量,固有频率和阻尼比,使对应于主系统第i阶模态的最大响应处于一个预先指定的范围.具体步骤为:(1)设在第J个坐标处安装动力吸振器,取第i阶振型为:{)一[纯仇.…1…儡(7)第i阶模态质量为;第1期阻尼动力吸振器碱振问题的进一步研究=m辑一…+m+…+m簖,(8)由(8)式可看出,当取第j点的质量为原来的值时,其余各点处的质量都必须乘上一个因子,例如第r点处应乘上因子秣,因此,M可理解为第i阶模态在第j点处的等效质量.类似地可对Kc进行讨论.(2)确定系统最大响应点允许的响应值范围,设最大响应点为第j点: X…∈(D—A,D+△)由x,一%.?q,则Q.一X…Q…∈(D一△,D+△)其中Q…表示最大模态坐标允许值,D表示允许的最大响应值,△表示其允许误差.(3)由公式Q=F/K决定对应于模态坐标的等效静位移值,再由公式&一Q…/Q|.决定放大因子(4)根据&值由表1查出所需要的质量比则吸振质量rll可取为:ma一M,.(5)应用单自由度主系统单吸振器的设计公式,决定吸振器的固有频率和阻尼比.1z…丁:P一/3一8(1+)若主系统是有阻尼的.则上述第(4),(5)二步应参照本文第二节进行.2.安装多个并联动力吸振器的单模态减振工程中的大型结构.往往在控制某一模态的振动时也需要在若干不同点分别附加动力吸振器.这类问题可归结为本文第三节逛一个单自由度主系统上并联多个动力吸振器的情况a假设需在r个点附加吸振器,具体设计步骤为:(1)确定吸振器的安装位置和最优控制力按文献[8]提供的方法确定r个吸振器的安装位置和最优控制力u1,u.-,u.(2)确定各吸振器的质量先按前面第三小节的方法确定总模态吸振质量m,再求出对应于各减振点的模态质量m.mm可按各点最优控制力的大小分配.“=∑”%一∑‟(9)m=m告(10)l”各点处的实际减振质量可按下式求得m—/蠢,(11)(3)确定各吸振器的P,℃值加上各吸振器后.设计问题可描述为:在对应于第i阶模态的等效单自由度系统上附加r个动力吸振器.它们的等效质量分别为Ma,使得在等效激振力作用下.坐标q,的最大响应值最小.设振动与冲击计模型与图2相似,具体设计可按类似本文第三节的方法进行,即对放大园子口进行优化计算,使口的最大值最小,即可得到各吸振器的最优P,的值.现举一例加以说明..图4所示为一简支梁,有关尺寸及参数见图.设在梁的中部作用一力F一49sinmtN.现需在A.B处各附加一个吸振器,使梁中点处对应于一阶模态的振动量在0.0005m左右.4对应于一阶模态的运动方程为i6.3询l+38100ocl一49sin~t最大模态静位移为Q:l一面4丽9一..O0013m模态放大园子为:p一89由表l查得模态质量比约为0.14.由于结构的对称性,可算碍A,B处的模态吸振质量均为1.14kg,实际的吸振质量均为1.71kg,吸振器的固有频率和阻尼比可算得为=13]rad/secP一146rad/sech一0.i2一0.095五多自由度系统多模态振动控制多自由度系统多模态振动控制主要有两种情况.第一种情况是外界激励频率复盖系统的多个固有频率,但这些固有频率彼此相隔较远,可以分别地当作单自由度系统处理,减振设计可按前面第四节的方法进行.第二种情况是外界激励频率复盖系统的多个固有频率,且这些固有频率相隔较近研究表明,当相邻固有频率的比值小于2时,各模态的相互影响很明显,不能将它们分开处理.这种情况下的减振设计可按以下步骤进行:1.按文献[8]提供的方法确定吸振器的最优安装位置和最优控制力2.确定各动力吸振器的质量m通常可用几个吸振器分别控制系统不同模态的振动,因此确定ma可按第四节的方法进行,由于各模态之间存在耦合,这样确定的m与真正的m之间会存在一定误差,但由于预先给定的响应水平也有一定范围,因此,可以经过试算对各吸振器质量作一定调整.3.进行优化计算确定各吸振器的P,值比较有效的方法是最小范数法..假定已求出最优控制力向量为u(t).由吸振器产生的对系统第1期阻尼动力吸振器减振问题的进一步研究7的作用力向量为s(t),定义误差激励向量e(t)(£)=s(£)一”“)将频率离散化,则Eu一5()一”()处激振频率为OOj时S(t)和U(t)的幅值.定义范数厂_IE一√(r为离散频率个数)其中El∑W…E(m为减振点的个数)—I上式中w是加权因子,一般可取为,当j固定时,第i个减振点处的位移帽值X.()通过使|IEI『取极小值的优化计算可求得吸振器的各参数.(本文于1991年9月14日收到)参考文献[1]J.P.DenHartogtMechaniealVibration,Mcgraw—Hill,l956—2]F.M.LewistExtendedTheoryoftheV[scoUNV[brationDamper,ASM EJournalofAppliedMechaniest22-377—389,1955[3]G.B.WarburlontOptimumAbsouberParametersforMinimizingVibratio nResponse,EarthquakeEng一gtStrut.Dynam,9,251—262,1981[4J.C.Snowdon,DynamicVibrationAbsorbersThatHaveIncreasedEffecti veness,Journa10fEngineeringforIndustry,96,840—945,l974[5:KazutoSETO.KouichiIWANAMI.AnInvestigationoftheVibrationIsol atorEquippedWithDualDynamicDampersas日DampingElement,IstReport-0ptimumAdjustmentConditionforDualDyna micDampers,Bulletin0ftheJSME.VOL.24,Nol97,NOVl982:6]碉千里,.多维动力吸振器对复杂悬臀结构减振之应用《航空》,第3卷No.2,1982-7]《振动控制》,南京航空学院振动工程研究所《振动控制》编写组,1987-8]伍良生,厩仲权,张阿舟,”具有多个主振模态振动系统的减振优化设计”,《振动工程》,VOI.3No.41990AFURTHERINVESTIGA TIONOFUSINGDYNAMICVIBRA T10N ABS0RBERT0REDUCEVIBRA T10NWuLiangsheng (HuazhongUniversityofScienceandTechnology)AbstractGuZhongquanZhangAzhou (NanjJngAeronauticalInstitute) Thispaperfurtherinvestigatestheproblemofusingdynamicvibrationabsorb ertoreducevi—bration,whichismainlyengagedinthecaseofinstallingoneorseveraldynami cvibrationab—sorbersonasystermofsingledegreeormultipledegreesoffreedom.Themaxi mumresponseina frequencydomainofasystemisstipulatedbeforehandinapermissivedomain ofamplitude.Theparametersoftheabsorbers.suchasmassratio,naturalfrequencyanddampin gratio,canbe determinedbyoptimizationproceduresaccordingtodifferentsystemandvib rationreductionde—mand.。
动力吸振器原理

动力吸振器原理《神奇的动力吸振器原理》嘿,朋友们!今天咱来聊聊一个挺有意思的东西,那就是动力吸振器。
你说这动力吸振器啊,就像是一个特别会安抚的小精灵。
想象一下,你正在被一些烦人的振动困扰,就好像你走在路上,地面老是晃来晃去让你站不稳。
这时候动力吸振器就出现啦!它能把那些让你不舒服的振动给“吸”走,让你重新找回稳稳当当的感觉。
比如说,在一些机器里面,会有各种零部件晃来晃去产生振动。
这些振动要是不处理,那可不得了,机器可能就没法好好工作啦,甚至还可能出故障呢。
这就好像一个人一直在那里抖腿,抖得你心烦意乱的。
但是有了动力吸振器,它就会悄悄地把那些多余的振动能量给吸收掉,让机器变得安静又乖巧。
动力吸振器的工作原理呢,其实也不难理解。
它就像是一个很会调节气氛的高手。
它有自己的固有频率,这个频率就像是它的独特“魅力”。
当机器的振动频率和它的固有频率对上了,嘿,那就像两个好朋友找到了共鸣一样。
动力吸振器就开始发挥作用啦,把振动能量给“拐”到自己身上,然后慢慢消耗掉。
咱再打个比方,就像你去参加一个聚会,里面有个人特别能和你聊得来,你们俩一聊就停不下来,把其他的嘈杂都给忽略掉了。
动力吸振器就是这样,专门针对那些让人头疼的振动,和它们“聊得火热”,然后把问题解决掉。
你可别小看了这个小小的动力吸振器,它在很多地方都能大显身手呢!在汽车里,它能让你的驾驶体验更舒适,不会因为抖动而让你觉得难受。
在各种工业设备中,它能保证设备的稳定运行,提高生产效率。
就好像一个默默付出的幕后英雄,虽然不显眼,但却非常重要。
我记得有一次去参观一个工厂,看到那些巨大的机器在运行。
本来以为会很吵很晃的,结果走近了发现居然很平稳很安静。
后来一打听,才知道是因为装了动力吸振器。
当时我就想,这东西可真是神奇啊!总之呢,动力吸振器就是这么一个有趣又有用的东西。
它就像是一个魔法小助手,专门来对付那些让人烦恼的振动。
有了它,我们的生活和工作都能变得更加美好和顺利。
动力吸振器的基础知识

二自由度系统的应用场景之一是为动力吸振器设计提供理论支撑,动力吸振器作为一种减振装置,其减振原理不是依靠耗损能力进行减振,而是通过吸振器质量的动力作用,使吸振器在主系统上产生一个与强迫振动力相抵消的反作用力,依次来达到减振目的。
一、无阻尼主系统的二自由度模型及幅频特性图1 无阻尼主系统的二自由度模型图1为无阻尼主系统的二自由度模型,m1,k1为主系统的质量、刚度;m2,k2,c2为吸振器的质量、刚度、阻尼;主系统的位移为x1,动力吸振器的位移为x2;应用牛顿第二定律,可得该系统的振动微分方程:m1ẍ1+c2(ẋ1−ẋ2)+k2(x1−x2)+k1x1=Fm2ẍ2+c2(ẋ2−ẋ1)+k2(x2−x1)=0当F为简谐激励时,F(t)=F0e jωt,系统的响应可以表示为:x1=X1e jωt,x2=X2e jωt将响应表达式代入振动微分方程,可得主系统的幅频特性曲线|X1X st|=√(γ2−λ2)2+(2γλξ2)2[(1−λ2)(γ2−λ2)−μγ2λ2]2+[1−(1+μ)λ2]2(2γλξ2)2式中,质量比μ=m2m1;主系统固有频率ωn1=√k1m1,单位rad/s;动力吸振器固有频率ωn2=√k2m2,单位rad/s;吸振器阻尼比ξ2=22m2k2=c22m2ωn2;主系统静变形为X st=F0k1;强迫振动比λ=ωωn1;固有频率比γ=ωn2ωn1。
二、有阻尼主系统的二自由度模型及幅频特性当主系统存在阻尼时,二自由度系统的模型如图2所示图2带阻尼主系统的二自由度模型其中m1,k1,c1为主系统的质量、刚度;m2,k2,c2为吸振器的质量、刚度、阻尼;主系统的位移为x1,动力吸振器的位移为x2;应用牛顿第二定律,可得该系统的振动微分方程:m1ẍ1+c2(ẋ1−ẋ2)+k2(x1−x2)+c1ẋ1+k1x1=Fm 2ẍ2+c 2(ẋ2−ẋ1)+k 2(x 2−x 1)=0将振动微分方程改写成矩阵方程为:[m 100m 2]{ẍ1ẍ2}+[c 1+c 2−c 2−c 2c 2]{ẋ1ẋ2}+[k 1+k 2−k 2−k 2k 2]{x 1x 2}={F0} 简写为[M ][X ]+[C ][X ]+[K ][X ]=[F]其中[M ],[C ],[K ]分别代表质量矩阵,阻尼矩阵和刚度矩阵,[X ],[X ],[X ],[F]分别代表加速度矩阵、速度矩阵、位移矩阵和激励力矩阵。
动力吸振器课程设计

动力吸振器课程设计一、课程目标知识目标:1. 学生能够理解动力吸振器的基本原理,掌握其工作方式和功能。
2. 学生能够描述动力吸振器在工程中的应用,并解释其对于机械设备稳定性和减震效果的重要性。
3. 学生能够掌握动力吸振器的结构组成及其参数对吸振效果的影响。
技能目标:1. 学生能够运用物理知识分析动力吸振器的动力学问题,具备设计和优化吸振器参数的能力。
2. 学生能够运用数学工具对动力吸振器的振动方程进行求解,预测其吸振效果。
3. 学生能够通过实验操作,验证动力吸振器的吸振性能,并能够分析实验数据,提出改进措施。
情感态度价值观目标:1. 学生能够培养对物理学科的兴趣,激发对工程技术的热爱。
2. 学生能够认识到科学技术在生活中的应用,增强实践与创新意识。
3. 学生能够养成合作、探究的学习习惯,培养面对工程问题积极解决的信心和责任感。
课程性质:本课程属于物理学科,结合实际工程应用,强调理论联系实际,注重培养学生的动手能力和实际问题解决能力。
学生特点:学生处于高中阶段,具有一定的物理基础和数学素养,对实际工程问题充满好奇心,但需要引导和激发。
教学要求:教师应注重理论与实践相结合,关注学生个体差异,提供多样化的教学手段,确保学生能够达到课程目标。
在教学过程中,分解目标为具体学习成果,以便进行有效的教学设计和评估。
二、教学内容1. 理论基础:- 动力吸振器的基本原理与分类- 振动系统的数学模型及振动方程- 动力吸振器参数对吸振性能的影响教学内容关联教材第十二章“机械振动与波”的相关内容。
2. 实践应用:- 动力吸振器在工程中的应用案例分析- 动力吸振器的设计原则与优化方法- 动力吸振器性能测试方法及数据分析教学内容关联教材第十五章“工程技术案例分析”的相关内容。
3. 实验操作:- 搭建动力吸振器实验装置,进行吸振性能测试- 分析实验数据,验证理论模型的正确性- 针对实验结果,提出优化措施,改进吸振性能教学内容关联教材第十六章“实验设计与操作”的相关内容。
动力吸振器在动力总成振动控制中的应用

中图 分 类 号 : 6 U4 41
文献标识码 : A
DO 编 码 : 03 6 /i n10 —3 52 1 0 . 7 I 1 9 9 .s 0 61 5—0 1 20 js 2
s er f r nc orsm ia ng n e i g om e e e ef i lre i e rn
Ke r s:v b ai n a dwa e; A : o r s e by r s n n e; i r t n c n r l y wo d i r t n v DV o p we s m l e o a c v b a i o t a o o
动力 吸振 器在 动 力 总成振 动控 制 中的应 用
l5 l
文章 编 号 :0 61 5 (0 0 -1 50 10 .3 52 1 )20 —4 1 1
动 力 吸振 器在 动 力总 成 振 动控 制 中的应 用
刘建 娅 李舜 酩 姜建 中 , 庄 , , 严 2 孙 勃 路 志尧 , ,
f q e c f h ir ins s m mp s do e o b l n s u t g B sdo e einte r f y a c ir in r u n yo e b a o t c e t v t y e o o e f h re a di ni ae nt s oy o n mi vba o t c t mo n h d g h d t
a s re ( A)ad mpn A a e nd sg e n se ldi ep we se l h e il et e ut so ta b o b r DV , a igDV h sb e e in da da smbe t o ra smby T ev hcets s l h w t nh r s h
动力吸振

1
第五章 动力吸振
5.1 5.2 5.3 5.4
无阻尼动力吸振器 阻尼动力吸振器 动力吸振器原理 动力吸振器设计步骤
3
5.1 无阻尼动力吸振器
5.1.1 无阻尼动力吸振器
如图所示的单自由度系统,质量为M,刚 度为K,在一个频率为ω、幅值为FA的简谐外 力激励下,系统将作强迫振动。
A
15
5.1.2 无阻尼动力吸振器使用条件 并非所有的振动系统都需要附加动 力吸振器,动力吸振器的使用是有条件 的,可简单归纳如下: 1. 激振频率 ω接近或等于系统固有频 且激振频率基本恒定; 率 ω0 ,且激振频率基本恒定; 主振系阻尼较小; 2.主振系阻尼较小; 主振系有减小振动的要求。 3.主振系有减小振动的要求。
产生的静位移为1cm,转速为300r/min,产生的动荷载幅值P=1kN 问:1)应加动力吸振器吗?2)设计吸振器。(许可位移为1cm)
9.81 g = = 31.3 1 s 解:1)ω = ∆ st 0.01
Psinθt k2 m2
2πn 2π ⋅300 θ= = = 31.4 1 s 60 60
F (t ) = FA sin ωt
4
回顾:单自由度强迫振动的解。 回顾:单自由度强迫振动的解。
ɺ ɺ mɺ + Cx + Kx = F(t) x
方程的通解由两部分组成, x(t) = x1(t) + x2 (t)
x1(t) = Xe−ζωnt sin( 1−ζ 2ωnt +ϕ)
F (t ) = FA sin ωt
33
Thank you for your listening!
高层建筑吸振器的最佳参数

高层建筑吸振器的最佳参数高层建筑吸振器是一种用于减小建筑物在风力作用下振动的装置。
它的最佳参数是指在设计和安装过程中需要考虑的关键参数,以确保吸振器的效果最大化,从而保证高层建筑的结构安全和使用舒适性。
一个重要的参数是吸振器的质量。
吸振器的质量越大,它对建筑物的振动衰减效果就越好。
因此,在选择吸振器时,应考虑使用足够重量的材料来制造吸振器,以增加其质量,并提高其吸振效果。
吸振器的刚度也是一个重要的参数。
吸振器的刚度越大,它对建筑物的振动影响就越小。
因此,在设计吸振器时,需要选择合适的材料和尺寸,以确保吸振器具有足够的刚度来抵抗建筑物的振动。
吸振器的阻尼也是一个关键参数。
阻尼是指吸振器对建筑物振动的能量耗散能力。
吸振器的阻尼越大,它对建筑物振动的衰减效果就越好。
因此,需要选择合适的材料和设计来增加吸振器的阻尼,以提高吸振效果。
吸振器的安装位置也是一个需要考虑的参数。
吸振器应该安装在高层建筑的关键位置,例如结构刚度较小的区域或振动较大的区域。
通过在这些位置安装吸振器,可以最大限度地减小建筑物的振动,提高结构的稳定性和安全性。
吸振器的数量和布置也需要合理考虑。
根据建筑物的大小和结构,需要确定合适的吸振器数量和布置方式。
吸振器应该均匀分布在建筑物的各个部位,以确保吸振效果的均衡和一致性。
高层建筑吸振器的最佳参数包括吸振器的质量、刚度、阻尼、安装位置以及数量和布置。
通过合理选择这些参数,可以最大限度地减小建筑物的振动,提高结构的安全性和使用舒适性。
在设计和安装过程中,需要综合考虑各个参数,以确保吸振器的效果最大化,从而保证高层建筑的稳定性和可靠性。
随机振动动力吸振器参数的最优设计

1 ∞ H 2Π - ∞
∫
2
x1
( Ξ) 2S ( Ξ) d Ξ =
S0
2Π -
∫H
∞
∞
x1ห้องสมุดไป่ตู้
( Ξ)
2
dΞ
( 6)
将式 ( 3) 代入式 ( 6) , 经积分运算并整理得吸振器的优化目标函数为
3 2 Π S 0 B 1Φ 2 + B 2Φ 2 + B 3Φ 2 + B 4 2 3 3 2 4M Ξ1 A 1 Φ 2 + A 2Φ 2 + A 3Φ 2 + A 4 2 2 2 3 ) ; A 2 = ( Λ+ 4Φ ); 其中: A 1 = 4Φ + 4Φ 1 Α ( 1+ Λ 1) Α 1 Α ( 1+ Λ 2 4 2 2 2 3 ) Α ]+ 2Φ 1 [ 1+ ( 1+ Λ 1 Α ( 2Φ 1 - 1) ; 1 Α; A 3= Φ A 4 = ΛΦ 2 2 [ 1+ ( 1+ Λ) Α ] 1Α B 1 = 4 ( 1+ Λ) Α; B 2 = 4Φ 2 2 2 4 3 ) Α + ( 1+ Λ) Α; 1 - 2- Λ 1 ΛΑ B 3 = 1+ ( 4Φ B 4= Φ
第 2 期 缪 等: 随机振动动力吸振器参数的最优设计
127
2 2 图 4 方差 Ρx 与固有频率比 Α的关系 图 5 方差 Ρx 与固有频率比 Φ 2 的关系 1 1
H H
x2
2 2 ( Ξ) = ( Α Ξ1 + J 2Φ Ξ1 Ξ) ∃ 2Α
( 4) ( 5)
∆2
( Ξ) = Ξ ∃
吸振实验实验报告

一、实验名称:吸振实验二、所属课程名称:振动与波三、学生姓名、学号、及合作者:张三,123456789;李四,987654321;王五,112233445四、实验日期和地点:2023年10月26日,物理实验室五、实验目的:1. 了解吸振器的基本原理和构造。
2. 掌握吸振器在振动系统中的应用。
3. 通过实验,验证吸振器对振动系统的减振效果。
六、实验原理:吸振器是一种用于降低振动能量的装置,其工作原理是通过吸振器内部的阻尼材料消耗振动能量,从而降低系统的振动幅度。
本实验采用线性阻尼吸振器,其阻尼系数与振动频率、质量等因素有关。
七、实验内容和步骤:1. 实验装置搭建:- 搭建一个振动系统,包括激振器、振动台、吸振器等。
- 将吸振器安装在振动台上,确保其与振动台接触良好。
2. 实验数据采集:- 开启激振器,使振动系统产生一定频率的振动。
- 利用传感器采集振动台上的振动数据,包括振动幅度和振动频率。
- 记录不同吸振器安装位置和阻尼系数下的振动数据。
3. 数据处理与分析:- 对采集到的振动数据进行处理,包括计算振动幅度、振动频率等。
- 分析不同吸振器安装位置和阻尼系数对振动系统减振效果的影响。
八、实验环境和器材:1. 实验环境:- 温度:25℃- 湿度:50%2. 实验器材:- 激振器- 振动台- 吸振器- 传感器- 数据采集系统- 计算机软件九、实验结果:1. 吸振器安装位置对振动系统减振效果的影响:- 实验结果表明,吸振器安装在振动台上时,对振动系统的减振效果较好。
- 随着吸振器安装位置的降低,减振效果逐渐增强。
2. 阻尼系数对振动系统减振效果的影响:- 实验结果表明,随着阻尼系数的增加,振动系统的减振效果逐渐增强。
- 当阻尼系数达到一定值时,减振效果趋于稳定。
十、实验结论:1. 吸振器可以有效地降低振动系统的振动幅度,提高系统的稳定性。
2. 吸振器的安装位置和阻尼系数对振动系统的减振效果有显著影响。
动力吸振器在改善车内轰鸣声中的应用与研究

动力吸振器在改善车内轰鸣声中的应用与研究随着汽车使用的频繁,车内噪音问题使许多车主感到不适。
轰鸣声特别是高速行驶时产生的噪音问题令人烦躁,严重影响驾驶的安全和舒适性。
为了改善车内轰鸣声,动力吸振器的应用得到越来越广泛的关注和研究。
动力吸振器是一种被广泛应用于汽车降噪领域的改善装置,它能够通过振动反向相消,从而减小车辆引擎和底盘传递到车身的振动和噪音。
动力吸振器由振铃器和驱动单元组成,其具体原理是:当车辆行驶时,引擎和底盘震动会通过悬挂系统传递到车身。
这些振动在车身上共振并形成压力波,导致车内出现噪音。
动力吸振器的作用是将这些压力波反向相消,从而在减小车内噪音的同时,提高驾驶的舒适性。
动力吸振器在汽车行业中应用出现较早,但是由于其成本高、安装复杂等原因,一直没有得到广泛的应用。
然而,随着现代汽车制造技术的发展和消费者对汽车舒适性要求的不断提高,动力吸振器在车内降噪领域的应用越来越受到关注和青睐。
相比于传统的降噪装置,动力吸振器的优点在于其能够快速、精确地反向相消振动波,从而能够更有效地减小车内噪音。
动力吸振器在改善车内轰鸣声中的研究也逐渐得到了重视。
一些研究表明,动力吸振器能够在多个频率范围内降低车内噪声的水平。
这一结论得到了汽车制造业和消费者的广泛认可,许多汽车制造商正开始将动力吸振器作为标准配备,为车主提供更加安静、舒适的驾驶体验。
总而言之,动力吸振器作为一种有效的车内降噪装置,已经在汽车制造业中发挥了重要的作用,同时也在不断得到改进和提高。
随着全球范围内人们对车辆舒适性的追求,动力吸振器的应用前景将越来越广阔,同时也将对未来汽车的研发与制造产生深远的影响。
动力吸振器除了在汽车行业中得到广泛应用,在航空、建筑等领域也被用于降低噪音和振动。
尤其是在高速铁路领域,动力吸振器的作用更加显著。
高速列车行驶时,由于刹车、钟摆等原因,车身会发生震动和噪音,这不仅影响旅客的乘车体验,还可能对车辆的安全产生影响。
《动力吸振器》课件

# 动力吸振器
简介
1 什么是动力吸振器?
动力吸振器是一种用来减少机械设备振动和噪音的装置,它能有效地吸收和消除机械设 备产生的震动。
2 动力吸振器的作用是什么?
动力吸振器主要用于保护设备的稳定运行,减少振动对设备造成的损坏,同时提升机械 设备的工作效率。
3 动力吸振器的特点和优势是什么?
3
动力吸振器是如何消除振动和噪音的?
通过减震橡胶和液压缓冲器的作用,动力吸振器能够将振动和噪音有效地传导到 地面,从而降低设备的振动和噪音水平。
应用领域
动力吸振器的主要应用 领域是什么?
动力吸振器广泛应用于工业 生产线、发电厂、航空航天 等领域,以及各种需要减振 和降噪的机电设备。
动力吸振器在哪些行业 中常常使用?
动力吸振器具有结构简单、使用方便、效果显著等特点,能够提供良好的减振效果和噪 音降低效果。
工作原理
1
动力吸振器的结构和组成部分
动力吸振器一般由弹簧、减震橡胶、液压缓冲器等组成,这些组件相互协作以达 到吸
动力吸振器通过弹簧和橡胶的弹性变形,吸收和抑制机械设备产生的振动和冲击。
动力吸振器常见于汽车制造、 船舶工程、建筑施工、石油 化工等行业,用于减少机械 设备的振动和噪音。
动力吸振器的应用实例 和案例分享
分享一些具体的实例和案例, 展示动力吸振器在不同行业 中的应用效果和成果。
市场前景
动力吸振器在未来市 场中的发展趋势
随着工业发展和环保意识的增 强,动力吸振器在未来市场中 将继续得到广泛应用和推广。
动力吸振器的市场规 模和增长率情况
介绍动力吸振器市场的规模和 增长率,展示市场的潜力和前 景。
动力吸振器未来的发 展和应用前景
低频动力吸振器原理

低频动力吸振器原理
低频动力吸振器是一种用于减少机械结构振动的装置,其工作原理基于振动能量的吸收和消散。
低频动力吸振器通常由质量块、弹簧和阻尼器组成。
质量块通过弹簧与主结构相连,阻尼器用于消耗质量块的振动能量。
当主结构受到振动激励时,质量块会在弹簧的作用下产生与主结构振动相反的运动,从而吸收主结构的振动能量。
具体来说,当主结构振动时,质量块会受到惯性力的作用,产生与主结构振动相反的运动。
弹簧则提供了一个弹性力,使质量块能够在一定范围内自由振动。
阻尼器则通过消耗质量块的振动能量,将其转化为热能等形式的能量,从而减少质量块的振动幅度。
通过合理设计质量块、弹簧和阻尼器的参数,可以使低频动力吸振器在特定的频率范围内具有良好的吸振效果。
通常,低频动力吸振器适用于低频振动的抑制,如机械设备的基座振动、建筑物的风振等。
需要注意的是,低频动力吸振器的效果受到其自身参数、安装位置和环境条件等因素的影响。
在实际应用中,需要根据具体情况进行合理的设计和安装,以达到最佳的吸振效果。
第五章_动力吸振器

(1) 通过计算或测试,确定激振频率 ,并估算激振力
幅值FA大小;
(2) 确定吸振器弹簧刚度 k,使得吸振器振幅为空间许
可的合理值,并且弹簧能够经受这一振幅下的疲劳应 力;
(3) 选择吸振器质量,满足 ,且k m m M 0.1
选择一定质量比的原因是为了使主振系能够安全工作, 在两个新的固有频率之间应有一定的间隔频带;
Psinθt
35
【作业】:如图示梁中点放一点动机。重2500N,电动机使梁中点
产生的静位移为1cm,转速为300r/min,产生的动荷载幅值P=1kN 问:1)应加动力吸振器吗?2)设计吸振器。(许可位移为1cm)
解:1)
g
st
9.81 0.01
31.3
1
s
Psinθt
2n
60
2 300
60
第五章 动力吸振 第六章 隔 振 第七章 阻尼减振 第八章 吸声降噪 第九章 隔声技术 第十章 消 声 器
1
第五章 动力吸振
5.1 无阻尼动力吸振器 5.2 阻尼动力吸振器 5.3 动力吸振器原理 5.4 动力吸振器设计步骤
3
5.1 无阻尼动力吸振器
5.1.1 无阻尼动力吸振器
如图所示的单自由度系统,质量为M,刚 度为K,在一个频率为ω、幅值为FA的简谐外 力激励下,系统将作强迫振动。
40
• 概述
减振器
• 减振器用来衰减由于弹性系统引起的振, 减振器的类型有筒式减振器,阻力可调式 新式减振器,充气式减振器。
• 在汽车悬架系统中广泛采用的是筒式减振 器,且在压缩和伸张行程中均能起减振作
用叫双向作用式减振器,还有采用新式减
振器,它包括充气式减振器和阻力可调式 减振器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D1 P k 22 2 m2 k12 P2 1 D2 P2 k11 2
k 21 k11 m1
2
m k
1
21P 1
D
k 21
0
如果荷载频率θ与任一个自振频率 ω1、 ω2重合,则D0=0, 当D1、D2 不全为零时,则出现共振现象
5
例:质量集中在楼层上m1、m2 ,层间侧移刚度为k1、k2 解:荷载幅值:P1=P,P2=0,求刚度系数: k11=k1+k2 , k21=-k2 , k22=k2 , k12=-k2
两个主振型相互正交,因与质量有关,称为第一正交关系。 3
由功的互等定理:
2 2 (m112Y11 )Y12 (m212Y21 )Y22 (m12 Y12 )Y11 (m22 Y22 )Y21
m1Y11Y12 m2Y21Y22 0(15.51)
上式分别乘以ω12、ω22,则得:
如图示对称结构在对称荷载作用下。
k11 k22 , k12 k21
与ω2相应的振型是
Psinθt m l/3 l/3
Psinθt m l/3
Y12 k12 2 2 =-1 k 22 2 m k11 2 m k12 k 21 2 2 m Y22 k11
当θ=ω2 ,D0=0 ,也有: 对称体系在对称荷载作用下时, 只有当荷载频率与对称主振型的自 2 D1 P k 22 2 m2 k12 P2 振频率相等时才发生共振;当荷载 P k 22 2 m k12 P 0 1 频率与反对称主振型的自振频率相 2 D2 P2 k11 2 m1 k 21P 等时不会发生共振。同理可知:对 P k11 2 m k 21P 0 1 称体系在反对称荷载作用下时,只 有当荷载频率与反对称主振型的自 D1 D2 不会趋于无穷大,不发生共振, Y1 , Y2 振频率相等时才发生共振。 D0 D0 共振区只有一个。
各个主振型能单独存在,而不相互干扰。
4
m1 y1 k11 y1 k12 y2 P1 (t ) 0 .. m2 y2 k 21 y1 k 22 y2 P2 (t ) 0
§15-5 ..
两个自由度体系在简谐荷载下的受迫振动
如 P (t ) P sint 1 1 P2 (t ) P2 sint y1 (t ) Y1 sint y2 (t ) Y2 sint
1 m k 2
层间动剪力:
Q1 1
2m
k
( 1 2 )
Q1 P 2 m(Y1 Y2 ) 2m P(1 ( 1 2 )) k
由此可见,在多自由度体系中,没有一个统一的动力系数。
9
例15-9:质量集中在楼层上m1、m2 ,层间侧移刚度为k1、k2 k11=k1+k2 , k21=-k2 , k22=k2 , k12=-k2 m2
(m112Y11 )Y12 (m212Y21 )Y22 0
2 2 (m12 Y12 )Y11 (m22 Y22 )Y21 0
第一主振型惯性力在第二主振型位移上所做的功等于零;
第二主振型惯性力在第一主振型位移上所做的功等于零; 某一主振型的惯性力在其它主振型位移上不做功,其能量 不会转移到其它主振型上,不会引起其它主振型的振动;
Pk 11 D D1 P(k 2 m22) k12 P2 2 P2 (k2 m1 ) k 21P1 1 22 m Y2 Y1 D0 D0 D0 D0 D0 D0
22
2
m2
Psint
m1
k2
D0 k1 k 2 m1 k 2
2
11
近似法求自振频率 1、能量法求第一频率——Rayleigh法
根据能量守恒定律,当不考虑阻尼自由振动时,振动体系在任何时刻的动 能T 和应变能U 之和应等于常数。 ※根据简谐振动的特点可知:在体系通过静力平衡位置的瞬间,速度最大(动 能具有最大值),动位移为零(应变能为零);当体系达到最大振幅的瞬间
※假设位移幅值函数Y(x)必须注意以下几点:
1、必须满足运动边界条件:
(铰支端:Y=0;固定端:Y=0,Y´=0) 尽量满足弯矩边界条件,以减小误差。剪力边界条件可不计。 2、所设位移幅值函数应与实际振型形状大致接近;如正好与第 n 主振 型相似,则可求的ωn的准确解。但主振型通常是未知的,只能假定一近
§15-4
一、刚度法
两自由度体系的自由振动
k12 ( k22 2m2 ) 0
特征方程
频率方程
D
( k11 2 m1 ) k21
(k11 2m1 )( k22 2m2 ) k12k21 0
1 k11 k22 k11k22 k12k21 1 k11 k22 m m 2 m m 2 1 m1m2 2 2 1
P1(t)
y2(t)
在平稳阶段,各质点也作简谐振动:
(k11 2 m1 )Y1 k12Y2 P 1 k 21Y1 (k 22 2 m2 )Y2 P2
D0 k11 m1
2
P2(t) y1(t)
Y1=D1/D0 Y2=D2/D0
k12 k 22 2 m2 k12 k 22 m2
§15-9
(变形能最大),速度为零(动能为零)。对这两个特定时刻,根据能量守恒
定律得:
Umax=Tmax
位移幅值
ω
. v ax ,Tmax
设: y( x, t ) Y ( x) sin(t ) l l l 1 1 2 2 1 2 Tmax m ( xv dx )Y 2 ( x)dx 2 (t ) m ( x)Y 2 ( x)dx ) m ( x cos ※求频率 2 02 2 0 0 l 2 EI[Y ( x)]2 dx l 2 0 l 1 1 l EI[ ( xy 2 dx 1 22 UU EI )] dx sin (lt ) EI[Y ( x )]2 dx Y max 2 x 2 20 2 0 m[Y ( )] dx miYi 2 0 x 2 0 12 如梁上还有集中质量mi, Yi为集中质量mi处的位移幅值。
2
2 m2 k 2
k1
当m1=m2=m,k1=k2=k
2 2 2 2 Pk12 P22 k11 2 m1 k 21P2 3k 2 2 k 2 2 2 D k 22P1 m m2 m2 Dk P 1k k 22 k12 P2 2 P 1 D0 2k2 44 m k m ) k m ( 1 Y1 Y2 2 m D m D0 D0 D0 D0 D00 D0 2 24 2 2 2 2 2 2 2 2 2 1 m k 2 Y1 2 D1 P k 22 m2 1 k12 P2 2 1 1 2 1 k11 2 2 m1 2 3 k k212 2 2 D0 (1 2 )(1 22 ) 2 P 1 2 2 2 2 2P 2 D2 2 2kk112 m1 k 21P k 21 1 m22 2m2 k k m (1 )(1 1 ) 2
1
21m1
0
2
令
1
2
2 ( 11m1 22m2 ) ( 11 22m1m2 12 21m1m2 ) 0
1 1 ( 11m1 22m2 ) ( 11m1 22m2 ) 2 4( 11 22 12 21 )m1m2 2 2
g 9.81 31.3 1 s 解:1) st 0.01
Psinθt k2 m2
2n 2 300 31.4 1 s 60 60
频率比在共振区之内应设置吸振器。
P 2)由 k 2 弹簧刚度系数为: Y2 1000 k2 110 5 N/m 0.01 k 2 110 5 =102 kg m2 2 2 31.4
m 3km k
22 11
Y2 2 2 k 1 1 2 2 2 m )(1 2 ) P (1 2 2 2 k 1
2 (1 )(1 m 1
m
2
2 m (( )( )) 2 ) ( m
2 2 22
)
6
1 m k 2 Y1 1 2 )(1 2 ) P (1 2 2 2 k 1
Y1
3.0 P 2.0 0.618 1.618 1.0 0 -1.0 -2.0 -3.0
k
Y2 1 2 2 2 P (1 2 )(1 2 ) k 1 2
1
主振型
1
Y11 12m2 1 Y21 11m1 2
1
2
1
1
Y12 12m2 1 Y22 11m1 2
2
2
2
三、主振型及主振型的正交性
12m1Y11 12 m2Y21
m1
2 2 m1Y12
m2 Y21
m1 Y12
Y22 m2
2 2 m2Y22
可以消除m1的振动(动力吸振器原理)。 设计吸振器时,先根据m2的许可振幅Y2,选定
Psint
m2 k2
m1
k1
P k2 Y2
,再确定 m2
2
10
k2
吸振器不能盲目设置,必须在干扰力使体系产生较大振动时才有必要设置。
例:如图示梁中点放一电动机。重2500N,电动机使梁中点产生 的静位移为1cm,转速为300r/min,产生的动荷载幅值P=1kN, 问:1)应加动力吸振器吗?2)设计吸振器。(许可位移为1cm)
