克鲁斯卡尔算法求最小生成树
求无向图的最小生成树算法——Prim与Kruskal

求无向图的最小生成树算法——Prim与Kruskal一.Prim算法1.算法思想对于图G=(V,E),用Prim算法求最小生成树T=(S,TE)的流程如下① 初始化:设S、TE为空集,任选节点K加入S。
② 选取一条权值最小的边(X,Y),其中X∈S,且not (Y∈S)即,选取一条权值最小的、连接着S中一点与S外一点的边。
将Y加入S中,边(X,Y)加入TE中重复② 直到V=S即所有G中的点都在S中,此时的T为G的最小生成树。
由此流程可见,Prim算法求最小生成树时任何时候的T都是一颗树。
2.实现显然,Prim算法的主要运行时间花在过程②的选边中。
看起来复杂度是O(VE)=O(V^3)不是么,效率也太低了吧……为了比较快速地选边,我们用两个数组lowcost、closest动态地维护每一个点到S的最短距离。
在某一状态下,lowcost[i]表示所有与i相连且另一端点在S中的边中的权值最小值,closest[i]表示在S中且与i相连的点中与i之间距离最小的点。
显然,lowcost[i]=w(i,closest[i])。
需要注意的是两个数组记录的都是边而不是路径。
若i没有边直接连向S,则lowcost[i]=∞。
另外,若i已在S 中,则lowcost[i]=0。
设出发点为x。
初始时对于任意k∈V,closest[k]=x,lowcost[k]=w(k,x)【w(i,j)表示i、j间的距离。
初始化时,若两点间没有边则w(i,j)赋为一个足够大的整数(如maxint),并且所有点到自身的距离赋为0,即w(i,i)=0】每一次找出lowcost中不为0的最小值lowcost[i],然后把i加入S(即lowcost[i]:=0),然后对于图中所有点k,若w(k,i)<lowcost[k],则把lowcost[k]赋为w(k,i),把closest[k]赋为i。
【由于s中所有点的lowcost都为0,所以只影响到s以外的点】以上操作重复|V|-1次结束。
最小生成树算法

最小生成树之克鲁斯卡尔(Kruskal)算法、普里姆(prim)算法分类:算法 2012-01-04 11:091159人阅读评论(0)收藏举报算法问题描述:在一个具有几个顶点的连通图G中,如果存在子图G'包含G中所有顶点和一部分边,且不形成回路,则称G'为图G的生成树,其中代价最小的生成树则称为最小生成树。
例如,设有下图G,找出连接图G所有顶点(v1,v2,v3,v4,v5,v6)的边,且这些边的权重之和最小。
那么如何生成该最小生成树呢?两个经典算法是普里姆 (Prim)算法和克鲁斯卡(Kruskal )算法。
克鲁斯卡尔(Kruskal)算法:克鲁斯卡尔(Kruskal)算法是以图上的边为出发点依据贪心策略逐次选择图中最小边为最小生成树的边,且所选的当前最小边与已有的边不构成回路。
在图G中,首先选择最小的边(V2,V3),(V4,V5),(V2,V4),因为(V4,V6)和(V5,V6)权重相等,所以可以任选其中一条(这也表明最小生成树不是唯一的)。
同样的道理,选择权重为5的边(V3,V5)(V2,V1),因为(V3,V5)和(V2,V3),(V2,V4),(V4,V5)构成了回路,所以舍弃(V3,V5)保留(V2,V1)。
这时该子图G‘已经包含了图G的所有的边,算法结束。
得到的最小生成树如下图:伪代码: Kruskal(G,W)1、按照权重从小到大顺序排序G的边{e1,e2,e3,e4,e5,...,em};2、for i = 1to m do3、如果ei的两个端点不在同一个连通分支,则将ei加到T中;算法特点:时间复杂度为O(eloge)(e为网中边数),适合于求稀疏的网的最小生成树。
普里姆(Prim)算法:普里姆(Prim)算法是以图上的顶点为出发点,逐次选择到最小生成树顶点集距离最短的顶点为最小生成树的顶点,并加入到该顶点集,直到包含所有的顶点。
在图G中,选择顶点V1加入到顶点集S,连接S中顶点的边为(V1,V2)(V1,V3),选择最小的即(V1,V2),并将V2加入到顶点集S。
最小生成树克鲁斯卡尔算法详解

最小生成树克鲁斯卡尔算法详解转载自:数据结构中图结构的最小生成树克鲁斯卡尔算法详解我一直想把克鲁斯卡尔算法实现,但是由于马上就要考试了,而且自己由于天气寒冷等各种原因没能如愿。
不过在昨天一天的努力中,我终于完成了克鲁斯卡尔算法的实现。
算法是c++的,图的数据结构是以邻接矩阵为基础,并且使用了模板,所以可以对任何类型的顶点进行最小生成树的生成。
克鲁斯卡尔算法中的核心思想就是逐个在边的集合中找到最小的边,如果满足条件就将其构造,最后生成一个最小生成树。
它首先是一系列的顶点集合,并没有边,然后我们从邻接矩阵中寻找最小的边,看看它是否和现有的边连接成一个环,如果连接成环,则舍弃,另外取其它的边。
如果不连接成环,则接受这个边,并把其纳入集合中。
以此类推。
我们知道,一课有n个顶点的树(无论是树还是二叉树),它必定有n-1个边。
我们只需要对上述操作循环至少n-1次(因为可能选出的边会构成环,不是我们需要的边)。
下面就是我寻找最小边的c++代码:Code:min=INFINITY;for(i=0;i vexnum;i++){for(j=i;j vexnum;j++){if(arcs[i][j].adj!=INFINITY&&minarcs[i][j].adj){if(arcs[i][j].adj=vexSet.lowcost&&!vexSet.IsAlreadyIn(i,j)){min=arcs[i][j].adj;track_i=i;track_j=j;}}}}首先让min为最大(INFINITY),然后让其与邻接矩阵的一个个元素进行比较,我在遍历邻接矩阵的时候使用的是上三角(◥)法,因为无向网的邻接矩阵是对称矩阵。
当然我们必须记录满足调件的顶点的下标,所以track_i、track_j就变得必要了。
又因为我们要满足每次选取的最小权值的边呈递增数列,所以arcs[i][j].adj vexSet.lowcost(其中vexSet.lowcost为上次保存的最小边)就变得必要了。
克鲁斯卡尔算法的时间复杂度

克鲁斯卡尔算法的时间复杂度
第一段:克鲁斯卡尔算法是一种求解最小生成树问题(MinimumSpanningTreeProblem)和求最短路径问题(ShortestPathProblem)的算法,是图论中最常用的算法之一。
它
有效地找到一幅给定的加权图中的最小生成树,并对相关的最短路径问题提供了优化的解决方案。
本文将讨论克鲁斯卡尔算法的时间复杂度,包括它的最佳情况和最坏情况。
第二段:克鲁斯卡尔算法的时间复杂度在最佳情况下是线性的,即O(n)。
具体而言,如果一个图中存在一个可以完全覆盖所有边的
最小生成树,则克鲁斯卡尔算法只需要遍历一次图来找到最小生成树,所以它的时间复杂度是O(n)。
第三段:然而,在最坏情况下,克鲁斯卡尔算法的时间复杂度是平方的,即O(n2)。
这是因为最坏情况下,算法将遍历图中的所有边,一共有O(n2)个边,这样它将在遍历完所有边之后才能完成寻找最小生成树的过程,所以它的时间复杂度是O(n2)。
第四段:此外,克鲁斯卡尔算法的时间复杂度还可能受到图的形状和连接方式的影响,这可能会严重影响算法的运行时间。
例如,如果一个图的边比较多,但是连接方式却比较规则,这样算法能够更快地找到最小生成树,导致克鲁斯卡尔算法的时间复杂度低于最坏情况下的O(n2)。
第五段:总而言之,克鲁斯卡尔算法的时间复杂度由图的状况决定。
它在最佳情况下是线性的,即O(n),在最坏情况下则是平方的,
即O(n2)。
然而,它的时间复杂度还可能受到图的形状和连接方式的影响,有时可能低于最坏情况下的O(n2)。
kruskal算法求最小生成树

数据结构课程设计Kruskal算法求最小生成树学院:班级:学号;姓名;指导老师;完成日期:目录(一)需求分析———————————(二)概要设计———————————(三)详细设计———————————(四)主函数设计—————————(五)经验体会——————————- (六)源代码及调试分析————————1、需求分析运用kruskal算法求最小生成树最短路径:①输入任意源点,求到其余顶点的最短路径。
②输入任意对顶点,求这两点之间的最短路径和所有路径。
2、概要设计首先要确定图的存储形式。
经过的题目要求的初步分析,发现该题的主要操作是路径的输出,因此采用数组(邻接矩阵)的方法构造无向图,比较方便以后的编程。
从而求得最小生成树。
3、函数详细设计(1)构造无向图本题中为了能够求得最小生成树,先要构造无向图,并且用领结矩阵的形式表现出来。
void Create(MGraph &G) //采用数组(邻接矩阵)表示法,构造无向图G。
{int i,j,k,w;char v1[10],v2[10];scanf("%d%d",&G.vexnum,&G.arcnum); //输入定点数和边数for(i=0; i<G.vexnum; i++)scanf("%s", G.vexs[i]);for(i=0; i<G.vexnum; i++) //初始化邻接矩阵{for(j=0; j<G.vexnum; j++)G.arcs[i][j] = INF;}for(k=0; k<G.arcnum; k++) //构造邻接矩阵{scanf("%s%s%d",v1,v2,&w); //输入一条边依附的顶点及权值i = Locate(G,v1); //确定v1在G中的位置j = Locate(G,v2); //确定v2在G中的位置G.arcs[i][j] = w; //弧<v1,v2>的权值G.arcs[j][i] = w; //弧<v2,v1>是权值}for(i=0; i<G.vexnum; i++){for(j=0; j<G.vexnum; j++){printf("%6d ",G.arcs[i][j]);}printf("\n");}}(2) kruskal算法。
克鲁斯卡尔算法伪代码

克鲁斯卡尔算法伪代码克鲁斯卡尔算法是一个用于求解最小生成树的算法。
最小生成树(Minimum Spanning Tree, MST)指的是在一张无向图G中找到一个树T,使得T中的边权之和最小。
克鲁斯卡尔算法的基本思路是将所有边按照权值从小到大排序,然后依次选取这些边,如果选取的边之间没有形成环,就将该边加入到最小生成树中去。
这样,直到最小生成树中有n-1条边为止,就得到了最小生成树。
1. 将边按照权值从小到大排序。
2. 初始化一个并查集,即每个点都是一个单独的子集。
3. 遍历排好序的边,依次将边加入最小生成树中。
4. 对于每条边,检查该边的两个端点是否在同一个子集中,如果不在同一个子集中,则将它们合并成一个子集,同时将这条边加入最小生成树中。
5. 直到最小生成树中有n-1条边为止。
下面是使用Java语言实现克鲁斯卡尔算法的代码示例://边的类定义class Edge implements Comparable<Edge> {int u; // 边的起点int v; // 边的终点int w; // 边的权值// 构造函数public Edge(int u, int v, int w) {this.u = u;this.v = v;this.w = w;}//并查集的类定义class UnionFind {int[] parent;int[] rank;//查找父节点public int find(int p) {while (p != parent[p]) {parent[p] = parent[parent[p]]; //路径压缩p = parent[p];}return p;}//判断两个节点是否在同一个集合中public boolean connected(int p, int q) {return find(p) == find(q);}}//求解最小生成树public void solve() {Collections.sort(edges); //按照权值从小到大排序UnionFind uf = new UnionFind(V); //初始化并查集Kruskal kruskal = new Kruskal(V, edges);kruskal.solve();System.out.println("最小生成树的边为:");for (Edge e : kruskal.mst) {System.out.println(e.u + " - " + e.v + " : " + e.w);}}输出结果如下:最小生成树的边为: 0 - 2 : 13 - 5 : 21 - 4 : 30 - 1 : 62 -3 : 5。
的最小生成树算法Prim和Kruskal算法

的最小生成树算法Prim和Kruskal算法Prim和Kruskal算法是求解最小生成树的两种常用算法。
最小生成树指的是在一个连通图中,找到一棵包含所有顶点的生成树,使得树上边的权重之和最小。
Prim算法基于贪心思想,从一个起始顶点开始,逐步向其他顶点扩展,每次选择权重最小的边连接已经选中的顶点和未选中的顶点。
具体步骤如下:1. 初始化一个空的集合S,用于存放已经选中的顶点。
2. 从图中任选一个顶点作为起始顶点,并将其加入集合S。
3. 重复以下步骤,直到集合S包含了所有顶点:a. 在未加入集合S的顶点中,找到与集合S中顶点相连的边中权重最小的边。
b. 将该边加入生成树中,并将与该边相连的顶点加入集合S。
4. 生成的树即为最小生成树。
Kruskal算法是基于边的权重排序的思想。
具体步骤如下:1. 初始化一个空的集合S,用于存放已经选中的边。
2. 将图中的所有边按照权重从小到大排序。
3. 重复以下步骤,直到生成的树中包含了所有顶点-1条边(其中顶点的数量为n):a. 从排序后的边列表中选取一条最小权重的边。
b. 若该边的两个顶点不在同一连通分量中,将该边加入生成树中。
c. 否则,舍弃该边,继续选择下一条边。
4. 生成的树即为最小生成树。
值得注意的是,在构建最小生成树时,如果图不是连通图,那么最小生成树就不存在。
Prim算法的时间复杂度为O(V^2),其中V表示顶点的数量。
在稠密图中效果较好。
而Kruskal算法的时间复杂度为O(ElogE),其中E表示边的数量。
在稀疏图中效果较好。
这两种算法在实际应用中都有一定的局限性。
Prim算法适合处理边稠密、顶点稀疏的图,而Kruskal算法适合处理边稀疏、顶点稀疏的图。
在选择使用算法时,需要根据具体问题的特点进行权衡。
最小生成树算法Prim和Kruskal算法在图论领域具有重要的地位,广泛应用于网络设计、电路布线、城市规划等领域。
通过构建最小生成树,可以在保证连通性的前提下,选择最经济、最高效的路径和连接方式,节约资源并提高效率。
数据结构-kruskal算法求最小生成树 实验报告

一、问题简述题目:图的操作。
要求:用kruskal算法求最小生成树。
最短路径:①输入任意源点,求到其余顶点的最短路径。
②输入任意对顶点,求这两点之间的最短路径和所有路径。
二、程序设计思想首先要确定图的存储形式。
经过的题目要求的初步分析,发现该题的主要操作是路径的输出,因此采用边集数组(每个元素是一个结构体,包括起点、终点和权值)和邻接矩阵比较方便以后的编程。
其次是kruskal算法。
该算法的主要步骤是:GENERNIC-MIT(G,W)1. A←2. while A没有形成一棵生成树3 do 找出A的一条安全边(u,v);4.A←A∪{(u,v)};5.return A算法设置了集合A,该集合一直是某最小生成树的子集。
在每步决定是否把边(u,v)添加到集合A中,其添加条件是A∪{(u,v)}仍然是最小生成树的子集。
我们称这样的边为A 的安全边,因为可以安全地把它添加到A中而不会破坏上述条件。
然后就是Dijkstra算法。
Dijkstra算法基本思路是:假设每个点都有一对标号 (dj , pj),其中dj是从起源点s到点j的最短路径的长度 (从顶点到其本身的最短路径是零路(没有弧的路),其长度等于零);pj则是从s到j的最短路径中j点的前一点。
求解从起源点s到点j的最短路径算法的基本过程如下:1) 初始化。
起源点设置为:① ds =0, ps为空;②所有其他点: di=∞, pi=?;③标记起源点s,记k=s,其他所有点设为未标记的。
2) 检验从所有已标记的点k到其直接连接的未标记的点j的距离,并设置:d j =min[dj, dk+lkj]式中,lkj是从点k到j的直接连接距离。
3) 选取下一个点。
从所有未标记的结点中,选取dj中最小的一个i:di =min[dj, 所有未标记的点j]点i就被选为最短路径中的一点,并设为已标记的。
4) 找到点i的前一点。
从已标记的点中找到直接连接到点i的点j*,作为前一点,设置:i=j*5) 标记点i。
克鲁斯卡尔(Kruskal)算法求无向网的最小生成树数据结构报告

数据结构上机报告(1) 姓名:张可心学号:14030188030 班级:1403018一、题目描述用克鲁斯卡尔(Kruskal)算法求无向网的最小生成树,分析你的算法的时空复杂度,必须有过程说明。
输入:输入数据第一行为两个正整数n和m,分别表示顶点数和边数。
后面紧跟m行数据,每行数据是一条边的信息,包括三个数字,分别表示该边的两个顶点和边上的权值。
输出:按顺序输出Kruskal算法求得的最小生成树的边集,每行一条边,包括三个数字,分别是该边的两个顶点和边上的权值,其中第一个顶点的编号应小于第二个顶点的编号。
示例输入8 111 2 31 4 51 6 182 4 72 5 63 5 103 8 204 6 154 7 115 7 85 8 12示例输出1 2 31 4 52 5 65 7 83 5 105 8 124 6 15二、解题思路(1)假定每对顶点表示图的一条边,每条边对应一个权值;(2)输入每条边的顶点和权值;(3)输入每条边后,计算出最小生成树;(4)打印最小生成树边的顶点及权值。
三、源代码#include<stdio.h>#include<stdlib.h>typedef struct {int a,b,value;}node;int stcmp(const void *p,const void *q){node *a=(node *)p;node *b=(node *)q;if(a->value>b->value){return 1;}else if(a->value==b->value){return 0;}else{return -1;}}int root(int a,int *b){for(;a!=b[a];a=b[a]);return a;}bool isgroup(int a,int b,int *c){if(root(a,c)==root(b,c))return true;return false;}void add(int a,int tob,int *c){c[root(a,c)]=root(tob,c);}int main (){int n,m;scanf("%d %d",&n,&m);node no[m];for(int u=0;u<m;u++){scanf("%d",&(no[u].a));scanf("%d",&(no[u].b));scanf("%d",&(no[u].value));}qsort(no,m,sizeof(no[0]),stcmp);int bcj[n+1];for(int u=1;u<=n;u++){bcj[u]=u;}int i=0;int cc=n;for(;i<m;i++){if(!isgroup(no[i].a,no[i].b,bcj)){add(no[i].a,no[i].b,bcj);cc--;printf("%d %d %d\n",no[i].a,no[i].b,no[i].value);}if(cc==1)break;}return 0;}四、运行结果。
最小生成树算法(克鲁斯卡尔算法和普里姆算法)

最⼩⽣成树算法(克鲁斯卡尔算法和普⾥姆算法)⼀般最⼩⽣成树算法分成两种算法:⼀个是克鲁斯卡尔算法:这个算法的思想是利⽤贪⼼的思想,对每条边的权值先排个序,然后每次选取当前最⼩的边,判断⼀下这条边的点是否已经被选过了,也就是已经在树内了,⼀般是⽤并查集判断两个点是否已经联通了;另⼀个算法是普⾥姆算法:这个算法长的贼像迪杰斯塔拉算法,⾸先选取⼀个点进⼊集合内,然后找这个点连接的点⾥⾯权值最⼩的点,然后每次在选取与集合内任意⼀点连接的点的边的权值最⼩的那个(这个操作可以在松弛那⾥修改⼀下,这也是和迪杰斯塔拉算法最⼤的不同,你每次选取⼀个点后,把这个点能达到的点的那条边的权值修改⼀下,⽽不是像迪杰斯塔拉算法那样,松弛单点权值);克鲁斯卡尔代码:#include<iostream>#include<algorithm>#define maxn 5005using namespace std;struct Node{int x;int y;int w;}node[maxn];int cmp(Node x,Node y){return x.w<y.w;}int fa[maxn];int findfa(int x){if(fa[x]==x)return x;elsereturn findfa(fa[x]);}int join(int u,int v){int t1,t2;t1=findfa(u);t2=findfa(v);if(t1!=t2){fa[t2]=t1;return1;}elsereturn0;}int main(){int i,j;int sum;int ans;int n,m;sum=0;ans=0;cin>>n>>m;for(i=1;i<=m;i++)cin>>node[i].x>>node[i].y>>node[i].w;sort(node+1,node+1+m,cmp);for(i=1;i<=n;i++)fa[i]=i;for(i=1;i<=m;i++){if(join(node[i].x,node[i].y)){sum++;ans+=node[i].w;}if(sum==n-1)break;}cout<<ans<<endl;return0;}普⾥姆算法:#include<iostream>#include<algorithm>#include<cstring>#include<cstdio>#define inf 0x3f3f3fusing namespace std;int Map[1005][1005];int dist[1005];int visit[1005];int n,m;int prime(int x){int temp;int lowcast;int sum=0;memset(visit,0,sizeof(visit)); for(int i=1;i<=n;i++)dist[i]=Map[x][i];visit[x]=1;for(int i=1;i<=n-1;i++){lowcast=inf;for(int j=1;j<=n;j++)if(!visit[j]&&dist[j]<lowcast){lowcast=dist[j];temp=j;}visit[temp]=1;sum+=lowcast;for(int j=1;j<=n;j++){if(!visit[j]&&dist[j]>Map[temp][j]) dist[j]=Map[temp][j];}}return sum;}int main(){int y,x,w,z;scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j)Map[i][j]=0;elseMap[i][j]=inf;}}memset(dist,inf,sizeof(dist)); for(int i=1;i<=m;i++){scanf("%d%d%d",&x,&y,&w); Map[x][y]=w;Map[y][x]=w;}z=prime(1);printf("%d\n",z);return0;}。
kruskal算法求最小生成树
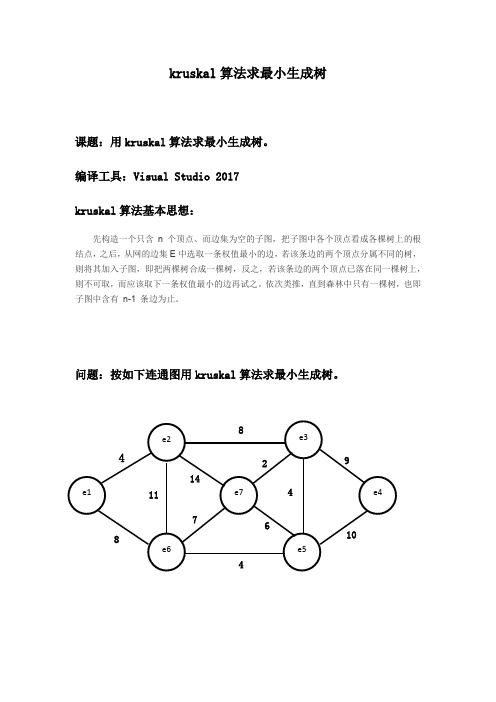
kruskal算法求最小生成树课题:用kruskal算法求最小生成树。
编译工具:Visual Studio 2017kruskal算法基本思想:先构造一个只含n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集E中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。
依次类推,直到森林中只有一棵树,也即子图中含有n-1 条边为止。
问题:按如下连通图用kruskal算法求最小生成树。
程序源码:#include <iostream>#include <algorithm>using namespace std;const int N = 100;int nodeset[N];int n, m;struct Edge { //定义结构体.int u;int v;int w;}e[N*N];bool comp(Edge x, Edge y) { //配合sort()方法对权值进行升序。
return x.w < y.w;}void Init(int n) //对集合号nodeset数组进行初始化. {for (int i = 1; i <= n; i++)nodeset[i] = i;}int Merge(int a, int b) //将e[i].u结点传递给a; e[i].v结点传递给b. {int p = nodeset[a]; //p为a结点的集结号,int q = nodeset[b]; //q为b 结点的集结号.if (p == q) return 0; //判断结点间是否回环。
若两个结点的集结号相同,则不操作,直接返回。
for (int i = 1; i <= n; i++)//若两个结点的集结号不相同,检查所有结点,把集合号是q的改为p.{if (nodeset[i] == q)nodeset[i] = p;}return 1;}int Kruskal(int n){int ans = 0;for (int i = 1; i<=m; i++)if (Merge(e[i].u, e[i].v)){cout << "A结点:" << e[i].u << "一>B结点:" << e[i].v << endl; //输出满足条件的各结点ans += e[i].w;n--;if (n == 1)return ans;}return 0;}int main() {cout << "输入总结点数(n)和总边数(m):" << endl;cin >> n >> m;Init(n);cout << "输入结点数(u),(v)和权值(w):" << endl;for (int i = 1; i <= m; i++)cin >> e[i].u >> e[i].v >> e[i].w;sort(e+1, e + m+1, comp);int ans = Kruskal(n);cout << "最小的花费是:" << ans << endl;return 0;}源码流程解析:(1)在main()中,输入结点数n与边m,n=7,m=12。
克鲁斯卡尔算法实现最小生成树

克鲁斯卡尔算法姓名:学号:班级:信工0808 成绩:1,原理由于克鲁斯卡尔算法是在图中从边长小的边开始查找,为了减少重复查找与比较的次数,直接使用快排,使边长按非降序排列。
为了使所构成的最小生成树不出现回路,则对顶点进行集合划定,father[i]保存顶点i所在的集合序号。
初始时每个顶点对应的集合序号为其顶点序号,只要两顶点a,b不再同一集合内,即可加入到最小生成树中,若father[a]<father[b]则b所在的集合序号全部改为father[a],否则,a所在的集合序号全部改为father[b]。
主要类型说明:2,struct edge{int pointA;//边的起点int pointB;//边的终点int cost;//边长};3程序代码#include<iostream>#include<iomanip>using namespace std;const int N = 6;const int MaxCost = 100;int m;//边长不为0且不重复的边的条数-1struct edge{int pointA;int pointB;int cost;};const int size = (N*N-N)/2;//无重复的边的条数,边长可能为0edge edgeList[size];//排好序的边的信息int father[N+1];//father[i]为顶点i所在的集合,按所在集合中顶点序号最小来赋值//edgecost[i][j]为顶点i+1到顶点j+1的距离int edgecost[N][N] = {0,6,1,5,0,0, 6,0,5,0,3,0, 1,5,0,5,6,4,5,0,5,0,0,2, 0,3,6,0,0,6, 0,0,4,2,6,0};void print(int edgecost[N][N]){cout<<" ";for (int i = 1; i<=N;i++){cout<<setw(4)<<i<<" ";}cout<<endl;for (int a = 0; a < N; a++){cout<<a+1<<" ";for (int b = 0; b < N; b++)cout<<setw(4)<<edgecost[a][b]<<" ";cout<<endl;}}void init(){for (int a = 1; a<=N;a++){father[a] = a;}m = 0;for (int i = 0;i<N;i++)for (int j = i+1; j<N;j++){if(edgecost[i][j] != 0){edgeList[m].cost = edgecost[i][j];}else{edgeList[m].cost = MaxCost;}edgeList[m].pointA = i+1;edgeList[m].pointB = j+1;m++;}}inline void exchang(edge &b,edge &a){edge temp;temp.cost = b.cost;temp.pointA = b.pointA;temp.pointB = b.pointB;b.cost = a.cost;b.pointA = a.pointA;b.pointB = a.pointB;a.cost = temp.cost;a.pointA = temp.pointA;a.pointB = temp.pointB;}int partion(edge * pa,int a,int b){edge * Num = pa+a;int i= a;int j= b;while(i<j){while((i<j)&(pa[i].cost<=Num->cost)) {i++;}while((i<j)&(pa[j].cost>Num->cost)) {j--;}exchang(pa[i],pa[j]);}if(pa[a].cost>pa[i].cost){exchang(pa[a],pa[i]);}return i;}void quick_sort(edge * p,int a,int b){if(a>=b) return;int r= partion(p,a,b);quick_sort(p,a,r-1);quick_sort(p,r,b);}void getMinTree(){int e =0;int a =0,b =0;int i = 0;int s;while(e<N-1){a = edgeList[i].pointA;b = edgeList[i].pointB;if ( father[a] != father[b])//a,b不在同一个集合中则不会形成回路{if (father[a] > father[b]){for (s = 1; s<=N; s++)if (father[s] == father[a] )father[s] = father[b];}else{for (s = 1; s<=N; s++)if (father[s] == father[b] )father[s] = father[a];}cout<<"<"<<a<<" , "<<b<<">"<<endl;e++;}i++;}}void main(){init();print(edgecost);quick_sort(edgeList,0,size-1);getMinTree();}4,程序结果。
最小生成树修路问题(普里姆算法,克鲁斯卡尔算法)

最⼩⽣成树修路问题(普⾥姆算法,克鲁斯卡尔算法)普⾥姆算法介绍普利姆(Prim)算法求最⼩⽣成树,也就是在包含 n 个顶点的连通图中,找出只有(n-1)条边包含所有 n 个顶点的连通⼦图,也就是所谓的极⼩连通⼦图应⽤场景-修路问题最⼩⽣成树修路问题本质就是就是最⼩⽣成树问题,先介绍⼀下最⼩⽣成树(Minimum Cost Spanning Tree),简称 MST。
给定⼀个带权的⽆向连通图,如何选取⼀棵⽣成树,使树上所有边上权的总和为最⼩,这叫最⼩⽣成树1) N 个顶点,⼀定有 N-1 条边2) 包含全部顶点3) N-1 条边都在图中4) 举例说明(如图:)5) 求最⼩⽣成树的算法主要是普⾥姆算法和克鲁斯卡尔算法思路分析1)设 G=(V,E)是连通⽹,T=(U,D)是最⼩⽣成树,V,U 是顶点集合,E,D 是边的集合2)若从顶点 u 开始构造最⼩⽣成树,则从集合 V 中取出顶点 u 放⼊集合 U 中,标记顶点 v 的 visited[u]=13)若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边,则寻找这些边中权值最⼩的边,但不能构成回路,将顶点 vj 加⼊集合 U 中,将边(ui,vj)加⼊集合 D 中,标记 visited[vj]=14)重复步骤②,直到 U 与 V 相等,即所有顶点都被标记为访问过,此时 D 中有 n-1 条边5)提⽰: 单独看步骤很难理解,我们通过代码来讲解,⽐较好理解.6)图解普利姆算法普⾥姆算法最佳实践(修路问题代码实现)import java.util.Arrays;public class PrimAlgorithm {public static void main(String[] args) {//测试看看图是否创建okchar[] data = new char[]{'A','B','C','D','E','F','G'};int verxs = data.length;//邻接矩阵的关系使⽤⼆维数组表⽰,10000这个⼤数,表⽰两个点不联通int [][]weight=new int[][]{{10000,5,7,10000,10000,10000,2},{5,10000,10000,9,10000,10000,3},{7,10000,10000,10000,8,10000,10000},{10000,9,10000,10000,10000,4,10000},{10000,10000,8,10000,10000,5,4},{10000,10000,10000,4,5,10000,6},{2,3,10000,10000,4,6,10000},};//创建MGraph对象MGraph graph = new MGraph(verxs);//创建⼀个MinTree对象MinTree minTree = new MinTree();minTree.createGraph(graph, verxs, data, weight);//输出minTree.showGraph(graph);//测试普利姆算法minTree.prim(graph, 1);//}}//创建最⼩⽣成树->村庄的图class MinTree {//创建图的邻接矩阵/**** @param graph 图对象* @param verxs 图对应的顶点个数* @param data 图的各个顶点的值* @param weight 图的邻接矩阵*/public void createGraph(MGraph graph, int verxs, char data[], int[][] weight) {int i, j;for(i = 0; i < verxs; i++) {//顶点graph.data[i] = data[i];for(j = 0; j < verxs; j++) {graph.weight[i][j] = weight[i][j];}}}//显⽰图的邻接矩阵public void showGraph(MGraph graph) {for(int[] link: graph.weight) {System.out.println(Arrays.toString(link));}}//编写prim算法,得到最⼩⽣成树/**** @param graph 图* @param v 表⽰从图的第⼏个顶点开始⽣成'A'->0 'B'->1...*/public void prim(MGraph graph, int v) {//visited[] 标记结点(顶点)是否被访问过int visited[] = new int[graph.verxs];//visited[] 默认元素的值都是0, 表⽰没有访问过// for(int i =0; i <graph.verxs; i++) {// visited[i] = 0;// }//把当前这个结点标记为已访问visited[v] = 1;//h1 和 h2 记录两个顶点的下标int h1 = -1;int h2 = -1;int minWeight = 10000; //将 minWeight 初始成⼀个⼤数,后⾯在遍历过程中,会被替换for(int k = 1; k < graph.verxs; k++) {//因为有 graph.verxs顶点,普利姆算法结束后,有 graph.verxs-1边//这个是确定每⼀次⽣成的⼦图,和哪个结点的距离最近for(int i = 0; i < graph.verxs; i++) {// i结点表⽰被访问过的结点for(int j = 0; j< graph.verxs;j++) {//j结点表⽰还没有访问过的结点if(visited[i] == 1 && visited[j] == 0 && graph.weight[i][j] < minWeight) {//替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最⼩的边)minWeight = graph.weight[i][j];h1 = i;h2 = j;}}}//找到⼀条边是最⼩System.out.println("边<" + graph.data[h1] + "," + graph.data[h2] + "> 权值:" + minWeight);//将当前这个结点标记为已经访问visited[h2] = 1;//minWeight 重新设置为最⼤值 10000minWeight = 10000;}}}class MGraph {int verxs; //表⽰图的节点个数char[] data;//存放结点数据int[][] weight; //存放边,就是我们的邻接矩阵public MGraph(int verxs) {this.verxs = verxs;data = new char[verxs];weight = new int[verxs][verxs];}}克鲁斯卡尔算法介绍克鲁斯卡尔(Kruskal)算法,是⽤来求加权连通图的最⼩⽣成树的算法。
克鲁斯卡尔算法求最小生成树

目录1.需求解析⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2目⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2任及要求⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2程思想⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2程序运行流程⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯21.5 硬件运行境及开工具⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯22.大纲⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯22.1 流程⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2抽象数据型 MFSet的定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3主程序⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4抽象数据型的定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4抽象数据型的定⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 3.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7程序⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 4.与操作明⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10果⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯104.2 解析⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯115.程与领悟⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11领悟⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯116.致⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯127.参照文件⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯121.需求解析1.1 设计题目:最小生成树1.2 设计任务及要求:随意创办一个图,利用克鲁斯卡尔算法,求出该图的最小生成树。
1.3 课程设计思想: Kruskal 算法采用了最短边策略 ( 设 G=(V,E)是一个无向连通网,令 T=(U,TE)是 G的最小生成树。
克鲁斯卡尔算法
最小生成树—克鲁斯卡尔算法克鲁斯卡其尔算法的时间复杂度为O (eloge )(e 为网中边的数目),因此它相对于普里姆算法而言,适合于求边稀疏的网的最小生成树。
克鲁斯卡尔算法从另一途径求网的最小生成树。
假设连通网N=(V ,{E}),则令最小生成树的初始状态为只有n 个顶点而无边的非连通图T=(V ,{∮}),图中每个顶点自成一个连通分量。
在E 中选择代价最小的边,若该边依附的顶点落在T 中不同的连通分量上,则将此边加入到T 中,否则舍去此边而选择下一条代价最小的边。
依次类推,直至T 中所有顶点都在同一连通分量上为止。
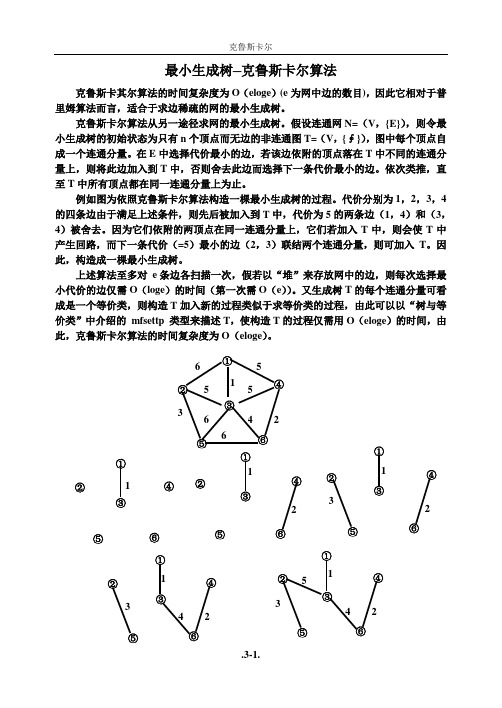
例如图为依照克鲁斯卡尔算法构造一棵最小生成树的过程。
代价分别为1,2,3,4的四条边由于满足上述条件,则先后被加入到T 中,代价为5的两条边(1,4)和(3,4)被舍去。
因为它们依附的两顶点在同一连通分量上,它们若加入T 中,则会使T 中产生回路,而下一条代价(=5)最小的边(2,3)联结两个连通分量,则可加入T 。
因此,构造成一棵最小生成树。
上述算法至多对 e 条边各扫描一次,假若以“堆”来存放网中的边,则每次选择最小代价的边仅需O (loge )的时间(第一次需O (e ))。
又生成树T 的每个连通分量可看成是一个等价类,则构造T 加入新的过程类似于求等价类的过程,由此可以以“树与等价类”中介绍的 mfsettp 类型来描述T ,使构造T 的过程仅需用O (eloge )的时间,由此,克鲁斯卡尔算法的时间复杂度为O (eloge )。
1 2 3 4 56 ① ② ③ ④ ⑤ ⑥6 5 5 6 1 2 3 4 ① ② ③ ④ ⑥5 1 ① ② ③ ④ ⑤ ⑥ 1 2 ① ② ③ ④ ⑤ ⑥ 1 2 3 ① ② ③ ④ 3 1 2 4 ① ② ③ ④ ⑤ ⑥program kruskal;label 10;const max=6;s:array[1..max,1..max] of byte=((0,6,1,5,0,0),(0,0,5,0,3,0),(0,0,0,5,6,4),(0,0,0,0,0,2),(0,0,0,0,0,6),(0,0,0,0,0,0));var p:array[1..(max*(max-1) div 2),0..2] of byte; 存所有边数(存权、两端点) f:array[1..max,1..max] of integer; 生成树邻接表q:array[1..max,1..2] of integer; 生成树链表i,j,l,m,n,zs:integer;beginfor i:=1 to max do q[i,2]:=0; 链表指针清零l:=0;for i:=1 to max do 找出所有边for j:=1 to max doif s[i,j]<>0 thenbeginl:=l+1;p[l,0]:=s[i,j];p[l,1]:=i;p[l,2]:=jend;for i:=1 to l-1 do 边按权升序排序for j:=i+1 to l doif p[i,0]>p[j,0] thenbeginzs:=p[i,0];p[i,0]:=p[j,0];p[j,0]:=zs;zs:=p[i,1];p[i,1]:=p[j,1];p[j,1]:=zs;zs:=p[i,2];p[i,2]:=p[j,2];p[j,2]:=zs;end;f[p[1,1],p[1,2]]:=p[1,0]; 第一条边加入生成树邻接表q[p[1,1],1]:=p[1,1];q[p[1,1],2]:=-p[1,1];端点加入链表,根节点链指针为负 q[p[1,2],1]:=p[1,2];q[p[1,2],2]:=p[1,1];i:=1;j:=0; I:所选边的序号,j:当前要选的边数repeati:=i+1;m:=p[i,1];n:=p[i,2]; 取当前选中边的两端点序号repeat 分别查找两端点的根if m>0 then m:=q[m,2]until m<=0;repeatif n>0 then n:=q[n,2]until n<=0;if (m<0) and (m=n) then goto 10; 若为同一根,则重选f[p[i,1],p[i,2]]:=p[i,0]; 当前边加入生成树邻接表if m=n then 当前边两端点均不在树中,则新建一棵树 beginq[p[i,1],1]:=p[i,1];q[p[i,1],2]:=-p[i,1];q[p[i,2],1]:=p[i,2];q[p[i,2],2]:=p[i,1]end;if (m<0) and (n=0) then 若一端点在某棵树中,则加入 beginq[p[i,2],1]:=p[i,2];q[p[i,2],2]:=p[i,1]end;if (n<0) and (m=0) then 若另一端点在某棵树中,则加入 beginq[p[i,1],1]:=p[i,1];q[p[i,1],2]:=p[i,2];end;if (m<0) and (n<0) then q[-n,2]:=-m; 边接两棵树j:=j+1;10:until j>max-1;for i:=1 to max do 输出生成树邻接表beginfor j:=1 to max do write(f[i,j]);writeln;end;end.。
JS实现最小生成树之克鲁斯卡尔(Kruskal)算法

JS实现最⼩⽣成树之克鲁斯卡尔(Kruskal)算法克鲁斯卡尔算法打印最⼩⽣成树: 构造出所有边的集合 edges,从⼩到⼤,依次选出筛选边打印,遇到闭环(形成回路)时跳过。
JS代码:1//定义邻接矩阵2 let Arr2 = [3 [0, 10, 65535, 65535, 65535, 11, 65535, 65535, 65535],4 [10, 0, 18, 65535, 65535, 65535, 16, 65535, 12],5 [65535, 18, 0, 22, 65535, 65535, 65535, 65535, 8],6 [65535, 65535, 22, 0, 20, 65535, 65535, 16, 21],7 [65535, 65535, 65535, 20, 0, 26, 65535, 7, 65535],8 [11, 65535, 65535, 65535, 26, 0, 17, 65535, 65535],9 [65535, 16, 65535, 65535, 65535, 17, 0, 19, 65535],10 [65535, 65535, 65535, 16, 7, 65535, 19, 0, 65535],11 [65535, 12, 8, 21, 65535, 65535, 65535, 65535, 0],12 ]1314 let numVertexes = 9, //定义顶点数15 numEdges = 15; //定义边数1617// 定义图结构18function MGraph() {19this.vexs = []; //顶点表20this.arc = []; // 邻接矩阵,可看作边表21this.numVertexes = null; //图中当前的顶点数22this.numEdges = null; //图中当前的边数23 }24 let G = new MGraph(); //创建图使⽤2526//创建图27function createMGraph() {28 G.numVertexes = numVertexes; //设置顶点数29 G.numEdges = numEdges; //设置边数3031//录⼊顶点信息32for (let i = 0; i < G.numVertexes; i++) {33 G.vexs[i] = 'V' + i; //scanf('%s'); //ascii码转字符 //String.fromCharCode(i + 65);34 }35 console.log(G.vexs) //打印顶点3637//邻接矩阵初始化38for (let i = 0; i < G.numVertexes; i++) {39 G.arc[i] = [];40for (j = 0; j < G.numVertexes; j++) {41 G.arc[i][j] = Arr2[i][j]; //INFINITY;42 }43 }44 console.log(G.arc); //打印邻接矩阵45 }4647function Edge() {48this.begin = 0;49this.end = 0;50this.weight = 0;51 }5253function Kruskal() {54 let n, m;55 let parent = []; //定义⼀数组⽤来判断边与边是否形成环路56 let edges = []; //定义边集数组5758for (let i = 0; i < G.numVertexes; i++) {59for (let j = i; j < G.numVertexes; j++) { //因为是⽆向图所以相同的边录⼊⼀次即可,若是有向图改为060if (G.arc[i][j] != 0 && G.arc[i][j] != 65535) {61 let edge = new Edge();62 edge.begin = i;63 edge.end = j;64 edge.weight = G.arc[i][j];65 edges.push(edge);66 }67 }68 }6970 edges.sort((v1, v2) => {71return v1.weight - v2.weight72 });7374 console.log('**********打印所有边*********');75 console.log(edges);7677for (let i = 0; i < G.numVertexes; i++) {78 parent[i] = 0;79 }8081for (let i = 0; i < edges.length; i++) {82 n = Find(parent, edges[i].begin)83 m = Find(parent, edges[i].end)84if (n != m) { //假如n与m不等,说明此边没有与现有⽣成树形成环路85 parent[n] = m;86 console.log("(%s,%s) %d", G.vexs[edges[i].begin], G.vexs[edges[i].end], edges[i].weight);87 }88 }89 }909192function Find(parent, f) { //查找连线顶点的尾部下标93while (parent[f] > 0) {94 f = parent[f]95 }96return f;97 }9899 createMGraph();100 console.log('*********打印最⼩⽣成树**********')101 Kruskal();打印结果:代码部分过程解析:当i=7时,第82⾏,调⽤Find函数,会传⼊参数edges[7].begin=5。
普里姆算法和克鲁斯卡尔算法

普里姆算法和克鲁斯卡尔算法普里姆算法和克鲁斯卡尔算法介绍在图论中,最小生成树是一种重要的概念。
最小生成树是指在一个加权连通图中,找到一棵生成树,使得所有边的权值之和最小。
其中,Prim算法和Kruskal算法是两种常用的求解最小生成树的方法。
Prim算法Prim算法是一种贪心算法,它从一个顶点开始构建最小生成树。
具体实现过程如下:1. 选取任意一个顶点作为起始点,并将其标记为已访问。
2. 遍历与该顶点相邻的所有边,并将这些边加入一个优先队列中。
3. 从优先队列中选取一条权值最小的边,并将与之相邻的未被访问过的顶点标记为已访问。
4. 重复步骤2和3,直到所有顶点都被访问过。
代码实现```def prim(graph, start):visited = set()visited.add(start)edges = []min_span_tree_cost = 0while len(visited) != len(graph.keys()):candidate_edges = []for node in visited:for edge in graph[node]:if edge[1] not in visited:candidate_edges.append(edge)sorted_edges = sorted(candidate_edges, key=lambda x:x[2]) min_edge = sorted_edges[0]edges.append(min_edge)min_span_tree_cost += min_edge[2]visited.add(min_edge[1])return edges, min_span_tree_cost```时间复杂度Prim算法的时间复杂度为O(ElogV),其中E为边数,V为顶点数。
因为每次需要从优先队列中选取一条权值最小的边,所以需要使用堆来实现优先队列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录1.需求分析 (2)1.1 设计题目 (2)1.2 设计任务及要求 (2)1.3课程设计思想 (2)1.4 程序运行流程 (2)1.5软硬件运行环境及开发工具 (2)2.概要设计 (2)2.1流程图 (2)2.2抽象数据类型MFSet的定义 (3)2.3主程序 (4)2.4抽象数据类型图的定义 (4)2.5抽象数据类型树的定义 (5)3.详细设计 (7)3.1程序 (7)4.调试与操作说明 (10)4.1测试结果 (10)4.2调试分析 (11)5.课程设计总结与体会 (11)5.1总结 (11)5.2体会 (11)6. 致谢 (12)7. 参考文献 (12)1.需求分析1.1 设计题目:最小生成树1.2 设计任务及要求:任意创建一个图,利用克鲁斯卡尔算法,求出该图的最小生成树。
1.3 课程设计思想:Kruskal算法采用了最短边策略(设G=(V,E)是一个无向连通网,令T=(U,TE)是G的最小生成树。
最短边策略从TE={}开始,每一次贪心选择都是在边集E中选择最短边(u,v),如果边(u,v)加入集合TE中不产生回路,则将边(u,v)加入边集TE中,并将它在集合E中删去。
),它使生成树以一种任意的方式生长,先让森林中的树木随意生长,每生长一次就将两棵树合并,最后合并成一棵树。
1.4程序运行流程:1)提示输入顶点数目;2)接受输入,按照项目要求产生边权值的随机矩阵;然后求解最小生成树;3)输出最小生成树并且退出;1.5 软硬件运行环境及开发工具:VC2.概要设计2.1流程图开始定义数据类型定义图定义树定义图的顶点数和边数Kruskal算法主程序图1流程图2.2抽象数据类型MFSet的定义:ADT MFSet {数据对象:若设S是MFSet型的集合,则它由n(n>0)个子集Si(i = 1,2...,n)构成,每个子集的成员代表在这个子集中的城市。
数据关系:S1 U S2 U S3 U... U Sn = S, Si包含于S(i = 1,2,...n)Init (n): 初始化集合,构造n个集合,每个集合都是单成员,根是其本身。
rank 数组初始化0Find(x):查找x所在集合的代表元素。
即查找根,确定x所在的集合,并路径压缩。
Merge(x, y):检查x与y是否在同一个集合,如果在同一个集合则返回假,否则按秩合并这两个集合并返回真。
}2.3主程序:int main(){初始化;while (条件){接受命令;处理命令;}return 0;}2.4抽象数据类型图的定义如下:ADT Graph{数据对象V:V是具有相同特性的数据元素的集合,成为顶点集。
数据关系R:R={VR} VR={<v,w>|v,w∈V且P(v,w),<v,w>表示从v 到w的弧,谓词P(v,w)定义了弧<v,w>的意义或信息}基本操作P:CreateGraph(&G,V,VR);初始条件:V是图的顶点集,VR是图中弧的集合。
操作结果:按V和的VR定义构造图G。
DestoryGraph(&G);初始条件:图G存在。
操作结果:销毁图G。
LocateVex(G,u);初始条件:图G存在,u和G中是顶点有相同特征。
操作结果:若G中存在顶点u,则返回该顶点在图中位置;否则返回其他信息。
GetVex(G,v);初始条件:图G存在,v是G中某个顶点。
操作结果:返回v的值。
PutVex(&G,v,value);初始条件:图G存在,v是G中某个顶点。
操作结果:对V赋值value,FirstAdjVex(G,v);初始条件:图G存在,v是G中某个顶点。
操作结果:返回v的第一个邻接顶点。
若顶点在G中没有顶点,则返回“空”。
NextAdjVex(G,v,w);初始条件:图G存在,v是G中某个顶点,w是v的邻接顶点。
操作结果:返回v的(相对于w的)下一个邻接顶点。
若w是v的最后一个邻接顶点,则返回“空”。
InsertVex(&G,v);初始条件:图G存在,v和途中顶点有相同特征。
操作结果:在图G中添加新顶点v。
DeleteVex(&G,v);初始条件:图G存在,v是G中某个顶点。
操作结果:删除G中顶点v及其相关的弧。
InsertArc(&G,v,w);初始条件:图G存在,v和w是G中两个顶点。
操作结果:在G中添加弧<v,w>,若G是无向的,则还增添对称弧<v,w>。
DeleteArc(&G,v,w);初始条件:图G存在,v和w是G中两个顶点。
操作结果:在G中删除弧<v,w>,若G是无向的,则还删除对称弧<v,w>。
DFSTravrese(G,Visit());初始条件:图G存在,Visit是顶点的应用函数。
操作结果:对图进行深度优先遍历。
在遍历过程中对每个顶点调用函数Visit一次且仅一次。
一旦Visit()失败,则操作失败。
BFSTravrese(G,Visit());初始条件:图G存在,Visit是顶点的应用函数。
操作结果:对图进行广度优先遍历。
在遍历过程中对每个顶点调用函数Visit 一次且仅一次。
一旦Visit()失败,则操作失败。
}ADT Graph2.5抽象数据类型树的定义如下:ADT Tree{数据对象D:D是具有相同特性数据元素的集合。
数据关系R:若D为空集,则称为空树;若D仅含一个元素数据,则R为空集,否则R={H},H是如下二元关系:(1)在D中存在唯一的称为根的数据元素root,它在关系H 下无前驱;(2)若D-{root}≠Φ,则存在D-{root}的一个划分D1,D2,…,D m(m>0),对任意j≠k(1≤j,k≤m)有D j∩D k=Φ,且对任意的I(1≤i≤m),惟一存在数据元素x i∈D i有<root,x i>∈H;(3)对应于D-{root}的划分,H-{<root,x1>,…,<roor,x m>}有惟一的一个划分H1,H2,…,H m(m>0),对任意j≠k(1≤j,k≤m)有H j∩H k=Φ,且对任意I(1≤i≤m),H i是D i上的二元关系,(D i,{H i})是一棵符合本定义的树,称为跟root的子树。
基本操作P:InitTree(&T);操作结果:构造空树T。
DestoryTree(&T);初始条件:树T存在。
操作结果:销毁树T。
CreateTree(&T,definition);初始条件:definition给出树T的定义。
操作结果:按definition构造树T。
ClearTree(&T);初始条件:树T存在。
操作结果:将树T清为空树。
TreeEmptey(T);初始条件:树T存在。
操作结果:若T为空树,则返回TRUE,否则FALSE。
TreeDepth(T);初始条件:树T存在。
操作结果:返回T的深度。
Root(T);初始条件:树T存在。
操作结果:返回T的跟。
Value(T,cur_e);初始条件:树T存在,cur_e是T中某个结点。
操作结果:返回cur_e的值。
Assign(T,cur_e,value);初始条件:树T存在,cur_e是T中某个结点。
操作结果:结点cur_e赋值为value。
Parent(T,cur_e);初始条件:树T存在,cur_e是T中某个结点。
操作结果:若cur_e是T的非根结点,则返回它的双亲,否则函数值为“空”。
LeftChild(T,cur_e);初始条件:树T存在,cur_e是T中某个结点。
操作结果:若cur_e是T的非叶子结点,则返回它的最左子,否则返回“空”。
RightSibling(T,cur_e);初始条件:树T存在,,cur_e是T中某个结点。
操作结果:若cur_e有右兄弟,则返回它的右兄弟,否则函数值为“空”。
InsertChild(&T,&p,I,c);初始条件:树T存在,P指向T中某个结点,1≤i≤p所指向的结点度数+1,非空树c与T不相交。
操作结果:插入c为T中p指结点的第i棵子树。
DeleteChild(&T,&p,i);初始条件:树T存在,p指向T中某个结点,1≤i≤p指结点的度。
操作结果:删除T中p所指结点的第i棵子树。
TraverseTree(T,Visit());初始条件:树T存在,Visit是对结点操作的应用函数。
操作结果:按某种次序对T的每个结点调用函数visit()一次且至多一次。
一旦vista()失败,则操作失败。
}ADT Tree3.详细设计3.1程序:如下#include<stdio.h>#include<stdlib.h>#include<string.h>#define MAX_NAME 5#define MAX_VERTEX_NUM 30typedef char Vertex[MAX_NAME];/*顶点名字数组*/typedef int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];/*邻接矩阵*/typedef struct /*定义图*/{Vertex vexs[MAX_VERTEX_NUM];AdjMatrix arcs;int vexnum,arcnum;}MGraph;int LocateVex(MGraph *G,Vertex u){int i;for(i=0;i<G->vexnum;++i)if(strcmp(G->vexs[i],u)==0)return i;return -1;}void CreateGraph(MGraph *G){int i,j,k,w;Vertex va,vb;printf("请输入无向网G的顶点数和边数(以空格作为间隔): \n");scanf("%d %d",&G->vexnum,&G->arcnum);printf("请输入%d个顶点的名字(小于%d个字符):\n",G->vexnum,MAX_NAME);for(i=0;i<G->vexnum;++i) /*构造顶点集*/scanf("%s",G->vexs[i]);for(i=0;i<G->vexnum;++i) /*初始化邻接矩阵*/for(j=0;j<G->vexnum;++j)G->arcs[i][j]=0x7fffffff;printf("请输入%d条边的顶点1 顶点2 权值(以空格作为间隔):\n",G->arcnum);for(k=0;k<G->arcnum;++k){scanf("%s%s%d%*c",va,vb,&w);i=LocateVex(G,va);j=LocateVex(G,vb);G->arcs[i][j]=G->arcs[j][i]=w; /*对称*/}}void kruskal(MGraph G){FILE *fpt;fpt = fopen("9.txt","w");/*打开文档,写入*/fprintf(fpt,"最小生成树的各条边为:\n");int i,j;int k=0,a=0,b=0,min=G.arcs[a][b],min_out;printf("最小生成树的各条边为:\n");while(k<G.vexnum-1){for(i=0;i<G.vexnum;++i)for(j=i+1;j<G.vexnum;++j)if(G.arcs[i][j]<min){min=G.arcs[i][j];a=i;b=j;}min_out=min;min=G.arcs[a][b]=0x7fffffff;printf("%s-%s-%d\n",G.vexs[a],G.vexs[b],min_out);fprintf(fpt,"%s-%s-%d\n",G.vexs[a],G.vexs[b],min_out);k++;}fclose(fpt);}void main(){MGraph g;CreateGraph(&g);kruskal(g);}4. 调试与操作说明4.1测试结果:如下图图2测试结果1图3测试结果24.2调试分析本程序利用克鲁斯卡尔算法求最小生成树数据结构清晰因而调试比较顺利。
