几种求解最小生成树的算法 (论文)
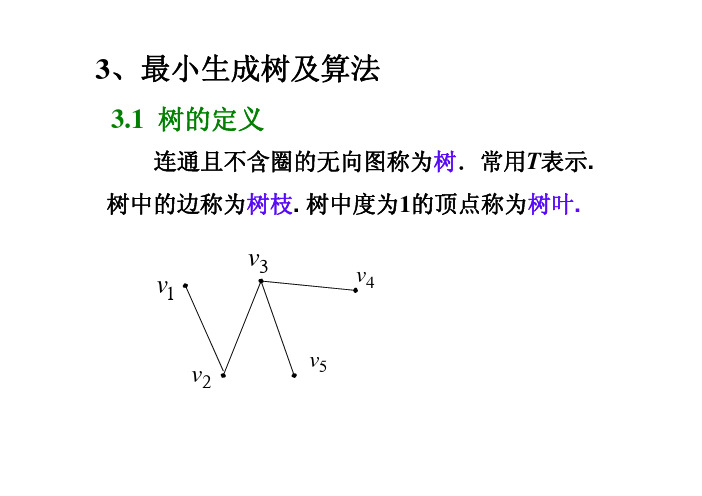
最小生成树及算法
|S|=n-1, 说明是树 最后S={a1, a2, a3,… ,an-1}
B. 破圈法
算法2 步骤如下: (1) 从图G中任选一棵树T1. (2) 加上一条弦e1,T1+e1中 生成一个圈. 去掉此圈中最大权边,得到新树T2, 以T2代T1,重复(2)再检查剩余的弦,直到全部弦 检查完毕为止.
例 n个城市,各城市之间的距离如下表(距离为 ∞,表示两个城市之间没有直接到达的线路)。 从一个城市出发走遍各个城市,如何选择最优的 旅行路线.
性质 任何一棵树至少有两片树叶。 证明 设树T=(V,E),结点数为v,因T是连通的,因 此,树中每个结点vi,有deg(vi)1,且 deg(vi)=2(v-1)=2v-2. 若T中结点度数都大于2,则 deg(vi) 2v,矛盾。 若T中只有一个结点度数为1,则 deg(vi) 2(v-1)+1=2v-1 矛盾。
4 3
v5 3 v6
3.5 生成树的计数
1、一些概念 • • ① 设 G 是一个连通图。 T , T 分别是 G 的两个生成树,如果 E (T ) E (T ) ,则认为 T , T 是 G 的两个不同的生成树。 G 的 不同的生成树个数用 (G) 表示。 如:
v1 v3 v2 v3 v1 v2 v3 v1 v2 v3 v1 v2
证明:⑴⑵ 当 n=2时, e=1, 显然 e=n-1. 假设n=k-1时命题成立,当n=k时,因G无圈、连 通,则至少有一条边(u,v),deg(u)=1,删去u,得到 连通无圈的图G1, G1的边数e1,结点数n1满足: e1=n1-1= k-2 将u,边(u,v)加到 G1中,得到T,且 e=n-1.
( K3 ) 3。 则:
② G-e: 从G中去掉边e后所得的图。
一种求解最小生成树问题的算法

c m pe t fteag rtm ea ay e . t p l steag rtm otehg wa y tm ngn ei gc nsrcinpln, er s l r v h aiiy o lxi o lo h a n lz d I pi lo i y h i r a e h h t h ih y s se e i e rn o t t a t e ut p o et ev l t u o h s d
摘
要: 基于节 点合并和反向追踪的思想 ,提出一种求解最小 生成树 问题 的算法 。该算法依据 网络邻接矩 阵,将与源 节点相邻 的节点逐步
合并 为新的源 节点 , 网络中的所有节点合树 ,对算法正确性与 算法复杂 度进 使 行分析 。将该算法应用于某高速公路 网工程建设 方案,结果证 明了算法的有效性。
o h e ag rt ft l o hm. i
[ e o d lMi m m S an g r ( T ; o e o b ao ;ee e i c o ai ; o t o t bl r y aj e t a i K yw r s n u n i e MS )n m i t n r r r t n c g f n i e a a; d c n m tx i p nT e d c ni v s d ei t n r p n l r r a a r D : 03 6 0 s . 0 — 2 . 1 . . 2 OI 1 . 9 .s 1 03 8 0 1 3 8 9 in 0 4 2 20
3 GeeaAr met e at n layR pee tt eO c inh i e in B oi 2 0 6 Chn ) . nrl ma n pr D met i r e rsna v f enTa su go , aj7 10 , ia Mit i i i R
量子遗传算法求解度约束最小生成树

中 图法分 类 号:P 0 . T 3 1 文 献标识 码 : 6 A 文章 编号 :6 2 2 6 (0 0 0 — 0 8 0 17 — 8 8 2 1 )6 0 3 — 5
( ) 度 约束 , 1为 约束 条 件 ( ) ( ) 2 ,3 保证 了所得 到 的是一 棵 生成树 。
22量 子遗 传 算 法 .
遗 传算 法 (e e ca oi m, A) 模拟 生 物进 化过 程 中优 胜劣 汰 规则 与 群体 内部 染 色体信 息 交换 gn t l r h G 是 i g t
mn =∑ ∑ i Z 鳓
i =l = 1
() 1
() 2
≤}f1 ̄ CV s S _ , S ,≠
i dE
∑ ∑ : 一 n1
i1 j l Leabharlann = () 3 ∈(, , , ∈V 0 1) iJ
这里, 1边(√ 在最优树中, , ) 产0为其他。 变量 II s为集合S中所含图 G的接点个数。 约束条件
有 成熟 的算法 进行 有 效求解 。 圆但如果 对生 成树 中的各 顶点 度数(er) d ge再加 上一 定 的限制 。 能超 过 即不 预 先 给定 的数值 , 问题 的性 质 将变 得截 然不 同 。在解 决不 同研 究领 域 中的实 际 问题 时 , 则 由于 要求 不 同 , 往会 对最 小 生成 树 问题 产 生许 多 限制 , 往 节点 带 有 度约束 的最小 生 成树 就 是其 中一类重 要 的度 约
求最小生成树问题,常用的方法

求最小生成树问题,常用的方法最小生成树(Minimum Spanning Tree)问题是一个经典的图论问题,其涉及到给定一个加权无向图,求其最小的生成树。
在实际问题中,求解最小生成树问题非常重要。
例如,最小生成树问题被广泛应用于网络设计、电路布线、机器学习等众多领域。
本文将介绍求解最小生成树问题的常用方法,包括Kruskal算法、Prim算法和Boruvka算法。
我们将详细介绍这些算法的原理和步骤,并给出各种算法的优缺点和适用情况。
1. Kruskal算法Kruskal算法是一种基于贪心策略的算法。
它首先将所有边按照权重大小排序,然后从小到大遍历边。
对于每个边,如果它连接了两个不同的连通块,则将这两个连通块合并成一个。
重复这个过程,直到所有的边都被考虑完。
最终的联通块就构成了最小生成树。
Kruskal算法具有简单、高效、容易实现的特点。
它的时间复杂度为O(E log E),其中E为边的数量。
Kruskal 算法的实现需要使用并查集。
Kruskal算法的优点是它是一种局部最优的策略,因此它能够在众多情况下得到最优解。
另外,它能够处理稀疏图和稠密图,因为它不需要全局访问图的结构。
2. Prim算法Prim算法也是一种基于贪心策略的算法。
它从一个任意的节点开始,不断加入与已经加入的节点相邻的最短边,直到所有节点都被加入。
这个过程类似于将一个连通块逐渐扩张为最小生成树。
Prim算法的时间复杂度为O(E log V),其中E为边的数量,V为节点的数量。
Prim算法的实现需要使用堆数据结构来进行边的最短距离的管理。
Prim算法的优点是它比Kruskal算法更加容易实现和理解。
另外,Prim算法能够处理不连通图,因为它从任意一个节点开始加入边。
此外,Prim算法也能够处理含有负权重的边的图。
3. Boruvka算法Boruvka算法是一种基于分治策略的算法。
它首先将所有的节点看作单独的连通块,然后每个连通块都选择当前权重最小的边加入。
用破圈法求最小生成树的算法

用破圈法求最小生成树的算法
求最小生成树是搜索树上每条边将权值加起来最小的那棵树,也就是要
求在给定顶点的一组边的条件下求出最小的生成树,一般采用贪心算法来求解。
其中最常用的算法就是破圈法。
破圈法实质上是 Prim 算法的改进,是一种贪心算法。
它的基本思想是:试着将边依次加入最小生成树中,当已生成的最小生成树中的边形成了一个
环的时候,其中的边中权值最大的一条被舍弃,存在于两个不同的顶点间。
破圈法求最小生成树算法基本步骤如下:
1.初始化最小生成树,构造一个空集合;
2.从贴源点开始,找出所有连接源点的边中权值最小的增加一条边到空集合中;
3.重复上述步骤,在剩余边权中选出最小值,增加一条边,并保证了加入当
前边后不产生环;
4.当把所有边都添加到集合中,即得到最小生成树;
破圈法的复杂度是O(n^2),由于它具有简单的求解过程和易于实现的特性,因而得到广泛的应用。
破圈法非常适合在网络中采用,它可以容易的获
得一条路径的最小权值生成树从而实现网络的最佳路径匹配。
破圈法可以证明:当每一条边都属于给定顶点集合时,最小生成树一定
存在。
因此它在可以用来求解最小生成树的问题中是非常有效的。
最小生成树及克鲁斯卡尔算法

最小生成树及克鲁斯卡尔算法
最小生成树是指在一个连通的无向图中,找到一棵生成树,使得所有
边的权值之和最小。
克鲁斯卡尔算法是一种用来求解最小生成树的贪
心算法。
克鲁斯卡尔算法的基本思想是将所有边按照权值从小到大排序,然后
依次加入生成树中,如果加入某条边会形成环,则不加入该边。
直到
生成树中有n-1条边为止,其中n为图中节点的个数。
克鲁斯卡尔算法的时间复杂度为O(ElogE),其中E为边的数量。
因为需要对所有边进行排序,所以时间复杂度与边的数量有关。
最小生成树的应用非常广泛,例如在网络设计、电力传输、交通规划
等领域都有重要的应用。
在网络设计中,最小生成树可以用来构建网
络拓扑结构,使得网络的总成本最小。
在电力传输中,最小生成树可
以用来确定输电线路的布局,使得电力传输的成本最小。
在交通规划中,最小生成树可以用来确定道路的布局,使得交通运输的成本最小。
除了克鲁斯卡尔算法,还有其他求解最小生成树的算法,例如Prim算法、Boruvka算法等。
这些算法的基本思想都是贪心算法,但具体实
现方式有所不同。
总之,最小生成树是图论中的一个重要问题,克鲁斯卡尔算法是一种常用的求解最小生成树的算法。
在实际应用中,需要根据具体情况选择合适的算法,并结合实际需求进行优化。
k-means论文

对k-means聚类算法的改进研究摘要:本文针对k-means算法对初值的依赖性,基于最小生成树原理选取聚类中心进行聚类。
根据寻找最优初值的思想提出了一种改进的k-means算法,将最小生成树的构造算法之一的卡斯克鲁尔(Kruskal Algorithm)算法以及贪心算法(Greedy Algorithm)的思想引入到k-means算法中。
关键字:k-means算法最小生成树贪心策略一、算法的改进思路的形成无论是原始的k-means算法还是加入了聚类准则函数的k-means算法,都有一个共同的特点,即采用两阶段反复循环过程,算法结束的条件是不再有数据元素被重新分配:1)指定聚类,即指定数据x i到某一个聚类,使得它与这个聚类中心的距离比它到其它聚类中心的距离要近;2)修改聚类中心。
k-means算法中急需解决的问题主要有三个:(l)在k-means算法中,k是事先给定的,这个k值的选定是很难估计的。
很多时候,我们事先并不知道给定的数据集应分成多少类最合适,这也是k-means 算法的一个不足。
有的算法是通过类的自动合并和分裂,得到较为合理的类型数目k,例如ISODALA算法。
关于k-means算法中聚类数目k值的确定,有些根据方差分析理论,应用混合F统计量来确定最佳分类数,并应用了模糊划分墒来验证最佳分类数的正确性。
在文献[26]中,使用了一种结合全协方差矩阵的RPCL算法,并逐步删除那些只包含少量训练数据的类。
而其中使用的是一种称为次胜者受罚的竞争学习规则,来自动决定类的适当数目。
它的思想是:对每个输入而言,不仅竞争获胜单元的权值被修正以适应输入值,而且对次胜单元采用惩罚的方法,使之远离输入值。
(2)在k-means算法中常采用误差平方和准则函数作为聚类准则函数,考察误差平方和准则函数发现:如果各类之间区别明显且数据分布稠密,则误差平方和准则函数比较有效;但是如果各类的形状和大小差别很大,为使误差平方和的值达到最小,有可能出现将大的聚类分割的现象。
克鲁斯卡尔算法求最小生成树完整代码

克鲁斯卡尔算法是一种用来求解最小生成树(Minimum Spanning Tree)的经典算法,它采用了贪心策略,能够高效地找到图中的最小生成树。
下面将为大家介绍克鲁斯卡尔算法的完整代码,希望对大家有所帮助。
1. 算法思路克鲁斯卡尔算法的基本思路是:首先将图中的所有边按照权值进行排序,然后从小到大依次考虑每条边,如果加入该边不会构成环,则将其加入最小生成树中。
在算法执行过程中,我们需要使用并查集来判断是否会构成环。
2. 代码实现接下来,我们将给出克鲁斯卡尔算法的完整代码,代码使用C++语言编写,具体如下:```cpp#include <iostream>#include <vector>#include <algorithm>using namespace std;// 定义图的边struct Edge {int u, v, weight;Edge(int u, int v, int weight) : u(u), v(v), weight(weight) {} };// 定义并查集class UnionFind {private:vector<int> parent;public:UnionFind(int n) {parent.resize(n);for (int i = 0; i < n; i++) {parent[i] = i;}}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}void Union(int x, int y) {int root_x = find(x);int root_y = find(y);if (root_x != root_y) {parent[root_x] = root_y;}}};// 定义比较函数用于排序bool cmp(const Edge a, const Edge b) {return a.weight < b.weight;}// 克鲁斯卡尔算法vector<Edge> kruskal(vector<Edge> edges, int n) { // 先对边进行排序sort(edges.begin(), edges.end(), cmp);// 初始化最小生成树的边集vector<Edge> res;UnionFind uf(n);for (int i = 0; i < edges.size(); i++) {int u = edges[i].u, v = edges[i].v, weight = edges[i].weight; // 判断是否构成环if (uf.find(u) != uf.find(v)) {uf.Union(u, v);res.push_back(edges[i]);}}return res;}// 测试函数int m本人n() {vector<Edge> edges;edges.push_back(Edge(0, 1, 4));edges.push_back(Edge(0, 7, 8));edges.push_back(Edge(1, 2, 8));edges.push_back(Edge(1, 7, 11));edges.push_back(Edge(2, 3, 7));edges.push_back(Edge(2, 5, 4));edges.push_back(Edge(2, 8, 2));edges.push_back(Edge(3, 4, 9));edges.push_back(Edge(3, 5, 14));edges.push_back(Edge(4, 5, 10));edges.push_back(Edge(5, 6, 2));edges.push_back(Edge(6, 7, 1));edges.push_back(Edge(6, 8, 6));edges.push_back(Edge(7, 8, 7));vector<Edge> res = kruskal(edges, 9);for (int i = 0; i < res.size(); i++) {cout << res[i].u << " " << res[i].v << " " << res[i].weight << endl;}return 0;}```3. 算法实例上述代码实现了克鲁斯卡尔算法,并对给定的图进行了最小生成树的求解。
克里斯卡尔算法最小生成树

克里斯卡尔算法最小生成树什么是克里斯卡尔算法?克里斯卡尔算法是一种求解最小生成树(Minimum Spanning Tree, MST)的算法,它采用贪心算法的思想,在给定一个连通图的情况下,通过逐步选择边来生成树,最终得到权值和最小的生成树。
为了更好地理解克里斯卡尔算法,我们首先要明确最小生成树的概念。
在一个连通图中,最小生成树是指连接图中所有顶点的树,并且树上所有边的权值之和最小。
生成树是一个无环的连通图,具有n个顶点的连通图的生成树必然含有n-1条边。
克里斯卡尔算法的步骤如下:1. 初始化:将图中的每个顶点看作是一个单独的树,每个树只包含一个节点。
同时,创建一个空的边集合用于存储最小生成树的边。
2. 对所有边按照权值进行升序排列。
3. 依次选择权值最小的边,并判断该边连接的两个节点是否属于不同的树(不属于同一个连通分量)。
4. 如果两个节点不属于同一个树,则将这条边添加到边集合中,并将两个节点合并为同一个连通分量。
5. 重复步骤3和步骤4,直到最小生成树的边数达到n-1条为止。
6. 返回边集合,即为最小生成树。
通过这个步骤的执行,克里斯卡尔算法能够保证运行过程中生成的树权值和是最小的。
这是因为在选择边时,我们总是选择权值最小且不会形成环路的边,这样生成的树就不会包含多余的边。
需要注意的是,克里斯卡尔算法适用于带权无向连通图,如果是带权有向图,需要先进行转化为无向图的操作。
另外,克里斯卡尔算法在实际应用中有着广泛的应用,比如网络设计、电路设计以及地图路线规划等领域。
总结一下,克里斯卡尔算法是一种通过贪心思想解决最小生成树问题的算法。
它通过逐步选择权值最小的边,并将不同的树合并为一个连通分量的方式,生成一个权值和最小的生成树。
在实际应用中,克里斯卡尔算法具有重要的意义,能够为我们提供高效、经济的解决方案。
通过了解和学习克里斯卡尔算法,我们能够更好地理解图论中的最小生成树问题,并运用其解决实际问题。
克鲁斯卡尔算法求最小生成树的最短路径

克鲁斯卡尔算法求最小生成树的最短路径克鲁斯卡尔算法的核心思想是从图的边集中选取边来构建最小生成树,首先将图中的所有边按照权重进行排序。
然后依次取最小权重的边,如果这条边的加入不会形成环路,则将它加入最小生成树的边集中。
重复这个过程,直到最小生成树中的边数等于顶点数减一,或者所有的边都已经考虑过。
假设有一个包含n个顶点的带权无向图G=(V,E),其中,V表示顶点的集合,E表示边的集合。
假设我们要求解G的最小生成树。
1.初始化边集E'为空集,集合S={v},v是图中任意一个顶点。
2.对所有的边进行排序,按照边的权重从小到大排列。
3.从排序后的边集中依次选取边e,如果边e的两个顶点都不在集合S中,则将边e加入集合S,并加入边集E'中。
4.重复步骤3,直到E'中的边数等于n-1在克鲁斯卡尔算法中,需要使用并查集来判断选定的边e是否会形成环路。
并查集是一种数据结构,用于维护元素的等价关系。
它有两个主要操作,即查找和合并。
使用并查集的步骤如下:1.初始化并查集,使得每个元素都是一个单独的集合。
2.对每一条边e=(u,v),如果u和v在同一个集合中,则说明加入这条边会形成环路;否则,将这两个集合合并。
3.重复步骤2,直到所有的边都考虑过。
接下来,我们通过一个具体的例子来说明克鲁斯卡尔算法的具体过程。
假设有以下的带权无向图G=(V,E),其中,V={A,B,C,D,E,F,G},E为边的集合,每条边的权重如下:AE:5AB:7AG:8BF:7BC:9CD:5CG:9DE:15DF:6EG:11EF:8FG:9按照权重对边进行排序:CD:5AE:5DF:6AB:7BF:7EF:8AG:8CG:9BC:9FG:9DE:15EG:11从最小的边开始选取,首先选取CD:5,加入到最小生成树的边集中。
最小生成树的边集:{"CD:5"}接下来选取AE:5,加入到最小生成树的边集中。
最小生成树的经典算法

最小生成树(Minimum Spanning Tree,简称MST)是一个连接图中所有节点且权值之和最小的树。
有两个经典算法可以解决最小生成树问题:普里姆算法(Prim's Algorithm)和克鲁斯卡尔算法(Kruskal's Algorithm)。
1. 普里姆算法(Prim's Algorithm):
普里姆算法是一种贪心算法,从一个初始节点开始,逐步选择与当前生成树相邻的边中权值最小的边,将其加入生成树,然后扩展到新加入的节点。
该算法的基本步骤如下:
1. 选择初始节点,将其标记为已访问。
2. 从已访问的节点中选择一条边,该边的权值最小且连接一个未访问的节点。
3. 将该边和相应的节点加入生成树,并标记该节点为已访问。
4. 重复步骤2和步骤3,直到所有节点都被访问。
2. 克鲁斯卡尔算法(Kruskal's Algorithm):
克鲁斯卡尔算法也是一种贪心算法,它通过按权值升序的顺序逐渐选择图中的边,如果选择某条边不形成回路,则将其加入生成树。
该算法的基本步骤如下:
1. 将图中所有边按照权值升序排列。
2. 从最小权值的边开始,依次选择每条边。
3. 如果选择某条边不形成回路,则将其加入生成树,否则舍弃该边。
4. 重复步骤2和步骤3,直到生成树中包含了所有节点。
这两种算法都能够有效地求解最小生成树问题,选择使用哪个算法通常取决于具体的问题需求、图的规模和边的数量。
在实际应用中,这两种算法都有广泛的应用。
国家集训队2004论文集_汪汀

可知如果(+a1,-b2)和(+a2,-b1)都是 T 的可行交换,则有ω(b2)≤ω(a1),ω(b1)≤ω (a2),故ω(b1)+ω(b2)≤ω(a1)+ω(a2); 否则,或者(+a1,-b2)或者(+a2,-b1)不是 T 的 可行交换,根据引理 1,T’=T+{a1,a2}-{b1,b2}仍然是 T 的 k 度限制生成树,则ω (T)≤ω(T’),故ω(b1)+ω(b2)≤ω(a1)+ω(a2)。 ⑵充分性
综上,求最小 k 度限制生成树算法总的时间复杂度为 O(Vlog2V+E+kV)。
3、次小生成树
3.1、次小生成树的定义
设 G=(V,E,w)是连通的无向图,T 是图 G 的一个最小生成树。如果有另一棵树 T1,满 足不存在树 T’,ω(T’)<ω(T1) ,则称 T1 是图 G 的次小生成树。
3.2、求解次小生成树的算法
通过上述定理,我们就有了解决次小生成树问题的基本思路。 首先先求该图的最小生成树 T。时间复杂度 O(Vlog2V+E) 然后,求 T 的邻集中权值和最小的生成树,即图 G 的次小生成树。 如果只是简单的枚举,复杂度很高。首先枚举两条边的复杂度是 O(VE),再判断该交换是否 可行的复杂度是 O(V),则总的时间复杂度是 O(V2E)。这样的算法显得很盲目。经过简单的 分析不难发现,每加入一条不在树上的边,总能形成一个环,只有删去环上的一条边,才能 保证交换后仍然是生成树,而删去边的权值越大,新得到的生成树的权值和越小。我们可以 以此将复杂度降为 O(VE)。这已经前进了一大步,但仍不够好。 回顾上一个模型——最小度限制生成树,我们也曾面临过类似的问题,并且最终采用动态规 划的方法避免了重复计算,使得复杂度大大降低。对于本题,我们可以采用类似的思想。首 先做一步预处理,求出树上每两个结点之间的路径上的权值最大的边,然后,枚举图中不在
《基于遗传算法的度约束最小生成树问题的研究》范文

《基于遗传算法的度约束最小生成树问题的研究》篇一一、引言度约束最小生成树问题(Degree-Constrained Minimum Spanning Tree Problem, DC-MST)是图论领域中的经典问题之一,它在计算机网络设计、交通网络优化、电信网络规划等领域有着广泛的应用。
近年来,随着大数据和人工智能的快速发展,遗传算法作为一种重要的优化算法,在解决复杂组合优化问题中发挥了重要作用。
本文旨在研究基于遗传算法的度约束最小生成树问题,并分析其求解性能和应用效果。
二、研究背景在无向加权图中,最小生成树问题是寻找连接所有节点的无环连通子图,并且使子图的所有边权之和最小。
而度约束最小生成树问题则是在此基础上增加了节点的度约束条件,即每个节点的连接边数不能超过给定的限制。
这一问题的求解对于网络结构的优化和设计具有重要意义。
传统的求解方法如Kruskal算法和Prim算法等在处理大规模问题时往往效率较低,因此需要寻找更高效的算法来求解度约束最小生成树问题。
三、遗传算法概述遗传算法是一种模拟自然进化过程的优化算法,它通过模拟生物进化过程中的选择、交叉和变异等操作来寻找最优解。
在求解度约束最小生成树问题时,遗传算法能够快速找到满足度约束的解,并且具有较高的求解效率。
本文将采用遗传算法来求解度约束最小生成树问题。
四、基于遗传算法的度约束最小生成树问题求解本文提出的基于遗传算法的度约束最小生成树问题求解方法主要包括以下步骤:1. 编码:将解空间中的解编码为遗传算法中的染色体,每个染色体代表一个可能的解。
在度约束最小生成树问题中,染色体通常采用实数编码或整数编码的方式表示节点的连接关系和度约束条件。
2. 初始化种群:随机生成一定数量的初始染色体作为种群的初始解。
这些初始解构成了遗传算法的初始种群。
3. 选择:根据适应度函数选择优秀的染色体进入下一代。
在度约束最小生成树问题中,适应度函数通常采用生成树的边权之和作为评价指标。
生成最小生成树的方法

生成最小生成树的方法
生成最小生成树的方法有以下几种:
1. Kruskal算法:该算法首先将图中的边按权值从小到大排序,然后依次考虑每条边,若加入该边不会形成环,则将该边加入最小生成树中,直到最小生成树的边数等于节点数减一为止。
2. Prim算法:该算法从任意一个节点开始,不断选择与当前
最小生成树相连的边中权值最小的边,将其加入最小生成树中,直到所有节点都被加入最小生成树为止。
3. Boruvka算法:该算法首先将图中的每个节点作为一个独立
的连通分量,并初始化一个空的最小生成树。
然后,依次遍历所有连通分量,每次选择与该连通分量相连的最小权值边,并将其加入最小生成树中。
当最小生成树中的边数等于节点数减一时,算法停止。
4. Reverse-Delete算法:该算法从图中的所有边中按权值从大
到小的顺序考虑,然后依次删除每条边,若删除该边后原图仍然是连通的,则继续删除下一条边,直到最小生成树的边数等于节点数减一为止。
这些方法都可以用来生成最小生成树,选择哪种方法取决于具体的应用场景和图的特点。
设计一个用破圈法求最小生成树的算法

设计一个用破圈法求最小生成树的算法
破圈法是一种求解最小生成树的算法,它基于Prim算法,用于求解最小生成
树(Minimum Spanning Tree, MST)问题。
破圈法同样也能解决切分图中(Cutting)边缘权重最小化的问题,是一种创建适应性结构的方法。
破圈法的原理可以理解为迭代式的选择最小边界的策略,其包括核心算法思想:
1. 首先计算图中的26未访问节点的最小边权重。
2. 然后添加最小权重边,将最小权重边连接的两个点打破圈。
3. 重复步骤1,其中只考虑不在圈中的节点的最小边权重,直至无节点可添加,完成最小生成树的构建。
破圈法具有稳定、高效和低内存占用特点。
它类似于Prim算法,但是它比
Prim算法更快,因为它节省了比较步骤,即只考虑不在圈中的节点的最小边权重。
破圈法可广泛用于互联网开发中的多种应用,比如路由器的简化、家庭网络构建、通信系统构建以及计算机科学和生物信息学中的最短路径问题等。
其优越性是,在构建复杂、动态网络中,能够准确地表示相互联系,加快了最短路径检索的过程;而且,它由于不需要建立额外的树结构,因此内存消耗比较小。
破圈法是最小生成树问题的一种很好的解决方案,它能够有效地避免圈死现象,构建一个没有重复的树或图;它的实现思路也比较简单,可以用来解决复杂网络中的最短路径问题。
最小生成树三种求解方法的分析与实现

最小生成树三种求解方法的分析与实现作者:李龙霞陈燕于晓倩来源:《电脑知识与技术》2021年第33期摘要:圖作为一种典型的非线性结构,用图来描述问题简明直观。
而最小生成树作为图的重要应用之一,用于解决优化路线,如何使网络通信线路成本最低,电话线路最短等问题。
将此类问题转化为最小生成树问题进行求解。
最小生成树是所有生成树中代价最小的生成树。
它以邻接矩阵的方式存储,采用Prim算法,Kruskal算法和破圈法的方法进行求解。
关键词:图;最小生成树;Prim算法;Kruskal算法;破圈法中图分类号:TP301.6;TP311.12 文献标识码:A文章编号:1009-3044(2021)33-0044-03开放科学(资源服务)标识码(OSID):Analysis and Realization of Three Methods of Solving Minimum Spanning TreeLI Long-xia, CHEN Yan, YU Xiao-qian(School of Maritime Economics and Management, Dalian Maritime University, Dalian 116026, China)Abstract: Graph, as a typical nonlinear structure, is simple and intuitive to describe the problem. As one of the most important applications of graphs, the minimum spanning tree is used to solve the problems of optimizing routes, minimizing the cost of network communication lines and the shortest telephone lines. This kind of problem is transformed into the minimum spanning tree problem to solve. The minimum spanning tree is the spanning tree with the least cost among all spanning trees. It is stored in the form of adjacency matrix and solved by Prim algorithm, Kruskal algorithm and loop breaking method.Key words: Graph; Minimum Spanning Tree; Prim algorithm; Kruskal algorithm; Broken Ring Method1 引言求解最小生成树是解决工程类问题的一种重要手段。
算法合集之《最小生成树算法及其应用》

第 5 页 共 29 页
IOI2004 国家集训队论文 吴景岳
图 3 Kruskal 算法的执行流程 Kruskal 算法在图 G=(V,E)上的运行时间取决于如何实现集合的合并。我们可 以采用路径压缩的优化方法,这是目前所知的最有效的。初始化需占用时间 O(V),第 4 行中对边进行排序需要的运行时间为 O(ElgE);对分离集的森林要进 行 O(E)次操作,总共需要时间为 O(Eα(E,V)),其中α函数为 Ackermann 函数的 反函数。因为α(E,V)=O(lgE)。所以 Kruskal 算法的全部运行时间为 O(ElgE)。 Prim 算法: 正如 Kruskal 算法一样。Prim 算法也是最小生成树一般算法的特例。它的执 行非常类似于寻找图的最短通路的 Dijkstra 算法。Prim 算法的特点是集合 A 中 的边总是只形成单棵树。如图 4 所示,阴影覆盖的边属于正在生成的树,树中的 结点为黑色。在算法的每一步,树中与树外的结点确定了图的一个割,并且通过 该割的轻边被加进树中。树从任意根结点 r 开始形成并逐渐生长直至该树跨越了 V 中的所有结点。在每一步,连接 A 中某结点到 V-A 中某结点的轻边被加入到 树中。由推论 1,该规则总是加入对 A 安全的边,因此当算法终止时,A 中的边 就成为一棵最小生成树。因为每次添加到树中的边都是使树的权尽可能小的边, 因此上述策略是“贪心”的。 有效实现 Prim 算法的关键是设法较容易地选择一条新的边添加到由 A 的边 所形成的树中,在下面的伪代码中,算法的输入是连通图 G 和将生成的最小生 成树的根 r。在算法执行过程中,不在树中的所有结点都驻留于优先级基于 key 域的队列 Q 中,对每个结点 v,key[v]是连结 v 到树中结点的边所具有的最小权 值;按常规,若不存在这样的边则 key[v]=∞。域π[v]表示点 v 的“父亲结点”。 在算法执行中,GENERIC-MST 的集合 A 隐含地满足: A={(v,π[v]):v∈V-{r}-Q} 当算法终止时,优先队列 Q 为空,因此 G 的最小生成树 A 满足: A={(v,π[v]): v∈V-{r}}
最小生成树的两种算法

最小生成树的两种算法包括:
1. Prim算法:
Prim算法是一种选择点加入树的算法。
首先选择任意一点作为树的第一个节点,然后枚举与它相连的所有点,将两点之间的边权记为这个点到生成树的距离,选择距离最近的点加入生成树,然后枚举与之相邻的节点,用边权更新该节点的距离,使距离等于两个节点之间的边的权重和。
再继续加入当前离生成树最近的点,在更新它相邻的点,以此类推,直到所有点全部加入生成树。
这样就求出了最小生成树。
2. Kruskal算法:
Kruskal算法也称为“加边法”。
首先把图中的所有边按代价从小到大排序,把图中的n个顶点看成独立的n棵树组成的森林,按权值从小到大选择边,所选的边连接的两个顶点应该属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
重复以上步骤,直到所有顶点都在一颗树内或者有n-1条边为止。
这样就可以得到最小生成树。
以上信息仅供参考,可以咨询计算机专业人士或者查看专业书籍,
以获取更准确更全面的内容。
上海海事大学09届本科毕业生优秀论文

学号:************上海海事大学本科生毕业设计(论文)基于最小生成树法的港口装船提箱模型学院:交通运输学院专业:交通运输专业班级:交通运输091******指导教师:罗**完成日期:2013年5月22日摘要集装箱港口在飞速的发展中正面临着前所未有的考验。
国内外发展实践表明,对于大型港口的提升,对堆场工作效率的优化整合仍然有很大的空间,并有着重要的意义。
为了继续发展航运事业,必须提高堆场的工作效率。
本文探讨了集装箱码头堆场的翻箱问题,对其产生的原因和解决思路进行了分析。
并提出了基于装船过程中的提箱优化模型。
本文对分支定界法进行了简介并指出了在应用到翻箱问题中此法的不足之处,本文模型应用了最小生成树的思想,尽可能控制了二次翻箱问题的出现。
关键词:翻箱问题,最小生成树,堆场效率AbstractContainer ports have been facing an unprecedented challenge through its booming period. Worldwide development experience has shown that there is a lot to do to optimize efficiency at container yards, which also means a lot to the improvement of international ports. It’s important to improve working efficiency at container yards.This article discusses about container turnover problems inside container yards, and analyzes its causes and how it can be solved. It also brings up a quick model to optimize the process of containers transportation from yard to ship. The article shines a little light on the method of branch and bound, points out its weaknesses in applying into container problems, and uses the idea of minimum spanning tree to solve the model and control the appearance of second-time container turnover problems.Key words: container turnover problem, minimum spanning tree, container yard efficiency目录1. 引言 (1)1.1 绪论 (1)1.2 国内外研究现状综述 (1)1.3 研究目的与意义 (4)1.4 本文主要研究内容 (4)1.5 论文结构 (5)2. 翻箱问题分析 (6)2.1 翻箱原因 (6)2.2 集装箱堆场的翻箱原则 (7)2.3 翻箱问题解决思路 (8)2.4 降低翻箱率的方法 (8)3. 提箱模型的建立 (10)3.1 模型简介 (10)3.2 模型假设条件 (10)3.3 参数设定 (11)3.4 目标函数确立及约束条件 (12)4. 算法详述及应用 (13)4.1 翻箱量的分支定界法 (13)4.2 最小生成树方法简介 (14)4.3 算法实现步骤 (15)4.4 算例说明及结果验证 (16)4.5 结果分析 (22)5. 总结与展望 (23)5.1 全文总结 (23)5.2 研究展望 (23)参考文献 (24)1. 引言1.1 绪论集装箱运输这一方式在其初露头角之时,就凭借其运量大,单位成本低,破损少的优势呈现出强劲的发展势头。
克鲁斯卡尔算法求最小生成树的最短路径

克鲁斯卡尔算法求最小生成树的最短路径在计算机科学领域中,克鲁斯卡尔算法是一种经典的图论算法,用于求解最小生成树和最短路径的问题。
在本文中,我将深入探讨克鲁斯卡尔算法的原理和应用,以及其在实际生活中的意义和影响。
我将从简单的概念入手,逐步深入,帮助你更好地理解和掌握这一重要的算法。
1. 算法原理克鲁斯卡尔算法是一种基于贪心策略的算法,用于求解带权无向连通图的最小生成树。
其基本思想是从图中的所有边中选择权值最小的边,且保证不构成回路,重复这个过程直到所有的顶点都已经联通。
通过这种方式,最终得到的就是图的最小生成树。
算法的具体步骤可以分为以下几个部分:- 将图中的所有边按照权值进行排序- 依次考虑所有的边,若当前边的两个顶点不属于同一连通分量,则将其加入最小生成树中- 重复上述步骤直到所有的顶点都已经联通2. 算法应用克鲁斯卡尔算法在实际生活中有着广泛的应用。
以通信网络建设为例,假设我们需要在若干个城市之间铺设光纤网络,我们希望在网络总成本最低的前提下建立通信链路。
这时候,我们可以将城市看作图的顶点,城市之间的光缆看作边的权值,然后利用克鲁斯卡尔算法求解最小生成树,就可以得到一个在总成本最低的情况下连接所有城市的方案。
3. 个人理解对于我个人而言,克鲁斯卡尔算法是一种非常优雅的算法。
它简单而高效地解决了一个看似复杂的问题,展现了计算机科学中贪心策略的魅力。
在学习和了解这一算法的过程中,我深刻体会到了算法设计的巧妙以及数学结构在计算机科学中的重要性。
我也意识到算法并不仅仅是理论上的概念,它们在实际生活中有着广泛的应用,并对我们的生活产生着深远的影响。
在本文中,我对克鲁斯卡尔算法的原理和应用进行了深入的探讨,希望能够帮助读者更好地理解和掌握这一算法。
通过分析算法的原理和应用,我相信读者们将对克鲁斯卡尔算法有更深入的理解,并能够在实际问题中灵活运用这一算法。
希望本文能够为读者们带来一些启发和帮助,让我们一起探索和学习计算机科学的奥秘吧!克鲁斯卡尔算法的应用广泛,不仅仅局限于通信网络建设,还涉及到诸如城市规划、交通规划、电力系统设计等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
孔祥男
(青海师范大学数学系,青海 810000) 摘要:本文讲述了几种求解最小生成树的算法(Kruskal 算法、Prim 算法、破圈法和 DNA 算法),重点介绍了一种求解最小生成树问题的 DNA 算法,进而比较这几种算法的优 缺点以及介绍最小生成树的几个实际应用。 关键字:最小生成树 Kruskal 算法 Prim 算法 破圈法 DNA 算法
4 key[r] ← 0 5 Q ←VG 6 while Q≠ ∅ 7 8 9 10 11 4.2 Prim 算法的复杂性 下面简单分析一下 Prim 算法的复杂性。第一次执行第 2 步是 n-2 次比较, 第二次为 n-3 次比较,第三次是 n-4 比较,„,因此总的比较为2 n − 2 (n − 1)次。在执行第 3 步时,第一次是 n-2 次比较,第二次 n-3 次比较,„,因此 总的比较为(n-2)(n-1)次。由此算法的总计算量约为 O n2 .
1 引言 最小生成树是网络最优化中一个重要的图论问题,它在交通网、电力网、 电话网、管道网等设计中均有广泛的应用。比如要在 n 个城市间建立通信联络 网,要考虑的是如何保证 n 点连通的前提下最节省经费,就应用到了最小生成 树。 求图的最小生成树有两种常见的算法,一种是 Kruskal(克鲁斯卡尔)算 法,另一种是 Prim(普里姆)算法。这两个算法的基本思想均是基于避圈法, 而从相反的角度,破圈法也可构造最小生成树算法。 本文讲述 Kruskal 算法、Prim 算法和破圈法的同时,也着重介绍了一种求 解最小生成树问题的 DNA 算法。 2 有关最小生成树的理论基础 2.1 有关最小生成树的概念 2.1.1 定义一(图) 一个图 G 定义为一个偶对(V,E),记作 G=(V,E),其中 (1) (2) V 是一个集合,其中的元素称为顶点; E 是无序积 V������V 中的一个子集合,其元素称为边;
Several algorithm of solving minimum spanning tree and its application
Xiangnan-kong
(Mathematics Department of Qinghai Normal University, Qinghai 810000) Abstract: This paper describes several algorithm of solving minimum spanning tree (Kruskal algorithm、Prim algorithm、Broken circle method and DNA algorithm), and focuses on discussing the DNA algorithm. Then it compares the advantages and disadvantages of several algorithms and introduces several practical applications of the minimum spanning tree . Keyword: Minimum spanning tree;Kruskal algorithm;Prim algorithm; Broken circle method ;DNA algorithm.
5
图4 6 一种求解最小生成树问题的 DNA 算法 6.1 DNA 算法介绍 基于生化反应的生物智能计算是现阶段计算领域研究的热点,DNA 计算是 通过 DNA 分子之间的生化反应来进行计算的一种计算模式,凭借运算巨大的并 行性和海量存储的优势,DNA 计算在解决复杂运算问题方面的计算能力显而易 见。设计了一种利用 DNA 计算来求解图的最小生成树的计算模型,采用一种特 殊的编码方式来对顶点,边和权值进行编码,从而解决最小生成树问题。 6.1.1 DNA 计算的基本原理 DNA 计算的本质就是利用大量不同的核酸分子杂交,产生类似于某种数学 过程的一种组合的结果,并根据限定条件对其进行筛选的。单链 DNA 可看作由 符号 A、C、G、T 组成的串,同电子计算机中编码 0 和 1 一样,可表示成 4 字母的 集合来译码信息。特定的酶可充当“软件”来完成所需的各种信息处理工作。 DNA 计算的基本思想是:利用 DNA 分子的双螺旋结构和碱基互补配对的性 质,将所要处理的问题编码成特定的 DNA 分子,在生物酶的作用下,生成各种数据
图5 从图 5 中 K-臂 DNA 分子的结构可以看出,通过连接酶,我们可以利用 K-臂(K ≤4)DNA 分子构造出任意顶点的最大度为 4 的图。正是利用这一思想,我们 用 K-臂分子来表示图或树中度为 n(n≤4)的顶点的结构,来实现最小生成树 问题解的节点结构。在求解最小生成树问题计算模型的编码方案中,使用的 DNA 分子是由单链和双链进行混合编码的不完全分子。 6.1.3 最小生成树编码的分子结构 本节介绍最小生成树中顶点、支架分子、权值和边的编码方式,以图 6 的 连1,转向第 2 步;否则,置j: = j + 1,转向第 2 步。 MST-KRUSKAL(G,w)
2
1 A→∅ 2 for each vertex ϑ ∈ V G 3 do Make-Set(v)
4 sort the edge of E into nondecreasing order by weight w 5 for each edge μ, ϑ ∈ E,taken in nondecreasing order by weight 6 7 8 9 retuen A 3.2 Kruskal 算法的复杂性 首先在第 1 步中把边按权的大小由小到大地排列起来,这约需 m﹒log 2 m 次比较;其次第 2 步最多循环 n 次;在第 3 步中判断 G [S⋃ aj ]是否构成回路, 判定加边后是否构成回路总共约需 m 次比较,而加边后点的重新标号最多需 n(n-1)次比较。所以总的计算量为 m﹒log 2 m+n+m+ n(n-1)~O n2 log 2 n 由定理一(1)易见上述算法的正确性。 3.3 例如在图 1 所示的网络中,求一个最小树,计算的迭代过程如图 2 所示 do if Find-Set(u)≠Find-Set(v) then A ← A ∪ u, v
2.1.2 定义二(树):不含圈的连通图称为树。
1
2.1.3 定义三(生成树):如果 T 是 G 的一个生成子图而且又是一棵树,则称 T 是图 G 的一棵生成树。 2.1.4 定义四(最小树):设T ∗ 是赋权图 G 的一颗生成树,若对 G 的任意生成 树 T 都有������ T ∗ < ������ (������),则称T ∗ 为 G 的最小树。 2.2 有关最小生成树的定理 2.2.1 定理一(最小树充要条件) 设 T 是 G 的一棵生成树,则下列条件都是 T 为最小树的充要条件 (1) 对任意连枝 e′∈G\T,有������ (e′)=maxe ∈C T (e ′) {(������(e))} (2) 对图 G 中任意圈 C,存在 e′∈C\T,有������ (e′)=maxe ∈C {������ (e)} (3)对任意树枝 e∈T,有������ (e)=mine ∈S T (e) {(������(e′))} (4)对 G 的任意割集 S,在 T∩S 中存在一条边 e,������ (e)=mine ′∈S T (e) {������(e′)} 2.2.2 定理二(唯一最小树充要条件) 设T ∗ 是 G 的一棵生成树,则下列条件都是T ∗ 是 G 的唯一最小树的充要条件 是下列两个条件中的任一个成立: (1)对任意 e∈G\T ∗ ,e 是CT ∗ (e)的唯一权最大的边。 (2)对任意e∗ ∈ T ∗ ,e∗ 是ST ∗ (e∗ )的唯一权最小的边。 3 Kruskal(克鲁斯卡尔)算法 3.1 Kruskal 算法介绍 Kruskal 算法是 1956 年首次提出的求最小生成树的算法。后来 Edmonds 把这个算法称为贪心算法。其基本思路是从 G 的 m 条边中选取 n-1 条权尽量小 的边,并且使得不构成回路,从而构成一个最小树。下面我们就来叙述这个算 法. 第 1 步 开始把图的边按权的大小由小到大地排列起来,即将图的边排序为 a1 , a2 , … , am ,使W a1 ≤ W a2 ≤ ⋯ ≤ W am 置 S=∅,������ = 0, ������ = 1. 第 2 步 若|S|= ������ = n − 1,则停止。这时 G [S]=T 即为所求;否则,转向第 3 步。 第3步 若 G [S⋃ aj ]不构成回路,则置e ������+1 = aj , S = S⋃{e ������+1 }, ������ ≔ ������ +
4
1
do u ← Extract − Min Q for each v ∈ Adj u do if v ∈ Q and w(u,v)< key[v] then π v ← u key[v] ← w(u, v)
4.3 例如在图 1 所示的网络中,求一个最小树,计算的迭代过程如图 3 所示
图3 5 破圈法 5.1 破圈法介绍 该算法的理论依据是存在性定理:连通图至少有一棵生成树。如果我们给 的连通图 G 中没有回路,那么 G 本身就是一棵生成树,若 G 中只有一个回路, 则删去 G 的回路上的一条边(不删除结点),则产生的图仍是连通的,且没有 回路,则得到的子图就是图 G 的一棵生成树,若 G 的回路不止一个,只要删去 每一个回路上的一条边,直到 G 的子图是连通没有回路且与图 G 有一样的结点 集,那么这个子图就是一棵生成树。由于我们破坏回路的方法可以不一样(即 删去的边不一样)所以可得到不同的生成树,但是在求最小生成树的时候,为 了保证求得的生成树的树权 W(T)最小,那么在删去回路上的边的时候,总是 在保证图仍连通的前提下删去权值较大的边。尽量保留权值较小的边。这就是 所谓的破圈法。破圈法就是在带权图的回路中找出权值最大的边,将该边去掉, 重复这个过程,直到图连通且没有圈为止,保留下来的边组成的图即为最小生 成树。破圈法的复杂程度为 O n3 . 5.2 例如在图 1 所示的网络中,求一个最小树,计算的迭代过程如图 4 所示
