北京理工大学信号与系统实验报告6 离散时间系统的z域分析
北京理工大学信号和系统实验报告材料

本科实验报告实验名称:信号与系统实验实验一信号的时域描述与运算一、实验目的①掌握信号的MATLAB表示及其可视化方法。
②掌握信号基本时域运算的MATLAB实现方法。
③利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形常用的信号产生函数2.连续时间信号的时域运算-1-0.8-0.6-0.4-0.200.20.40.60.81Time(seconds)图1 利用向量表示连续时间信号-1-0.50.51t图 2 利用符号对象表示连续时间信号sin(t)对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
第6章离散时间信号与系统的z域分析

6.4.2 LTI离散时间系统零状态响应的 zT分析法 p188
若已知LTI离散时间系统的单位冲激序列响应
h[n]和输入信号f[n] 。计算
h[n]H(z),| z|:(ah,bh) f[n]F(z),| z|:(af,bf ) y[z]F(z)H(z),| z|:公共部分
则:yf [n]Z1[Y(z),]| z|:公共部分 当因果信号通过散 因LT果系 I 离统时, 由于公共收敛域在 一, 定因 存此可 不再讨再讨论收敛
区外极点是反因果分量 的贡献。
收敛边界a
pk
,b
max
pk'
。
min
j Im[ z ]
0a
b
Re[ z ]
图6-1 (a)
2、因果序列的ZT的收敛域是Z平面上某园的
园外部分 z:(a,) ,全部极点为区内极点 pk
,收敛边界 a pk max
如图6-1(b)所示。
j Im[ z ]
0a
Re[ z ]
若f: [n]F(z),z:(a,)
则n: [fn]zF/(z),z:(a,)
证明:
F ( z ) f [ k ] z k , | z |: ( a . ) k0
上式两端对 z求导,得:
F ' ( z ) f [ n ]( n ) z n 1 n0
z 1 nf [ n ] z n n0
M
bM (z i )
则
H(z)
i1 N
(z pj )
j1
j Im[z]
1
0
1
Re[ z]
图6-5 H(z)极点分布与h[k]的关系
2.离散时间系统的因果性 3.因果LTI离散时间系统的稳定性p196
北京理工大学信号与系统实验实验报告
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MA TLAB实现方法。
3. 利用MA TLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
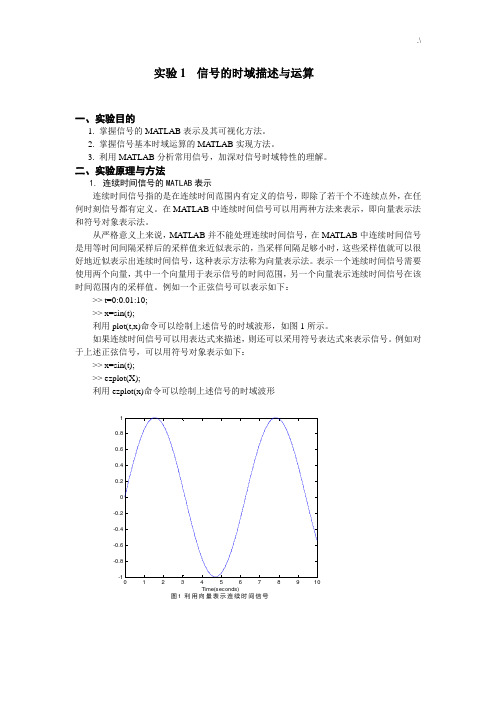
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形Time(seconds)图1 利用向量表示连续时间信号t图 2 利用符号对象表示连续时间信号sin(t)2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
采用符号对象表示的两个信号,可以直接根据符号对象的运算规则运算。
北京理工大学信号与系统信号的频域分析

x(t ) a0 ak cos kw0t bk sin kw0t
k 1 k 1
(3)
其中:
a0
1 2 2 T0 x(t )dt , ak T x(t ) cos kw0tdt , bk T x(t ) sin kw0tdt 0 T0 T0 T0 0
(4)
4、离散非周期时间信号的频域分析
非周期序列 x( n) 可以表示成一组复指数序列的连续和
x ( n)
其中
1 2
X (e
2
j
)e jn d
(15)
X (e j )
n
x ( n )e
jn
(16)
式(16)称为 x( n) 的离散时间傅里叶变换,式(15)和式(16)确立了非周期离散时 间信号 x( n) 及其离散时间傅里叶变换 X (e 称为频谱函数,且 X (e
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
N=20;T=1;a=0.5;A=1;
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
③利用 MATLAB 绘出周期矩形脉冲信号的频谱,观察参数 T 和变 化时对频谱波形的影响。
Answer:频谱包络形状不变,过零点不变,普贤间隔随着 T 变大而缩小。
2、已知 x(t)是如图所示的矩形脉冲信号。 ①求该信号的傅里叶变换; ②利用 MATLAB 绘出矩形脉冲信号的频谱,观察矩形脉冲信号宽 度变化时对频谱波形的影响; ③让矩形脉冲信号的面积始终等于 1,改变矩形脉冲宽度,观察 矩形脉冲信号时域波形和频谱随矩形脉冲宽度的变化趋势。
数字信号处理实验离散系统的Z域分析

数字信号处理实验报告实验名称:离散系统的Z 域分析学号:姓名: 评语: 成绩: 一、实验目的1、掌握离散序列z 变换的计算方法。
2、掌握离散系统系统函数零极点的计算方法和零极点图的绘制方法,并能根据零极点图分析系统的因果性和稳定性。
3、掌握利用MATLAB 进行z 反变换的计算方法。
二、实验原理与计算方法1、z 变换离散序列x (n )的z 变换定义为:。
∑∞-∞=-=n n z n x Z X )()(在MATLAB 中可以利用符号表达式计算一个因果序列的z 变换。
其命令格式为:syms n; f=(1/2)^n+(1/3)^n;ztrans(f)2、离散系统的系统函数及因果稳定的系统应满足的条件一个线性移不变离散系统可以用它的单位抽样响应h (n )来表示其输入与输出关系,即y (n )= x (n )* h (n )对该式两边取z 变换,得: Y (z )= X (z )· H (z )则: )()()(z X z Y z H =将H (z )定义为系统函数,它是单位抽样响应h (n )的z 变换,即∑∞-∞=-==n n z n h n h Z z H )()]([)(对于线性移不变系统,若n <0时,h (n )=0,则系统为因果系统;若,则系统稳∞<∑∞-∞=n n h |)(|定。
由于h (n )为因果序列,所以H (z )的收敛域为收敛圆外部区域,因此H (z )的收敛域为收敛圆外部区域时,系统为因果系统。
因为,若z =1时H (z )收敛,即∑∞-∞=-=n n z n h z H )()(,则系统稳定,即H(z)的收敛域包括单位圆时,系统稳定。
∞<=∑∞-∞==n z n h z H |)(||)(1因此因果稳定系统应满足的条件为:,即系统函数H (z )的所有极点全部落在1,||<∞≤<ααz z 平面的单位圆之内。
3、MATLAB 中系统函数零极点的求法及零极点图的绘制方法MATLAB 中系统函数的零点和极点可以用多项式求根函数roots ()来实现,调用该函数的命令格式为:p=roots(A)。
北京理工大学信号与系统实验报告

北京理工大学信号与系统实验报告本科实验报告实验名称:信号与系统实验实验1 信号的时域描述与运算(基础型实验)一、实验目的1.掌握信号的MATLAB表示及其可视化方法。
2.掌握信号基本时域运算的MATLAB实现方法。
3.利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理及方法1.连续时间信号的MATLAB表示连续时间信号在连续时间范围内除若干不连续点外在任何时刻都有定义,在MATLAB中的表示法包括向量表示法和符号对象表示法。
1)向量表示法MATLAB从严格意义上来说并不能处理连续时间信号,但可以通过等时间间隔采样后的采样值来近似表示,如果采样间隔足够小,则采样值就可以很好地近似表示出连续时间信号。
这种方法称为向量表示法。
表示一个连续时间信号需要用到两个向量,一个表示时间范围,另一个表示连续时间信号在相对应时间范围内的采样值。
2)符号对象表示法如果连续时间信号可以用表达式来描述,则可以采用符号对象表达法。
例:对于余弦信号,采用两种方式来表示:>> t=0:0.01:10;>> x=sin(t);>> subplot(121)>> plot(t,x)>> title('向量表示法')>> clear>> syms t>> x=sin(t);>> subplot(122)>> ezplot(x)>> title('符号对象表示法')符号对象表示法向量表示法t常用信号产生函数2.连续时间信号的时域运算连续时间信号的运算包括两信号相加、相乘、微分、积分,以及移位、反转、尺度变换等。
1) 相加和相乘信号的相加和相乘指两信号对应时刻值相加或相乘。
两个采用向量表示法的信号可以直接使用‘+’和‘*’进行运算,此时要求二者的向量时间范围以及采样间隔相同。
信号与系统 第六章 离散时间系统的Z域分析

2z z X ( z) z 1 z 0.5
z 1, 即x n 为因果序列
x n = 2-0.5n u n
第六节 z变换的基本性 质
一、 Z变换的基本性质
1线性性:
若x(n) X ( z ) (R x1 < z <R x2 )
n
-n
<1 x(n) Rx1
即: z lim
n
看出:
z Rx1
则该级数收敛.其中Rx1是级数的收敛半径. 可见:右边序列的收敛域是半径为Rx1的圆外部分。 1)如果n10,则收敛域包括z=。即收敛域为 z Rx1 2)如果n1<0,则收敛域不包括z=。即收敛域为 Rx1< z 3)如果n1=0,则右边序列变成因果序列,即因果 序列是右边序列的一种特殊情况,其收敛域为: z Rx1
b0 b1 z = a0 a1 z br 1 z r 1 br z r ak 1 z k 1 ak z k
对因果序列 z R为X z 的收敛域, 需k r保证X z 在z=处收敛。
逆Z变换
则(1)当X(z)仅含一阶极点时 X z 部分分式展开 k Am 先
二、 典型序列的Z变换
Z 1 单位样值序列 ( n ) 1
( n)
1
0
z , z 1 2 单位阶跃序列 u(n) z 1
Z
Z 3 斜变序列 nu(n)
n u ( n)
1
z
0
2
z 1
z , 1
n
典型序列的Z变换
4 单边指数序列 a u(n)
举例
求序列 a u(n) a u(n 1)的z变换.
《信号与系统》第六章 离散系统z域分析

(z
z2 1)(z
2)
z2
z2 z
2
其收敛域如下,分别求其相对应的原序列f(k)。 (1) |z| > 2 (2) |z|< 1 (3) 1< |z| < 2
解(1) 由于F(z)的收敛域在半径为2的圆外,故f(k) 为因果序列。用长除法将F(z)展开为z-1的幂级数:
z2/(z2-z-2)=1+ z-1 + 3z-2 + 5z-3 + …
例:f1(k)=2k(k)←→F1(z)=
z z2
, z>2
f2(k)=
–2k(–
k
–1)←→F2(z)=
z
z
2
, z<2
对单边z变换,其收敛域比较简单,一定
是某个圆以外的区域。可以省略。
常用序列的z变换: (k) ←→ 1 ,z>0
(k)
z ,z>1
–(– k –1)
z 1 ,z<1
书p276
若 f(k) ←→ F(z) , <z< , 且有常数a0
则 akf(k) ←→ F(z/a) , a<z<a
证明:
Z[akf(k)]=
ak f (k)z k
f (k)
z k
F( z )
k
k
a
a
例1:akε(k) ←→ z
za
例2:cos(k)ε(k) ←→? cos(k)ε(k)=0.5(ejk+ e-jk)ε(k) ←→
方程取单边z变换yzz1yzy12z2yzy2y1z1fz2z2fz12224212121221212222212211??????????????????????????zzzzzzzzzzfzzzzzyyzzy1221221242kkyzzzzzzzzzykkzizi??????????????231212123121221kkyzzzzzzzykkzszs?????????????二系统函数zazbzfzyzhzs??2与时域的关系
第六章离散时间信号与系统的z域分析

例6.1 求双边序列 f k a
k
a 1
的Z变换,并确定它的收敛域。
解:双边指数序列可写为右边序列和左边序列之和,即 a k a k k a k k 1
右边序列
a k k 的Z变换 Fa z
k
z Fa z , z a za
以后我们的讨论将限于单边z变换,记做F ( z ) Z f (k )
k 0
2、s平面和z平面间的对应关系 z e sT e ( j )T eT e jT z e j z eT
Im[ z ] j
s平面 z平面 Re[z ]
T
二、z变换的收敛域 z变换是z的幂级数,F ( z ) z变换存在的充要条件是
Z [ f (k-m) (k m)] z m F ( z ) Z [ f (k m) ( k m)] z m F ( z )
例如:
Z [ f ( k 1) ( k )] zF ( z ) zf (0) Z [ f ( k 2) ( k )] z 2 F ( z ) z 2 f (0) zf (1)
则左移后 f (k m) (k ) z m [ F ( z ) f (k ) z k ]
k 0 m 1
右移后 f (k m) (k ) z [ F ( z )
m
k m
1
f (k ) z k ]
(3) 若f (k )是因果序列,其单边 变换为 f ( k ) (k ) F ( z ) z Z [ f (k-m) (k )] z m F ( z ) m 1 常用 Z [ f (k m) (k )] z m F ( z ) z m f (k ) z k k 0
北京理工大学信号与系统实验实验报告

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB实现方法。
3. 利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
第6章离散时间信号与系统的z域分析

2 双边ZT的移位特性p173
若 f [n] F(z), z : (a,b ) 则 f [n m] zmF(z), z : (a,b )
(m为整数)
5.时域反转特性p176
若 f [n] F (z), z : (a,b )
则:f [n] F (1), z : ( 1 ,1)
z
ab
3 序列指数加权(Z域尺度变换)特性 p174
证明: f1[n] f2[n] f1[n] f2[n]zn n
f1[k] f2[n k ]zn
n k
交换求和次序
f1[k ]
f
2[n
k
]z
k
k
n
当 z : (a2,b 2 ) f1[k]F2 (z)zk k
f1[k
]z
k
F2
(
z
)
k
当 z : (a1,b 1)F1(z)F2 (z)
z : (0.)
6.1.3 双边z变换的性质 p172
1 线性特性p172
若 f1[n] F1(z), z : (a1,b 1)
f2[n] F2 (z), z : (a2,b 2 )
则 c1 f1[n] c2 f2[n] c1F1(z) c2F2 (z), z : 公共部分
其中c,c 为常数 12
Z 1 F (z) 1 F (z)zn1dz f [n], z : (a, )
2j c
6.3.2 单边ZT的性质 p181
除具双边ZT的全部性质外,还具有如下性质: 1、序列乘线性加权(Z域微分)特性p181
若:f [n] F (z), z : (a, )
则:nf [n] zF / (z), z : (a, )
《信号与系统》讲义教案第6章离散信号与系统的Z域分析

第 6 章离散信号与系统的Z 域分析6.0 引言与拉氏变换是连续时间傅立叶变换的推广相对应,Z 变换是离散时间傅立叶变换的推广。
Z 变换的基本思想、许多性质及其分析方法都与拉氏变换有相似之处。
当然, Z 变换与拉氏变换也存在着一些重要的差异。
6.1 双边 Z 变换6.1.1双边Z变换的定义前面讨论过,单位脉冲响应为h[n] 的离散时间 LTI 系统对复指数输入z n的响应y[n]为y[ n]H ( z) z n(6.1)其中H ( z)h[ n] z n(6.2)n式 (6. 2) 就称为 h[n] 的双边 Z 变换。
当 z= e j时, Z 变换就转变为傅立叶变换。
因此一个离散时间信号的双边Z 变换定义为:X ( z)x[ n]z n(6.3)n式中 z 是一个复变量。
而x[n]与它的双边z 变换之间的关系可以记做zx[n]X (z)6.1.2双边Z变换的收敛域x[n] 的双边 Z 变换为一无穷级数,因此存在级数是否收敛的问题,即一方面并非所有信号的Z 变换都存在;另一方面即使某信号的Z 变换存在,但并非Z 平面上的所有点都能使X(z)收敛。
那些能够使X(z)存在的点的集合,就构成了X(z)的收敛域,记为ROC。
只有当式 (6.3) 的级数收敛,X (z) 才存在。
X ( z) 存在或级数收敛的充分条件是x[n]z n(6.4)n在 x[ n] 给定的条件下,式 (6.4)级数是否收敛取决于 z 的取值。
在 z 复平面上,使式 (6.4)级数收敛的 z取值区域就是 X(z)的收敛域。
6.1.3零极点图如果X(z) 是有理函数,将其分子多项式与分母多项式分别因式分解可以得到:N ( z)(z z i )X ( z)i(6.5)M(zD ( z)z p )p则由其全部的零极点即可表示出X ( z) ,最多相差一个常数因子。
在Z 平面上表示出全部的零极点,即构成X ( z) 的几何表示——零极点图。
北京理工大学信号与系统实验报告6离散时间系统的z域分析

北京理工大学信号与系统实验报告6-离散时间系统的z域分析————————————————————————————————作者:————————————————————————————————日期:实验6 离散时间系统的z 域分析(综合型实验)一、 实验目的1) 掌握z 变换及其反变换的定义,并掌握MAT LAB实现方法。
2) 学习和掌握离散时间系统系统函数的定义及z 域分析方法。
3) 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。
二、 实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ (1)Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰(2)MA TLA B中可采用符号数学工具箱z trans 函数和iz trans 函数计算z 变换和z 反变换: Z=ztran s(F)求符号表达式F的z 变换。
F=iztra ns(Z)求符号表达式Z 的z 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应h(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ (3)此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = (4)由(4)式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ (5) 3. 离散时间系统的零极点分析MATLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根,从而得到系统的零极点。
此外还可采用MATL AB 中zpl ane 函数来求解和绘制离散系统的零极点分布图,zp lane 函数的调用格式为:zplane(b,a) b、a 为系统函数分子分母多项式的系数向量(行向量) zplane (z,p) z 、p为零极点序列(列向量) 系统函数是描述系统的重要物理量,研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化,还可以了解系统频率特性响应以及判断系统的稳定性; 系统函数的极点位置决定了系统的单位抽样响应的波形,系统函数零点位置只影响冲激响应的幅度和相位,不影响波形。
信号与系统 实验报告 实验六 离散信号与系统的Z变换分析报告

实验六 离散信号与系统的Z 变换分析学院 班级 学号一、 实验目的1.熟悉离散信号Z 变换的原理及性质2.熟悉常见信号的Z 变换3.了解正/反Z 变换的MATLAB 实现方法4.了解离散信号的Z 变换与其对应的理想抽样信号的傅氏变换和拉氏变换之间的关系5.了解利用MATLAB 实现离散系统的频率特性分析的方法二、 实验原理1. 正/反Z 变换Z 变换分析法是分析离散时间信号与系统的重要手段。
如果以时间间隔s T 对连续时间信号f (t)进行理想抽样,那么,所得的理想抽样信号()f t δ为:()()*()()*()Ts s k f t f t t f t t kT δδδ∞=-∞==-∑理想抽样信号()f t δ的双边拉普拉斯变换F (s)为:()()*()()s ksT st s s k k F s f t t kT e dt f kT e δδ∞∞∞---∞=-∞=-∞⎡⎤=-=⎢⎥⎣⎦∑∑⎰ 若令()()s f kT f k = ,sTs z e =,那么()f t δ的双边拉普拉斯变换F (s)为:()()()sTs k z e k F s f k z F z δ∞-==-∞==∑则离散信号f (k )的Z 变换定义为:()()k k F z f k z ∞-=-∞=∑从上面关于Z 变换的推导过程中可知,离散信号f (k )的Z 变换F(z)与其对应的理想抽样信号()f t δ的拉氏变换F (s)之间存在以下关系:()()sTs z e F s F z δ==同理,可以推出离散信号f (k )的Z 变换F(z)和它对应的理想抽样信号()f t δ的傅里叶变换之间的关系为()()j Ts z e F j F z ωδω==如果已知信号的Z 变换F(z),要求出所对应的原离散序列f (k ),就需要进行反Z 变换,反Z变换的定义为: 11()()2k f k F z z dz j π-=⎰Ñ 其中,C 为包围1()k F z z -的所有极点的闭合积分路线。
信号与系统 第六章离散系统的Z域分析

Z平面
k 1 k (1 z ) ( 3z ) 3 k 1 k 0
0
|z|<3时,第一项收敛于
z ,对应于左边序列。 z 3 z |z|>1/3时,第二项收敛于 ,对应于右边序列。 1 收敛域 z3
1 3
3
1 当 | z | 3 时, 3
8 z z 3 z F ( z) 1 z 3 z 3 ( z 3)( z 1 3)
应用尺度变换:
k
sin k (k )
z a
z sin z 2 2 z cos 1
0< a <1
sin a z sin a sin k (k ) z 2 z ( a ) 2( a ) cos 1 z 2 2 a z cos a 2
§6.2
Z变换的性质
| k-3|(k)
解:(1) F z
k k k z 1
k 1
(2) 双边z变换: F z
k
f k z
k
2 1 z 2z 3 2 z z
2
0 z
单边z变换: F z f k z
k 0
长春理工大学
零点:0 极点:3,1/3
§6.1
Z 变换
Z变换的收敛域
收敛域内不包含任何极点,在极点处,F(z)为无穷大, Z变换不收敛。 有限长序列的收敛域为整个Z平面, 可能不含z=0, z=。 因果有限长序列: F(z)=f (1)z -1+ f (2)z -2+· · · · |z|>0 反因果有限长序列: F(z)=f (-1)z 1+ f (-2)z2+· · · · |z|< 如果是因果序列,收敛域为|z|>0圆的外部。 如果是左边序列,收敛域为|z|<0 。 如果是双边序列,收敛域由圆环组成。
北京理工大学信号与系统实验讲义电子版
实验1 信号的时域描述与运算 一、实验目的①掌握信号的MATLAB 表示及其可视化方法。
②掌握信号基本时域运算的MA TLAB 实现方法。
③利用MA TLAB 分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB 表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB 中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB 并不能处理连续时间信号,在MATLAB 中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
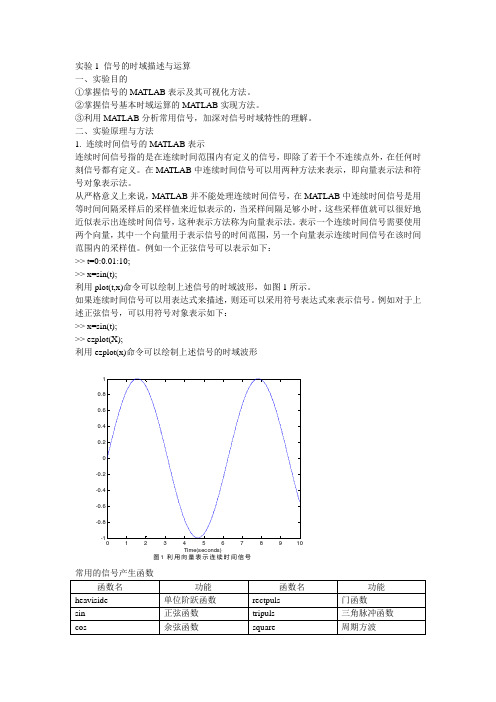
例如一个正弦信号可以表示如下: >> t=0:0.01:10; >> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下: >> x=sin(t); >> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形012345678910-1-0.8-0.6-0.4-0.200.20.40.60.81Time(seconds)图1 利用向量表示连续时间信号常用的信号产生函数 函数名 功能 函数名 功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos余弦函数square周期方波sinc sinc 函数 sawtooth 周期锯齿波或三角波 exp指数函数-6-4-20246-1-0.50.51t图 2 利用符号对象表示连续时间信号sin(t)2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
北理工信号与系统实验报告

������������ ������ ������������ ������ 0 ������
������������ =
1 ������0
������(������)������ −������������ ������ 0 ������ ������������
������0
上述两式定义为周期信号复指数形式的傅里叶级数,系数 Ck 称为 x(t)的傅 里叶级数。周期信号的傅里叶级数还可以由三角函数的线性组合来表示,即
xlabel('n') title('y[n]') 程序运行结果如下:
x[n] 1 0.5 0 -0.5 -1 1 0.5 0 -0.5 -1 y[n] 4 h[n]
0
5
10 n
15
20
0
5
10 n
15
20
2
0
-2
0
5
10
15
20 n
25
30
35
40
7.已知两个连续时间信号,求两个信号的卷积。 程序如下: w1=2; w2=4; dt=0.01; t1=-2:dt:2; t2=-4:dt:4; x1=2*rectpuls(t1,w1) x2=rectpuls(t2,w2) x=conv(x1,x2); x=x*dt; t0=t1(1)+t2(1); t3=length(x1)+length(x2)-2; t=t0:dt:(t3*dt+t0); plot(t,x); axis([-4 4 -2 6]); xlabel('t'); title('x(t)'); 程序运行结果如下:
an y (n) (t ) an1 y (n1) (t ) a1 y ' (t ) a0 y(t ) bm x (m) (t ) bm1 x (m1) (t ) b1 x ' (t ) b0 x(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验6 离散时间系统的z 域分析(综合型实验)一、实验目的1) 掌握z 变换及其反变换的定义,并掌握MATLAB 实现方法。
2) 学习和掌握离散时间系统系统函数的定义及z 域分析方法。
3) 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。
二、实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ (1)Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰(2)MATLAB 中可采用符号数学工具箱ztrans 函数和iztrans 函数计算z 变换和z 反变换: Z=ztrans(F)求符号表达式F 的z 变换。
F=iztrans(Z)求符号表达式Z 的z 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应h(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ (3)此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = (4)由(4)式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ (5) 3. 离散时间系统的零极点分析MATLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根,从而得到系统的零极点。
此外还可采用MATLAB 中zplane 函数来求解和绘制离散系统的零极点分布图,zplane 函数的调用格式为:zplane(b,a) b 、a 为系统函数分子分母多项式的系数向量(行向量) zplane(z,p) z 、p 为零极点序列(列向量) 系统函数是描述系统的重要物理量,研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化,还可以了解系统频率特性响应以及判断系统的稳定性; 系统函数的极点位置决定了系统的单位抽样响应的波形,系统函数零点位置只影响冲激响应的幅度和相位,不影响波形。
系统的频率响应取决于系统函数的零极点,根据系统的零极点分布情况,可以通过向量法分析系统的频率响应。
因果的离散时间系统稳定的充要条件是H(z)的全部极点位于单位圆内。
三、实验内容(1) 已知两个因果离散时间系统的系统函数,采用MATLAB 画出零极点分布图,求解系统的冲激响应h(n)和频率响应(e)j H Ω,并判断系统是否稳定。
1)23221()0.50.0050.3z z H z z z z ++=--+ >> b=[1 2 1];>> a=[1 -0.5 -0.005 0.3]; >> zplane(b,a)>> impz(b,a)全部极点都在单位圆内,系统稳定。
>> [H,w]=freqz(b,a); >> subplot(211)>> plot(w/pi,abs(H)); >> xlabel('\omega(\pi)'); >> ylabel('Magnitude'); >> title('|H(e^j^\Omega)|'); >> grid on>> subplot(212)>> plot(w/pi,angle(H)/pi); >> xlabel('\omega(\pi)'); >> ylabel('Phase(\pi)'); >> title('theta(\Omega)'); >> grid onReal PartI m a g i n a r y P a r tn (samples)A m p l i t u d eω(π)M a g n i t u d e|H(e j Ω)|ω(π)P h a s e (π)theta(Ω)2)324322()3331z z H z z z z z -+=+-+->> b=[1 -1 0 2]; >> a=[3 3 -1 3 -1]; >> zplane(b,a)>> impz(b,a)有极点在单位圆外,系统不稳定。
>> [H,w]=freqz(b,a); >> subplot(211)>> plot(w/pi,abs(H)); >> xlabel('\omega(\pi)'); >> ylabel('Magnitude'); >> title('|H(e^j^\Omega)|'); >> grid on>> subplot(212)>> plot(w/pi,angle(H)/pi); >> xlabel('\omega(\pi)'); >> ylabel('Phase(\pi)'); >> title('theta(\Omega)'); >> grid on(2) 用MATLAB 绘制以下六种情况系统函数的零极点分布图,并绘制相应单位抽样响应的时域波形,观察分析系统函数极点位置对单位抽样响应时域特性的影响和规律。
1) z=0,p=0.25b=[1 0]; a=[1 -0.25]; subplot(211)zplane(b,a); subplot(212) impz(b,a)Real PartI m a g i n a r y P a r tn (samples)A m p l i t u d eImpulse Responseω(π)M a g n i t ud e|H(e j Ω)|ω(π)P h a s e (π)theta(Ω)2) z=0,p=1b=[1 0]; a=[1 -1]; subplot(211)zplane(b,a); subplot(212) impz(b,a)3) z=0,p=-1.25b=[1 0]; a=[1 1.25]; subplot(211)zplane(b,a); subplot(212) impz(b,a)Real PartI m a g i n a r y P a r tn (samples)A m p l i t u d eReal PartI m a g i n a r y P a r tn (samples)A m p li t u d eReal PartI m a g i n a r y P a r t6n (samples)A m p l i t u d eImpulse Response4)66120,0.8,0.8jjz p ep eππ-===b=[1 0];a=poly([0.8*exp(j*pi/6) 0.8*exp(-j*pi/6)]); subplot(211)zplane(b,a); subplot(212) impz(b,a)5)88120,,jjz p ep eππ-===b=[1 0];a=poly([exp(j*pi/8) exp(-j*pi/8)]); subplot(211)zplane(b,a); subplot(212) impz(b,a)6)3344120, 1.2,jj z p ep eππ-===b=[1 0];a=poly([1.2*exp(j*3*pi/4) 1.2*exp(-j*3*pi/4)]); subplot(211)zplane(b,a); subplot(212) impz(b,a)Real PartI m a g i n a r y P a r tn (samples)A m p l i t u d eImpulse ResponseReal PartI m a g i n a r y P a r tn (samples)A m p l i t u d eImpulse Response综合分析以上六个图可知:如果只有一个极点,响应波形为指数型。
当极点在单位圆内时,呈指数衰减;当极点在单位圆上,为定值(单位阶跃响应);当极点在单位圆外时,呈指数增长。
如果有一对共轭极点,响应为振荡型。
当极点在单位圆内,呈衰减振荡;当极点在单位圆上,为等幅振荡;当极点在单位圆外时,呈增幅振荡(3) 以下两个系统具有相同的极点,但零点不同,用MATLAB 分别绘制两个系统的零极点分布图及相应单位抽样响应的时域波形,观察分析系统函数零点位置对单位抽样响应时域特性的影响。
1)66(z 2)(z)(z 0.8e )(z 0.8e)jjz H ππ-+=--b=poly([0 -2]);a=poly([0.8*exp(j*pi/6) 0.8*exp(-j*pi/6)]); subplot(211) zplane(b,a); subplot(212) impz(b,a)Real PartI m a g i n a r y P a r t6n (samples)A m p l i t u d eImpulse ResponseReal PartI m a g i n a r y P a r tn (samples)A m p l i t u d eImpulse Response2)66(z 2)(z)(z 0.8e )(z 0.8e)jjz H ππ--=--b=poly([0 2]);a=poly([0.8*exp(j*pi/6) 0.8*exp(-j*pi/6)]); subplot(211) zplane(b,a); subplot(212) impz(b,a)分析以上两图可知:当零点沿纵轴对折时,时域波形图近似沿横轴对折。
但只是波形的对称,各点的值并没有等幅改变。
四、实验收获与体会本次实验通过MATLAB 实现z 变换及其反变换,进一步加深了对z 域分析法的理解,理清了系统零极点分布与系统特性的关系。
Real PartI m a g i n a r y P a r tn (samples)A m p l i t u d e。
