热学模拟试题(一)
热学专项模拟测试题

热学专项模拟测试题高垚骏(安徽省宣城市宣州区新田中心初中)一、选择题(每题3分,共36分)1.下列物态变化,需要吸热的是()A.初春,皑皑的白雪开始消融 B.初夏,青青的小草挂上露珠C.深秋,红红的苹果蒙上白霜 D.严冬,静静的池塘覆上薄冰2.根据下表所提供的数据,在标准大气压下,以下判断正确的是()A.80℃的酒精是液态B.气温接近-50℃时.应选用水银做温度计的测温液体C.-39℃的水银吸热,温度可能不变D.铅的凝固点是-328℃3.给一定质量的水加热,其温度随时间变化的关系如图所示。
若其它条件不变,仅将水的质量增加,则水的温度随时间变化的图线应该是()4.下面是某同学“物理学习笔记”中的摘录,其中错误的是()A.燃料的热值与燃料的质量没有关系B.温度越高的物体含有的热量越多C.做功和热传递在改变物体的内能上是等效的D.汽油机工作时,在压缩冲程中机械能转化为内能5.暑假去植物园游玩,同学们的感受与物理知识的联系不正确的是()A.在园内散步时闻到花香,是升华现象B.中午坐公园的椅子感觉很烫,是热传递改变了物体的内能C.人出汗后,微风吹过感到凉爽,是因为汗液蒸发加快,带走更多的热量D.同学们感到植物园是避暑的好去处,是因为园内树木多且有人工湖,起到调温作用6.小明和小华同学在做“探究:比较水与煤油吸收热量时温度升高的快慢”的实验时,使用了如图5所示的装置。
设计实验方案时,他们确定以下需控制的变量,其中多余的是()A.采用完全相同的加热方式B.酒精灯里所加的酒精量相同C.取相同质量的水和煤油D.盛放水和煤油的容器相同7.冰在熔化过程中,下列判断正确的是()A.内能不变,比热容不变 B.吸收热量,温度不变C.比热容、内能、温度都不变 D.比热容变大,内能增加,温度升高8.如图所示的四个现象中,属于内能转化为机械能的是()9.爆米花是将玉米放入铁锅内,边加热边翻动一段时间后,“砰”的一声变成了玉米花。
重庆大学_837传热学一_《传热学》(第一版)王厚华模拟题(2套)_考研专业课分析

重庆⼤学_837传热学⼀_《传热学》(第⼀版)王厚华模拟题(2套)_考研专业课分析模拟试题⼀⼀、填空题(共20分,每⼩题2分)1.传热过程是由导热、A、B三种基本传热⽅式组合形成的。
2.导热微分⽅程式是根据热⼒学第⼀定律和 A定律所建⽴起来的描写物体的温度随 B 变化的关系式。
3.对流换热过程是靠 A和 B 两种作⽤来完成热量传递的。
4.⽓体只能辐射和吸收某⼀定波长范围的能量,即⽓体的辐射和吸收具有明显的A。
5.对服从兰贝特定律的物体,辐射⼒E与任意⽅向辐射强度I之间的关系式为 A 。
6.热⽔瓶的双层玻璃中抽真空是为了 A 。
7.⾃然对流换热在 A 条件下发⽣关于特征长度的⾃模化现象。
8.有效辐射包括 A 和 B 两部分能。
9.不稳态导热采⽤有限差分⽅法求解温度场,节点的隐式差分⽅程是采⽤ A 差分⽅法获得的,此差分⽅程 B 稳定性条件。
10.常物性流体管内受迫流动的充分发展段,沿管长流体的断⾯平均温度在常壁温边界条件下呈 A 规律变化。
⼀、判断题,对的画√,错的画×(共10分,每⼩题2分)1.流体外掠光滑管束换热时,第⼀排管⼦的平均表⾯传热系数最⼤。
()2.为减少保温瓶的辐射散热,将瓶胆的两层玻璃之间抽成真空。
()3.⽔在⽔平圆管内受迫流动,管外是空⽓⾃然对流,为强化传热应把肋⽚安装在圆管外表⾯。
()4.由两种不同材料制成的⼤平壁紧密接触时进⾏稳态导热过程,若已知121223,t t t t δδδ==->-,则 12<λλ。
() 5. 有⼀冷凝器,饱和蒸汽在管外凝结成饱和液体,冷却⽔在管内流,则其平均温差m t ?与流动⽅式⽆关。
()⼆、解释名词与基本概念(20分,每⼩题4分)1. 温度梯度2. 努谢尔特准则及其物理本质3. 肋⽚效率4. 辐射强度5. 传热过程三、简答及说明题(共40分,每⼩题8分)1. 为什么潮湿的多孔材料的导热系数不但⽐⼲多孔材料的导热系数⼤,⽽且还⽐⽔的导热系数⼤?2. 流体在管内受迫流动换热的其它条件相同时,直管和弯管(如螺旋管)何者换热强?为什么?3. 试说明Bi 数的物理意义。
热一 试题

一、选择题:1 对于理想气体的内能有下述四种理解:(1) 状态一定,内能也一定(2) 对应于某一状态的内能是可以直接测定的(3) 对应于某一状态,内能只有一个数值,不可能有两个或两个以上的数值(4) 状态改变时,内能一定跟着改变其中正确的是: ( )(A) (1),(2) (B) (3),(4) (C) (2),(4) (D) (1),(3)2 下面陈述中,正确的是: ( )(A) 虽然Q和W是过程量,但由于Q V =ΔU,Q p=ΔH,而U和H是状态函数,所以Q V和Q p是状态函数(B) 热量是由于温度差而传递的能量,它总是倾向于从含热量较多的高温物体流向含热量较少的低温物体(C) 封闭体系与环境之间交换能量的形式非功即热(D) 两物体之间只有存在温差,才可传递能量,反过来体系与环境间发生热量传递后, 必然要引起体系温度变化3 在SI单位中,压力的单位是: ( )(A) atm (B) kg×m-2 (C) Pa (D) mmHg4 现有两个微分式:d Z1=Y(3X2+Y2)d X+X(X2+2Y2)d Yd Z2=Y(3X2+Y)d X+X(X2+2Y)d Y式中d Z2代表体系的热力学量,Y,Z是独立变量。
若分别沿Y=X与Y=X 2途径从始态X=0,Y=0 至终态X=1,Y=1 积分,可以证明d Z2为全微分的应是: ( )(A) d Z1 (B) d Z2 (C) d Z1和d Z2 (D) 都不是5 如图,在绝热盛水容器中,浸有电阻丝,通以电流一段时间,如以电阻丝为体系,则上述过程的Q、W和体系的ΔU值的符号为: ( )(A) W = 0, Q < 0, ΔU < 0(B) W < 0, Q < 0, ΔU > 0(C) W = 0, Q > 0, ΔU > 0(D) W < 0, Q = 0, ΔU > 06 有一高压钢筒,打开活塞后气体喷出筒外,当筒内压力与筒外压力相等时关闭活塞,此时筒内温度将: ( )(A) 不变 (B) 升高 (C) 降低 (D) 无法判定7 1 mol 373 K,p$下的水经下列两个不同过程变成373 K,p$下的水气,(1) 等温等压可逆蒸发 (2) 真空蒸发这两个过程中功和热的关系为: ( )(A) W1> W2Q1> Q2(B) W1< W2Q1< Q2(C) W1= W2Q1= Q2(D) W1> W2Q1< Q28 有一真空绝热瓶子,通过阀门和大气隔离,当阀门打开时,大气(视为理想气体)进入瓶内,此时瓶内气体的温度将: ( )(A) 升高 (B) 降低 (C) 不变 (D) 不定9 苯在一个刚性的绝热容器中燃烧,则: ( )C6H6(l) + (15/2)O2(g) 6CO2+ 3H2O(g)(A) ΔU = 0 , ΔH < 0 , Q = 0(B) ΔU = 0 , ΔH > 0 , W = 0(C) ΔU = 0 , ΔH = 0 , Q = 0(D) ΔU≠0 , ΔH≠0 , Q = 010 恒容下,一定量的理想气体,当温度升高时内能将: ( )(A) 降低 (B) 增加 (C) 不变 (D) 增加、减少不能确定11 对于孤立体系中发生的实际过程,下列关系中不正确的是: ( )(A) W = 0 (B) Q = 0 (C) ΔU= 0 (D) ΔH = 012 下图为某气体的p-V图。
传热学模拟试题一

传热学复习题一。
选择恰当的答案填入空格中(每题2分,共30分)1.传热学是研究()的科学。
①热量传导规律;②热量传递规律;③对流传热规律;④辐射传热规律。
2.采暖时,热量从90℃的热水通过1mm厚的钢板传给25℃的室内空气。
在这个综合传热过程中,()。
①水到钢板的传热强于通过钢板的传热强于钢板到空气的传热;②钢板到空气的传热强于通过钢板的传热强于水到钢板的传热;③钢板到空气的传热弱于水到钢板的传热弱于通过钢板的传热;④钢板到空气的传热强于水到钢板的传热强于通过钢板的传热。
3.傅立叶定律中的负号表示热量传递的方向与温度梯度的方向(),即热量必须从高温处向低温处传递。
①相反;②垂直;③相交;④相同。
4.工程材料在使用时表现出来的导热系数还常常与材料内部结构有关,是一种综合导热系数,不再单纯是()。
①物性参数;②过程参数;③几何参数;④边界条件。
5.导热问题(导热数学模型)的三类边界条件分别是()。
①速度边界条件、流量边界条件和温度边界条件;②温度边界条件、热流量边界条件和对流边界条件;③克希霍夫边界条件、基尔霍夫边界条件和霍金边界条件;④导热边界条件、辐射边界条件和对流边界条件。
()。
6.()远远小于()是肋片导热的必要条件,反过来的话肋片不仅不增大传热,反而削弱传热。
①肋片表面对流换热热阻、肋片内导热热阻;②肋基接触热阻、肋片内导热热阻;③肋基导热热阻、肋片内导热热阻;④肋片内导热热阻、肋片表面对流换热热阻。
7.周期性的非稳态导热过程由于边界条件变化程度与周期不同,可能分为也可能不分()等两个阶段。
①非稳态阶段和稳态阶段;②非正规状况阶段和正规状况阶段;③非周期性阶段和周期性阶段;④非定常阶段和定常阶段。
8.集总参数法使用条件是()。
①物体内部单位导热面积上的导热热阻远远小于传热过程总传热热阻;②物体内部单位导热面积上的导热热阻远远大于传热过程总传热热阻;③物体内部单位导热面积上的导热热阻(内热阻)远远小于物体表面同周围环境进行换热的换热热阻(外热阻);④物体内部单位导热面积上的导热热阻(内热阻)远远小于物体表面同周围环境进行换热的换热热阻(外热阻),即Bi很小(<0.1)。
传热传质学模拟试题之一

传热学模拟考试试题1
14、空气在圆管内的湍流对流换热,若保持质量流量及其它条件不变,将圆管的直径减小一半,换热系数如何变化?总换热量如何变化?
5、流量为39m3/h的透平油,在冷油器中从初温60℃冷却到40℃,冷测器采用1-2型壳管式结构,管子为铜管,外径为15mm,壁厚为1mm,每小时47t的流水作为冷却水在管侧流过,进口温度为30℃,油安排在壳侧,油侧的表面传热系数为450W/m2K,水侧的表面传热系数为5850 W/m2K,已知透平油在运行温度下的物性为ρ1=879kg/m3,c1=2kJ/kgK,管内外污垢热阻分别为0.0005m2K/W和0.0002m2K/W,管壁热阻可不计,试求所需的传热面积。
(10分)(用图附后)
7、一根长径比为10的金属柱体,从加热炉中取出置于静止的空气中冷却。
从加速冷却的观点,柱体应水平放置还是竖直放置(设两种情况下的辐射散热相同)?试估算开始冷却的瞬间在两种放置的情形下自然对流冷却散热量的比值,两种情况下流动均为层流(端面散热不计)。
己知准则关联式为Nu=C (GrPr)n,其中对竖板和横管来说C和n分别为0.59、1/4和0.48、1/4。
(10分)
附题二(5)用图如下:。
热力学基础测试题

热力学基础测试题(一)的标准摩尔生成焓的反应是………(1) 表示CO2(2)下列情况中属于封闭体系的是………………………(A) 用水壶烧开水(B)氯气在盛有氯气的密闭绝热容器中燃烧(C) 氢氧化钠与盐酸在烧杯里反(D)反应在密闭容器中进行应(3)下列叙述中正确的是………………………(A) 恒压下ΔH=Q p及ΔH=H2-H1。
因为H2和H1均为状态函数,故Qp也为状态函数。
(B) 反应放出的热量不一定是该反应的焓变(C) 某一物质的燃烧焓愈大,其生成焓就愈小(D) 在任何情况下,化学反应的热效应只与化学反应的始态和终态有关,而与反应的途径无关(4) 按通常规定,标准生成焓为零的物质有…………………(A) C(石墨)(B) Br2(g) (C) N2(g)(D) 红磷(p)(5)下列叙述中正确的是………………(A) 由于反应焓变的常用单位是KJ/mol,故下列两个反应的焓变相等:(B) 由于CaCO3的分解是吸热的,故它的生成焓为负值(C) 反应的热效应就是该反应的焓变(D) 石墨的焓不为零(6)CO2(g)的生成焓等于…………………(A) CO2(g)燃烧焓的负值(B) CO(g)的燃烧焓(C) 金刚石的燃烧焓(D) 石墨的燃烧焓(7)由下列数据确定键N-F的键能为…………………………(A) 833.4KJ/mol(B) 277.8 KJ/mol(C) 103.2 KJ/mol(D) 261.9 KJ/mol(8)由下列数据确定水分子中键O-H的键能应为………………………(A) 121KJ/mol(B) 231.3 KJ/mol(C) 464 KJ/mol (D) 589 KJ/mol(9)由下列数据确定 CH4(g)的为…………(A) 211 KJ /mol(B) -74.8KJ/mol(C) 890.3KJ/mol(D) 缺条件,无法算。
(10)已知结晶态硅和无定形硅(Si)的燃烧热各为-850.6KJ/mol 和-867.3KJ/mol 则由无定形硅转化为结晶态硅的热效应为…………(A) 吸热(B) 放热(C) 16.7KJ/mol(D) 不能判断正确答案:1:(D)、2:(D)、3:(B)、4:(A)、5:(D)6:(D)、7:(B)、8:(C)、9:(B)、10:(B)热力学基础测试题(二)(1) 由下列数据确定 NH4Cl(s)溶解成NH4Cl(aq)的热效应应为(A) -6.1KJ/mol (B) +6.1 KJ/mol(C) -108.8 KJ/mol(D) +108.8 KJ/mol(2) 下列叙述中肯定正确的是………………………(A) 由于熵是体系内部微粒混乱程度的量度,所以盐从饱和溶液中结晶析出的过程总是个熵减过程。
传热学核心考点模拟试题

3.如图所示的二维、含有内热源、常物性的稳态导热问题,试导出内角顶节点 O(m,n)的 离散方程式。且Δx=Δy时,解出内角顶节点 O(m,n)的温度分布
4.一直径为 0.8m的薄壁球形液氧贮存容器,被另一个直径为 1.2m的同心薄壁 容器所包围。两容器表面为不透明漫灰表面,发射率均为 0.05,两容器表面之 间是真空的,如果外表面的温度为 300K,内表面温度为 95K,试求由于蒸发使 液氧损失的质量流量。液氧的蒸发潜热为 2.13×105J/kg。 5.在一逆流式水-水换热器中,管内为热水,进口温度 =100℃,出口温度 =80℃;管外 流过冷水,进口温度 =20℃,出口温度 =70℃。总换热量Ф=350kW,共有 53 根内径为 16mm、壁厚为 1mm的管子,管壁导热系数λ=40W/(m·K),管外流体的表 面传热系数 h0=1500W/(m2·K),管内流体为一个流程。假设管子内、外表面都是洁 净的,试确定所需的管子长度。(17分) 准则方程: 水的物性简表:
准则方程:
水的物性简表:
℃
20 45 70 80 90 100
4.183 4.174 4.187 4.195 4.208 4.220
998.2 990.1 977.7 971.8 965.3 958.4
59.9 64.15 66.8 67.4 68.0 68.3
1004 601.4 406.1 355.1 314.9 282.5
一.填空题
传热学模拟试题(一)
1.导热系数是由式
定义的,式中符号 q表示沿 n方向的
,
是
。
2.可以采用集总参数法的物体,其内部的温度变化与坐标
。
3.温度边界层越________,则对流换热系数越小,为了强化传热,应使温度边界层
热学试题及答案
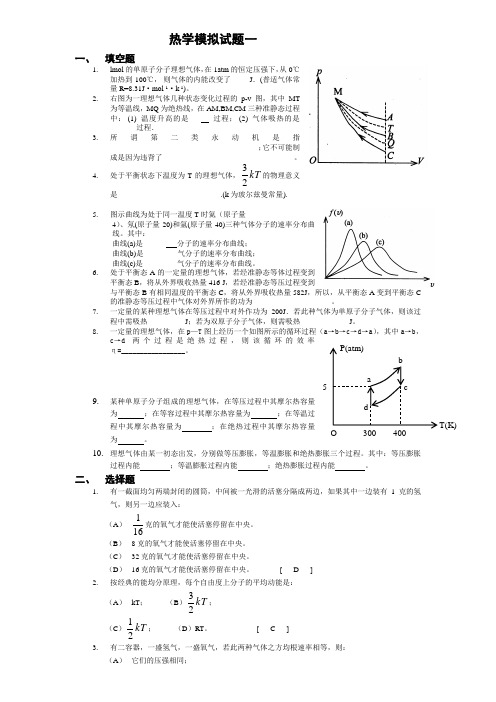
热学模拟试题一一、 填空题1.lmol 的单原子分子理想气体,在1atm 的恒定压强下,从0℃加热到100℃, 则气体的内能改变了_____J .(普适气体常量R=8.31J ·mol -1·k -1)。
2.右图为一理想气体几种状态变化过程的p-v 图,其中MT 为等温线,MQ 为绝热线,在AM,BM,CM 三种准静态过程中: (1) 温度升高的是___ 过程; (2) 气体吸热的是______ 过程. 3.所谓第二类永动机是指 _______________________________________ ;它不可能制成是因为违背了___________________________________。
4.处于平衡状态下温度为T 的理想气体,kT 23的物理意义是 ___________________________.(k 为玻尔兹曼常量).5.图示曲线为处于同一温度T 时氦(原子量 4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中:曲线(a)是______ 分子的速率分布曲线; 曲线(b)是_________气分子的速率分布曲线; 曲线(c)是_________气分子的速率分布曲线。
6.处于平衡态A 的一定量的理想气体,若经准静态等体过程变到平衡态B ,将从外界吸收热量416 J ,若经准静态等压过程变到与平衡态B 有相同温度的平衡态C ,将从外界吸收热量582J ,所以,从平衡态A 变到平衡态C 的准静态等压过程中气体对外界所作的功为_____________________。
7. 一定量的某种理想气体在等压过程中对外作功为200J .若此种气体为单原子分子气体,则该过程中需吸热__________J ;若为双原子分子气体,则需吸热_____________J 。
8.一定量的理想气体,在p —T 图上经历一个如图所示的循环过程(a→b→c→d→a),其中a→b,c→d 两个过程是绝热过程,则该循环的效率η=_________________。
热工学试题 00(1)

热工学习题(一)名词解释:1.Thermodynamics:Work is defined as the mechanical form of energy that is transferred between systems and its surrounding through boundary.2.conservation of energy principle(1)Energy can be neither created nor destroyed, it can only change forms.(2)In the nature, every substance has energy, which has different change forms. It can change from one form to another, but during the change, the total energy is unchangeable.3. closed system:energy, but not matter, can be exchanged with the environment. Examples:a tightly cappedNeither energy nor matter can be exchanged with the environment - in fact, no interactions with the environment are possible at all.4.open system:Both energy and matter can be exchanged with the environment. Example: an open cup of coffee.5 isolated system :Without any contact with the environment.过程:指热力系由一个状态变化到另一个状态时所经历的全部状态的集合。
热学试题(1)

大学物理竞赛训练题 热学(1)一、选择题(每题3分)1. 在标准状态下,任何理想气体在1 m 3中含有的分子数都等于 [ ](A) ×1023. (B)×1021.(C) ×1025. (D)×1023.(玻尔兹曼常量k =×1023 J ·K 1) 2. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常量,R 为普适气体常量,则该理想气体的分子数为: [ ](A) pV / m . (B) pV / (kT ).(C) pV / (RT ). (D) pV / (mT ).3. 若室内生起炉子后温度从15℃升高到27℃,而室内气压不变,则此时室内的分子数减少了 [ ] (A)00. (B) 400.(C) 900. (D) 2100.4. 两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内的气体质量,分别有如下关系: [ ](A) n 不同,(E K /V )不同,不同. (B) n 不同,(E K /V )不同,相同. (C) n 相同,(E K /V )相同,不同. (D) n 相同,(E K /V )相同,相同.5. 在一容积不变的封闭容器内理想气体分子的平均速率若提高为原来的2倍,则(A) 温度和压强都提高为原来的2倍. [ ](B) 温度为原来的2倍,压强为原来的4倍.(C) 温度为原来的4倍,压强为原来的2倍.(D)温度和压强都为原来的4倍.6. 关于温度的意义,有下列几种说法:(1) 气体的温度是分子平均平动动能的量度.(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义.(3) 温度的高低反映物质内部分子运动剧烈程度的不同.(4) 从微观上看,气体的温度表示每个气体分子的冷热程度.这些说法中正确的是 [ ](A) (1)、(2) 、(4). (B) (1)、(2) 、(3).(C) (2)、(3) 、(4). (D) (1)、(3) 、(4).7. 一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们 [ ](A) 温度相同、压强相同.(B) 温度、压强都不相同.(C) 温度相同,但氦气的压强大于氮气的压强.(D) 温度相同,但氦气的压强小于氮气的压强.8. 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()2/122/122/12::C B A v v v =1∶2∶4,则其压强之比A p ∶B p ∶C p 为: [ ](A) 1∶2∶4. (B) 1∶4∶8.(C) 1∶4∶16. (D) 4∶2∶1.9. 水蒸气分解成同温度的氢气和氧气,内能增加了百分之几(不计振动自由度和化学能)(A) %. (B) 50%. [ ](C) 25%. (D) 0.10. 有容积不同的A 、B 两个容器,A 中装有单原子分子理想气体,B 中装有双原子分子理想气体,若两种气体的压强相同,那么,这两种气体的单位体积的内能(E / V )A 和(E / V )B的关系 [ ](A) 为(E / V )A <(E / V )B .(B) 为(E / V )A >(E / V )B .(C) 为(E / V )A =(E / V )B .(D) 不能确定.11. 有N 个分子,其速率分布如图所示,v > 5v 0时分子数为0,则: [ ] (A) a = N / (2 v 0). (B) a = N / (3 v 0). (C) a = N / (4 v 0). (D) a = N / (5 v 0). 12. 设图示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线;令()2O p v 和()2H p v 分别表示氧气和氢气的最概然速率,则 [ ](A) 图中a表示氧气分子的速率分布曲线;()2O p v /()2H p v =4. (B) 图中a表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4. (C) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4. (C) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v = 4. 13. 下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线 [ ]2a/a/ 00000f (v )14. 若氧分子[O 2]气体离解为氧原子[O]气后,其热力学温度提高一倍,则氧原子的平均速率是氧分子的平均速率的 [ ](A) 1 /2倍. (B) 2倍. (C) 2倍. (D) 4倍.15. 已知分子总数为N ,它们的速率分布函数为f (v ),则速率分布在v 1~v 2区间内的分子的平均速率为 [ ](A)⎰21d )(v v v v v f . (B) ⎰21d )(v v v v v f /⎰21d )(v v v v f . (C) ⎰21d )(v v v v v f N . (D) ⎰21d )(v v v v v f /N . 16. 气缸内盛有一定量的氢气(可视作理想气体),当温度不变而压强增大一倍时,氢气分子的平均碰撞频率Z 和平均自由程λ的变化情况是: [ ] (A) Z 和λ都增大一倍. (B) Z 和λ都减为原来的一半. (C) Z 增大一倍而λ减为原来的一半. (D) Z 减为原来的一半而λ增大一倍.17. 一固定容器内,储有一定量的理想气体,温度为T ,分子的平均碰撞次数为 1Z ,若温度升高为2T ,则分子的平均碰撞次数2Z 为 [ ] (A) 21Z . (B) 12Z . (C) 1Z . (D) 121Z .18. 在恒定不变的压强下,气体分子的平均碰撞频率Z 与气体的热力学温度T 的关系为 (A) Z 与T 无关. (B) Z 与T 成正比. [ ] (C) Z 与T 成反比. (D) Z 与T 成正比.19. 容积恒定的容器内盛有一定量某种理想气体,其分子热运动的平均自由程为0λ,平均碰撞频率为0Z ,若气体的热力学温度降低为原来的1/4倍,则此时分子平均自由程λ和平均碰撞频率Z 分别为 [ ] (A) λ=0λ,Z =0Z . (B) λ=0λ,Z =210Z .v v(C) λ=20λ,Z =20Z . (D) λ=20λ,Z =210Z . 20. 一定量的理想气体,在体积不变的条件下,当温度降低时,分子的平均碰撞频率Z 和平均自由程λ的变化情况是: [ ] (A) Z 减小,但λ不变. (B) Z 不变,但λ减小.(C) Z 和λ都减小. (D) Z 和λ都不变.21. 在一个体积不变的容器中,储有一定量的理想气体,温度为T 0时,气体分子的平均速率为0v ,分子平均碰撞次数为0Z ,平均自由程为0λ.当气体温度升高为4T 0时,气体分子的平均速率v ,平均碰撞频率Z 和平均自由程λ分别为: [ ](A) v =40v ,Z =40Z ,λ=40λ.(B) v =20v ,Z =20Z ,λ=0λ.(C) v =20v ,Z =20Z ,λ=40λ.(D) v =40v ,Z =20Z ,λ=0λ.二、填空题1. (3分) 已知某种理想气体分子的最概然速率为p v ,气体的压强为p .则此气体的密度为__________.2. (3分) 氢分子的质量为 ×1024 g ,如果每秒有1023 个氢分子沿着与容器器壁的法线成45°角的方向以105 cm / s 的速率撞击在 2.0 cm 2 面积上(碰撞是完全弹性的),则此氢气的压强为____________.3. (3分) A 、B 、C 三个容器中皆装有理想气体,它们的分子数密度之比为n A ∶n B ∶n C =4∶2∶1,而分子的平均平动动能之比为A w ∶B w ∶C w =1∶2∶4,则它们的压强之比A p ∶B p ∶C p =__________.4. (3分) 若某种理想气体分子的方均根速率()4502/12=vm/ s ,气体压强为p =7×104 Pa ,则该气体的密度为=_______________.5. (5分) 某容器内分子数密度为10 26 m -3,每个分子的质量为 3×10-27 kg ,设其中 1/6分子数以速率v = 200 m / s 垂直地向容器的一壁运动,而其余 5/6分子或者离开此壁、或者平行此壁方向运动,且分子与容器壁的碰撞为完全弹性的.则(1) 每个分子作用于器壁的冲量ΔP =_______________;(2) 每秒碰在器壁单位面积上的分子数0n =________________;(3) 作用在器壁上的压强p =___________________.6. (3分)下面给出理想气体的几种状态变化的关系,指出它们各表示什么过程.(1) p d V= (M / M mol)R d T表示____________________过程.(2) V d p= (M / M mol)R d T表示____________________过程.(3) p d V+V d p= 0 表示____________________过程.7. (3分) 某理想气体在温度为27℃和压强为×10-2 atm情况下,密度为 g/m3,则这气体的摩尔质量M mol=____________.(普适气体常量R= J·mol1·K1)8. (3分)在一个以匀速度u运动的容器中,盛有分子质量为m的某种单原子理想气体.若=________________.使容器突然停止运动,则气体状态达到平衡后,其温度的增量T9. (5分) 容器中储有1 mol 的氮气,压强为 Pa,温度为 7 ℃,则(1) 1 m3中氮气的分子数为_____________;(2) 容器中的氮气的密度为_________________;(3) 1 m3中氮分子的总平动动能为___________.(玻尔兹曼常量k=×1023 J·K1 , N2气的摩尔质量M mol=28×103 kg·mol1 , 普适气体常量R= J·mol1·K1 )10. (5分) 在相同的温度和压强下,氢气(视为刚性双原子分子气体)与氦气的单位体积内能之比为____________,氢气与氦气的单位质量内能之比为___________.11. (3分) 储有某种刚性双原子分子理想气体的容器以速度v=100 m/s运动,假设该容器突然停止,气体的全部定向运动动能都变为气体分子热运动的动能,此时容器中气体的温度上升K,由此可知容器中气体的摩尔质量M mol=_____. (普适气体常量R= J·mol1·K1) 12. (3分) 一铁球由10 m高处落到地面,回升到 m高处.假定铁球与地面碰撞时损失的宏观机械能全部转变为铁球的内能,则铁球的温度将升高______.(已知铁的比热c=J·kg1·K1)13. (3分) 一能量为1012 eV的宇宙射线粒子,射入一氖管中,氖管内充有 mol的氖气,若宇宙射线粒子的能量全部被氖气分子所吸收,则氖气温度升高了_______________K.(1 eV=×1019J,普适气体常量R= J/(mol·K))14. (3分) 1 mol的单原子分子理想气体,在1 atm的恒定压强下,从0℃加热到100℃,则气体的内能改变了_______________J.(普适气体常量R= J·mol1·K1 )15. (3分) 一氧气瓶的容积为V,充入氧气的压强为p1,用了一段时间后压强降为p2,则瓶中剩下的氧气的内能与未用前氧气的内能之比为__________.16.(3分)若某容器内温度为 300 K的二氧化碳气体(视为刚性分子理想气体)的内能为×103 J,则该容器内气体分子总数为___________________.(玻尔兹曼常量k=×10-23 J·K1,阿伏伽德罗常量N A=×1023 mol1)17. (3分)体积和压强都相同的氦气和氢气(均视为刚性分子理想气体),在某一温度T下混合,所有氢分子所具有的热运动动能在系统总热运动动能中所占的百分比为_________.18. (3分)一气体分子的质量可以根据该气体的定体比热来计算.氩气的定体比热c V = k J·kg1·K1,则氩原子的质量m=__________.(波尔兹曼常量k=×1023 J / K)19. (3分)若某容器内温度为 300 K的二氧化碳气体(视为刚性分子理想气体)的内能为×103 J,则该容器内气体分子总数为___________________.(玻尔兹曼常量k =×10-23 J ·K 1,阿伏伽德罗常量N A =×1023 mol 1)20. (3分)一定量H 2气(视为刚性分子的理想气体),若温度每升高1 K ,其内能增加 J ,则该H 2气的质量为________________.(普适气体常量R = J ·mol 1·K 1)21. (3分) 体积为103 m 3、压强为 ×105 Pa 的气体分子的平动动能的总和为 _____________J .22.(3分)某气体在温度为T = 273 K 时,压强为p =×102 atm ,密度 = ×102 kg/m 3,则该气体分子的方均根速率为___________. (1 atm = ×105 Pa)23. (4分) 图示氢气分子和氧气分子在相同温度下的麦克斯韦速率分布曲线.则氢气分子的最概然速率为______________,氧分子的最概然速率为____________.24. 当理想气体处于平衡态时,若气体分子速率分布函数为f (v ),则分子速率处于最概然速率v p 至∞范围内的概率△N / N =________________.25. (4分) 一定量的理想气体,经等压过程从体积V 0膨胀到2V 0,则描述分子运动的下列各量与原来的量值之比是(1) 平均自由程0λλ=__________. (2) 平均速率0v v =__________. (3) 平均动能0K K εε=__________. 26.(4分)氮气在标准状态下的分子平均碰撞频率为×108 s -1,分子平均自由程为 6×10-6 cm ,若温度不变,气压降为 atm ,则分子的平均碰撞频率变为_______________;平均自由程变为_______________.27.一定量的某种理想气体,先经过等体过程使其热力学温度升高为原来的2倍;再经过等压过程使其体积膨胀为原来的2倍,则分子的平均自由程变为原来的__________倍.*28. (3分) 处于重力场中的某种气体,在高度z 处单位体积内的分子数即分子数密度为n .若f (v )是分子的速率分布函数,则坐标介于x ~x +d x 、y ~y +d y 、z ~z +d z 区间内,速率介于v ~ v + d v 区间内的分子数d N =____________________.*29. (3分) 一个很长的密闭容器内盛有分子质量为m 的理想气体,该容器以匀加速度a ϖ垂直于水平面上升(如图所示).当气体状态达到稳定时温度为T ,容器底部的分子数密度为n 0,则容器内离底部高为h 处的分子数密度n =____________. *30. (3分) 已知大气压强随高度h 变化的规律为 f ()v 1000 h n n 0 a ϖ⎪⎭⎫ ⎝⎛-=RT gh M p p mol 0exp 拉萨海拔约为 3600 m ,设大气温度t =27℃,而且处处相同,则拉萨的气压p =________________. (空气的摩尔质量M mol = 29×103 kg/mol , 普适气体常量R =J ·mol 1·K 1 , 海平面处的压强p =1 atm ,符号exp(a ) ,即e a)*31. 已知大气压强随高度h 的变化规律为 ⎪⎭⎫ ⎝⎛-=RT gh M p p mol 0exp 设气温t =5 ℃,同时测得海平面的气压和山顶的气压分别为 750 mmHg 和 590 mmHg ,则山顶的海拔h =__________m. (普适气体常量R = J ·mol -1·K -1,空气的摩尔质量M mol =29×10-3kg / mol ,p 0为h =0处的压强.符号exp(a ),即e a )三、计算题1. (5分) 一氧气瓶的容积为V ,充了气未使用时压强为p 1,温度为T 1;使用后瓶内氧气的质量减少为原来的一半,其压强降为p 2,试求此时瓶内氧气的温度T 2.及使用前后分子热运动平均速率之比21/v v .2. (5分) 黄绿光的波长是5000οA (1οA =1010 m).理想气体在标准状态下,以黄绿光的波长为边长的立方体内有多少个分子(玻尔兹曼常量k =×1023J ·K 1) 3. (10分) 一密封房间的体积为 5×3×3 m 3,室温为20 ℃,室内空气分子热运动的平均平动动能的总和是多少如果气体的温度升高 K,而体积不变,则气体的内能变化多少气体分子的方均根速率增加多少已知空气的密度= kg/m 3,摩尔质量M mol =29×103 kg /mol ,且空气分子可认为是刚性双原子分子.(普适气体常量R = J ·mol 1·K 1)4. (5分) 已知某理想气体分子的方均根速率为 400 m ·s 1.当其压强为1 atm 时,求气体的密度.5. (5分) 质量m = ×1017 g 的微粒悬浮在27℃的液体中,观察到悬浮粒子的方均根速率为1.4 cm ·s 1.假设粒子速率服从麦克斯韦速率分布,求阿伏伽德罗常数.(普适气体常量R = J ·mol 1·K 1 )6. (10分) 容积为20.0 L(升)的瓶子以速率v =200 m ·s 1匀速运动,瓶子中充有质量为100g 的氦气.设瓶子突然停止,且气体的全部定向运动动能都变为气体分子热运动的动能,瓶子与外界没有热量交换,求热平衡后氦气的温度、压强、内能及氦气分子的平均动能各增加多少(摩尔气体常量R = J ·mol -1·K 1,玻尔兹曼常量k =×10-23 J ·K 1)7. (10分)有 2×103 m 3刚性双原子分子理想气体,其内能为×102 J .(1) 试求气体的压强;(2) 设分子总数为 ×1022个,求分子的平均平动动能及气体的温度.8. (5分) 一氧气瓶的容积为V ,充了气未使用时压强为p 1,温度为T 1;使用后瓶内氧气的质量减少为原来的一半,其压强降为p 2,试求此时瓶内氧气的温度T 2.及使用前后分子热运动平均速率之比21/v v .9. (10分) 当氢气和氦气的压强、体积和温度都相等时,求它们的质量比()()e H H 2M M 和内能比()()e H H 2E E .(将氢气视为刚性双原子分子气体) 10. (5分) 计算下列一组粒子的平均速率和方均根速率.粒子数N i 2 4 6 8 2速率v i (m/s) 11. (10分) 导体中自由电子的运动可看成类似于气体中分子的运动.设导体中共有N 个自由电子,其中电子的最大速率为v m ,电子速率在v ~v + d v 之间的概率为⎩⎨⎧=0d d 2v v A N N 式中A 为常数.(1) 用N ,v m 定出常数A ;(2) 试求导体中N 个自由电子的平均速率.12. (10分) 由N 个分子组成的气体,其分子速率分布如图所示. (1) 试用N 与0v 表示a 的值.(2) 试求速率在0v ~0v 之间的分子数目.(3) 试求分子的平均速率.13. (10分) N 个粒子,其速率分布如图所示(v > 50v 时粒子数为零). (1) 试用N 与0v 表示a 的值.(2) 试求速率在 20v ─ 30v 间的粒子数.(3) 试求粒子的方均根速率. 14. (5分) 某种气体由大量分子组成,试证明:分子热运动的方均根速率恒大于或等于平均速率,即()2/12v ≥ v .15. (5分) 今测得温度为t 1=15℃,压强为p 1= m 汞柱高时,氩分子和氖分子的平均自由程分别为:Ar λ= ×108 m 和Ne λ=×108 m ,求:(1) 氖分子和氩分子有效直径之比d Ne / d Ar =(2) 温度为t 2=20℃,压强为p 2= m 汞柱高时,氩分子的平均自由程/Ar λ=16. (5分) 在什么条件下,气体分子热运动的平均自由程λ与温度T 成正比在什么条件下,λ与T 无关(设气体分子的有效直径一定)aNf (v ) v v 0 0O a/3 a 2a/3Nf (v ) v v 0 2v 0 3v 0 4v 0 5v 0 O0≤v ≤v mv >v m答:从()p d kT 2π2/=λ可见,对于分子有效直径一定的气体,当压强p 恒定时,λ与T 成正比.从()n d 2π2/1=λ和n = N / V 可见,对于分子有效直径一定的气体,当分子 总数N 和气体体积V 恒定时,λ与T 无关.17. (5分) 在A 、B 、C 三个容器中,装有不同温度的同种理想气体,设其分子数密度之比n A ∶n B ∶n C =1∶2∶4,方均根速率之比()()()2/122/122/12::C B A v v v =1∶2∶4.则其算术平均速率之比为C B A v v v ::=1∶4∶16,压强之比为p A ∶p B ∶p C =1∶4∶16. 以上关于算术平均速率之比值与压强之比值是否正确如有错误请改正.18.(10分) 根据22123v m n p =和kT m 23212=v 两式,从气体分子动理论角度推导气体实验三定律:即玻意耳马略特定律、盖吕萨克定律和查理定律.19.(5分)试以分子动理论的观点解释玻意耳定律(T 不变,pV =C ).*20. (5分)试由麦克斯韦速度分布函数 )2/exp()2()(2/3kT m kTm f v v v ϖϖϖ⋅-π=导出麦克斯韦速率分布函数F (v ).*21. (10分) 假定大气层各处温度相同均为T ,空气的摩尔质量为M mol .试根据玻尔兹曼分布律 ()/kT E P n n -=e 0证明大气压强p 与高度h (从海平面算起,海平面处的大气压强为p 0)的关系是 ⎪⎪⎭⎫ ⎝⎛=p p g M RT h 0mol ln .大学物理竞赛训练题 热学(1)参考答案:一、选择题(每题3分) 1. C 2331002.6104.221⨯⨯⨯- 2. B P =nkT , nV=pV/kT 3. B P =nkT ,nkT+nk T=0 -n/n =T/T 4. C P =nkT , E K /V=n kT nw 23=,RT M M pV mol =, RT pM mol =ρ 5. D kT nw 23= 6. B7. C RT M M pV mol =, p RT M mol =ρ, kT w 23=, 8. C 231υnm p = 9. C 2H 2O. RT v E O H 26202=,RT v RT v RT v E O H 25325252000,22=+= 25.01212152222,=-=-OH OH O H E E E 2i E v RT = pV vRT = 2i E pV = 11.B N a a a a a =++++000003223υυυυυ 12. B 22p molkT RT m M υ== 14. C mol mol M RT M RT m kT 60.188≈==ππυ; 2132162222=⋅==o o o o o o T M M T υυ 15. B16. C kT p d Z υπ22=, p d kT 22πλ= 17. B n d Z υπ22=, mol M RT m kT ππυ88==18. C kTpM RT d n d Z mol ππυπ82222==19. B 20. A 21. B二、填空题 1. RTpM V M mol==ρ ,molp M RT2=υ. 22p p υρ=2. 4233274230100.210707.010103.32100.21045cos 2---⨯⨯⨯⨯⨯⨯=⨯⨯=υm p = ×10 3Pa 3. P=nkT , kT w 23=, w n w k nk p 3232==. 1∶1∶1 4. RT M M pV mol =, p RTMmol =ρ; molM RTmkT332==υ p RT M mol =ρp 22)(3υ=24)450(1073⨯⨯==1.037kg.m -3. kg ·m 35. ix ix ix m m m P υυυ2])[(=---=∆=×10-24kg m / sn 0=122826010312001061--⨯=⨯⨯==∆∆⨯⨯=s m n S S n n x x υυP n p ∆=0=4×103Pa 6. 等压; 等体; 等温. 7. g/mol 8. m u 2/ 3k9. ×1020; ×105kg/m 3; 2 J . 10. RT i v E 2=,V vRT i V E 2=, vRT pV =, p i V E 2=, 5 / 3molM RT i M E 2=, 10 / 3 11. 28×103kg / mol 12. K 13. ×10714. ×10315. p 1V =RT 1 p 2V =RT 2; E 1=21i RT 1=21i p 1V , E 2=21i RT 2=21i p 2V∴ E 2 / E 1=p 2 / p 116. kT i N E 2=, 3001038.161074.322233⨯⨯⨯⨯⨯==-ikT E N =×1023个 17. % 18. ×1026kg19. ×1023个 20. ×103kg 21. ×102 22. 495 m/s 23. mol p M RTmkT22==υ, O 2: 1000m/s , 4==molHmolOPopH M M υυ, H 2: 4000m/s,24.⎰∞pf v v v d )(25. n d 221πλ=,20==n n λλ , mol M RT πυ8=,vRT pV =,2T 0=T , 200==T T υυkT iK 2=ε 2 26. n d Z υπ22=kTpd υπ22=; pd kTn d Z 22221ππυλ=== ×107s -1; 6×10-5cm27. 2*28. dN=N f (v ) d v=n f (v )d x d y d z d v *29. kTmgh n -e0, 相对加速度g +a , kTh a g m n )(0e+-*30. 329109.836001exp 8.31300p -⎛⎫⨯⨯⨯=⨯- ⎪⨯⎝⎭=*31. 1950 三、计算题1. 解: p 1V =RT 1 p 2V =21RT 2∴ T 2=2 T 1p 2 / p 12121212P P T T ==v v2.解:理想气体在标准状态下,分子数密度为n = p / (kT )=×1025 个/ m 3以5000οA 为边长的立方体内应有分子数为N = nV =×106个.3.解:根据 kT m 23212=v , 可得 NkT m N 23212=v , 即=()RT M M mol /23=()V M RT ρmol /23=×106 . 又 ()T iR M M E ∆=∆21/mol =()T iR M V ∆21/mol ρ=×104J .及 ()()()2/1212/1222/12v v v-=∆= ()()122/1mol /3T TM R -= m/s .4.解: 223131v v ρ==nm p ∴ 90.1/32==v p ρ kg/m 35.解:据 ()m N RT M RT A /3/3mol 2/12==v,得 N A =3RT / (m 2v )=×1023mol -1.6.解:定向运动动能221v Nm ,气体内能增量T ik N ∆21,i =3 .按能量守恒应有: 221v Nm =T ik N ∆21∴ AN T iR m /2∆=v(1) ()()===∆iR M iR m N T A //2mol 2v v K(2) ()V T R M M p //mol ∆=∆=×104Pa . (3) ()T iR M M E ∆=∆21/mol =×103J .(4) T ik ∆=∆21ε=×1022 J . 7. 解:(1) 设分子数为N .据 E = N (i / 2)kT 及 p = (N / V )kT 得 p = 2E / (iV ) = ×105Pa(2) 由 kT N kT Ew2523=ϖϖ得 ()21105.75/3-⨯==N E w J又 kT NE 25= 得 T = 2 E / (5Nk )=362k 8.解: p 1V =RT 1 p 2V =21RT 2∴ T 2=2 T 1p 2 / p 12121212P P T T ==v v 9.解: 由 pV =()()mol22H H M M RT 和pV =()()mol e H e H M M RT得 ()()e H H 2M M =()()m ol m ol 2e H H M M =42=21.由 E (H 2)=()()mol 22H H M M 25RT 和RT M M E 23)He ()He ()He (mol =得 ()()e 2H E H E =()()()()molmol22e H /He 3H /H 5M M M M∵()()mol 22H M H M = ()()mole H M e H M (p 、V 、T 均相同), ∴ ()()e H E H E 2=35.10. 解:平均速率∑∑=ii i N N /v v= m/s 方均根速率 ()∑∑=iii NN 22/12v v= m/s .11. 解:(1) 根据已知条件可知电子速率分布函数为⎩⎨⎧==0d d )(2v v v A N Nf 根据速率分布函数的归一化条件1d )(0=⎰∞v v f有13d 0d 22==+⎰⎰∞m A A mmv v v v v v 0解得 33mA v =(2) 根据平均速率定义 NN ⎰=d v v可得 ⎰∞=0d )(v v v v f ⎰=mf v v v v 0d )(0≤v ≤v m v > v mm m A A mv v v v v v 4341d 402===⎰ 12. 解:(1) 由分布图可知:0→v 0: N f (v ) = ( a / v 0) v , f (v ) = av /(N v 0).v 0→2 v 0: N f (v ) = a , f (v ) = a /N .2v 0 f (v ) = 0由归一化条件1d )(0=⎰∞v v f , 有 1d /d )/(020=+⎰⎰v v v v v vv N a N a ,得: ( 3 /2 ) ( av 0 /N ) = 1 , ∴ a = ( 2 /3 ) ( N /v 0).(2) ⎰⎰==∆0000223223d d )(v v v v v v v N a NNf N 021v a =, 将a 代入得 N N N 31)3/(22100=⨯=∆v v . (3) 0→v 0: f (v ) = a v /(N v 0) = (v / N v 0)×2 N / (3 v 0) )3/(220v v =. v 0→2 v 0: f (v ) = a /N = ( 1 / N )×( 2 N / 3 v 0) = 2 / (3 v 0).⎰∞=0d )(v v v v f v vv v v v v v v v d )3/(2d )3/(20202⎰⎰⨯+⨯=0092v v +==11 v 0 /913. 解:(1) 曲线下的面积代表总分子数N ,N a a a a a =++++0000032313231v v v v v , ∴ )3(0v N a =.(2) 速率在2v 0 ─3 v 0间的粒子数3/)3/(000N N a N ===∆v v v .(3) ⎰∞=022d )(v v v v f ⎰∞=02d )()/1(v v v Nf N⎢⎢⎣⎡=⎰002d )()/1(v v v v Nf N ++⎰0022d )(v v v v v Nf⎰+00322d )(v v v v v Nf ⎰+00432d )(v v v v v Nf ⎥⎥⎦⎤+⎰00542d )(v v Nf v v v{+-+=])2[(313231311303030v v v a a N +-+-+])3()4[(3132])2()3[(3130303030v v v v a a}])4()5[(31313030v v -+a 2v 20323v =()02/1202/1277.2])3/23[(v v v ==.14.证法1:设速率分布函数为 F (v )则 1d )(0=⎰∞v v F , ⎰∞=022d )(v v v v F ,⎰∞=0d )(v v v v F由于定积分性质: 2]d )()([⎰b ax x g x f ≤⎰⋅⎰bab ax x g xx f d )]([d )]([22所以有: ()22]d )()([v v v v v ⋅⋅=⎰∞F F ≤⎰⎰∞∞⋅020d )(d )(v v v v v F F 2v =即 ()2v ≤2v 或 ()2/12v≥v证法2:因为 2)(v v -≥0而 2)(v v -22222)()(22v v v v v v v +-=+-=()22v v -= ∴ ()22v v -≥02/12)(v ≥v15. 解:(1) 据 ()p d kT 22/π=λ得 d Ne / d Ar =()2/1NeAr /λλ= .(2) /Ar λ=Ar λ(p 1 / p 2)T 2 / T 1=()()2732731221Ar ++t p t p λ=×107m .16. 答:从()p d kT 2π2/=λ可见,对于分子有效直径一定的气体,当压强p 恒定时,λ与T 成正比.从()n d 2π2/1=λ和n = N / V 可见,对于分子有效直径一定的气体,当分子总数N 和气体体积V 恒定时,λ与T 无关.17.答:以上两个比值的结果是错误的,改正如下: 对于不同温度的同种理想气体,有CB A v v v ::=()()()2/122/122/12::CB A v v v =1 : 2 : 4根据理想气体压强公式231v nm p =可得 Ap B p C p =()()()222::CC B B A A n n n v v v =1:8:6418.推导:由22123v m n p =及kT m 23212=v 得 nkT p =.即 ()kT V N nkT p /==, NkT pV =. 一定量的气体N 不变,在温度T 不变时,NkT = 恒量.故 pV = 恒量 玻意耳马略特定律 又 p = nkT , p / T = nK = (N /V )k . 一定量的气体N 不变,在体积V 不变时,(N /V )k = 恒量.故 (p / T ) = 恒量 查理定律. 再由 p = nkT = (N / V )kT 得 (V / T ) = (Nk ) / p . 一定量的气体N 不变,在压强p 不变时,Nk / p = 恒量. 故 V / T = 恒量 盖吕萨克定律19.答:当一定质量的理想气体的温度保持一定时,其压强与体积的乘积等于常量,即pV =C .也就是说:压强p 与体积V 成反比.根据分子运动论的观点,压强p 应正比于分子每次碰壁所施于器壁的平均冲量和分子在单位时间内碰撞单位面积器壁的次数这二者的乘积. 2分前者取决于分子的平均平动动能w ,也就是说取决于气体的温度T (kT w 23=),后者则正比于分子的数密度n ,而在总分子数一定时,n 又是反比于V 的.所以在T 一定的情况下,p 反比于V ,这就是玻意耳定律. 3分*20.解:设F (v )为速率分布函数,则有vv d d )(N NF =, ∴ v v d )(d NF N = ①①式的物理意义为速率分布在v ~v + d v 区间内的分子数.v ~v + d v 区间在速度空间里为一半径为v 厚度为d v 的球壳(如图所示).)(v ϖf 的物理意义为速度空间中的概率密度.在本题中)(v ϖf 为速度空间中的球对称函数.图中球壳的体积为v v d π42.速度分布在球壳中的分子数为v v v d 4)(d 2π=ϖNf N ②比较①式和②式得 24)()(v v v π=ϖf F 22v 2/32)2(4v kT m e kTm -ππ= *21.证:设空气分子的质量为m ,则在离海平面高度为h 处,空气分子的势能为E p =mgh ,于是有 h RTgM h kTN mgN h kTmg n n n n AAmol eee000---=== 2分那么,由 p = nkT =h RTgM h RTgM p kT n mol mol ee00--= 1分取对数 ln(p / p 0) =-M mol g h / RTh = RT ln (p 0/p ) / M mol g 2分。
传热学模拟试题及参考答案

传热学课程试卷(A卷)题号一二三四总分得分一、填空题(本大题共14分,每题2分)1.导温系数又称热扩散率,它表征了物体内部各部分温度趋于均匀一致的能力(或材料传播温度变化的能力。
2.对同一种工质,自然对流换热系数h自、强制对流换热系数h强和沸腾换热系数h沸的大小关系为:h自<h强<h沸。
3.半径为R的半球内表面和圆底面组成封闭系统,则半球内表面对圆底面的角系数X2,1=1/2 。
4.定向辐射强度是指单位时间,单位可见辐射面积,单位立体角内的辐射能量。
5.从换热表面的结构而言,强化凝结换热的基本思想是尽量减薄粘滞在换热表面上的液膜厚度;强化沸腾换热的基本思想是尽量增加换热表面上的汽化核心数。
6.已知炉墙表面与空气的对流换热系数为h c,辐射换热系数为h r,则其单位面积复合换热热阻为1/(h c+h r) 。
7.圆管的临界热绝缘直径d cri的计算式为d cri=2λ/h,其物理意义为当d=d cri时对流与导热热阻之和最小,散热量最大。
二、选择题(本大题共16分,每小题2分)在每题列出的四个选项中只有一个选项正确,请将正确选项前的字母填在题后的括号内。
1.公式tKq∆=称为( D )。
A.傅里叶定律 B. 牛顿冷却公式 C. 热平衡方程 D. 传热方程式2.物体表面黑度不受下述(D)条件的影响。
A.物质种类 B. 表面温度 C. 表面状况 D. 表面位置3.某热力管道采用两种导热系数不同的保温材料进行保温,为了达到较好的保温效果,应将哪种材料放在内层?( B )A .导热系数较大的材料 B. 导热系数较小的材料 C .任选一种即可 D. 无法确定 4.下列各参数中,属于物性参数的是( C )。
A .传热系数 B. 吸收率 C. 普朗特数 D. 对流换热系数 5.将保温瓶的双层玻璃中间抽成真空,其目的是( D )。
A .减少导热 B. 减少对流换热 C .减少对流与辐射换热 D. 减少导热与对流换热 6.沸腾的临界热流密度q cri 是( C )。
热学试题1---4及答案

热学模拟试题一一、 填空题1.lmol 的单原子分子理想气体,在1atm 的恒定压强下,从0℃加热到100℃, 则气体的内能改变了_____J .(普适气体常量R=8.31J ·mol -1·k -1)。
2.右图为一理想气体几种状态变化过程的p-v 图,其中MT 为等温线,MQ 为绝热线,在AM,BM,CM 三种准静态过程中: (1) 温度升高的是___ 过程; (2) 气体吸热的是______ 过程. 3.所谓第二类永动机是指 _______________________________________ ;它不可能制成是因为违背了___________________________________。
4.处于平衡状态下温度为T 的理想气体,kT 23的物理意义是 ___________________________.(k 为玻尔兹曼常量).5.图示曲线为处于同一温度T 时氦(原子量 4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中:曲线(a)是______ 分子的速率分布曲线; 曲线(b)是_________气分子的速率分布曲线; 曲线(c)是_________气分子的速率分布曲线。
6.处于平衡态A 的一定量的理想气体,若经准静态等体过程变到平衡态B ,将从外界吸收热量416 J ,若经准静态等压过程变到与平衡态B 有相同温度的平衡态C ,将从外界吸收热量582J ,所以,从平衡态A 变到平衡态C 的准静态等压过程中气体对外界所作的功为_____________________。
7. 一定量的某种理想气体在等压过程中对外作功为200J .若此种气体为单原子分子气体,则该过程中需吸热__________J ;若为双原子分子气体,则需吸热_____________J 。
8.一定量的理想气体,在p —T 图上经历一个如图所示的循环过程(a→b→c→d→a),其中a→b,c→d 两个过程是绝热过程,则该循环的效率η=_________________。
全国10月高等教育自学考试工程热力学(一)试题及答案解析

全国2018年10月高等教育自学考试工程热力学(一)试题课程代码:02248一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1.简单可压缩热力系统的状态可由( )A.两个状态参数决定B.两个具有物理意义的状态参数决定C.两个可测状态参数决定D.两个相互独立的状态参数决定2.热能转变为机械能的唯一途径是通过工质的( )A.膨胀B.压缩C.凝结D.加热3.q=△h+w t 适宜于( )A.稳流开口系统B.闭口系统C.任意系统D.非稳流开口系统4.锅炉空气预热器中,烟气入口温度为1373K ,经定压放热后其出口温度为443K ,烟气的入口体积是出口体积的( )A.3.1倍B.6.47倍C.0.323倍D.2.864倍5.理想气体定压过程的势力学能变化量为( )A.c p △tB.c v △TC.h-p vD.q-w t6.理想气体等温过程的技术功=( )A.0B.v(p 1-p 2)C.p 1v 1ln 21P P D.h 1-h 2 7.在p —v 图上,经过同一状态点的理想气体等温过程线斜率的绝对值比绝热过程线斜率的绝对值( )A.大B.小C.相等D.可能大,也可能小8.不可逆机与可逆机相比,其热效率( )A.一定高B.相等C.一定低D.可能高,可能低,也可能相等9.若弧立系内发生的过程都是可逆过程,系统的熵( )A.增大B.减小C.不变D.可能增大,也可能减小10.水蒸汽热力过程热力学能变化量△u=( )A.q-w tB.△h-△(pv)C.c v (T 2-T 1)D.21t t v c (T 2-T 1)11.理想气体绝热流经节流阀,节流后稳定截面处的温度( )A.升高B.降低C.不变D.无法确定12.热力计算时,回热加热器的出口水温取决于( )A.回热抽气量B.回热抽汽压力C.加热器的给水量D.加热器的进口温度13.若再热压力选择适当,则朗肯循环采用再热后( )A.汽耗率上升,热耗率下降B.汽耗率下降,热耗率上升C.汽耗率与热耗率都上升D.汽耗率与热耗率都下降14.在定压加热燃气轮机循环中,为达到提高循环热效率的目的,可采用回热技术来提高工质的( )A.循环最高温度B.循环最低温度C.平均吸热温度D.平均放热温度15.湿空气中水蒸汽所处的状态( )A.可以是饱和状态,也可以是过热蒸汽状态B.只能是饱和状态C.既不是饱和状态,也不是过热蒸汽状态D.只能是过热蒸汽状态二、多项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的五个选项中有二至五个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
热学试题1---4及答案

热学模拟试题一一、 填空题1.lmol 的单原子分子理想气体,在1atm 的恒定压强下,从0℃加热到100℃, 则气体的内能改变了_____J .(普适气体常量R=8.31J ·mol -1·k -1)。
2.右图为一理想气体几种状态变化过程的p-v 图,其中MT 为等温线,MQ 为绝热线,在AM,BM,CM 三种准静态过程中: (1) 温度升高的是___ 过程; (2) 气体吸热的是______ 过程. 3.所谓第二类永动机是指 _______________________________________ ;它不可能制成是因为违背了___________________________________。
4.处于平衡状态下温度为T 的理想气体,kT 23的物理意义是 ___________________________.(k为玻尔兹曼常量).5.图示曲线为处于同一温度T 时氦(原子量 4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中:曲线(a)是______ 分子的速率分布曲线; 曲线(b)是_________气分子的速率分布曲线; 曲线(c)是_________气分子的速率分布曲线。
6.处于平衡态A 的一定量的理想气体,若经准静态等体过程变到平衡态B ,将从外界吸收热量416 J ,若经准静态等压过程变到与平衡态B 有相同温度的平衡态C ,将从外界吸收热量582J ,所以,从平衡态A 变到平衡态C 的准静态等压过程中气体对外界所作的功为_____________________。
7. 一定量的某种理想气体在等压过程中对外作功为200J .若此种气体为单原子分子气体,则该过程中需吸热__________J ;若为双原子分子气体,则需吸热_____________J 。
8.一定量的理想气体,在p —T 图上经历一个如图所示的循环过程(a→b→c→d→a),其中a→b,c→d 两个过程是绝热过程,则该循环的效率η=_________________。
热学专项模拟测试题(参考答案)

热学专项模拟测试题(参考答案)高垚骏(安徽省宣城市宣州区新田中心初中)
一、选择题
二、填空题
13.(1)惯性小长(2)小快低
14.汽化做功
15.液化放出上水汽化吸热
16.热量沸点
17.如下表:
18.压缩体积增加吸收
19.压强(压力)摩擦力(摩擦、阻力)
20.35~42 0.1 A 凸透镜成正立放大的虚像或放大镜的原理21.(1)温度计的玻璃泡与容器底部接触;读数时视线与温度计上表面不相平(2)不变增大减小
(3)增大热传递
(4)水银吸收的热量5.6J
三、实验与探究
22.(1)6.72×104
(2)D
(3)继续吸热且温度保持不变
(4)①水太多了②水的初温度太低③提高水的初温度(或减少水的质量或在杯子上加盖等)
(5)温度计不准确,或当地的气压低,水的沸点不到100℃
23.(1)羽绒
(2)4.4l×105J
(3)热水与外界温差越大时,放热速度越快(或热水放热先快后慢)
四、综合解答
24.。
传热学试卷

传热学(一)第一部分选择题•单项选择题(本大题共 10 小题,每小题 2 分,共 20 分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1. 在稳态导热中 , 决定物体内温度分布的是 ( )A. 导温系数B. 导热系数C. 传热系数D. 密度2. 下列哪个准则数反映了流体物性对对流换热的影响 ?( )A. 雷诺数B. 雷利数C. 普朗特数D. 努谢尔特数3. 单位面积的导热热阻单位为 ( )A. B.C. D.4. 绝大多数情况下强制对流时的对流换热系数 ( ) 自然对流。
A. 小于B. 等于C. 大于D. 无法比较5. 对流换热系数为 100 、温度为 20 ℃的空气流经 50 ℃的壁面,其对流换热的热流密度为()A. B.C. D.6. 流体分别在较长的粗管和细管内作强制紊流对流换热,如果流速等条件相同,则()A. 粗管和细管的相同B. 粗管内的大C. 细管内的大D. 无法比较7. 在相同的进出口温度条件下,逆流和顺流的平均温差的关系为()A. 逆流大于顺流B. 顺流大于逆流C. 两者相等D. 无法比较8. 单位时间内离开单位表面积的总辐射能为该表面的()A. 有效辐射B. 辐射力C. 反射辐射D. 黑度9. ()是在相同温度条件下辐射能力最强的物体。
A. 灰体B. 磨光玻璃C. 涂料D. 黑体10. 削弱辐射换热的有效方法是加遮热板,而遮热板表面的黑度应()A. 大一点好B. 小一点好C. 大、小都一样D. 无法判断第二部分非选择题•填空题(本大题共 10 小题,每小题 2 分,共 20 分)11. 如果温度场随时间变化,则为。
12. 一般来说,紊流时的对流换热强度要比层流时。
13. 导热微分方程式的主要作用是确定。
14. 当 d 50 时,要考虑入口段对整个管道平均对流换热系数的影响。
15. 一般来说,顺排管束的平均对流换热系数要比叉排时。
高考物理专练题热学(试题部分)

高考物理专练题热学(试题部分)考点一分子动理论1.[2018河南八市第一次测评,16(1)](多选)关于热现象和热学规律,以下说法正确的有()A.随分子间的距离增大,分子间的斥力减小,分子间的引力增大B.液体表面层分子间距离大于液体内部分子间距离,液体表面存在张力C.晶体熔化时吸收热量,分子平均动能不变D.自然界中的能量虽然是守恒的,但并非所有的能量都能利用E.气体的温度升高时,分子的热运动变得剧烈,分子的平均动能增大,撞击器壁时对器壁的作用力增大,从而气体的压强一定增大答案BCD2.(多选)关于布朗运动,下列说法正确的是()A.布朗运动是液体中悬浮微粒的无规则运动B.液体温度越高,液体中悬浮微粒的布朗运动越剧烈C.在液体中的悬浮颗粒只要大于某一尺寸,都会发生布朗运动D.布朗运动是液体分子永不停息地做无规则运动E.液体中悬浮微粒的布朗运动是液体分子对它的撞击作用不平衡所引起的答案ABE3.[2020届河南五校联考,33(1)]在“用油膜法估测分子的大小”实验中,用amL的纯油酸配制成bmL的油酸酒精溶液,再用滴管取1mL油酸酒精溶液,让其自然滴出,共n滴。
现在让其中一滴落到盛水的浅盘内,待油膜充分展开后,测得油膜的面积为Scm2,则:(1)估算油酸分子的直径大小是cm。
(2)用油膜法测出油酸分子的直径后,要测定阿伏加德罗常数,还需要知道油酸的。
A.摩尔质量B.摩尔体积C.质量D.体积(2)B答案(1)abSn考点二固体、液体、气体1.[2019广西梧州联考,33(1)](多选)以下说法正确的是()A.当一定量气体吸热时,其内能可能减小B.单晶体有固定的熔点,多晶体和非晶体都没有固定的熔点C.一定量的理想气体在等温变化的过程中,随着体积减小,气体压强增大D.已知阿伏加德罗常数、气体的摩尔质量和密度,可估算出该气体分子间的平均距离E.给自行车打气时越往下压,需要用的力越大,是因为压缩气体使得分子间距减小,分子间作用力表现为斥力导致的答案ACD2.[2015课标Ⅰ,33(1),5分](多选)下列说法正确的是()A.将一块晶体敲碎后,得到的小颗粒是非晶体B.固体可以分为晶体和非晶体两类,有些晶体在不同方向上有不同的光学性质C.由同种元素构成的固体,可能会由于原子的排列方式不同而成为不同的晶体D.在合适的条件下,某些晶体可以转变为非晶体,某些非晶体也可以转变为晶体E.在熔化过程中,晶体要吸收热量,但温度保持不变,内能也保持不变答案BCD3.[2016课标Ⅲ,33(2),10分]一U形玻璃管竖直放置,左端开口,右端封闭,左端上部有一光滑的轻活塞。
热工基础模拟试题(附答案)

热工基础模拟试题(附答案)一、单选题(共55题,每题1分,共55分)1.测量容器中气体压力的压力表读数发生变化一定是因为:()A、有气体泄漏B、气体的热力状态发生变化C、大气压力发生变化D、以上三者均有可能正确答案:D2.下面属于水蒸气定压产生过程的温熵图上最少有()线A、2B、3C、1D、0正确答案:A3.热力学第二定律描述的是能量转化遵守的()A、数量规律B、能质规律C、数量与质量规律D、以上都不对正确答案:B4.朗肯循环的绝热膨胀过程在(____)中完成的。
A、锅炉B、给水泵C、凝汽器D、汽轮机正确答案:D5.不是状态参数的是(____)。
A、熵B、焓C、比功D、比内能正确答案:C6.与实际循环热效率相等的卡诺循环称为(____)。
A、适用循环B、实用循环C、等效卡诺循环D、动力循环正确答案:C7.热力系与外界交换的能量有()A、功B、热能C、热D、热和功正确答案:D8.功的符号是()A、WB、J/KGC、wD、j正确答案:A9.在锅炉中吸收的热量转化为了工质的()A、热量B、焓C、熵D、动能正确答案:B10.在现有火力发电技术中,提高朗肯循环初温受制于(____)。
A、乏汽干度B、循环C、冷源D、材料正确答案:D11.温度越高,则过热蒸汽的焓(____)。
A、不变B、越低C、前三个都可能D、越高正确答案:C12.功的单位是()A、kgB、JC、kg/JD、J/kg正确答案:B13.朗肯循环的等压散热过程在(____)中完成的。
A、锅炉B、汽轮机C、给水泵D、凝汽器正确答案:D14.10Kg蒸汽的焓是10KJ,则其比焓是(____)KJ/kg。
A、1B、0C、0.5D、2正确答案:A15.朗肯循环()有汽化过程A、一定B、可能C、一定没D、以上都不对正确答案:B16.热与功一定在()上具有不同A、能质B、过程C、状态D、数量正确答案:A17.朗肯循环中具有绝热升压作用的是(____)。
B、凝汽器C、给水泵D、汽轮机正确答案:C18.朗肯循环中工质在汽轮机内发生是(____)过程。
热力学考试试题

热力学考试试题一、选择题(每题 5 分,共 30 分)1、下列关于热力学第一定律的表述中,正确的是()A 系统从外界吸收的热量等于系统内能的增加量与系统对外做功之和B 系统内能的增加量等于系统从外界吸收的热量减去系统对外做功C 系统对外做功等于系统从外界吸收的热量减去系统内能的增加量D 以上表述都不正确2、一定质量的理想气体,在绝热膨胀过程中()A 气体的内能增大,温度升高B 气体的内能减小,温度降低C 气体的内能不变,温度不变D 气体的内能不变,温度升高3、对于热机,下列说法中正确的是()A 热机效率越高,做的有用功越多B 热机效率越高,消耗的燃料越少C 热机效率越高,燃料燃烧释放的内能转化为机械能的比例越大D 热机效率可以达到 100%4、下列过程中,可能发生的是()A 某一物体从外界吸收热量,内能增加,但温度降低B 某一物体从外界吸收热量,内能增加,温度升高C 某一物体对外做功,内能减少,但温度升高D 以上过程都不可能发生5、一定质量的理想气体,在等容变化过程中,温度升高,则()A 气体压强增大B 气体压强减小C 气体压强不变D 无法确定气体压强的变化6、关于热力学第二定律,下列说法正确的是()A 不可能使热量从低温物体传向高温物体B 不可能从单一热源吸收热量并把它全部用来做功,而不引起其他变化C 第二类永动机不可能制成,是因为它违反了能量守恒定律D 热力学第二定律说明一切宏观热现象都具有方向性二、填空题(每题 5 分,共 20 分)1、热力学温度与摄氏温度的关系为_____,当热力学温度为 273K 时,摄氏温度为_____℃。
2、一定质量的理想气体,在等温变化过程中,压强与体积成_____比。
3、卡诺循环包括_____个等温过程和_____个绝热过程。
4、熵增加原理表明,在任何自然过程中,一个孤立系统的熵总是_____。
三、计算题(每题 15 分,共 30 分)1、一定质量的理想气体,初始状态为压强 p₁= 10×10⁵ Pa,体积 V₁= 10×10⁻³ m³,温度 T₁= 300 K。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热学模拟试题(一)
(时间:120分钟 共100分)
一、单项选择题:下面每题的选项中,只有一个是正确的,请将正确答案填在下面的答题表格内。
(本题共15小
题,每小题2分,共30分)
1、 有一截面均匀、两端封闭的圆筒,中间被一光滑的活塞分成两边,如果其中的一边装有1克的氢
气,则为了使活塞停留在正中央,另一边应装入的氧气质量为( ) A 、
16
1
克;B 、8克;C 、16克;D 、32克。
2、 如果只能用绝热方法使系统从初态变到终态,则( )
A 、 对联结这两态的不同绝热路径,所做功不同;
B 、 对联结这两态的所有绝热路径,所做功都相同;
C 、 由于没有热能传递,故没有做功;
D 、 系统的总内能将不变。
3、 下列说法正确的是( )
A 、一个热力学系统吸收的热量越多,则其温度就越高,内能也就越大;
B 、理想气体在自由膨胀过程中,体积从1V 变到2V ,则所作的功⎰
⋅=
2
1
V V dV P A ;
C 、任意准静态过程中,理想气体的内能增量公式T C U m V ∆=∆,ν都适用;
D 、理想气体被压缩,其温度必然会升高。
4、 由热力学第二定律,下面哪个说法正确( )
A 、功可完全转变为热,但热不可能完全转为功;
B 、热量不可能由低温物体传向高温物体;
C 、两条绝热线可以相交;
D 、一条绝热线与一条等温线只能有一个交点。
5、 一摩尔单原子理想气体,在一个大气压的恒定压强下,从0C 被加热到100C ,此时气体的内能增
加了( )
A 、150J ;
B 、;
C 、;
D 、。
6、 将氦气液化的设备装在温度为K 3001=T 的房间内,如果该设备中氦气的温度为K 0.51=T ,则释
放给房间的热量1Q 和从氦气吸收的热量2Q 的最小比值为( ) A 、
601;B 、60;C 、59
1
;D 、59。
7、 在固定的容器中,若将理想气体的温度T 0提高为原来的两倍,即T =2T 0,分子的平均动能和气体
压强分别用ε和P 表示,则( )
A 、02εε=,P = 2P 0;
B 、02εε=,P = 4P 0;
C 、04εε=,P = 2P 0;
D 、ε和P 都不变。
8、 摩尔数一定的理想气体,由体积V 1,压强P 1绝热自由膨胀到体积V 2=2V 1,则气体的压强P 2、内
能变化U ∆和熵的变化S ∆分别为( ) A 、
21P ,0,0; B 、2
1P
,0,2ln R ν C 、
21
P ,2ln R ν,0;; D 、γ2
1P ,0,2ln R ν。
9、 理想气体起始时温度为T ,体积为V ,经过三个可逆过程,先绝热膨胀到体积为2V ,再等体升压
到使温度恢复到T ,再等温压缩到原来的体积。
则此循环过程( ) A 、每个过程中,气体的熵保持不变;
B 、每个过程中,外界的熵保持不变;
C 、每个过程中,气体与外界的熵之和保持不变;
D 、整个过程中,气体与外界的熵之和增加。
10、 若用N 表示总分子数,f (v )表示麦克斯韦速率分布函数,以下哪一个积分表示分布在速率区间
v 1~v 2内所有气体分子的总和( )
A 、⎰2
1
)(v v dv v f ;B 、⎰2
1
)(v v dv v Nf ;C 、⎰2
1
)(v v dv v vf ;D 、⎰2
1
)(v v dv v Nvf 。
11、 某容器内盛有标准状态下的氧气O 2,其均方根速率为v 。
现使容器内氧气绝对温度加倍,O 2被
分离成原子氧O ,则此时原子氧的均方根速率为( ) A 、
2
1
v ;B 、v ;C 、2v ;D 、2v 。
12、 若气体分子服从麦克斯韦速率分布律,如果气体的温度降为原来的二分之一,与最概然速率v p
相应的速率分布函数f (v p )变为原来的( ) A 、
21
;B 、2;C 、2
1;D 、2。
13、 一容器贮有气体,其平均自由程为λ,当绝对温度降为原来的一半,体积增大一倍,分子作用
半径不变。
此时平均自由程为( ) A 、
21
λ; B 、2
1λ; C 、λ; D 、2λ; E 、2λ。
14、 气体温度和压强都提高为原来的2倍,则扩散系数D 变为原来的( )
A 、2倍;
B 、
2
1倍;C 、2倍;D 、
2
1
倍;E 、22倍。
15、 若在温度为T ,压强为P 时,气体的粘滞系数为,则单位体积内的分子在每秒钟相互碰撞的总次
数为( )
A 、πη34P ;
B 、πη
38P
;C 、kT P πη342;D 、kT P πη382。
二、填空题:根据题意将正确答案填在题目中的空格内。
(本题共9小题,10个空,每空2分,共20分) 1、 一摩尔单原子分子理想气体,从温度为300K ,压强为1atm 的初态出发,经等温过程膨胀至原
来体积的2倍,则气体所作的功为 。
2、 设空气温度为0℃,且不随高度变化,则大气压强减为地面的75%时的高度为 。
3、 某种气体分子在温度为T 1时的方均根速率等于温度为T 2时的平均速率,则2
1
T T = 。
4、 氮气分子的最概然速率为450m/s 时的温度为 。
5、 1摩尔双原子分子理想气体由300K 经可逆定压过程从 m 3膨胀到 m 3,则气体的熵变
为 。
6、 在室温300K 下,一克氢气的内能是 。
7、 kT 23
的物理意义是 。
8、 已知氧在标准状态下的粘滞系数为26Nsm 102.19--⨯,则氧分子的平均自由程为 ,分
子的有效直径为 。
9、 一温度为400K 的热库在与另一温度为300K 的热库短时间的接触中传递给它1kJ 的热量,两热
库构成的系统的熵改变了 。
三、计算题:按照下面题目的要求,将完整答案写在题目后面的空白处,不够可另加附页。
1、(16分)如图所示为1摩尔理想气体氦所经历的循环,其中bc 过程为绝热过程。
求:
(1) c 状态的体积V c ; (2) b c 过程系统对外作的功; (3) a b 过程系统的熵变; (4) 循环abca 的效率。
2、(8分)在两个共轴圆筒之间充满氮气,内筒的筒壁上绕有电阻丝加热,已知内筒半径为m 10531-⨯=r ,每米长度上所绕电阻丝的阻值为Ω=10R ,加热电流A 0.1=I ;外筒半径为m 1022
2-⨯=r 。
保持外筒温度恒定t 2=0℃,过程稳定后内筒的温度t 1=100℃。
则氮气的导热系
数是多少
3、(8分)处在平衡态下的气体分子热运动的速率分布是麦克斯韦速率分布f (v ),分子的平动动能
22
1
mv =ε,求气体分子按的分布律f (),以及分子的平均平动能平ε和最概然值p 。
4、(8分)有一台实际致冷机工作于两个恒温热源之间,热源温度分别为T 1=500K 和T 2=300K ,设工质在每一循环中从低温热源吸收热量为2kJ ,向高温热源放热6kJ ,试求:
(1)每一循环中,外界对致冷机作了多少功
(2)该致冷机的致冷系数是多少
(3)每一循环中热源和工质的总熵变为多少
(4)假定上述致冷机为可逆机,那么每一循环中热源和工质的总熵变为多少致冷系数为多少
5、(10分)设由N 个气体分子组成的热力学系统,分子质量为m ,其速率分布函数为:
⎩⎨
⎧>≤≤--=)
(0
)0()()(000v v v v v
v v k v f
试求:(1)分布函数中的常数k (v 0为已知);(2)最概然速率v p ;(3)平均速率v ;
(4)气体分子的平均平动能平ε;(5)速率在0~间的分子数N 。
