铅球投掷模型
数学实验之铅球投掷
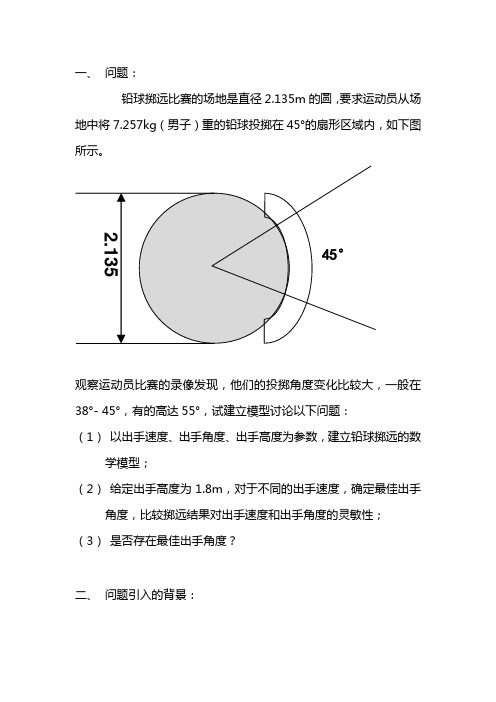
一、问题:铅球掷远比赛的场地是直径2.135m的圆,要求运动员从场地中将7.257kg(男子)重的铅球投掷在45°的扇形区域内,如下图所示。
观察运动员比赛的录像发现,他们的投掷角度变化比较大,一般在38°- 45°,有的高达55°,试建立模型讨论以下问题:(1)以出手速度、出手角度、出手高度为参数,建立铅球掷远的数学模型;(2)给定出手高度为1.8m,对于不同的出手速度,确定最佳出手角度,比较掷远结果对出手速度和出手角度的灵敏性;(3)是否存在最佳出手角度?二、问题引入的背景:铅球比赛是奥运会中一项重要的比赛项目,在铅球比赛中,运动员在投掷圈中站立开始投掷。
投掷圈外围是金属镶边,有6毫米厚,顶端涂白。
投掷时,运动员不能接触铁边的顶端或者投掷圈以外的地面,铅球的投掷圈直径2.135米。
圈内地面由水泥或者有相似的硬度又能防滑的物质构成,它的高度略低于地面高度。
铅球投掷圈的正前方放着一个木质的抵趾板,用来防止运动员滑出圈外。
运动员可以碰抵趾板的内侧,但不能碰抵趾板的顶部。
运动员进入圈内开始投掷后,如果运动员身体的任何部位触及圈外地面,或触及铁圈和抵趾板上面,或以不符合规定的方式将铅球推出,均判为一次试掷失败。
铅球必须完全落在落地区角度线内沿以内,试掷方为有效。
每次有效试掷后,应立即测量成绩。
从铅球落地痕迹的最近点取直线量至投掷圈内沿,测量线应通过投掷圈圆心。
运动员在器械落地后方可离开投掷圈。
离开投掷圈时首先触及的铁圈上沿或圈外地面必须完全在圈外白线的后面,白线后沿的延长线应能通过投掷圈圆心。
铅球的投掷运动是运动员单手托住7.264kg(16磅)重的铅球在直径为2.135m的投掷圆内将铅球掷出并且使铅球落入开角为45°的有效扇形区域内。
以铅球的落地点与投掷圆间的距离度量铅球投掷的远度,并以铅球投掷远度的大小评定运动员的成绩。
在铅球的训练和比赛中,铅球投掷距离的远与近是人们最关心的问题。
完整的数学建模(铅球投掷)

承诺书我们仔细阅读了四川理工学院大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果设置报名号的话):所属学校(请填写完整的全名):四川理工学院黄岭校区参赛队员(打印并签名) :1.2.3.日期: 2012 年 05 月21 日编号专用页评阅编号(由评委团评阅前进行编号):评阅记录表铅球投掷问题摘要本文通过对投掷铅球的水平距离的讨论,研究了根据实际怎样控制水平距离的因素,才能使得铅球飞行更远.运用了力学知识,抛物线规律及数学软件的辅助,建立了各种最佳投掷模型。
即运动员应该根据自身的的具体身高与其习惯的出手姿势计算并得出最佳的出手角度,一般而言使出手速度在14m/s左右,对应的出手角度在37.2707°左右时能使得投掷距离最大,而且可以通过各种方式.增大手与铅球间的摩擦力,同时采用旋转投掷法,从腰间发力,在投掷点采用前后脚交替等方法可达到增大初速度从而增加投掷距离的作用.关键词:铅球投掷投掷距离出手角度出手速度最佳一、问题的提出铅球的投掷运动是运动员单手托住7.264kg(16磅)重的铅球在直径为2.135m的投掷圆内将铅球掷出并且使铅球落入开角为45o的有效扇形区域内。
以铅球的落地点与投掷圆间的距离度量铅球投掷的远度,并以铅球投掷远度的大小评定运动员的成绩。
如图1:图1 铅球投掷场地根据优秀运动员的投掷数据看出他们的投掷角度一般为35°—41°,出手速度一般为13.1m/s—14.1m/s,出手高度一般为1.9m—2.1m……………[1]。
铅球掷远问题的数学模型

铅球掷远问题的数学模型颜学友1,黄兰香1,黄旺林21.韶关学院2001级数学系数学与应用数学(1)班,广东韶关512005; 2. 韶关学院2002级计算机系本科(2)班,广东韶关512005[摘要]:本文综合考虑铅球的受力情况,抓住出手角度、出手速度、出手高度与投掷距离的关系,从解析几何角度考虑铅球的运动方程,进而得出了反映铅球掷远距离与三者函数关系的模型Ⅰ.为了得到更为合理的数学模型,我们进一步观察整个投掷过程,将整个过程分为滑步用力阶段和展臂脱手两个阶段.再对两个阶段分别进行合理的分析,进一步考虑推力、初速度、加速度、出手速度等因素之间的相互关系,对以上模型进行了改进,得到了更为合理的模型Ⅱ.在以上模型的基础上固定出手高度,求出了最佳出手角度为πθk 2±]4/,0(π∈,N k ∈,其中))/(arccos(2/12v gh gh +=θ.另外,运用数值极差法和图象分析法,得出了速度的灵敏性高于出手角度.关键词:出手速度;出手角度;出手高度;灵敏性1 问题的提出铅球掷远比赛要求运动员在直径2.135m 的圆内将重7.257kg 的铅球投掷在 45的扇形区域内,如右图.综合分析铅球的运动过程建 立分别符合以下要求的两个数学模型:1.以出手速度、出手角度、出手高度为参数,建立铅球掷远的数学模型; 2.考虑运动员推铅球时用力展臂的动作,改进以上模型.3.在此基础上,给定出手高度,对于 不同的出手速度,确定最佳出手角度4.比较掷远结果对出手速度和出手角度的灵敏性.2 模型的分析2.1 模型Ⅰ2.1.1 模型的假设与符号约定1 忽略空气阻力对铅球运动的影响.2 出手速度与出手角度是相互独立的.3 不考虑铅球脱手前的整个阶段的运动状态. 2.1.2 符号约定v 铅球的出手速度 θ 铅球的出手角度 h 铅球的出手高度 t 铅球的运动时间 L 铅球投掷的距离g 地球的重力加速度(2/8.9s m g =)2.1.3 问题的分析问题1要求我们以出手速度、出手角度、出手高度为参数,建立铅球掷远的数学模型.我们只需求出掷远的距离关于三者的函数关系式.这样,我们合理地简化其他影响因素,从物理、数学上得出关系式即可. 2.1.4 模型的建立与求解铅球出手后,由于是在一个竖直平面上运动.我们,以铅球出手点的铅垂方向为y 轴,以y 轴与地面的交点到铅球落地点方向为x 轴构造平面直角坐标系.这样,铅球脱手后的运动路径可用平面直角坐标系表示,如图(1).因为,铅球出手后,只受重力作用(假设中忽略空气阻力的影响),所以,在x 轴上的加速度0=,在y 轴上的加速度g a y -=.如此,从解析几何角度上,以时间 t 为参数,易求得铅球的运动方程:⎪⎩⎪⎨⎧+-==h gt t v y t v x 221sin cos θθ 对方程组消去参数t ,得h x x v gy ++-=)(tan cos 2222θθ……………………………………………(1) 当铅球落地时,即是0=y ,代入方程(1)解出x 的值v ggh gh v g v x θθθθθ2222sin 22cos sin cos sin 2-++=对以上式子化简后得到铅球的掷远模型θθθ22222cos 22sin 222sin g v h g v g v L +⎪⎪⎭⎫ ⎝⎛+=………………………………(2) 2.1.5 模型的检验以下是我国两名优秀女运动员一次投掷的成绩: 从以上数据,我们可以看出由模型Ⅰ计算的结果与实际投掷距离是比较吻合的.但也有一定的误差,这是由于我们忽略了过多的因素,下面我们尽量考虑所涉及到的因素建立模型Ⅱ.2.2 模型Ⅱ2.2.1 模型的假设1 忽略空气阻力对铅球运动的影响.2 手对铅球的推力是一个恒力.3 在铅球脱手前,铅球的运动方向与出手角度一致.4 铅球从静止到运动期间运动的路径是直线的.5 不考虑运动员的身体素质和心理素质对投掷铅球的影响.6 铅球出手瞬间肩部恰在场地边界. 2.2.2 符号约定v 铅球的出手速度 θ 铅球的出手角度 h 铅球的出手高度g 地球的重力加速度(2/8.9s m g =) F 手对铅球的推力m 铅球的质量(m=7.257kg)'h 铅球出手瞬间肩部的高度L 铅球出手后运动的距离1L 手臂的长度 2L 铅球加速的距离S 铅球投掷的总成绩 2.2.3 问题的分析在模型Ⅰ中,我们假设出手速度和出手角度是相互独立的.事实上,整个投掷过程包括滑步用力阶段和展臂脱手阶段,(如图(2)).它们是相互联系的.所以,模型Ⅰ中假设出手速度和出手角度相互独立是不合理的.现在,我们观察以上两个阶段,铅球从A 点运动到B 点,其运动状态是匀加速直线运动的,加速距离是2L 段.且出手高度与手臂长及出手角度是有一定的联系,进而合理地细化各个因素对掷远成绩的约束,改进模型Ⅰ.2.2.4 模型的建立与求解在投掷角度为θ上进行受力分析,如图(3)由牛顿第二定 律可得,ma mg F =-θsin 再由上式可得,θsin g mFa -=………………………………………(3) 又,22022aL v v =-,即22022aL v v += (4)将(3)代入(4)可得,θsin 2222202g L m FL v v -⎪⎭⎫⎝⎛+= ………………………(5) (5)式进一步说明了,出手速度v 与出手角度θ有关,随着θ的增加而减小.模型Ⅰ假设出手速度与出手角度相互独立是不合理的. 又根据图(2),有θsin 1'L h h += (6)由模型Ⅰ,同理可以得到铅球脱手后运动的距离θθθ22222cos 22sin 222sin g v h g v g v L +⎪⎪⎭⎫ ⎝⎛+= 将 (4)、(5)、(6)式代入上式整理,得到铅球运动的距离()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛++++-⎪⎭⎫ ⎝⎛+=θθθθθ22220'2220sin sin 22sin 2112sin 2sin 22g L m FL v h g g g L m FL v L 对上式进行化简:将m=7.257kg,2/8.9s m g = 代入上式,再令m h 60.1'= (我国铅球运动员的平均肩高),代入上式进一步化简得,()⎪⎪⎭⎫ ⎝⎛-++-++⨯θθθθθ2222232222sin sin 6.192756.06.19sin 6.19sin 2756.0sin 1L FL v L FL v ………………(7) 所以,运动员投掷的总成绩θcos 1L L S +=即为模型Ⅱ.一般情况下,129.1L L =.将2L 代入以上模型,得到S 关于F 和θ的函数关系式(手臂()θθ2sin sin 6.192756.051.0222L FL v L -+=长1L 是常数).为了了解S 对F 和θ的关系,我们令m L 8.01=,分别用数学软件MAPLE 作出S 对F (令θ=37.6)和S 对θ的图象(令F=350N)供参考:2.3给定出手高度,对于不同的出手速度,要确定最佳的出手角度.显然,是求极值的问题,根据微积分的知识,我们要先求出驻点,首先,模型一中L 对θ求导得,g hv g v g hv v g v d dL θθθθθθθθ22224242cos 82sin sin cos 42cos 2sin 2cos +-+=令0=θd dL,化简后为, 0sin cos 42cos 2sin cos 82sin 2cos 2422242=-++θθθθθθθhgv v hgv v v根据倍角与半角的三角关系,将以上方程转化成关于θ2cos 的方程,然后得,hv g g vgh gh222cos +=+=θ (3)从(3)式可以看出,给定铅球的出手高度h ,出手速度v 变大,相应的最佳出手角度θ也随之变大.对(3)式进行分析,由于0,0>>θh ,所以02cos >θ,则40πθ≤<.所以,最佳出手角度为)arccos(212v gh gh +=θθ是以π2为周期变化的,当且仅当N k k ∈⎪⎭⎫⎝⎛∈±,4,02ππθ时,πθk 2±为最佳出手角度.特别地,当h=0时(即出手点与落地点在同一高度),最佳出手角度︒=45α. 2.4 参数灵敏性分析 2.4.1 数值极差法模型Ⅰ、Ⅱ是铅球掷远的数学模型,运动员最为关心是怎样才能有效地提高掷远成绩,也就是怎样从出手高度、出手角度、出手速度三个自变量中抓住其中的主要因素,提高掷远成绩.由于出手高度是没有多大变化的,所以,我们应该从出手角度和出手速度着手找出其中对掷远成绩影响较大的变量.也就是比较出手速度和出手角度的灵敏性.这里,我们引入数值分析中的极差来比较两者的灵敏性.根据我国优秀铅球运动员三个因素的具体情况,我们令0.2=h 米,出手速度在10m/s ─15m/s 之间变化,出手角度在37─43变化.用数学软件MA TLAB 编程得到下表:从上表可以看出,出手角度在其可能范围内所引起的成绩的最大改变量在0.06─0.42m 之间;出手速度在其可能范围内所引起的成绩的最大改变量在12.48─12.88m .这表明,出手速度是影响成绩的主要因素,即出手速度的灵敏性高于出手角度的灵敏性. 2.4.2 图象分析法极差法从数值上分析了出手角度和出手速度的灵敏性,图象法是从得到的模型出发,观察L 关于速度的图象(4)和L 关于角度的图象(5).分析:图(4)和图(5)是根据我国优秀运动员正常情况下投掷时作出的, 图(4)是s m v m h /10,2==时,θ在一个周期内的图象;图(5)是 37,2==θm h 时,v 在s m s m /15/10-时的图象.图(4)的曲线明显比图(5)的曲线递增要快,几乎任意一点的斜率都要比图(5)中的任意点的斜率要大.也就是说,改变等量的L,θ的变化量比v 的变化量要更大.换言之,改变少量的v 则可以使得L 变化较大.所以,v 的灵敏性较高.3 模型的优缺点模型Ⅰ以出手速度、出手角度以及出手高度为参数建立的数学模型,通过假设出手速度和出手角度是相互独立的,较为简单地描述了掷远距离与三者的关系.缺点是忽略了过多的因素,该模型相对简单且与实际问题有一定距离,不适合精确的计算和要求较高的铅球运动员训练参考.模型Ⅱ综合考虑铅球从静止到脱手整个运动过程,将整个过程分成滑步用力阶段和展臂脱手阶段.合理地假设铅球脱手前作直线运动,利用出手速度与初速度和出手角度的关系,得出的结果更为合理和精确.给定出手高度,对于不同的出手速度,解出了最佳出手角度,这样铅球运动员可以根据不同的出手速度确定最佳出手角度,使投掷距离最远.在模型Ⅰ的基础上,对出手速度和出手角度的灵敏性进行了分析,确定了出手速度的灵敏性高于出手角度.所以,运动员要提高成绩,应该抓住出手速度这一主要矛盾.缺点是数值分析法只能从数值上进行比较,图象分析法是观察图象比较的,较为粗糙.参考文献:[1] 姜启源.数学模型(第三版)[M].北京:高等教育出版社,2003.8 [2] 刘来福.数学模型与数学建模[M].北京:北京师范大学出版社,1997.9 [3] 王庚.实用计算机数学建模[M].安徽:安徽大学出版社,2000.7 [4] 郑永令.力学[M].上海:复旦大学出版社,1989.10 [5] 程稼夫.力学[M].北京:中国科学技术大学出版社,1996.3The mathematics model of the shot putYAN Xue-you 1, HUANG Lan-xiang 1, HUANG Wang-lin 2(1. Department of Mathematics, Shaoguan University, Shaoguan 512005 Guangdong China; 2. Department of Computer, Shaoguan University, Shaoguan 512005 Guangdong China)Abstract: This text synthesizes the consideration shot put suffers the dint circumstance, holding tight the handangle,out the hand speed and out the hand the high degree with the relation that throw the distance, consider the square distance in sport of the shot put from the analytic geometry angle, then have to out to reflect the shot put distance with three equation the model Ⅰ that function relation. For getting more reasonable mathematics model, we are further to observe whole foundation for throwing process,Whole process is divided into slipping a correlation for making an effort stage with exhibition arm selling two stages. Again to two stages distinguishing reasonable analysis in proceeding, further considering pushing dint, beginning speed, acceleration, outing hand speed etc. Bases the above model proceeding improvement, getting more reasonable model Ⅱ. In the above model is last fix out hand high degree, beg a the best out hand angle is N k k ∈∈±],4/,0(2ππθ,thereinto ))/(arccos(2/12v gh gh +=θ.In addition,the number ofapplication differs the method very to analyze the method with portrait, get flat-out and intelligent higher than out hand angle.Key wrods: Out the hand the speed;Out the hand angle;Out the hand the high degree; Intelligent。
数学建模铅球掷远

数学建模铅球掷远一、引言铅球掷远是田径项目中的一项,它要求选手将铅球尽可能远地抛掷出去。
而在数学建模中,我们可以通过一系列的分析和计算,来研究铅球掷远所需的最佳策略。
本文将从数学角度出发,探讨铅球掷远的建模方法和优化策略。
二、问题分析铅球掷远的关键在于角度和速度的选择。
我们首先假设铅球在空中的运动符合平抛运动模型,并不考虑空气阻力和风力的影响。
那么,我们可以将铅球的运动轨迹分解为水平和竖直方向的运动。
三、数学建模1. 铅球的水平方向运动模型在水平方向上,铅球的运动速度恒定且不受外界因素的影响。
设铅球的水平速度为v_x, 则铅球在x方向上的运动可以用以下公式表示:x = v_x * t其中,x为铅球的水平位移,t为时间。
2. 铅球的竖直方向运动模型在竖直方向上,铅球的运动受到重力的影响。
设铅球在竖直方向上的初速度为v_y,重力加速度为g,那么铅球在y方向上的运动可以用以下公式表示:y = v_y * t - (1/2) * g * t^2其中,y为铅球的竖直位移。
3. 最佳投掷角度的计算为了将铅球掷得更远,我们需要确定最佳的投掷角度。
根据上述的数学模型,我们可以列出铅球在水平和竖直方向上的运动方程。
然后,通过对这两个方程进行求解,可以得到最佳投掷角度的表达式。
首先,根据水平方向的运动方程x = v_x * t,可以得到时间t与水平速度v_x的关系:t = x / v_x将t代入竖直方向的运动方程y = v_y * t - (1/2) * g * t^2,可以得到铅球的竖直位移y与水平位移x、竖直初速度v_y和重力加速度g的关系:y = (x / v_x) * v_y - (1/2) * g * (x / v_x)^2接下来,我们需要求解这个关系式的极大值点,从而确定最佳的投掷角度。
通过对上述关系式进行求导和求解极值的过程,可以得到最佳投掷角度的表达式。
四、优化策略1. 初始速度的选择除了求解最佳投掷角度外,我们还需考虑初始速度的选择。
投掷铅球的数学模型

分 析表 中 数据变 化 规 律 可 以 发 现 ¹ 初 速 度 V 是 影 响投 掷 距 离 的 最 主
要 因 素 初 速 度提 高 1 米 / 秒
,
:
½ 表
测量
,
1
可 为 运 动 员 寻 找个 人差 距
。
、
改
进 投掷 技 术 提 供 参 照 均值
h
;
。
铅 球 出手 高 度 易 于
,
,
则投 掷 距 离
.
或 4 o 0 则 投 掷 距离 均不 高 于 3 4’
, ,
若 实 际 投距 与 表
。
6 2 米
2
厘米 的差 距 离 对 于 高水 平 的
,
中 的 距 离 有 较大 差 距
,
,
则很 可 能是 由 于 出
,
运动 员 来 说 是 极 其 宝 贵 的
往往决定 能否
球 角度 不 佳 所致 运动 员 应 调 整 出 球 角度
0
.
’
41 47
0
.
’
42 0 6
0
.
’
4 2 14
0
.
,
42 25
0
.
’
42 35
0
.
’
42 46
0
.
’
42 53
0
.
’
43 59
0
.
’
(1 3 9 4 ) (1 5 0 9 ) ( 1 6 3 1 ) (1 7
4 1 20
0
.
,
1 75
.
4 1 42
0
.
’
5 6 ) (1 8 8 6 ) ( 2 0 2 3 ) ( 2 1 6 3 ) ( 2 3 0 9 ) ( 2 4 6 0 ) 0 0 , 0 , 0 ’ 0 , 0 , 0 ’ 4 1 59” 42 0 8 4 2 21 42 32 42 42 42 50 42 58
铅球掷远研究-数学建模-论文

铅球掷远研究目录一、问题的提出 (3)二、问题分析 (3)三、模型假设 (4)四、符号定义 (4)五、模型建立与求解 (4)六、模型的评价 (10)七、参考文献 (10)八、附录 (10)摘要:本文研究了铅球掷远的问题,分析了掷远距离和出手速度、出手角度、出手高度的关系。
得出了对于不同的出手速度,确定的了最佳出手角度,比较了掷远结果对出手速度和出手角度的灵敏度。
铅球投掷作为田径比赛的一个重要组成项目,投掷距离s(米)的远近是教练员和运动,员最关心的问题。
由投掷常识知道,影响投掷距离远近的因素主要有三个: 铅球出手时的初、速度v(米/秒)、出手角度A(度) 和出手高度h(米)。
迄今为止,利用物理中运动学知识研究铅球投掷运动现象比较多, 而且在研究时很少考虑出手高度的影响[2, 3]。
通过建立模型,寻求初速度v、出手角度A和出手高度h三个因素对投掷距离s的影响度的大小,从而在训练和比赛中对运动员和教练员有一定的理论指导意义.关键词:铅球掷远投掷距离出手角度灵敏度一、问题提出球掷远比赛要求运动员在直径2.135m 的圆内将重7.257kg (男子)的铅球投掷在45的扇形区域内,如图1所示。
观察运动员比赛的录像发现,他们的投掷角度变化较大,一般在38°- 45°,有的高达55°,建立模型讨论以下问题 :1.以出手速度、出手角度、出手高度为参数,建立铅球掷远的数学模型。
2.在此基础上,给定出手高度,对于不同的出手速度,确定最佳出手角度。
比较掷远结果对出手速度和出手角度的灵敏性。
二、问题分析针对如何使铅球掷得最远,只需求得铅球在空中停留时间以及铅球在水平方向的速度即可,铅球投掷后在空中停留的时间可以凭借铅球投掷后在垂直方向上先以向上的速度运动到静止,再做自由落体运动落到地面求出。
【1】三、模型假设1、 人的高度h 和铅球投掷初速度v 是一定的,当投掷出时间1t 后,铅球到达最高点,当时间在2t 时刻时铅球落地,重力加速度28.9s m g =,速度方向与投掷的水平方向所成角为θ时)900(︒≤≤θ,此情况下铅球落地点与人的距离是S 。
最新铅球掷远研究-数学建模-

铅球掷远研究目录一、问题的提出 (3)二、问题分析 (3)三、模型假设 (4)四、符号定义 (4)五、模型建立与求解 (4)六、模型的评价 (10)七、参考文献 (10)八、附录 (10)摘要:本文研究了铅球掷远的问题,分析了掷远距离和出手速度、出手角度、出手高度的关系。
得出了对于不同的出手速度,确定的了最佳出手角度,比较了掷远结果对出手速度和出手角度的灵敏度。
铅球投掷作为田径比赛的一个重要组成项目,投掷距离s(米)的远近是教练员和运动,员最关心的问题。
由投掷常识知道,影响投掷距离远近的因素主要有三个: 铅球出手时的初、速度v(米/秒)、出手角度A(度) 和出手高度h(米)。
迄今为止,利用物理中运动学知识研究铅球投掷运动现象比较多, 而且在研究时很少考虑出手高度的影响[2, 3]。
通过建立模型,寻求初速度v、出手角度A和出手高度h三个因素对投掷距离s的影响度的大小,从而在训练和比赛中对运动员和教练员有一定的理论指导意义.关键词:铅球掷远投掷距离出手角度灵敏度一、问题提出球掷远比赛要求运动员在直径2.135m的圆内将重7.257kg(男子)的铅球投45的扇形区域内,如图1所示。
观察运动员比赛的录像发现,他们的投掷掷在角度变化较大,一般在38°- 45°,有的高达55°,建立模型讨论以下问题:1.以出手速度、出手角度、出手高度为参数,建立铅球掷远的数学模型。
2.在此基础上,给定出手高度,对于不同的出手速度,确定最佳出手角度。
比较掷远结果对出手速度和出手角度的灵敏性。
二、问题分析针对如何使铅球掷得最远,只需求得铅球在空中停留时间以及铅球在水平方向的速度即可,铅球投掷后在空中停留的时间可以凭借铅球投掷后在垂直方向上先以向上的速度运动到静止,再做自由落体运动落到地面求出。
【1】三、模型假设1、 人的高度h 和铅球投掷初速度v 是一定的,当投掷出时间1t 后,铅球到达最高点,当时间在2t 时刻时铅球落地,重力加速度28.9s m g =,速度方向与投掷的水平方向所成角为θ时)900(︒≤≤θ,此情况下铅球落地点与人的距离是S 。
数学建模铅球投掷问题(四川理工学院)

2011年四川理工学院数学建模摘要:在铅球投掷训练和比赛中,教练和运动员关心的核心问题是铅球的投掷距离的远近,而距离的远近主要取决于铅球的出手速度、出手角度、出手高度等等,它们对铅球投掷距离的远近主次影响是怎样的呢?因为空气阻力等的影响相对比较微小,可以忽略不计,本文主要运用牛顿力学等物理、数学知识建立了铅球投掷过程的数学模型探讨出手速度、出手高度、出手角度这三个影响铅球投掷成绩的主要因素,然后运用数值法进行分析,计算出各影响因素对铅球投掷距离的影响程度,确定出各影响因素的主次关系,为制定科学的铅球训练计划提供依据。
关键词:铅球投掷、数值法、最优出手角度、最远投掷距离1问题的提出众所周知,铅球的投掷运动是运动员单手托住7.264kg(16磅)重的铅球在直径为2.135m 的投掷圆内将铅球掷出并且使铅球落入开角为45o的有效扇形区域内。
以铅球的落地点与投掷圆间的距离度量铅球投掷的远度,并以铅球投掷远度的大小评定运动员的成绩。
在铅球的训练和比赛中,铅球投掷距离的远与近是人们最关心的问题。
而对于教练和运动员最为关心的问题是如何使铅球掷得最远。
影响铅球投掷远度的因素有哪些?建立一个数学模型,将预测的投掷距离表示为初始速度和出手角度的函数。
最优的出手角度是什么?如果在采用你所建议的出手角度时,该运动员不能使初始速度达到最大,那么他应该更关心出手角度还是出手速度?应该怎样折中?哪些是影响远度的主要因素?在平时训练中,应该更注意哪些方面的训练?试通过组建数学模型对上述问题进行分析,给教练和运动员以理论指导。
参考数据资料如下:表1 李素梅与斯卢皮亚内克铅球投掷成绩姓名出手速度)/(smv 出手高度)(mh出手角度)(oα实测成绩李梅素13.75 1.90 37.60 20.95李梅素13.52 2.00 38.69 20.30斯卢皮亚内克13.77 2.06 40.00 21.41表2 我国优秀运动员的铅球投掷数据姓名成绩s(m) 出手速度)/(smv 出手角度)(oα出手高度)(mh李梅素19.40 13.16 40.27 2.02李梅素 20.30 13.51 38.69 2.00 黄志红 20.76 13.58 37.75 2.02 隋新梅 21.66 13.95 39.00 2.04 李梅素21.7614.0835.131.952 问题的分析针对如何使铅球掷得最远,只需求得铅球在空中停留时间以及铅球在水平方向的速度即可,铅球投掷后在空中停留的时间可以凭借铅球投掷后在垂直方向上先以向上的速度运动到静止,再做自由落体运动落到地面求出。
铅球掷远模型

铅球掷远模型一、问题重述建立铅球掷远模型,不考虑阻力,建立投掷距离与铅球初速,出手高度,出手角度(与水平地面夹角)的关系式,并求出在铅球初速和出手高度一定的条件下的最佳出手角度。
二、模型假设1、不考虑铅球的旋转对铅球速度和运行轨迹的影响2、不考虑空气的阻力3、选取9.8为重力加速度的数值4、不考虑投掷铅球的过程中手对铅球运动状态的影响5、把铅球的看做一个质点三、符号说明V:铅球初速A:出手角度H:出手高度L:投掷距离G:重力加速度T:表示时间V x:水平方向分速度V y:竖直方向分速度四、问题分析针对这个模型,画出铅球的运行轨迹,并分解速度到水平和竖直两个方向,根据运动学规律建立方程组,联立可以得到L与V,H,A的关系式,第二个问题,可以让L对A求导,使倒数为零的点就是函数的极值点,可以得到最佳出手角度。
五、建立模型建立如图所示直角坐标系,画出铅球的运动轨迹对速度做如上分解:V x =VcosA;V y =VsinA;球抛出时,在第一段过程中,先是竖直方向做加速度为—G 的匀减速运动,减速到0后又做加速度为G 的匀加速运动,所以当铅球到达抛出点时,竖直方向速度仍为V y ,方向向下,所以在这段运动过程内,所花时间2)(1⨯÷=g V T y 。
在第二段过程中,球做加速度为G ,初速度为V y 的匀加速运动,所以可以列出路程与时间的关系式T T V G H y 22221⨯⨯+⨯=求解可以得到H G y V T ⨯+=222.因此,)(21T T V x L +⨯=代入T 1,T 2,V x ,V y 得到 )2sin sin 2(cos 22H GA G A V A V L V ++= 令0d =dA L 得到最佳出手角度)(2sin 21GH V A V +=- 令H=15m/s,V=10m/s,可以算出A= 4.41o L=11.4m.六、模型改进及推广对于这个模型,有很多因素没有考虑,简化成了最理想的情形,在建模过程中可以把球的旋转等对球的运动状态影响较大的因素考虑进来。
铅球抛掷问题数学建模

我们知道,抄袭别人的成果是违反竞赛章程和参赛规则的,如果引用别人的成果或
其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文
引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛章程和参赛规则,以保证竞赛的公正、公平性。如有
违反竞赛章程和参赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展
铅球抛掷问题
摘要
本文探究了铅球投掷远度的影响因素等一系列问题。运用了牛顿力学等物理、数 学知识建立了铅球投掷过程的数学物理模型探讨了出手速度v(m/s),出手高度 h(m),出 手角度 α(度),这三个影响铅球投掷水平位移s(m)的主要因素。然后运用数值法进行 分析,计算各影响因素的主次关系。
问题一的分析:根据斜抛运动及牛顿运动定理求解铅球抛掷的水平距离s(m)以及求 出水平距离s 与出手速度v(cm/s)出手高度h(m),出手角度α(度)的影响。用 Mathematica 软件求出理论抛掷距离s0,并用 Matlab 软件对题中数据进行筛选,最终得 到实际抛掷距离s0与理论值 s 之间的误差百分比。再分析表1、表 2 中的数据,得出出 手速度v在10m/s~15m/s之间变化,出手角度 α 在37°~43°之间变化, 并对这之间的速度、角度分别求出对应的投掷距离。再运用 Excel 做出角度与投掷 距离的关系图。最后得出运动员投掷铅球存在最佳角度,角度是在 40°~42°间。
一、问题重述
众所周知,铅球的投掷运动是运动员单手托住 7.264kg (16 磅)重的铅球在直径为 2.135m 的投掷圆内将铅球掷出并且使铅球落入开角为 45 的有效扇形区域内。以铅球 的落地点与投掷圆间的距离度量铅球投掷的远度,并以铅球投掷远度的大小评定运动 员的成绩(以国际男子铅球比赛为例)。如图:
铅球掷远模型

2.135m
45 ο
综合分析铅球的运动过程,可以分为两种情况:
1、在不考虑铅球展臂的情况下,以出手速度、出手高度、出手角度为参数, 建立第一种数学模型。
2、在考虑铅球展臂的情况下,以出手速度、出手高度、出手角度、展臂为 参数,建立第二种数学模型。
3. 在铅球整个运动过程中,空气阻力虽然一直存在,但是其影响极其微小, 因而忽略不计。
2.3 问题三的分析 针对问题三我们运用以上所建立的模型一,求出水平投掷的距离,再借助
Matlab7.0 软件对水平距离求导,确定最优解,即铅球在不同出手速度下的最佳 出手角度。
2.4 问题四的分析 对于问题四我们同样运用模型二来解决掷远结果对速度和角度的灵敏度。
分别求 S (v,θ ) 对 v 和θ 的一阶导数,对二者比较大小,可以得出出手速度对掷远
我们运用 Matlab7.0 软件分别求出 ∂S (已求出)Leabharlann ∂S ,可以得出结果。∂θ
∂v
∂S 的求导过程如下: ∂v
PDF 檔案使用 "pdfFactory Pro" 試用版本建立 /FinePrint
通过 Matlab7.0 我们可以比较 ∂S 和 ∂S 的大小,比较的结果为 ∂S > ∂S ,因而可
对于问题二:当考虑运动员臂展对投掷结果的影响的条件下,我们对模型
一进行了适当的改进,在引进臂展这一参数之后重新建立了以出手速度、出手角
度、出手高度以及臂展为参数的掷远模型二,应用模型一中相同的知识,我们建
立
的
模
型
二
为
:
S(F,θ ) = (2FL − 2mgL sinθ )sinθ cosθ + mg
第五章 微分方程建模 第四节 铅球掷远模型

a = sin
和最佳成绩为
∗
−1
v ; 2 2(v + gh)
v 2 R = v + 2gh . g
∗
第四节
铅球掷远模型
如果测得该运动员的出手高度 h = 1.5 m,铅球初速 , 度为 v = 10m/s,则有 , 得最佳出手角度为 最佳成绩为
a ∗ ≈ 41.4 ,
R∗ = 11.4m .
第四节
铅球掷远模型
在右图坐标系下, 在右图坐标系下,铅球运动方程为
x ɺɺ = 0 ; ɺ x(0) = 0 , x(0) = v cos a .
y ɺɺ = − g ; ɺ y(0) = h , y(0) = v sin a .
第四节
铅球掷远模型
分= x(t ) = sinacos a + 2 sin a + v cos a , g g g
这个关系式还可以表示为
1 2
R2 g = 2v2 cos2 a(h + Rtana) .
第四节
铅球掷远模型
dR = 0 ,得最佳出手角度为 由此计算 da a∗
x ( t ) = ( v cos a )t ;
1 2 y ( t ) = (v sin a )t − gt + h . 2
又令 y ( t ) = 0 ,可得
1 t = v sin a + v 2 sin 2 a + 2 gh , g
∗
(
)
第四节
铅球掷远模型
代入 x ( t ) 可以求得铅球的投掷距离为
第四节
铅球掷远模型
某铅球运动员正在训练,如果不考虑阻力, 某铅球运动员正在训练,如果不考虑阻力,设铅球初 与地面夹角), 速度为 v,出手高度为 h,出手角度为 a (与地面夹角 , , , 与地面夹角 试建立投掷距离 R 与 v,h,a 的关系式的数学模型。并 , , 的关系式的数学模型。 在 v,h 一定的条件下求该运动员的最佳出手角度和最佳 , 成绩。 成绩。
铅球投掷中的数学模型

距离 角 度 37° 38° 39° 40° 41° 42° 43° 极差
速度 10m/s 11.78 11.81 11.82 11.83 11.83 11.82 11.79 0.05 11m/s 13.86 13.90 13.93 13.95 13.96 13.95 13.93 0.10 12m/s 16.12 16.18 16.23 16.26 16.28 16.28 16.26 0.16 13m/s 18.57 18.65 18.71 18.76 18.79 18.79 18.78 0.22 14m/s 21.20 21.30 21.39 21.45 21.49 21.51 21.50 0.31 15m/s 21.89 22.08 22.25 22.39 22.51 22.60 22.66 0.77
4.来稿请 在 左 上 方 注 明 文 稿 适 合 初 中 生 还 是 高 中 生 阅 读,标 题 下 方 请 写 明 作 者 的 通 讯 地 址 、邮 编 、作 者 姓 名 、电 子 信 箱 及 电 话 .
5.来稿切忌一稿 多 投,如 发 现 抄 袭 现 象 我 们 将 作出公开批评.来稿一律不退,请作者自留底稿.
(4 5
)x ,
x<2 时 ,
g(x)=
(3 5
)x +
(4 5
)x >
(3 5
)2+
(4 5
)2=1;
x>2 时 ,
欢迎投稿
来稿须知 1.稿 件 的 内 容 要 新 颖 、形 式 要 活 泼,以 适 合
中 学 生 阅 读 ,应 避 免 写 成 教 学 交 流 文 章 . 2.提倡短小精 悍 的 文 章,讲 清 一、两 个 问 题,
(责 审 余 炯 沛 )
铅球投掷模型 终极版

10.43
10.56
10.68
10.78
10.87
2.8最优出手角度
由上述模型可以看出,一个运动员投掷铅球,在能力一定时,即出手高度 和出手速度确定的时候,他所投掷的距离 只与投掷角度 有关,要看 是否存在最大值,即要看 关于 的函数式在其定义域范围内是否有最大值(在实际中,投掷距离 自然是大于等于零的数,当然求最小值是没有意义的,所以 的极值存在且为极大值就是 最大值).
2.04
13.95
39.00
21.66
21.68
+0.1%
李梅素
1.95
14.08
35.13
21.76
21.50
-1.2%
从表1的数据中我们可以看出,由铅球投掷的抛射体模型计算出得出的理论成绩与实际成绩是比较相符的,所以模型的建立是较为成功的.
2.7参数灵敏度测试
相比其他数据来看,运动员投掷铅球时的出手高度 是相对稳定的,这主要与运动员的身高、臂长以及对专业技术的掌握程度有关.
,
则有
可得,当 时,投掷距离最远(因为 ,所以 ),即 达到最大值.
由 可得速度 对应的 的函数图像[7]如图3所示.
在图像中我们可以很直观地看出,在运动员的实际出手速度( )范围内,最优出手角度在 左右[8].有的研究认为,铅球的最优出手角度在 度之间,这显然有些笼统.有的资料表示,最优出手角度趋于 ,但这是在出手速度
表1实际与理论成绩比对
姓名
出手
高度
( )
出手
速度
( )
出手
角度
( )
实际
成绩
( )
理论
成绩
( )
与实际
铅球掷远模型

铅球掷远模型一、问题重述不考虑阻力,铅球初速度为v ,出手高度为h ,出手角度为a (与地面夹角),建立投掷距离与v ,h ,a 的关系,并在v ,h 一定的条件下求最佳出手角度。
二、基本假设1、设当地的重力加速度为g ,且取值为9.8m/s 2,并在抛铅球的任意点都相等;2、不考虑空气阻力,摩擦力以及风速等其他因素的影响;3、铅球运动轨迹在同一平面内;4、地面处处水平。
三、问题分析由题目所述,再根据物理知识可得,铅球投掷轨迹为一抛物线,且由题目知,初速度v 和高度h 一定,因此可以建立一个平面直角坐标系,分别对x ,y 方向进行分析。
对y 即竖直方向,铅球做竖直向上抛运动,对x 即水平方向,铅球做匀速直线运动,所以轨迹为两个运动的叠加。
照此,根据物理知识可建立模型。
四、模型建立由题目可知,铅球初速度为v ,高度为h ,出手角度为a ; 设铅球质量为m ;抛出的水平距离为s ;抛出至落地的时间为t 。
以铅球抛出点在水平地面投影点为原点,原点与落地点方向为x 轴正方向,原点与抛出点方向为y 轴正方向,建立平面直角坐标系。
由物理知识有:y 方向:h+t*v*sina-1/2*g*t^2;x 方向:t*v*cosa=s.五、模型计算由于h 和s 是正相关的,因此当求出h (max )时,即对应的s 也为s (max ) v y xs a h由上面两关系式,联立消去t得-h=-1/2*g*(s/v*cosa)^2+s*tana=-(gs^2/2v^2)*(tana-v^2/gs)^2-g/2*(s/v)^2+v^2/2g可知在a变化时,-h的最大值为-h=-g/2*(s/v)^2+v^2/2g此时tana=v^2/g*s;所以有s=v*sqrt(v*v+2*g*h)/g,然后将tana=v^2/g*s代入得tana=v/sqrt(v*v+2*g*h)另外,对抛物线分析,设最高点距地面H,且前后两段时间为t1、t2,则有:(v*sina)^2=2*g*(H-h)1/2*g*t2^2=Hv*sina=g*t1所以s=(sqrt(2*g*h+(v*sina)^2)+v*sina)*v*cosa/g由上,s、h、v、a的关系式如下:s=(sqrt(2*g*h+(v*sina)^2)+v*sina)*v*cosa/g且当a=arctan(v/sqrt(v*v+2*g*h))时,s最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西北农林科技大学实验报告学院名称:理学院专业年级:2011级信计1班姓名:学号:2011014816课程:数学模型与数学建模报告日期:2013年11月7日1 实验题目:铅球投掷模型2 实验问题陈述:众所周知,铅球运动是指运动员单手托住铅球在投掷圆内将铅球掷出并且使千秋在有效区域中,以铅球的落地点与投掷圆间的距离度量铅球投掷的远度,并以铅球投掷远度的大小评定运动员的成绩。
在铅球的训练和比赛中,铅球投掷的距离的远近使人们最关心的问题,而对于教练和运动员最为关心的问题是如何使铅球投掷得最远?由普通的投掷常识我们知道,在投掷铅球的过程中,有两个重要的因素:投掷角和初速度。
对于教练来说,平时的训练中,应更注意哪方面的训练呢?3 实验目的:建立模型进行分析如何能使铅球投掷的最远,在投掷角和初速度两个重要因素上运动员在训练时应该更加注重哪一项的训练。
选择一个最优的方法使得训练更加具有针对性,使运动员提高起来更加容易。
4 实验内容抛射模型:在这个模型中,我们不考虑投掷者在投掷圆内用力阶段的力学过程,只考虑前球脱手使得初速度和投掷的角度对铅球投掷远度的影响。
为此,我们不妨把铅球视为一个抛射体,关于它的运动可以在如下三个家设置下来分析。
⑴铅球被看成是一个质点,其初速度为v ,运动轨迹如图一。
⑵铅球运动中忽略空气的阻力。
⑶投掷角α和初速度v 是相互独立的,并且衡量成绩的远度记为s 。
⑷运动员具有身高h 。
以铅球出手点的铅垂方向为y 轴(向上为正),以y 轴与地面的交点到铅球落地点方向为x 轴构成平面直角坐标系。
在此坐标系内考虑铅球的运动,由物理学的知识可以得到铅球运动方程: ()()⎪⎩⎪⎨⎧-+⋅⋅=⋅⋅=221sin cos gt h t v y t v x αα,/8.9,2,0秒米=⎥⎦⎤⎢⎣⎡∈g πα 解这个方程,得()()222tan 2cos gx y f x x h v αα=-++ ① 图中显示铅球落在地面A 点,此时的远度是s ,也即轨迹与x 轴相交于点(s ,0)处。
代入①解出s ,得 s =② 这个公式中已经体现了初速度、投掷角度和远度之间的简单关系。
也指明了铅球投掷的远度是如何依赖于前两者的。
这就是我们需要的铅球投掷模型I ——投射模型。
模型II ——投掷模型在实际中我们从奥运会的女子铅球比赛中获得这样一组数据可以看到第二组数据h与α都提高了,但v与s却降低了。
也就是说随着α的提高,即使是更接近于最佳出手角度,成绩反而降低了,主要原因在于v降低了,因此我们可以得出结论,α与v之间一定有某种关系。
因此模型I中假设3是不恰当的。
实际上模型I只是刻画了铅球出手时与出手后的情形,而要刻画出手速度与出手角度之间的依赖关系,我们必须对铅球出手前的运动情况进行研究。
也就是分析在投掷圆中的运动过程。
我们将投掷过程大致分为滑步和用力阶段。
假设:⑴滑步运动为水平运动,铅球随人的身体产生一个水平的初速度v。
⑵在用力阶段,运动员从开始用力推铅球到铅球出手有一段时间,记为0到t。
⑶在运动员用力的时间内,运动员作用在铅球上的推力大小F是不变的,力的方向与铅球的出手角度α相同。
现在用这三个假设代替模型I的假设⑶,运动轨迹如图二,进一步建立模型II——投掷模型。
记()()t yx,为开始用力后铅球运动轨迹的水平和铅垂方向坐标,则t根据牛顿第二定律。
()()⎩⎨⎧-=''=''mgF t y m F t x m ααsin cos ③ m 为铅球质量,F 是推力,α为力的方向(出手角度)。
根据整个运动方式,我们知道0=t 时开始用力,0t t =时铅球出手。
于是可将③在()0,0t 上积分得()()⎩⎨⎧+-='+='20010sin cos C mgt Ft t y m C Ft t x m αα 21,C C 分别是0=t 时铅球的水平与垂直的初速度。
由假设⑴知0,201==C v C ,代入上式:()()⎩⎨⎧-='+='0000sin cos mgt Ft t y m v Ft t x m αα 上式表明了在F 作用下,铅球在水平与垂直方向上的运动速度,可由此得到合速度v ,可以看到它是一个与α有关系的量。
()()ααcos 2sin 200202022222v t m F v t g m F g m F t y t x v ++⎪⎪⎭⎫ ⎝⎛-+='+'= ④将②与④合并就得到模型II ——铅球的投掷模型αααααcos 2sin 22cos 4sin 2sin 0020202222222v t m F v t g m F g m F v ggh v v v s ++⎪⎪⎭⎫ ⎝⎛-+=+⋅+= ⑤至此我们已经将投铅球的整个过程完整地转换为一组公式,我们可以通过这个公式对投铅球运动的各项关键因素进行深入分析,以帮助运动员得到最好的成绩。
1.建立掷远距离随出手速度和出手角度变化的函数文件function f=fun_s(a,v)f=(2.*1.8.*v.*v.*cos(a).*cos(a)./9.8+(v.*v.*sin(2.*a)./19.6).^2).^0.5+v.*v.*sin(2*a)./19.6;2运行程序一,在matlab中绘出函数图像结果如下图所示:图3.不同出手速度和角度对应的抛掷距离图像Matlab命令:1.在给定出手速度v下要达到最大射程时对应的角度,运行程序二结果如下图所示:图4.出手速度不同时得到最大投掷距离对应的角度曲线3.2比较掷远结果对出手速度和出手角度的灵敏性。
1.对角度θ求导运行程序三结果如下图:2.s对速度v求导运行程序四结果如下图:5 实验结果分析与讨论可以看出,v 与h 越大,远度s 越大。
也就是说当一个运动员具有较优秀的身高和力量能使成绩更好,但另一方面这两个因素又是非常有限的。
因此选择一个最佳的出手角度α是一个更实用的提高成绩的方式。
针对模型I 就是求一个值可以使s 最大,这是一个求函数极值的问题。
即利用算法0=∂∂αs 解出α。
得h v g gv gh gh 222cos +=+=α上式表明:给定v ,当h 变小,则相应的最佳角度α随之变大;当h 变大,则相应的最佳角度α随之减小。
由于⎥⎦⎤⎢⎣⎡∈2,0πα,当h =0时,最佳出手角度α=45︒。
这个结论是符合物理学规律的,但运动员是有身高的即h >0,那么实际情况中会出现什么样的情况呢?这就需要对模型II 进行分析。
给定h ,当v 变大,相应的最佳角度α也变大。
6 实验程序(Matlab 或者其它软件语言陈述)程序一:v=linspace(0,30,100);a=linspace(0,pi/2.100);[A,V]=meshgrid(a,v);S=fun_s(A,V);surf(A,V,S)ylabel('速度V m/s');xlabel('角度');zlabel('投掷距离 m');title('不同出手速度和角度对应的抛掷距离图像');axis([0 pi/2 0 30 0 100]);程序二:function f=fun_sv(v)f=0.5*acos(1.8*9.8/(1.8*9.8+v*v))/pi*180;绘出图像:fplot('fun_sv',[0,100]);xlabel('速度V m/s');ylabel('角度');title('v不同得到最大投掷距离时对应的角度曲线 ');axis([0 50 0 60]);程序三:函数文件:function f=fun_da(a,v)h=1.8f=(v.^4.*sin(2*a).*cos(2*a)/9.8/9.8-2.*h.*v.*v.*sin(2*a)./9.8)./9.8./sqrt(8*9.8*h.*v.*v.*cos(a).^2+v.^4.*sin(2*a).^2)+v.^2.*cos(2*a)./9.8;绘出图像:da=fun_da(A,V);surf(A/3.14*180,V,da)ylabel('速度V m/s');xlabel('角度');zlabel('不同角度对应的da');title('不同速度和角度下S对θ求导图像');axis([0 90 0 30 -100 100]);程序四:函数文件:function f=fun_dv(v,a)w=4.*1.8.*v.*cos(a).*cos(a)./9.8+v.*v.*v.*sin(2.*a).*sin(2.*a)./9.8./9.8;q=(2.*1.8.*v.*v.*cos(a)./9.8+(v.*v.*sin(2.*a)./19.6).^2).^0.5;f=1/2.*w./q+v.*sin(2.*a)./19.6;绘出图像:dv=fun_dv(V,A)surf(A/3.14*180,V,dv)ylabel('速度V m/s');xlabel('角度');zlabel('不同角度对应的dv');title('不同速度和角度下S对V求导图像');axis([0 90 0 30 0 5]);。
