土方方格网
方格网计算土方量原理

方格网计算土方量原理方格网法是一种常用的土方量计算方法,它通过将地块划分为等距的方格,然后通过对每个方格的高程进行测量,从而计算出土方量。
这种方法简单易行,且精度较高,因此在土方工程中得到了广泛应用。
下面我们将详细介绍方格网计算土方量的原理及具体步骤。
首先,进行地块的测量和划分。
在进行土方量计算之前,需要对地块进行测量,并将其划分为等距的方格。
方格的大小可以根据实际情况进行调整,一般情况下选择较小的方格可以提高计算精度。
接下来,对每个方格的高程进行测量。
利用测量工具,对每个方格的四个角以及中心点的高程进行测量记录。
在记录高程时,需要注意测量的准确性,以确保计算结果的准确性。
然后,进行土方量的计算。
通过测量得到的高程数据,可以利用方格网法进行土方量的计算。
具体计算步骤为,首先计算每个方格的平均高程,然后根据相邻方格的高程差值,计算出每个方格的土方量。
最后将所有方格的土方量相加,即可得到整个地块的土方量。
在进行方格网计算土方量时,需要注意一些问题。
首先是高程测量的准确性,高程数据的准确性直接影响土方量计算结果的准确性。
其次是方格的划分和选择,合理的方格划分可以提高计算精度,而过大或过小的方格都会影响计算结果的准确性。
最后是计算的精度和误差控制,需要对计算结果进行合理的校核和误差控制,以确保计算结果的可靠性。
总的来说,方格网法是一种简单有效的土方量计算方法,通过合理的测量和计算步骤,可以得到较为准确的土方量结果。
在实际的土方工程中,可以根据具体情况选择合适的土方量计算方法,以确保工程的顺利进行和计算结果的准确性。
通过本文的介绍,相信大家对方格网计算土方量的原理及具体步骤有了更深入的了解。
在实际工程中,希望大家能够根据本文所述的方法进行合理的土方量计算,为工程的顺利进行提供有力的支持。
同时也希望大家能够在实际工作中不断总结经验,不断提高土方量计算的准确性和精度。
这样才能更好地为土方工程的顺利进行和计算结果的准确性做出贡献。
方格网及断面法计算土方

先操作完成面里程,保存后重新打开CASS,重复以上 操作完成原始面设计里程。
三、断面法计算土方
三、断面法计算土方
三、断面法计算土方
三、断面法计算土方
3、断面法计算过程
1)生成原始地面土方断面
工程应用——断面法土方计算——场地断面——选择 原始面里程文件(.hdm)——选择原始面里程数据文 件(.dat)——绘图参数修改——绘制纵断面图比 例——确定——图纸空白处点击出断面图
•Байду номын сангаас目录
一、计算准备 二、方格网计算土方 三、断面法计算土方
一、计算准备
• 土方计算由三个要素组成:
土方计 算
1.计算范围 2.原地面标高数据文件
3.完成面标高数据文件
一、计算准备
1、计算范围 用复合线(PL)画计算范围
注:一定要闭合,按C闭合
2、标高数据文件 要将标高生成高程点坐标数据文件(*.dat),
注:有可能回车后看不到计算结果,这时要重新设定窗口范围, 命令栏输入zoom—— a 。
二、方格网计算土方
二、方格网计算土方
三、断面法计算土方
1、导入坐标(针对没有电子版图纸) 绘图处理——展高程点——导入已有坐标数据文件 (*.dat)
2、生成里程文件(先完成面后原始面) 1)绘制纵断面线 2)工程应用——生成里程文件——由纵断面生成—
方法有两种: 1)文本输入
2)图纸获取
一、计算准备
1)文本输入 对有坐标数据(X,Y,H)的,直接在记事本上按以
下格式(序号,,Y,X,H)操作: 1,,Y,X,H 2,,Y,X,H ……….
另存为*.dat文件 例如:
一、计算准备
土方方格网计算公式图示及推导
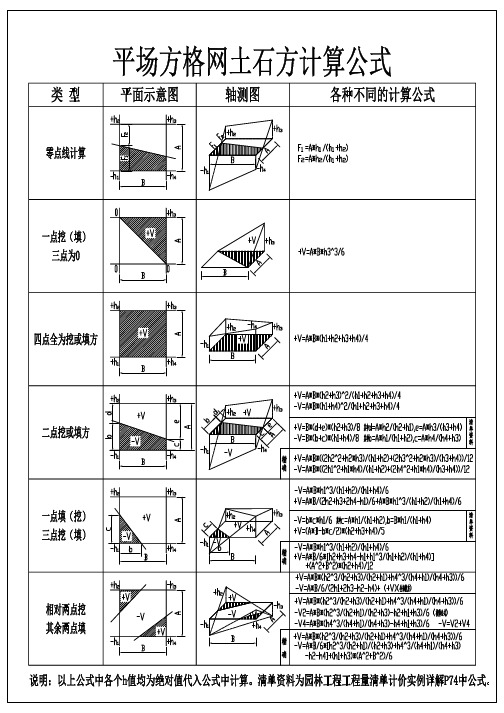
方格网土方计算公式推导:1、两点开挖工程量计算公式:如上图示:d=A*h2/(h1+h2); e=A*h3/(h3+h4); S1=d*h2/2; S2=e*h3/2S0=(d+e)/2*(h2+h3)/2/2根据拟柱体体积计算公式:V=B/6*(S1+4*S0+S2)将上面已知数代入公式可得:V=B/6*{A*h2/(h1+h2)*h2/2+4*[A*h2/(h1+h2)+A*h3/(h3+h4)]/2*(h2+h3)/2/2+h3*A*h3/(h3+h4)/2}=A*B/6*{h2*h2/(h1+h2)+ h2*(h2+h3)/(h1+h2)+ h3*(h2+h3)/(h3+h4)+h3*h3/(h3+h4)}/2=A*B/12*{(2h2^2+h2*h3)/ (h1+h2)+(2*h3^2+h2*h3)/(h3+h4)}2、三点开挖的挖方量计算公式:由图分解可得,挖方体积=v1+v2-(v3-v4),由拟柱体体积计算公式可以得出:V1={A*(h3+h4)/2+4*A/2*(h3+h2+h2+h4)/4}*B/6=A*B/12*{h3+h4+2*h2+h3+h4}=A*B*(h2+h3+h4)/6V2、V3、V4分别按四棱锥、三棱锥、三棱锥体积计算公式进行计算(体积=底面积*高/3)V2= [√(A^2+B^2)]*1/2*1/3*[√(A^2+B^2)]*(h2+h4)/2= (A^2+B^2)*(h2+h4) /12V3=A*B/2/3*h1=A*B*h1/6V4=h1/3*(B*h1/(h1+h4)*A*h1/(h1+h2)/2=A*B/6*h1^3/(h1+h2)/(h1+h4)V=V1+V2-V3+V4= A*B*(h2+h3+h4)/6+(A^2+B^2)*(h2+h4) /6+A*B/6*h1^2/(h1+h2)/(h1+h4)- A*B*h1/6= A*B /6*[ h2+h3+h4-h1+h1^3/(h1+h2)/(h1+h4)] +(A^2+B^2)*(h2+h4) /123、不机邻两点回填方量计算公式推导:如图示:从h1和h3处将图形分成平面为两个直角三角形体:h4侧的体积公式如下:Vh4=V1+V3-V2根据锥体体积公式:底面积*高/3可得V1=(h1+h3)/2*[√(A^2+B^2)] /3*[√(A^2+B^2)]/2=(h1+h3)*(A^2+B^2) /12 V2=A*B/2*h4/3= A*B*h4/6V3= h4/3*(B*h4/(h4+h1)*A*h4/(h4+h3)/2=A*B/6*h4^3/(h4+h1)/(h4+h3) V=(h1+h3)*(A^2+B^2) /12- A*B*h4/6+ A*B/6*h4^3/(h4+h1)/(h4+h3)= A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12h2侧的体积公式推导方法h4侧的体积公式:Vh2=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12V=Vh2+Vh4=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12+ A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12= A*B/6*[ h2^3/(h2+h1)/(h2+h3) + h4^3/(h4+h1)/(h4+h3) -h2-h4]+ (h1+h3)*(A^2+B^2) /6。
土方工程—土方工程量方格网法ppt

对于第①种情况:
Hx
hx
Ha
x
L
Hb
h
hx x
hL
xh hx L
Hx
Ha
xh L
对于第②种情况:
Hb h hx
L
h
L
h hx L x
Ha
xh hx L
Hx
Hx
Ha
xh L
x
对于第③种情况:
Hx
h L hx x
xh
hx h
hx L
xh Hx Ha L
Hb
Ha L x
对角点1-1,属第 一种情况,则:
Hx
20.00
7.4 0.5 12.6
20.29m
对角点1-2,属第三种情况,则:
Hx
20.00 13 0.5 12
20.54m
依次将其余各角点一一求出,并标写图上。
(二)求平整标高(计划标高)
平整标高概念:对原有高低不平的地面在保证土方 平衡的前提下,挖高垫低使地面成为水平,这个水平 地面的高程即为平整标高。
0.36 3-3
列出方格Ⅶ的土方 计算公式?
-0.54 4-2
-0.49 4-3
b c
VVII
6
h 12 8.47 0.36 6.10m3 6
(2a2 b c)
VVII
10
h (2 202 128.47) (0.24 0.54 0.49) 10
88.5m3
同理,依法将其余各个方格的土方量逐一 求出,并将结果汇总填入土方量计算表。
代入公式(1-19) N=8
H0
1 4N
(
h1 2
h2 3
h3 4
土方方格网计算方法

土方方格网计算方法土方方格网是土方工程中常用的一种计算方法,通过将土地分割成方格网,对每个方格内的土方进行计算,可以更精确地评估土地的开挖量和填方量。
本文将介绍土方方格网的计算方法,包括方格网的划分、土方量的计算等内容。
1. 方格网的划分。
在进行土方计算之前,首先需要对土地进行方格网的划分。
一般来说,可以根据土地的实际情况确定方格的大小,通常情况下,方格的大小可以选择为10米×10米或20米×20米。
在确定了方格的大小后,可以利用测量工具对土地进行划分,确保每个方格都能够清晰地被划分出来。
2. 土方量的计算。
一旦完成了方格网的划分,接下来就是对每个方格内的土方进行计算。
土方量的计算可以通过以下步骤进行:(1)测量每个方格的高程。
首先,需要对每个方格的高程进行测量。
可以利用测量仪器对方格内的几个关键点进行高程测量,然后通过插值法计算出整个方格的平均高程。
(2)计算土方量。
在得到了每个方格的平均高程后,可以通过以下公式计算出每个方格内的土方量:土方量 = 方格面积×(挖方高程填方高程)。
其中,方格面积可以直接通过方格的大小得到,挖方高程和填方高程分别为该方格内的地面高程和设计高程。
3. 土方量的累加。
完成了每个方格内土方量的计算后,就可以将所有方格内的土方量进行累加,得到整个土地的总土方量。
通过这种方法,可以更准确地评估土地的开挖量和填方量,为土方工程的施工提供重要参考。
4. 注意事项。
在进行土方方格网计算时,需要注意以下几点:(1)方格网的划分应当尽量均匀,确保每个方格内的土方量计算准确;(2)测量方格内的高程时,应当选择代表性的点进行测量,确保计算结果的准确性;(3)在进行土方量累加时,需要对累加的结果进行核对,确保计算结果的准确性。
总之,土方方格网计算方法是土方工程中常用的一种计算方法,通过对土地进行方格网的划分,可以更精确地评估土地的土方量。
在实际应用中,需要严格按照计算步骤进行操作,并注意各项计算的准确性,以确保土方计算结果的准确性和可靠性。
-建筑工程技术土方量(方格网)计算

fl]点编、 ?/ % 1血锲+0^0Zi=3%o4^ 65地伺菲窟/、设讣标髙】r0 392 +0 023 小 94 -0 556 理如建筑工程技术土方量(方格网)计算、方格网识图:方格网图由设计单位(一般在1: 500的地形图上)将场地划分为边长a=10〜40m 的若干方格,与测 量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高 (H )和设计标高(Hn ),如图 1-3所示.图1-3 方格网法计算土方工程量图场地平整土方计算考虑的因素:① 满足生产工艺和运输的要求;② 尽量利用地形,减少挖填方数量; ③ 争取在场区内挖填平衡,降低运输费; ④ 有一定泄水坡度,满足排水要求.43 6343 67*17^043 73 4-1 34 43 81-27000*11700+ U6ODL0-0 4043 65 +0.97+Q 71+ 044 151342.58 4^5543 67歸73⑤场地设计标高一般在设计文件上规定,如无规定:A. 小型场地——挖填平衡法;B. 大型场地一一最佳平面设计法(用最小二乘法,使挖填平衡且总土方量最小)。
1、初步标高(按挖填平衡),也就是设计标高。
如果已知设计标高,1.2步可跳过。
场地初步标高:H0=(刀 H1+2E H2+3E H3+迟 H4)/4MH1———个方格所仅有角点的标高;H2 H3 H4——分别为两个、三个、四个方格共用角点的标高 .M——方格个数.2. 地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整 .按泄水坡度调整各角点设计标高:①单向排水时,各方格角点设计标高为:Hn = H0 ± Li②双向排水时,各方格角点设计标高为:Hn = H0 土 Lx ix ± L yi y3. 计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差,是以角点设计标高为基准的挖方或填方的施工高度•各方格角点的施工高度按下式计算:h n = H n-H式中hn——角点施工高度即填挖高度(以“ +”为填,“-”为挖),mn------方格的角点编号(自然数列1,2, 3,…,n).Hn --- 角点设计高程,H——角点原地面高程.4. 计算“零点”位置,确定零线方格边线一端施工高程为“ +” ,若另一端为“-”,则沿其边线必然有一不挖不填的点,即“零点”(如图1-4所示).图1-4 零点位置零点位置按下式计算:工=式中 x1、x2——角点至零点的距离,m;hl、h2 ――相邻两角点的施工高度(均用绝对值),m ; a —方格网的边长,m.5. 计算方格土方工程量按方格底面积图形和表1-3所列计算公式,逐格计算每个方格内的挖方量或填方量表1-3常用方格网点计算公式6. 边坡土方量计算场地的挖方区和填方区的边沿都需要做成边坡,以保证挖方土壁和填方区的稳定。
方格网计算土方例题

方格网图由设计单位(一般在 1:500 的地形图上)将场地划分为边长 a=10~40m 的若干方格,与测量的纵横坐标相对应 ,在各方格角点规定的位置上标注角点的自然地面标高 (H)和设计标高(Hn),.①满足生产工艺和运输的要求;②尽量利用地形,减少挖填方数量;③争取在场区内挖填平衡,降低运输费;④有一定泄水坡度,满足排水要求 .⑤场地设计标高一般在设计文件上规定,如无规定:A.小型场地――挖填平衡法;B.大型场地――最佳平面设计法 (用最小二乘法,使挖填平衡且总土方量最小 )。
场地初步标高:H0=(∑ H1+2∑H3+4∑ H4)/4MH1 --一个方格所仅有角点的标高;H2、 H3、 H4 --分别为两个、三个、四个方格共用角点的标高 .M ——方格个数 .按泄水坡度、土的可松性、就近借弃土等调整 .按泄水坡度调整各角点设计标高①单向排水时,各方格角点设计标高为 : Hn = H0 ± Li②双向排水时,各方格角点设计标高为: Hn = H0 ± Lx ix ± L yi y施工高度为角点设计地面标高与自然地面标高之差,是以角点设计标高为基准的挖方或填方的施工高度 .各方格角点的施工高度按下式计算:式中 hn------角点施工高度即填挖高度 (以“+”为填,“ -”为挖),m;n------方格的角点编号(自然数列 1,2,3 ,…, n).Hn------角点设计高程,H------角点原地面高程 .方格边线一端施工高程为”,若另一端为“ -”,则沿其边线必然有一不挖不填的点,零点位置按下式计算:式中 x1、x2 ——角点至零点的距离 ,m;h1、 h2 ——相邻两角点的施工高度 (均用绝对值),m;a —方格网的边长, m.按方格底面积图形和所列计算公式,逐格计算每个方格内的挖方量或填方量 .场地的挖方区和填方区的边沿都需要做成边坡 ,以保证挖方土壁和填方区的稳定。
土方计算方格网法与DTM三角网两期间土方计算比较案列
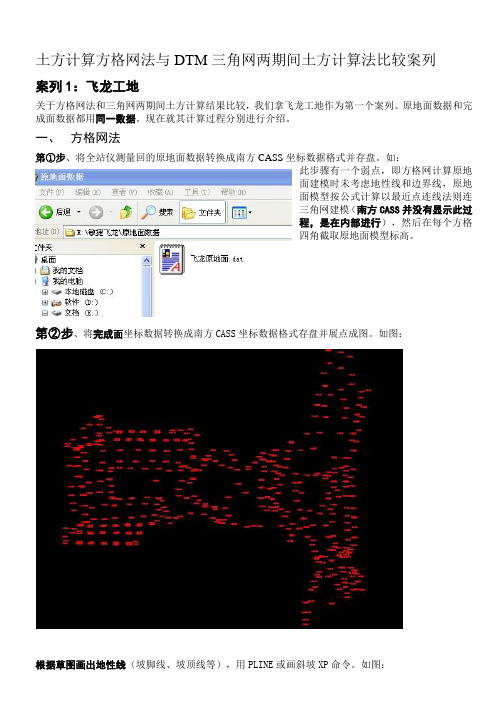
土方计算方格网法与DTM三角网两期间土方计算法比较案列案列1:飞龙工地关于方格网法和三角网两期间土方计算结果比较,我们拿飞龙工地作为第一个案列。
原地面数据和完成面数据都用同一数据。
现在就其计算过程分别进行介绍。
一、方格网法第①步、将全站仪测量回的原地面数据转换成南方CASS坐标数据格式并存盘。
如:此步骤有一个弱点,即方格网计算原地面建模时未考虑地性线和边界线,原地面模型按公式计算以最近点连线法则连三角网建模(南方CASS并没有显示此过程,是在内部进行),然后在每个方格四角截取原地面模型标高。
第②步、将完成面坐标数据转换成南方CASS坐标数据格式存盘并展点成图。
如图:根据草图画出地性线(坡脚线、坡顶线等),用PLINE或画斜坡XP命令。
如图:建立DTM(就是建立完成面三维模型),如图:但是一定要保证数据的完整性和不可重复性,建模过程一定要考虑地性线,最好关闭捕捉(可以输入OSMODE 回车16384回车)。
选择所有高程点,然后选择所有地性线生成三角网。
删除边界线以外的三角形。
建立好的三角网模型如图:点击等高线---修改结果存盘。
再点击等高线---绘制等高线---等高距0.5米,检查等高线图与实际地形相不相吻合。
如果不吻合,应该检查等高线突然密集处是否有异常高程、坡坎处三角网是否穿越地性线,是否有高程点因为坡太陡平距太小没有参加组网导致遗漏;解决办法是删除异常高程(若关键位置高程错误要补测),用等高线->加入地性线功能修改穿越地性线的三角形,删除关联错误高程点的三角形,删除连接错误的三角形,用等高线->图面DTM完善或者增加三角形命令补齐因为删除错误三角形引起的空洞。
再点击->修改结果存盘。
反复检查无误后将正确的三角网写入文件存盘第③步、方格网土方计算----点击计算结果如下二、DTM三角网两期间土方计算法A、步骤一:处理原地面数据,方法跟方格网法第②步一样,不再重复介绍。
以下是处理好的地性线图和等高线图:B、步骤二:处理完成面数据,同方格网法第②步。
方格网计算土方量

方格网计算土方量
在土建工程中,计算土方量是非常重要的一个环节。
而计算土方量的方法也有很多,其中一种方法就是通过方格网来计算。
方格网计算法通常适用于分块比较规则的场地。
下面将详细介绍如何使用方格网来计算土方量。
步骤一:绘制方格网
首先,需要绘制方格网,即把场地按照一定的比例划分成小块。
具体的比例应该根据场地大小和地形情况来确定。
划分好方块之后,可以用绳子或者直尺来把方块连接起来,形成方格网。
步骤二:测量地形高度
接着,需要在方格网的交点处,即每个小块的四个角落处进行地形高度测量。
可以使用测高仪等工具来进行测量。
在测量时,需要保证精度,以确保计算的土方量准确无误。
步骤三:计算每个小块的体积
有了每个小块的高度数据之后,就可以计算每个小块的体积。
计算公式如下:体积 = 面积 × 平均高度
其中,面积可以通过方格网的尺寸来直接计算,平均高度则是该小块四个角高度的平均值。
步骤四:计算总体积
所有小块体积计算完毕之后,需要把它们加起来,得到场地的总体积。
为了便于计算,可以把各个小块的体积逐个列出来,然后进行累加,最终得到总体积。
步骤五:检查计算结果
计算出总体积之后,需要对结果进行检查。
可以再次对各个小块的高度进行测量,以确保计算结果的准确性。
另外,也需要检查方格网的划分是否准确,以及每个小块的面积是否计算正确。
方格网计算法是一种简单易行的土方量计算方法,适用于场地比较规则且地形比较平缓的情况。
在进行方格网计算时,需要注意测量高度的精度,以及对结果进行检查。
土建工程土方方格网方案

土建工程土方方格网方案1. 简介土方方格网是土建工程中常用的测量方法之一,用于确定土方工程中各个点的坐标和高程。
通过土方方格网测量,可以准确且高效地完成土方工程的测绘任务。
本文档将介绍土方方格网方案的实施步骤和注意事项,以及相关的技术要点。
2. 实施步骤2.1 建立基准点在土方工程区域内选择适当的位置,建立基准点。
基准点的选择应满足以下条件: - 位置稳定,不易受外力干扰 - 距离土方工程区域相对较近 - 测量基准点高程的工作量相对较小2.2 布设方格网在土方工程区域内,按照一定的间距和方向,布设方格网。
方格网的间距和方向的选择应根据具体工程要求和场地条件来确定。
一般来说,在大面积土方工程中,方格网的间距可以适当放大,以提高测量效率。
2.3 测量土方坐标和高程使用全站仪等测量设备,对方格网上的各个点进行测量。
测量时,需要注意以下事项: - 测量要准确,尽量避免误差 - 测量数据要及时记录,确保完整性 - 测量过程中要注意安全,保护设备2.4 数据处理将测量得到的数据进行处理,计算出各个点的坐标和高程。
数据处理的过程中,需要注意以下技术要点: - 坐标计算方法:可以使用简化的平差方法,也可以使用较为复杂的最小二乘法,根据具体情况选择合适的方法。
- 高程计算方法:可以使用直接法,即将基准点高程作为起点,逐点相加,也可以使用平差法,通过对测量数据进行处理,得到更精确的高程数据。
2.5 结果输出将处理后的数据整理成表格或文本文件,输出为可供使用的格式。
一般情况下,输出的数据包括点的编号、坐标和高程信息。
3. 注意事项在实施土方方格网测量时,需要根据具体情况和实际需求,注意以下事项:•网格布设要合理:方格网的布设应尽量覆盖整个土方工程区域,并考虑不同地形条件下的适应性。
•测量要精确:测量时要严格按照操作规范进行,尽量避免误差产生。
•数据处理要准确:数据处理过程中要注意计算方法的选择和计算精度的控制,以确保结果的准确性。
方格网计算土方量原理

方格网计算土方量原理
方格网计算土方量原理即通过在地面上划分方格网,并计算每个方格中的土方体积,进而得出总的土方量。
具体原理可分为以下几步:
1. 划分方格网:首先在待测量区域的地面上进行方格网的划分,通常使用水平标杆和粉笔线等工具,将地面划分为等大的方格。
2. 计算单个方格的土方体积:对每个方格进行土方体积的计算。
土方体积的计算可以通过以下公式进行:
土方体积 = 方格面积 ×层高
其中,方格面积为方格的水平投影面积,层高为该方格内土
方堆积的高度,可以通过测量或估算得出。
3. 累加各个方格的土方体积:将所有方格内的土方体积累加起来,得到总的土方体积。
可以通过逐个方格计算土方体积,并将其累加到总体积中的方法来实现。
4. 随机抽查方格:为了验证计算结果的准确性,可以随机抽取部分方格进行测量和计算,然后与计算结果进行对比。
需要注意的是,在进行方格网计算土方量时,应当注意以下几点:
- 方格的大小应根据实际情况进行选择,一般应适当缩小,以
提高计算精度。
- 方格网的划分应在待测量区域的整个范围内进行,确保所有
区域被覆盖。
- 土方体积计算中的方格面积和层高都应该准确测量或者经过合理估算。
- 测量时要确保准确性,避免误差的产生,可选用高精度的测量工具,并进行多次测量取平均值。
综上所述,方格网计算土方量原理是通过划分方格网,计算每个方格内的土方体积,累加得到总的土方体积。
该方法可以提高土方量计算的准确性和效率。
《土石方方格网》计算

一、读识方格网图方格网图由设计单位(一般在1:500的地形图上)将场地划分为边长a=10~40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图1-3所示.图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素:① 满足生产工艺和运输的要求;② 尽量利用地形,减少挖填方数量;③争取在场区内挖填平衡,降低运输费;④有一定泄水坡度,满足排水要求.⑤场地设计标高一般在设计文件上规定,如无规定:A.小型场地――挖填平衡法;B.大型场地――最佳平面设计法(用最小二乘法,使挖填平衡且总土方量最小)。
1、初步标高(按挖填平衡),也就是设计标高。
如果已知设计标高,1.2步可跳过。
场地初步标高:H0=(∑H1+2∑H2+3∑H3+4∑H4)/4MH1--一个方格所仅有角点的标高;H2、H3、H4--分别为两个、三个、四个方格共用角点的标高.M——方格个数.2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整.按泄水坡度调整各角点设计标高:①单向排水时,各方格角点设计标高为: Hn = H0 ±Li②双向排水时,各方格角点设计标高为:Hn = H0± Lx ix± L yi y3.计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差,是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算:式中hn------角点施工高度即填挖高度(以“+”为填,“-”为挖),m;n------方格的角点编号(自然数列1,2,3,…,n).Hn------角点设计高程,H------角点原地面高程.4.计算“零点”位置,确定零线方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点,即“零点”(如图1-4所示).图1-4 零点位置零点位置按下式计算:式中x1、x2 ——角点至零点的距离,m;h1、h2 ——相邻两角点的施工高度(均用绝对值),m;a —方格网的边长,m.5.计算方格土方工程量按方格底面积图形和表1-3所列计算公式,逐格计算每个方格内的挖方量或填方量.表1-3 常用方格网点计算公式6.边坡土方量计算场地的挖方区和填方区的边沿都需要做成边坡,以保证挖方土壁和填方区的稳定。
《土石方方格网》计算,很全啊

一、读识方格网图方格网图由设计单位(一般在1:500的地形图上)将场地划分为边长a=10~40m的若干方格,与测量的纵横坐标相对应,在各方格角点规定的位置上标注角点的自然地面标高(H)和设计标高(Hn),如图1—3所示。
图1-3 方格网法计算土方工程量图二、场地平整土方计算考虑的因素:① 满足生产工艺和运输的要求;② 尽量利用地形,减少挖填方数量;③争取在场区内挖填平衡,降低运输费;④有一定泄水坡度,满足排水要求.⑤场地设计标高一般在设计文件上规定,如无规定:A。
小型场地――挖填平衡法;B.大型场地――最佳平面设计法(用最小二乘法,使挖填平衡且总土方量最小)。
1、初步标高(按挖填平衡),也就是设计标高。
如果已知设计标高,1。
2步可跳过。
场地初步标高:H0=(∑H1+2∑H2+3∑H3+4∑H4)/4MH1--一个方格所仅有角点的标高;H2、H3、H4--分别为两个、三个、四个方格共用角点的标高。
M——方格个数。
2、地设计标高的调整按泄水坡度、土的可松性、就近借弃土等调整。
按泄水坡度调整各角点设计标高:①单向排水时,各方格角点设计标高为: Hn = H0 ±Li②双向排水时,各方格角点设计标高为:Hn = H0± Lx ix± L yi y3。
计算场地各个角点的施工高度施工高度为角点设计地面标高与自然地面标高之差,是以角点设计标高为基准的挖方或填方的施工高度.各方格角点的施工高度按下式计算:式中hn————--角点施工高度即填挖高度(以“+”为填,“—"为挖),m;n------方格的角点编号(自然数列1,2,3,…,n).Hn-—-—-—角点设计高程,H---—--角点原地面高程.4。
计算“零点”位置,确定零线方格边线一端施工高程为“+”,若另一端为“-”,则沿其边线必然有一不挖不填的点,即“零点”(如图1-4所示)。
图1-4 零点位置零点位置按下式计算:式中x1、x2 ——角点至零点的距离,m;h1、h2 ——相邻两角点的施工高度(均用绝对值),m;a —方格网的边长,m。
土方工程量计算方格网法课件

Ha——位于低边的等高线高程(m); x——角点至低边等高线的距离(m); h——等高距(m); L——相邻两等高线间最短距离(m)。
土方工程量计算方格网法
插入法求高程通常会遇到3种情况: (1) 待求点标高Hx在二等高线之间(如下图①)
=〔(S1+Sn)/2+S2+S3+…+Sn-1土方〕工程*量h计1算方+格S网法n*h2/3
无论是垂直断面法还是水平断面法,不规则的断面面 积的计算工作总是比较繁琐的。一般说来,对不规则 面积的计算可采用以下几种方法: (1)求积仪法 运用求积仪进行测量,此法比较简便,精确度也比较 高。 (2)方格纸法 用方格纸蒙在图纸上,通过数方格数,再乘以每个方 格的面积而求取。此法方格网越密,精度越大。 一般在数方格数时,测量对象占方格单元超过1/2, 按一整个方格计;小于1/2者不计。最后进行方格数 的累加,再求取面积既可。
§ ∑h1=角点之和 =(20.29+20.23+19.37+19.64+18.79+19.32)=117.75
§ 2∑h2=2*(边点之和) =2*(20.54+20.89+21.00+19.50+19.39+19.35)=241.34
§ 3∑h3=3*(拐点之和) =3*(19.91+20.15)=120.18
土方工程量计算方格网法
土方工程量计算方格网法
土方工程量计算方格网法
三、方格网法 方格网法是一种相对比较精确的方法。 多用于平整场地,将原来高低不平、比较破碎的地 形按设计要求整理成平坦的具有一定坡度的场地。
土方工程量计算方格网法

土方工程量计算方格网法土方工程量计算是土方工程建设的重要环节,准确计算土方工程量可以为土方工程施工提供准确的数据支持,保证土方工程的顺利进行。
方格网法是一种常用的土方工程量计算方法,其原理简单,操作方便,下面将详细介绍方格网法的计算步骤和注意事项。
方格网法是一种将土地表面划分为固定大小的网格,然后通过对网格内全填全挖的体积进行计算,得出土方工程量的方法。
该方法主要分为以下几个步骤。
第一步,确定网格大小。
网格大小的确定需要根据具体情况而定,一般来说,土方工程量计算的精度要求高时,网格的大小要适当缩小。
而计算的范围较大时,网格的大小可以适当加大。
根据实际情况选择合适的网格大小可以减少计算量,并提高计算效率。
第二步,划分网格。
将土地表面按照网格大小进行划分,一般情况下,常用的方法是将土地表面划分为正方形或长方形的网格。
划分网格时需要注意网格之间的重叠与缝隙,做到严密贴合,以确保计算结果的准确性。
第三步,测量高程。
在每个网格内需测量地面高程,可以使用测高仪进行测量,获取每个网格内地面的高程数据。
第四步,计算体积。
根据测得的高程数据,对每个网格进行体积计算,包括填方体积和挖方体积。
填方体积表示网格内地面相对基准面升高的土方体积,挖方体积表示网格内地面相对基准面降低的土方体积。
体积的计算需将每个网格的填方体积和挖方体积累加求和,得到整个土方工程的总体积。
需要注意的是,在计算填方和挖方体积时,需确定基准面的高程。
一般来说,基准面的选取应符合工程设计要求,并保持统一方格网法计算土方工程量的优点是计算简便、操作方便,适用于较小的土方工程量计算。
但同时也存在一些局限性,在计算大范围土方工程量时会受到网格大小和形状的影响,可能造成计算误差较大。
在实际应用中,可以结合其他方法并综合考虑,提高计算的准确性和可靠性。
综上所述,方格网法是一种简便易行的土方工程量计算方法,适用于较小范围的土方工程量计算。
通过确定网格大小、划分网格、测量高程和计算体积等步骤,可以准确计算土方工程的填方和挖方体积,为土方工程施工提供可靠的数据支持。
