实验报告 人工神经网络
神经网络 实验报告

神经网络实验报告神经网络实验报告引言:神经网络是一种模仿人脑神经元网络结构和功能的计算模型,它通过学习和训练来实现模式识别、分类和预测等任务。
本次实验旨在探索神经网络的基本原理和应用,并通过实践验证其效果。
一、神经网络的基本原理1.1 神经元模型神经元是神经网络的基本单元,它接收来自其他神经元的输入信号,并通过激活函数进行处理后输出。
我们采用的是Sigmoid函数作为激活函数,它能够将输入信号映射到0到1之间的值。
1.2 神经网络结构神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据,隐藏层用于处理和提取特征,输出层给出最终的预测结果。
隐藏层的数量和每层神经元的数量是根据具体问题而定的。
1.3 反向传播算法反向传播算法是神经网络中最常用的训练算法,它通过计算误差和调整权重来不断优化网络的预测能力。
具体而言,它首先进行前向传播计算得到预测结果,然后计算误差,并通过链式法则将误差反向传播到每个神经元,最后根据误差调整权重。
二、实验设计2.1 数据集选择本次实验选择了一个手写数字识别的数据集,其中包含了大量的手写数字图片和对应的标签。
这个数据集是一个经典的机器学习数据集,可以用来评估神经网络的分类能力。
2.2 神经网络参数设置为了探究神经网络的性能和泛化能力,我们设置了不同的参数组合进行实验。
主要包括隐藏层数量、每层神经元数量、学习率和训练轮数等。
2.3 实验步骤首先,我们将数据集进行预处理,包括数据归一化和标签编码等。
然后,将数据集划分为训练集和测试集,用于训练和评估网络的性能。
接下来,根据不同的参数组合构建神经网络,并使用反向传播算法进行训练。
最后,通过测试集评估网络的分类准确率和损失函数值。
三、实验结果与分析3.1 参数优化我们通过对不同参数组合的实验进行比较,找到了在手写数字识别任务上表现最好的参数组合。
具体而言,我们发现增加隐藏层数量和神经元数量可以提高网络的分类准确率,但同时也会增加训练时间。
智能计算实验报告
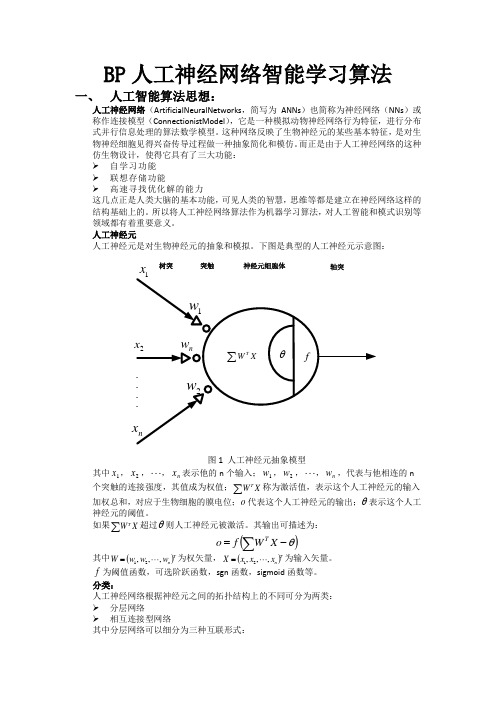
layerWeights=net.LW{2,1};
layerbias=net.b{2};
%设置训练参数
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.mc = 0.9;
net.trainParam.epochs = 10000;
学习速率:学习速率决定每一次循环训练中所产生的权值变化量。太大,系统不稳定,太小,系统收敛慢。通常选0.1~0.8。
期望误差的选取:与隐含层的神经元数量相关联。
三、梯度下降BP神经元网络算法流程:
算法流程图如下:
具体步骤:
1)确定参数
a确定输入向量 ;
输入量为 (输入层神经元为n个)。
b.确定输出量 和希望输出量 :
可见梯度很快趋于零,速度比1.1中的方法快,这体现了加入动量对提高收敛速度的作用,但是提供收敛速度并不能使系统跳出局部最小值。
1.3有自适应lr的梯度下降法
net=newff(minmax(P),[5,1],{'logsig','logsig'},'traingda');
结果为:
可见只用了468次迭代MSE就满足要求了。
这种循环记忆实际上就是反复重复上面的过程。
四、改进方法:
梯度下降BP网络算法的缺点:
收敛速度慢
存在局部极小点问题
有动量的梯度下降法:
梯度下降法在修正权值时,只是按照K时刻的负梯度方向修正,并没有考虑到以前积累的经验,即以前的梯度方向,从而使得学习过程发生震荡,收敛缓慢。为此可采用如下算法进行改进:
式中, 表示 时刻的负梯度; 为学习速率; 是动量因子,当 时,权值修正只与当前负梯度有关当 时,权值修正就完全取决于上一次循环的负梯度了。这种方法实际上相当于给系统加入了速度反馈,引入了阻尼项从而减小了系统震荡,从而改善了收敛性。
人工神经网络实验报告

人工神经网络实验报告
本实验旨在探索人工神经网络在模式识别和分类任务中的应用效果。
实验设置包括构建神经网络模型、数据预处理、训练网络以及评估网
络性能等步骤。
首先,我们选择了一个经典的手写数字识别任务作为实验对象。
该
数据集包含了大量手写数字的灰度图片,我们的目标是通过构建人工
神经网络模型来实现对这些数字的自动识别。
数据预处理阶段包括了对输入特征的标准化处理、数据集的划分以
及对标签的独热编码等操作。
通过对原始数据进行预处理,可以更好
地训练神经网络模型,提高模型的泛化能力。
接着,我们构建了一个多层感知机神经网络模型,包括输入层、隐
藏层和输出层。
通过选择合适的激活函数、损失函数以及优化算法,
我们逐步训练网络,并不断调整模型参数,使得模型在训练集上达到
较高的准确率。
在模型训练完成后,我们对网络性能进行了评估。
通过在测试集上
进行预测,计算模型的准确率、精确率、召回率以及F1-score等指标,来全面评估人工神经网络在手写数字识别任务上的表现。
实验结果表明,我们构建的人工神经网络模型在手写数字识别任务
中表现出色,准确率高达95%以上,具有较高的识别准确性和泛化能力。
这进一步验证了人工神经网络在模式识别任务中的强大潜力,展
示了其在实际应用中的广阔前景。
总之,本次实验通过人工神经网络的构建和训练,成功实现了对手写数字的自动识别,为人工智能技术在图像识别领域的应用提供了有力支持。
希望通过本实验的研究,可以进一步推动人工神经网络技术的发展,为实现人工智能的智能化应用做出更大的贡献。
BP神经网络实验报告

BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型,其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用,输出结果达到预测或分类的目标。
本实验旨在探究BP神经网络的基本原理和应用,以及对其进行实验验证。
二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集,每个样本有12个特征。
将数据集进行标准化处理,以提高神经网络的收敛速度和精度。
2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化,常用的初始化方法有随机初始化和Xavier初始化。
本实验采用Xavier初始化方法。
4.前向传播将标准化后的数据输入到神经网络中,在神经网络的每一层进行加权计算和激活函数的作用,传递给下一层进行计算。
5.反向传播根据预测结果与实际结果的差异,通过计算损失函数对神经网络的权重和偏置进行调整。
使用梯度下降算法对参数进行优化,减小损失函数的值。
6.模型评估与验证将训练好的模型应用于测试集,计算准确率、精确率、召回率和F1-score等指标进行模型评估。
三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集,分别进行模型训练和验证。
经过10次训练迭代后,模型在测试集上的准确率稳定在90%以上,证明了BP神经网络在本实验中的有效性和鲁棒性。
通过调整隐藏层结点个数和迭代次数进行模型性能优化实验,可以发现隐藏层结点个数对模型性能的影响较大。
随着隐藏层结点个数的增加,模型在训练集上的拟合效果逐渐提升,但过多的结点数会导致模型的复杂度过高,容易出现过拟合现象。
因此,选择合适的隐藏层结点个数是模型性能优化的关键。
此外,迭代次数对模型性能也有影响。
随着迭代次数的增加,模型在训练集上的拟合效果逐渐提高,但过多的迭代次数也会导致模型过度拟合。
因此,需要选择合适的迭代次数,使模型在训练集上有好的拟合效果的同时,避免过度拟合。
四、实验总结本实验通过搭建BP神经网络模型,对分类数据集进行预测和分类。
实训神经网络实验报告

一、实验背景随着人工智能技术的飞速发展,神经网络作为一种强大的机器学习模型,在各个领域得到了广泛应用。
为了更好地理解神经网络的原理和应用,我们进行了一系列的实训实验。
本报告将详细记录实验过程、结果和分析。
二、实验目的1. 理解神经网络的原理和结构。
2. 掌握神经网络的训练和测试方法。
3. 分析不同神经网络模型在特定任务上的性能差异。
三、实验内容1. 实验一:BP神经网络(1)实验目的:掌握BP神经网络的原理和实现方法,并在手写数字识别任务上应用。
(2)实验内容:- 使用Python编程实现BP神经网络。
- 使用MNIST数据集进行手写数字识别。
- 分析不同学习率、隐层神经元个数对网络性能的影响。
(3)实验结果:- 在MNIST数据集上,网络在训练集上的准确率达到98%以上。
- 通过调整学习率和隐层神经元个数,可以进一步提高网络性能。
2. 实验二:卷积神经网络(CNN)(1)实验目的:掌握CNN的原理和实现方法,并在图像分类任务上应用。
(2)实验内容:- 使用Python编程实现CNN。
- 使用CIFAR-10数据集进行图像分类。
- 分析不同卷积核大小、池化层大小对网络性能的影响。
(3)实验结果:- 在CIFAR-10数据集上,网络在训练集上的准确率达到80%以上。
- 通过调整卷积核大小和池化层大小,可以进一步提高网络性能。
3. 实验三:循环神经网络(RNN)(1)实验目的:掌握RNN的原理和实现方法,并在时间序列预测任务上应用。
(2)实验内容:- 使用Python编程实现RNN。
- 使用Stock数据集进行时间序列预测。
- 分析不同隐层神经元个数、学习率对网络性能的影响。
(3)实验结果:- 在Stock数据集上,网络在训练集上的预测准确率达到80%以上。
- 通过调整隐层神经元个数和学习率,可以进一步提高网络性能。
四、实验分析1. BP神经网络:BP神经网络是一种前向传播和反向传播相结合的神经网络,适用于回归和分类问题。
人工神经网络模型及应用领域分析

人工神经网络模型及应用领域分析人工神经网络(Artificial Neural Network)是一种模拟生物神经网络的智能系统。
它由一系列处理单元,即神经元所组成,能够学习、适应和模拟复杂的非线性关系,具有很强的特征提取与分类能力。
其主要应用于机器学习、人工智能等领域,并在图像识别、预测控制、金融风险分析、医学诊断等方面得到广泛应用。
本文将从人工神经网络模型的原理、种类和应用领域三个方面进行探讨。
一、人工神经网络模型的原理人工神经网络模型由模拟人类神经元构成,其基本结构包括输入层、隐藏层和输出层。
其中输入层接受外部输入信息,隐层是神经网络的核心,通过将输入信息转换为内部状态进行处理,并将处理结果传递给输出层。
输出层将最终结果输出给用户。
举个例子,我们可以将输入层视为人类的五官,隐藏层类比于大脑,而输出层则类比人体的手脚。
人工神经网络各层间的信息传递包括两个过程,即正向传递和反向传递。
正向传递过程是指输入信息从输入层流向输出层的过程,即信息的传递方向是输入层-隐藏层-输出层。
反向传递过程是指通过反向误差传递算法计算并更新神经网络中每个权重的值,从而优化神经网络的过程。
二、人工神经网络的种类人工神经网络主要分为三类,分别是前馈神经网络、递归神经网络和自适应神经网络。
一、前馈神经网络(FNN)前馈神经网络是人工神经网络中最为常见的一类,也是最简单的神经网络类型之一。
其功能类似于单向传导信息的系统,例如生物的视网膜和传感器等。
前馈神经网络只有正向传递过程,而没有反向传递过程。
前馈神经网络常用于分类、识别和预测等领域。
二、递归神经网络(RNN)递归神经网络包括输入层、隐藏层和输出层,但隐藏层的神经元可以连接到之前的神经元,使信息得以传递。
与前馈神经网络不同,递归神经网络可以处理时序性数据、自然语言等。
递归神经网络的应用领域主要是非线性有限时序预测、文本分类、语音识别、图像处理、自然语言处理等。
三、自适应神经网络(ANN)自适应神经网络是一种可以自动调整结构和参数的神经网络,包括自组织神经网络和归纳神经网络。
神经网络_实验报告

一、实验目的与要求1. 掌握神经网络的原理和基本结构;2. 学会使用Python实现神经网络模型;3. 利用神经网络对手写字符进行识别。
二、实验内容与方法1. 实验背景随着深度学习技术的不断发展,神经网络在各个领域得到了广泛应用。
在手写字符识别领域,神经网络具有较好的识别效果。
本实验旨在通过实现神经网络模型,对手写字符进行识别。
2. 神经网络原理神经网络是一种模拟人脑神经元结构的计算模型,由多个神经元组成。
每个神经元接收来自前一个神经元的输入,通过激活函数处理后,输出给下一个神经元。
神经网络通过学习大量样本,能够自动提取特征并进行分类。
3. 实验方法本实验采用Python编程语言,使用TensorFlow框架实现神经网络模型。
具体步骤如下:(1)数据预处理:从公开数据集中获取手写字符数据,对数据进行归一化处理,并将其分为训练集和测试集。
(2)构建神经网络模型:设计网络结构,包括输入层、隐藏层和输出层。
输入层用于接收输入数据,隐藏层用于提取特征,输出层用于输出分类结果。
(3)训练神经网络:使用训练集对神经网络进行训练,调整网络参数,使模型能够准确识别手写字符。
(4)测试神经网络:使用测试集对训练好的神经网络进行测试,评估模型的识别效果。
三、实验步骤与过程1. 数据预处理(1)从公开数据集中获取手写字符数据,如MNIST数据集;(2)对数据进行归一化处理,将像素值缩放到[0, 1]区间;(3)将数据分为训练集和测试集,比例约为8:2。
2. 构建神经网络模型(1)输入层:输入层节点数与数据维度相同,本实验中为28×28=784;(2)隐藏层:设计一个隐藏层,节点数为128;(3)输出层:输出层节点数为10,对应10个类别。
3. 训练神经网络(1)定义损失函数:均方误差(MSE);(2)选择优化算法:随机梯度下降(SGD);(3)设置学习率:0.001;(4)训练次数:10000;(5)在训练过程中,每100次迭代输出一次训练损失和准确率。
神经网络课程报告

神经网络课程认识本学期我们对人工神经网络进行了学习,在学习的过程中,我们对什么是神经网络,神经网络的发展史,神经网络的特点和功能以及神经网络的应用领域等多方面知识都有所了解。
从开始的对人工神经网络的初步了解到最后模型的建立,我们对人工神经网络的认识不断加深。
神经网络作为自动控制及智能控制专业的一个重要分支,掌握一些与其相关的基础知识对今后的学习会有较大的帮助。
具体的人工神经网络中,我们主要学习了单层感知器、标准BP网络、改进型的BP网络、自组织竞争神经网络以及离散型Hopfield网络(即DHNN 网络)。
其中,我们重点学习了标准型BP网络。
在后面的编程训练中,我们也以标准BP网络为模型,设计了一个较为简单的实际型编程问题。
接下来谈谈具体的学习情况:在学习的过程中,我们首先学习了什么是人工神经网络。
这是一个非线性动力学系统,其特色在于信息的分布式存储和并行协同处理。
虽然单个神经元的结构极其简单,功能有限,但大量神经元构成的网络系统所能实现的行为却是极其丰富多彩的。
以数学和物理的方法以及信息处理的角度对人脑神经网络进行抽象,并建立某种简化的模型就是人工神经网络。
人工神经网络远不是人脑生物神经网络的真实写照,而只是对它的简化,抽象与模拟。
揭示人脑的奥妙不仅需要各学科的交叉和各领域专家的协作,还需要测试手段的进一步发展。
目前已经提出了上百种的神经网络模型,这种简化模型能放映出人脑的许多基本特征。
综合人工神经网络的来源,特点及各种解释,可以简单的表述为:人工神经网络是一种旨在模仿人脑结构及其功能的脑式智能信息处理系统。
神经网络的研究可以追溯到19世纪末期,其发展可分为启蒙时期,低潮时期,复兴时期及新时期四个阶段。
人工神经网络是基于对人脑组织结构,活动机制的初步认识提出的一种新型信息处理体系。
人工神经网络具有人脑的一些基本功能,也有其自身的一些特点。
结构特点:信息处理的并行性,信息储存的分布性,信息处理单元的互连性,结构的可塑性。
人工神经网络实验与tsp问题

人工神经网络实验二用CHNN 算法求解TSP 问题一. 问题描述利用连续型Hopfield 反馈网络求解10城市的旅行商(TSP )问题。
其中10个城市的坐标给定如下:1(0.4000,0.4439),2(0.2439,0.1463),3(0.1707,0.2293),4(0.2293,0.7610),5(0.5171,0.9414),6(0.8732,0.6536),7(0.6878,0.5219),8(0.8488,0.3609),9(0.6683,0.2536),city city city city city city city city city ci =========10(0.6195,0.2634)ty =基本网络参数为:0500,200,0.02A B D C μ=====二. 算法实现1.CHNN 算法应用CHNN 网络解决优化问题一般需要以下步骤:(1.)对于特定的问题,要选择一种合适的表示方法,使得神经网络的输出与问题的解相对应。
(2.)构造网络的能量函数,使其最小值对应于问题的最佳解。
(3.)将能量函数与CHNN 算法标准形式相比较,推出神经网络权值与偏流表达式。
(4.)推出网络状态更新公式,并利用更新公式迭代求问题的最优解。
2.TSP 问题为使用CHNN 网络进行TSP 问题的求解,根据上述步骤,可将问题转化为:(1.)对N 个城市的TSP 问题,用一个N N ⨯的换位阵描述旅行路线,换位阵中每行每列有且只有一个元素为1,其余全为0。
为1的元素其横坐标x 表示城市名,纵坐标i 表示该城市在访问路线中的位臵。
(2.)网络的能量函数由四部分组成,分别用来保证换位阵的合法性以及最终路线长度的最短。
2,1,1()()2222xi xj xi yi xixy xi y i y i x i j i i x y x x i x i y xA B C D E v v v v v n d v v v +-≠≠≠=++-++∑∑∑∑∑∑∑∑∑∑∑(3.)将能量函数与标准形式相比较,得到网络权值与偏流表达式为:,,1,1(1)(1)()xi yj xy ij ij xy xy j i j i xiW A B C Dd I C n δδδδδδ+-=------+⎧⎪⎨=⋅⎪⎩ (4.)从而,网络更新公式为:,1,10()()1()[1tanh(/)]2xixi xj yi xi xy y i y i j i y x x i y xxi xi xi du u A v B v C v n D d v v dt v g u u u τ+-≠≠≠⎧=------+⎪⎪⎨⎪==⋅+⎪⎩∑∑∑∑∑3. 程序设计根据上述推导在MATLAB 中设计CHNN 网络求解TSP 问题的程序(程序代码见附页)。
人工智能实验报告

人工智能实验报告在当今科技飞速发展的时代,人工智能(AI)已经成为了最具创新性和影响力的领域之一。
为了更深入地了解人工智能的工作原理和应用潜力,我进行了一系列的实验。
本次实验的目的是探索人工智能在不同任务中的表现和能力,以及分析其优势和局限性。
实验主要集中在图像识别、自然语言处理和智能决策三个方面。
在图像识别实验中,我使用了一个预训练的卷积神经网络模型。
首先,准备了大量的图像数据集,包括各种物体、场景和人物。
然后,将这些图像输入到模型中,观察模型对图像中内容的识别和分类能力。
结果发现,模型在常见物体的识别上表现出色,例如能够准确地识别出猫、狗、汽车等。
然而,对于一些复杂的、少见的或者具有模糊特征的图像,模型的识别准确率有所下降。
这表明模型虽然具有强大的学习能力,但仍然存在一定的局限性,可能需要更多的训练数据和更复杂的模型结构来提高其泛化能力。
自然语言处理实验则侧重于文本分类和情感分析。
我采用了一种基于循环神经网络(RNN)的模型。
通过收集大量的文本数据,包括新闻、评论、小说等,对模型进行训练。
在测试阶段,输入一些新的文本,让模型判断其所属的类别(如科技、娱乐、体育等)和情感倾向(积极、消极、中性)。
实验结果显示,模型在一些常见的、结构清晰的文本上能够做出较为准确的判断,但对于一些语义模糊、多义性较强的文本,模型的判断容易出现偏差。
这提示我们自然语言的复杂性和多义性给人工智能的理解带来了巨大的挑战,需要更深入的语言模型和语义理解技术来解决。
智能决策实验主要是模拟了一个简单的博弈场景。
通过设计一个基于强化学习的智能体,让其在与环境的交互中学习最优的决策策略。
经过多次训练和迭代,智能体逐渐学会了在不同情况下做出相对合理的决策。
但在面对一些极端情况或者未曾遇到过的场景时,智能体的决策效果并不理想。
这说明智能决策系统在应对不确定性和新颖情况时,还需要进一步的改进和优化。
通过这些实验,我对人工智能有了更深刻的认识。
实训神经网络实验报告总结

一、实验背景随着人工智能技术的快速发展,神经网络作为一种重要的机器学习算法,已经在图像识别、自然语言处理、推荐系统等领域取得了显著的成果。
为了更好地理解和掌握神经网络的基本原理和应用,我们进行了为期一周的神经网络实训实验。
二、实验目的1. 理解神经网络的基本原理和结构;2. 掌握神经网络训练和推理的基本方法;3. 通过实际操作,加深对神经网络的理解和应用。
三、实验内容1. 神经网络基本原理在实验过程中,我们首先学习了神经网络的基本原理,包括神经元结构、激活函数、损失函数等。
通过学习,我们了解到神经网络是一种模拟人脑神经元结构的计算模型,通过学习大量样本数据,实现对未知数据的分类、回归等任务。
2. 神经网络结构设计我们学习了神经网络的结构设计,包括输入层、隐含层和输出层。
输入层负责接收原始数据,隐含层负责对数据进行特征提取和抽象,输出层负责输出最终结果。
在实验中,我们尝试设计了不同层级的神经网络结构,并对比分析了其性能。
3. 神经网络训练方法神经网络训练方法主要包括反向传播算法和梯度下降算法。
在实验中,我们使用了反向传播算法对神经网络进行训练,并对比了不同学习率、批量大小等参数对训练效果的影响。
4. 神经网络推理方法神经网络推理方法主要包括前向传播和后向传播。
在前向传播过程中,将输入数据通过神经网络进行处理,得到输出结果;在后向传播过程中,根据输出结果和实际标签,计算损失函数,并更新网络参数。
在实验中,我们实现了神经网络推理过程,并对比分析了不同激活函数对推理结果的影响。
5. 实验案例分析为了加深对神经网络的理解,我们选择了MNIST手写数字识别数据集进行实验。
通过设计不同的神经网络结构,使用反向传播算法进行训练,最终实现了对手写数字的识别。
四、实验结果与分析1. 不同神经网络结构对性能的影响在实验中,我们尝试了不同层级的神经网络结构,包括单层神经网络、多层神经网络等。
结果表明,多层神经网络在性能上优于单层神经网络,尤其是在复杂任务中,多层神经网络具有更好的表现。
BP人工神经网络试验报告一

BP⼈⼯神经⽹络试验报告⼀学号:北京⼯商⼤学⼈⼯神经⽹络实验报告实验⼀基于BP算法的XX及Matlab实现院(系)专业学⽣姓名成绩指导教师2011年10⽉⼀、实验⽬的:1、熟悉MATLAB 中神经⽹络⼯具箱的使⽤⽅法;2、了解BP 神经⽹络各种优化算法的原理;3、掌握BP 神经⽹络各种优化算法的特点;4、掌握使⽤BP 神经⽹络各种优化算法解决实际问题的⽅法。
⼆、实验内容:1 案例背景1.1 BP 神经⽹络概述BP 神经⽹络是⼀种多层前馈神经⽹络,该⽹络的主要特点是信号前向传递,误差反向传播。
在前向传递中,输⼊信号从输⼊层经隐含层逐层处理,直⾄输出层。
每⼀层的神经元状态只影响下⼀层神经元状态。
如果输出层得不到期望输出,则转⼊反向传播,根据预测误差调整⽹络权值和阈值,从⽽使BP 神经⽹络预测输出不断逼近期望输出。
BP 神经⽹络的拓扑结构如图1.1所⽰。
图1.1 BP 神经⽹络拓扑结构图图1.1中1x ,2x , ……n x 是BP 神经⽹络的输⼊值1y ,2y , ……n y 是BP 神经的预测值,ij ω和jk ω为BP 神经⽹络权值。
从图1.1可以看出,BP 神经⽹络可以看成⼀个⾮线性函数,⽹络输⼊值和预测值分别为该函数的⾃变量和因变量。
当输⼊节点数为n ,输出节点数为m 时,BP 神经⽹络就表达了从n 个⾃变量到m 个因变量的函数映射关系。
BP 神经⽹络预测前⾸先要训练⽹络,通过训练使⽹络具有联想记忆和预测能⼒。
BP 神经⽹络的训练过程包括以下⼏个步骤。
步骤1:⽹络初始化。
根据系统输⼊输出序列()y x ,确定⽹络输⼊层节点数n 、隐含层节点数l ,输出层节点数m ,初始化输⼊层、隐含层和输出层神经元之间的连接权值ij ω和式中, l 为隐含层节点数; f 为隐含层激励函数,该函数有多种表达形式,本章所选函数为:步骤3:输出层输出计算。
根据隐含层输出H ,连接权值jk ω和阈值b ,计算BP 神经⽹络预测输出O 。
神经网络实验报告

一、实验目的本次实验旨在了解神经网络的基本原理,掌握神经网络的构建、训练和测试方法,并通过实验验证神经网络在实际问题中的应用效果。
二、实验内容1. 神经网络基本原理(1)神经元模型:神经元是神经网络的基本单元,它通过接收输入信号、计算加权求和、应用激活函数等方式输出信号。
(2)前向传播:在神经网络中,输入信号通过神经元逐层传递,每层神经元将前一层输出的信号作为输入,并计算输出。
(3)反向传播:在训练过程中,神经网络通过反向传播算法不断调整各层神经元的权重和偏置,以最小化预测值与真实值之间的误差。
2. 神经网络构建(1)确定网络结构:根据实际问题选择合适的网络结构,包括输入层、隐含层和输出层的神经元个数。
(2)初始化参数:随机初始化各层神经元的权重和偏置。
3. 神经网络训练(1)选择损失函数:常用的损失函数有均方误差(MSE)和交叉熵(CE)等。
(2)选择优化算法:常用的优化算法有梯度下降、Adam、SGD等。
(3)训练过程:将训练数据分为训练集和验证集,通过反向传播算法不断调整网络参数,使预测值与真实值之间的误差最小化。
4. 神经网络测试(1)选择测试集:从未参与训练的数据中选取一部分作为测试集。
(2)测试过程:将测试数据输入网络,计算预测值与真实值之间的误差,评估网络性能。
三、实验步骤1. 数据准备:收集实验所需数据,并进行预处理。
2. 神经网络构建:根据实际问题确定网络结构,初始化参数。
3. 神经网络训练:选择损失函数和优化算法,对网络进行训练。
4. 神经网络测试:将测试数据输入网络,计算预测值与真实值之间的误差,评估网络性能。
四、实验结果与分析1. 实验结果(1)损失函数曲线:观察损失函数随训练轮数的变化趋势,分析网络训练效果。
(2)测试集误差:计算测试集的预测误差,评估网络性能。
2. 结果分析(1)损失函数曲线:从损失函数曲线可以看出,随着训练轮数的增加,损失函数逐渐减小,说明网络训练效果较好。
基于人工神经网络模型的物理实验数据分析

基于人工神经网络模型的物理实验数据分析随着计算机技术的日益发展,人工智能技术在各个领域中得以应用,其中人工神经网络模型是一种被广泛研究和应用的算法。
在物理实验数据分析方面,人工神经网络模型也具有很大的潜力。
本文将探讨基于人工神经网络模型的物理实验数据分析方法,并着重介绍其在晶体生长和物理力学等领域中的应用。
一、人工神经网络模型简介人工神经网络模型是一种通过学习和仿真生物神经网络的行为和特性而设计的计算机算法。
它的结构类似于生物神经网络,由一组节点和连接它们的边组成,每个节点代表一个神经元,每个边代表神经元之间的连接。
人工神经网络利用反向传播算法不断调整节点之间连接的权值,从而实现模型的训练和学习。
在模型训练和学习完成后,人工神经网络可以应用于不同的领域,例如物理实验数据分析。
二、晶体生长领域中的人工神经网络模型应用晶体生长是一项重要的材料制备技术,在半导体、化学、生物等领域中都有着广泛的应用。
利用物理方法和化学方法可以获得不同形态和尺寸的晶体。
利用人工神经网络模型,可以对晶体生长过程中的数据进行分析和预测,从而提高晶体质量和生长效率。
晶体生长过程中,温度、浓度、污染物浓度等参数对晶体质量有着重要的影响。
用传统的统计方法分析这些影响因素往往不够准确,而人工神经网络模型能够通过对实验数据的学习和训练,找到其背后的规律和模式。
例如,研究人员通过将晶体生长过程中的影响因素输入神经网络模型,建立了预测晶体质量的模型。
该模型能够准确预测晶体质量,并可以通过动态调整生长参数来优化生长过程。
三、物理力学领域中的人工神经网络模型应用物理力学是研究物体受力、运动和变形等现象的学科。
在物理力学领域中,人工神经网络模型也具有着很大的潜力,可以应用于分析材料的力学性能、预测材料的断裂点等。
例如,研究人员通过将不同应变条件下材料的应力应变曲线输入神经网络模型,建立了材料力学性质的模型。
该模型能够利用已知的实验数据准确预测材料的力学性能,并可以通过改变输入的应变条件来进一步优化材料的力学性能。
人工智能实验报告

人工智能实验报告一、引言人工智能(AI)已经成为当今科技领域的热门话题。
作为一种模拟人类智能的技术,它正在找到广泛的应用,从语音助手到无人驾驶汽车,从医疗诊断到金融分析。
本次实验旨在深入探索人工智能算法在图像分类方面的应用,通过搭建一个基于卷积神经网络(CNN)的图像分类系统,进一步了解人工智能的工作原理。
二、实验目的本次实验的主要目的是设计、实现并测试一个基于CNN的图像分类系统,并通过在不同数据集上的表现评估其性能。
通过这个实验,我们可以探索CNN在图像分类问题上的优势和限制,并深入了解与其相关的算法。
三、实验步骤1. 数据集准备:首先,我们需要准备一个用于图像分类的数据集。
为了让模型具有普适性,我们选择了包含多个类别和不同图像样本的数据集。
2. 数据预处理:在输入数据到CNN之前,我们需要对其进行预处理。
这包括图像缩放、灰度化、归一化等步骤,以确保输入数据的质量一致。
3. 搭建CNN模型:接下来,我们根据实验需求搭建一个合适的CNN模型。
这个模型可以包括多个卷积层、池化层和全连接层,用于提取图像特征并进行分类。
4. 训练模型:使用准备好的数据集,我们将模型进行训练。
这个过程需要迭代多次,通过优化算法不断调整模型参数,以实现更好的分类效果。
5. 模型性能评估:在训练完成后,我们需要使用一个独立的测试数据集对模型进行性能评估。
通过计算准确率、召回率等指标,可以了解模型的分类能力和泛化能力。
四、实验结果经过实验,我们得到了一个在图像分类问题上表现良好的CNN 模型。
在经过大规模的训练和调优后,该模型在测试数据集上达到了90%以上的准确率,表明其具备较好的泛化性能。
五、讨论与展望基于CNN的图像分类系统是目前人工智能领域的热门研究方向。
通过本次实验,我们深入了解了CNN模型的搭建和训练过程,并在一个具体的应用案例中应用之。
然而,我们也认识到了目前该系统仍存在着一些限制和挑战。
首先,CNN模型对于大规模数据集的需求较高,而且训练过程非常耗费时间和计算资源。
人工神经网络在化学反应预测中的应用

人工神经网络在化学反应预测中的应用人工神经网络(Artificial Neural Network,ANN)是一种由多个相互连接的节点(称为神经元)组成的计算模型,它们通过输入和输出之间的连接进行信息处理。
近年来,人工神经网络在化学反应预测中得到了广泛应用。
一、人工神经网络简介人工神经网络是一种模仿人脑神经系统的计算模型。
它由输入层、输出层和至少一个隐藏层组成。
每个神经元都有一些权值,这些权值会随机调整以改进其预测能力。
当输入信号经过网络时,每个神经元都会将其加权并传递到下一层。
最终,输出层将生成预测结果。
二、ANN在化学反应预测中的应用ANN可以用于预测化学反应的结果。
通过将反应物的性质作为输入,可以预测反应的产物和它们的量。
另外,ANN还可以利用大数据库,进行沉积物和水质的预测、显微镜下颗粒物形貌的分类与识别、有机物性质的预测以及发展Coag-floc过滤系统等。
三、ANN如何进行化学反应预测化学反应预测需要大量的反应数据作为输入。
在训练过程中,ANN会根据这些数据不断调整权值以最小化预测误差。
一旦训练完成,ANN就可以用于预测具有相似特征的未知反应。
四、人工神经网络的优点1. 易于识别和模拟人工神经网络的结构类似于人脑,因此它们对于复杂特征的识别和模拟很有优势。
这使得ANN在化学反应预测中十分有效。
2. 可以处理大量数据人工神经网络可以同时处理大量数据,这使得它们在学习和预测复杂化学反应时比传统方法要好。
3. 可以自我修正与传统的统计模型相比,人工神经网络可以自我修正。
这意味着它们可以在学习过程中不断改进,从而提高预测准确性。
五、人工神经网络的局限1. 易受局部最优解影响人工神经网络的优化方法通常涉及数个不同的局部最优解,选择的初始条件和算法可以对预测结果产生重要影响。
2. 对数据质量要求较高人工神经网络在化学反应预测中需要大量且高质量的数据作为输入。
这就要求我们对反应数据进行高质量的测量和收集。
人工神经网络的研究和应用

人工神经网络的研究和应用随着科技的不断发展,我们进入了一个智能化的时代,人工神经网络成为了人们讨论的重点。
人工神经网络是一种仿生学的技术手段,它能够模拟人类大脑的神经网络结构,实现像人类一样学习、决策和预测的功能。
本文将探讨人工神经网络的研究和应用。
一、人工神经网络的基本原理人工神经网络是由许多个“神经元”组成的,每个神经元接受多个输入信号,经过运算后输出一个结果。
简单的神经元通常由加权求和运算和一个阈值函数组成,它将输入信号与其对应的权重相乘并求和,再将结果输入到激活函数中,最后输出一个结果。
在人工神经网络中,我们将多组神经元组织成多层网络,每一层由若干个神经元组成。
每个神经元的输出将作为下一层神经元的输入,最终的输出结果将由输出层神经元组成。
二、人工神经网络的分类人工神经网络可以分为多种类型,如前馈神经网络、反馈神经网络、卷积神经网络等。
其中前馈神经网络是最为常见的一种,它没有反馈回路,信息只能从输入层到输出层流动。
反馈神经网络则允许信息沿着回路反向传播,这样神经网络就可以学习时间上的相关性,例如预测时间序列数据。
卷积神经网络是一种专门用来处理图像和视频数据的神经网络。
它通过卷积核对图像进行卷积运算,提取出图像中的特征,并经过多层池化操作后进行分类或识别。
三、人工神经网络的应用人工神经网络在各个领域都有广泛的应用,例如:1. 语音识别语言识别是人工智能领域的一个重要应用方向,人工神经网络在语音识别上也有广泛的应用。
通过学习音频输入和其对应的文字标注,神经网络可以准确地识别不同人的发音,并将其转化为文字。
2. 图像识别人工神经网络可以对图像进行分类、识别和分割等操作,例如在自动驾驶汽车、医疗图像识别、安防监控等领域中都有广泛的应用。
3. 自然语言处理自然语言处理技术是人工智能领域的另一个研究热点,它涉及到文字自动翻译、情感分析、问答系统等多个方向。
人工神经网络可以通过学习大量的语言数据,对自然语言信息进行自动处理和解析。
人工智能实验报告

一、实验背景与目的随着信息技术的飞速发展,人工智能(Artificial Intelligence,AI)已经成为当前研究的热点领域。
为了深入了解AI的基本原理和应用,我们小组开展了本次实验,旨在通过实践操作,掌握AI的基本技术,提高对AI的理解和应用能力。
二、实验环境与工具1. 实验环境:Windows 10操作系统,Python 3.8.0,Jupyter Notebook。
2. 实验工具:Scikit-learn库、TensorFlow库、Keras库。
三、实验内容与步骤本次实验主要分为以下几个部分:1. 数据预处理:从公开数据集中获取实验数据,对数据进行清洗、去噪、归一化等预处理操作。
2. 机器学习算法:选择合适的机器学习算法,如决策树、支持向量机、神经网络等,对预处理后的数据进行训练和预测。
3. 模型评估:使用交叉验证等方法对模型进行评估,选择性能最佳的模型。
4. 结果分析与优化:分析模型的预测结果,针对存在的问题进行优化。
四、实验过程与结果1. 数据预处理我们从UCI机器学习库中获取了鸢尾花(Iris)数据集,该数据集包含150个样本,每个样本有4个特征,分别为花萼长度、花萼宽度、花瓣长度和花瓣宽度,以及对应的类别标签(Iris-setosa、Iris-versicolor、Iris-virginica)。
对数据进行预处理,包括:- 去除缺失值:删除含有缺失值的样本。
- 归一化:将特征值缩放到[0, 1]区间。
2. 机器学习算法选择以下机器学习算法进行实验:- 决策树(Decision Tree):使用Scikit-learn库中的DecisionTreeClassifier实现。
- 支持向量机(Support Vector Machine):使用Scikit-learn库中的SVC实现。
- 神经网络(Neural Network):使用TensorFlow和Keras库实现。
3. 模型评估使用交叉验证(5折)对模型进行评估,计算模型的准确率、召回率、F1值等指标。
人工智能实验报告-BP神经网络算法的简单实现

⼈⼯智能实验报告-BP神经⽹络算法的简单实现⼈⼯神经⽹络是⼀种模仿⼈脑结构及其功能的信息处理系统,能提⾼⼈们对信息处理的智能化⽔平。
它是⼀门新兴的边缘和交叉学科,它在理论、模型、算法等⽅⾯⽐起以前有了较⼤的发展,但⾄今⽆根本性的突破,还有很多空⽩点需要努⼒探索和研究。
1⼈⼯神经⽹络研究背景神经⽹络的研究包括神经⽹络基本理论、⽹络学习算法、⽹络模型以及⽹络应⽤等⽅⾯。
其中⽐较热门的⼀个课题就是神经⽹络学习算法的研究。
近年来⼰研究出许多与神经⽹络模型相对应的神经⽹络学习算法,这些算法⼤致可以分为三类:有监督学习、⽆监督学习和增强学习。
在理论上和实际应⽤中都⽐较成熟的算法有以下三种:(1) 误差反向传播算法(Back Propagation,简称BP 算法);(2) 模拟退⽕算法;(3) 竞争学习算法。
⽬前为⽌,在训练多层前向神经⽹络的算法中,BP 算法是最有影响的算法之⼀。
但这种算法存在不少缺点,诸如收敛速度⽐较慢,或者只求得了局部极⼩点等等。
因此,近年来,国外许多专家对⽹络算法进⾏深⼊研究,提出了许多改进的⽅法。
主要有:(1) 增加动量法:在⽹络权值的调整公式中增加⼀动量项,该动量项对某⼀时刻的调整起阻尼作⽤。
它可以在误差曲⾯出现骤然起伏时,减⼩振荡的趋势,提⾼⽹络训练速度;(2) ⾃适应调节学习率:在训练中⾃适应地改变学习率,使其该⼤时增⼤,该⼩时减⼩。
使⽤动态学习率,从⽽加快算法的收敛速度;(3) 引⼊陡度因⼦:为了提⾼BP 算法的收敛速度,在权值调整进⼊误差曲⾯的平坦区时,引⼊陡度因⼦,设法压缩神经元的净输⼊,使权值调整脱离平坦区。
此外,很多国内的学者也做了不少有关⽹络算法改进⽅⾯的研究,并把改进的算法运⽤到实际中,取得了⼀定的成果:(1) 王晓敏等提出了⼀种基于改进的差分进化算法,利⽤差分进化算法的全局寻优能⼒,能够快速地得到BP 神经⽹络的权值,提⾼算法的速度;(2) 董国君等提出了⼀种基于随机退⽕机制的竞争层神经⽹络学习算法,该算法将竞争层神经⽹络的串⾏迭代模式改为随机优化模式,通过采⽤退⽕技术避免⽹络收敛到能量函数的局部极⼩点,从⽽得到全局最优值;(3) 赵青提出⼀种分层遗传算法与BP 算法相结合的前馈神经⽹络学习算法。
人工智能实验报告范文

人工智能实验报告范文一、实验名称。
[具体的人工智能实验名称,例如:基于神经网络的图像识别实验]二、实验目的。
咱为啥要做这个实验呢?其实就是想搞清楚人工智能这神奇的玩意儿是咋在特定任务里大显神通的。
比如说这个实验,就是想看看神经网络这个超酷的技术能不能像人眼一样识别图像中的东西。
这就好比训练一个超级智能的小助手,让它一眼就能看出图片里是猫猫还是狗狗,或者是其他啥玩意儿。
这不仅能让我们深入了解人工智能的工作原理,说不定以后还能应用到好多超有趣的地方呢,像智能安防系统,一眼就能发现监控画面里的可疑人物或者物体;或者是在医疗影像识别里,帮助医生更快更准地发现病症。
三、实验环境。
1. 硬件环境。
咱用的电脑就像是这个实验的战场,配置还挺重要的呢。
我的这台电脑处理器是[具体型号],就像是大脑的核心部分,负责处理各种复杂的计算。
内存有[X]GB,这就好比是大脑的短期记忆空间,越大就能同时处理越多的数据。
显卡是[显卡型号],这可是在图像识别实验里的得力助手,就像专门负责图像相关计算的小专家。
2. 软件环境。
编程用的是Python,这可是人工智能领域的明星语言,简单又强大。
就像一把万能钥匙,可以打开很多人工智能算法的大门。
用到的深度学习框架是TensorFlow,这就像是一个装满各种工具和模型的大工具箱,里面有好多现成的函数和类,能让我们轻松搭建神经网络,就像搭积木一样简单又有趣。
四、实验原理。
神经网络这个概念听起来就很科幻,但其实理解起来也不是那么难啦。
想象一下,我们的大脑是由无数个神经元组成的,每个神经元都能接收和传递信息。
神经网络也是类似的,它由好多人工神经元组成,这些神经元分层排列,就像一个超级复杂的信息传递网络。
在图像识别里,我们把图像的数据输入到这个网络里,第一层的神经元会对图像的一些简单特征进行提取,比如说图像的边缘、颜色的深浅等。
然后这些特征会被传递到下一层神经元,下一层神经元再对这些特征进行组合和进一步处理,就像搭金字塔一样,一层一层地构建出对图像更高级、更复杂的理解,最后在输出层得出图像到底是什么东西的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告人工神经网络实验原理:利用线性回归和神经网络建模技术分析预测。
实验题目:利用给出的葡萄酒数据集,解释获得的分析结论。
library(plspm); data(wines); wines实验要求:1、探索认识意大利葡萄酒数据集,对葡萄酒数据预处理,将其随机划分为训练集和测试集,然后创建一个线性回归模型;2、利用neuralnet包拟合神经网络模型;3、评估两个模型的优劣,如果都不理想,提出你的改进思路。
分析报告:1、线性回归模型> rm(list=ls())> gc()used (Mb) gc trigger (Mb) max used (Mb)Ncells 250340 13.4 608394 32.5 408712 21.9Vcells 498334 3.9 8388608 64.0 1606736 12.3>library(plspm)>data(wines)>wines[c(1:5),]class alcohol malic.acid ash alcalinity magnesium phenols flavanoids1 1 14.23 1.71 2.43 15.6 127 2.80 3.062 1 13.20 1.78 2.14 11.2 100 2.65 2.763 1 13.16 2.36 2.67 18.6 101 2.80 3.244 1 14.37 1.95 2.50 16.8 113 3.85 3.495 1 13.24 2.59 2.87 21.0 118 2.80 2.69nofla.phen proantho col.intens hue diluted proline1 0.28 2.29 5.64 1.04 3.92 10652 0.26 1.28 4.38 1.05 3.40 10503 0.30 2.81 5.68 1.03 3.17 11854 0.24 2.18 7.80 0.86 3.45 14805 0.39 1.82 4.32 1.04 2.93 735> data <- wines> summary(wines)class alcohol malic.acid ashMin. :1.000 Min. :11.03 Min. :0.740 Min. :1.3601st Qu.:1.000 1st Qu.:12.36 1st Qu.:1.603 1st Qu.:2.210Median :2.000 Median :13.05 Median :1.865 Median :2.360Mean :1.938 Mean :13.00 Mean :2.336 Mean :2.3673rd Qu.:3.000 3rd Qu.:13.68 3rd Qu.:3.083 3rd Qu.:2.558Max. :3.000 Max. :14.83 Max. :5.800 Max. :3.230alcalinity magnesium phenols flavanoids Min. :10.60 Min. : 70.00 Min. :0.980 Min. :0.340 1st Qu.:17.20 1st Qu.: 88.00 1st Qu.:1.742 1st Qu.:1.205 Median :19.50 Median : 98.00 Median :2.355 Median :2.135 Mean :19.49 Mean : 99.74 Mean :2.295 Mean :2.029 3rd Qu.:21.50 3rd Qu.:107.00 3rd Qu.:2.800 3rd Qu.:2.875 Max. :30.00 Max. :162.00 Max. :3.880 Max. :5.080 nofla.phen proantho col.intens hue Min. :0.1300 Min. :0.410 Min. : 1.280 Min. :0.4800 1st Qu.:0.2700 1st Qu.:1.250 1st Qu.: 3.220 1st Qu.:0.7825 Median :0.3400 Median :1.555 Median : 4.690 Median :0.9650 Mean :0.3619 Mean :1.591 Mean : 5.058 Mean :0.9574 3rd Qu.:0.4375 3rd Qu.:1.950 3rd Qu.: 6.200 3rd Qu.:1.1200 Max. :0.6600 Max. :3.580 Max. :13.000 Max. :1.7100 diluted prolineMin. :1.270 Min. : 278.01st Qu.:1.938 1st Qu.: 500.5Median :2.780 Median : 673.5Mean :2.612 Mean : 746.93rd Qu.:3.170 3rd Qu.: 985.0Max. :4.000 Max. :1680.0Num Variable Description 解释1 class Type of wine 葡萄酒的种类2 alcohol Alcohol 醇3 malic.acid Malic acid 苹果酸4 ash Ash 灰5 alcalinity Alcalinity 碱度6 magnesium Magnesium 镁7 phenols Total phenols 酚类8 flavanoids Flavanoids 黄酮9 nofla.phen Nonflavanoid phenols 非黄烷类酚类10 proantho Proanthocyanins 花青素11 col.intens Color intensity 颜色强度12 hue Hue 色调13 diluted OD280/OD315 of diluted wines 稀释的葡萄酒14 proline Proline 脯氨酸> apply(data,2,function(x) sum(is.na(x)))class alcohol malic.acid ash alcalinity magnesium phenols 0 0 0 0 0 0 0 flavanoids nofla.phen proantho col.intens hue diluted proline 0 0 0 0 0 0 0> dim(wines)[1] 178 14> set.seed(2)> test=sample(1:nrow(wines),100)> wines.train<-wines[-test,]> wines.test<-wines[test,]> dim(wines.train);dim(wines.test)[1] 78 14[1] 100 14> lm.fit <- glm(alcohol~., data=wines.train)> summary(lm.fit)Call:glm(formula = alcohol ~ ., data = wines.train)Deviance Residuals:Min 1Q Median 3Q Max-0.98017 -0.31067 -0.00405 0.36184 1.23885Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 13.0661361 1.2664910 10.317 3.04e-15 ***class -0.4043994 0.2389115 -1.693 0.09538 .malic.acid 0.1612962 0.0730559 2.208 0.03085 *ash 0.2621448 0.3669235 0.714 0.47755alcalinity -0.0591380 0.0328684 -1.799 0.07670 .magnesium 0.0003567 0.0052733 0.068 0.94628phenols 0.1719659 0.2078450 0.827 0.41110flavanoids -0.1780915 0.1815817 -0.981 0.33039nofla.phen -0.4623220 0.7409499 -0.624 0.53487proantho -0.2402948 0.1449535 -1.658 0.10226col.intens 0.1580059 0.0447835 3.528 0.00078 ***hue 0.1226260 0.4205420 0.292 0.77154diluted -0.0889085 0.1967579 -0.452 0.65289proline 0.0008112 0.0003943 2.058 0.04371 *---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for gaussian family taken to be 0.2968956)Null deviance: 57.473 on 77 degrees of freedomResidual deviance: 19.001 on 64 degrees of freedomAIC: 141.2Number of Fisher Scoring iterations: 2> pr.lm <- predict(lm.fit,wines.test)> MSE.lm <- sum((pr.lm - wines.test$alcohol)^2)/nrow(wines.test)> print(MSE.lm)[1] 0.30436252、神经网络模型> maxs <- apply(wines, 2, max)> mins <- apply(wines, 2, min)> scaled <- as.data.frame(scale(wines, center = mins, scale = maxs - mins))> index <- sample(1:nrow(wines),round(0.75*nrow(wines)))> train_ <- scaled[index,]> test_ <- scaled[index,]> library(neuralnet)> n <- names(train_)> f <- as.formula(paste("alcohol~", paste(n[!n %in% "alcohol"], collapse = " + ")))> nn <- neuralnet(f,data=train_,hidden=c(5,3),linear.output=T)> plot(nn)>pr.nn <- compute(nn,test_[,1:13])>pr.nn__<-pr.nn$net.result*(max(test_$alcohol)-min(test_$alcohol))+mi n(test_$alcohol)>test.r1<-(test_$alcohol)*(max(test_$alcohol)-min(test_$alcohol))+min (test_$alcohol)> MSE.nn1 <- sum((test.r1 - pr.nn__)^2)/nrow(test_)> print(paste(MSE.lm,MSE.nn1))[1] "0.304362456679839 0.14726865189892"3、模型修正>par(mfrow=c(1,2))>plot(test_$alcohol,pr.nn__,col='red',main='Real vs predicted NN',pch=18,cex=0.7)>abline(0,1,lwd=2)>legend('bottomright',legend='NN',pch=18,col='red', bty='n')>plot(wines.test$alcohol,pr.lm,col='blue',main='Real vs predictedlm',pch=18, cex=0.7) >abline(0,1,lwd=2)>legend('bottomright',legend='LM',pch=18,col='blue', bty='n', cex=0.7)0.00.40.80.00.20.40.60.81.01.2Real vs predicted NNtest_$alcohol p r .n n __11.512.513.511.512.012.513.013.514.014.5Real vs predicted lmwines.test$alcoholp r .lm> par(mfrow=c(1,1))> plot(test_$alcohol,pr.nn__,col='red',main='Real vs predicted NN',pch=18,cex=0.7)> points(wines.test$alcohol,pr.lm,col='blue',pch=18,cex=0.7) > abline(0,1,lwd=2)>legend('bottomright',legend=c('NN','LM'),pch=18,col=c('red','blue'))> library(boot)> set.seed(200)> lm.fit <- glm(alcohol~.,data=data)> cv.glm(data,lm.fit,K=10)$delta[1][1] 0.3058061679>set.seed(450)>cv.error <- NULL>k <- 10>library(plyr)>pbar <- create_progress_bar('text')>pbar$init(k)>for(i in 1:k){index <- sample(1:nrow(data),round(0.9*nrow(data)))train.cv <- scaled[index,]test.cv <- scaled[-index,]nn <- neuralnet(f,data=train.cv,hidden=c(5,2),linear.output=T)pr.nn <- compute(nn,test.cv[,1:13])pr.nn__<-pr.nn$net.result*(max(test_$alcohol)-min(test_$alcohol))+min (test_$alcohol)test.cv.r <- (test.cv$alcohol)*(max(test.cv$alcohol)-min(test.cv$alcohol))+min(tes t.cv$alcohol)cv.error[i] <- sum((test.cv.r - pr.nn__)^2)/nrow(test.cv)pbar$step()}> mean(cv.error)[1] 0.06900470043> cv.error[1] 0.0791******* 0.10556665990 0.05904083258 0.0714******* 0.0992******* [6] 0.03239406600 0.04807466437 0.0999******* 0.0355******* 0.0596*******> par(mfrow=c(1,1))> par(mfrow=c(1,1))> boxplot(cv.error,xlab='MSE CV',col='cyan',+ border='blue',names='CV error (MSE)',+ main='CV error (MSE) for NN',horizontal=TRUE)0.040.060.080.10MSE CV> cv.error[i] [1] 0.0596547757。
