水文地质学课件 04地下水运动的基本规律
水文地质基础知识 ppt课件

空隙性
指岩石空隙的大小、多少、形状、分 布特点以及连通情况等。这些特性 对于地下水的埋藏、分布、运动有 重要的影响。
岩石中的空隙
松散岩层孔隙特点
孔隙率(度):一定体积岩石(包括孔隙)中孔隙体积所占的比例。
n Vn 100% V
影响松散岩层孔隙度的因素
“理想土”模型
颗粒排列方式和密实程度 颗粒大小和形状 分选程度 土壤结构(单粒、团粒结构) 其他因素:次生裂隙、根孔、虫孔等
裂隙
成岩裂隙 构造裂隙 风化裂隙
裂隙性
裂隙的方向、宽度、延伸方向、充填情况等。 裂隙率
Kr Vr V
溶穴
发生在可溶性岩石之中 具有继承性 岩溶率(溶隙率)
岩石空隙的特性(均匀性、方向性、连通性)
松散岩类:空隙分布均匀、连通性好 基岩裂隙:不均匀、具方向性、不同方向裂隙可形成裂隙网
络 可溶岩溶隙:极不均匀、很强的方向性、容易形成各自的岩
溶水流系统。
按含水介质的地下水分类
层。
支持毛细带 中间带 土壤水带
水文地质学研究的重点是饱水带。但包气 带作为补给通道作用也不容忽视。
地下水赋存
含水层
定义:饱含水的透水层,或能够透过并给出相当数量水的岩 层。
辨异:饱含水的弱透水层(粘土、沿粘土等);不含水的透 水层(沙漠、被疏干的含水层等)
隔水层
定义:不透水的岩层,或不能透过并给出一定水量的岩层。 辨异:隔水层的相对性,并非完全隔水-弱透水层
下可以进行三种状态的相互转化 全球水文循环是闭合系统,局部为开放系统 水文循环过程伴随着能量的转换和其他物质的运移和聚集
地下水运动的基本规律

地下水运动的基本规律
因为流速V=Q/A,故达西定律也可以用式(56)来表达。 V=Ki(5-6) 式中,V为渗透流速(m/d或cm/s)。
由式(5-6)可知,K是水力坡度为1时的 渗透流速,称为渗透系数。渗透系数可以用来 比较不同岩石的透水性,是水文地质学中一个 非常重要的水文地质参数。
地下水运动的基本规律
地下水运动的基本规律
在满足生产要求和方便研究的前提下,可以不将含 水层概括为均质各向同性、均质各向异性、非均质各向 同性和非均质各向异性的含水层。所谓均质各向同性就 是指渗透系数在含水层的任何空间位置上、任何渗透方 向上均为一个常数;如不为常数则属非均质各向异性, 其余可类推。
对于渗透系数的测定,一般采用室内土柱试验(达 西试验)和野外抽水试验两种方法。一些松散岩石的渗 透系数参考值见表5-4,表见下页。
应该明确,渗透系数不仅取决于 岩石的空隙性质及水在空隙中的存在 形式,而且与地下水的一些物理性质 ,如黏滞性等有关。在具有同样空隙 的岩石中,当水力坡度相等时,黏滞 性大的水(或液体)渗透系数小。
一般情况下,当地下水的黏 滞性相近时可以不予考虑,但在 研究卤水时,不可忽视。因此, 除个别特殊情况外,可以把渗透 系数看作衡量岩石透水性能的参 数。岩石的透水性能在不同空间 位置和渗透方向上是不一致的, 即渗透系数是不相等的。
地下水运动的基本规律
工程地质Βιβλιοθήκη 工程地质地下水运动的基本规律
地下水在岩石空隙(孔隙、裂隙及溶穴) 中的运动称为渗流(渗透),地下水运动的 场所称为渗流场。渗流是在与介质发生密切 联系的条件下进行的,由于受到介质的阻滞, 地下水的运动远较地表水缓慢。
在岩层空隙中渗流时,水的质点有秩序 地、互不混杂地流动,称为层流运动。水的 质点无秩序地、互相混杂地流动,称为紊流 运动。一般认为渗流属于层流。
水文地质-地下水的运动
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
(2)抽水井流量与井径的关系
但实际情况远非如此,井径 对流量的影响比Dupuit公 式反映的关系要大得多。
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
(3)水跃对裘布依公式计算结果的影响
在潜水的出口处一般都存 在渗出面。当潜水流入井 中时也存在渗出面,也称水 跃,即井壁水位hs高于井 中水位hw(图4一10),而潜 水井的Dupuit公式并没有 考虑渗出面的存在。
H Z p
图4-5 流网示意图
在渗流场中,把水头值相等的点连成线或面就构成了等水 头线或等水头面。
流网是由等水头线和流线所组成的正交网格。流网直观地 描述了渗流场(或流速场)的特征。它可以是正方形、长 方形或曲边方形。
第二节 地下水运动规律
水流类型
一维流任意点的水力坡度均相等(
图4-6a);
s1=1.00 m s2=1.75 m s3=2.50 m 求K?
Q1=4500 m3/d; Q2=7850 m3/d; Q3=11250 m3/d;
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
1、承压水非完整井 当α=1时,A=0,就变成 完整井公式,当α很小, A值很大,则公式变为:
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
2、潜水非完整井 潜水非完整井可以看做上段 是潜水完整井,下段是承压 水非完整井。这样可以近似 的看做总流量Q等于两段Q1 和Q2的和。
第三节 地下水向井的稳定运动
裘布衣假设:
天然水力坡度为0,井附近水力坡度<1/4; 含水层是均质各向同性的,含水层的底板
地下水运动的基本规律

断面的水头,水头差为h;两断面相距L; (5)下端出口测定流量为Q。
0
0
图4-1 达西实验装置图
5.4.1.2 实验成果
Q KA h KAI L
Q AV
V KI
5.4.2 达西公式中各项的物理意义
5.4.2.1 渗透流速(V) >>在达西定律表达公式中,渗透流速是一个宏观概念,并且
它很容易测量。 >>因此,必须把它与单个水质点在砂粒中寻路而曲折前进的
地下水迹线示意图
5.1.2.3 二者区别
流线和迹线都是流场中的一簇曲线,都与流 体的运动有关,但各自代表了不同的概念:
>>流线反映的是某时刻流体的流速向量,迹线 是反映流体中某一质点不同时间走过的轨迹;
>>因此流线可看作水质点运动的摄影,迹线则 可看作对水质点运动所拍摄的电影。
5.1.3 过水断面与流量
5.4 地下水运动的基本规律
5.4.1 达西定律
达西定律是法国水利学家H.Darcy通过大量的实验,得到的线 性渗透定律。
5断面面积A;
(2)上游置一个稳定的溢水装置→保持稳定
水头;
(3)实验上端进水,下端出水→示意流线;
(4)圆筒中上、下断安装测压管→测定两个
>>稳定流条件下,流体的流线与迹线重合!
>>严格说来,自然界中的地下水都属于非稳定流,但是, 但为了便于分析和运算,也可以将某些运动要素变化微小的 渗流,近似地看作稳定流。
5.1.7 均匀流与非均匀流
>>均匀流——在实际水流中,如果流线是彼此平行的直线, 而且在同一流线上的点,其实际流速相等,即沿水流方向实 际流速的大小和方向皆不变。显然,在均匀流中,质点的时 变加速度和位变加速度都等于零。亦即流体在运动过程中, 其运动要素不随坐标位置而改变!
水文地质学第4章 地下水运动的基本规律改.ppt

u =Q/w′
渗透流速:假想水流通过单位过水断面的流量称
为渗透流速。
V=Q/ w
松散岩石孔隙中的水示意图
渗流必须满足下列条件:
1)通过任一断面的渗透流量等于通过该断 面的实际流量;
2)作用于任一面积的渗透压力或水头等于 作用于该面积的实际压力或水头;
3)渗透通过任一体积所受的阻力等于实际 水流通过该体积所受到的阻力。
2、达西定律的讨论与适用范围 1)达西定律的讨论
公式:V=K × I 反映通过任一断面一维流的
渗流速度与其水力坡度之间的关系式,这种关系的
微分表达式:V=-K×dh/dL,对于二维流和三维
流同样适用。
达西定律是在稳定运动条件下得到的,当地下 水为非稳定运动时,渗流中任一点处瞬时流速与水 力坡度之间的关系仍可用上面关系表征,只是渗透 流速和水力坡度随时间在变化。
(1)渗透流速: 根据水力学流速与流量的关系,上式可转化:
与(2)式比较
Q = W ·V
V = K·I
(3)
称为渗透流速(seepage velocity \Darcy velocity \specific discharge)
上式为单位面积上的流量——称比流量。 由此看出,达西定律中: 渗透流速与水力梯度的一次方成正比,故达西定律又称为线性渗透定律
水力梯度:渗流通过A点单位渗流途径长度
上的水头损失称为水力坡度。
I = dH/dL 或 I =(H1-H2)/ L
水 力 梯 度 示 意 图
3、流线、迹线、等水头线和流网: 流线:同一时间内不同液流质点的连线,这 根连线上的各液流质点速度矢量都与这根连 线相切。 迹线:某一液流质点在某一时间段内的运动 轨迹。 等水头线:水头值相等点的连线。
水文地质第四章1

3、当抽水井是建在无充分就地补给(无定 水头)广阔分布的含水层之中。若观测孔中 的s值在s-lgr曲线上能连成直线,则可根据 观测井的数据用裘布依型公式来计算含水层 的渗透系数
4、在取水量远小于补给量的地区,可以先 用上述方法求得含水层的渗透系数,然后 再用裘布依公式大致推测在不同取水量的 情况下境内及附近的地下水位降值
只有当雷诺数小于1~10时地下水运动才服 从达西公式。 大多情况下地下水的雷诺数一般不超过1; 例如,地下水以u=10m/d的流速在粒径为 20mm的卵石层中运动,卵石间的孔隙直径 为3mm(0.003m),当地下水温为15℃时, 运动粘滞系数γ=0.1m2/d,则雷诺数为?
(二)非线性渗透定律
当地下水在岩石的大孔隙,大裂隙,大溶洞中及取 水构筑物附近流动时,Re>10,紊流。 紊流运动的规律称为谢才公式(哲才公式)
D、地下水径流从水位高处向低处流动
达西定律要满足条件为( ) A、地下水流的雷诺数Re<1~10 B、地下水流的雷诺数1~10<Re<20~60 C、地下水流的雷诺数Re>20~60 D、地下水流的雷诺数可以为任何值
一潜水含水层均质,各向同性,渗透系数 为15m/d,其中某过水断面A的面积为 100m2,水位为38m,距离A断面100米的 断面B的水位为36m,则断面A的日过流量 是( )m3
裘布依公式推导的假设条件
1、水力坡度:天然水力坡度等于零,抽水时为了 用流线倾角的正切代替正弦,则井附近的水力坡 度不大于1/4。 2、含水层是均质各向同性的,含水层的底板是隔 水的。 3、边界条件:抽水时影响半径的范围内无入渗, 无蒸发,每个过水断面上流量不变;在影响半径 范围以外的地方流量为零;在影响半径的圆周上 为定水头边界。 4、抽水井内及附近都是二维流(即抽水井内不同 深度处的水头降低是相同的。
水文地质学基础 第四章 地下水运动的基本规律.
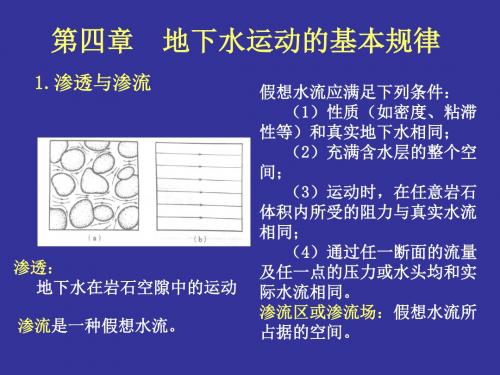
1.渗透与渗流
渗透: 地下水在岩石空隙中的运动
渗流是一种假想水流。
假想水流应满足下列条件: (1)性质(如密度、粘滞
性等)和真实地下水相同; (2)充满含水层的整个空
间; (3)运动时,在任意岩石
体积内所受的阻力与真实水流 相同;
(4)通过任一断面的流量 及任一点的压力或水头均和实 际水流相同。 渗流区或渗流场:假想水流所 占据的空间。
• 流线:是渗流场中某一瞬时的一条线,线上各水 质点在此瞬时的流向均与此线相切。
• 迹线:则是对水质点运动所拍的电影。在稳定流 条件下,流线与迹线重合。
一、均质各向同,流线与等水头线构成 正交网格。 • 分析均质各向同性介质中的稳定流网。 • 徒手绘制定性流网
地下水的运动绝大多数服从Darcy定律。
二、非线性渗透定律—哲才(Chezy)定律
地下水在较大的空隙中运动且流速较大时,呈紊 流运动,此时的渗流服从哲才定律。有:
1
Q KI 2
1
V KI 2
即此时渗透流速V与水力梯度I的1/2次方成正比.
4.2 流 网
• 流网:在渗流场的某一典型剖面或切面上,由一 系列等水头线与流线组成的网格.
2.层流和紊流
层流运动:水质点作有秩序的、互不混杂的流动. 紊流运动:水质点无秩序的、互相混杂的流动.
地下水在岩石空隙中的运动速度一般较慢,大多为层流 运动。只有在大裂隙、溶洞中地下水流速大,才可能出现紊 流运动。此外,在抽水井附近小范围内,当降深很大时,流 速增大,也可出现紊流现象。
3. 稳定流和非稳定流
实际流速,ω有:
Q Kw h KwI Vw L
Q= ω/·u= ω·ne·u=
4.水文地质学基础-地下水的基本运动规律

4.1 重力水运动的基本规律
渗透系数(K)的影响因素:
d0 —— 孔隙直径;γ——水的重率;μ——动力粘滞系数
K与岩石空隙性质、水的某些物理性质有关。
(1)孔隙直径大则渗透性强,取决于最小孔隙直径。 (2)圆管通道:形状弯曲而变化时,渗透性较差。 (3)颗粒分选性:比对孔隙度的影响要大。 (4)水的物理性质:粘滞性大的液体K<粘滞性小的液体
4.1 重力水运动的基本规律
4.1.4渗透系数 渗透系数(K)是水力梯度等于1时的渗透流速,单位:m/d,cm/s. 关系: V = K I 1)I为定值时,K大,V大;K小,V小(V=KI); 2)V为定值时,K大,I小等水位线疏;K小,I大等水位线密。 渗透系数可定量说明岩石的渗透性:K大→渗透性强;K小→渗 透性弱。
Q K ω I K M 1 I H H H H b a b K a 2 L K 2 2 Ha H b 2L
4.2 流 网
流线(flow line, stream line)是渗流场中某一瞬时的一条 线,线上各个水质点在此时刻的流向均与此线相切。 迹线(path line)是渗流场中某一时间段内某一水质点的运动 轨迹。
h1 0
K
M
h2
0’ L
dh dx 单宽流量为: v K dh dh q v K M 1 KM dx dx
qdx KMdh
L
0
qdx KMdh
h1 L h2 0 h1
h2
分离变量并积分:
q dx KM dh h1 h2 q KM KMI L
0 h1 L h2
h1 h2 h1 h2 qK KM I 2 L
第4章 地下水的运动5--3

非稳定流:在渗流场内,水质点的运动要素随时间而变化的 水流运动。与空间、时间有关的函数。
缓变流动:在天然条件下地下水流一般都呈缓变流动,流线 弯曲度很小,近似于一条直线。
二、地下水运动的基本规律
h I J 水力梯度 L
hydraulic gradient
( 2)
Q = K Iω
Company Logo
马氏瓶 测压板 排水装置
测压管
试样筒
水力梯度(I) 从达西公式: V = KI 来看: 当I 增大时,V 也愈大; 即流速V 愈大,单位渗流途径上损失的能量也愈大; 反过来,水力梯度I愈大时,驱动水流运动与速度 也愈大 注意:水头损失一定要与渗流途径相对应
渗流运动取决于空隙大小、形状、连通性。
一、地下水运动的特点
曲折复杂的水流通道;
是缓慢的流速, 层流和紊流; 非稳定的、缓变运动。
层流:在岩石空隙中渗流时,水的质点作有秩序、 平行而互不混杂的流动。
层流示意图
紊流示意图
紊流:在岩石空隙中渗流时,水的质点作无 秩序、互相混杂、互相碰撞的流动。
稳定流与非稳定流
达西公式微分形式
dH vK dx dH Q KA dx
dx dH
沿水流方向无穷小的距离 相应dx水流微分段上的水头损失
渗透系数
渗透系数 K
重要的水文地质参数,它表征岩石对某种流体的渗透 能力。
也称为水力传导率
定义:水力梯度为 I =1 时的渗透流速 (V=KI)
具有速度量纲 L T-1 由公式V = K I 分析 当I一定时,岩层的 K 愈大,则 V 也愈大, Q 大
第四章 地下水运动规律

有效孔隙度 ne:重力水流动的空隙体积(不包括结合水占据
的空间)与岩石体积之比。 ne>μ
既然ω不是实际的过水断面,可知V也并非真实的流速,而是
假设水流通过包括颗粒骨架与空隙在内的整个断面( ω )。 因此,渗透流速是一种虚拟流速。
渗透流速与实际流速:令通过实际过水断面ω’ 的流速为实际
2 d 0 ne 32
K与液体的物理性质有关,与液 体的容重γ成正比,与动力粘滞系 数μ成反比;在研究卤水或热水的 运动时需要考虑液体物理性质的 差异。 K与岩石的空隙性质有关,与空 隙大小( d02)成2次方、与空隙 多少( ne )成一次方正比关系。
2013-9-7
12
表4-1
2013-9-7 19
2013-9-7
图4—3 等水头线、流线与各类边界的关系 1—含水层;2—隔水层;3—潜水面;4—等水头线;5—流线; 6—河渠水面;7—降水入渗
20
b. 绘制步骤(参见河间地块流网图P40,图4-4):
寻找已知边界(湿周,隔水边界,水位线);
分水线、源、汇的确定;流线总是由源指向汇;
地下水在多孔介质的细小空隙中流动,水流很慢——渗流,
多为层流(除在宽大空隙中,如岩溶管道、宽大裂隙)。
2013-9-7 2
第4章
地下水运动的基本规律
层流:水质点有秩序的、互不混杂的流动。
紊流:水质点无秩序地、相互混杂的流动。
稳定流与非稳定流:若流场中所有空间点上一切运 动要素(水位、流速、流向)都不随时间改变时, 称为稳定流。否则称为非稳定流。 水头:水流中空间上某点所具有的总势能。根据水 动力学原理,水流运动中任意点总水头(总势能) 可表示为:
地下水运动的基本规律54页PPT

1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
水文地质学基础ppt课件

3.2.2 概念的相对性
定义中的模糊概念—“相当水量,微不足道,较大水力梯度”等
严格的“是与非”的逻辑思维,在很多情况下是相对的和模糊 的概念相对性的意义:
从实际应用角度来看划分的相对性——相当水量
满足需要就可以了。如在某处一口井出水量80m3/d,作为1万人的
供水,非含水层;作为饮料厂、装瓶生产则为含水层。又如一个小 泉水流量0.11/s≈8.6m3/d,大厂——非,村用——是。
地下水污染地下水污染地下水污染主要分布在城区附近和地表水污染严重的地区地下水污染主要分布在城区附近和地表水污染严重的地区心脑血管病是世界卫生组织总干事讲过只要采取预防措施就能减少一半的死亡也就是说一半的死亡完全是可以预防的1012020自然界的水循环自然界的水循环心脑血管病是世界卫生组织总干事讲过只要采取预防措施就能减少一半的死亡也就是说一半的死亡完全是可以预防的1012020自然界的水循环自然界的水循环心脑血管病是世界卫生组织总干事讲过只要采取预防措施就能减少一半的死亡也就是说一半的死亡完全是可以预防的1012020第二章岩土中的空隙和水a分选好的高孔隙度沉积b分选差的低孔隙度沉积c分选好的高孔隙度卵石沉积d分选好的矿物充填沉积e岩体溶解空隙f岩体裂隙21岩土中的空隙孔隙度是指某一体积岩石包括孔隙在内中孔隙体积所占的比例心脑血管病是世界卫生组织总干事讲过只要采取预防措施就能减少一半的死亡也就是说一半的死亡完全是可以预防的1012020心脑血管病是世界卫生组织总干事讲过只要采取预防措施就能减少一半的死亡也就是说一半的死亡完全是可以预防的1012020裂隙
全国60%的耕地 全部或部分使用地下水灌 溉
全国95%以上的农 村饮用地下水
95%
Company Logo
8
农村饮用地下水 饮用其它水
《水文地质》课件

● 06
第六章 总结与展望
水文地质的基本 概念
水文地质是研究地下水运动规律和地下水与地质环境关系 的学科,通过对地下水系统的深入了解,可以更好地应用 于环境保护和工程建设中。地下水的开发利用也是未来的 重要方向。
地下水运动规律
地下水循环
描述地下水在地球 中的循环方式
地下水排泄
解释地下水的排泄 方式
01 矿区地下水的运动规律
地下水在矿区中的流动特点
02 矿产开采影响
矿产开采对地下水资源的影响
03
矿产开采对地下水的影 响
矿产开采活动可能导致矿区地下水位下降,地下水紧缺,地 下水质污染等问题。矿产开采对周边环境和生态系统的影响 较大,需要进行科学评估和合理控制,以保护地下水资源的 可持续利用。
学习方法
结合理论与实 践
多进行案例分析
加强动手能力
多进行田野调查和 实验
评估方式
课堂测验
考察学生对课程内容的掌握程 度
作业与实验报告
加强学生的实践能力和独立思 考能力
参考书目
《水文地质学》
深入了解水文地质 领域的理论知识
《水文地质与 水文地质工程》
应用水文地质知识 解决实际工程问题
● 02
第2章 地下水的形成与分布
● 04
第4章 地下水与地质环境
岩溶地质特点
岩溶地质是一种特殊的地质构造,其特点包括岩溶溶蚀作用 强烈、地下水流动通道复杂等。岩溶地质景观丰富多样,例 如溶洞、溶岩地貌等,对地下水运动有重要影响。
岩溶地下水运动规律
溶蚀作用影响
溶蚀作用形成的裂 隙是地下水流动通
道
水文特性
地下水水位波动大, 水质多变
能够运用水文地质知识解决实际问题
第五章地下水运动基本规律

地下水运动的本质
VKIK•H1H2 L
L
HH1H2
V• K
H:势能 V:流速(动能)
由此可以看出,地下水的运动是由势能转化为地下水 流动的动能的过程,也即符合质量/能量守衡定律的基本 物理定律。
第五章地下水运动基本规律
地下水运动本质:也即,由势能转化为地下水流动的过程, 符合质量,能量守衡定律。
1)ne<n;
2)一般重力释水时,空隙中有结合水、毛细水,所以 <ne;
3)对于粘性土,空隙细小、结合水所占的比例大,所以ne很小,尽管n很 大;
4)对于空隙大的岩层(如大的溶隙、裂隙),ne≈ ≈n。
∵ 由于ω不是实际过水断面,
∴ V不是真实流速(假设水流通过骨架与空隙在内的流速),虚拟流速–––
对于井半径也可用公式求得 合理的井半径。半径和抽水量成 正相关,半径增加10培,水量增 加40%左右。
第五章地下水运动基本规律
影响半径
齐姆(法国)提出了影响半径的概念,最早称补给半径。后改为引 用半径,然后提出为影响半径。即超过影响半径后水位不发生变 化。
1)稳定井流(经验公式) (1)潜水井的库萨金公式
实验中过水断面ω
1)颗粒––––无水通过; 2)孔隙––––有水通过。
水流实际流过的面积(扣除结合水)––––实际过水断面ω’: ω’=ωne (ne<n) 有效孔隙度(ne)––––为重力水流动的孔隙体积(不包括结合水占 据的空间)与岩石体积之比。(对重力水的运动有效)
第五章地下水运动基本规律
关于有效孔隙度ne:
第五章 地下水运动的基本规律
第五章地下水运动基本规律
5.1 重力水运动的基本规律 5.2 达西定律的应用 5.3 流网 5.4 饱水粘土中水的运动规律
地质大水文地质学基础讲义04地下水运动的基本规律

第四章 地下水在岩石空隙中的运动称为渗流(渗透)。
发生渗流的区域称为渗流场。
由于受到地下水运动的基本规律 介质的阻滞,地下水的流动远较地表水为缓慢。
在岩层空隙中渗流时,水的质点作有秩序的、互不混杂的流动,称作层流运动。
在具狭小空隙的岩石(如砂、裂隙不很宽大的基岩)中流动时,重力水受介质的吸引力较大,水的质点排列较有秩序,故均作层流运动。
水的质点无秩序地、互相混杂的流动,称为紊流运动。
作紊流动时,水流所受阻力比层流状态大,消耗的能量较多。
在宽大的空隙中(大的溶穴、宽大裂隙),水的流速较大时,容易呈紊流运动。
水只在渗流场内运动,各个运动要素(水位、流速、流向等)不随时间改变时,称作稳定流。
运动要素随时间变化的水流运动,称作非稳定流。
严格地讲,自然界中地下水都属于非稳定流。
但是,为了便于分析和运算,也可以将某些运动要素变化微小的渗流,近似地看作稳定流。
4.1 重力水运动的基本规律4.1.1 达西定律1856年,法国水力学家达西(H. Darcy )通过大量的实验,得到线性渗透定律。
实验是在装有砂的圆筒中进行的(图4—1)。
水由筒的上端加入,流经砂柱,由下端流出。
上游用溢水设备控制水位,使实验过程中水头始终保持不变。
在圆筒的上下端各设一根测压管,分别测定上下两个过水断面的水头。
下端出口处设管嘴以测定流量。
根据实验结果,得到下列关系式:I K Lh K Q ωω== (4—1) 式中:Q ——渗透流量(出口处流量,即为通过砂柱各断面的流量); ω——过水断面(在实验中相当于砂柱横断面积);h ——水头损失(12h H H =−,即上下游过水断面的水头差);L ——渗透途径(上下游过水断面的距离); I ——水力梯度(相当于h /L ,即水头差除以渗透途径);K ——渗透系数。
此即达西公式。
从水力学已知,通过某一断面的流量Q 等于流速V 与过水断面ω的乘积,即:Q V ω= (4—2)即/V Q ω=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
普通水流的流向是从总水头高的地方流向总水头低的地方 水流量的大小取决于水头差和水头损失 地下水水的流向也是从高水头流向低水头 流量的大小也取决于水头差和水头损失 普通水流在管道中运动取决于管道大小、形状及管壁的粗糙度 渗流运动取决于多孔介质空隙大小、形状以及其连通性
第四章 地下水运动的基本规律
4.1.4 渗透系数(K)
第四章 地下水运动的基本规律
4.1.4 渗透系数(K)
K
V I
渗透系数可定量说明岩石的渗透性能。 渗透系数愈大,岩石的透水能力愈强。
水流在岩石空隙中运动,需要克服隙壁与水及水质点 之间的摩擦阻力;
所以:渗透系数不仅与岩石的空隙性质有关,还与 水的某些物理性质有关。(水和石油)
C)渗流场任意一点的水头H和流速矢量V等运动要素 与实际水流在该点周围一个小范围内的平均值相等。
第四章 地下水运动的基本规律
3)渗流的微观分析——各种流速的比较
第四章 地下水运动的基本规律
4.1.6 达西定律的适用范围
雷诺数是指流体流动时的惯性力Fe和和粘性力F之比,
用Re表示,即:
Re
ul
ρ 为流体密度; u 为流体流速; μ 为流体动力粘性系数; l 为过流断面有效长度。
⑤稳定流:水在渗流 场内运动,各个运动 要素(水位、流速、 流向等)不随时间改 变时,称作稳定流
第四章 地下水运动的基本规律
⑥非稳定流:运动要素随时间 变化的水流运动,称作非稳定 流
第四章 地下水运动的基本规律
4.1 重力水运动的基本规律
4.1.1 达西定律—线性渗透定律
Q
KA
h L
KAI
Q V A
第四章 地下水运动的基本规律
结合水的运动规律: 曲线通过原点,说明只要施加微小的水力梯度,
结合水就会流动,但此时的渗透流速 V 十分微小。随 着 I 加大,曲线斜率(表征渗透系数 K )逐渐增大, 然后趋于定值。
结合水:
非牛顿流体,性质介于固体与液体之间的异常液体, 外力必须克服其抗剪强度才能流动。
有的学者主张用临界流速Vcr来划分这一界限,并认为 Vcr=0.3~0.5cm/s。
当V>Vcr后,达西定律可修改为:V=KIm(m<1)。
第四章 地下水运动的基本规律
4.1.6 达西定律的适用范围
纯砾以上的很粗的土中 V-I关系曲线
粘性很强的致密粘土中 V-I关系曲线
第四章 地下水运动的基本规律
例如:在狭小空隙(如砂,砂土)中流动时,重力水 受介质的吸引力较大,水的质点排列较有秩序,可以认为 是层流运动。
④紊流运动:水的质点无秩序的、互相混杂的流动,称作 紊流运动
第四章 地下水运动的基本规律
第四章 地下水运动的基本规律
第四章 地下水运动的基本规律
第四章 地下水运动的基本规律
4.0 几个概念
第四章 地下水运动的基本规律
h
L
h
L
第四章 地下水运动的基本规律
如图,上方不断滴水,使砂柱顶端经常保持一极薄的水
层。已知渗透流量 Q 和过水断面面积ω,求渗透系数 K ,
并在图上标明达西公式相应的项。
Q
K
h L
KI
K
Q
1 I
Q
L h
第四章 地下水运动的基本规律
第四章 地下水运动的基本规律
4.1.2 渗透流速(V)
设有粘滞性不同的两种液体在同一岩石中运动。则 粘滞性大的液体渗透系数就会小于粘滞性小的液体。
在研究卤水、热水的运动时,就要考虑液体粘滞性
第三章 地下水的赋存
②确定潜水面的水面坡度 水面坡度:相邻两条等水位线的水位差除以其水平距离 水力梯度:沿渗透途径水头损失与相应渗透途径长度的比值
当潜水面坡度不大时,潜水面坡度可视为潜水水力梯度
砂柱的横断面积,包括砂颗粒所占据的面积及空隙所占据的面积 扣除结合水所占据的范围以外的水流实际流过的空隙面积
ne ne ——有效空隙度
第四章 地下水运动的基本规律
n ne
空间(孔隙度)
n
重力水所占据的空间——给水 度
毛细水所占据的空间
结合水所占据的空间
有
效 孔
ne
隙
度
对于粘性土,由于空隙细小,结合水所占比例大,所以 有效孔隙度很小。
本
4.3.0 岩层透水特征分类
规
4.3.1 均匀各向同性介质中的流网(信手流网的绘制)
律
4.3.2 层状非均质介质中的流网
第四章 地下水运动的基本规律
4.0 几个概念
①渗流:地下水在岩石空隙中的运动称为渗流 ②渗流场:发生渗流的区域称为渗流场
③层流运动:在岩层空隙中渗流时,水的质点做有秩序 的,互不混杂的流动,称作层流运动
第四章 地下水运动的基本规律
4.1.6 达西定律的适用范围
1<Re<10,层流,适用,地下水低速运动,粘滞 力占优势;
10<Re<100,层流,不适用,地下水流速增大, 为过渡带,由粘滞力占优势的层流转变为以惯性 力占优势的层流运动;
Re>100,紊流,不适用。
达西定律是描述层流状态下渗透流速与水头损失关系的 规律,即渗流速度V与水力坡度I成线性关系只适用于层流范 围。在水利工程中,绝大多数渗流,无论是发生于砂土中或 一般的粘性土中,均属于层流范围,故达西定律均可适用。
第四章 地下水运动的基本规律
结合水的抗剪强度随着离颗粒表面距离的加大而降 低;
施加的水力梯度很小时,只有孔隙中心(距离颗粒 较远)抗剪强度较小的那部分结合水发生运动;
随着 I 增大,参与流动的结合水层厚度加大,即对 水流动有效的孔隙断面扩大。
因此,隐渗流阶段的 K 值是 I 的函数。
由于内层结合水的抗剪强度随着靠近颗粒表面而迅 速增大,当 I 进一步增大时,参与流动的结合水的厚度 没有明显扩大,此时,K 即趋于定值。
第四章 地下水运动的基本规律
4.1.4 渗透系数(K)
大风对田径比赛影响很大,田径比赛场地上风速超过 限制,所创造出的成绩将不被承认。
田径比赛规则上明文规定:距离200米和200米以下的 径赛以及跳远、三级跳远等项目,凡顺风时平均风速超过 每秒2米者,所创纪录不予承认。
国际业余田径联合会的规则规定,在田径比赛中,有 一部分项目要测定风速,主要有:100米、110米栏、200 米、跳远和三级跳远等项目。规则规定,当顺风风速超过 2米/秒时,比赛成绩只能用于决定当场比赛名次,而不能 作为比赛记录。
对于空隙大的岩层(例如溶穴发育的可溶岩,有宽大裂
隙的裂隙岩层), n n e
第二章 岩石中的空隙与水分
2.3.5 透水性——岩石允许水透过的能力
以松散岩石为例,分析一个理想孔隙通道中水的运动情况
第四章 地下水运动的基本规律
4.1.3 水力梯度(I)
水力梯度(I):沿渗透途径水头损失与相应渗透途径 长度的比值
水流通过单位长度渗透途径为克服摩擦阻力所耗失的 机械能
克服摩擦阻力使水以一定速度流动的驱动力
补充→液体(水)的粘滞性:液体具有易流动性,处 于静止状态时不能承受剪切力而抵抗剪切变形,但在运动 状态时,其内部会出现抵抗变形的特性。
液体在运动状态时抵抗剪切变形的性质称为液体的粘 滞性。
第四章 地下水运动的基本规律
=100分
=10分x10分 =10分/个x10个
=0.1元x0.1元 =0.1元/个x10个
=0.01元
=0.01元/个×100个
=1分
第四章 地下水运动的基本规律
第四章 地下水运动的基本规律
4.2 饱水粘性土中水(结合水)的运动规律
①V—I关系为通过原点的直线,服从达西定律 ②V—I曲线不通过原点,水力梯度小于某一值I0时无 渗透;大于I0时,起初为一向I轴凸出的曲线,然后转 为直线
第四章 地下水运动的基本规律
③V—I曲线通过原点,I小时曲线向I轴凸出,I大时为直线。
但以下两种情况可认为超出达西定律适用范围。
第四章 地下水运动的基本规律
4.1.6 达西定律的适用范围
一种情况是在纯砾以上的很粗的土中的渗流,且水力 坡降较大时,流态已不再是层流而是紊流。这时,达西定 律不再适用,渗流速度V与水力坡降I之间的关系不再保持 直线而变为次线性的曲线关系,如图所示。
层流进入紊流的界限,即为达西定律适用的上限。
4.0 几个概念
第 四 章
4.1 重力水运动的基本规律
4.1.1 达西定律—线性渗透定律
4.1.2 渗透流速(V)
地 下 水
4.1.3 水力梯度(I) 4.1.4 渗透系数(K) 4.1.5 地下水渗流的思考、总结
运
4.1.6 达西定律的适用范围
动 4.2 饱水粘性土中水(结合水)的运动规律
的 基
4.3 流网
第四章 地下水运动的基本规律
4.3 流网——准备知识
H
Z
p
g
u2 2g
m
m
kg
N/ / m3
m2 m/
s2
(m / s)2 2m/ s2
m
m
kg m / kg / m3
s2 / m2 m/ s2
(m / s)2 2m/ s2
mmmm
第四章 地下水运动的基本规律
4.3 流网——准备知识
1元
=100分
(以此种情况居多)
说明:只要施加微小的水力梯度,结合水就会流动,但 此时的V十分微小;随着I加大,曲线斜率(K)逐渐增大,然 后趋于定值
较多的学者认为,粘性土(包括相当致密的粘土在内)中 的渗透,通常仍然服从达西定律。例如,奥尔逊曾用高岭土作 渗透试验,加压固结使高岭土孔隙度从58.8%降到22.5%,施 加水力梯度I =0.2~40,结果得出V - I 关系为一通过原点的直 线。他解释说,这是因为高岭土颗粒表面的结合水层厚度相当 于20~40 个水分子,仅占孔隙平均直径的2.5%~3.5%,所以 对渗透影响不大;对于颗粒极其细小的粘土,尤其是膨润土, 结合水则有可能占据全部或大部孔隙,从而呈现非达西渗透。
