倒立摆MATLAB建模
基于MATLAB的单级旋转倒立摆建模与控制仿真
基于MATLAB的单级旋转倒立摆建模与控制仿真一、分析课题,选择数据源外文数据库多种多样,对于工程应用所研究的课题,通常选取比较常用的数据库为:IEEE Xplore(/Xplore/home.jsp)、Google学术搜索(/)以及SpringerLink(/)。
二、选取检索词单级旋转倒立摆的英文名称为:single rotational inverted pendulum,故以此为检索词进行检索。
三、构造检索式Single (and)rotational inverted pendulum四、实施检索,调整检索策略由于搜索步骤较多,此处只详细给出使用IEEE Xplore数据库的检索过程,另外两个数据库提供大概检索过程及结果截图。
由于搜索结果只有9条,数量较少,故调整检索词,过程如下:Google学术搜索:SpringerLink数据库:五、检索结果1、题目:Analysis of human gait using an Inverted Pendulum Model基于倒立摆模型的人体步态分析Zhe Tang ; Meng Joo Er ; Chien, C.-J. Fuzzy Systems, 2008. FUZZ-IEEE 2008. (IEEE World Congress on Computational Intelligence). IEEE International Conference onAbstract: IPM(Inverted Pendulum Model) has been widely used for modeling of human motion gaits. There is a common condition in most of these models, the reaction force between the floor and the humanoid must go through the CoG (Center of Gravity) of the a humanoid or human being. However, the recent bio-mechanical studies show that there are angular moments around the CoG of a human being during human motion. In other words, the reaction force does not necessarily pass through the CoG. In this paper, the motion of IPM is analyzed by taking into consideration two kinds of rotational moments, namely around the pivot and around the CoG. The human motion has been decomposed into the sagittal plane and front plane in the double support phase and single support phase. The motions of the IPM in these four different phases are derived by solving four differential equations with boundary conditions. Simulation results show that a stable human gait is synthesized by using our proposed IPM.摘要:IPM(倒立摆模型)已被广泛用于人体运动步态建模。
直线二级倒立摆建模与matlab仿真LQR
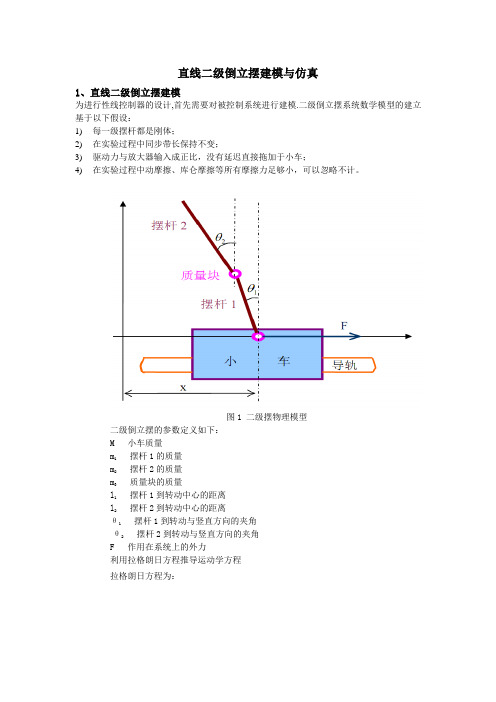
直线二级倒立摆建模与仿真1、直线二级倒立摆建模为进行性线控制器的设计,首先需要对被控制系统进行建模.二级倒立摆系统数学模型的建立基于以下假设:1)每一级摆杆都是刚体;2)在实验过程中同步带长保持不变;3)驱动力与放大器输入成正比,没有延迟直接拖加于小车;4)在实验过程中动摩擦、库仑摩擦等所有摩擦力足够小,可以忽略不计。
图1 二级摆物理模型二级倒立摆的参数定义如下:M 小车质量m1摆杆1的质量m2摆杆2的质量m3质量块的质量l1摆杆1到转动中心的距离l2摆杆2到转动中心的距离θ1摆杆1到转动与竖直方向的夹角θ2摆杆2到转动与竖直方向的夹角F 作用在系统上的外力利用拉格朗日方程推导运动学方程拉格朗日方程为:其中L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的势能其中错误!未找到引用源。
,错误!未找到引用源。
为系统在第i 个广义坐标上的外力,在二级倒立摆系统中,系统有三个广义坐标,分别为x,θ1,θ2,θ3。
首先计算系统的动能:其中错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
分别为小车的动能,摆杆1的动能,摆杆2的动能和质量块的动能。
小车的动能:错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆1的平动动能和转动动能。
错误!未找到引用源。
,其中错误!未找到引用源。
,错误!未找到引用源。
分别为摆杆2的平动动能和转动动能。
对于系统,设以下变量: xpend1摆杆1质心横坐标 xpend2摆杆2质心横坐标 yangle1摆杆1质心纵坐标 yangle2摆杆2质心纵坐标 xmass 质量块质心横坐标 ymass 质量块质心纵坐标 又有:(,)(,)(,)L q q T q q V q q =-则有:系统总动能:系统总势能:则有:求解状态方程:可解得:使用MATLAB对得到的系统进行阶跃响应分析,执行命令:A=[0 0 0 1 0 0;0 0 0 0 1 0;0 0 0 0 1 01;0 0 0 0 0 0;0 86.69 -21.62 0 0 0;0 -40.31 39.45 0 0 0];B=[0;0;0;1;6.64;-0.808];C=[1 0 0 0 0 0;0 1 0 0 0 0;0 0 1 0 0 0];D=[0;0;0];sys=ss(A,B,C,D);t=0:0.001:5;step(sys,t)求取系统的单位阶跃响应曲线:图2 二级摆阶跃响应曲线由图示可知系统小车位置、摆杆1角度和摆杆2角度均发散,需要设计控制器以满足期望要求。
倒立摆系统建模及MATLAB仿真

倒立摆系统的建模及MATLAB仿真通过建立倒立摆系统的数学模型,应用状态反馈控制配置系统极点设计倒立摆系统的控制器,实现其状态反馈,从而使倒立摆系统稳定工作。
之后通过MA TLAB 软件中Simulink工具对倒立摆的运动进行计算机仿真,仿真结果表明,所设计方法可使系统稳定工作并具有良好的动静态性能。
倒立摆系统是1个经典的快速、多变量、非线性、绝对不稳定系统,是用来检验某种控制理论或方法的典型方案。
倒立摆控制理论产生的方法和技术在半导体及精密仪器加工、机器人技术、导弹拦截控制系统和航空器对接控制技术等方面具有广阔的开发利用前景。
因此研究倒立摆系统具有重要的实践意义,一直受到国内外学者的广泛关注。
本文就一级倒立摆系统进行分析和研究,建立倒立摆系统的数学模型,采用状态反馈极点配置的方法设计控制器,并应用MA TLAB 软件进行仿真。
1 一级倒立摆系统的建模1. 1 系统的物理模型如图1 所示,在惯性参考系下,设小车的质量为M ,摆杆的质量为m ,摆杆长度为l ,在某一瞬间时刻摆角(即摆杆与竖直线的夹角)为θ,作用在小车上的水平控制力为f 。
这样,整个倒立摆系统就受到重力,水平控制力和摩擦力的3 外力的共同作用。
图1 一级倒立摆物理模型1. 2 系统的数学模型在系统数学模型中,本文首先假设:(1) 摆杆为刚体。
(2)忽略摆杆与支点之间的摩擦。
(3)忽略小车与导轨之间的摩擦。
然后根据牛顿第二运动定律,求得系统的运动方程为:方程(1) , (2) 是非线性方程,由于控制的目的是保持倒立摆直立,在施加合适的外力条件下,假定θ很小,接近于零是合理的。
则sinθ≈θ,co sθ≈1 。
在以上假设条件下,对方程线性化处理后,得倒立摆系统的数学模型:1. 3 系统的状态方程以摆角θ,角速度θ',小车的位移x ,速度x'为状态变量,输出为y 。
即令:则一级倒立摆系统的状态方程为:2 控制器设计及MATLAB 仿真2. 1 极点配置状态反馈的基本原理图2 状态反馈闭环控制系统极点配置的方法就是通过一个适当的状态反馈增益矩阵的状态反馈方法,将闭环系统的极点配置到任意期望的位置。
倒立摆PID控制及MATLAB仿真

摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:一级倒立摆,PID,MATLAB仿真目录第1章自动控制概述 (1)1.1 自动控制概念 (1)1.1.1 开环控制 (1)1.1.2 闭环控制 (2)1.2 自动控制系统的分类 (2)1.2.1 恒值系统、随动系统和程序控制系统 (2)1.2.2 随机系统与自动调整系统 (3)1.2.3 线性系统和非线性系统 (3)1.2.4 连续系统与离散系统 (3)1.2.5 单输入单输出系统和多输入多输出系统 (3)1.2.6 集中参数系统和分布参数系统 (4)1.3 对控制系统的性能要求 (4)1.4 典型环节 (5)1.4.1 比例环节 (5)1.4.2 积分环节 (5)1.4.3 微分环节 (6)1.4.4 惯性环节 (6)1.4.5 时滞环节 (7)第2章 MATLAB仿真软件的应用 (9)2.1 MATLAB的基本介绍 (9)2.2 MATLAB的仿真 (9)2.3 控制系统的动态仿真 (10)2.4 小结 (12)第3章直线一级倒立摆系统及其数学模型 (13)3.1 系统组成 (13)3.1.1 倒立摆的组成 (14)3.1.2 电控箱 (14)3.1.3 其它部件图 (14)3.1.4 倒立摆特性 (15)3.2 模型的建立 (15)3.2.1 微分方程的推导 (16)3.2.2 传递函数 (17)3.2.3 状态空间结构方程 (18)3.2.4 实际系统模型 (20)3.2.5 采用MATLAB语句形式进行仿真 (21)第4章 PID控制理论 (23)4.1 PID控制概述 (23)4.2 PID的控制规律 (24)4.3 数字PID控制 (25)4.3.1 位置式PID控制算法 (26)4.3.2 增量式PID控制算法 (27)4.4 常用的PID控制系统 (27)4.4.1 串级PID控制 (27)4.4.2 纯滞后系统的大林控制算法 (28)4.4.3纯滞后系统的Smith控制算法 (29)4.4.4 PID控制原理的特点 (30)4.4.5 PID参数的调整 (31)4.4.6 PID控制回路的运行 (32)第5章直线一级倒立摆的PID控制器设计与调节 (33)5.1 PID控制器的设计 (33)5.2 PID控制器设计MATLAB仿真 (35)结论 (40)致谢.......................................................................................................................错误!未定义书签。
基于MATLAB的旋转倒立摆建模和控制仿真

倒立摆系统作为一个被控对象具有非线性、强耦合、欠驱动、不稳定等典型特点,因此一直被研究者视为研究控制理论的理想平台,其作为控制实验平台具有简单、便于操作、实验效果直观等诸多优点。
倒立摆具有很多形式,如直线倒立摆、旋转倒立摆、轮式移动倒立摆等等。
其中,旋转倒立摆本体结构仅由旋臂和摆杆组成,具有结构简单、空间布置紧凑的优点,非常适合控制方案的研究,因此得到了研究者们广泛的关注[1-2]。
文献[3]介绍了直线一级倒立摆的建模过程,并基于MATLAB 进行了仿真分析;文献[4]通过建立倒立摆的数学模型,采用MATLAB 研究了倒立摆控制算法及仿真。
在倒立摆建模、仿真和研究中大多数研究者常用理论建模方法,也可以利用SimMechanics 搭建三维可视化模型仿真;文献[5]使用SimMechanics 工具箱建立旋转倒立摆物理模型,通过极点配置、PD 控制和基于线性二次型控制实现了倒立摆的平衡控制;文献[6]通过设计的全状态观反馈控制器来实现单极旋转倒立摆SimMechanics 模型控制,表明了SimMechanics 可用于不稳定的非线性系统;文献[7]通过单级倒立摆SimMechanics 仿真,研究了Bang-Bang 控制和LQR 控制对倒立摆的自起摆和平衡控制;文献[8]基于Sim⁃Mechanics 建立了直线六级倒立摆模型,并基于LRQ 设计状态反馈器进行了仿真控制分析。
本文首先采用Lagrange 方法建立了旋转倒立摆的动力学模型,在获得了旋转倒立摆动力学微分方程后建立了s-func⁃tion 仿真模型;然后,本文采用SimMechanics 建立了旋转的可视化动力学模型。
针对两种动力学模型,采用同一个PID 控制器进行了控制,从控制结果可以看出两种模型的响应曲线完全一致,这两种模型相互印证了各自的正确性。
1旋转倒立摆系统的动力学建模旋转倒立摆是由旋臂和摆杆构成的系统,如图1所示,旋臂绕固定中心旋转(角度记为θ)带动摆杆运动,摆杆可以绕旋臂自由转动,角度记为α。
直线一级倒立摆MATLAB仿真报告
1便携式倒立摆实验简介倒立摆装置被公认为是自动控制理论中的典型试验设备,是控制理论教学和科研中不可多得的典型物理模型。
本实验基于便携式直线一级倒立摆试验系统研究其稳摆控制原理。
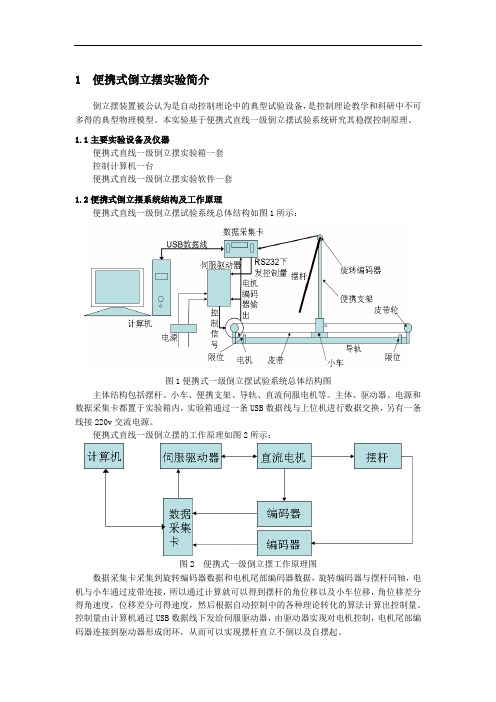
1.1主要实验设备及仪器便携式直线一级倒立摆实验箱一套控制计算机一台便携式直线一级倒立摆实验软件一套1.2便携式倒立摆系统结构及工作原理便携式直线一级倒立摆试验系统总体结构如图1所示:图1 便携式一级倒立摆试验系统总体结构图主体结构包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主体、驱动器、电源和数据采集卡都置于实验箱内,实验箱通过一条USB数据线与上位机进行数据交换,另有一条线接220v交流电源。
便携式直线一级倒立摆的工作原理如图2所示:图2 便携式一级倒立摆工作原理图数据采集卡采集到旋转编码器数据和电机尾部编码器数据,旋转编码器与摆杆同轴,电机与小车通过皮带连接,所以通过计算就可以得到摆杆的角位移以及小车位移,角位移差分得角速度,位移差分可得速度,然后根据自动控制中的各种理论转化的算法计算出控制量。
控制量由计算机通过USB数据线下发给伺服驱动器,由驱动器实现对电机控制,电机尾部编码器连接到驱动器形成闭环,从而可以实现摆杆直立不倒以及自摆起。
2便携式倒立摆控制原理方框图便携式倒立摆是具有反馈功能的闭环系统,其控制目标是实现在静态和动态下的稳摆。
当输入量为理想摆角,即∅∅=0时,偏差为0,控制器不工作;当输入量不为理想摆角时,偏差存在,控制器做出决策,驱动电机,使小车摆杆系统发生相应位移,输出的摆角通过角位移传感器作用于输出量,达到减小偏差的目的。
根据控制原理绘制出控制方框图如图3所示:图3 便携式一级倒立摆控制原理方框图3建立小车-摆杆数学模型便携式倒立摆系统主要由小车、摆杆等组成,它们之间自由连接。
小车可以在导轨上自由移动,摆杆可以在铅垂的平面内自由地摆动。
在忽略了空气阻力和各种摩擦之后,可将便携式倒立摆系统抽象成小车和匀质杆组成的刚体系统,在惯性坐标内应用经典力学理论建立系统的动力学方程,采用力学分析方法建立小车-摆杆的数学模型。
—倒立摆状态反馈系统的建模及matlab仿真

倒立摆状态反馈系统的建模及matlab仿真课题名称:倒立摆状态反馈系统的建模及matlab仿真学生姓名:谢凯学号:2011330380229班级:电气工程及其自动化2班指导老师:高金凤2013年12月20日倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。
通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。
同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等。
故其研究意义广泛。
一、倒立摆系统的建模1.系统的物理模型如图1所示,在惯性参考系下,设小车的质量为M,摆杆的质量为m,摆杆长度为l,在某一瞬间时刻摆角(即摆杆与竖直线的夹角)为Θ,作用在小车上的水平控制力为f。
这样,整个倒立摆系统就受到重力,水平控制力和摩擦力的3外力的共同作用。
图a一级倒立摆物理模型图b摆杆隔离受力图2.系统的数学模型在系统数学模型中,本文首先假设:(1)摆杆为刚体;(2)忽略摆杆与支点之间的摩擦;(3)忽略小车与导轨之间的摩擦。
然后根据牛顿第二运动定律,求得系统的运动方程为: ()2222sin M d x l d x m f dt dtθ++= (1) ()22sin cos sin d x l ml mgl dtθθθ++= (2) 方程(1),(2)是非线性方程,由于控制的目的是保持倒立摆直立,在施加合适的外力条件下,假定θ很小,接近于零是合理的。
则sin θθ≈,cos 1θ≈.在以上假设条件下,对方程线性化处理后,得到倒立摆系统的数学模型如下:()M m x ml f θ++=&&&& (3) 2ml mlx mgl θθ+=&&&& (4) 3. 系统的状态方程以摆角θ,角速度θ,小车的位移x ,速度x 为状态变量,输出为y 。
单级移动倒立摆建模及控制器设计matlab

单级移动倒立摆建模及控制器设计matlab 单级移动倒立摆是一种常见的控制系统模型,它在机器人控制、自动驾驶等领域有着广泛的应用。
本文将介绍如何使用MATLAB进行单级移动倒立摆的建模和控制器设计。
首先,我们需要了解单级移动倒立摆的基本原理。
单级移动倒立摆由一个垂直的杆和一个可以在水平方向上移动的小车组成。
小车上有一个可以旋转的杆,杆的一端连接着小车,另一端有一个质量块。
通过控制小车的位置和杆的角度,我们可以实现倒立摆的平衡。
接下来,我们开始建立单级移动倒立摆的数学模型。
首先,我们需要定义系统的状态变量。
在这个模型中,我们可以选择小车的位置x、小车的速度v、杆的角度θ和杆的角速度ω作为状态变量。
然后,我们可以根据物理原理建立系统的动力学方程。
根据牛顿第二定律和角动量守恒定律,我们可以得到如下的动力学方程:m*x'' = F - m*g*sin(θ) - m*l*θ'^2*cos(θ)m*l^2*θ'' = -m*g*l*sin(θ) + m*l*x''*cos(θ) - b*θ'其中,m是小车和质量块的总质量,l是杆的长度,F是施加在小车上的外力,g是重力加速度,b是杆的阻尼系数。
接下来,我们可以使用MATLAB进行模型的建立和仿真。
首先,我们需要定义系统的参数和初始条件。
然后,我们可以使用ode45函数来求解系统的动力学方程。
ode45函数是MATLAB中用于求解常微分方程的函数,它可以根据给定的初始条件和参数,计算出系统在一段时间内的状态变化。
在求解动力学方程之后,我们可以得到系统的状态变量随时间的变化。
通过绘制状态变量随时间的曲线,我们可以观察到系统的动态行为。
例如,我们可以绘制小车位置随时间的变化曲线,以及杆角度随时间的变化曲线。
最后,我们需要设计一个控制器来实现单级移动倒立摆的平衡。
常见的控制器设计方法包括PID控制器和模糊控制器。
用Matlab完成倒立摆系统的分析与综合

现代控制理论用Matlab 完成倒立摆系统的分析与综合2013/5/23 Thursday 学号:**********杨 博用Matlab 完成倒立摆系统的分析与综合一、实验要求1、熟悉非线性系统数学模型的建立过程。
2、非线性数学模型的近似线性化。
3、判断系统的能控性及能观性。
4、学习利用MATLAB 来分析系统的能观性、能控性和稳定性(Lyapunov 第一法)。
5、掌握状态反馈极点配置控制,并能用MATLAB 仿真软件进行控制算法的仿真验证与分析。
二、实验原理底座导轨摆杆XFϕl图1 一级倒立摆系统模型 图2 小车水平方向受力分析图3 摆杆垂直方向的受力分析Pb ẋ N F小车水平方向受力: Mẍ+bẋ+N =F摆杆水平方向受力:2(sin )2d N m x l dtθ=+即: N =mẍ+mlθcos θ−mlθsin θ得第一个运动方程:(M +m )ẍ+bẋ+mlθcos θ−mlθsin θ=F摆杆垂直方向受力:2(cos )2d P mg m l dtθ-=力矩平衡方程:−Pl sin θ−Nl cos θ=Iθ=+θπφ,cos cos φ=-sin sin φθ=-第二个运动方程:(I +ml 2)θ+mgl sin θ=−mlẍcos θ 两个运动方程化简得:{(I +ml 2)ϕ−mgl∅=mlẍ(M +m )ẍ+bẋ−mlϕ=u拉普拉斯变换得:222()()()()22()()()()()I ml s s mgl s mlX s sM m X s s bX s s ml s s U s ⎧+Φ-Φ=⎪⎨⎪++-Φ=⎩三、实验内容1、一级直线倒立摆传递函数的建立 摆杆输出角度和电机作用力的传递函数为:2()2()()()432ml s s qU s b I ml mgl M m bmgls s s sq q q⋅Φ=+++⋅-⋅-⋅ 其中22[()()()]q M m I ml ml =++-2、一级直线倒立摆状态空间方程的建立求解可得ẍ、ϕ,整理后得到系统的状态空间方程为:010002222()00222()()()00010()00222()()()x x I ml b m gl I ml x xI M m Mml I M m Mml I M m Mml umlbmgl M m ml I M m Mml I M m Mml I M m Mml φφφφ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++++++⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎢⎥++++++⎣⎦⎣⎦1000000100x x x y u φφφ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦3、MATLAB 仿真要求 ➢ 求出状态空间表达式矩阵。
Invertedpendulum倒立摆的matlab建模

ECE451 Controll EngineeringInverted pendulum09/29/2013Introduction:Inverted pendulum is a typical fast, multi-varaibles, nonlinear, unstable system, ithas significant meaning. We choose the PID controller to fot the inverted pendulum. Assume the input is a step signal , the gravitational acceleration g=9.8m/s^2 and linearize the nonlinear model around the operating point.1.Mathematic ModlingM mass of the car 0.5 kgm mass of the pendulum 0.2 kgb coefficient of friction for cart 0.1 N/m/secl length to pendulum center of mass 0.3 mI mass moment of inertia of the pendulum 0.006 kg.m^2F force applied to the cartx coordinate of cart positionθpendulum angle from vertical (down)N and F are the force from horizontal and vertical direction.)Force analysisConsider the horizontal direction cart force, we get the equation:Consider the horizontal direction pendulum force, we get the equation:To get rid of P and N, we get this equation:Merge these two equations, about to P And N, to obtain a second motion equation:u to represent the controlled object with the input force F, linearized two motion equationsApply Laplace transform to the equation aboveThe transfer function of angle and positionLet v =put the equation above into the second equationWe get the transfer functionState space equation:Solve the algebraic equation, obtain solution as follows:Finally we get the system state space equations.2. PID Controller DesignWe now design a PID controller for the inverted pendulum system.KD(s) is the transfer function of the controller.G(s) is the transfer function of the controlled car.Considering that the input r(s) =0, the block diagram can be transformed as: The output of the system is()()()()()()()()()()()()()()()()sFnumnumPIDdendenPIDdenPIDnumsFdendenPIDnumnumPIDdennumsFsGskDsGsy+=+=+=11num —the numerator of the objectden —the denominator of the objectnumPID – the numerator of the PID controller transfer functiondenPID – the denominator of the PID controller transfer functionThe object transfer function is()()()()dennumsqbmglsqmglMmsqmlIbssqmlsUs=-+-++=Φ23242,in which[()()()]22mlmlIMmq-++=.PID Controller Transfer Function is()22sKsKsKsKKsKsKD IpDIPD++=++=Now, we add the car’s position as another output, we getin which G1 is the transfer function of the pendulum, G2 is the transfer function of the car.The output of the car’s position is()()()()()()()()()()sFdendenPIDnumnumPIDdennumsFsGsKDsGsX11221211+=+=in which, num1,den1,num2,den2 are separately mean the controlled object 1 and object 2 and PID controller‘s numerators and denominators.From ()()()s s g ml ml I s X Φ⎥⎦⎤⎢⎣⎡-+=22, we could get thatIn which,[()()()]22ml ml I M m q -++=.We can easily simplified the equation as()()()()()()()()s F num numPID k den denPID denPID num s X 12+=3. Matlab SimulationIn design, the cart's position will be ignored. Under these conditions, the design criteria are:1) settling time is less than 5 seconds2) pendulum should not move more than 0.05 radians away from the vertical When kd=1,k=1,ki=1:numc1=4.5455 0 0 0, denc1=1 4.7273 -26.6364 0.0909 0 0, num2= -1.8182 0 44.5455 0, denc2=1 4.7273 -26.6364 0.0909 0()()()()()()s qbmgl s q mgl M m s q ml I b s s qbmgls q ml I s U s X s G -+-++-+==2324222Then we tried many times to adjust the parameter to satisfy the requirements: Ts <=5 s and overshoot M<0.05.We find the optimal parameters of kd,k,ki which is the second situation.2. When kd=20,k=300,ki=1:Numc1= 4.5455 0 0 0, denc1=0.001 0.09111.3325 0.0001 0 0, numc2= -1.8182 0 44.5455 0, denc2=0.001 0.09111.3325 0.0001 0 0The results:Matlab codesM=0.5;m=0.2;b=0.1;I=0.006;g=9.8;l=0.3;q=(M+m)*(I+m*l^2)/q-(m*l)^2;num1=[m*l/q 0 0];den1=[1 b*(I+m*l^2)/q-(M+m)*m*g*l/q-b*m*g*l/q 0];num2=[-(I+m*l^2)/q 0 m*g*l/q];den2=den1;kd=1;k=1;ki=1;numPID=[kd k ki];denPID=[1 0];numci=conv (num1 denPID);denc1=polyadd(conv(denPID,den1),conv(numPID,num1)); t=0:0.1:20;figure(1)impulse(numc1,denc1,t)title(‘Angle’)figure(2)impulse(numc2,denc2,t)title(‘Position’)M=0.5;m=0.2;b=0.1;I=0.006;g=9.8;l=0.3;q=(M+m)*(I+m*l^2)/q-(m*l)^2;num1=[m*l/q 0 0];den1=[1 b*(I+m*l^2)/q-(M+m)*m*g*l/q-b*m*g*l/q 0]; num2=[-(I+m*l^2)/q 0 m*g*l/q];den2=den1;kd=20;k=300;ki=1;numPID=[kd k ki];denPID=[1 0];numci=conv (num1 denPID);denc1=polyadd(conv(denPID,den1),conv(numPID,num1)); t=0:0.1:20;figure(1)impulse(numc1,denc1,t)title(‘Angle’)figure(2)impulse(numc2,denc2,t)title(‘Position’)Simulation:We will build a closed-loop model with reference input of pendulum position and a disturbance force applied to the cart.We now begin to simulate the closed-loop system. The physical parameters are set as follows.M=0.5, m=0.2, b=0.1, I=0.006, g=9.8, l=0.3After 20s simulation, we see the response as followThe response is very much like what have been done in Matlab codes.。
基于ADAMS与MATLAB的倒立摆联合仿真实验5篇

基于ADAMS与MATLAB的倒立摆联合仿真实验5篇第一篇:基于ADAMS与MATLAB的倒立摆联合仿真实验基于ADAMS与MATLAB的倒立摆联合仿真实验一、实验目的在传统的机电一体化研究设计过程中,机械工程师和控制工程师虽然在共同设计开发一个系统,但是他们各自都需要建立自己的模型,然后分别采用不同的分析软件,对机械系统和控制系统进行独立的设计、调试和试验,最后进行机械系统和控制系统各自的物理样机联合调试,如果发现问题又要回到各自的模型中分别修改,然后再联合调试,显然这种方式费时费力。
基于多领域的建模与联合仿真技术很好的解决了这个问题,为机械和控制系统进行联合分析提供了一种全新的设计方法。
机械工程师和控制工程师就可以享有同一个样机模型,进行设计、调试和试验,可以利用虚拟样机对机械系统和控制系统进行反复联合调试,直到获得满意的设计效果,然后进行物理样机的建造和调试。
ADAMS与MATLAB是机械系统仿真和控制系统仿真领域应用较为广泛的软件,其中ADAMS为用户提供了强大的建模、仿真环境,使用户能够对各种机械系统进行建模、仿真和分析,具有十分强大的运动学和动力学分析功能;而MATLAB具有强大的计算功能、极高的编程效率及模块化的建模方式,因此,把ADAMS与MATLAB联合起来仿真,可以充分将两者的优势相结合,将机械系统仿真分析同控制系统设计有机结合起来,实现机电一体化的联合分析。
本实验以倒立摆为例,进行ADAMS与MATLAB的联合仿真,对倒立摆的运动性能和运动规律进行分析。
二、实验方法软件环境:MD ADAMS R3,MATLAB R2009b 2.1 建立倒立摆的动力学模型启动ADAMS/View模块弹出如图1所示对话框,建立小车及摆杆模型。
首先选择“Create a new model”选项,创建一个新的模型,将该文件保存在相应的文件夹下,本实验将结果保存在E:daolibai_adams文件夹下,将文件名取为“daolibai_adams”,其余选项保持默认。
单级倒立摆控制系统设计及MATLAB中的仿真

单级倒立摆控制系统设计及MATLAB中的仿真第一步是建立单级倒立摆的数学模型。
单级倒立摆可以通过旋转关节将一根质量均匀的细杆与一个平台相连。
细杆的一端固定在平台上,另一端可以自由旋转。
细棒的旋转角度用θ表示,质心的位置用x表示。
根据牛顿力学和杆的动力学方程,可以得到如下数学模型:1.摆杆的运动方程:Iθ'' + mgl sin(θ) = u - F (1)其中,I是摆杆的转动惯量,m是摆杆的质量,g是重力加速度,l是摆杆的长度,u是控制输入(摆杆上的转动力矩),F是摩擦力。
2.质心的运动方程:m(x'' - lθ'²cos(θ)) = F (2)接下来是设计控制器来控制单级倒立摆。
一个常用的控制方法是使用线性化控制理论,其中线性化是将系统在一些工作点附近线性近似。
在这种情况下,将摆杆保持在垂直方向,并使质心静止作为工作点。
线性化系统的转移函数为:H(s) = θ(s)/u(s) = (ml²s² + mg)/(s(ml² + I))为了稳定单级倒立摆,可以使用自动控制理论中的反馈控制方法,特别是状态反馈。
状态反馈根据系统的状态变量来计算控制器输入。
为了设计状态反馈控制器,首先需要判断系统的可控性和可观测性。
根据控制系统理论,如果系统是可控和可观测的,则可以设计一个线性状态反馈控制器来稳定系统。
在MATLAB中,可以使用控制系统工具箱来设计单级倒立摆的控制系统。
首先,通过建立系统的传递函数模型(由线性化系统得到)来定义系统。
然后,使用控制系统工具箱中的函数来计算系统的稳定极点,并确定所需的反馈增益以稳定系统。
最后,可以使用MATLAB的仿真工具来模拟单级倒立摆的响应,并进行性能分析。
在进行仿真时,可以将倒立摆的初始状态设置为平衡位置,并应用一个输入来观察系统的响应。
可以通过调整控制器增益和系统参数来改变系统响应的性能,例如收敛时间、超调量和稳态误差。
基于MATLAB的单级倒立摆控制系统设计

基于MATLAB的单级倒立摆控制系统设计单级倒立摆是一种常见的控制系统,其结构简单,但具有较强的动态控制性能。
本文基于MATLAB对单级倒立摆控制系统进行设计,并详细介绍了设计过程和结果。
首先,我们需要了解单级倒立摆的结构和动力学模型。
单级倒立摆由轴、电机和旋转杆组成,电机通过轴和旋转杆相连。
倒立摆的目标是使旋转杆竖直,即使旋转杆的角度保持为0°。
为了实现倒立摆的控制,我们借助PID(Proportional-Integral-Derivative)控制器。
PID控制器是一种常用的线性控制系统,其中,比例系数(P)、积分系数(I)和微分系数(D)能够根据系统的需求进行调整。
接下来,我们需要确定系统的控制目标。
倒立摆的目标是使旋转杆的角度保持为0°。
因此,我们需要设计一个控制器,使得当旋转杆角度发生偏差时,控制器能够迅速响应,并产生相应的控制信号。
首先,我们需要获取倒立摆的角度信息。
我们可以通过连接传感器获取角度信息,并将其输入到MATLAB中进行处理。
然后,我们需要设计PID控制器来控制倒立摆。
在MATLAB中,可以使用pid函数来创建PID控制器对象,然后使用tune函数来调整PID控制器对象的参数。
调整PID控制器参数的过程通常可以通过试验和观察实现。
我们可以将倒立摆设置为初始状态,并控制器输出控制信号,然后观察倒立摆的响应。
根据实际观察,我们可以逐步调整PID控制器的参数,以达到系统的稳定性和响应速度的要求。
在完成PID控制器的参数调整后,我们可以进行仿真实验。
在MATLAB中,可以使用sim函数来进行仿真实验。
通过仿真实验,我们可以观察倒立摆的控制效果,并根据需要进行进一步的调整。
通过在MATLAB中进行控制器设计和仿真实验,我们可以对单级倒立摆进行控制系统设计。
该设计可以帮助我们理解控制系统的工作原理,并为实际应用提供参考。
同时,我们还可以根据具体需求对设计进行进一步调整和优化。
倒立摆MATLAB建模
Matlab程序设计上交作业要求:1)纸质文档:设计分析报告一份(包括系统建模、系统分析、系统设计思路、程序及其执行结果)。
2)Matlab程序:按班级统一上交后备查。
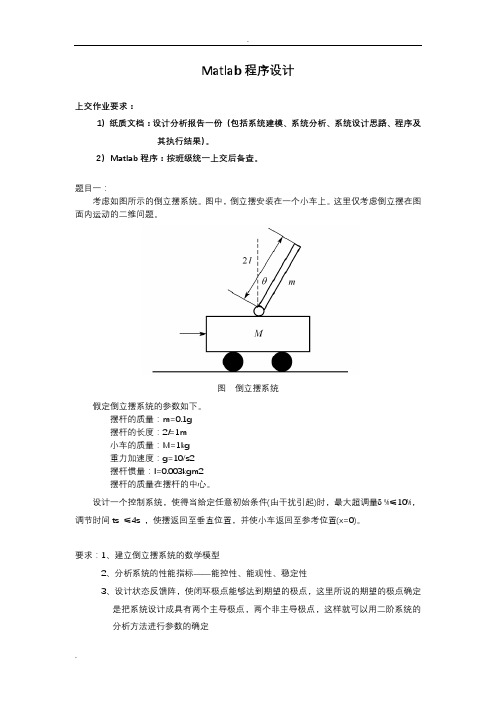
题目一:考虑如图所示的倒立摆系统。
图中,倒立摆安装在一个小车上。
这里仅考虑倒立摆在图面内运动的二维问题。
图倒立摆系统假定倒立摆系统的参数如下。
摆杆的质量:m=0.1g摆杆的长度:2l=1m小车的质量:M=1kg重力加速度:g=10/s2摆杆惯量:I=0.003kgm2摆杆的质量在摆杆的中心。
设计一个控制系统,使得当给定任意初始条件(由干扰引起)时,最大超调量 %≤10%,调节时间ts ≤4s ,使摆返回至垂直位置,并使小车返回至参考位置(x=0)。
要求:1、建立倒立摆系统的数学模型2、分析系统的性能指标——能控性、能观性、稳定性3、设计状态反馈阵,使闭环极点能够达到期望的极点,这里所说的期望的极点确定是把系统设计成具有两个主导极点,两个非主导极点,这样就可以用二阶系统的分析方法进行参数的确定4、用MATLAB 进行程序设计,得到设计后系统的脉冲响应、阶跃响应,绘出相应状态变量的时间响应图。
题目二:根据自身的课题情况,任意选择一个被控对象,按照上题所示步骤进行分析和设计,并给出仿真程序及其执行结果。
题目一:考虑如图所示的倒立摆系统。
图中,倒立摆安装在一个小车上。
这里仅考虑倒立摆在图面内运动的二维问题。
图倒立摆系统假定倒立摆系统的参数如下。
摆杆的质量:m=0.1g摆杆的长度:2l=1m小车的质量:M=1kg重力加速度:g=10/s2摆杆惯量:I=0.003kgm2摆杆的质量在摆杆的中心。
设计一个控制系统,使得当给定任意初始条件(由干扰引起)时,最大超调量 %≤10%,调节时间ts ≤4s ,使摆返回至垂直位置,并使小车返回至参考位置(x=0)。
要求:1、建立倒立摆系统的数学模型2、分析系统的性能指标——能控性、能观性、稳定性3、设计状态反馈阵,使闭环极点能够达到期望的极点,这里所说的期望的极点确定是把系统设计成具有两个主导极点,两个非主导极点,这样就可以用二阶系统的分析方法进行参数的确定4、用MATLAB 进行程序设计,得到设计后系统的脉冲响应、阶跃响应,绘出相应状态变量的时间响应图。
倒立摆控制系统设计matlab

倒立摆控制系统设计matlab倒立摆控制系统设计是一个在工程领域中非常重要的课题。
倒立摆是一个经典的控制系统问题,通过控制电机的力矩来使倒立摆保持平衡。
在这篇文章中,我们将使用Matlab来设计一个倒立摆控制系统,并逐步回答其中的关键问题。
首先,我们需要明确设计的目标。
在倒立摆控制系统中,我们的目标是使摆杆保持垂直位置。
为了实现这个目标,我们需要采用逆向控制方法,即通过测量摆杆当前状态以及目标状态之间的差异,并控制力矩,从而使摆杆回复到垂直位置。
接下来,我们需要构建倒立摆的模型。
倒立摆模型可以采用Euler-Lagrange动力学方程进行描述。
具体地,我们可以使用如下的动力学方程来描述倒立摆:m*L^2*θ''(t) + m*g*L*sin(θ(t)) = u(t) - b*θ'(t) - c*sat(θ(t)) 其中,m是摆杆的质量,L是摆杆的长度,θ(t)是摆杆的角度,u(t)是电机的力矩,b是摩擦系数,c是控制器增益。
在上述动力学方程中,μ(t)表示补偿力,其作用是抵消由于重力引起的非线性成分。
有了动力学方程之后,我们可以使用Matlab来进行数值仿真。
首先,我们需要定义模型的初始状态和控制器增益。
我们可以选择一个合适的初始状态,比如θ(0)=pi/4,θ'(0)=0,然后根据模型的特性来选择控制器增益c。
接下来,我们可以使用Matlab的ode45函数来求解动力学方程的数值解。
ode45函数是一种常用的数值积分器,可以对常微分方程进行数值求解。
在本例中,我们可以将动力学方程与初始条件传递给ode45函数,然后使用该函数来求解摆杆的角度θ(t)和角速度θ'(t)的变化。
在求解得到角度和角速度之后,我们可以使用反馈控制方法来设计控制器。
一种常见的控制器设计方法是使用PID控制器。
PID控制器基于当前状态与目标状态之间的差异来计算控制信号。
具体地,PID控制器的输出可以通过如下公式来计算:u(t) = Kp*e(t) + Ki*∫e(t)dt + Kd*e'(t)其中,u(t)是控制器的输出,Kp、Ki和Kd分别是比例、积分和微分增益,e(t)=θ(t)-θd(t)是当前状态与目标状态之间的差异,e'(t)=θ'(t)-θd'(t)是当前状态与目标状态之间的差异的一阶导数。
直线二级倒立摆系统MATLAB模型的建立与仿真

直线二级倒立摆系统模型的建立与仿真1 引言倒立摆是一个高阶次、非线性、快速、多变量、强藕合、不稳定的系统。
在控制理论发展过程中,倒立摆常常被做为典型的被控对象来验证某一理论的正确性,以及在实际应用中的可行性,通过对倒立摆引入一个适当的控制方法使之成为一个稳定系统,来检验控制方法对不稳定性、非线性和快速性系统的处理能力。
该控制方法在军工、航天、机器人等领域和一般工业过程中都有广泛应用。
本文主要讨论二级倒立摆系统模型的建立和仿真。
2二级倒立摆系统数学模型直线二级倒立摆系统是由直线运动模块和两级倒立摆组件组成。
主要包括导轨、小车和各级摆杆、编码器等元件。
由驱动电机给小车施加一个控制力,迫使小车在导轨上左右移动。
而小车的位移和各级摆杆角度由编码器测得。
倒立摆的控制目标是使倒立摆的摆杆能在有限长的导轨上快速的达到竖直向上的稳定状态,以实现系统的动态平衡,并且小车位移和摆杆角度的振荡幅度较小,系统具有一定的抗干扰能力。
系统简化后的直线二级倒立摆系统物理结构图如图2.1所示。
图1.二级倒立摆系统模型系统模型建立所用的各参数如下:应用Lagrange 方程建立的数学模型为012221221211121221222212212222cos (,)cos()cos cos()1121111121111m +m +m (m l +m L )cos m l H (m l +m L )cos J m l m L m l L m l m l L J m l θθθθθθθθθθ⎡⎤⎢⎥=++-⎢⎥⎢⎥-+⎣⎦.1011...1221212122.11222cos (,,,)0(0(112222222f m l +m L sin m l H f f m l L sin f m l L sin f f θθθθθθθθθθθθθ⎡⎤-•⎢⎥⎢⎥=--•+⎢⎥⎢⎥-•+-⎢⎥⎣⎦111()-)-) 312(,)h θθ= [0 11211()sin m l m L g θ+ 212sin m l g θ] T0h =[1 0 0]T()1121212121312022(,)(,,,),x x H H h h u θθθθθθθθθθθθ⎡⎤⎡⎤⎢⎥⎢⎥=++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦3 倒立摆PID控制器系统PID控制是比例积分微分控制的简称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线控大作业
如图所示的倒立摆系统。
图中,倒立摆安装在一个小车上。
这里仅考虑倒立摆在图面内运动的二维问题。
图倒立摆系统
假定倒立摆系统的参数如下。
摆杆的质量:m=0.1g
摆杆的长度:2l=1m
小车的质量:M=1kg
重力加速度:g=10/s2
摆杆惯量:I=0.003kgm2
摆杆的质量在摆杆的中心。
设计一个控制系统,使得当给定任意初始条件(由干扰引起)时,最大超调量 %≤10%,
调节时间ts ≤4s ,使摆返回至垂直位置,并使小车返回至参考位置(x=0)。
要求:1、建立倒立摆系统的状态方程
2、定量分析,定性分析系统的性能指标——能控性、能观性、稳定性
3、极点配置
设计分析报告
1 系统建模
在忽略了空气阻力和各种摩擦之后,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统。
如下如所示。
图 一级倒立摆模型 其中:
φ 摆杆与垂直向上方向的夹角
θ 摆杆与垂直向下方向的夹角(考虑到摆杆初始位置为竖直向下) 图是系统中小车和摆杆的受力分析图。
其中,N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量。
注意:在实际倒立摆系统中检测和执行装置的正负方向已经完全确定,因而矢量方向定义如图所示,图示方向为矢量正方向。
分析小车水平方向所受的合力,可以得到以下方程:
N x b F x
M --= 由摆杆水平方向的受力进行分析可以得到下面等式:
)sin (22
θl x dt d m N += 即:
θθθθsin cos 2 ml ml x
m N -+= 把这个等式代入式(3-1)中,就得到系统的第一个运动方程:
F ml ml x b x
m M =-+++θθθθsin cos )(2 为了推出系统的第二个运动方程,我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:
)cos (22
θl dt
d m mg P =- θθθθ
cos sin 2 ml ml mg P --=- 力矩平衡方程如下:
θ
θθ I Nl Pl =--cos sin 注意:此方程中力矩的方向,由于θφθφφπθsin sin ,cos cos ,-=-=+=,故等式前面有负号。
合并这两个方程,约去P 和N ,得到第二个运动方程:
θθθcos sin )(2x
ml mgl ml I -=++ 设φπθ+=(φ是摆杆与垂直向上方向之间的夹角),假设φ与1(单位是弧度)相比很小,即1<<φ,则可以进行近似处理:0)(,sin ,1cos 2=-=-=dt
d θφθθ。
用u 来代表被控对象的输入力F ,线性化后两个运动方程如下: 2(+)()I ml mgl mlx M m x bx ml u ϕϕϕ⎧-=⎨++-=⎩
对式(3-9)进行拉普拉斯变换,得到
⎪⎩⎪⎨⎧=Φ-++=Φ-Φ+)
()()()()()()()()(22222s U s s ml s s bX s s X m M s s mlX s mgl s s ml I 注意:推导传递函数时假设初始条件为0。
由于输出为角度φ,求解方程组的第一个方程,可以得到:
)(])([)(22s s
g ml ml I s X Φ-+= 或 mgl
s ml I mls s X s -+=Φ222
)()()( 如果令x
v =,则有:
mgl
s ml I ml s V s -+=Φ22)()()( 把上式代入方程组的第二个方程,得到:
)()()()()()(2222s U s s ml s s s g ml ml I b s g ml
ml I m M =Φ-Φ⎥⎦⎤⎢⎣⎡+++⎥⎦⎤⎢⎣⎡-++ 整理后得到传递函数:
s q
bmgl s q mgl m M s q ml I b s s q ml s U s -+-++=Φ23242)()()()( 其中 []
22)())((ml ml I m M q -++=
设系统状态空间方程为: Du CX y Bu AX X
+=+=
方程组 对φ
,x 解代数方程,得到解如下: ⎪⎪⎪⎪⎩
⎪⎪⎪⎪⎨⎧+++++++++-==++++++++++-==u Mml m M I ml Mml m M I m M mgl x Mml m M I mlb u Mml m M I ml I Mml m M I gl m x Mml m M I b ml I x x x 2222222222)()()()()()()()()(φφφ
φφ 整理后得到系统状态空间方程:
u Mml m M I ml Mml m M I ml I x x Mml m M I m M mgl Mml m M I mlb Mml m M I gl m Mml m M I b ml I x x ⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎢⎣⎡++++++⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+++++-+++++-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡2222222
222)(0)(00)()()(010000)()()(00010φφφφ u x x x y ⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0001000001φφφ 代入倒立摆系统的参数。
摆杆的质量:m=0.1g
摆杆的长度:2l =1m
小车的质量:M=1kg
重力加速度:g=10/s2
摆杆惯量:I=0.003kgm2
010
000010100010001101x x x x u ϕϕϕϕ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥'=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦ u x x x y '⎥⎦⎤⎢⎣⎡+⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=0001000001φφφ 另外,也可以利用 MATLAB 中 tf2ss 命令对(3-13)式进行转化,求得上述状态方程。
2 系统分析
2.1 判断系统能控性和能观性
在MATLAB 中,可以利用ctrb()和obsv()函数直接求出能控性和能观性矩阵 A=[0 1 0 0;0 0 1 0;0 0 0 1;0 0 11 0];
B=[0;1;0;1];
C=[1 0 0 0;0 0 1 0];
D=[0;0];
Uc=ctrb(A,B);rc=rank(Uc);
n=size(A);
if rc==n
disp('system is controlled.')
elseif rc<n
disp('system is uncontrolled.')
end
V o=obsv(A,C);
ro=rank(V o);
if ro==n
disp('system is observable.')
elseif ro~=n disp('system is no observable.')
End
运行情况如下:
2.2 系统稳定性
A=[0 1 0 0;0 0 1 0;0 0 0 1;0 0 11 0];
B=[0;1;0;1];
C=[1 0 0 0;0 0 1 0];
D=[0;0];
P=poly(A),v=roots(P)
运行结果如下:
特征值为0(二重),3.3166,-3.3166,显然,其中一个极点在右半平面,该系统不稳定。
3 系统设计 极点配置与控制器设计
极点配置的方法就是通过一个适当的状态反馈增益矩阵的状态反馈方法 ,将闭环系统的极点配置到任意期望的位置。
()()()X t Ax t Bu t ,其中x 是状态变量(n 维),u 是控制信号,这里选取控制信号为u Kx ,
()()()x t A BK x t ,该方程的解为()()(0)A BK t x t e x ,
系统的稳态响应和瞬态响应特性由矩阵 A - B K 的特征决定。
1234K K K K K x ,闭环系统的方程为
()x
Ax Bf A BK x
,选取所希望的极点值为,1234p p p p 设计状态反馈阵时,要使系统的极点设计成具有两个主导极点,两个非主导
极点,这样就可以用二阶系统的分析方法进行参数的确定。
最大超调量小于等于10%,调节时间为4S ,
运用超调量的计算公式,
21%100%e ,其中为阻尼系数,有该公式可求得,阻尼系数=0.59,小于1,是欠阻尼。
33()s
n t 为极点实部,可以求得n =1.27 则极点公式为2
1,21n n p j ,得到两个共轭极点为
1,20.75 1.025p j .
配置非主导极点3415,15p p ,
在MATLAB 的控制系统工具箱中提供了单变量系统极点配置acker(),其格式为 K=acker(A,B,p)
程序如下:
A=[0 1 0 0;0 0 -2 0;0 0 0 1;0 0 22 0];
B=[0;1;0;-1];
C=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
D=0;
rc=rank(ctrb(A,B));
p=[-0.75+1.025j,-0.75-1.025j,-15,-15];
K=acker(A,B,p)
运行结果如下:
4 程序及其执行结果
该二阶系统的阶跃响应为下图所示
脉冲响应:。
