信息论和编码理论习题集答案解析

合集下载

信息论与编码理论习题答案

信息论与编码理论习题答案LG GROUP system office room 【LGA16H-LGYY-LGUA8Q8-LGA162】第二章信息量和熵八元编码系统，码长为3，第一个符号用于同步，每秒1000个码字，求它的信息速率。

解：同步信息均相同，不含信息，因此每个码字的信息量为 2⨯8log =2⨯3=6 bit因此，信息速率为 6⨯1000=6000 bit/s掷一对无偏骰子，告诉你得到的总的点数为：(a) 7; (b) 12。

问各得到多少信息量。

解：(1) 可能的组合为 {1，6},{2，5},{3，4},{4，3},{5，2},{6，1})(a p =366=61得到的信息量 =)(1loga p =6log = bit (2) 可能的唯一，为 {6，6})(b p =361得到的信息量=)(1logb p =36log = bit 经过充分洗牌后的一副扑克（52张），问：(a) 任何一种特定的排列所给出的信息量是多少？(b) 若从中抽取13张牌，所给出的点数都不相同时得到多少信息量？解：(a) )(a p =!521信息量=)(1loga p =!52log = bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C = bit 随机掷3颗骰子，X 表示第一颗骰子的结果，Y 表示第一和第二颗骰子的点数之和，Z 表示3颗骰子的点数之和，试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。

信息论和编码理论第二章习题集答案解析(王育民)

部分答案，仅供参考。

2.1信息速率是指平均每秒传输的信息量点和划出现的信息量分别为3log ,23log ，一秒钟点和划出现的次数平均为415314.0322.01=⨯+⨯一秒钟点和划分别出现的次数平均为45.410那么根据两者出现的次数，可以计算一秒钟其信息量平均为253log 4153log 4523log 410-=+2.3 解：(a)骰子A 和B ，掷出7点有以下6种可能：A=1,B=6; A=2,B=5; A=3,B=4; A=4,B=3; A=5,B=2; A=6,B=1 概率为6/36=1/6，所以信息量-log(1/6)=1+log3≈2.58 bit(b) 骰子A 和B ，掷出12点只有1种可能： A=6,B=6概率为1/36，所以信息量-log(1/36)=2+log9≈5.17 bit 2.5解：出现各点数的概率和信息量：1点：1/21，log21≈4.39 bit ； 2点：2/21，log21-1≈3.39 bit ； 3点：1/7，log7≈2.81bit ； 4点：4/21，log21-2≈2.39bit ； 5点：5/21，log （21/5）≈2.07bit ； 6点：2/7，log(7/2)≈1.81bit平均信息量：(1/21)×4.39+(2/21)×3.39+(1/7)×2.81+(4/21)×2.39+(5/21)×2.07+(2/7)×1.81≈2.4bit 2.7解：X=1:考生被录取； X=0:考生未被录取； Y=1:考生来自本市；Y=0:考生来自外地； Z=1: 考生学过英语；Z=0：考生未学过英语P(X=1)=1/4, P(X=0)=3/4; P(Y=1/ X=1)=1/2； P(Y=1/ X=0)=1/10； P(Z=1/ Y=1)=1, P(Z=1 / X=0, Y=0)=0.4, P(Z=1/ X=1, Y=0)=0.4, P(Z=1/Y=0)=0.4 (a) P(X=0,Y=1)=P(Y=1/X=0)P(X=0)=0.075, P(X=1,Y=1)= P(Y=1/X=1)P(X=1)=0.125P(Y=1)= P(X=0,Y=1)+ P(X=1,Y=1)=0.2P(X=0/Y=1)=P(X=0,Y=1)/P(Y=1)=0.375, P(X=1/Y=1)=P(X=1,Y=1)/P(Y=1)=0.625I (X ;Y=1)=∑∑=====xx)P()1Y /(P log)1Y /(P )1Y (I )1Y /(P x x x x;x=1)P(X )1Y /1X (P log)1Y /1X (P 0)P(X )1Y /0X (P log)1Y /0X (P =====+===== =0.375log(0.375/0.75)+0.625log(0.625/0.25)=(5/8)log5-1≈0.45bit (b) 由于P(Z=1/ Y=1)=1, 所以 P （Y=1，Z=1/X=1）= P （Y=1/X=1）=0.5 P （Y=1，Z=1/X=0）= P （Y=1/X=0）=0.1那么P （Z=1/X=1）= P （Z=1,Y=1/X=1）+ P （Z=1,Y=0/X=1）=0.5+ P （Z=1/Y=0，X=1）P （Y=0/X=1）=0.5+0.5*0.4=0.7P(Z=1/X=0)= P （Z=1,Y=1/X=0）+ P （Z=1,Y=0/X=0）=0.1+P(Z=1/Y=0，X=0)P(Y=0/X=0)=0.1+0.9*0.4=0.46P （Z=1,X=1）= P （Z=1/X=1）*P(X=1)=0.7*0.25=0.175P （Z=1,X=0）= P （Z=1/X=0）*P(X=0)= 0.46*0.75=0.345 P(Z=1) = P(Z=1,X=1)+ P(Z=1,X=0) = 0.52 P(X=0/Z=1)=0.345/0.52=69/104 P(X=1/Z=1)=35/104I (X ;Z=1)=∑∑=====x x )P()1Z /(P log )1Z /(P )1Z (I )1Z /(P x x x x;x=1)P(X )1Z /1X (P log )1Z /1X (P 0)P(X )1Z /0X (P log )1Z /0X (P =====+======(69/104)log(23/26)+( 35/104)log(35/26) ≈0.027bit(c)H （X ）=0.25*log(1/0.25)+0.75*log(1/0.75)=2-(3/4)log3=0.811bit H(Y/X)=-P(X=1,Y=1)logP(Y=1/X=1) -P(X=1,Y=0)logP(Y=0/X=1)-P(X=0,Y=1)logP(Y=1/X=0) -P(X=0,Y=0)logP(Y=0/X=0)=-0.125*log0.5-0.125*log0.5-0.075*log0.1-0.675*log0.9=1/4+(3/40)log10-(27/40)log(9/10)≈0.603bitH(XY)=H(X)+H(Y/X)=9/4+(3/4)log10-(21/10)log3=1.414bitP(X=0,Y=0,Z=0)= P(Z=0 / X=0, Y=0)* P( X=0, Y=0)=(1-0.4)*(0.75-0.075)=0.405 P(X=0,Y=0,Z=1)= P(Z=1 / X=0, Y=0)* P( X=0, Y=0)=0.4*0.675=0.27 P(X=1,Y=0,Z=1)= P(Z=1/ X=1,Y=0)* P(X=1,Y=0)=0.4*(0.25-0.125)=0.05 P(X=1,Y=0,Z=0)= P(Z=0/ X=1,Y=0)* P(X=1,Y=0)=0.6*0.125=0.075 P(X=1,Y=1,Z=1)=P(X=1,Z=1)- P(X=1,Y=0,Z=1)=0.175-0.05=0.125 P(X=1,Y=1,Z=0)=0 P(X=0,Y=1,Z=0)=0P(X=0,Y=1,Z=1)= P(X=0,Z=1)- P(X=0,Y=0,Z=1)= 0.345-0.27=0.075H(XYZ)=-0.405*log0.405-0.27*log0.27-0.05*log0.05-0.075*log0.075-0.125*log0.125-0.07 5*log0.075=(113/100)+(31/20)log10-(129/50)log3=0.528+0.51+0.216+0.28+0.375+0.28=2.189 bitH(Z/XY)=H(XYZ)-H(XY)= -28/25+(4/5)log10-12/25log3 =0.775bit2.9 解：A，B，C分别表示三个筛子掷的点数。

《信息论与编码》习题答案(高等教育出版社)仇佩亮编

――――――――――――――――――――――――――课外习题1．设某信道，其信道矩阵为若信道的输入符号a1,a2,a3先验等概，（1）若使平均错误译码概率最小,请选择译码函数。

（2）求出此错误译码概率Pemin。

解：(1)因为先验等概,所以选择最大似然译码准则F(b1)=a1 F(b2)=a3 F(b3)=a2(2) Pemin=2. 有二进制对称信道p=0.01 =0.99(1) 采用最大似然译码准则确定译码函数,(2) 求出最小平均错误译码概率。

(3) 对该信道进行扩展,采用简单重复编码，000,111, 采用最大似然译码准则确定译码规则。

(4) 求出扩展后的最小平均错误译码概率。

(5) 求出扩展后的信道传输率解：（1）P(j/i)= 译码函数为F(b1)=a1，F(b2)=a2(2) P emin=(0.01+0.01)/2=0.01(3)译码函数F(β1)= F(β2)= F(β3)= F(β4)=000=α 1F(β5)= F(β6)= F(β7)= F(β8)=000=α2（4）平均错误最小概率为（5）R==3．αi，βj是两个码符号{0,1}组成的符号序列，求αi，βj之间的汉明距离解：D(αi，βj)=4．W:{000,001,010,100,011,110,101,111}的最小汉明距离解：D min=15．设有一离散信道，其信道矩阵为(1) 当信源X的概率分布为p(a1)=2/3，p(a2)=p(a3)=1/6时，按最大后验概率准则选择译码函数，并计算其平均错误译码概率P emin(2) 当信源是等概率是分布时，选择最大似然译码准则选择译码函数，并计算其平均错误译码概率P emin。

解：(1) 联合概率：后验概率根据最大后验概率准则F(b1)=a1，F(b2)=a1，F(b3)=a1最小错误译码概率为(2) 当信源是等概率分布时采用最大似然译码准则F(b1)=a1，F(b2)=a2，F(b3)=a36．设离散无记忆信道的输入符号集X:{0,1}，输出符号集Y:{0,1,2}，信道矩阵为P=若某信源输出两个等该消息x1，x2，现在用信道输入符号集对x1，x2进行编码，W1=00，W2=11代表x1，x2。

《信息论与编码理论》(王育民李晖梁传甲)课后习题问题详解高等教育出版社

信息论与编码理论习题解第二章-信息量和熵2.1解: 平均每个符号长为:1544.0312.032=⨯+⨯秒每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以信息速率为444.34159183.0=⨯比特/秒2.2 解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特；所以信息速率为600010006=⨯比特/秒2.3 解:(a)一对骰子总点数为7的概率是366 所以得到的信息量为 585.2)366(log 2= 比特 (b) 一对骰子总点数为12的概率是361 所以得到的信息量为 17.5361log 2= 比特 2.4 解: (a)任一特定排列的概率为!521,所以给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为13521313521344!13C A =⨯所以得到的信息量为 21.134log 1313522=C 比特.2.5 解:易证每次出现i 点的概率为21i,所以比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 解: 可能有的排列总数为27720!5!4!3!12= 没有两棵梧桐树相邻的排列数可如下图求得， Y X Y X Y X Y X Y X Y X Y X Y图中X 表示白杨或白桦，它有⎪⎪⎭⎫⎝⎛37种排法，Y 表示梧桐树可以栽种的位置，它有⎪⎪⎭⎫⎝⎛58种排法，所以共有⎪⎪⎭⎫ ⎝⎛58*⎪⎪⎭⎫⎝⎛37=1960种排法保证没有两棵梧桐树相邻，因此若告诉你没有两棵梧桐树相邻时，得到关于树排列的信息为1960log 27720log 22-=3.822 比特 2.7 解: X=0表示未录取，X=1表示录取； Y=0表示本市，Y=1表示外地；Z=0表示学过英语，Z=1表示未学过英语，由此得比特比特比特)01(log )01()0()00(log )00()0()(8113.04log 4134log 43)()(02698.04110435log 104354310469log 10469)1()01(log )01()0()00(log )00()0;(104352513/41)522121()0(/)1())11()1,10()10()1,00(()01(104692513/43)104109101()0(/)0())01()0,10()00()0,00(()00()(4512.04185log 854383log 83)1()01(log )01()0()00(log )00()0;(8551/4121)0(/)1()10()01(8351/43101)0(/)0()00()00()(,251225131)1(,2513100405451)10()1()00()0()0(,54511)1(,51101432141)10()1()00()0()0(,41)1(,43)0(222222222222+=====+=======+==+======+========⨯⨯+========+=========⨯⨯+========+=========+======+========⨯=========⨯=========-===⨯+====+======-===⨯+⨯====+=========x y p x y p x p x y p x y p x p X Y H X H c x p z x p z x p x p z x p z x p z X I z p x p x y p x y z p x y p x y z p z x p z p x p x y p x y z p x y p x y z p z x p b x p y x p y x p x p y x p y x p y X I y p x p x y p y x p y p x p x y p y x p a z p y z p y p y z p y p z p y p x y p x p x y p x p y p x p x p2.8 解:令{}{}R F T Y B A X ,,,,==，则比特得令同理03645.0)()(5.0,02.03.0)2.05.0(log 2.0)()2.05.0(log )2.05.0()2.03.0(log )2.03.0(5.0log 5.03.0log 3.0)5log )1(2.02log )1(5.0log )1(3.05log 2.0log 3.02log 5.0(2.0log 2.0)2.05.0(log )2.05.0()2.03.0(log )2.03.0()()();()(2.0)(,2.05.0)(2.03.0)1(3.05.0)()()()()(5.0max 2'2222223102231022222==∴==+-=---++-+=-+-+-+++-----++-=-===-=+=-⨯+=+==p p I p I p pp p I p p p p p p p p p p p p p p X Y H Y H Y X I p I R P p F P pp p B P B T P A P A T P T P2.9 & 2.12解:令X=X 1,Y=X 1+X 2,Z=X 1+X 2+X 3, H(X 1)=H(X 2)=H(X 3)= 6log 2 比特 H(X)= H(X 1) = 6log 2 =2.585比特 H(Y)= H(X 2+X 3)=6log 61)536log 365436log 364336log 363236log 36236log 361(2222222+++++ = 3.2744比特 H(Z)= H(X 1+X 2+X 3)=)27216log 2162725216log 2162521216log 2162115216log 2161510216log 216106216log 21663216log 2163216log 2161(222222222++++++= 3.5993比特所以H(Z/Y)= H(X 3)= 2.585 比特 H(Z/X) = H(X 2+X 3)= 3.2744比特 H(X/Y)=H(X)-H(Y)+H(Y/X) = 2.585-3.2744+2.585 =1.8955比特H(Z/XY)=H(Z/Y)= 2.585比特 H(XZ/Y)=H(X/Y)+H(Z/XY) =1.8955+2.585 =4.4805比特 I(Y;Z)=H(Z)-H(Z/Y) =H(Z)- H(X 3)= 3.5993-2.585 =1.0143比特 I(X;Z)=H(Z)-H(Z/X)=3.5993- 3.2744 =0.3249比特 I(XY ;Z)=H(Z)-H(Z/XY) =H(Z)-H(Z/Y)=1.0143比特 I(Y;Z/X)=H(Z/X)-H(Z/XY) = H(X 2+X 3)-H(X 3) =3.2744-2.585 =0.6894比特 I(X;Z/Y)=H(Z/Y)-H(Z/XY) =H(Z/Y)-H(Z/Y) =02.10 解:设系统输出10个数字X 等概,接收数字为Y,显然101)(101)()()(919===∑∑==i j p i j p i Q j w i iH(Y)=log10比特奇奇奇奇偶18log 81101452log 211015)(log)()()(log )()(0)(log ),()(log ),()(22,2222=⨯⨯⨯⨯+⨯⨯⨯=--=--=∑∑∑∑∑∑∑≠====x y p x y p x p x x p x x p x p x y p y x p x y p y x p X Y H x y x i y x y x所以I(X;Y)= 3219.2110log 2=-比特2.11 解:（a ）接收前一个数字为0的概率 2180)0()()0(==∑=i i i u p u q wbits p pw u p u I )1(log 11log )0()0(log )0;(2212121-+=-==（b ）同理 418)00()()00(==∑=ii iu p u q wbits p p w u p u I )1(log 22)1(log )00()00(log )00;(24122121-+=-== （c ）同理 818)000()()000(==∑=ii iu p u q wbits p p w u p u I )1(log 33)1(log )000()000(log )000;(28132121-+=-== （d ）同理 ))1(6)1(()0000()()0000(4226818p p p p u p u q w ii i+-+-==∑=bitsp p p p p p p p p p w u p u I 42264242268142121)1(6)1()1(8log ))1(6)1(()1(log )0000()0000(log )0000;(+-+--=+-+--==2.12 解:见2.9 2.13 解: (b))/()/()/(1log)()/(1log)()/()/(1log)()/(1log)()/(XY Z H X Y H xy z p xyz p x y p xyz p xy z p x y p xyz p x yz p xyz p X YZ H x y z xyzxyzxyz+=+===∑∑∑∑∑∑∑∑∑∑∑∑(c))/()/(1log)/()()/(1log)/()()/(X Z H x z p xy z p xy p xy z p xy z p xy p XY Z H xyzxyz=≤=∑∑∑∑∑∑（由第二基本不等式）或)1)/()/((log )/()()/()/(log)/()()/(1log)/()()/(1log)/()()/()/(=-⨯≤=-=-∑∑∑∑∑∑∑∑∑∑∑∑xy z p x z p e xy z p xy p xy z p x z p xy z p xy p x z p xy z p xy p xy z p xy z p xy p X Z H XY Z H xyzxyzxyzxyz（由第一基本不等式）所以)/()/(X Z H XY Z H ≤(a))/()/()/()/()/(X YZ H XY Z H X Y H X Z H X Y H =+≥+等号成立的条件为)/()/(x z p xy z p =,对所有Z z Y y X x ∈∈∈,,,即在给定X 条件下Y 与Z 相互独立。

信息论与编码_习题解答

2.5 居住某地区的女孩子有25%是大学生，在女大学生中有75%是身高160厘米以上的，而女孩子中身高160厘米以上的占总数的一半。

假如我们得知“身高160厘米以上的某女孩是大学生”的消息，问获得多少信息量？解：设随机变量X 代表女孩子学历X x 1（是大学生） x 2（不是大学生） P(X) 0.25 0.75设随机变量Y 代表女孩子身高Y y 1（身高>160cm ） y 2（身高<160cm ） P(Y) 0.5 0.5已知：在女大学生中有75%是身高160厘米以上的即：bit x y p 75.0)/(11=求：身高160厘米以上的某女孩是大学生的信息量即：bit y p x y p x p y x p y x I 415.15.075.025.0log )()/()(log)/(log )/(11111111=⨯-=-=-=2.7 设有一离散无记忆信源，其概率空间为123401233/81/41/41/8X x x x x P ====⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭（1）求每个符号的自信息量（2）信源发出一消息符号序列为{202 120 130 213 001 203 210 110 321 010 021 032 011 223 210}，求该序列的自信息量和平均每个符号携带的信息量解：122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit ===因为信源无记忆，所以此消息序列的信息量就等于该序列中各个符号的信息量之和就有：123414()13()12()6()87.81I I x I x I x I x bit =+++=平均每个符号携带的信息量为87.811.9545=bit/符号 2.13 有两个二元随机变量X 和Y ，它们的联合概率为并定义另一随机变量Z = XY （一般乘积），试计算： (1) H(X), H(Y), H(Z), H(XZ), H(YZ)和H(XYZ)；(2) H(X/Y), H(Y/X), H(X/Z), H(Z/X), H(Y/Z), H(Z/Y), H(X/YZ), H(Y/XZ)和H(Z/XY)；(3) I(X;Y), I(X;Z), I(Y;Z), I(X;Y/Z), I(Y;Z/X)和I(X;Z/Y)。

信息论与编码陈运主编答案完整版

2.10 一阶马尔可夫信源的状态图如下图所示。信源 X 的符号集为{0, 1, 2}。 (1) 求平稳后信源的概率分布； (2) 求信源的熵 H∞。
解： (1)
⎧p e( 1 ) = p e p e( 1 ) ( 1 /e1 ) + p e( 2 ) (p e1 /e2 ) ⎪ ⎨p e( 2 ) = p e( 2 ) (p e2 /e2 ) + p e( 3 ) (p e2 /e3 )
i
)
p x( )log p x( )
信源 = 1
⎡ X ⎤ ⎧ x 2.6 设 x2
x3 x4
⎢P X( )⎥⎦ ⎨⎩0.2 0.19 0.18 0.17 0.16
⎣
H(X) > log6 不满足信源熵的极值性。
解：
x5 0.17⎬⎭
x6 ⎫ ，求这个信源的熵，并解释为什么
HX
i
px px
=−(0.2log0.2 + 0.19log0.19 + 0.18log0.18+ 0.17log0.17 + 0.16log0.16 + 0.17log0.17) = 2.657 bit symbol/ H X( ) > log 62 = 2.585

p x x( i1 i3 )log p x( i3 / xi1)
i1 i2 i3
i1 i3
∑∑∑ ∑∑∑ = −
p x x x( i1 i2i3 )log p x( i3 / x xi1 i2 ) +
p x x x( i1 i2i3 )log p x( i3 / xi1)
i1
i2 i3 i1 i2 i3 p x( i3 / xi1)

信息论与编码理论习题答案全解

第二章信息量和熵2.2 八元编码系统，码长为3，第一个符号用于同步，每秒1000个码字，求它的信息速率。

解：同步信息均相同，不含信息，因此每个码字的信息量为 2⨯8log =2⨯3=6 bit因此，信息速率为 6⨯1000=6000 bit/s2.3 掷一对无偏骰子，告诉你得到的总的点数为：(a) 7; (b) 12。

问各得到多少信息量。

解：(1) 可能的组合为 {1，6},{2，5},{3，4},{4，3},{5，2},{6，1})(a p =366=61得到的信息量 =)(1loga p =6log =2.585 bit (2) 可能的唯一，为 {6，6})(b p =361得到的信息量=)(1logb p =36log =5.17 bit2.4 经过充分洗牌后的一副扑克（52张），问：(a) 任何一种特定的排列所给出的信息量是多少？(b) 若从中抽取13张牌，所给出的点数都不相同时得到多少信息量？解：(a) )(a p =!521信息量=)(1loga p =!52log =225.58 bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C =13.208 bit2.9 随机掷3颗骰子，X 表示第一颗骰子的结果，Y 表示第一和第二颗骰子的点数之和，Z 表示3颗骰子的点数之和，试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。

信息论与编码理论习题答案

= 3、3 设有一离散无记忆信源,U＝，其熵为。考察其长为得输出序列，当时满
足下式
（a）在=0、０５,=0、1 下求 (b）在＝，＝下求（c)令就是序列得集合，其中
试求Ｌ=时情况（a)(b）下,T 中元素个数得上下限. 解：＝==０、８１ bit
= ＝=—
= =0、471 则根据契比雪夫大数定理
0、2
00１
10０
a４
0、１
０00１
10００
(a) 各码就是否满足异字头条件？就是否为唯一可译码？
(b) 当收到 1 时得到多少关于字母 a 得信息？
(c) 当收到 1 时得到多少关于信源得平均信息?
２、14 对于任意概率事件集 X，Y,Z，证明下述关系式成立 (ａ）＋,给出等号成立得条件 (ｂ）=+ （c）
证明：(b) =-
=＝—-
=+ (c) ＝-
=［—］ [-］
＝—
= 当=，即Ｘ给定条件下，Y 与 Z 相互独立时等号成立 (ａ）上式(ｃ)左右两边加上，可得＋＋于就是+ ２、2８令概率空间，令 Y 就是连续随机变量。已知条件概率密度为，求： (a)Y 得概率密度 (ｂ) （ｃ) 若对 Y 做如下硬判决
求，并对结果进行解释. 解：（a) 由已知,可得
= ＝
＝＋
= （ｂ) ==2、５ bｉt
=
= =2 bｉt =-＝0、5 ｂit （c) 由可得到Ｖ得分布律
Ｖ
—１
p
1/4
再由可知
V
－1
p(V|x=－１）
１/2
p(V｜x=1）
0
bｉt
=1 bit ＝= 0、5 bit
０ 1/2
0 1/2 1/2

彭代渊王玲-信息论与编码理论-第二章习题解答精选全文

1第2章信息的度量2.1 同时扔一对质地均匀的骰子，当得知“两骰子面朝上点数之和为5”或“面朝上点数之和为8”或“两骰子面朝上点数是3和6”时，试问这三种情况分别获得多少信息量？解：某一骰子扔得某一点数面朝上的概率是相等的，均为1/6，两骰子面朝上点数的状态共有36种,其中任一状态出现都是等概率的,出现概率为1/36。

设两骰子面朝上点数之和为事件a ，有：⑴ a=5时，有1+4，4+1，2+3，3+2，共4种，则该事件发生概率为4/36=1/9，则信息量为I(a)=-logp(a=5)=-log1/9≈3.17(bit)⑵ a=8时，有2+6，6+2，4+4，3+5，5+3，共5种，则p(a)=5/36,则I(a)= -log5/36≈2.85(bit) ⑶ p(a)=2/36=1/18,则I(a)=-log1/18≈4.17(bit)2.2 如果你在不知道今天是星期几的情况下问你的朋友“明天是星期几”，则答案中含有多少信息量？如果你在已知今天是星期三的情况下提出同样的问题，则答案中你能获得多少信息量（假设已知星期一至星期日的排序）？解：设“明天是星期几”为事件a ：⑴ 不知道今天是星期几：I(a)=-log1/7≈2.81(bit) ⑵ 知道今天是星期几：I(a)=-log1=0 (bit)2.3 居住某地区的女孩中有20%是大学生，在女大学生中有80%是身高1米6以上的，而女孩中身高1米6以上的占总数的一半。

假如我们得知“身高1米6以上的某女孩是大学生”的消息，求获得多少信息量？解：设“居住某地区的女孩是大学生”为事件a ，“身高1米6以上的女孩”为事件b ，则有： p(a)= 0.2，p(b|a)=0.8，p(b)=0.5，则“身高1米6以上的某女孩是大学生”的概率为：32.05.08.02.0)()|()()|(=⨯==b p a b p a p b a p信息量为：I=-logp(a|b)=-log0.32≈1.64(bit)2.4 从大量统计资料知道，男性中红绿色盲的发病率为7%，女性发病率为0.5%，如果你问一位男同志：“你是否是红绿色盲？”，他回答“是”或“否”，问这两个回答中各含有多少信息量？平均每个回答中含有多少信息量？如果你问一位女同志，则答案中含有的平均自信息量是多少？解：⑴ 男同志回答“是”的概率为7%=0.07，则信息量I=-log0.07≈3.84(bit) 男同志回答“否”的概率为1-7%=0.93，则信息量I=-log0.93≈0.10(bit) 平均信息量为：H 1=-(0.07×log0.07+0.93×log0.93) ≈0.37(bit/符号) ⑵ 问女同志的平均自信息量：H 2=-[0.05×log0.05+(1-0.05) ×log(1-0.05)] ≈0.045(bit/符号)2.5 如有7行9列的棋型方格，若有两个质点A 和B ，分别以等概率落入任一方格内，2且它们的坐标分别为（X A ，Y A ）、（X B ，Y B ），但A 、B 不能落入同一方格内。

信息论与编码理论-第3章信道容量-习题解答-071102

第3章信道容量习题解答3-1 设二进制对称信道的转移概率矩阵为2/31/31/32/3⎡⎤⎢⎥⎣⎦解: (1) 若12()3/4,()1/4P a P a ==，求(),(),(|),(|)H X H Y H X Y H Y X 和(;)I X Y 。

i i 2i=13311H(X)=p(a )log p(a )log()log()0.8113(/)4444bit -=-⨯-=∑符号111121*********j j j=132117p(b )=p(a )p(b |a )+p(a )p(b |a )=43431231125p(b )=p(a )p(b |a )+p(a )p(b |a )=4343127755H(Y)=p(b )log(b )=log()log()0.9799(/)12121212bit ⨯+⨯=⨯+⨯=---=∑符号 22i j j i j i j i ,H(Y|X)=p(a ,b )logp(b |a )p(b |a )logp(b |a )2211log()log()0.9183(/)3333i jjbit -=-=-⨯-⨯=∑∑符号I(X;Y)=H(Y)H(Y|X)=0.97990.91830.0616(/)bit --=符号 H(X|Y)=H(X)I(X;Y)=0.81130.06160.7497(/bit --=符号)(2)求该信道的信道容量及其达到信道容量时的输入概率分布。

二进制对称信息的信道容量H(P)=-plog(p)-(1-p)log(1-p)1122C =1-H(P)=1+log()+log()=0.0817(bit/)3333符 BSC 信道达到信道容量时，输入为等概率分布，即：{0.5，0.5} 注意单位3-2 求下列三个信道的信道容量及其最佳的输入概率分布。

1b 2b 3b 3a 2a 1a Y X 1b 2b 3a 2a 1a Y X 1b 2b 2a 1a Y X 3b 11111110.70.3第一种：无噪无损信道，其概率转移矩阵为： 1 0 0P=0 1 00 0 1⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦信道容量：()max (;)P X C I X Y @ bit/符号()()()()max{(;)}max{()(|)}(|)0max{(;)}max{()}p x p x p x p x C I X Y H X H X Y H X Y C I X Y H X ==-∴=∴==离散无记忆信道(DMC)只有输入为等概率分布时才能达到信道容量，C=log3=1.5850 bit/符号输入最佳概率分布如下：111,,333⎧⎫⎨⎬⎩⎭第二种：无噪有损信道，其概率转移矩阵为： 1 0P=0 10 1⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，离散输入信道， ()()()()max{(;)}max{()(|)}(|)0max{(;)}max{()}p x p x p x p x C I X Y H Y H Y X H Y X C I X Y H Y ==-∴=∴==H(Y)输出为等概率分布时可达到最大值，此值就是信道容量此时最佳输入概率：123p(a )+p(a )=0.5,p(a )=0.5 信道容量：C=log(2)=1 bit/符号第三种：有噪无损信道，由图可知：()()()()max{(;)}max{()(|)}(|)0max{(;)}max{()}p x p x p x p x C I X Y H X H X Y H X Y C I X Y H X ==-∴=∴==输入为等概率分布时可达到信道容量，此时信道容量p(x)C=max{H(X)}=log(2)=1 bit/符号输入最佳概率分布：11,22⎧⎫⎨⎬⎩⎭3-3 设4元删除信道的输入量{1,2,3,4}X ∈，输出量{1,2,3,4,}Y E ∈，转移概率为(|)1(|)1-ε 0 0 0 ε0 1-ε 0 0 ε P=0 0 1-ε 0 ε0 0 0 1-ε ε1-ε 0 0 0 ε0 1-ε 0 0 ε p1= p2=0 0 1-ε 0 ε0 0 0 1-ε εP Y i X i P Y E X i εε===-===⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦其中1,2,3,4i = 1）该信道是对称DMC 信道吗？ 2）计算该信道的信道容量；3）比较该信道与两个独立并联的二元删除信道的信道容量。

信息论与编码理论-习题答案-姜楠-王健-编著-清华大学

第1章绪论1.1 信源、编码器、信道、干扰、译码器、信宿 1.2 香农1.3 通信系统模型1.4信号是消息的表现形式，是物理的，比如电信号、光信号等。

消息是信息的载荷者，是信号的具体容，不是物理的，但是又比较具体，例如语言、文字、符号、图片等。

信息包含在消息中，是通信系统中被传送的对象，消息被人的大脑所理解就形成了信息。

1.5 略第2章信息的统计度量2.1 少2.2 y 的出现有助于肯定x 的出现、y 的出现有助于否定x 的出现、x 和y 相互独立 2.3 FTTTF 2.4 2.12比特2.5依题意，题中的过程可分为两步，一是取出一枚硬币恰好是重量不同的那一枚，设其发生的概率为1p ，由于每枚硬币被取出的概率是相同的，所以1181p =所需要的信息量()()1log 6.34I A p bit =-=二是确定它比其他硬币是重还是轻，设其发生的概率为2p ，则212p =总的概率12111812162p p p ==⨯=所需要的信息量()log log1627.34I p bit =-==2.6 设A 表示“大学生”这一事件，B 表示“身高1.60m 以上”这一事件，则()()()0.250.5|0.75p A p B p B A ===故()()()()()()|0.750.25|0.3750.5p AB p A p B A p A B p B p B ⨯====()()()11|loglog 1.42|0.375I A B bit p A B ===2.7 四进制波形所含的信息量为()log 42bit =，八进制波形所含信息量为()log 83bit =，故四进制波形所含信息量为二进制的2倍，八进制波形所含信息量为二进制的3倍。

2.8()()()()()()2322log 3log 32log 3 1.585I p bit I p bit I I =-=-==故以3为底的信息单位是比特的1.585倍。

信息论与编码试卷及答案解析

一、（11’）填空题（1）1948年，美国数学家香农发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。

（2）必然事件的自信息是0 。

（3）离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的N倍。

（4）对于离散无记忆信源，当信源熵有最大值时，满足条件为__信源符号等概分布_。

（5）若一离散无记忆信源的信源熵H（X）等于2.5，对信源进行等长的无失真二进制编码，则编码长度至少为 3 。

（6）对于香农编码、费诺编码和霍夫曼编码，编码方法惟一的是香农编码。

（7）已知某线性分组码的最小汉明距离为3，那么这组码最多能检测出_2_______个码元错误，最多能纠正___1__个码元错误。

（8）设有一离散无记忆平稳信道，其信道容量为C，只要待传送的信息传输率R__小于___C（大于、小于或者等于），则存在一种编码，当输入序列长度n足够大，使译码错误概率任意小。

（9）平均错误概率不仅与信道本身的统计特性有关，还与___译码规则____________和___编码方法___有关三、（5 ）居住在某地区的女孩中有25%是大学生，在女大学生中有75%是身高1.6米以上的，而女孩中身高1.6米以上的占总数的一半。

假如我们得知“身高1.6米以上的某女孩是大学生”的消息，问获得多少信息量？解：设A表示“大学生”这一事件，B表示“身高1.60以上”这一事件，则P(A)=0.25 p(B)=0.5 p(B|A)=0.75 （2分）故 p(A|B)=p(AB)/p(B)=p(A)p(B|A)/p(B)=0.75*0.25/0.5=0.375 （2分） I(A|B)=-log0.375=1.42bit （1分）四、（5'）证明：平均互信息量同信息熵之间满足I(X;Y)=H(X)+H(Y)-H(XY) 证明：()()()()()()()()()()Y X H X H y x p y x p x p y x p x p y x p y x p Y X I X X Y j i j i Y i j i XYi j i j i -=⎥⎦⎤⎢⎣⎡---==∑∑∑∑∑∑log log log; （2分）同理()()()X Y H Y H Y X I -=; （1分）则()()()Y X I Y H X Y H ;-= 因为()()()X Y H X H XY H += （1分）故()()()()Y X I Y H X H XY H ;-+=即()()()()XY H Y H X H Y X I -+=; （1分）五、（18’）.黑白气象传真图的消息只有黑色和白色两种，求：1）黑色出现的概率为0.3，白色出现的概率为0.7。

信息论与编码课后习题答案

1．有一个马尔可夫信源，已知p(x 1|x 1)=2/3，p(x 2|x 1)=1/3，p(x 1|x 2)=1，p(x 2|x 2)=0，试画出该信源的香农线图，并求出信源熵。

解：该信源的香农线图为： 1/3○○2/3(x 1) 1 (x 2)在计算信源熵之前，先用转移概率求稳定状态下二个状态x 1和 x 2的概率)(1x p 和)(2x p 立方程：)()()(1111x p x x p x p =+)()(221x p x x p=)()(2132x p x p + )()()(1122x p x x p x p =+)()(222x p x x p=)(0)(2131x p x p + )()(21x p x p +=1 得431)(=x p 412)(=x p 马尔可夫信源熵H = ∑∑-IJi j i jix x p x xp x p )(log )()( 得 H=0.689bit/符号2．设有一个无记忆信源发出符号A 和B ，已知4341)(.)(==B p A p 。

求： ①计算该信源熵；②设该信源改为发出二重符号序列消息的信源，采用费诺编码方法，求其平均信息传输速率； ③又设该信源改为发三重序列消息的信源，采用霍夫曼编码方法，求其平均信息传输速率。

解：①∑-=Xiix p x p X H )(log )()( =0.812 bit/符号②发出二重符号序列消息的信源,发出四种消息的概率分别为1614141)(=⨯=AA p 1634341)(=⨯=AB p 1634143)(=⨯=BA p 1694343)(=⨯=BB p 用费诺编码方法代码组 b iBB 0 1 BA 10 2 AB 110 3 AA 111 3 无记忆信源 624.1)(2)(2==X H X H bit/双符号平均代码组长度 2B =1.687 bit/双符号BX H R )(22==0.963 bit/码元时间③三重符号序列消息有8个,它们的概率分别为641)(=AAA p 643)(=AAB p 643)(=BAA p 643)(=ABA p 649)(=BBA p 649)(=BAB p 649)(=ABB p 6427)(=BBB p用霍夫曼编码方法代码组 b i BBB 6427 0 0 1 BBA 649 0 )(6419 1 110 3 BAB 649 1 )(6418)(644 1 101 3 ABB 649 0 0 100 3AAB 643 1 )(646 1 11111 5 BAA 643 0 1 11110 5ABA 643 1 )(6440 11101 5AAA 6410 11100 5)(3)(3X H X H ==2.436 bit/三重符号序列 3B =2.469码元/三重符号序列3R =BX H )(3=0.987 bit/码元时间 3．已知符号集合{ 321,,x x x }为无限离散消息集合，它们的出现概率分别为 211)(=x p ，412)(=x p 813)(=x p ···i i x p 21)(=···求： ① 用香农编码方法写出各个符号消息的码字（代码组）； ② 计算码字的平均信息传输速率； ③ 计算信源编码效率。

信息论与编码习题参考答案(全)

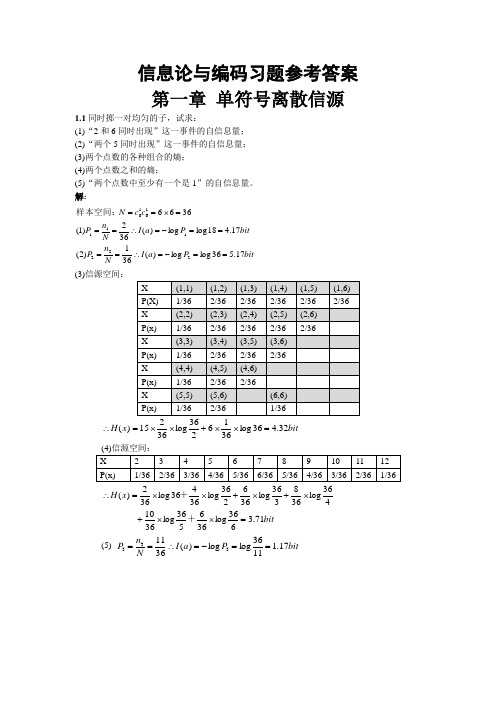
信息论与编码习题参考答案第一章单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。

解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。

（1）若仅有质点A ，求A 落入任一方格的平均信息量；（2）若已知A 已落入，求B 落入的平均信息量；（3）若A ，B 是可辨认的，求A ，B 落入的平均信息量。

解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。

信息论与编码理论-习题答案-姜楠-王健-编著-清华大学

第1章绪论1.1 信源、编码器、信道、干扰、译码器、信宿 1.2 香农1.3 通信系统模型1.4信号是消息的表现形式，是物理的，比如电信号、光信号等。

消息是信息的载荷者，是信号的具体内容，不是物理的，但是又比较具体，例如语言、文字、符号、图片等。

信息包含在消息中，是通信系统中被传送的对象，消息被人的大脑所理解就形成了信息。

2.8()()()()()()2322log 3log 32log 3 1.585I p bit I p bit I I =-=-==故以3为底的信息单位是比特的1.585倍。

信息论与编码试题集与答案(新)

1. 在无失真的信源中，信源输出由 H (X ) 来度量；在有失真的信源中，信源输出由 R (D ) 来度量。

2. 要使通信系统做到传输信息有效、可靠和保密，必须首先信源编码，然后_____加密____编码，再______信道_____编码，最后送入信道。

3. 带限AWGN 波形信道在平均功率受限条件下信道容量的基本公式，也就是有名的香农公式是log(1)C W SNR =+；当归一化信道容量C/W 趋近于零时，也即信道完全丧失了通信能力，此时E b /N 0为 -1.6 dB ，我们将它称作香农限，是一切编码方式所能达到的理论极限。

4. 保密系统的密钥量越小，密钥熵H (K )就越小，其密文中含有的关于明文的信息量I (M ；C )就越大。

5. 已知n ＝7的循环码42()1g x x x x =+++，则信息位长度k 为 3 ，校验多项式 h(x)= 31x x ++ 。

6. 设输入符号表为X ＝{0，1}，输出符号表为Y ＝{0，1}。

输入信号的概率分布为p ＝(1/2，1/2)，失真函数为d (0，0) = d (1，1) = 0，d (0，1) =2，d (1，0) = 1，则D min ＝ 0 ，R (D min )＝ 1bit/symbol ，相应的编码器转移概率矩阵[p(y/x )]＝1001⎡⎤⎢⎥⎣⎦；D max ＝ 0.5 ，R (D max )＝ 0 ，相应的编码器转移概率矩阵[p(y/x )]＝1010⎡⎤⎢⎥⎣⎦。

7. 已知用户A 的RSA 公开密钥(e,n )=(3,55)，5,11p q ==,则()φn = 40 ，他的秘密密钥(d,n )＝(27,55) 。

若用户B 向用户A 发送m =2的加密消息，则该加密后的消息为 8 。

二、判断题1. 可以用克劳夫特不等式作为唯一可译码存在的判据。

（√ ）2. 线性码一定包含全零码。

（√ ）3. 算术编码是一种无失真的分组信源编码，其基本思想是将一定精度数值作为序列的编码，是以另外一种形式实现的最佳统计匹配编码。

信息论与编码理论习题答案全解

信息论与编码理论习题答案全解第二章信息量和熵2.2 八元编码系统，码长为3，第一个符号用于同步，每秒1000个码字，求它的信息速率。

问各得到多少信息量。

解：(1) 可能的组合为 {1，6},{2，5},{3，4},{4，3},{5，2},{6，1})(a p =366=61得到的信息量 =)(1loga p =6log =2.585 bit (2) 可能的唯一，为 {6，6})(b p =361得到的信息量=)(1logb p =36log =5.17 bit2.4 经过充分洗牌后的一副扑克（52张），问：(a) 任何一种特定的排列所给出的信息量是多少？(b) 若从中抽取13张牌，所给出的点数都不相同时得到多少信息量？解：(a) )(a p =!521信息量=)(1loga p =!52log =225.58 bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C =13.208 bit即)0;(1u I ，)00;(1u I ，)000;(1u I ，)0000;(1u I)0(p =4)1(81⨯-p +481⨯p =21)0;(1u I =)0()|0(log1p u p =211log p-=1+)1log(p - bit)00(p =]2)1(4)1(2[8122p p p p +-+-=41)00;(1u I =)00()|00(log 1p u p =4/1)1(log 2p -=)]1log(1[2p -+ bit)000(p =])1(3)1(3)1[(813223p p p p p p +-+-+-=81)000;(1u I =3[1+)1log(p -] bit)0000(p =])1(6)1[(814224p p p p +-+- )0000;(1u I =42244)1(6)1()1(8logp p p p p +-+-- bit2.12 计算习题2.9中);(Z Y I 、);(Z X I 、);,(Z Y X I 、)|;(X Z Y I 、)|;(Y Z X I 。

信息论和编码陈运主编答案解析(完整版)

⇒ H X( 2 )
≥ H X( 2 / X1 ) I X( 3;X X1 2 ) ≥ 0
⇒ H X( 3 ) ≥ H X( 3 / X X1 2 )
... I X( N;X X1 2...Xn−1) ≥ 0
⇒ H X( N ) ≥ H X( N / X X1 2...Xn−1)
WORD 完美格式
专业整理
不满足极值性的原因是
。
i
2.7 证明：H(X3/X1X2) ≤ H(X3/X1)，并说明当 X1, X2, X3 是马氏链时等式成立。证明：
H X(3 / X X12 ) − H X(3 / X1)
∑∑∑ ∑∑ = −
p x x x( i1 i2i3 )log p x( i3 / x xi1 i2 ) +
⎢p e( 1 ) = p e( 2 ) = p e( 3 ) ⎢
⎢p e( 1 ) + p e( 2 ) + p e( 3 ) =1
⎢p e( 1 ) =1/3 ⎢ ⎢p e( 2 )
⎢
=1/3 ⎢p e( 3 ) =1/3
⎢p x( 1 ) = p e( 1 ) (p x1 /e1 ) + p e( 2 ) (p x1 /e2 ) = p p e⋅( 1 ) + p p e⋅ ( 2 ) = (p + p)/3 =1/3 ⎢⎢ ⎢p x( 2 ) = p e( 2 ) (p x2 /e2 ) + p e( 3 ) (p x2 /e3 ) =p p e⋅( 2 ) + p p e⋅ ( 3 ) = (p + p)/3 =1/3
解： (1)
这个信源是平稳无记忆信源。因为有这些词语：“它在任意时间．．．．而且不论以前发生过什么符号．．．．．．．．．．．……”

《信息论与编码理论》(王育民李晖梁传甲)课后习题答案高等教育出版社

信息论与编码理论习题解第二章 -信息量和熵2.1 解: 平均每个符号长为 :20.2 10.4 4 秒3315每个符号的熵为 2log31 log 3 0.9183 比特 /符号 32 3所以信息速率为 0.9183 15 3.444 比特 /秒42.2 解: 同步信号均相同不含信息,其余认为等概 ,每个码字的信息量为 3*2=6 比特；所以信息速率为 6 10006000 比特 /秒2.3 解:(a) 一对骰子总点数为 7 的概率是 636所以得到的信息量为log 2( 6) 2.585 比特36(b)一对骰子总点数为 12 的概率是 136所以得到的信息量为log 21 比特5.17362.4 解: (a)任一特定排列的概率为1,所以给出的信息量为52!1log252 !225.58比特(b) 从中任取 13 张牌 ,所给出的点数都不相同的概率为13! 413413A 5213C 135213所以得到的信息量为 log 2C 5213.21 比特 .4132.5 解:易证每次出现 i 点的概率为i,所以21I (x i )log 2i, i 1,2,3,4,5,6 21I (x1) 4.392 比特I (x2) 3.392 比特I (x3) 2.807 比特I (x4) 2.392比特I (x5) 2.070 比特I (x6) 1.807 比特6i log2i比特H(X)212.398i 1212.6 解: 可能有的排列总数为12!277203! 4! 5!没有两棵梧桐树相邻的排列数可如下图求得，Y X Y X Y X Y X Y X Y X Y X Y图中 X 表示白杨或白桦，它有73种排法， Y 表示梧桐树可以栽种的位置，它有8种排法，所以共有8 *7=1960种排法保证没有553两棵梧桐树相邻，因此若告诉你没有两棵梧桐树相邻时，得到关于树排列的信息为 log2 27720log 2 1960 =3.822比特2.7 解: X=0 表示未录取， X=1 表示录取；Y=0 表示本市， Y=1 表示外地；Z=0 表示学过英语， Z=1 表示未学过英语，由此得p( x0) 3 ,p(x1)4 p( y0)p( x 0) p( y 1 1 3 142 410 p( y 1)1 1 4 ,5 5p( z 0)p( y 0) p(z 14405 5 100 p( z 1)1 13 12 ,25 25(a) p( x0 y 0) p( yp( x1 y 0) p( y1 , 40 x 0)p( x 1) p( y 0 x 1)1 , 50 y 0) p( y 1) p( z 0 y 1)13 , 250 x 0) p( x 0) / p( y0)13 1310/5 84 0 x 1) p( x 1) / p( y0) 1 1 / 152 4 58I ( X ; y 0)p(x0 y p(x 0 y 0) p( x 1 y 0)0) log 2p(x 1 y 0) log 2p( x 0)p( x 1)3 log 2 35log 2 58 8 8 3 8 14 40.4512比特(b) p( x0 z 0)( p( z 0 y 0, x 0) p( y 0 x 0) p( z 0 y 1, x 0) p( y 1x 0)) p(x0) / p( z 0)(19 4 ) 3/1369 10 10 10 4 25 104p( x 1z 0)( p( z 0 y 0, x 1) p( y 0 x 1) p(z 0 y1, x 1) p( y 1 x 1)) p( x1) / p(z 0)(11 2) 1/13 3522 5 4 25104I ( X ; z 0)p( x 0 zp( x 0 z 0)p( x p(x 1 z 0)0) log 21z 0) log 21)p( x 0)p( x6969log 2104104343510435log 21041 40.02698 比特(c) H ( X )3 log 24 1 log 2 40.8113 比特4 3 4H(Y X)p( x 0) p( y 0 x 0) log 2 p( y 0 x 0) p( x 0) p( y 1 x 0) log 2 p( y 1x 0)p( x 1) p( y 0 x1) log 2 p( y 0 x 1)p( x 1) p( y 1 x1) log 2 p( y 1 x1)3 1log 2 10 3 9log 2 10 1 1 log 2 2 11log 2 2 410410 9 4 2 4 20.6017比特2.8 解:令X A,B,Y T,F,R ，则P(T)P(T A)P(A)P(T B)P(B)0.5 p0.3(1p)0.3 0.2 p同理P(F )0.50.2 p,P(R)0.2I ( p) I ( X ; Y)H (Y)H(Y X)(0.30.2p) log2 (0.30.2 p)(0.50.2p) log2 (0.50.2 p)0.2log 2 0.2(0.5 p log2 20.3 plog 21030.2 p log2 50.3(1p) log2103 0.5(1 p) log2 20.2(1p) log2 5)0.3log 2 0.30.5log 2 0.5(0.30.2p) log2 (0.30.2 p)(0.50.2 p) log2 (0.5 0.2 p)令I '( p)0.2 log2(0.50.2 p)0,得p0.50.30.2 pI ( p)max I ( p) p0 .50.03645比特2.9 & 2.12解:令 X=X 1,Y=X 1+X 2,Z=X 1+X 2+X 3, H(X 1)=H(X 2)=H(X 3)= log26比特H(X)= H(X 1) = log26=2.585 比特H(Y)= H(X 2+X 3)=2( 1log 2 362log 2363log 2364log 2365log 236 )1log 2 6363623633643656 = 3.2744 比特H(Z)= H(X 1+X 2+X 3)=2( 1 log 2 216 3 log 2 216 6log 2 216 10 log 2 216 15 log 2 216216 216 3 216 6 216 10 216 15 21 216 25 216 27 216 )log 2 21 log 2 log 2 27216 216 25 216= 3.5993 比特所以H(Z/Y)= H(X 3)= 2.585 比特H(Z/X) = H(X 2+X 3)= 3.2744 比特H(X/Y)=H(X)-H(Y)+H(Y/X)= 2.585-3.2744+2.585 =1.8955 比特H(Z/XY)=H(Z/Y)= 2.585 比特 H(XZ/Y)=H(X/Y)+H(Z/XY)=1.8955+2.585=4.4805 比特I(Y;Z)=H(Z)-H(Z/Y)=H(Z)- H(X 3)= 3.5993-2.585 =1.0143 比特I(X;Z)=H(Z)-H(Z/X)=3.5993- 3.2744=0.3249 比特I(XY ;Z)=H(Z)-H(Z/XY)=H(Z)-H(Z/Y)=1.0143 比特I(Y;Z/X)=H(Z/X)-H(Z/XY)=H(X 2+X 3)-H(X3) =3.2744-2.585=0.6894 比特I(X;Z/Y)=H(Z/Y)-H(Z/XY)=H(Z/Y)-H(Z/Y)=02.10 解:设系统输出10 个数字 X 等概 ,接收数字为 Y,9191显然 w( j )Q(i ) p( j i )p( j i )i010 i 110H(Y)=log10H(YX)p( x, y) log 2 p( y x)p( x, y) log2 p( y x)y x 偶y x 奇0p( x) p( x x) log 2 p( x x)p(x) p( y x) log 2 p( y x) i奇y x,奇 x奇511log2 2 5 411log2 81021081比特所以I(X;Y)=log 2 10 1 2.3219比特2.11 解:（a）接收前一个数字为0 的概率81w( 0)q(u i ) p( 0 u i )2i 0I (u1 ;0)log2p(0 u1)1p(1 p) bitslog 21 1 log 2w(0)28（b ）同理w(00)q(u ) p(00 u ) 41iI (u 1;00)p(00u 1)log 2 (1p)22 2 log 2 (1 p) bitslog 2 w(00)14（c ）同理 w(000)8q(u i ) p(000 u i )81i 0I (u 1;000) log 2 p(000u 1 ) log 2 (1 p)33 3log 2 (1p)bitsw(000)18（d ）同理 w(0000 )8q(u i ) p(0000 u i )81((1p)66 p 2 (1 p)2p 4 )i 0p(0000u 1 )(1 p)4I (u 1;0000)log 2w(0000)log 281((1 p)6 6 p 2 (1p) 2p 4 )log 2 8(1 p) 4bits(1 p) 6 6 p 2 (1 p) 2p 42.12 解:见 2.92.13 解:(b)H(YZ/ X)xyzxyzxyzH(Y/ X)1p( xyz)logp( yz / x)1p( xyz) logp( y / x) p(z / xy)11p( xyz) logp(xyz)logp( y / x)x yzp( z / xy)H(Z/ XY)(c)H (Z / XY )p(xy)p( z / xy) log1xyzp(xy)xyzH(Z / X)p(z / xy)1p( z/ xy) log （由第二基本不等式） p(z / x)或H(Z/XY)H(Z/X)p(xy)1p( z / xy) logxyzp(z / xy)p( xy)p( z/ xy) log1p( z / x)xyzp( xy)p( z/ xy) logp(z / x)（由第一基xyzp( z / xy )p( xy)p(z / xy) log e( p(z / x)1)xyzp(z / xy)本不等式）所以H(Z/XY) H(Z/X)(a)H(Y/ X) H(Z / X)H(Y/ X) H(Z/XY) H(YZ/X)等号成立的条件为 p(z / xy) p( z / x) ,对所有 xX , y Y, z Z ,即在给定 X条件下 Y 与 Z 相互独立。

信息论与编码理论(最全试题集+带答案+各种题型)

6.相比于模拟通信系统，简述数字通信系统的优点。
答：抗干扰能力强，中继时可再生，可消除噪声累计；差错可控制，可改善通信质量；便于加密和使用DSP处理技术；可综合传输各种信息，传送模拟系统时，只要在发送端增加莫属转换器，在接收端增加数模转换器即可。
7.简述信息的性质。
答：存在普遍性；有序性；相对性；可度量性；可扩充性；可存储、传输与携带性；可压缩性；可替代性；可扩散性；可共享性；时效性；
A.形式、含义和安全性
B.形式、载体和安全性
C.形式、含义和效用
D.内容、载体和可靠性
20.（D）是香农信息论最基本最重要的概念
A.信源B.信息C.消息D.熵
三．简答（
1.通信系统模型如下：
2.信息和消息的概念有何区别？
答：消息有两个特点：一是能被通信双方所理解，二是能够互相传递。相对于消息而言，信息是指包含在消息中的对通信者有意义的那部分内容，所以消息是信息的载体，消息中可能包含信息。
31．简单通信系统的模型包含的四部分分别为信源、有扰信道、信宿、干扰源。
32．的后验概率与先念概率的比值的对数为对的互信息量。
33．在信息论中，互信息量等于自信息量减去条件自信息量。
34．当X和Y相互独立时，互信息为0。
35．信源各个离散消息的自信息量的数学期望为信源的平均信息量，也称信息熵。
第一章
一、填空（
1．1948年，美国数学家香农发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。
2．按照信息的性质，可以把信息分成语法信息、语义信息和语用信息。
3．按照信息的地位，可以把信息分成客观信息和主观信息。
4．人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。