倾向值评分匹配方法PSM

合集下载

倾向得分匹配方法步骤

倾向得分匹配方法步骤倾向得分匹配方法（Propensity Score Matching, PSM）是一种用于评估因果效应的经典方法之一。

该方法通过倾向得分（Propensity Score）将处理组和对照组进行配对，以减少处理组和对照组之间的混淆偏倚。

下面是倾向得分匹配方法的步骤：1. 研究问题和数据准备：首先明确研究问题，并收集相关的观测数据。

数据应包括处理组和对照组的特征变量，以及因果变量。

2. 变量选择：根据研究问题，选择适当的特征变量作为倾向得分模型的输入变量。

这些变量应具有影响处理组选择的潜在因素，且与因果变量相关。

通常选择的变量包括年龄、性别、教育水平、收入水平等。

3. 倾向得分估计：倾向得分是处理组与对照组之间的条件概率，表示个体被分到处理组的概率。

可以使用各种统计方法来估计倾向得分，包括逻辑回归、梯度提升树等。

估计得到的倾向得分应在0到1之间。

4. 匹配样本选择：通过选择与处理组匹配的对照组样本，减少混淆偏倚。

常见的匹配方法包括最近邻匹配、卡尔曼匹配等。

匹配前，可以根据倾向得分的近似程度设置质量标准，例如最大汉明距离。

5. 匹配效果评估：在匹配完成后，对匹配样本进行处理效果评估。

通常使用平均处理效应（Average Treatment Effect, ATE）或平均处理效应对受处理样本的平均效应（Average Treatment Effect on the Treated, ATT）进行估计。

处理效果的估计可以使用插补法、回归法等。

6. 效果检验和敏感性分析：对匹配效果进行检验，常用的方法有t检验、Bootstrap法等。

此外，还需要进行敏感性分析，检验结果对于倾向得分估计的敏感性。

常见的敏感性分析方法包括皮贝根评分、加入未观测因素等。

7. 结果解读：根据匹配效果评估、效果检验和敏感性分析的结果，对研究问题进行解读。

解读应注意结果的可靠性、合理性和一致性，并结合文献综述和实证研究来进行解释。

倾向计分(积分,匹配)法PSM_SSWR_2004

“comparison” group are compared to only the best cases from the treatment group, the result may be regression toward the mean
• makes the comparison group look better • Makes the treatment group look worse.
focused on the problem of selection biases, and traditional approaches to program evaluation, including randomized experiments, classical matching, and statistical controls. Heckman later developed “Difference-in-differences” method
NSCAW data used to illustrate PSM were collected under funding by the Administration on Children, Youth, and Families of the U.S. Department of Health and Human Services. Findings do not represent the official position or policies of the U.S. DHHS. PSM analyses were partially funded by the Robert Wood Johnson Foundation and the Childrens Bureau’s Child Welfare Research Fellowship. Results are preliminary and not quotable. Contact information: sguo@

倾向得分匹配法步骤

倾向得分匹配法步骤
倾向得分匹配法（Propensity Score Matching, PSM）是一种常用的统计方法，用于处理因果推断中的选择偏差。

下面我将从多个角度介绍倾向得分匹配法的步骤。

1. 确定研究目的，在使用倾向得分匹配法之前，首先需要明确研究的目的和问题，确定需要进行匹配的变量和研究对象。

2. 计算倾向得分，倾向得分是指个体被暴露于某个处理（例如接受某种治疗）的概率。

通常使用logistic回归等方法来计算每个个体的倾向得分，得到一个介于0到1之间的概率值。

3. 匹配处理组和对照组，根据计算得到的倾向得分，将处理组和对照组中的个体进行配对，使得处理组和对照组在倾向得分上尽可能接近，从而达到减少选择偏差的效果。

4. 检验匹配质量，匹配完成后，需要进行匹配质量的检验，通常会使用标准化差异（Standardized Mean Difference, SMD）等指标来评估匹配的效果，确保处理组和对照组在匹配后的特征上没有显著差异。

5. 进行因果推断，匹配完成后，可以利用匹配后的样本进行因果效应估计，比较处理组和对照组在结果变量上的差异，从而得出处理对结果变量的影响。

6. 稳健性检验，最后，为了确保结果的稳健性，可以进行一些敏感性分析，例如倾向得分模型的选择、不同的匹配算法等，来检验结果的稳健性。

综上所述，倾向得分匹配法的步骤包括确定研究目的、计算倾向得分、匹配处理组和对照组、检验匹配质量、进行因果推断以及稳健性检验。

这些步骤有助于减少因果推断中的选择偏差，提高研究结论的可信度。

stata：倾向得分匹配（PSM）

stata：倾向得分匹配（PSM）导读：在经济学中，我们常常希望评估项目实施后的效应，一般的做法是加入虚拟变量，但是这种做法并不科学。

例如政府推行就业培训计划，该项目的参与者，我们将其称作处理组（treatment group），未参与的培训的样本称作控制组（control group）也叫对照组。

PSM考虑就业培训的处理效应评估。

我们一般的做法是比较两组的收入状况。

如果这样处理，可能得到的结论是参加培训的收入低于未参加培训者。

这是由于一开始选择控制组的样本时，选择范围比较广阔，存在选择偏差。

所以在此介绍倾向得分匹配方法（PSM）。

本文在此就不介绍相关理论了，因为小编的理论也不是特别的好，如果想学习的可以参阅连玉君老师的相关视频（重点推介），大概有5个课时；同时也可以参考陈强老师的《高级计量经济学及stata应用》中的第28章处理效应。

在此小编仅仅介绍stata的相关操作。

1、安装psmatch2ssc install psmatch2，replace2、导入数据，方法比较多，可以粘贴复制、也可以使用命令use E:\BaiduNetdiskDownload\A\labor.dta,clear3、命令语法格式介绍psmatch2 D x1 x2 x3 ,outcome(y) logit ties ate common odds /// pscore(varname) qui对以上的标准命令进行解析D为处理变量，是虚拟变量即是否参加培训x1 x2 x3是协变量，一般的称呼也叫解释变量outcome(varname)是输出变量，例如收入logit 表示计算得分的时候使用logit模型，如果不写Logit，默认为probit模型计算得分，在连玉君的视频中论述了二者并不存在明显的差异。

ties表示包括所有倾向得分相同的并列个体，默认按照数据排序选择其中一位个体。

ATE表示同是汇报ATE、ATU、ATT，大家看书重点了解common表示仅对共同取值范围内的个体进行匹配odds使用几率比（odds ratio）算法为p/(1-p),熟悉logit模型的应该了解qui屏幕中不显示logit模型估计过程，可以节省运算时间4 匹配方法连玉君的视频教程讲了三种：最近0匹配、半径匹配、核匹配；陈强老师讲了6种，如果想详细学习，可以参考他们的相关视频与书籍。

1:1倾向性评分匹配(PSM)-SPSS教程

1:1倾向性评分匹配(PSM)-SPSS教程一、问题与数据谈起临床研究，如何设立一个靠谱的对照，有时候成为整个研究成败的关键。

对照设立的一个非常重要的原则就是可比性，简单说就是对照组除了研究因素外，其他的因素应该尽可能和试验组保持一致，这里就不得不提随机对照试验。

众所周知，随机对照试验中研究对象是否接受干预是随机的，这就保证了组间其他混杂因素均衡可比。

但是有些时候并不能实现随机化，比如说观察性研究。

这时候倾向性评分匹配(propensity score matching, PSM)可以有效降低混杂偏倚，并且在整个研究设计阶段，得到类似随机对照研究的效果。

与常规匹配相比，倾向性评分匹配能考虑更多匹配因素，提高研究效率。

这么“高大上”的倾向性评分匹配，是不是超级难学？错矣！今天就带大家轻松搞定1:1倾向性评分匹配。

作为“稀罕”大招，并不是在所有版本的SPSS都可以实现倾向性评分匹配，仅在SPSS22及以上自带简易版PSM。

本次使用SPSS22为大家演示1:1倾向性评分匹配。

某研究小白想搞明白吸烟和高血压之间的关系，准备利用某项调查的资料进一步随访研究吸烟和高血压的关联，该项研究包括233名吸烟者，949 名不吸烟者。

如果全部随访，研究小白感觉鸭梨山大，所以打算从中选取部分可比的个体进行随访。

这两组人群一些主要特征的分布存在显著差异（见表1），现准备采用PS最邻近匹配法选取可比的个体作为随访对象。

表1. 两组基线情况比较（匹配前）二、SPSS操作1. 数据录入(1) 变量视图(2) 数据视图2. 倾向性评分匹配选择Data→Propensity Score Matching，就进入倾向性评分匹配的主对话框。

将分组变量Smoke放入Group Indicator中（一般处理组赋值为“1”，对照组赋值为“0”）；将需要匹配的变量放入Predictors中；Name for Propensity Variable为倾向性评分设定一个变量名PS；Match Tolerance用来设置倾向性评分匹配标准（学名“卡钳值”），这里设定为0.02，即吸烟组和不吸烟组按照倾向性评分±0.02进行1：1匹配（当然，卡钳值设置的越小，吸烟组和不吸烟组匹配后可比性越好，但是凡事有个度，太小的卡钳值也意味着匹配难度会加大，成功匹配的对子数会减少，需要综合考虑~~~）；Case ID确定观测对象的ID；Match ID Variable Name设定一个变量，用来明确对照组中匹配成功的Match_ID；Output Dataset Name这里把匹配的观测对象单独输出一个数据集Match。

SPSS—倾向性评分匹配法（PSM）

SPSS—倾向性评分匹配法（PSM）倾向评分匹配(propensity score matching, PSM)的概念由Rosenbaum和Rubin在1983年首次提出。

2010年之后，这一方法日益受到人们的关注。

国际上越来越多的研究者将倾向指数法应用到流行病学、健康服务研究、经济学以及社会科学等许多领域。

在流行病学研究中，该方法可以在分析和设计阶段有效平衡非随机对照研究中的混杂偏倚，使研究结果接近随机对照研究的效果。

在观察性研究中，如病例对照研究，经常会见到匹配的概念，即按照某些因素或特征，将病例组（或暴露组）和对照组的研究对象进行匹配，以保证两组研究对象具有可比性，从而排除匹配因素的干扰。

同样，既然倾向性评分是一个能够反映多个混杂因素影响的综合评分，我们也可以将两组人群按照倾向性评分从小到大来进行匹配，仅用匹配倾向性评分一个指标来达到同时控制多个混杂因素的目的。

倾向性评分匹配是倾向性分析中应用最为广泛的一种方法。

首先我们要计算出每一个研究对象的倾向性评分，然后从小到大进行排序，对于每一个暴露/处理组的研究对象，从对照组中选取与其倾向性评分最为接近的所有个体，并从中随机抽取一个或N个研究对象作为匹配对象，直至所有的研究对象均匹配完毕，未匹配上的研究对象则进行舍去。

当然，有多少研究对象可以成功匹配，常常与选择匹配的比例和匹配的标准有关。

匹配的比例最常见的为1:1匹配，需要根据两组人群的数量来决定合适的匹配比例，建议不要超过1:4匹配。

对于匹配标准，如果匹配的标准很高，则能够成功匹配的对象就可能会少，甚至出现匹配不上的现象，造成研究对象信息的浪费，如果匹配的标准很宽泛，则匹配的效果就会较差，有可能出现两组人群在匹配后依然存在混杂因素分布不均衡的现象。

例如某个个体的倾向性评分为0.8，如果设定匹配标准为±0.02，则需要为其寻找倾向性评分在0.78-0.82之间的对照进行匹配，匹配范围太窄就可能出现匹配不上的情况；如果设定匹配标准为±0.2，则需要为其寻找倾向性评分在0.8-1.0之间的对照进行匹配，匹配范围太宽则可能降低匹配的效果。

stata倾向得分匹配法

stata倾向得分匹配法英文回答：Propensity score matching (PSM) is a statistical technique used to estimate the causal effect of a treatment or intervention. PSM is based on the assumption that, conditional on a set of observed covariates, treatment assignment is random. This assumption is known as the conditional independence assumption (CIA).The CIA can be tested using a variety of methods, including the Rosenbaum-Rubin test and the covariate balance test. If the CIA is satisfied, then PSM can be used to estimate the average treatment effect (ATE).To estimate the ATE, PSM first estimates the propensity score for each individual. The propensity score is the probability of receiving the treatment, conditional on the observed covariates. Once the propensity scores have been estimated, PSM matches treated individuals to untreatedindividuals who have similar propensity scores.Matching can be done using a variety of methods, including nearest neighbor matching, caliper matching, and kernel matching. After matching, the ATE can be estimated by comparing the outcomes of the treated and untreated individuals.PSM is a powerful tool for estimating the causal effect of a treatment or intervention. However, it is important to note that PSM is only valid if the CIA is satisfied. If the CIA is not satisfied, then PSM may produce biased estimates of the ATE.中文回答：倾向得分匹配法（PSM）是一种统计技术，用于估计治疗或干预的因果效应。

倾向匹配得分教程（附PSM操作应用、平衡性检验、共同取值范围、?核密度函数图）

倾向匹配得分教程（附PSM操作应用、平衡性检验、共同取值范围、核密度函数图）本文主要包括倾向匹配得分命令简介、语法格式、倾向匹配得分操作步骤思路，涉及倾向匹配得分应用、平衡性检验、共同取值范围检验、核密度函数图等内容。

1命令简介Stata does not have a built-in command for propensity score matching, a non-experimental method of sampling that produces a control group whose distribution of covariates is similar to that of the treated group. However, there are several user-written modules for this method. The following modules are among the most popular:Stata没有一个内置的倾向评分匹配的命令，一种非实验性的抽样方法，它产生一个控制组，它的协变量分布与被处理组的分布相似。

但是，这个方法有几个用户编写的模块。

以下是最受欢迎的模块（主要有如下几个外部命令）psmatch2.adopscore.adonnmatch.adopsmatch2.ado was developed by Leuven and Sianesi (2003) and pscore.ado by Becker and Ichino (2002). More recently, Abadie, Drukker, Herr, and Imbens (2004) introduced nnmatch.ado. All three modules support pair-matching as well as subclassification.You can find these modules using the .net command as follows:net search psmatch2net search pscorenet search nnmatchYou can install these modules using the .ssc or .net command, for example:ssc install psmatch2, replaceAfter installation, read the help files to find the correct usage, for example:help psmatch2上述主要介绍了如何获得PSM相关的命令，总结一下目前市面上用的较好的命令为psmatch2.PSM 相关命令help psmatch2help nnmatchhelp psmatchhelp pscore持续获取最新的 PSM 信息和程序findit propensity scorefindit matchingpsmatch2 is being continuously improved and developed. Make sure to keep your version up-to-date as follows ssc install psmatch2, replacewhere you can check your version as follows:which psmatch22语法格式语法格式为：help psmatch2••••••psmatch2 depvar [indepvars] [if exp] [in range] [, outcome(varlist) pscore(varname) neighbor(integer) radius caliper(real) mahalanobis(varlist) ai(integer) population altvariance kernel llr kerneltype(type) b width(real) spline nknots(integer) common trim(real ) noreplacement descending odds index logit ties q uietly w(matrix) ate]选项含义为：depvar因变量；indepvars表示协变量；outcome(varlist)表示结果变量；logit指定使用logit模型进行拟合，默认的是probit模型；neighbor(1)指定按照1:1进行匹配，如果要按照1:3进行匹配，则设定为neighbor(3)；radius表示半径匹配核匹配 (Kernel matching)其他匹配方法广义精确匹配(Coarsened Exact Matching) || help cem局部线性回归匹配 (Local linear regression matching)样条匹配 (Spline matching)马氏匹配 (Mahalanobis matching)pstest $X, both做匹配前后的均衡性检验，理论上说此处只能对连续变量做均衡性检验，对分类变量的均衡性检验应该重新整理数据后运用χ2检验或者秩和检验。

倾向得分匹配法命令 -回复

倾向得分匹配法命令-回复倾向得分匹配法命令的使用指南引言：倾向得分匹配法（Propensity Score Matching，PSM）是一种常用的非实验研究设计方法，用于评估某个干预对于特定结果的影响。

本文将一步一步介绍如何使用倾向得分匹配法命令进行数据分析。

第一步：定义研究目标在使用倾向得分匹配法前，首先需要明确研究的目标是什么。

例如，我们想评估某种药物对患者生存率的影响。

这个目标会指导我们后续的研究设计和数据分析。

第二步：准备数据倾向得分匹配法需要有一组观测数据，包括干预组和对照组。

干预组是接受干预的个体/单位，而对照组是没有接受干预的个体/单位。

这两组个体/单位应当具有相似的特征，以便进行可靠的比较。

通常，我们会根据实际情况选择与研究目标相关的变量，如性别、年龄、病史等作为控制变量。

第三步：估计倾向得分倾向得分是根据个体特征而计算的一个概率值，用于评估个体被分配到干预组的倾向程度。

估计倾向得分有多种方法，包括逻辑回归、矩阵分解等。

常见的统计软件都提供了相应的命令，如R语言的"MatchIt"包中的"matchit"命令。

该命令可以帮助我们估计倾向得分，并生成用于匹配的变量。

第四步：匹配样本在得到倾向得分后，我们需要将干预组和对照组进行匹配，以便比较它们的特征。

匹配样本可以采用一对一匹配、多对一匹配等方法。

常见的匹配算法有最近邻匹配、卡尔曼滤波匹配等。

在R语言中，可以使用"MatchIt"包中的"match.data"命令实现样本匹配。

第五步：比较结果匹配样本后，我们可以进行结果比较。

通常会比较干预组和对照组在某个特定结果上的差异，如患者生存率。

可以使用各种统计方法，如t检验、卡方检验等，来评估差异的显著性。

同时，我们也可以计算倾向得分匹配法的保守性、平衡性等指标，以评估匹配的质量。

第六步：结果解释和结论在得到结果后，我们需要解释和分析结果。

真实世界研究统计分析方法（二）：倾向性评分匹配（PSM）

真实世界研究统计分析方法（二）：倾向性评分匹配（PSM）试验性研究（例如RCT）做随机化分组目的是：控制混杂。

真实世界研究，不人为分配X（Assigned Exposure X），不做随机分组，需要通过数据分析的方法控制混杂。

2006年美国流行病学杂志Am J Epidemiol 总结了真实世界研究控制混杂常用的五种方法[1]，包括：1. 多元回归模型调整混杂2. 倾向性评分匹配（PSM）后构建回归模型3. 回归模型调整倾向性评分（PS）4. 回归模型加权（IPTW）处理5. 回归模型加权（SMR）处理本文分享第二种方法：倾向性评分匹配（PSM）往期相关资料：真实世界研究统计分析方法（一）：调整混杂2015年在NEJM发表了一项研究[2]，支架和CABG手术相比，对于多支病变的冠心病的疗效。

研究对象：冠心病患者X：两种治疗方式，第二代药物支架（PCI）与冠脉搭桥（CABG）相比Y：预后包括死亡、心梗、再次血运重建和卒中研究设计：观察性研究（observational）中的队列（cohort）研究。

没有随机分配治疗方案，不是RCT，是在真实世界中观察不同治疗方案的疗效。

纳入了3万多人，PSM后剩下不到2万人，样本量少了很多。

目的是控制混杂：挑出一部分人，使得接受不同治疗方案（X）的患者基线情况相似。

这一点非常重要。

试想，如果病情重的人偏向于做搭桥手术，病情重的人预后不好，就会得出搭桥手术疗效差的假象。

解决办法：研究设计时通过PSM的方法选择患者，使得不同X组的人基线相似。

即纳入的人既有可能接受PCI，又有可能接受CABG。

给定一个病例，从数据库里找出满足配对条件的所有可能的对照，然后根据匹配数随机选择对照。

如1：1匹配，随机选一个作对照；1：2匹配，随机选2个配对。

因此PSM的方法又被成为事后随机化，相当于在队列里面构建RCT。

这个就厉害了！正因为倾向性评分（Propensity score ，PS）在控制混杂方面有独特的优势，肿瘤领域的真实世界研究，近年运用PS方法论文的比例出现了爆发[3]：使用PS分析方法的论文数量随发表年份的变化图2017年发布了PS论文报告标准，规范了19条需要在论文中描述的重要内容[3]。

倾向值评分匹配方法PSMppt课件

倾向值匹配法（PSM）
1
RCT：很多限制，如费用，伦理学要求，操作困难，不适合发病率很低的疾病非RCT：避免以上繁杂的问题，容易组间基线不齐，使之成为处理效应的混杂因素从而产生偏移
2
• 为了消除混杂因素的影响，传统的解决方式是，用多变量配对，多变量分析模型，M-H分层分析，协变量分析。
14
• 比较的效果是接受治疗后1 年内的生存率，成本是所有疾病相关的医疗成本，研究分别对成本和效果未经过调整的结果、多元回归结果、基于倾向值匹配的结果和基于倾向值分层的结果进行了比较。
15
讨论
倾向值分析只能尽量减少混杂因素产生的影响，并不能完全消除，其消除程度取决于可以被观测和控制的变量数量以及匹配的质量。此外，倾向值分析只能对可观测的混杂因素进行平衡和控制，并不能够控制不可观测的混杂因素，当有重要的混杂因素缺失或不可观测时，采用倾向值分析所得结果可能与真实值存在较大偏差。
8
估计倾向值
• Logistic 回归模型 • 令y=组别，x为各协变量每个个体在给定可观测混杂因素的条件下接受干预的条件概率。
9
选择匹配方法
最近邻匹配
卡钳匹配马氏距离匹配
贪婪匹配法
10
匹配后的均衡性检验
• 协变量的平衡可通过均值上的绝对标准化差值来衡量
• 通常dX＞dXm，说明在匹配后样本的平衡程度有所改善。
• 目的：将多个变量（多维）转化为一个中间变量（一维） • 特点：不在关注每个需要控制的混杂因素的具体取值，转为关注将这
些变量纳入logistic回归方程后预测出来的倾向值。只要保证倾向值匹配，这些所有需要控制的混杂因素都考虑了。
5
PSM适用情形
• 前提：logistic多因素分析已经无法校正 • 1：实验组与对照组人数相差甚远（＞4:1） • 2：两组变量差异太大，可比性差，如基线不齐，或混杂因素多 • 3：变量过多，样本量偏少

倾向评分匹配法

倾向评分匹配法（Propensity Score Matching, PSM）是一种常用的非实验研究方法，用于解决因果推断问题。

它通过将参与某个处理（例如接受某项政策、干预或治疗）的个体与没有参与该处理的个体进行匹配，以消除因群体选择偏差带来的潜在混杂变量的影响。

PSM的基本步骤如下：
1. 确定研究问题和处理变量：明确需要进行因果分析的研究问题，并确定影响因变量的处理变量。

2. 构建倾向评分模型：利用回归分析等方法，建立一个预测参与处理的倾向评分模型，该模型能够根据个体的特征预测其选择处理的概率。

3. 匹配样本：根据个体的倾向评分，将参与处理的个体与未参与处理的个体进行配对匹配，使得两组个体在处理前的特征上尽可能相似。

4. 检验平衡性：检验匹配后的样本是否在处理前的特征上达到平衡状态，以确保匹配的有效性。

5. 进行因果推断：比较处理组和对照组在因变量上的差异，以得出因果效应的估计结果。

6. 敏感性分析：进行敏感性分析，检验倾向评分模型的稳健性，并评估结果对潜在假设的依赖程度。

PSM方法在通过实验研究来解决问题存在困难或不可行的情况下，为研究人员提供了一种处理群体选择偏差的有效工具。

然而，PSM也有
一些限制，如依赖于建模假设、匹配质量和结果的解释等方面存在一定挑战。

因此，在应用PSM时需要谨慎选择合适的方法和适用范围，并结合其他方法进行结果验证和分析。

倾向性得分匹配（PSM）

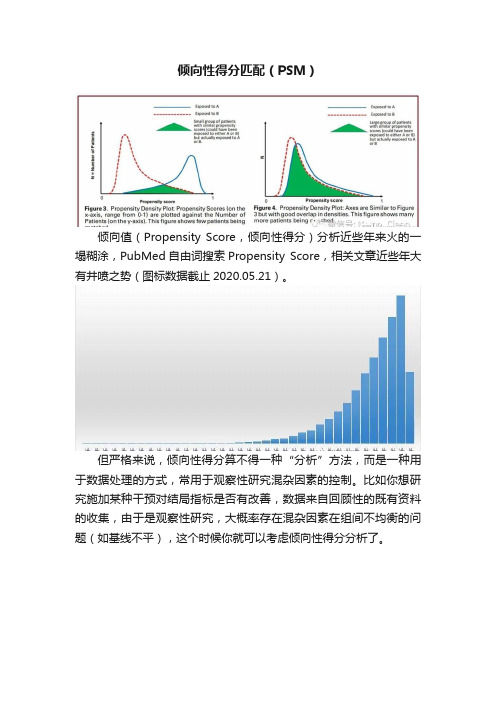
倾向性得分匹配（PSM）倾向值（Propensity Score，倾向性得分）分析近些年来火的一塌糊涂，PubMed自由词搜索Propensity Score，相关文章近些年大有井喷之势（图标数据截止2020.05.21）。

但严格来说，倾向性得分算不得一种“分析”方法，而是一种用于数据处理的方式，常用于观察性研究混杂因素的控制。

比如你想研究施加某种干预对结局指标是否有改善，数据来自回顾性的既有资料的收集，由于是观察性研究，大概率存在混杂因素在组间不均衡的问题（如基线不平），这个时候你就可以考虑倾向性得分分析了。

PS就是以干预因素（组别）为因变量，以所有观测到的非研究性因素为自变量进行logistic或probit回归，在给定的协变量条件下，个体接受干预因素处理的概率。

根据PS，我们就可以对试验组和对照组进行筛选，使得不同组的非研究性因素实现均衡，从而达到控制的目的。

倾向性得分本身并不能控制混杂，而是通过PS匹配、加权、分层或进入回归模型直接调整混杂等方式，不同程度地提高对比组间的均衡性，从而削弱或平衡协变量对效应估计的影响，达到“类随机化”的效果，又称为事后随机化。

简单理解，就是从大量的样本数据中将具有共同特征的干预组和对照组样本挑选出来，然后对这些符合要求的样本进行分析。

倾向性得分可以同时调整大量的混杂因素，省时间省钱，但是需要的样本量较大，只能均衡已观测的指标变量，而且可能会以丢失样本为代价。

大部分软件给出的是两水平的干预因素的倾向性得分，SPSS直接给出了1:1的倾向性得分匹配结果。

数据来自STATA16的自带数据，是一项关于孕期妇女吸烟对新生儿体重的影响的观察性研究，由Cattaneo (2010)报道。

调查数据涉及众多变量包括新生儿出生体重(bweight)外，还有孕母的婚姻状况(mmarried)、孕期是否饮酒(alcohol)、年龄(mage)、教育水平(medu)、是否吸烟(mbsmoke)、母亲是否白人(mrace)、是否首胎(fbaby)、首次产前检查是否在头三个月内(prenatal1)以及父亲的年龄(fage)、是否白人(frace)等众多变量。

倾向得分匹配法原理 -回复

倾向得分匹配法原理-回复倾向得分匹配法（Propensity Score Matching，PSM）是一种常用于处理因果推断问题的统计方法。

它的基本原理是通过构建倾向得分模型，将被处理的个体（处理组）与未处理的个体（对照组）进行配对，以便在某些特定的变量上达到类似或相同的分布，从而减少处理选择引起的偏倚。

PSM方法主要适用于在实验条件不具备的情况下进行因果推断。

在实验研究中，研究人员可以通过随机分组将个体分配到处理组和对照组，从而控制潜在的混淆因素。

然而，在实际应用中，一些因果问题无法通过实验进行研究，因此需要使用非实验数据来进行推断。

在这种情况下，倾向得分匹配法就能派上用场。

PSM方法的核心思想是通过估计个体的倾向得分，来度量个体进入处理组的概率。

倾向得分（Propensity Score）是指个体进入处理组的条件概率。

我们可以使用一些统计模型，例如逻辑回归模型，来估计这个得分。

这个模型会基于一系列观察到的协变量（confounding variables），也就是可能影响个体进入处理组的变量，比如年龄、性别、教育水平等，来预测个体进入处理组的概率。

在得到个体的倾向得分后，我们可以使用这个得分来进行配对。

具体来说，我们首先将处理组中的个体与对照组中的个体按照倾向得分进行配对。

一般可以使用一对一匹配、一对多匹配或者多对多匹配等方式。

匹配的目标是使处理组和对照组在倾向得分上的分布相似。

配对完成后，我们可以比较处理组和对照组在结果变量上的差异，来得到处理的因果效应。

这种比较可以通过计算平均处理效应（Average Treatment Effect，ATE）来实现。

ATE表示处理组与对照组在结果变量上的平均差异。

在计算ATE时，常常还会考虑到一些非随机选择问题带来的偏倚。

例如，可能存在选择性个体退出、数据缺失或者其他特殊情况。

为了解决这些问题，可以使用倾向得分匹配法的改进方法，如加权倾向得分匹配法（Weighted Propensity Score Matching）或者可接受性函数（Acceptance Function）等。

倾向匹配得分教程（附PSM操作应用、平衡性检验、共同取值范围、

核密度函数图）倾向匹配得分教程（附PSM操作应⽤、平衡性检验、共同取值范围、核密度函数图）本⽂主要包括倾向匹配得分命令简介、语法格式、倾向匹配得分操作步骤思路，涉及倾向匹配得分应⽤、平衡性检验、共同取值范围检验、核密度函数图等内容。

1命令简介Stata does not have a built-in command for propensity score matching, a non-experimental method of sampling that produces a control group whose distribution of covariates is similar to that of the treated group. How following modules are among the most popular:Stata没有⼀个内置的倾向评分匹配的命令，⼀种⾮实验性的抽样⽅法，它产⽣⼀个控制组，它的协变量分布与被处理组的分布相似。

但是，这个⽅法有⼏个⽤户编写的模块。

以下是最受欢迎的模块（主要有如下⼏个psmatch2.adopscore.adonnmatch.adopsmatch2.ado was developed by Leuven and Sianesi (2003) and pscore.ado by Becker and Ichino (2002). More recently, Abadie, Drukker, Herr, and Imbens (2004) introduced nnmatch.ado. All three modules suppo You can find these modules using the .net command as follows:net search psmatch2net search pscorenet search nnmatchYou can install these modules using the .ssc or .net command, for example:ssc install psmatch2, replaceAfter installation, read the help files to find the correct usage, for example:help psmatch2上述主要介绍了如何获得PSM相关的命令，总结⼀下⽬前市⾯上⽤的较好的命令为psmatch2.PSM 相关命令help psmatch2help nnmatchhelp psmatchhelp pscore持续获取最新的 PSM 信息和程序findit propensity scorefindit matchingpsmatch2 is being continuously improved and developed. Make sure to keep your version up-to-date as followsssc install psmatch2, replacewhere you can check your version as follows:which psmatch22语法格式语法格式为：help psmatch2psmatch2 depvar [indepvars] [if exp] [in range] [,outcome(varlist) pscore(varname) neighbor(integer) radius caliper(real) mahalanobis(varlist) ai(integer) population altvariance kernel llr kerneltype(type) bwidth(real) spline nknots(integer) common trim(real) no 选项含义为：depvar因变量；indepvars表⽰协变量；outcome(varlist)表⽰结果变量；logit指定使⽤logit模型进⾏拟合，默认的是probit模型；neighbor(1)指定按照1:1进⾏匹配，如果要按照1:3进⾏匹配，则设定为neighbor(3)；radius表⽰半径匹配核匹配 (Kernel matching)其他匹配⽅法⼴义精确匹配(Coarsened Exact Matching) || help cem局部线性回归匹配 (Local linear regression matching)样条匹配 (Spline matching)马⽒匹配 (Mahalanobis matching)pstest $X, both做匹配前后的均衡性检验，理论上说此处只能对连续变量做均衡性检验，对分类变量的均衡性检验应该重新整理数据后运⽤χ2检验或者秩和检验。

倾向得分匹配法(PSM)举例及stata实现

倾向得分匹配法（PSM ）举例及stata 实现——读书笔记【例】培训对工资的效应1政策背景：国家支持工作示范项目（National Supported Work,NSW ）研究目的：检验接受该项目（培训）与不接受该项目（培训）对工资的影响。

基本思想：分析接受培训组（处理组，treatment group ）接受培训行为与不接受培训行为在工资表现上的差异。

但是，现实可以观测到的是处理组接受培训的事实，而处理组没有接受培训会怎样是不可能观测到的，这种状态也成为反事实（counterfactual ）。

匹配法就是为了解决这种不可观测事实的方法。

在倾向得分匹配方法（Propensity Score Matching ）中，根据处理指示变量将样本分为两个组，一是处理组，在本例中就是在NSW 实施后接受培训的组；二是对照组（comparison group ），在本例中就是在NSW 实施后不接受培训的组。

倾向得分匹配方法的基本思想是，在处理组和对照组样本通过一定的方式匹配后，在其他条件完全相同的情况下，通过接受培训的组（处理组）与不接受培训的组（对照组）在工资表现上的差异来判断接受培训的行为与工资之间的因果关系。

变量定义：变量定义TREAT * 处理指示变量，1表示接受培训（处理组），0表示没有接受培训（对照组）AGE 年龄（年）EDUC 受教育年数（年）BLACK 种族虚拟变量，黑人时，1BLACK =HSIP 民族虚拟变量，西班牙人时，=1HSIPMARR婚姻状况虚拟变量，已婚，1MARR = 74RE 1974年实际工资（1982年美元）75RE 1975年实际工资78RE 1978年实际工资74U 当在1974年失业，741U =75U当在1975年失业，751U = NODEGREE 当12EDUC <时，1NODEGREE =，否则为0 AGESQAGE AGE × 1 本例选自Cameron&Trivedi 《微观计量经济学：方法与应用》（中译本，上海财经大学出版社，2010）pp794-800 所有数据及程序均来自于本书的配套网站（/mmabook/mmaprograms.html ）。

倾向得分匹配法介绍

倾向得分匹配法介绍本研究主要考察政府对企业研究开发补贴的影响，由于传统的模型例如采用普通最小二乘法（OLS）估计的多元线性模型难以有效地解决可能存在的样本选择性偏差和遗漏关键变量所造成的内生性这两个关键性问题。

因此，本研究主要采用倾向得分匹配法（propensityscorematching，PSM）对政府对企业研究开发的补贴与企业发展水平的实证关系进行稳健性的因果推断。

一、模型构建）；另一D s={0，1}lnincome1Rubin（ATT）、。

样本（获取政府补贴的企业样本）在获取政府补贴前后发展水平变化的期望值；控制组平均处理效应（ATU）测度的是对照组样本（未获取政府补贴的企业样本）在获取政府补贴前后发展水平变化的期望值；平均处理效应（ATE）测度的是样本满足“个体处理效应稳定假设”前提下，同一样本企业在获取政府补贴前后发展变化的期望值。

3、倾向得分匹配过程（matching）在公式（1）和（2）中，E(lnincome0|X,subside=1)表示获得补贴的企业如果不接受政府补贴时的企业发展水平，E(lnincome1|X,subside=0)表示没有获得补贴的企业如果接受政府补贴时的企业发展水平，由此可以看出，这两个期望均值是非事实以及不可观测的。

解决这一问题的关键思路是，如果可以找到与获得政府补贴的企业“相似”的未获取政府补贴的企业，那么，就可以通过观察未获取补贴企业来判断接受补贴的企业在反事实情况下的发展水平，这一过程被称之为匹配过程（matching）。

通过匹配，可以使得获取补贴的企业和未获取补贴的企业所有的特征变量都尽量相同，但这些特征变量的权重在很多情况下难以衡量。

基于此，采用倾向得分匹配法则可以将众多指标合成（。