七年级数学下学期周练试卷7无答案苏科版

合集下载

苏科版七级下数学周练试卷()

苏科版七级下数学周练试卷()泰兴市黄桥初级中学2016年春学期七年级数学周测32016-03-15(满分：100分，时间50分钟)姓名：得分:一、选择题（每题只有一个正确结论，把正确结论的题号填入下表，每题2分，共16分）题号 1 2 3 4 5 6 7 8答案1.下列运算不正确．．．的是（）A.()1025aa= B.()532632aaa-=-⋅ C.65bbb=⋅D.2555bbb=⋅2．如图，下列条件中，不能判断直线l1∥l2的是（）A．∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°3.长度为1cm、2cm、3cm、4cm、5cm的五条第5第2第7（第8题周测3 第 2 页共 11 页周测3 第 3 页共 11 页线段，若以其中的三条线段为边构成三角形，可以构成不同的三角形共有（）A.2个 B.3个 C.4个 D.5个 4．下列各题中，计算正确的有( )． ①3a 3·2a 3＝6a 3； ②4a 3·ba n＝4a 3nb ； ③(4xm ＋1z 3) ·(－2x 2y z 2)＝－8x2m ＋2yz 6；④(－ab 3c 2)·(－4b c)·(－3ab 2)＝－12a 2b 6c 3．A ．1个B ．2个C ．3个D ．4个5．如图，△ABC 中，∠ACB＝90°，沿CD 折叠△CBD，使点B 恰好落在AC 边上的点E 处．若∠A＝22°，则∠BDC 等于（） A ．44° B ．60° C ．67° D ．77° 6．若,32=m42=n ，则322m n-等于( )A ．1 B ．89 C ． 827 D ．1627 7.如图，在△ABC 中，已知点D 、E 、F 分别是BC 、AD 、BE 上的中点，且△ABC 的面积为82cm ，则△BCF的面积为（）A．0.52cm B．12cm C．22cm D．42cm8．如图，长方形的长为a，宽为b，横向阴影部分为长方形，另一阴影部分为平行四边形，它们的宽都为c,则空白部分的面积是( )A. ab－bc＋ac－c2B. ab－bc－ac ＋c2C. ab－ac－bcD. ab－ac－bc－c2二、填空题：（每空3分，共33分，把正确答案填在相对应的位置上）9.10. . 11.12. ______________13._______________ 14.15. 16.17. 18.（1）周测3 第 4 页共 11 页（2）9.已知等腰△ABC的两边长分别为2和5，则这个等腰三角形的周长为．10.计算:()()yxyx-+2=________________11．一个多边形的每个外角都等于36°，那么该多边形的边数是．12.如图，在△ABC中，点D E、分别在AB AC、上，若120B C∠+∠=︒，则12∠+∠=．13.如图，长方形由8个边长为3cm的小正方形组成，图中阴影部分的面积是2cm．第15第13题第12题第14题周测3 第 5 页共 11 页14．如图，在四边形ABCD中∠A+∠D=260°，∠ABC的平分线与∠BCD的平分线交于∠P，则∠P 为__________°．15.如图所示，则∠A+∠B-∠C+∠D+∠E的度数为°16. 如图，小亮从A点出发前进10m，向右转15，再前进10m，又向右转15，…，这样一直走下去，他第一次回到出发点A时，一共走了________m．17.若662332)(⨯=x，则x=__________．18.如图，已知射线DM与直线BC交于点A，AB∥DE.∠DAC=80°，∠BCE=120°，点P从点C出发沿射线CA方向运动，第16第18题周测3 第 6 页共 11 页周测3 第 7 页共 11 页（1）当∠CEP= °时，可判定 MD ∥EP ；（2）当∠CEP= °时，，△CEP 是直角三角形。

江苏省大丰市万盈第二中学七年级数学下学期第7周假期作业(无答案) 苏科版

七年级（下）第七周数学假期作业一、选择题（8×3分=24分．）题号 1 2 3 4 5 67 8 答案1.)12)(12(+-+x x 的计算结果是（）A.142+x B. 241x - C. 241x + D. 142--x 2.已知2,5x y =⎧⎨=-⎩是关于x 、y 的二元一次方程3x-ay=7的一个解，则a 的值为（）A ．5B ．15 C ．-15D ．-5 3. 把多项式xy xy y x 412422+-分解因式,结果是（）A. )3(4y x xy -B. )13(4+-y x xyC. )13(4-+y x xyD. )13(4++y x xy 4.将方程154-=+-y x 用含y 的代数式表示x 是（）A. 154-=-y xB. 154-=y xC. 154+=y xD. 154+-=y x 5.下列由左到右的变形中,属于因式分解的是（）A ．4)3(432-+=-+x x x x B ．x x x x x 3)2)(2(342+-+=+- C ．)2)(2(42-+=-x x x D ．4)2)(2(2-=+-x x x6.如果1212++ax x 是两个数的和的平方的形式，那么a 的值是（） A ．22 B ．11 C ．±22 D ．±11 7．下列各式中,能直接运用完全平方公式进行因式分解的是( ) A ．1842++x x B ．14122+-xy y x C ．1642+-x x D ．2296y xy x -- 8.某次知识竞赛共计25道题，评分标准如下：答对1题加4分，答错1题扣1分，她的总分为75分，则她答对了（）A ．18题B ．19题C ．20题D ．21题二、填空题（8×2分=16分）9．方程x －4y=5中，用含x 的代数式表示y ＝。

10．写出一个以 ⎩⎨⎧-==32y x 为解的二元一次方程组．11．若方程653342=-+-b a y x 是关于x 、y 的二元一次方程,则___________,==b a ．12．若⎩⎨⎧-==12y x 是二元一次方程53=+my x 的解,则m= ．13．=--2)52(a _________ _．14. 利用因式分解计算：20142013201422--＝． 15. 若2=+b a ，1=ab ，则22b a +＝，2)(b a -＝． 16. 若m 2+n 2－6n ＋4m ＋13＝０，则m 2－n 2=_________；三、解答题17．计算（4×3分=12分）(1))2)(3(n m n m -+ (2)5－16×(－2)－3（3）()()223131x x +- （4）)1)(1)(1)(1(42-+++x x x x18．把下列各式分解因式: （4×4分=16分）(1)32124x x - (2) 4(a+b)2－9(a －b)2（3）50182-a （4）811824+-a a19.解下列方程（4×4分=16分）（1） ⎩⎨⎧=+=-.52,4y x y x （2） ⎩⎨⎧-=--=-.2354,42y x y x（3）⎩⎨⎧+=--=-)10(2)1(522)1(3x y y x （4）131441141340x y x y +=⎧⎨+=⎩20. （5分）若关于x ，y 的二元一次方程组⎩⎨⎧=-=+k y x ,k y x 95的解也是二元一次方程632=+y x 的解，求k 的值。

苏科版七年级下册数学周练试卷

2021年苏科版七年级下册数学周练试卷一、填空题(每空3分，共45分)1、在△ABC中， A=40，C，则C=.2、一个三角形三个内角度数的比是2∶3∶4，那么这个三角形是三角形.3、在△ABC中， B=36，C=2B，则C= .4、如图，DE∥BC，ADE=60，C=50，则A= .5、多边形的每个内角都是每个外角的4倍，则这个多边形的边数是.6、多边形的边数增加1，则内角和增加度，而外角和=度.7、如果一个多边形的内角和是它外角和的3倍，那么那么这个多边形是边形.8、直角三角形中，有一个锐角是另一个锐角的2倍，则这两个锐角的度数为 .9、如图，在四边形ABCD中1、2分别是BCD和BAD的补角，ADC=140，则2= .10、一个多边形的外角中钝角的个数最多只能有个.11、一个多边形每个内角都相等，且一个外角等于一个内角的，这个多边形是边形.12、如图，BC∥DE，ADDF，l=30，2=50，则A= .13、如图，AB∥CD，FE平分GFD，GF与AB相交于点H.若GHA=40，则BEF= .14、如图，一束光线与水平镜面的夹角为，该光线先照射到平面镜上，然后在两个平面镜上反射.如果=60，=50，那么= .二、选择题(每小题3分，共15分)15、将一张宽度相等的纸条按如图所示的方式折叠，则图中l的度数为( )A.60B.55C.45D.3516、如图，AB∥DE，C+D等于 ( )A.180B.270C.360D.54017、如图，C、l、2之间的大小关系是 ( )A.CB.CC.2D.C18、一个三角形的3个内角度数之比为5：3：1，则与之对应的3个外角的度数之比为( )A.4：3：2B.2：3：4C.3：2：4D.3：1：519、如图，两个平面镜a、b的夹角为，平行于b的光线AO 入射到上，经过两次反射后的反射光线0B平行于a，则角等于 ( )A.70B.60C.45D.30三、解答题(共40分 )20、(本题5分)如图，求的度数.21、(本题7分)一个多边形的所有内角与它的一个外角的和等于2021度，求这个多边形的边数。

苏科版数学七年级下册江苏省昆山市锦溪中学周周练(第7章)

七年级数学周周练（第7章）一、选择题(每题3分，共30分)1．能把一个三角形分成两个面积相等部分的是三角形的（）A．中线B．高C．角平分线D．以上都不是2．△ABC的高的交点一定在外部的是( )A．锐角三角形B．钝角三角形C．直角三角形D．有一个角是60°的三角形3．现有两根木棒，它们的长分别是40 cm和50 cm，若要钉或一个三角形木架，则在下列四根木棒中应选取( )A．10 cm的木棒B．40 cm的木棒C．90 cm的木棒D．100 cm的木棒4．已知等腰三角形的两边长分别为3 cm，4 cm，则它的周长为( )A．10 cm B．11 cmC．10 cm或11 cm D．无法确定5．在△ABC中，∠A＝12∠B＝13∠C，则△ABC的形状为( )A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形6．在四边形的4个内角中，钝角的个数最多为( )A．1 B．2 C．3 D．47．如图，已知直线AB∥CD，∠C =115°，∠A=25°，∠E= ( )A．70°B．80°C．90°D．100°(第7题) (第8题) (第10题)8．如图，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C的个数是( )A．2 B．3 C．4 D．59．若△ABC的三边长分别为整数，周长为11，且有一边长为4，则这个三角形的最大边长为( ) A．7 B．6 C．5 D．410．在△ABC中，已知点D、E、F分别是边BC、AD、CE上的中点，且S△ABC=4 cm2，则S△BEF的值为( )A．2 cm2B．1 cm2 C．0．5 cm2D．0．25 cm2姓名成绩二、填空题(每题3分，共24分)11．在△ABC中，∠A：∠B=2：1，∠C=60°，则∠A=_________．12．一个凸多边形的内角和与外角和相等，它是_________边形．13．如图，线段DE由线段AB平移而得，AB=4，EC=7－CD，则△DCE的周长为______cm．14．如图，直线a ∥b ，c ∥d ，∠1=115°，则∠3=_______．15．若一个多边形的每一个外角都是72°，则这个多边形的内角和为___ __．16．根据下图所表示的已知角的度数，求出其中∠α的度数为。

苏科版七年级数学下册第7章测试题(附答案)

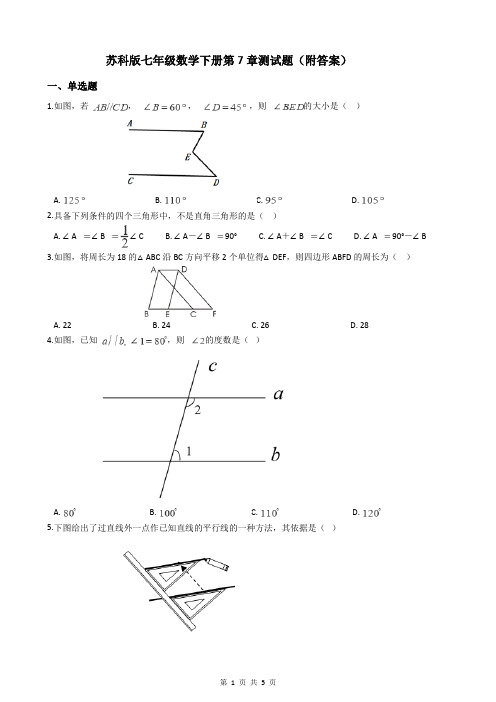
苏科版七年级数学下册第7章测试题（附答案）一、单选题1.如图，若，，，则的大小是（）A. B. C. D.2.具备下列条件的四个三角形中，不是直角三角形的是（）A. ∠A ∠B ∠CB. ∠A－∠B 90°C. ∠A＋∠B ∠CD. ∠A 90°－∠B3.如图，将周长为18的△ABC沿BC方向平移2个单位得△DEF，则四边形ABFD的周长为（）A. 22B. 24C. 26D. 284.如图，已知，则的度数是（）A. B. C. D.5.下图给出了过直线外一点作已知直线的平行线的一种方法，其依据是（）A. 同位角相等，两直线平行B. 内错角相等，两直线平行C. 同旁内角互补，两直线平行D. 平行于同一直线的两条直线平行6.如图所示,△DEF经过平移可以得到△ABC，那么∠C的对应角和ED的对应边分别是（）A. ∠F，ACB. ∠BOD，BAC. ∠F，BAD. ∠BOD，AC7.如图，下列条件能判定的是（）A. B.C. D. 且8.如图，下列条件中不能判断直线与直线平行的是（）.A. B. C. D.9.如图所示，平移后得到，已知，，则（）A. B. C. D.10.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=20°,那么∠2等于( )A. 30°B. 25°C. 20°D. 15°11.已知一个多边形的内角和为720°，则这个多边形为（）A. 三角形B. 四边形C. 五边形D. 六边形12.如图，能判定EB∥AC的条件是（）A. ∠1＝∠2B. ∠3＝∠4C. ∠5＝∠6D. ∠2＝∠3二、填空题13.一个多边形的每一个外角都等于18°，则这个多边形的边数是________.14.已知三角形的三边长均为整数，其中两边长分别为1和3，则第三边长为________.15.如图，在△ABC中，∠A＝60°，若剪去∠A得到四边形BCDE，则∠1+∠2＝________°.16.如图，在△ABC中，E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别S、S1、S2，且S=36，则S1-S2=________.17.小张同学观察如图1所示的北斗七星图，小张同学把北斗七星：摇光、开阳、玉衡、天权、天玑、天璇、天枢按图2分别标为点A、B、C、D、E、F、G，然后将点A、B、C、D、E、F、G顺次首尾连接，发现AG 恰好经过点C，且∠B－∠DCG=115°，∠B－∠D=10°，若AG//EF，则∠E=m°，这里的m=________.18.如图是用三角尺和直尺画平行线的示意图，将三角尺沿着直尺平移到三角尺的位置，就可以画出的平行线.若，，则直线平移的距离为________cm.19.如图，将三角形ABC沿水平方向向右平移到三角形DEF的位置，若BF=11，EC=5，则A，D之间的距离为________.20.如图，在ABC 中，AD、CE 是中线，若四边形BDFE 的面积是6，则ABC 的面积为________.三、解答题21.已知：如图，直线AB∥CD，直线EF与直线AB、CD分别交于点M、N，MG平分∠AMF，NH平分∠END.求证：MG∥NH.22.如图，在ABC中，F、H是BC上的点，FG⊥AC，HD⊥AC，垂足分别为G、D，在AB上取一点E，使∠BED＋∠B＝180°.求证：∠CFG＝∠HDE.23.如图，AB∥CD，∠AFE=140°，∠C=30°，求∠CEF的度数.24.如图，已知∠1=∠2，∠GFA=40°，∠HAQ=15°，∠ACB=70°，AQ平分∠FAC，求证：BD∥GE∥AH．答案一、单选题1. D2. B3. A4. B5. A6. C7. D8. B9. C 10. B 11. D 12. D二、填空题13. 20 14. 3 15. 240 16. 6 17. 18. 5.5 19. 3 20. 18三、解答题21. 证明：∵AB CD，∴∠AMF＝∠END，∵MG平分∠AMF，NH平分∠END，∴∠GMN＝∠AMF，∠HNM＝∠END，∴∠GMN＝∠HNM，∴GM NH.22. 证明：∵HD⊥AC，FG⊥AC，∴∠CDH＝∠CGF＝90°.∴ FG∥HD.∴∠CFG＝∠CHD.∵∠BED＋∠B＝180°，∴ BC∥ED.∴∠CHD＝∠HDE.∴∠CFG＝∠HDE.23. 解：延长FE交CD于G点，∵AB∥CD，∴∠AFE+∠CGF=180°，∵∠AFE=140°，∴∠CGF=40°，∵∠CEF=∠C+∠CGE，∠C=30°，∠CGE=∠CGF=40°，∴∠CEF=∠C +∠CGE =70°.24. 证明：∵∠1=∠2，∴AH∥GE，∴∠GFA=∠FAH．∵∠GFA=40°，∴∠FAH=40°，∴∠FAQ=∠FAH+∠HAQ，∴∠FAQ=55°．又∵AQ平分∠FAC，∴∠QAC=∠FAQ=55°，∵∠HAC=∠QAC+∠HAQ，∴∠HAC=55°+15°=70°=∠ACB，∴BD∥AH，∴BD∥GE∥AH．。

苏科版数学七年级下册江苏省昆山市锦溪中学周周练(第8章)

七年级数学周周练（第8章）一、选择（每题3分，共30分）1．下列各式中，正确的是（）A ．844m m m =⋅ B.25552m m m =⋅ C.933m m m =⋅ D.66y y ⋅122y = 2．实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为0.00000156m ，则这个数用科学记数法表示是（）A ．5106.15-⨯mB ．710156.0-⨯mC ．61056.1-⨯mD ．71056.1-⨯m3．在等式⋅⋅23a a ( )11a =中，括号里面的代数式是（）A ．7aB ．8aC ．6aD ．3a4．在下列括号中应填入4a 的是（）A.212)(=aB.312)(=aC.412)(=aD.612)(=a5．下列运算正确的是 ( )A ．(2a )2=2a 2B ．a 2·a 3=a 6C ．2a +3a =5aD ．(a 2) 3=a 56．若2=m a ，3=n a ，则n m a +等于（）A ．5B ．6C ．8D ．97．若1593)(y x y x n m =，则m 、n 的值分别为（）A ．9，5B ．3，5C ．5，3D ．6，128．n x -与n x )(-的正确关系是（）A.相等B.互为相反数C.当n 为奇数时它们互为相反数，当n 为偶数时相等D.当n 为奇数时相等，当n 为偶数时互为相反数 9．如果()02010a =-，()11.0--=b ，235-⎪⎭⎫ ⎝⎛-=c ，那么c b a ,,三数的大小为（） A.b a c >> B.a b c >> C.b c a >> D.c b a >>10．b a 28•等于（）A.ab 16B.b a +16C.b a +10D.b a +32 二、填空（每题3分，共30分）11．计算：（1）()=32y x （2）()()=-•342a a （3）()()=-÷-a a 4 12．填上适当的指数：（1）()54a a a =• （2）()45a a a =÷ （3）()()84a a = 13．若a x =2，则a 3x =___________． 14. 计算:(1) =÷+22x x n . (2) ()=÷-44ab ab .15．用小数表示=⨯-41014.3 . 16．计算：()022π--+的结果是 .17．若83a a a a m =••，则=m .18．若3=-b a ，则=-⋅-2332])[(])[(a b b a ________.(用幂的形式表示）19．计算：200920108(0.125)-⨯-= . 20．已知3=m a ，9=n a ，则=-n m a 3 .姓名成绩三、用心解答（共40分）21．（本题20分）计算：（1）()()524232)(a a a -÷⋅ （2）()()()34843222b a b a ⋅-+-（3）()123041323--⎪⎭⎫ ⎝⎛--+- （4）()a b - ()3a b -()5b a -22．（本题5分）已知3×9m ×27m =316，求m 的值．23．（本题5分）先化简，再求值：32233)21()(ab b a -+-⋅，其中441==b a ，24．（本题5分）若922)2(162=⋅n ，解关于x 的方程24=+nx .25．（本题5分）已知b a 92762==，求ab a 222+的值.初中数学试卷。

苏科版数学七年级下7.5 多边形的内角和与外角和同步练习(无答案)

7.5 多边形的内角和与外角和第1课时三角形三个内角之间的关系基础练知识点三角形三个内角之间的关系1.在△ABC中,若∠C=100°,∠B=10°,则∠A=_______2.在△ABC中,若∠A=80°,∠B=∠C,则∠B =_______3.在Rt△ABC中,∠C=90,∠B=54°,则∠A的度数是( )A. 66°B.36°C.56°D.46°4.如图,直线AB∥CD,∠B=50°,∠C=40,则∠E等于( )A.70°B.80°C.90°D.100°第4题图第5题图第8题图5.一个缺角的三角形ABC残片如图所示,量得∠A=45°,∠B=60°,则这个三角形残缺前的∠C 的度数为( )A.75°B.65C.55D.45°6.若三角形的一个内角等于另外两个内角和的2倍,则此三角形的最大角是( )A. 90°B.115°C.120°D.135°7.已知在△ABC中,∠A=45°,∠B=46°,那么△ABC的形状为( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形8.如图,在△ABC中,点D,E分别在AB,BC上,且DE∥AC,∠A=80°,∠BED=55°,则∠B=_____9.在△ABC中, ∠B比∠A大360，∠C比∠A小360，求△ABC各内角的度数.10.如图, △ABC中,∠A=460，CE是∠ACB的平分线，B、C、D在同一直线上，FD//EC , ∠D=42°,求∠B的度数.易错点因忽视三角形的形状而漏解11.已知AD是△ABC的高,并且∠ACD=70°,∠ABD=30°,则∠BAC=_____能力练12.在△ABC中,若∠A：∠B：C=1：2：3，.则△ABC的形状是（）A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形13.一副三角尺按如图所示的方式叠放在一起,则图中∠α等于( )A. 105°B.115°C.120°D.135°14.如图,直线a∥b,直线l与a,b分别相交于A,B两点,AC⊥AB交b于点C,∠1=40°,则∠2的度数是( )A. 40°B.45°C.50°D.60°第13题图第14题图第15题图15.如图,已知∠ACB=90°,CD⊥AB于点D,那么图中与∠A相等的角是_______16.在下列条件中:①∠A+∠B=∠C;②∠A:∠B: ∠C=1:2:3;③∠A=90°-∠B;④∠A=∠B=∠C.其中能确定△ABC是直角三角形的条件有________(填序号)17.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=______18.如图,已知DF⊥AB于点F,∠A=40°,∠D=50°,求∠ACB的度数.19.如图,在△ABC中,BD,CD是内角平分线,BD,CD 交于点D,BE,CE是外角平分线,BE,CE交于点E 试猜想∠D与∠E的关系,并说明理由.素养练20.如图,在△ABC中,AD⊥BC于点D,AE平分∠BAC.(1)若∠C=70°,∠B=40°,求∠DAE的度数;(2)若∠C-∠B=30°,则∠DAE=_______(3)若∠C-∠B=α(∠C>∠B),求∠DAE的度数(用含a的式子表示)第2课时多边形的内角和基础练知识点多边形的内角和定理1.一个十二边形的内角和等于( )A.2160°B.2080°C.1980°D.1800°2.将一个n边形变成(n+2)边形,内角和将( )A.减少180°B.增加180°C.减少360°D.增加360°3.若一个正多边形每个内角度数是方程-2x+140=-130的解,则这个正多边形的边数是( )A.9B.8C.7D.64.一个n边形的内角和等于720°,则n=________5.在五边形ABCDE中,若∠A +∠B+∠C+∠D=440°,则∠E=________6.正六边形从一个顶点出发可以画_________条对角线,这些对角线把正六边形分割成______个三角形.7.如图,该硬币边缘镌刻的正九边形每个内角的度数是_______能力练8.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得800°,则这个多边形应该是( )A六边形 B.七边形 C.八边形 D.九边形9.把一个多边形割去一个角后,得到的多边形内角和为1440°,请问这个多边形原来的边数为( )A.9B.10C.11D.以上都有可能10.如图,过正五边形ABCDE的顶点B作一条射线与其内角∠EAB的平分线相交于点P,且∠ABP=60°,则∠APB=________度.11.如图,在五边形ABCDE中,已知AB∥CD,则x=______12.如图,在正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=_______度.13.如图所示,∠A+∠B+∠C+∠D+∠E+∠F=_______度14.两个正多边形的边数之比为1:2,内角和之比为3:8,求这两个多边形的边数素养练15.如图,三角形的对角线有0条,四边形的对角线有2条,五边形的对角线有5条,六边形的对角线有9条.通过分析,请计算:(1)十边形的对角线条数为________(2)n边形的对角线条数为________(用含n的代数式表示)第3课时多边形的内角和基础练知识点多边形的外角及外角和1.正十边形的外角和为( )A180° B360° C.720° D.1440°2.已知正多边形的一个外角为36°,则该正多边形的边数为( )A.12,B.10C.8D.63.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )A.10B.11C.12D.134.若正多边形的一个外角是60°,则这个正多边形的内角和是_______5.若一个多边形的内角和等于它的外角和,则这个多边形的边数为_________6.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是_______7.已知一个多边形的每个内角都比相邻的外角大120°, 求这个多边形的边数易错点因混淆内角和与外角和而出错8.当一个凸多边形的边数由原来的3增加到n(n>3,且n为正整数)时,它的外角和( )A.增加(n-2)·180° B减小(n-2)·180° C.增加(n-1)·180° D.没有改变能力练9.如图,某人从点A出发,前进8m后向右转60°,再前进8m后又向右转60°,按照这样的方式一直走下去,当他第一次回到出发点A时, 共走了A.24mB.32mC.40 mD.48m第9题图第10题图10.如图,在七边形ABODEFG中, AB.ED的延长线交于点Q.若∠1,∠2,∠3,∠4对应的邻补角的和等于225°,则∠BOD的度数为( )A.35°B.40°C.45°D.50°11.在各个内角都相等的多边形中,一个外角等于一个内角的13,求这个多边形每个内角的度数和它的边数.12.一个多边形的每个外角都相等, 如果它的一个内角与一个外角的度数之比为13:2,求这个多边形的边数及对角线的条数13.如图,请猜想∠A+∠B+ ∠C+∠D+∠E+∠F的度数,并说明理由。

苏科版数学七年级下册第2周数学周练试卷(B).docx

七年级数学试题（B ）满分值时间制卷审核得分 100 45分钟潘明朱广庆一、选择题（每题5分，共25分）1．下列各式中错误的是( )A.()[]()623y x y x -=-B.84216)2(a a =-C.363227131n m n m -=⎪⎭⎫ ⎝⎛- D.6333)(b a ab -=-2．已知n 是大于1的自然数,则 ()()11+--⋅-n n c c 等于 ( )A.()12--n c B.nc 2- C.n c 2- D.n c 2 3．5．(-3)100×(-13)101等于 ( )A ．-1B ．1C ．-13 D ．134．如果等式(2a —1)a+2=1成立，则a 的值可能有 ( )A ．4个B ．1个C ．2个D ．3个二、填空题（每题5分，共30分）5．若3n =2，3m =5，则32m+3n-1=_______．6．计算9910022）（）（-+-所得的结果是7．计算(-3)0+(-12)-2÷|-2|的结果是8．︱x ︱＝(x －1)0 ，则x = ． 9．若3=-b a ，则=-⋅-2332])[(])[(a b b a ________.(用幂的形式表示）10．用小数表示3.14×10-4 =________．三、计算：（10分+10分+10分+10分+10分=50分）11、已知10a =5, 10b =6, 求(1)102a +103b 的值；(2)102a+3b 的值。

12、已知 n x m x ==53，用含有n m 、的代数式表示14x .班级姓名学号…………….……………..…………..密……...封……...线……...内……...请……...勿……...答……...题……………………..…….……….13、已知 222444555632---===c b a ，，请用“>”把它们按从小到大的顺序连接起来，并说明理由.14．若922)2(162=⋅n ，解关于x 的方程24=+nx .15．已知b a 92762==，求ab a 222+的值.初中数学试卷马鸣风萧萧。

苏科版七年级下学期数学周周测平行线

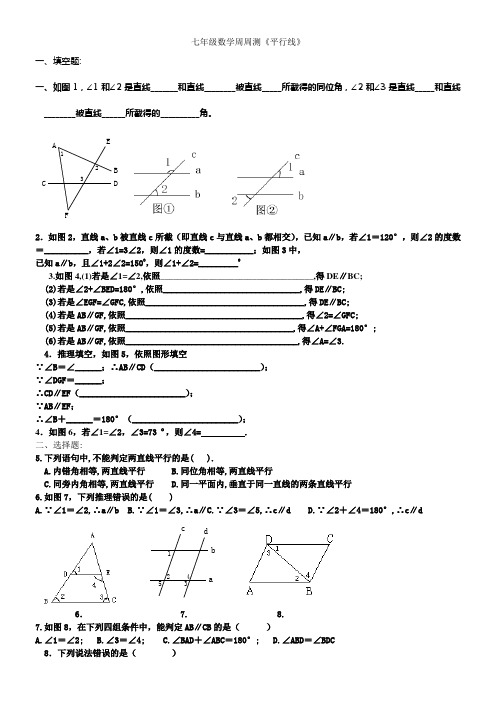
七年级数学周周测《平行线》一、填空题:一、如图1，∠1和∠2是直线_______和直线________被直线_____所截得的同位角，∠2和∠3是直线_____和直线________被直线______所截得的__________角。

321FEDCB A2．如图2，直线a 、b 被直线c 所截（即直线c 与直线a 、b 都相交），已知a ∥b ，若∠1＝120°，则∠2的度数＝__________，若∠1=3∠2，则∠1的度数=___________；如图3中，已知a ∥b ，且∠1+2∠2=1500，则∠1+∠2=_________03.如图4,(1)若是∠1=∠2,依照___________________________________,得DE ∥BC; (2)若是∠2+∠BED=180°,依照_______________________________,得DE ∥BC; (3)若是∠EGF=∠GFC,依照____________________________________,得DE ∥BC; (4)若是AB ∥GF,依照________________________________________,得∠2=∠GFC;(5)若是AB ∥GF,依照______________________________________,得∠A+∠FGA=180°; (6)若是AB ∥GF,依照_______________________________________,得∠A=∠3. 4．推理填空，如图5，依照图形填空∵∠B ＝∠______；∴AB ∥CD （________________________）； ∵∠DGF ＝______；∴CD ∥EF （________________________）； ∵AB ∥EF ；∴∠B ＋______＝180°（________________________）； 4．如图6，若∠1=∠2，∠3=73 º，则∠4= . 二、选择题:5.下列语句中,不能判定两直线平行的是( ).A.内错角相等,两直线平行B.同位角相等,两直线平行C.同旁内角相等,两直线平行D.同一平面内,垂直于同一直线的两条直线平行 6.如图7，下列推理错误的是( )A.∵∠1＝∠2,∴a ∥bB.∵∠1＝∠3,∴a ∥C.∵∠3＝∠5,∴c ∥dD.∵∠2＋∠4＝180°,∴c ∥dd cb a543216． 7. 8. 7.如图8，在下列四组条件中，能判定AB ∥CB 的是（）A.∠1＝∠2;B.∠3＝∠4;C.∠BAD ＋∠ABC ＝180°;D.∠ABD ＝∠BDC 8．下列说法错误的是（）Ａ.在同一平面内，垂直于同一直线的两直线平行Ｂ.两条直线被第三条直线所截，同旁内角互补Ｃ.平行于同一直线的两条直线平行Ｄ.若两条平行线被第三条直线所截，一组同旁内角的角平分线相互垂直三、解答题:9.如图，已知直线AB 、CD 被直线EF 所截，若是∠BMN ＝∠D NF ，∠1＝∠2，那么MQ ∥NP ，试写出推理，PQMN 21FEDCB A10、已知DE ∥BC ，CD 是∠ACB 的角平分线，∠B=80°，∠ACB=50°。

七年级数学下册周周测二无答案苏科版

江苏省连云港市新浦中学七年级数学下册周周测（二）苏科版一、选择题（每小题3分，共24分）1．下列计算正确的是 ( )A ．x 2 + x 2 = 2x4 B ．x 2•x 3=x 6 C ．(2x 3)2 = 2x 6 D ．628)(x x x =÷- 2.若2=m a ，3=n a ，则n m a +等于 ( ) A.5 B.6 C.8 D.93.在等式⋅⋅23a a （）11a =中，括号里填入的代数式应当是 ( )A.7aB. 8aC.6aD.3a4.计算m m 525÷的结果为（）A.5B.20C.m 5D.m 205.计算3112)(n n x xx +-⋅⋅的结果为( ) A.33+n x B.36+n x C.n x 12 D.66+n x 6.若0222)31()31(33.0-=-=-=-=--d c b a 则正确的为……（）A.a<b<c<dB.c<a<d<bC.a<d<c<bD.b<a<d<c7.下列算式，计算正确的有（）①10－3＝0.0001 ②(0.0001)0＝1 ③32-a ＝231a④(－x )3÷(－x )5＝－2-x A ．1个 B ．2个 C ．3个 D ．4个8.已知 n 是大于1的自然数,则 ()()11+--⋅-n n c c 等于 ( ) A.()12--n c B.nc 2- C.n c 2- D. n c 2二、填空题（每空2分，共36分）9.最薄的金箔的厚度为m 000000091.0，用科学记数法表示为 _________m ；每立方厘米的空气质量约为g 310239.1-⨯，用小数把它表示为 g . 10.（21）-1= ，（-3）-3= ，（π-3）0 = ，(-21)100×2101= 11.()=-⋅⎪⎭⎫ ⎝⎛n n 221 ；=÷-++112n n y y ；=-23])[(m .11.=+⋅+32)()(a b b a ；=-⋅-23)2()2(m n n m .12.( )242b a =； 32122+-=⨯n n ；x 10÷(x 4÷x 2)= 13.已知4x =2x+3，则x= 。

苏科版数学七年级下册周检试卷0517.docx

七年级数学周检试卷20150517班级：姓名：得分：一、选择题。

（每题2分）题号 1 2 3 4 5 6 7 8 9 10 答案1.下列说法错误的是（）A.－3x >9的解集为x <－3B.不等式2x >－1的整数解有无数多个C.－2是不等式3x <－4的解D.不等式x >－5的负整数解有无数多个 2.如图1—3—1表示的是以下哪个不等式的解集（）图1—3—1A.x >－1B.x <－1C.x ≥－1D.x ≤－1 3. 不等式－4≤x ＜2的所有整数解的和是( )A.－4B.－6C.－8D.－9 4. 已知a ＜b ，下列式子中，错误的是( )A 、4a ＜4bB 、－4a ＜－4b C.、a ＋4＜b ＋4 D 、a －4＜b －4 5.若不等式(a +1)x ＜a +1的解集为x ＜1，那么a 必须满足( ) A.a ＜0 B.a ≤－1 C.a ＞－1 D.a ＜－1 6、下列不等式中，是一元一次不等式的是（）A ．3x(x+5)＞3x 2+7； B ．x ≥0； C ．xy-2＜3； D ．x+y ＞5． 7、若x ＞y ，则ax ＞ay.那么一定有( )A 、a ＞0B 、a ≥0C 、a ＜0D 、a ≤0 8．若|m-5|=5-m ，则m 的取值范围是（）A ．m ＞5；B ．m ≥5；C ．m ＜5；D ．m ≤5．（）A ．x ＞15；B ．x ≥15；C ．x ＜15；D ．x ≤15． 10．若关于x 的方程3x+3k=2的解是正数，则k 的值为（）A. k ﹤32 B. k ﹥32C ．k 为任何实数；D ．以上答案都不对．二、填空题（每空2分）1.如果3+2x 是正数，则x 的取值范围是_______，2.x 的3倍不大于－8，用不等式表示为_______ _，其解集是_______ _.3.不等式2x －1≥5的最小整数解为________.4.若a ＞b,c ＜0, 用“>”或“<”号填空．（1）13a 13b （2）-a -b （3）ac 2 bc 2（4）ac bc 5.如果关于x 的不等式0 x k 正整数解为1,2,3,正整数k 应满足。

苏科版七年级数学下册周练试卷

苏科版七年级数学下册周练试卷
A.88mm
B.96mm
C.80mm
D.84mm
图10 图11
5.如图11，OP∥QR∥ST，则下列各式中正确的是 ( )
A.2+3=180
B.2-3=90
C.2+3=90
D.3-1=180
6.在△ABC中,三边长分别为a,b,c,且都是整数且bc,b=5,则满足条件的三角形的个数为( )
A. 2个
B. 3个
C. 4个
D. 5个
三、解答题：
1. 如图，请你根据图中的信息，把小船ABCD通过平移后到的位置，画出平移后的小船位置.
2. 如图13，平移方格纸中的图形，使点A平移到处，画出放大一倍后的图形.(所画的图形用阴影表示)
图13
3.如图，如果4=180，那么1与2是否相等?为什么?
4：如图，从下列三个条件中：(1)AD∥CB (2)AB∥CD (3)C，任选两个作为条件，另一个作为结论，编一道数学题，并说明理由。

已知：
结论：
理由：
5：如图，AD∥BC，C，BE、DF分别平分ABC和CDA，试说明
BE∥DF的理由?
4.如图，如果AB//CD，B=37，D=37，那么BC与DE平行吗? 为什么?
5.如图，AD//BC，C.AB与DC平行吗?为什么?
6.已知等腰三角形的周长为14cm，底边与腰的比为3：2，求各边长。

(苏科版)初中数学七年级下册第7章综合测试(含答案)

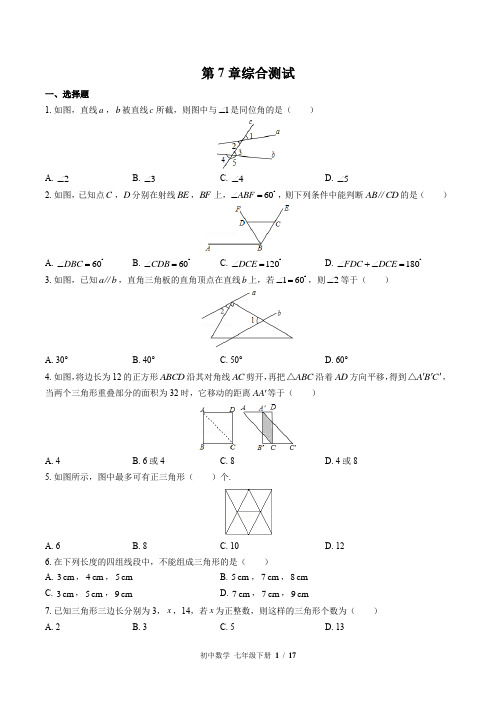
第7章综合测试一、选择题1.如图，直线a ，b 被直线c 所截，则图中与1∠是同位角的是（）A .2∠B .3∠C .4∠D .5∠2.如图，已知点C ，D 分别在射线BE ，BF 上，°60ABF ∠=，则下列条件中能判断AB CD ∥的是（）A .°60DBC ∠=B .°60CDB ∠=C .°120DCE ∠=D .°180FDC DCE ∠+∠=3.如图，已知a b ∥，直角三角板的直角顶点在直线b 上，若°160∠=，则2∠等于（）A .30°B .40°C .50°D .60°4.如图，将边长为12的正方形ABCD 沿其对角线AC 剪开，再把ABC △沿着AD 方向平移，得到A B C '''△，当两个三角形重叠部分的面积为32时，它移动的距离AA '等于（）A .4B .6或4C .8D .4或85.如图所示，图中最多可有正三角形（）个.A .6B .8C .10D .126.在下列长度的四组线段中，不能组成三角形的是（） A .3cm ，4cm ，5cm B .5cm ，7cm ，8cm C .3cm ，5cm ，9cmD .7cm ，7cm ，9cm7.已知三角形三边长分别为3，x ，14，若x 为正整数，则这样的三角形个数为（） A .2B .3C .5D .138.在三角形的三个外角中，锐角最多只有（） A .3个B .2个C .1个D .0个9.如图，点A 、B 、C 、D 、E 、F 是平面上的6个点，则A B C D E F ∠+∠+∠+∠+∠+∠的度数是（）A .180°B .360°C .540°D .720°10.已知一个多边形内角和为720°，则该多边形的对角线条数为（） A .9B .12C .15D .1811.若一个多边形的每个内角都为144°，则这个多边形是（） A .七边形B .八边形C .九边形D .十边形12.三角形的高、中线和角平分线都是（） A .直线B .射线C .线段D .以上答案都不对13.下列ABC △中，正确画出AC 边上的高的是（）A .B .C .D .14.下列说法错误的是（）A .三角形的三条高一定在三角形内部交于一点B .三角形的三条中线一定在三角形内部交于一点C .三角形的三条角平分线一定在三角形内部交于一点D .三角形的三条高所在直线可能相交于外部一点15.如图，ABC △中，°90ACB ∠＞，AD BC ⊥，BE AC ⊥，CF AB ⊥，垂足分别为D 、E 、F ，ABC △中边BC 上的高是（）A .FCB .BEC .ADD .AE二、填空题16.如图，ACD ∠是ABC △的外角，若°80ACD B ∠-∠=，则A ∠=________°.17.如图，在一块长为12cm ，宽为6cm 的矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是2cm ），则空白部分表示的草地面积是________.18.如图，点G 为ABC △三边的重心，若12ABC S =△，则图中阴影部分的面积是________.19.如图所示°3118∠=，°148∠=，则2∠=________.20.将一副三角尺按如图方式进行摆放，则1∠的度数为________.三、解答题21.如图，四边形ABCD 中，外角DCG A ∠=∠，点E 、F 分别是边AD 、BC 上的两点，且EF AB ∥.D ∠与1∠相等吗？为什么？22.如图1，在ABC △中，OB 、OC 是ABC ∠、ACB ∠的角平分线；（1）填写下面的表格.（2）试猜想A ∠与BOC ∠之间存在一个怎样的数量关系，并证明你的猜想；（3）如图2，ABC △的高BE 、CD 交于O 点，试说明图中A ∠与BOD ∠的关系.23.（1）观察下列各图，第①个图中有1个三角形，第②个图中有3个三角形，第③个图中有6个三角形，第④个图中有10个三角形，……，根据这个规律可知第n 个图中有()12n n -个三角形（用含正整数n 的式子表示）；（2）（1）中是否存在一个图形，该图形中共有29个三角形？若存在，请画出图形；若不存在，请通过具体计算说明；（3）图③中，点B 线段AC 的中点，D 为AC 延长线上一个动点，记PDA △的面积为1S ；PCB △的面积为2S ；PDC △的面积为3S .下列两个结论①132S S S +是定值；②132S S S -是定值.有且只有一个结论是正确的，请作出选择并求值.24.如图，每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，四边形ABCD 四个顶点的坐标分别为()20A -，，()12B -，，()33C ，，()40D ，.（1）画出四边形ABCD ；（2）把四边形ABCD 向下平移4个单位长度，再向左平移2个单位长度得到四边形A B C D ''''，画出四边形A B C D ''''，并写出C '的坐标；（3）求出四边形ABCD 的面积.25.如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形，建立如图所示的平面直角坐标系，已知点()10A ，，()40B ，，()33C ，，()14D ，（1）描出A 、B 、C 、D 、四点的位置，并顺次连接ABCD .（2）四边形ABCD 的面积是________.（3）把四边形ABCD 向左平移5个单位，再向下平移2个单位得到四边形A B C D ''''，写出点A '、B '、C '、D '的坐标.26.如图，已知AC ED ∥，ED GF ∥，°90BDF ∠=.（1）若°150ABD ∠=，求GFD ∠的度数；（2）若ABD θ∠=，求GFD CBD ∠-∠的度数.27.如图是一个汉字“互”字，其中，AB CD ∥，12∠=∠，MGH MEF ∠=∠.求证：MEF GHN ∠=∠.第7章综合测试答案解析一、 1.【答案】B【解析】利用同位角、内错角、同旁内角的定义判断即可. A .2∠是1∠的对顶角，所以此选项错误； B .3∠是1∠的同位角，所以此选项正确； C .4∠与1∠不是同位角，所以此选项错误； D .5∠与1∠不是同位角，所以此选项错误. 故选B.此题主要考查了“三线八角”，同位角的边构成“F ”形，内错角的边构成“Z ”形，同旁内角的边构成“U ”形是解答此题的关键.【考点】同位角，内错角，同旁内角 2.【答案】B【解析】根据内错角相等，两直线平行，即可得到AB CD ∥. 当°60DBC ∠=时，不能判断AB CD ∥；当°60CDB ∠=时，根据°60ABF ∠=，可得ABF CDB ∠=∠，故能判断AB CD ∥；当°120DCE ∠=时，不能判断AB CD ∥；当°180FDC DCE ∠+∠=，不能判断AB CD ∥；故选：B.本题主要考查了平行线的判定，解题时注意：内错角相等，两直线平行. 【考点】平行线的判定 3.【答案】A【解析】先根据平行线的性质求出3∠的度数，再由余角的定义即可得出结论.a b ∵∥，°160∠=， °3160∠=∠=∴，°°°°2903906030∠=-∠=-=∴.故选：A.本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等.【考点】平行线的性质 4.【答案】D【解析】设AA x '=，AC 与A B ''相交于点E ，判断出AA E '△是等腰直角三角形，根据等腰直角三角形的性质可得A E x '=，再表示出A D '，然后根据平行四边形的面积公式列方程求解即可. 设AA x '=，AC 与A B ''相交于点E ，ACD ∵△是正方形ABCD 剪开得到的， ACD ∴△是等腰直角三角形， °45A ∠=∴，AA E '∴△是等腰直角三角形， A E AA x ''==∴， 12A D AD AA x ''=-=-，∵两个三角形重叠部分的面积为32，()1232x x -=∴，整理得，212320x x -+=，解得14x =，28x =，即移动的距离AA '等4或8. 故选D.本题考查了平移的性质，正方形的性质，等腰直角三角形的判定与性质，熟记平移的性质并用平移距离表示出重叠部分的底与高是解题的关键. 【考点】平移的性质 5.【答案】B【解析】分单个的正三角形和几个三角形复合的正三角形两种情况计算个数. 单个的正三角形有6个，复合正三角形有2个，所以正三角形共有8个. 故选B.分单个的正三角形和复合的正三角形两种情况找出正三角形，要注意做到不重不漏. 【考点】三角形 6.【答案】C【解析】根据三角形的三边关系定理：三角形两边之和大于第三边进行分析即可.A .345+＞，能够组成三角形，故此选项不合题意；B .578+＞，能够组成三角形，故此选项不合题意；C .359+＜，不能够组成三角形，故此选项符合题意；D .779+＞，能够组成三角形，故此选项不合题意. 故选：C.此题主要考查了三角形的三边关系，运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形. 【考点】三角形三边关系 7.【答案】C【解析】直接根据三角形的三边关系求出x 的取值范围，进而可得出结论.∵三角形三边长分别为3，x ，14，143143x -+∴＜＜，即1117x ＜＜. x ∵为正整数，12x =∴，13，14，15，16，即这样的三角形有5个.故选C.本题考查的是三角形的三边关系，熟知三角形两边之和大于第三边，两边之差小于第三边是解答此题的关键.【考点】三角形三边关系 8.【答案】C【解析】利用三角形的内角和外角之间的关系分析.根据三角形的内角和是180°可知，三角形内角最多只能有1个钝角，所以在三角形的三个外角中，锐角最多只有1个.故选：C.主要考查了三角形的内角和外角之间的关系.（1）三角形的外角等于与它不相邻的两个内角和.（2）三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件. 【考点】三角形内角和定理 9.【答案】B【解析】先根据三角形外角的性质得出1A B ∠+∠=∠，2E F ∠+∠=∠，3C D ∠+∠=∠，再根据三角形的外角和是360°进行解答.1∠∵是ABG △的外角， 1A B ∠=∠+∠∴， 2∠∵是EFH △的外角， 2E F ∠=∠+∠∴，3∠∵是CDI △的外角， 3C D ∠=∠+∠∴，1∠∵、2∠、3∠是GIH △的外角，°123180∠+∠+∠=∴，°=360A B C D E F ∠+∠+∠+∠+∠+∠.故选B.本题考查的是三角形外角的性质及三角形的外角和，熟知三角形的外角和是360度是解答此题的关键. 【考点】三角形内角和定理 10.【答案】A【解析】根据多边形内角和的计算方法()°2180n -，先求出边数，再求出对角线的条数. 依题意有()°°2180720n -=，解得6n =.该多边形为六边形，故对角线条数为()66329⨯-÷=条. 故选：A.此类题考查的是多边形内角和的计算方法，难度属简单，考生应识记该公式. 【考点】多边形内角与外角，多边形的对角线 11.【答案】D【解析】先求出每一个外角的度数，再根据360︒=÷边数一个外角的度数计算即可.°°°18014436-=， °°3603610÷=，故这个多边形的边数是10. 故选：D.本题主要考查了多边形的内角与外角的关系，求出每一个外角的度数是关键. 【考点】多边形内角与外角 12.【答案】C【解析】根据三角形的高、中线和角平分线的定义可知它们都是线段.三角形的高、中线和角平分线都是线段.故选C.本题考查了三角形的高、中线和角平分线的定义，用到的知识点：从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高；三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线；三角形一边的中点与此边所对顶点的连线叫做三角形的中线；三角形有三条中线，有三条高线，有三条角平分线，它们都是线段.【考点】三角形的角平分线、中线和高13.【答案】D△中AC边上的高是过点B垂直于AC边的线段，只有D选【解析】根据三角形高线的定义解答即可.ABC项正确.故选D.本题考查了三角形的高线的定义，是基础题，熟记高线的概念是解题的关键.【考点】三角形的角平分线、中线和高14.【答案】A【解析】三角形的三条中线和三条角平分线都交于三角形的内部，而三条高线可以交在三角形的内部，或外部，或一角的顶点.A.错误，三条高线可以交在三角形的内部，或外部，或一角的顶点；B.正确；C.正确；D.正确.故选A.本题考查了三角形的高线、角平分线、中线的性质.【考点】三角形的角平分线、中线和高15.【答案】C⊥，根据三角形高的定义即可得到AD为三角形ABC的边BC上的高.【解析】由于AD BC∵，⊥AD BC∴为三角形ABC的边BC上的高.AD故选C.本题考查了三角形的角平分线、中线和高：过三角形的一个顶点引对边的垂线，这个点与垂足的连线段叫三角形的高.【考点】三角形的角平分线、中线和高二、16.【答案】80【解析】根据三角形的外角的性质列式计算即可.°∠=∠-∠=，A ACD B80故答案为：80.本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.【考点】三角形的外角性质60cm17.【答案】2【解析】根据矩形面积公式可求矩形的面积；因为柏油小路的任何地方的水平宽度都是2，所以其面积与同宽的矩形面积相等，故可求草地面积.()21262660cm =-=⨯-⨯=草地面积矩形面积小路面积.故答案为：260cm .此题考查生活中的平移现象，化曲为直是解决此题的关键思路.【考点】生活中的平移现象18.【答案】4【解析】根据重心的概念和性质分别求出BGF S △和CGE S △，计算即可.∵点G 为ABC △三边的重心，AD ∴是ABC △的中线，AF 是ABC △的中线，2AG GD =，162ABD ABC S S ==△△∴， 24ABG CBD S S ==△△∴，2BGF S =△∴，同理2CGE S =△，∴图中阴影部分的面积是4，故答案为：4.本题考查的是重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍.【考点】三角形的重心19.【答案】70°【解析】根据三角形外角的性质即可得到结论.312∠=∠+∠∵，°23170∠=∠-∠=∴，故答案为：70°.本题考查了三角形外角的性质，熟练掌握三角形外角的性质是解题的关键.【考点】三角形的外角性质20.【答案】120°【解析】根据三角形的一个外角等于和它不相邻的两个内角的和计算即可.如图，°°°1239030120∠=∠+∠=+=，故答案为：120°.本题考查的是三角形的外角的性质，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.【考点】三角形的外角性质，三角形内角和定理三、21.【答案】解：1D ∠=∠，DCG A ∠=∠∵，°180DCG DCB ∠+∠=，°180A DCB ∠+∠=∴，°360A B DCB D ∠+∠+∠+∠=∵，°180D B ∠+∠=∴，EF AB ∵∥，°1180B ∠+∠=∴，1D ∠=∠∴.【解析】首先证明°180A DCB ∠+∠=，再根据四边形内角和为360°可得°180D B ∠+∠=，根据平行线的性质可得°1180B ∠+∠=，进而可得1D ∠=∠.此题主要考查了多边形的内角，以及平行线的性质，关键是掌握四边形内角和为360°.【考点】多边形内角与外角，平行线的性质22.【答案】解：（1）（2）猜想：°902BOC A ∠=+∠.理由：∵在ABC △中，OB 、OC 是ABC ∠、ACB ∠的角平分线；12OBC ABC ∠=∠∴，12OCB ACB ∠=∠， °180ABC ACB A ∠+∠=-∠∵，()()°°11118090222OBC OCB ABC ACB A A ∠+∠=∠+∠=-∠=-∠∴， ()°°°°11180180909022BOC OBC OCB A A ⎛⎫∠=-∠+∠=--∠=+∠ ⎪⎝⎭∴．（3）证明：ABC ∵△的高BE 、CD 交于O 点，°90BDC BEA ∠=∠=∴，°90ABE BOD ∠+∠=∴，°90ABE A ∠+∠=，A BOD ∠=∠∴.【解析】（1）由°1902A BOC ∠=+∠，代入数值即可求得答案；（2）由在ABC △中，OB 、OC 是ABC ∠、ACB ∠的角平分线，根据三角形的内角和定理即可求得OBC OCB ∠+∠的值，然后在OBC △中，再利用三角形的内角和定理，即可求得答案；（3）由ABC △的高BE 、CD 交于O 点，即可得°90BDC BEA ∠=∠=，然后利用同角的余角相等，即可求得A ∠与BOD ∠的关系.此题考查了三角形的内角和定理与同角的余角相等，以及角平分线的定义.此题难度适中，解题的关键是整体思想与数形结合思想的应用.【考点】三角形内角和定理23.【答案】解：（1）由题意得出规律，第n 个图时，应该有三角形的个数为()12n n +个；（2）当()1292n n +=，化简得：2580n n +-=，由于这个方程中没有正整数解，因此不管是第几个图形，都不可能有29个三角形；（3）1322S S S -=， AB BC =∵，且三角形ABP 和三角形BCP 的底边AB ，CD 上的高相等，12ABP BCP APC S S S ==△△△∴，因此1322APC APD PCD S S S S S S =-=-=△△△，即1322S S S -=. 【解析】（1）我们看到后一个图形的三角形的个数与上一个图形中三角形的个数的差是递增的（1，12+，33+，64+，105+，……），因此我们可得出到第n 个图时，应该有三角形的个数为()12n n +个；（2）将29代入（1）得出的式子中，看看是否有整数解即可；（3）可根据AB BC =得出三角形ABP ，BCP 的面积相等，因此三角形BCP 的面积就是三角形APC 的面积的一半，APC APD PCD =-三角形的面积三角形的面积三角形的面积，因此1322S S S -=是成立的. 本题考查了三角形和规律性等知识点，读懂题中给出的条件是解题的关键.【考点】三角形的面积，三角形24.【答案】解：（1）如图所示，四边形ABCD 即为所求；（2）如图所示，四边形AB C D '''即为所求，且()11C '-，；（3）如图所示，11131241134212812.5 2222 ABCDS=⨯⨯+⨯⨯+⨯⨯+⨯=+++=四边形.【解析】（1）在坐标系内描出各点，再顺次连接即可；（2）根据图形平移的性质画出四边形AB C D'''，并写出C'点的坐标即可；（3）把四边形分为三个直角三角形和一个矩形，再求其面积即可.本题考查的是作图——平移变换，熟知图形平移不变性的性质是解答此题的关键.【考点】作图——平移变换25.【答案】解：（1）如图，四边形ABCD即为所求；（2）连接AC，则1124338.522ACD ABCABCDS S S=+=⨯⨯+⨯⨯=△△四边形.故答案为：8.5；（3）如图，四边形AB C D'''即为所求，()42A'--，，()12B'--，，()21C'-，，()42D'-，.【解析】（1）在坐标系内描出各点，并顺次连接ABCD即可；（2）连接AC，利用三角形的面积公式即可得出结论；（3）画出四边形AB C D'''，写出点A'、B'、C'、D'的坐标即可.本题考查的是作图——平移变换，熟知图形平移不变性的性质是解答此题的关键.【考点】作图——平移变换26.【答案】解：（1）AC ED ∵∥，°180ABD BDE ∠+∠=∴，°150ABD ∠=∵，°30BDE ∠=∴，°90BDF ∠=∵，°60EDF ∠=∴，ED GF ∵∥，°180EDF F ∠+∠=∴，°120F ∠=∴；（2）AC ED ∵∥，°180ABD BDE ∠+∠=∴，ABD θ∠=∵，BDE θ∠=∴，°90BDF ∠=∵，()°90EDF θ∠=-∴，ED GF ∵∥，°180EDF F ∠+∠=∴， ()°90F θ∠=+∴，ABD θ∠=∵， ()°180CBD θ∠=-∴，()()()°°°90180290GFD CBD θθθ∠-∠=+--=-∴.【解析】（1）根据平行线的性质可得°180ABD BDE ∠+∠=，进而可得°30BDE ∠=，然后再计算出EDF ∠的度数，再根据平行线的性质可得°180EDF F ∠+∠=，进而可得GFD ∠的度数；（2）与（1）类似，表示出F ∠的度数，再表示出CBD ∠的度数，再求差即可.此题主要考查了平行线的性质，关键是掌握两直线平行，同旁内角互补.【考点】平行线的性质27.【答案】证明：延长ME 交CD 于P 点，AB CD ∵∥，13∠=∠∴，12∠=∠∵，23∠=∠∴，ME HN ∴∥，MGH GHN ∠=∠∴，MGH MEF ∠=∠∵，MEF GHN ∠=∠∴.【解析】延长ME 交CD 于P 点，然后由AB CD ∥.可得13∠=∠，等量代换易得23∠=∠，由平行线的判定定理可得ME HN ∥，易得MGH GHN ∠=∠，等量代换易得结论.此题考查了平行线的性质与判定，熟记同位角相等⇔两直线平行，内错角相等⇔两直线平行，同旁内角互补⇔两直线平行是解题的关键.【考点】平行线的性质。

苏科版七年级数学下册第7-8章达标检测卷附答案

苏科版七年级数学下册第7章达标检测卷一、选择题(每题3分，共24分)1．下列长度的3根小木棒不能搭成三角形的是( )A．2 cm，3 cm，4 cm B．1 cm，2 cm，3 cmC．3 cm，4 cm，5 cm D．4 cm，5 cm，6 cm2．如图，直线a∥b，∠1＝130°，则∠2等于( )A．70°B．60°C．50°D．40°3．如图，在下列给出的条件中，不能判定AB∥EF的是( )A．∠B＝∠3B．∠1＝∠4C．∠1＝∠BD．∠B＋∠2＝180°4．如图，将周长为7的△ABC沿BC方向平移2个单位长度得到△DEF，则四边形ABFD的周长为( )A．16 B．9 C．11 D．125．如图，AD，BE，CF是锐角三角形ABC的三条高，它们交于点H，则图中直角三角形的个数是( )A．6 B．8 C．10 D．126．如图，已知直线AB∥CD，直线EF与AB相交于点O，且∠BOE＝140°.直线l 平分∠BOE交CD于点G，那么∠CGO＝( )A．110°B．105°C．100°D．70°7．如图，直角三角形ABC的顶点A在直线m上，分别测量下列角的度数：①∠1，∠2，∠C；②∠2，∠3，∠B；③∠3，∠4，∠C；④∠1，∠2，∠3.可判断直线m与直线n是否平行的是( )A．①B．②C．③D．④8．如图，△ABC中，AD是BC边上的高，AE，BF分别是∠BAC，∠ABC的平分线，∠BAC＝50°，∠ABC＝60°，则∠EAD＋∠ACD＝( )A．75°B．80°C．85°D．90°二、填空题(每题3分，共30分)9．若线段AD是△ABC的中线，且BD＝3，则BC的长为________．10．如图，请填写一个条件，使结论成立：因为________，所以a∥b.11．若长度分别为3，4，a的三条线段能组成一个三角形，则整数a的值可以是________．(写出一个即可)12．在△ABC中，∠ACB是钝角，AD是BC边上的高，若AD＝2，BD＝3，CD＝1，则△ABC的面积等于________．13．如图，直线m与∠AOB的一边射线OB相交，∠1＝30°，向上平移直线m得到直线n，直线n与∠AOB的另一边射线OA相交，则∠2＋∠3＝________．14．如图，有一块长为a m，宽为3 m的长方形地，其中阴影部分是一条小路，空白部分为草地，小路的左边线向右平移1 m能得到它的右边线，若草地的面积为12 m2，则a＝________．15．两个直角三角尺如图摆放，其中∠BAC＝∠EDF＝90°，∠E＝45°，∠C＝30°，AB与DF交于点M.若BC∥EF，则∠BMD的大小为________．16．一机器人在平地上按如图设置的程序行走，则该机器人从开始到停止所行走的路程为________．17．将一个长方形纸片折叠成如图所示的图形，若∠ABC＝26°，则∠ACD＝________°.18．一副直角三角尺按如图①所示方式叠放，现将含45°角的三角尺ADE固定不动，将含30°角的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行．如图②，当∠CAE＝15°时，BC∥DE.则∠CAE(0°＜∠CAE＜180°)其他所有可能符合条件的度数为______________．三、解答题(19，20题每题6分，21，22题每题8分，23，24题每题9分，其余每题10分，共66分)19．在△ABC中，AB＝8，BC＝2，并且AC的长为偶数，求△ABC的周长．20．如图，点E在AB的延长线上，指出下面各题中的两个角是哪两条直线被哪一条直线所截形成的？它们是什么角？(1)∠A和∠D；(2)∠A和∠CBA；(3)∠C和∠CBE.21．已知一个多边形的边数为n.(1)若n＝5，求这个多边形的内角和．(2)若这个多边形的内角和的14比一个四边形的内角和多90°，求n的值．22．如图，在方格纸中，△ABC的顶点都在方格纸的格点上．将△ABC平移后得到△A′B′C′，图中已画出B点的对应点B′.(1)请补全△A′B′C′；(2)画出△A′B′C′的高C′H以及中线A′D；(3)连接BB′，CC′，BB′和CC′的数量关系为__________．23．如图，已知AD，AE分别是△ABC的中线和高，△ABD的周长比△ACD的周长多3 cm，且AB＝9 cm.(1)求AC的长；(2)求△ABD与△ACD的面积的关系．24．如图，已知∠1＋∠2＝180°，且∠3＝∠B.(1)试说明：∠AFE＝∠ACB；(2)若CE平分∠ACB，且∠2＝110°，∠3＝50°，求∠ACB的度数．25．如图，在四边形ABCD中，AD∥BC，∠BDC＝∠C，DE⊥DC交AB于点E.(1)试说明：DE平分∠ADB.(2)若∠ABD的平分线与CD的延长线交于点F，与DE交于点G，设∠F＝α°.①若α＝50，求∠A的度数；②若∠F＜12∠ABC，试确定α的取值范围．26．已知MN∥EF，C为两直线之间的一点，连接AC，BC.(1)如图①，∠CAM与∠CBE的平分线相交于点D，若∠ACB＝100°，求∠ADB的度数．(2)如图②，若∠CAM与∠CBE的平分线相交于点D，∠ACB与∠ADB有何数量关系？请说明理由．(3)如图③，若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D，请写出∠ACB与∠ADB的数量关系，并说明理由．答案一、1．B 2．C 3．C 4．C 5．D 6．A 7．B8．A 二、9．6 10．∠1＝∠4(答案不唯一)11．5(答案不唯一) 12．2 13．210°14．5 15．75°16．32 m 17．12818．60°或105°或135°点拨：如图①，当BC∥AE时，∠CAE＝∠C＝60°；如图②，当DE∥AB时，则∠E＋∠EAB＝180°，所以∠EAB＝135°，所以∠CAE＝135°－30°＝105°，此时AD∥BC；如图③，当AC∥DE时，则∠E＋∠CAE＝180°，所以∠CAE＝135°.三、19．解：根据三角形的三边关系得8－2＜AC＜8＋2，即6＜AC＜10.因为AC的长为偶数，所以AC＝8，所以△ABC的周长为8＋2＋8＝18.20．解：(1)∠A和∠D是由直线AE，CD被直线AD所截形成的，它们是同旁内角．(2)∠A和∠CBA是由直线AD，BC被直线AE所截形成的，它们是同旁内角．(3)∠C和∠CBE是由直线CD，AE被直线BC所截形成的，它们是内错角．21．解：(1)当n＝5时，(5－2)×180°＝540°，所以这个多边形的内角和为540°.(2)由题意，得14×(n－2)×180°－360°＝90°，解得n＝12.所以n的值为12.22．解：(1)如图，△A′B′C′即为所求．(2)如图，C′H，A′D即为所求，(3)BB′＝CC′23．解：(1)因为AD是△ABC的中线，所以BD＝CD.因为△ABD的周长比△ACD的周长多3 cm，所以AB＋BD＋AD－(AD＋AC＋DC)＝3 cm，即AB－AC＝3 cm.因为AB＝9 cm，所以AC＝6 cm.(2)因为S△ABD＝12BD·AE，S△ACD＝12CD·AE，BD＝CD，所以S△ABD＝S△ACD.24．解：(1)因为∠1＋∠2＝180°，∠1＋∠FDE＝180°，所以∠FDE＝∠2.因为∠3＋∠FEC＋∠FDE＝180°，∠2＋∠B＋∠ECB＝180°，∠B＝∠3，所以∠FEC＝∠ECB，所以EF∥BC，所以∠AFE＝∠ACB.(2)因为∠3＝∠B，∠3＝50°，所以∠B＝50°.因为∠2＋∠B＋∠ECB＝180°，∠2＝110°，所以∠ECB＝20°.因为CE平分∠ACB，所以∠ACB＝2∠ECB＝40°.25．解：(1)因为AD∥BC，所以∠ADC＋∠C＝180°.因为DE⊥DC，所以∠EDC＝90°，所以∠BDE＋∠BDC＝90°，∠ADE＋∠C＝90°.因为∠BDC＝∠C，所以∠BDE＝∠ADE，即DE平分∠ADB.(2)①因为DE平分∠ADB，BF平分∠ABD，所以∠EDB＝12∠ADB，∠DBF＝12∠ABD，所以∠EDB＋∠DBF＝12(∠ADB＋∠ABD)．因为∠A＋∠ADB＋∠ABD＝180°，所以∠EDB＋∠DBF＝90°－12∠A.由题意知∠EDF＝90°，∠F＝α°＝50°，所以∠FGD＝40°.因为∠BGD＋∠FGD＝180°，∠BGD＋∠EDB＋∠DBF＝180°，所以∠FGD＝∠EDB＋∠DBF，所以90°－12∠A＝40°，所以∠A＝100°.②因为AD∥BC，所以∠ADB＝∠DBC，所以∠EDB＋∠DBF＝12(∠ADB＋∠ABD)＝12∠ABC.由(2)①知∠FGD＝∠EDB＋∠DBF，所以∠FGD＝12∠ABC.因为∠F＜12∠ABC，所以∠F＜∠FGD.易知∠F＋∠FGD＝90°，所以0°＜∠F＜45°，即0＜α＜45.26．解：(1)如图①，过点C作CG∥MN，过点D作DH∥MN，因为MN∥EF，所以MN∥CG∥EF，MN∥DH∥EF，所以∠1＝∠ADH，∠2＝∠BDH，∠MAC＝∠ACG，∠EBC＝∠BCG.因为∠CAM与∠CBE的平分线相交于点D，所以∠1＝12∠MAC＝12∠ACG，∠2＝12∠EBC＝12∠BCG，所以∠ADB＝∠ADH＋∠BDH＝∠1＋∠2＝12∠ACG＋12∠BCG＝12(∠ACG＋∠BCG)＝12∠ACB.因为∠ACB＝100°，所以∠ADB＝50°.(2)∠ADB＝180°－12∠ACB.理由如下：如图②，过点C作CG∥MN，过点D作DH∥MN，因为MN∥EF，所以MN∥CG∥EF，MN∥DH∥EF，所以∠1＝∠ADH，∠2＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，∠MAC＋∠ACG＝180°，∠EBC＋∠BCG＝180°.因为∠MAC与∠EBC的平分线相交于点D，所以∠1＝12∠MAC，∠2＝12∠EBC，所以∠ADB＝∠ADH＋∠BDH＝∠1＋∠2＝12(∠MAC＋∠EBC)＝12(180°－∠ACG＋180°－∠BCG)＝12(360°－∠ACB)，所以∠ADB＝180°－12∠ACB.(3)∠ADB＝90°－12∠ACB.理由如下：如图③，过点C作CG∥MN，过点D作DH∥MN，因为MN∥EF，所以MN∥CG∥EF，MN∥DH∥EF，所以∠DBE＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，∠MAC＋∠ACG＝180°，∠NAD＋∠ADH＝180°.因为∠MAC的平分线与∠FBC的平分线所在的直线相交于点D，所以∠CAD＝12∠MAC，∠BDH＝∠DBE＝12∠CBF，所以∠ADB＝180°－∠CAD－∠CAN－∠BDH＝180°－12∠MAC－∠ACG－12∠CBF＝180°－12∠MAC－∠ACG－12∠BCG＝180°－12(180°－∠ACG)－∠ACG－12∠BCG＝180°－90°＋12∠ACG－∠ACG－12∠BCG＝90°－12∠ACG－12∠BCG＝90°－12(∠ACG＋∠BCG)＝90°－12∠ACB.苏科版七年级数学下册期中达标检测卷一、选择题(每题3分，共24分)1．下列运算正确的是( )A．(a2)3＝a5B．a4·a2＝a8C．a6÷a3＝a3D．(－ab2)5＝－a5b7 2．将下面的图形进行平移，能得到的图形是( )3．下列长度的三条线段，能组成三角形的是( )A．3，4，8 B．5，6，10C．5，5，11 D．5，6，114．如图，可以判定AC∥BD的是( )A．∠2＝∠3B．∠2＝∠5C．∠1＝∠4D．∠4＝∠55．把多项式(x－y)2－2(x－y)－8分解因式，正确的结果是( )A．(x－y＋4)(x－y＋2) B．(x－y－4)(x－y－2)C．(x－y－4)(x－y＋2) D．(x－y＋4)(x－y－2)6．将一副直角三角尺(∠A＝30°，∠E＝45°)按如图所示的位置摆放，使AB∥EF，则∠DOC的度数是( )A．70°B．75°C．80°D．85°7．若259＋517能被n整除，则n的值可能是( )A．20 B．30 C．35 D．408．已知(x2＋px＋8)(x2－3x＋q)乘积中不含x2与x3项，则p，q的值分别是( ) A．0，0 B．3，1 C．－3，－9 D．－3，1 二、填空题(每题3分，共30分)9．如图，直线a，b被直线c所截，a∥b，∠1＝60°，那么∠2＝________°.10．计算：12x·(－2x2)3＝________．11．分解因式：－12a2＋2a－2＝____________．12．肥皂泡的泡壁厚度大约为0.000 7 mm，用科学记数法表示0.000 7＝________．13．已知2x＋y＋1＝0，则52x·5y＝________．14．若x2＋(m－2)x＋9是一个完全平方式，则m的值是________．15．如图，将△ABE向右平移3 cm得到△DCF，如果△ABE的周长是16 cm，那么四边形ABFD的周长是________cm.16．若a＋b＝10，ab＝11，则代数式a2－ab＋b2的值是________．17．如图，在五边形ABCDE中，∠A＋∠B＋∠E＝300°，DP，CP分别平分∠EDC，∠BCD，则∠P＝______．18．如图，将一副三角尺按如图放置，则下列结论：①∠1＝∠3；②若∠2＝30°，则BC∥AE；③若∠1＝∠2＝∠3，则BC∥AE；④若∠2＝30°，则∠3＝∠E.其中正确的是________(填序号)．三、解答题(19，20题每题6分，21，22题每题8分，23，24题每题9分，其余每题10分，共66分)19．计算：(1)(12)－1＋(π＋3)0－|－3|＋(－1)2 023; (2)x·x5＋(－2x3)2－3x8÷x2.20．把下列各式分解因式：(1)a4－16; (2)18a2－50.21．先化简，再求值：(a －2b )(a ＋2b )－(a －2b )2＋8b 2，其中a ＝－2，b ＝12.22．如图，将方格纸中的△ABC (顶点A ，B ，C 均在格点上)向右平移6个单位长度，得到△A 1B 1C 1. (1)画出平移后的图形；(2)连接AA 1，BB 1，则线段AA 1，BB 1的位置关系是________； (3)如果每个小方格的边长是1，那么△ABC 的面积是________．23．如图是一个长为10 cm ，宽为6 cm 的长方形，在它的4个角上分别剪去边长为x cm 的小正方形，再沿虚线折成一个有底无盖的长方体盒子，求盒子的体积．24．如图，点F是线段BA延长线上一点，点E，G是线段CD上的两点，在△ADE 中，∠D＝∠DAE，AD平分∠EAF，AG∥BC，若∠B＝140°，求∠AGD的度数．25．如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“奇巧数”，如12＝42－22，20＝62－42，28＝82－62，…，因此12，20，28这三个数都是“奇巧数”．(1)52，72都是“奇巧数”吗？(2)设两个连续偶数为2n，2n＋2(其中n为正整数)，由这两个连续偶数构造的“奇巧数”是8的倍数吗？为什么？(3)试说明：任意两个连续“奇巧数”之差是同一个数．26．【数学经验】三角形的中线能将三角形分成面积相等的两部分．【经验发展】面积比和线段比的联系：如果两个三角形的高相同，那么它们的面积比等于对应底边的比．如图①，△ABC的边AB上有一点M，试说明：S△ACMS△BCM ＝AM BM.【结论应用】如图②，S△CDE＝1，CDAC＝14，CECB＝13，求S△ABC.【拓展延伸】如图③，△ABC的边AB上有一点M，D为CM上任意一点，请利用上述结论，试说明：S△ACDS△BCD ＝AM BM.【迁移应用】如图④，在△ABC中，M是AB上一点，且AM＝13AB，N是BC的中点，若S△ABC＝1，则S四边形BMDN＝________．答案一、1．C 2．C 3．B 4．C 5．C 6．B 7．B 8．B二、9．60 10．－4x711．－12(a－2)212．12．7×10－413．1 514．8或－4 15．22 16．6717．60°18．①③④三、19．解：(1)原式＝2＋1－3－1＝－1.(2)原式＝x6＋4x6－3x6＝2x6.20．解：(1)原式＝(a2＋4)(a2－4)＝(a2＋4)(a＋2)(a－2)．(2)原式＝2(9a2－25)＝2(3a＋5)(3a－5)．21．解：原式＝a2－4b2－a2＋4ab－4b2＋8b2＝4ab，当a＝－2，b＝12时，原式＝4×(－2)×12＝－4.22．解：(1)如图，△A1B1C1即为所求．(2)平行(3)423．解：盒子的体积为x(10－2x)(6－2x)＝x(4x2－32x＋60)＝4x3－32x2＋60x(cm3)．24．解：因为AD平分∠EAF，所以∠DAF＝∠DAE.又因为∠D＝∠DAE，所以∠D＝∠DAF.所以BF∥CD.所以∠B＋∠C＝180°.所以∠C＝180°－∠B＝180°－140°＝40°.又因为AG∥BC，所以∠AGD＝∠C＝40°.25．解：(1)因为52＝142－122，68＝182－162，76＝202－182，所以52是“奇巧数”，72不是“奇巧数”．(2)不是．因为(2n＋2)2－(2n)2＝(2n＋2＋2n)(2n＋2－2n)＝4(2n＋1)，所以这两个连续偶数构造的“奇巧数”不是8的倍数．(3)设三个连续偶数分别为2k，2k＋2，2k＋4(k为正整数)，因为[(2k＋2)2－(2k)2]－[(2k＋4)2－(2k＋2)2]＝(2k＋2＋2k)(2k＋2－2k)－(2k＋4＋2k＋2)(2k＋4－2k－2)＝4(2k＋1)－4(2k＋3)＝8k＋4－8k－12＝－8，所以任意两个连续“奇巧数”之差是同一个数．26．解：【经验发展】如图①，过C作CH⊥AB于H.因为S△ACM＝12AM×CH，S△BCM＝12BM×CH，所以S△ACMS△BCM ＝12AM×CH12BM×CH＝AMBM，即S△ACMS△BCM＝AMBM.【结论应用】如图②，连接AE.因为CDAC＝14，所以S△CDE＝14S△ACE.因为CECB＝13，所以S△ACE＝13S△ABC，所以S△CDE＝14×13S△ABC＝112S△ABC.又因为S△CDE＝1，所以S△ABC＝12.【拓展延伸】因为M是AB上任意一点，所以S△ACMS△BCM ＝AM BM.因为D是CM上任意一点，所以S△ACDS△ACM ＝CDCM，S△BCDS△BCM＝CDCM，所以S△ACD＝CDCM×S△ACM，S△BCD＝CDCM×S△BCM，所以S△ACDS△BCD ＝CDCM×S△ACMCDCM×S△BCM＝S△ACMS△BCM，即S△ACD S△BCD ＝AM BM.【迁移应用】512点拨：如图③，连接BD.因为AM＝13 AB，所以AM＝12 BM，所以S△ACDS△BCD ＝AMBM＝12，S△ADMS△BDM ＝AMBM＝12，即S△ACD＝12S△BCD，S△ADM＝12S△BDM.因为N是BC的中点，所以CN＝BN，所以S△ACDS△ABD ＝CNBN＝1，S△CDNS△BDN＝CNBN＝1，即S△ACD＝S△ABD，S△CDN＝S△BDN.设S△ADM＝a，则S△BDM＝2a，所以S△ACD＝S△ABD＝3a，所以S△CDN＝S△BDN ＝12S△BCD＝S△ACD＝3a，所以S 四边形BMDN ＝5a ，S △ABC ＝12a ，所以S 四边形BMDN ＝512S △ABC ＝512×1＝512. 苏科版七年级数学下册第8章达标检测卷一、选择题(每题3分，共24分) 1．计算(－a )2·a 4的结果是( )A ．a 6B ．－a 6C ．a 8D ．－a 82．－3－2的倒数是( )A ．－9B ．9C ．19D ．－193．下列运算正确的是( )A ．2a －a ＝2B ．a 3·a 2＝a 6C ．a 3÷a ＝a 2D ．(2a 2)3＝6a 54．计算：(a ·a 3)2＝a 2·(a 3)2＝a 2·a 6＝a 8，其中，第一步运算的依据是( )A ．同底数幂的乘法法则B ．幂的乘方法则C ．乘法分配律D ．积的乘方法则5．数据0.000 000 12用科学记数法可表示为( )A ．1.2×10－7B ．0.12×10－6C ．12×10－8D ．1.2×10－66．定义一种新的运算：若a ≠0，则有a ▲b ＝a －2＋ab ＋|－b |，那么(－12)▲2的值是( ) A ．－3B ．5C ．－34D ．327．已知10a＝20，100b＝50，则12a ＋b ＋32的值是( )A ．2B ．52C ．3D ．928．已知(x －1)|x |－1有意义且值为1，则x 的值为( )A ．±1B ．－1C ．－1或2D ．2二、填空题(每题3分，共30分) 9．计算：(1)(2a 2)2＝________；(2)(x 2)3÷(x ·x 2)2＝________； (3)[(a －b )2]3·[(b －a )3]3＝________． 10．计算：⎝ ⎛⎭⎪⎫12－3＋2 0230＝________．11．计算：(－5)2 021×⎝ ⎛⎭⎪⎫15 2 022＝________．12．若(m －2)0无意义，则代数式(－m 2)3的值为________．13．纳秒(ns)是非常小的时间单位，1 ns ＝10－9s.北斗全球导航系统的授时精度优于20 ns.用科学记数法表示20 ns 是__________s. 14．若0＜x ＜1，则x －1，x ，x 2的大小关系是____________． 15．若x ＋3y －4＝0，则3x ·27y 的值为________．16．设x ＝5a ，y ＝125a ＋1(a 为正整数)，用含x 的代数式表示y ，则y ＝________． 17．梯形的上、下底的长分别是4×103 cm 和8×103 cm ，高是1.6×104 cm ，此梯形的面积是__________．18．对于数a ，b ，定义运算a ▲b ＝⎩⎨⎧a b（a ＞b ，a ≠0），a －b （a <b ，a ≠0），如2▲3＝2－3＝18，4▲2＝42＝16.照此定义的运算方法计算[2▲(－4)]×[(－4)▲(－2)]的结果为________．三、解答题(19，20题每题6分，21，22题每题8分，23，24题每题9分，其余每题10分，共66分) 19．计算：(1)a 3·a 2·a ＋(a 2)3;(2)(2m 3)3＋m 10÷m －(m 3)3.20．计算：(1)0.62 023×(－53)2 022; (2)(－23)2 022×(－32)2 023.21．已知2a＝4b(a，b是正整数)且a＋2b＝8，求2a＋4b的值．22．(1)比较221与314的大小；(2)比较86与411的大小．23．(1)已知m＋2n＝4，求2m×4n的值；(2)已知n为正整数，且x2n＝4，求(x3n)2－2(x2)2n的值．24．某农科所要在一块长1.2×105 cm，宽为2.4×104 cm的长方形实验地上培育新品种粮食，已知培育每种新品种需一块边长为1.2×104 cm的正方形实验地，这块实验地最多可以培育多少种新品种粮食？25．已知a m＝2，a n＝3.(1)求a m＋2n的值；(2)求a2m－3n的值．26．阅读以下材料：苏格兰数学家纳皮尔是对数的创始人．他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉才发现指数与对数之间的联系．对数的定义：一般地，若a x＝N(a＞0且a≠1)，那么x叫做以a为底N的对数，记作x＝log a N.比如指数式24＝16可以转化为对数式4＝log216，对数式2＝log39可以转化为指数式32＝9.我们根据对数的定义可得到对数的一个性质：log a(M·N)＝log a M＋log a N(a＞0，a≠1，M＞0，N＞0)，理由如下：设log a M＝m，log a N＝n，则M＝a m，N＝a n，所以M·N＝a m·a n＝a m＋n，由对数的定义得m＋n＝log a(M·N)．又因为m＋n＝log a M＋log a N，所以log a(M·N)＝log a M＋log a N.根据上述材料，结合你所学的知识，解答下列问题：(1)填空：①log232＝________，②log327＝________，③log71＝________；(2)试说明：log a MN＝log a M－log a N(a＞0，a≠1，M＞0，N＞0)；(3)拓展运用：计算log5125＋log56－log530.答案一、1．A 2．A 3．C 4．D 5．A 6．B7．C 8．C 二、9．(1)4a 4 (2)1 (3)(b －a )15 10．9 11．－15 12．－6413．2×10－8 14．x 2＜x ＜x －1 15．81 16．125x 3 17．9.6×107 cm 2 18．1三、19．解：(1)原式＝a 6＋a 6＝2a 6.(2)原式＝8m 9＋m 9－m 9＝8m 9. 20．解：(1)原式＝0.62 022×⎝ ⎛⎭⎪⎫－53 2 022×0.6＝⎣⎢⎡⎦⎥⎤0.6×⎝ ⎛⎭⎪⎫－53 2 022×0.6＝(－1)2 022×0.6＝1×0.6＝0.6. (2)原式＝⎣⎢⎡⎦⎥⎤－23×⎝ ⎛⎭⎪⎫－32 2 022×⎝ ⎛⎭⎪⎫－32＝1×⎝ ⎛⎭⎪⎫－32＝－32.21．解：因为2a ＝4b ＝22b ，所以a ＝2b .又因为a ＋2b ＝8，所以4b ＝8，解得b ＝2，所以a ＝4，所以2a ＋4b ＝24＋42＝32. 22．解：(1)221＝(23)7＝87，314＝(32)7＝97，因为8＜9，所以87＜97，即221＜314.(2)86＝(23)6＝218， 411＝(22)11＝222，因为18＜22，所以218＜222，即86＜411.23．解：(1)因为m ＋2n ＝4，所以原式＝2m ×22n ＝2m ＋2n ＝24＝16.(2)因为x2n＝4，所以原式＝(x2n)3－2(x2n)2＝43－2×42＝32.24．解：[(1.2×105)÷(1.2×104)]×[(2.4×104)÷(1.2×104)]＝20(种)，所以这块实验地最多可以培育20种新品种粮食．25．解：(1)因为a m＝2，a n＝3，所以a m＋2n＝a m·a2n＝a m·(a n)2＝2×32＝2×9＝18.(2)因为a m＝2，a n＝3，所以a2m－3n＝a2m÷a3n＝(a m)2÷(a n)3＝22÷33＝4 27.26．解：(1)①5 ②3 ③0(2)设log a M＝m，log a N＝n，则M＝a m，N＝a n，所以MN＝a ma n＝a m－n.由对数的定义得m－n＝log a M N .又因为m－n＝log a M－log a N，所以log a MN＝log a M－log a N.(3)原式＝log5(125×6÷30)＝log525＝2.。

江苏省灌南县实验中学七年级数学下学期第7周周练试题(B)(无答案) 苏科版

七年级数学试题（B ）一、选择题（每题5分，共25分） 1．已知 n 是大于1的自然数,则 ()()11+--⋅-n n c c 等于 ( ) A.()12--n c B.nc 2- C.n c 2- D.n c 2 2．已知125y x =-，223y x =-+，如果12y y <，则x 的取值范围是（） A 、2x > B 、2x < C 、2x >- D 、2x <- 3．数a 、b 、c 在数轴上对应的点如图所示，则下列式子中正确的是 A ．a －c>b －c B ．a ＋c<b ＋c C ．ac>bc D ．a c b b < 4．设a 、b 、c 的平均数为M ，a 、b 的平均数为N ，N 、c 的平均数为P ，若a>b ≥c ，则M 与P 的大小关系是 ( ) A. M < P B. M > P C. M ≥ P D. 不确定 5．不等式组1(1)22331x x x ⎧+≤⎪⎨⎪-<+⎩的解集在数轴上表示正确的是（）二、填空题（每题5分，共30分） 6．计算：498×502－5002＝． 7．已知不等式30x m -≤有5个正整数解，则m 的取值范围是． 8．已知不等式组1x x n <⎧⎨>⎩有解，则n 的取值范围是． 9．已知关于x 的方程x －(2x －a)＝2的解是负数，则a 的取值范围是． 10．计算9910022）（）（-+-所得的结果是三、计算：（7分+12分+9分+10分+12分=50分）11、解不等式组⎪⎩⎪⎨⎧+≤-+<+23531)2(213x x x x ，并把解集在数轴上表示出来,同时写出解集中的所有整数解．A B C D …………….……………..…………..密……...封……...线……...内……...请……...勿……...答……...题……………………..…….……….12、因式分解：（1）242a a -（2）42816x x -+13．若关于x 、y 的方程组325233x y a x y a -=-⎧⎨+=+⎩的解都为正数，求a 的取值范围．14．甲、乙两商场以同样价格出售同样的商品，并且又推出不同的优惠方案：在甲商场累计购物超过100元后，超出100元的部分按90%收费；在乙商场累计购物超过50元后，超出50元的部分按95%收费．(1)若小明妈妈准备用120元去商场购物，你建议小明妈妈去商场花费少（直接写“甲”或“乙”）；(2)根据两家商场的优惠活动方案，问顾客到哪家商场购物花费少？请说明理由．15、某电脑经销商计划同时购进一批电脑机箱和液晶显示器，若购进电脑机箱10台和液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液晶显示器5台，共需要资金4120元．(1)每台电脑机箱、液晶显示器的进价各是多少元?(2)该经销商计划购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?。

苏科版七年级数学下第周围周测试卷

4321DAB C（第2题）七年级数学（下）第四周周测试卷一．选择题：1.下列各角不是多边形的内角的是（）．（Ａ）1800（B）5400（C）19000 （D）108002.如图，下列推理正确的是A．∵∠2＝∠4，∴AD∥BC．B．∵∠1＝∠3，∴AD∥BC．C．∵∠4＋∠D＝180°，∴AD∥BC．D．∵∠4＋∠B＝180°，∴AD∥BC．3.在等式a3·a2·( )＝a11中，括号里面人代数式应当是（）(A)a7 (B)a8 (C)a6 (D)a34.已知n是大于1的自然数,则()c-1-n()1+-•nc等于 ( )A. ()12--nc B.nc2- C.c-n2 D.nc25.已知OA OB⊥，O为垂足，且AOC∠∶1AOB∠=∶2，则BOC∠是（）.A、45︒B、135︒C、45︒或135︒D、60︒或20︒6.下列运算中与44aa•结果相同的是 ( )A.82aa• B.()2a4 C.()44a D.()()242aa•47.一个三角形的两边长是2cm和7cm，第三边长是偶数，则那个三角形的周长是( ) A．15cm B．17cm C．15cm或17cm D．16cm和18cm8.已知a m=3，a n=2，那么a m+n+2的值为（）A 8B 7C 6a2D 6+a29.在△ABC中，∠A=80°，∠B、∠C的平分线交于O，则∠BOC等于（）A. 80°B. 60°C. 100°D. 130°10.如图14，若AB∥CD，则∠A、∠E、∠D之间的关系是( )图14A.∠A+∠E+∠D=180°B.∠A－∠E+∠D=180°C.∠A+∠E－∠D=180°D.∠A+∠E+∠D=270°二．填空题：1.若52=m，62=n，则nm+2＝．2.木工师傅有两根长别离为80㎝、150㎝的木条，要再找一根木条，将它们钉成一个三角形框架，现有70㎝、200㎝、300㎝三根木条，他可选择长为的木条．3.若一个多边形的每一个外角都等于72°，则那个多边形是__________边形，它共有_______条对角线.4.(a ＋b)2·(b＋a)3＝，(2m －n)3·(n－2m)2＝ ;5.已知：。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3
2
1
七年级数学下学期周练试卷7 苏科版
学校班级学号姓名 1、六边形的内角和是度，外角和是度，它共有条对角线. 2、如图，直线a ∥b ，那么∠A= .
第8题图
3、将一个正方体木块表面涂上红色, 如果每面等距离地切4刀, 则可以得到 ___ _ 个三面红色的小正方体, ______ 个两面红色的小正方体, _______ 个一面红色的小正方体, ______ 个没有涂色的小正方体; 如果要得到各面都没有涂色的小正方体100个, 则每面至少需切 ______ 刀.
4、如果一个等腰三角形的两条边长分别为2、4，那么这个三角形的周长是 .
5、图中阴暗部分的面积是 .
6、如图，平面镜A 与B 之间的夹角为120°，光线经平面镜A 反射后射在平面镜B 上，再反射出去，若∠1＝∠2，则∠1的度数为 .
7、已知：2a －b －3c ＝4，且a 2
＋b 2
＋c 2
＝ab ＋bc ＋ca ，则a －1
＋b 0
－c 3
＝ .
8、如图，给出了过直线外一点作已知直线的平行线的方法，其依据是 . 9、如果把多项式x 2
-8x ＋m 分解因式得(x-10)(x ＋n)，那么m ＝，n ＝ . 10、若多项式2
25x kx ++是一个完全平方式，则k ＝ .
11、(1)当a 时，1)3(0
=+a ． (2)已知2
10,t t +-=则32
2t t ++2008= .
12、我们知道，1nm=10-9
m ，一种花粉的直径为35 000nm ，那么这种花粉的直径用科学记数法可记为___________m 。

13、右图为6个边长等的正方形的组合图形，则123∠+∠+∠= ．
（第13题）
A B
C
a b
28°
50°
第2题图
120°
第6题图
1
2
a b
a 21
b 2
1
第5题图
A
B D
A′ D ′ C ′
B ′ （第14题）
A B
C
D
E
F （第15题）
A B
C
D
E
F
（第16题）
绿化园地
14、如图，边长为4cm 的正方形ABCD 先向上平移2cm ，再向右平移1cm ，得到正方形A′B′C′D′，此时阴影部分的面积为_______cm 2
．
15、如图，它是由6个面积为1的小正方形组成的长方形，点A 、B 、C 、D 、E 、F 是小正方形的顶点，以这六个点中的任意三点为顶点，可以组成________个面积是1的三角形．
16、已知在△ABC 中，已知点D 、E 、F 分别为BC 、AD 、CE 的中点，且S △ABC ＝4cm 2
，则S △BEF 的值为________cm 2
． 17、已知1639273m m ⨯⨯=,则m= .
18、如果一个多边形的每个内角都相等，且内角比与它相邻的外角大100°，则这个多边形的内角和等于度
19、已知△ABC 中， 2∠A=3∠B= 4∠C，则此三角形是
（）
A 、锐角三角形
B 、直角三角形
C 、钝角三角形
D 、以上都有可能
20、下列各式从左到右的变形，是因式分解的是（） A 、x x x x x 6)3)(3(692
+-+=+- B 、()()103252
-+=-+x x x x
C 、()2
2
4168-=+-x x x D 、623ab a b =⋅
21、下面计算中，正确的是（） A 、(m+n)(-m+n)=－m 2
+n 2
B 、5
523)()(n m n m n m +=++
C 、6
9323)(b a b a -=-- D 、a a a =-2
323
22、为了美化城市，经统一规划，将一正方形．．．草坪的南北方向增加3m ，东西方向缩短3m ，则改造后的长方形草坪面积与原来正方形草坪面积相比（）
Ａ、增加6m 2 Ｂ、增加9m 2 Ｃ、保持不变Ｄ、减少9m 2
23、下列各式中，能用平方差公式计算的是
（） A ．)3)(3(+--x x B ．)2)(2(b a b a -+ C ．)1)(1(---a a
D ．2
)3(-x
24、如图，在一个长方形花园ABCD 中，AB=a ，AD=b ，花园中建有一条长方形道路LMPQ 及一条平行四边形道路RSKT ，若LM=RS=c ，则花园中可绿化部分的面积为（）
A 、2
b a
c ab bc ++- B 、ac bc ab a -++2
C 、2
c ac bc ab +-- D 、ab a bc b -+-2
2
（第24题图）（第26题图）（第27题图）
25、篮子里有若干苹果，可以平均分给)1(+x 名同学，也可以平均分给)3(-x 名同学（x 为大于3的正整
A B
C D G
E
F
数），用代数式表示苹果数量不可能是（）
A ．322-+x x
B ．322--x x
C ．)3)(1(3-+x x
D ．)32(2
--x x x
26、如图，正方形ABCD 和CEFG 的边长分别为m 、n ，那么∆AEG 的面积的值（） A ．与m 、n 的大小都有关 B ．与m 、n 的大小都无关 C ．只与m 的大小有关 D ．只与n 的大小有关
27、如图，一块四边形绿化园地，四角都做有半径为R 的圆形喷水池，则这四个喷水池占去的绿化园地的面积为（） A 、2
2R π B 、2
4R π C 、2
R π D 、不能确定 28、计算
(1) （π-3）0
－(12)－1+ ()200820092 1.53⎛⎫⨯- ⎪⎝⎭
(2) （2）)2)(2(282
-+-x x x —8
(3)310
5322334)()2()(2a a a a a a ÷+-⋅-+ (4)（2x-3y ）2(2x+3y)2
29、将下列各式因式分解
（1）4x 2
－16 （2）223363xy y x x -+- （3）)x y ()y x (x 2
-+-
（4）2
22x 16)4x (-+ （5）9(x+y)2
-16(x-y)2
（6）16)5(8)5(222+-+-x x
30、先化简，再求值
2(21)(21)(2)a a a +-+-4(1)a -+(2)a -，其中2=a ．
31、如图AB ∥DE ，且有∠1＝∠2，∠3＝∠4，试说明：BC ∥EF 解：∵AB ∥DE(已知)∴∠1＝_____ (两直线平行，同位角相等)
∵∠1＝∠2，∠3＝∠4 (已知)∴∠2＝ (等量代换) ∴BC ∥EF (________________________)
32、如图，在△ABC 中，∠BAC 是钝角，请画出AB 边上的高CD ，BC 边上的中线AE ，∠B 的平分线BF 。

33、已知2m
a =，5n
a =，求 2m n
a +的值
34、如图，把长方形ABCD 的两角折叠，折痕为EF 、HG ，使HD 与BF 在同一直线上，已知长方形的两组对边分别平行，试说明两条折痕也相互平行.
35、如图，在△ABC 中，AD ⊥BC 于D ，AE 平分∠BAC ．（1）若∠B ＝30°，∠C ＝70°，则∠DAE ＝______．（2）若∠C－∠B＝30°，则∠DAE ＝______．（3）若∠C－∠B＝α（∠C＞∠B），求∠DAE 的度数（用含α的代数式表示）．
B
A
C
C
D
F
E H
G
B 1
C
1
A
C
B
D E
36、好学的小红在学完三角形的角平分线后，遇到下列4个问题，请你帮她解决．如图，在ABC中，∠BAC= 50°，点I是两角B、C平分线的交点．
问题(1)：填空：∠BIC＝°．
问题(2)：若点D是两条外角平分线的交点；填空：∠Array问题(3)：若点E是内角∠ABC、外角∠ACG
试探索：∠BEC与∠BAC的数量关系，并说明理由．
问题(4)：在问题（3）的条件下，当∠ACB等于多少
度时，CE∥AB．。