用灰色理论分析的水箱水流量问题

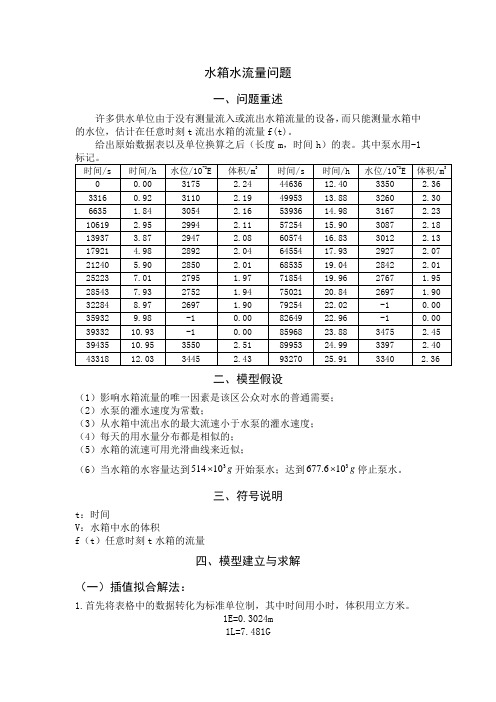
水箱水流量问题
一、问题重述
许多供水单位由于没有测量流入或流出水箱流量的设备，而只能测量水箱中的水位，估计在任意时刻t流出水箱的流量f(t)。

给出原始数据表以及单位换算之后（长度m，时间h）的表。

其中泵水用-1
二、模型假设
（1）影响水箱流量的唯一因素是该区公众对水的普通需要；
（2）水泵的灌水速度为常数；
（3）从水箱中流出水的最大流速小于水泵的灌水速度；
（4）每天的用水量分布都是相似的；
（5）水箱的流速可用光滑曲线来近似；
（6）当水箱的水容量达到3
⨯停止泵水。

51410g
677.610g
⨯开始泵水；达到3
三、符号说明
t：时间
V：水箱中水的体积
f（t）任意时刻t水箱的流量
四、模型建立与求解
（一）插值拟合解法：
1.首先将表格中的数据转化为标准单位制，其中时间用小时，体积用立方米。

1E=0.3024m
1L=7.481G
2.（1）水塔中水的体积计算：
24
V D h π
=
式中：D 为水塔的直径；h 为水塔中的水位高度。

（2）水塔中水流速度的估计。

水流速度应该是水塔中水的体积对时间的导数，但由于没有每一时刻水体积的具体数学表达式，这里我们用插商近似导数。

由于在两个时间段，水泵向水塔供水，无法确定水位的高度，因此计算水流速度要分3段进行计算。

第一段从0省道32284s ，第二段从39435s 到75021s ，第三段从85968s 到93270s
3.为了得到流速的连续曲线可以使用三次样条插值处理，然后做出时间-流速的散点图。

图1：时间流速散点图
4.曲线拟合
用MATLAB 进行三次样条插值拟合的曲线如下
图2：时间-流速曲线
5.对水流速度进行数值积分可以得到24小时的用水量为1358.43m
（二）GM （2,1）模型解法：
1.
-1
2.设时间序列为n t ，体积序列为n V 将11i i
i i
V V t t ++--组成新的一个数组n Q 并存储在文件名为data2.txt 的纯文本文件
中。

然后对序列n Q 建立GM （2,1）模型。

计算出
可以看出用GM（2,1）对本问题进行估计误差较大，所以不建议使用。

GM(2,1)模型流速图
其中蓝线是GM（2,1）模型给出的流速图。

五、附录
计算的MATLAB程序如下：
首先把原始数据粘贴到纯文本文件data.txt中，并把其中的泵水用-1标记。

clc,clear
a=load('data.txt');
t0=a(:,[1,3]);to=t0(:);%Ìá³öʱ¼äÊý¾Ý£¬²¢Õ¹¿ª³ÉÁÐÏòÁ¿
h0=a(:,[2,4]);h0=h0(:);%Ìá³ö¸ß¶ÈÊý¾Ý£¬²¢Õ¹¿ª³ÉÁÐÏòÁ¿
hs=0.3024;%µ¥Î»»»ËãÊý¾Ý
D=57*hs;%Ë®ËþÖ±¾¶£¬µ¥Î»m
h=h0/100*hs;%¸ß¶ÈÊý¾Ý£¬µ¥Î»m
t=t0/3600;%ʱ¼äת»¯³ÉСʱ
V=pi/4*D^2*h;%¼ÆËã¸÷¸öʱ¿ÌµÄÌå»ý
dv=gradient(V,t);%¼ÆËã¸÷ʱ¿ÌµÄÊýÖµµ¼Êý
no1=find(h0==-1);%ÕÒ³öÔ-ʼÎÞЧÊý¾ÝµÄµØÖ·
no2=[no1(1)-1:no1(2)+1,no1(3)-1:no1(4)+1];%ÕÒ³öµ¼ÊýÊý¾ÝÎÞЧµÄµØÖ·tt=t;tt(no2)=[];%ɾ³ýµ¼ÊýÊý¾ÝÎÞЧµÄµØÖ·µÄʱ¼ä
dv2=-dv;dv2(no2)=[];%¸ø³ö¸÷ʱ¿ÌµÄÁ÷ËÙ
plot(tt,dv2,'*')%»-³öÁ÷ËÙµÄÉ¢µãͼ
pp=csape(tt,dv2);%¶ÔÁ÷ËÙ½øÐвåÖµ
tt0=0:0.1:tt(end);%¸ø³ö²åÖµµã
fdv=ppval(pp,tt0);%¼ÆËã¸÷²åÖµµãµÄÁ÷ËÙÖµ
hold on,plot(tt0,fdv)%»-³ö²åÖµÇúÏß
I=trapz(tt0(1:241),fdv(1:241))%¼ÆËã24hÄÚ×ÜÁ÷Á¿µÄÊýÖµ»ý·Ö
clc,clear
a=load('data2.txt');%ÌáÈ¡Êý¾Ý
tt=a(:,1);
x0=a(:,2);
x0=x0/7.481
x0=x0'
n=length(x0);
x1=cumsum(x0)
a_x0=diff(x0)'
z=0.5*(x1(2:end)+x1(1:end-1))';
B=[-x0(2:end)',-z,ones(n-1,1)];
u=B\a_x0
x=dsolve('D2x+a1*Dx+a2*x=b','x(0)=c1,x(26)=c2');
x=subs(x,{'a1','a2','b','c1','c2'},{u(1),u(2),u(3),x1(1),x1(27)}); yuce=subs(x,'t',0:n-1);
x=vpa(x,6)
ezplot(x,[1,26])
x0_hat=[yuce(1),diff(yuce)]
epsilon=x0-x0_hat
plot(tt,x0_hat,tt,x0)
delta=abs(epsilon./x0)。