水箱水流量问题-第二十章建立数学建模案例分析

水箱的水流量估计【范本模板】

水箱的水流量估计摘要本文主要讨论了水箱在任意时刻流量随时间的变化问题。

对于问题一,应用EXCEL公式将所给的原始数据化为标准形式得到时间中点与平均流量值，用matlab软件的三次样条插值函数计算出水泵工作时空缺的流量值，做出时间-流量散点图，观察点的分布特征,考虑其最佳的拟合函数形式，最后通过matlab曲线拟合得到在一天内时间与流量的函数关系式：f(x)=97566−16.8x3+0.013x5−83143cos(0.1x)−27478sin(0.1x)在该模型中应用曲线插值和曲线拟合得到时间与流量的关系式,最后利用水泵泵水速度为常数这一原理来检验模型的拟合程度，操作简单结果真实.关键字：时间中点平均流量曲线插值多项式拟合一、问题重述准确地对短时段水塔水流量的预测在良好的用水管理机构中越来越成为至关紧要的一个步骤,对各个城镇的发展也具有重要的意义。

许多供水单位由于没有测量流入或流出水箱流量的设备，只能测量水箱中的水位，试通过测得的某时刻水箱中的水位的数据，估计在任意时刻t流出水箱的流量f(t)。

二、模型假设2)；1、忽略水位高度对流量的影响（根据托里拆利定律V=√2gH2、影响水箱水流量的唯一因素是该区公众对水的普通需求；3、水泵泵水速度为常数；4、从水箱中流出水的最大流速小于水泵的灌水速度；5、流量与水泵是否工作无关。

三、符号说明t: 时间V：水箱的水量V t: t时刻水箱的水量f(t)：任意t时刻流出水箱的流量P:水泵的泵水速度四、模型建立与求解4。

1模型分析问题要求是分析水箱流量与时间的关系，因此我们需要得到具体时间点所对应的流量数据,由于原始数据中只有一个时间段所对应的水量变化值，于是我们用一个时间段的平均流量作为该时间段时间中点所对应的流量值，然后再通过曲线插值拟合得出时间和流量的函数关系式。

4。

2数据处理首先我们要将表中数据换算为标准单位制，其中:时间用小时（h）、水箱水量用加仑（G）换算公式有:1E=0.3024m ， 1m3=1000L, 1L=7.481G用EXCEL公式进行换算，结果如表一:平均流量v̅：v̅=(区间左端水量−区间右端水量)÷时间间隔用EXCEL公式进行计算，计算结果为表二:4。

第十一讲估计水箱水流量模型

5．每天的用水量分布都是相似的。因为公众对水的消耗量是以全天的活动（诸如洗澡、做饭、洗衣服等）为基础的，所以每日用水类型是相似的。
6．水箱的流水速度可用光滑曲线来近似。每个用户的用水需求量与整个区的用水需求量相比微不足道，而且它与整个社区需求量的增减情况是不相似的。
四、分析与建模
引入如下记号： V、Vi — 水的容积，时刻ti水的容积G）； ti — 时刻（h）； p — 水泵的灌水速度（G/h）; T0 — 初始数据的当天测量时间; T — 当天的时间（以24小时制）; f(t) — 流出水箱的流速是时间的函数（G/h）;
18.49 14.0
2.369 10.0 10.94
/
19.50 16.0
3.411
9.6
11.49 18.6 20.40 15.0
4.425
9.6
12.49 20.0 21.43
/
5.439
8.9
13.42 19.0 22.49
/
6.45
9.6
14.43 16.0 23.42
/
7.468
8.9
15.44
0
606.1 9.981
/ 19.038 542.6
0.921 593.7 10.926
/
19.959 528.2
1.843 583.0 10.954 677.7 20.839 514.8
2.950 571.6 12.033 657.7 22.015
/
3.871 562.6 12.954 639.5 22.958
本问题中使用的长度单位为E(=30.24cm）;容积单位为G(=3.785L(升))。水箱为圆柱体，其直径为57E.

二维水箱流场问题

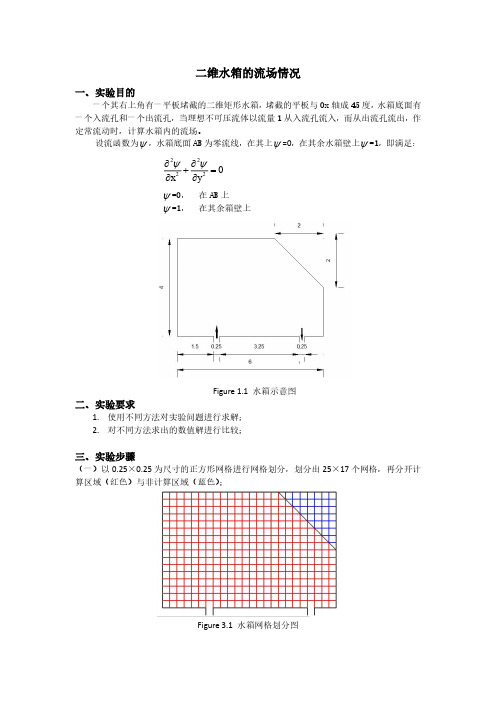
二维水箱的流场情况一、实验目的一个其右上角有一平板堵截的二维矩形水箱，堵截的平板与Ox 轴成45度，水箱底面有一个入流孔和一个出流孔，当理想不可压流体以流量1从入流孔流入，而从出流孔流出，作定常流动时，计算水箱内的流场。

设流函数为ψ，水箱底面AB 为零流线，在其上ψ=0，在其余水箱壁上ψ=1，即满足：02222=∂∂+∂∂yx ψψ ψ=0，在AB 上ψ=1，在其余箱壁上Figure 1.1 水箱示意图二、实验要求1. 使用不同方法对实验问题进行求解；2. 对不同方法求出的数值解进行比较；三、实验步骤（一）以0.25×0.25为尺寸的正方形网格进行网格划分，划分出25×17个网格，再分开计算区域（红色）与非计算区域（蓝色）；Figure 3.1 水箱网格划分图（二）使用SOR 方法（超松弛迭代法）进行求解1.差分方程：Ψi,j k+1=ω4(Ψi−1,j k+1+Ψi,j−1k+1+Ψi+1,j k +Ψi,j+1k )+(1−ω)Ψi,j k其中k 为迭代次数，ω为超松弛因子。

一般超松弛因子ω为1<ω<2。

当超松弛因子选择恰当，会大大加快迭代收敛的速度。

而对于边长为1的正方形区域第一边值问题，采用等步长正方形网格的研究表明，它的最佳松弛因子为：{ω最佳=2μ=12(cos πN +cos πM )N ×M 为网格数量。

因此：μ=12(cos π25+cos π17)≈0.9875ω最佳=21+√1−0.98752≈1.72772.用fortran 编程（附件1）进行计算，求出数值解（更改ω和允许误差的值进行不同计算）；再用matlab 程序进行绘图（附件3），进行比较。

（三）使用ADI 方法（交替方向隐格式）进行求解 1.差分方程Ψi,j k+12=Ψi,j k +∆t 2(∆x )2(Ψi−1,j k+12−2Ψi,j k+12+Ψi+1,j k+12)+∆t 2(∆y )2(Ψi,j−1k −2Ψi,j k +Ψi,j+1k ) Ψi,jk+1=Ψi,jk+12+∆t 2(∆x )2(Ψi−1,j k+12−2Ψi,j k+12+Ψi+1,j k+12)+∆t 2(∆y )2(Ψi−1,j k+1−2Ψi,j k+1+Ψi+1,j k+1) 2.用fortran 编程（附件2）进行计算，求出数值解（更改∆t 和允许误差的值进行不同计算）；再用matlab 程序进行绘图（附件3），进行比较。

数学建模案例分析

数学建模案例分析数学建模是将现实问题转化为数学模型，并利用数学方法对模型进行求解的过程。

它是数学与实际问题结合的重要手段，能够帮助人们深入理解问题的本质，提供科学的决策依据。

以下是一个数学建模案例分析。

市有4个城区，现准备改造城市供水系统，以满足未来的供水需求。

根据过往的数据分析，每个城区的用水量与其人口数量、平均收入以及大型工厂的数量有关。

现在的问题是如何设计供水系统，使得满足各城区的用水需求，并且降低总成本。

为了解决这个问题，我们需要进行数学建模。

首先，我们需要确定影响用水量的因素。

1.人口数量：根据过往数据，我们可以得到人口数量与用水量之间的关系。

假设每增加1个人口，用水量增加A升，其中A为一个常数。

2.平均收入：平均收入的提高可能会促使人们增加用水量。

假设平均收入每提高1个单位，用水量增加B升，其中B为一个常数。

3.大型工厂数量：大型工厂对水的需求较大，可能对城区的用水量产生较大的影响。

假设每增加1个大型工厂，用水量增加C升，其中C为一个常数。

通过对过往数据的分析和回归分析，我们可以得到A、B和C的具体数值。

然后，我们可以建立供水系统的数学模型：设城区1、城区2、城区3和城区4的人口分别为x1、x2、x3和x4，平均收入分别为y1、y2、y3和y4，大型工厂数量分别为z1、z2、z3和z4设城区1、城区2、城区3和城区4的用水量分别为w1、w2、w3和w4根据前述的假设，我们可以得到数学模型：w1=A*x1+B*y1+C*z1w2=A*x2+B*y2+C*z2w3=A*x3+B*y3+C*z3w4=A*x4+B*y4+C*z4此外，由于我们希望降低总成本，我们还需要引入成本模型。

假设供水系统的建设成本与每个城区的用水量成正比，并且平均每增加1升用水量，建设成本增加D元，其中D为一个常数。

设城区1、城区2、城区3和城区4的建设成本分别为cost1、cost2、cost3和cost4根据成本因素，我们可以得到成本模型：cost1 = D * w1cost2 = D * w2cost3 = D * w3cost4 = D * w4接下来，我们需要优化这个数学模型。

水流问题数学建模

估计水塔的水流量1问题提出某居民区的民用自来水是由一个圆柱形的水塔提供．水塔高12.2米，直径17．4米．水塔是由水泵根据水塔内水位高低自动加水，一般每大水泵工作两次．现在需要了解该居民区用水规律与水泵的工作功率．按照设计，当水塔的水位降至最低水位，约8．2米时，水泵自动启动加水；当水位升；高到一个最高水位，约10．8米时，水泵停止工作．可以考虑采用用水率（单位时间的用水量）来反映用水规律，并通过间隔一段时间测量水塔里的水位来估算用水率．表4．2是某一天的测量记录数据，测量了28个时刻，但是由于其中有3个时刻遇到水泵正在向水塔供水，而无水位作功率．2问题分析与数据处理由问题的要求，关键在于确定用水率函数，即单位时间内用水体积，记为f(t)，又称水流速度．如果能够通过测量数据，产生若干个时刻的用水率，也就是f(t)在若干个点的函数值，则f(t)的计算问题就可以转化为插值问题．1．假设1）水塔中水流量是时间的连续光滑函数，与水泵工作与否无关，并忽略水位高度对水流速度的影响．2）水泵工作与否完全取决于水塔内水位的高度，且每次加水的工作时间为2小时3）水塔为标准圆柱体．考虑到假设2）结合表4．2中具体数据，推断得出4）水泵第一次供水时间段为［8．967，10．954］，第二次供水时间段为「20．839，22．958］．2．体积计算水塔是一个圆柱体，体积为h D V 24π=．其中D 为底面直径，h 为水位高度。

水流速度应该是水塔中水的体积对时间的导数（微商）由于没有水的体积关于时间的函数表达式，而只有一个离散的函数值表4．3，因此考虑用差商代替微商，这也是离散反映连续的常用思想．为提高精度，采用二阶差商，即i i v t f 2)(-∇=具体地，因为所有数据被水泵两次工作分割成三组数据，对每组数据的中间数据采用中心差商，前后两个数据不能够采用中心差商，改用向前或向后差商．中心差商公式模型及计算结果问题已经转变为根据流速f(t)的一个函数值表，产生函数f(t)在整个区间（二十四小时）上的函数或函数值，插值和拟合是两种最常用的方法．如果建立拟合模型，需要根据散点图的趋势，选择适当的拟合函数形式．如果采用插值模型，可以考虑分段线性插值。

水箱流量

这里我们取级数前5项进行近似（如果想要更
精确可以取更多项）对上式进行积分得：
H （t ）
其中：
令
，
是常数，，
，
我们就得到了一个多元线性回归方程：
6vt 6vt
2.下面把加水过程也考虑在内因为假设了加水速度是均匀的，所以我们设第一次加水和第二次加水过程中由于加水使得水位上升的速度分别是 v(t),和u(t)。第一次加水可以表示成在水位表达式中加上一个 β6v(t)，第二次加水是在水位表达式中加上一个 β7u(t)。当水箱的水容量达到514 g（27E）时开始泵水，达到677.6 g（35.50E）时停止泵水。所以无法准确知道泵水时间，但是可以知道是在 [32284,39435]和 [75021,85968]这两个时间段内，不妨假设水泵就是在这两个时间段内泵水的。
D2 d
用MATLAB做出的f（t）图像如图所示：
水箱水流量问题
模型假设
（1）影响水箱流量的唯一因素是该区公众对
水的普通需要；（2）水泵的灌水速度为常数；（3）从水箱中流出水的最大流速小于水泵的灌水速度；（4）每天的用水量分布都是相似的；（5）水箱的流速可用光滑曲线来近似；（6）当水箱的水容量达到开始泵水；达到停止泵水。
模型建立与求解

1. 先不考虑泵水过程，设在t时刻水箱中水位（单位E）为：H=H（t）则水箱的水的体积（单位，E3）为：其中，D=47E为水塔直径则在t时刻流出水塔的水流量为：反过来有：
由于假设小镇中每天的86400s为周期的周期函数，任何以时间T为周期的函数都可以展开为下列的傅里叶函数：
f (t ) H (t ) 4 dt ^ ^ ^ 2 D2 ^ T 2 t ^ 2 t 4 t 4 t cos sin 2 cos 2 1 2 4 5 sin 3 2T 2 T T T T

水箱水流量问题

水箱水流量问题班级：计算122姓名：***学号：*********1水箱的水流量问题（一）问题的提出：许多供水单位由于没有测量流入或流出水箱流量的设备，而只能测量水箱中的水位。

试着通过测得的某时刻水箱中水位的数据，估计在任意时刻（包括水泵灌水时间）t流出水箱的流量f(t)。

假设：(1)影响水箱流量的唯一因素是该区域公众对水的普通需要。

(2)水泵的灌水速度为常数。

(3)从水箱中流出水的最大流速小于水泵的灌水速度。

(4)每天的用水量分布都是相似的。

(5)水箱的流水速度可用光滑曲线来近似。

(6)当水箱的水容量达到514.8g时，开始泵水；达到677.6时，便停止泵水。

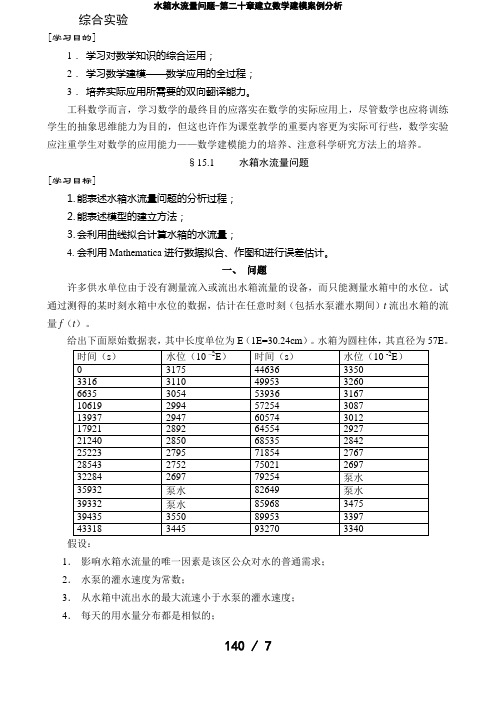
给出下面原始数据表，其中长度单位为E（1E=30.24cm）。

水箱为圆柱体，其直径为57E。

23（二）关键字水箱，水流量，水箱容积，时间。

（三）问题分析与建立模型引入如下记号： V ——水的容积； V i ——时刻t i （h ）水的容积（单位G ，1G=3.785L （升）；f （t ）——时刻t i 流出水箱的水的流速，它是时间的函数（G/h ）；p ——水泵的灌水速度（G/h ）。

根据要求先将上表中的数据做变换，时间单位用小时（h ），水位高转换成水的体积（V =πR 2h ），得下表。

32284 35932 39332 39435 433182697 泵水泵水 3550 344579254 82649 85968 89953 93270泵水泵水 3475 3397 33402由于要求的是水箱流量与时间的关系，因此须由上表的数据计算出相邻时间区间的中点及在时间区间内水箱中流出的水的平均速度：平均流速=（区间左端点的水量―区间右端点的水量）/区间中点值得下表：410.45/10.94/11.4918.612.4920.013.4219.014.4316.015.4416.016.3716.017.3814.018.4914.019.5016.020.4015.021.43/22.49/23.42/24.4314.025.4512.0做出散点图如图15-1:图15-1 散点图从图中可以看出数据分布不均匀，局部紧密，因此不能采用插值多项式处理数据，而用曲线拟5合的最小二乘法。

数学建模之水厂供水的优化问题

数学建模在实际中的应用水厂供水的优化问题学号姓名专业选址是生活中经常遇到的问题，如向居民输送自来水等都是实际需要考虑的问题，在解决此类问题时，可以将实际问题具体化，首先将总区域建立成一个平面坐标，接着将居民区简化成坐标，如此，便可将复杂的生活问题化成数学建模问题。

本模型正是研究了一个向六个居民区输水的A、B水厂的选址问题，本模型把其定义为双选址问题，首先对六个居民点，分成两个区域，然后分别求解。

为了简单易求，也可以首先选择重心法，对其求解，但通过对其结果的分析，发现重心法存在着缺点。

所以采取对模型进行重建的方法，列出了一个二元方程，然后对其最小值进行求解。

一、问题描述（优化选址问题）某城市拟建A、B两个水厂。

水厂分小、中、大三种规模，日均贮水量分别为30万吨、40万吨及50万吨，A、B两个水厂日进水量总和不超过80万吨。

A、B两个水厂共同担负供应六个居民区（由表一给出坐标）用水任务，每户日均用水量为1.0吨，水厂供应居民点用水的成本为1.05元/吨公里。

表1：各居民区的位置和拥有的家庭户数表一问题：若A、B两个水厂的位置尚未确定，请确定它们的位置及供水方案使总成本最低。

二、模型假设1.假设水厂与居民点的距离为直线距离，即忽略掉输水管道的路线问题。

2.假设水厂与居民点之间的供水费用仅与供水长度有关，和输水量无关。

3.假设水厂的建设资金是确定的，不会因规模的大小而改变。

成本仅为供水成本。

4.假设水厂和居民区都是理性化的质点。

5.假设居民的用水量就为人均用水量乘上人口数。

而且，长期不变。

三、符号表示四、问题分析通过简单的分析可以的知，总的用水量为74吨，而A、B两厂的总进水量为80吨，所以B两厂的规模只能为（30，50）、（40，40）、（50，30）三种方式。

对于问题一，是典型的线性最优化问题，我们分三种方式对其求解。

而对于问题二，我们则是采用将完全不同的模型：首先，利用聚类算法思想，把六个居民点化分成为两个区域，然后利用重心选址法初步判断和偏微分法求解地方法，分别对A、B两个水厂的位置进行确定。

水箱模型模拟实例

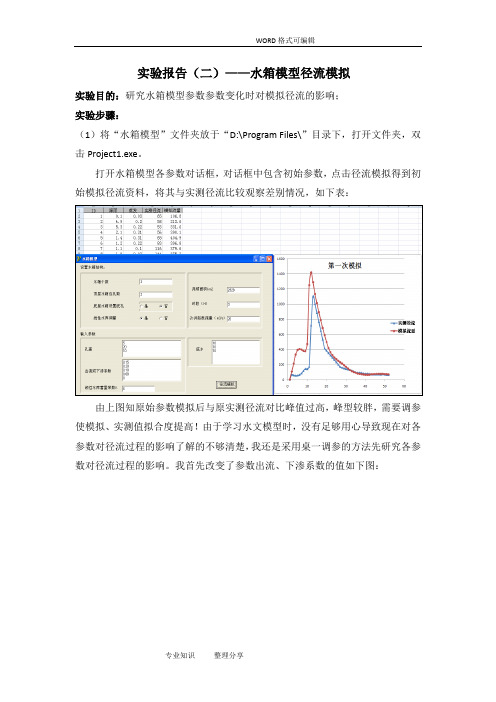
实验报告（二）——水箱模型径流模拟实验目的：研究水箱模型参数参数变化时对模拟径流的影响；实验步骤：（1）将“水箱模型”文件夹放于“D:\Program Files\”目录下，打开文件夹，双击Project1.exe。

打开水箱模型各参数对话框，对话框中包含初始参数，点击径流模拟得到初始模拟径流资料，将其与实测径流比较观察差别情况，如下表：由上图知原始参数模拟后与原实测径流对比峰值过高，峰型较胖，需要调参使模拟、实测值拟合度提高！由于学习水文模型时，没有足够用心导致现在对各参数对径流过程的影响了解的不够清楚，我还是采用桌一调参的方法先研究各参数对径流过程的影响。

我首先改变了参数出流、下渗系数的值如下图：通过对模拟、实测径流过程的拟合度的观察，我发现减小出流或下渗的前三个参数时逢高变小了；拟合度显著增大！增大这一参数时峰值增大。

翻阅书籍才知道原来前三个参数代表水箱模型第一层水箱！在了解了出流、下渗系数对流量过程的影响后我开始调节第二个参数底水的大小，如下图：观察发现，减小底水后模拟流量峰前蜂后与实测更加吻合，峰值进一步变小，模拟流量过程线变得瘦高；进一步减小底水第一个参数结果使得模拟流量峰前降低，蜂后也有下降；说明底水主要是对峰前峰后产生影响进而改变流量过程！如下图：了解了底水、出流或下渗系数变化对流量过程的影响后，我开始固定这两参数，来研究孔高对径流过程的影响，如下图：由上图观察发现第二个孔高影响峰高；第一个孔高影响峰前和蜂后，增大孔高第一个参数蜂后进一步下降，模拟流量过程更加瘦高；最后固定前三个参数，研究K值对径流过程的影响，如下图：由上图，增大K值模拟流量峰高降低，过程线变得矮胖；减小K值峰高增高，过程线瘦高，且稍往前移；在对几个参数对径流过程影响了解过后，我又做了一些实验，来研究具体每个参数内部各参数对流量的影响如下列图：改变出流下渗前三个参数，也就是上层水箱的参数，使得模拟流量峰高增加而，而其他形状不变！！改变出流或下渗系数后三个值，如果是减小它们则模拟流量过程线变得更瘦尖，而其他形状不变；在上边一系列实验，获得了各参数对径流过程的影响之后，我便开始进行同参数两次流量过程的模拟了！首先需要改变所给模型中的原始值，即调换sheet1，sheet3位置模拟第二个径流，如此反复替换反复模拟知道再同一参数下两个径流模拟过程都能和实测过程拟合完好为止！如下图：减小出流或下渗系数第一个参数，改变低水值，使得模拟流量过程线蜂后前移；将第二个径流模拟相对吻合的参数再次用于模拟第一个实测径流过程，发现吻合还算精确；说明这一参数可以使得两个实测径流过程都和模拟径流过程都拟合良好符合要求：最终得使两个径流过程都拟合相对较好的参数如下图标：。

水塔流量估计的数学建模

水塔流量估计的数学建模水塔是城市供水系统中的重要组成部分，它们储存着大量的水资源，为城市居民提供生活用水。

在城市供水系统中，水塔的流量是一个非常重要的参数，它直接影响着供水系统的运行效率和水资源的利用率。

因此，如何准确地估计水塔的流量是一个非常重要的问题。

水塔的流量估计可以通过数学建模来实现。

首先，我们需要了解水塔的基本结构和工作原理。

水塔通常由水箱、进水管、出水管、溢流管等组成。

当水箱内的水位下降时，进水管会自动打开，将外部的水源引入水箱中，同时出水管会自动关闭，防止水箱内的水流失。

当水箱内的水位上升到一定高度时，溢流管会自动打开，将多余的水流出水箱，以保持水箱内的水位稳定。

在水塔的运行过程中，我们可以通过测量进水管和出水管的水流速度来估计水塔的流量。

根据流量的定义，流量等于单位时间内通过某一截面的液体体积。

因此，我们可以通过测量进水管和出水管的截面积和水流速度来计算水塔的流量。

具体地，假设进水管的截面积为A1，出水管的截面积为A2，进水管的水流速度为v1，出水管的水流速度为v2，则水塔的流量Q可以表示为：Q = A1v1 - A2v2其中，A1v1表示进水管的流量，A2v2表示出水管的流量。

由于进水管和出水管的截面积和水流速度可能会随着时间的变化而发生变化，因此我们需要不断地对它们进行测量和调整，以保证水塔的流量估计的准确性。

除了测量进水管和出水管的水流速度外，我们还可以通过其他的方法来估计水塔的流量。

例如，我们可以通过测量水塔内部的水位变化来估计水塔的流量。

具体地，我们可以安装水位传感器在水塔内部，通过测量水位的变化来计算水塔的流量。

这种方法的优点是不需要对进水管和出水管进行测量，但是需要安装水位传感器，成本较高。

水塔流量估计的数学建模是一个非常重要的问题。

通过测量进水管和出水管的水流速度或者测量水塔内部的水位变化，我们可以准确地估计水塔的流量，从而保证城市供水系统的正常运行。

水箱流量数学建模论文 (2) - 副本

问题重述：许多供水单位由于没有测量流入或流出水箱流量的设备，而只能测量水箱中的水位．试通过测得的某时刻水箱中的水位的数据，估计在任意时刻（包括水泵灌水期间）t流出水箱的流量f(t).模型假设：除题目中的假设，另加如下假设：(1)影响水箱流量的唯一因素是该区民众对水的普通需求；(2)水塔中的水位不影响水流量的大小。

可根据物理学的Torricelli定律得出；(3)水泵起止工作时间由水塔的水位决定；(4)水塔的水流量与水泵状态独立,并不因水泵工作而增加或减少水流量的大小；符号说明：t:时间Y：水量V:水流量I：总用水量模型求解：首先，将时间换算成小时，水位高度变换成水的体积，如表1所示：表1：某一时刻水的体积因为水量达到514×10³g时开始泵水；达到667.6×10³g时停止泵水。

根据表1中的数据，可以近似认为在8.968h时开始第一次泵水，10.954h时第一次泵水停止；在20.839h时开始第二次泵水，22.880h时第二次泵水停止。

根据表1中的数据，计算相邻时间区间中点以及相应的时间段内平均水流量：记水量为y，时间为t，流量为v：（t i，t i+1）区间内平均流量v i=（y i+1-y i）/（t i+1-t i）区间首尾点流量为：v0= (3y0-4y1+y2)/(t2-t0)v n= (-3y n+4y n-1-y n-2)/(t n-t n-2)表2:某一时刻的对应流量将表二中的数据写入名为“data2”的txt文件中，以供计算使用。

方法1：插值与拟合法：在数据中水泵工作时的流量数据并没有给出，为了模拟拟合的准确性，采用插值拟合方法作出水箱中水的流速图，如图1所示：对流速积分，计算一天中的总流量，部分计算结果如图2所示：计算出24小时之内总用水量：I=363.4×10³g=364×3.78=1373.65m³图1：插值与拟合计算出的每个时间水流量图2：插值与拟合运行结果部分显示计算的matlab程序如下：clc,cleara=load('data2.txt');tt=a(:,1)dv2=a(:,2);plot(tt,dv2,'*')%画出流速的散点图pp=csape(tt,dv2);%对流量进行插值tt0=0:0.1:tt(end);%给出插值点fdv=ppval(pp,tt0);%计算各插值点的流量值hold on,plot(tt0,fdv)%画出插值曲线I=trapz(tt0(1:260),fdv(1:260))%计算24h内总流量的数值积分方法2：灰色理论：对表2中计算出来的流量，因为是非单调的摆动发展序列，故采用灰色理论中的GM(2,1)模型，预测流量随时间的变化关系：计算得到的时间影响序列为：x =482.495*exp(0.0239263*t) - 0.0463653*exp(0.276532*t) - 468.238计算出来的预测数据、残差以及相对误差如表3所示：表3：灰色理论预测出的流量值画出原始数据以及预测值的图像如图3所示：图3：流量原始值以及灰色理论预测值图由图3和表3可以看出用灰色理论预测得到的流量值与原始值差别较大，主要是由于模型建立不完善引起的，仍需进一步修改与提高。

水箱水流量问题-第二十章建立数学建模案例分析

1如能知道水泵的抽水速度就能更准确地估算水泵灌水期间水的流速
水箱水流量问题 -第二十章建立数学建模案例分析
1．优点：（1）任意时刻从水箱中流出的水速都可通过该模型计算出来；（2）可推测几天的流速；
（3）可以将该建模过程推广到用电及用气的估算上。 2．缺点：（1）如能知道水泵的抽水速度，就能更准确地估算水泵灌水期间水的流速；（2）通过考虑体积测量的差异建模，该作法包含着某种不准确性。源程序： L={{0.460，14.0}，{1.382，12.0}，{2.396，10.0}，{3.411，9.6}，{4.425，9.6}，{5.439，8.9}，{6.45，9.6}，{7.468，8.9}， {8.448，10.0}，{11.49，18.6}，{12.49，20.0}，{13.42，19.0}， {14.43，16.0}，{15.44，16.0}，{16.37，16.0}，{17.38，14.0}， {18.49，14.0}，{19.50，16.0}，{20.40，15.0}，{24.43，14.0}， {25.45，12.0}} fx=Fit[L，{1，x^3，x^5，Sin[0.1x]，Cos[0.1x]}，x] graph1=ListPlot[L，DisplayFunction→Identity] graph2=ListPlot[fx，{x，0.46，25.45}，DisplayFunction→Identity]； Show[graph1，graph2，DisplayFunction→$DisplayFunction， PlotRange→All]
图15-2水箱水流量拟合图 v1=677600-514800； t2=10.926-8.968； m1=v1/t1； v2=677600-514800； t1=22.958-20.839； m2=v2/t2； p1=m1+Integrate[fx，{x，8.96{x，20.839，22.958}]/t2 %=（p1-p2）p2 运行结果为：

计算机过程控制实验报告单容水箱液位数学模型的测定实验

实验1 单容水箱液位数学模型的测定实验1、试验方案：水流入量Qi 由调节阀u 控制，流出量Qo 则由用户通过负载阀R 来改变。

被调量为水位H 。

分析水位在调节阀开度扰动下的动态特性。

直接在调节阀上加定值电流，从而使得调节阀具有固定的开度。

（可以通过智能调节仪手动给定，或者AO 模块直接输出电流。

）调整水箱出口到一定的开度。

突然加大调节阀上所加的定值电流观察液位随时间的变化，从而可以获得液位数学模型。

通过物料平衡推导出的公式：μμk Q H k Q i O ==,那么 )(1H k k Fdt dH -=μμ，其中，F 是水槽横截面积。

在一定液位下，考虑稳态起算点，公式可以转换成μμR k H dtdH RC =+。

公式等价于一个RC 电路的响应函数，C=F 就是水容，k H R 02=就是水阻。

如果通过对纯延迟惯性系统进行分析，则单容水箱液位数学模型可以使用以下S 函数表示：)1()(0+=TS S KR S G 。

相关理论计算可以参考清华大学出版社1993年出版的《过程控制》，金以慧编著。

2、实验步骤：1) 在现场系统A3000-FS 上，将手动调节阀JV201、JV206完全打开，使下水箱闸板具有一定开度，其余阀门关闭。

2) 在控制系统A3000-CS 上，将下水箱液位（LT103）连到内给定调节仪输入端，调节仪输出端连到电动调节阀（FV101）控制信号端。

3) 打开A3000-CS 电源，调节阀通电。

打开A3000-FS 电源。

4) 在A3000-FS 上，启动右边水泵（即P102），给下水箱（V104）注水。

给定值图1 单容水箱液位数学模型的测定实验5) 调节内给定调节仪设定值，从而改变输出到调节阀（FV101）的电流，然后调节JV303开度，使得在低水位时达到平衡。

6) 改变设定值，记录水位随时间的曲线。

3、参考结果单容水箱水位阶跃响应曲线，如图2所示：图2 单容水箱液位飞升特性此时液位测量高度184.5 mm ，实际高度184 mm -35 mm =149 mm 。

水箱水流量问题-第二十章建立数学建模案例分析

综合实验[学习目的]1．学习对数学知识的综合运用；2．学习数学建模——数学应用的全过程；3．培养实际应用所需要的双向翻译能力。

工科数学而言，学习数学的最终目的应落实在数学的实际应用上，尽管数学也应将训练学生的抽象思维能力为目的，但这也许作为课堂教学的重要内容更为实际可行些，数学实验应注重学生对数学的应用能力——数学建模能力的培养、注意科学研究方法上的培养。

§15.1水箱水流量问题[学习目标]1.能表述水箱水流量问题的分析过程；2.能表述模型的建立方法；3.会利用曲线拟合计算水箱的水流量；4.会利用Mathematica进行数据拟合、作图和进行误差估计。

假设：1．影响水箱水流量的唯一因素是该区公众对水的普通需求；2．水泵的灌水速度为常数；3．从水箱中流出水的最大流速小于水泵的灌水速度；4．每天的用水量分布都是相似的；5．水箱的流水速度可用光滑曲线来近似；6．当水箱的水容量达到514.8×103g时，开始泵水；达到667.6×103g时，便停止泵水。

二、问题分析与建立模型1.引入如下记号：6.45 9.67.468 8.98.448 10.09.474 /10.45 /10.94 /11.49 18.612.49 20.013.42 19.014.43 16.015.44 16.016.37 16.017.38 14.018.49 14.019.50 16.020.40 15.021.43 /22.49 /23.42 /24.43 14.025.45 12.0做出散点图如图15-1。

图15-1 散点图从图中可以看出数据分布不均匀，局部紧密，因此不能采用插值多项式处理数据，而用曲线拟合的最小二乘法。

三、计算过程1．算法：第1步输入数据{x i，y i}；第2步进行拟合；第3步作出散点图；第4步作出拟合函数图；第5步进行误差估算。

2．实现在算法步2中使用Fit[ ]函数，步3、步4使用Plot[ ]，步5选用Integrate[ ]函数。

用灰色理论分析的水箱水流量问题

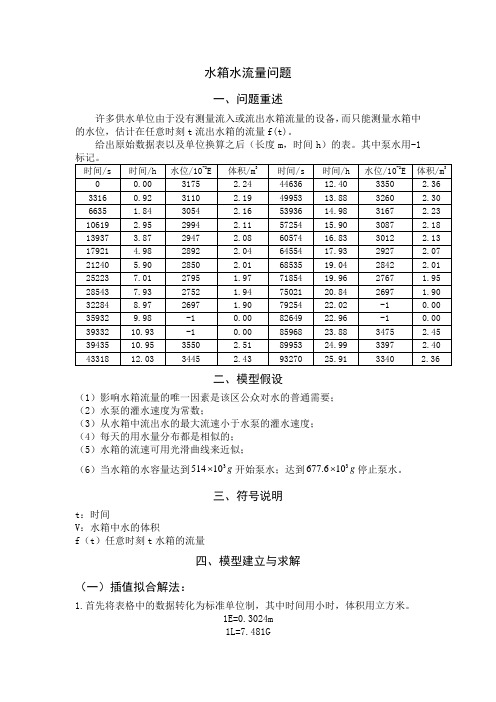
水箱水流量问题一、问题重述许多供水单位由于没有测量流入或流出水箱流量的设备，而只能测量水箱中的水位，估计在任意时刻t流出水箱的流量f(t)。

给出原始数据表以及单位换算之后（长度m，时间h）的表。

其中泵水用-1二、模型假设（1）影响水箱流量的唯一因素是该区公众对水的普通需要；（2）水泵的灌水速度为常数；（3）从水箱中流出水的最大流速小于水泵的灌水速度；（4）每天的用水量分布都是相似的；（5）水箱的流速可用光滑曲线来近似；（6）当水箱的水容量达到3⨯停止泵水。

51410g677.610g⨯开始泵水；达到3三、符号说明t：时间V：水箱中水的体积f（t）任意时刻t水箱的流量四、模型建立与求解（一）插值拟合解法：1.首先将表格中的数据转化为标准单位制，其中时间用小时，体积用立方米。

1E=0.3024m1L=7.481G2.（1）水塔中水的体积计算：24V D h π=式中：D 为水塔的直径；h 为水塔中的水位高度。

（2）水塔中水流速度的估计。

水流速度应该是水塔中水的体积对时间的导数，但由于没有每一时刻水体积的具体数学表达式，这里我们用插商近似导数。

由于在两个时间段，水泵向水塔供水，无法确定水位的高度，因此计算水流速度要分3段进行计算。

第一段从0省道32284s ，第二段从39435s 到75021s ，第三段从85968s 到93270s3.为了得到流速的连续曲线可以使用三次样条插值处理，然后做出时间-流速的散点图。

图1：时间流速散点图4.曲线拟合用MATLAB 进行三次样条插值拟合的曲线如下图2：时间-流速曲线5.对水流速度进行数值积分可以得到24小时的用水量为1358.43m（二）GM （2,1）模型解法：1.-12.设时间序列为n t ，体积序列为n V 将11i ii iV V t t ++--组成新的一个数组n Q 并存储在文件名为data2.txt 的纯文本文件中。

然后对序列n Q 建立GM （2,1）模型。

数学建模

4
表2 一天内水塔水位记录
时间/h 时间 0 0.92 1.84 2.95 3.87 4.98 5.90 7.00 7.93 8.97 9.98 10.93 10.95 12.03 水位/m 水位 9.68 9.45 9.31 9.13 8.98 8.81 8.69 8.52 8.39 8.22 水泵开动水泵开动 10.82 10.50 时间/h 时间 12.95 13.88 14.98 15.90 16.83 17.93 19.04 19.96 20.84 22.02 22.96 23.88 24.99 25.91 水位/m 水位 10.21 9.94 9.65 9.41 9.18 8.92 8.66 8.43 8.22 水泵开动水泵开动 10.59 10.35 10.18
3
有了任何时刻的流量，就能计算一天的总用水量。有了任何时刻的流量，就能计算一天的总用水量。其实，其实，水泵不工作时段的用水量可以由测量记录直接得到，由表1中下降水位乘以水搭的截面积就是这一时得到，由表中下降水位乘以水搭的截面积就是这一时段的用水量。段的用水量。这个数值可以用来检验数据插值或拟合并且用MATLAB软件实现插值法）。软件实现插值法）。的结果（并且用软件实现插值法问题求解为了表示方便，我们将问题中所给表1中的数据全为了表示方便，我们将问题中所给表中的数据全部化为国际标准单位（），时间用小时部化为国际标准单位（表2），时间用小时（h），），时间用小时（），高度用米（）：高度用米（m）：
由表2知由表知，第1未供水时段的总用水高未供水时段的总用水高度为146(=968－822)，可见上述三种插值度为－，方法计算的结果与实际值（方法计算的结果与实际值（146）相比都）比较接近。比较接近。考虑到三次样条插值方法具有更加良好的性质，我们采取该方法。有更加良好的性质，我们采取该方法。其他三段的处理方法与第1未供水时段的其他三段的处理方法与第未供水时段的处理方法类似，这里不再详细叙述，处理方法类似，这里不再详细叙述，只给出数值结果和函数图像（），图出数值结果和函数图像（图4～图6），图～），中曲线标记同图3。中曲线标记同图。

水流问题(数学建模)

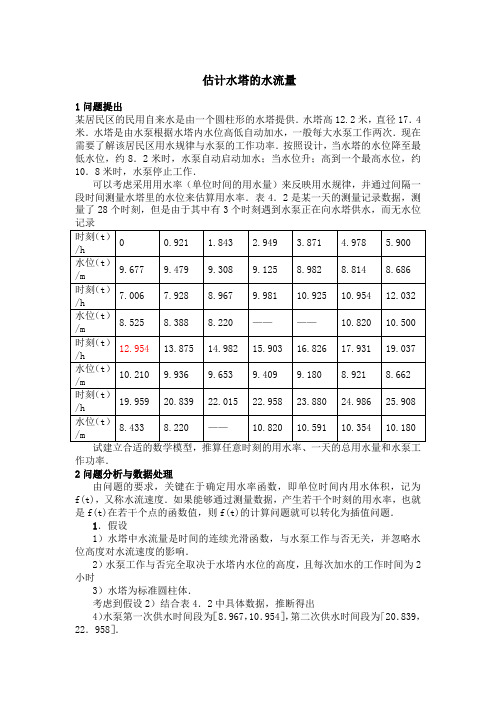
估计水塔的水流量1问题提出某居民区的民用自来水是由一个圆柱形的水塔提供．水塔高12.2米，直径17．4米．水塔是由水泵根据水塔内水位高低自动加水，一般每大水泵工作两次．现在需要了解该居民区用水规律与水泵的工作功率．按照设计，当水塔的水位降至最低水位，约8．2米时，水泵自动启动加水；当水位升；高到一个最高水位，约10．8米时，水泵停止工作．可以考虑采用用水率（单位时间的用水量）来反映用水规律，并通过间隔一段时间测量水塔里的水位来估算用水率．表4．2是某一天的测量记录数据，测量了28个时刻，但是由于其中有3个时刻遇到水泵正在向水塔供水，而无水位作功率．2问题分析与数据处理由问题的要求，关键在于确定用水率函数，即单位时间内用水体积，记为f(t)，又称水流速度．如果能够通过测量数据，产生若干个时刻的用水率，也就是f(t)在若干个点的函数值，则f(t)的计算问题就可以转化为插值问题．1．假设1）水塔中水流量是时间的连续光滑函数，与水泵工作与否无关，并忽略水位高度对水流速度的影响．2）水泵工作与否完全取决于水塔内水位的高度，且每次加水的工作时间为2小时3）水塔为标准圆柱体．考虑到假设2）结合表4．2中具体数据，推断得出4）水泵第一次供水时间段为［8．967，10．954］，第二次供水时间段为「20．839，22．958］．2．体积计算水塔是一个圆柱体，体积为h D V 24π=．其中D 为底面直径，h 为水位高度。

水流速度应该是水塔中水的体积对时间的导数（微商）由于没有水的体积关于时间的函数表达式，而只有一个离散的函数值表4．3，因此考虑用差商代替微商，这也是离散反映连续的常用思想．为提高精度，采用二阶差商，即i i v t f 2)(-∇=具体地，因为所有数据被水泵两次工作分割成三组数据，对每组数据的中间数据采用中心差商，前后两个数据不能够采用中心差商，改用向前或向后差商．中心差商公式模型及计算结果问题已经转变为根据流速f(t)的一个函数值表，产生函数f(t)在整个区间（二十四小时）上的函数或函数值，插值和拟合是两种最常用的方法．如果建立拟合模型，需要根据散点图的趋势，选择适当的拟合函数形式．如果采用插值模型，可以考虑分段线性插值。

单容水箱建模分析

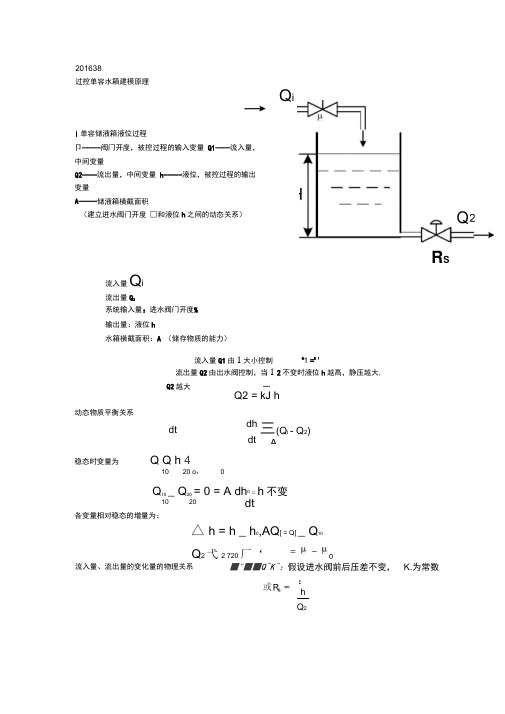
流入量Q i流出量Q 2系统输入量：进水阀门开度%输出量：液位h水箱横截面积：A （储存物质的能力）流入量Q1由1大小控制Q 1 =K 1 流出量Q2由出水阀控制，当1 2不变时液位h 越高，静压越大,Q2越大一 Q2 = kJ h动态物质平衡关系稳态时变量为 Q Q h 4 10 20 o ，0 Q 10 _ Q 20 = 0 = A dh 0 = h 不变10 20 dt各变量相对稳态的增量为：△ h = h _ h 0,AQ [ = Q[ _ Q 10■"■■Q ^K ^：假设进水阀前后压差不变， K.为常数 201638 过控单容水箱建模原理Q i i 单容储液箱液位过程卩-----阀门开度，被控过程的输入变量 Q1——流入量，中间变量 Q2——流出量，中间变量 h-----液位，被控过程的输出变量 A-----储液箱横截面积（建立进水阀门开度 □和液位h 之间的动态关系）R SQ 2 弋2 720 厂‘ ：hQ 2dtdh dt三(Q i - Q 2) A 流入量、流出量的变化量的物理关系由©二丄(Q-Q)的增量形式 at A '结论： -J A L.令T 二 A&,K 二 K.R ，则有：T-^- +：h=K ：JdtT s H(s) H(s)二 K 」(s)得到：四 —%s) T s + 1T 为液位过程的时间常数 ^A Rs,显然与水箱存储能力和出水阀液阻有关，A 、Rs 越大，T 越大K 为液位过程的放大系数，与进水阀流量比例系数和出水阀液阻有关容量系数的影响容积系数是衡量一个过程对象存贮物质(或能量)的能力的物理量，在此水箱对象的容量系数就是水箱的截面积 A 。

若水箱截面积A 越大，对于出现同样大小的不平衡流量(Q1 - Q2)，水箱液位h 变化的速度就越小，即抵抗扰动的能力强。

从这一方面来说，容量系数描述了对象抵抗扰动的能力。

时间常数T = Rs A ，当阀阻Rs 不变时，水槽的截面积A 越大，说明要使液位上升一个单位所需的存水量就越大，因此在同样的阶跃扰动量输入下，起始上升的速度就越小，因此水位h 以该起始速度达到稳态值所需的时间就越长，即时间常数 T 越大。