电力系统暂态分析 (4)

合集下载

大学考试试卷《电力系统暂态分析》及参考答案

电力系统暂态分析一、判断题（本大题共10分，共 5 小题，每小题 2 分）1. 对称短路时仅有正序分量，不对称短路时会出现正序、负序和零序分量。

2. 三相变压器负序电抗与其正序电抗相同。

3. 同步发电机负序电抗与其正序电抗相同。

4. 短路时网络中任意处的电流、电压均都满足用相量或序分量表示的边界条件。

5. 自耦变压器的零序电抗通常不会为无穷大。

二、填空题（本大题共60分，共 20 小题，每小题 3 分）1. 具有转子阻尼绕组的同步发电机机端短路瞬时的状态称为 ______ ，电枢反应磁通的路径是 ______ 。

2. 单相短路的复合序网图中三序网络是 ______ 关系。

3. 计算三相短路电流交流分量初始值时，远离短路点的电动机按 ______ 模型处理，短路点附近的电动机均按 ______ 模型处理。

4. 节点阻抗矩阵是 ______ 的逆矩阵。

5. 一般在工程实用计算中为了简便，通常用 ______ 替代交轴暂态电动势6. 同步发电机机端三相短路至稳态后，电枢反应磁通的路径是 ______ 、______ 、 ______ 。

7. 极限切除角度对应的切除时间被称为 ______ 。

8. 短路计算时通常假设各电源的电动势相位 ______ 。

9. 当接地短路点位于变压器三角形或不接地星形绕组侧时，变压器的零序电抗为 ______ 。

10. 通常，同步发电机和异步电动机定子绕组通常是 ______ 接线，其零序电抗为 ______ 。

11. 同步发电机负载三相短路时，定子绕组交轴感应电动势在短路前后是______ 。

12. ______ 定则可用于分析简单系统的暂态稳定性问题。

13. 利用节点导纳矩阵求解系统中三相短路，通常采用 ______ 方法求解网络方程。

14. 由于存在转子阻尼绕组，同步发电机定子绕组的次暂态电抗值比同步电抗值和暂态电抗值都 ______ 。

15. 同步发电机三相短路时，转子绕组电流存在交流分量的原因是 ______ 、______ 。

《电力系统暂态分析》习题集 answer

6、某同步发电机处于稳定运行状态，其端电压 u = 1.0 ，输出功率为 0.8+j0.5，发电机参数为 xd = 1.8, xq = 0.9, xσ = 0.15, r = 0.05,ω = 1，计算：
(1) δ ,Ud ,Uq , id , iq ,ϕd ,ϕq , if ,ϕ f , Eq ；
2 0.3 + x 0.6 + x
x>0.9
4、有一台无阻尼绕组的同步发电机具有恒定的励磁电压，现以δ0 超前无穷大系统母线电压时合到母线上。
4
Us = 1.0∠00
G 无穷大系统母线
求： a) 发电机机端电压与无穷大母线电压幅值相等时的合闸电流 id (t),iq (t), (rf = 0, r = 0) ；
Peq max
=
EqU xd
sin δ
+U2 2
xd − xq xd xq
sin 2δ
= 1.3984
(3) Peq = 1.298sin δ + 0.2778sin 2δ = 0.8*(1+ 5 /100) = 0.84 sin δ cosδ + 2.3364sin δ −1.4347 = 0
14. 系统接线示于题图，已知各元件参数如下：发电机 SN = 30MVA,Vn = 10.5KV , x = 27% 。
110kV G 10kV T-1
T-2
6kV
R
T-3
试作不含磁耦合关系的等值电路并计算其标么值参数。 [解]
xG
Eq
= EQ
xd ∑ xq ∑
− U cosδ
xd ∑ − xq∑ xq ∑
=
1.3 1.41

电力系统暂态分析部分习题答案

电力系统暂态分析部分习题答案电力系统暂态分析部分习题答案3电力系统暂态分析部分习题答案(参考)第一章电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量，它们的额定电压分别为6.3kV 和10.5kV ，若以它们的额定值为基本条件的发电机电抗的标么值是相同的，问这两个发电机电抗的欧姆值的比值是多少？解：X G1*(N)＝X G1*S N1/U N12 X G2*(N)＝X G2*S N2/U N22∵X G1*(N)＝X G2*(N) ∴X G1*S N1/U N12＝X G2*S N2/U N22 故：X G1/ X G2＝U N12/ U N22＝6.32/10.52＝0.36 1-4、求：①准确计算各元件电抗的标么值，基本段取I 段U BI ＝10.5kV 。

②工程近似计算各元件电抗的标么值，S B ＝100MVA 。

解：① 精确计算法U BI ＝10.5kV S B ＝100MVA U BII ＝5.101215.10⨯＝10.5kV U BIII ＝1106.65.101215.10⨯⨯＝7.26kV T 1X LT 2II III50MVA 10.5kV X d ’’=0.15 60MVA 10.5kV/121kV U k %=10.5 0.4Ω/km 100km30MVA110kV/6.6kV U k %=10.543.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法U B ＝U av S B ＝100MVA3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X 302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X 1-5、某一线路上安装一台Xk%＝5的电抗器，其额定电流为150A ，额定电压为6kV ，若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它，并要求保持线路的电抗欧姆值不变，问这台电抗器的电抗百分数值应是多少？解：∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=5∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、 (1) 若短路前空载，计算短路电流的周期分量及短路电流最大有效值；(2) 若A 相非周期分量电流的初值为零及最大时，计算相应的B 、C 相非周期分量电流的初始值；(3) 若短路前变压器满负荷运行，功率因数为0.9（低压侧），计算最大非周期分量电流的初始值，并与空载时短路比较。

电力系统暂态分析

电力系统暂态分析第一章1、电力系统运行状态的分类答：电力系统的运行状态分为稳态运行和暂态过程两种，其中暂态过程又分为波过程、电磁暂态过程和机电暂态过程。

波过程主要研究与大气过电压和操作过电压有关的电压波和电流波的传递过程；电磁过渡过程主要研究与各种短路故障和断线故障有关的电压、电流的变化，有时也涉及功率的变化；机电暂态过程主要研究电力系统受到干扰时，发电机转速、功角、功率的变化。

2、电力系统的干扰指什么？答：电力系统的干扰指任何可以引起系统参数变化的事件。

例如短路故障、电力元件的投入和退出等。

3、为什么说电力系统的稳定运行状态是一种相对稳定的运行状态？答：由于实际电力系统的参数时时刻刻都在变化，所以电力系统总是处在暂态过程之中，如果其运行参量变化持续在某一平均值附近做微小的变化，我们就认为其运行参量是常数（平均值），系统处于稳定工作状态。

由此可见系统的稳定运行状态实际是一种相对稳定的工作状态。

4、为简化计算在电力系统电磁暂态过程分析和机电暂态过程分析中都采用了那些基本假设？答：电磁暂态分析过程中假设系统频率不变，即认为系统机电暂态过程还没有开始；机电暂态过程中假设发电机内部的机电暂态过程已经结束。

第一章：1、电力系统的故障类型答：电力系统的故障主要包括短路故障和断线故障。

短路故障（又称横向故障）指相与相或相与地之间的不正常连接，短路故障又分为三相短路、两相短路、单相接地短路和两相短路接地，各种短路又有金属性短路和经过渡阻抗短路两种形式。

三相短路又称为对称短路，其他三种短路称为不对称短路；在继电保护中又把三相短路、两相短路称为相间短路，单相接地短路和两相短路接地称为接地短路。

断线故障（又称纵向故障）指三相一相断开（一相断线）或两相断开（两相断线）的运行状态。

2、短路的危害答：短路的主要危害主要体现在以下方面：1）短路电流大幅度增大引起的导体发热和电动力增大的危害；2）短路时电压大幅度下降引起的危害；3）不对称短路时出现的负序电流对旋转电机的影响和零序电流对通讯的干扰。

电力系统暂态分析第四版课后答案方万良

电力系统暂态分析第四版课后答案方万良电力系统暂态分析（暂态过程）是以电力系统为研究对象，对其进行科学的分析、预测，并通过分析得出其所需的信息，从而为规划决策提供参考。

电力系统暂态分析中，有一个重要的组成部分就是变功率系统。

该系统具有一定的数学模型、时间同步特性以及电气化条件（高压或低压）等，能够为电力系统结构优化提供参考。

该部分内容主要包括变功率系统的数学模型与时间同步特性、变功率系统与输电通道间速度场、变电所内各种保护等几个方面。

一、变功率系统的数学模型与时间同步特性变功率系统在电力系统暂态分析中，主要起到变流器的作用，其时间同步特性是其暂态分析的重要参数之一。

变流器、滤波器与变压器等主要元件组成了变功率系统理论上的各个部分的数学模型。

例如，在电力系统中，变流器等主要元件是由电磁铁来工作的。

此外，变功率系统中所产生的电压与电流也会直接影响到电力系统电网中变流器、滤波器所受负载对电压电流的承受能力。

通过数学模型分析得出结论，在不同情况下，变功率系统具有不一样的时间同步特性。

通常，这些时间同步特性可分为：主电源不能超过最大瞬时输出电压、功率因数偏高或无功补偿电压、以及电流为零等四种类型。

二、变功率系统与输电通道间速度场在电力系统暂态分析中，电网中的各个系统是相互联系、相互制约的，它们之间的速度场可以看作是一种相互联系的网络，也可以看作是一种相互制约的系统。

如果网络中节点数量相匹配，则电力系统各节点之间是处于静止状态，速度场中的各点也处于静止状态。

当电力系统发生事故时，首先要分析事故原因，然后对事故进行建模分析和计算得出结论。

三、变电所内各种保护在电力系统暂态分析中，对变电所内各种保护的研究，是根据电力系统现有发展情况，通过理论分析得到的结果和试验结果，并将理论设计值与实际情况进行比较而进行设计。

对于电力系统暂态分析而言，保护方法主要有隔离法、电压法、断路器脱扣法和断路器跳闸法。

对于一般电网和高压电网而言，可以通过以下方法来保护电力网线路：在电压、电流正常时，对其进行保护；在发生故障时，对其进行保护；在电网发生事故时，对其进行保护；在运行正常时，对其进行保护；在故障时恢复正常时，对其进行保护。

电力系统暂态分析试卷及答案5套

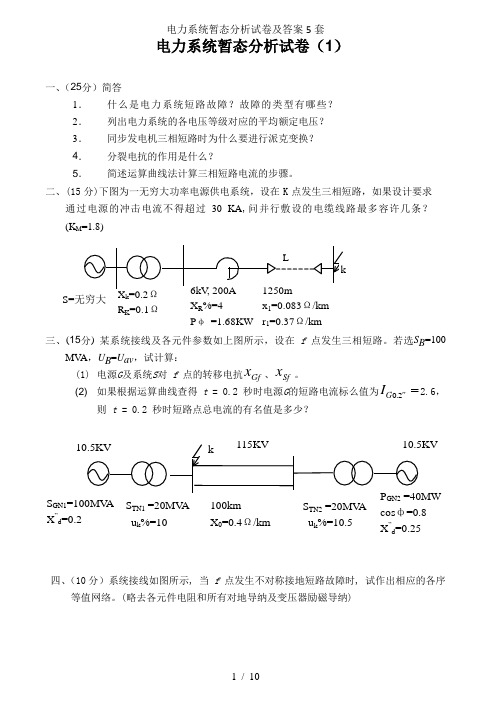
电力系统暂态分析试卷（1）一、（25分）简答1．什么是电力系统短路故障？故障的类型有哪些？2．列出电力系统的各电压等级对应的平均额定电压？3．同步发电机三相短路时为什么要进行派克变换？4．分裂电抗的作用是什么？5．简述运算曲线法计算三相短路电流的步骤。

二、(15分)下图为一无穷大功率电源供电系统，设在K点发生三相短路，如果设计要求通过电源的冲击电流不得超过30 KA,问并行敷设的电缆线路最多容许几条？(K M=1.8)三、(15分)某系统接线及各元件参数如上图所示，设在 f 点发生三相短路。

若选S B=100MV A，U B=U av，试计算：(1) 电源G及系统S对f 点的转移电抗xGf、xSf。

(2) 如果根据运算曲线查得t = 0.2 秒时电源G的短路电流标么值为I G02.''=2.6，则t = 0.2 秒时短路点总电流的有名值是多少？四、（10分）系统接线如图所示, 当f 点发生不对称接地短路故障时, 试作出相应的各序等值网络。

(略去各元件电阻和所有对地导纳及变压器励磁导纳)五、（10分）如图所示系统，电抗为归算到统一基准值下的标么值（S B =100MVA ，U B =平均额定电压），用正序等效定则计算以下各种情况短路时，短路点的A 相正序电流有名值，（1）三相短路；（2）A 相接地短路；六、（10分）如图所示系统，求发电机电势E q 和静态稳定储备系数K p ？（注：图中参数为归算到统一基准值下的标么值S B =100MV A ，U B =平均额定电压）七、（15分）有一简单系统，已知发电机参数2.0='dx ，E΄ =1.2，原动机功率P T =1.5，线路参数如图所示，无穷大电源电压000.1∠=c U ，如果开关K 突然合上，电容电抗Xc=0.3试判断该系统能否保持暂态稳定?电力系统暂态分析试卷(2)一、简答（25分）1. 什么是短路？简述短路的现象和危害？2. 什么是短路冲击电流？出现冲击电流的条件是什么？3. 为什么同步发电机定、转子绕组的电感系数矩阵中会有零元素？4. 变压器中性点接小电阻的作用是什么？简要分析理由。

电力系统分析实验报告四(理工类)

西华大学实验报告（理工类）开课学院及实验室：实验时间：年月日学生姓名学号成绩学生所在学院年级/专业/班课程名称课程代码实验项目名称电力系统功率特性和功率极限实验项目代码指导教师项目学分一、实验目的1)初步掌握电力系统物理模拟实验的基本方法。

2)加深理解功率极限的概念，在实验中体会各种提高功率极限措施的作用。

3)通过对实验中各种现象的观察，结合所学的理论知识，培养理论结合实际及分析问题的能力。

二、实验原理所谓简单电力系统，一般是指发电机通过变压器、输电线路与无限大容量母线联接而且不计各元件的电阻和导纳的输电系统。

对于简单系统，如发电机至系统d 轴和g 轴总电抗分别为d X ∑和q X ∑，则发电机的功率特性为2()sin sin 2q d q Eq d d q E UX X U P X X X δδ∑∑∑∑∑-=+⨯⨯当发电机装有励磁调节器时，发电机电势q E 随运行情况而变化，根据一般励磁调节器的性能，可认为保持发电机'q E （或'E ）恒定。

这时发电机的功率特性可表示成''2'''''()sin sin 2Eq q d q d d q E UX X U P X X X δδ∑∑∑∑∑-=+⨯⨯ 或''''sin E q d E UP Xδ∑=这时功率极限为'''Em q d E UP X∑=随着电力系统的发展和扩大，电力系统的稳定性问题更加突出，而提高电力系统稳定性和输送能力的最重要手段之一，就是尽可能提高电力系统的功率极限。

从简单电力系统功率极限的表达式看，要提高功率极限，可以通过发电机装设性能良好的励磁调节器，以提高发电机电势、增加并联运行线路回路数；或通过串联电容补偿等手段，以减少系统电抗，使受端系统维持较高的运行电压水平；或输电线采用中继同步调相机、中继电力系统等手段以稳定系统中继点电压。

(完整版)电力系统暂态分析习题答案

电力系统暂态分析李光琦习题答案第一章电力系统分析基础知识1-2-1 对例1-2，取kV 1102=B U ，MVA S B 30=,用准确和近似计算法计算参数标幺值。

解：①准确计算法：选取第二段为基本段，取kV 1102=B U ，MVA S B 30=，则其余两段的电压基准值分别为：9.5kV kV 1101215.10211=⨯==B B U k U 电流基准值：各元件的电抗标幺值分别为：发电机：32.05.930305.1026.0221=⨯⨯=*x 变压器1T ：121.05.3130110121105.02222=⨯⨯=*x 输电线路：079.011030804.023=⨯⨯=*x 变压器2T ：21.01103015110105.02224=⨯⨯=*x电抗器：4.03.062.26.6605.05=⨯⨯=*x 电缆线路：14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值：16.15.911==*E ②近似算法：取MVA S B 30=，各段电压电流基准值分别为：kV U B 5.101=，kA I B 65.15.103301=⨯=kV U B 1152=，kA I B 15.01153301=⨯=kV U B 3.63=，kA I B 75.23.63301=⨯=各元件电抗标幺值：发电机：26.05.1030305.1026.0221=⨯⨯=*x 变压器1T ：11.05.3130115121105.0222=⨯⨯=*x 输电线路：073.011530804.023=⨯⨯=*x 变压器2T ：21.01530115115105.0224=⨯⨯=*x电抗器：44.03.075.23.6605.05=⨯⨯=*x 电缆线路：151.03.6305.208.026=⨯⨯=*x 电源电动势标幺值：05.15.1011==*E 发电机：32.05.930305.1026.0221=⨯⨯=*x 变压器1T ：121.05.3130110121105.02222=⨯⨯=*x 输电线路：079.011030804.023=⨯⨯=*x 变压器2T ：21.01103015110105.02224=⨯⨯=*x电抗器：4.03.062.26.6605.05=⨯⨯=*x 电缆线路：14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值：16.15.911==*E 1-3-1 在例1-4中，若6.3kV 母线的三相电压为：在空载情况下f 点突然三相短路，设突然三相短路时 30=α。

电力系统中的暂态分析

电力系统中的暂态分析概述电力系统中的暂态分析是电力系统研究中的一个非常重要的领域。

暂态分析是指电力系统中瞬时电压、电流等物理量随时间的变化过程及其特性的研究。

电力系统暂态分析的目的是为了了解系统在发生暂态过程时的变化情况，并通过研究暂态特性，掌握电力系统的运行状况，为系统的优化运行提供有力的理论基础。

电力系统中的暂态过程包括各种故障事件，例如三相短路、单相接地故障、线路开关跳闸等。

这些故障事件都会导致电力系统中电压、电流等物理量的瞬时变化，对电力系统的运行稳定性产生直接的影响。

因此，电力系统的暂态分析成为了电力系统研究中一个重要的领域。

暂态分析包括以下几个方面：短路故障分析在电力系统中，三相短路是最常见的故障之一。

当它发生时，瞬态电流会产生高电压和高电流，对设备和电力系统的安全稳定性产生严重的影响。

因此，对于电力系统中的短路故障，进行详细的暂态分析非常重要。

暂态电压稳定分析电力系统在发生各种故障时，电压经常会发生瞬时的变化，这种变化会引起电力设备的故障或系统崩溃。

因此，在电力系统的暂态分析中，电压稳定性也是一项非常重要的内容。

暂态功率稳定分析电力系统的暂态功率稳定性是电力系统的重要特性之一。

当电力系统的暂态功率稳定性不足或损坏时，会导致各种不稳定的暂态事件或系统的崩溃。

暂态过电压分析暂态过电压是电力系统中常见的暂态现象，通常是由于雷击或开关操作导致的。

过电压从物理上来说是一种瞬时的电压变化，但它会对设备和系统产生破坏性的影响。

总结电力系统中的暂态分析是一种关键的技术，它可以帮助工程师和研究人员确定电力系统在发生暂态过程时的情况。

暂态分析不仅可以为电力系统的设计和改进提供理论基础，还可以为实际的电力系统运行提供指导。

在电力系统的建设和运行中，暂态分析技术正在不断地发展和更新，以提高电力系统的稳定性、可靠性和安全性。

电力系统暂态分析(第四章习题答案)

za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
1) 当 za = zb = zc 时，非对角元素 Z1 = za 1 + a2 +
a = Z2 = 0，则三序分量可以解藕。
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流：
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流：
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
零序电压标幺值：
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流：
0.0787 I1 = −0.12＋(−0.014)//0.244） = 0.748
0.244 I2 = I1 × （ − 0.014 + 0.244） = 0.794
I3 = I1 − I2 = −0.0455 电流有名值：
障时的正序、负序、零序等效电路；解：正序：负序：
零序：

电力系统暂态分析(第二、四章习题答案)

第2章作业参考答案 2-1 为何要对同步发电机的基本电压方程组及磁链方程组进行派克变换？
答：由于同步发电机的定子、转子之间存在相对运动，定转子各个绕组的磁路会发生周期性的变化，故其电感系数（自感和互感）或为1 倍或为2倍转子角θ的周期函数（θ本身是时间的三角周期函数），故磁链电压方程是一组变系数的微分方程，求解非常困难。因此，通过对同步发电机基本的电压及磁链方程组进行派克变换，可把变系数微分方程变换为常系数微分方程。 2-2 无阻尼绕组同步发电机突然三相短路时，定子和转子电流中出现了哪些分量？其中哪些部分是衰减的？各按什么时间常数衰减？试用磁链守恒原理说明它们是如何产生的？
8、已知电力系统原理接线如下图所示，如果不计各元件对地导纳支路、各元件电阻以及负荷影响，请画出图中f点发生接地短路时，系统的正序、负序和零序等值电路。
解：
答：不能。因为对称分量法实际上是迭加原理的应用，而迭加原理不能用于非线性电路的分析计算，所以对称分量法不能用于非线性三相电力系统的分析计算。
7、什么叫做分析不对称故障的基本相？基本相如何选取？答：利用对称分量法分析计算时，以哪一相的序分量为未知数列方程求解，则那一相就称为分析计算的基本相。基本相通常选择特殊相。
答：架空输电线路正序电抗、负序电抗、零序电抗三者之间的关系是；因为架空输电线路任何一相的磁链都是由本相电流产生的自感磁链和其它两相电流产生的互感磁链组成，正序和负序情况下，其它两相所产生的互感磁链对自感磁链起去磁作用，零序情况下互感磁链对自感磁链起助磁作用，所以输电线路的正序电抗与负序电抗相等，而小于零序电抗。 4、为什么电动机的零序阻抗总可以视为无限大？答：因为电力元件的某序阻抗等于在该元件端点施加的该序电压和由它产生的流过元件端点的该序电流的比值。电动机三相绕组采用三角形接线和中性点不接地的星形接线方式，当在其端点施加零序电压时，在端口产生的零序电流为零，根据序阻抗的定义其零序阻抗为无限大。 5、变压器的正序励磁电抗和负序励磁电抗都可以视为无限大，从而用开路代替，变压器的零序励磁电抗是否也可以视为无限大？在什么情况下，变压器的零序励磁电抗才可以视为无限大？答：变压器的正序励磁电抗和负序励磁电抗之所以都可以视为无限大，是因为不管变压器采用什么样的铁芯形式，其励磁磁通都是通过铁芯形成回路的，由于铁芯的磁阻很小，所以与之相对应的励磁电抗非常大，近似计算中可以视为无限大；而变压器的零序励磁磁通通道与变压器铁芯的结构有关，在三相芯式变压器中，其励磁磁通只能通过铁芯、油箱与铁芯之间间隙和油箱形成回路，由于间隙的磁阻很大，所以对应的励磁电抗较小，因而不能视为无限大。只有在变压器的铁芯形式能够使零序励磁磁通通过铁芯形成通道时（如三相变压器组、三相五柱式变压器、壳式三相变压器等）才可以将其零序励磁电抗视为无限大。另外当变压器有三角形接线绕组时，由于在零序等值电路中三角形绕组对零序而言相当于短路，其漏抗与励磁电抗并联连接，由于漏抗远小于励磁电抗，所以此时变压器的零序励磁电抗也可以视为无限大。 6、对称分量法能否用于非线性三相电力系统的分析计算？为什么？

电力系统暂态分析第四章

上式说明三组对称相量合成得三个不对称相量。其逆关系为：
FFaa(( 12)) Fa(0)

1 13a1
a a2 1
a2 a
FFba

1 Fc
（4－6）
《电力系统分析》
2019/10/31
或写为：
FS T1FP
上式说明三个不对称的相量可以唯一地分解成为三组对称的相量(即对称分量): 正序分量、负序分量和零序分量。
2、同步发电机的正序参数及正序等值电路
由于不对称短路时，正序基频电流对发电机的作用与
三相短路相同，所以同步发电机的正序参数就是发电机
三相短路时的参数（即
）。
《电力系统分析》
2019/10/31
3、同步发电机的负序参数和等值电路发电机无负序电动势；发电机负序电抗定义为：发电机机端负序基频电压与
流入发电机的负序基频电流的比值。按照发电机负序电抗的定义在不同的情况下发电机具有不同负序电抗值，实用计算中取
zm zs
zm zm
IIba

Uc zm zm zs Ic
可简写为： UPZPIP
《电力系统分析》
2019/10/31
则：
TUS ZPTSI
即
U ST 1Z P TS IZ SIS
式中：
zs zm 0 ZST1ZPT 0 zs zm
分量同基频分量一样衰减，短路达到稳定状态时仍然存在。
而定子绕组中的非周期分量在转子绕组产生各种奇次谐波电流并在定子绕组产生正序、负序、零序偶次谐波电流，这些谐波电流都随定子绕组非周期分量逐渐衰减到零。隐极机和有阻尼绕组凸极机情况下定子绕组非周
《电力系统分析》

电力系统暂态分析

电力系统暂态分析概述电力系统暂态分析是电力系统工程中的重要环节，它主要研究电力系统在暂态过程中的运行状态和稳定性。

暂态过程是指系统发生突发故障后，从故障发生到系统恢复正常运行的过程。

电力系统暂态分析的目的是评估系统在故障情况下的电压、电流和功率等参数的变化，以便采取相应的措施来保障系统的平安运行。

暂态分析的方法暂态分析的方法主要有以下几种：1. 数值计算法数值计算法是一种较为常用的暂态分析方法。

它通过建立电力系统的数学模型，采用数值计算的技术来模拟系统在暂态过程中的行为。

数值计算法可以分为直接法和迭代法两种。

直接法是指直接求解系统方程组，得到系统在每个时刻的状态；迭代法是指通过屡次迭代求解，逐步逼近真实解。

数值计算法的优点是适用范围广，可以模拟各种不同类型的暂态过程，但计算量大，耗时较长。

2. 等效方法等效方法是一种简化计算的暂态分析方法。

它通过将电力系统中的各个元件等效为简化的模型，来简化暂态分析的计算过程。

等效方法主要包括等值电路法和等值参数法。

等值电路法是指将电力系统中的元件用等效电路来代替，以简化计算；等值参数法是指将电力系统中的元件用等效参数来代替，以简化计算。

等效方法的优点是计算速度快，但往往精度较低。

3. 软件仿真法软件仿真法是一种基于计算机软件的暂态分析方法。

它利用计算机软件来构建电力系统的模型，并通过仿真计算得到系统在暂态过程中的行为。

常用的电力系统暂态分析软件有PSS/E、EMTP等。

软件仿真法的优点是模型灵巧性高，能够模拟复杂的暂态过程，但需要具备一定的计算机编程和模拟仿真的技术。

暂态分析的应用暂态分析在电力系统工程中有广泛的应用。

以下是几个常见的应用场景：1. 故障分析暂态分析可以用于故障分析，即在系统发生故障后，分析故障对系统的影响。

通过暂态分析，可以评估故障引起的电压暂降、电压暂升和电流过载等情况，以及评估故障后的系统稳定性和可靠性。

2. 保护设备设计暂态分析可以用于保护设备的设计。

电力系统暂态分析（自己总结的）

电力系统暂态分析（自己总结的）电力系统暂态分析过程（复习提纲）第一篇电力系统电磁暂态过程分析（电力系统故障分析）1 第一章电力系统故障分析的基本知识1.1故障概述1.2标幺制1.2.1标幺值1.2.2基准值的选取1.2.3基准值改变时标幺值的换算1.2.4变压器联系的不同电压等级电网中各元件参数标幺值的计算一、准确计算法二、近似计算法1.3无限大功率电源供电的三相短路电流分析1.3.1暂态过程分析1.3.2短路冲击电流和短路电流有效值一、短路冲击电流二、短路电流有效值习题2 第二章同步发电机突然三相短路分析2.1同步发电机在空载情况下定子突然三相短路后的电流波形及其分析2.2同步发电机空载下三相短路后内部物理过程以及短路电流分析2.2.1短路后各绕组的此联及电流分量一、定子绕组磁链和短路电流分量1、励磁主磁通交链定子三相绕组的磁链2、短路瞬间三相绕组磁链的瞬时值3、磁链守恒原理的作用4、三相短路电流产生的磁链5、对应的i 的三相短路电流二、励磁绕组磁链和电流分量1、强制励磁电流产生的磁链2、电子三相交流电流的电枢反应3、定子直流电流的磁场对励磁绕组产生的磁链4、按照磁链守恒原理励磁回路感生的电流和磁链三、等效阻尼绕组的电流四、定子和转子回路（励磁和阻尼回路的统称）电流分量的对应关系和衰减2.2.2短路电流极基频交流分量的初始和稳态有效值一、稳态值二、初始值1、不计阻尼回路时基频交流分量初始值2、计及阻尼回路作用的初始值2.2.3 短路电流的近似表达式一、基频交流分量的近似表达式二、全电流的近似表达式2.3 同步发电机负载下三相短路交流电流初始值2.3.1 正常稳态运行时的相量图和电压平衡关系2.3.2 不计阻尼回路时的初始值'I 和暂态电动势'q|0|E 、'|0|E一、交轴方向二、直轴方向2.3.3 计及阻尼回路的''I 和次暂态电动势''|0|E一、交轴方向二、直轴方向2.4 同步发电机的基本方程2.4.1 同步发电机的基本方程和坐标转换一、发电机回路电压方程和磁链方程二、派克变换及d 、q 、0、坐标系统的发电机基本方程1、磁链方程的坐标变换2、电压平衡方程的坐标变换2.4.2 基本方程的拉氏运算形式和运算电抗一、不计阻尼绕组时基本方程的拉氏运算形式，运算电抗和暂态电抗二、计及阻尼绕组时基本方程的拉氏运算形式，运算电抗和暂态电抗2.5 应用同步发电机基本方程分析突然三相短路电流2.5.1 不计阻尼绕组时的短路电流一、忽略所有绕组的电阻以分析d i 、q i 各电流分量的初始值二、dq i 的稳态值三、计及电阻后的dq i 各分量的衰减1、d i 直流分量的衰减时间常数2、dq i 中基频交流分量的衰减时间常数3、计及各分量衰减的dq i四、定子三相短路电流五、交轴暂态电动势2.5.2 计及阻尼绕组时的短路电流一、dq i 各分量的初始值二、dq i 的稳态直流三、计及电阻后的dq i 各分量的衰减1、d i 直流分量的衰减2、q i 直流分量的衰减3、dq i 中基频交流分量的衰减时间常数四、定子三相短路电流五、次暂态电动势1、交轴次暂态电动势''Eq 2、直轴次暂态电动势''Ed2.6自动调节励磁装置对短路电流的影响3 第三章电力系统三相短路电流的实用计算3.1短路电流交流分量初始值计算3.1.1计算的条件和近似3.1.2简单系统''I计算3.1.3复杂系统计算3.2计算机计算复杂系统短路电流交流分量初始值的原理3.2.1等值网络3.2.2用节点阻抗矩阵的计算方法3.2.3用节点导纳矩阵的计算方法一、应用节点导纳矩阵计算短路电流的原理二、三角分解法求导纳型节点方程3.2.4短路点在线路上任意处的计算公式3.3其他时刻短路电流交流分量有效值的计算3.3.1运算曲线法一、方法的基本原理二、运算曲线的制定三、应用运算曲线计算的步骤四、合并电源简化计算五、转移阻抗3.3.2应用计算系数计算一、无限大功率电源二、发电机和异步电动机4 第四章对称分量法及电力系统元件的各序参数和等值电路4.1对称分量法4.2对称分量法在不对称故障分析中的应用4.3同步发电机的负序和零序电抗4.3.1同步电机不对称短路时的高次谐波电流4.3.2同步发电机的负序电抗4.3.3同步发电机的零序电抗4.4异步电动机的负序和零序电抗4.5变压器的零序电抗和等值电路4.5.1双绕组变压器一、YNd接线变压器二、YNy接线变压器三、YNyn接线变压器4.5.2三绕组变压器4.5.3自耦变压器4.6输电线路的零序阻抗和电纳4.6.1输电线路的零序阻抗一、单根导线——大地回路的自阻抗二、双回路架空输电线路的零序阻抗三、架空地线的影响四、电缆线路的零序阻抗4.6.2架空线路的零序电容（电纳）一、分析导线电容的基本公式二、单回线路的零序电容三、同杆双回路的零序电容4.7零序网络的构成5 第五章不对称故障的分析计算5.1各种不对称短路时故障处的短路电流和电压5.1.1单相接地短路[(1)f]5.1.2两相短路[(2)f]5.1.3两相接地短路[(11)f，]5.1.4正序增广网络的应用一、正序增广网络二、应用运算曲线求故障处正序短路电流5.2非故障处电流、电压的计算5.2.1计算各序网中任意处各序电流、电压5.2.2对称分量经变压器后的相位变化5.3非全相运行的分析计算5.3.1三序网络及其电压方程5.3.2一相断线5.3.3两相断线5.4计算机计算程序原理框图第二篇电力系统机电暂态过程分析（电力系统的稳定性）6 第六章电力系统稳定性问题概述和各元件机电特征6.1概述6.2同步发电机组的机电特性6.2.1同步发电机组转子运动方程6.2.2发电机的电磁转矩和功率一、简单系统中发电机的功率二、隐极同步发电机的功-角特性三、凸极式发电机的功-角特性四、发电机功率的一般近似表达式6.2.3电动势变化过程的方程式6.3自动调节励磁系统的作用原理和数学模型6.3.1主励磁系统一、直流励磁机励磁二、交流励磁机励磁三、他励直流励磁机的方程和框图6.3.2自动调节励磁装置及其框图6.3.3自动调节励磁系统的简化模型6.4负荷特性6.4.1恒定阻抗（导纳）6.4.2异步电动机的机电特性——变化阻抗一、异步电动机转子运动方程二、异步电动机转差率的变化——等值阻抗的变化6.5柔性输电装置特性6.5.1静止无功补偿器（SVC）一、晶闸管控制的电抗器二、晶闸管投切的电容器三、SVC的静态特性和动态模型6.5.2晶闸管控制的串联电容器（TCSC）一、基本原理二、导通阶段三、关断阶段7 第七章电力系统静态稳定7.1简单电力系统的静态稳定7.2小干扰法分析简单系统表态稳定7.2.1小干扰法分析简单系统的静态稳定一、列出系统状态变量偏移量的线性状态方程二、根据特征值判断系统的稳定性7.2.2阻尼作用对静态稳定的影响7.3自动调节励磁系统对静态稳定的影响7.3.1按电压偏差比例调节励磁一、列出系统状态方程二、稳态判据的分析三、计及T时系统的状态方程和稳定判据e7.3.2励磁调节器的改进一、电力系统稳定器及强力式调节器二、调节励磁对静态稳定影响的综述7.4多机系统的静态稳定近似分析7.5提高系统静态稳定性的措施7.5.1采用自动调节励磁装置7.5.2减小元件的电抗一、采用分裂导线二、提高线路额定电压等级三、采用串联电容补偿7.5.3改善系统的结构和采用中间补偿设备一、改善系统的结构二、采用中间补偿设备8 第八章电力系统暂态稳定8.1电力系统暂态稳定概述8.2简单系统的暂态稳定性8.2.1物理过程分析一、功率特性的变化二、系统在扰动前的运行方式和扰动后发电机转子的运动情况8.2.2等面积定则8.2.3发电机转子运动方程的求解一、一般过程二、改进欧拉法8.3发电机组自动调节系统对暂态稳定的影响8.3.1自动调节系统对暂态稳定的影响一、自动调节励磁系统的作用二、自动调节系统的作用8.3.2计及自动调节励磁系统作用时的暂态稳定分析8.4复杂电力系统的暂态稳定计算8.4.1假设发电机暂态电动势和机械功率均为常数，负荷为恒定阻抗的近似计算法一、发电机作为电压源时的计算步骤二、发电机作为电流源时的计算步骤8.4.2假设发电机交轴暂态电动势和机械功率为常数一、坐标变换二、发电机电流源与网络方程求解8.4.3等值发电机8.5提高暂态稳定性的措施8.5.1故障的快速切除和自动重合闸装置的应用8.5.2提高发电机输出的电磁功率一、对发电机实行强行励磁二、电气制动三、变压器中性点经小电阻接地8.5.3减少原动机输出的机械功率8.5.4系统失去稳定后的措施一、设置解析点二、短期异步运行和再同步的可能性。

电力系统暂态分析要点与分析

电力系统电磁暂态分析Ch11.电力系统暂态指电力系统受突然的扰动后，运行参数发生较大的变化即引起电磁暂态、机电暂态过程。

电磁暂态是电压电流等电气运行参数的快速变化过程。

机电暂态是角速度等机械运行参数的慢速变化。

电力系统电磁暂态分析是研究交流电力系统发生短路（断线）后电压电流的变化。

2.元件参数指发电机、变压器、线路的属性参数，运行参数指反映电力系统运行状态的电气、机械参数。

3.故障类型：短路（三相短路、两相短路、两相短路接地、单相短路接地）、断线（一相断线、两相断线）。

对称故障（三相短路）、不对称故障（不对称短路、断线故障）。

短路故障（横向故障）、断线故障（纵向故障、非全相运行）。

简单故障：指电力系统中仅有一处发生短路或断线故障，复杂故障：指电力系统中有多处同时发生不对称故障。

4.短路危害：短路电流大使设备过热并产生一定的电动力、故障点附件电压下降、功率不平衡失去稳定、不对称故障产生不平衡磁通影响通信线路。

短路计算目的:电气设备选型、继电保护整定、确定限制短路电流措施、电气接线方式的选择。

短路解决措施：继电保护快速隔离、自动重合闸、串联电抗器。

5.无限大功率电源指短路点距离电源的电气距离较远时，短路导致电源输出功率的变化量远小于电源所具有的功率的电源。

6.无限大功率电源的三相突然短路电流：1.短路电流含有二种分量：基频稳态分量、直流暂态分量。

2.基频稳态分量比短路前电流大，其大小受短路后回路的阻抗值决定。

3.直流暂态分量其大小由短路前电流和短路后电流的交流稳态值决定，并按短路后回路的时间常数Ta 衰减为0（出现原因：短路前后电感电流不能突变）。

7.最大短路电流条件：短路前线路空载、短路后回路阻抗角90°、电压初始角为0°或180°。

出现时间：在短路后0.01秒时刻出现。

短路冲击电流：指在短路时可能达到的最大短路电流瞬时值。

三相电流中那相的直流分量起始值越大，则其短路电流越大。

电力系统暂态分析

电力系统暂态分析电力系统暂态分析是指对电力系统在暂态过程中的电压、电流、功率等参数进行研究和分析的过程。

暂态过程是指系统发生突变、故障等原因引起的瞬时变化过程，一般持续时间很短，但对电力系统的稳定运行和设备安全具有重要影响。

本文将介绍电力系统暂态分析的基本原理、方法和应用。

一、电力系统暂态分析的基本原理在电力系统中，暂态过程主要包括大电流暂态和大电压暂态。

大电流暂态一般是由于系统突发故障引起的，如短路故障；大电压暂态则是由于系统发生突变，如开关切换等。

暂态过程中，电力系统的电压、电流和功率等参数会发生瞬时的变化，因此需要进行暂态分析来研究这些变化对系统和设备的影响。

暂态分析的基本原理是根据电力系统的物理特性和传输线路的数学模型，通过求解微分方程组或差分方程组，获得系统在暂态过程中各个时刻的电压、电流和功率等参数。

在电力系统暂态分析中，常用的数学模型包括传输线模型、发电机模型、变压器模型等，这些模型可以描述不同设备在暂态过程中的响应特性。

二、电力系统暂态分析的方法电力系统暂态分析的方法主要包括数值计算方法和仿真计算方法。

数值计算方法是通过数学公式和数值计算技术，求解电力系统暂态过程的物理方程。

常用的数值计算方法包括龙格-库塔法和差分法等。

仿真计算方法是通过建立电力系统的数学模型，利用计算机软件进行模拟计算，得到系统在暂态过程中各个时刻的参数。

常用的仿真计算软件包括PSCAD、EMTP-RV等。

在进行电力系统暂态分析时，需要先确定系统的故障类型、故障位置和故障参数等。

然后，根据故障类型选择适当的暂态分析方法，并进行故障电流和故障电压等参数的计算。

最后，根据计算结果进行参数比较和评估，确定系统在暂态过程中的稳定性和设备的安全性。

三、电力系统暂态分析的应用电力系统暂态分析在电力系统的设计、运行和维护中起着重要的作用。

具体应用包括：1. 设备选择和配置：通过对电力系统暂态过程的分析，可以评估不同设备的暂态稳定性，选择合适的设备并进行合理配置，确保系统在暂态过程中能够正常运行。

《电力系统暂态分析》第四章提纲

第四章对称分量法及电力系统元件的各序等值电路三相短路属对称短路，短路电流交流分量是对称的。

在对称三相电路中，三相阻抗相同，三相电压、电流有效值相等。

因此对称三相系统三相短路的分析与计算，可只分析和计算其中一相。

单相接地短路、两相短路、两相接地短路以及单相断线、两相断线属不对称故障故障。

不对称故障时，三相阻抗不同，三相电压、电流的有效值不等，相与相之间相位差也不相等。

因此不对称故障的分析与计算，就不能只分析其中一相。

通常采用对称分量法。

第一节对称分量法适用于线性电路：可应用叠加原理。

一、对称分量法的基本思想1918年，美国学者C.L.Fortescue 提出：n 相的不对称分量，可以分解为n 组的对称分量。

应用于三相交流电力系统，对称分量法的基本思想是：任意3个不对称相量，可以分解为3组对称分量。

即(1)a F 、(1)b F 、(1)c F ——称为正序分量 a F 、b F 、c F (2)a F 、(2)b F 、(2)c F ——称为负序分量 (0)a F、(0)b F 、(0)c F ——称为零序分量这3组对称分量具有不同的相序。

然后对3组对称分量系统分别进行求解，求得3组对称分量，最后在进行叠加，求得3个不对称分量。

相量F可以是：电流、电压、电势或磁链等电路学中的相量。

二、基本公式1．正序分量：(1)a F 、(1)b F 、(1)c F )1(c F三相分量大小：相等；相位：互差120°电角度；相序：b 相超前a 相240°电角度，c 相超前a 相120°电角度。

因此，有如下关系)1(2)1(240)1(0a a j b F a F e F == )1()1(120)1(0a a j c F a F e F == 式中2321120101200jea j +-=∠==； 2321240102402jea j --=∠==。

2．负序分量：(2)a F 、(2)b F 、(2)c F)2F三相分量大小：相等；相位：互差120°电角度；相序：b 相超前a 相120°电角度，c 相超前a 相240°电角度。

电力系统暂态分析要点总结

第一章1.短路的概念和类型概念：指一切不正常的相与相与地（对于中性点接地的系统）之间发生通路或同一绕组之间的匝间非正常连通的情况。

类型：三相短路、两相短路、两相接地短路、单相接地短路。

2.电力系统发生短路故障会对系统本身造成什么危害？1）短路故障是短路点附近的支路中出现比正常值大许多倍的电流，由于短路电流的电动力效应，导体间将产生巨大的机械应力，可能破坏导体和它们的支架。

2）比设备额定电流大许多倍的短路电流通过设备，会使设备发热增加，可能烧毁设备。

3）短路电流在短路点可能产生电弧，引发火灾。

4）短路时系统电压大幅度下降，对用户造成很大影响。

严重时会导致系统电压崩溃，造成电网大面积停电。

5）短路故障可能造成并列运行的发电机失去同步，破坏系统稳定，造成大面积停电。

这是短路故障的最严重后果。

6）发生不对称短路时，不平衡电流可能产生较大的磁通在邻近的电路内感应出很大的电动势，干扰附近的通信线路和信号系统，危及设备和人身安全。

7）不对称短路产生的负序电流和电压会对发电机造成损坏，破坏发电机的安全，缩短发电机的使用寿命。

3．同步发电机三相短路时为什么进行派克变换？目的是将同步发电机的变系数微分方程式转化为常系数微分方程式，从而为研究同步发电机的运行问题提供了一种简捷、准确的方法。

4.同步发电机磁链方程的电感系数矩阵中为什么会有变数、常数或零？变数：因为定子绕组的自感系数、互感系数以及定子绕组和转子绕组间的互感系数与定子绕组和转子绕组的相对位置θ角有关，变化周期前两者为π，后者为2π。

根本原因是在静止的定子空间有旋转的转子。

常数：转子绕组随转子旋转，对于其电流产生的磁通，其此路的磁阻总不便，因此转子各绕组自感系数为常数，同理转子各绕组间的互感系数也为常数，两个直轴绕组互感系数也为常数。

零：因为无论转子的位置如何，转子的直轴绕组和交轴绕组永远互相垂直，因此它们之间的互感系数为零。

5.同步发电机三相短路后，短路电流包含哪些分量？各按什么时间常数衰减？1）定子短路电流包含二倍频分量、直流分量和交流分量；励磁绕组的包含交流分量和直流分量；D轴阻尼绕组的包含交流分量和直流分量；Q轴阻尼包含交流分量。