1二次函数的最值问题总结

合集下载

解题秘诀二次函数最值的4种解法

解题秘诀二次函数最值的4种解法二次函数是高中数学中的一个重要知识点，掌握了解题的秘诀和方法，就可以更好地解决与二次函数相关的各种问题。

本文将介绍四种解法来求解二次函数的最值问题。

一、二次函数的最值根据导数解法要求解二次函数的最值，可以通过求导数的方法来解决。

具体步骤如下：1. 将二次函数表示为一般式：f(x) = ax^2 + bx + c。

2. 对函数进行求导，得到导函数：f'(x) = 2ax + b。

3.导函数表示了二次函数的斜率，要求函数的最值，就是要求导函数为零点时的x值。

4. 解方程2ax + b = 0，求得x = -b / 2a。

5.将求得的x值代入二次函数，计算得到对应的y值。

6.x和y的值就是二次函数的最值。

二、二次函数的最值根据顶点法解法顶点法也是求解二次函数的最值的一种方法，具体步骤如下：1. 将二次函数表示为一般式：f(x) = ax^2 + bx + c。

2.求出二次函数的顶点坐标，顶点的x值为-x/2a。

3.将求得的x值代入二次函数，计算得到对应的y值。

4.x和y的值就是二次函数的最值。

三、二次函数的最值根据平移法解法平移法是一种通过平移变换求解二次函数最值的方法，具体步骤如下：1. 将二次函数表示为一般式：f(x) = ax^2 + bx + c。

2.将二次函数表示为顶点形式：f(x)=a(x-h)^2+k，其中(h,k)为顶点坐标。

3.根据函数的几何性质，二次函数的最值就是顶点的纵坐标k。

四、二次函数的最值根据因式分解解法因式分解是一种求解二次函数最值的常用方法，具体步骤如下：1. 将二次函数表示为一般式：f(x) = ax^2 + bx + c。

2.将二次函数进行因式分解：f(x)=a(x-x1)(x-x2)，其中x1和x2为二次函数的两个零点。

3.根据函数的几何性质，二次函数的最值为x轴与二次函数的拐点处的纵坐标。

通过以上四种解法，我们可以灵活地解决二次函数的最值问题。

二次函数的最值与极值总结

二次函数的最值与极值总结二次函数是高中数学中常见的一类函数，具有形如y=ax^2+bx+c的一般式。

在研究二次函数的性质时，最值与极值是非常重要的概念。

本文将对二次函数的最值与极值进行总结和讨论。

一、最值的概念在数学中，最值指的是函数在定义域内取得的最大值或最小值。

对于二次函数来说，最值的存在与二次项的系数a的正负有关。

1. 当a>0时，二次函数的抛物线开口向上，函数的最小值存在。

这个最小值即为函数的最小值。

2. 当a<0时，二次函数的抛物线开口向下，函数的最大值存在。

这个最大值即为函数的最大值。

二、最值的求解方法1. 最值的求解方法一：利用函数的对称性二次函数关于x轴对称，对称轴方程为x = -b/(2a)。

所以，函数的最值点的横坐标一定在对称轴上。

当对称轴上有x值时，带入函数表达式即可求得对应的y值，确定最值点。

2. 最值的求解方法二：利用二次函数的顶点公式二次函数的顶点公式为x = -b/(2a)，y = f(x)。

通过求得的顶点坐标，就可以确定最值点的坐标。

根据二次函数的性质，当a>0时，对应的顶点为最小值点；当a<0时，对应的顶点为最大值点。

三、极值的概念在数学中，极值是指函数在一定范围内取得的最大值或最小值。

对于二次函数来说，极值的存在与一阶导数的符号有关。

1. 当一阶导数大于0时，函数递增，没有极小值。

2. 当一阶导数小于0时，函数递减，没有极大值。

3. 当一阶导数等于0时，函数可能存在极值或拐点。

此时，需要通过二阶导数或其他方法来进一步判断。

四、极值的求解方法1. 极值的求解方法一：利用导数法对二次函数进行求导，得到一阶导数f'(x)。

将一阶导数f'(x)等于0解方程，求得x的值。

然后，将求得的x值代入原函数f(x)中，求得对应的y值，确定极值点。

2. 极值的求解方法二：利用二阶导数法对二次函数进行求导，得到一阶导数f'(x)和二阶导数f''(x)。

二次函数最值知识点总结_典型例题及习题

二次函数在闭区间上的最值一、知识要点：一元二次函数的区间最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论。

一般分为：对称轴在区间的左边，中间，右边三种情况.设f x ax bx c a ()()=++≠20，求f x ()在x m n ∈[]，上的最大值与最小值。

分析：将f x ()配方，得顶点为--⎛⎝ ⎫⎭⎪b aac b a 2442，、对称轴为x b a =-2 当a >0时，它的图象是开口向上的抛物线，数形结合可得在[m ，n]上f x ()的最值：（1）当[]-∈b a m n 2，时，f x ()的最小值是f b a ac b a f x -⎛⎝ ⎫⎭⎪=-2442，()的最大值是f m f n ()()、中的较大者。

（2）当[]-∉b am n 2，时若-<b am 2，由f x ()在[]m n ，上是增函数则f x ()的最小值是f m ()，最大值是f n () 若n b a<-2，由f x ()在[]m n ，上是减函数则f x ()的最大值是f m ()，最小值是f n () 当a <0时，可类比得结论。

二、例题分析归类：（一）、正向型是指已知二次函数和定义域区间，求其最值。

对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。

此类问题包括以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1. 轴定区间定二次函数是给定的，给出的定义域区间也是固定的，我们称这种情况是“定二次函数在定区间上的最值”。

例1. 函数y x x =-+-242在区间[0，3]上的最大值是_________，最小值是_______。

练习. 已知232x x ≤，求函数f x x x ()=++21的最值。

2、轴定区间变二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是“定函数在动区间上的最值”。

二次函数中的最值问题【八大题型】(举一反三)(浙教版)(解析版)

二次函数中的最值问题【浙教版】【题型1 已知二次函数的对称轴及自变量取值范围求最值】 (1)【题型2 已知含参二次函数的对称轴及最值求参】 (3)【题型3 已知二次函数解析式及最值求自变量取值范围】 (5)x=-【例1】二次函数y＝x2﹣2x+m．当﹣3≤x≤3时，则y的最大值为15+m（用含m的式子表示）．【分析】根据题目中的函数解析式，可以得到该函数的对称轴，然后根据二次函数的性质，即可得到当﹣3≤x≤3时，y的最大值．【解答】解：∵二次函数y＝x2﹣2x+m＝（x﹣1）2﹣1+m，∴该函数的对称轴是直线x＝1，该函数图象开口向上，当x＝1时，有最小值，∴当﹣3≤x≤3时，y取得最大值时对应的x的值是﹣3，∵当x＝﹣3时，y＝（﹣3﹣1）2﹣1+m＝15+m，∴当﹣3≤x≤3时，y的最大值为15+m，故答案为：15+m．【变式1-1】当x≥2时，二次函数y＝x2﹣2x﹣3有（）A．最大值﹣3B．最小值﹣3C．最大值﹣4D．最小值﹣4【分析】用配方法配方成顶点式，可求得对称轴，然后根据二次函数的性质即可求得．【解答】解：∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线开口向上，对称轴为直线x＝1，∴当x＞1时，y随x的增大而增大，∴当x≥2时，函数有最小值y＝22﹣2×2﹣3＝﹣3，故选：B．【变式1-2】已知二次函数y＝x2，当﹣1≤x≤2时，求函数y的最小值和最大值．小王的解答过程如下：解：当x＝﹣1时，y＝1；当x＝2时，y＝4；所以函数y的最小值为1，最大值为4．小王的解答过程正确吗？如果不正确，写出正确的解答过程．【分析】根据二次函数的性质和小王的做法，可以判断小王的做法是否正确，然后根据二次函数的性质即可解答本题．【解答】解：小王的做法是错误的，正确的做法如下：∵二次函数y＝x2，∴该函数图象开口向上，该函数的对称轴是y轴，∵﹣1≤x≤2，∴当x＝0时取得最小值，最小值是0，当x＝2时取得最大值，此时y＝4，由上可得，当﹣1≤x≤1时，函数y的最小值是0，最大值是4．【变式1-3】已知二次函数y＝x2+bx﹣c的图象经过点（3，0），且对称轴为直线x＝1．（1）求b+c的值．（2）当﹣4≤x≤3时，求y的最大值．（3）平移抛物线y＝x2+bx﹣c，使其顶点始终在二次函数y＝2x2﹣x﹣1上，求平移后所得抛物线与y轴交点纵坐标的最小值．=1，求出b的值，再将点（3，0）代入y＝x²+bx﹣c，即可【分析】（1）由对称轴−b2求解析式；（2）由题意可得抛物线的对称轴为直线x ＝1，结合函数图像可知当x ＝﹣4时，y 有最大值21；（3）设顶点坐标为（h ，2h 2﹣h ﹣1），可求平移后的解析式为y ＝（x ﹣h ）2+2h 2﹣h ﹣1，设平移后所得抛物线与y 轴交点的纵坐标为w ，则w ＝3h 2﹣h ﹣1＝3（h −16）2−1312，即可求解．【解答】解：（1）∵二次函数y ＝x ²+bx ﹣c 的对称轴为直线x ＝1， ∴−b2=1， ∴b ＝﹣2，∵二次函数y ＝x ²+bx ﹣c 的图象经过点（3，0）， ∴9﹣6﹣c ＝0， ∴c ＝3， ∴b +c ＝1；（2）由（1）可得y ＝x ²﹣2x ﹣3＝（x ﹣1）2﹣4， ∴抛物线的对称轴为直线x ＝1， ∵﹣4≤x ≤3，∴当x ＝﹣4时，y 有最大值21；（3）平移抛物线y ＝x 2﹣2x ﹣3，其顶点始终在二次函数y ＝2x 2﹣x ﹣1上，∴．设顶点坐标为（h ，2h 2﹣h ﹣1），故平移后的解析式为y ＝（x ﹣h ）2+2h 2﹣h ﹣1， ∴y ＝x 2﹣2hx +h 2+2h 2﹣h ﹣1＝x 2﹣2hx +3h 2﹣h ﹣1，设平移后所得抛物线与y 轴交点的纵坐标为w ，则w ＝3h 2﹣h ﹣1＝3（h −16）2−1312，∴当h =16时，平移后所得抛物线与y 轴交点纵坐标的最小值为−1312．【题型2 已知含参二次函数的对称轴及最值求参】【例2】已知二次函数y ＝mx 2﹣4mx （m 为不等于0的常数），当﹣2≤x ≤3时，函数y 的最小值为﹣2，则m 的值为（） A ．±16B ．−16或12C ．−16或23D ．16或2【分析】由二次函数y ＝mx 2﹣4mx 可得对称轴为x ＝2，分为m ＞0和m ＜0两种情况，当m ＞0时，二次函数开口向上，当﹣2≤x ≤3时，函数在x ＝2取得最小值﹣2，将x ＝2，y ＝﹣2代入y ＝mx 2﹣4mx 中，解得m =12，当m ＜0时，二次函数开口向下，当﹣2≤x ≤3时，函数在x ＝﹣2取得最小值﹣2，将x ＝﹣2，y ＝﹣2代入y ＝mx 2﹣4mx 中，解得m =−16，即可求解．【解答】解：∵二次函数为y ＝mx 2﹣4mx ，∴对称轴为x =−b 2a=4m 2m=2，①当m ＞0时， ∵二次函数开口向上，∴当﹣2≤x ≤3时，函数在x ＝2取得最小值﹣2，将x ＝2，y ＝﹣2代入y ＝mx 2﹣4mx 中，解得：m =12， ②当m ＜0时， ∵二次函数开口向下，∴当﹣2≤x ≤3时，函数在x ＝﹣2取得最小值﹣2，将x ＝﹣2，y ＝﹣2代入y ＝mx 2﹣4mx 中，解得：m =−16，综上，m 的值为12或−16，故选：B ．【变式2-1】已知关于x 的二次函数y ＝x 2+2x +2a +3，当0≤x ≤1时，y 的最大值为10，则a 的值为 2 ．【分析】根据抛物线的关系式可知，抛物线的开口方向向上，对称轴为直线x ＝﹣1，所以可得0≤x ≤1在对称轴的右侧，然后进行计算即可解答．【解答】解：∵y ＝x 2+2x +2a +3 ＝x 2+2x +1+2a +2 ＝（x +1）2+2a +2，∴抛物线的对称轴为：直线x ＝﹣1， ∵a ＝1＞0，∴抛物线的开口方向向上，∴当x ＞﹣1时，y 随x 的增大而增大， ∵当0≤x ≤1时，y 的最大值为10， ∴当x ＝1时，y ＝10，把x ＝1时，y ＝10代入y ＝x 2+2x +2a +3中可得： 1+2+2a +3＝10， ∴a ＝2，故答案为：2．【变式2-2】已知二次函数y ＝ax 2﹣2ax +c ，当﹣1≤x ≤2时，y 有最小值7，最大值11，则a +c 的值为（） A ．3B ．9C ．293D ．253【分析】先求得抛物线的对称轴，根据二次函数图象上点的坐标特征，当﹣1≤x≤2时，函数的最值为y＝﹣a+c和y＝3a+c，即可得出﹣a+c+（3a+c）＝7+11，即2a+2c＝18，从而求得a+c＝9．【解答】解：∵二次函数y＝ax2﹣2ax+c，∴该二次函数的图象的对称轴为直线x=−−2a2a=1，∵当x＝1时，y＝a﹣2a+c＝﹣a+c；当x＝﹣1时，y＝a+2a+c＝3a+c；∴当﹣1≤x≤2时，函数的最值为y＝﹣a+c和y＝3a+c，∵当﹣1≤x≤2时，y有最小值7，最大值11，∴﹣a+c+（3a+c）＝7+11，即2a+2c＝18，∴a+c＝9，故选：B．【变式2-3】已知二次函数y＝x2+bx+c，当x＞0时，函数的最小值为﹣3，当x≤0时，函数的最小值为﹣2，则b的值为（）A．6B．2C．﹣2D．﹣3【分析】根据二次函数y＝x2+bx+c，当x＞0时，函数的最小值为﹣2，可知该函数的对称轴在y轴右侧，4×1×c−b 24×1=−3，−b2＞0，再根据当x≤0时，函数的最小值为﹣2，即可得到c的值，然后将c的值代入入4×1×c−b 24×1=−3，即可得到b的值．【解答】解：∵二次函数y＝x2+bx+c，当x＞0时，函数的最小值为﹣3，∴该函数的对称轴在y轴右侧，4×1×c−b 24×1=−3，−b2＞0，∴b＜0，∵当x≤0时，函数的最小值为﹣2，∴当x＝0时，y＝c＝﹣2，将c＝﹣2代入4×1×c−b 24×1=−3，可得b1＝2（舍去），b2＝﹣2，故选：C．【题型3 已知二次函数解析式及最值求自变量取值范围】【例3】当0≤x≤m时，函数y＝﹣x2+4x﹣3的最小值为﹣3，最大值为1，则m的取值范围是（）A．0≤m≤2B．0≤m＜4C．2≤m≤4D．m≥2【分析】根据题意和二次函数的性质，可以得到m的取值范围，本题得以解决．【解答】解：∵y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴该函数的对称轴是直线x＝2，当x＝2时，该函数取得最大值1，该函数图象开口向下，∵当0≤x≤m时，此函数的最小值为﹣3，最大值为1，当x＝0时，y＝﹣3，∴2≤m≤4，【变式3-1】已知二次函数y ＝﹣x 2﹣4x +5，当m ≤x ≤m +3时，求y 的最小值（用含m 的代数式表示）．【分析】分四种情况讨论：①当m +3≤﹣2时，即m ≤﹣5，y 的最小值为﹣m 2﹣4m +5；②当m +32＜−2＜m +3时，即﹣4＜m ＜﹣3，y 的最小值为﹣m 2﹣4m +5；③当m ＜﹣2≤m +32时，即﹣3≤m ＜﹣2，y 的最小值为﹣m 2﹣8m ﹣7；④当m ≥﹣2时，y 的最小值为﹣m 2﹣8m ﹣7，【解答】解：y ＝﹣x 2﹣4x +5＝﹣（x +2）2+9， ∴对称轴为直线x ＝﹣2，当m ≥﹣2时，则当x ＝m +3时，y 有最小值为﹣（m +3）2﹣4（m +3）+5＝﹣m 2﹣10m ﹣16，当m ＜﹣2＜m +3时，即﹣5＜m ＜﹣2，当对称轴位于范围内时，谁离对称轴远，谁就小，若m +3+2≥﹣2﹣m ，即−72≤m ＜﹣2时，当x ＝m +3时，y 有最小值为﹣（m +3）2﹣4（m +3）+5＝﹣m 2﹣10m ﹣16，当m +3+2＜﹣2﹣m ，即﹣5＜m ＜−72时，当x ＝m 时，y 有最小值为﹣m 2﹣4m +5，当m +3+2≤﹣2时，即m ≤﹣5， y 的最小值为﹣m 2﹣4m +5；综上所述：m ≥−72时y 的最小值为﹣m 2﹣10m ﹣16；当m ＜−72时，y 的最小值为﹣m 2﹣4m +5．【变式3-2】（2022•庐阳区一模）设抛物线y ＝ax 2+bx ﹣3a ，其中a 、b 为实数，a ＜0，且经过（3，0）．（1）求抛物线的顶点坐标（用含a 的代数式表示）；（2）若a ＝﹣2，当t ﹣2≤x ≤t 时，函数的最大值是6，求t 的值；（3）点A 坐标为（0，4），将点A 向右平移3个单位长度，得到点B ．若抛物线与线段AB 有两个公共点，求a 的取值范围．【分析】（1）把已知点坐标代入抛物线的解析式，求得a 、b 的数量关系，把抛物线解析式中的b 换成a 的代数式，再将抛物线的解析式化成顶点式，便可求得顶点坐标；（2）分x ＝t 和x ＝t ﹣2在对称轴右侧、左侧或两侧三种情况，讨论求解即可；（3）抛物线经过（﹣1，0）和（3，0），与线段AB 有两个公共点时，结合图象即可判断出a 的取值范围．【解答】解：（1）把（3，0）代入y ＝ax 2+bx ﹣3a 得，9a +3b ﹣3a ＝0，∴抛物线的解析式为y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣1）2﹣4a ， ∴抛物线的顶点坐标为（1，﹣4a ）；（2）∵a ＝﹣2，∴抛物线的解析式为y ＝﹣2（x ﹣1）2+8， ∴对称轴为直线：x ＝1，∴当x ＞1时，y 随x 的增大而减小，当x ＜1时，y 随x 的增大而增大， ∵当t ﹣2≤x ≤t 时，函数的最大值是6，∴①当x ＝t 和x ＝t ﹣2在对称轴右侧时，有{−2(t −2−1)2+8=6t −2＞1，解得t ＝4，②当x ＝t 和x ＝t ﹣2在对称轴左侧时，有{−2(t −1)2+8=6t ＜1，解得t ＝0，③当x ＝t 和x ＝t ﹣2在对称轴左侧或两侧时，函数的最大值为8，不可能为6，此时无解，综上，t 的值为0或4；（3））∵点A 坐标为（0，4），将点A 向右平移3个单位长度，得到点B ， ∴B （3，4），∵y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣3）（x +1）， ∴抛物线经过点（3，0）和（﹣1，0），若此二次函数的图象与线段AB 有两个交点，则如图所示，抛物线的图象只能位于图中两个虚线的位置之间，当抛物线经过点A 时，为一种临界情况，将A （0，4）代入，4＝0﹣0﹣3a ，解得a ＝−43，当抛物线的顶点在线段AB 上时，为一种临界情况，此时顶点的纵坐标为4，∴﹣4a ＝4，解得a ＝﹣1，∴−43≤a ＜﹣1．【变式3-3】已知抛物线y ＝﹣x 2+bx +c 与x 轴的一个交点为（﹣1，0），且经过点（2，c ）．（1）求抛物线与x 轴的另一个交点坐标．（2）当t ≤x ≤2﹣t 时，函数的最大值为M ，最小值为N ，若M ﹣N ＝3，求t 的值．【分析】（1）由抛物线经过（2，c ）和（0，c ），可得到抛物线的对称轴为直线x ＝1，即可根据点（﹣1，0），确定抛物线与x 轴的另一个交点坐标为（3，0）；（2）根据t ≤2﹣t ，确定t ≤1，2﹣t ≥1，求出当＝1时取得最大值4，解得N ＝1，令y ＝1求出值．【解答】解：（1）∵抛物线经过（2，c ）和（0，c ）， ∴抛物线的对称轴为直线x ＝1， ∴（﹣1，0）的对称点为（3，0）．即抛物线与x 轴的另一个交点坐标为（3.0）；（2）∵与x 轴的一个交点为（﹣1，0），对称轴为直线x ＝1， ∴{0=−1−b +c −b 2×(−1)=1，解得：{b =2c =3，∴y ＝﹣x 2+2x +3． ∵t ≤x ≤2﹣t ， ∴t ≤1，2﹣t ≥1．∴当t ≤x ≤2﹣t 时，当x ＝1时取得最大值4，即M ＝4，当x ＝t 或x ＝2﹣t 时取得最小值N ，∵M ﹣N ＝3，∴N ＝1．令y ＝l 得，1＝﹣t 2+2t +3，解得t 1=√3+1（舍），t 2=−√3+1，∴t =−√3+1．令y ＝l 得，1＝﹣（2﹣t ）2+2（2﹣t ）+3，解得t 1=√3+1（舍），t 2=−√3+1． ∴t =−√3+1．综上：t =−√3+1．。

二次函数的最值与极值问题

二次函数的最值与极值问题二次函数是数学中常见的一种函数类型，在很多实际问题中都可以用二次函数来描述。

在解决二次函数的最值与极值问题时，可以运用一些方法和技巧来求解。

本文将介绍一些常见的解题思路和方法。

一、二次函数的最值问题二次函数的最值指的是函数在定义域内的最大值或最小值。

当求解二次函数的最值时，可以利用二次函数的顶点和开口方向进行判断。

1. 定理1：对于开口向上的二次函数 f(x) = ax^2 + bx + c，其中 a > 0，顶点的 y 值是函数的最小值。

使用该定理时，可以先求得二次函数的顶点，再将顶点的坐标代入原函数，得到最小值。

2. 定理2：对于开口向下的二次函数 f(x) = ax^2 + bx + c，其中 a < 0，顶点的 y 值是函数的最大值。

同样地，使用该定理时，先求得二次函数的顶点，再将顶点的坐标代入原函数，得到最大值。

需要注意的是，二次函数的最大值或最小值可能在定义域内的某个点上出现，因此除了顶点外还需要考虑其他可能的极值点。

二、二次函数的极值问题二次函数的极值指的是函数在定义域内的局部最大值或最小值。

当求解二次函数的极值时，可以利用二次函数的导数和零点来寻找。

1. 求解极值的一般步骤如下：a) 求二次函数的导函数；b) 解二次函数的导函数为零的方程，得到零点；c) 将零点带入原函数，求得对应的函数值，得到极值。

2. 一个特殊情况是在二次函数的定义域 [a, b] 上求极值时，可以先求出导数，然后导数大于零的部分即是函数的递增区间，导数小于零的部分即是函数的递减区间。

接着，再对边界点和零点进行比较，得到极值。

三、综合练习与例题为了更好地理解二次函数的最值与极值问题，我们来进行一些练习和解题。

【练习题一】已知二次函数 f(x) = -2x^2 + 4x + 1，1. 求二次函数的顶点及对应的最值；2. 求二次函数的极值。

【解答】1. 对于二次函数 f(x) = -2x^2 + 4x + 1，a = -2 < 0，可以判断开口向下，顶点的 y 值是最大值。

初中数学最值问题总结

初中数学最值问题总结初中数学中的最值问题主要涉及到以下知识点：1. 一次函数的最值：一次函数 y = kx + b（k ≠ 0）在闭区间 [a, b] 上的最大值和最小值。

当 k > 0 时，函数在区间 [a, b] 上单调递增，最小值为 f(a)，最大值为 f(b)；当 k < 0 时，函数在区间 [a, b] 上单调递减，最小值为 f(b)，最大值为 f(a)。

2. 二次函数的最值：二次函数 y = ax^2 + bx + c（a ≠ 0）的最值主要出现在顶点处。

对于开口向上的抛物线（a > 0），最小值出现在顶点处；对于开口向下的抛物线（a < 0），最大值出现在顶点处。

3. 反比例函数的最值：反比例函数 y = k/x（k ≠ 0）在 x > 0 的范围内单调递减，所以最大值为 k/x = k/x₁，最小值为 k/x = k/x₂。

在 x < 0 的范围内单调递增，所以最小值为 k/x = k/x₁，最大值为 k/x = k/x₂。

4. 对数函数和指数函数的最值：对数函数和指数函数都有其定义域和值域，因此在定义域内求解最值需要考虑函数的性质和定义域的限制。

5. 利用基本不等式求最值：基本不等式如算术平均数大于等于几何平均数等，可用于求解一些特定形式的最值问题。

解决最值问题的一般步骤包括：1. 分析问题：明确最值是在什么条件下取得，以及这个最值是最大值还是最小值。

2. 选择合适的方法：根据问题的性质选择合适的方法来求解最值，如一次函数、二次函数、反比例函数等。

3. 建立数学模型：根据问题的要求建立相应的数学模型，利用适当的公式和不等式来求解最值。

4. 解方程或不等式：解方程或不等式得到最值的取值范围或具体数值。

5. 检验答案：对答案进行检验，确保其符合问题的实际情况。

通过以上知识点和解题步骤的总结，学生可以更好地理解和掌握初中数学中的最值问题，提高解决这类问题的能力。

二次函数的最值问题总结

二次函数的最值问题二次函数2(0)y ax bx c a =++≠是初中函数的主要内容，也是高中学习的重要基础．在初中阶段大家已经知道：二次函数在自变量x 取任意实数时的最值情况(当0a >时，函数在2b x a =-处取得最小值244ac b a -，无最大值；当0a <时，函数在2b x a=-处取得最大值244ac b a-，无最小值．本节我们将在这个基础上继续学习当自变量x 在某个范围内取值时，函数的最值问题．同时还将学习二次函数的最值问题在实际生活中的简单应用．二次函数求最值（一般范围类）例1．当22x -≤≤时，求函数223y x x =--的最大值和最小值．分析：作出函数在所给范围的及其对称轴的草图，观察图象的最高点和最低点，由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值．解：作出函数的图象．当1x =时，min 4y =-，当2x =-时，max 5y =．例2．当12x ≤≤时，求函数21y x x =--+的最大值和最小值．解：作出函数的图象．当1x =时，min 1y =-，当2x =时，max 5y =-．由上述两例可以看到，二次函数在自变量x 的给定范围内，对应的图象是抛物线上的一段．那么最高点的纵坐标即为函数的最大值，最低点的纵坐标即为函数的最小值．根据二次函数对称轴的位置，函数在所给自变量x 的范围的图象形状各异．下面给出一些常见情况：例3．当0x ≥时，求函数(2)y x x =--的取值范围．解：作出函数2(2)2y x x x x =--=-在0x ≥内的图象．可以看出：当1x =时，min 1y =-，无最大值．所以，当0x ≥时，函数的取值范围是1y ≥-．例4．当1t x t ≤≤+时，求函数21522y x x =--的最小值(其中t 为常数)．分析：由于x 所给的范围随着t 的变化而变化，所以需要比较对称轴与其范围的相对位置．解：函数21522y x x =--的对称轴为1x =．画出其草图． (1) 当对称轴在所给范围左侧．即1t >时：当x t =时，2min 1522y t t =--； (2) 当对称轴在所给范围之间．即1101t t t ≤≤+⇒≤≤时：当1x =时，2min 1511322y =⨯--=-； (3) 当对称轴在所给范围右侧．即110t t +<⇒<时：当1x t =+时，22min 151(1)(1)3222y t t t =+-+-=-．综上所述：2213,023,0115,122t t y t t t t ⎧-<⎪⎪=-≤≤⎨⎪⎪-->⎩在实际生活中，我们也会遇到一些与二次函数有关的问题：二次函数求最值(经济类问题)例1．为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y （台）与补贴款额x （元）之间大致满足如图①所示的一次函数关系．随着补贴款额x 的不断增大，销售量也不断增加，但每台彩电的收益Z （元）会相应降低且Z 与x 之间也大致满足如图②所示的一次函数关系．（1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？（2）在政府补贴政策实施后，分别求出该商场销售彩电台数y 和每台家电的收益Z 与政府补贴款额x 之间的函数关系式；（3）要使该商场销售彩电的总收益w （元）最大，政府应将每台补贴款额x 定为多少？并求出总收益w 的最大值．分析：（1）政府未出台补贴措施前，商场销售彩电台数为800台，每台彩电的收益为200元；（2）利用两个图像中提供的点的坐标求各自的解析式；（3）商场销售彩电的总收益＝商场销售彩电台数×每台家电的收益，将（2）中的关系式代入得到二次函数，再求二次函数的最大值.解：（1）该商场销售家电的总收益为800200160000⨯=（元）；（2）依题意可设1800y k x =+，2200Z k x =+，∴有14008001200k +=，2200200160k +=，解得12115k k ==-，．所以800y x =+，12005Z x =-+．（3）1(800)2005W yZ x x ⎛⎫==+-+ ⎪⎝⎭21(100)1620005x =--+，政府应将每台补贴款额x 定为100元，总收益有最大值，其最大值为162000元．说明：本题中有两个函数图像，在解题时要结合起来思考，不可顾此失彼.例2．凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包房费100元时，包房便可全部租出；若每间包房收费提高20元，则减少10间包房租出，若每间包房收费再提高20元，则再减少10间包房租出，以每次提高20元的这种方法变化下去.（1）设每间包房收费提高x （元），则每间包房的收入为y 1（元），但会减少y 2间包房租出，请分别写出y 1、y 2与x 之间的函数关系式.（2）为了投资少而利润大，每间包房提高x （元）后，设酒店老板每天晚餐包房总收入为y （元），请写出y 与x 之间的函数关系式，求出每间包房每天晚餐应提高多少元可获得最大包房费收入，并说明理由.分析：（1）提价后每间包房的收入＝原每间包房收包房费+每间包房收包房提高费，包房减少数＝每间包房收包房提高费数量的一半；（2）酒店老板每天晚餐包房总收入＝提价后每间包房的收入×每天包房租出的数量，得到二次函数后再求y 取得最大值时x 的值.解：（1）x y +=1001，x y 212=；（2）)21100()100(x x y -•+=y 11250)50(212+--=x ，因为提价前包房费总收入为100×100=10000，当x=50时，可获最大包房收入11250元，因为11250>10000又因为每次提价为20元，所以每间包房晚餐应提高40元或60元. 说明：本题的答案有两个，但从“投资少而利润大”的角度来看，因尽量少租出包房，所以每间包房晚餐应提高60元应该更好.例3．某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价1y （元）与销售月份x （月）满足关系式1y ＝36x 83+-，而其每千克成本2y （元）与销售月份x （月）满足的函数关系如图所示．（1）试确定b c 、的值；（2）求出这种水产品每千克的利润y （元）与销售月份x （月）之间的函数关系式；（3）“五·一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？分析：（1）将点（3，25），（4，24）代入求b 、c 的值；（2）y ＝1y -2y ；（3）将（2）中的二次函数配方为顶点式，再利用二次函数的增减性，在满足“五·一”之前的前提下求最大值.解：（1）由题意：22125338124448b c b c ⎧=⨯++⎪⎪⎨⎪=⨯++⎪⎩，解得7181292b c ⎧=-⎪⎪⎨⎪=⎪⎩；（2）12y y y =-23115136298882x x x ⎛⎫=-+--+ ⎪⎝⎭21316822x x =-++；（3）21316822y x x =-++ 2111(1236)46822x x =--+++21(6)118x =--+. ∵108a =-<，∴抛物线开口向下．在对称轴6x =左侧y 随x 的增大而增大．由题意5x <，所以在4月份出售这种水产品每千克的利润最大．最大利润211(46)111082=--+=（元）．说明：本题在x ＝6，即6月份时取得最大值，但题目要求在“五·一”之前，所以要将二次函数配方为顶点式，利用二次函数的增减性来求解.例4.某商场以每件30元的价格购进一种商品，试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤．(1) 写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式；(2) 若商场要想每天获得最大销售利润，每件商品的售价定为多少最合适？最大销售利润为多少？解：(1) 由已知得每件商品的销售利润为(30)x -元，那么m 件的销售利润为(30)y m x =-，又1623m x =-．y 22 (30)(1623)32524860,3054y x x x x x ∴=--=-+-≤≤(2) 由(1)知对称轴为42x =，位于x 的范围内，另抛物线开口向下 ∴当42x =时，2max 342252424860432y =-⨯+⨯-=∴当每件商品的售价定为42元时每天有最大销售利润，最大销售利润为432元．二次函数求最值(面积最值问题)例1.在矩形ABCD 中，AB=6cm ，BC=12cm ，点P 从点A 出发，沿AB 边向点B 以1cm ／s 的速度移动，同时点Q 从点B 出发沿BC 边向点C 以2cm ／s 的速度移动，如果P 、Q 两点同时出发，分别到达B 、C 两点后就停止移动．（1）运动第t 秒时，△PBQ 的面积y(cm²)是多少？（2）此时五边形APQCD 的面积是S(cm²)，写出S 与t 的函数关系式，并指出自变量的取值范围．（3）t 为何值时s 最小，最小值时多少？答案：6336333607266126262621)1(2222有最小值等于时；当）（）（）（）（）（）（S t t S t t t t t S t t t t y =∴+-=<<+-=+--⨯=+-=⋅-=例2.小明的家门前有一块空地，空地外有一面长10米的围墙，为了美化生活环境，小明的爸爸准备靠墙修建一个矩形花圃，他买回了32米长的不锈钢管准备作为花圃的围栏，为了浇花和赏花的方便，准备在花圃的中间再围出一条宽为一米的通道及在左右花圃各放一个1米宽的门（木质）．花圃的长与宽如何设计才能使花圃的面积最大？解：设花圃的宽为x 米，面积为S 平方米则长为：x x 4342432-=+-(米)则：)434(x x S -=x x 3442+-= 4289)417(42+--=x ∵104340≤-<x ∴2176<≤x∵6417<，∴S 与x 的二次函数的顶点不在自变量x 的范围内，而当2176<≤x 内，S 随x 的增大而减小， ∴当6=x 时，604289)4176(42max =+--=S (平方米) 答：可设计成宽6米，长10米的矩形花圃，这样的花圃面积最大．例3.已知边长为4的正方形截去一个角后成为五边形ABCDE （如图），其中AF=2，BF=1．试在AB 上求一点P ，使矩形PNDM 有最大面积．解：设矩形PNDM 的边DN=x ，NP=y ，则矩形PNDM 的面积S=xy （2≤x≤4）易知CN=4-x ，EM=4-y ．过点B 作BH ⊥PN 于点H则有△AFB ∽△BHP∴PHBH BF AF =，即3412--=y x ， ∴521+-=x y ， x x xy S 5212+-==)42(≤≤x ，此二次函数的图象开口向下，对称轴为x=5，∴当x≤5时，函数值y 随x 的增大而增大，对于42≤≤x 来说，当x=4时，12454212=⨯+⨯-=最大S ．【评析】本题是一道代数几何综合题，把相似三角形与二次函数的知识有机的结合在一起，能很好考查学生的综合应用能力．同时，也给学生探索解题思路留下了思维空间．例4.某人定制了一批地砖，每块地砖（如图(1)所示）是边长为0.4米的正方形ABCD ，点E 、F 分别在边BC 和CD 上，△CFE 、△ABE 和四边形AEFD 均由单一材料制成，制成△CFE 、△ABE 和四边形AEFD 的三种材料的每平方米价格依次为30元、20元、10元，若将此种地砖按图(2)所示的形式铺设，且能使中间的阴影部分组成四边形EFGH ．(1)判断图(2)中四边形EFGH 是何形状，并说明理由；(2)E 、F 在什么位置时，定制这批地砖所需的材料费用最省？解：(1) 四边形EFGH 是正方形．图(2)可以看作是由四块图(1)所示地砖绕C 点按顺(逆)时针方向旋转90°后得到的，故CE =CF =CG ．∴△CEF 是等腰直角三角形因此四边形EFGH 是正方形．(2)设CE =x , 则BE =0.4－x ，每块地砖的费用为y 元那么：y =x ×30+×0.4×(0.4-x )×20+[0.16-x -×0.4×(0.4-x )×10]=xx)-102+242.0.0(-=x)4.0102+3.2()1.0<x0(<当x=0.1时，y有最小值，即费用为最省，此时CE=CF=0.1．答：当CE=CF=0.1米时，总费用最省．。

二次函数最值知识点总结典型例题及习题

二次函数最值知识点总结典型例题及习题必修一二次函数在闭区间上的最值一、知识要点：对于一元二次函数在闭区间上的最值问题，关键在于讨论函数的对称轴与区间的相对位置关系。

一般分为对称轴在区间左侧、中间和右侧三种情况。

例如，对于函数f(x) = ax^2 + bx + c (a ≠ 0)，求其在闭区间[x1.x2]上的最大值和最小值。

分析：将函数f(x)配方，得到其顶点为(-b/2a。

c - b^2/4a)。

因此，对称轴为x = -b/2a。

当a。

0时，函数f(x)的图像为开口向上的抛物线。

结合数形结合可得在闭区间[x1.x2]上f(x)的最值：1）当对称轴在[x1.x2]之外时，f(x)的最小值为f(-b/2a)，最大值为f(x1)和f(x2)中的较大者。

2）当对称轴在[x1.x2]之间时，若x1 ≤ -b/2a ≤ x2，则f(x)的最小值为f(-b/2a)，最大值为f(x1)和f(x2)中的较大者；若x1.-b/2a或x2 < -b/2a，则f(x)在闭区间[x1.x2]上单调递增或单调递减，最小值为f(x1)，最大值为f(x2)。

当a < 0时，情况类似。

二、例题分析归类：一）正向型此类问题是指已知二次函数和定义域区间，求其最值。

对称轴与定义域区间的相互位置关系往往成为解决这类问题的关键。

此类问题包括以下四种情形：（1）轴定，区间定；（2）轴定，区间变；（3）轴变，区间定；（4）轴变，区间变。

1.轴定区间定二次函数和定义域区间都是给定的，我们称这种情况是“定二次函数在定区间上的最值”。

例如，对于函数y = -x^2 + 4x - 2在区间[0.3]上的最大值为2，最小值为-2.2.轴定区间变二次函数是确定的，但它的定义域区间是随参数而变化的，我们称这种情况是“定函数在动区间上的最值”。

例如，对于函数f(x) = (x-1)^2 + 1，在区间[t。

t+1]上的最值为f(t)和f(t+1)中的较大者。

二次函数最值问题及解题技巧(个人整理)

二次函数最值问题及解题技巧(个人整理)一、二次函数线段最值问题1、平行于x轴的线段最值问题1）首先表示出线段两个端点的坐标2）用右侧端点的横坐标减去左侧端点的横坐标3）得到一个线段长关于自变量的二次函数4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值2、平行于y轴的线段最值问题1）首先表示出线段两个端点的坐标2）用上面端点的纵坐标减去下面端点的纵坐标3）得到一个线段长关于自变量的二次函数解析式4）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值3、既不平行于x轴，又不平行于y轴的线段最值问题1）以此线段为斜边构造一个直角三角形，并使此直角三角形的两条直角边分别平行于x轴、y轴2）根据线段两个端点的坐标表示出直角顶点坐标3）根据“上减下，右减左”分别表示出两直角边长4）根据勾股定理表示出斜边的平方（即两直角边的平方和）5）得到一个斜边的平方关于自变量的二次函数6）将其化为顶点式，并根据a的正负及自变量的取值规模判断最值7）根据所求得的斜边平方的最值求出斜边的最值即可2、二次函数周长最值问题1、矩形周长最值问题1）一般会给出一点落在抛物线上，从这点向两坐标轴引垂线构成一个矩形，求其周长最值2）可先设此点坐标，点p到x轴、y轴的距离和再乘以2，即为周长3）将其化为顶点式，并根据a的正负及自变量的取值范围判断最值2、利用两点之间线段最短求三角形周长最值1）首先判断图形中那些边是定值，哪些边是变量2）使用二次函数轴对称性及两点之间线段最短找到两条变革的边，并求其和的最小值3）周长最小值即为两条变革的边的和最小值加上不变的边长3、二次函数面积最值问题1、规则图形面积最值问题（这里规则图形指三角形必有一边平行于坐标轴，四边形必有一组对边平行于坐标轴）1）首先表示出所需的边长及高2）使用求面积公式表示出面积3）得到一个面积关于自变量的二次函数4）将其化为顶点式，并根据a的正负及自变量的取值规模判断最值2、不划定规矩图形面积最值问题1）支解。

二次函数求最值方法总结

二次函数求最值方法总结二次函数是高中数学中一个非常重要的内容，它的研究主要是通过函数的图像和性质来分析。

求二次函数的最值是我们在解决实际问题时经常需要用到的一个重要问题，下面我将对二次函数求最值的几种常用方法进行总结。

一、求二次函数的最值的基本思路：求解二次函数的最大值或最小值，就是要找出二次函数图像上的顶点。

根据二次函数的解析式f(x) = ax^2 + bx + c (a ≠ 0)，顶点的横坐标为 x = -b/2a，纵坐标为 f(-b/2a)。

二、二次函数的变形：通过对二次函数的变形，将其转化为标准的完全平方形式，可以更方便地求解最值。

1.完全平方形式：f(x)=a(x-h)^2+k2.平移变形：f(x)=a(x-h)^2+k+c三、利用函数图像特征求解最值：1.如果a>0，则二次函数的图像开口向上，顶点为最小值；如果a<0，则二次函数的图像开口向下，顶点为最大值。

2.如果函数的常数项c>0，则函数的最小值为c；如果函数的常数项c<0，则函数的最大值为c。

四、利用导数的方法求解最值：1. 求二次函数的一阶导数 f'(x) = 2ax + b，并令其为零，求出顶点的横坐标 x = -b/2a。

2.将顶点的横坐标代入二次函数的解析式，求出纵坐标f(-b/2a)即可得到顶点的坐标。

五、利用求根公式求解最值：求根公式是指二次函数求根的公式，即二次函数的解为 x = (-b ± √(b^2 - 4ac))/(2a)。

1. 如果二次函数的判别式Δ = b^2 - 4ac < 0，则二次函数没有实数解，从而也没有最值。

2. 如果二次函数的判别式Δ = b^2 - 4ac > 0，则二次函数有两个实数解 x1 和 x2，取其中更接近顶点的一侧的解作为最值。

3. 如果二次函数的判别式Δ = b^2 - 4ac = 0，则二次函数有且只有一个实数解 x = -b/2a，此时该解即为最值。

二次函数最值问题及解题技巧(个人整理)

一、二次函数线段最值问题之阳早格格创做1、仄止于x轴的线段最值问题1）最先表示出线段二个端面的坐标2）用左侧端面的横坐标减去左侧端面的横坐标3）得到一个线段少闭于自变量的二次函数4）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值2、仄止于y轴的线段最值问题1）最先表示出线段二个端面的坐标2）用上头端面的纵坐标减去底下端面的纵坐标3）得到一个线段少闭于自变量的二次函数剖析式4）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值3、既没有服止于x轴，又没有服止于y轴的线段最值问题1）以此线段为斜边构制一个曲角三角形，并使此曲角三角形的二条曲角边分别仄止于x轴、y轴2）根据线段二个端面的坐标表示出曲角顶面坐标3）根据“上减下，左减左”分别表示出二曲角边少4）根据勾股定理表示出斜边的仄圆（即二曲角边的仄圆战）5）得到一个斜边的仄圆闭于自变量的二次函数6）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值7）根据所供得的斜边仄圆的最值供出斜边的最值即可二、二次函数周少最值问题1、矩形周少最值问题1）普遍会给出一面降正在扔物线上，从那面背二坐标轴引垂线形成一个矩形，供其周少最值2）可先设此面坐标，面p到x轴、y轴的距离战再乘以2，即为周少3）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值2、利用二面之间线段最短供三角形周少最值1）最先推断图形中那些边是定值，哪些边是变量2）利用二次函数轴对于称性及二面之间线段最短找到二条变更的边，并供其战的最小值3）周少最小值即为二条变更的边的战最小值加上没有变的边少三、二次函数里积最值问题1、准则图形里积最值问题（那里准则图形指三角形必有一边仄止于坐标轴，四边形必有一组对于边仄止于坐标轴）1）最先表示出所需的边少及下2）利用供里积公式表示出头积3）得到一个里积闭于自变量的二次函数4）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值2、没有准则图形里积最值问题1）分隔.将已有的没有准则图形通太过隔后得到几个准则图形2）再分别表示出分隔后的几个准则图形里积，供战3）得到一个里积闭于自变量的二次函数4）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值或者1）利用大减小，没有准则图形的里积可由准则的图形里积减去一个或者几个准则小图形的里积去得到2）得到一个里积闭于自变量的二次函数3）将其化为顶面式，并根据a的正背及自变量的与值范畴推断最值。

二次函数最值问题类型题总结

二次函数得最大值或最小值问题知识点：1、配方法:将二次函数得一般式化为顶点式（1）若,有最小值、当时，取得最小值（2）若，有最大值、当时,取得最大值2、公式法:直接利用二次函数图像得顶点坐标求解、（1）若,有最小值，没有最大值,当时,、（2）若,有最大值,没有最小值,当时，、考察方向:一、１、已知二次函数得图像确定二次函数得最值例1、二次函数得部分图象如图１、3-3所示，则该函数有最值,最值为、2、已知二次函数表达式求函数最值①在函数整个定义域内求函数最值例2、二次函数有( )A.最大值Ｂ、最小值C、最大值D、最小值②在给定定义域区间范围内求函数最值二次函数在自变量得给定范围内，对应得图象就是抛物线上得一段.那么最高点得纵坐标即为函数得最大值,最低点得纵坐标即为函数得最小值.根据二次函数对称轴得位置，函数在所给自变量得范围得图象形状各异.下面给出一些常见情况:例３、当时,求函数得最大值与最小值例4、二次函数,当且时，y 散文最小值为2m,最大值为2n ，则得值为多少？3、由二次函数得最大值或最小值求二次函数表达式中得待定系数(解答最值问题忽略二次项系数得符号)例5、已知二次函数有最小值1,则得大小关系就是什么？例6、已知二次函数有最小值0，则m 得值就是多少?二、4、二次函数最值在实际应用题间得应用(①生活中得应用②几何图形面积最值问题)例７、某水产品养殖企业为指导该企业某种水产品得养殖与销售,对历年市场行情与水产品养殖情况进行了调查．调查发现这种水产品得每千克售价(元)与销售月份(月)满足关系式＝，而其每千克成本(元)与销售月份(月)满足得函数关系如图所示.(1）试确定得值; (2)求出这种水产品每千克得利润（元)与销售月份(月)之间得函数关系式; “五·一”之(3)前,几月份出售这种水产品每千克得利润最大?最大利润就是多少？例8、已知边长为4得正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,ＢＦ＝1．试在ＡＢ上求一点P,使矩形ＰND Ｍ有最大面积. 25 24 y 2(元)x (月) 1 2 3 4 5 6 7 8 9 O。

中考数学最值问题总结

中考数学最值问题总结中考数学中最值问题是一个重要的考点，通常涉及到二次函数、一次函数、不等式等问题。

以下是一些常见的最值问题及解决方法：1. 二次函数最值问题二次函数的最值问题是最常见的最值问题之一。

解决这类问题的一般步骤是：首先确定自变量的取值范围，然后利用二次函数的顶点式或开口方向来求最值。

如果二次函数的开口向上，那么在顶点处取得最小值（当x<0时），在x轴上取得最大值（当x>0时）。

如果二次函数的开口向下，那么在顶点处取得最大值（当x<0时），在x轴上取得最小值（当x>0时）。

2. 一次函数最值问题一次函数的最值问题通常涉及到一次函数的单调性和自变量的取值范围。

如果一次函数是递增的，那么在自变量取值范围内的最大值是当x取最大值时的函数值，最小值是当x取最小值时的函数值。

如果一次函数是递减的，那么在自变量取值范围内的最大值是当x取最小值时的函数值，最小值是当x取最大值时的函数值。

3. 不等式最值问题不等式的最值问题通常涉及到不等式的性质和不等式的取值范围。

解决这类问题的一般步骤是：首先确定不等式的取值范围，然后利用不等式的性质来求最值。

如果是不等式左边是一个定值，右边是一个变量的形式，那么当变量取最大或最小值时，不等式取得最值。

如果是不等式两边都是变量，那么需要利用不等式的性质来求解。

4. 代数式的最值问题代数式的最值问题通常涉及到代数式的化简和代数式中字母的取值范围。

解决这类问题的一般步骤是：首先将代数式进行化简，然后根据代数式中字母的取值范围来确定最值。

如果代数式中包含有二次项，那么可以利用配方法将其化简为顶点式或开口方向式来求解最值。

如果代数式中包含有绝对值，那么需要先去掉绝对值符号再化简求解最值。

解决中考数学最值问题需要掌握各种知识点和方法，包括二次函数、一次函数、不等式、代数式等，同时需要注意自变量的取值范围和函数的单调性等问题。

二次函数最值问题解题技巧

二次函数最值问题解题技巧二次函数最值问题是高中数学中常见的一类问题，也是中考、高考中经常出现的题型之一。

解题时需要掌握一些解题技巧，下面就介绍一些二次函数最值问题的解题技巧。

1. 求最值的方法二次函数的最值可以通过求解二次函数的顶点来得到，顶点即为最值点。

二次函数的顶点公式为：(-b/2a , f(-b/2a))。

其中，a、b、c分别为二次函数的系数，f(x)表示函数值。

2. 求最值的条件要求二次函数的最值，必须先要满足二次函数的a值不为0，否则该函数就不是二次函数。

其次，需要根据二次函数的符号来判断最值，当a>0时，函数的最小值为f(-b/2a)，当a<0时，函数的最大值为f(-b/2a)。

3. 求最值的步骤求解二次函数的最值，一般可以分为以下几个步骤：（1）将二次函数化简为标准形式：y=ax+bx+c。

（2）求出二次函数的顶点坐标：(-b/2a , f(-b/2a))。

（3）判断二次函数的最值：当a>0时，函数的最小值为f(-b/2a)；当a<0时，函数的最大值为f(-b/2a)。

（4）用最值来解题：根据题目要求，将二次函数的x值代入函数中求出对应的y值，从而得到函数的最值。

4. 拓展除了方法和步骤外，还有一些需要注意的点：（1）二次函数最值问题常常伴随着图像问题，需要将函数的图像画出来，从而更直观地理解问题。

（2）对于一些复杂的二次函数，可以借助计算器等工具来求解，但需要掌握求解方法和步骤。

（3）对于二次函数最值问题的解题，需要练习多种不同类型的题目，从而提高解题能力。

总之，掌握二次函数最值问题的解题技巧，需要学生在学习中不断积累，多加练习，从而提高数学解题能力。

二次函数的最值与极值问题

二次函数的最值与极值问题二次函数是一种具有一次项和二次项的多项式函数，通常用以下的一般形式表示：f(x) = ax^2 + bx + c其中，a、b、c是实数，且a ≠ 0。

在本文中，我们将讨论二次函数的最值与极值问题。

一、最值问题二次函数的最值表示函数的取值范围的极值点。

要确定二次函数的最值，首先需要弄清楚二次函数的开口方向。

当a > 0时，二次函数开口向上，此时函数的最小值为最值；当a < 0时，二次函数开口向下，此时函数的最大值为最值。

我们以一个具体的例子来说明。

考虑二次函数f(x) = 2x^2 - 3x + 1，根据题目要求，我们需要找到它的最值。

1. 确定二次函数的开口方向：由于a = 2 > 0，所以二次函数的开口向上。

2. 求出二次函数的顶点：二次函数的顶点是一个非常重要的概念，它是确定函数的最值的关键。

顶点的横坐标可以通过以下公式计算得到：x = -b/2a在这个例子中，我们可以计算得出：x = -( -3 ) / ( 2 × 2 ) = 3/4顶点的纵坐标可以通过将横坐标代入函数中计算得到：y = f(3/4) = 2 × (3/4)^2 - 3 × (3/4) + 1 = 11/8所以该二次函数的顶点为(3/4, 11/8)。

3. 确定最值：由于二次函数开口向上，所以顶点代表了函数的最小值。

所以函数f(x)的最小值是11/8，此时x取3/4。

二、极值问题极值点是指函数在某一点上的局部最值点。

对于二次函数来说，极值点就对应着函数的顶点。

回顾刚才的例子，我们已经计算出了二次函数f(x) = 2x^2 - 3x + 1的顶点为(3/4, 11/8)。

这个顶点就是该函数的极小值点。

在极值问题中，有两种情况需要注意：1. 当二次函数开口向上时，顶点为极小值点；2. 当二次函数开口向下时，顶点为极大值点。

所以，在求二次函数的极值问题时，需要先找到顶点，再根据开口方向确定极值类型。

二次函数的最值与优化问题

二次函数的最值与优化问题二次函数是数学中的一种常见函数形式，其一般形式为：f(x) = ax^2 + bx + c其中，a、b、c为实常数，且a≠0。

在本文中，我们将探讨二次函数的最值问题以及与之相关的优化问题。

一、二次函数的最值对于给定的二次函数f(x) = ax^2 + bx + c，我们希望确定其在定义域内的最大值或最小值。

为此，我们可以采用两种主要方法来求解。

1.1 完全平方与顶点根据二次函数的形式，我们可以将其转化为完全平方式，即通过提取二次项系数a来得到形如(x + p)^2 + q的表达式。

其中，p和q是与原函数相关的实数常数。

为了找到二次函数的最值，我们可以通过在完全平方形式下确定顶点来实现。

顶点坐标为(-p, q)，其中q为二次函数的最值。

顶点对应着二次函数的最值点。

1.2 导数与极值点除了利用完全平方形式来确定顶点之外，我们还可以应用导数的概念来解决二次函数的最值问题。

具体而言，我们计算出二次函数的导数，并找出导数为零的点。

这些点将对应着二次函数的极值点。

在计算导数时，我们可以使用幂函数的求导法则，得到二次函数的导函数f'(x) = 2ax + b。

令f'(x) = 0，我们可以解得x = -b/2a。

将该值代入原函数，即可得到最值点的纵坐标。

通过以上两种方法，我们可以有效地求解二次函数的最值问题，并得到有效的数学模型。

二、二次函数的优化问题除了求解最值问题外，二次函数还可以应用于优化问题。

在优化问题中，我们希望找到二次函数在一定条件下的最优解。

2.1 最优解的定义在优化问题中，我们需要明确定义何为最优解。

针对二次函数的优化问题，最优解通常是指使得目标函数取得最大值或最小值的变量取值。

2.2 约束条件的设定在确定最优解之前，我们需要设定一些约束条件。

这些条件可能来自于实际问题的限制或者其他相关要求。

常见的约束条件包括：定义域的范围、一些限制性条件（如非负性、连续性等）等。

第一讲二次函数的最值问题

第一讲二次函数的最值问题一、知识要点：1.二次函数的最值：当a>0，二次函数有最小值；当a<0，二次函数有最小值。

2.二次函数的最值类型：(1)自变量取全体实数；(2)自变量在某个范围二典型例选知识点1:自变量取全体实数的二次函数最值例1．（1） (2017兰州)二次函数y=x2+4x﹣3的最小值是．（2）已知二次函数y=ax2+4x+a﹣1的最小值为2，则a的值为（）.A．3 B．﹣1 C．4 D．4或﹣1（3）函数的最小值是．知识点2:自变量在某个范围内的二次函数最值例2已知关于x的函数y=x2+2ax+2在﹣5≤x≤5上．（1）当a=﹣1时，求函数的最大值和最小值；（2）当a为实数时，求函数的最大值．练习1 （2017•德阳）已知0≤x≤，那么函数y=﹣2x2+8x﹣6的最大值是（）. A．﹣10.5 B．2 C．﹣2.5 D．﹣6知识点3:含字母系数的二次函数最值例3 （2017.德州）函数y=（m+2）是关于x的二次函数，求：（1）满足条件的m值；（2）m为何值时，抛物线有最低点？求出这个最低点．这时，当x为何值时，y随x的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？这时，当x为何值时，y随x的增大而减小．练习1：已知二次函数y=a（x﹣1）2+b有最小值﹣1，则a，b的大小关系为（）. A．a＜b B．a=b C．a＞b D．大小不能确定2：(2017天津)已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）.A．1或﹣5 B．﹣1或5 C．1或﹣3 D．1或3知识点4: 二次函数最值的应用例3．对称轴为直线x=﹣1的抛物线y=x2+bx+c，与x轴相交于A，B两点，其中点A的坐标为（﹣3，0）．（1）求点B的坐标．（2）点C是抛物线与y轴的交点，点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．练习1如图所示，二次函数y=x2﹣（a﹣2）x+a﹣5的图象交x轴于A和B，交y轴于C，当线段AB最短时，线段OC的长是．2.（2017•宁德）如图，P是抛物线y=﹣x2+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则求四边形OAPB周长的最大值．例4（2017•鄄城）如图，△ABC是直角三角形，∠A=90°，AB=8cm，AC=6cm点P从点A出发，沿AB方向以2cm/s的速度向点B运动；同时点Q从点A出发，沿AC方向以1cm/s的速度向点C运动，其中一个动点到达终点，则另一个动点也停止运动，则三角形APQ的最大面积是多少？练习：（2017•贵港）如图，抛物线y=﹣x2+x+与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（）.A．（4，3） B．（5，） C．（4，） D．（5，3）三．课后作业1．对于抛物线y=x2﹣m，若y的最小值是1，则m=（）.A．﹣1 B．0 C．1 D．22若抛物线y=x2﹣2x+m的最低点的纵坐标为n，则m﹣n的值是 .3.在二次函数y=x2﹣2x﹣3中，当0≤x≤3时，y的最大值是，最小值是 . 4．如图，线段AB=10，点P是AB的动点，分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF，连结ME，则ME的最小值是．5.（2017•大连）如图，抛物线y=x2﹣3x+与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一点，过点D作y轴的平行线，与直线BC相交于点E（1）求直线BC的解析式；（2）当线段DE的长度最大时，求点D的坐标．。

二次函数的最值问题总结

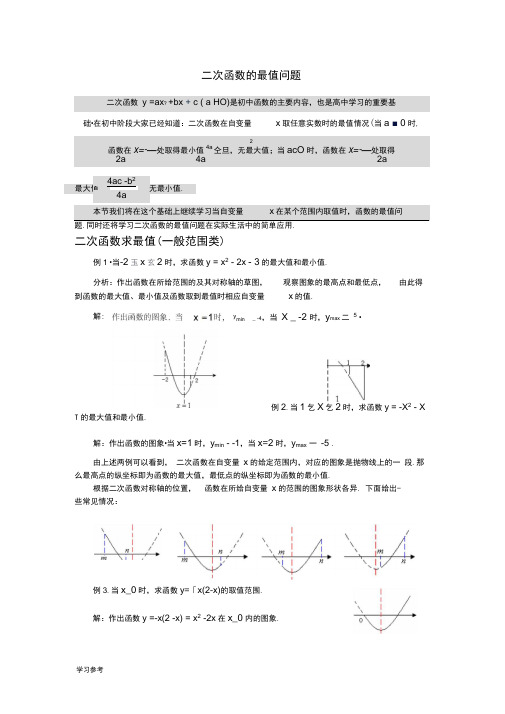
例3.当x_0时，求函数y =「x(2-x)的取值范围. 解：作出函数y =-x(2 -x) = x 2 -2x 在x_0内的图象.二次函数的最值问题二次函数 y =ax ? +bx + c ( a HO)是初中函数的主要内容，也是高中学习的重要基础•在初中阶段大家已经知道：二次函数在自变量x 取任意实数时的最值情况(当a ■ 0时,2函数在x=-—处取得最小值4a 仝旦，无最大值；当acO 时，函数在x=-—处取得2a4a2a本节我们将在这个基础上继续学习当自变量x 在某个范围内取值时，函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用.二次函数求最值(一般范围类)例1 •当-2玉x 玄2时，求函数y = x 2 - 2x - 3的最大值和最小值. 分析：作出函数在所给范围的及其对称轴的草图，观察图象的最高点和最低点，由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值._ -4，当X _ -2 时，y max 二 5 •例2.当1乞X 乞2时，求函数y = -X 2 - XT 的最大值和最小值.解：作出函数的图象•当x=1时，y min - -1，当x =2时，y max 一 -5 .由上述两例可以看到，二次函数在自变量 x 的给定范围内，对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值，最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置，函数在所给自变量 x 的范围的图象形状各异. 下面给出- 些常见情况：最大值4ac -b 2 4a无最小值.解:ymin1 25 解：函数y x -x的对称轴为x = 1 .画出其草图.221 5 （1）当对称轴在所给范围左侧•即t .1时：当x =t 时，y mint 2-t- 22⑵ 当对称轴在所给范围之间•即t _ 1 _ t • 1二0 _ t _ 1时：1 2 5当 x = 1 时，y min=2 1一1—㊁二一3 ； ⑶ 当对称轴在所给范围右侧•即 t 1 .^= t ：. 0时：1 25 1 2 当 X =t 1 时，y min (t 1)2 - (t 1) t 2 -3 .1 2—t — 3,t < 0 2y - -3,0 zt ^132 —t —5,t>1 .2 2在实际生活中，我们也会遇到一些与二次函数有关的问题：二次函数求最值（经济类问题）例1•为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴. 规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y （台）与补贴款额x （元）之间大致满足如图①所示的一次函数关系•随着补贴款额x 的不断增大，销售量也不断增加，但每台彩电的收益 Z （元）会相应降低且Z 与x 之间也大致满足如图②所示的一次函数关系.置.可以看出：当X =1时，y min 二-1，无最大值. 所以，当x _ 0时，函数的取值范围是 y _ -1 •例4.当t 乞X 乞t • 1时，求函数- x -号的最小值（其中t 为常数）.分析：由于X 所给的范围随着t 的变化而变化，所以需要比较对称轴与其范围的相对位综上所述:政府补贴款额x 之间的函数关系式；（3）要使该商场销售彩电的总收益 w （元）最大，政府应将每台补贴款额 x 定为多少？并求出总收益 w 的最大值.分析：（1）政府未出台补贴措施前，商场销售彩电台数为 800台，每台彩电的收益为200元；（2）禾U 用两个图像中提供的点的坐标求各自的解析式；（3）商场销售彩电的总收益=商场销售彩电台数X 每台家电的收益，将（ 2）中的关系式代入得到二次函数，再求二次函数的最大值.解：（1）该商场销售家电的总收益为800 200=160000 （元）;（2 ）依题意可设 y =k ,x 800 , Z =k 2x 200 ,.有 400k , 800 =1200 ,1 1 200k2 200 =160，解得 k =1, k 2•所以 y =x 800 , Z x 200.55r 1、 1（3） W = yZ = （x 800） x 200（x-100）2 162000，政府应将每台补 I 5丿5贴款额x 定为100元，总收益有最大值，其最大值为162000元.说明：本题中有两个函数图像，在解题时要结合起来思考，不可顾此失彼例2•凯里市某大型酒店有包房 100间，在每天晚餐营业时间，每间包房收包房费100 元时，包房便可全部租出；若每间包房收费提高20元，则减少10间包房租出，若每间包房收费再提高20元，则再减少10间包房租出，以每次提高 20元的这种方法变化下去.（1）设每间包房收费提高 x （元），则每间包房的收入为 y 1 （元），但会减少y 2间包房租出，请分别写出 y 1、y 2与x 之间的函数关系式.（2）为了投资少而利润大，每间包房提高 x （元）后，设酒店老板每天晚餐包房总收入为y （元），请写出y 与x 之间的函数关系式，求出每间包房每天晚餐应提高多少元可获得最大包房费收入，并说明理由•分析：（1）提价后每间包房的收入=原每间包房收包房费 +每间包房收包房提高费，包房减少数=每间包房收包房提高费数量的一半；（2）酒店老板每天晚餐包房总收入=提价后每间包房的收入X 每天包房租出的数量，得到二次函数后再求y 取得最大值时x 的值.1解：（1） y 1 =100 x , y 2x ； 21 12（2） y =（100 • x ） "100 x ）y （x -50）11250 ,因为提价前包房费总收入2 2(1)(2)为100X 100=10000,当x=50时，可获最大包房收入11250元，因为11250>10000又因为每次提价为20元，所以每间包房晚餐应提高40元或60元.说明：本题的答案有两个，但从“投资少而利润大”的角度来看，因尽量少租出包房，所以每间包房晚餐应提高60元应该更好•例3•某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价y1（元）与销售月份x （月）3满足关系式y1 = x 36，而其每千克成本y（元）与销售月份x （月）满足的函数关8系如图所示.y 2 (兀)（1）试确定b 、c 的值；（2）求出这种水产品每千克的利润 y （元）与销售月份x （月）之间的函数关系式;（3） “五•一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？分析：（1）将点（3, 25）, （4, 24）代入求 b 、c 的值；（2） y = y 1- y 2 ；（3）将（2）中的二次函数配方为顶点式，再利用二次函数的增减性，在满足“五•一”之前的前提下求x 5 ,所以在4月份出售这种水产品每千克的利润最大.最大利润1 2 1 （4 -6）2 11 =10—（元）. 8 2说明：本题在x = 6,即6月份时取得最大值，但题目要求在“五•一”之前，所以要将二次函数配方为顶点式，利用二次函数的增减性来求解例4.某商场以每件 30元的价格购进一种商品，试销中发现这种商品每天的销售量（1）写出商场卖这种商品每天的销售利润（2）若商场要想每天获得最大销售利润, y 与每件销售价x 之间的函数关系式；每件商品的售价定为多少最合适？最大销售利润为多少?解：（1）由已知得每件商品的销售利润为（x-30）元,那么m 件的销售利润为y 二m （x - 30），又m =162 -3x .m （件）与每件的销售价x （元）满足一次函数 m =162 —3x,30 空 x ^54 .解：（1 ）由题意:25V 32 24三 423b c 4b c—7 ，解得 81c = 29 —I 2(2) y 十 -丫2=一3 x 36 _ 1X 2 _15 X 291 二-1 x 28 8 8 2 83- 2十2X一x 61 — 】(x 2 -12x 36) 4」6」一】(x-6)2 11. 2 8 2 2 8•- --0,•••抛物线开口向下.8在对称轴x = 6左侧y 随x 的增大而增大.由题意\17.y =(x-30)(162 -3x) =—3x 2 252x -4860,30 乞 x 乞 54(2)由⑴ 知对称轴为x = 42，位于x 的范围内，另抛物线开口向下2.当 x = 42时，y max - -3 42 252 42 -4860 =432.当每件商品的售价定为 42元时每天有最大销售利润，最大销售利润为432元.二次函数求最值(面积最值问题)例1.在矩形ABCD 中, AB=6cm BC=12cm 点P 从点A 出发，沿 AB 边向点B 以1cm/s 的速度移动，同时点 Q 从点B 出发沿BC 边向点C 以2cm /s 的速度移动，如果 P 、Q 两点同时出发，分别到达B 、C 两点后就停止移动.(1) 运动第t 秒时，△ PBQ 的面积y(cm2 )是多少？(2) 此时五边形 APQCD 勺面积是S(cm2 )，写出S 与t 的函数关系式，并指出自变量的取值范围.(3) t 为何值时s 最小，最小值时多少？答案：1 2(1) y = -(6 -t ) 2t 一t 6t2(2) S =6 12 一( 一t 2 6t )t 2 -6t • 72(0 ：：t ：：：6) (3) S (t -3)2 63.当t =3时；S 有最小值等于63例2.小明的家门前有一块空地，空地外有一面长 10米的围墙，为了美化生活环境，小明的爸爸准备靠墙修建一个矩形花圃，他买回了32米长的不锈钢管准备作为花圃的围栏，为了浇花和赏花的方便，准备在花圃的中间再围出一条宽为一米的通道及在左右花圃各放一个 1米宽的门(木质).花圃的长与宽如何设计才能使花圃的面积最大？解：设花圃的宽为x 米，面积为S 平方米贝U 长为：32 -4x • 2 =34 -4x (米) 则:S=x(34-4x)--4x 2 34x••• 0 ： 34—4x ^106*卫二％-乎)2 4289而当6乞x 内，S 随x 的增大而减小，2 17 289•••当 X=6 时，S max 一 4(6 -二)2 = 60(平方米)4 4答：可设计成宽6米，长10米的矩形花圃，这样的花圃面积最大.例3.已知边长为4的正方形截去一个角后成为五边形 ABCD (如图)，其中AF=2, BF=1.试在AB 上求一点P ,使矩形PNDM 有最大面积.1 2S = xy x 5x (2 _ x _ 4),此二次函数的图象开口向下，对称轴为x=5,•••当x W5时，函数值y 随x 的增大而增大，1 2对于2^x^4来说，当x=4时，S 最大4—5 4=12 .【评析】本题是一道代数几何综合题，把相似三角形与二次函数的知识有机的结合在一起, 能很好考查学生的综合应用能力•同时，也给学生探索解题思路留下了思维空间.例4.某人定制了一批地砖，每块地砖(如图(1)所示)是边长为0.4米的正方形 ABCD 点 E F 分别在边BC 和CD 上, △ CFE △ ABE 和四边形 AEFD 均由单一材料制成，制成△ CFE △ ABE 和四边形AEFD 勺三种材料的每平方米价格依次为30元、20元、10元，若将此种地砖按图(2)所示的形式铺设，且能使中间的阴影部分组成四边形EFGH(1) 判断图 ⑵ 中四边形EFGH1何形状，并说明理由；(2) E 、F 在什么位置时，定制这批地砖所需的材料费用最省？解：⑴四边形EFG!是正方形.图⑵ 可以看作是由四块图(1)所示地砖绕C 点按顺(逆)时针方向旋转90°后得到的，故 CE=CF =CG• △CEF 等腰直角三角形因此四边形EFGH 是正方形.(2)设CE=x ,则BE =0.4 — x ,每块地砖的费用为 y 元那么：y = X 」X30+ X 0.4 X (0.4 -x ) X 20+[0.16 - x - X 0.4 X (0.4 -x ) X 10]匚17 67 6，S 与x 的二次函数的顶点不在自变量 x 的范围内,解:设矩形PNDM 勺边DN=x NP=y, 则矩形PNDM 勺面积S=xy (2W x < 4) 易知 CN=4-x , EM=4-y .D 8HC2 2 2 2=10(x2 _0.2x 0.24)= 10(x -0.1)2 2.3 (0 :：: x :: 0.4)当x=0.1时，y有最小值，即费用为最省，此时CE=CF=0.1 .答：当CE=CF=0.1米时，总费用最省.。