数学建模Word使用
数学建模word排版

码删除,这时所有m页的页码都消失了。
论文题目用三号黑体字、一级标题用四号黑 体字,并居中;二级、三级标题用小四号黑 体字,左端对齐(不居中)。论文中其他汉 字一律采用小四号宋体字,行距用单倍行距, 打印时应尽量避免彩色打印。
参考文献按正文中的引用次序列出,其中书 籍的表述方式为: [编号] 作者,书名,出版地:出版社,出版年。 参考文献中期刊杂志论文的表述方式为: [编号] 作者,论文名,杂志名,卷期号:起止 页码,出版年。 参考文献中网上资源的表述方式为: [编号] 作者,资源标题,网址,访问时间(年 月日)。
全国大学生数学建模竞赛论文格式规范 论文题目和摘要写在论文第三页上,从第四 页开始是论文正文。(在第三页摘要后插入 分页符)
全国大学生数学建模竞赛论文格式规范 论文从第三页开始编写页码,页码必须位于 每页页脚中部,用阿拉伯数字从“1”开始 连续编号。
1.ቤተ መጻሕፍቲ ባይዱ2.
3.
4.
将鼠标移至第2页最后的位置,然后点击 插入—〉分隔符—〉分节符类型 选为“下一页”,点击确定,此时鼠标移动到了第3页; 点击插入—〉页码—〉首页显示页码—〉格式—〉选择所要插入的数字 格式,并选择起始页码为1,点击确定就可以了。这时我们可以看到从第 三页开始页码分别为1,2,3………,但是前面的m页也插入了页码,用 如下步骤3,4解决; 双击第3页插入页码的地方,这时会弹出“页眉页脚”的工具栏,点击其 中的“同前”(或高版本为“链接到前一个”)按钮(默认是启用这个功 能,点一下相当于取消这个链接,页脚的右上方“与上一节相同”6个字 消失,这就是有些资料上说的“关闭‘与上一节相同’”),然后关闭 “页眉页脚”工具栏; 这时可以回到第m页中任何插入页码的地方双击,按delete,将其中的页
数学建模的支撑材料的格式

数学建模的支撑材料的格式
数学建模的支撑材料可以采用不同的格式,具体要根据具体情况和要求来确定。
以下是一些常见的数学建模支撑材料的格式:
1. 报告格式:采用报告格式的支撑材料通常包括标题、摘要、引言、问题分析、模型建立、模型求解、结果分析和结论等部分。
可以按照规定的模板或格式要求来编写。
2. 论文格式:采用论文格式的支撑材料通常包括封面、摘要、引言、相关理论、模型建立、模型求解、结果分析和结论等部分。
要按照学术论文的写作规范和要求来编写。
3. PPT格式:采用PPT格式的支撑材料通常包括标题页、目
录页、问题分析、模型建立与求解、结果展示和结论等部分。
要注意简洁明了,配合幻灯片演示使用。
4. LaTeX格式:采用LaTeX格式的支撑材料通常是用LaTeX
编辑软件编写的,具有复杂的数学符号和公式排版能力。
可以根据需要选择适当的LaTeX模板来编写。
5. 表格和图表格式:数学建模中常涉及数据分析和可视化展示,支撑材料中可以包括各种表格、图表、图像等格式,以直观地呈现模型的结果和分析。
除了以上常见的格式,还可以根据项目要求和个人喜好选择其他适合的格式,如Markdown格式、Word文档格式等。
在选
择格式时要注意清晰、简洁、科学、规范和易于理解。
如何做数学建模

数学建模竞赛新手教程(1)--数学建模竞赛是什么?数学建模竞赛,就是在每年秋收的时候开始的一项数学应用题比赛。
大家都做过数学应用题吧,不知道现在的教育改革了没有,如果没有大变化,大家都应该做过,比如说[树上有十只鸟,开枪打死一只,还剩几只],这样的问题就是一道数学应用题(应该是小学生的吧),正确答案应该是9只,是吧?这样的题照样是数学建模题,不过答案就不重要了,重要的是过程。
真正的数学建模高手应该这样回答这道题。
“树上有十只鸟,开枪打死一只,还剩几只?”“是无声手枪或别的无声的枪吗?”“不是。
”“枪声有多大?”“80-100分贝。
”“那就是说会震的耳朵疼?”“是。
”“在这个城市里打鸟犯不犯法?”“不犯。
”“您确定那只鸟真的被打死啦?”“确定。
”“OK,树上的鸟里有没有聋子?”“没有。
”“有没有关在笼子里的?”“没有。
”“边上还有没有其他的树,树上还有没有其他鸟?”“没有。
”“有没有残疾的或饿的飞不动的鸟?”“没有。
”“算不算怀孕肚子里的小鸟?”“不算。
”“打鸟的人眼有没有花?保证是十只?”“没有花,就十只。
”“有没有傻的不怕死的?”“都怕死。
”“会不会一枪打死两只?”“不会。
“所有的鸟都可以自由活动吗?”“完全可以。
”“如果您的回答没有骗人,打死的鸟要是挂在树上没掉下来,那么就剩一只,如果掉下来,就一只不剩。
”不是开玩笑,这就是数学建模。
从不同的角度思考一个问题,想尽所有的可能,正所谓的智者千虑,绝无一失,这,才是数学建模的高手。
然后,数学建模高手的搭挡----论文写作高手(暂称为写手吧),会把以上的思想用最好的方式表达出来。
一般的写手会直接把以上的文字放到论文里就成了。
但是专职的数学建模论文的写手不会这样做,她们会先分析这些思想,归整好条理;然后,她们会试着用图画来深入浅出的表达这些思想,或者再使用一些表格;这些都是在Word中进行,她们都是这一行的专家,相信Word什么的使用技巧,都够她们写一篇论文的了。
全国大学生数学建模竞赛论文格式规范(2020年修订稿)

全国大学生数学建模竞赛论文格式规范(全国大学生数学建模竞赛组委会,2020年修订稿)为了保证竞赛的公平、公正性,便于竞赛活动的标准化管理,根据评阅工作的实际需要,竞赛要求参赛队分别提交纸质版和电子版论文,特制定本规范。
一、纸质版论文格式规范第一条论文用白色A4纸打印(单面、双面均可);上下左右各留出至少2.5厘米的页边距;从左侧装订。
第二条论文第一页为承诺书,第二页为编号专用页,具体内容见本规范第三、第四页。
第三条论文第三页为摘要专用页。
摘要内容(含标题和关键词,无需翻译成英文)不能超过一页;论文从此页开始编写页码,页码位于页脚中部,用阿拉伯数字从“1”开始连续编号。
第四条论文从第四页开始是正文内容(不要目录,尽量控制在20页以内);正文之后是论文附录(页数不限),附录内容必须打印并与正文装订在一起提交。
第五条论文附录内容应包括支撑材料的文件列表,建模所用到的全部完整、可运行的源程序代码(含EXCEL、SPSS等软件的交互命令)等。
如果缺少必要的源程序、程序不能运行或运行结果与论文不符,都可能会被取消评奖资格。
如果确实没有用到程序,应在论文附录中明确说明“本论文没有用到程序”。
第六条论文正文和附录中任何地方都不能有显示参赛者身份和所在学校及赛区的信息。
第七条所有引用他人或公开资料(包括网上资料)的成果必须按照科技论文的规范列出参考文献,并在正文引用处予以标注。
第八条本规范中未作规定的,如论文的字号、字体、行距、颜色等不做统一要求。
在不违反本规范的前提下,各赛区可以对论文做相应的要求。
二、电子版论文格式规范第九条参赛队应按照《全国大学生数学建模竞赛报名和参赛须知》的要求提交参赛论文和支撑材料两个电子文件。
第十条参赛论文电子版内容必须与纸质版内容及格式(包括附录)完全一致;必须是一个单独的文件,文件格式为PDF或者Word格式之一(建议使用PDF格式);文件大小不超过20MB。
注意参赛论文电子版文件不要压缩,承诺书和编号专用页不要放在电子版论文中,即电子版论文的第一页必须为摘要页。
截断切割大学生数学建模word版

截断切割数学建模论文摘要 本文讨论了将一个待加工长方体经过六次截断切割成一个成品长方体的切割方式问题,利用重心偏移法,考虑了第七及第k+1次切割之间的联系,建立了动态规划的数学模型,并用直接搜索法进行了求解。
本文接着用此模型对某些部门的切割准则作了正确的评价,并给了当e=0时的简明优化准则,最后用具体实例验证了模型的可靠性,并对一些初值进行了详细的讨论,给出了所有的最优解。
本文还对模型进行了误差分析,并对模型进行了推广。
关键词 动态规划 切割方式 f-原则一、问题的提出与分析某些工业部门(如贵重石材加工等)采用截断切割的加工方式。
这里“截断切割”是指将物体沿某个切割平面分成两部分。
从一个长方体中加工出一个已知尺寸,位置预定的长方体(这两个长方体的对应表面是平行的),通常要经过6次截断切割。
设水平切割单位面积的费用是垂直切割单位面积的费用的r 倍,且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用e 。
试为这些部门设计一种安排各面加工次序(称“切割方式”)的方法,使加工费用最少。
并对某部门用的如下准则作出评论:每次选择一个加工费用最少的待切割面进行切割。
该问题可以采用重心偏移法。
在切割之前,长方体的重心是确定的,每切割一次它的重心就偏移一次,而且偏移有一定的规律,它只是沿着长、宽或高的方向偏移。
待原长方体加工成成品长方体之后,长方体的重心经过六次偏移已与成品长方体的重心重合了。
这就是长方体的重心偏移过程。
该问题是一个动态规划问题,是分级决策方法和最佳化原理的综合应用。
首先是建立分级决策的模型。
用d k 表示第k 次决策,J k 表示第k 级的级收益,现在一定条件下,寻求一组可行决策变量{}621,,,d d d ,使问题的总收益J 为最佳。
二、基本假设与符号约定(一) 基本假设1. 由工艺要求,与水平工作台接触的待加工长方体底面是事先指定的,成品长方体的尺寸已知,位置预定,且两个长方体和对应表面是平行的。
数学有关的电脑操作方法

数学有关的电脑操作方法
以下是数学有关的电脑操作方法:
1. 数学符号输入:使用键盘上的符号键输入数学符号,例如加号(+)、减号(-)、乘号(*)、除号(/)、等号(=)、大于号(>)、小于号(<)、不等号(≠)等。
2. 数学公式编辑:使用数学公式编辑器软件,如Microsoft Word中的公式编辑器,LaTeX等,输入和编辑复杂的数学公式和符号。
3. 数学计算软件:使用数学计算软件,如Matlab、Mathematica等,进行数学计算、图形绘制、数据分析等操作。
4. 数学图形绘制:使用绘图软件,如GeoGebra、Desmos等,绘制数学图形,如函数图像、几何图形等。
5. 数学求解器:使用数学求解器软件,如Wolfram Alpha等,可以输入数学问题,自动求解并显示结果。
6. 数学统计分析软件:使用统计分析软件,如SPSS、R等,进行数学统计分析,包括数据处理、概率分布、假设检验等。
7. 数学建模软件:使用数学建模软件,如Matlab、Simulink等,进行数学建
模和仿真分析,用于求解实际问题。
总之,数学有关的电脑操作方法包括数学符号输入、数学公式编辑、数学计算软件、数学图形绘制、数学求解器、数学统计分析软件和数学建模软件等。
数学建模

写 Lingo 程序求解。
X0kg 原料
0.5X0kg 洗衣粉 0.3X0kg 洗涤剂
X1kg 普通洗衣粉 X2kg 浓缩洗衣粉
X1kg 普通洗衣粉 X2kg 浓缩洗衣粉
图 13-1 洗衣粉和洗涤剂加工示意图
14. 柴油机生产问题☆☆☆
某柴油厂接到今年 1 至 4 季度柴油机生产订单分别为:3000 台,4500 台,3500 台,5000 台,该厂每季度正常生产量为 3000 台,若加班可多生产 1500 台。正常生 产成本为每台 5000 元,加班生产还要追加成本每台 1500 元。库存成本为每台每季 度 200 元,问该柴油机厂该如何组织生产才能使生产成本最低?试编写 Lingo 程序 求解。
利润最大?试编写 Lingo 程序求解。
表 12-1 原料油的质量及成本数据
序号(i) 原料
辛烷值 含硫量/% 成本/(元·t-1) 可用量(t·日-1)
1
直馏汽油
62
1.5
600
2000
2
催化汽油
78
0.8
900
1000
3
重整汽油
90
02
1400
500
序号(i) 1 2 3
表 12-2
产品 70 号汽油 80 号汽油 85 号汽油
图 6.1 飞机降落曲线
已知飞机的飞行高度为 h ,飞机的着陆点为原点 O ,且在整个降落过程中,飞机的水 平速度始终保持为常数 u ,出于安全考虑,飞机垂直加速度的最大绝对值不得超过 g ,此
10 处 g 是重力加速度。 (1) 若飞机从 x = x0 处开始下降,试确定出飞机的下落曲线; (2) 设 h = 1000米 , u = 540公里 / 小时 ,求开始下降点 x = x0 所能允许的最小值;
数学建模简介word文档-华南师范大学数学科学学院

1.1 关于数学建模一、数学、数学模型、数学建模的定义二、数学建模过程流程图三、数学建模的特点和分类四、数学建模的应用和现代科学五、历年全国和美国大学生数学建模竞赛六、如何学好数学建模七、数学建模的例子:火炮的射击、椅子能在不平的地上放稳吗、人中预报问题一、数学、数学模型、数学建模的定义数学――是一门研究数量关系和空间变化关系的学科数学模型――对于现实世界的一个特定对象,一个特定目的,根据特有的内在规律,做出一些必要的假设,运用适当的数学工具,得到一个数学结构。
数学建模――构造数学模型的过程,利用数学方法解决实际问题的一种实践。
即通过抽象、简化、假设、引进变量等处理过程后,将实际问题用数学方式表达,建立起数学模型,然后运用先进的数学方法及计算机技术进行求解,得到定量的结果,以供人们作分析、预报、决策和控制。
例1:火炮的射击―――数学建模的大致全过程模型一:假设不考虑空气的阻力、重力影响――抛物运动模型二:假设不考虑重力影响,并且空气的阻力与速度成正比。
模型三:假设不考虑重力影响,并且空气的阻力与速度的平方成正比。
――适用于火炮的射击模型四:考虑重力影响,并且空气的阻力与速度的平方成正比。
―――适用于卫星的发射。
二、数学建模过程流程图众多的因素(主要和次要)--合理的假设――建立数学模型――用数学方法(或数学软件)求解模型――检验(得解与实际问题作比较)――修改完善模型。
上述数学建模过程可用流程图表述如下:三、数学建模的特点和分类数学建模是一个实践性很强的学科,它具有以下特点:1.应用领域广,如物理学、力学、工程学、生物学、医学、经济学、军事学、体育运动学等.而不少完全不同的实际问题,在一定的简化层次下,它们的模型是相同或相似的.这就要求我们培养广泛的兴趣,拓宽知识面,从而发展联想能力,通过对各种问题的分析、研究、比较,逐步达到触类旁通的境界.2.需要各种数学知识,应用已学到的数学方法和思想进行综合应用和分析,进行合理的抽象及简化的能力如微分方程、运筹学、概率统计、图论、层次分析、变分法等,去描述和解决实际问题.3.需要各种技术手段的配合,如查阅各种文献资料、使用计算机和各种数学软件包等.4.与求解数学题目的差别.求解数学题目往往有唯一正确的答案,而数学建模没有唯一正确的答案。
投资问题数学建模(Word最新版)

投资问题数学建模通过整理的投资问题数学建模相关文档,渴望对大家有所扶植,感谢观看!数学模型第一次探讨作业问题:某部门现有资金10万元,五年内有以下投资项目供选择:项目A:从第一年到第四年每年初投资,次年末收回本金且获利15%;项目B:第三年初投资,第五年末收回本金且获利25%,最大投资额为4万元;项目C:其次年初投资,第五年末收回本金且获利40%,最大投资额为3万元;项目D:每年初投资,年末收回本金且获利6%;问如何确定投资策略使第五年末本息总额最大?问题分析:用表示第i年对第j个项目的投资金额要使第五年年末本息总额最大,应当在每年将全部可用资金都用于投资,以确保资金的充分利用,由于项目投资均发生在年初,故以下只探讨年初的投资状况:第一年:其次年:手上资金(即第一年年末收回资金)为,全部用来对可投资项目投资,则有= 第三年:同理,有= 第四年:= 第五年:= 第五年年末本息和为(即第五年所能收回的全部资金)建立模型:= = = = ,求解模型:Lingo解法:可编写lingo程序如下:model: max=1.06*x54+1.15*x41+1.25*x32+1.4*x23;!目标函数; x11+x14=10;!以下约束条件表示每年资金全部用于投资;1.06*x14=x21+x23+x24; 1.15*x11+1.06*x24=x31+x32+x34;1.15*x21+1.06*x34=x41+x44; 1.15*x31+1.06*x44=x54; x23<=3;!限制B,C项目的最大投资额; x32<=4; end 运行结果如下:Global optimal solution found. Objective value: 14.37500 Infeasibilities:0.000000 Total solver iterations:1 Variable Value Reduced Cost X54 0.000000 0.000000 X41 4.500000 0.000000 X32 4.000000 0.000000 X23 3.000000 0.000000 X11 7.169811 0.000000 X14 2.830189 0.000000 X21 0.000000 0.000000 X24 0.000000 0.3036000E-01 X31 0.000000 0.000000 X34 4.245283 0.000000 X44 0.000000 0.2640000E-01 Row Slack or Surplus Dual Price1 14.37500 1.0000002 0.000000 1.4018503 0.000000 -1.3225004 0.000000 -1.2190005 0.000000 -1.1500006 0.000000 -1.0600007 0.000000 0.7750000E-018 0.000000 0.3100000E-01 所得最优值为14.375万元,对应的最优解为: x11=7.169811,x14=2.830189,x23=3,x32=4,x34=4.245283,x41=4.5,其余值为0 即第一年对A项目投资7.169811万元,对D项目投资2.830189万元;其次年对C项目投资3万元;第三年对B项目投资4万元,对D项目投资4.245283万元;第四年对A项目投资4.5万元。
最新数学建模格式规范及word模板

数学建模论文格式规范•论文用白色A4纸单面打印;上下左右各留出至少2.5厘米的页边距;从左侧装订。
•论文第一页的内容是:论文题目、组员姓名、学号、所属专业、联系电话、电子邮箱。
•论文题目和摘要写在第二页上, 从第三页开始是论文正文。
•论文从第二页开始编写页码,页码必须位于每页页脚中部,用阿拉伯数字从“1”开始连续编号。
•论文不能有页眉,论文中不能有任何可能显示答题人身份的标志。
•论文题目用三号黑体字、一级标题用四号黑体字,并居中;二级、三级标题用小四号黑体字,左端对齐(不居中)。
论文中其他汉字一律采用小四号宋体字,行距用单倍行距,打印时应尽量避免彩色打印。
•提请大家注意:摘要应该是一份简明扼要的详细摘要(包括关键词),在整篇论文评阅中占有重要权重,请认真书写(注意篇幅不能超过一页,且无需译成英文)。
评阅时将首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选。
•引用别人的成果或其他公开的资料(包括网上查到的资料) 必须按照规定的参考文献的表述方式在正文引用处和参考文献中均明确列出。
正文引用处用方括号标示参考文献的编号,如[1][3]等;引用书籍还必须指出页码。
参考文献按正文中的引用次序列出,其中书籍的表述方式为:[编号] 作者,书名,出版地:出版社,出版年。
参考文献中期刊杂志论文的表述方式为:[编号] 作者,论文名,杂志名,卷期号:起止页码,出版年。
参考文献中网上资源的表述方式为:[编号] 作者,资源标题,网址,访问时间(年月日)。
题目(三号黑体居中)摘要:此处写摘要。
摘要在整篇论文评阅中占有重要权重,请认真书写摘要(注意篇幅不能超过一页)。
组委会评阅时将首先根据摘要和论文整体结构及概貌对论文优劣进行初步筛选。
简要论述本文所要解决的问题及意义,解决问题的思路与方法、主要结果(数值结果或结论),建模的创新之处与特色等。
①短:字数尽量控制在500字内;语言精简,用词准确;②精:阐述细致具体的方法;列出主要结论③完整:写出主要模型(名称)、方法和结果,解决了什么问题,有何特色等;摘要应具有独立性和自明性,应是一篇完整的短文。
数学建模 建立函数模型解决实际问题2019版 新高一word讲义

数学建模建立函数模型解决实际问题课标要求素养要求收集、阅读一些现实生活、生产实际或者经济领域中的数学模型,体会人们是如何借助函数刻画实际问题,感悟数学模型中参数的现实意义.通过生活中具体的数学模型,进行提出问题、分析数据、建立模型、检验模型来发展数据分析、数学抽象及数学建模素养.新知探究数学建模是在20世纪60和70年代进入一些西方国家大学的,我国的几所大学也在80年代初将数学建模引入课堂.经过30多年的发展现在绝大多数本科院校和许多专科学校都开设了各种形式的数学建模课程和讲座,为培养学生利用数学方法分析、解决实际问题的能力开辟了一条有效的途径.大学生数学建模竞赛最早是1985年在美国出现的,1989年在几位从事数学建模教育的教师的组织和推动下,我国几所大学的学生开始参加美国的竞赛,而且积极性越来越高,近几年参赛校数、队数占到相当大的比例.可以说数学建模竞赛是在美国诞生,在中国开花、结果的.问题你知道什么是数学建模吗?提示数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.主要过程包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,求解模型、检验结果、得出结论,最终解决实际问题.1.用函数构建数学模型解决实际问题的步骤(1)观察实际情景:对实际问题中的变化过程进行分析;(2)发现和提出问题:析出常量、变量及其相互关系;(3)收集数据、分析数据:明确其运动变化的基本特征,从而确定它的运动变化类型;(4)选择函数模型:根据分析结果,选择适当的函数类型构建数学模型,将实际问题化归为数学问题;(5)求解函数模型:通过运算推理,求解函数模型;(6)检验模型:利用函数模型的解说明实际问题的变化规律,达到解决问题的目的.2.数学建模活动的要求(1)组建团队;(2)开展研究报告;(3)撰写研究报告;(4)交流展示.拓展深化[微判断]1.在构建函数模型时,经常会遇到没有现成数据可用的情况,这时就需要先收集数据.(√)2.在用函数构建数学模型解决实际问题时,首先要对实际问题中的变化过程进行分析,析出其中的常量、变量及其相互关系.(√)3.求出函数模型后,还需要利用函数模型的解说明实际问题的变化规律,从而达到解决问题的目的.(√)[微思考]数学建模活动是一个科学的研究过程,科学研究通常要经历哪几个步骤?提示科学研究通常需要经历四个基本步骤(1)选题;(2)开题;(3)做题;(4)结题.题型一数学建模主要步骤的探究【例1】[提出问题]在小傅家门口有一个十字型的交通路口(如图所示),小傅就想了,警察叔叔需要指挥多少种情况的汽车运行线路?[建立模型]此问题需要分是否可以原路调头的情况来讨论.(1)每条线路都有往返双向线;(2)设4条路分别为A,B,C,D;(3)以A为起始,①如允许原路调头,则有A→A,A→B,A→C,A→D,②如不允许原路调头,则有A→B,A→C,A→D.[求解模型]第一步:始线路条数;第二步:终线路条数.①如允许原路调头:则N=4×4=16(种)可能;②如不允许原路调头:则N=4×3=12(种)可能.[检验结果]如果允许汽车原路调头,那么在此交通路口共有16种不同的行车情况,如果不允许汽车原路调头,那么在此交通路口共有12种不同的行车情况. 【例2】[提出问题]两根同样长的蜡烛,点完粗蜡烛要3小时,点完细蜡烛要1小时.现同时点燃两根蜡烛.一段时间后同时熄灭,发现粗蜡烛的长度是细蜡烛的3倍.问两根蜡烛燃烧了多长时间?[建立模型] ①设两根蜡烛的长度为l 厘米,粗、细蜡烛的燃烧速度分别为x 、y (厘米/小时),则有y =l =3x ;②点燃两根蜡烛一段时间后同时熄灭,剩余粗、细蜡烛的长度分别为R 、r ,则R =3r .[求解模型] 根据条件有:l -r y =l -3rx (燃烧时间相同)化简为l =4r ,即细蜡烛燃烧后的长度是原来长度的14⎝ ⎛⎭⎪⎫也即燃烧了34,所以燃烧的时间为34l y =34l l =34(小时).[检验结果] 为了明确各量之间的相互关系,在必要的地方可以加注.【例3】 [提出问题] 李明玩套圈游戏,游戏规则为:套中小鸡一次得9分,套中小猴一次得5分,套中小狗一次得2分,李明共套10次,且每个小玩具都至少被套中一次.已知李明共得61分,求其中小鸡被套中过多少次. [建立模型] ①设每次不可能同时套中2个及2个以上的玩具;②为了保证“每个小玩具都至少被套中一次”,可设小鸡、小猴、小狗分别被套中x ,y ,z 次,x ,y ,z ∈N +,然后解不定方程组. [求解模型] 由条件得不定方程组 ⎩⎪⎨⎪⎧x +y +z =10,①9x +5y +2z =61,②②-2×①消去z 得7x +3y =41.正整数解为⎩⎪⎨⎪⎧x =2,y =9(不合方程①),⎩⎪⎨⎪⎧x =5,y =2⇒⎩⎪⎨⎪⎧x =5,y =2,z =3,[检验结果] 验证得小鸡、小猴、小狗分别被套中5、2、3次,总共得分61分. 【例4】 [提出问题] 甲、乙两人去沙漠中探险,他们每天向沙漠深处走20千米,已知每人最多可带一个人4天的食物和水.如果允许将部分食物存放于途中,问其中1人最远可深入沙漠多少千米?(要求最后两人返回出发点)[建立模型]要使其中一位探险者尽可能走得远,另一位须先回,留下食物和水给另一位,所以必须分头行动.问题是在何处留下食物和水?①经过商议让甲走得更远(最远走4×20=80(千米),但回程就没有食物和水了),需要乙在适当的地点留下足够的食物和水.②第1天乙在10千米处留下1份食物和水,到20千米处吃1份留下1份,第2天走到30千米处留下1份食物和水后马上往回返,到20千米处再吃1份,第3天走20千米回出发点.③第1天甲20千米处吃1份,第2天走到40千米处吃1份,第3天走到60千米处吃1份,第4天走到65千米处然后往返,到50千米处吃1份(到此为止甲自带的食物和水已吃完),第5天走到30千米处吃1份(此处食物和水是乙留下的),第6天走到10千米处吃1份,然后回出发点.[求解模型]所谓“错位推进法”,对于本题来说,关键点为“乙在30千米和10千米处给甲留下食物和水”,根据分析与假设推知结论:其中的一位沙漠探险家最多可深入沙漠65千米.[检验结果]从“第6天走到10千米处吃1份,然后回出发点”,感觉似乎还有10千米可以走,但已经回出发点了,考虑一下甲还可以再往前推进5千米吗?题型二数学建模活动主要过程的探究【例5】关于外卖垃圾问题的分析与解决[选题]餐饮业作为我国第三产业中一个传统服务性行业,经历了改革开放进步、数量型扩张、规模连锁发展和品牌提升战略4个阶段,取得突飞猛进的发展.为了满足当今社会快速的生活节奏,“外卖”这一餐饮方式便应运而生.“外卖”这个词是舶来品,原意是离店销售.目前,无论是地处繁华地带的市中心,还是相对冷清的城郊地区,原先并不涉足外卖的餐馆都经营了外卖快餐.外卖有好有坏,它既方便了我们的生活,但同时也制造了大量的垃圾,这些垃圾造成了生态环境的破坏,海洋动物的死亡,也已经威胁到了我们的生活.本文就此问题,展开对外卖垃圾该如何处理的分析与讨论.[开题]从具体的处理方式考虑.通过资料我们了解到填埋是我国最重要的垃圾处理方式.而填埋对环境的影响则大多体现在填埋场对周围土地的污染.因此,我们想要在不减少填埋场地所能填埋垃圾的数量的情况下,减少对土地的污染.而填埋数量与填埋场的体积有关.目前,填埋场的深度基本已达最大.因此我们通过改变填埋场的形状,寻找更好的可建为填埋场的图形.在此过程中,我们猜测填埋场对周围土地的污染是以c为半径的.并假设填埋场形状可以为任意形状.在尝试过长方形、正方形、圆形、正三角形后,我们通过公式及定量分析得出圆形为更好的一种选择.因此,在一定的条件下,填埋场建为圆形可以更有效的减少对周围土地的污染.一、固体废物数据的搜集与处理我们通过技术手段(代码见附件),在知名外卖网站“饿了么”上面定点抓取了一个地区方圆7 500 m左右所有已在该网站上注册的店铺的数据约32 109条,合计月销量267 305份,并写了一个简单的基于字典的分类算法,分类了135 655份月销量,并按照一个理想数值为每一种商品产生的垃圾进行估算.分类结果如下:外卖网站数据分类结果网站ele.me理论单月垃圾产生量根据网络搜集的市场份额与分类算法的处理偏差可以合理计算出附近外卖垃圾的月总量.线上外卖网站理论单月垃圾产生量①饭类、面类、菜类占比较高,根据本小组的实践,这类外卖都会产生塑料碗、塑料袋、一次性筷子,而这些塑料是最难处理的,当塑料上沾上油的时候,清洗也是件困难的事情.②在这些外卖产生的垃圾中,塑料袋最多,一次性筷子其次,塑料碗也较多. 二、固体废弃物处理情况由问题一我们推出的一个区域的废弃物再结合网络上的数据我们可以合理推理:垃圾回收方式占比①大部分的塑料都是以填埋的方式处理;②筷子、包装纸等可回收的一般是能回收则回收,但是难以回收的会放弃;③塑料制品一般是填埋.根据以上的信息并结合我们手上的数据,可以猜想:预测垃圾单类回收方法占比回收(kg) 1 346.8241.68356.0131.49466.63[1.问题分析填埋作为重要的处理方式,可以优化填埋所进行的具体措施来减少污染.我们了解到,填埋的污染主要为土地污染,因此减少土地污染即可.我们通过查找资料得知,填埋对土地的污染大多是以填埋场地为中心,并往四周拓展一定区域,我们假定其是以均匀半径进行拓展.因此可以尝试在同体积的情况下减小其污染的土地.因为目前的填埋场深度基本已达最大深度,所以在此暂不考虑对深度的拓展.假设垃圾填埋场为规则的立体图形.因此要保证同体积的情况下,深度一样,则表面积一样.所以我们的目的便是使在相同的表面积下,什么图形所构成的表面会对土地污染数量最小.2.模型建立我们通过网上的信息了解到,目前的填埋场形状大多为长方形.如图:(周围为污染区)设长为a,宽为b,对四周土地进行污染的半径为c,总污染面积为S.那么S=ab+2ac+2bc+πc2=ab+2c(a+b)+πc2在表面积固定的情况下:ab为定值,c、π均为定值,因此使(a+b)最小即可.由均值不等式可得:a+b≥2ab且当a=b时取等号.因此若使S最小,即a=b,因此我们得出结论:垃圾填埋场呈正方形比呈长方形要好.之后,我们再比较其他形状的垃圾填埋场和传统垃圾填埋场谁更好.为了方便计算和更好的解决问题,以下模型均与正方形所造成的土地污染进行对比,若更好,则模型优化成立.(1)圆形在这里为方便,把正方形的图与圆形的图放在一起做对比.设正方形边长为d ,对四周土地进行污染的半径为c ,圆的半径为r . d 2=πr 2, r =d π,正方形总污染为S 正方形=πc 2+4dc +d 2,圆形总污染为S 圆形=⎝ ⎛⎭⎪⎫d π+c 2π=⎝ ⎛⎭⎪⎫d 2π+2dc ππ+c2·π=d 2+2dc π+c 2·π, 作差得S 圆形-S 正方形=c 2π+2dc π+d 2-πc 2-4dc -d 2 =2dc π-4dc =2dc (π-2), 又因为π-2<0,因此S 圆形<S 正方形,所以圆形更好. 因此在之后的比较中用圆形即可. (2)正三角形设正三角形边长为e ,则S 三角形=34e 2, 因为我们要使圆形与三角形的表面积相同,则 34e 2=πr 2,r =e 23π, 因此通过计算可得S 三角形污染面积=34e 2+πc 2+3ce ,S 圆形污染面积=⎝⎛⎭⎪⎫e23π+c 2·π =⎝ ⎛⎭⎪⎫e 24·3π+ec 3π+c 2·π =34e 2+ec3π+c 2·π,S 圆形污染面积-S 三角形污染面积=34e 2+ec3π+c 2·π-34e 2-πc 2-3ce =ec (3π-3)<0,因此S 圆形污染面积<S 三角形污染面积,所以圆形更好.综上所述,目前的填埋场形状为长方形,而我们通过计算得出,圆形实则为更好的一种方案.因此我们可以通过把长方形的填埋场改建为圆形的填埋场,这样可以有效的减少土地污染体积.模型优化成立. [结题] 1.模型优点:A.该模型可以有效的减少土地污染体积;B.该模型不需要耗费大量的人力物力. 2.模型缺点:A.该模型没有考虑渗滤液处理区等方面的限制条件;B.该模型只能用于填埋场形状为圆形的填埋场.3.我们了解到填埋是我国目前最重要的垃圾处理方式.而填埋造成的环境污染主要体现在对周围土地的污染.因此我们想在不影响填埋数量的情况下,通过改变填埋场形状来减少对土地的污染.在此模型中,我们采用了枚举法,通过比较不同的形状带来的污染,最后得出结论.在一定的条件下,圆形较好.最后,我们通过调查问卷和数据抓取的方式,得到订外卖的主体为服务业的年轻人.大量的外卖垃圾正威胁着我们的环境,但并非无解决方法.但是,最重要的还是我们自身需建立起环境保护意识,自觉保护环境,维护生态平衡.只有这样,我们才能继续绿色、健康的生存和发展下去. 【例6】 牙膏价格与重量关系的数学建模[选题] 在超市购物时,我们注意到大包装商品比小包装商品便宜,比如洁银牙膏50 g 装的每支1.50元,120 g 装的每支3.00元.我们可以通过单位商品价格关于商品重量的函数来分析大包装便宜还是小包装便宜. [开题] 1.分析问题商品价格是由成本决定的,成本可分为生产成本、包装成本和其他成本.生产成本与重量W成正比,包装成本与表面积成正比,其他成本与W无关.单位重量商品价格c=总价格总重量.牙膏可以近似为圆柱体来思考.2.模型假设设如下变量:商品价格为C,商品重量为W,单位重量价格为c,商品包装面积为S,生产成本为C1,包装成本为C2,其它成本为C3.3.研究的大体思路、方法与步骤(1)分析商品价格C与商品重量W的关系.价格由生产成本、包装和其它成本等决定,这些成本中有的与重量W成正比,有的与表面积成正比,还有与W无关的因素.(2)求单位重量价格c与W的关系,可以用简图分析.最后结合实验结论,对商家或顾客提出合理的建议.4.研究此问题的意义实际生活中,经常会遇到大、小包装的问题,如洗衣粉、洗发水、纯净水等.在选择购买时,可依据下面的数学模型做选择.[做题] 1.模型建立与求解商品价格由成本决定,商品成本=生产成本+包装成本+其他成本,故C=C1+C2+C3,生产成本与重量W成正比,设C1=k1W(k1为大于0的常数),包装成本与表面积S成正比,商品包装包括牙膏包装和牙膏盒包装,牙膏包装与牙膏表面积有关,牙膏盒为长方体,设牙膏盒包装面积S2,牙膏可以近似为无底的圆柱体,设牙膏包装面积S1即圆柱体侧面积.设此圆柱体的半径为R,高为L,S1=2πRL,①由题意,我们需要将包装面积与商品重量联系在一起,故我们将牙膏体积V近似为圆柱体积的一半,则V=12πR2L,②设牙膏密度为ρ,则V=W ρ,③一般地,为了美观,牙膏的半径与长度有一定比例关系,在这里:设R =k 2L (k 2为大于0的常数),④根据②③④,可以得出:半径R =⎝ ⎛⎭⎪⎫2k 2W ρπ13,⑤ 由①④⑤得出S 1=2πk 2⎝⎛⎭⎪⎫2k 2W ρπ23, 我们可以把牙膏盒看成一个长为L ,宽高都为2R 的长方体,故牙膏盒包装面积S 2=8R 2+8RL ,再根据④⑤求得S 2=8⎝ ⎛⎭⎪⎫1+1k 2⎝⎛⎭⎪⎫2k 2W ρπ23, 则包装成本C 2=k 32πk 2⎝⎛⎭⎪⎫2k 2W ρπ23+k 48⎝ ⎛⎭⎪⎫1+1k 2⎝ ⎛⎭⎪⎫2k 2W ρπ23, k 3、k 4为大于0的常数,是包装价格与包装面积的比值.其他成本C 3为固定常数,与W 、S 无关.即C =C 1+C 2+C 3=k 1W +k 32πk 2⎝⎛⎭⎪⎫2k 2W ρπ23+k 48⎝ ⎛⎭⎪⎫1+1k 2⎝ ⎛⎭⎪⎫2k 2W ρπ23+C 3. 由于k 1,k 2,k 3,k 4,ρ都是大于零的常数,所以商品价格关于商品重量的函数是单调增函数,所以商品重量增大,商品价格增大.对于单位重量价格c 与商品重量W 的关系,我们已知c =C W ,由于k 1,k 2,k 3,k 4,ρ都是大于零的常数,我们发现包装成本与商品重量成正比,可以简化为C 2=k 5×W 23,所以c =C W =k 1+k 5×13W+C 31W . 2.模型解释c -W 的简图如图所示:由函数解析式及图象可知单位商品价格关于商品重量的函数是一个减函数,即随着W的增加,c的减少幅度减少,当W很大时,则c不再减少,所以说,不要盲目追求大包装商品.[结题]对于商家,一般来说,小包装商品的利润较高,但成本也相应的增多,所以应该包装大小适宜,在适当情况下,可以尽量生产小包装的商品;对于顾客,在用得完的情况下,尽量买较大的包装,可以节省包装的费用,但是也不能盲目地认为越大包装的商品就越便宜,可能会有其他消耗,如用不完的情况.数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法、数学模型解题的过程.在构建模型时,经常会遇到没有现成数据可用的情况,这时就需要先收集数据,再进行分析、建模.下面摘录一些中学生曾经研究过的问题供参考,同学们可根据情况组织团队进行建模活动.自然方面的问题公路上雪的融化速度;都江堰宝瓶口的水有多深;圭表与日晷原理的数学分析;利用灯光促进植物生长的实验;由氢键理论推算冰的密度;从拼图游戏到人类基因组计划;水草治理问题;天体日、月相在旋转点阵屏上运行的数学模型;云南白马雪山地区树木年轮宽度与气候变化的相关性研究;植物叶表粗糙程度与吸附大气颗粒物能力的关系探究;孔雀鱼体色基因类型初步研究.社会方面的问题“110”巡警站的位置安排;公路护栏的改良;防错拨的城市电话号码设置方案;对小区学生择校问题的研究;如何使防护林达到最佳防护效果;保安巡更路线方案及软件流程设计;高峰期学校门前十字路口红绿灯周期时间的设计;利用数码相机测量桥梁裂纹;埙的容积对音高的影响;考试焦虑的影响因素分析;老年人免费乘公交车的社会成本;“梦之队”组建的最优化选择;汉字结构特征及其识别;“月上柳梢头,人约黄昏后”——古诗中的天文学问题;中国古建筑建造中“举折法”屋面曲线猜想;泰森多边形在环境空气监测网络布设中的应用.生活方面的问题流行歌曲的流行趋势分析;地铁站旅客流通情况及优化方案;暖瓶的最佳保温水位;讨论适合拼音输入法的键盘布局;游览卢浮宫的最佳路线;抽取式面巾纸的包装盒优化设计;汽车后视镜的角度分析及安装改进;14款笔记本电脑性价比报告;地区加油站各区域分布数量方案;为数独定难度;太阳能电池板发电设备优化;区域养老院规划;城市周边地区住房入住率估算与分析;碘酸钾碘盐在烹饪食物时碘损失率的研究.结束语数学建模是一个让纯粹数学家(指只懂数学不懂数学在实际中的应用的数学家)变成物理学家、生物学家、经济学家甚至心理学家等等的过程.。
数学建模大赛一等奖作品Word 文档

数学建模论文高速公路道路交通事故分析预测摘要我国目前的道路交通安全状况相对于世界水平要差得多,高速公路道路交通事故所造成的损失非常高。
因此,改善交通安全状况、预防和减少高速公路交通事故具有重大的现实意义。
针对这样的现状,我们必须进行高速公路交通事故的预测,从而及早采取措施进行预防工作,从而减少事故发生次数及损失程度。
针对此次建模的要求,在对此问题的深入研究下,我们提出了合理的假设,将本问题归结为一个预测分析的问题,其基本思想是通过聚类分析、SPSS软件求解、GM(1,1)灰色预测模型、多元线性回归分析,组合模型等方法的运用得到最优的预测结果。
针对问题一,我们首先运用了聚类分析的思想,建立了基于聚类分析的模型Ⅰ,通过聚类分析方法对给定的信息的筛选、加工、延伸和扩展,从而将评价对象确定在某一范围内,通过了该方法,最终得到了各类评价等级方法,为科学预测交通事故提供了依据。
针对问题二,本文选取受伤人数这一单项指标作为预测的对象,首先运用了GM(1,1)灰色预测模型,建立模型Ⅱ,通过对给定的事故原始数据,通过MATLAB 软件预测了五年内的交通事故受伤人数;运用多元线性回归方法建立模型Ⅲ,在模型Ⅱ和模型Ⅲ的基础之上,通过基于组合模型思想的模型Ⅳ,求解得出了交通事故受伤人数在五年内的预测。
关键词:SPSS聚类分析 GM(1,1)灰色预测模型组合预测模型 MATLAB目录一.问题重述 (3)二.问题的分析 (4)三.模型假设与符号系统 (5)3.1模型假设 (5)3.2符号系统 (6)四.模型的建立及求解 (7)4.1 问题一 (7)4.1.1建立模型Ⅰ (7)4.1.2模型Ⅰ的求解及结果 (8)4.1.3实验结果的分析说明 (9)4.2 问题二 (12)4.2.1建立GM(1,1)模型Ⅱ (12)4.2.2 用MATLAB求解模型Ⅱ (16)4.2.3 建立模型Ⅲ (19)4.2.4 建立优化模型Ⅳ (20)4.2.5最优组合模型的求解 (21)五.模型的评价 (22)参考文献 (23)附录 (24)一.问题重述随着道路交通事业的发展,高速公路交通事故也在不断增加,对人类的生命和财产安全构成了极大的威胁。
数学建模教案(word版)

数学建模教案要求应用和创新是数学建模的特点,也是素质教育的灵魂;不论用数学方法解决哪类实际问题,还是与其他学科想结合形成交叉学科,首先的和关键的一步是用数学的语言表述所研究的对象,即建立数学模型。
在高科技,特别是计算机技术迅速发展的今天,计算和建模正成为数学科学技术转化的主要途径。
本课程旨在提高学生数学应用能力和数学知识的获取能力。
根据课程特点,要求同学们做到一些几个环节:1、认真听讲,认真体会,善于思考,勤于总结。
2、学会查阅资料,认真完成作业,要勤于动手,做好每一个实验,认真对待每一个计算步骤。
3、有问题及时提问,及时解决。
参考书1.《数学模型》谭永基复旦大学出版社1997年2.《数学模型》姜启源高等教育出版社2003年3.《数学建模与数学实验》赵静但琦高等教育出版社2000年4.《大学生数学建模竞赛辅导教材》叶其孝湖南教育出版社2003年按学校规定,缺交作业或缺课达1/3者不得参加本课程的考试。
前言1、数学史简介(包括数学建模史)数学,作为一门研究现实世界数量关系和空间形式的科学,它的内容是从实际中抽象出来,与实际想脱离的,但在它生产和发展的历史长河中,一直是和人们生活的实际需要密切相关。
数学具有三大特点:(1)、抽象性(2)、严密性(3)、应用的广泛性数学的任务和发展动力应用是数学的主要任务,也是数学发展的主要动力。
数学的发展阶段数学发展经历了五个主要阶段[1]雅典时期,泰勒斯,毕达哥拉斯开始对命题加以证明(勾股定理,无理数),没留下书籍;亚历山大时期,欧几里德,阿基米德,阿波罗泥,海伦,丢番图等作出了永载史册的功绩。
[2]三次四次方程的求根公式,韦达和符号代数学,三角的发展,小数与对数的发明。
笛卡儿力求用代数的方法来解决几何问题,建立了解析几何,标志着变量数学时期的到来。
[3]牛顿和莱布尼兹创立了微积分,通过微积分的完善建立了分析数学。
数学建模是指用数学的语言和方法对实际问题进行近似地刻划和描述,数学建模并不是中新事物,自从有了数学并用数学去解决问题时,就有了数学建模。
2020年全国大学生数学建模论文规范与模板

全国大学生数学建模竞赛论文格式规范(全国大学生数学建模竞赛组委会,2020年修订稿)为了保证竞赛的公平、公正性,便于竞赛活动的标准化管理,根据评阅工作的实际需要,竞赛要求参赛队分别提交纸质版和电子版论文,特制定本规范。
一、纸质版论文格式规范第一条论文用白色A4纸打印(单面、双面均可);上下左右各留出至少2.5厘米的页边距;从左侧装订。
第二条论文第一页为承诺书,第二页为编号专用页,具体内容见本规范第三、第四页。
第三条论文第三页为摘要专用页。
摘要内容(含标题和关键词,无需翻译成英文)不能超过一页;论文从此页开始编写页码,页码位于页脚中部,用阿拉伯数字从“1”开始连续编号。
第四条论文从第四页开始是正文内容(不要目录,尽量控制在20页以内);正文之后是论文附录(页数不限),附录内容必须打印并与正文装订在一起提交。
第五条论文附录内容应包括支撑材料的文件列表,建模所用到的全部完整、可运行的源程序代码(含EXCEL、SPSS等软件的交互命令)等。
如果缺少必要的源程序、程序不能运行或运行结果与论文不符,都可能会被取消评奖资格。
如果确实没有用到程序,应在论文附录中明确说明“本论文没有用到程序”。
第六条论文正文和附录中任何地方都不能有显示参赛者身份和所在学校及赛区的信息。
第七条所有引用他人或公开资料(包括网上资料)的成果必须按照科技论文的规范列出参考文献,并在正文引用处予以标注。
第八条本规范中未作规定的,如论文的字号、字体、行距、颜色等不做统一要求。
在不违反本规范的前提下,各赛区可以对论文做相应的要求。
二、电子版论文格式规范第九条参赛队应按照《全国大学生数学建模竞赛报名和参赛须知》的要求提交参赛论文和支撑材料两个电子文件。
第十条参赛论文电子版内容必须与纸质版内容及格式(包括附录)完全一致;必须是一个单独的文件,文件格式为PDF或者Word格式之一(建议使用PDF格式);文件大小不超过20MB。
注意参赛论文电子版文件不要压缩,承诺书和编号专用页不要放在电子版论文中,即电子版论文的第一页必须为摘要页。
数学建模竞赛论文的撰写及Word排版

用了目标规划与粒子群算法进行配时优化的模型[1]
3.问题分析
切忌:问题分析中不要讲述问题的解法, 关键是分析问题本身(包括问题间的联系)。 问题分析一般不要超过一页半,最好能够控 制在一页。
3. 摘要和正文中行距最好使用1.25倍行距,摘要行距视情况而 定,如果摘要篇幅过长,可使用单倍行距;
4. 摘要中的特殊符号最好使用Mathtype编辑;
5. 摘要和正文中插入公式后行距可能会发生变化,这种情况下 除了调整公式大小外,还可以尝试如下操作:点击鼠标右键 >>段落>>点击如果定义了文档网格,则对齐到网格,这种方 法相当奏效;
[编号] 作者.书名[M].出版地:出版社,出版年.
[2]高昆(原著),韩汝琦(改编).固体物理学[M].北京:高等教育出版社,1988.
•期刊杂志论文的表述方式为:
[编号] 作者.论文名[J].期刊名,出版年,卷(期):起止页码.
• 正文[3]引陈宗用胜.中处国用居民方收入括分配号差表别的示深入参研究考[J].文经济献研究的,20编00, 6号(8):68-72. 如[1][2],排队论[1] 、随机数的选取[2]
• 对于正文中用到的符号给出说明,可以用表格的形式 给出
5.模型的建立
(1) 模型: (2)模型要实用,有效,有特色,以解决问
题有效为原则 (3)鼓励创新,但要切实,不要离题搞标新
立异 (4)在问题分析推导过程中,需要注意的问
题:
(1) 模型:
• 基本模型:要求完整,正确,简明 • 简化后模型:尽可能完整给出,要明
6. 关键词与上文空2~3行,关键词3~5个为宜,逗号隔开。
数学建模论文写作论文写作——word排版使用

论文写作——word使用论文是建模中最后的一环也是最关键的一环,这环做好了那就圆满了,做砸了全功尽弃了。
关于怎么写论文已经有很多文章介绍了,这就足以可见写论文的重要性了。
下面我就结合我们的几次比赛,就写作分享一下自己的经验.先介绍下写论文的工具,或许很多朋友要纳闷了,写论文什么工具,不就是电脑呗,还有朋友会进一步说用word呗,两者都对,当然用电脑的这个说法绝对正确,如果说是用手那更对了,呵呵,其实偶指的工具是软件,由于各方面的原因,大家主要还是用Word编辑论文。
Word在写科技论文方面虽然有一些先天不足,但却提供了非常强大的功能。
如果不能充分利用这些功能,可能经常要为不断地调整格式而烦恼。
我把自己以前使用Word的经验和教训总结一下,抛块砖。
原则:内容与表现分离。
一篇论文应该包括两个层次的含义:内容与表现,前者是指文章作者用来表达自己思想的文字、图片、表格、公式及整个文章的章节段落结构等,而后者则是指论文页面大小、边距、各种字体、字号等。
相同的内容可以有不同的表现,例如一篇文章在不同的出版社出版会有不同的表现;而不同的内容可以使用相同的表现,例如一个期刊上发表的所有文章的表现都是相同的。
这两者的关系不言自明。
在排版软件普及之前,作者只需关心文章的内容,文章表现则由出版社的排版工人完成,当然他们之间会有一定交互。
Word倡导一种所见即所得(WYSIWYG)的方式,将编辑和排版集成在一起,使得作者在处理内容的同时就可以设置并立即看到其表现。
可惜的是很多作者滥用WYSIWYG,将内容与表现混杂在一起,花费了大量的时间在人工排版上,然而效率和效果都很差。
本文所强调的“内容与表现分离”的原则就是说文章作者只要关心文章的内容,所有与内容无关的排版工作都交给Word去完成,作者只需将自己的排版意图以适当的方式告诉Word。
因为Word不仅仅是一个编辑器,还是一个排版软件,不要只拿它当记事本或写字板用。
主要建议如下。
(完整word版)数学建模——人员安排问题(word文档良心出品)
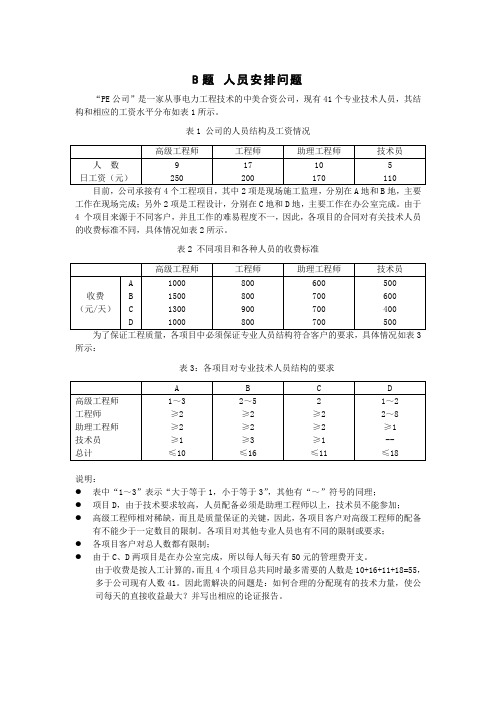
B题人员安排问题“PE公司”是一家从事电力工程技术的中美合资公司,现有41个专业技术人员,其结构和相应的工资水平分布如表1所示。
表1 公司的人员结构及工资情况目前,公司承接有4个工程项目,其中2项是现场施工监理,分别在A地和B地,主要工作在现场完成;另外2项是工程设计,分别在C地和D地,主要工作在办公室完成。
由于4 个项目来源于不同客户,并且工作的难易程度不一,因此,各项目的合同对有关技术人员的收费标准不同,具体情况如表2所示。
表2 不同项目和各种人员的收费标准为了保证工程质量,各项目中必须保证专业人员结构符合客户的要求,具体情况如表3 所示:表3:各项目对专业技术人员结构的要求说明:●表中“1~3”表示“大于等于1,小于等于3”,其他有“~”符号的同理;●项目D,由于技术要求较高,人员配备必须是助理工程师以上,技术员不能参加;●高级工程师相对稀缺,而且是质量保证的关键,因此,各项目客户对高级工程师的配备有不能少于一定数目的限制。
各项目对其他专业人员也有不同的限制或要求;●各项目客户对总人数都有限制;●由于C、D两项目是在办公室完成,所以每人每天有50元的管理费开支。
由于收费是按人工计算的,而且4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41。
因此需解决的问题是:如何合理的分配现有的技术力量,使公司每天的直接收益最大?并写出相应的论证报告。
问题重述:本问题是人事安排,在满足客户要求,和公司人员结构的前提下,公司获得最大利润问题,即: 4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41。
因此需解决的问题是:如何合理的分配现有的技术力量,使公司每天的直接收益最大?要建立模型:1,客户要求:不同工种的人数,见表3. 2,公司人员结构:见表1.3,不同项目,和各种人员收费标准:见表2.建立最佳收益模型f(x)max,并列出不同项目的人员结构.模型假设:假设四个项目同时开始,并且同时结束,所有人都工作.同等级别的人的能力一样. C 、D 项开支由公司支付。
数学建模-论文字体字号规格样式
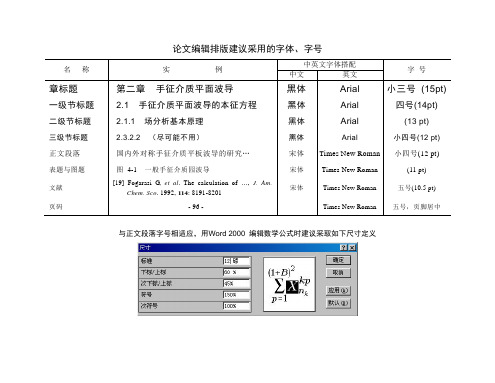
名称
实例
中英文字体搭配
字号
中文
英文
章标题
第二章手征介质平面波导
黑体
Arial
小三号(15pt)
一级节标题
2.1手征介质平面波导的本征方程
黑体
Arial
四号(14pt)
二级节标题
2.1.1场分析基本原理
黑体Байду номын сангаас
Arial
(13 pt)
三级节标题
2.3.2.2(尽可能不用)
黑体
Arial
小四号(12 pt)
正文段落
国内外对称手征介质平板波导的研究…
宋体
Times New Roman
小四号(12 pt)
表题与图题
图4-1一般手征介质园波导
宋体
Times New Roman
(11 pt)
文献
[19]Fogarasi G,et al. The calculation of,J. Am. Chem. Sco. 1992,114: 8191-8201
宋体
Times New Roman
五号(10.5 pt)
页码
- 96 -
Times New Roman
五号,页脚居中
与正文段落字号相适应,用Word 2000编辑数学公式时建议采取如下尺寸定义
mworks建模流程

mworks建模流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 问题定义与分析明确建模的目标和问题。
确定系统的边界和输入输出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模竞赛利用好Word教程
花一天时间学好Word排版,绝对是一劳永逸的事。
Word不是最重要的,但绝对是影响建模表达、写作效率和修改方便性的关键。
所有与内容无关的排版工作都交给Word去完成吧。
记得初识数模时,Word曾让下天同志郁闷了半个夏天;后来参加了几次大赛,自以为Word 用得还可以,结果毕业设计时经高人提点,发现Word竟可以这样用。
好东西当然要大家一起分享,现介绍***(网上down的,未能核实真身)的大作如下,以抛砖引玉:
用Word编辑论文的几个建议由于各方面的原因,大家主要还是用Microsoft Word (以下简称Word)编辑论文。
Word在写科技论文方面虽然有一些先天不足,但却提供了非常强大的功能。
如果不能充分利用这些功能,可能经常要为不断地调整格式而烦恼。
我把自己以前使用Word的经验和教训总结一下,抛块砖。
原则: 内容与表现分离
一篇论文应该包括两个层次的含义:内容与表现,前者是指文章作者用来表达自己思想的文字、图片、表格、公式及整个文章的章节段落结构等,而后者则是指论文页面大小、边距、各种字体、字号等。
相同的内容可以有不同的表现,例如一篇文章在不同的出版社出版会有不同的表现;而不同的内容可以使用相同的表现,例如一个期刊上发表的所有文章的表现都是相同的。
这两者的关系不言自明。
在排版软件普及之前,作者只需关心文章的内容,文章表现则由出版社的排版工人完成,当然他们之间会有一定交互。
Word倡导一种所见即所得(WYSIWYG)的方式,将编辑和排版集成在一起,使得作者在处理内容的同时就可以设置并立即看到其表现。
可惜的是很多作者滥用WYSIWYG,将内容与表现混杂在一起,花费了大量的时间在人工排版上,然而效率和效果都很差。
本文所强调的“内容与表现分离”的原则就是说文章作者只要关心文章的内容,所有与内容无关的排版工作都交给Word去完成,作者只需将自己的排版意图以适当的方式告诉Word。
因为Word不仅仅是一个编辑器,还是一个排版软件,不要只拿它当记事本或写字板用。
主要建议如下。
1. 一定要使用样式,除了Word原先所提供的标题、正文等样式外,还可以自定义样式。
如果你发现自己是用选中文字然后用格式栏来设定格式的,一定要注意,想想其他地方是否需要相同的格式,如果是的话,最好就定义一个样式。
对于相同排版表现的内容一定要坚持使用统一的样式。
这样做能大大减少工作量和出错机会,如果要对排版格式(文档表现)做调整,只需一次性修改相关样式即可。
使用样式的另一个好处是可以由Word自动生成各种目录和索引。
2. 一定不要自己敲编号,一定要使用交叉引用。
如果你发现自己打了编号,一定要小心,这极可能给你文章的修改带来无穷的后患。
标题的编号可以通过设置标题样式来实现,表格和图形的编号通过设置题注的编号来完成。
在写“参见第x章、如图x所示”等字样时,不要自己敲编号,应使用交叉引用。
这样做以后,当插入或删除新的内容时,所有的编号和引用都将自动更新,无需人力维护。
并且可以自动生成图、表目录。
公式的编号虽然也可以通过题注来完成,但我另有建议,见5。
3. 一定不要自己敲空格来达到对齐的目的。
只有英文单词间才会有空格,中文文档没有空格。
所有的对齐都应该利用标尺、制表位、对齐方式和段落的缩进等来进行。
如果发现自己打了空格,一定要谨慎,想想是否可以通过其他方法来避免。
同理,一定不要敲回车来调整段落的间距。
4. 绘图。
统计图建议使用Execel生成,框图和流程图建议使用Visio画。
如果不能忍受Visio对象复制到Word的速度,还可以试试SmardDraw,功能不比Visio弱,使用不比Visio 难,速度却快多了。
如果使用Word的绘图工具绘图,最好以插入Word图片的方式,并适当使用组合。
5. 编辑数学公式建议使用 MathType5.0,其实Word集成的公式编辑器是它的3.0版。
安装MathType后,Word会增加一个菜单项,其功能一目了然。
一定要使用 MathType 的自动编号和引用功能。
这样首先可以有一个良好的对齐,还可以自动更新编号。
Word 正文中插入公式的一个常见问题是把上下行距都撑大了,很不美观,这部分可以通过固定行距来修正。
6. 参考文献的编辑和管理。
如果你在写论文时才想到要整理参考文献,已经太迟了,但总比论文写到参考文献那一页时才去整理要好。
应该养成看文章的同时就整理参考文献的习惯。
手工整理参考文献是很痛苦的,而且很容易出错。
Word没有提供管理参考文献的功能,用插入尾注的方法也很不地道。
我建议使用 Reference Manager,它与Word集成得非常好,提供即写即引用(Citewhile you write,简称Cwyw)的功能。
你所做的只是像填表格一样地输入相关信息,如篇名、作者、年份等在文章中需要引用文献的的方插入标记,它会为你生成非常美观和专业的参考文献列表,并且对参考文献的引用编号也是自动生成和更新的。
这除了可以保持格式上的一致、规范,减少出错机会外,更可以避免正文中对参考文献的引用和参考文献列表之间的不匹配。
并且从长远来说,本次输入的参考文献信息可以在今后重复利用,从而一劳永逸。
类似软件还有Endnote和Biblioscape。
Endnote优点在于可以将文献列表导出到BibTeX格式,但功能没有ReferenceManager强大。
可惜这两个软件都不支持中文,据说Biblioscape对中文支持的很好,我没有用过,就不加评论了。
7.使用节。
如果希望在一片文档里得到不同的页眉、页脚、页码格式,可以插入分节符,并设置当前节的格式与上一节不同。
上述7点都是关于排版的建议,还是要强调一遍,作者关心的重点是文章的内容,文章的表现就交给Word去处理。
如果你发现自己正在做与文章内容无关的繁琐的排版工作,一定要停下来学一下Word的帮助,因为Word 早已提供了足够强大的功能。
我不怀疑Word的功能,但不相信其可靠性和稳定性,经常遇到“所想非所见”、“所见非所得”的情况让人非常郁闷。
如果养成良好的习惯,这些情况也可以尽量避免,即使遇上,也可以将损失降低到最低限度。
建议如下:
8.使用子文档。
学位论文至少要几十页,且包括大量的图片、公式、表格,比较庞大。
如果所有的内容都保存在一个文件里,打开、保存、关闭都需要很长的时间,且不保险。
建议论文的每一章保存到一个子文档,而在主控文档中设置样式。
这样每个文件小了,编辑速度快,而且就算文档损坏,也只有一章的损失,不至于全军覆灭。
建议先建主控文档,从主控文档中创建子文档,个人感觉比先写子文档再插入到主控文档要好。
9.及时保存,设置自动保存,还有一有空就ctrl+s。
10.多做备份,不但Word不可靠,windows也不可靠,每天的工作都要有备份才好。
注意分清版本,不要搞混了。
Word提供了版本管理的功能,将一个文档的各个版本保存到一个文件里,并提供比较合并等功能。
不过保存几个版本后文件就大得不得了,而且一个文件损坏后所有的版本都没了,个人感觉不实用。
还是多处备份吧
11.插入的图片、和公式最好单独保存到文件里另做备份。
否则,哪天打文档时发现自己辛辛苦苦的编辑的图片和公式都变成了大红叉,哭都来不及了。
其他建议:
12. 使用大纲视图写文章的提纲,调整章节顺序比较方便
13. 使用文档结构图让你方便的定位章节
14. 使用文档保护,方便文章的审阅和修改
15. Word表格的排序、公式和转换的功能也是很值得学习的上面的建议并不全面,但相信比较管用。
如果还有疑问,自己花些时间研究一下Word的帮助,相信会有事半功倍的效果。
建议数模小组事先为本组的数模论文建立一个适合本组写作风格的模板,第一次可能会累一点,以后就只需套用模板,建模效率提高不少哦另外,大力推荐上文中Word自定义样式、交叉引用、分隔符等功能的使用;子文档就不必了,因为数模论文一般不长,不会超过20页;至于编辑公式是MathType5.0还是EQNEDIT好,见仁见智吧,用了就知道了。
当然,以上只是建议,使用与否,大家视情况而定,希望能有所帮助。
