连续介质力学习题二

合集下载

连续介质力学

1. 推导（2.8.10）后两式第二式：T T Xi F F G g G g G g G g g g F l kkK kK k KK T T ki k K k K j K K K j x x t t X X tv x v X X x <><><>>>⎛⎫⎛⎫∂∂∂∂∂⎛⎫⎪==⊗=⊗ ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎪⎝⎭⎝⎭⎛⎫⎛⎫∂∂∂=⊗=⊗⊗= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭（1）或Tl F FT-T>>><<>=得到0TT Tl F F F F F F T-T-T-T>>><<>><<>><<>===+ （2）⇒TTF F F FT -T<><>><<>=- （3）（我这一步得到的和书上有点差别，为什么呢？）第三式：由（1）、（3）得到TT F F F F F lT -TT T<><>><<><>>>=-=由（2）、（3）得到TTTFF F Fl F-T-T T ><><<>><>>><--=-=-2.推导（2.8.16）后两式第三式： d d d d d div d v VvVv v=∴===v J J J J第四式：d d Tv FA ><><-= Jd d d TTvF A F A ><><><<--∴=+J J(这步最右式和书上的也不同)d d d div d d tr d d T T T T TTv F A F A F A F A d F A FA ><><><><><<<<----><><>><<--⎛⎫⎛⎫ ⎪ ⎪∴=+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫ ⎪=+ ⎪ ⎪⎝⎭ ⎪⎝⎭v J J J J JT tr tr TTd l Fl F><>>><>>>>--⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭,（2.8.10）T d tr d d T T v l F A l F A ><>>><>>><<--⎛⎫⎛⎫∴=- ⎪ ⎪⎝⎭⎝⎭J3．证明第二单元章后习题变形基本定理：FV R R U ==R 为转动张量，且是正交张量T V R U R ⇒=U V ⇒、互为正交相似矩阵，因而有相同的特征值记,k K k k k k UN N V n n λλ=⊗=⊗T V R U R =k k k ij i j K k k i j ji R R n n e e N N e e λλ⇒⊗=⊗⊗⊗令k ij i j K k R n e e N λ=⊗证得k k n R N =4．简要说明四类应力的共同点和差异点（1）Cauchy 应力张量，kirchhoff 应力张量，第二类P-K 应力都是对称张量，而第一类P-K 应力无所谓对称性。

《连续体力学》习题及解答2_工学_高等教育_教育专区.doc

2二阶张量及其若干运算法则（一）概念.理论和公式提要2-1张量的乘法① 张量的外乘（并乘）张量的外乘用0表示，其外积为张量，其阶数等于外乘诸张量阶数之和。

② 张量的内乘（点乘）张量的点乘用匕”表示（有时也可省去“•” ）, 其内积为张量，其阶数为内乘诸张量阶数之和减去2倍内乘的次数。

③ 张量的双点乘记作“：”（两次点乘），例如A ：B ；其积为张量，其阶数为诸张量阶数之和减2倍点乘次数。

设A 为CT （m ）, B 为CT （〃），C 为CT （p ）, 则A ：B ：C =D 9 D 为 CT （m + 斤 + p - 2 x 4）（2-1-1）取加=4, n = 4, p = 2,则D 为CT （2）,其分量为D a = A ij inn B ,nn r P C r P （2T-2）其中A 分量的后两个指标与B 分量的前两个指标，B 分量的后两个指标与C 分量的询两个指标依次相同O二阶张量T 的范数记为||7|定义为T ：T = 为正方根，且有||T|| > 0,只当T = o 吋才取等号|a r|| = |a|||T||, |a|为标量◎的绝对值 ||r+i?||<||r||+W T ：国聊|・|网 |八忤制问为矢量"的模，/?亦为二阶张量。

⑤ 设A 和B 分是是CT0）和CT （" 则4和B 外积的s 次缩拼为张量C ,记为C S A®B = CC 为O + / - 25）阶张量，其分量关系为(2-1-3) (2-1-4)(2-1-5)(2-1-6)(2-1-7)C ij …mn — Aj ……k$B k'kfks. 反Z,如果已知B 和C 为张量，其分量与带指标的量务•满足上式，则务•为张量A 的分量，称为商法则或张量识别定理。

A 的阶数等于C 的阶数加减去 B 的阶数。

特别地当s = t, B 的分量的全部指标都是哑标时，则A 的阶数等于B 和c 的阶数Z 和。

流体力学第1、2、3、4章课后习题答案

第一章习题答案选择题（单选题）1.1按连续介质的概念，流体质点是指：（ d ）（ a ）流体的分子；（ b ）流体内的固体颗粒；（ c ）几何的点；（ d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

1.2作用于流体的质量力包括：（ c ）（ a ）压力；（b ）摩擦阻力；（ c ）重力；（ d ）表面张力。

1.3 单位质量力的国际单位是：（ d ）（ a ） N ；（ b ） Pa ；（ c ） N / kg ；（d ） m / s 2 。

1.4与牛顿内摩擦定律直接有关的因素是：（ b ）（ a ）剪应力和压强；（ b ）剪应力和剪应变率；（ c ）剪应力和剪应变；（ d ）剪应力和流速。

1.5 水的动力黏度 μ 随温度的升高：（ b ）（ a ）增大；（b ）减小；（ c ）不变；（ d ）不定。

1.6 流体运动黏度的国际单位是：（ a ）222（ a ）） N / m ；（）；（） N s/ m 。

bc kg / m d1.7 无黏性流体的特征是：（ c ）（ a ）黏度是常数；（ b ）不可压缩；（c ）无黏性；（ d ）符合pRT 。

1.8 当水的压强增加 1 个大气压时，水的密度增大约为：（ a ）（ a ） 1/20000；（ b ） 1/10000；（ c ） 1/4000 ；（ d ） 1/2000。

1.9 水的密度为 1000 kg/m 3 ，2L 水的质量和重量是多少？解：m V 1000 （ kg ）0. 002Gmg2 9.80719.614 （ N ）答： 2L 水的质量是 2 kg ，重量是 19.614N 。

1.10 体积为 0.5 m 3的油料，重量为 4410N ，试求该油料的密度是多少？解：m G g 4 4 1 0 9 . 8 0879 9 . 3 （58kg/m 3）V V0 . 5答：该油料的密度是899.358 kg/m 3。

大连理工研究生连续介质力学作业题

f = xT Ax ， grad（f ）= ∂x T Ax = 2Ax ∂x
f ′ = (RT x′)T ART x′ = x′T RART x′
grad(f' ) = ∂x′TRART x′ = 2RART x′ ∂x′
= 2RA(RT x′) = 2RAx = R ⋅ 2Ax = R ⋅ grad(f)
（3） a1 = p, a 2 = q, a3 = r
⎡2 0 1⎤ 由[gij ] = ⎢⎢0 4 2⎥⎥
⎢⎣1 2 2⎥⎦ 及 ai = gij a j 得 a1 = 2 p+ r, a2 = 4 q+ 2 r, a3 = p+ 2 q+ 2 r
1
2. 已知笛卡尔坐标系 e1 , e3 , e3 ，一个新的坐标系定义为
2 3
x2'
+
2 3
x2'
−
4 3
x2'
+
2 3 x3' 4 3 x3' 2 3 x3'
⎫ ⎪ ⎪⎪ ⎬ ⎪ ⎪ ⎪⎭
= grad（f ′）
3
3.
二维情况下，一质点应力张量 σ 主值 λ1σ = 1.6 ， λσ2 = 2.3 。主方向 N1 =
3 2
e1
−
1 2
e2
，
N2
=
1 2 e1
+
3 2
e
（2）求向量 x 参考新坐标系的表示形式 x = xi′ ei′ （3）求函数 f 在新的坐标系下的表达形式 f ′(x1′ , x2′ , x3′ ) （4）判断 grad（f ）的客观性。
¾ 解答：
（1） grad（f ）＝ (2 x1 , 0, − 2 x3 )T

连续介质力学-2d

度
23
量
H
=
1 2
ln(I
+
2E)
=
ln(I
+
E工 )
=
1 2
(2E
−
1 2
(2E)2
+
1 (2E)3 3
− ...)
=
E工
−
1 2
E工2
+
1 3
E工3
−
...
Green应变,工程应变和对数应变张量之间的关系
18
第二
同理, 对参考构形中随体坐标系{ xi, t0 }变形状态的描
章述还可定义工程应变张量 e工和对数应变张量 h ：
(C AB
− GAB )
(2.69)
应
称为Green应变张量
变
度量
Green应变张量 E 是对当前构形中随体坐标系
{ XA, t }的变形状态描述,称为空间应变张量。
—
E的主方向：Lα ,α = 1,2,3
E的主值：
1 2
( λ α2
− 1), α
= 1,2,3
14
第二章
任取变形前在参考构形R中的单位矢量 L ，记
L ⋅ E ⋅ L 为Green应变张量在 L方向的法分量：
变形和运
∴L ⋅ E ⋅ L = 1 (L ⋅C ⋅ L − L ⋅ I ⋅ L) 2
=
1 2
(λ2L
−1)
=
ds2 − dS 2dS 2
2
(2.70)
动
2.考虑{ xi, t0 }
{xi} 线元长度的改变(E描述)：
—
应 ds2 − dS 2 = dx ⋅ i ⋅ dx − dx ⋅ c ⋅ dx = dx ⋅ (i − c) ⋅ dx

张量分析——精选推荐

《连续介质力学》例题和习题第一张、矢量和张量分析第一节矢量与张量代数一、矢量代数令 11223A A A =++A e e e 112233B B B =++B e e e 则有 11223A A A αααα=++A e e e 11122233()()()A B A B A B +=+++++A B e ee 1122331122331122()()A A A B B B A B A B A B ∙=++∙++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e 又因为 11⨯=e e 0 123⨯=e e e 132⨯=-e e e 213⨯=-e e e 22⨯=e e 0 231⨯=e e e 312⨯=e e e 321⨯=-e e e 33⨯=e e 0则 2332131132122(_)()()A B A B A B A B A B A B⨯=+-+-A B e e e习题1、证明下列恒等式：1）[]2()()()()⨯∙⨯⨯⨯=∙⨯A B B C C A A B C2) [][]()()()()⨯∙⨯=∙⨯-∙⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 单位为正交的基矢量。

*补充知识：矩阵及矩阵运算1、定义：[]()111213212223313233,1,2,3ij A A A A A A A i j A AA ⎡⎤⎢⎥⎡⎤===⎣⎦⎢⎥⎢⎥⎣⎦A i 表示行，j 表示列；m 和n 相等表示为方阵，称为m （或n ）阶矩阵。

连续介质力学-例题与习题

《连续介质力学》例题和习题第一章矢量和张量分析第一节矢量与张量代数一、矢量代数令112233A A A =++A e e e ,112233B B B =++B e e e ,则有112233A A A αααα=++A e e e111222333()()()A B A B A B +=+++++A B e e e112233112233112233()()A A A B B B A B A B A B •=++•++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为: 11⨯=e e 0;123⨯=e e e ;132⨯=-e e e ;213⨯=-e e e ;22⨯=e e 0;231⨯=e e e ; 312⨯=e e e ;321⨯=-e e e ;33⨯=e e 0则: 233213113212213(_)()()A B A B A B A B A B A B ⨯=+-+-A B e e e 习题:1、证明下列恒等式：1）[]2()()()()⨯•⨯⨯⨯=•⨯A B B C C A A B C2) [][]()()()()⨯•⨯=•⨯-•⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 为单位正交基矢量。

3、试判断[]816549782-⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 是否有逆矩阵；如有，请求出其逆阵[]1-A 。

二、张量代数例1：令T 是一个张量，其使得矢量a ，b 经其变换后变为2=+Ta a b ，=-Tb a b ，假定一个矢量2=+c a b ，求Tc 。

连续介质力学习题二答案

连续介质力学习题二答案连续介质力学是力学中的一个重要分支，研究的是连续介质的宏观性质和行为。

在学习连续介质力学的过程中，习题是不可或缺的一部分。

下面将为大家提供一些连续介质力学习题的答案，希望能对大家的学习有所帮助。

1. 一个均匀的弹性杆，长度为L，横截面积为A，杨氏模量为E。

如果在杆的一端施加一个拉力F，另一端固定，求杆的伸长量。

解答：根据胡克定律，弹性杆的伸长量与施加的拉力成正比。

所以，伸长量可以用下面的公式表示：ΔL = (F * L) / (A * E)其中，ΔL表示伸长量，F表示施加的拉力，L表示杆的长度，A表示横截面积，E表示杨氏模量。

2. 一个圆柱形的液体容器，底面半径为R，高度为H。

如果在容器的底部施加一个压力P，求液体容器内部的压强分布。

解答：液体容器内部的压强分布可以用下面的公式表示：P(z) = P + ρ * g * z其中，P(z)表示液体容器内部距离底部高度为z处的压强，P表示底部施加的压力，ρ表示液体的密度，g表示重力加速度。

3. 一个均匀的弹性球体，半径为R，杨氏模量为E。

如果在球体的表面施加一个压力P，求球体的压缩量。

解答：根据胡克定律，弹性球体的压缩量与施加的压力成正比。

所以，压缩量可以用下面的公式表示：ΔR = (P * R^3) / (3 * E)其中，ΔR表示压缩量，P表示施加的压力，R表示球体的半径，E表示杨氏模量。

4. 一个均匀的弹性体，体积为V，体积弹性模量为K。

如果在弹性体的体积上施加一个压力P，求弹性体的体积变化量。

解答：弹性体的体积变化量可以用下面的公式表示：ΔV = -(P * V) / K其中，ΔV表示体积变化量，P表示施加的压力，V表示弹性体的体积，K表示体积弹性模量。

以上是一些连续介质力学习题的答案，希望对大家的学习有所帮助。

在学习连续介质力学的过程中，多做习题是非常重要的，通过解答习题可以加深对理论知识的理解和运用。

同时，也希望大家能够在学习中保持耐心和积极性，相信通过不断的努力，一定能够掌握连续介质力学的知识。

连续介质力学习题二

连续介质力学习题二二．变形与运动2-1 如果物体在运动过程中保持任意两点间的距离不变，则称这样的运动为刚体运动，试证：物体的运动若为刚体运动，则参考构形中的物质点X变换到当前构形中的空间位置x时，必满足：)()()(t a A X t Q x +-⋅=，其中)(t Q 为正常正交仿射量。

2-2 现取物质坐标系}{A X 和空间坐标系}{i x 为同一个直角坐标系，其单位基向量为),,(321e e e，有一物体的变形为：33222011,,X x X x X k X x ==+=，试写出以下各量：1）变形梯度张量F 和变形梯度张量之逆1-F ；2）右，左Cauchy-Green 张量B C ,；并计算C 和B的三个主不变量；3）写出C 和B的特征方程，并求出三个特征值αη和相应的特征方向αL 和αl)3,2,1(=α。

4）试给出极分解R V F ⋅=中的左伸长张量V 和正交张量R的矩阵表示。

2-3 现取物质坐标系}{A X 为直角坐标系{X ，Y ，Z}，空间坐标系}{i x 为圆柱坐标系},,{z r θ，令z 轴与Z 轴重合，0=θ与X 轴重合，图示长方体发生纯弯曲，题2-3图变形满足),(X r r =),(Y θθ=)(Z z z =，且存在逆关系：),(r X X =，),(θY Y =)(z Z Z =，试写出以下各量：1）变形梯度张量F 和变形梯度张量之逆1-F ；2）右，左Cauchy-Green 张量B C ,；并计算C 和B的三个主不变量；3）写出C 和B的特征方程，并求出三个特征值αη和相应的特征方向αL 和αl)3,2,1(=α。

2-4 现取空间坐标系}{i x 为直角坐标系，其单位基向量为),,(321e e e，有一物体的小变形位移场为3212323213131))(())((e x x e x x x x e x x x x u-+++--=，试求：（1）P （0，2，-1）点的小应变张量e ，小转动张量Ω 及其反偶矢量ω；（2）求P 点在9/)48(321e e e+-=ν方向上的线应变；（3）求P 点在9/)48(321e e e +-=ν和9/)744(321e e e-+=μ二方向上的直角的变化量。

连续介质力学作业(第二章)习题和答案

连续介质力学作业（第二章）参考答案1、初始构型和当前构型的转换关系：21122X X x +=，21222X X x +=，33X x = 其中()321,,X X X 为一个物质点在初始构型上的坐标，()321,,x x x 为同一个物质点在当前构型上的坐标。

参考基是~3~2~1,,e e e 标准正交基求：（1）变形梯度F（2）右Cauchy-Green 变形张量C （3）Green 变形张量E（4）初始构型上一向量~33~22~11~e X e X e X X ++=，变形后在当前构型上是~x ，证明~~~~X C X x x ••=•和()~~~~~~2X E X X X x x ••=•−•（5）左Cauchy-Green 变形张量b （6）Almansi 变形张量A解答：（1）⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛3213211001220221X X X x x x （2）⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=•=100232022310012202211001220221TTF F C（3）()⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=−=000041220224121I C E （4）~33~221~121~2222e X e X X e X X x +⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+=[]~~3213212321222123221221~~100023202232223232222XC X X X X X X X X X X X X X X X X X x x ••=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=+++=+⎟⎟⎠⎞⎜⎜⎝⎛++⎟⎟⎠⎞⎜⎜⎝⎛+=• []()~~321321212221~~~~210002120221222121XE X X X X X X X X X X X X X x x ••=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=++=•−• （5）⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=1001220221F ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡•⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=•=1000232022310012202211001220221TTF F b（6）()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡−−=−=−10005.2220225.2211b I A2、一个连续体内的任意一点，初始时刻坐标为()Y X ,，经过t 时刻后，变为()y x ,，其中：atY X x +=，Y y = ，其中a 是常数。

《连续体力学》习题及解答9

9 塑性物质（一）概念、理论和公式提要9-1 经典塑性理论本章只介绍经典塑性理论和粘塑性本构方程，且都限于小变形情况。

塑性变形是不可逆变形，塑性本构方程是非线性的，属于物理非线性。

经典塑性理论虽有其广泛的应用领域，但在一些情况下，它就显得不足。

例如，对于岩土类物质、粒状物质及高强度钢等力学性能的深入研究，经典塑性理论中的正交法则和塑性体积应变为零等经典假设就不适用；而要研究变形局部化问题，需要从大变形本构模型入手，在大变形条件下，往往伴随材料的损伤，因此在研究从变形到破坏的全过程中，必然要考虑大变形塑性-损伤本构方程等。

经典塑性理论有两个基本假设或基本前提：①在应力(或应变)空间内，存在屈服曲面。

在小变形条件下，屈服曲面可表示为αθεq ij 及，(内变量)的函数，即表示成ααθσθεq q g ij ij ，，；也可表示成，，0)(=的函数，即0)(=αθσq f ij ，，。

在屈服曲面之内，)0(0<<f g 或，状态变化，塑性变形不变化；屈服曲面之上)0(0==f g 或，塑性变形处于可变化的状态，称为弹塑性状态。

②加载过程和卸载过程服从不同的本构关系，加载过程是指塑性变形继续发展的过程，而塑性变形不变化的过程称为卸载过程。

这两个基本假设在轴向拉伸试验中是可以观测到的。

图9-1示一拉伸曲线，包括从任一点B 卸载沿直线到达反向(压缩)屈服点,B 处，此后又呈现曲线变化。

从试验中可观测到下列结果。

EBB AA epeσεεεε=+=，∥''图9-1以上关系仅在变形不大时近似成立。

在''BB AA 和范围内，应力变化与应变化之间遵循εσεσd d E E ==或△△分别称''B B A A 、和、点为初始和相继弹性范围的边界，边界点)()(''B B A A 、和、对应于弹塑性状态。

当应力从B 点向内变化时(卸载过程)，有εσd d E =当应力从C 点沿曲线变化到B 点时(加载过程)有 )d d (d d p e t t E E εεεσ+==由E e σεd d =及上式，易得pp E σεd d =(9-1-1) EE E t p 111-= (9-1-2) 是切线模量，称为塑性模量，t p E E 一般地它们都不是常数。

连续介质力学作业(第一章)答案

连续介质力学作业（第一章）习题1. 向量~~~~k z j y i x a ++=。

~i ，~j ，~k 表示三维空间中标准正交基。

给定一组协变基~~12i g =，~~~2j i g +=，~~~3k j g +=。

（1）求逆变基1g ，2g ，3g 。

（2）求ij g（3）向量~a 参考逆变基~1g ，~2g ，~3g 表示时，~~i i g a a =，求i a 。

（1）[]222~~~~~~~~~3~2~1= +•= +• +×=• ×=k j k k j j i i g g g g+−=+× += ×=~~~~~~~~3~2~121211i j k k j j i g g g g~~~~~~1~3~22211j k i k j g g g g +−= × += ×=~~~~~2~1~32211k j i i g g gg =+×= ×=(2) g ij =gg ii ⋅gg jj �g ij �=�3/4−11/2−12−11/2−11�(3)a i =aa ⋅gg ii a 1=2x,a 2=x +y,a 3=y +z2. 已知笛卡尔坐标系331e e e ,,，一个新的坐标系定义为−−−= ′′′32132161312161312162310e e e e e e 向量321e e e x 321x x x ++=，给定函数2321x x )f(−=x 。

（1）求函数f 的梯度）（f grad（2）求向量x 参考新坐标系的表示形式i ′′=e x i x（3）求函数f 在新的坐标系下的表达形式),,(321′′′′x x x f （4）判断）（f grad 的客观性。

3. 二维情况下，一质点应力张量σ主值6.11=σλ，3.22=σλ。

主方向2112123e e N −=，2122321e e N +=。

流体力学作业题库及答案..

流体⼒学作业题库及答案..第⼀章绪论思考题1- 1何谓流体连续介质模型？含有⽓泡的液体是否适⽤连续介质模型？答：所谓流体的连续介质模型，即把流体视为没有间隙地由流体质点充满它所占据的整个空间的⼀种连续介质其物理性质和物理量也是连续的。

若⽓泡相对于液体⽽⾔可以看作孤⽴的点的话，则含有⽓泡的液体可以适⽤连续介质模型。

习题11-3如题图所⽰，设平⾏板间隙为 0.5mm ，中间充满液体，上板以 U = 0.25m/s 的速度平移，施于单位⾯积的⼒为 2Pa ,试求液体的粘度为多少？解：F A液体粘度1-4求题图所⽰的轴与轴套之间的流体粘度。

解：F duA dy A dLFY dLU第⼆章流体静⼒学习题22-5⽤多管⽔银测压计测压，，题图中标⾼的单位为m ,试求⽔⾯的压强 p o 。

解：P A P 0 ⽔ g(3.0m 1.4m) P A P B 汞 g(2.5m 1.4m) P B P C ⽔ g(2.5m 1.2 m) P C P D汞 g(2.3m1.2m)P D 0 padu U dy Y3FY 20.5 104 10 3Pa sAU 0.250.0648Pa s3.14 (120 140) 100.4932-9 —盛⽔的敞⼝容器作加速运动，试求下列两种情况下容器内静压强的分布规律:(1) P0汞g 2.2m ⽔g52.9m 133416 2.2 9800 2.9 2.65 10 Pa⾃由降落;解：（2）以等加速度a 向上运动。

p P 0(g a si n )h（1）90 ,相对压强P 0P 0（2）90 ,绝对压强P 0 P a P P ah(g a)2- 12试求开启题图所⽰⽔闸闸门所需的单宽拉⼒F 。

不计闸门⾃重及转轴摩擦⼒。

解：闸门所受的单宽静压⼒ F 1b⼀2—9800[3 (3 2)] 1 2 ⼆249.05 10 NF i 作⽤点 y c 匹h12(h1h2)1.25m 3si n60 h(h 1所求拉⼒ F 98.05kNsin602-16试定性绘出题图中各 ABC 曲⾯的压⼒体图。

连续介质力学作业

6
k z
k
r
r

r
j j
i

i

设柱坐标对应 x r , , z ，球坐标对应 X R, , ，则有对应关系：
r R sin z R cos
Jacobi 矩阵为：
sin 0 R cos x xi 1 0 0 X X j cos 0 R sin
这些参数在前面题目中均已求出，不再冗述。 2.13 证明单位张量 I g j gi g gi g g j gij g g g gi g j 。
i j j i i j ij
证明：
I gi g i gij g j g i gij g j g i gij g i g j gi g ij g j g ij gi g j gij g j g il gl gij g il g j gl l j g j gl g i gi

div v v i xi vi xi

vi vi xi xi
divv v
div u v div e u j vk ei
ijk
eijk u j vk xi vk xi vk xi
2 于是， C 的谱表示为： C L L ，其中 L L1 T
L2
2 L3 , L 为对应于的
12 2 特征向量，

2 2
2 3
定义与之对应的唯一对称正定张量 U ，谱表示为：

Tu Tv Tw u v w

连续介质力学2-2

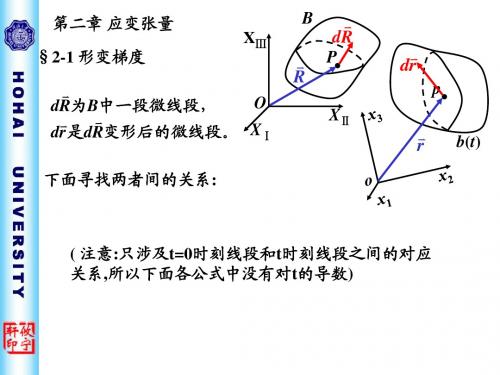
记E IJ
1 x i x j ij IJ 2 X I X J
E IJ
1 x i x j ij IJ 2 X I X J
ˆ 1 x i x j E E E ij IJ I J 2 X I X J
N K N L KL 1
取泛函 N K N K N L E KL 1 KL N K N L
其中Ψ为Lagrange乘子
泛函 N K N K N L E KL 1 KL N K N L
由d dN K d 0 N K
ˆ ˆ U P T diag 1
ˆ 2 3 P

2
ˆ 3 P

ˆ U
1
1 ˆ P diag 1
T
1
2
1 ˆ P 3
ˆ ˆ ˆ R F U 1
例1. 图示二维线元变形 ˆ dx F dX FiK ei E K dX L E L FiK dX K ei
同理:
2 E IJ U I , J U J , I U M , I U M , J 2e ij ui , j u j ,i um ,i um , j
注：U与u是同一个矢量。
讨论：
dr2 dr dr ij dxi dx j
x i x i dX I dX J X I X J
ˆ dr F dR
( 2) dR (1) dR
dr ( 2 )
(1) dr
ˆ 1 FT F I ˆ ˆ ˆ E 2 ˆ T U I ˆ F X

2011年连续介质力学试题

2010—2011学年第 3学期连续介质力学课程期末考试试卷(A卷）2010—2011学年第 3学期连续介质力学课程期末考试试卷（A卷）O Ox x y y2010—2011学年第 3学期连续介质力学课程期末考试试卷（A卷）2010—2011学年第 3学期连续介质力学课程期末考试试卷（A卷）答案及评分标准2010—2011学年第 3学期连续介质力学课程期末考试试卷（A卷）答案及评分标准2、axy y x 622=∂∂=φσ22212ax xy =∂∂=φσ 223ay yx xy-=∂∂∂-=φτ（3分）3ah 23ah 23al 23alh3ah 2xy（4分）五、证明题（本大题25分）1、证明：假想从物体内任意点P 取出一个微分四面体元PABC ，如图。

斜截面ABC 离开O 点一微小距离 h ，它的外法线为 n 。

（2分）设已知作用于截面 PBC ，PAC ，PAB 上的合应力矢量分别为T 1，T 2，T 3，于是，作用于与坐标轴X i 垂直的面元上的合应力矢量i T 可由沿坐标轴方向的分量表示为j ij ie T σ=。

（3分）设面元 ABC 的面积为 dA ，则其余与轴 x j 垂直的各截面的面积为()dA n n x dA dA j j j ==,cos ，这里的n j 是斜截面ABC 的外法线n 的方向余弦。

（2分）根据应力连续性的假设，应力矢量在物体内是连续变化的，作用在截面ABC 上的应力分量的合力为dA T i n；同理作用在PBC ，PCA 与PAB 等截面上的应力分量的合力为dA n j ij σ-，前取负号是因为dA j 的外法线与X j 轴的正方向相反；体力F 的分量为F i hdA/3，其中hdA/3是四面体的体积。

（3分）至此，可以列出四面体的平衡方程：2010—2011学年第 3学期连续介质力学课程期末考试试卷（A卷）答案及评分标准。