建筑力学李前程教材第四章习题解
建筑力学-第4章 平面力系的简化与平衡方程.

平面固定端约束
=
=
≠
=
3、 平面任意力系的简化结果分析
=
FR 0 M O 0
合力
合力作用线过简化中心
FR 0 M O 0
合力
合力作用线距简化中心M O
FR
其中
MO d FR
M o FRd
M o ( FR ) M O M O ( Fi )
FR FR FR
q 20 kN
求: 固定端A处约束力.
, l 1m; F 400kN, m
解: 取T型刚架,画受力图. 1 其中 F1 q 3l 30kN 2 Fx 0 FAx F1 F sin 600 0 解得 FAx 316.4kN
F Ay P F cos 60 0 Fy 0 解得 FAy 300kN
A
M
解得
0
12 FBy 10 P 6 P 1 4P 2 2 P 5F 0
FBy 77.5kN
iy
F
解得
0 FAy FBy 2 P P 1P 2 0
FAy 72.5kN
取吊车梁,画受力图.
M
解得
D
0
8FE' 4P 1 2P 2 0
Fx 0
Fy 0
FAx FB 0
FAy P 1P 2 0
M
解得
A
0
FB 5 1.5 P 1 3.5 P 2 0
FAy 50kN
FB 31kN
FAx 31kN
例4-4 已知: P, q, a, M pa; 求: 支座A、B处的约束力. 解:取AB梁,画受力图.
建筑力学习题及答案1-4
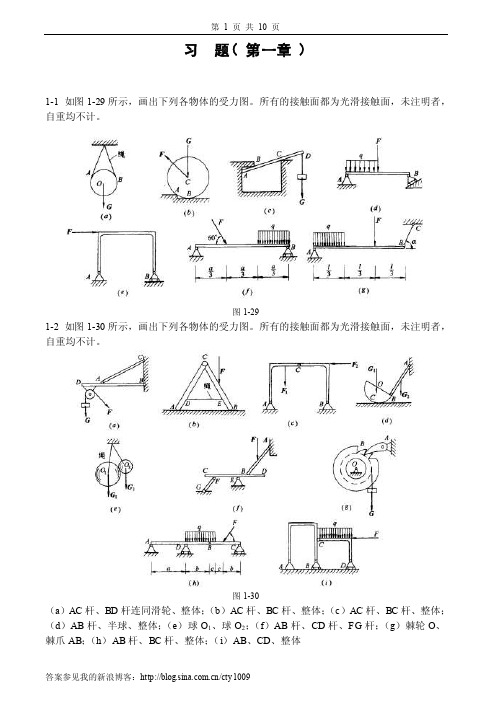
1-1 如图1-29所示,画出下列各物体的受力图。
所有的接触面都为光滑接触面,未注明者,自重均不计。
图1-291-2 如图1-30所示,画出下列各物体的受力图。
所有的接触面都为光滑接触面,未注明者,自重均不计。
图1-30(a)AC杆、BD杆连同滑轮、整体;(b)AC杆、BC杆、整体;(c)AC杆、BC杆、整体;(d)AB杆、半球、整体;(e)球O1、球O2;(f)AB杆、CD杆、FG杆;(g)棘轮O、棘爪AB;(h)AB杆、BC杆、整体;(i)AB、CD、整体2-1 如图2-14所示,四个力作用于O点,设F1=50N,F2=30N,F3=60N,F4=100N。
试分别用几何法和解析法求其合力。
2-2 拖动汽车需要用力F=5kN,若现在改用两个力F1和F2,已知F1与汽车前进方向的夹角α=20o,分别用几何法和解析法求解:(1)若已知另外一个作用力F2与汽车前进方向的夹角β=30o,试确定F1和F2的大小;(2)欲使F2为最小,试确定夹角β及力F1、F2的大小。
图2-14 图2-152-3 支架由杆AB、AC构成,A、B、C三处都是铰链约束。
在A点作用有铅垂力W,用几何法求在图2-16所示两种情况下杆AB、AC所受的力,并说明所受的力是拉力还是压力。
图2-16 图2-172-4 简易起重机如图2-17所示,重物W=100N,设各杆、滑轮、钢丝绳自重不计,摩擦不计,A、B、C三处均为铰链连接。
求杆件AB、AC受到的力。
习题( 第三章 )3-1 计算下列各图中F力对O点之矩。
图3-163-2求图示梁上分布荷载对B点之矩。
图3-173-3 求图示各梁的支座反力。
图3-183-4 如图3-19所示,已知挡土墙重G1=90kN,垂直土压力G2=140kN,水平压力P=100kN,试验算此挡土墙是否会倾覆?3-5 如图3-20所示,工人开启闸门时,常将一根杆穿入手轮中,并在杆的一端C加力,以转动手轮。
设杆长l=1.4m,手轮直径D=0.6m。
建筑力学_Chapter4

其它力系的平衡条件
汇交力系平衡的充分必要条件: 汇交力系平衡的充分必要条件: 空间问题
∑ Fx = 0 ∑ F y = 0, ∑ Fz = 0
平面问题
∑ Fx = 0 , ∑ Fy = 0
力偶系平衡的充分必要条件: 力偶系平衡的充分必要条件:
∑ M x ( F ) = 0 ∑ M y ( F ) = 0, ∑ M z ( F ) = 0
F
重为W 例 :重为 的均质正方形板 (边长a)水平支承在铅垂墙壁 边长a)水平支承在铅垂墙壁 a) 上,求绳1、2的拉力, BC杆 求绳1 的拉力, 杆 的内力和球铰链A的约束力。 的内力和球铰链A的约束力。 解:[板] 受力分析如图 基本方程
z
1 A 2
θ
ϕ
B
y
x
W
F z 1 Fz A
C
F 2
3m 1m
0
P1
P2
x
q=γy A y
3m 1m
解:
P2
水比重 :γ=9.8kN/m3
h
0
P1
y
Q
q=γy A y
dy yc
yQ xR
α
1 2 水合力: 水合力 Q = ∫ qdy = h γ = 314kN 0 2 x h 2 2 水作用点: 水作用点 yC = ∫0 γ y dy/Q = h 3 1 y Q = h = 2.67m 3
θ
∑ Fx = 0 ∑ Fy = 0 ∑ Fz = 0
∑ M x (F ) = 0 ∑ M y (F ) = 0, ∑ M z (F ) = 0
A F Ay
Fx A
ϕ
建筑力学 第四章

O
I A 1 B C 2 D
在体系运动的过程中,瞬铰的位臵随之变 化。 用瞬铰替换对应的两个链杆约束,这种约 束的等效变换只适用于瞬时微小运动。
八、无穷远处的瞬铰
∞
如果用两根平行的链杆把刚片I和基础相连,则其 瞬铰在无穷远处—瞬时平动。 在几何构造分析中应用无穷远瞬铰的概念时,采 用影射几何中关于∞点和∞线的四点结论:
B 1
I II A
2
C
3、对于A点增加两根共线的链杆后,仍然具有1个自由度。 可见在链杆1和2这两个约束中有一个是多余约束。
一般来说,在任一瞬变体系中必然存在多余约束。
七、瞬铰 点O: 瞬时转动中心 此时刚片I 的瞬时运动情况与刚片I在O点 用铰和基础相连的运动情况完全相同。 从瞬时微小运动来看,两根链杆所起的约 束作用相当于在链杆交点处的一个铰所起 的约束作用,这个铰称为 瞬铰(虚铰)
I II A
1 2
I
C
A
II
B
1 B
2 C
两根链杆彼此共线 1、从微小运动的角度看,这是一个可变体系。 左图两圆弧相切,A点可作微小运动; 右图两圆弧相交,A点被完全固定。
B 1
I II A
2
C
2、当A点沿公切线发生微小位移后,两根链杆不再共线, 因而体系就不再是可变体系。 本来是几何可变,经微小位移后又成为几何不变的体系 称为瞬变体系。 可变体系分为瞬变体系和常变体系,如果一个几何可变 体系可以发生大位移,则称为常变体系。
一点在平面内有两个自由度
一个刚片在平面内有三个自 由度
三、自由度
一般来说,如果一个体系有 n 个独立的运动方式,则这 个体系有 n 个自由度。
一个体系的自由度,等于这个体系运动时可以独立改变 的坐标的数目。 普通机械中使用的机构有一个自由度,即只有一种运动 方式; 一般工程结构都是几何不变体系,其自由度为零。 凡是自由度大于零的体系就是几何可变体系。
《建筑力学》第4章计算题

计 算 题( 第四章 )试作图示各杆的轴力图。
图题4. 1图示等截面混凝土的吊柱和立柱,已知横截面面积A 和长度a ,材料的重度γ,受力如图示,其中10F Aa γ=。
试按两种情况作轴力图,并求各段横截面上的应力,⑴不考虑柱的自重;⑵考虑柱的自重。
图题一起重架由100×100mm2 的木杆BC 和直径为30mm 的钢拉杆AB 组成,如图所示。
现起吊一重物WF =40kN 。
求杆AB 和BC 中的正应力。
图题图示钢制阶梯形直杆,各段横截面面积分别为21100mm A =,2280mm A =,23120mm A =,钢材的弹性模量GPa E 200=,试求:(1)各段的轴力,指出最大轴力发生在哪一段,最大应力发生在哪一段;(2)计算杆的总变形;图题4.5 图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm 。
试求F 值。
已知:(E 钢=200GPa ,E 铝=70GPa)。
4.6 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
题图 题图两块钢板用四个铆钉连接,受力kN 4=F 作用,设每个铆钉承担4F 的力,铆钉的直径mm 5=d ,钢板的宽mm 50=b ,厚度mm 1=δ,连接按(a )、(b )两种形式进行,试分别作钢板的轴力图,并求最大应力max σ。
题图用钢索起吊一钢管如图所示,已知钢管重kN10=G F ,钢索的直径mm 40=d ,许用应力[]MPa 10=σ,试校核钢索的强度。
正方形截面的阶梯混凝土柱受力如图示。
设混凝土的320kN m γ=,载荷kN 100=F ,许用应力[]MPa 2=σ。
试根据强度选择截面尺寸a 和b 。
题图 题图图示构架,30=α,在A 点受载荷kN 350=F 作用,杆AB 由两根槽钢构成,杆AC 由一根工字钢构成,钢的许用拉应力[]MPa 160t =σ,许用压应力[]MPa 100c =σ,试为两杆选择型钢号码。
《理论力学》第四章 力系的简化习题解
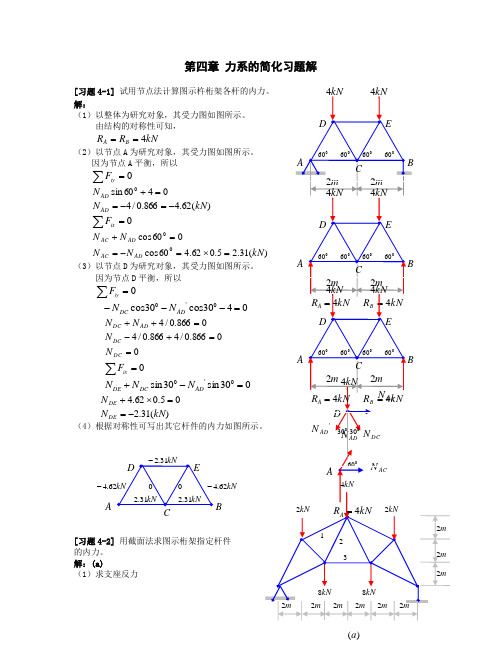
(1)确定悬索的形状
根据对称性,建立如图所示的坐标系。
由公式(4-6)得:
悬索的边界条件为: , , , 。
所以悬索线方程为:
悬索线的斜率:
边界条件:
故悬索线方程为:
(2)求
(3)求最大拉力
由公式 得:
(出现在A、B两点处)。
[习题4-12]输电线之两塔相距 ,塔顶高差 ,垂度 ,电线每米重 ,并假定沿水平跨度均匀分布,求最低点水平拉力及最大拉力。
最大静摩擦力,那 么圆轮水平向右滑动,不
发生滚动。在这种情况下,杆OC的受力图如
图(a)所示。
由OC的平衡条件得:
圆轮的力图如图(b)所示。
由圆轮的平衡条件得:
(2)如果A先达到最大静摩擦力,那么圆轮将
沿地面滚动。此时,
由圆轮的平衡条件得:
(3)如果B先达到最大静摩擦力,那么圆轮将沿OC滚动。此时,
所示。由AB的平衡条件得:
………(1)
………(2)
………(3)
(1)/(2)得:
当物块M靠近B端时,板AB的受力如图(b)
所示。由AB的平衡条件得:
………(a)
………(b)
………(c )
(a)/(b)得:
综合考虑图(a)、(b)两种情况下的 值可知, 的范围是 。
[习题4-22] 攀登电线杆的脚套钩如图所示。设电线杆直径 ,A、B间的铅垂距离为 。若套钩与电线杆之间摩擦因为 ,求工人操作时,为了安全,站在套钩上的最小距离 应为多大?
故悬索线方程为:
…………(3)
(3) 代入(2)得:
当 时, ,即:
。故悬索线方程为:
(2)确定水平力
当 时, ,即:
令
建筑力学第4章习题解答

[习题4-2] 试求图示拉杆1-1、2-2、3-3截面上的轴力,并作出轴力图。
[解题要点]1、分段计算轴力(1)计算CD 段轴力a 、用3-3截面截开CD 段杆件,取右段分析,右段截面上內力用N 3代替,受力图如图(a )。
b 、根据静力平衡条件计算N 1值 ∑F x =0 N 3+2F =0 N 3=-2F(2)计算BC 段轴力a 、用2-2截面截开BC 段杆件,取右段分析,右段截面上內力用N 2代替,受力图如图(b)。
b 、根据静力平衡条件计算N 2值 ∑F x =0 N 2+2F -3F =0 N 2=F (3)计算AB 段轴力a 、用1-1截面截开AB 段杆件,取右段分析,右段截面上內力用N 1代替,受力图如图(c)。
b 、根据静力平衡条件计算N 3值∑F x =0 N 3+2F +3F -3F =0 N 3=-2F 2、 绘制轴力图(图(d ))[习题4-3] 杆件的受力情况如图所示,试绘出轴力图。
[解题要点]1、分段计算轴力 (1)计算DE 段轴力a 、用3-3截面截开DE 段杆件,取右段分析,右段截面上內力用N 3代替,受力图如图(a )。
b 、根据静力平衡条件计算N 1值 ∑F x =0 N 3-40KN =0 N 3=40KN(2)计算CD 段轴力a 、用2-2截面截开CD 段杆件,取右段分析,右段截面上內力用N 2代替,受力图如图(b)。
b 、根据静力平衡条件计算N 2值∑F x =0 N 2+60KN -40KN =0 N 2=-20KN(3)计算AC 段轴力(AB 、BC 段尽管截面不同,但轴力相同) a 、用1-1截面截开AC 段杆件,取右段分析,右段截面上內力用N 1代替,受力图如图(c)。
b 、根据静力平衡条件计算N 3值∑F x =0 N 3+60KN -40KN -80KN =0D C B A 轴力图(a )(b )(c )(d )2F2F F(d )(c )(b )(a )轴力图 (单位:KN )A B C D406020EN 3=60KN2、 绘制轴力图(图(d ))[例4-2]:计算图示杆1-1、2-2截面上的正应力。
【工程力学 课后习题及答案全解】第4章 刚体静力学专题习题解

工程力学(1)习题全解第4章 刚体静力学专题4-1 塔式桁架如图所示,已知载荷F P 和尺寸d 、l 。
试求杆1、2、3的受力。
解:截面法,受力如图(a ) dl=αtan ,22cos dl d +=α0=∑x F ,0cos 2P =−αF FP 222F dd l F +=(拉) 0=∑AM ,02P 1=⋅−l F d FP 12F dlF =(拉)0=∑y F ,0sin 231=++αF F FP 33F dlF −=(压)4-2 图示构件AE 和EQ 铰接在一起做成一个广告牌。
它承受给定的分布风载。
试求解:(1)先将分布载荷合成于E 点88894.2)7.7402963(8.47.740=×−+×=F N由节点C ,显然 F CQ = 0 (1) (2)截面法,图(a )0=∑D M ,08.4538.4=××+×−QG F F ,F QG = 14815 N (拉) (2)0=∑B M ,F QD = 00=∑y F ,054=+×BC QG F F ,11852−=BC F N (压) (3) (3)截面法,图(b )习题4-3图习题4-4图0=∑E M ,08.04.2)7.7402963(212.14.27.7404.253=××−−××−××−AB F2963−=AB F N (压) (4) (4)节点B ,图(c )0=∑y F ,05454=−−′BQ BC AB F F F ,05411852296354=−+×−BQ F F BQ = 11852 N (拉)(5)0=∑x F ,0)(53=++′BE BQ ABF F F ,0)118522963(53=++−BE F ,5333−=BE F N (压) (6) 又 11852−==BC CD F F N (压)(7)4-3 桁架的载荷和尺寸如图所示。
《建筑力学》第4章计算题知识讲解

《建筑力学》第4章计算题计 算 题( 第四章 )4.1 试作图示各杆的轴力图。
图题4. 14.2 图示等截面混凝土的吊柱和立柱,已知横截面面积A 和长度a ,材料的重度γ,受力如图示,其中10F Aa γ=。
试按两种情况作轴力图,并求各段横截面上的应力,⑴不考虑柱的自重;⑵考虑柱的自重。
图题4.24.3 一起重架由100×100mm2 的木杆BC 和 直径为30mm 的钢拉杆AB 组成,如图所示。
现起吊一重物WF =40kN 。
求杆AB 和BC 中的正应力。
图题4.34.4 图示钢制阶梯形直杆,各段横截面面积分别为21100mm A =,2280mm A =,23120mm A =,钢材的弹性模量GPa E 200=,试求:(1)各段的轴力,指出最大轴力发生在哪一段,最大应力发生在哪一段; (2)计算杆的总变形;图题4.44.5 图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm2;下段为 铝制,长300mm ,截面尺寸 为200×200mm 2。
当柱顶受F 力作 用时,柱子总长度减少了0.4mm 。
试求F 值。
已知:(E 钢=200GPa ,E 铝=70GPa)。
4.6 图示等直杆AC ,材料的容重为ρg , 弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
题4.5图 题4.6图4.7 两块钢板用四个铆钉连接,受力kN 4=F 作用,设每个铆钉承担4F 的力,铆钉的直径mm 5=d ,钢板的宽mm 50=b ,厚度mm 1=δ,连接按(a )、(b )两种形式进行,试分别作钢板的轴力图,并求最大应力max σ。
题4.7图4.8 用钢索起吊一钢管如图所示,已知钢管重kN10=G F ,钢索的直径mm 40=d ,许用应力[]MPa 10=σ,试校核钢索的强度。
4.9 正方形截面的阶梯混凝土柱受力如图示。
设混凝土的320kN m γ=,载荷kN 100=F ,许用应力[]MPa 2=σ。
建筑力学课后习题答案,建筑力学课后习题答案李前程

建筑力学课后习题答案,建筑力学课后习题答案李前程《建筑力学》习题集一、单项选择题在下列每小题的四个备选答案中选出一个正确的答案,并将其字母标号填入题干的括号内。
1.三力平衡定理是指()A.共面不平行的三个力若平衡必汇交于一点B.共面三力若平衡,必汇交于一点C.三力汇交于一点,则这三个力必互相平衡D.三力若平衡,必汇交于一点2.光滑面对物体的约束反力,作用点在接触面上,其方向沿接触面的公法线,并且有()A.指向受力物体,为拉力B.指向受力物体,为压力C.背离物体,为压力D.背离物体,为拉力3.两根拉杆的材料、横截面积和受力均相同,而一杆的长度为另一杆长度的两倍。
试比较它们的轴力、横截面上的正应力、轴向正应变和轴向变形。
正确的是()A.两杆的轴力、正应力、正应变和轴向变形都相同B.两杆的轴力、正应力相同,而长杆的正应变和轴向变形较短杆的大C.两杆的轴力、正应力和正应变都相同,而长杆的轴向变形较短杆的大D.两杆的轴力相同,而长杆的正应力、正应变和轴向变形都较短杆的大4.圆轴扭转时,若已知轴的直径为d,所受扭矩为T,试问轴内的最大剪应力τma x和最大正应力σmax各为()A.τmax=16T/(πd),σmax=0B.τmax=32T/(πd),σmax=0C.τmax=16T/(πd),σmax=32T/(πd)D.τmax=16T/(πd),σmax=16T/(πd)5.梁受力如图示,则其最大弯曲正应力公式:σmax=Mymax/Iz中,ymax为()333333A.dB.(D-d)/2C.DD.D/26.工程中一般是以哪个指标来区分塑性材料和脆性材料的()A.弹性模量B.强度极限C.比例极限D.延伸率7.一悬臂梁及其所在坐标系如图所示。
其自由端的()A.挠度为正,转角为负C.挠度和转角都为正B.挠度为负,转角为正D.挠度和转角都为负8.梁的横截面是由一个圆形中央去除一个正方形而形成的,梁承受竖直方向上的载荷而产生平面弯曲。
建筑力学(第四章)

Da a
Fx 0 :
FAx FCcon45 0
FAx FCcon45
2F
2 2
F
FAx
A
M0=Fa
C
FAy FC
B F
Fy 0 : FAy FC sin 45 F 0
FAy FC sin 45 F
2F
2 2
F
第二节 平面一般力系向作用面内任一点简化
简化中心 F1
OA
F3 C
B
F2 =
m1F'1′ F′3 O
m2
F'2′ =
m3
M0 O
FR
主矢(FR’ ):将平面汇交力系 (F1’、F2’、 F3’ )合成, 可得一合力FR’,这个力称为原力系的主矢。通过0点。
大小:
FR ( Fx)2 ( Fy)2 ( Fx )2 ( Fy )2
0
aa
负号说明约束反力FAX的实际方向与图中
假定方向相反。
应用举例
例4-4:求图示梁支座的
y
F
F
约束反力。已知 :
Fy
F 2kN a 2m A
解:取梁为研究对象。
Fx
受力图如图示。建立坐标
a
a
FB
Bx
a
系,列平衡方程:
Fx 0 Fy 0
M
O
(
F
)
0
(2) 主矢、主矩均不为零 FR≠0 M0≠0 根据力的平移定理的逆过程可知,主矢FR和主矩MO也可
以合成为一个 合力FR。
材料力学习题解答[第四章]
![材料力学习题解答[第四章]](https://img.taocdn.com/s3/m/989c254a336c1eb91a375dfd.png)
材料力学(周建方版本)习题解答第四章 变形计算4-1 解:(一)绘制轴力图 (二)计算:4-2 解4-3 解(一)求反力(二)根据条件求解4-4解,如图伸长)(5)10002100010002(100102001020)22(33321mm l l l EAF EAl F l i Ni =⨯++⨯⨯⨯⨯=++==Λ∑mmmm EA l F l ii Ni 1625.010625.11025.11075.3102010150250101520201015015010151123333=⨯=⨯+⨯==⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯==∆---∑l x l F F AB )(-=lx FF CD =lx xx l r r A A F F A E l F A E l F l l CA C A C A C C C C AA A A CDAB 544122=-====∆=∆则:即:⎰⎰⎰⎰⎰==-==∆=∆∴==-=-=-==∆llA B llllB EAWl EAqldx x l EAq x EA dx x N l EAWl l Wql EAqlxl EAq dx x l EAq EA qdxx l x EA dx x N l 8383)()()(2]2[)()()()(222224-5(b )4-5(c )EAql CC BB B EAql CC EAql EAl ql CD qll l q l F M DC DCA22228'2'24'4224'24F 02220====⋅===⋅⋅-=∑点的位移:则故:求反力:qEAFl CC BB B EAFl CC EC CC EAFl EAl F EC Fl F lF M CD DC DC DC A6'23'4''23'322'3F 032320====⋅====⋅-⋅=∑点位移:根据图的关系:则:故:杆反力:计算BB'C C'E DAEAFl EAFl EAFl EAFl EAlF EA lF EA Fl EA l F FF l F l F MF F M CO A O C O C O DA O C)124(242)(222222222(202200(12312131211111+=+=+=+=+=⋅=⋅=====⋅+⋅-===∑∑δδδδδδδδδ二)求变形因此:算一)受力分析,反力计BF O1CO2Cδ1δ2δ34-7 解4-8 解4-9 解EAFl EAFl EAFl HF BE B EAFl BD B EAFl EAl F BE EAFl BD F F F F y x BC AB )221(222222222+=+=+⋅=∆==∆=⋅====则:由根据静力学容易求得:B DE GH Fmmtg C C mm C mmEAFl AA F F F y x y 476.045476.0476.01001021010005.0102002'203321=⋅∆=∆=∆=⨯⨯⨯⨯⨯====根据静力学容易求得:A B B'ΔC x2)/24.2(/109.305.01416.31090321015.23224934m m rad GIM DI Px P -⨯=⨯⨯⨯⨯⨯===θπ)55.0(10589.93.02.0/10746.2)/57.1(/10746.204.014.310903210208.6)/387.0(/10755.007.014.310903210432.110208.6200139********.820017955010432.1200309550955033221312max 0249233203493121232231rad mrad m m rad GIM m m rad GI M m N Mm N M m N M n P MPP x---------⨯=⨯+⨯=⨯=⨯=⨯⨯⨯⨯⨯==⨯=⨯⨯⨯⨯⨯==⋅⨯=⨯=⋅⨯=⨯=⋅⨯=⨯==θθϕθθθ因此4-11 解4-12解)48.8(10481.024010270.510902.325.010902.3180/9550355.710270.510587.6108010587.6])6050(1[3206.014.3)1(32142022479474444rad l GIM Mml GI ml GImxdx MGI mD I Px lxPPxP P ---⨯=⨯⨯⨯=⋅====⨯=⨯=⨯=⨯⨯⨯=⨯=-⨯=-=⎰ϕϕαπ故:其中:32.0172.8122161272.8110172.810277.110833.32.0102.010833.3322161016.225414.3113.010*******28384523=-⨯=-==⨯=⨯⨯⨯⨯⨯==⨯===⨯=⨯⨯⨯⨯=⋅∆=---GE GPaPa I l M G D I GPaMPa Al l F E P x P N γϕπ)(332))(()(332)11()(32)3()(32)()(32)()(:)(1)](1[132)](1[32)()(1)(1222121323132312221211212323112312121412112104121041211211122121d d d d dd G Tl dd d d d d d d d d G Tld d d d G TlKd d lG T d d l d K dKG T d d l d K x d d x ld K dxd d x ld G T dx d d x ld GM dx GIx M d d x l d xd ld xdldx d d d d lllxP++=++-⋅-=--=--=--=--=-+=-+=-+==-+=-+=--⎰⎰⎰⎰πππππϕππϕ上面积分转换为:则令d 1d 2Lx已知:h=100mm ,b=45mm ,T=2kN ·m ,G=80GPa ;4-14(a )解: 由挠曲线方程:4-14(b )解:mm rad b h b h b h b h hbG Mx /66.0/10157.1045.01.0237.01080102237.00.25.20.22.2229.0249.0229.0249.05.2/229.00.2/2.2//023933=⨯=⨯⨯⨯⨯⨯==---+=======-θβββββθ)(,,,,插值有关和其中,EIMlw w EIMxw D w x DMxD Cx MxEIw EI Ml EI Mx C x CMx C MdxCdx x M EI M x M B A Z B Z A Z 220002121000)()(2max 222max -==-=∴===+-=++-=-==-====+-=+-=+=-=⎰⎰,所以时,当故:,故,当θθθθθEIqlEI qlww qlC l xD w x DCx qx qlxw EI CqxqlxC q x l x q Cdx x xl qC dx x M EI x xl q x M B A Zl Z Z 243845,24020,002411216141614)(2)()(2)(3max42max 343323222==-=-==-====∴==++-=+-=+-=+-=+=-=⎰⎰θθθθθ则,从而,时,当时,当qq/24-15(a )解:4-15(b)解EI ql EIqlEI l ql EI l ql EIl ql w w w w w EIqlEIqlEIqlEIl ql EIql w B B B B BC C B C B C B C C C C C C CB C 12214131)2(2)5.0(3)(6)6(5.02.,442222332133323)'(4)'(3)'(2)'(14321-=⎥⎦⎤⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+-=++=-=+-+--=+++=+++=(二)求(一)求求:θθθθθθθθθθθc2ql M =(B')(1)2ql221ql (B')(3)(2)(B')+q(4)EIFlEIFlEIFlEIMlEIFlw w w w EIFlEIl Fl EIFlB B B BC C C C62323 233233323212221=+-=+-=+==+-=+=(二)求(一)θθθθ4-16(b )解EIFl EI Fl EIFll EIl Fl l EI FlEI lFl EI Flw l l w w w EI FlEI Fl EI FlEI l Fl EI FlB FlC FC FlC FC B BFlB F B B 333223211112222211max 23)3121414161(32)()2(2)2(2)2(345)212141(22)2(2-=-----=-⋅-⋅-⋅--=+⋅+⋅++=-=---=-⋅--=++==θθθθθθθ(二)最大挠度(一)最大转角F BB BA B D B B B B B B B B B B B B B BB B B B B B B Bw w w w ql w EIqll EI qll w EI qll EI qll w ql EI l q w l l w w w w w w EIqlEIqlEI l qlEI ql EIql EI l q ==<<-=-=⋅-=⋅==⋅=⋅=-=-=⋅+⋅+=++=-=++=-=⋅-==-=-=max max 443334322441311321332132332331,,)3(128:4822424822421288)2(22)2(482438124486)2()1(θθθθθθθθθθθθθθθθθC经过验算,故qll/2qB1B2w B376804.546.0076851283)241483(11283)61163(1128312830]2,0[)61163(1)2183(1)(1]20[],2[81]2,0[283M Q,)3(38476476)(6))((66))(()()2(128336496416)2)((6)2)((66))(()()1(4max max 423433323130132121max2max max2343234220432ql w l x w w EIqlw xEIqlql qlxEIw EI qlqx qlx EI EIqlC EIql x l x C qx qlxEI C dx qx qlx EI C dx x M EI l Ml l x qlx l x qx qlx Mw w w EIqllEIl qdx x x l EIlq dx x l x l x EIl q EIlx l x l x qdx d EIqll EIl qx lx x l EIl qdx x l x l x EIlqdxx l x l x EIl q EIlx l l x l x qdx d x x l x x x xCl B B BllA A A-=≈==-=--=--=-=-==∈+-=+-=+=⎪⎪⎩⎪⎪⎨⎧∈∈-=≠==-=+-=+-=-=-=⎥⎦⎤⎢⎣⎡+--=---=---=-+--=⎰⎰⎰⎰代入:即:时,当则所以因此时,当,位于图,根据求求θθθθθθθθθθ4-16(e) 4-16(f)4-17 解384134838454851624444)()(max333)()(maxqlEIqlqlwwwwwEIqlEIqlEIqlqlBqBBBqlAqAAcA-=--=+==-=--=+==-=θθθθθθ)43(246862131231412max31maxllEIqllEIqlEIqllwwwEIqlBBCB+-=--=⋅+==-==θθθAEIqlwwwwwEIqlEIqlwEIqlEIlqlEIqlwEIqllEIqEIqlwEIqlDD48133165333221163163)2(1283864321max3321max43323423324131-=++==-=++==-=-=⋅-====-=-=θθθθθθθθqDw2w3mmEIFlqlwGPaEmmcmIcx5.221025001020048)106(101010250010200384)106()10/104(548384520010250025004333343433334444=⨯⨯⨯⨯⨯⨯⨯-⨯⨯⨯⨯⨯⨯⨯⨯-=--==⨯==4-18(b)解4-19解EIqlEIqlEIl ql EIl q w w w qlF F c q c c yc 4434)()(32)382(3)2(8)2(=+-=+-=+=-=A AEIqlw w w w w w EIqlw EIql w EIql w EIql w EIqll EIqll w ql F MC YC D853836332/0454321454443424311-=++++=-=-=-=-==⋅=⋅===∑θ212345)(232)(343)()(22)(22223322322顺时针向下向右EIFlEIFlEIFl EI Fl EIFll EIFl w l EIFlEIFlEIl Fl EI MlCF B C BCcP B CY B CX =+=+==+⋅=+⋅===⋅==θθθθδθδ。
建筑力学第四章答案.doc

COS (p D =解:(1)画出三皎拱的等代梁,求三皎拱的约束反力yf =5kN, K ; = 35kN , M^=120kN-m故,匕=妇州%=侣35翊,码四=苧=字=3。
玳M^A =5x4 = 20(kN-m),崂=5x4 + 80 = 100(kN ・ni),成=哄=5kNM^=^c =35x4 = 140(kN-m) , V^B = -35kN , V^c = 5kN(2)计算D 、E 截面的内力 因为拱轴线方程为y=^x(l-x),4 f1 , 故,(/ - 2x) = tan , cos =,sinQ =),'cos 仞 ①计算D 截面的内力 4x4y D 二斯-x4x(16-4) = 3(m)4x4 i .K =-j^r (16-2x4) = m = tan%― =J-—=车,sinQ=y ;cos0)=Lx3 = )。
故, 1 + (《)2 切 +(1/2)2 75 * c 昨 2 & &4-1设三饺拱的为拱轴线方程为),二¥心/一同,拱的尺寸及承受的荷载如图所示。
试求 支反力及D 、E 截面的内力。
,sin (p=y D cos (p DM [)A =M^A -Hy D =20-30x3 = -70(kN• m), =岭—Hy 。
=100 —30x3 = 10(kN ・m)n i.A = V DC = V* cos 物 一 H sin 们)=5x 了 - 30 x 了二 -4后二-8. 94 (kN) J5 A /5i pN DA - N DC 二一崂\ sin% - Hcos 。
=-5x-3=-30x-y= = -13^5 = -29. 07(kN) J5 J5 ②计算E截面的内力)板=4x4 = -^r xl2x(16-12) = 3(m) 4x4 i 二 (16 2x ⑵= =tan% lb~ 2 M =140 —30x3 = 50(kN ・ni),n i V EB = V* cos 代 一 H sin 饥=—35x 了 - 30x (—-)二-8^5 二 T 7. 89 (kN) J5 v5=暖 cos 牲一 H sin 件=5 x j - 30x (-土)= 8后=17. 89 (kN) i 2 N EB = -V*B sin (pE - H COS (P E = —(—35)X (— )-30x 厂=-42. 49 (kN) J5 yj5i 2 N EC = —V ;;, sin (p E — H cos (p E — —5 x (— ) - 30 x 厂——24. 60 (kN)A /5 A /54-2如图所示半圆弧三钗拱, 左半跨承受水平竖向荷载。
建筑力学 李前程第4章习题课

习题课的要求: 学生需要认真听 讲积极参与讨论 按时完成作业并 做好笔记和复习
习题课的授课方式
讲解习题:详细讲 解习题包括解题思 路、解题步骤等
互动讨论:鼓励学 生参与讨论分享自 己的解题思路和想 法
实践操作:让学生 动手操作实践解题 过程加深理解
反馈评价:对学生 的解题过程和结果 进行评价提出改进 建议
超静定结构的内力计算习题解析
超静定结构的定义和特点
内力计算的基本原理和方 法
习题解析:超静定结构的 内力计算实例
习题解析:超静定结构的 内力计算注意事项
习题解析:超静定结构的 内力计算常见错误及解决 方法
习题解析:超静定结构的 内力计算技巧和经验分享
04
解题技巧与思路
静力学基础解题技巧与思路
理解静力学基本概念:力、力矩、力偶、力系等 掌握静力学基本定理:静力平衡条件、力矩平衡条件等 学会分析受力图:找出所有作用在物体上的力并画出受力图 运用静力学基本定理求解:根据静力平衡条件或力矩平衡条件求解未知力或力矩
静定结构内力计算解题技巧与思路
确定结构类型:梁、柱、桁架等
确定计算步骤:受力分析、内力计算、 应力计算等
确定荷载类型:集中荷载、分布荷载法:截面法、位移法等
确定计算误差:误差分析、误差修正等
静定结构的位移计算解题技巧与思路
确定位移计算公式:根据静定结构的特点确定位移计算公式。 确定位移边界条件:根据题目要求确定位移边界条件。 确定位移计算方法:根据题目要求确定位移计算方法如积分法、图解法等。
利用计算机 软件求解未 知内力
05
习题课总结与展望
习题课总结
习题课内容:建筑力学李前程第4章习题 习题类型:选择题、填空题、计算题等 习题难度:中等难度适合初学者 习题解析:详细讲解帮助学生理解知识点 习题课效果:提高学生解题能力加深对建筑力学的理解 习题课展望:未来将继续开展习题课提高教学质量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P 4 3
A 2m (a)
B YB
q4-7】如图所示,已知P,求支座A的反力和杆BC受的力。 【解】BC为二力杆,BC杆受的力为轴力SBC。 由∑mA=0 得 SBClsin30o-Pl/2=0 P SBC=P l/2 l/2 X C 30 A 由∑Xi=0 得 Y o XA+SBCcos30 =0 B XA=-0.866P S 由∑Yi=0 得 YA+SBCsin30o-P=0 YA=0.5P
o
A
A
B
A
A
B
【4-6】已知:(a)m=2.5kN.m,P=5kN;(b)q=1kN/m, P=3kN。求刚架的支座A和B的约束反力。 m 【解】(a)受力分析图如右图 2.5m 由∑Xi=0 得 XA-P×3/5=0 XA=3P/5=3kN ;由∑mB=0 得 X Y m-YA×2+3P/5 ×2.5=0 , YA=5kN 由∑Yi=0 得 YA+YB-4P/5=0 , YB=-1kN (↓) (b)受力分析图如右图 由∑Xi=0 得 XA+P=0 , XA=-P=3kN 2m P 由∑mB=0 得 4q×2-P×3-YA×4=0 3m YA=-0.25kN X Y 由∑Yi=0 得 YA+YB-4q=0 , YB=4.25kN
A o A BC
[4-8]如图,已知P=2kN , q=500N/m。求支座A和B反力。 【解】由∑Xi=0 得 XB=P q 由∑mB=0 得 B P YA ×2-4q ×2=0 Y 2m YA=4q A 由∑Yi=0 得 2m 2m YB+YA-4q=0 Y YB=0
B A
XB
【4-15】已知q=10kN/m , m=40kN.m,求支座A反力。 【解】由于结构上没有水平方向的主动外力, q 故A铰支座水平方向的反力为零。 A B C 由图(a)可知,由三个竖向未知反力, 2m 2m 2m 平行力系只有两个方程,不能求解, Y Y (a) 那么,先看CD杆,见图(b), q C 由∑mC=0 得 D Y 2m 2m YD ×4-2q ×1-m=0 Y (b) YD=15kN; 再看整个结构,由∑mB=0 得 YD ×6-m-4q ×2-YA ×2=0 YA=-15kN(↓)
A B C
m D 2m YD
D
建筑力学第四章习题解
平面力系与平衡方程
【4-3】已知F=2kN,m=2kN.m,求支座A、B的反力。 【解】(a) 由∑Xi=0 得 XA+Fcos45o=0 F m A 45 X B XA=-Fcos45o=-1.41kN Y Y 由∑mB=0 得 -YA×4-F×2× sin45o-m=0 4m 2m (a) YA=-1.21kN(↓) 由∑Yi=0 得 YA+YB-F×sin45o=0 YB=2.62kN (b)由∑Xi=0 得 XA=0 F m A X B 由∑mB=0 得 YA×4-F×2 +m=0 Y Y 2m 2m 2m YA=0.5kN (b) 由∑Yi=0 得 YA+YB-F=0 YB=1.5kN
