初中常用数学模型

合集下载

初中数学63个几何模型

初中数学63个几何模型
1. 点
2. 直线
3. 射线
4. 线段
5. 角
6. 直角
7. 钝角
8. 锐角
9. 平角
10. 三角形
11. 直角三角形
12. 等腰三角形
13. 等边三角形
14. 直线角平分线
15. 外角
16. 内角
17. 同位角
18. 对顶角
19. 同旁内角
20. 同旁外角
21. 三线合一定理
22. 利用同旁内角、三线合一求外角
23. 利用对顶角求角度
24. 正方形
25. 矩形
26. 平行四边形
27. 菱形
28. 梯形
29. 等腰梯形
30. 同底同高面积公式
31. 全等三角形
32. 相似三角形
33. 欧拉线
34. 垂线
35. 点到直线距离公式
36. 垂线段定理
37. 中线
38. 角平分线
39. 中垂线
40. 外心
41. 垂心
42. 重心
43. 内切圆
44. 外切圆
45. 位似比
46. 「半周角」公式
47. 内角和公式
48. 细分
49. 长度单位转换
50. 平面直角坐标系
51. 平移变换
52. 旋转变换
53. 对称变换
54. 条件语句
55. 循环语句
56. 取模 %
57. 迭代过程
58. Turtle库
59. 折线
60. 多边形
61. 圆
62. 起重机问题
63. 网格问题。

初中几何48种数学模型系统讲解

初中几何48种数学模型系统讲解初中几何是数学中非常重要的一个分支，涉及到许多基础知识和技能。

在初中几何学习中，数学模型是非常重要的一环，它能够帮助学生更好地理解和掌握几何知识，并提高解题的能力。

下面我们就来介绍一下初中几何中常见的48种数学模型系统。

1. 平面几何模型：平面几何模型是研究平面上的图形和变换的数学模型，例如平移、旋转、对称等。

2. 立体几何模型：立体几何模型是研究空间中的图形和变换的数学模型，例如立体的投影、旋转、平移等。

3. 直线模型：直线模型是用来表示直线的数学模型，例如在平面几何中，可以使用坐标系来表示一条直线。

4. 线段模型：线段模型是用来表示线段的数学模型，例如在平面几何中，可以使用坐标系来表示一条线段。

5. 角度模型：角度模型是用来表示角度的数学模型，例如在平面几何中，可以使用角度制和弧度制来表示角度。

6. 相交模型：相交模型是用来表示图形相交的数学模型，例如在平面几何中，可以使用交点来表示两条直线相交的情况。

7. 平行模型：平行模型是用来表示平行线的数学模型，例如在平面几何中，可以使用平行线的定义来表示两条直线平行的情况。

8. 垂直模型：垂直模型是用来表示垂直线的数学模型，例如在平面几何中，可以使用垂直线的定义来表示两条直线垂直的情况。

9. 对称模型：对称模型是用来表示对称图形的数学模型，例如在平面几何中，可以使用对称轴来表示对称图形的情况。

10. 相似模型：相似模型是用来表示相似图形的数学模型，例如在平面几何中，可以使用相似比例来表示两个相似图形之间的关系。

11. 等比模型：等比模型是用来表示等比数列的数学模型，例如在几何中，可以使用等比数列来表示一些几何问题。

12. 等分模型：等分模型是用来表示等分线段的数学模型，例如在几何中，可以使用等分线段来表示将一个线段分成若干等分的情况。

13. 圆模型：圆模型是用来表示圆形的数学模型，例如在平面几何中，可以使用圆心、半径来表示一个圆。

初中48个数学模型

初中48个数学模型
1. 直线方程模型
2. 一次函数模型
3. 二次函数模型
4. 指数函数模型
5. 对数函数模型
6. 三角函数模型
7. 幂函数模型
8. 反比例函数模型
9. 绝对值函数模型
10. 分段函数模型
11. 等差数列模型
12. 等比数列模型
13. 等差数列求和模型
14. 等差数列通项求值模型
15. 等差数列前n项和求值模型
16. 等差数列前n项平均值模型
17. 等比数列求和模型
18. 等比数列通项求值模型
19. 等比数列前n项和求值模型
20. 等差数列与等差数列之和关系模型
21. 平方根模型
22. 平方根与二次方程关系模型
23. 正方形面积模型
24. 三角形面积模型
25. 平行四边形面积模型
26. 斜率模型
27. 切线斜率模型
28. 余弦定理模型
29. 正弦定理模型
30. 几何相似模型
31. 三角形相似模型
32. 平行线与平行线之间的角关系模型
33. 同位角与内错角模型
34. 相交弦定理模型
35. 角平分线定理模型
36. 体积模型
37. 圆锥体积模型
38. 圆柱体积模型
39. 球体积模型
40. 柱台体积模型
41. 三维图形表面积模型
42. 立体图形展开模型
43. 均值不等式模型
44. 不等式求解模型
45. 组合数学模型
46. 排列数学模型
47. 方程求解模型
48. 实际问题建模模型
以上是初中数学常见的48个数学模型，希望对你有所帮助！。

(完整版)初中常用数学模型

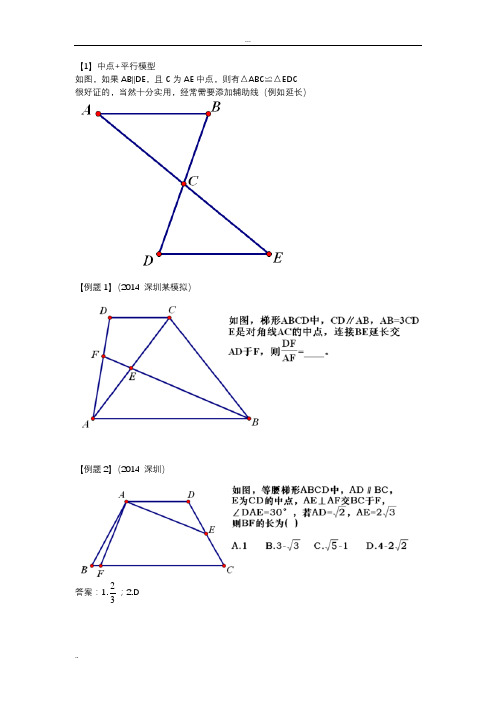
如图，如果AB ‖DE ，且C 为AE 中点，则有△ABC ≌△EDC 很好证的，当然十分实用，经常需要添加辅助线（例如延长）【例题1】（2014 深圳某模拟）【例题2】（2014 深圳）答案：1.32；2.D如图，若∠B=∠C=∠DEF=α（0<α≤90)则一定有△BDE与△CEF相似。

十分好证（外角和什么一大堆），并且也很实用。

经常在矩形里出题。

【例题1】（2009 太原）【例题2】（2006 河南）【例题3】（原创）答案：1. 2或3-24或25 2.(5453-，) 【3】巧造旋转模型在某些几何题中，往往有一些奇怪的结论，此时可以通过几何三大变换之一【旋转】求解。

巧造旋转往往要有一定的等量关系和特殊角度，如下题：通过观察可得∠ABC=∠C=45°，AB=AC 。

我们可以将△ACD 绕A 顺时针旋转90°得到△ABE ，使得AC 与AB 重合。

那么就有EB ⊥BC ，而在RT △AED 中，DE ²=2AD ²（等腰直角三角形）所以BE ²+BD ²=DE ²，即BD ²+CD ²=2AD ²是不是赶脚很难想到？要学会判断，这种感觉是要练出来的！【例题1】（2014 武汉）【例题2】【例题3】（2014 菏泽改编）答案：1.41 2.9 3.(1.)2，(2.)直角三角形，旋转后证全等，证明略【4】等腰模型这是一个很基础的模型——什么样的结构会生成等腰三角形首先：平行+角平分线，如图，若AD‖BE，BC平分∠ABE，则AB=AC，很好证的，导角即可。

其次：垂直+角平分这个不难理解，因为等腰三角形三线合一。

这种模型很常用，常常需要做辅助线（延长之类）【例题1】（原创）AB‖CD【例题2】（原创）【例题3】（改编）1.112.33.延长CD交AB于M，利用中位线，证明略【5】倍长中线法常考，选填大证明都可能会用。

(全)初中数学｜23种模型汇总

(全)初中数学｜23种模型汇总1. 数列模型数列模型是一组按照特定规律排列的数字，常见的数列有等差数列和等比数列。

在解题中，需要掌握其通项公式和求和公式。

2. 几何模型几何模型是通过图形来表示问题，需要熟练掌握各种几何图形的性质和定理，如圆、三角形、直线等。

3. 等式模型等式模型是通过等式来表示问题，需要掌握化简等式、配方、移项等技巧。

4. 方程模型方程模型是通过方程来表示问题，需要掌握解方程的方法和技巧，如消元法、相似变形法、套公式法等。

5. 数据分析模型数据分析模型需要对给定的数据进行处理和分析，如找出最大值、最小值、平均值等。

6. 概率模型概率模型需要根据事件发生的可能性来计算概率，需要掌握概率的基本原理和计算方法。

8. 百分数模型百分数模型需要将数值转化为百分数进行计算，需要掌握百分数的计算方法和应用。

9. 推理模型推理模型需要根据已知的信息推出未知的结果，需要掌握逻辑思维和推理技巧，如分类讨论法、反证法等。

10. 图表模型图表模型是通过图表来表示问题，需要掌握读图和解决图表问题的技巧。

11. 统计模型统计模型需要对给定的数据进行统计分析，如频数分布、统计量计算等。

12. 函数模型函数模型需要根据函数的定义和性质来计算未知量，需要掌握函数的基本概念和图像变化规律。

13. 同余模型同余模型需要根据同余关系来计算未知量，需要掌握同余关系的基本性质和计算方法，如模运算等。

14. 最优化模型最优化模型需要找出满足特定条件下的最优解，需要掌握最优化方法和技巧，如最大值最小值法、拉格朗日乘数法等。

16. 排列组合模型排列组合模型需要计算不同元素之间的排列和组合方式，需要掌握排列组合的基本概念和计算方法。

17. 质数模型质数模型需要计算满足质数条件的解，需要掌握质数的基本性质和计算方法，如质因数分解等。

23. 递推模型递推模型需要利用递推公式来计算未知项，需要掌握递推公式的推导方法和递推问题的解法。

初中数学30种模型汇总(最全几何知识点)

10.等面积模型:D是BC的中点
20.平移构造全等
30.二次函数中平行四边形存在性模型
01.三线八角
同位角：找F型
内错角：找Z型
同旁内角：找U型
02.拐角模型
一.锯齿型
1
1
3
2
2
3
4
∠1+∠3=∠2
∠1+∠2=∠3 +∠4
左和＝右和
二.鹰嘴型
1
1
2
3
3
2
∠1+∠3=∠2
∠1+∠3=∠2
鹰嘴＋小＝大
一.大小等边三角形
虚线相等，且夹角为60°
（全等，八字形）
四.大小等腰三角形（顶角为α）
结论：虚线相等，且夹角为α
（全等，八字形）
三. 大小等腰直角三角形
结论：虚线相等，且夹角为90°
（全等，八字形）
二.大小正方形
结论：虚线相等，且夹角为90°
（全等，八字形）
15.半角模型
条件：正方形ABCD
∠EDF=45°
证：EF=AE+CF
条件：CD=AD,∠ADC=90°
∠EDF=45°
∠A+∠C=180°
证明：EF=AE+CF
条件：AB=AD
∠B+∠D=180°
∠EAF=1 ∠BAD
2
证明：EF=BE+DF
条件：AB=AC,∠BAC=90°
∠DAE=45°
证明：DE2=BD2+CE2
△CEF为直角三角形
初中数学30种模型汇总
(最全几何知识点)
01.三线八角
02.拐角模型
03.等积变换模型

初中数学模型23种(53张PPT)

等积变换模型
S△ACD=S△BCD
初二数学模型
八字模型
A B
E
C
D
角：∠A+ ∠B= ∠C+ ∠D 边：AD+BC＞AB+CD
飞镖模型
A
D B
角：∠D = ∠B+ ∠C+ ∠A 边：AB+AC＞BD+CD
C
内内角平分线模型
A
D
B
C
D 90 1 A 2
内外角平分线模型
A D
B
CE
D 1 A 2
外外角平分线模型
A
B E
D
C F
∠��=90°−
1 2
∠��
平行平分出等腰模型
E G A
C
H
M
F
B
HG=HM
D
等面积模型:D是BC的中点
A
h
B
a
D
b
C
��△�� △ ��
Smax

SOBM
S OAB

1 MN
2
max
OG
1 OA BG 2
1 4 4 1 5 4 18
2
2
M t, t2 5t
h
N t,t G
二次函数中等腰三角形存在性模型
A、B固定，找点C，使得△ABC是等腰三角形，C在两圆一线上
A
B
二次函数中直角三角形存在性模型
证明：DE2=BD2+CE2 △CEF为直角三角形
将军饮马模型

初中数学｜23种模型汇总

初中数学｜23种模型汇总初中数学中，有许多不同的模型方法可以帮助学生理解和解决问题。

这些模型方法以图形、物体和实际情境等形式呈现，通过具象化和抽象化的方式引导学生建立数学概念和解题能力。

以下是初中数学中常用的23种模型汇总：1.长方形模型：将实际问题或数学关系转化为长方形的长度和宽度，以便解决各种问题。

2.正方形模型：通过将关系表达为正方形的边长和面积来解决问题。

3.圆形模型：将实际问题或数学关系转换为圆的直径、半径、周长和面积，以解决相应的问题。

4.三角形模型：通过将问题转化为三角形的底边、高和面积来解决问题。

5.平行四边形模型：通过将问题转化为平行四边形的底边、高和面积来解决问题。

6.梯形模型：将问题转化为梯形的上底、下底、高和面积，以解决相应的问题。

7.直角三角形模型：通过将问题转化为直角三角形的直角边、斜边和面积来解决问题。

8.立体模型：通过制作模型或利用图形来解决与立体图形相关的问题，如长方体、正方体、圆柱体、圆锥体、球体等。

9.比例模型：通过将问题转化为比例关系来解决问题，如平均速度、单位价格等。

10.百分比模型：将问题转化为百分比的概念和计算来解决问题，如打折、涨价等。

11.质量守恒模型：通过将问题转化为质量守恒的原理来解决问题。

12.可视化模型：通过绘制图形、示意图或使用图表来解决问题，以帮助学生更好地理解和分析问题。

13.数轴模型：通过在数轴上表示数值和位置来解决问题，如正数、负数、小数、分数等。

14.曲线图模型：通过绘制曲线图或利用曲线图来解决问题，如成长曲线、销售曲线等。

15.关系图模型：通过绘制关系图或利用关系图来解决问题，如家族关系、人际关系等。

16.流程图模型：通过绘制流程图或利用流程图来解决问题，如计算、制作工艺等。

17.条形图模型：通过绘制条形图或利用条形图来解决问题，如统计数据、比较等。

18.平面几何模型：通过绘制图形和利用几何关系来解决问题，如平行线、垂直线、对称等。

初中数学23种数学模型汇总

初中数学23种数学模型汇总数学模型是数学在实际问题中的应用，它可以帮助我们理解和解决各种问题。

下面是初中数学中常见的23种数学模型汇总：1. 线性函数模型：描述一个变量与另一个变量之间的简单关系，可以用方程 y = kx + b 表示。

2. 平方函数模型：描述一个变量与另一个变量之间的二次关系，可以用方程 y = ax^2 + bx + c 表示。

3.指数函数模型：描述一个变量与另一个变量之间的指数关系，可以用方程y=a*b^x表示。

4. 对数函数模型：描述一个变量与另一个变量之间的对数关系，可以用方程 y = log_b(x) 表示。

5. 正比例函数模型：描述两个变量之间的正比例关系，可以用方程y = kx 表示。

6.反比例函数模型：描述两个变量之间的反比例关系，可以用方程y=k/x表示。

7.几何模型：使用几何图形和关系来解决问题，如平面几何和立体几何问题。

8.统计模型：使用统计方法和数据来分析和解释问题，如平均数、中位数和众数等。

9.概率模型：使用概率理论来解决问题，如计算概率、期望值和方差等。

10.贝叶斯模型：使用贝叶斯定理来评估和预测事件的概率。

11.数列模型：描述一系列数字之间的关系和规律，如等差数列和等比数列等。

12.方程模型：使用代数方程来表示问题中的关系，如一元一次方程、一元二次方程等。

13.不等式模型：使用不等式来表示问题中的关系，如一元一次不等式、一元二次不等式等。

14.三角函数模型：使用三角函数来描述问题中的关系，如正弦函数、余弦函数等。

15.空间几何模型：描述三维空间中物体和其属性的关系，如平行四边形、正方体等。

16.排列组合模型：使用排列和组合方法来计算问题中的可能性，如计算排列数和组合数等。

17.图论模型：使用图论方法来解决问题，如最短路径问题、连通性问题等。

18.线性规划模型：使用线性规划方法来优化问题，如最大化利润、最小化成本等。

19.矩阵模型：使用矩阵和线性代数来解决问题，如线性方程组和矩阵运算等。

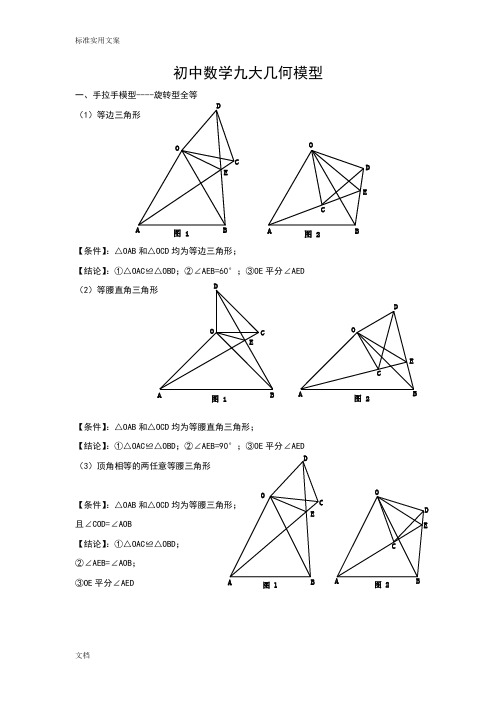
(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90°将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

初中数学48个几何模型及题型

初中数学的几何模型是学生学习数学时的重要内容之一，通过学习几何模型和解题，可以帮助学生对几何知识有更深层次的理解，提高数学解题能力。

本文将介绍初中数学中常见的48个几何模型及其相关题型，希望可以帮助学生系统地掌握几何知识。

一、直线和角1. 直线概念直线是由一点不停地延伸而成的。

在平面几何中，直线没有宽度和厚度，只有长度。

2. 角的概念两条相交直线之间的夹角叫做角。

角可以分为锐角、直角、钝角和平角。

3. 直线和角相关题型- 计算夹角的大小- 判断角的种类二、多边形1. 三角形三角形是最简单的多边形，其内角和为180度。

根据边的长度和角的大小，可以分为等腰三角形、等边三角形、直角三角形等不同种类。

2. 四边形四边形是具有四条边的几何图形，常见的四边形有矩形、正方形、平行四边形和菱形等。

3. 多边形相关题型- 计算多边形的内角和- 判断多边形的种类三、圆1. 圆的概念圆是由一个点到另一个点距离恒定的点的集合。

其中，点到圆心的距离为半径，圆上任意两点之间的距离称为弦。

2. 圆的性质圆的直径是圆的两个相对的端点，圆的周长和面积分别为2πr和πr²。

3. 圆相关题型- 计算圆的周长和面积- 判断圆的种类四、平面图形的平移、旋转和对称1. 平移平移是指将一个物体按照一定的规则移动到另一位置，移动前后的图形位置关系不变。

学生需要了解不同平移的规律和图形的位置关系。

2. 旋转旋转是指以某一点为中心，按一定角度将图形进行旋转。

学生需要掌握图形旋转的规律和性质。

3. 对称对称是指一个图形绕某条直线或点对称，对称轴可以分为水平对称轴、垂直对称轴和斜对称轴。

五、三视图和展开图1. 三视图三视图是指物体分别从正视图、侧视图和俯视图所得的图形。

学生需要根据给定的三视图还原出物体的整体图形。

2. 展开图展开图是将立体图形按一定规则展开成平面图形。

学生需要了解展开图的规律和方法。

六、空间图形1. 空间图形的概念空间图形是三维几何中的图形，包括圆柱、圆锥、球体、棱体等。

初中数学16种模型必背

初中数学16种模型必背初中数学学习中，积累掌握各种数学模型是非常重要的。

下面将介绍16种常见的数学模型，希望能为同学们提供一定的指导和帮助。

1.等式思想模型：如解方程、组合等式的题目，需要将问题转化为等式，并运用代数法解决。

2.比重模型：涉及到相对比较、平均数、集合比较的题目，要掌握将问题转化为比重关系的方法。

3.图形关系模型：如几何图形的面积、周长、体积等问题，需要通过图形关系进行解答。

4.倍数关系模型：涉及到最小公倍数、最大公约数等题目，需要掌握倍数关系的应用。

5.增量模型：如等差数列、等比数列的题目，需要观察数值之间的增量规律，并进行计算。

6.比例模型：涉及到长度比、面积比、速度比等题目，需要掌握比例关系的应用。

7.排列组合模型：如从一组元素中选择若干个进行排列、组合的题目，需要利用排列组合的原理进行解答。

8.图表模型：运用柱状图、折线图、饼图等图表进行数据分析、比较和计算。

9.分数模型：涉及到分数的加减乘除、比较大小等问题，需要熟练掌握分数的运算和应用。

10.百分数模型：涉及到百分数的比较、计算和应用，需要掌握百分数在实际生活中的应用。

11.方程模型：如利用二次方程解决问题的题目，需要将实际问题转化为方程，并进行求解。

12.三角形模型：涉及到三角形的边长、角度、面积等问题，需要熟悉三角形的性质和应用。

13.函数模型：如利用函数关系解决问题的题目，需要了解函数的概念、性质和应用。

14.平方根模型：涉及到平方根的计算和应用，需要熟练掌握平方根的性质和运算。

15.几何变换模型：如平移、旋转、镜像等几何变换的题目，需要了解几何变换的规律和应用。

16.几何证明模型：涉及到几何定理的证明题目，需要运用几何定理和逻辑推理进行证明。

以上就是初中数学学习中常见的16种数学模型。

通过熟练掌握这些模型，同学们能更好地解决数学问题，并在实际生活中应用数学知识。

希望同学们能够在学习中不断积累，并灵活运用这些数学模型，提高数学解题的能力。

初中数学八大几何模型归纳

初中数学几何模型总结归纳1.中点模型【模型1】倍长1、倍长中线；2、倍长类中线；3、中点遇平行线延长相交ABCD E ABC DEFEDCBA【模型2】遇多个中点，构造中位线1、直接连接中点；2、连对角线取中点再相连GABCDEFABCD E【例1】在菱形ABCD 和正三角形BEF 中，∠ABC ＝60°，G 是DF 的中点，连接GC 、GE ．（1）如图1，当点E 在BC 边上时，若AB ＝10，BF ＝4，求GE 的长；（2）如图2，当点F 在AB 的延长线上时，线段GE 、GC 有怎样的数量和位置关系，写出你的猜想，并给予证明；（3）如图3，当点F 在CB 的延长线上时，（2）问中的关系还成立吗？写出你的猜想，并给予证明．图3图2图1ACDEFGDEFGCDEGABBFCBA【解答】（1）延长EG 交CD 于点H 易证明△CHG ≌△CEG ，则GE ＝HBEGCFAD（2）延长CG 交AB 于点I ，易证明△BCE ≌△FIE ，则△CEI 是等边三角形，GE ＝3GC 错误!未找到引用源。

，且GE ⊥GCF（3）EJ【例2】如图，在菱形ABCD 中，点E 、F 分别是BC 、CD 上一点，连接DE 、EF ，且AE ＝AF ，∠DAE ＝∠BAF .（1）求证：CE ＝CF ；（2）若∠ABC ＝120°，点G 是线段AF 的中点，连接DG 、EG ，求证：DG ⊥EG .GFE DC BAE H GF EDCBA【解答】（1）证明△ABE ≌△ADF 即可；（2）延长DG 与AB 相交于点H ，连接HE ，证明△HBE ≌△EFD 即可【例3】如图，在凹四边形ABCD 中，AB ＝CD ，E 、F 分别为BC 、AD 的中点，BA 交EF 延长线于G 点，CD 交EF 于H 点，求证：∠BGE ＝∠CHE . 【解答】取BD 中点可证，如图所示：JA BCDE F GH2.角平分线模型【模型1】构造轴对称【模型2】角平分线遇平行构等腰三角形【例4】如图，平行四边形ABCD 中，AE 平分∠BAD 交BC 边于E ，EF ⊥AE 交边CD 于F 点，交AD 边于H ，延长BA 到G 点，使AG ＝CF ，连接GF .若BC ＝7，DF ＝3，EH ＝3AE ，则GF 的长为_______.HGFEDCBA【解答】延长FE 、AB 交于点I ，易得CE ＝CF ，BA ＝BE ，设CE ＝x ，则BA ＝CD ＝3＋x ，BE ＝7－x ， 3＋x ＝7－x ，x ＝2，AB ＝BE ＝5，AE ＝，作AJ ⊥BC ，连接AC ，求得GF ＝AC ＝3JIAB CDEFGH3.手拉手模型【条件】OA ＝OB ，OC ＝OD ，∠AOB ＝∠COD【结论】△OAC ≌△OBD ，∠AEB ＝∠AOB ＝∠COD （即都是旋转角）；OE 平分∠AEDDC EBAOOABEC D 导角核心图形：八字形CBAO【例5】（2014重庆市A 卷）如图，正方形ABCD 的边长为6，点O 是对角线AC 、BD 的交点，点E 在CD 上，且2DE CE ，连接BE ．过点C 作CF ⊥BE ，垂足是F ，连接OF ，则OF 的长为________．FABCOEDDE CBA【例6】如图，△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC 于点D ，点E 在AC 边上，连接BE ，AG ⊥BE于F ，交BC 于点G ，求∠DFG ． GFE DCBAABC【答案】45°【例7】（2014重庆B 卷）如图，在边长为ABCD 中，E 是AB 边上一点，G 是AD 延长线一点，BE ＝DG ，连接EG ，CF ⊥EG 交EG 于点H ，交AD 于点F ，连接CE 、BH ．若BH ＝8，则FG＝_____________．HGDE CBAFABE G【答案】4.邻边相等对角互补模型【模型1】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＋∠BCD ＝∠ABC ＋∠ADC ＝180° 【结论】AC 平分∠BCDEB【模型2】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＝∠BCD ＝90° 【结论】① ∠ACB ＝∠ACD ＝45°； ② BC ＋CDABCECB【例8】如图，矩形ABCD 中，AB ＝6，AD ＝5，G 为CD 中点，DE ＝DG ，FG ⊥BE 于F ，则DF 为_____.F ABCEDGG DE【例9】如图，正方形ABCD 的边长为3，延长CB 至点M ，使BM ＝1，连接AM ，过点B 作BN ⊥AM ，垂足为N ，O 是对角线AC 、BD 的交点，连结ON ，则ON 的长为__________. OMN DCBA【例10】如图，正方形ABCD 的面积为64，△BCE 是等边三角形，F 是CE 的中点，AE 、BF 交于点G ，则DG 的长为___________. GFEABCDEC【答案】45.半角模型【模型1】【条件】如图，四边形ABCD 中，AB ＝AD ，∠BAD ＋∠BCD ＝∠ABC ＋∠ADC ＝180°，∠EAF ＝12∠BAD ，点E 在直线BC 上，点F 在直线CD 上【结论】BE 、DF 、EF 满足截长补短关系FEDCBA【模型2】【条件】如图，在正方形ABCD 中，已知E 、F 分别是边BC 、CD 上的点，且满足∠EAF ＝45°，AE 、AF 分别与对角线BD 交于点M 、N ．【结论】①BE ＋DF ＝EF ； ② ABE ADF AEF S S S ∆∆∆+=；③AH ＝AB ；④2ECF C AB ∆=；⑤BM 2＋DN 2＝MN 2；⑥△ANM ∽△DNF ∽△BEM ∽△AEF ∽△BNA ∽△DAM （由AO ：AH ＝AO ：AB ＝1：可得到△ANM 和△AEF 相似比为1）⑦AMN MNFE S S ∆=四边形；⑧△AOM ∽△ADF ；△AON ∽△ABE ；⑨△AEN 为等腰直角三角形，∠AEN ＝45°，△AFM 为等腰直角三角形，∠AFM ＝45°；⑩A 、M 、F 、D 四点共圆，A 、B 、E 、N 四点共圆，M 、N 、F 、C 、E 五点共圆．H NM FEDCBA【模型2变形】【条件】在正方形ABCD 中，已知E 、F 分别是CB 、DC 延长线上的点，且满足∠EAF ＝45° 【结论】BE ＋EF ＝DFFEDCB A【模型2变形】【条件】在正方形ABCD 中，已知E 、F 分别是BC 、CD 延长线上的点，且满足∠EAF ＝45° 【结论】DF ＋EF ＝BEAB C DEF【例11】如图，△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC ＝∠EDF ＝90°，△DEF 的顶点E与△ABC 的斜边BC 的中点重合，将△DEF 绕点E 旋转，旋转过程中，线段DE 与线段AB 相交于点P ，射线EF 与线段AB 相交于点G ，与射线CA 相交于点Q .若AQ ＝12，BP ＝3，则PG ＝__________.Q PGD FECBA【解答】连接AE ，题目中有一线三等角模型和半角模型设AC ＝x ，由△BPC ∽△CEQ 得BP CE ＝BE CQ ， 3/（22x ）＝22x /（x ＋12），解得x ＝12 设PG ＝y ，由AG 2＋BP 2＝PG 2得32＋(12－3－x )2＝x 2，解得x ＝5【例12】如图，在菱形ABCD 中，AB ＝BD ，点E 、F 在AB 、AD 上，且AE ＝DF ．连接BF 与DE 交于点G ，连接CG 与BD 交于点H ，若CG ＝1，则S 四边形BCDQ ＝__________．HGFED CB A【解答】346.一线三等角模型【条件】∠EDF ＝∠B ＝∠C ，且DE ＝DF 【结论】△BDE ≌△CFDFEDCBA【例13】如图，正方形ABCD 中，点E 、F 、G 分别为AB 、BC 、CD 边上的点，EB ＝3，GC ＝4，连接EF 、FG 、GE 恰好构成一个等边三角形，则正方形的边为__________.GA B CDEF【解答】如图，构造一线三等角模型，△EFH ≌△FGI 则BC ＝BF ＋CF ＝HF －BH ＋FI －CI ＝GI －BH ＋HE －CI ＝733IH F ED C B A G7.弦图模型【条件】正方形内或外互相垂直的四条线段【结论】新构成了同心的正方形LK JIHGFECDB AHG FEDCBA【例14】如图，点E 为正方形ABCD 边AB 上一点，点F 在DE 的延长线上，AF ＝AB ，AC 与FD 交于点G ，∠F AB 的平分线交FG 于点H ，过点D 作HA 的垂线交HA 的延长线于点I .若AH ＝3AI ，FH ＝22，则DG ＝__________．I H AGFEDCB【解答】1742【例15】如图，△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC 于点D ，点E 是AC 中点，连接BE ，作AG ⊥BE 于F ，交BC 于点G ，连接EG ，求证：AG ＋EG ＝BE ．FE CGDBABC【解答】过点C 作CH ⊥AC 交AG 的延长线于点H ，易证8.最短路径模型【两点之间线段最短】 1、将军饮马Q2、费马点【垂线段最短】【两边之差小于第三边】【例16】如图，矩形ABCD 是一个长为1000米，宽为600米的货场，A 、D 是入口，现拟在货场内建一个收费站P ，在铁路线BC 段上建一个发货站台H ，设铺设公路AP 、DP 以及PH 之长度和为l ，求l 的最小值．【解答】3500600 ，点线为最短．【例17】如图，E 、F 是正方形ABCD 的边AD 上的两个动点，满足AE ＝DF，连接CF 交BD 于G ，连接BE 交AG 于H ，若正方形的边长为2，则线段DH 长度的最小值为______________________．【解答】如图，取AB 中点P ，连接PH 、PD ，易证PH ≥PD -PH 即DH ≥15-．【例18】如图所示，在矩形ABCD 中，AB ＝4，AD ＝24，E 是线段AB 的中点，F 是线段BC 上的动点，△BEF 沿直线EF 翻折到△EF B '，连接B D '，B D '最短为________________．【解答】4【例19】如图1，□ABCD 中，AE ⊥BC 于E ，AE ＝AD ，EG ⊥AB 于G ，延长GE 、DC 交于点F ，连接AF ．（1）若BE ＝2EC ，AB ＝13，求AD 的长；（2）求证：EG ＝BG ＋FC ；（3）如图2，若AF ＝25，EF ＝2，点M 是线段AG 上一动点，连接ME ，将△GME 沿ME 翻折到△ME G '，连接G D '，试求当G D '取得最小值时GM 的长．图1 图2 备用图【解答】（1）3（2）如图所示（3）当DG ′最小时D 、E 、G '三点共线解得43173-=+'=MN N G GMEH【练习1】如图，以正方形的边AB为斜边在正方形内作直角三角形ABE，∠AEB＝90°，AC、BD交于O．已知AE、BE的长分别为3、5，求三角形OBE的面积．【解答】25【练习2】问题1：如图1，在等腰梯形ABCD 中，AD∥BC，AB＝BC＝CD，点M，N分别在AD，CD上，∠MBN21∠ABC，试探究线段MN，AM，CN有怎样的数量关系？请直接写出你的猜想；问题2：如图2，在四边形ABCD中，AB＝BC，∠ABC＋∠ADC＝180°，点M，N分别在DA，CD延长线，若∠MBN＝12∠ABC仍然成立，请你进一步探究线段MN，AM，CN又有怎么样的关量关系？写出你的猜想，并给予证明。

初中数学48个解题模型

初中数学48个解题模型数学是一门需要理解和掌握的学科，而解题模型则是数学学习中非常重要的一部分。

解题模型是指在解决数学问题时，根据问题的特点和要求，采用合适的方法和步骤，运用数学知识进行分析、计算和推理的一种解题方式。

在初中数学学习中，掌握一定的解题模型，可以更好地提高数学解题的能力和效率。

下面，我们将介绍初中数学中常用的48个解题模型，其中包括了初中数学的各个方面，希望对初中数学学习有所帮助。

1. 等式变形模型：根据等式变形的性质，对等式进行变形，使其更加简单易解。

2. 分式化简模型：根据分式化简的原理，对分式进行化简，使其更加简单易解。

3. 去括号模型：根据去括号的原理，将括号内的式子进行展开，使其更加简单易解。

4. 合并同类项模型：根据合并同类项的原理，将同类项进行合并，使其更加简单易解。

5. 因式分解模型：根据因式分解的原理，将式子进行因式分解，使其更加简单易解。

6. 基本不等式模型：根据基本不等式的原理，对不等式进行变形，使其更加简单易解。

7. 二次函数解析式模型：根据二次函数解析式的原理，求出二次函数的解析式。

8. 三角函数解析式模型：根据三角函数解析式的原理，求出三角函数的解析式。

9. 解方程模型：根据解方程的原理，对方程进行变形，求出方程的解。

10. 解不等式模型：根据解不等式的原理，对不等式进行变形，求出不等式的解。

11. 平面几何基本定理模型：根据平面几何基本定理的原理，对几何问题进行求解。

12. 空间几何基本定理模型：根据空间几何基本定理的原理，对几何问题进行求解。

13. 三角形的性质模型：根据三角形的性质，对三角形问题进行求解。

14. 相似三角形模型：根据相似三角形的原理，对相似三角形问题进行求解。

15. 同余模型：根据同余的原理，对同余问题进行求解。

16. 勾股定理模型：根据勾股定理的原理，对勾股定理问题进行求解。

17. 三角函数基本关系式模型：根据三角函数的基本关系式，对三角函数问题进行求解。

初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOCD E图 1图 2二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90° 将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB BC AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CO CDEOB CDEOC DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

初中数学十大模型

初中数学中考总复习几何十大模型1、模型一：“12345”模型
2、模型二：“半角”模型
对称半角模型
旋转半角模型
3、模型三：“角平分线”模型
角平分线定理角平分线+垂线=等腰三角
形
角分线+平行线=等腰三角必呈现
角平分线+垂线=等腰三角形
4、模型四：“手拉手”模型
条件：1、两个等腰三角形；2、顶角相等；3、顶点重合。

结论：1、手相等；2、三角形全等；3、手的夹角相等；
4、顶点连手的交点得平分。

5、模型五：“将军饮马”模型
6、模型六：“中点”模型
【模型1】倍长
1、倍长中线；
2、倍长类中线；
3、中点遇平行延长相交
【模型2】遇多个中点，构造中位线
1.直接连接中点；
2.连对角线取中点再相连
7、模型七：“邻边相等的对角互补”模型
【模型1】
【条件】如图，四边形ABCD中，AB=AD，∠BAD+∠BCD=∠ABC+∠ADC=180°【结论】AC平分∠BCD
【模型2】
【条件】如图，四边形ABCD中，AB=AD，∠BAD=∠BCD=90°
【结论】①∠ACB=∠ACD=45°②BC+CD=V2AC
8、模型八：“一线三角”模型
【条件】∠EDF=∠B=∠C，且DE=DF
【结论】△BDE=△CFD
9、模型九：“弦图”模型
【条件】正方形内或外互相垂直的四条线段
【结论】新构成了同心的正方形
10、模型十：费马点。

初中常用数学模型

初中常用数学模型数学模型是数学和实际问题相结合的产物，通过建立相应的数学关系，对实际问题进行抽象和描述，从而帮助我们更好地理解和解决问题。

在初中数学中，一些常用的数学模型能够帮助我们更好地理解和应用数学知识。

本文将介绍一些常见的数学模型及其应用。

1. 几何模型几何模型是基于几何图形的形状和属性的数学模型。

例如，在初中几何学中，我们常常使用平面几何模型来解决与平面图形相关的问题。

通过建立几何模型，我们可以计算图形的面积、周长等属性，进而解决实际问题。

例如，当我们在初中学习矩形的面积和周长时，可以将其建立为一个几何模型，并通过计算得到具体数值。

2. 代数模型代数模型是基于代数式和方程的数学模型。

在初中代数学中，我们经常使用代数模型进行问题的抽象和求解。

代数模型可以帮助我们描述抽象的数学关系，并通过代数运算求解未知数的值。

例如，当我们在初中学习一元一次方程时，可以将问题建立为一个代数模型，通过方程的解来确定未知数的值。

3. 概率模型概率模型是用于描述随机事件发生概率的数学模型。

在初中概率论中，我们常常使用概率模型来分析和计算事件的概率。

通过建立概率模型，我们可以预测事件发生的可能性，并进行相应的决策。

例如，在投掷硬币的实验中，我们可以建立一个概率模型来计算正面朝上的概率，从而得出预测结果。

4. 统计模型统计模型是用于描述和分析数据的数学模型。

在初中统计学中，我们经常使用统计模型来分析数据的分布、变化趋势等。

通过建立统计模型，我们可以从大量数据中提取有用的信息，并进行相关的推断。

例如，在调查班级学生身高的数据中，我们可以建立一个统计模型来计算平均身高、身高的分布等。

5. 动力学模型动力学模型是用于描述物体运动和力学规律的数学模型。

在初中物理学中，我们常常使用动力学模型来分析物体的运动状态和受力情况。

通过建立动力学模型，我们可以预测物体的运动轨迹和速度，进而解决相关的物理问题。

例如，在初中学习直线运动时，我们可以建立一个动力学模型来计算物体的位移、速度和加速度。

【收藏】初中数学经典几何模型大全

【收藏】初中数学经典几何模型大全
中点模型
【模型1】倍长
1、倍长中线；
2、倍长类中线；
3、中点遇平行延长相交
【模型2】遇多个中点，构造中位线
1、直接连接中点；
2、连对角线取中点再相连
【例】在菱形ABCD和正三角形BEF中，∠ABC=60°，G是DF 的中点，连接GC、GE．
（1）如图1，当点E在BC边上时，若AB=10，BF=4，求GE的长；（2）如图2，当点F在AB的延长线上时，线段GC、GE有怎样的数量和位置关系，写出你的猜想；并给予证明；（3）如图3，当点F在CB的延长线上时，(2)问中关系还成立吗？写出你的猜想，并给予证明.
角平分线模型
【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形
【例】如图，平行四边形ABCD中，AE平分∠BAD交BC边于E，EF⊥AE交CD边于F，交AD边于H，延长BA到点G，使AG=CF，连接GF．若BC=7，DF=3，EH=3AE，则GF的长为 .
手拉手模型
【例】如图，正方形ABCD的边长为6，点O是对角线AC、BD 的交点，点E在CD上，且DE=2CE，过点C作CF⊥BE，垂足为F，连接OF，则OF的长为 .
邻边相等的对角互补模型
【例】如图，矩形ABCD中，AB=6，AD=5，G为CD中点，DE=DG，FG⊥BE于F，则DF 为 .
半角模型
一线三角模型
弦图模型
最短路径模型
【两点之间线段最短】1、将军饮马
2、费马点【垂线段最短】
【两边之差小于第三边】。

初中三年常用的数学模型大汇总

1 全等变换平移：平行等线段〔平行四边形〕。

对称：角平分线或垂直或半角。

旋转：相邻等线段绕公共顶点旋转。

2 对称全等模型说明：以角平分线为轴在角两边进展截长补短或者作边的垂线，形成对称全等。

两边进展边或者角的等量代换，产生联系。

垂直也可以做为轴进展对称全等。

3 对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称〔翻折〕，翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

4 旋转全等模型半角：有一个角含1/2角及相邻线段。

自旋转：有一对相邻等线段，需要构造旋转全等。

共旋转：有两对相邻等线段，直接寻找旋转全等。

中点旋转：倍长中点相关线段转换成旋转全等问题。

5 旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

6 自旋转变换构造方法：遇60度旋60度，造等边三角形；遇90度旋90度，造等腰直角；遇等腰旋顶点，造旋转全等；遇中点旋180度，造中心对称。

7 共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的容。

通过“8〞字模型可以证明。

8 模型变形说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

9 中点旋转模型说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和的等腰直角三角形〔或者正方形〕公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

10 几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明：通过对称进展等量代换，转换成两点间距离及点到直线距离。