4线性多步方法
【国家自然科学基金】_线性多步方法_基金支持热词逐年推荐_【万方软件创新助手】_20140731
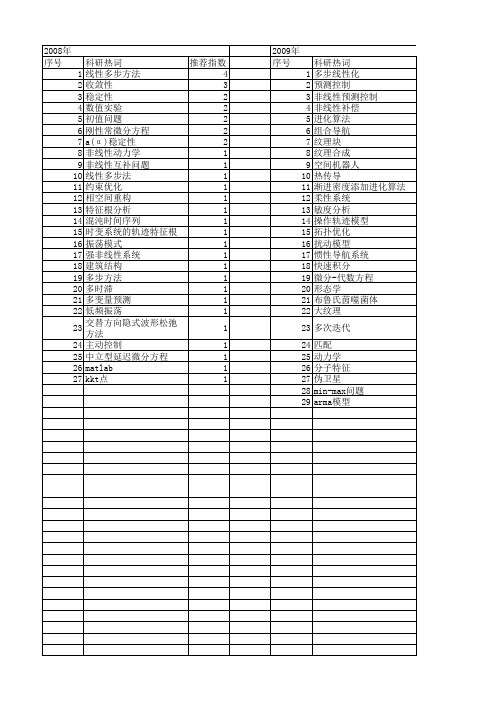
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 颤振 预测控制 零偏vsp 迭代算法 轨控 耦合 线性组合 线性矩阵方程 线性二次型调节器 波场分离 气动弹性 极小范数解 最佳逼近 手指 广义自反矩阵 姿控 多步检验量 多模态 多指抓取 四旋翼飞行器 同相轴排齐 叶轮机 双置信因子 动力学模型异常 力优化 初值 vlbi svd rbf-arx模型
科研热词 推荐指数 气动弹性 2 颤振 1 预测补偿 1 超限插值 1 调度算法 1 解的存在唯一性 1 膜蛋白质 1 综合 1 线性时不变系统 1 线性多步方法 1 紧耦合 1 空分氮塞 1 相空间重构 1 热解过程 1 热分析动力学 1 混沌预测 1 永磁同步电机 1 柚皮苷 1 极限环 1 最小二乘支持向量机 1 时滞积分微分方程 1 无序量测 1 数值方法 1 径向基函数 1 常微分方程初值问题 1 峰值功耗 1 小鼠肝脏 1 多维离子交换色谱 1 多步runge-kutta方法 1 多核学习 1 多变量时间序列分析 1 变量预测 1 反相高效液相色谱 1 卡尔曼滤波 1 单调性 1 十二烷基硫酸钠-聚丙烯酰胺凝胶电泳 1 功耗控制 1 串联质谱 1 一般线性方法 1 tg-dtg/dta 1 rom 1 rbf神经网络 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
数值分析(26)线性多步法

其局部截断误差为
Rn1
19 720
h5
yn(5) (
)
xn2 xn1
由于积分区间在插值区间[ xn2 , xn1 ]内,故Adams隐式
公式又称为Adams内插公式
数值分析
数值分析
(3)米尔尼( Miline )公式
4 yn1 yn3 3 h(2 fn fn1 2 fn2 ) 称为Miline公式,其局部截断误差为
这就是四阶Adams显式公式。由于积分区间在插值
区间[ xn3 , xn ]外面,又称为四阶Adams外插公式。
由插值余项公式可得其局部截断误差为
Rn1
xn1 xn
F (4) ( x )
4!
3 j0
(x
xn j )dx
xn1 xn
y(5) ( x )
4!
3
(x
j0
xn j )dx
数值分析
2!
h2
y(4) n
3!
h3
y(5) n
4!
h4 O(h(5) )
数值分析
数值分析
将以上各公式代入并整理,得
yn1 (0 1 ) yn (1 1 0 1 ) yn' h
(1
2
1
1 ) yn''h2
( 1
6
1
2
1
2
) yn'''h3
(1
24
1
6
1
6
)
y(4) n
h4
(
1
120
5!
yn1 (0 1 ) yn (1 1 0 1 ) yn' h
(1
数值计算方法 线性多步法 - 线性多步法

由四阶Adams隐示公式有
h yn1 yn 24 (9 fn1 19 fn 5 fn1 fn2 )
1
典
24 (0.9 yn1 22.1 yn 0.5 yn1 0.1 yn2 0.24n 0.12)
型
例
由上式可解出
题
1
yn1 24.9 (22.1 yn 0.5 yn1 0.1 yn2 0.24n 0.12)
式公式对预测值进行校正,求出 y( xn1)的近似值 yn1.
思 考 题
线性多步法的构造基于泰勒展开或数值积分, 从数值积分出发,如何推导出线性多步法? 如何估计误差?
的数值解.
典
y x y 0 x 1
y(0)
0
取h 0.1
型 例
根据题意, xn nh 0.1n, fn xn yn,
题
由四阶Adams显示公式有
h yn1 yn 24 (55 fn 59 fn1 37 fn2 9 fn3 )
1 24 (18.5 yn 5.9 yn1 3.7 yn2 0.9 yn3 0.24n 0.12)
一 般 公
Rn k
L[
y(
xn
);
h]
k 1
k
y( xnk ) i y( xni ) h i y( xni )
式
i0
i0
若Rn+k=O(hp+1),则称方法是 p阶的.
对Rn+k在xn处泰勒展开,由于
线
y( xn
ih)
y( xn ) ihy(xn )
(ih)2 2!
y(xn )
式
其中 c0 1 (0 1 k1 ),
c1 k [1 22 (k 1)k1] (0 1 k ),
Milne—Hamming线性多步法在求解姿态四元数微分方程中的应用

mut se r c s n —o r ci g ag r h s ito u e n t i p p r l —t p f e a t g c re t o t m wa n r d c d i h s a e .Th r c s e fs l ig at u e q ae o i o i n l i e p o e s s o o vn t t d u tmin i
解姿 态四元数微分方程 的有效方法, 其稳定度明显优于 四阶龙格一 库塔算法并且计算量小。
关 键 词 : 联 惯 性 导航 系 统 ; leH m n 性 多步 法 ; 态 四元 数 ; 捷 Mi — a mi n g线 姿 龙格 库塔 法 文 献 标 识 码 : A 中图 分 类 号 :2 8 P2
Ap ia i n o in - mm i n a u t- t p Fo e a tng Co r c i g pl to f M l e Ha c ng Li e r M lise r c si ・ r e tn
A g r h t ov t td aeno i e e t l q ain loi m oS leA t u eQu tr in D f rni u t t i aE o
摘要 : 姿态微分方程 的求解是 SN (t pdw nra N vgt nSs m) IS Sr —o nIetl aiao yt 导航解算 中一项重要 的内容 , a i i e 对算法
的稳 定 性 、 度 和 计 算 量 有 较 高 的要 求 。 引入 了一 种 求 解 姿 态 四 元 数 微 分 方 程 的 新 方 法— — Mi — a m n 精 MeH m ig 线 性 多步 预 测 校 正 方法 , 细推 导 了应 用 此 方 法 求 解姿 态 四元 数 微 分 方 程 的过 程 。 应用 仿 真 数据 和 实 测 数 据 详 对 此算 法 和 四阶 龙格 一 塔 算 法 进 行 了对 比 验 证 , 果 表 明 Mi eH m n 库 结 l — a mig线 性 多步 预 测 校 正 方 法 是 一 种 求 n
线性规划问题的两种求解方式

线性规划问题的两种求解⽅式线性规划问题的两种求解⽅式线性规划是运筹学中研究较早、发展较快、应⽤⼴泛、⽅法较成熟的⼀个重要分⽀,它是辅助⼈们进⾏科学管理的⼀种数学⽅法。
线性规划所研究的是:在⼀定条件下,合理安排⼈⼒物⼒等资源,使经济效果达到最好。
⼀般地,求线性⽬标函数在线性约束条件下的最⼤值或最⼩值的问题,统称为线性规划问题。
解决线性规划问题常⽤的⽅法是图解法和单纯性法,⽽图解法简单⽅便,但只适⽤于⼆维的线性规划问题,单纯性法的优点是可以适⽤于所有的线性规划问题,缺点是单纯形法中涉及⼤量不同的算法,为了针对不同的线性规划问题,计算量⼤,复杂繁琐。
在这个计算机⾼速发展的阶段,利⽤Excel建⽴电⼦表格模型,并利⽤它提供的“规划求解”⼯具,能轻松快捷地求解线性模型的解。
⽆论利⽤哪种⽅法进⾏求解线性规划问题,⾸先都需要对线性规划问题建⽴数学模型,确定⽬标函数和相应的约束条件,进⽽进⾏求解。
从实际问题中建⽴数学模型⼀般有以下三个步骤;1、根据所求⽬标的影响因素找到决策变量;2、由决策变量和所求⽬标的函数关系确定⽬标函数;3、由决策变量所受的限制条件确定决策变量所要满⾜的约束条件。
以下是分别利⽤单纯形法和Excel表格中的“规划求解”两种⽅法对例题进⾏求解的过程。
例题:某⼯⼚在计划期内要安排⽣产I、II两种产品,已知⽣产单位产品所需的设备台时分别为1台时、2台时,所需原材料A分别为4单位、0单位,所需原材料B分别为0单位、4单位,⼯⼚中设备运转最多台时为8台时,原材料A、B的总量分别为16单位、12单位。
每⽣产出I、II产品所获得的利润为2和3,问I、II两种产品的⽣产数量的哪种组合能使总利润最⼤?这是⼀个典型的产品组合问题,现将问题中的有关数据列表1-1如下:表1-1I II 限量设备 1 2 8台时原材料A 4 0 16单位原材料B 0 4 12单位所获利润 2 3⾸先对例题建⽴数学模型。
问题的决策变量有两个:产品I的⽣产数量和产品II的⽣产数量;⽬标是总利润最⼤;需满⾜的条件是:(1)两种产品使⽤设备的台时<= 台时限量值(2) ⽣产两种产品使⽤原材料A、B的数量<= 限量值(3)产品I、II的⽣产数量均>=0。
常微分方程的数值解法

第六章 常微分方程的数值解法 §6.0 引言§6.1 算法构造的主要途径§6.2 Runge-Kutta Method 算法§6.3 线性多步法§6.4 线性多步法的一般形式§6.5 算法的稳定性、收敛性§6.0 引 言1. 主要考虑如下的一阶常微分方程初值问题的求解:()()00,dy f x y dx y x y ⎧=⎪⎪⎨=⎪⎪⎩ 微分方程的解就是求一个函数y=y(x),使得该函数满足微分方程并且符合初值条件。
2. 例如微分方程:xy '-2y=4x ;初始条件: y(1)=-3。
于是可得一阶常微分方程的初始问题24(1)3y y x y ⎧'=+⎪⎨⎪=-⎩。
显然函数y(x)=x 2-4x 满足以上条件,因而是该初始问题的微分方程的解。
3. 但是,只有一些特殊类型的微分方程问题能够得到用解析表达式表示的函数解,而大量的微分方程问题很难得到其解析解,有的甚至无法用解析表达式来表示。
因此,只能依赖于数值方法去获得微分方程的数值解。
4. 微分方程的数值解:设微分方程问题的解y(x)的存在区间是[a,b ],初始点x 0=a ,将[a,b ]进行划分得一系列节点x 0 , x 1 ,...,x n ,其中a= x 0< x 1<…< x n =b 。
y(x)的解析表达式不容易得到或根本无法得到,我们用数值方法求得y(x)在每个节点x k 的近似值y(x k ),即y≈y(x k ),这样y 0 , y 1 ,...,y n 称为微分方程的数值解。
如图所示:§6.1 算法构造的主要途径x 0 x 1 x 2 ...1 欧拉公式1.1 构造的思想:利用差商代替一阶导数,即010()()x x y x y x dy dx h =-≈,则 1000()()(,)y x y x f x y h -≈。
常微分方程数值解法2线性多步法

03
常见的线性多步法
欧拉方法
总结词
欧拉方法是常微分方程数值解法中最简单的一种方法,它基于线性近似,通过已知的函 数值来估计新的函数值。
详细描述
欧拉方法的基本思想是利用已知的函数值来估计下一个点的函数值。具体来说,假设我 们有一个函数 (y = f(x)),在已知 (x_0) 处的函数值 (y_0 = f(x_0)) 的情况下,欧拉方法 通过线性插值来估计 (x_1) 处的函数值 (y_1),即 (y_1 = y_0 + h f(x_0)),其中 (h) 是
05
线性多步法的优缺点
优点
稳定性好
线性多步法在处理常微分方程时具有较好的数值稳定性, 能够有效地抑制数值振荡,提高计算结果的精度。
01
易于实现
线性多步法的计算过程相对简单,易于 编程实现,适合于大规模数值计算。
02
03
精度可调
通过选择不同的步长和线性多步法公 式,可以灵活地调整计算结果的精度, 满足不同的数值模拟需求。
改进方法的收敛性
研究收敛性条件
深入研究线性多步法的收敛性条件,了解哪些情况下方法可能不收 敛,并寻找改进措施。
优化迭代算法
通过优化迭代算法,提高方法的收敛速度和精度,减少迭代次数, 提高计算效率。
引入预处理技术
利用预处理技术对线性系统进行预处理,改善系统的条件数,提高方 法的收敛性。
拓展应用领域
在工程问题中的应用
控制系统设计
在工程领域中,线性多步法可以用于控制系统设计,通过 建立控制系统的数学模型,设计控制算法和控制器,实现 系统的稳定性和性能优化。
ADAMS方法和一般线性多步法

Created with SmartPrinter trail version
2. l 步隐式Adams(亚当姆斯)方法(内插法)
公式: 用过点 ( xk i , fk i ),i = 1,0,L,l 1 的插值多项式
~p(x) = l 1 fk
i= 1
l1 x x i
fk 5
fk
fk 2) 1 + fk
2)
yk+1 = yk + 7h20(251fk+1 + 646fk 264fk 1 + 106fk 2 19fk 3)
表 8.3
显式Adams方法
步数(l ) 方法阶 ( p)
公式
1
1
2
2
3
3
4
4
yk+1 = yk + hfk
yk+1
=
yk
+
h(3 2
fk
fk 1)
= xk+1 [ f (x, y(x))
i=0
p( x)]dx
xk
t=x
xk
= xk+1 y(l+1)( (x))(x
xk
l!
xk )(x
xk 1)L(x
xk l+1)dx
h
=
ቤተ መጻሕፍቲ ባይዱ
y(l +1)(
( x )) {
1
t(t + 1)(t + 2)L(t + l
1)dt }hl +1
l!
0
Created with SmartPrinter trail version
xx xxkk i
8.4-8.5线性多步法及收敛性与稳定性分析

f x ( x0 , y0 )
]
在平移一下,即化成检验方程形式.
y' y y ( x0 ) y0
--------------(2)
y y0e
当 Re 0时, 当 Re 0时,
其关系式为
( x x0 )
( y0 0)
y ( x) | (as x ); y ( x) | 0 (as x ), 此时, 试验方程是稳定的.
(5) Simpson 2步4阶隐式公式
h yn 1 y n 1 ( f n 1 4 f n 2 f n 1 ) 3
1 5 (5) Tn 1 h y ( xn ) O (h 6 ) 90
多步方法的特点: (1)、 因初始条件只有一个,多步方法的启动要借助 高阶的单步方法来开始. (2)、多步方法比较简单,只要在这几个点的函数 值的线性组合, 而且每步中所用函数值, 有些下一 步还可使用。
要使 |1 h | 1,
即 |1 h | 1 给出了绝对稳定区域 {z | z 1| 1|},
这是复平面上以 (1,0)为圆心的单位圆, 绝对稳定区间为(-2,0).
2. 隐式Euler公式
yn1 yn hf ( xn1, yn1 ) yn hyn1
2. 一个方法的整体截断误差比局部截断误差低一阶.
若某些引入的误差, 在以后的传播中被压缩, 衰减或增长 可以控制, 就认为数值方法 (1) 是数值稳定的, 反之, 若在传 播中被放大而无法控制, 就认为是数值不稳定.其中, 若误 差的传播可以被压缩, 衰减, 则称绝对稳定.
y ' =f ( x, y ), x D 定义8.5.2 对初值问题 对于固定的 y ( x0 ) y 0 , 步长 h,在数值计算中, 节点值 yi 产生一扰动 i (包括初值y 0 ), 而仅由这一个扰动引起的以后各节点值 y j ( j i ) 的变化 j 都不超过 i , 即 | j || i |, 就称这个数值方法是稳定的.
数值分析线性多步法讲解

fn-
r
yn+1 = yn + h bri fn-i
i=0
其 中 :b ri
=
(-1)i
r j=i
j
i a j
§5 线性多步法 © 2009, Henan Polytechnic University
77
第五章 常微分方程数值解法
局部截断误差为:Rr
=
y(xn+1) - yn+1 = h
j fn- j =
i=0
-1
i
j
i
fn-i
r
r
j
a j j fn- j = a j
j=0
j=0 i=0
-1
i j
i
fn-i
=
r i=0
-1
i
r j =i
j i
a
j
fn-i
=
r i=0
bri
1
0 Rr (xn + th) h dt
Newton 插值余项
§5 线性多步法 © 2009, Henan Polytechnic University
55
第五章 常微分方程数值解法
xn+1
f
(x,
y(x)) dx
x=xn +th
=
xn
1
0 Nr (xn + th) h dt +
1
0 Rr (xn + th) h dt
构造 r 阶牛顿后插多项式, 有
Nr (xn
线性多步法

y ( x i 1 ) y ( x i ) x
xi 1 i
f ( x, y ( x ))dx
为了近似计算式中的积分,以xi−k , xi−k+1, , xi−1, xi 为插值节点,作函数f (x, y (x)) 的k 次插值多项 式pk (x),从而有 f (x, y (x) ) = pk (x) + R (x), 其中,R (x)为插值余项
i 2, , N 1
将 f (x, y) = 2x + y, h = 0.1, xi = 0.1i 代入,得
1 yi 1 (0.9 yi 1 25.9 yi 0.5 yi 1 0.2 yi 2 0.48i 0.24) 24
本例可以解出yi+1 使其成为显式
几个常用的Adams外插公式如下 ① 单步法(k=0)
y i 1 y i hy i
1 2 ei 1 h y( i ) 2
② 二步法(k=1)
i 0,1,, N 1
h yi 1 yi (3 y y ) i 0,1, , N 1 i i 1 2
§5 线性多步法 /*Linear multistep method*/
一、Adams外插法 二、Adams内插法 三、Taylor级数法
求解初值问题的数值方法都是“步进式”的,即 求 解过程从初值y0开始,顺着节点的排列次序,一 步一步地向前推进.所以,在计算yi+1 时,前面 的i + 1 个值y0, y1, , y i 都是已知的.如果在计算 yi+1 时能充分利用这些已有的信息,而不是像单 步法中那样,只用其前一步的值yi,则可望构造 出精度高,但计算量小的求解公式.线性多步法 k k 就是基于这一思想发展起来的,其计算公式可表 yi 1 r yi r h r y 示为 i r
线性多步法

(6)计算 f3 f ( x3 , y3 ) x x3 h 4 112 p y0 (2 f3 f 2 2 f1 ) m p (c0 p0 ) 3 121 1 3 c (9 y3 y1 ) h[ f ( x, m) 2 f 3 f 2 ] 8 8 9 y c (c p ) 输出(x, y ) 121 (7)若n N,置n 1 n, x j 1 x j , y j 1 y j , f j 1 f j ( j 0,1, 2), x x3 , y y3 , p p0 , c c0 , 转6; 否则停机。
算法 ba (1)输入 a, b, f ( x, y ), N , y0 (2)置h , x0 a, n 1 N (3)计算 f n 1 f ( xn 1 , yn 1 ) K1 hf n 1 h K1 K 2 hf ( xn 1 , yn 1 ) 2 2
(i 1, 2, , N ) (i 1, 2, , N )
若对 y 和 f 采用向量的记号 y ' f ( x, y); y( x0 ) y 0 ;
f ( f1 , f 2 , f N ) ;
T
或表达为 h yi ,n 1 yin ( K i1 2 K i 2 2 K i 3 K i 4 ) 6 (i 1, 2, , N ), 其中 K i1 fi ( xn , y1n , y2n , , yNn ); h h h h K i 2 fi ( xn , y1n K11 , y2 n K 21 , , y Nn K N 1 ); 2 2 2 2 h h h h K i 3 fi ( xn , y1n K12 , y2 n K 22 , , yNn K N 2 ); 2 2 2 2 K i 4 fi ( xn h, y1n hK13 , y2 n hK 23 , , y Nn hK N 3 );
求解微分方程的线性多步法

讯 * 一k hI -
展 式得 u= 0h( ,0 ,1 是 ut 的近 似值 。N Iu又可 算 出 Iu+ft U)1就 0 1 () 1  ̄l l
U , 此 下 去可 算 出U 所 有 结 点 上 的值 , 般 递推 公 式 为u 1 ,如 在 一 = 由文 献 [ ] , 解 该 类 方 程分 为单 步法 和多 步 法 。只 要 1知 求 N , N u 即可 算 出u 的算 法 称 为单 步 方 法 ,单 步 法 包 括 J J t l Nh
… , m+k-I才 能 求 U
出u+(> ) k 1 的算 法 称 为 多 步 方 法 , 性 多 步 法 包 括 数值 积 分 线 法 和待 定 系 数法 , 一 般 形 式 为 其 u。 h B , 里 , : 这
-
( 0 1K, ) 常数 , j ,, k是 = 它需 要 有k 初 值 u, … ,k才 能 得 到 个 。U , U 1
060 ) 6 0 4
用 低 阶微 商 构 造 高 精 度 的 方 法对 实 际计 算 是 很 有 意 义 的 。 u 对 ( 1= ( ). u ()t 用u () 点t 1 处 的 函数 值 及 其 各 t ) u t + td利 r t在 , t
阶 导数 值 构 造 H ri 型 插 值 多项 式 , 代 积 分 。 去 误 差 项 即 ent e 再 舍
【()u uc =。 0
㈩
由 于F 是 已 知 的 , 是 ( ) m 于 2 式可 用 迭 代 法 求 解 。 迭 代 法 都 需 要有 u , n的 迭 代初 值 。 取 一 个好 的u 即u+ 选
其 中伪 t 的 已知 函 数 , 给 定 的初 值 。我 们假 设 函数 和U u为
线性多步法

1.待求解问题描述
⎧ y ' = f (t , y ) ⎨ ⎩ y (t0 ) = y0
(1)
2、线性多步法表达式建立
Lk ( y (t ), h) = ∑ [α j y (t + jh) − hβ j y ' (t + jh)]
j =0
k
(2)
将
y (t + jh )
和
y ' ( t + jh )
公式性质: 1. 公式左边j=k项为我们需要求取得项,j<k的项为已 得项; 2. 公式右边可以使用f(t,y)直接带入求取; 3. 当右边 β k ≠ 0 时,公式所得到的算法为隐式算法;否
则为显式算法。 4. (4) 式中,我们可以要求α k =1,因为如果α <>1,只需 公式两边同时除以 α k 即可使得 =1 k
⎧ ⎪c = α + α + α + ... + α = 0 k 0 1 2 ⎪0 ⎪c1 = α1 + 2α2 + ... + kαk − (β0 + β1 + β2 + ... + βk ) = 0 ⎪ ⎨... ⎪ 1 1 ⎪c p = (α1 + 2 p α2 + ... + k pαk ) − (β1 + 2 p−1 β2 + ... + k p−1βk ) = 0, p ≥ 2 p! ( p −1)! ⎪ ⎪ p = 2,3,... ⎩
⎪c = α + 2 − (β + β + β ) = 0 0 2 2 ⎪1 1 ⎪ 1 ⎨c2 α=0α1 + 4) − (β1 + 2β2 ) = 0 1、 = ( 2 ⎪ h yn+2 = yn+1 + [5fn+2 +8fn+1 − fn ] ⎪ 1 12 ⎪c3 = (α1 + 8) − 12(β1 + 4β2 ) = 0 6 ⎩
ADAMS方法和一般线性多步法

x
l i=
1
f ( xk i ,
1
xk +1 )( x
y( xk
xk
l1
i ))[
j= 1 ji
)L( x
x xk i
xk
xk j xk j
l +1 )
]
l1
则 y( xk+1) yk+1 = y( xk +1 ) { y( xk ) + h
l,i f ( xk i , y( xk i ))}
i= 1
(5.2)
i=0
Created with SmartPrinter trail version
由插值多项式余项: Rl 1(x) = f ( x, y(x)) p( x)
= f ( x, y( x))
l1
f ( xk
i=0
i , y( xk
l1 x
i ))[
j =0
xk
l 几种低阶显式Adams方法的公式及主局部截断误差的系数
l1
当 l =1 时,p( x) = fk ,
yk +1 = yk + h f l,i k i (5.2)
( ) yk+1 = yk +
x k +1 xk
fkdx,
或者
yk +1
=
yk
+h
i=0
1,0 fk ,
1,0 = 1.
l =1
即
yk+1 = yk + hfk ,
(5.3)
ji
x xk j = x xk + xk xk j = th + jh xk i xk j = xk i xk + xk xk j = ih+ jh
数值计算方法课后习题答案吕同富

数值计算方法课后习题答案吕同富【篇一:《数值计算方法》(二)课程教学大纲】txt>课程编号: l124008课程类别:专业必修学分数: 3 学时数:48 适用专业:信息与计算科学应修(先修)课程:数学分析、高等代数一、本课程的地位和作用数值分析(二)为数值分析课程的第二部分,它是信息与计算科学专业的一门专业必修课。
主要内容包括函数最佳逼近、数值积分、数值微分、常微分方程数值解法。
通过本课程的学习,学生将初步具备用计算机去有效地解决实际问题的能力。
二、本课程的教学目标通过本课程的学习,使学生了解和掌握求解函数最佳逼近、数值积分、数值微分、常微分方程等问题所涉及的各种常用的数值计算方法、数值方法的构造原理及适用范围。
本课程坚持理论与实践教学并重的原则,理论上主要讲述求解函数最佳逼近、数值积分、数值微分、常微分方程等问题的基本理论和基本方法。
与此同时,通过上机实验加深学生对各种计算方法的理解,为今后用计算机去有效地解决实际问题打下基础。
三、课程内容和基本要求(“*”记号标记难点内容,“▽”记号标记重点内容,“▽*”记号标记既是重点又是难点的内容)第六章函数最佳逼近 1.教学基本要求(1)理解:几类常用的正交多项式。
(2)掌握:最佳一致逼近和最佳平方逼近。
(3)掌握:曲线拟合的最小二乘法。
2.教学内容(1)*正交多项式。
(2)▽*最佳一致逼近。
(3)▽最佳平方逼近。
(4)正交多项式的逼近性质。
(5)▽曲线拟合的最小二乘法。
第七章数值积分 1.教学基本要求(1)理解:机械求积公式的基本思想、插值型求积公式的特点。
(2)掌握:newton-cotes求积公式、复合求积公式。
(3)掌握:romberg求积公式、gauss求积公式。
2.教学内容(1)*机械求积公式。
(2)▽newton-cotes求积公式。
(3)▽复合求积公式。
(4)变步长求积公式。
(5)▽romberg求积公式。
(6)▽*gauss求积公式第八章数值微分 1.教学基本要求(1)了解:数值微分的中点法。
11-时间积分

时间积分以三维非定常可压缩无粘流的Euler 方程组为例。
在直角坐标系下,流动控制方程的形式为0U F G Ht x y z∂∂∂∂+++=∂∂∂∂ (1)1. 半离散化方法将计算区域进行空间离散化,则在每一个网格点上有()ijk ijk dU t F G H dtx yz ⎛⎫∂∂∂=-++ ⎪∂∂∂⎝⎭ (2)将上式右端用适当的差分格式近似代替,即ijk ijk F G H R x yz ⎛⎫∂∂∂=-++ ⎪∂∂∂⎝⎭ 就得到半离散化格式()ijk ijk dU t R dt=(3)设整个计算区域内共有M 个空间网格点,对所有的网格点列出(2)式并将它们联立在一起。
为此,将所有的M 个未知向量 ()ijk U t 组合在一起,形成总体的未知向量 ()Q Q t = ,再将所有的M 个右端向量 ijk R 组合在一起,形成总体的右端项(向量)()R R Q = ,就得到常微分方程组()()dQ t R Q dt=(4)根据与控制方程组(1)相应的初始条件,可为方程组(4)给定初值,使其成为常微分方程组初值问题。
2. 显式Runge-Kutta 方法显式Runge-Kutta 方法的一般形式为()()()()1112211122,11 2,3,,+--⎧=+∆+++⎪⎪=⎪⎪⎨⎪⎡⎤=+∆+++⎣⎦⎪⎪=⎪⎩n n s s n n r r r r r r Q Q t b K b K b K K R Q K R Q t a K a K a K r s (5)这里 ()n n Q Q t = 是 n t t = 时刻的流场解(已知), ()()11n n n Q Q t Q t t ++==+∆ 则是 1n t t += 时刻的流场解(待求),t ∆ 为时间步长。
(5)式中,s 称为方法的步数。
若(5)式的(时间)精度为p 阶,则称(5)式为s 步p 阶显式Runge-Kutta 方法。
理论上已经证明了s 步显式Runge-Kutta 方法的最高所能达到的精度,如下表所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、k步隐式线性多步法
j 0
k
j
yn j h j f n j
j 0
k
( )
k
2 2 , 其中 j j 均为常数,且 k 0, k 0,0 0 0
等价形式: yn k
j 0
k 1
j
yn j h j f n j
2 xn 2 xn1 h yn [55( yn ) 59( yn1 ) 24 yn yn1
xi
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
R-K方法
Adams预-校法
精确解
1 1.095446 1.183217 1.264912 1.3416413571 1.4142138334 1.4832398242 1.5491933804 1.6124515364 1.6733199993
5 f ( xn1 , yn1 ) f ( xn 2 , yn 2 )]
(隐式)
2x dy 例3:用Adams预报-校正公式 y y x [0,1] 求解下列初值问题h 0.1 。 dx y ( 0) 1 解: Adams预报-校正公式:
y
( 0) n 1
2 2
x xn m f ( x , y ) L3 ( x ) ( ) f ( x n k , yn k ) k 1 m 1 xn k xn m
k 1
yn1 yn
2
mk
f ( x n k , yn k )
xn1 xn
x xn m dx m 1 xn k xn m
j 0
隐式线性多步法的求法: 记 yn k h k f n k g
其中 g
(h
j 0
k 1
j
f n j j yn j ) 已知
( s 1) n k
采用下列迭代法求解 y
h k f ( xn k , y
( s) n k
) g
四、线性多步法的收敛阶和局部截断误差: 根据线性多步法的迭代公式
Adams显式公式的局部截断误差:
由Lagrange插值余项知
4
4阶方法
d ( x) f ( x , y ) L3 ( x ) [ 4 f ( x , y( x )]x dx 4!
xn1 xn
其中 ( x) ( x xn )( x xn1 )( x xn 2 )( x xn3 )
1.0000000000 1.0954451153 1.1832159566 1.2649110640 1.3416407864 1.4142135623 1.4832396974 1.5491933384 1.6124515496 1.6733200530
1.0
1.7320507198 1.7320508075
2 mk
h yn1 yn [9 f ( xn1 , yn1 ) 19 f ( xn , yn ) 24
5 f ( xn1 , yn1 ) f ( xn 2 , yn 2 )]
Adams三步隐式公式的局部截断误差:
19 5 ( 5 ) 5 y( xn1 ) yn1 h y ( ) O( h ) 720
Def 3 若在 Lh 的表达式中,系数满足
c0 c1 ... c p 0; c p1 0
则称线性差分算子 Lh[ y( x ), h] 和与之对应的线性 多步法(*)是 p 阶的。
Def 4 线性多步法(*)在 xn k 上的局部截断误差为
Tn k Lh [ y( xn ), h] [ j y( xn j ) h j y( xn j )]
j 0
k 1
j
yn j h j f n j
j 0
如果 k 0 ,则(*)式称为显式k步法; 直接求解 如果 k 0 ,则(*)式称为隐式k步法; 迭代求解
二、阿达姆斯(Adams)方法
基本思想:
dy 对微分方程 f ( x , y ) 两边在区间[ xn , xn1 ] 上积分: dx
y( xn1 ) yn1
[ f ( x, y) L3 ( x )]dx
xn1 xn
d ( x) [ 4 f ( x , y )]x dx(第二积分中值定理) dx 4!
4
1 d 5 y( x ) |x 5 4 ! dx
xn1 xn
251 5 ( 5 ) 5 h y ( ) O( h ) ( x )dx 720
k 0
3
m0 mk
3
x xn m dx xn k xn m
h yn1 yn [55 f ( xn , yn ) 59 f ( xn1 , yn1 ) 24
37 f ( xn2 , yn2 ) 9 f ( xn3 , yn3 )]
称之为Adams四步显式公式(或Adams外插公式)
构造 f ( x , y ) 的3次Lagrange插值多项式:
f ( x , y ) L3 ( x ) (
k 0 m0 mk
3
3
x xn m ) f ( x n k , yn k ) x n k xn m
xn1 xn
yn1 yn f ( xn k , yn k )
k步线性多步法的一般形式
yn k j yn j h j f n j
j 0 j 0
k 1
k
Adams四步显式公式(四阶方法):
选取下列4个等距节点作为插值节点:
xn3 , xn2 , xn1 , xn
h yn1 yn [55 f ( xn , yn ) 59 f ( xn1 , yn1 ) 24
§4 线性多步法/*Linear Mutistep Method*/
一、k步线性多步法的一般形式
j 0
k
j
yn j h j f n j
j 0
k
( )
fn f ( xn , yn )
k
2 2 , 其中 j j 均为常数,且 k 0,0 0 0
等价形式: yn k
Tn k 与 y( xn k ) yn k的首项相同
37 f ( xn2 , yn2 ) 9 f ( xn3 , yn3 )]
Adams三步隐式公式(或Adams内插公式):
选取下列4个等距节点作为插值节点:
xk x0 kh; k n 2, n 1, n, n 1
构造 f ( x , y ) 的3次Lagrange插值多项式:
2 xn 2 2 xn 3 37( yn 2 ) 9( yn3 )] yn 2 yn3 2 xn1 2 xn h ( 0) yn1 yn [9( yn1 ( 0 ) ) 19( yn ) 24 yn1 yn 2 xn1 2 xn 2 5( yn1 ) ( yn 2 )] yn1 yn 2
Adams预报-校正公式:
y
(0) n 1
初值由4阶R-K方法计算 (显式)
h yn [55 f ( xn , yn ) 59 f ( xn1 , yn1 ) 24
37 f ( xn2 , yn2 ) 9 f ( xn3 , yn3 )]
h (0) yn1 yn [9 f ( xn1 , yn 1 ) 19 f ( xn , yn ) 24
j 0
k
Tn k 按 h 展开的首项称为主局部截断误差(主项)
类似单步法的讨论,假设 yn j y( xn j ); j 0,1,..., k 1 易验证,对于显式多步法:
Tn k y( xn k ) yn k
说明:显式线性多步法的局部截断误差相当于假设 计算 yn k之前的各步是精确的,再向前一步的误差 对于隐式多步法,易证:
k k
j 0
j
yn j h j f n j
j 0
( )
定义线性差分算子:
Lh [ y( x ); h] [ j y( x jຫໍສະໝຸດ ) h j y( x jh)]
j 0
k
利用一元函数的Taylor展开公式
2 q (q) Lh c0 y( x) c1hy ( x) c2h y ( x) ... cqh y ( x) ...
y( xn1 ) y( xn )
xn1
xn
f ( x, y )dx
在积分区间 [ xn , xn1 ] 上用 f ( x , y ) 的插值多项式近似代替
Adams四步显式公式:
选取下列4个等距节点作为插值节点:
xk x0 kh; k n 3, n 2, n 1, n
