复习:几个典型例题
中考历史复习题:中华人民共和国成立---典型例题_学习指导

中考历史复习题:中华人民共和国成立---典型例题_学习指导中考历史复习题:中华人民共和国成立---典型例题1、中国民主革命胜利的基本经验中,最重要的一条是A.中国共产党的领导B.开展武装斗争C.走社会主义道路D.建立统一战线答案:A分析:四条经验均为中国民主革命胜利的基本经验,但最重要的是能对其它三条起决定作用的一条。
只有在中国共产党的领导下,再开展武装斗争、建立统一战线、团结一切可以团结的人、走社会主义道路,才能赢得中国民主革命的胜利。
2、请思考:中国人民政治协商会议第一次会议是在什么条件下召开的?这次会议为新中国的成立做了哪些准备?新中国成立有什么历史意义?解题思路:本题是分析、说明题。
此题共三问:第一、二问,通过中国人民政协第一次会议召开的历史条件和会议主要内容的分析,认识新中国成立的必然性和可能性;第三问是要通过对新中国成立这一历史性大事的分析,认识其重大历史意义。
有的学生对新政治协商会议召开的条件,容易出现只答一个条件,而不答中国共产党为召开新政治协商会议所做的努力,为会议的召开创造了有利条件。
错误原因:审题不准,把召开新政治协商会议的条件误认为只是问客观上的条件,而没有全面地考虑还包括召开会议的具体条件,这样,就造成答案不全的错误。
在新政协为新中国成立作了哪些准备一问中,学生会出现漏答知识点的错误。
此问实际就是要求答出中国人民政治协商会议的内容。
这次会议内容实质上是两部分。
一部分是制定了起临时宪法作用的(共同纲领),它规定了中华人民共和国的国家性质、领导阶级及建设新中国的总政策、总原则等。
另一部分内容就是为建立新中国做了全面的准备:成立政府、选出主席、确定国旗和国歌、确定首都和纪年方法等。
如果用这种分类的方法,掌握了重点,在答题过程中就不会出现漏答知识点的错误。
中华人民共和国的建立,标志着新民主主义革命的胜利。
所以,此题要求答出新中国成立的伟大历史意义,也就是中国新民主主义革命胜利的伟大历史意义,其内容基本上是相同的。
数与代数(整理与复习)

数与代数(整理与复习)【典型例题】例1.小华上午8时30分出发去姥姥家,下午2时到达姥姥家,她一共用了多长时间?例2.甲船每时行24千米,乙船第时行16千米,两船同时同地北向出发,2时后,甲船因有事转头追赶乙船,几时才能追上乙船?例3.煤气公司铺设一条煤气管道,第一周铺了全长得30%,第二周铺了全长的40%,两周共铺了2800米,这条煤气管道全长多少米?4,四月份生产了2300个零件,二月份生产了例4.某工厂三月份生产的零件比二月份多15%,比四月份少25多少个零件?例5.商店一、二楼柜台数量的比是6:5,如果从一楼调9个柜台给二楼,这时一二楼柜台数量的比是3:4,商店一共有多少个柜台?例6.正方形操场边长增加它的四分之一后,得到新操场的周长是500米原操场的边长是?(用方程解)【课堂练习】1.填空:(1)0.4=( )( ) =10( ) =( )35=( )% (2)一个数个位上是最小的合数,十位上是最小的奇数,百位上是最小的偶数,千位上是最小的质数,万位上是最小的1位数,十万位上是最小的自然数,百万位上是5的倍数,这个数是( )。
(3)最小的五位数是( ),减少1是( );最大的三位数加上1是( )。
(4)10以内的质数有( );合数有( );既是奇数又是合数的最小两位数是( )。
(5)18和36的最大公因数是( );12和42的最小公倍数是( )。
(6)能被2、3、5整除的最大两位数是( );比最大的三位数多1的数是( )。
(7)13628中的“6”表示( );70.6中的“6”表示( );611中的“6”表示( )。
(8)280004320读作( ),四舍五入改写成用“万”作单位的数是( ),省略亿位后的尾数得到的近似数是( )(9)一个数由3个一,5个百分之一和7个千分之一组成,这个数写作( ),读作( ),把这个数精确到十分位是( )。
(10)把0.85吨:170克化简成最简整数比是( )(11)如果男生人数是女生人数的2/3,那么女生人数占全班人数的( )%。
线性代数复习第1-6章典型例题

按最后一列展开再提取每列的公因子
-8-
Dn = ( −1) n+1 (a1 − a n )(a 2 − a n )⋯(a n−1 − a n ) ×
1 a1
2 a1
1 a2
2 a2
⋯
1
1 a n −1
2 a n −1
⋯ a n− 2
2 ⋯ a n− 2
⋮
n a1 − 2
⋮
⋮
⋮
n− 2 a n −1 ( n −1 )
n
x2 ⋯ xn a2 ⋱ an
xk yk ) = a 2 a 3 ⋯ a n (a1 − ∑ k = 2 ak
-6-
n
例9
范德蒙德(Vandermonde)行列式 行列式 范德蒙德
1 a1 Dn =
2 a1
1 a2
2 a2
⋯
1
2 a n −1
1 an
2 an
− an − an
⋯ a n −1 ⋯ ⋮
n n− 2 a 2 − 2 ⋯ a n− 2
Dn = ( a n − a1 )(a n − a 2 )⋯(a n − a n−1 ) Dn −1
Dn − 1 = (a n − 1 − a1 )(a n − 1 − a 2 ) ⋯ (a n − 1 − a n − 2 ) Dn − 2
⋯⋯
D3 = (a 3 − a1 )(a 3 − a 2 ) D2 D2 = (a 2 − a1 ) D1 = a 2 − a1
-17-
例8
设 n 阶方阵 A 满足 A2 = E ,
证明 r ( E + A) + r ( E − A) = n
证
A 2 = E ⇒ ( A + E )( A − E ) = O
六年级上册数学期末应用题专题复习

第一章转化单位1【典型例题】1、小红用三天时间看完一本故事书。
第一天看完了全书的1\3,第二天看了余下的2\5,已知第二天比第三天少看24页,这本故事书一共有多少页?2、某工程队修一段公路,第一天修了全长的1\5多100米,第二天修的比第一天修的4\5多20米,第三天修了600米,正好修完。
这段公路全长多少米?3、有两袋大米,第二袋比第一袋重6千克,已知第一袋大米的重量的1\3恰好与第二袋大米重量的2\7相等,问两袋大米各重多少千克?4、甲乙丙三人买股票,甲买股票用的钱是乙、丙两人所用钱数的1\2,乙买股票用的钱是甲、丙两人所用钱数的1\3。
已知丙用了3000元,求甲、乙共用了多少元?5、瓶内原来盐的重量是水的1\11,加进30克盐后,盐的重量站盐水的重量的1\9。
瓶内原来有盐水多少克?6、某运输队分三次运完一批货物。
第一次运了这批货物的1\4,第二次运了余下的1\3,第三次比第二次多运15吨,这批货物一共有多少吨?7、王叔叔运一堆煤,第一天运了总数的1\4多4吨,第二天运的比第一天的3\4多3吨,第三天运了35吨,正好运完。
这堆煤共有多少吨?8、有两个粮仓,乙仓的存粮比甲仓少120吨,已知甲仓存粮的1\4等于乙仓存粮的1\3,问甲、乙两个仓库各存粮多少吨?9、兄弟三人一起去合买一台电脑,老大带去的钱是另外两个人所带钱数的一半,老二带去的钱是另外两个所带钱数的1\4.已知老三带了2100元,那么老大和老二各带了多少元?10、瓶内原来盐的重量是水的1\10,加进40克盐后,盐的重量站盐水的重量的1\7。
瓶内原来有盐水多少克?【展示平台】1、运进一批水泥,第一天运了这批水泥的1\4,第二天运了第一天的3\5,已知第一天比第二天多运20吨,这批水泥有多少吨?2、某工程队修一段公路,第一天修了全长的2\5,第二天修了余下部分的3\10 多24米,第三天修的是第一天的3\4多60米,正好修完。
这段公路全长多少米?3、甲乙两个仓库共存粮840吨,已知甲仓库存粮的1\4等于乙仓库存粮的1\3问甲、乙两个仓库各存粮多少吨?4、某工厂的甲乙丙三个车间向灾区捐款,甲车间捐款数是另外两个车间捐款数的2\3,乙车间捐款数是另外两个车间捐款数的3\5.已知丙车间捐款数1800元,这三个车间共捐款多少元?5、一个盒子里装有黑白两种棋子,黑子的颗数是总数的五分之三盒子里有黑白两种棋子,黑子的颗数是总数的3\5,把12颗白子放入盒子后,黑子的颗数占总数的3\7,盒子里有黑子多少颗?6、一瓶酒精,第一次倒出2\3又20千克,第二次倒出的是第一次的1\4,瓶中还剩下35克酒精,原来瓶中有多少酒精?7、水果店运来梨和苹果共180千克,梨卖出2\5,苹果卖出1\10,这时梨和苹果剩下的千克数正好相等。
数列专题复习之典型例题(含答案)

数列知识点-——-求通项一、由数列的前几项求数列的通项:观察法和分拆与类比法-—-—-猜测———-证明(略)二、由a n 与S n 的关系求通项a n例1已知数列{a n }的前n 项和为S n =3n -1,则它的通项公式为a n =________。
答案2·3n -1练1 已知数列{a n }的前n 项和S n =3n 2-2n +1,则其通项公式为________. 答案a n =错误!三、由数列的递推公式求通项例3、(1)设数列{}n a 的前n 项和为n S .已知1a a =,13n n n a S +=+,*n ∈N .设3n n n b S =-,求数列{}n b 的通项公式;答案: 13(3)2n n n n b S a -=-=-,*n ∈N .(2)(4)在数列{}n a 中,11a =,22a =,且11(1)n n n a q a qa +-=+-(2,0n q ≥≠).(Ⅰ)设1n n n b a a +=-(*n N ∈),证明{}n b 是等比数列;(Ⅱ)求数列{}n a 的通项公式;答案: 11,,.1,111n n q q q a n q-≠=⎧-+⎪=-⎨⎪⎩(3)在数列{}n a 中,1112(2)2()n n n n a a a n λλλ+*+==++-∈N ,,其中0λ>.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列{}n a 的前n 项和n S ;答案:(1)2nnn a n λ=-+21212(1)22(1)(1)n n n n n n S λλλλλ+++--+=+-≠- 1(1)22(1)2n n n n S +-=+-λ=(4)已知数列{}n a 满足:()213,22n n a a a n n N *+=+=+∈(1)求数列{}n a 的通项公式; (2)设1234212111n n nT a a a a a a -=+++,求lim n n T →∞答案: 11,,.1,111n n q q q a n q-≠=⎧-+⎪=-⎨⎪⎩注意:由数列的递推式求通项常见类型(请同学们查看高一笔记)1.)(1n f a a n n +=+ 2 . n n a n f a )(1=+.3 q pa a n n +=+1(其中p,q 均为常数,)0)1((≠-p pq )。
初中物理各单元经典例题

1复习第一章+走进实验室例1. 用皮卷尺测量球场的宽度,记录的数据是25.36米,这个皮卷尺的最小刻度值是()A. 1mmB. 1cm2-1认识运动、2-2运动的描述【典型例题】例 1. “小小竹排江中游,巍巍青山两岸走”这歌词中“竹排江中游”是以为参照物,“青山两岸走”是以为参照物.例2. 下列现象中,能够说明物体的分子在不停地做无规则运动的是()A. 房间几天不打扫就会有一层灰尘B. 水从高处流向低处C. 放在空气中的铁器过段时间生锈了D. 在一杯白开水中放入白糖,这杯水就有甜味了例4. 关于机械运动的说法中,正确的是A. 宇宙间一切物体都是运动的B. 只有静止的物体才能被选作参照物C. 运动快慢不变的物体,一定在做匀速直线运动D. 对同一物体,选用不同的参照物,其运动情况一定不同2-3[1].运动的速度、2-4能量【典型例题】例1. 关于匀速直线运动的速度,下列讨论正确的说法是()A. 物体运动速度v越大,通过的路程s越长B. 物体运动速度v越大,所用时间t越少C. v的大小由s/t决定,但与s、t的大小无关D. 上述说法都正确例3. 一短跑运动员沿直线跑了5s,前2s内通过16m的路程,后3s通过了30m的路程,这个运动员在5s内的平均速度是()A. 8m/sB. 10m/sC. 9m/sD. 9.2 m /s2运动与能量复习【典型例题】例1. 中国长江科学考察探险队乘坐的中华勇士号橡皮艇在长江上游顺流而下,下面几种说法中正确的是()A. 以橡皮艇为参照物,江水是静止的B. 以江水为参照物,探险队员是静止的C. 以岸边的树为参照物,探险队员是静止的D. 以探险队员为参照物,橡皮艇是运动的例2. 小汽车在平直的公路上匀速行驶,1分钟通过了1200米的路程,小汽车的行驶速度是()A. 1200米/秒B. 20米/秒C. 60米/秒D. 0.5米/秒3-1[1].什么是声音、3-2乐音的三个特征【典型例题】例1. 在装满水的长铁管的一端敲一下,在较远处的另一端将听到次响声。
中考语文现代文阅读复习句式特点训练

中考语文现代文阅读复习句式特点训练一、典型例题考题一:从句式特点的角度,赏析第⑨段画线句。
(3分) 23济南中考《一桌人生》春风从远处的山谷里挤过来,暖暖的。
答案示例:倒装句,将“暖暖的"后置(1),突出了春风的温暖和煦(1),烘托了我看到新桌子时的喜悦心情(1)。
考题二:从句式特点的角度,赏析第⑩段画线句。
(2分) 24济南样题《雪落菘叶》拢上套袖,奶奶横起面板,竖起擀面杖,烧旺炉火。
答案示例:连用多个短句,形象地呈现了奶奶烙饼的劳动场景,表现出奶奶厨艺娴熟、勤劳能干。
(共2分。
句式特点1分,表达效果1分。
意思对即可)二、知识讲析常见句式特点有:长短句结合、句子对仗工整、双重否定句、排比句、反问句、倒装句。
(1)长句和短句:长句的修辞效果是表意严密、精确、细致;短句的修辞效果是表意简洁、明快、有力。
(2)对仗工整:使句子整齐匀称,节奏鲜明;富有音乐美;表意凝练集中,概括力强. (3)双重否定:表示肯定的意思。
双重否定句比一般的肯定句语气更强,更加肯定。
(4)排比:加强句子语气,给人以一气呵成之感,节奏感强,增强语言气势。
(5)反问:可以加强语气,增强文中的气势和说服力,把本来已确定的思想表现得更加鲜明、强烈。
倒装:起到强调、突出的作用。
三、课内回顾例题一:小草偷偷地从土里钻出来,嫩嫩的,绿绿的。
园子里,田野里,瞧去,一大片一大片满是的。
坐着,躺着,打两个滚,踢几脚球,赛几趟跑,捉几回迷藏。
风轻悄悄的,草软绵绵的。
问题:从句式的角度赏析选文中画横线的句子,说说其表达效果。
答案:本句运用短句和倒装句,强调了小草嫩绿的特点,表现了小草的生机勃勃的样子,表达了作者的喜悦之情。
例题二:这腰鼓,使冰冷的空气立即变得燥热了,使恬静的阳光立即变得飞溅了,使困倦的世界立即变得亢奋了。
赏析:运用排比句式,使语言气势充沛、节奏鲜明、感情强烈。
排比中还应用了三组反义词,在强烈的对比中,更能突出安塞腰鼓的特点。
高考数学复习---《类周期函数》典型例题讲解

高考数学复习---《类周期函数》典型例题讲解【典型例题】例1、(2022·天津一中高三月考)定义域为R 的函数()f x 满足()()22f x f x +=,当[]0,2x 时,()[)[)232,0,11,1,22x x x x f x x −⎧−∈⎪⎪=⎨⎛⎫−∈⎪ ⎪⎪⎝⎭⎩,若当[)4,2x ∈−−时,不等式()2142m f x m ≥−+恒成立,则实数m 的取值范围是( )A .[]2,3B .[]1,3C .[]1,4D .[]2,4【答案】B【解析】 因为当[)4,2x ∈−−时,不等式()2142m f x m ≥−+恒成立,所以()2min 142m f x m ≥−+, 当[)[)4,2,40,2x x ∈−−+∈时,()()()112424f x f x f x =+=+ ()()[)[)2342144,40,1411,41,242x x x x x +−⎧⎡⎤+−++∈⎪⎣⎦⎪=⎨⎛⎫⎪−+∈ ⎪⎪⎝⎭⎩当[)40,1x +∈时,()()()211114444416f x x x ⎡⎤=+−+≥−⨯=−⎣⎦,当[)41,2x +∈时, ()342111424x f x +−⎛⎫=−≥− ⎪⎝⎭,因此当[)4,2x ∈−−时,()2min 1113442m f x m m =−≥−+∴≤≤,选B . 例2、(2022·浙江·杭州高级中学高三期中)定义域为R 的函数()f x 满足(2)3()f x f x +=,当[0,2]x ∈时,2()2f x x x =−,若[4,2]x ∈−−时,13()()18≥−f x t t恒成立,则实数t 的取值范围是( )A .(](],10,3−∞− B.((,0,3⎤−∞⎦ C .[)[)1,03,−+∞ D .))3,⎡⎡+∞⎣⎣【答案】C【解析】因为[]4,2x ∈−−,所以[]40,2x +∈,因为[]0,2x ∈时,()22f x x x =−,所以()()()22442468f x x x x x +=+−+=++, 因为函数()f x 满足()()23f x f x +=, 所以()()()4329f x f x f x +=+=,所以()()()21146899f x f x x x =+=++,[]4,2x ∈−−, 又因为[]4,2x ∈−−,()13t 18f x t ⎛⎫≥− ⎪⎝⎭恒成立, 故()131t 189min f x t ⎛⎫−≤=− ⎪⎝⎭, 解不等式可得t 3≥或1t 0−≤<.例3、(2022山西省榆林市高三二模理科数学试卷)定义域为R 的函数()f x 满足()()22f x f x +=,当[)0,2x ∈时,()[)[)2213,0,1{ln ,1,2x x x f x x x x −+∈=∈,若当[)4,2x ∈−−时,函数()22f x t t ≥+恒成立,则实数t 的取值范围为A .30t −≤≤B .31t −≤≤C .20t −≤≤D .01t ≤≤【答案】C【解析】 当[)0,2x ∈时,()min 0f x =,又()()22f x f x +=,因此当[)4,2x ∈−−时,函数()min 0f x =,从而20220t t t ≥+⇒−≤≤,选C .。
场论典型例题汇编

场论典型例题第一章 矢量分析 例题1、(基本矢量计算)已知两个矢量j i 2+=A ,j i 34+=B ,求(1)B A + (2)B A - (3)B A •(4)B A ⨯ (5)若A 和B 两矢量夹角为α,求αcos 。
解:(1)B A +=)34()2(j i j i +++=j i )32()41(+++=j i 55+ (2)B A -=)34()2(j i j i +-+=j i )32()41(-+-=j i --3 (3)B A •=)34()2(j i j i +•+=)32()41(⨯+⨯=64+=10(4)B A ⨯=)34()2(j i j i +⨯+=0 3 4 0 21 kj i =k 5- (5)根据内积的定义有:B A •=αcos B A ,其中A ,B 为矢量的模。
所以:BΑBA •=αcos 其中B A •在(2)中已经得到B A •=10,而A =5021222=++,B =5034222=++ 因此B ΑB A •=αcos =5510=52说明:此题可以用于掌握矢量运算法则。
例题2、(矢性函数的极限)设t t t cos sin )(B A F += )20(π<≤t ,式中A ,B 为矢量,分别为j i -=A ,j i +=B 。
求下列极限。
(1))(lim 3/t F t π→ (2)|)(|lim 3/t F t π→解:(1)整理)(t F 。
t j i t j i t t t F cos )(sin )(cos sin )(++-=+=B A=j t t i t t )sin (cos )sin (cos -++而 3/|)sin (cos π→+t t t =231+ 3/|)sin (cos π→-t t t =231- 所以)(lim 3/t F t π→=i 231++j 231- (2)|)(|t F =|j t t i t t )sin (cos )sin (cos -++| =22)sin (cos )sin (cos t t t t -++ =2=→|)(|lim 3/t F t π2说明:对矢性函数的极限,归结为对各坐标分量求极限,因此,需要温习高等数学中微积分中关于“函数极限”的内容,特别是一些常用极限的求法。
2023年高考数学复习----排列组合多面手问题典型例题讲解

2023年高考数学复习----排列组合多面手问题典型例题讲解【典型例题】例1.我校去年11月份,高二年级有10人参加了赴日本交流访问团,其中3人只会唱歌,2人只会跳舞,其余5人既能唱歌又能跳舞.现要从中选6人上台表演,3人唱歌,3人跳舞,有种不同的选法.A .675B .575C .512D .545【答案】A【解析】分析:根据题意可按照只会左边的2人中入选的人数分类处理,分成三类,即可求解.详根据题意可按照只会左边的2人中入选的人数分类处理.第一类2个只会左边的都不选,有3355100C C ⋅=种; 第二类2个只会左边的有1人入选,有123256400C C C ⋅=种;第三类2个只会左边的全入选,有213257175C C C ⋅=种,所以共有675种不同的选法,故选A .例2.某国际旅行社现有11名对外翻译人员,其中有5人只会英语,4人只会法语,2人既会英语又会法语,现从这11人中选出4人当英语翻译,4人当法语翻译,则共有( )种不同的选法A .225B .185C .145D .110【答案】B【解析】根据题意,按“2人既会英语又会法语”的参与情况分成三类. ①“2人既会英语又会法语”不参加,这时有4454C C 种; ②“2人既会英语又会法语”中有一人入选, 这时又有该人参加英文或日文翻译两种可能,因此有134413254524C C C C C C +种; ③“2人既会英语又会法语”中两个均入选,这时又分三种情况:两个都译英文、两个都译日文、两人各译一个语种,因此有22442213132545242514C C C C C C C C C C ++种. 综上分析,共可开出441344132244221313542545242545242514185C C C C C C C C C C C C C C C C C C +++++=种. 故选:B .例3.“赛龙舟”是端午节的习俗之一,也是端午节最重要的节日民俗活动之一,在我国南方普遍存在端午节临近,某单位龙舟队欲参加今年端午节龙舟赛,参加训练的8名队员中有3人只会划左桨,3人只会划右桨,2人既会划左桨又会划右桨.现要选派划左桨的3人、划右桨的3人共6人去参加比赛,则不同的选派方法共有( )A .26种B .30种C .37种D .42种【答案】C【解析】根据题意,设{A =只会划左桨的3人},{B =只会划右桨的3人},{C =既会划左桨又会划右桨的2人},据此分3种情况讨论:①从A 中选3人划左桨,划右桨的在(B C ⋃)中剩下的人中选取,有35C 10=种选法, ②从A 中选2人划左桨,C 中选1人划左桨,划右桨的在(B C ⋃)中选取,有213324C C C 24=种选法,③从A 中选1人划左桨,C 中2人划左桨,B 中3人划右桨,有13C 3=种选法,则有1024337++=种不同的选法. 故选:C .。
复习关系及关联词语

复习关系及关联词语一、常见复句关系及典型例题。
1、并列复句:分句之间不分主次,彼此平等。
例题:他一边..走,一边..在考虑问题。
2、递进复句:后一分句在意思上比前一分句更进一层。
例题:她不但..能唱歌,而且..唱得非常好。
3、选择复句:分贝说出几种情况,从中选择一种。
例题:最近我们的小队活动,不是..参观工厂,就是..举办读书会。
4、转折复句:前后两个分句的意思相对立或相矛盾。
例题:虽然..丝毫阻止不了我们前进。
..前进的道路上还有困难,但是5、因果复句:前后分句分别表示原因与结果。
例题:因为..看上去只有一个盘子那么大。
..太阳离地球太远了,所以6、假设复句:前一分句假设一种情况,后一分句说出假设情况后的结果。
例题:即使..山高路远,我们也.要努力向上攀登。
7、条件复句:前一分句提出条件,后一分句说出在这个条件下出现的情况。
例题:只有..刻苦学习,才.能取得优异成绩。
8、承接复句:各分句表示连续发生的事情或动作,分句有先后顺序。
例题:下雨了,于是..比赛就终止了。
二、复句中的关联词语:复句是由两个或两个以上的单句组合而成,表达更加复杂的内容。
复句中的单句是复句的组成部分,失去了独立性,称为分句,书面上各用逗号隔开。
复句中的虚词在分句间起着重要的关联作用,依靠它们把分句间的意义联系起来,所以叫关联词语。
能够充当关联词语的大都是连词,也有些是副词。
各复句类型中的关联词语:1、并列关系:又……又……既……又……那么……那么……时而……时而……一会儿……一会儿有时……有时……不是……而是……2、递进关系:不但(不光、不仅)……而且(并且、还)…………更…………甚至……3、选择关系:是……还是……不是……就是……或者……或者……要么……要么……4、转折关系:尽管……可是(还是、还)……虽然……但是(可是、还)5、因果关系:因为……所以……既然……就…………因而(因此)……6、假设关系:如果……就……即使……也…………假如……就是……也……7、条件关系:只要……就……只有……才……无论……都……不管……总是……8、承接关系:……于是…………就…………也……三、填写关联词语时应注意以下几点:1]要先认真读句子,清楚前后句子之间的关系。
小学六年级 阴影部分面积 专题复习 典型例题 (1)
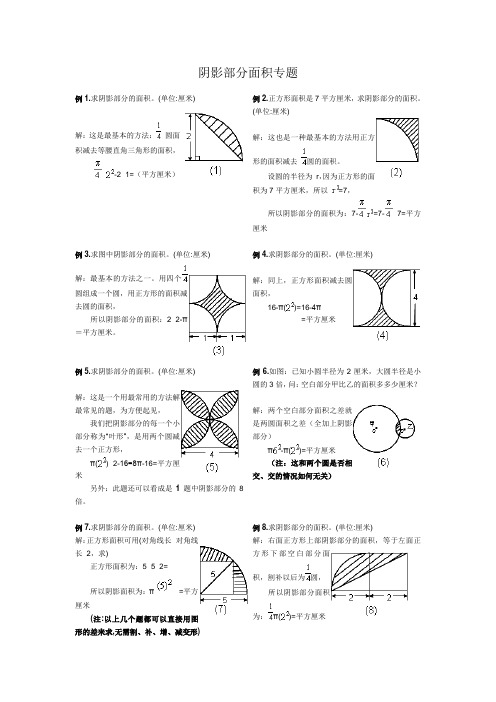
阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=所以阴影面积为:π÷=平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
高考复习——《力 物体的平衡》典型例题复习

一、力物体的平衡1、力:力是物体对物体的作用。
⑴力是一种作用,可以通过直接接触实现(如弹力、摩擦力),也可以通过场来实现(重力、电场力、磁场力)⑵力的性质:物质性(力不能脱离物体而独立存在);相互性(成对出现,遵循牛顿第三定律);矢量性(有大小和方向,遵从矢量运算法则);效果性(形变、改变物体运动状态,即产生加速度)⑶力的要素:力的大小、方向和作用点称为力的三要素,它们共同影响力的作用效果。
力的描述:描述一个力,应描述力的三要素,除直接说明外,可以用力的图示和力的示意图的方法。
⑷力的分类:按作用方式,可分为场力(重力、电场力)、接触力(弹力、摩擦力);接效果分,有动力、阻力、牵引力、向心力、恢复力等;接性质分,有重力、弹力、摩擦力、分子力等;按研究系统分,内力、外力。
2、重力:由于地球吸引,而使物体受到的力。
(1)重力的产生:由于地球的吸引而使物体受到的力叫重力。
(2)重力的大小:G=mg ,可以用弹簧秤测量,重力的大小与物体的速度、加速度无关。
(3)重力的方向:竖直向下。
(4)重心:重力的作用点。
重心的测定方法:悬挂法。
重心的位置与物体形状的关系:质量分布均匀的物体,重心位置只与物体形状有关,其几何中心就是重心;质量分布不均匀的物体,其重心的位置除了跟形状有关外,还跟物体的质量分布有关。
3、弹力(1)弹力的产生:发生弹性形变的物体,由于要恢复原来的形状,对跟它接触的物体产生力的作用,这种力叫弹力。
(2)产生的条件:两物体要相互接触;发生弹性形变。
(3)弹力的方向:①压力、支持力的方向总是垂直于接触面。
②绳对物体的拉力总是沿着绳收缩的方向。
③杆对物体的弹力不一定沿杆的方向。
如果轻直杆只有两个端点受力而处于平衡状态,则轻杆两端对物体的弹力的方向一定沿杆的方向。
例题:如图所示,光滑但质量分布不均的小球的球心在O ,重心在P ,静止在竖直墙和桌边之间。
试画出小球所受弹力。
解析:由于弹力的方向总是垂直于接触面,在A 点,弹力F 1应该垂直于球面所以沿半径方向指向球心O ;在B 点弹力F 2垂直于墙面,因此也沿半径指向球心O 。
高考数学复习----《斜率之和差商积问题》典型例题讲解

高考数学复习----《斜率之和差商积问题》典型例题讲解【规律方法】在面对有关等角、倍角、共线、垂直等几何特征时,可设法将条件翻译成关于斜率的关系式,然后将斜率公式代入其中,得出参数间的关系式,再根据要求做进一步的推导判断.【典型例题】例1、(2022·浙江·模拟预测)已知曲线C上的任意一点到点)F和直线x =. (1)求曲线C 的方程;(2)记曲线的左顶点为A ,过()4,0B 的直线l 与曲线C 交于P ,Q 两点,P ,Q 均在y 轴右侧,直线AP ,AQ 与y 轴分别交于M ,N 两点.若直线MB ,NB 的斜率分别为1k ,2k ,判断12k k 是否为定值.若是,求出该定值;若不是,请说明理由.【解析】(1)设曲线C 上一点的坐标为(),x y=,化简得:2214x y −= ; (2)依题意作上图,设PQ 方程为4x my =+ ,()()1122,,,P x y Q x y ,则m 必定是存在的, 联立方程22144x y x my ⎧−=⎪⎨⎪=+⎩得2212304m y my ⎛⎫−++= ⎪⎝⎭ ,12122223,1144m y y y y m m +=−=−− , ()()221212121212228168,4161144m x x m y y x x m y y m y y m m++=++=−=+++=−−− AP 的方程为()110022y y x x −−=++ ,令x =0,则M 点的坐标为1120,2y x ⎛⎫ ⎪+⎝⎭, 同理,N 点的坐标为2220,2y x ⎛⎫⎪+⎝⎭,()()()12111212121212121222002211,,0404422424y y x x y y y y k k k k x x x x x x −−++∴===⨯=⨯−−+++++ 2222311341684144241144m m m m −=⨯=−+−−⨯+−− ,是定值;综上,曲线C 的方程为2214x y −=,123144k k =− 是定值.例2、(2022春·云南昆明·高三昆明市第三中学校考期末)如图,已知抛物线C :24y x =,过焦点F 斜率大于零的直线l 交抛物线于A 、B 两点,且与其准线交于点D .(1)若线段AB 的长为5,求直线l 的方程;(2)在C 上是否存在点M ,使得对任意直线l ,直线,,MA MD MB 的斜率始终成等差数列,若存在求点M 的坐标;若不存在,请说明理由.【解析】(1)抛物线24y x =的焦点为1,0F (),因为直线l 的斜率不为0,所以可设l 的方程为1x my =+,设()()1122,,A x y B x y ,,联立214x my y x=+⎧⎨=⎩消x ,得2440y my −−=,方程2440y my −−=的判别式216160m ∆=+>,12124,4y y m y y +==−,21212()242x x m y y m +=++=+,2221212(4)14416y y x x −=⋅==,∴212||2445AB x x m =++=+=,∴214m =,设直线l 的斜率为k ,则10k m =>,所以12m =,所以直线l 的方程为220x y −−=; (2)设()2,2M a a ,1122121122424MA y a y a k x a y a y a −−===−+−, ,同理, 242MBk y a =+,又联立11x my x =+⎧⎨=−⎩可得12x y m =−⎧⎪⎨=−⎪⎩,即点D 的坐标为21,m ⎛⎫−− ⎪⎝⎭, 所以2221MDa m ka +=+, ∵直线,,MA MD MB 的斜率始终成等差数列,所以21222442122a m a y a y a +⨯=++++恒成立; ∴122212121412()4a y y a m a y y a y y a +++=++++,又∵12124,4y y m y y +==−,所以221121a a m m a a am ++=++−,()()()221121am m a a a am m +++=+−,()2110a m m ⎛⎫−+= ⎪⎝⎭,因为10m m+≠,所以1a =±, 所以存在点1,2M ()或1,2M −(),使得对任意直线l , 直线,,MA MD MB 的斜率始终成等差数列.例3、(2022·安徽·校联考二模)已知椭圆2222:1(0)x y C a b a b +=>>经过点12⎫⎪⎭,其右焦点为)F.(1)求椭圆C 的标准方程;(2)椭圆C 的右顶点为A ,若点,P Q 在椭圆C 上,且满足直线AP 与AQ 的斜率之积为120,求APQ △面积的最大值.【解析】(1)依题可得22222311,4,c a b a b c ⎧=⎪⎪+=⎨⎪=+⎪⎩解得2,1,a b c ⎧=⎪=⎨⎪=⎩所以椭圆C 的方程为2214x y +=;(2)易知直线AP 与AQ 的斜率同号,所以直线PQ 不垂直于x 轴, 故可设()()1122:,,,,PQ y kx m P x y Q x y =+,由221,4x y y kx m ⎧+=⎪⎨⎪=+⎩可得,()222148440k x mkx m +++−=, 所以()222121222844,,Δ164101414mk m x x x x k m k k−−+===+−>++,即2241k m +>, 而120AP AQ k k =,即121212220y y x x ⋅=−−, 化简可得()()()()12122022kx m kx m x x ++=−−,()()221212121220202024k x x km x x m x x x x +++=−++,222222224484482020202414141414m mk m mk k km m k k k k −−−−⋅+⋅+=−⨯+++++化简得2260k mk m +−=, 所以2m k =−或3m k =,所以直线():2PQ y k x =−或()3y k x =+, 因为直线PQ 不经过点A , 所以直线PQ 经过定点()3,0−.所以直线PQ 的方程为()3y k x =+,易知0k ≠, 设定点()1212153,0,22APQABPABQB S SSAB y y k x x −=−=−=−52=52==因为Δ0>,且3m k =,所以2150k −>,所以2105k <<,设29411,5t k ⎛⎫=+∈ ⎪⎝⎭,所以53APQS==, 当且仅当97t =,即2114k =时取等号,即APQ △面积的最大值为53.例4、(2022春·云南·高三校联考阶段练习)已知椭圆C :()222210x y a b a b +=>>的离心率为,H ⎛ ⎝⎭是C 上一点. (1)求C 的方程.(2)设A ,B 分别为椭圆C 的左、右顶点,过点()1,0D 作斜率不为0的直线l ,l 与C 交于P ,Q 两点,直线AP 与直线BQ 交于点M ,记AP 的斜率为1k ,BQ 的斜率为2k .证明:①12k k 为定值;②点M 在定直线上.【解析】(1,H ⎛ ⎝⎭是椭圆C 上一点, 所以22222222123121c e a a b c a b⎧==⎪⎪⎪=+⎨⎪⎪+=⎪⎩,解得2224,2,2a b c ===,所以椭圆的方程为22142x y +=; (2)①因为过点()1,0D 且斜率不为0,所以可设l 的方程为1x ty =+,代入椭圆方程22142x y +=得()222230t y ty ++−=,方程()222230t y ty ++−=的判别式()2241220t t ∆=++>,设()11,P x y ,()22,Q x y ,则12222t y y t +=−+,12232y y t =−+. 两式相除得121223y y t y y +=,()121232ty y y y =+. 因为,A B 分别为椭圆C 的左、右顶点,所以点A 的坐标为()2,0−,点B 的坐标为()2,0,所以1111123y y k x ty ==++,2222221y y k x ty ==−−. 从而()()()()1211211212221122313123393323y y y y ty k y y y y k y ty y y y +−−+====++++; ②由①知1231k k =,设1k m =,则23k m =,所以直线AP 的方程为:2y mx m =+,直线BQ 的方程为36y mx m =−,联立236y mx m y mx m =+⎧⎨=−⎩可得46x y m =⎧⎨=⎩,所以直线AP 与直线BQ 的交点M 的坐标为()4,6m ,所以点M 在定直线4x =上.。
集合复习题

A {x | x2 5x q 0} , B {x | x2 px 12 0} ,且 (CU A) B {1, 2,3, 4,5} ,求实数 p、q 的值.
7. 已知集合 A={x|x2-3x+2=0},B={x|x2-ax+3a-5=0}.若 A∩B=B,求实数 a 的取值范围.
例题 4:设 A {x | x2 8x 15 0} , B {x | ax 1 0},若 B A,求实数 a 组成的集合、.
例题 5. 设 A {x | x2 ax 6 0} , B {x | x2 x c 0} ,且 A∩B={2},求 A∪B. 例题 6. 已知 A={x|x<-2 或 x>3},B={x|4x+m<0},当 A B 时,求实数 m 的取值范围。
A.U A B
B. U (CU A) B
C.U A (CU B)
D.U (CU A) (CU B)
4.
满足条件{1,2,3}
M
{1,2,3,4,5,6}的集合 M 的个数是
.
5. 设集合 M {y | y 3 x2} , N {y | y 2x2 1} ,则 M N
.
6. 设全集U {x | x 5,且x N*},集合
例题 2 已知全集U {1, 2,3, 4,5},若 A B U , A B , A (CU B) {1, 2},求集合 A、 B.
例 题 3 若 A x x2 4x 3 0 , B x x2 ax a 1 0 , C x x2 mx 1 0 且A B A, A C C ,求实数 a、m 的值或取值范围.
集合复习题
复习题 1:什么叫交集、并集、补集?符号语言如何表示?图形语言.
复习题 2:交、并、补有如下性质.
《微积分初步》期末复习典型例题

《微积分初步》期末复习典型例题一、函数、极限与连续(一)考核要求1.了解常量和变量的概念;理解函数的概念;了解初等函数和分段函数的概念.熟练掌握求函数的定义域、函数值的方法;掌握将复合函数分解成较简单函数的方法.2.了解极限概念,会求简单极限.3.了解函数连续的概念,会判断函数的连续性,并会求函数的间断点. (二)典型例题 1.填空题(1)函数)2ln(1)(-=x x f 的定义域是 .答案:2>x 且3≠x .(2)函数24)2ln(1)(x x x f -++=的定义域是 .答案:]2,1()1,2(-⋃--(3)函数74)2(2++=+x x x f ,则=)(x f .答案:3)(2+=x x f(4)若函数⎪⎩⎪⎨⎧≥<+=0,0,13sin )(x k x xx x f 在0=x 处连续,则=k .答案:1=k(5)函数x x x f 2)1(2-=-,则=)(x f . 答案:1)(2-=x x f (6)函数1322+--=x x x y 的间断点是 .答案:1-=x (7)=∞→xx x 1sinlim .答案:1(8)若2sin 4sin lim=→kxx x ,则=k .答案:2=k 2.单项选择题 (1)设函数2e exxy +=-,则该函数是( ).A .奇函数B .偶函数C .非奇非偶函数D .既奇又偶函数 答案:B(2)下列函数中为奇函数是( ).A .x x sinB .2e exx+- C .)1ln(2x x ++ D .2x x +答案:C(3)函数)5ln(4+++=x x xy 的定义域为( ).A .5->xB .4-≠xC .5->x 且0≠xD .5->x 且4-≠x答案:D(4)设1)1(2-=+x x f ,则=)(x f ( ) A .)1(+x x B .2x C .)2(-x x D .)1)(2(-+x x 答案:C(5)当=k ( )时,函数⎩⎨⎧=≠+=0,0,2)(x k x e x f x 在0=x 处连续.A .0B .1C .2D .3 答案:D(6)当=k ( )时,函数⎩⎨⎧=≠+=0,0,1)(2x k x x x f ,在0=x 处连续.A .0B .1C .2D .1- 答案:B (7)函数233)(2+--=x x x x f 的间断点是( )A .2,1==x xB .3=xC .3,2,1===x x xD .无间断点 答案:A 3.计算题 (1)423lim222-+-→x x x x .解:4121lim)2)(2()1)(2(lim423lim22222=+-=+---=-+-→→→x x x x x x x x x x x x(2)329lim 223---→x x x x解:234613lim)1)(3()3)(3(lim 329lim33223==++=+-+-=---→→→x x x x x x x x x x x x(3)4586lim224+-+-→x x x x x解:3212lim )1)(4()2)(4(lim 4586lim 44224=--=----=+-+-→→→x x x x x x x x x x x x x (4)计算极限xx x 11lim 0--→.解:)11(11lim)11()11)(11(lim11lim00+---=+-+---=--→→→x x x x x x x xx x x x21)11(1lim 0-=+--=→x x(5)计算极限xx x 4sin 11lim 0--→解:xx x 4sin 11lim0--→)11(4sin 11lim)11(4sin )11)(11(lim0+---=+-+---=→→x x x x x x x x x81)11(4sin 44lim)11(4sin lim-=+--=+--=→→x x xx x xx x二、 导数与微分 (一)考核要求1.了解导数概念,会求曲线的切线方程.2.熟练掌握求导数的方法(导数基本公式、导数的四则运算法则、复合函数求导法则),会求简单的隐函数的导数.3.了解微分的概念,掌握求微分的方法.4.了解高阶导数的概念,掌握求显函数的二阶导数的方法. (二)典型例题1.填空题 (1)曲线1)(+=x x f 在)2,1(点的切斜率是 .答案:21(2)曲线x x f e )(=在)1,0(点的切线方程是 . 答案:e x y +=(3)已知x x x f 3)(3+=,则)3(f '= . 答案:3ln 33)(2x x x f +=')3(f '=27()3ln 1+(4)已知x x f ln )(=,则)(x f ''= . 答案:xx f 1)(=',)(x f ''=21x-(5)若x x x f -=e )(,则='')0(f.答案:xx x x f --+-=''e e 2)(='')0(f 2-2.单项选择题 (1)若x x f xcos e)(-=,则)0(f '=( ).A. 2B. 1C. -1D. -2答案:C(2)设y x =lg 2,则d y =( ).A .12d xx B .1d x x ln 10C .ln 10xx d D .1d xx答案:B(3)设)(x f y =是可微函数,则=)2(cos d x f ( ). A .x x f d )2(cos 2' B .x x x f d22sin )2(cos ' C .x x x f d 2sin )2(cos 2' D .x x x f d22sin )2(cos '- 答案:D(4)若3sin )(a x x f +=,其中a 是常数,则='')(x f ( ).A .23cos a x +B .a x 6sin +C .x sin -D .x cos 答案:C3.计算题(1)设x x y 12e =,求y '.解: )1(e e 22121xx x y xx-+=')12(e 1-=x x(2)设x x y 3cos 4sin +=,求y '.解:)sin (cos 34cos 42x x x y -+='x x x 2c o s s i n 34c o s 4-=(3)设xy x 2e 1+=+,求y '.解:2121(21exx y x -+='+(4)设x x x y cos ln +=,求y '. 解:)sin (cos 12321x xx y -+=' x x tan 2321-=(5)设)(x y y =是由方程422=-+xy y x 确定的隐函数,求y d .解:方程两边对x 求导,得0)(22='+-'+y x y y y xxy x y y --='22于是得到x xy x y y d 22d --=(6)设2e e cos y x y x =++,求y d . 解:方程两边对x 求导,得y y y x yx'='++-2e e sin yx y yx 2e e sin --='于是得到x yx y yx d 2e e sin d --=三、导数应用 (一)考核要求1.掌握函数单调性的判别方法.2.了解极值概念和极值存在的必要条件,掌握极值判别的方法.3.掌握求函数最大值和最小值的方法. (二)典型例题1.填空题(1)函数y x =-312()的单调增加区间是 . 答案:),1(+∞ (2)函数1)(2+=axx f 在区间),0(∞+内单调增加,则a 应满足 .答案:0>a 2.单项选择题(1)函数2)1(+=x y 在区间)2,2(-是( ) A .单调增加 B .单调减少 C .先增后减 D .先减后增 答案:D(2)满足方程0)(='x f 的点一定是函数)(x f y =的( ). A .极值点 B .最值点 C .驻点 D . 间断点 答案:C(3)下列结论中( )不正确. A .)(x f 在0x x =处连续,则一定在0x 处可微. B .)(x f 在0x x =处不连续,则一定在0x 处不可导. C .可导函数的极值点一定发生在其驻点上.D .函数的极值点可能发生在不可导点上. 答案:A(4)下列函数在指定区间(,)-∞+∞上单调增加的是( ).A .x sinB .x eC .2xD .x -3 答案:B3.应用题(以几何应用为主)(1)欲做一个底为正方形,容积为108立方米的长方体开口容器,怎样做法用料最省? 解:设底边的边长为x ,高为h ,用材料为y ,由已知22108,108xh h x ==xx xx x xh x y 432108442222+=⋅+=+=令043222=-='xx y ,解得6=x 是唯一驻点,且04322263>⨯+=''=x xy ,说明6=x 是函数的极小值点,所以当6=x ,361082==h 用料最省.(2)用钢板焊接一个容积为43m 的正方形的水箱,已知钢板每平方米10元,焊接费40元,问水箱的尺寸如何选择,可使总费最低?最低总费是多少? 解:设水箱的底边长为x ,高为h ,表面积为S ,且有24xh =所以,164)(22xx xh x x S +=+=2162)(xx x S -='令0)(='x S ,得2=x ,因为本问题存在最小值,且函数的驻点唯一,所以,当1,2==h x 时水箱的面积最小. 此时的费用为 1604010)2(=+⨯S (元) 4.证明题(1)证明函数x x f 23)(-=,在定义区间上是单调下降的.证明 因为x x f 23)(-=的定义区间为),(+∞-∞,且02)(<-='x f ,所以x x f 23)(-=在),(+∞-∞是单调下降的.(2)证明函数x x x f e )(-=在()0,∞-是单调增加的.证明:因为在()0,∞-上,有0e 1)(>-='x x f ,所以函数x x x f e )(-=在()0,∞-是单调增加的.四、 一元函数积分 (一)考核要求1.理解原函数与不定积分的概念、性质,掌握积分基本公式,掌握用直接积分法、第一换元积分法和分部积分法求不定积分的方法.2.了解定积分的概念、性质,会计算一些简单的定积分.3. 了解广义积分的概念,会计算简单的无穷限积分。
高一物理必修2期末复习知识-典型例题

高一物理必修2期末复习知识-典型例题高中物理必修2综合总复习典型例题:1、过河问题例1.小船在200m 的河中横渡,水流速度为2m/s ,船在静水中的航速是4m/s ,求: 1.小船怎样过河时间最短,最短时间是多少? 2.小船怎样过河位移最小,最小位移为多少?解:如右图所示,若用v1表示水速,v2表示船速,则:①过河时间仅由v2的垂直于岸的分量v ⊥决定,即⊥=v dt ,与v1无关,所以当v2⊥岸时,过河所用时间最短,最短时间为2v dt =也与v1无关。
②过河路程由实际运动轨迹的方向决定,当v1<v2时,最短路程为d ; 2、连带运动问题指物拉绳(杆)或绳(杆)拉物问题。
由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题原则是:把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相同求解。
例2 如图所示,汽车甲以速度v1拉汽车乙前进,乙的速度为v2,甲、乙都在水平面上运动,求v1∶v2解析:甲、乙沿绳的速度分别为v1和v2cos α,两者应该相等,所以有v1∶v2=cos α∶13、平抛运动例3平抛小球的闪光照片如图。
已知方格边长a 和闪光照相的频闪间隔T ,求:v0、g 、vc解析:水平方向:T av 20=竖直方向:22,T a g gT s =∴=?先求C 点的水平分速度vx 和竖直分速度vy ,再求合速度vC :412,25,20Tav T a v T a v v c y x =∴===(2)临界问题典型例题是在排球运动中,为了使从某一位置和某一高度水平扣出的球既不触网、又不出界,扣球速度的取值范围应是多少?例4 已知网高H ,半场长L ,扣球点高h ,扣球点离网水平距离s 、求:水平扣球速度v 的取值范围。
解析:假设运动员用速度vmax 扣球时,球刚好不会出界,用速度vmin 扣球时,球刚好不触网,从图v 2v 1v 1 甲乙α v 1v 2ABCDE中数量关系可得:()h g s L g h s L v 2)(2/max +=+=;)(2)(2/min H h gs g H h s v -=-=实际扣球速度应在这两个值之间。
高考数学复习压轴题归类解析06 妙用洛必达法则

高考数学复习压轴题归类解析 第06讲妙用洛必达法则【典型例题典型例题】】 例1.已知()(1)f x x lnx =+. (1)求()f x 的单调区间;(2)若对任意1x …,不等式()[]01f x x ax a x −++…恒成立,求a 的取值范围. 【解析】解:(1)()f x 的定义域为(0,)+∞,1()1f x lnx x′=++,令1()1(0)g x lnx x x=++>,则22111()x g x xx x−′=−= 所以当01x <<时,()0g x ′<;当1x >时,()0g x ′>,所以()g x 在(0,1)单调递减,在(1,)+∞单调递增,所以0x >时,()g x g >(1)20=>, 即()f x 在(0,)+∞上单调递增,所以()f x 的增区间为(0,)+∞,无减区间.(2)对任意1x …,不等式()[]01f x x ax a x −++…恒成立等价于对任意1x …,1(0lnx a x x−−…恒成立.当1x =,a R ∈对任意1x >,不等式()[]01f x x ax a x −++…恒成立等价于对任意1x >,21xlnx a x −…恒成立.记2()(1)1xlnx m x x x =>−,则22222222222212(1)(1)(1)21(1)11()(1)(1)(1)lnx lnx x x lnx x x lnx x x m x x x x −−+−−−−+++′===−−−,记22()1(1)1t x lnx x x =−−>+, 则22222222222414(1)(1)()0(1)(1)(1)x x x x t x x x x x x x −+−′=−==−<+++,所以()t x 在(1,)+∞单调递减,又t (1)0=, 所以,1x >时,()0t x <,即()0m x ′<, 所以()m x 在(1,)+∞单调递减.所以1122110111()(1)lim lim ()||111(1)2maxx x x x xlnxxlnx xlnx x lnx x m x m x x x x ′==→→−+−+<=====−−++, 综上所述,a 的取值范围是1[,)2+∞.例2.设函数2()(1)()f x ln x a x x =++−,其中a R ∈.(1)1a =时,求曲线()y f x =在点(1,f (1))处的切线方程; (2)讨论函数()f x 极值点的个数,并说明理由; (3)若0x ∀>,()0f x …成立,求a 的取值范围. 【解析】解:(1)当1a =时,切点为(1,2)ln ,则1()211f x x x ′=+−+,所以3(1)2f ′=, 切线方程为32(1)2y ln x −=−,即322230x y ln −+−=, 所以切线方程为:322230x y ln −+−=;(2)由题意可知,函数()f x 的定义域为(1,)−+∞,则2121()(21)11ax ax a f x a x x x +−+′=+−=++,令2()21g x ax ax a =+−+,(1,)x ∈−+∞, ①当0a =时,()0f x ′>,函数()f x 在(1,)−+∞上单调递增,无极值点, ②当0a >时,△(98)a a =−,当809a <…时,△0…,()0g x …,()0f x ′…, 所以()f x 在(1,)−+∞上单调递增,无极值点,当89a >时,△0>,设方程2210ax ax a +−+=的两个根,1x ,2x ,且1x =,2x =,此时12x x <,因为1212x x +=−,114x <−,214x >−,(1)10g −=>,所以1114x −<<−, 因为1(1,)x x ∈−,2(x ,)+∞时,()0g x >,()0f x ′>,函数()f x 单调递增,1(x x ∈,2)x 时,()0g x <,()0f x ′<,函数()f x 单调递减,所以函数有两个极值点,当0a <时,△0>,设方程2210ax ax a +−+=的两个根,1x ,2x ,且1x =,2x =,此时12x x >,因为(1)10g −=>,所以21x <−,所以,1(1,)x x ∈−时,()0g x >,()0f x ′>,函数()f x 单调递增, 当2(x x ∈,)+∞时,()0g x <,()0f x ′<,函数()f x 单调递减, 所以函数有一个极值点,综上可知,当0a <时,函数()f x 有一个极值点; 当809a剟时,函数()f x 无极值点; 当89a >时,函数()f x 有两个极值点;(3)当809a剟时,函数()f x 在(0,)+∞上单调递增,因为(0)0f =,所以(0,)x ∈+∞时,()0f x >,符合题意, 当819a <…时,(0)0g >,得20x <, 所以函数()f x 在(0,)+∞上单调递增,又因为(0)0f =,所以(0,)x ∈+∞时,()0f x >,符合题意, 当1a >时,由(0)0g <,得20x >, 所以2(0,)x x ∈时,函数()f x 单调递减,因为(0)0f =,所以2(0,)x x ∈时,()0f x <时,不符合题意, 当0a <时,设()(1)h x x ln x =−+, 因为(0,)x ∈+∞时,1()1011x h x x x ′=−=>++,所以()h x 在(0,)+∞上单调递增, 所以当(0,)x ∈+∞时,()(0)0h x h >=,即(1)h x x +<, 可得22()()(1)f x x a x x ax a x <+−=+−,当11x a>−时,2(1)0ax a x +−<,此时()0f x <,不合题意, 综上,a 的取值范围为[0,1]. 例3.已知函数2()1x f x x mx e =−−+.(1)若函数()f x 在点(1,f (1))处的切线l 经过点(2,4),求实数m 的值; (2)若关于x 的方程|()|f x mx =有唯一的实数解,求实数m 的取值范围.【解析】解:(1)()2x f x x m e ′=−−,∴在点(1,f (1))处的切线l 的斜率k f ′=(1)2e m =−−,又f (1)2e m =−−,∴切线l 的方程为(2)(2)(1)y e m e m x −−−=−−−, 即:(2)l y e m x =−−,由l 经过点(2,4), 可得42(2)e m m e =−−⇒=−.(2)证明:易知|(0)|000f m x ==×⇒=为方程的根, 由题只需说明当0x >和0x <时原方程均没有实数解即可.①当0x >时,若0m <,显然有0mx <,而|()|0f x …恒成立,此时方程显然无解, 若0m =,2()1()2x x f x x e f x x e ′=−+⇒=−,()2x f x e ′′=−,令()02f x x ln ′′>⇒<,故()f x ′在(0,2)ln 单调递增,在(2,)ln +∞单调递减, 故()(2)2220()f x f ln ln f x ′′<=−<⇒在(0,)+∞单调递减()(0)0f x f ⇒<=, 从而|()|0f x >,00mx x =×=,此时方程|()|f x mx =也无解.若0m >,由1|()|||xe f x mx m x m x x =⇒=+−−,记1()x e g x x m x x=+−−,则2(1)(1)()x x x e g x x −+−′=, 设()1x h x x e =+−,则()10x h x e ′=−<有(0,)+∞恒成立,()(0)0h x h ∴<=恒成立,故令()001()g x x g x ′>⇒<<⇒在(0,1)上递增,在(1,)+∞上递减()g x g ⇒…(1)20|()|2e m g x e m m =−−<⇒−+>…,可知原方程也无解,由上面的分析可知0x >时,m R ∀∈,方程|()|f x mx =均无解.②当0x <时,若0m >,显然有0mx <,而|()|0f x …恒成立,此时方程显然无解, 若0m =,和①中的分析同理可知此时方程|()|f x mx =也无解.若0m <,由1|()|||xe f x mx m x m x x =⇒−=+−−,记1()x e g x x m x x =+−−,则2(1)(1)()x x x e g x x −+−′=,由①中的分析知()10x h x x e =+−<,故()0g x ′>在(,0)−∞恒成立,从而()g x 在(,0)−∞上单调递增,当0x →时,200012()lim ()lim lim 11x xx x x x e x e g x g x m m m x−−−→→→+−−→=−=−=−−, 如果10m −−…,即1m −…,则|()|1g x m >+,要使方程无解,只需112m m m −+⇒−剠,即有102m −<…如果10m −−>,即1m <−,此时|()|[0g x ∈,)+∞,方程|()|m g x −=一定有解,不满足. 由上面的分析知0x <时,1[,)2m ∀∈−+∞,方程|()|f x mx =均无解,综合①②可知,当且仅当1[,)2m ∈−+∞时,方程|()|f x mx =有唯一解,m ∴的取值范围为1[,)2−+∞.【同步练习同步练习】】1.设函数2()1x f x e x ax =−−−, (1)若0a =,求()f x 的单调区间; (2)若当0x ≥时()0f x ≥,求a 的取值范围. 【解析】(1)0a =时,()1x f x e x =−−,'()1x f x e =−.当(,0)x ∈−∞时,'()0f x <;当(0,)x ∈+∞时,'()0f x >.故()f x 在(,0)−∞单调减少,在(0,)+∞单调增加.(2)当0x =时,()0f x =,对于任意实数a ,()0f x ≥恒成立;当0x >时,()0f x ≥等价于21x e x a x−−≤, 令21()(0)x e x g x x x −−=>,则322()x x xe e x g x x −++′=, 令()22(0)x x h x xe e x x =−++>,则()1x x h x xe e ′=−+,()0x h x xe ′′=>, 所以()h x ′在(0,)+∞上为增函数,()(0)0h x h ′′>=,所以()h x 在(0,)+∞上为增函数,()(0)0h x h >=, 所以()0g x ′>,()g x 在(0,)+∞上为增函数.而0lim (1)0x x e x +→−−=,20lim ()0x x +→=,由洛必达法则知,2000111lim lim lim 222x x x x x x e x e e x x +++→→→−−−===,故21≤a . 综上得a 的取值范围为1(,2−∞.2.设函数2()ln(1)()f x x a x x =++−,其中a R ∈. (1)讨论函数()f x 极值点的个数,并说明理由; (2)若0x ∀>,()0f x ≥成立,求a 的取值范围. 【解析】(1)2()ln(1)()f x x a x x =++−,定义域为(1,)−+∞21(21)(1)121()(21)111a x x ax ax af x a x x x x −++++−′=+−==+++, 当0a =时,1()01f x x ′=>+,函数()f x 在(1,)−+∞为增函数,无极值点. 设222()21,(1)1,8(1)98g x ax ax a g a a a a a =++−−=∆=−−=−,当0a ≠时,根据二次函数的图像和性质可知()0g x =的根的个数就是函数()f x 极值点的个数.若(98)0a a ∆=−≤,即809a <≤时,()0g x ≥,()0f x ′≥函数在(1,)−+∞为增函数,无极值点.若(98)0a a ∆=−>,即89a >或0a <,而当0a <时(1)0g −≥此时方程()0g x =在(1,)−+∞只有一个实数根,此时函数()f x 只有一个极值点;当89a >时方程()0g x =在(1,)−+∞都有两个不相等的实数根,此时函数()f x 有两个极值点;综上可知当809a ≤≤时()f x 的极值点个数为0;当0a <时()f x 的极值点个数为1;当89a >时,()f x 的极值点个数为2.(2)函数2()ln(1)()f x x a x x =++−,0x ∀>,都有()0f x ≥成立,即2ln(1)()0x a x x ++−≥恒成立,设()2ln 1()x h x x x−+=−,则2222221(21)ln(1)()(21)ln(1)(21)(1)1()()()x x x x x x x x x x x h x x x x x −−−++ −−+−+−+ +′==−−, 设2()ln(1)(21)(1)x x x x x x ϕ−=−++−+,则222()(41)()(21)(1)x x x x x x ϕ−+′=−+,所以1(0,)2x ∈和1(,1)2x ∈时,()0x ϕ′<,所以()x ϕ在对应区间递减,(1,)x ∈+∞时,()0x ϕ′>,所以()x ϕ在对应区间递增,因为(0)0ϕ=,212lim 0(21)(1)x x x x x →+−−>−+,(1)ln 20ϕ=>, 所以(0,1)x ∈和(1,)x ∈+∞时,()0h x ′>,所以()h x 在(0,1)与(1,)+∞上递增. 当()0,1x ∈时,20x x −<,所以()2ln 1x a x x−+≤−,由()h x 的单调性得,()()()20001ln 111lim lim lim 121211x x x x x a x xx x x →→→−−+−+≤===−−−+; 当1x =时,()0f x =,恒成立; 当()1,x ∈+∞时,20x x −>,所以()2ln 1x a x x −+≥−,由()h x 的单调性得,所以()()()()221ln 1ln 111lim lim lim 021211x x x x x x a x x x xx x x →+∞→+∞→+∞−−+−+−+≥====−−−−+,综上,[]1,0∈a3.已知函数()x f x e =,()1g x bx =+,若()()f x g x ≥对于任意x R ∈恒成立,求b 的取值集合. 【解析】1x e bx ≥+恒成立,即1x e bx −≥. 当0x =时显然成立,即b R ∈.当0x >时,1x e b x −<,令1()x e F x x −=,则2(1)1()x e x F x x−+′=,令()(1)1x G x e x =−+, 则()0x G x xe ′=>,所以()G x 递增,所以()(0)0G x G >=,所以()F x ′在(0,)+∞上恒成立. 所以()F x 在(0,)+∞上递增,根据洛必达法则得,001lim lim 11x xx x e e x ++→→−==,所以1b ≤. 同理,当0x <时,1b ≥. 综上所述,b 的取值集合为{}1.4.设函数()ln(1)f x x =+,()()g x xf x ′=,0x ≥,其中()f x ′是()f x 的导函数,若()()f x ag x ≥恒成立,求实数a 的取值范围.【解析】已知()()f x ag x ≥恒成立,即ln(1)1axx x +≥+恒成立. 当0x =时,a 为任意实数,均有不等式恒成立. 当时0x >,不等式变形为(1)ln(1)x x a x++≤恒成立. 令(1)ln(1)()x x h x x ++=,则2ln(1)()x x h x x −+′=,再令()ln(1)x x x ϕ=−+,则()1xx x ϕ′=+.因为0x >,所以()0x ϕ′>,所以()x ϕ在(0,)+∞上递增,从而有()(0)0x ϕϕ>=. 进而有()0h x ′>,所以()h x 在(0,)+∞上递增. 当0x +→时,有(1)ln(1)0x x ++→,0x →, 由洛必达法则得000(1)ln(1)ln(1)1lim ()limlim 11x x x x x x h x x +++→→→++++===,所以当0x +→时,()1h x →.所以(1)ln(1)x x a x++≤恒成立,则1a ≤. 综上,实数的取值范围为(,1]−∞.5.若不等式3sin x x ax >−对于0,2x π∈ 恒成立,求a 的取值范围.【解析】当0,2x π ∈时,原不等式等价于3sin x x a x −>.记3sin ()x x f x x −=,则43sin cos 2()x x x x f x x′−−=. 记()3sin cos 2g x x x x x =−−,则()2cos sin 2g x x x x ′=+−. 因为()cos sin cos (tan )g x x x x x x x ′′=−=−,()sin 0g x x x ′′′=−<,所以()g x ′′在0,2π上单调递减,且()0g x ′′<,所以()g x ′在0,2π上单调递减,且()0g x ′<.因此()g x 在0,2π上单调递减, 且()0g x <,故4()()0g x f x x ′=<,因此3sin ()x x f x x −=在0,2π上单调递减.由洛必达法则有320000sin 1cos sin cos 1lim ()limlim lim lim 3666x x x x x x x x x x f x x x x →→→→→−−===== 即当0x →时,1()6g x →,即有1()6f x <. 故16a ≥时,不等式3sin x x ax >−对于0,2x π ∈恒成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、选电梯参考系,电梯参考系是非惯 性系,那么我们就用非惯性系中的力学 定律来解决此问题。 在非惯性系中,物体除了真实受力外, 还要受到一个假想的惯性力的作用。 设 m1、 m 2相对于的电梯的加速 度 a ' ,相对于地的加速度分别 为 a1、a2 受力分析如图。 在非惯性系中,利用牛顿第二定律:
2.光滑的水平桌面上, 有一长为 2L、质量为 m 的匀质细杆,可绕过其中点且垂直于杆的竖 直光滑固定轴自由转动,其转动惯量为 mL2/3, 起初杆静止,桌面上有两个质量均为 m 的小 球,各自在垂直于杆的方向上,正对着杆的一端, 以相同速率 v 相向运动,当两个小球同时与 杆的两个端点发生完全非弹性碰撞后,与杆粘 在一起转动,则这一系统碰撞后的转动角速度 m v 应为:
T
a m2
'
T
a
m1
m1 g
a'
m2 g
m : m g T m a m : T m g m a
1
1
1
(1) (2)
2
2
2
2
根据相对运动公式:
am地 am梯 a梯地
得到:
T
a1 a a
'
( 3) ( 4)
a m2
'
T
a
m1
m1 g
a'
a2 a a
'
m2 g
a
再根据相对运动公式:
am地 am梯 a梯地
a
'
T
m2
m2 g
T
m2 a
m1
m1 g
a'
m1a
得到:
a1 a a
'
a2 a a
'
m1 g m2 g 2a a1 m1 m2 m1 g 2a m2 g a2 m1 m2
2、一轻绳跨过两个质量均为m、半径均为r的 均匀滑轮,绳的两端分别挂着质量为m和2m的 重物。绳与滑轮间无相对滑动,滑轮轴光滑。 两个定滑轮的转动惯量均为 J 1 mr 2,求两滑 2 轮之间的绳内张力。 解:在地面参考系中,分别以两个物 体和两个滑轮为研究对象,用隔离体 法,分别以牛顿第二定律和刚体定轴 转动定律建立方程。
x
A外 k x
1 2 2
1 2
1 3
m1 L2 m2 L2 2
联立可解
kx m2 L
2
例:质量为 m 、长为 l 的细杆两端用细线 悬挂在天花板上,当其中一细线烧断的瞬间另 一根细线中的张力为多大? 解:在线烧断瞬间,以 杆为研究对象,细杆受 重力和线的张力,
B
解:受力分析如图
由题意 a人=aB=a
由牛顿第二定律
人 : Mg T 2 Ma
①
o T2 1 (T 2 T 1)R J M R 2 ③ A
4
附加 : a R
由转动定律 : 对滑轮 :
1 1 B : T 1 Mg Ma ② 4 4
T1
④
Mg
B
1 Mg 4
由此可解出所求值
3 4
o M L c
v0
1 4
L m
1.一个人站在有光滑固定转轴的转动平 台上,双臂伸直水平地举起二哑铃,在该 人把此二哑铃水平收缩到胸前的过程中, 人、哑铃与转动平台组成的系统的 (A)机械能守恒,角动量守恒; (B)机械能守恒,角动量不守恒, (C)机械能不守恒,角动量守恒; (D)机械能不守恒,角动量不守恒. [ C ]
联立上面四个式子,得:
m1 g a m2 g a a m1 m2
'
2m1m2 g a T m1 m2
m1 g m2 g 2a a1 m1 m2 m1 g 2a m2 g a2 m1 m2
如果电梯是加速向下运动呢? 不过是把上式中的 a 都换成 a 罢了
2m : 2mg T 2ma (1) m : T mg ma (2)
1
2
mg
2mg
a r
(5)
1 2 T1r Tr mr 2 1 2 Tr T2 r mr 2
(3) (4)
联立上面的式子,可得:
11mg T 8
物体A和B叠放在水平面上,由跨过定滑轮的不 可伸长的轻质细绳相互连接,如图所示。今用 大小为F的水平力拉A。设A、B和滑轮质量都为m, 1 滑轮的半径为R,对轴的转动惯量 J mR 2 AB之间、A与桌面之间、滑轮与轴之间均无摩擦, m 绳与滑轮之间无相对滑动,且绳子不可伸长。已 知F=10N,m=8.0 kg,R=0.050m, T 求:滑轮的角加速度。
o
F
L0 L J 0 0 J
0
2
mr0 0 mr r r0 /2 4 0
2
r0 m F
o
F
半径减小角速度增加。 (2)拉力作功。请考虑合外力矩为0, 为什么拉力还作功呢? W Md
0
在定义力矩作功时, 我们认为只有切向力 作功,而法向力与位 移垂直不作功。 但在例题中,小球 受的拉力与位移并 不垂直,小球的运 动轨迹为螺旋线, 法向力要作功。
L
系统最初静止,在外力矩作用下绕竖直轴无摩擦转 动。当 m2 缓慢滑到端点A时,系统角速度为 求:此过程中外力矩的功 请自行列式
o
k
m2
解:m1 + m2+k 系统非刚体, A
m1
缓慢滑动,不计 m2 沿杆径 向运动的动能。
L
A外 A内 Ek
1 A内 A弹 kx d x k ( x ) 2 0 2
1 4
L m
3 4 Lmv0 cos
LM 0
撞后
3 4
Lmv0 cos
m L Lm
3 4 2
2 1 ; LM ML 3
9 1 m M 16 3
L
2
②摆动: M + m + 地球系统 E 守恒 势能Ep 动能 Ek 初态: 末态:
1 9 2 16
4.人造地球卫星,绕地球作椭圆轨道运动, 地球在椭圆的一个焦点上,则卫星的 (A)动量不守恒,动能守恒。 (B)动量守恒,动能不守恒。 (C)角动量守恒,动能不守恒。 (D)角动量不守恒,动能守恒。
[ C ]
5.一轻绳绕过一定滑轮,滑轮轴 光滑,滑轮的质量为 M/4,均匀 分布在其边远上,绳子 A 端有 一质量为 M的人抓住了绳端,而 A 在绳的另一端 B 系了一质量为 M /4 的重物,如图。已知滑轮 对 o 轴的转动惯量 J=MR2/4 , 设人从静止开始以相对绳匀速向 上爬时,绳与滑轮间无相对滑动, 求 B 端重物上升的加速度?
3 4
o
L
M c
v0
m M L 3 M 2 4 m gL 1 cos
1 9 2 16
1 4
L m
3 4
Lmv0 cos m M L
9 16 1 3 2
1 9 2 16
2 2 3 M m 1 M L m gl 1 cos 3 2 4
v om
o
( A) ( C)
2v 3L 6v 7L
4v ( B) 5L 8 v ( D) 9L
v m
o
m v
[ C ]
3.一块方板,可以其一边为轴自由转动.最初板 自由下垂.今有一小团粘土,垂直板面撞击方板 并粘在板上,对粘土和方板系统,如果忽略空气 阻力,在碰撞中守恒的量是:
(A)动能. (B)绕木板转轴的角动量. (C)机械能. (D)动量. [ B ]
m M L
1 3 2
2
1 mg 3 L Mg 4 2 L
1 ( mg 3 4 L Mg 2 L ) (1 cos )
0
EK1 Ep1 Ek 2 Ep 2 Ep Ep 2 Ep1 EK1 Ek 2 EK
1 3 2 2
a
'
a
T
m2
m2 g
T
m2 a
m1
m1 g
a'
m1a
m : m g m a T m a
1
'
1
1
1
(1)
'
m : T m g m a m a
2
2
2
2
(2)
联立两式可得:
m1 g a m2 g a ' a m1 m2
2m1m2 g a T m1 m2
a
联立① ② ③ ④求解
1 a g 2
练习
1.以下五种运动中, a 保持不变的运动是 (A) (B) (C) (D) (E) 单摆的运动。 匀速率圆周运动。 行星的椭圆轨道运动。 抛体运动。 圆锥摆运动。 [ D ]
2.一质点在平面上运动,已知质点位置矢 量的表达式为 r = at2 i + bt2 j ,(其中a、b为常量.) 则该质点作 (A)匀速直线运动。 (B)变速直线运动。 (C) 抛物线运动。 (D)一般曲线运动。 [ B ]
3.质点沿 x 轴作直线运动,其 v ~ t 曲线如图所示,如 t = 0 时,质点位于坐 标原点,则 t = 4.5s时,质点在 x 轴上的位置为: ( A) 0. v (B) 5m. 2 (C) 2m. 1 2. 5 o (D)–2m. 4 . 5 1 2 4 3 t (E) –5m. 1 [ C ]
