二叉树构造方法
二叉树的建立与基本操作

二叉树的建立与基本操作二叉树是一种特殊的树形结构,它由节点(node)组成,每个节点最多有两个子节点。
二叉树的基本操作包括建立二叉树、遍历二叉树、查找二叉树节点、插入和删除节点等。
本文将详细介绍二叉树的建立和基本操作,并给出相应的代码示例。
一、建立二叉树建立二叉树有多种方法,包括使用数组、链表和前序、中序、后序遍历等。
下面以使用链表的方式来建立二叉树为例。
1.定义二叉树节点类首先,定义一个二叉树节点的类,包含节点值、左子节点和右子节点三个属性。
```pythonclass Node:def __init__(self, value):self.value = valueself.left = Noneself.right = None```2.建立二叉树使用递归的方法来建立二叉树,先构造根节点,然后递归地构造左子树和右子树。
```pythondef build_binary_tree(lst):if not lst: # 如果 lst 为空,则返回 Nonereturn Nonemid = len(lst) // 2 # 取 lst 的中间元素作为根节点的值root = Node(lst[mid])root.left = build_binary_tree(lst[:mid]) # 递归构造左子树root.right = build_binary_tree(lst[mid+1:]) # 递归构造右子树return root```下面是建立二叉树的示例代码:```pythonlst = [1, 2, 3, 4, 5, 6, 7]root = build_binary_tree(lst)```二、遍历二叉树遍历二叉树是指按照其中一规则访问二叉树的所有节点,常见的遍历方式有前序遍历、中序遍历和后序遍历。
1.前序遍历前序遍历是指先访问根节点,然后访问左子节点,最后访问右子节点。
```pythondef pre_order_traversal(root):if root:print(root.value) # 先访问根节点pre_order_traversal(root.left) # 递归访问左子树pre_order_traversal(root.right) # 递归访问右子树```2.中序遍历中序遍历是指先访问左子节点,然后访问根节点,最后访问右子节点。
平衡二叉树构造过程

平衡二叉树构造过程
平衡二叉树的构造过程主要分为以下几个步骤:
1.定义平衡二叉树的结构:平衡二叉树的结构类似于普通二叉树,每
个节点的左子树和右子树的深度差不超过1。
2.插入节点:当往平衡二叉树中插入一个节点时,需要先通过二叉搜
索树的方式找到新节点的插入位置。
然后,通过旋转操作将树重新平衡。
旋转分为左旋和右旋两种操作。
3.左旋:当一个节点的右子树深度大于左子树深度时,需要进行左旋
操作。
左旋操作是将该节点的右子树进行旋转,使其成为该节点的父节点,该节点成为该节点的右子树的左子树。
4.右旋:当一个节点的左子树深度大于右子树深度时,需要进行右旋
操作。
右旋操作是将该节点的左子树进行旋转,使其成为该节点的父节点,该节点成为该节点的左子树的右子树。
5.删除节点:当从平衡二叉树中删除一个节点时,需要通过旋转操作
将树重新平衡,避免树退化成非平衡二叉树,导致性能下降。
6.重新计算节点深度:平衡二叉树的关键是保证每个节点的左子树和
右子树深度差不超过1,因此在进行节点插入和删除操作后,需要重新计
算每个节点的深度,并检查是否满足平衡二叉树的结构。
通过以上步骤,可以构造一个平衡二叉树。
在应用中,平衡二叉树常
用于高效的查找和排序操作。
最优二叉树(哈夫曼树)的构建及编码

最优⼆叉树(哈夫曼树)的构建及编码参考:数据结构教程(第五版)李春葆主编⼀,概述1,概念 结点的带权路径长度: 从根节点到该结点之间的路径长度与该结点上权的乘积。
树的带权路径长度: 树中所有叶结点的带权路径长度之和。
2,哈夫曼树(Huffman Tree) 给定 n 个权值作为 n 个叶⼦结点,构造⼀棵⼆叉树,若该树的带权路径长度达到最⼩,则称这样的⼆叉树为最优⼆叉树,也称为哈夫曼树。
哈夫曼树是带权路径长度最短的树,权值较⼤的结点离根较近。
⼆,哈夫曼树的构建1,思考 要实现哈夫曼树⾸先有个问题摆在眼前,那就是哈夫曼树⽤什么数据结构表⽰? ⾸先,我们想到的肯定数组了,因为数组是最简单和⽅便的。
⽤数组表⽰⼆叉树有两种⽅法: 第⼀种适⽤于所有的树。
即利⽤树的每个结点最多只有⼀个⽗节点这种特性,⽤ p[ i ] 表⽰ i 结点的根节点,进⽽表⽰树的⽅法。
但这种⽅法是有缺陷的,权重的值需要另设⼀个数组表⽰;每次找⼦节点都要遍历⼀遍数组,⼗分浪费时间。
第⼆种只适⽤于⼆叉树。
即利⽤⼆叉树每个结点最多只有两个⼦节点的特点。
从下标 0 开始表⽰根节点,编号为 i 结点即为 2 * i + 1 和 2 * i + 2,⽗节点为 ( i - 1) / 2,没有⽤到的空间⽤ -1 表⽰。
但这种⽅法也有问题,即哈夫曼树是从叶结点⾃下往上构建的,⼀开始树叶的位置会因为⽆法确定⾃⾝的深度⽽⽆法确定,从⽽⽆法构造。
既然如此,只能⽤⽐较⿇烦的结构体数组表⽰⼆叉树了。
typedef struct HTNode // 哈夫曼树结点{double w; // 权重int p, lc, rc;}htn;2,算法思想 感觉⽐较偏向于贪⼼,权重最⼩的叶⼦节点要离根节点越远,⼜因为我们是从叶⼦结点开始构造最优树的,所以肯定是从最远的结点开始构造,即权重最⼩的结点开始构造。
所以先选择权重最⼩的两个结点,构造⼀棵⼩⼆叉树。
然后那两个最⼩权值的结点因为已经构造完了,不会在⽤了,就不去考虑它了,将新⽣成的根节点作为新的叶⼦节加⼊剩下的叶⼦节点,⼜因为该根节点要能代表整个以它为根节点的⼆叉树的权重,所以其权值要为其所有⼦节点的权重之和。
哈夫曼树构造方法

哈夫曼树构造方法哈夫曼树,又称最优二叉树,是一种带权路径长度最短的树,广泛应用于数据压缩和编码领域。
其构造方法主要是通过贪心算法来实现,下面我们将详细介绍哈夫曼树的构造方法。
首先,我们需要了解哈夫曼树的基本概念。
哈夫曼树是一种二叉树,其叶子节点对应着需要编码的字符,而非叶子节点则是字符的权重。
构造哈夫曼树的目标是使得树的带权路径长度最小,即字符的编码长度最短。
接下来,我们来介绍哈夫曼树的构造步骤。
首先,我们需要准备一个包含所有字符及其权重的集合,然后按照字符的权重进行排序。
接着,我们选择权重最小的两个字符,将它们作为左右子节点构造一个新的节点,其权重为两个子节点的权重之和。
然后将新节点插入到集合中,并重新按照权重排序。
重复这个过程,直到集合中只剩下一个节点为止,这个节点就是哈夫曼树的根节点。
在构造哈夫曼树的过程中,我们需要使用一个辅助数据结构来辅助构造。
通常我们会选择最小堆作为辅助数据结构,因为它能够快速找到最小权重的节点,并且在插入新节点后能够快速调整堆的结构。
除了使用最小堆外,我们还可以使用其他数据结构来构造哈夫曼树,比如使用优先队列或者手动实现堆结构。
无论使用何种数据结构,核心的思想都是贪心算法,即每一步都选择当前最优的解决方案,最终得到全局最优解。
在实际应用中,哈夫曼树常常用于数据压缩,其编码长度与字符的权重成正比。
权重越大的字符,其编码长度越短,从而实现了对数据的高效压缩。
除此之外,哈夫曼树还被广泛应用于通信领域,比如无线电通信和光通信中的信道编码。
总之,哈夫曼树是一种非常重要的数据结构,其构造方法基于贪心算法,能够实现带权路径长度最短的树。
通过合理选择辅助数据结构,我们可以高效地构造出哈夫曼树,并且在实际应用中取得良好的效果。
希望本文能够帮助读者更好地理解哈夫曼树的构造方法,以及其在实际应用中的重要性。
数据结构二叉排序树

05
13
19
21
37
56
64
75
80
88
92
low mid high 因为r[mid].key<k,所以向右找,令low:=mid+1=4 (3) low=4;high=5;mid=(4+5) div 2=4
05
13
19
low
21
37
56
64
75
80
88
92
mid high
因为r[mid].key=k,查找成功,所查元素在表中的序号为mid 的值
平均查找长度:为确定某元素在表中某位置所进行的比 较次数的期望值。 在长度为n的表中找某一元素,查找成功的平均查找长度:
ASL=∑PiCi
Pi :为查找表中第i个元素的概率 Ci :为查到表中第i个元素时已经进行的比较次数
在顺序查找时, Ci取决于所查元素在表中的位置, Ci =i,设每个元素的查找概率相等,即Pi=1/n,则:
RL型的第一次旋转(顺时针) 以 53 为轴心,把 37 从 53 的左上转到 53 的左下,使得 53 的左 是 37 ;右是 90 ,原 53 的左变成了 37 的右。 RL型的第二次旋转(逆时针)
一般情况下,假设由于二叉排序树上插入结点而失去 平衡的最小子树的根结点指针为a(即a是离插入结点最 近,且平衡因子绝对值超过1的祖先结点),则失去平衡 后进行调整的规律可归纳为下列四种情况: ⒈RR型平衡旋转: a -2 b -1 h-1 a1
2.查找关键字k=85 的情况 (1) low=1;high=11;mid=(1+11) / 2=6
05
13
19
21
二叉排序树的构造方法

二叉排序树的构造方法二叉排序树又称二叉查找树,是一种经典的数据结构,它具有快速的插入、删除和查找等操作。
在实际应用中,二叉排序树被广泛地使用,因此了解二叉排序树的构造方法至关重要。
本文将介绍二叉排序树的构造方法,帮助读者深入理解这一数据结构。
一、二叉排序树基本概念二叉排序树是一种二叉树,每个节点包含一个值,并且满足以下性质:1. 左子树上所有节点的值均小于其父节点的值;2. 右子树上所有节点的值均大于其父节点的值;3. 左右子树也分别为二叉排序树。
根据上述性质,可以得出二叉排序树的中序遍历结果为有序序列。
这一特点使得二叉排序树成为一种非常有效的数据结构,用于快速查找和排序。
二、二叉排序树的构造方法在构造二叉排序树时,一般采用递归或循环遍历的方法。
下面将分别介绍这两种构造方法。
1. 递归构造方法递归构造方法是一种常见且直观的构造二叉排序树的方式。
其基本原理为,将新节点插入到当前节点的左子树或右子树上,直至找到合适的位置。
具体流程如下所示:(1)若二叉排序树为空,直接将新节点作为根节点插入;(2)若新节点值小于当前节点值,则递归地将其插入到左子树上;(3)若新节点值大于当前节点值,则递归地将其插入到右子树上。
通过递归构造方法,可以很方便地构造出一棵满足二叉排序树性质的树。
2. 循环构造方法循环构造方法是另一种构造二叉排序树的方式,通过使用迭代的方式,逐步构建二叉排序树。
其基本思路为:(1)从根节点开始,若树为空,则直接将新节点插入为根节点;(2)若树不为空,则利用循环遍历的方式,找到新节点应插入的位置,直至找到合适的叶子节点;(3)将新节点插入到找到的叶子节点的左子树或右子树上。
循环构造方法相对于递归构造方法,更加迭代化,适合于对二叉排序树进行迭代构造和遍历。
三、二叉排序树构造方法的实现在实际编程中,可以通过使用递归或循环的方式,实现二叉排序树的构造。
下面将简要介绍二叉排序树构造方法的实现过程。
1. 递归实现递归实现二叉排序树的构造方法一般通过编写递归函数,不断地将新节点插入到当前节点的左子树或右子树上。
哈夫曼树的构造

哈夫曼树的构造关键思想: 依据哈弗曼树的定义,⼀棵⼆叉树要使其WPL值最⼩,必须使权值越⼤的叶⼦结点越靠近根结点,⽽权值越⼩的叶⼦结点越远离根结点。
哈弗曼根据这⼀特点提出了⼀种构造最优⼆叉树的⽅法,其基本思想如下:1。
根据给定的n个权值{w1, w2, w3 ... w n },构造n棵只有根节点的⼆叉树,令起权值为w j2。
在森林中选取两棵根节点权值最⼩的树作为左右⼦树,构造⼀颗新的⼆叉树,置新⼆叉树根节点权值为其左右⼦树根节点权值之和。
注意,左⼦树的权值应⼩于右⼦树的权值。
3。
从森林中删除这两棵树,同时将新得到的⼆叉树加⼊森林中。
(换句话说,之前的2棵最⼩的根节点已经被合并成⼀个新的结点了)4。
重复上述两步,直到只含⼀棵树为⽌,这棵树即是哈弗曼树以下演⽰了⽤Huffman算法构造⼀棵Huffman树的过程:考研题⽬:三、哈夫曼树的在编码中的应⽤在电⽂传输中,须要将电⽂中出现的每⼀个字符进⾏⼆进制编码。
在设计编码时须要遵守两个原则:(1)发送⽅传输的⼆进制编码,到接收⽅解码后必须具有唯⼀性,即解码结果与发送⽅发送的电⽂全然⼀样;(2)发送的⼆进制编码尽可能地短。
以下我们介绍两种编码的⽅式。
1. 等长编码这样的编码⽅式的特点是每⼀个字符的编码长度同样(编码长度就是每⼀个编码所含的⼆进制位数)。
如果字符集仅仅含有4个字符A,B,C,D,⽤⼆进制两位表⽰的编码分别为00,01,10,11。
若如今有⼀段电⽂为:ABACCDA,则应发送⼆进制序列:00010010101100,总长度为14位。
当接收⽅接收到这段电⽂后,将按两位⼀段进⾏译码。
这样的编码的特点是译码简单且具有唯⼀性,但编码长度并⾮最短的。
2. 不等长编码在传送电⽂时,为了使其⼆进制位数尽可能地少,能够将每⼀个字符的编码设计为不等长的,使⽤频度较⾼的字符分配⼀个相对照较短的编码,使⽤频度较低的字符分配⼀个⽐較长的编码。
⽐如,能够为A,B,C,D四个字符分别分配0,00,1,01,并可将上述电⽂⽤⼆进制序列:000011010发送,其长度仅仅有9个⼆进制位,但随之带来了⼀个问题,接收⽅接到这段电⽂后⽆法进⾏译码,由于⽆法断定前⾯4个0是4个A,1个B、2个A,还是2个B,即译码不唯⼀,因此这样的编码⽅法不可使⽤。
哈夫曼树构造例题

哈夫曼树构造例题【原创版】目录1.哈夫曼树的概念和基本性质2.哈夫曼树的构造方法3.哈夫曼树的应用实例正文哈夫曼树(Huffman Tree)是一种带权路径长度最短的二叉树,它是由美国计算机科学家 David A.Huffman 在 1952 年提出的。
哈夫曼树的主要应用是在数据压缩和编码领域,通过将原始数据转换成对应的哈夫曼编码,可以大大减少数据的存储空间和传输时间。
一、哈夫曼树的概念和基本性质哈夫曼树是一棵满二叉树,它的构造方法是将权值最小的两个节点合并为一个新节点,新节点的权值为两个节点权值的和。
重复这个过程,直到所有的节点都被合并为一个根节点。
哈夫曼树的基本性质包括:1.哈夫曼树是一棵满二叉树,即除了最后一层外,其他层的节点数都是满的。
2.哈夫曼树的叶节点(即最后一层的节点)对应于原始数据中的每个字符,且权值最小的叶节点在最左边。
3.哈夫曼树的每个父节点的权值等于其左右子节点权值之和。
二、哈夫曼树的构造方法构造哈夫曼树的方法可以分为两个步骤:1.根据原始数据中的字符出现频率构建一个哈夫曼树。
首先将原始数据中的每个字符作为叶子节点,权值为该字符出现的频率。
然后在这些节点中选择权值最小的两个节点合并为一个新节点,新节点的权值为两个节点权值的和。
重复这个过程,直到所有的节点都被合并为一个根节点。
2.对哈夫曼树进行编码。
从根节点到每个叶节点的路径代表一个字符的编码,其中左子节点的边表示 0,右子节点的边表示 1。
例如,如果某个字符的叶节点位于路径“001”,那么该字符的编码就是“001”。
三、哈夫曼树的应用实例哈夫曼树在数据压缩和编码领域有着广泛的应用,以下是一个简单的实例:假设有如下一段原始数据:“aaabbbccc”,对应的哈夫曼树如下:```10/a c/ /a b b c```根据哈夫曼树,我们可以得到该数据集的哈夫曼编码为:“101 102 103 11 10”。
其中,“101”代表字符“a”,“102”代表字符“b”,“103”代表字符“c”。
平衡二叉树-构造方法(绝妙)
平衡二叉树构造方法平衡二叉树对于二叉查找树,尽管查找、插入及删除操作的平均运行时间为O(logn),但是它们的最差运行时间都是O(n),原因在于对树的形状没有限制。
平衡二叉树又称为AVL树,它或者是一棵空树,或者是有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左右子树的深度之差的绝对值不超过1。
二叉树的的平衡因子BF为:该结点的左子树的深度减去它的右子树的深度,则平衡二叉树的所有结点的平衡因子为只可能是:-1、0和1一棵好的平衡二叉树的特征:(1)保证有n个结点的树的高度为O(logn)(2)容易维护,也就是说,在做数据项的插入或删除操作时,为平衡树所做的一些辅助操作时间开销为O(1)一、平衡二叉树的构造在一棵二叉查找树中插入结点后,调整其为平衡二叉树。
若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树(1)插入点位置必须满足二叉查找树的性质,即任意一棵子树的左结点都小于根结点,右结点大于根结点(2)找出插入结点后不平衡的最小二叉树进行调整,如果是整个树不平衡,才进行整个树的调整。
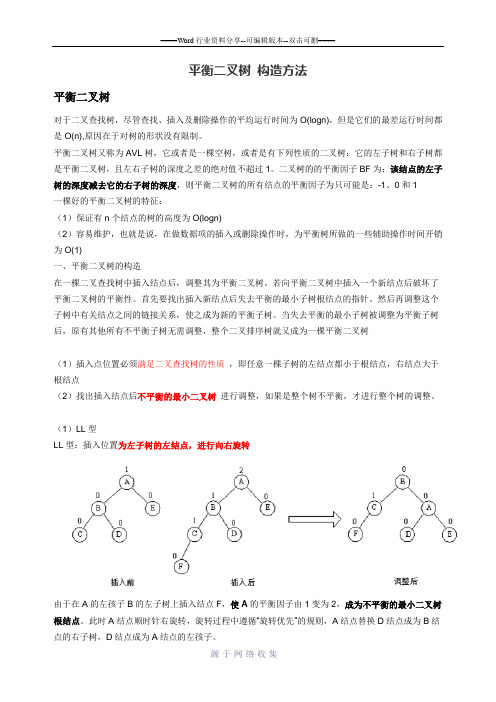
(1)LL型LL型:插入位置为左子树的左结点,进行向右旋转由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1变为2,成为不平衡的最小二叉树根结点。
此时A结点顺时针右旋转,旋转过程中遵循“旋转优先”的规则,A结点替换D结点成为B结点的右子树,D结点成为A结点的左孩子。
(2)RR型RR型:插入位置为右子树的右孩子,进行向左旋转由于在A的右子树C的右子树插入了结点F,A的平衡因子由-1变为-2,成为不平衡的最小二叉树根结点。
此时,A结点逆时针左旋转,遵循“旋转优先”的规则,A结点替换D结点成为C的左子树,D结点成为A的右子树。
平衡二叉树构造过程

平衡二叉树构造过程1.插入操作:插入新节点是平衡二叉树构造过程中的基本操作之一、首先,将新节点插入到二叉树中的合适位置,然后检查树的平衡性。
在插入过程中,需要更新每个节点的高度,并验证是否需要进行旋转操作,以保持树的平衡。
具体插入操作的步骤如下:1.1在树中查找合适的位置插入新节点,按照二叉树的规则:-如果新节点值小于当前节点值,则继续在当前节点的左子树中查找合适位置插入新节点;-如果新节点值大于当前节点值,则继续在当前节点的右子树中查找合适位置插入新节点;-如果当前节点为空,则将新节点插入到此位置。
1.2更新每个节点的高度,从插入的节点开始,向上遍历到根节点。
计算每个节点的左子树高度和右子树高度,然后取其中较大值加1作为节点的新高度。
1.3验证平衡性。
对于每个节点,计算其左右子树高度差的绝对值,如果超过1,则需要进行旋转操作。
2.旋转操作:旋转是平衡二叉树构造过程中的关键步骤,用来调整树的结构,使其保持平衡。
2.1左旋:将当前节点的右子树变为新的根节点,当前节点成为新的根节点的左子树,新的根节点的左子树成为当前节点的右子树。
2.2右旋:将当前节点的左子树变为新的根节点,当前节点成为新的根节点的右子树,新的根节点的右子树成为当前节点的左子树。
2.3左右旋:先对当前节点的左子树进行左旋操作,然后再对当前节点进行右旋操作。
2.4右左旋:先对当前节点的右子树进行右旋操作,然后再对当前节点进行左旋操作。
旋转操作的目的是调整树的结构,使得左右子树的高度差不超过1,并保持二叉树的性质。
3.删除操作:删除节点是平衡二叉树构造过程中的另一个重要操作。
删除操作也需要更新树的高度和进行旋转操作。
删除操作的步骤如下:3.1在树中查找要删除的节点。
如果要删除的节点是叶子节点,则直接删除即可。
3.2如果要删除的节点只有一个子节点,则将子节点替换成当前节点的位置。
3.3如果要删除的节点有两个子节点,则找到当前节点的后继节点(即比当前节点大的最小节点)或前驱节点(即比当前节点小的最大节点),将后继节点或前驱节点的值复制到当前节点,并删除后继节点或前驱节点。
构造表达式二叉树

构造表达式二叉树构造表达式二叉树,需要先确定二叉树的构造规则,然后将表达式按照规则转换为对应的二叉树结构。
下面是一个简单的例子,演示如何构造一个表达式的二叉树:假设我们有一个简单的四则运算表达式:3 + 4 2 - 1 / 2。
根据二叉树的构造规则,我们可以将这个表达式转换为如下的二叉树结构:```+/ \3/ \4 2/ \- 1/ \/ 2```这个二叉树表示的表达式是:3 + (4 2) - (1 / 2)。
其中,根节点表示运算符"+",左子树表示3,右子树是一个二叉树,根节点表示运算符"",左子树表示4,右子树表示2。
在右子树的下面是一个三叉树,根节点表示运算符"-",左子树是空,中子树表示1,右子树是一个二叉树,根节点表示运算符"/",左子树是空,右子树表示2。
在构造这个二叉树时,需要注意以下几点:1. 先处理运算符和操作数。
在表达式中,运算符和操作数之间有一个空格。
在构造二叉树时,我们需要保留这个空格,将其视为两个节点的分隔符。
2. 根据运算符的优先级和结合性,确定子树的构造顺序。
在本例中,""的优先级高于"+",所以先构造""的子树。
同时,""是左结合的,所以先构造左子树。
3. 对于复杂的表达式,需要使用括号来明确运算顺序。
在本例中,"1 / 2"被括起来,表示先进行除法运算。
在构造二叉树时,需要将括号视为一个节点,并将其作为父节点包含其它的子节点。
二叉树广义表表示法 -回复

二叉树广义表表示法-回复什么是二叉树广义表表示法?二叉树广义表表示法是一种用括号来表示二叉树结构的方法。
它是对二叉树的一种抽象描述,将二叉树的各个节点及其子树以括号表示出来,从而形成了一种类似于数学表达式的结构,方便存储和解析二叉树。
具体来说,二叉树广义表表示法由一系列由逗号分隔的项组成,每个项可以是一个节点,也可以是空树。
对于一个非空节点,其形式是"(L, D, R)",其中L表示左子树,D表示节点本身的数据,R表示右子树。
对于一个空树,它的形式是"()"。
通过组合这些项,我们可以构建出二叉树的广义表表示。
下面,我将逐步详细解释二叉树广义表表示法的构造过程和使用方法。
第一步:构造树的根节点和左子树我们可以从根节点开始构造二叉树的广义表表示。
假设我们有一个根节点,且它的左子树不为空。
那么我们将根节点的数据和左子树看作一个项,构成一个括号对,即"(L, D)"。
这里的L表示左子树,D表示根节点的数据。
如果左子树为空,我们可以直接将根节点的数据写入括号中,即"(D)"。
这样,我们就成功构造了根节点和左子树的括号对。
第二步:构造右子树现在,我们需要构造二叉树的右子树。
同样地,如果右子树不为空,我们将右子树看作一个括号对,构成一个项,即"(L, D)"。
如果右子树为空,我们可以直接将括号闭合,即"(L, D)"。
这样,我们就成功构造了二叉树的右子树。
第三步:构造更多节点如果二叉树还有更多的节点,我们可以按照上述的方法继续构造。
具体地说,对于一个非空节点,我们将它的数据和左子树构成一个项,右子树构成另一个项。
这两个项可以按顺序写入广义表表示中,用逗号隔开。
如果节点的左子树和右子树都为空,我们可以直接将节点的数据写入表示中。
第四步:组合项构成广义表表示通过上述步骤,我们可以逐个构造出二叉树的各个节点及其子树的括号对,将它们按顺序以逗号分隔,从而形成二叉树的广义表表示。
最优二叉树(哈夫曼树)

第八节最优二叉树(哈夫曼树)一、概念在具有n个带权叶结点的二叉树中,使所有叶结点的带权路径长度之和(即二叉树的带权路径长度)为最小的二叉树,称为最优二叉树(又称最优搜索树或哈夫曼树),即最优二叉树使(W k—第k个叶结点的权值;P k—第k个叶结点的带权路径长度)达到最小。
二、最优二叉树的构造方法假定给出n个结点ki(i=1‥n),其权值分别为Wi(i=1‥n)。
要构造以此n个结点为叶结点的最优二叉树,其构造方法如下:首先,将给定的n个结点构成n棵二叉树的集合F={T1,T2,……,Tn}。
其中每棵二叉树Ti中只有一个权值为wi的根结点ki,其左、右子树均为空。
然后做以下两步⑴在F中选取根结点权值最小的两棵二叉树作为左右子树,构造一棵新的二叉树,并且置新的二叉树的根结点的权值为其左、右子树根结点的权值之和;⑵在F中删除这两棵二叉树,同时将新得到的二叉树加入F 重复⑴、⑵,直到在F中只含有一棵二叉树为止。
这棵二叉树便是最优二叉树。
三、最优二叉树的数据类型定义在最优二叉树中非叶结点的度均为2,为满二叉树,因此采用顺序存储结构为宜。
如果带权叶结点数为n个,则最优二叉树的结点数为2n-1个。
Const n=叶结点数的上限;m=2*n-1;{最优二叉树的结点数}Typenode=record{结点类型}data:<数据类型>;{权值}prt,lch,rch,lth:0‥m;{父指针、左、右指针和路径长度}end;wtype=array[1‥n] of <数据类型> ;{n个叶结点权值的类型}treetype=array[1‥m] of node;{最优二叉树的数组类型}Var tree:treetype;{其中tree [1‥n]为叶结点,tree [n+1‥2n-1]为中间结点,根为tree [2n-1]}四、构造最优二叉树的算法。
哈夫曼树构造方法

哈夫曼树构造方法哈夫曼树,又称最优二叉树,是一种带权路径长度最短的树。
它是由美国数学家大卫·哈夫曼于1952年提出的一种树形编码方法。
哈夫曼树的构造方法是通过给定n个权值{w1, w2, …, wn},构造一棵具有n个叶子结点的二叉树,其带权路径长度达到最小。
在实际应用中,哈夫曼树常用于数据压缩算法中,能够有效地减少数据的存储空间,提高数据传输效率。
构造哈夫曼树的方法主要包括以下几个步骤:1. 初始化,将n个权值看作是n棵二叉树的根节点,构造n棵只有一个结点的二叉树,每棵树的权值即为给定的权值。
2. 选择权值最小的两棵树,在n棵树中选择两棵根节点权值最小的树作为左右子树,构造一棵新的二叉树。
将这两棵树的根节点权值相加作为新树的根节点权值。
3. 删除已选择的两棵树,从n棵树中删除已选择的两棵树,将新的二叉树加入到n棵树中。
4. 重复步骤2和3,重复进行步骤2和3,直到所有的树都被选中,最终构造出一棵哈夫曼树。
接下来,我们通过一个例子来演示哈夫曼树的构造过程。
假设有一组权值{5, 29, 7, 8, 14, 23, 3, 11},我们将按照上述步骤来构造哈夫曼树。
首先,我们将这些权值看作是8棵只有一个结点的二叉树:[5] [29] [7] [8] [14] [23] [3] [11]接着,我们选择权值最小的两棵树3和5,构造一棵新的二叉树,根节点权值为3+5=8:[3 5]/ \。
3 5。
然后,我们删除已选择的两棵树,并将新的二叉树加入到剩下的树中:[8] [29] [7] [8] [14] [23] [11] [3 5]接着,我们选择权值最小的两棵树7和8,构造一棵新的二叉树,根节点权值为7+8=15:[7 8]/ \。
7 8。
再次删除已选择的两棵树,并将新的二叉树加入到剩下的树中:[15] [29] [14] [23] [11] [8] [3 5 7 8]依次类推,我们重复进行步骤2和3,直到所有的树都被选中,最终构造出一棵哈夫曼树:[100]/ \。
二叉树的构造方法

二叉树的构造方法
二叉树是一种树形数据结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。
下面将介绍二叉树的构造方法。
二叉树的构造方法主要有两种:递归和迭代。
递归构造方法是指从根节点开始,递归地构造二叉树。
具体地,我们可以定义一个函数,该函数接收一个数组或者列表作为输入,返回一个二叉树。
在该函数中,我们首先找到根节点,然后递归地构造左子树和右子树。
每次递归时,输入的数组或列表都会被缩小,直到只剩下一个元素或者没有元素为止。
此时,递归终止,返回一个节点或者空值,作为当前子树的根节点的左子节点或右子节点。
迭代构造方法是指利用栈或队列实现非递归的构造二叉树。
具体地,我们可以定义一个栈或队列,并将根节点入栈或入队。
然后,我们循环地弹出栈或队列的顶部元素,并将其作为当前子树的根节点。
接着,我们检查当前子树是否存在左子树和右子树。
如果存在,我们将左子树和右子树入栈或入队。
循环结束的条件是栈或队列为空。
无论使用递归方法还是迭代方法,构造二叉树的时间复杂度均为O(n),其中n为二叉树的节点数。
但是,递归方法可能会因为递归深度过大
而导致栈溢出的风险,而迭代方法则需要额外的空间来存储栈或队列。
因此,在实际应用中,我们需要根据实际情况选择相应的构造方法。
从前序和中序遍历构造二叉树算法

+1); //建右子树
return t:
l (二 )算法1的复杂性分析
设 r(/7)是从长为n的前序和 中序遍 历序列构造二又 树的H ̄1 ̄1复杂度,设分 划节点在 中序遍历序列 的第k个 节点 ,则 有 如下 递 推公 式
fro)=1
(,1)=r(k一1)+ (,l一七)+,l 最坏情况下,时间复杂度是 0(/7 ),空间复杂度是 D(力);平均情况下,时间复杂度是0(nlogn),空间复杂 度 是 0(1ogn)。
时间复 杂度是O(n )的主要原因是 ,在每次调用递归函 数 的时候 ,根 据在前序遍历得 到的根廿|点的关 键 字的 值 ,需要一 个循环来在中序遍历序列中 “定位”分 划节 点,这就是造成算法慢 的症结所在。如果要得到一个更 快 的算法 ,很 自然要考虑能否减少这个 “定位 ”所 花的 时 间开 销 。
t_->Leff=Build(InFrom,i-1,PreFrom+1);//建左 子 树
t->Right=Build(i+l,InTo,PreFrom +i—InFrom
+1);∥建右子树
2012年 。第 2期 投稿 邮箱 hnfc@21cn.net J 61
实务 ·软件服务
栏 目编 辑 梁 丽 雯 E—mail:liven 01@163 COrn
re[Urn t:
} 2.算 法2的复杂 性 分析 设 )是从长为n的前序和中序遍历序列构造二叉 树 的时间复杂度 ,设分划节 在中序遍历序列的第k个 节 ,则有如下递推公式
哈夫曼树构造方法

哈夫曼树构造方法哈夫曼树(Huffman Tree)是一种广泛应用于数据压缩和编码的二叉树结构。
它是一种最优二叉树,即带权路径长度最短的二叉树。
哈夫曼树的构造方法主要有两种:贪心算法和分治算法。
1. 贪心算法:哈夫曼树的贪心算法是一种自底向上(从叶子节点到根节点)的构造方法。
首先,根据给定的权值列表,将每个权值看作一个独立的节点,并按照权值从小到大的顺序构建一个森林。
然后,从森林中选择权值最小的两个节点(可以使用最小堆来实现),将它们合并为一个新的节点,并将新节点的权值设为两个被合并节点的权值之和。
将新节点插入到森林中,并移除原来的两个节点。
重复上述步骤,直到森林中只有一个节点为止,该节点就是哈夫曼树的根节点。
贪心算法构造哈夫曼树的时间复杂度为O(nlogn),n为节点数量。
2. 分治算法:哈夫曼树的分治算法是一种自顶向下(从根节点到叶子节点)的构造方法。
首先,将给定的权值列表按照权值从小到大的顺序排序。
然后,将权值最小的两个节点合并为一个新的节点,并将新节点的权值设为两个被合并节点的权值之和。
将新节点插入到排序后的列表中,并移除原来的两个节点。
重复上述步骤,直到列表中只有一个节点为止,该节点就是哈夫曼树的根节点。
分治算法构造哈夫曼树的时间复杂度为O(n^2),n为节点数量。
无论是贪心算法还是分治算法,构造出的哈夫曼树都具有最优性质,即带权路径长度最短。
由于贪心算法的时间复杂度较低,因此在实际应用中更为常用。
另外,构造哈夫曼树的方法除了贪心算法和分治算法外,还可以使用动态规划等其他方法。
对于哈夫曼树的应用,最常见的是数据压缩和编码。
哈夫曼树可以根据字符出现的频率构建对应的编码表,将频率高的字符用较短的编码表示,将频率低的字符用较长的编码表示,从而实现对数据的压缩。
在压缩的过程中,利用哈夫曼树可以实现对数据的高效编码和解码。
此外,哈夫曼树还有其他应用,比如在路由表的构建和图像压缩等领域也有广泛应用。
平衡二叉树构造方法

平衡二叉树构造方法构造平衡二叉树的方法有很多,其中一种绝妙的方法是通过AVL树进行构造。
AVL树是一种平衡二叉树,它的左子树和右子树的高度差不超过1、利用这种特性,我们可以通过以下步骤构造平衡二叉树:1.将需要构造平衡二叉树的数据按照升序或者降序排列。
2.选择数据的中间元素作为根节点。
3.将数据分成左右两个部分,分别作为根节点的左子树和右子树的数据。
4.递归地对左子树和右子树进行构造。
下面我们通过一个例子来具体说明这个方法:假设我们需要构造一个平衡二叉树,并且数据为1,2,3,4,5,6,7,8,9首先,我们将数据按照升序排列得到1,2,3,4,5,6,7,8,9、选择中间的元素5作为根节点。
然后,我们将数据分成两部分:1,2,3,4和6,7,8,9、递归地对这两个部分进行构造。
对于左子树,我们选择中间元素2作为根节点,将数据分成两部分:1和3,4、递归地构造这两个部分。
对于右子树,我们选择中间元素8作为根节点,将数据分成两部分:6,7和9、递归地构造这两个部分。
重复这个过程,直到所有的数据都被构造为节点。
最后得到的树就是一个平衡二叉树。
这个构造方法的时间复杂度是O(nlogn),其中n是数据的数量。
虽然它的时间复杂度比较高,但是它保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
总结起来,通过AVL树进行构造是一种有效的方法来构造平衡二叉树。
它将数据按照升序或者降序排列,选择中间元素作为根节点,然后递归地对左子树和右子树进行构造。
这种方法保证了构造的树是一个平衡二叉树,从而提高了数据的查找、插入和删除等操作的效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
பைடு நூலகம்
R->data = ch;
Create(R->lch); Create(R->rch);
//创建左子树 //创建右子树
}
}
2)根据前序遍历序列和中序遍历序列构造二叉链表的二叉树
如图 5-2 所示的二叉树的前序序列和中序序列为:ABDEFCGH 和 DBFEAGHC,则如 何创建二叉链表的二叉树呢?
编程思路:
递归实现创建操作时用来表示的结点的类型为指针的引用*&,这是通过函数参数传 递来使用的,目的是将指针本身传递给函数;非递归实现过程中没有参数调用,无法使 用*&类型,因此使用 **来传递结点指针的地址。
c.以类前序序列做为输入进行实现。
程序代码:
template <class T>
void BiTree<T>::Create(BiNode<T>** R)
{ BiNode<T>** stack[MAXSIZE]; int top =-1;
//定义顺序栈 //栈顶指针
char ch;
do
{
cin>>ch;
while(ch!=’#’)
{ *R = new BiNode<T>;
//创建结点,保存根结点指针的地址
(*R)->data=ch;
(*R)->lch =(*R)->rch = NULL;
b.使用非递归的方法创建二叉树必须要注意输入的参数类型**;
首先,**是指针的指针,也就是**类型的变量存储的数据是一个指针的地址。举个 例子,已知 int a=5;则 int *p=&a; int **pp = &p;则变量 a、p、pp 的关系如图所示:
p a=5
pp p=&a
p 是一个指针变量,该变量存储的是变量 a 的地址;pp 就是一个指针的指针,该变 量存储的是指针 p 的地址。
所有创建二叉树的思路有其通用性,都是先创建根结点,再递归创建左子树和右子树, 那么本题就转化成如何查找根结点和左右子树的问题。
a. 如何找到二叉树的根呢?
这就需要在前序序列中找根结点,就是当前前序序列数组的首字符;
b. 如何找出这个根的左子树和右子树呢?
根据前序序列[1..n]中找出的根结点,查找在中序序列[1..n]中的位置 pos,则前序 序列中[2,pos]部分是左子树,[pos,n]部分就是右子树;
R->data = PreData[s1];
(*R)->lch =(*R)->rch = NULL;
int pos = find(InData,PreData[s1],s2,e2); //获取根结点在中序序列中的下标
Create(R->lch,PreData,InData, s1+1,s1+pos-s2,s2,pos-1); //创建左子树 Create(R->rch,PreData,InData, s1+pos-s2+1,e1,pos+1,e2); //创建右子树
程序代码:
使用模板类的形式实现该函数如下:
template <class T>
void BiTree<T>::Create(BiNode<T> *&R)
{
char ch;
cin>>ch; if (ch=='#')
//如果结点不存在
R = NULL;
else
{
R = new BiNode<T>;
//创建新的结点
stack[++top]= R;
//R入栈
R = &((*R)->lch);
//R指向当前结点的左孩子指针
cin>>ch;
} R = &((*stack[top])->rch); top--;
//R指向栈顶元素的右孩子指针 //栈顶元素出栈
}while((top!=-1)|| (a[i]!=0)); }
B D
A E
C G
F
H
9
图 5-2 示例二叉树
1)根据类前序序列构造二叉链表的二叉树
如 5-2 所示的二叉树可表示为如图 5-3 所示的扩展二叉树,即为每一个结点的空指针引 入一个虚结点“#”,该扩展二叉树的前序序列表示为:ABD##EF###CG#H###,其中结点 的顺序是前序序列,结点之间的“#”代表空结点。因此,从键盘输入该序列,可以唯一的 构造一个二叉树。
程序代码:
template <class T>
void BiTree<T>::Create(BiNode<T>*& R,T PreData[], T InData[],
int s1, int e1,int s2, int e2)
{
if (s1<=e1)
{ R = new BiNode<T>;
//创建根结点
3)使用非递归的方法创建二叉链表的二叉树 编程思路:
可以参考教材上前序遍历非递归实现的思路来编程。创建二叉树和前序遍历对每个结点 的访问顺序一致,因此二者程序结构基本相同,其区别有二点:一是是否创建新的结点,二 是是否需要将新结点的左右孩子指针传递到下一层;因此,在实现过程中注意以下 3 点就可。
a.非递归必须要使用栈来实现;
}
}
template <class T> int BiTree<T>::find(T InData[],T e,int s2,int e2) //寻找字符e在中序序列中的下标 {
for (int i=s2; i<=e2; i++) if (InData[i] == e) return i;
}
当然,第二种方法也可以使用后序序列和中序序列作为输入构造二叉树,其编程思想 和实现方法同上。请同学们自行编程实现。
二叉树构造方法
这里,给出另外两种常用的二叉树的创建方法,一是根据类前序序列作为输入构造二 叉链表的二叉树,二是根据前序遍历序列和中序遍历序列做为输入构造二叉链表的二叉树。 此外,二叉树的创建非常适合使用递归的方法来实现,逻辑简单易于实现;但是在非递归的 环境下也是可以实现的,实现逻辑较为复杂,因此也在本部分进行讨论。
A
B
C
D
E
#
#
F
#
9
9
#
#
9
G
#
9
#
H
9
#
#
9
编程思路:
图 5-3 扩展二叉树
根据创建二叉链表的思维方式,我们可以这么考虑该问题:若输入的是“#”如何处理? 若是结点字符,如何处理?显然当输入的是结点字符时,需要创建一个新结点,然后呢?递 归创建左子树,递归创建右子树。若输入的是“#”,则表明该二叉树为空树,即 R=NULL。
c. 递归创建 将[2,pos]看成是一棵二叉树,反复进行步骤 a 和 b;将[pos, n]看成是一棵二叉树,
反复进行步骤 a 和 b,直到该树为空结束。 d. 表示方法:
字符数组 PreData[]:表示前序序列 字符数组 InData[]:表示中序序列 s1 和 e1:表示当前处理的前序序列的起始和终止位置; s2 和 e2:表示当前处理的中序序列的起始和终止位置; find(InData,e,s2,e2):查找指定字符 e 在中序序列 InData 中的下标。
