并行计算PC11
并行计算的现状与发展

2
2 1
并行计算的现状
对当前发展形势的基本估计 当前 , 并行计算发展的基本状况是 : ( 1) 并行软件的发展远远落后于并行计算体
收稿日期 : 2000 11 06 作者简介 : 刘赫男 ( 1972- ) , 女 , 河北唐山人 , 太原理工大学矿业学院助教 , 研究方向为监 控系统工程。
56
Coal 1/ 2001
4
结
语
超级计算机已走过了整整 20 年 , 这是一段可扩 展性与可编程性这一对矛盾相互作用直至统一的历 史。市场需求是发展的动力 , 技术进步是发展的条 件。有专家 估计 , 从 现在 起直 到 21 世纪 若干 年, DSM 结构将是超级计算机的主流 , 将稳固地占领超 级计算机的主要市场。 参考文献:
Present Status and Future Development of Parallel Computing
L IU He nan, L UO Xiao, GAO Xiao dong
( T aiy uan Univer sity of T echnology , T aiyuan 030024 , China)
[ 1] [ 2] [ 3] 陆鑫达 . 并行和 分布计算 技术 现状 及发展 策略 [ J] . 中 国计算机世界 , 1998. 王鼎兴 , 董春雷 . 可 扩展并行机群系统 [ J] . 中国计算 机 世界 , 1998. 陈 国良 . 并行 算法 # # # 排 序和 选择 [ M ] . 合肥 : 中国 科 技大学出版社 , 1990. [ 责任编辑 : 李巧英 ]
高计算机的运行速度, 并且已经取得非常显著的成 绩。然而这种努力不用多久就会因趋于物理器件的 极限而终止。人们在研制新一代计算机的努力中 , 一个共同的特点就是采用并行技术。增加同一时间 间隔内操作数量的技术即所谓并行处理技术; 为并 行处理所设计的计算机统称之为并行计算机; 在并 行计算机上求解问题称之为并行计算; 在并行计算 机上实现求解问题的算法可称之为并行算法。 并行处理, 是一门综合性的计算机学科, 它包括 硬件技术 , 也包括算法、 语言、 程序设计等软件方面 的问 题, 当然 , 还包括各种理论上的探讨。严格地 说, 并 行性 ( parallelism ) 有两 种 含义 : 一是 同 时 性 ( simutaneit y) , 亦即并行性, 指两个或多个事件在同 一时间发生; 二是并发性 ( concurrency) , 指两个或多 个事件在同一时间间隔内发生。 按照常用的分类方法, 可以把并行计算机的结 构分为: 单指令流单数据流 ( SISD) ; 单 指令流 多数据流 ( SIMD) ; ! 多指令 流单数据流 ( M ISD) ; ∀ 多指令流多数据流 ( M IMD) 。
2024版计算机发展历史

巴贝奇的差分机
19世纪初,英国数学家查尔斯·巴贝奇设计了差分机,这是一种能够进行复杂数 学运算的机械计算机,但由于技术和资金问题,最终未能完成。
电子计算机的雏形
真空管的出现
20世纪初,真空管技术的出现为电子计算机的发展奠定了基础。 真空管具有放大和开关功能,使得电路的设计和制造变得更加 灵活和高效。
UNIVAC
UNIVAC(Universal Automatic Computer)是第一台商用电子计算机,于1951年由美国雷明顿兰德公司推出。 它采用了5000多个电子管,每秒可进行1000次运算,被广泛应用于商业、政府和军事等领域。
电子管计算机的应用领域
军事领域
在军事领域,电子管计算机被用于弹 道计算、密码破译、雷达控制等方面, 为战争的胜利提供了重要支持。
业领域。
集成电路计算机的技术创新与影响
技术创新
集成电路计算机的出现标志着计算机技术 进入了一个新的时代。与之前的电子管计 算机和晶体管计算机相比,集成电路计算 机具有更高的性能、更小的体积和更低的 功耗。此外,它还引入了微程序设计技术、 多道程序设计技术等先进技术,进一步提 高了计算机的运算速度和效率。
DEC PDP-8
数字设备公司(DEC)推出的8位晶体 管计算机,采用小型化设计,广泛应用 于科研、工业等领域。
晶体管计算机的性能提升与应用拓展
性能提升
与第一代电子管计算机相比,晶体管计算机在运算速度、存储容量和可靠性等方面有了显著提升。
应用拓展
随着晶体管计算机性能的提升,其应用领域也不断拓展,包括科学计算、数据处理、自动控制、人工智能 等。同时,计算机编程语言也得到了进一步的发展和完善,使计算机的应用更加普及和便捷。
numeca并行计算培训教程xp

NUMECA FINE/Turbo™6.x 并行计算培训教程WINDOWS NT/2K/XP/2003操作系统并行计算前提条件1.为保证软件能够进行并行计算功能,需要在软件安装时安装并行计算功能(Parallel Computation)2.软件许可证需要包含并行计算特征(可电话咨询尤迈克公司进行许可证验证,以确认是否有并行计算功能。
多台PC分布式并行计算设定如果是单机多CPU并行计算设定,请跳至PageStep 1: 用户管理1. 添加用户在每一台并行机上创建一个相同的帐号及相同的密码。
例如,创建用户名numeca(也可是其它任意用户名),2. 为用户创建本地路径在用户属性中,添加本地路径,路径可为硬盘上任何已经存在的目录Step 2: 配置管理1. 编辑rhost.txt用文本编辑器打开c:\winnt\rhost.txt文件。
假设共有三台机器并行,主机名分别为PC1、PC2、PC3,则在rhost.txt文件中添加以下语句:PC1 numeca (注释:主机名用户名)PC2 numecaPC3 numeca2. 运行用户注册工具在NUMECA安装目录下(以FINE61-4版本为例),运行FINE61-4\bin\MPIRegister.exe,出现以下提示窗口:输入做并行的用户名,并连续输入两次用户登陆密码,“y”确认。
3. 重新启动计算机Step 3: pvm管理1.关闭所有用于并行机器上的正在运行的FINE软件2. 从任务管理器中删除pvm*.exe的进程,或者重新启动计算机3. 清除所有并行机器上c:\tmp目录下的pvm*.* 文件Step 4: 界面管理1.在主控机上以numeca用户登陆(其它机器可意任何帐户登录)2.启动FINE界面,并通过菜单Modules ÆTask Manager切换至Task Manager窗口,双击左侧的HOSTDEFINITION,进入HOSTS Definition页面3. 点击Add Host,在弹出是对话框中输入主机名、用户名以及操作系统Step 4: 界面管理(续) 4. Accept后弹出如下菜单系统完成主机添加,在HOSTNAME中会多出一计算机名。
ansys多cpu并行计算设置

关于ansys程序运行大内存多核CPU的设置问题转载近期出现这些问题找了些资料并整理下放这里了。
下面这些方法并没有一一试过。
1.ansys结果文件过大如何处理解决超大结果文件的方案主要有四种方法方法一将磁盘格式转换为NTFS 方法二在begin level的时候加上一条命令/configfsplitvalue其中value is the size of file the final size equal to nvalven is the number of sub-file在PC机上面一般1单位4M则/configfsplit750 生成每个分割后的文件都是3G的大小在这个命令下不只是rst文件被分割只要是由ansys所产生的binary文件都会。
如下面命令大概会产生6个rst文件/configfsplit1 14MB /prep7 et145 mpex12e11 mpprxy10.3 blc41011 esize0.1 vmeshall /solu da5all sfa2pres0.1 solve 方法三将不同时间段内的结果分别写入一序列的结果记录文件使用/assign命令和重启动技术ANSYS采用向指定结果记录文件追加当前计算结果数据方式使用/assign指定的文件所以要求指定的结果记录文件都是新创建的文件否则造成结果文件记录内容重复或混乱。
特别是反复运行相同分析命令流时在重复运行命令流文件之前一定要删除以前生成的结果文件序列。
方法四采用载荷步文件批处理方式求解在结果文件大小达到极限而终止计算时同样可以接着计算不过在重新计算时在重启动对话框里选择—create .rst并且read上次的计算结果。
转simwe 2.ansys中物理内存和虚拟内存设置增大物理内存是提高解题效率的关键。
虚拟内存理想配置为物理内存250Mansys的运行速度与内存大小直接有关对于同一台机器内存由256M增大到512M时计算同一题目的速度可以提高几倍解体规模可以达10万自由度以上。
云计算-知识点

1 云计算的计算模式为(B/C )。
2( 分布式)是公有云计算基础架构的基石。
3(虚拟化)是私有云计算基础架构的基石.4(并行计算)是一群同构处理单元的集合,这些处理单元通过通信和协作来更快地解决大规模计算问题5(集群)在许多情况下,能够达到99。
999%的可用性.6 网格计算是利用(因特网)技术,把分散在不同地理位置的计算机组成一台虚拟超级计算机。
7 B/S网站是一种(3层架构)的计算模式。
8 云计算就是把计算资源都放到上( 因特网)。
9(云用户端)提供云用户请求服务的交互界面,也是用户使用云的入口,用户通过Web浏览器可以注册、登录及定制服务、配置和管理用户.打开应用实例与本地操作桌面系统一样.10(服务目录)帮助云用户在取得相应权限(付费或其他限制)后可以选择或定制的服务列表,也可以对已有服务进行退订的操作,在云用户端界面生成相应的图标或列表的形式展示相关的服务.11( 管理系统和部署工具)提供管理和服务,能管理云用户,能对用户授权、认证、登录进行管理,并可以管理可用计算资源和服务,接收用户发送的请求,根据用户请求并转发到相应的相应程序,调度资源智能地部署资源和应用,动态地部署、配置和回收资源。
12( 监控端)监控和计量云系统资源的使用情况,以便做出迅速反应,完成节点同步配置、负载均衡配置和资源监控,确保资源能顺利分配给合适的用户。
13(服务器集群)提供虚拟的或物理的服务器,由管理系统管理,负责高并发量的用户请求处理、大运算量计算处理、用户Web应用服务,云数据存储时采用相应数据切割算法采用并行方式上传和下载大容量数据.14用户可通过( 云用户端)从列表中选择所需的服务,其请求通过管理系统调度相应的资源,并通过部署工具分发请求、配置Web应用.15 在云计算技术中,(中间件)位于服务和服务器集群之间,提供管理和服务即云计算体系结构中的管理系统。
16虚拟化资源指一些可以实现一定操作具有一定功能,但其本身是(虚拟)的资源,如计算池,存储池和网络池、数据库资源等,通过软件技术来实现相关的虚拟化功能包括虚拟环境、虚拟系统、虚拟平台。
ANSYS并行计算设置选项

ANSYS并行计算设置我的电脑是双核心的但是我发现算得很慢很慢貌似没有用到双核请问怎么设计双核并行计算越详细越好谢谢我用的ANSYS10.0 支持支持并行计算么?在线等谢谢问题补充:我想请问一下 90 10.0 版本支持并行运算么??最多即核心??我们学校有个工作站16个4核心CPU但是不清楚ANSYS并行运算有没有CPU这方面限制我知道内存是无限制有多少内存他都承认最佳答案使用AMG算法,可以使多个核同时工作。
使用方法1或2.方法1:(1). 在ansys product lancher 里面lauch标签页选中parallel performance for ansys.(2). 然后在求解前执行如下命令:finish/config,nproc,n!设置处理器数n=你设置的CPU数。
/solueqslv,amg !选择AMG算法solve !求解方法2:(1). 在ansys product lancher 里面lauch标签页选中parallel performance for ansys.(2). 在D:\professional\Ansys Inc\v90\ANSYS\apdl\start90.ans中添加一行:/config,nproc,2.别忘了把目录换成你自己的安装目录.没遇到过这么好的电脑我自己只是双核的去试试吧我觉得可以这也是我找的资料既然说N 那就表示有可能1.我有一个ANSYS输入文件,如何并行计算?答:最简单的办法是以批处理的方式提交。
有以下几个步骤:(1)系统配置。
一般已设置好,如有疑问或需进一步信息,请参考回答5。
(2)修改并行求解器脚本,指定使用CPU的个数。
a.在家目录下找到ansddsmpich文件。
b.其中的"-np"参数后带的数目,即为求解器所用的进程(或CPU)数目。
必须指定为偶数。
(3)修改ansys输入文件,指定使用的求解器类型和使用方式(必须指定为script),以及求解器域分解的数目(必须大于如前指定的CPU的个数)。
【国家自然科学基金】_pc集群_基金支持热词逐年推荐_【万方软件创新助手】_20140729
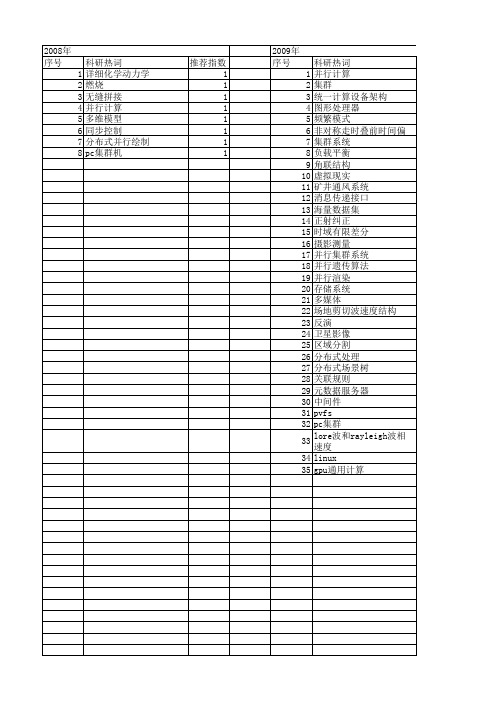
科研热词 详细化学动力学 燃烧 无缝拼接 并行计算 多维模型 同步控制 分布式并行绘制 pc集群机
推荐指数 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
2011年 科研热词 集群式供应链 集群 金融研究 近似 置信区间 网络游戏 网络处理单元 经济实验室建设 硬件加速 生长模拟模型 混合并行遗传算法 消息传递 沉浸式显示 横向合作 概率集群 技术创新 并行计算集群 并行计算 并行绘制 并行算法 多核集群系统 多投影系统 图像合成 响应面 分布式集群 共享内存 作物 优化 产业集群 主仆式并行化 pargeant4 openmp mpi geant4 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
并行计算的现状与发展

问题探讨并行计算的现状与发展刘赫男,罗霄,高晓东(太原理工大学,山西太原030024)摘要:从当前并行计算的实际出发,总结和分析了并行计算发展的现状,并对并行计算今后的发展做出了展望。
与此同时,客观分析了目前我国并行计算发展的状况和与国外发达国家的差距,使我们能够认清形势,更好地发展。
关键词:并行计算;分布计算;机群中图分类号:TP3文献标识码:B文章编号:1005—2798(2001)0卜0056-021并行计算概述从计算机诞生之日起,人们就不断努力加倍提高计算机的运行速度,并且已经取得非常显著的成绩。
然而这种努力不用多久就会因趋于物理器件的极限而终止。
人们在研制新一代计算机的努力中,一个共同的特点就是采用并行技术。
增加同一时间间隔内操作数量的技术即所谓并行处理技术;为并行处理所设计的计算机统称之为并行计算机;在并行计算机上求解问题称之为并行计算;在并行计算机上实现求解问题的算法可称之为并行算法。
并行处理,是一门综合性的计算机学科,它包括硬件技术,也包括算法、语言、程序设计等软件方面的问题,当然,还包括各种理论上的探讨。
严格地说,并行性(parallelism)有两种含义:一是同时性(simutaneity),亦即并行性,指两个或多个事件在同一时间发生;二是并发性(concurl‘ency),指两个或多个事件在同一时间间隔内发生。
按照常用的分类方法,可以把并行计算机的结构分为:①单指令流单数据流(SISD);②单指令流多数据流(SIMD);③多指令流单数据流(MISD);④多指令流多数据流(MIⅧ)。
2并行计算的现状2.1对当前发展形势的基本估计当前,并行计算发展的基本状况是:(1)并行软件的发展远远落后于并行计算体系结构的发展。
(2)并行计算的应用远远落后于并行计算技术的发展。
(3)大规模并行处理系统已不再是主要研究领域。
(4)由高速网联成的各种类型的、规模可伸缩计算机群,将进一步促使并行计算应用有较大的发展。
【小型微型计算机系统】_网络并行计算_期刊发文热词逐年推荐_20140724
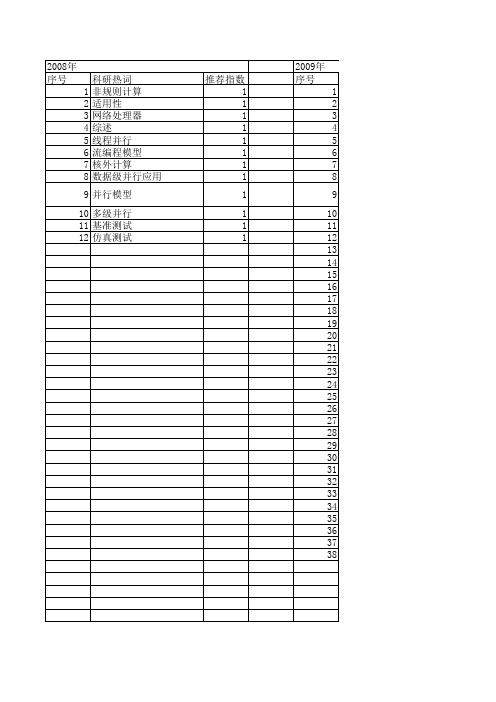
2009年 科研热词 推荐指数 并行算法 2 集成学习 1 近似词典匹配 1 调度 1 触发细胞自动机 1 网络处理器 1 移植 1 注册消息 1 数据加密 1 排序 1 归并 1 异构机群系统 1 并行计算 1 并行处理系统 1 并行处理 1 并行 1 工作站网络(now) 1 对称耦合结构 1 密钥共享与分存 1 学习系统 1 存储受限 1 大规模接入汇聚路由器 1 多目标串近似匹配 1 可分负载 1 协议无关组播-稀疏模式 1 包分类算法 1 动态负载均衡(dlb) 1 信道分配 1 交通流预测 1 wimax 1 webit 1 trie树 1 rapwbn模型 1 mesh网络 1 idcx 1 avr单片机at90s8515 1 8051单片机 1 51操作系统 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
科研热词 并行计算 社会化标签系统 标签共现关系 mapreduce模型 高速网络 零拷贝技术 通信协议 远程过程调用 软件定义的网络 负载均衡 计算域分解 网络安全 编译优化 等几何分析 程序执行模型 流级别 数据集群 数据流程序 数据密集型 并行网络文件系统 并行处理 多核技术 可扩展性 动态流量划分 分布式文件系统 共享内存 伪随机哈希 x10 psram(h) openflow mtf启发法
科研热词 推荐指数 高性能计算 1 马尔可夫链 1 通信轮回时间 1 转弯模型 1 资源共享 1 负载均衡 1 视频点播系统 1 视频点播 1 虫孔 1 虚信道 1 网络处理器 1 网格计算 1 组件 1 硬件设计 1 流水线 1 流媒体直播 1 模逆运算 1 模拟器 1 检查点文件 1 服务发现 1 无线视频传输 1 无死锁路由 1 性能优化 1 志愿者计算 1 弹性构造 1 并行处理 1 局域网 1 对等覆盖网 1 对等网络 1 实时性优化 1 实时性 1 实体排序 1 多链路聚合 1 多核心 1 多核 1 合作关系网络 1 半虚拟化 1 分布式计算平台 1 分布式计算 1 全局地址空间 1 任务调度 1 互连网络 1 云服务传递网络 1 二进制扩展的欧几里德算法 1 主题和时间敏感 1
3.4.2并行程序设计环境和工具(向量化的并行化编译器,并行程序性能分析,计算可视化等)

并行计算PC机群的构建随着计算机硬件技术的高速发展,处理器和网络的性能不断地迅速提高和价格的日益下降,使得并行计算日益从传统的超级计算平台转移到由一组高性能节点或工作站/PC机构成的称之为机群的计算平台上,从而机群成为构建可扩放并行计算机的一大趋势。
机群在计算机界有很多称呼,其中松耦合的工作站/PC机群也被称为工作站机群COW(Cluster of Workstation)或工作站网络NOW(Network of Workstation);而紧耦合的高性能服务器节点机群也被称为构筑高端大规模并行机的机群系统(如SP2和Option Red)。
本文将主要从PC机群软、硬件环境的选择及配置出发给出一个逐步的PC机群构建手册,以使广大的科研工作者能够更为方便的在PC机群环境中开展自己的工作。
并行计算机群是目前由于硬件的时效性很强,所以给出例子的意义并不是很大。
我们这里给出一套配置主要是为了以后叙述的方便,读者应该根据当前最新的硬件信息进行选择。
1PC机群硬件部件的选择在PC机群的构建过程中,硬件部件应根据所要部署应用的类型又针对性的加以选择,具体原则请参见《并行算法实践》第2.2节(硬件的选择与安装)。
本文沿用该章所给出的示例配置,如下:该PC机群包括1个服务节点(兼作计算节点)和63个计算节点。
(1)服务节点配置:Ⅳ(512KB全速二级缓存)CPU:Pentium 2.0G内存:1G(2⨯512M)Rambus硬盘:80GB IDE主板:ASUS P4T Socket 423网卡:3com 905 –TX(两个)显卡、显示器、键盘、鼠标、光驱、软驱:略(2)计算节点配置:CPU:Pentium 1.5GⅣ(512KB全速二级缓存)内存:512MB(2⨯256M) Rambus硬盘:40GB IDE主板:ASUS P4T Socket 423网卡:3com 905 –TX另外,交换设备由2个3com 3c16980和1个3com 3c16985的交换机通过一个matrix module堆叠而成,并安装了一个千兆光纤模块,以备服务接点连接内部机群的网卡升级为千兆网卡。
ANSYS并行计算设置选项

ANSYS并⾏计算设置选项ANSYS并⾏计算设置我的电脑是双核⼼的但是我发现算得很慢很慢貌似没有⽤到双核请问怎么设计双核并⾏计算越详细越好谢谢我⽤的ANSYS10.0 ⽀持⽀持并⾏计算么?在线等谢谢问题补充:我想请问⼀下 90 10.0 版本⽀持并⾏运算么??最多即核⼼??我们学校有个⼯作站16个4核⼼CPU但是不清楚ANSYS并⾏运算有没有CPU这⽅⾯限制我知道内存是⽆限制有多少内存他都承认最佳答案使⽤AMG算法,可以使多个核同时⼯作。
使⽤⽅法1或2.⽅法1:(1). 在ansys product lancher ⾥⾯lauch标签页选中parallel performance for ansys.(2). 然后在求解前执⾏如下命令:finish/config,nproc,n!设置处理器数n=你设置的CPU数。
/solueqslv,amg !选择AMG算法solve !求解⽅法2:(1). 在ansys product lancher ⾥⾯lauch标签页选中parallel performance for ansys.(2). 在D:\professional\Ansys Inc\v90\ANSYS\apdl\start90.ans中添加⼀⾏:/config,nproc,2.别忘了把⽬录换成你⾃⼰的安装⽬录.没遇到过这么好的电脑我⾃⼰只是双核的去试试吧我觉得可以这也是我找的资料既然说N 那就表⽰有可能1.我有⼀个ANSYS输⼊⽂件,如何并⾏计算?答:最简单的办法是以批处理的⽅式提交。
有以下⼏个步骤:(1)系统配置。
⼀般已设置好,如有疑问或需进⼀步信息,请参考回答5。
(2)修改并⾏求解器脚本,指定使⽤CPU的个数。
a.在家⽬录下找到ansddsmpich⽂件。
b.其中的"-np"参数后带的数⽬,即为求解器所⽤的进程(或CPU)数⽬。
必须指定为偶数。
(3)修改ansys输⼊⽂件,指定使⽤的求解器类型和使⽤⽅式(必须指定为script),以及求解器域分解的数⽬(必须⼤于如前指定的CPU的个数)。
Fluent的并行计算设置方法总结

并行计算资料来自傲雪论坛和流体中文网!Winnt平台下搭建Fluent并行计算的一些经验以下是本人在NT平台下搭建Fluent并行计算的一些经验,不足和错误的地方请各位高手指出!系统配置:winnt,win2000操作系统,每台主机只有一个CPU,Fluent6.1,每台主机有自己的IP地址,安装好TCP/IP协议1、 Fluent安装光盘上找到RSHD.exe这个文件。
(注意,必须使用Fluent公司提供的这个远程控制软件)2、用管理员的身份登陆计算机,拷贝该软件到系统盘的winnt目录下,在MS-DOS方式下执行 RSHD -install。
3、配置RSHD。
WINNT系统下:控制面板-〉服务-〉RSH Daemon,双击之,在Logon里面输入用户名/密码。
(一般情况下,为了您的计算机的安全,请不要使用具有管理员权限的用户名和口令。
)您可以在开始-〉程序-〉管理工具 -〉用户管理器里面设定,给guest权限就可以了。
Win2000系统下:控制面板-〉管理工具-〉服务-〉RSH Daemon,以下同于NT的操作。
完成上述操作后,请启动RSH服务。
4、资源管理器里面将Fluent的安装目录设置为共享。
注意:这个时候要分别从其他的计算机登陆到本机这个被共享的目录。
这个步骤一定不可缺少。
同样所有的计算机上的Fluent的安装目录都要被设置为共享,然后分别登陆.....5、编写hosts.txt文件,文件的格式在Fluent的帮助文件中又很详细的描述,这里不再复述。
hosts文件中应这样写computer1’s IP, com puter1’s namecomputer1’‘s IP,computer1’s namecomputer2’s IP,computer2’s namecomputer2’s IP,computer2’s name在命令行输入:fluent 3d -pnet然后在parallel-network-configuer菜单下配置即可。
计算机体系结构试题库—名词解释

计算机体系结构试题库名词解释(100题)1.计算机体系结构:计算机体系结构包括指令集结构、计算机组成和计算机实现三个方面的内容。
2.透明性:在计算机技术中,对这种本来是存在的事物或属性,但从某种角度看又好像不存在的概念称为透明性(transparency)。
3.程序访问的局部性原理:程序总是倾向于访问最近刚访问过的信息,或和当前所访问的信息相近的信息,程序对信息的这一访问特性就称之为程序访问的局部性原理。
4.RISC:精简指令集计算机。
5.CPI——指令时钟数(Cycles per Instruction)。
6.Amdahl定律——加快某部件执行速度所获得的系统性能加速比,受限于该部件在系统中的所占的重要性。
7.系列机:在一个厂家内生产的具有相同的指令集结构,但具有不同组成和实现的一系列不同型号的机器。
8.软件兼容:同一个软件可以不加修改地运行于体系结构相同的各档机器,而且它们所获得的结果一样,差别只在于有不同的运行时间。
9.基准程序:选择一组各个方面有代表性的测试程序,组成的一个通用测试程序集合,用以测试计算机系统的性能。
10.合成测试程序:首先对大量的应用程序中的操作进行统计,得到各种操作的比例,再按照这个比例人为制造出的测试程序。
11.Benchmarks:测试程序包,选择一组各个方面有代表性的测试程序,组成的一个通用测试程序集合。
12.核心程序:从真实程序提取出来的用于评价计算机性能的小的关键部分。
13.通用寄存器型机器:指令集结构中存储操作数的存储单元为通用寄存器的机器,称之为通用寄存器型机器。
14.Load/Store型指令集结构:在指令集结构中,除了Load/Store指令访问存储器之外,其它所有指令的操作均是在寄存器之间进行,这种指令集结构称之为Load/Store型指令集结构。
15.虚拟机器:(virtual machine),由软件实现的机器。
16.操作系统虚拟机:直接管理传统机器中软硬件资源的机器抽象,提供了传统机器所没有的某些基本操作和数据结构,如文件系统、虚拟存储系统、多道程序系统和多线程管理等。
云计算

计算机科学前沿技术之云计算摘要本文意围绕计算机前沿技术云计算展开研究,随着云计算的不断发展,使电脑的运算速度越来越快,也使很多大而复杂的问题得以解决。
本文分别介绍云计算的定义、云计算的相关应用、云计算存在的问题与云计算未来的发展趋势。
关键字云计算、云应用、云安全前言“云计算”被Google提出后,随着它的不断发展,为信息界带来了一场新的革命。
它使依靠掌上终端移动办公成为可能,这个超级计算模式具有高达每秒超过十万亿次的运算能力。
这个强大的互联网模式解决了原始的互联网系统和服务设计不能解决的种种问题。
云计算为我们带来了不可预料的前景。
一、云计算的定义[1]1.并行计算的定义并行计算或称平行计算是相对于串行计算来说的。
它是一种一次可执行多个指令的算法,目的是提高计算速度,及通过扩大问题求解规模,解决大型而复杂的计算问题。
所谓并行计算可分为时间上的并行和空间上的并行。
时间上的并行就是指流水线技术,而空间上的并行则是指用多个处理器并发的执行计算。
2.分布式计算的定义分布式计算是研究如何把一个需要非常巨大的计算能力才能解决的问题分成许多小的部分,然后把这些部分分配给许多计算机进行处理,最后把这些计算结果综合起来得到最终的结果。
3.网格计算的定义网格计算是利用互联网把地理上广泛分布的各种资源连成一个逻辑整体,就像一台超级计算机一样,为用户提供一体化信息和应用服务。
4.云计算的定义云计算是分布式计算、并行计算、网格计算、网络存储、虚拟化、负载均衡、热备份冗余等传统计算机和网络技术发展融合的产物。
是基于互联网的相关服务的增加、使用和交付模式,通常涉及通过互联网来提供动态易扩展且经常是虚拟化的资源。
是一种基于互联网的计算方式,通过这种方式,共享的软硬件资源和信息可以按需提供给计算机和其他设备。
二、云计算的相关应用云计算的相关应用简称“云应用”。
它们的工作原理是把传统软件“本地安装、本地运算”的使用方式变为”即取即用”的服务,通过互联网或局域网连接并操控远程服务器集群,完成业务逻辑或运算任务的一种新型应用。
第11章并行计算机体系结构简介

11.3.3 集群机系统Cluster
1. Cluster简介
计算机体系结构的研究就是当时的超级计 算机的研究,超级计算机共经历了五代。第 一代为早期的单芯片系统,第二代为向量处 理系统,第三代为大规模并行处理系统,第 四代为共享内存处理系统,第五代为集群系 统,目前全球五百强超级计算机排名已经有 半数以上是集群式系统。
第三代计算机(MPP)与第五代计算机:
相同:(Cluster)在体系结构上是同构的,同属 于分布式内存处理方式(DMP—Distributed Memory Processing)
差别:是否采用物美价廉的普通商品组件。MPP 与Cluster从互连角度看,区别在于MPP使用专 用高性能互连网络,而Cluster使用商用网络。 从CPU角度看MPP要用单独设计的高性能处理 器,而Cluster采用高性能成品处理器,从价格 方面看,MPP比Cluster要贵的多。
• 多计算机系统特点:每个CPU都有自己的内存,即自 己独立的物理地址空间;执行自己的操作系统,再加 上对外通信的通信处理器。
• 图11-4a和图11-4b分别说明了多处理器系统与多计 算机系统的区别。
多处理器系统特点:软件设计简单,易 实现,硬件设计比较复杂。
多计算机系统特点:正好相反。
图11-4a 多处理器系统
MESI协议是一种比较常用的写回Cache一致性协议,它 是用协议中用到的四种状态的首字母(M、E、S、I) 来命名的。目前,Pentium 4和许多其他的CPU都使用了 MESI协议来监听总线。每个Cache项都处于下面四种状 态之一:
(1)无效(Invalid)——该Cache项包含的数据无效。
每个CPU都带有Cache,当同时操作内存中某 一块数据时,会出现Cache一致性问题。例如, CPU1与CPU2同时读取内存中一块数据到自己的 Cache中,CPU1先对Cache内容进行了修改,此 后CPU2读自己Cache中数据就已成为旧内容,因 为CPU1修改自己的Cache后还没有写回内存,而 CPU2读的数据相对CPU1来讲是旧数据。解决 Cache一致性问题有两种方法,一种是监听型的 Cache(本书不再详述,请查阅有关书籍),另 一种是“MESI”Cache一致性协议。
PC1-3--系统互联系统结构

国家高性能计算中心(合肥)
2015/12/24
15
嵌入
1000 1001 1011 1010
1100
1101
1111
1110
0100
0101
0111
0110
0000
0001
0011
0010
0110 0100 0101
0111 1100
(a)二叉树
(b)星形连接
(c)二叉胖树
国家高性能计算中心(合肥)
2015/12/24
13
超立方 :
静态互连网络(4)
n
一个n-立方由 N 2 个顶点组成,3-立方如图(a)所示;4-立 方如图(b)所示,由两个3-立方的对应顶点连接而成。 n-立方的节点度为n,网络直径也是n ,而对剖宽度为N / 2 。 如果将3-立方的每个顶点代之以一个环就构成了如图(d)所示 的3-立方环,此时每个顶点的度为3,而不像超立方那样节点 度为n。
国家高性能计算中心(合肥)
2015/12/24
19
单级交叉开关级联起来形成多级互连网络MIN (Multistage Interconnection Network)
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
动态互联网络 (3)
(a)4种可能的开关连接
输入 000 001 010 011 100 101 110 111 第0级 第1级 第2级 输出 000 001 010 011 100 101 110 111
并行计算
——结构•算法•编程
并行计算——结构•算法•编程
并行计算的参考题目

1、讨论某一种算法的可扩放性时,一般指什么?88答:讨论某一种算法的可扩放性时,实际上是指该算法针对某一特定机器结构的可扩放性2、使用“Do in Parallel”语句时,表示的是什么含义105答:表示算法的若干步要并行执行3、并行计算机的存储访问类型有哪几种?26答:存储访问类型有:UMA(均匀存储访问)、NUMA(非均匀存储访问)、COMA(全高速缓存存储访问)、CC-NUMA(高速缓存一致性非均匀存储访问)、NORMAl(非远程存储访问)4、什么是同步?它有什么作用?如何实现?107答:同步是在时间上强使各执行进程在某一点必须相互等待。
作用:确保个处理器的正确工作顺序以及对共享可写数据的正确访问(互斥访问)。
实现方法:用软件、硬件和固件的方法实现。
5 在并行加速比的计算中,常用的三种加速比定律分别是哪三种?(P83)答:常用的三种加速比定律分别是:适用于固定计算负载的Amdahl定律,适用于可扩放问题的Gustafson定律和受限于存储器的Sun和Ni定律。
6、试比较Amdahl定律、Gustafson定律、Sun和Ni定律三种加速定律的应用场合。
83 答:Amdahl定律适用于固定计算负载的问题Gustafson定律适用于可扩放性问题Sun和Ni定律适用于受限于存储器的问题。
7.并行算法的基本设计技术有哪些?它们的基本思想是什么?139答:(1)基本技术有:划分设计技术(又分为均匀划分技术、方根划分技术、对数划分技术和功能划分技术)、分治设计技术、平衡树设计技术、倍增设计技术、流水线设计技术等。
(2)基本思想分别如下:a.划分设计技术:(P139) 将一原始问题分成若干部分,然后各部分由相应的处理器同时执行。
b.分治设计技术:(P144)将一个大二复杂的问题分解成若干特性相同的子问题分而治之。
若所得的子问题规模仍嫌过大,可反复使用分治策略,直至很容易求解诸子问题为止。
c.平衡树设计技术:(P149)将输入元素作为叶节点构筑一颗平衡二叉树,然后自叶向根往返遍历。
未来的并行计算

于 网络技术的消息传递和各节点机具 体的 计 算处 理 ,采用 的语 言用 传统 的语 言就 足够 了 ,如现在的 “ C+MP ”在局域 网 r 内的编 程 。对于 单机 或单 独的嵌 入 式设 备 而言 ,则 使用 专 门的并 行编程 语 言来 处理 并行 计算 。不管 怎样 ,正 如加 州大 学 伯克利 分校 的研 究人 员所 说 ,并 行计 算今后发 展的核心 目标就是使编写能在高
更大的运算规模 , “ 而 第三 代”( 大规模并
行 处 理 )和 “ 五 代 ”( 群 )正 是 由于 采 第 机
的 发 展 。 这 样 , 有 一 个 必 要 条 件 就 是 软 件 的 易 用 性 。 软 件 的 易 用 性 首 先 需 要 操 作 系 统 的 支 持 。 Mir s f2 0 c o o t0 6年 已 经推
3并行计算的应用领域
目前 ,并 行 计算 主要 集 中在高 端应
用领 域 ,例如 气象 、 石 油 、航 天 航空 。
理 并 行 程 序 不 再 像 以 前 一 样 困难 。但 并行计算机系统 ,或者说超级计算机 是 ,相对 串行 程序 来讲 ,并 行 程序 的编 系 统发 展 到 目前 已经 有 五 代 了。 近 几 年 , 最 写 、 调 试 、 运 行 还 是 具 有 较 大 的 难 度 的。现 在运用基于 MP 和 P I VM 的并行编 C mp t g 高性能计算 ) 中机群系统 所 程 ,主要是 集 中在大 公 司 、高校 和研 究 o ui , n 之 占的比重越来越大 ,在最新公布的 “ 超级 院 /所 。笔者 相信 ,并行 计算 因为其 强 计算机 5 0强”排行榜上 ,有 2 1 0 9 台系统 大 的 性 能 , 并 且 由于 是 目前 和 今 后 比 较 都 属于机群 ( lse )系统 。超级 计算机 长 的一段时间内解决计算机运算速度的几 Cu tr 的 “ 一 代 ” “ 二 代 ” 和 “ 四代 ” 由 乎 唯一 的选择 ,必将 会在 中低 端得 到大 第 、 第 第
ansys多cpu并行计算设置

关于ansys程序运行大内存多核CPU的设置问题转载近期出现这些问题找了些资料并整理下放这里了。
下面这些方法并没有一一试过。
1.ansys结果文件过大如何处理解决超大结果文件的方案主要有四种方法方法一将磁盘格式转换为NTFS 方法二在begin level的时候加上一条命令/configfsplitvalue其中value is the size of file the final size equal to nvalven is the number of sub-file在PC机上面一般1单位4M则/configfsplit750 生成每个分割后的文件都是3G的大小在这个命令下不只是rst文件被分割只要是由ansys所产生的binary文件都会。
如下面命令大概会产生6个rst文件/configfsplit1 14MB /prep7 et145 mpex12e11 mpprxy10.3 blc41011 esize0.1 vmeshall /solu da5all sfa2pres0.1 solve 方法三将不同时间段内的结果分别写入一序列的结果记录文件使用/assign命令和重启动技术ANSYS采用向指定结果记录文件追加当前计算结果数据方式使用/assign指定的文件所以要求指定的结果记录文件都是新创建的文件否则造成结果文件记录内容重复或混乱。
特别是反复运行相同分析命令流时在重复运行命令流文件之前一定要删除以前生成的结果文件序列。
方法四采用载荷步文件批处理方式求解在结果文件大小达到极限而终止计算时同样可以接着计算不过在重新计算时在重启动对话框里选择—create .rst并且read上次的计算结果。
转simwe 2.ansys中物理内存和虚拟内存设置增大物理内存是提高解题效率的关键。
虚拟内存理想配置为物理内存250Mansys的运行速度与内存大小直接有关对于同一台机器内存由256M增大到512M时计算同一题目的速度可以提高几倍解体规模可以达10万自由度以上。
MCNP程序并行计算性能分析

第26卷 第4期核科学与工程Vol.26 No.4 2006年 12月Chinese Journal of Nuclear Science and EngineeringDec. 2006收稿日期:2006204224;修回日期:2006205231作者简介:王 磊(1981—),男,清华大学工程物理系硕士研究生MCNP 程序并行计算性能分析王 磊,王 侃,余纲林(清华大学工程物理系,北京100084)摘要:并行计算可以有效地减少MCN P 程序的计算时间。
利用MPI 消息传递软件,可以在安装Win 2dows 操作系统的PC 集群上实现MCNP5的并行计算。
MCN P 程序的并行计算性能与所计算问题的类型、复杂程度及参数设置等因素有关,对此进行了分析并提出了改善MCNP 程序并行计算性能的措施。
关键词:MCNP ;并行计算中图分类号:TL32 文献标识码:A 文章编号:025820918(2006)0420301206Analysis of parallel computing performance of the code MCNPWAN G Lei ,WAN G Kan ,YU Gang 2lin(Depart ment of Engineering Physics ,Tsinghua University ,Beijing 100084,China )Abstract :Parallel comp uting can reduce t he running time of t he code MCN P effectively.Wit h t he M PI message t ransmitting software ,MCN P5can achieve it s parallel comp u 2ting on PC cluster wit h Windows operating system.Parallel comp uting performance of MCN P is influenced by factors such as t he type ,t he complexity level and t he parameter configuration of t he comp uting p roblem.This paper analyzes t he parallel comp uting per 2formance of MCN P regarding wit h t hese factors and gives measures to improve t he MC 2N P parallel comp uting performance.K ey w ords :MCN P ;parallel comp uting MCN P (Monte Carlo Neut ron and PhotonTransport Code )是美国Lo s Alamos 国家实验室编制的一个通用的多功能蒙特卡罗程序[1],可用于计算中子、光子、中子2光子耦合以及光子2电子耦合的输运问题,也可以计算临界系统(包括次临界及超临界)的本征值问题,适用于核科学与工程方面的多种问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
国家高性能计算中心(合肥)
2019/9/26
11
串行FFT递归算法
FFT的蝶式递归计算图(由计算原理推出)
a0
a1
. .
.
a
n 2
-1
an 2
a
n 2
+1
.
.
.
a n-1
+
a
0+a
n 2
+
a 1+a
n 2
+1
.
.
.
+
an 2
-1+a n-1
1 -
ω -
n
ω2
-1
-
a
0-a
n 2
ω(a1-a
n 2
+1
)
.
.
.
n
ω2
-1(a n 2
-1-an-1)
. DFT(n/2) .
.
DFT(n/2)
. .
.
国家高性能计算中心(合肥)
2019/9/26
12
串行FFT递归算法
特别地,n=8的FFT蝶式计算图(展开的)
a0
+
+
+
b0
a1
+
+
_
1
b4
a2
+
1
+
_
b2
a3
+
ω2 _
_
1
b6
a4
1
+
_
+
b1
a5
ω
~
l
n 2
1
(a n
2
1
n 2
1
an 1 )
n 2
1
~
k
l
k
(
ak
a
n 2
k
)
k 0
l
0,1,,
n 2
1
因此,向量(b1, b3,...,bn1)T 是((a0
an
2
),(a1
a
n 2
1
)
,
.
.
.
,
(a n
2
1
n 2
1
an 1 ) )T 的DF T
)T 是(a0
an
2
,
a1
a
n 2
1
,
.
.
.
,a
n 2
1
an 1 )T 的DF T
国家高性能计算中心(合肥)
2019/9/26
10
串行FFT递归算法
n1
奇数时:bl b2l1
a (2l1)k k
k 0
a0
2l1a1
a 2(2l 1) 2
2(n1)
(
n1)(n1)
an1
国家高性能计算中心(合肥)
2019/9/26
5
11.1 快速傅里叶变换(FFT)
11.1.1 离散傅里叶变换(DFT) 11.1.2 DFT的顺序代码 11.1.3 串行FFT递归算法 11.1.4 串行FFT非递归算法
DFT的顺序代码
,bn21
)T
注意推导中反复使用 n 1, n/ 2 1, ln 1, sn p p ,
ω2 =( 0,i)
ω3
ω1
ω4 =(-1,0)
ω8 =(1,0)
ω5
ω7
国家高性能计算中心(合肥) ω6 =(0,-i) 2019/9/26
9
串行FFT递归算法
n1
偶数时:bl b2l 2lk ak
k 0
a0
2l a1
4la2
a 2
l
n 2
1
n 2
1
an
2
a 2l
n 2
1
a 4l
n 2
2
2l
n 2
1an
1
(a0
an
2
)
2l
(a1
a ) n
2
1
4l
(a2
0 j n 1
k 0
这里=e2i/n为n次单位元根,i 1; 写成矩阵形式为
b0 0 0 0 0 a0
b1
0
1
2
n1
Hale Waihona Puke a1
bn1
0
n1
b[j]=b[j]+s*a[k] s=s*w end for w=w*ω end for
国家高性能计算中心(合肥)
2019/9/26
7
11.1 快速傅里叶变换(FFT)
11.1.1 离散傅里叶变换(DFT) 11.1.2 DFT的顺序代码 11.1.3 串行FFT递归算法 11.1.4 串行FFT非递归算法
+
_
_
1
b5
a6
ω2
1
+
_
_
b3
a7
ω3 _
ω2 _
_
1
b7
图11.4
国家高性能计算中心(合肥)
n 2
1
n 2
a 1 n1
(a0
an
2
)
2l(a1
a ) n
2
1
4l 2 (a2
an
2
2
)
2l
n 2
1
(a n
2
1
n 2
1
an 1 )
(a0
an
2
)
~ l (a1
a ) n
2
1
~2l 2 (a2
a ) n
2
2
代码1
for j=0 to n-1 do b[j]=0 for k=0 to n-1 do b[j]=b[j]+ωk*ja[k] end for
end for
注:代码1需要计算ωk*j
代码2的复杂度为O(n2)
代码2
w=ω0 for j=0 to n-1 do
b[j]=0, s=ω0 for k=0 to n-1 do
11.1.1 离散傅里叶变换(DFT) 11.1.2 DFT的顺序代码 11.1.3 串行FFT递归算法 11.1.4 串行FFT非递归算法
离散傅里叶变换(DFT)
定义
给定向量A=(a0,a1,…,an-1)T,DFT将A变换为B=(b0,b1,…,bn-1)T
n1
即
bj ak kj
串行FFT递归算法
蝶式递归计算原理
令 ~=e2 i /(n/ 2)为n/2次单位元根,则有~= 2.
将b向量的偶数项(b0 , b2 ,..., bn2 )和T 奇数项(b1,b3,..., bn1)T分别记为
(b0
,
b1,..
.
,bn
2
1
)T和
(b0,
b1,..
.
并行计算
中国科学技术大学计算机科学与技术系 国家高性能计算中心(合肥)
2004年12月
第三篇 并行数值算法
第八章 基本通讯操作 第九章 稠密矩阵运算 第十章 线性方程组的求解 第十一章 快速傅里叶变换
第十一章 快速傅里叶变换
11.1 快速傅里叶变换 11.2 并行FFT算法
11.1 快速傅里叶变换(FFT)
a ) n
2
2
2l
n 2
1
(a
n 2
1
an1
)
(a0
an
2
)
~l
(a1
a ) n
2
1
~ 2l
(a2
an
2
2
)
~
l
n 2
1(a
n 2
1
an1
)
n 2
1
~
k
l
(ak
a
n 2
k
)
k 0
l
0,1,,
n 2
1
因此,向量(b0 , b2 ,...,bn2
n
2
1
(2l
1)
an
2
1
a a a n 2
(
2l
1)
n
2
n 2
1
(2l
1)
n 2
1
n1(2l 1)
n1
a0
2la1
4l 2a2
2l
n 2
1
a n
2
1
n 2
1
an
2
2la
n 2
1
2l
